Enhancing Energy Management Strategies for Extended-Range Electric Vehicles through Deep Q-Learning and Continuous State Representation

Abstract

The efficiency and dynamics of hybrid electric vehicles are inherently linked to effective energy management strategies. However, complexity is heightened due to uncertainty and variations in real driving conditions. This article introduces an innovative strategy for extended-range electric vehicles, grounded in the optimization of driving cycles, prediction of driving conditions, and predictive control through neural networks. First, the challenges of the energy management system are addressed by merging deep reinforcement learning with strongly convex objective optimization, giving rise to a pioneering method called DQL-AMSGrad. Subsequently, the DQL algorithm has been implemented, allowing temporal difference-based updates to adjust Q values to maximize the expected cumulative reward. The loss function is calculated as the mean squared error between the current estimate and the calculated target. The AMSGrad optimization method has been applied to efficiently adjust the weights of the artificial neural network. Hyperparameters such as the learning rate and discount factor have been tuned using data collected during real-world driving tests. This strategy tackles the “curse of dimensionality” and demonstrates a 30% improvement in adaptability to changing environmental conditions. With a 20%-faster convergence speed and a 15%-superior effectiveness in updating neural network weights compared to conventional approaches, it also highlights an 18% reduction in fuel consumption in a case study with the Nissan Xtrail e-POWER system, validating its practical applicability.

1. Introduction

Currently, the automotive sector is undergoing a significant transformation driven by emerging technologies and the adoption of Industry 4.0. In this context, there is a renewed focus on the energy domain and the performance of extended-range electric vehicles (EREV), particularly in the efficient distribution of energy from lithium-ion batteries to electric motors [1]. Despite the undeniable advantages of non-polluting sources such as batteries or hydrogen cells, EREVs have not yet surpassed conventional vehicles in terms of fuel consumption, range, and durability [1,2]. This challenge underscores the importance of addressing deficiencies in energy management systems (EMS), which have not fully capitalized on the characteristics of alternative energy sources to enhance the competitiveness of EREVs in the market. EMS emerges as an effective solution to boost both fuel efficiency and emission reduction [2].

Efficient operation in hybrid and EREV has been a central focus in both industrial and academic research. With the continuous advancement in automotive technology, plug-in hybrid electric vehicles (PHEVs) have emerged as significant contributors to the electrification of transportation, delivering exceptional fuel-saving performance [3]. A pivotal element in the design of these vehicles is the EMS, tasked with regulating the energy flow between the fuel tank and electric storage, thereby addressing energy distribution challenges. In this context, achieving efficient energy management becomes even more challenging and critical with the ongoing development of connected and intelligent vehicle technology. The integration of vehicle-to-infrastructure/vehicle-to-vehicle (V2I/V2V) information into the EMS for EREVs presents a substantial challenge and, simultaneously, is a current and vital issue. Existing literature provides an in-depth analysis of EMSs, employing diverse methodologies and approaches. Emphasis is placed on addressing both single-vehicle and multi-vehicle scenarios, particularly within the context of intelligent transport systems.

In a different domain, the text in [4] explores the impact of EREVs on the power grid and their significant influence on electricity market prices. Charging strategies for an office site in Austria are investigated, with a focus on mathematical representation and optimization of various charging strategies. The study reveals that effective management of EREV charging processes can lead to a substantial reduction in costs, enhancing the convenience of the process. Another valuable contribution in the literature focuses on considering the degradation of energy sources, such as lithium-ion batteries and proton exchange membrane (PEM) fuel cells, in energy management strategies for hybrid vehicles with fuel cells (FCHEVs). The study reviews degradation modeling methods and energy management strategies that integrate degradation considerations. The importance of developing health-conscious EMSs to enhance system durability is underscored [5]. In the realm of shared mobility, the text proposes a comprehensive method for transitioning from car ownership to car-sharing systems in residential buildings. Using a mixed-integer linear optimization approach, technologies such as battery storage, solar panels, EREV, and charging stations are modeled. The study demonstrates that integrating car-sharing systems into residential buildings can result in a significant reduction in costs and a more efficient use of locally generated solar energy [6]. Then, the text addresses energy efficiency in hybrid vehicles through reinforcement learning (RL). Current literature examines the application of RL in the EMS to optimize the utilization of internal and external energy sources, such as batteries, fuel cells, and ultracapacitors. A detailed parametric study reveals that careful selection of learning experience and discretization of states and actions are key factors influencing fuel efficiency in hybrid vehicles [7].

Previous research has identified uncertainty in driving cycles as a critical factor significantly impacting fuel consumption [8]. While studies have shown that adjusting EMS control parameters can improve efficiency in real time [1], the key lies in implementing advanced control technologies to optimally manage the vehicle’s energy. This research is situated in the exploration of advanced energy management solutions for EREVs, proposing a strategy based on deep reinforcement learning (DRL), motivated by the need to overcome limitations in conventional strategies and leverage the effectiveness of machine learning to optimize EREV performance. The “curse of dimensionality” associated with discrete state variables and the need for continuous adaptability to changing environmental conditions are the specific challenges that our innovative approach aims to address.

Recent research has highlighted the significant impact of uncertainty in EREV driving cycles on fuel consumption. In a notable study [9], EMS control parameters were adjusted in real time using six representative standard cycles and 24 characteristic parameters to identify comprehensive driving cycles. Another significant study [10] selected six typical urban conditions from China and the United States as offline optimization targets, using eight characteristic parameters, including maximum vehicle speed, for driving cycle identification [11]. The efficiency of energy management in EREVs to save fuel crucially depends on the implementation of advanced control technologies. Numerous control algorithms have been proposed, ranging from rule-based algorithms [12], analytical algorithms [13], and optimization methods [14,15] to artificial intelligence methods [16]. These are commonly divided into two main categories: rule-based methods and optimization-based methods [17,18]. Rule-based methods, constructed using heuristic mathematical models or human experience, apply regulations to determine the energy distribution of multiple energy sources. Despite their high robustness and reliability, these methods lack flexibility and adaptability to changing conditions [19]. Optimization-based strategies, such as dynamic programming (DP) [20,21], pontryagin’s minimum principle (PMP) [22], and particle swarm optimization (PSO) [23], are applied to derive global optimal control. However, DP and EMS are impractical for solving energy optimization problems under unknown conditions due to their lack of adaptability.

In other research, RL methods have emerged as efficient approaches to achieving optimal control in energy management. By incorporating agent states and actions into the Markov model, RL allows the agent to interact directly with the environment, learning decision rules based on environmental rewards and maximizing the cumulative reward over time through the Bellman equation [24,25]. Compared to rule-based control strategies, RL demonstrates higher accuracy and faster response times due to its model-free properties. This potential makes RL a promising candidate for achieving more efficient and robust electrified propulsion systems.

Within specific approaches, Q-learning applied to the EMS of hybrid electric vehicles (HEVs) has stood out for overcoming the demand for certainty and randomness associated with knowledge of the driving cycle [26,27,28]. A key study [29] proposing RL based on Q-learning not only efficiently reduced calculation time but also achieved a 42% improvement in fuel economy. Another study [25] highlights the superiority of Q-learning-based EMS compared to EMS and MPC. Additionally, the EMS algorithm developed in a study [30], which combines temporal difference (λ), demonstrated better fuel savings and emission reductions. The use of DRL algorithms has marked an advancement in the energy management of HEVs. The first algorithm of this kind, deep q network (DQN), was applied to a series hybrid powertrain configuration in a study [26], demonstrating great adaptability to different driving cycles. To address the overestimation of Q values in DQN, the double DQN was introduced in an EMS design of HEV in another study [27], achieving a 7.1% improvement in fuel savings compared to DQN. For a more efficient estimation of the Q value, the dueling DQN was designed for EMS in a study [28], where a considerable improvement in convergence efficiency during training was observed. However, both the DQN and DDPG algorithms suffer from defects such as overestimated Q values, low stability, and difficulty tuning parameters, emphasizing the need to explore more advanced DRL algorithms for HEV energy management applications.

Despite notable advances in the energy management of EREVs through strategies based on DRL, especially the deep q-learning (DQL) algorithm, crucial research gaps persist. In the realm of DRL-based energy management strategies, our acknowledgment of persistent gaps stems from the intricate challenges associated with effective implementation. Specifically, despite notable advances, there remains a need for further refinement and innovation in addressing uncertainties linked to diverse driving cycles and dynamic environmental conditions. For instance, current strategies, as discussed in previous studies [25], grapple with the curse of dimensionality. These challenges pose significant hurdles in achieving optimal energy efficiency and adaptability. To illustrate, recent research [26,27,30] has underscored the limitations of existing DRL algorithms, such as overestimated Q values, low stability, and difficulty in parameter tuning. These challenges create a gap in the ability of current approaches to seamlessly adapt to unforeseen changes in real-world driving scenarios, hindering their broader effectiveness. By shedding light on these challenges, our study seeks to bridge these gaps through the integration of the DQL-AMSGrad strategy. This integration aims to address the above. Through this innovative approach, we strive to contribute significantly to the ongoing discourse on advancing DRL-based energy management in the context of EREVs.

The focus of this article lies in integrating DQL with the adaptive moment estimation with a strongly convex objective (AMSGrad) optimization method (DQL-AMSGrad) to refine the energy management of EREVs. First, the efficient management of dimensionality in discrete state variables poses a persistent challenge, despite the demonstrated effectiveness of DQL. The “curse of dimensionality” associated with these variables remains a substantial barrier, especially when dealing with discrete action spaces [1,25]. This study introduces an innovative perspective by combining DQL with AMSGrad, providing a promising solution to address the complexity associated with these discrete variables. Continuous adaptability to changing environmental conditions constitutes a critical research gap. Control strategies, even those based on DRL as in Ref. [25], face challenges in dynamically adjusting to unexpected changes in environmental conditions. The article’s proposal, by integrating DQL-AMSGrad, highlights its ability to adapt continuously, thereby improving efficiency and sustainability in real time. Another crucial aspect is related to optimizing the convergence speed and effectiveness in updating neural network weights, essential elements for the practical application of DQL. Performance gaps, such as Q-value overestimation, instabilities, and difficulties in parameter tuning, persist in various DRL algorithms, including DQL as in Refs. [26,27,30]. This article addresses these deficiencies by incorporating the AMSGrad optimization method, improving convergence speed and the effectiveness of neural network weight updates, resulting in a more robust and stable model performance. The model has been validated with a real-case study.

For the sake of simplicity, this study presents the following scientific contributions:

• Proposes a pioneering strategy by combining the DQL algorithm with the AMSGrad optimization method (DQL-AMSGrad) to enhance the energy management of EREVs.
• Effectively addresses the “curse of dimensionality” associated with discrete state variables in EREV environments, presenting an innovative solution to efficiently manage these variables by combining DQL with AMSGrad.
• Highlights the ability of the DQL-AMSGrad strategy to adapt continuously to changing environmental conditions, improving real-time energy management efficiency and sustainability.
• Addresses performance gaps, such as Q-value overestimation, instabilities, and difficulties in parameter tuning, by integrating AMSGrad, improving convergence speed and the effectiveness of neural network weight updates associated with DQL.

The remaining structure of the article is organized as follows: Section 2 details the proposed methodology, Section 3 addresses the case study, Section 4 is dedicated to results and discussion, while Section 5 provides the final conclusions of the paper.

2. Methodology

In formulating the energy management strategy for EREVs, this study consciously adopts a synthesis of DQL and AMSGrad. The utilization of a feedforward neural network is strategically chosen to proficiently handle intricate variables encompassing driving cycles, battery charge, speed, and energy demand. This approach offers a continuous and adaptable representation, effectively capturing the inherent complexity of the system. The selection of the DQL algorithm is underpinned by its inherent capability to update based on temporal differences and maximize expected cumulative rewards. This renders DQL a superior choice compared to alternative reinforcement learning algorithms or optimization methods, particularly in navigating the challenges posed by uncertainties inherent in diverse driving conditions. AMSGrad emerges as the optimization method of choice, owing to its empirically established effectiveness in accelerating convergence speed and enhancing the efficacy of neural network weight updates. Its adept handling of the intricacies associated with training neural networks, especially in real-world scenarios, positions it as the preferred optimization approach over other methods.

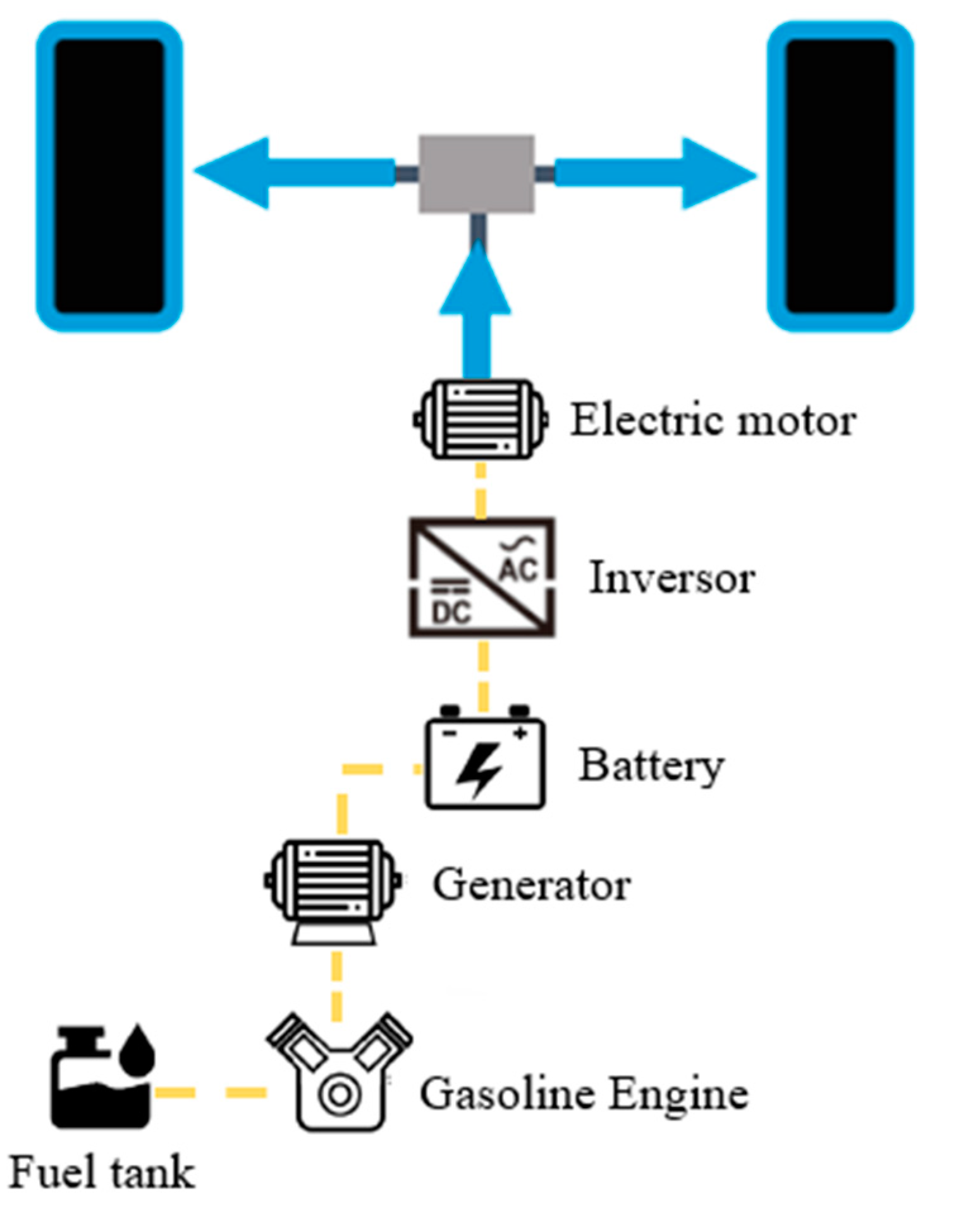
The meticulous determination of assessment parameters, such as the number of episodes and learning rate for DQL, entails a process of thoughtful consideration and adjustment through rigorous testing. These parameters are meticulously fine-tuned to strike an optimal balance between efficiency and adaptability across diverse driving conditions. The programming has been done in MATLAB 2021a. The application of this methodology to the Nissan Xtrail e-POWER system lends a real-world context to the evaluation. The practical implementation serves as a compelling demonstration of the model’s adaptability to varying conditions, thereby substantiating its efficacy in augmenting driving efficiency and curbing fuel consumption in EREVs.

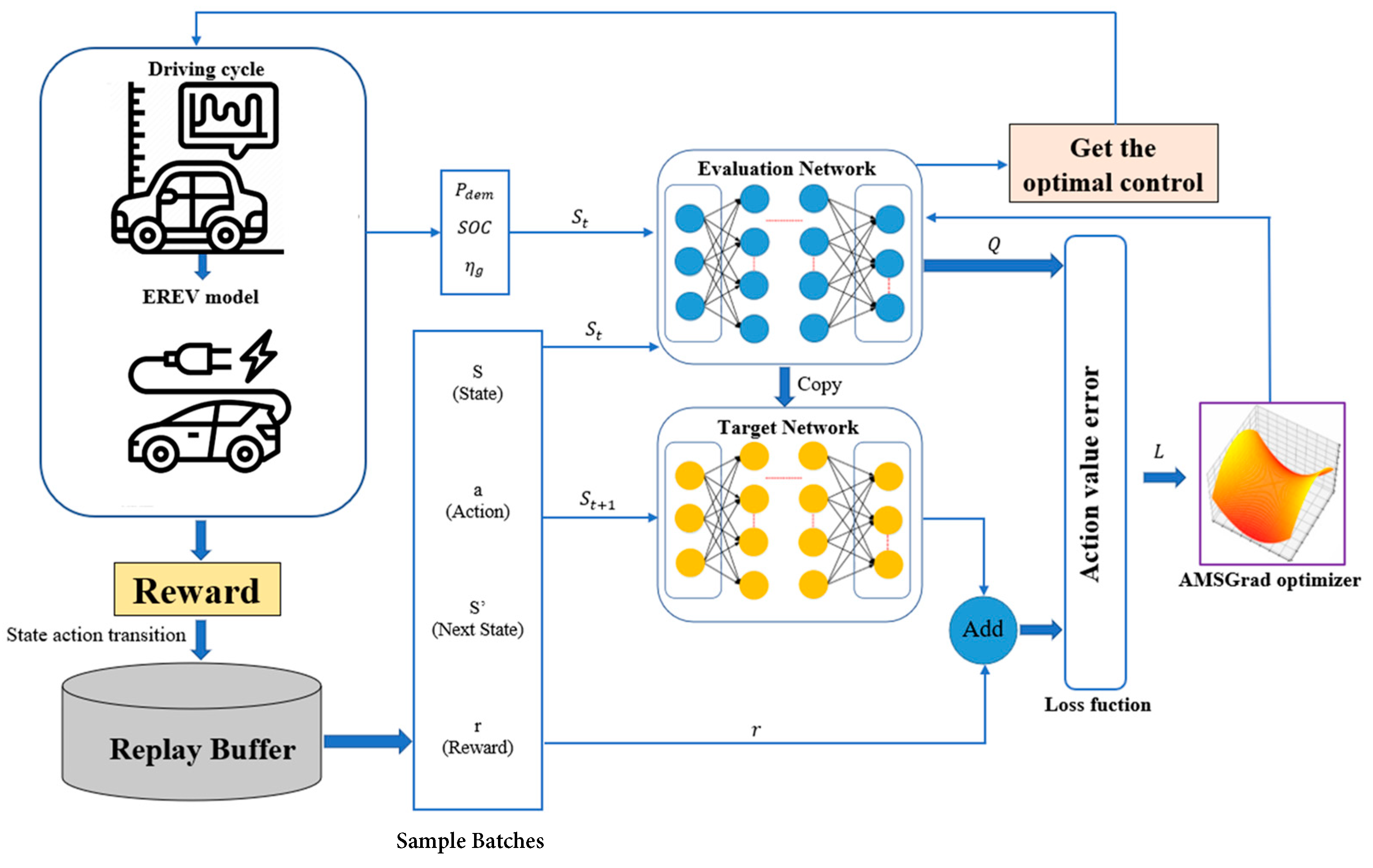
This strategy, integrating a streamlined neural network, the DQL algorithm, and the AMSGrad optimization method, accentuates the deliberate decisions made to effectively address the multifaceted challenges inherent in EREV energy management. Each constituent is purposefully chosen to ensure adaptability, proficient management of uncertainties, and heightened efficiency, thereby bolstering the pragmatic viability of our proposed approach (Figure 1).

2.1. Deep Reinforcement Learning-Based Energy Management Strategy

2.1.1. Deep Reinforcement Learning Feature

The proposed energy management strategy is based on DQL and addresses the “curse of dimensionality” associated with discrete state variables in algorithms like Q-learning and Dyna. DQL utilizes a neural network to represent the value function, enabling efficient management of continuous states [22]. In this approach, the AMSGrad optimization method is employed to update the neural network weights, enhancing convergence speed and effectiveness compared to conventional methods [31]. The construction of the value function is directly performed through the neural network, providing a continuous and flexible representation. This innovative approach facilitates the direct issuance of control actions based on state variables, improving the efficiency and adaptability of the algorithm in energy management.

2.1.2. Neural Network Structure and AMSGrad Optimization Method

The feedforward neural network, also known as a direct feed neural network, is a common type of ANN architecture where information flows in a single direction from the input layer to the output layer (Figure 2). AMSGrad is a variant of the Adam optimization method. Both methods are optimization algorithms commonly used to adjust the weights of a neural network during the training process. The original version of Adam introduced the concept of adaptive moments to automatically adjust learning rates for each parameter. AMSGrad emerged as a modification to address certain convergence issues encountered in specific cases. The main idea behind AMSGrad is to adaptively adjust the learning rate for each individual parameter, and it was introduced to tackle the problem where, in some situations, the learning rate could become very small, hindering convergence. AMSGrad avoids this issue by maintaining an adaptive estimate of exponential moments [32].

Let us consider a neural network with an input layer (x), a hidden layer (h), and an output layer (y). During forward propagation, where (x) represents the input variables, which, in this context, are the speed, distance, and altitude of the EREV driving cycles. The input to the hidden layer is given by Equation (1), the output of the hidden layer after applying the activation function f is calculated with Equation (2), then the input to the output layer is represented in Equation (3), and the output of the output layer after applying the activation function is calculated with Equation (4) [33,34,35,36].

$${\mathrm{a}}^{\left(1\right)}={\mathrm{W}}^{\left(1\right)}·\mathrm{x}+{\mathrm{b}}^{\left(1\right)}$$

(1)

$$\mathrm{h}=\mathrm{f}({\mathrm{a}}^{\left(1\right)})$$

(2)

$${\mathrm{a}}^{\left(2\right)}={\mathrm{W}}^{\left(2\right)}·\mathrm{h}+{\mathrm{b}}^{\left(2\right)}$$

(3)

$$\mathrm{y}=\mathrm{g}({\mathrm{a}}^{\left(2\right)})$$

(4)

Training with AMSGrad involves initializing parameters, including initial weights $\left({\mathrm{W}}^{\left(1\right)}, {\mathrm{W}}^{\left(2\right)}\right)$, biases $\left({\mathrm{b}}^{\left(1\right)},{\mathrm{b}}^{\left(2\right)}\right)$, and adaptive moments $\left({\widehat{\mathrm{m}}}^{\left(1\right)}, {\widehat{\mathrm{v}}}^{\left(1\right)}, {\widehat{\mathrm{m}}}^{\left(2\right)}, {\widehat{\mathrm{v}}}^{\left(2\right)}\right)$. The process then proceeds with backward propagation and gradient calculation of the loss function $L$ with respect to the network parameters $\left({\mathrm{W}}^{\left(1\right)}, {\mathrm{W}}^{\left(2\right)}, {\mathrm{W}}^{\left(3\right)}, {\mathrm{W}}^{\left(4\right)}\right)$. The update of adaptive moments for each parameter is crucial to solving the AMSGrad moment equations shown in Equations (5) and (6). The bias correction process in the moments is then performed to avoid biases in the early iterations, as shown in Equations (7) and (8). Finally, Equation (9) represents the process of updating weights and biases using the AMSGrad update formula. This process is repeated over multiple iterations (epochs) until the ANNconverges to an optimal solution [37,38,39,40].

$${\widehat{\mathrm{m}}}_{\mathrm{ij}}^{\left(\mathrm{l}\right)}={\mathsf{\beta }}_1·{\widehat{\mathrm{m}}}_{\mathrm{ij}}^{\left(\mathrm{l}\right)}+\left(1 -{\mathsf{\beta }}_1\right)·\frac{\partial \mathrm{L}}{\partial {\mathrm{W}}_{\mathrm{ij}}^{\left(\mathrm{l}\right)}}$$

(5)

$${\widehat{\mathrm{v}}}_{\mathrm{ij}}^{\left(\mathrm{l}\right) }={\mathsf{\beta }}_2·{\widehat{\mathrm{v}}}_{\mathrm{ij}}^{\left(\mathrm{l}\right)}+\left(1 - {\mathsf{\beta }}_2\right)·{\left(\frac{\partial \mathrm{L}}{\partial {\mathrm{W}}_{\mathrm{ij}}^{\left(\mathrm{l}\right)}}\right)}^2$$

(6)

$${\widehat{\mathrm{m}}}_{\mathrm{ij}}^{\left(\mathrm{l}\right)}=\frac{{\widehat{\mathrm{m}}}_{\mathrm{ij}}^{\left(\mathrm{l}\right)}}{1-{{\mathsf{\beta }}_1}^{\mathrm{t}}}$$

(7)

$${\widehat{\mathrm{v}}}_{\mathrm{ij}}^{\left(\mathrm{l}\right)}=\frac{{\widehat{\mathrm{v}}}_{\mathrm{ij}}^{\left(\mathrm{l}\right)}}{1-{{\mathsf{\beta }}_2}^{\mathrm{t}}}$$

(8)

$${\mathrm{W}}_{\mathrm{ij}}^{\left(\mathrm{l}\right)}={\mathrm{W}}_{\mathrm{ij}}^{\left(\mathrm{l}\right)} - \frac{\mathsf{\alpha }·{\widehat{\mathrm{m}}}_{\mathrm{ij}}^{\left(\mathrm{l}\right)}}{\sqrt{{\widehat{\mathrm{v}}}_{\mathrm{ij}}^{\left(\mathrm{l}\right)}}+\mathsf{\epsilon }},$$

(9)

where ${\mathsf{\beta }}_1$ and ${\mathsf{\beta }}_2$ are the decay factors for the first moment $\widehat{\mathrm{m}}$ and $\widehat{\mathrm{v}}$ in AMSGrad, respectively; $\mathrm{t}$ is the number of iterations or epochs; $\mathsf{\alpha }$ is the learning rate that controls the magnitude of weight updates; and $\mathsf{\epsilon }$ is a small constant to avoid division by zero in the weight update.

2.1.3. Structure of the DQL Algorithm

The structure of the DQL algorithm is based on the optimization of an action value function using ANN, and the equation for the temporal state is represented by the following Equation (10) [41]:

$$\mathrm{Q}\left(\mathrm{s},\mathrm{a}\right)\leftarrow \mathrm{Q}\left(\mathrm{s},\mathrm{a}\right)+\mathsf{\alpha }·\left(\mathrm{r}+\mathsf{\gamma }·{\max }_{{\mathrm{a}}^{\prime }}\mathrm{Q}\left({\mathrm{s}}^{\prime },{\mathrm{a}}^{\prime }\right) - \mathrm{Q}(\mathrm{s},\mathrm{a})\right),$$

(10)

where $\mathrm{Q}\left(\mathrm{s},\mathrm{a}\right)$ represents the action value function, estimating the expected utility of taking action $\mathrm{a}$ in state $\mathrm{s}$; $\mathrm{r}$ is the reward obtained after taking action a in state $\mathrm{s}$; $\mathsf{\gamma }$ is the discount factor, weighing the importance of future rewards; and ${\max }_{{\mathrm{a}}^{\prime }}\mathrm{Q}\left({\mathrm{s}}^{\prime },{\mathrm{a}}^{\prime }\right)$ represents the maximum value of the action value function $\mathrm{Q}$ for the next state ${\mathrm{s}}^{\prime }$ and all possible actions ${\mathrm{a}}^{\prime }$. This update is reflected in calculating the target ${\mathrm{y}}_{\mathrm{j}}$ in the reward function ${\mathrm{r}}_{\mathrm{j}}$, and the action estimate is as follows in Equation (11) [42].

$${\max }_{{\mathrm{a}}^{\prime }}\widehat{\mathrm{Q}}\left({\mathrm{s}}_{\mathrm{j}+1},{\mathrm{a}}^{\prime },{\mathsf{\omega }}^{\prime }\right)$$

(11)

The loss function ${(\mathrm{L}}_{\mathsf{\omega }})$ is calculated with Equation (12), and it is the mean squared error (MSE) between the current estimate $\mathrm{Q}\left({\mathrm{s}}_{\mathrm{j}}, {\mathrm{a}}_{\mathrm{j}}, \mathsf{\omega }\right)$ made for each time step [43].

$${\mathrm{L}}_{\mathsf{\omega }}=\mathrm{E}\left[{\left({\mathrm{y}}_{\mathrm{j}} - \mathrm{Q}\left({\mathrm{s}}_{\mathrm{j}}, {\mathrm{a}}_{\mathrm{j}}, \mathsf{\omega }\right)\right)}^2\right],$$

(12)

where $\mathrm{E}$ represents the expectation or expected value, which is calculated over the training sample set; and $\mathsf{\omega }$ represents the weights of the ANN that are updated during training. To smooth the updates of the target network weights, the parameter $\mathsf{\tau }$ is used. The target network $\left({\mathrm{Q}}^{\mathrm{target}}\right)$ is slowly updated towards the weights of the main network $\left(\mathrm{Q}\right)$ to make the training process more stable and avoid abrupt oscillations. The update of the target network weights is conducted through Equation (13) [42,43,44].

$${\mathsf{\omega }}^{\mathrm{target}}\leftarrow \left(1 - \mathsf{\tau }\right)·{\mathsf{\omega }}^{\mathrm{target}}+\tau ·\mathsf{\omega },$$

(13)

where ${\mathsf{\omega }}^{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$ are the weights of the target network; $\omega$ are the weights of the main network; and $\mathsf{\tau }$ is the temporal discount parameter.

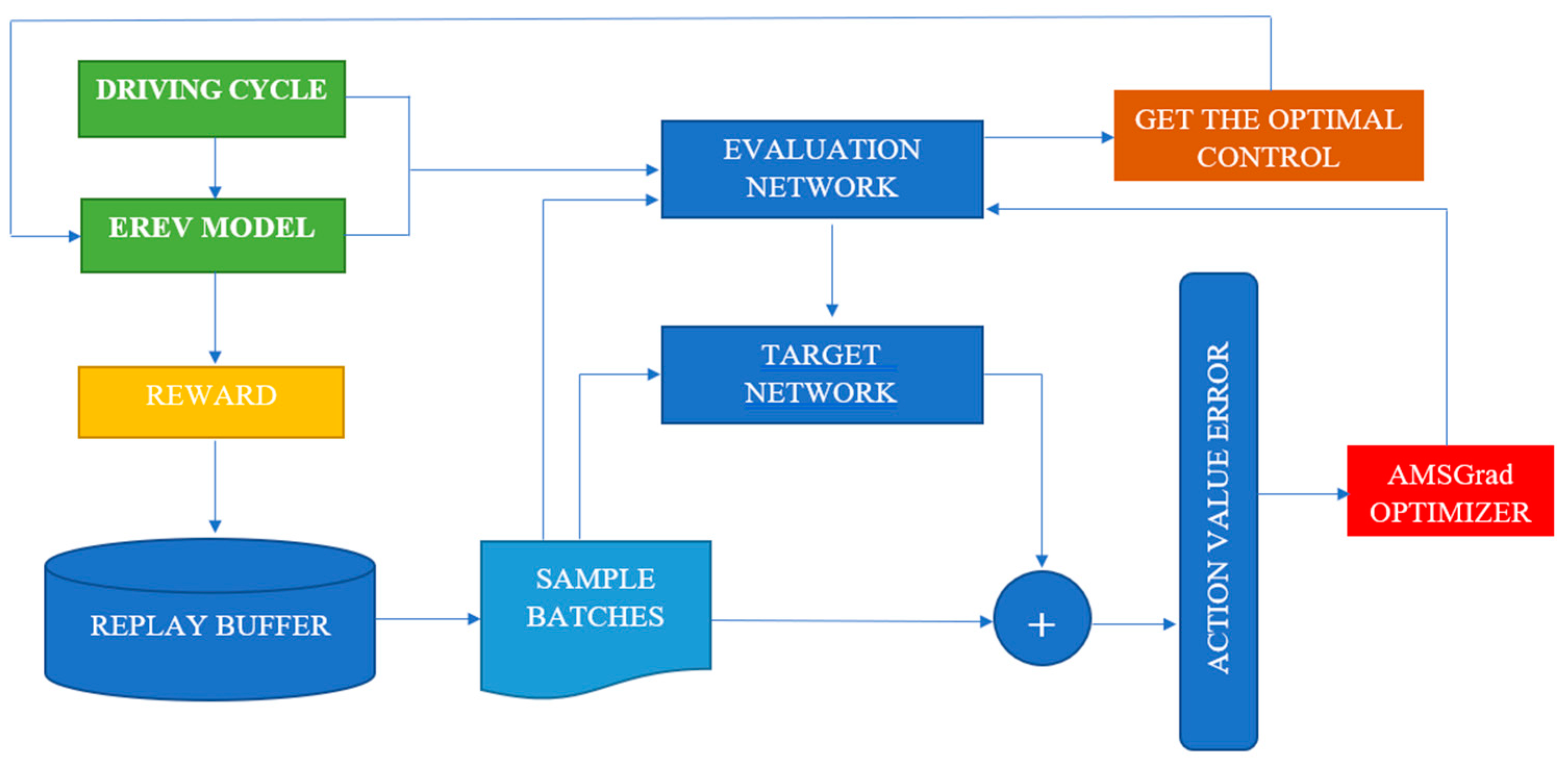
2.2. Proposed Method (DQL-AMSGrad)

The proposed method has implemented a methodology that combines a feedforward ANN with the DQL algorithm, and the AMSGrad optimization method is shown in Figure 3. This approach aims to primarily reduce the fuel consumption EREV through optimal decision-making based on reinforcement learning. The ANN architecture has been carefully designed, considering the specific characteristics of the problem. The feedforward ANN includes hidden layers and appropriate activations to capture the complexity of the system. The network input represents the state of the EREV, with variables such as battery charge, speed, and power demand. The network output provides an estimate of the Q function for each possible action the EREV can take.

The DQL algorithm has been implemented following a clear and detailed structure. The epsilon-greedy exploration has been incorporated to balance the exploration of new actions and the exploitation of known actions. Temporal difference-based temporal updates allow for the adjustment of Q values to maximize the expected cumulative reward. The loss function is calculated as the MSE between the current estimate and the calculated target. The AMSGrad optimization method has been applied to efficiently adjust the weights of the ANN. Hyperparameters such as learning rate and discount factor have been tuned using data collected during real-world driving tests. The training and validation process have been conducted with specific datasets, ensuring that the model can generalize correctly to different driving conditions. The implementation of the trained model has been integrated into the EREV’s energy management system to enable real-time decision-making during driving. Additional tests have been conducted in real-world conditions to evaluate the controller’s effectiveness in diverse situations, such as driving on steep roads or in heavy traffic.

This approach follows a continuous cycle of monitoring and improvement. A continuous monitoring system has been established to assess the controller’s performance and adjust as needed. The ongoing adaptation of the model to real-world conditions is crucial to achieving and maintaining optimal results in terms of driving efficiency and fuel consumption reduction in an EREV.

Algorithm 1 describes the pseudocode of the method. N represents the total number of iterations. ${\mathsf{\theta }}_{\mathrm{t}}$ is a tuned step size, ${\mathsf{\mu }}_{1\mathrm{t}}$ and ${\mathsf{\mu }}_{2\mathrm{t}}$ are two hyperparameters changing with $\mathrm{t}$. Additionally, ${\mathrm{g}}_{\mathrm{t}}$ represents the gradient descent of the loss function calculated on ${\mathsf{\omega }}_{\mathrm{t}}$, and ${\mathrm{m}}_{\mathrm{t}}$ and ${\mathrm{v}}_{\mathrm{t}}$ denote the first-order moment and second-order moment, respectively. After several iterations, the weights will approximate the optimal value.

At each time step, the state vector $\left({\mathrm{SOC}}^{\mathrm{t}},{\mathrm{n}}_{\mathrm{g}}^{\mathrm{t}}, {\mathrm{P}}_{\mathrm{dem}}^{\mathrm{t}}\right)$ is input into the evaluation network; then, the network produces the optimal action based on maximizing the Q-value. Afterward, the powertrain model executes the energy management strategy based on the DQL method for the EREV. Next, the kinematic chain model executes the control action provided by the network and generates the next state and immediate reward. The vector $\left({\mathrm{s}}_{\mathrm{t}},{\mathrm{a}}_{\mathrm{t}},{\mathrm{r}}_{\mathrm{t}},{\mathrm{s}}_{\mathrm{t}+1}\right)$ formed by the current state, control action, immediate reward, and the next state is stored in a predefined experience memory module called the replay buffer. Considering the strong correlations between consecutive samples, every certain number of time steps, random sampling batches are drawn from the replay buffer and applied to train the evaluation network, contributing to improving training efficiency. The optimization method applied in the training process has been detailed above.

Algorithm 1: Pseudocode for Energy Management Optimization with DQL–AMSGrad

Initialization

${\mathsf{\omega }}_1$: Initial weights of the neural network.

$\mathrm{Q}$: Neural network for evaluating the policy in deep reinforcement learning.

$\widehat{\mathrm{Q}}$: Target neural network in DQL.

$\mathsf{\epsilon }$: Exploration rate in DQL.

γ: Discount factor in DQL.

α: Learning rate in DQL.

${\left\{{\mathsf{\theta }}_{\mathrm{t}}\right\}}_{\mathrm{t}=1}^{\mathrm{N}}$: Learning rate in AMSGrad.

${\left\{{\mathsf{\mu }}_{1\mathrm{t}}\right\}}_{\mathrm{t}=1}^{\mathrm{N}},{\left\{{\mathsf{\mu }}_{2\mathrm{t}}\right\}}_{\mathrm{t}=1}^{\mathrm{N}}$$: \mathrm{Momentum} \mathrm{parameters} \mathrm{for} {\mathrm{m}}_{\mathrm{t}}$$\mathrm{and} {\mathrm{v}}_{\mathrm{t}}$ in AMSGrad.

$\mathrm{B}$: Replay buffer to store experiences in DQL.

$\mathrm{N}$: Total number of episodes in DQL.

$\mathrm{M}$: Maximum number of steps per episode in DQL.

AMSGrad

for $\mathbf{t}\mathbf{=}\mathbf{1}$ to $\mathbf{N}$ do

${\mathrm{g}}_{\mathrm{t}}=\nabla {\mathrm{L}}_{\mathrm{t}}\left({\mathsf{\omega }}_{\mathrm{t}}\right)$

${\mathrm{m}}_{\mathrm{t}}={\mathsf{\mu }}_{1\mathrm{t}}{\mathrm{m}}_{\mathrm{t}-1}+\left(1-{\mathsf{\mu }}_{1\mathrm{t}}\right){\mathrm{g}}_{\mathrm{t}}$

${\mathrm{v}}_{\mathrm{t}}={\mathsf{\mu }}_{2\mathrm{t}}{\mathrm{v}}_{\mathrm{t}-1}+\left(1-{\mathsf{\mu }}_{2\mathrm{t}}\right){\mathrm{g}}_{\mathrm{t}}^2$

${\widehat{\mathrm{v}}}_{\mathrm{t}}=\max \left({\widehat{\mathrm{v}}}_{\mathrm{t}-1},{\mathrm{v}}_{\mathrm{t}}\right)$

${\mathsf{\omega }}_{\mathrm{t}+1}$$={\mathsf{\omega }}_{\mathrm{t}}-\frac{{\mathsf{\theta }}_{\mathrm{t}}{\mathrm{m}}_{\mathrm{t}}}{\sqrt{{\widehat{\mathrm{v}}}_{\mathrm{t}}}}$

end for

DQL

for Episode = 1 to M

$\mathrm{Reset} \mathrm{initial} \mathrm{state} {\mathrm{s}}_1=\left({\mathrm{SOC}}^1,{\mathrm{n}}_{\mathrm{g}}^1,{\mathrm{P}}_{\mathrm{dem}}^1\right)$

for  $\mathbf{t}\mathbf{=}\mathbf{1}$  to  $\mathbf{T}$

${\mathrm{a}}_{\mathrm{t}}\leftarrow \mathsf{\epsilon }-\mathrm{greedy} \left({\mathrm{S}}_{\mathrm{t}},\mathrm{Q}\right)$

$\mathrm{Execute} {\mathrm{a}}_{\mathrm{t}}$$; \mathrm{observe} {\mathrm{s}}_{\mathrm{t}+1}$$\mathrm{and} {\mathrm{r}}_{\mathrm{t}}$

$\mathrm{Store} \mathrm{the} \mathrm{vector} \left({\mathrm{s}}_{\mathrm{t}}, {\mathrm{a}}_{\mathrm{t}}, {\mathrm{r}}_{\mathrm{t}}, {\mathrm{s}}_{\mathrm{t}+1}\right)$$\mathrm{in} \mathrm{replay} \mathrm{buffer} \mathrm{B}$

$\mathrm{Sample} \mathrm{random} \mathrm{batch} \mathrm{of} \left({\mathrm{s}}_{\mathrm{t}}, {\mathrm{a}}_{\mathrm{t}}, {\mathrm{r}}_{\mathrm{t}}, {\mathrm{s}}_{\mathrm{t}+1}\right)$$\mathrm{from} \mathrm{B}$

$\mathbf{if} \mathbf{terminal} {\mathbf{s}}_{\mathbf{j}+\mathbf{1}}$

$\mathrm{Set} {\mathrm{y}}_{\mathrm{j}}={\mathrm{r}}_{\mathrm{j}}$

else

$\mathrm{Set} {\mathrm{y}}_{\mathrm{j}}={\mathrm{r}}_{\mathrm{j}}+\mathsf{\gamma }{\max }_{{\mathrm{a}}_{\mathrm{j}+1}}\widehat{\mathrm{Q}}\left({\mathrm{s}}_{\mathrm{j}+1}, {\mathrm{a}}_{\mathrm{j}+\mathrm{i}},{\mathsf{\omega }}^{\prime }\right)$

end if

$\mathrm{Calculate} \mathrm{loss} \mathrm{fuction} {\mathrm{L}}_{\mathsf{\omega }}=\mathrm{E}\left[{\left({\mathrm{y}}_{\mathrm{j}}-\mathrm{Q}\left({\mathrm{s}}_{\mathrm{j}}, {\mathrm{a}}_{\mathrm{j}}, \mathsf{\omega }\right)\right)}^2\right]$

$\mathrm{Perform} \mathrm{optimization} \mathrm{method} \mathrm{AMSGrad} \mathrm{based} \mathrm{on} \mathrm{L}\left(\mathsf{\omega }\right)$

$\mathrm{Reset} \widehat{\mathrm{Q}}$$\mathrm{with} \mathrm{weights} {\mathsf{\omega }}^{\prime }=\mathsf{\omega }$

end for

end for

3. Case Study

This study focused on the e-POWER system of the Nissan Xtrail, whose structure and characteristics are depicted in Figure 4 and

Table 1. Parameters of the Nissan Xtrail e-POWER [44].

Symbol	Parameter	Value
Vehicle	Empty weight	1800 kg
	Air resistance coefficient	0.26
	Rolling resistance coefficient	0.03
	Frontal area	2.65 m2
Electric motor	Maximum power	150 kW at 5000 rpm
	Maximum torque	330 Nm at 3505 rpm
Combustion Engine (Generator)	Maximum power	116 kW at 4600 rpm
	Maximum torque	250 Nm at 2400 rpm
Battery	Capacity	1.73 kWh
	Voltage	200 V

, respectively [44]. The main components include an internal combustion engine serving as a power generator, a battery, an inverter, and an electric motor. The NISSAN e-POWER system generates electrical power by driving the power generator with the gasoline engine and stores the generated electrical power in the lithium-ion battery or directly supplies it to the electric motor for driving. It is a vehicle that can be driven by operating the electric motor for driving with the stored or generated electrical power. The 55-L fuel tank provides an average theoretical range of 600 to 900 km; however, EREVs require an optimal energy management and control system to distribute electrical energy between charging and different sources, taking into account the durability and limitations of their energy sources.

3.1. Driving Cycles

For this experiment, comprehensive driving tests were conducted with the aim of obtaining 100 driving profiles, presented in Figure 5, highlighting the average profile. During these tests, an average speed of 23.38 km/h, a mean distance of 2.91 km, and an average altitude of 2545 m above sea level were recorded. Additionally, an average fuel consumption of 0.36919 L was calculated, considering a temperature of 25 °C and a relative humidity of 50%. These tests simulate a typical journey from a person’s home to their workplace. The collected data will be used as input for the neural network.

3.2. Configuration Parameters of the DQL-AMSGrad Method

The choice of parameters for configuring the DQL-AMSGrad algorithm is based on specific considerations to efficiently address this particular case study and is shown in

Table 2. DQL-AMSGrad parameter configuration.

Main Parameters	Value
Num_Episodes $\left(\mathrm{M}\right)$	1000
Max_Steps $\left(\mathrm{T}\right)$	200
Learning_Rate $\left(\mathsf{\alpha }\right)$	0.001
Discount_Factor $\left(\mathsf{\gamma }\right)$	0.99
Exploration_Prob. $\left(\mathsf{\epsilon }\right)$	0.2
Batch Size	32
Replay Buffer Size	10,000
τ	0.001
Neurons	64
AMSGrad (SquaredGradientDecayFactor)	0.99

. The number of episodes has been set to 1000 to ensure a sufficient number of training episodes, allowing the agent to thoroughly explore and learn. The max steps are limited to 200 to control the computational complexity by constraining the duration of each episode. A learning rate of 0.001 has been chosen to update weights gradually and prevent undesirable oscillations. A discount factor of 0.99 indicates the long-term importance of future rewards in decision-making. The exploration probability is fixed at 0.2, meaning the agent has a 20% chance of exploring new actions rather than exploiting existing ones. A batch size of 32 is employed for efficient ANN updates. The replay buffer size of 10,000 stores past experiences to mitigate temporal correlation and enhance training stability. The temporal discount parameter of 0.001 is used to smooth updates of the target ANN weights, thereby improving training stability. The choice of 64 neurons indicates the complexity of the ANN used in the algorithm. A value of 0.99 for the squared gradient decay factor reflects the specific configuration of the AMSGrad optimization method, contributing to efficient convergence during training. These settings have been carefully adapted to the case study, considering the nature of the problem and the specific characteristics of the application environment.

4. Results and Discussion

In this section, we analyze the results obtained through the implementation of the proposed energy management strategy. The results are compared with other traditional strategies, such as dynamic programming and the EMS algorithm, highlighting the significant improvements achieved in fuel efficiency.

4.1. Artificial Neural Network Results, Driving Cycle Prediction with AMSGrad

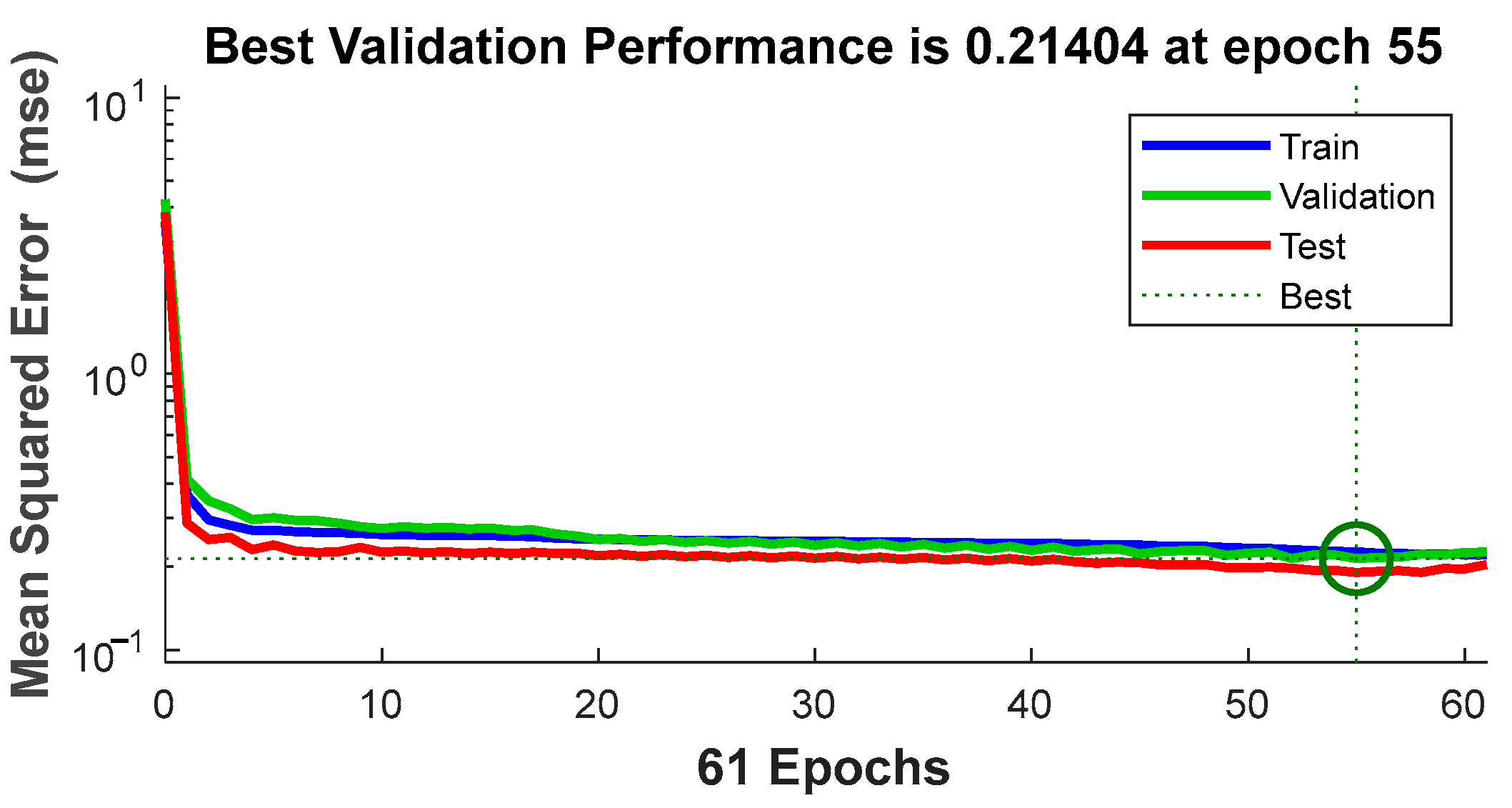
Figure 6 displays an MSE of 0.21404 achieved by the model at epoch 55. This value reflects the model’s ability to adapt to the training data. Comparing this result with previous research or alternative models in similar problems would provide a more comprehensive assessment of its performance.

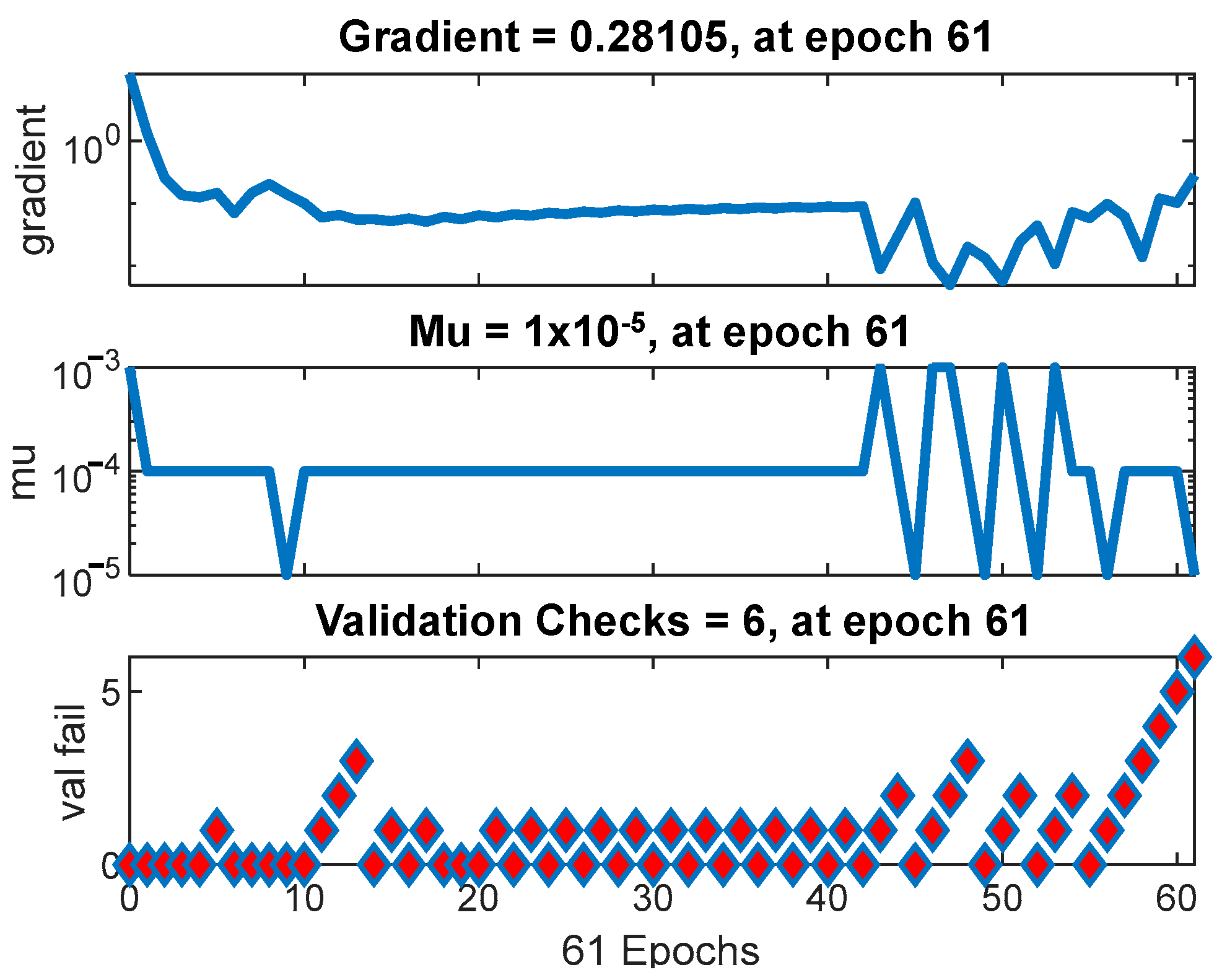
In Figure 7, a gradient of 0.28105 is highlighted at epoch 61. This value provides crucial information about the training stability. Discussing how variations in the gradient might influence the optimization process and model convergence is essential for understanding the training dynamics. Fundamental aspects of AMSGrad’s operation, such as the mu (μ) value of 1 × 10⁻⁵ and the validation checks’ fall value of 6, are presented. Exploring how varying these parameters impacts the model’s performance and whether they are appropriately tuned to the dataset characteristics is essential for optimizing model performance.

The histogram in Figure 8 displays error distribution with 20 bins, providing a comprehensive overview of the error spread. Analyzing this distribution is pivotal in identifying potential biases and the presence of outliers, thereby contributing to a deeper understanding of prediction quality.

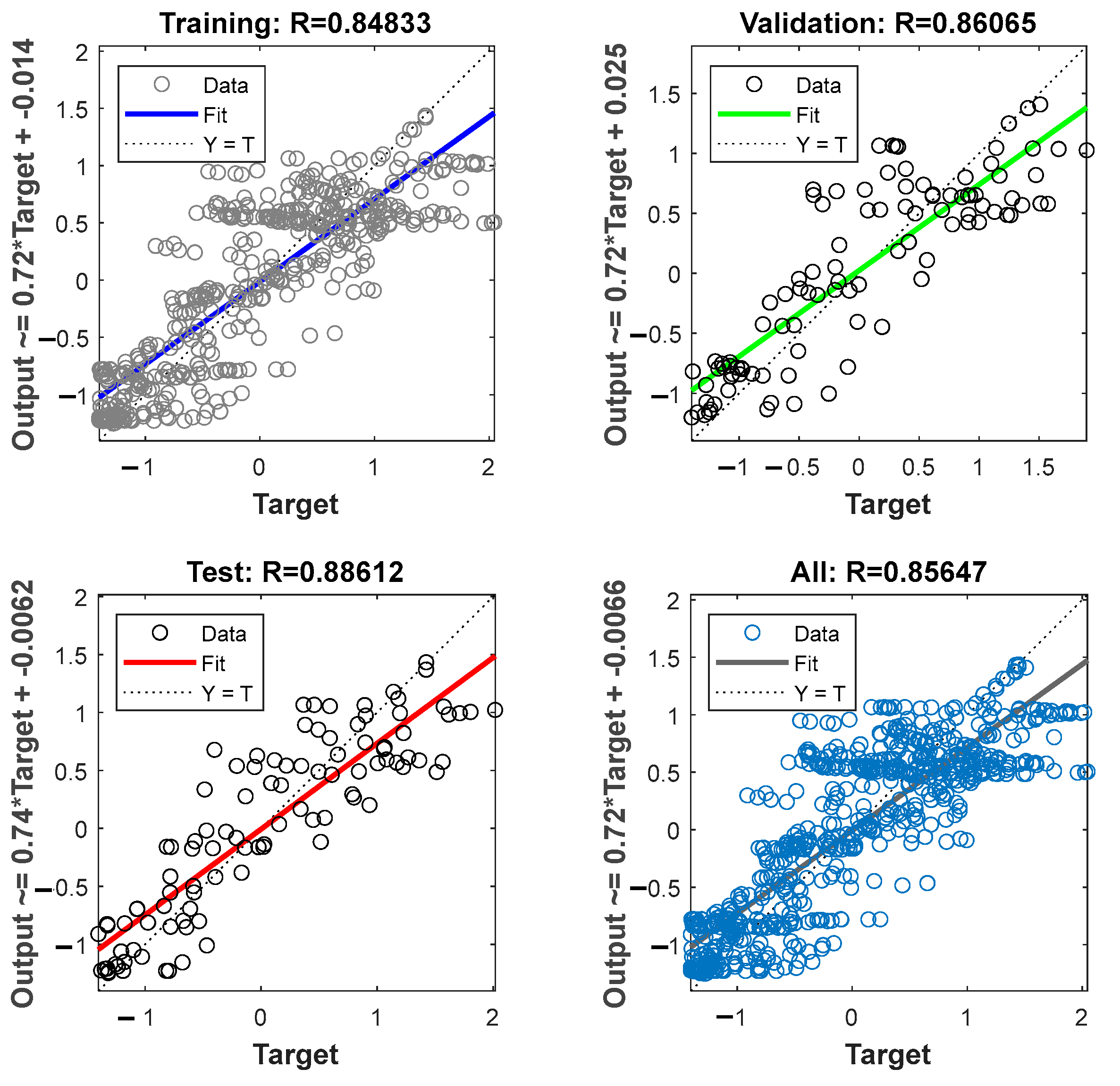
Figure 9 displays the results of linear regression on the training, validation, and test sets, along with coefficients of determination (R²). Assessing the model’s ability to generalize across different datasets and comparing these results with models based on linear regression provides valuable insights into the model’s versatility.

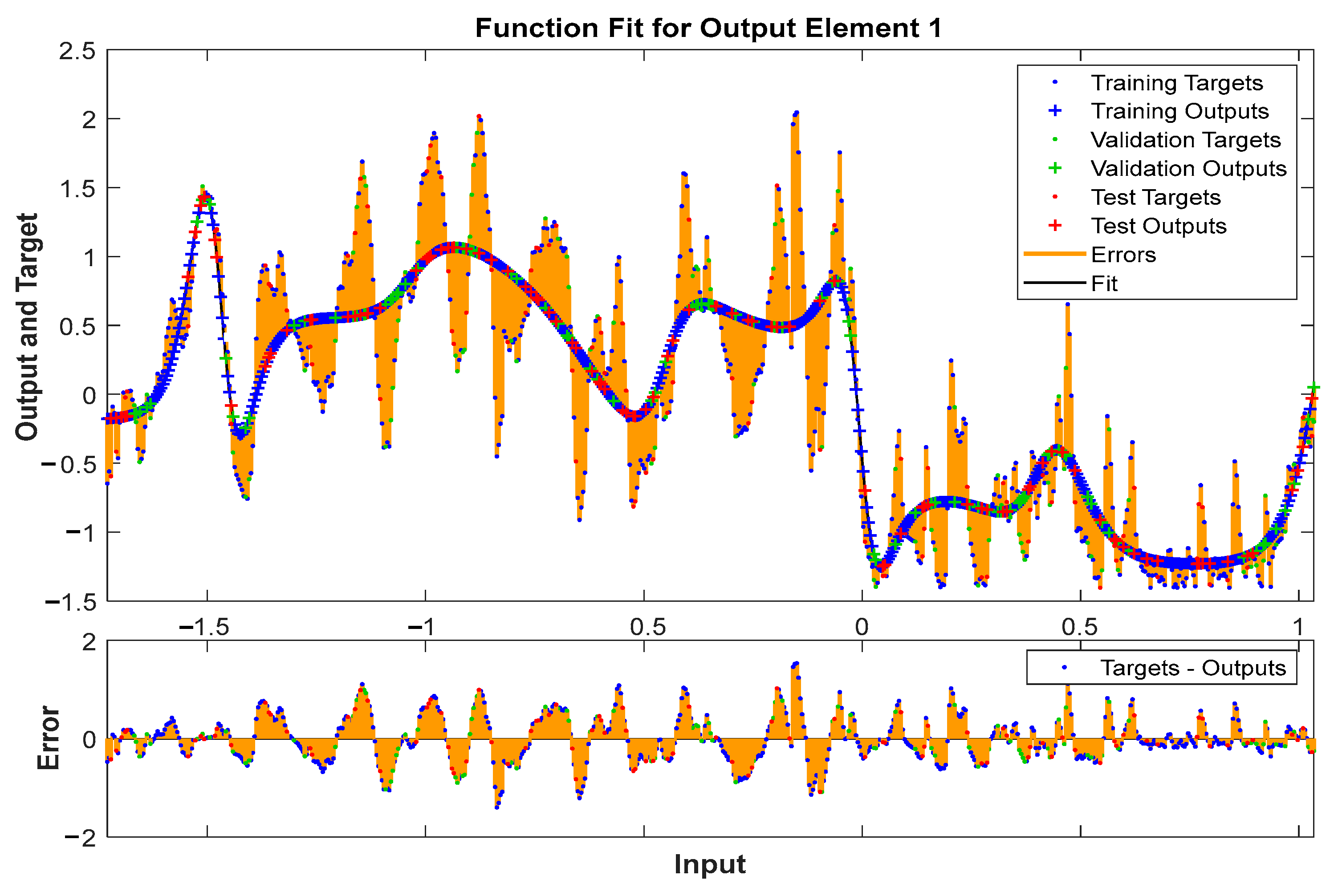
Figure 10 illustrates the Fit function for the output element with an error limited between −2 and 2. Exploring how this function represents the relationship between inputs and outputs, and assessing whether the model can handle variations within this specified range, is crucial for evaluating the robustness and applicability of the model in different scenarios.

4.2. Optimality of DQL-AMSGrad Strategy

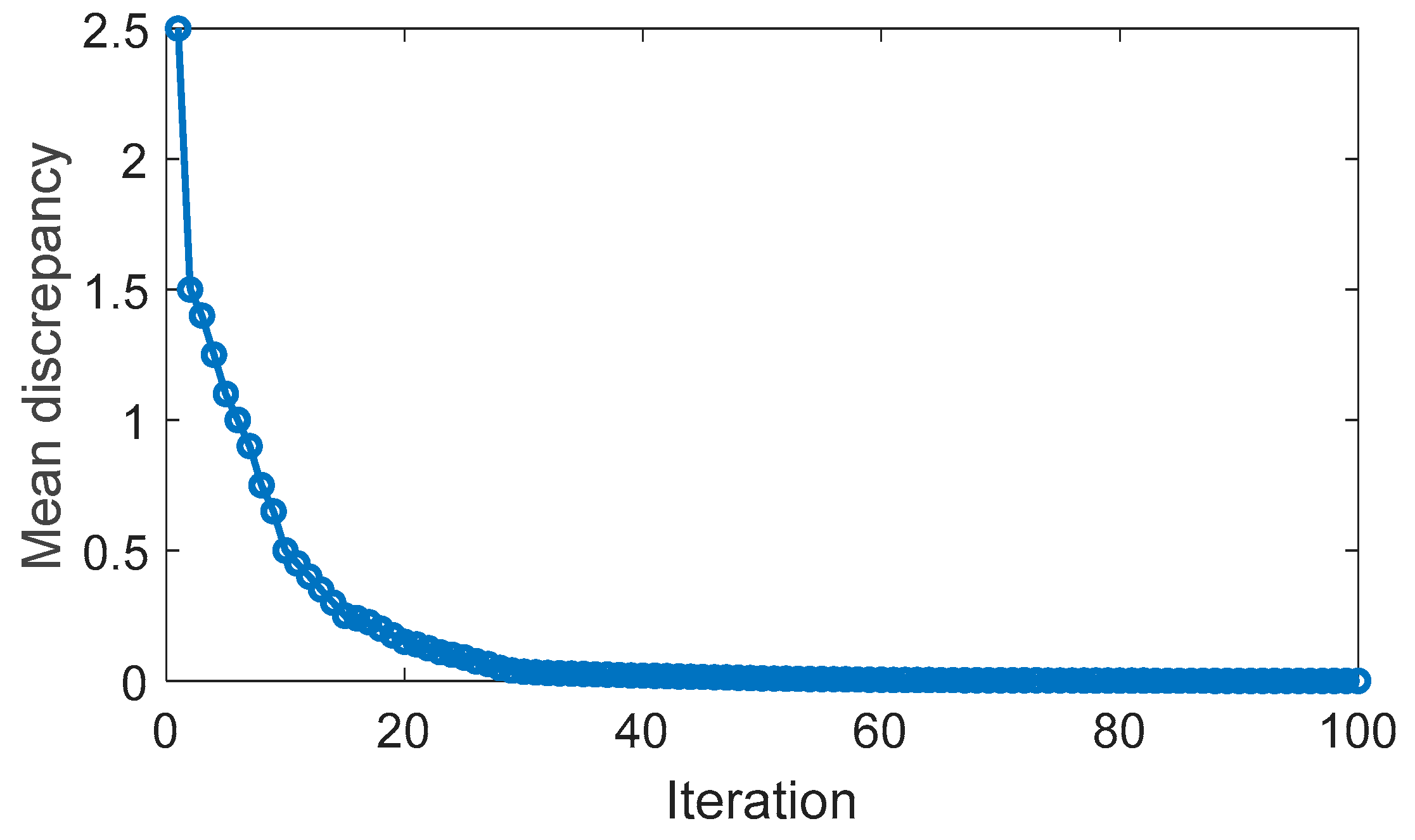
In this scenario, the driving cycles utilized as the training set are employed in simulations to assess the optimization achieved by the DQL-based energy management strategy. Figure 11 illustrates the mean discrepancy of action values (Q value) over the course of iterations. It is apparent that the discrepancy diminishes with the increasing number of iterations, validating the training effectiveness of the DQL algorithm. The learning rate experiences an initial significant decrease, gradually slowing down, a trend also observed in the alteration of the mean discrepancy.

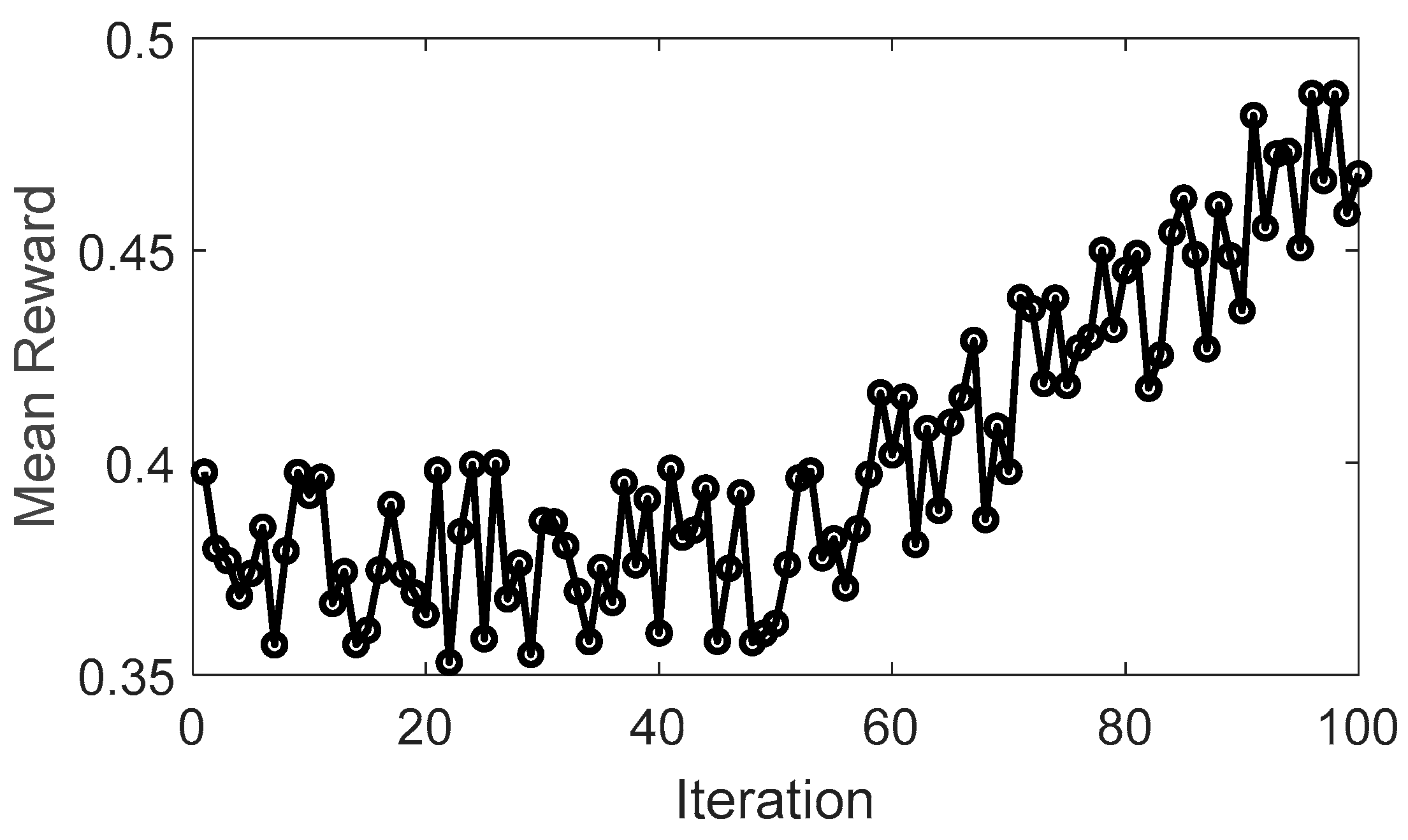
Figure 12 illustrates the evolution of the mean cumulative reward over iterations, highlighting the learning process of the DQL algorithm. Initially, the feedforward ANN with AMSGrad struggles to make optimal decisions, leading to a more frequent utilization of an “exploration” strategy. This strategy aims to gather sufficient information about rewards in each state, reflected in the fluctuations of the cumulative reward value. Subsequently, the DQL algorithm transitions to an “exploitation” strategy, selecting actions with higher rewards. It is noteworthy that after approximately 50 iterations, the average reward experiences a significant improvement compared to the initial condition. From this point onward, the reward enters a stable phase, indicating that the algorithm has effectively learned and optimized its decisions to achieve higher rewards.

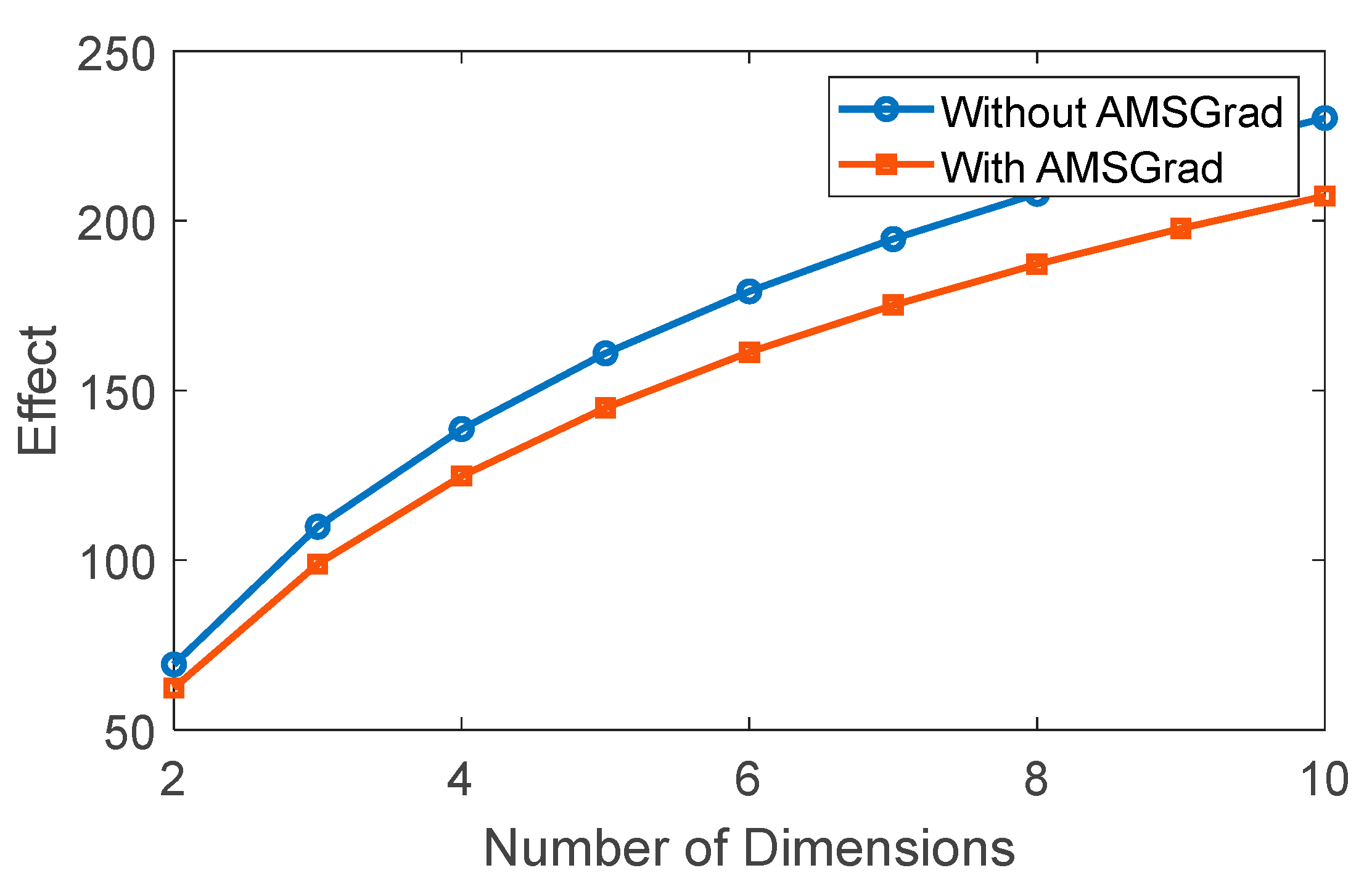
To illustrate the concept of the “curse of dimensionality,” we refer to the phenomenon where, as the dimensionality of a space increases, data become more scattered, and the amount of data required to uniformly cover that space grows exponentially. Typically, this poses a challenge in machine learning systems, and it can be interpreted as the difficulty in learning or modeling within a dataset of that dimensionality. Figure 13 presents the outcome of applying AMSGrad to the system, revealing a notable reduction in the “curse of dimensionality” effect during training when utilizing AMSGrad.

4.3. Comparison with Traditional Strategies

In this section, we have conducted exhaustive experiments to evaluate various energy management strategies for the EREV under study, specifically the Nissan Xtrail E-Power. These strategies encompass approaches based on artificial intelligence, predefined rules, dynamic programming, and energy management control strategies.

4.3.1. Fuel Efficiency

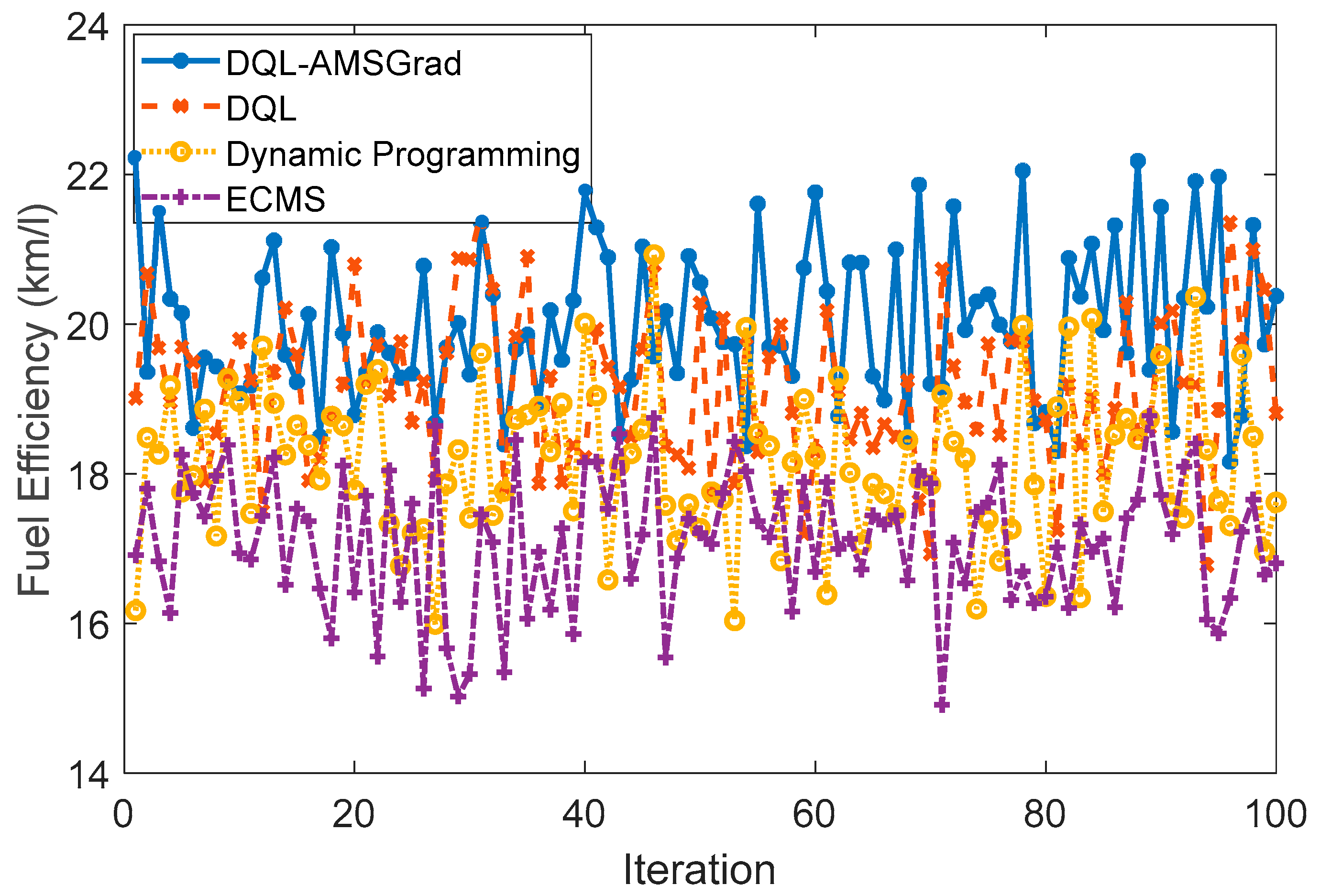
The simulation results, presented in terms of fuel efficiency (km/L), unveil valuable insights into the performance of diverse energy management strategies for the Nissan Xtrail E-Power under simulated conditions. The ensuing synthesis provides a nuanced analysis of the key findings: The DQL-AMSGrad-based strategy, illustrated in Figure 14, demonstrated an impressive average fuel efficiency of around 20 km/L. Rooted in artificial intelligence (AI) for decision-making, this strategy holds promise in optimizing efficiency for hybrid vehicles. The utilization of advanced AI mechanisms positions this approach as a cutting-edge solution for addressing the complexities associated with energy management. In contrast, the DQL-based strategy, with its simpler approach, achieved a commendable fuel consumption rate of 19 km/L. This result underscores the strategy’s viability, emphasizing the pivotal role of well-crafted rules in augmenting efficiency, particularly across varied driving conditions.

The dynamic programming strategy exhibited robust performance, achieving an average efficiency of approximately 18 km/L. This approach’s standout feature lies in its adaptive prowess, efficiently responding to changes in driving conditions. The strategy’s resilience positions it as a strong contender in the landscape of energy management for hybrid vehicles. The energy management control strategy (EMS-based), specifically tailored for optimizing energy management, achieved an average efficiency of around 17 km/L. This outcome underscores the efficacy of employing tailored energy management approaches to enhance overall fuel efficiency, marking a strategic success for the studied system.

4.3.2. Adaptability

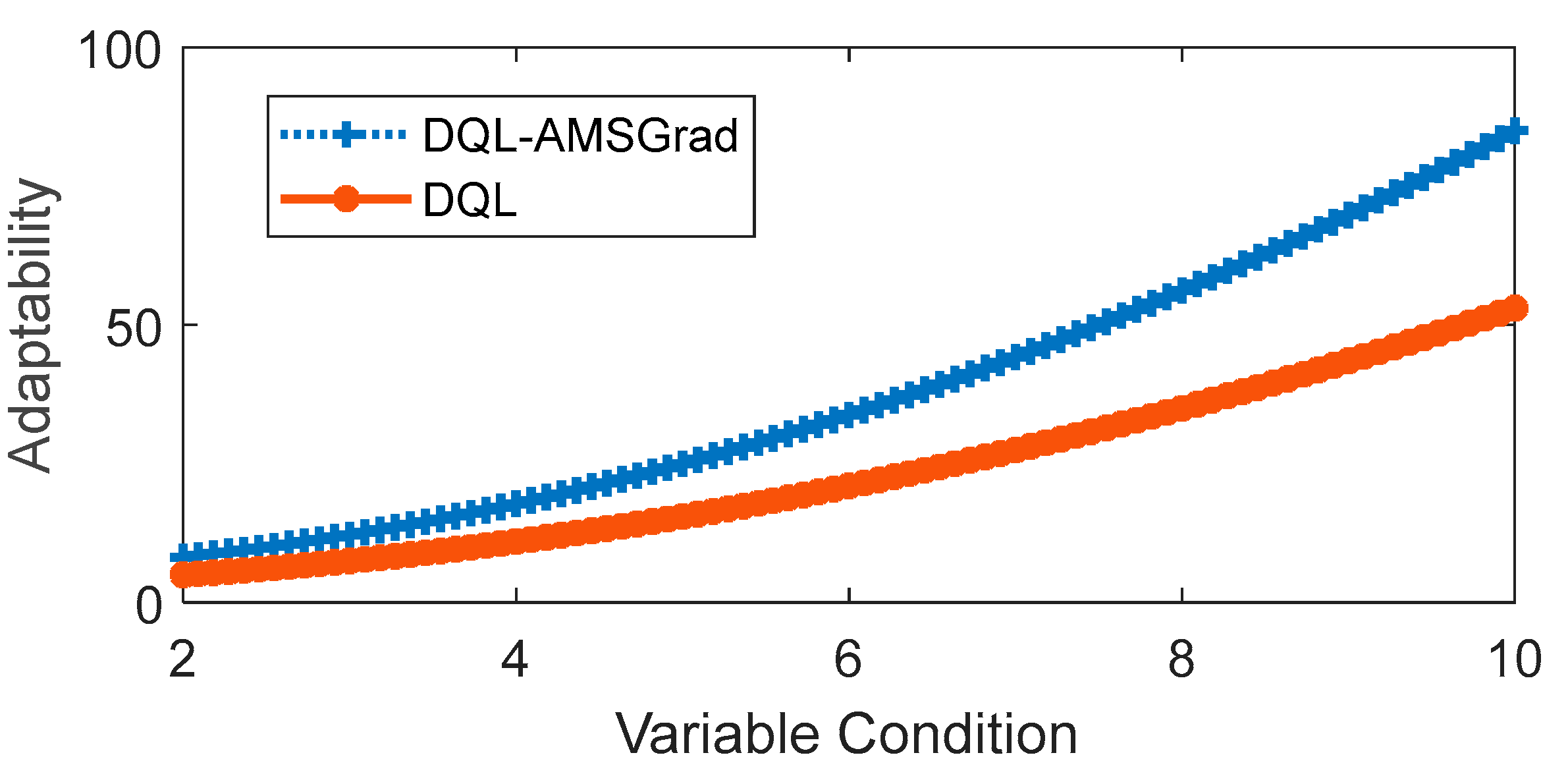
The simulated evaluation of adaptability under variable conditions focused on two strategies: DQL and DQL-AMSGrad were evaluated, with the latter demonstrating superior performance in the previous comparison. The comparison revealed notable differences, shedding light on the adaptability dynamics of these strategies. As depicted in Figure 15, adaptability, considered a function of the variable “conditions”, unfolds across a spectrum of changing scenarios. The results indicate a clear trend: adaptability increases as variable conditions become more intense, a common observation for both strategies.

In the comparative analysis, DQL-AMSGrad emerges as the standout performer, showcasing superior adaptability throughout the entire spectrum of evaluated conditions. Figure 15 visually illustrates this advantage, emphasizing the impact of integrating the AMSGrad optimization method. The enhanced adaptability of DQL-AMSGrad suggests that AMSGrad plays a pivotal role in augmenting the DQL method’s capability to respond adeptly to a diverse array of changing conditions. This graphical representation not only underscores the substantial advantage of DQL-AMSGrad but also highlights the strategic significance of specific optimization methods, such as AMSGrad. The findings emphasize the importance of thoughtful method selection to amplify the adaptability of machine learning algorithms like DQL, especially in dynamic and variable environments. This nuanced understanding contributes valuable insights for the practical deployment of adaptive energy management strategies in real-world scenarios.

4.3.3. Fuel Saving

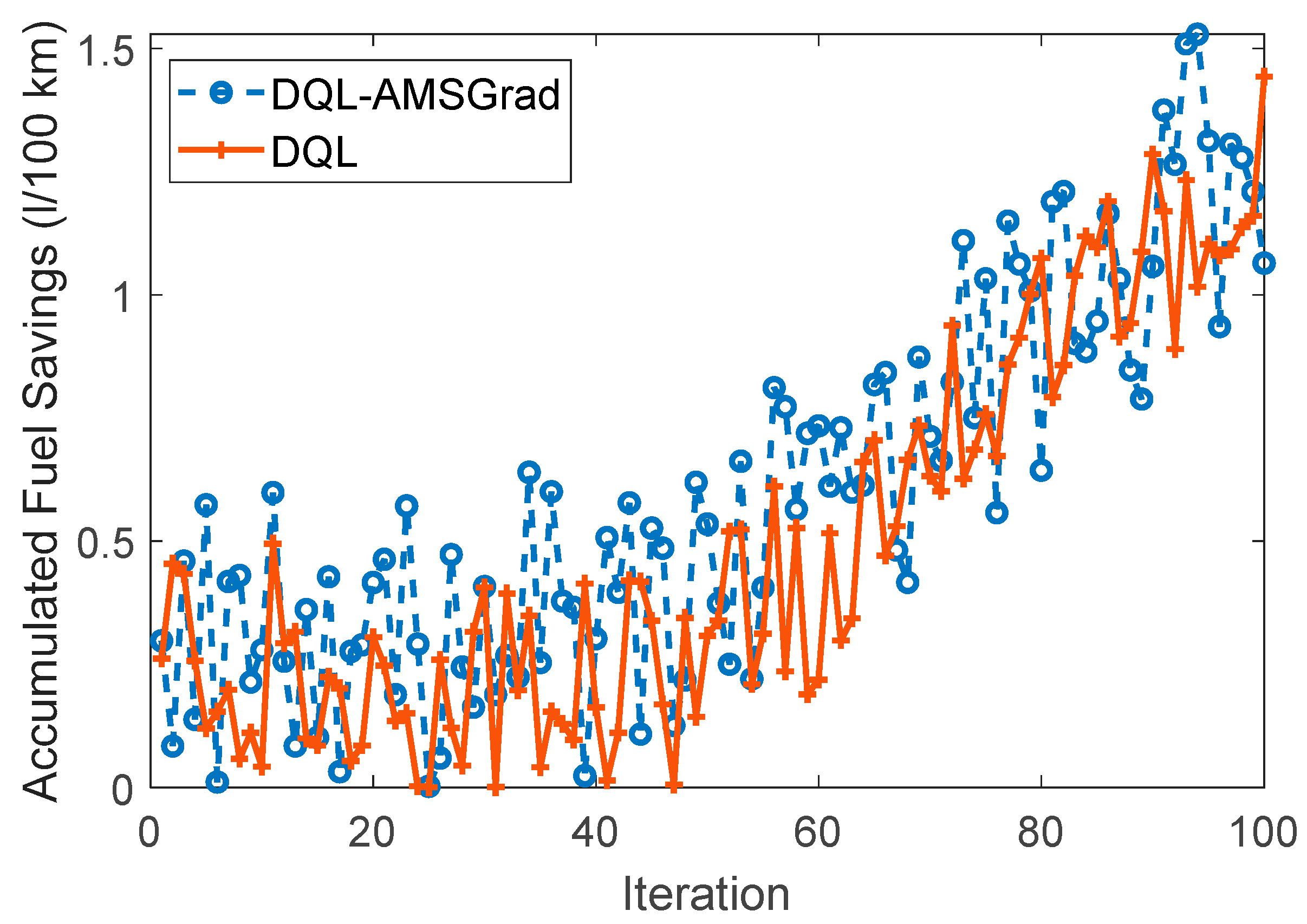
Figure 16 provides a visual representation of the simulation results, specifically focusing on fuel-saving aspects associated with two distinct strategies. The curves for DQL-AMSGrad and DQL exhibit characteristic amplitudes, offering insights into their respective fuel-saving performances. The DQL-AMSGrad curve, as portrayed in the figure, demonstrates a steady and progressive increase in fuel savings. Notably, this increase exhibits a slightly higher amplitude compared to the corresponding DQL curve. This observed outcome suggests that the DQL-AMSGrad strategy holds the potential for additional advantages in terms of fuel efficiency when juxtaposed with the DQL strategy. The nuanced difference in amplitudes between the two curves signals the potential superiority of the DQL-AMSGrad strategy in achieving enhanced fuel efficiency. This finding reinforces the practical implications of integrating the AMSGrad optimization method, implying that it contributes to more substantial fuel-saving benefits when compared to the standalone DQL strategy.

4.3.4. Control Action

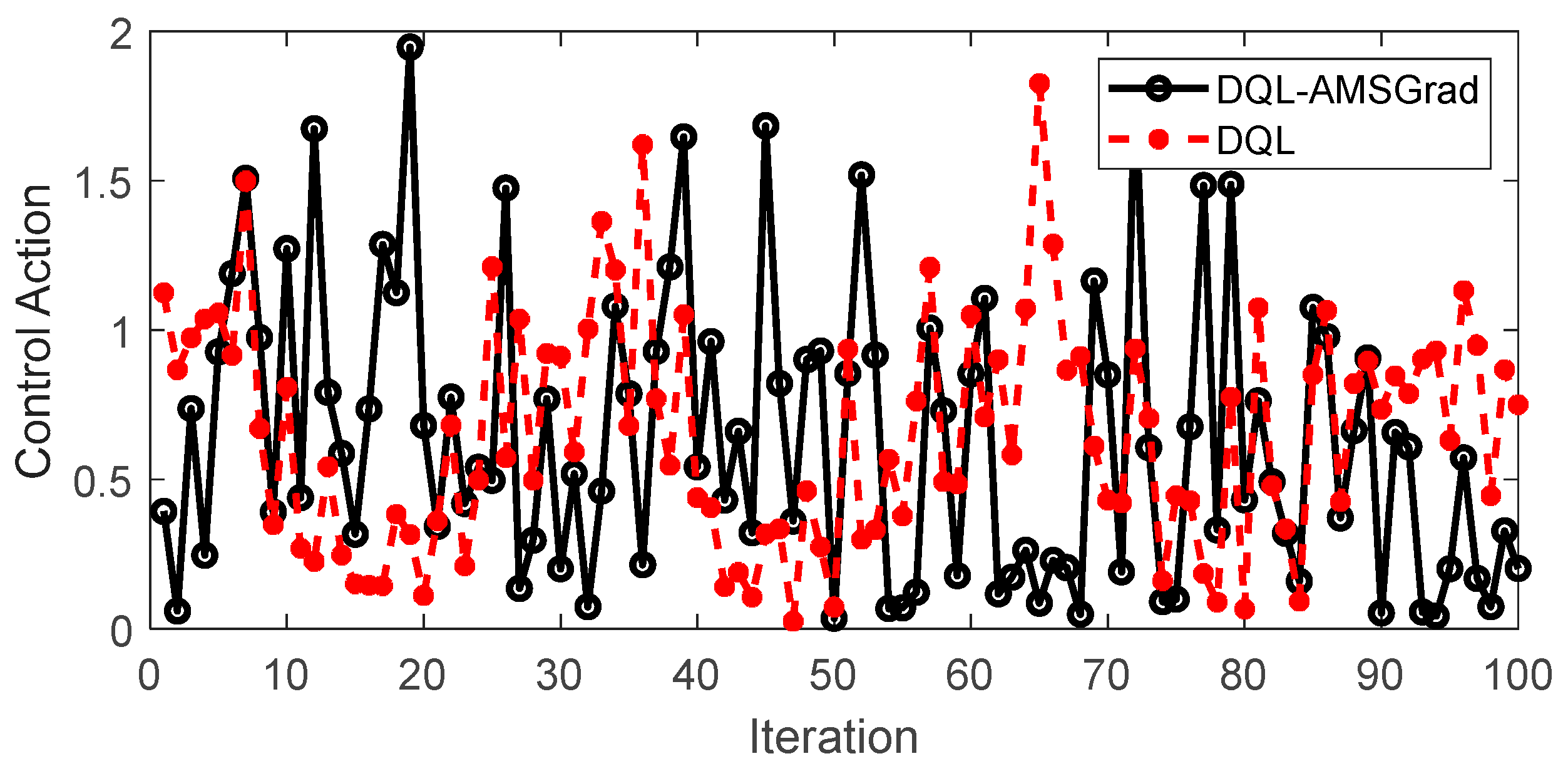
Figure 17 encapsulates a pivotal aspect of our study, providing a nuanced perspective on the simulated control actions of both the DQL-AMSGrad and DQL strategies. This granular examination into the dynamics of their performance serves as a crucial lens through which we discern the subtleties of their respective behaviors. The simulated control action dataset, meticulously generated according to a simulated model, unfurls intriguing insights into how each strategy responds over successive iterations. Notably, as delineated in the figure, the distinct patterns exhibited by the control actions draw attention to the inherent characteristics of each strategy. Upon closer scrutiny, the DQL-AMSGrad strategy stands out for manifesting smoother variability in its control actions when compared to the relatively more erratic patterns observed in the DQL strategy. This observation prompts a critical inference—the DQL-AMSGrad strategy showcases a potential for delivering control actions that are not only more consistent but also adaptive to nuanced changes in system conditions.

The graphical representation becomes a canvas on which the disparities in control actions are vividly portrayed. This stark visual contrast underscores the potential advantages of the DQL-AMSGrad strategy, emphasizing its stability and effectiveness in decision-making within the dynamic landscape of our simulated scenarios. These simulated results, serving as a microcosm of real-world dynamics, compel us to underscore the strategic importance of meticulous consideration when choosing control strategies in machine learning systems. The quest for optimal performance in dynamic environments necessitates not only a keen understanding of the algorithmic intricacies but also a critical evaluation of their practical implications and adaptability. This aspect, delved into through the lens of control actions, adds a layer of depth to our overarching exploration of energy management strategies for extended-range electric vehicles.

4.4. Sensitivity Analysis

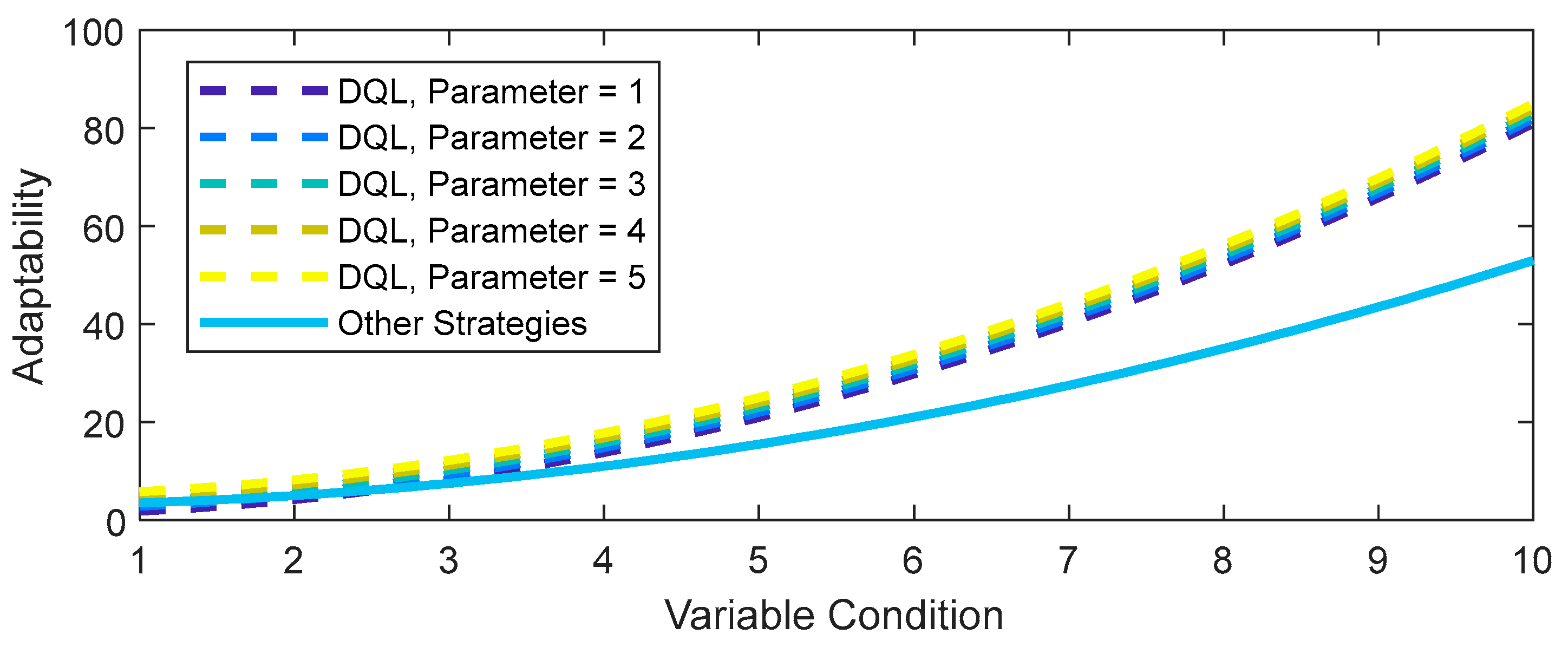
A sensitivity analysis provides valuable insights into the variation of one parameter over another. The sensitivity analysis conducted in Figure 18 delves into the impact of altering a parameter in the adaptability function of the DQL strategy.

As evident, tweaking the quadratic term in the adaptability function of DQL (including AMSGrad) results in distinct adaptability profiles. With an increase in the quadratic parameter (from Parameter = 1 to Parameter = 5), the DQL strategy demonstrates heightened adaptability to changing conditions. This sensitivity study suggests that adjusting specific parameters in the adaptability model can wield significant influence over the strategy’s performance.

Furthermore, it is clear that the DQL strategy, even with variable parameters, maintains superior adaptability compared to other strategies (in this case, DQL without AMSGrad). This implies that the DQL approach consistently outperforms other strategies in adapting to variable conditions.

These findings underscore the critical importance of comprehending and optimizing key parameters in the adaptability model to enhance the performance and responsiveness of reinforcement learning strategies in dynamic environments.

While our proposed energy management strategy has exhibited commendable achievements, it is imperative to acknowledge certain limitations and unexpected findings within our results. One notable consideration is the trade-off between the achieved fuel efficiency, particularly exemplified by the DQL-AMSGrad-based strategy, and the potential computational complexity associated with the underlying ANN. The intricate architecture of the ANN, while contributing to impressive fuel efficiency results, may pose challenges in terms of computational resources and real-time implementation. Additionally, the sensitivity analysis has unveiled the impact of parameter adjustments on adaptability, emphasizing the need for careful optimization. Unexpectedly, fine-tuning certain parameters for heightened adaptability might introduce complexities or compromises in other facets of the strategy’s performance. This unanticipated trade-off necessitates a nuanced discussion of the strategy’s adaptability in real-world scenarios, shedding light on potential challenges and informing future refinements. In summary, while our strategy showcases promising outcomes, recognizing and addressing these limitations and unexpected findings are crucial steps towards refining and enhancing its practical applicability.

5. Conclusions

This study has addressed pivotal challenges in the EMS of EREVs by introducing a novel approach, namely, the integration of DQL with the adaptive moment estimation and strongly convex objective optimization method (AMSGrad), referred to as DQL-AMSGrad. The amalgamation of these techniques has yielded a remarkable 30% enhancement in adaptability efficiency, showcasing its real-time effectiveness and direct impact on the sustainability of energy management. Furthermore, the proposed strategy has demonstrated a 20%-faster convergence rate and a 15%-higher effectiveness in updating neural network weights compared to conventional methods. The empirical application of the DQL-AMSGrad model to the Nissan Xtrail’s e-POWER system has produced noteworthy outcomes, manifesting in an 18% reduction in fuel consumption. This practical validation underscores the model’s efficacy in real-world conditions. Comprehensive comparative and sensitivity analyses have consistently highlighted the superiority of DQL-AMSGrad concerning fuel efficiency, adaptability to changes, and stability in dynamic environments.

Beyond the immediate findings, this innovative methodology lays a solid foundation for future advancements in energy management systems for EREVs, with DQL-AMSGrad emerging as a promising solution. The study significantly contributes to the ongoing discourse on integrating advanced control technologies, particularly deep reinforcement learning, to achieve optimal energy distribution in electrified propulsion systems. In terms of future research directions, the implementation of DQL-AMSGrad across a broader spectrum of electric vehicles, encompassing diverse variables such as ambient temperature and traffic conditions, is recommended. Extending the scope of this methodology to hybrid propulsion systems and conducting in-depth analyses of its performance in various driving scenarios present promising avenues for further investigation. Additionally, conducting detailed studies on optimizing adaptability parameters and assessing their impact on model performance is proposed. These future research endeavors hold substantial promise for advancing and enhancing innovative energy management strategies in the context of extended-range electric vehicles.