1. Introduction
In the era of rapid development, the proliferation of emerging applications has resulted in a substantial upsurge in the demand for network communication traffic. While 5G communication systems exhibit noteworthy advancements over their predecessors [
1], forthcoming wireless communications necessitate even higher throughput, enhanced security, reduced latency, lower energy consumption, extensive connectivity, network densification, and improved Quality of Service (QoS) [
2]. Additionally, the exponential growth of numerous emerging mobile application models and the surge in network traffic will engender an immense and escalating need for the radio spectrum. To effectively cope with the burgeoning mobile data traffic in future wireless network communications, it is imperative to address the scarcity of spectrum resources [
3].
Cognitive Radio Network (CRN) is widely acknowledged as a promising solution to enhance the efficient utilization of spectrum resources. CRN utilizes dynamic spectrum access and reconfiguration, enabling it to comprehend its surroundings and adapt its operating parameters according to the changes in the radio frequency (RF) environment. This breakthrough innovation in radio technology, Cognitive Radio (CR), paves the way for significant improvements in the utilization of congested radio spectra [
4].
In CRN systems, CR serves as an effective technique to enhance Spectrum Efficiency (SE), and its users are classified into PU and SU. A PU is a licensed user who possesses higher priority in accessing the spectrum. On the other hand, an SU is typically an unlicensed user who can share the spectrum of the PU while ensuring that no harmful interference is caused to the PU [
5]. For secondary users, the primary concern is to share the spectrum of the PU while minimizing interference and maintaining QoS for themselves, thereby maximizing spectrum efficiency.
While CRNs offer significant improvements in the spectral efficiency of wireless networks, they also face challenges related to optimizing performance for both PUs and SUs, as well as ensuring robust security [
6]. Practical applications of CRNs encounter persistent obstacles concerning network energy consumption and hardware costs. Additionally, like traditional wireless networks, CRNs are susceptible to security issues. As previously mentioned, the ability of the physical layer in CRNs to sense and comprehend the surrounding RF environment becomes a vulnerability that adversaries can exploit for malicious activities.
The dynamic and open nature of the physical layer in CRNs renders cognitive communications highly vulnerable to various internal and external malicious activities. In recent years, numerous research efforts have focused on developing secure transmission techniques at the physical layer specifically tailored for CRNs. These techniques include Artificial Noise (AN)-assisted beamforming, Cooperative Jamming (CJ), and Cooperative Relaying schemes [
7]. However, these approaches primarily concentrate on signal processing at the receiver and transmitter to adapt to changes in the wireless environment. They are unable to completely mitigate the negative effects caused by the uncontrollable electromagnetic wave propagation environment. Moreover, the deployment of a large number of relays in a secure wireless system inevitably leads to excessive costs. Additionally, collaborative interference and artificial noise introduce additional power consumption. Considering the limitations of these existing approaches, there is an urgent need for a new wireless security paradigm that is both cost-effective and energy-efficient.
In recent years, the emergence of Intelligent Reflecting Surface (RIS) technology, made possible by advancements in technology and metamaterials, has provided new opportunities. RIS is a planar array comprising numerous reconfigurable passive elements, each capable of independently modulating the incident signal to induce a specific phase shift. This collective manipulation of the reflected signal’s propagation characteristics enables RIS to significantly enhance the spectral efficiency and security of wireless networks at a low cost [
8]. RIS technology offers a high level of flexibility for resource allocation and CRN systems. Moreover, researchers have started exploring the application of RIS to enhance the physical layer security of wireless communications. By adjusting the phase shift of the reflected signals, RIS can reshape the wireless propagation environment. This adjustment increases the data rate for legitimate receivers while decreasing the data rate for potential eavesdroppers, thereby reducing information leakage and enhancing overall system security [
9]. Consequently, the integration of RIS into CRN systems holds promise as a solution to address the challenges faced by CRNs, improving spectral efficiency and energy efficiency, and facilitating green and secure communications.
1.1. Related Work
Reference [
10] focused on a MISO CR system and demonstrates the benefits of beamforming in increasing the secrecy rate. Reference [
11] considered a MIMO CR network and introduced a robust secure beamforming design to obtain the maximum achievable secrecy rate for the worst-case SU. Furthermore, several scholars have utilized various auxiliary techniques, such as the introduction of AN, relaying, and Collaborative Jamming to enhance the secure transmission performance of CR communication systems. In reference [
12], AN was introduced to enhance secure communication in fast-fading environments for SUs. Reference [
13] explored secure transmission in CR networks using relay-assisted orthogonal frequency division multiple access, considering latent eavesdroppers. Additionally, reference [
14] investigated bidirectional relaying in CR communication systems, showing significant improvements in secrecy and rate for SUs. Moreover, reference [
15] proposed a wireless energy-harvesting Collaborative Jammer-assisted transmission scheme to enhance CR system security. However, these studies have two main drawbacks. Firstly, deploying relays or auxiliary devices for secure output incurs high hardware costs and additional energy consumption. Secondly, ensuring satisfactory confidentiality performance in harsh wireless transmission environments remains challenging, even with AN or jamming signals.
The above energy consumption problems can be addressed well by introducing an RIS in CR networks. Due to full-duplex transmission and low power consumption, RIS has received a great deal of attention from both academia and industry as a promising technology that can significantly improve energy efficiency in 6G communications. It is a new cost-effective and energy-efficient technology that can shape the radio propagation environment and is well-suited to improve the energy efficiency of CR systems. In reference [
16], RIS was proposed as a means to enhance the data transfer rate of SUs in MIMO CR systems. Reference [
17] investigated RIS-assisted MISO CR systems to maximize the transmission rate of SUs. However, security considerations were not addressed. Subsequent studies focused on the security aspect. In reference [
18], the authors examined the security performance of RIS-assisted underlay-mode CR systems, enhancing the secrecy rate of SUs. In reference [
19], the problem of improving SUs’ secrecy in the presence of multiple eavesdroppers was investigated. The extension to the MIMO model was explored in reference [
20] to maximize SUs’ secrecy rate with RIS. However, the trade-off between secrecy rate and energy consumption was considered in reference [
21], aiming to maximize the Secrecy Energy Efficiency (SEE) of SUs by utilizing RIS.
1.2. Contributions
However, the aforementioned studies primarily focused on the secrecy rate and energy consumption of SU, neglecting the security and energy consumption aspects of the entire CR system in the presence of PU. Therefore, building upon the existing research, we propose a novel communication scenario to address the secure communication problem in the downlink and introduce the concept of an RIS to enhance the secure communication performance of the entire CR system. The main contributions of our work are as follows:
In a novel CR downlink communication scenario, a PBS communicates with a PU, while a CBS communicates with a SU. The entire CR system is subject to eavesdropping by an external entity;
We balance the secrecy rate and energy consumption by formulating a secure energy efficiency objective function, transforming the maximization of secrecy rate into a secure energy efficiency problem;
To efficiently solve the non-convex objective function in the subproblem, we employ an SCA-like (Sequential Convex Approximation-like) lemma. This approach helps overcome the nonconvexity and enables effective optimization of the objective function;
We propose an efficient algorithm based on alternating optimization, semidefinite relaxation, and Dinklbach’s method to solve the resulting optimization problem. Our method effectively improves the safety energy efficiency of the overall CR system, as demonstrated by simulation results.
3. Alternating Optimization-Based Algorithm
3.1. Given , Optimize
First, we define the following symbols below:
, .
, .
, .
, .
, .
, .
Then, Equation (5) can be simplified to
Let tr(Z) and rank(Z) denote the trace and rank of the matrix Z, respectively, where the semidefinite relaxation (SDR) algorithm [
22] is applied. Equation (15) can be written as
To further address the nonconvexity of the objective function, we quote the following lemma [
23].
Lemma 1. For any , consider the function . Then, we have The optimal solution is
. Lemma 1 provides an upper bound for
, which is tight when
. For
, applying Lemma 1, let
and
; then,
can be written as
where
Similarly, we set
and
, and
can then be written as
where
Let
and
; the,
can be written as
where
Let
,
,
can be written as
where,
By applying the semidefinite relaxation (SDR), we relax the rank(
) = rank(
) = 1 constraint and apply Dinklbach’s algorithm [
24]. Then, subproblem (P1.1) can be written as
where
, where
is the auxiliary variable introduced by applying Dinkelbach’s algorithm to solve this fractional programming problem. It can be shown that (P1.1) is convex for
or
. Therefore, it can be solved by applying alternating optimization techniques. According to Lemma 1, the optimal
for fixed
can be derived in closed form as follows:
On the other hand, for a given
, the optimal
is solved by each fixed
iteration. Since (P1.1) is convex, it can be solved efficiently by using a convex optimization solver (e.g., CVX), and, eventually, the optimal solution is obtained by alternately updating
and
. Note that the obtained
and
are not guaranteed to be rank 1 matrices because the rank 1 constraint is discarded in (P1.2) by applying SDR. To solve the omitted constraint rank equal to 1, we apply a Gaussian randomization method reduction, the details of which are omitted here for the sake of brevity. Algorithm 1 is summarized as follows.
| Algorithm 1 Alternating optimization solves P1.1 |
![Energies 17 00515 i001]() |
3.2. Given , Optimize
First, we let ; then, .
Let . And we define the following symbols below:
,
,
,
,
,
.
According to Lemma 1, we can obtain
where
Similarly,
where
where
where
By the semidefinite relaxation (SDR) method, we relax the
constraint, and the subproblem of (P1.2) can be written as follows:
It can be shown that (P1.2) is convex for
or (
). Therefore, it can be solved by applying alternating optimization techniques. According to Lemma 1, the optimal (
) for a fixed
can be derived in closed form as follows:
For a given (
), the optimal
can be solved iteratively. The overall solution method is similar to the subproblem (P1.1), which is finally solved with the help of the CVX tool. The complete Algorithm 2 for solving the entire problem is as follows.
| Algorithm 2 Alternating optimization solves P1 |
![Energies 17 00515 i002]() |
3.3. Algorithm Complexity
The overall algorithm for solving the problem is shown in Algorithm 2. The complexity of the algorithm comes from solving the two subproblems (P1.1) and (P1.2), the complexity of the algorithm in solving
is
, and the complexity of the algorithm in solving
is
[
25]. Assuming that the number of iterations in the two subproblems are
and
, the complexity is
and
, respectively. Thus, we know that the number of iterations in the overall iterative process is
, and the complexity of the whole algorithm is
.
4. Simulation Results
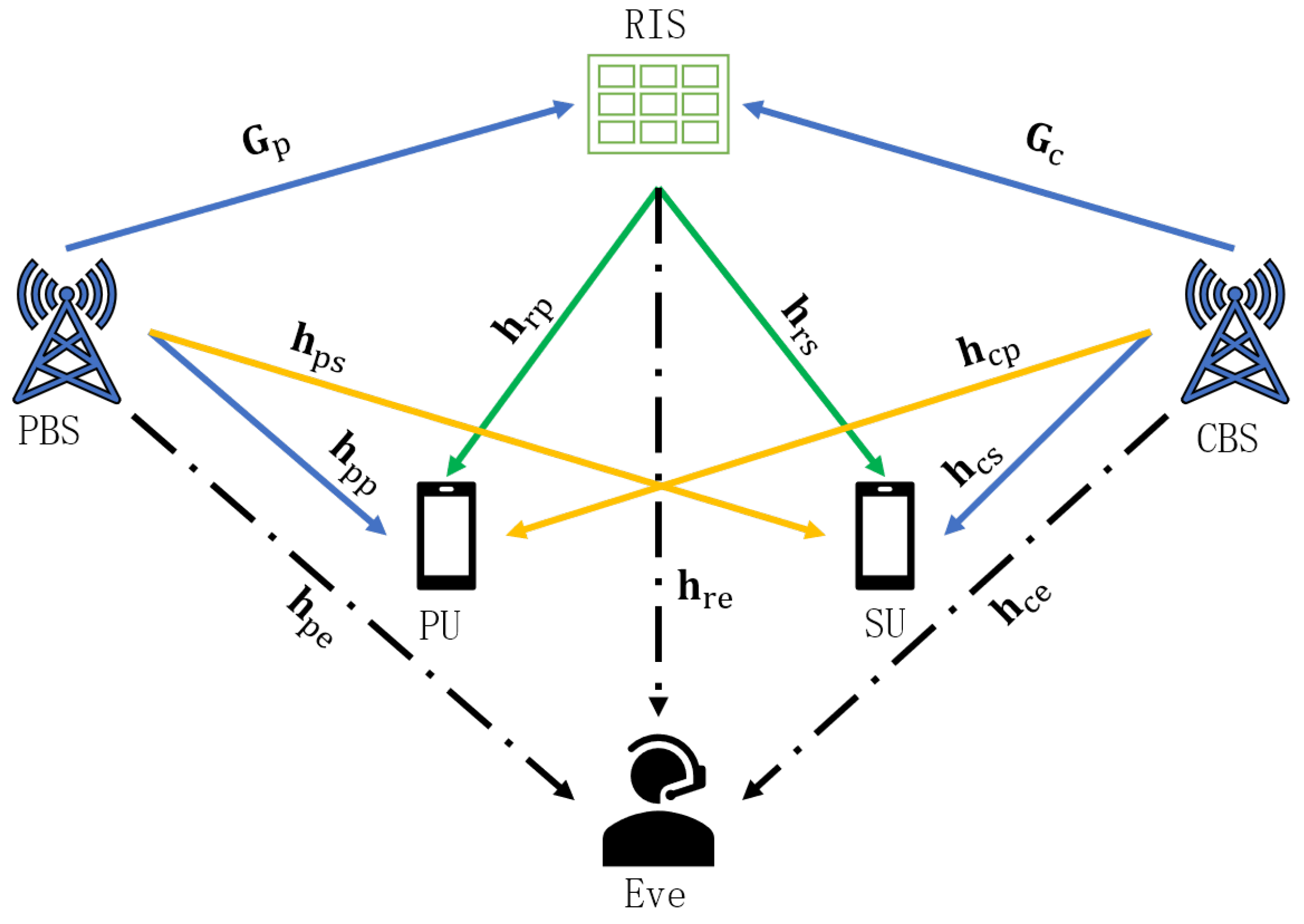
In this section, the effectiveness of the algorithm in this system model problem scenario is demonstrated by comparing it with the scheme without RIS and the RIS random phase algorithm scheme. We assume that the locations of primary user PU and secondary user SU are (100, 20) and (50, 0), respectively, the locations of PBS and CBS are (150, 0) and (0, 0), respectively, the locations of RIS and Eve are (50, 30), (100, −10), respectively, and the noise variance is set to . The path loss of all channels is given by the equation , where denotes the path loss at the reference distance m, d denotes the straight-line distance from communication end a to communication end b, is the path loss exponent, and the path loss coefficients of PBS to RIS, CBS to RIS, RIS to PU, RIS to SU, Eve to RIS, PBS to PU, PBS to SU, CBS to PU, CBS to SU, PBS to Eve, and CBS to Eve have path loss coefficients of , and , respectively.
It is assumed that the small-scale fading of the channels from PBS to RIS, RIS to PU, CBS to RIS, RIS to SU, and Eve to RIS all follow the Rayleigh fading model. The small-scale fading is expressed in the form of the equation
, where
denotes the Rician factor, and
and
represent the deterministic line-of-sight component and non-deterministic line-of-sight component of the channel of interest between the a and b ends, respectively. Other specific parameters are set as follows (
Table 1).
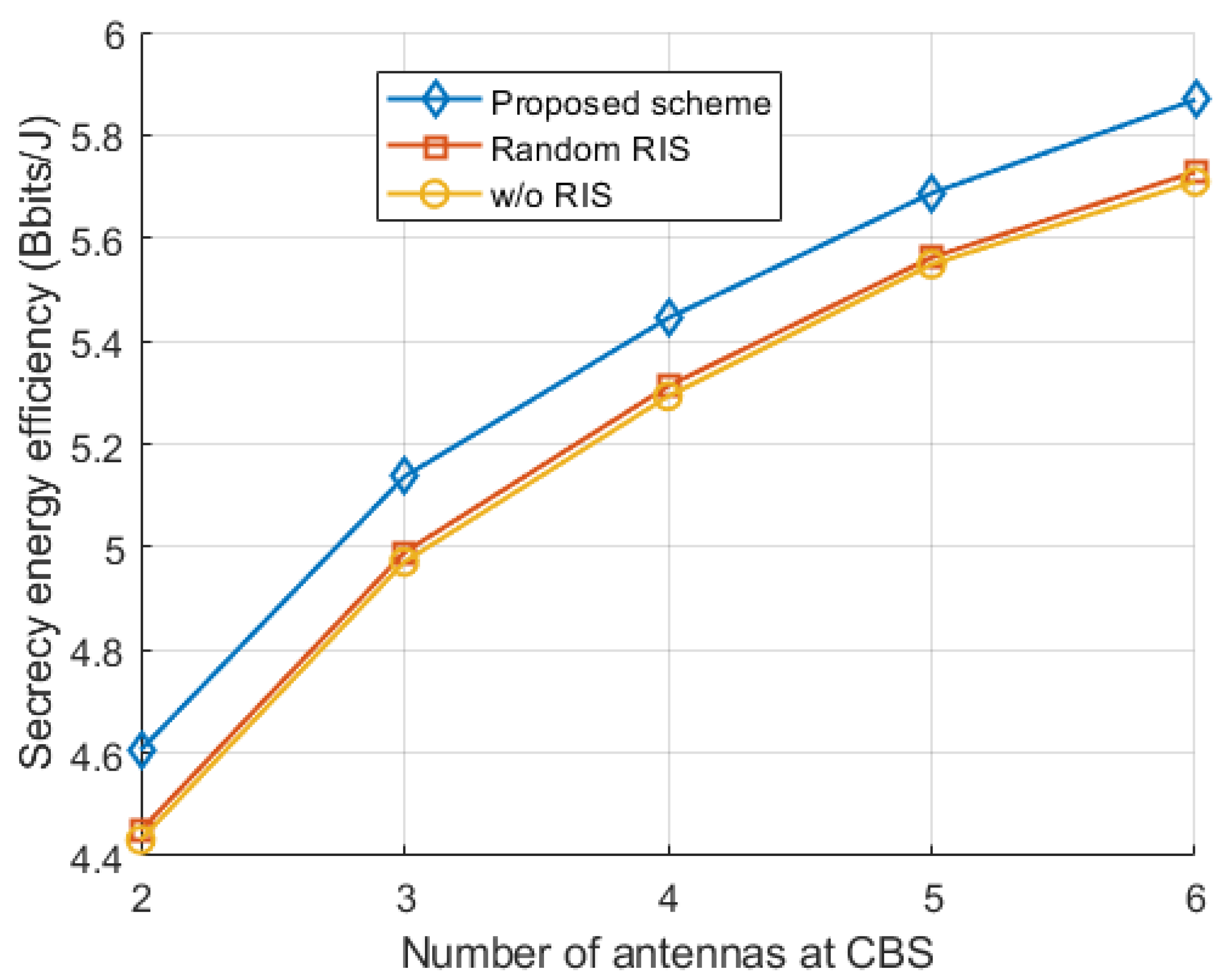
Figure 2 shows the variation of the safety energy efficiency with the number of CBS antennas for different schemes with a fixed number of PBS base station antennas
, with a maximum transmit power of 30 dBm, and a number of RISs
.
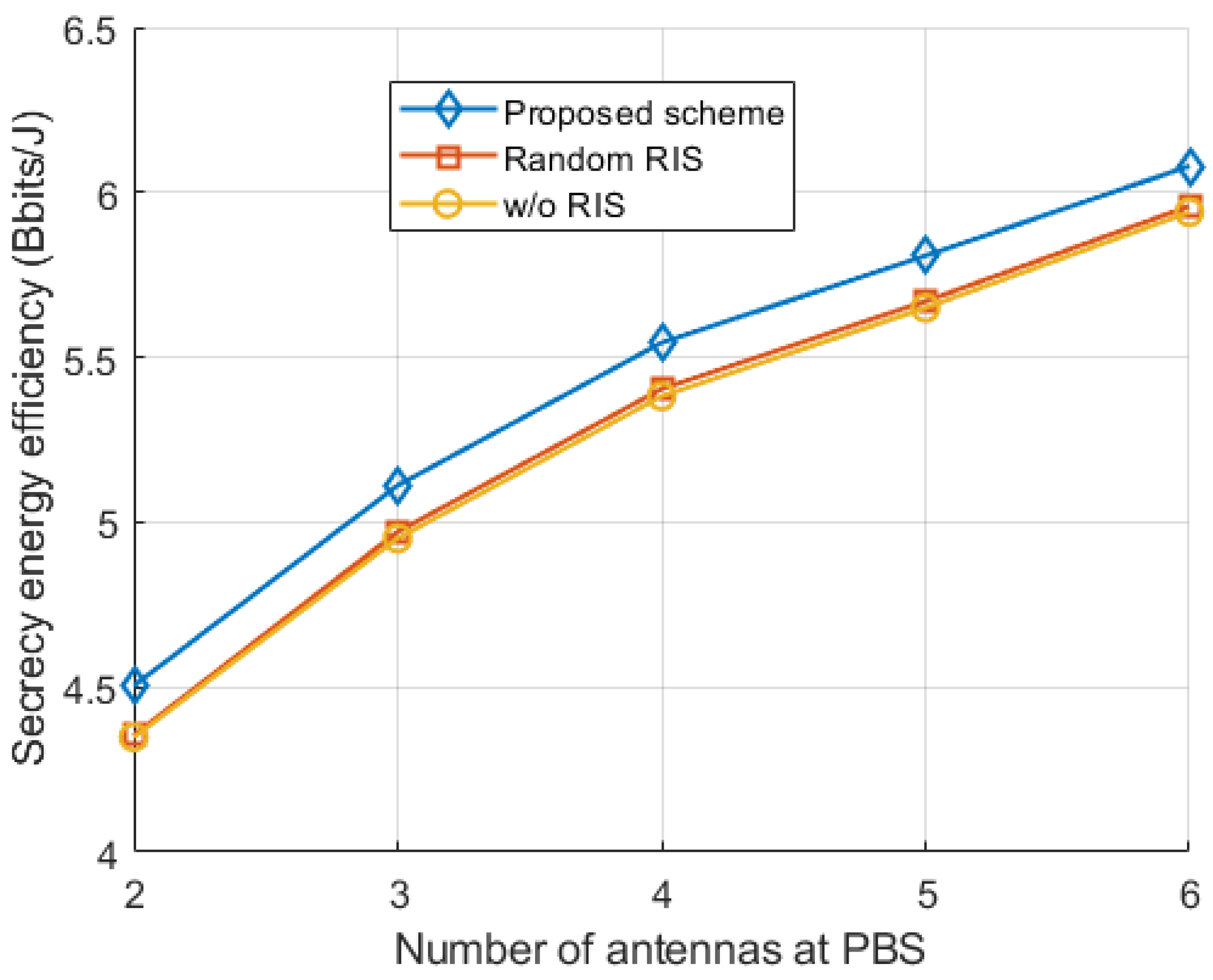
Figure 3 shows the variation of different schemes with a fixed number of CBS base station antennas. It can be seen that, with the increase in the number of antennas, the system safety performance is improved to a certain extent, and the proposed algorithm is better than the other two schemes. In addition, the system with random RIS assistance is slightly better than the system without RIS assistance in terms of safety energy efficiency gain.
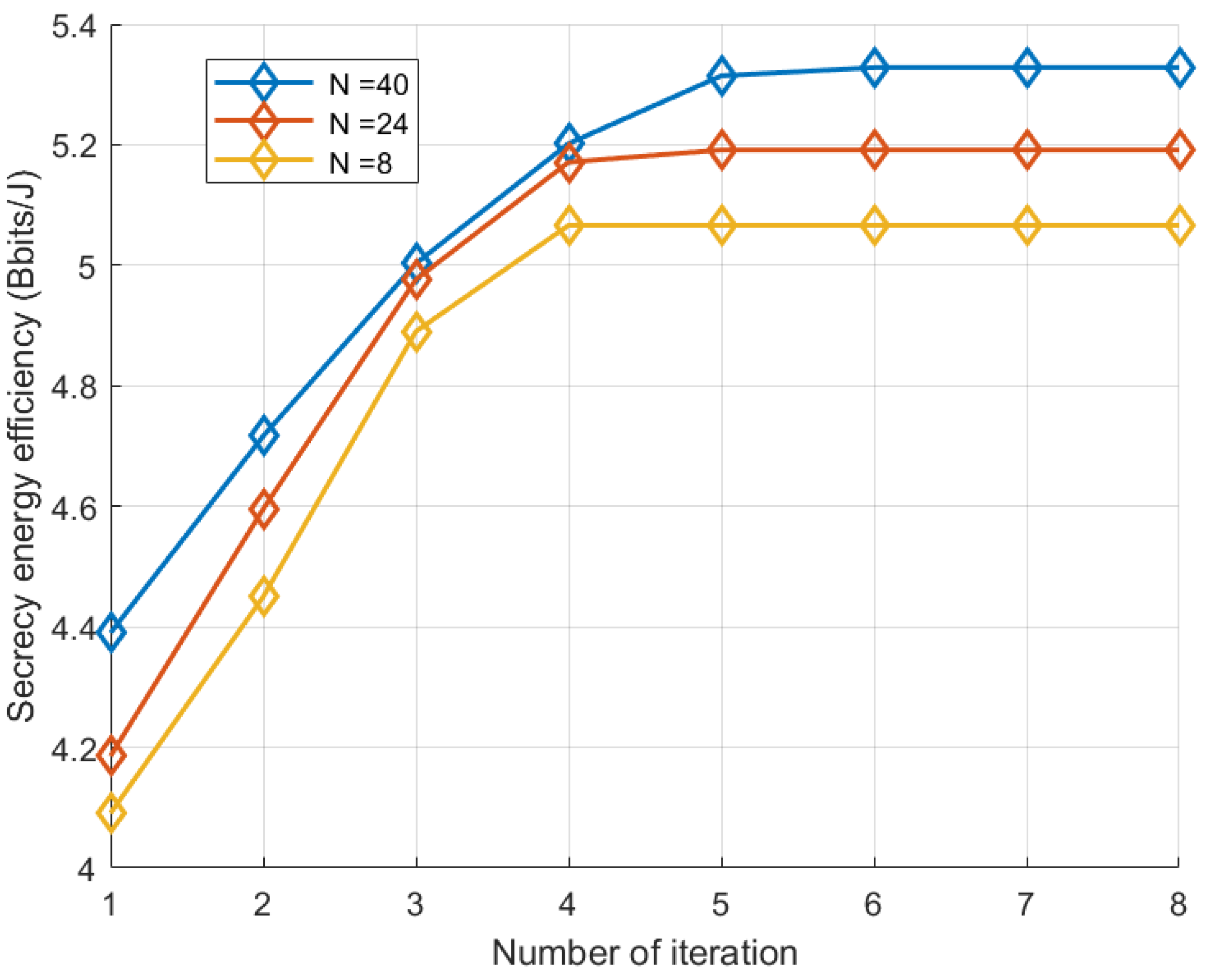
The convergence of the algorithm in this paper when
is given in
Figure 4. It can be seen that, as the number of iterations increases, the safety energy efficiency of the system increases monotonically until it maintains a steady state, which proves the effectiveness of the algorithm. Moreover, the more RIS reflection units, the greater the convergence value, which can be explained by the fact that the greater the number of RIS elements, the stronger the reflection of the signal in the expected direction.
Figure 5 shows the variation of the average security energy efficiency with the number of RIS reflective elements
N for different schemes with a fixed number of base station antennas. At this time, the
is 30 dBm, the number of antennas of both base stations is 4, and the interference temperature threshold is
−90 dBm. From the figure, it can be seen that, with the increase in the number of RIS reflector units in a certain range, the security energy efficiency of the two schemes—our proposed scheme and the RIS random phase-shift—becomes larger, whereas the security energy efficiency of the scheme without the assistance of the RIS remains unchanged. By increasing the number of RIS reflector units, the RIS gains more flexibility in channel design for the PBS/CBS–RIS–PU/SU link. This increased flexibility leads to improved beamforming gain. And the more RIS elements in the communication system, the more signal paths and energy the RIS reflects to improve the signal quality of the PUs and SUs while reducing the signal quality of the eavesdropper. However, it is worth noting that increasing the number of RISs is beneficial to improve the security energy efficiency of the whole communication system only within a certain range.
Figure 6 and
Figure 7 show the variation of the security energy efficiency with CBS and PBS transmitting power for different schemes for
N = 16. It can be observed that the gain effect of the proposed algorithm is significantly better than the other two schemes at different transmission powers. In addition, the safety energy efficiency of the three schemes gradually increases and then slowly decreases as the transmitted power
gradually increases. Because the applied scheme optimizes the phase shift of the RIS reflection unit, it harnesses the additional degrees of freedom in the channel, resulting in a gradual increase in the safety energy efficiency of the system. This is achieved despite the associated increase in energy consumption as the maximum power (
) gradually increases. As
increases further, the increase in system energy consumption dominates the system energy efficiency performance, leading to a decrease in safety energy efficiency. As
increases even further, the increased system rate begins to dominate the system safety energy efficiency, leading to a slow start of the decrease. Overall, the applied scheme is significantly better than the other two schemes.
Figure 8 shows the variation of the system safe energy efficiency for different
thresholds. As can be seen from the figure, the safe energy efficiency of all schemes is improved with the gradual increase in
. This is because the interference tolerance of the PU is greater when the interference temperature threshold
increases, which relaxes the constraints on the safe energy efficiency of the SU, and, thus, the safe energy efficiency of the whole communication system is improved. It can also be seen that the secure energy efficiency of our proposed scheme is significantly better than the benchmark scheme. Theoretically, the safe energy efficiency of the whole communication system should be saturated when the
increases to a certain value, which means that the interference temperature is no longer a factor affecting the safe energy efficiency of the system, which may be limited by the transmission power
or other factors.
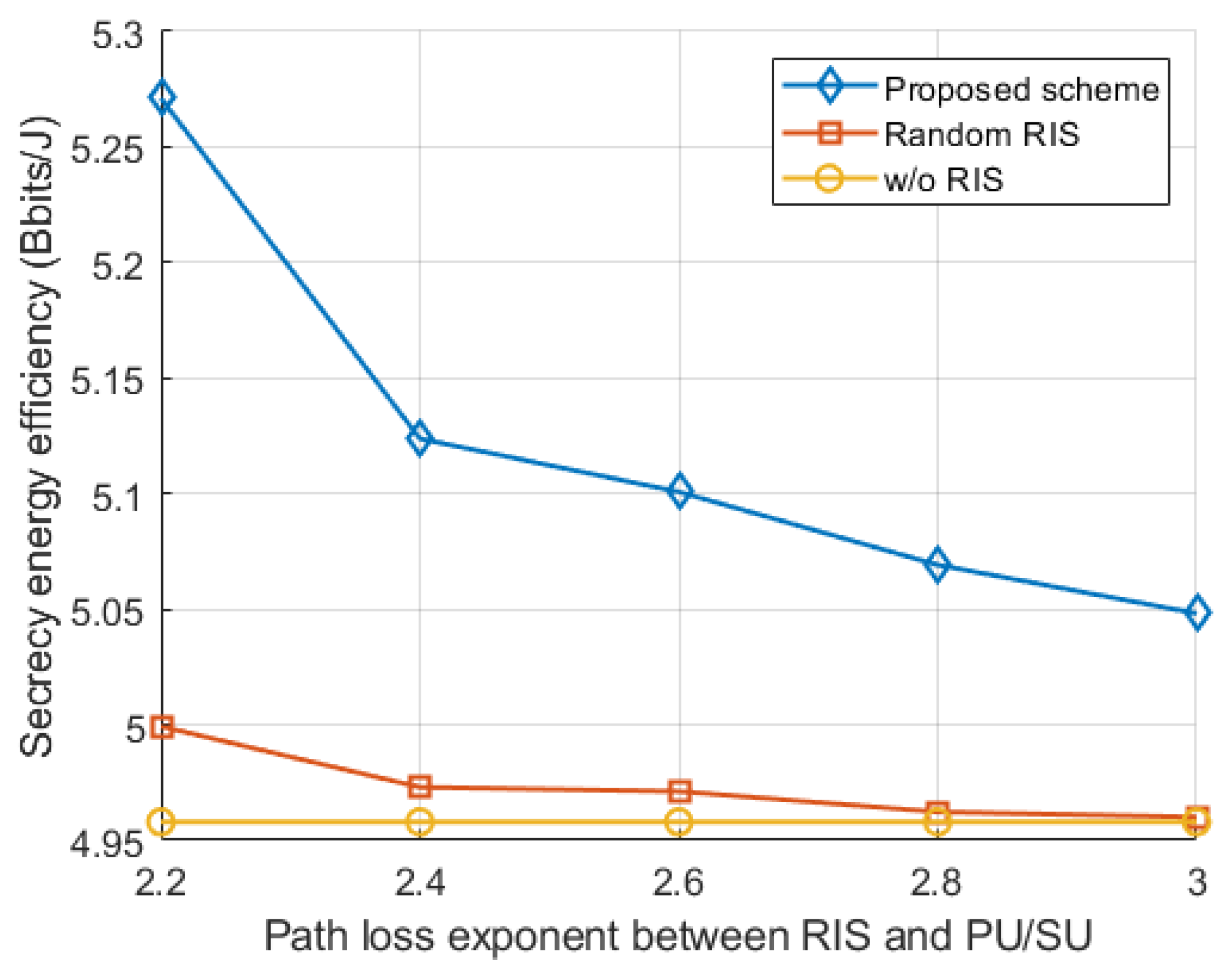
Figure 9 shows the system safety energy efficiency versus the path loss between the RIS and the base station. Path loss being an important parameter in communication, it is obvious that a greater path loss causes the associated safe energy efficiency to gradually decrease. However, we can clearly notice from the figure that, for the same path loss parameter, the scheme with RIS is better than the scheme without RIS assistance. More importantly, our proposed scheme with phase-shift optimization for RIS is superior to the one with random phase-shift, which is due to the disordered nature of the random phase-shift of RIS, which appears to weaken the communication quality of the legitimate link. Overall, the simulation results demonstrate the superiority and necessity of our proposed scheme.