A Performance Simulation Methodology for a Whole Turboshaft Engine Based on Throughflow Modelling
Abstract
1. Introduction
2. Throughflow Simulation Methods
2.1. Throughflow Methods for Components
2.1.1. Turbo-Machinery Modeling
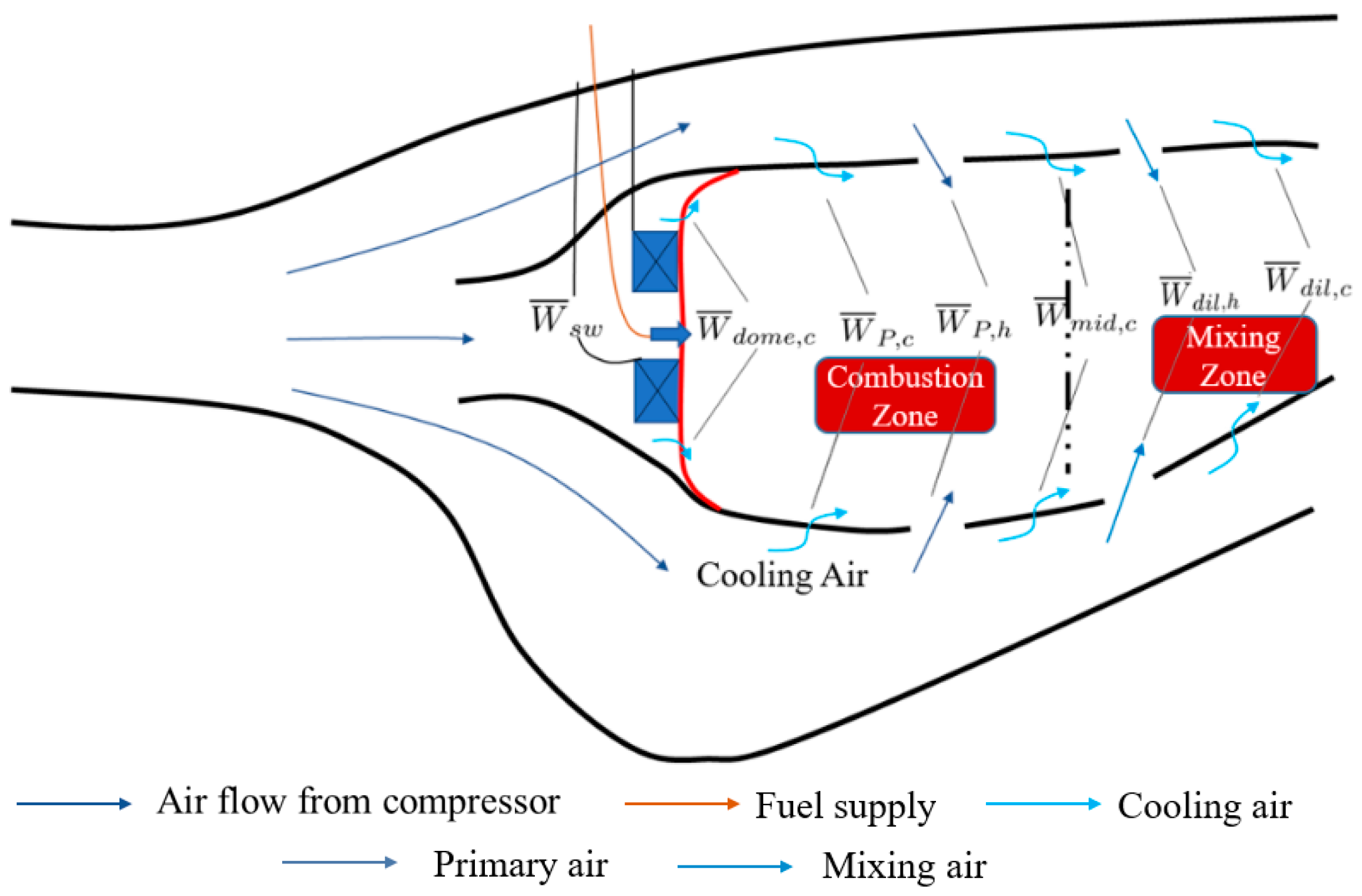
2.1.2. Combustor Modeling
- Retain the main structural characteristics of the flame tube and the main flow features in the flame tube, including swirler jets, primary hole jets, mixing hole jets, etc.;
- Maintain the flow distribution in the combustion zone and mixing zone;
- Neglect detailed processes such as fuel atomization and evaporation.
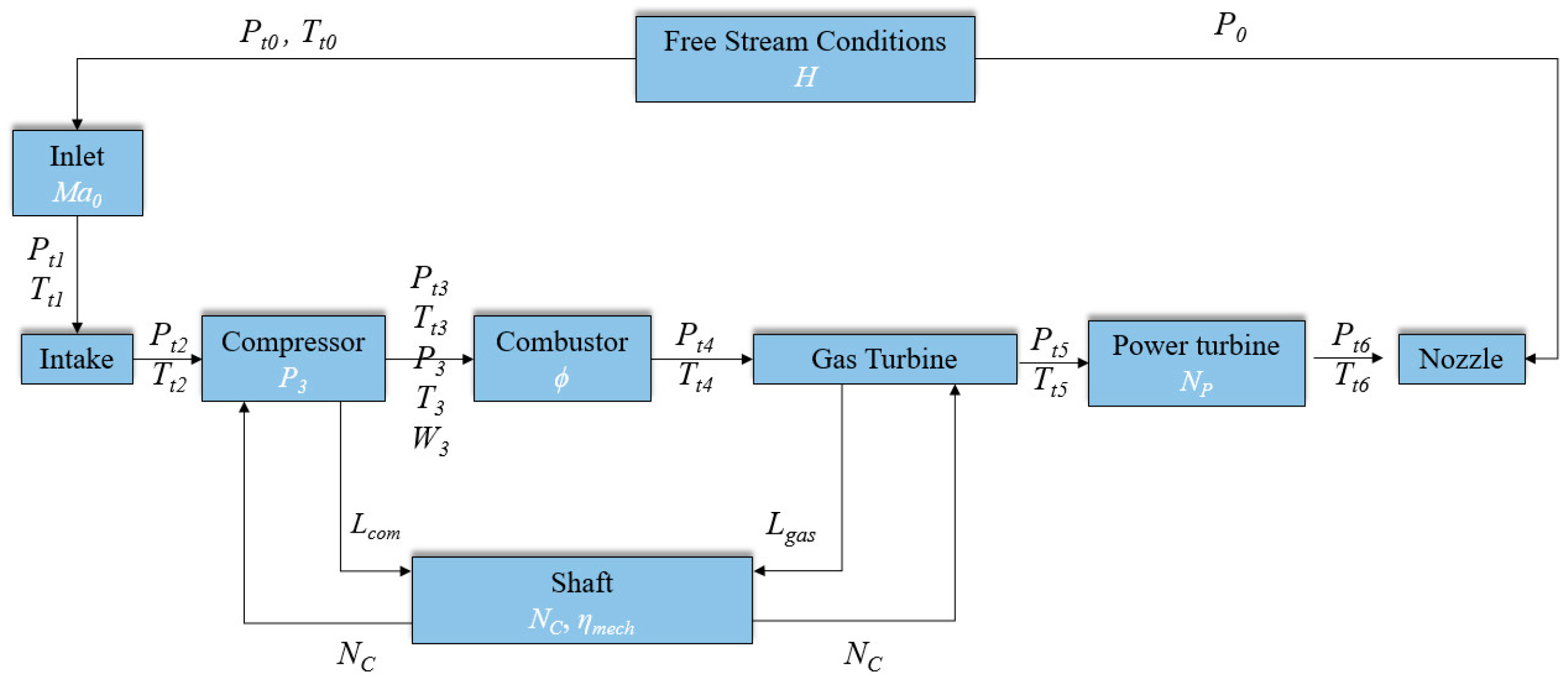
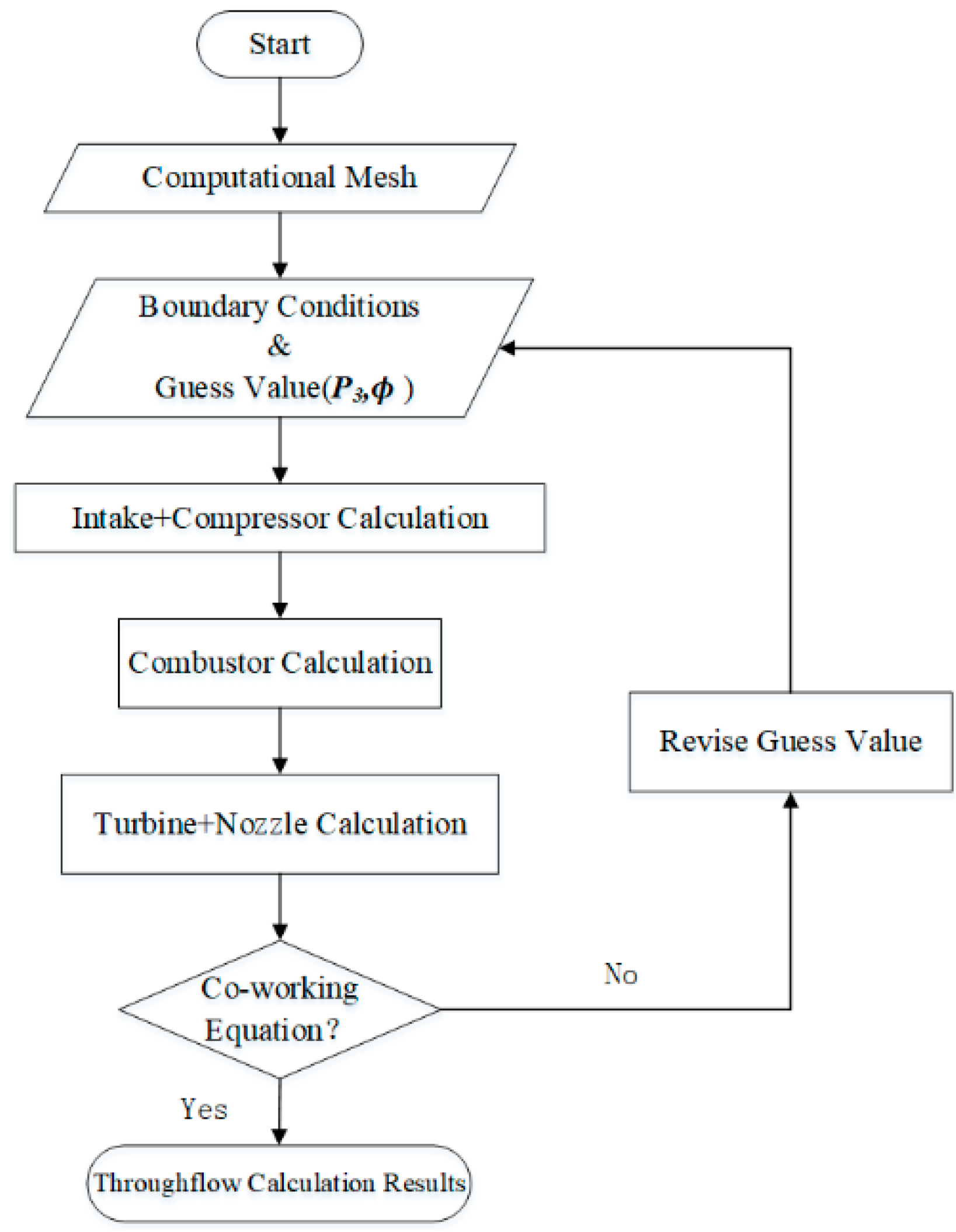
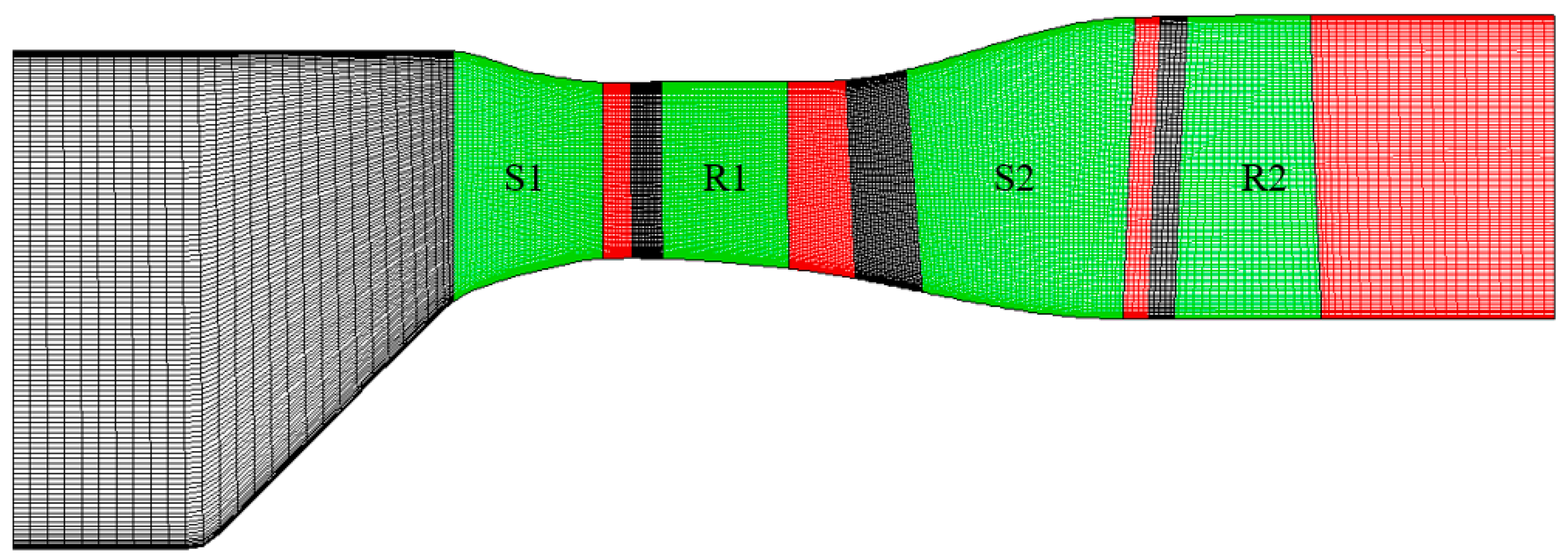
2.2. Whole Engine Simulation Platform
3. Component Validation Cases
3.1. P&W3S1 Axial Compressor
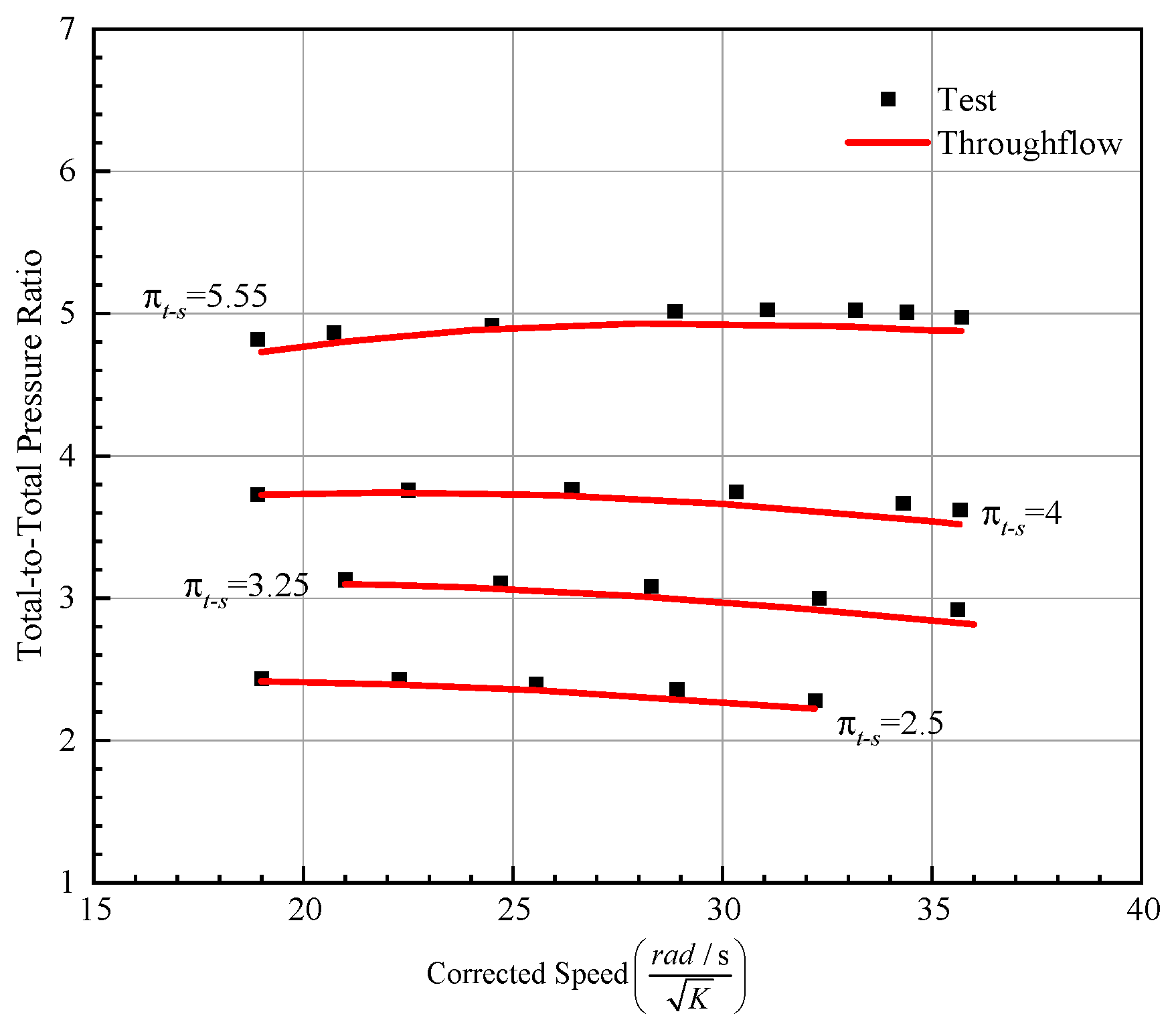
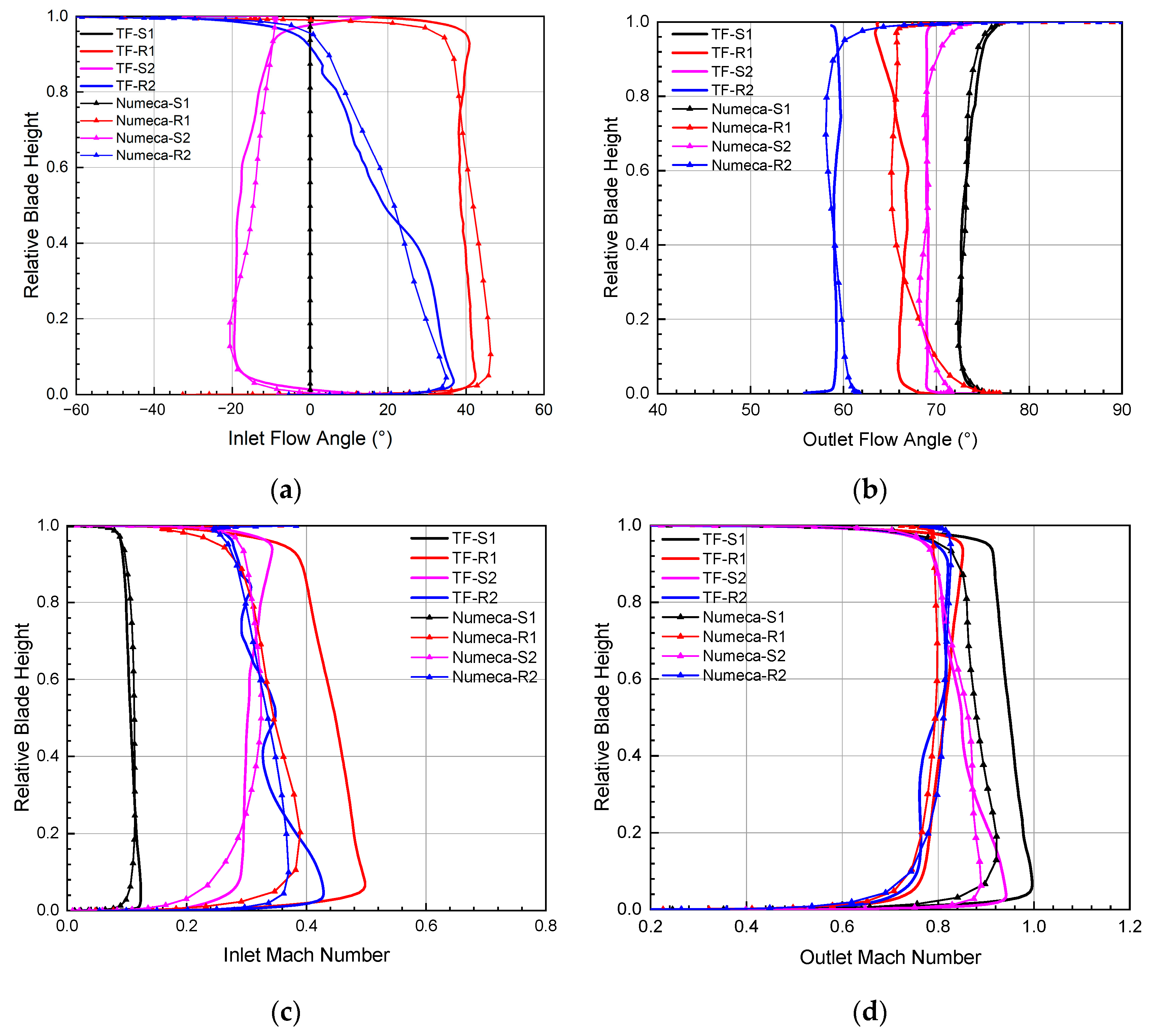
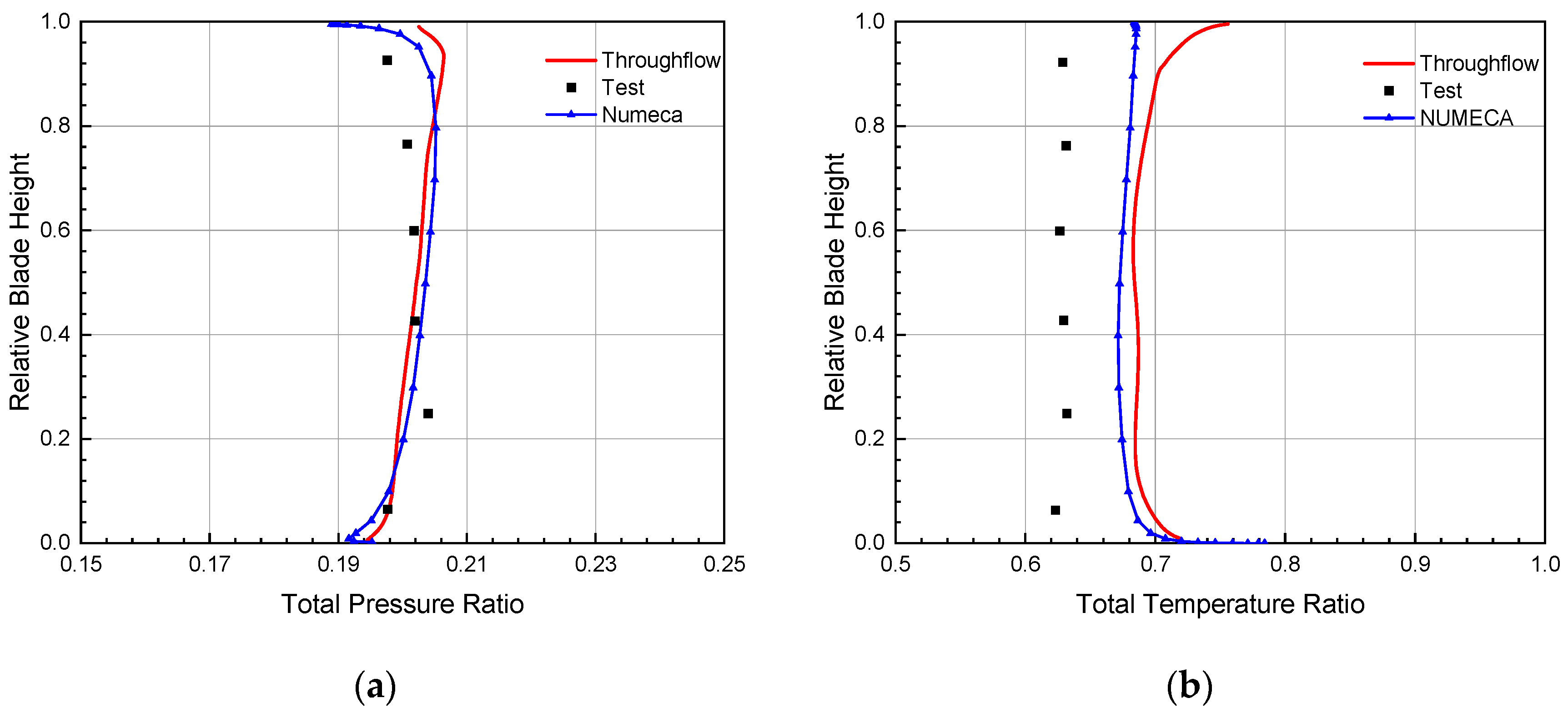
3.2. GE-EEE High-Pressure Turbine
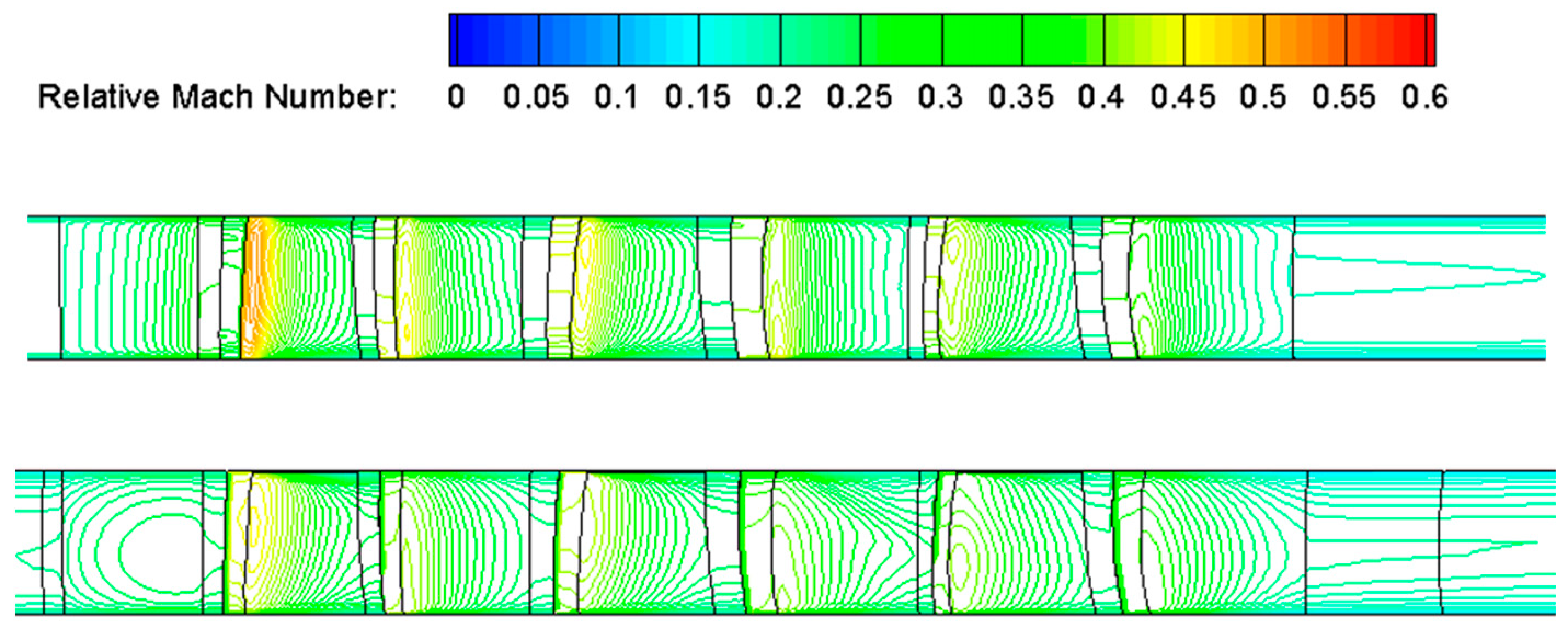
4. Whole Engine Validations Case
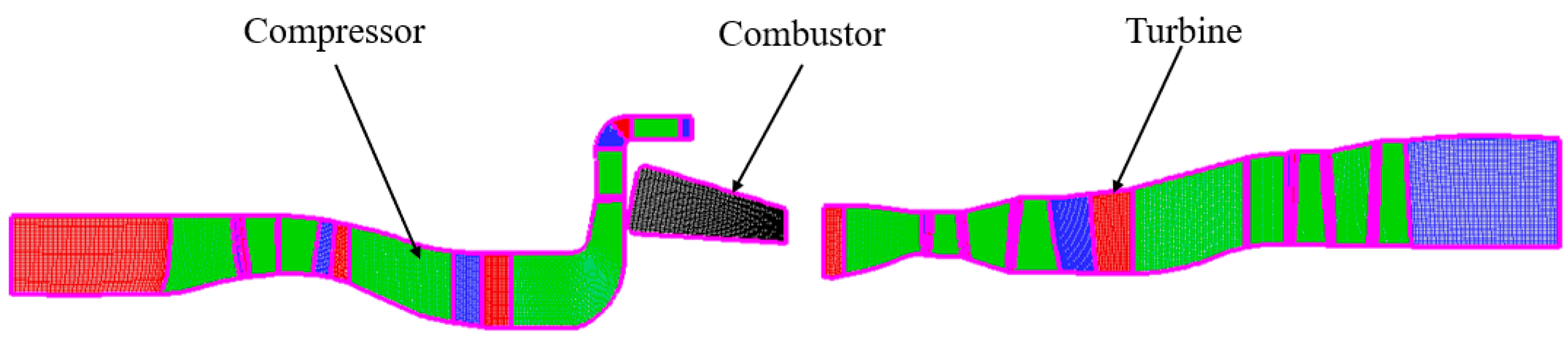
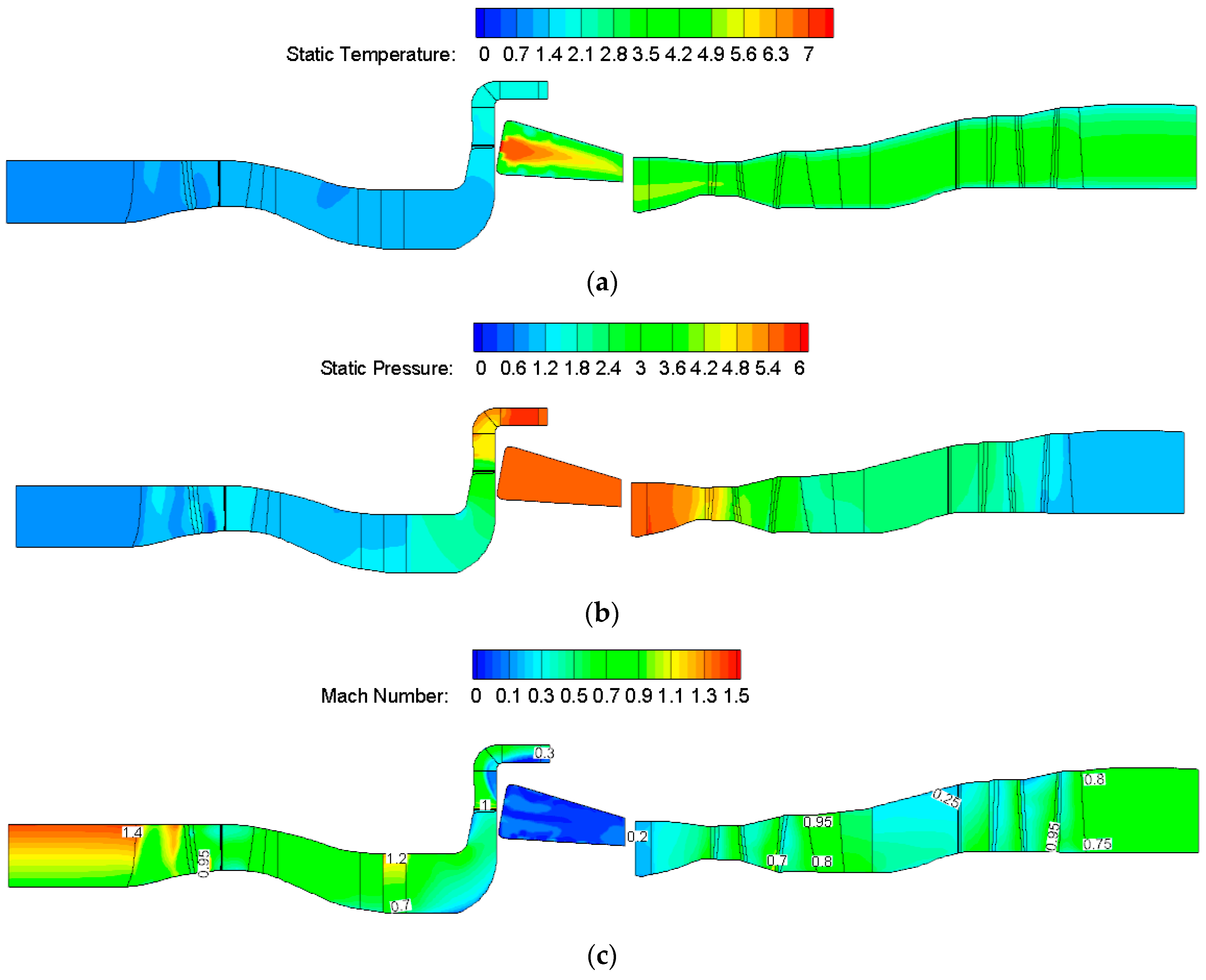
4.1. Case Background
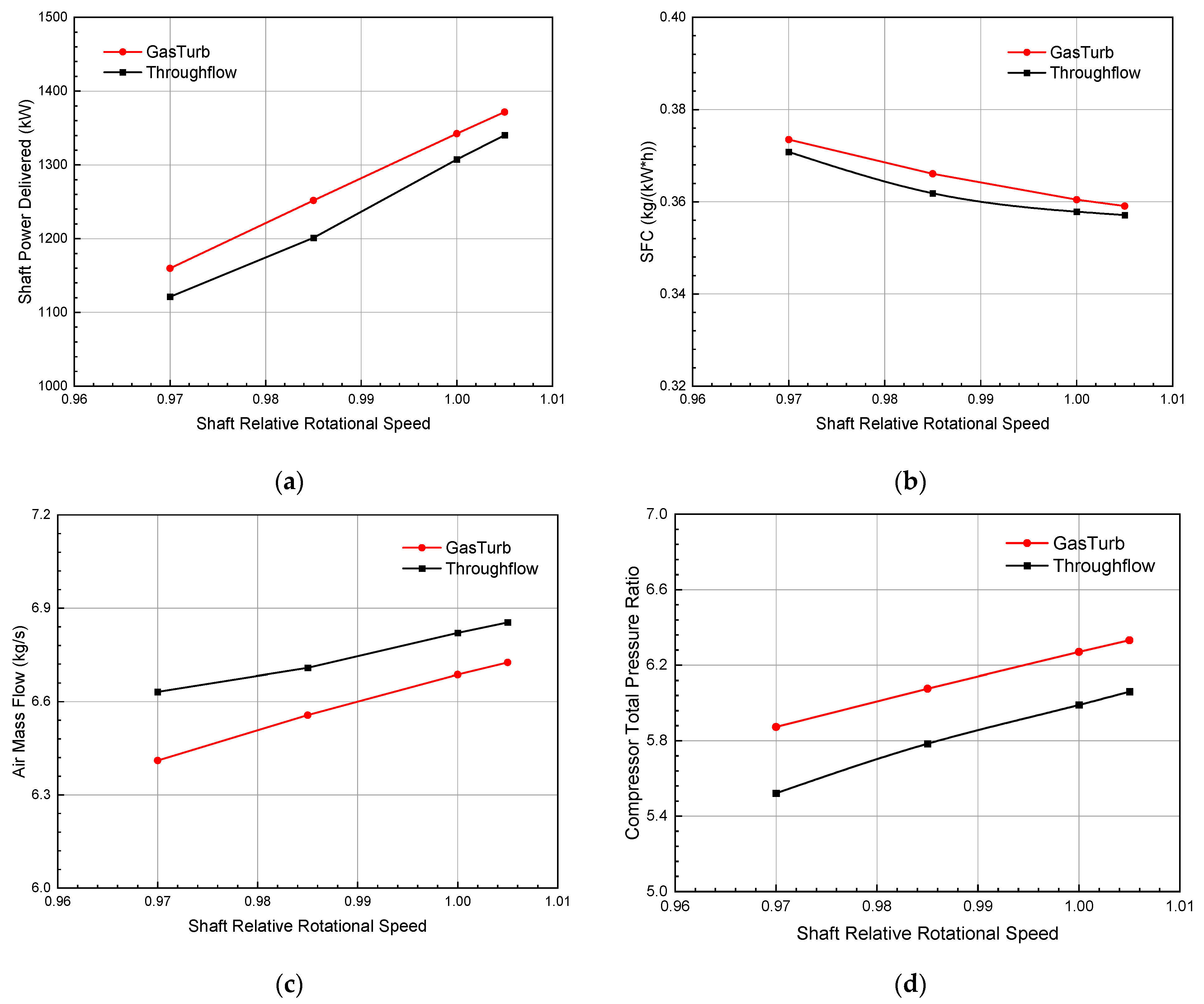
4.2. Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cao, J.G. Development Opportunities and Application Prospects of Aero-Engine Simulation Technology under Digital Transformation. J. Syst. Simul. 2021, 1, 1. (In Chinese) [Google Scholar] [CrossRef]
- Nichols, L.D.; Chamis, C.C. Numerical Propulsion System Simulation: An Interdisciplinary Approach. In Proceedings of the AIAA/NASA/OAI Conference on Advanced SEI Technologies, Cleveland, OH, USA, 4–6 September 1991. [Google Scholar]
- Homsi, P.; Tobias, L. VIVACE-Value Improvement through a Virtual Aeronautical Collaborative Enterprise; Technical Leaflet Final; VIVACE Public: Helsinki, Finland, 2007. [Google Scholar]
- Alexiou, A.; Tsalavoutas, T. Introduction to Gas Turbine Modelling with PROOSIS, 1st ed.; Empresarios Agrupados Internacional, S.A.: Madrid, Spain, 2011. [Google Scholar]
- Cao, J.G. Status, Challenges and Perspectives of Aero-Engine Simulation Technology. J. Propul. Techno. 2018, 39, 961–970. (In Chinese) [Google Scholar] [CrossRef]
- Wu, C.H. A General Theory of Three-Dimensional Flow in Subsonic and Supersonic Turbomachines of Axial-, Radial-, and Mixed-Flow Type; Technical Note; NASA: Washington, DC, USA, 1952.
- Hosseinimaab, S.M.; Tousi, A.M. A New Approach to Off-Design Performance Analysis of Gas Turbine Engines and Its Application. Energy Conv. Manag. 2021, 243, 114411. [Google Scholar] [CrossRef]
- Wen, Q.; Li, Y.J.; Liu, T.; Wei, G.; Fu, Q. Advances in the Research of 3D Full Engine Aerodynamics Simulation. Aerosp. Power 2021, 2, 46–51. (In Chinese) [Google Scholar]
- Teixeira, M.; Romagnosi, L.; Mezine, M.; Yannick, B.; Anker, J.; Claramunt, K.; Hirsch, C. A Methodology for Fully-Coupled CFD Engine Simulations, Applied to a Micro Gas Turbine Engine. In Proceedings of the ASME Turbo Expo 2018 Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Romagnosi, L.; Li, Y.C.; Mezine, M.; Teixeira, M.; Vilmin, S.; Anker, J.E.; Claramunt, K.; Baux, Y.; Hirsch, C. A Methodology for Steady and Unsteady Full-Engine Simulations. In Proceedings of the ASME Turbo Expo 2019 Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
- Pérez Arroyo, C.; Dombard, J.; Duchaine, F.; Gicquel, L.; Martin, B.; Odier, N.; Staffelbach, G. Towards the Large-Eddy Simulation of a Full Engine: Integration of a 360 Azimuthal Degrees Fan, Compressor and Combustion Chamber. Part I: Methodology and Initialisation. J. Glob. Power Propuls. Soc. 2020, 133115. [Google Scholar] [CrossRef] [PubMed]
- Pérez Arroyo, C.; Dombard, J.; Duchaine, F.; Gicquel, L.; Martin, B.; Odier, N.; Staffelbach, G. Towards the Large-Eddy Simulation of a Full Engine: Integration of a 360 Azimuthal Degrees Fan, Compressor and Combustion Chamber. Part II: Comparison Against Stand-Alone Simulations. J. Glob. Power Propuls. Soc. 2020, 133116. [Google Scholar] [CrossRef]
- Ricci, M.; Pacciani, R.; Marconcini, M. The exploitation of CFD legacy for the meridional analysis and design of modern gas and steam turbines. In Proceedings of the E3S Web of Conferences, Virtual Event, 15–16 September 2020. [Google Scholar] [CrossRef]
- Nigmatullin, R.Z.; Ivanov, M.J. The Mathematical Models of Flow Passage for Gas Turbine Engines and Their Components. In Proceedings of the AGARD Lecture Series, Paris, France, 15–16 December 1994. [Google Scholar]
- Stewart, E.M. Axisymmetric Aerodynamic Numerical Analysis of a Turbofan Engine. In Proceedings of the ASME 1995 International Gas Turbine and Aeroengine Congress and Exposition, Houston, TX, USA, 5–8 June 1995. [Google Scholar] [CrossRef]
- Petrovic, M.V.; Ahmed, A.-R.; Wiedermann, A. A Quick Method for Full Flange-to-Flange Industrial Gas Turbine Analysis Based on Through-Flow Modelling. J. Gas. Propuls. Power 2015, 8, 9–18. [Google Scholar] [CrossRef]
- Wiedermann, A.; Petrovic, M.V. Through-Flow Modeling of Single- and Two-Shaft Gas Turbines at Wide Operating Range. In Proceedings of the ASME Turbo Expo 2018 Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Petkovic, D.; Banjac, M.; Milic, S.; Petrovic, M.V.; Wiedermann, A. Modeling the Transient Behavior of Gas Turbines. J. Turbomach. 2020, 142, 081005. [Google Scholar] [CrossRef]
- Yang, C.; Wu, H.; Du, J.; Zhang, H.W.; Yang, J.G. Full-Engine Simulation of Micro Gas Turbine Based on Time-Marching Throughflow Method. Appl. Therm. Eng. 2022, 217, 119213. [Google Scholar] [CrossRef]
- Yang, C.; Wu, H.; Du, J.; Zhang, H.W.; Yang, J.G. Numerical Study on Throughflow Simulation of Components and Full Engine of Aero-Engine. J. Eng. Thermophys. 2023, 44, 894–902. (In Chinese) [Google Scholar]
- Liu, X.H.; Zhou, C.H.; Song, M.X.; Jin, D.H.; Gui, X.M. Overall Simulation of a Turbojet Engine Based on Throughflow Modeling. Acta Aeronaut. Astronaut. Sin. 2020, 41, 123199. (In Chinese) [Google Scholar]
- Dawes, W.N. Toward Improved Throughflow Capability: The Use of Three-Dimensional Viscous Flow Solvers in a Multistage Environment. J. Turbomach. Trans. ASME 1992, 114, 8–17. [Google Scholar] [CrossRef]
- Simon, J.F. Contribution to Throughflow Modelling for Axial Flow Turbomachines. Ph.D. Thesis, University of Liege, Liege, Belgium, 2007. [Google Scholar]
- Yang, X.F. Analysis and Design of Combined Compressor with Throughflow Model. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2016. (In Chinese). [Google Scholar]
- Zhu, L.S.; Zhang, S.; Ge, N. Application Research of Two Different Turbulence Models in Through-Flow Calculation. J. Propul. Techno. 2021, 42, 1223–1234. (In Chinese) [Google Scholar] [CrossRef]
- Hou, K.X. Research on Numerical Simulation of Reactive Flow in Combustor with Detailed Chemical Kinetic. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2007. (In Chinese). [Google Scholar]
- Jin, H.L.; Jin, D.H.; Li, X.J.; Gui, X.M. A Time-marching Throughflow Model and Its Application in Transonic Axial Compressor. J. Therm. Sci. 2010, 19, 519–525. [Google Scholar] [CrossRef]
- Horlock, J.H. On Entropy Production in Adiabatic Flow in Turbomachines. J. Basic Eng. 1971, 93, 587–593. [Google Scholar] [CrossRef]
- Wright, P.I.; Miller, D.C. An Improved Compressor Performance Prediction Model; Rolls-Royce Report; Rolls-Royce Ltd.: Manchester, UK, 1991. [Google Scholar]
- Dunham, J. Compressor Off-Design Performance Prediction Using an Endwall Model. In Proceedings of the ASME 1996 International Gas Turbine and Aeroengine Congress and Exhibition, Birmingham, UK, 10–13 June 1996. [Google Scholar] [CrossRef]
- Wiesner, F.J. A Review of Slip Factors for Centrifugal Impellers. J. Eng. Power 1967, 89, 558–566. [Google Scholar] [CrossRef]
- Zhu, J.Q.; Sjolander, S.A. Improved Profile Loss and Deviation Correlations for Axial-turbine Blade Rows. In Proceedings of the GT2005 ASME Turbo Expo 2005: Power for Land, Sea and Air, Reno-Tahoe, NV, USA, 6–9 June 2005. [Google Scholar]
- Kacker, S.C.; Okapuu, U. A Mean Line Prediction Method for Axial Flow Turbine Efficiency. J. Eng. Power 1982, 104, 111–119. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications, 3rd ed.; Hayton, J., Ed.; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar] [CrossRef]
- Baldwin, B.S.; Lomax, H. Thin Layer Approximation and Algebraic Model for Separated Turbulent Flows. In Proceedings of the AIAA 16th Aerospace Sciences Meeting, Huntsville, AL, USA, 16–18 January 1978. [Google Scholar] [CrossRef]
- Gatlin, B. An Implicit, Upwind Method for Obtaining Symbiotic Solutions to the Thin-Layer Navier-Stokes Equations. Ph.D. Thesis, Mississippi State University, Starkville, MS, USA, 1987. [Google Scholar]
- Chen, J.P. Unsteady Three-Dimensional Thin Layer Navier-Stokes Solutions for Turbomachinery in Transonic Flow. Ph.D. Thesis, Mississppi State University, Starkville, MS, USA, 1991. [Google Scholar]
- Degani, D.; Schiff, L.B. Computation of Turbulent Supersonic Flows around Pointed Bodies Having Crossflow Separation. J. Comput. Phys. 1986, 66, 173–196. [Google Scholar] [CrossRef]
- Hamer, A.; Roby, R.J. CFD Modeling of a Gas Turbine Combustor Using Reduced Chemical Kinetic Mechanisms. In Proceedings of the 33rd Joint Propulsion Conference and Exhibit, Seattle, WA, USA, 6–9 July 1997. [Google Scholar] [CrossRef]
- Yan, Y.W.; Song, S.W.; Hu, H.S.; Wang, Y.Y.; Lei, Y.B.; Zhao, J.X.; Lin, Z.Y. Numerical Investigations of Two-Phase Spray Combustion Flow Fields in Slinger Annular Combustor. J. Aerosp. Power 2011, 26, 1003–1010. (In Chinese) [Google Scholar] [CrossRef]
- Xu, R.; Li, J.H.; Zhao, J.X.; Liu, Y.; Wang, S.F. Effects of Turbulent Combustion Models on Spray Combustion Flow of Dual-Stage Swirl Combustor. J. Propuls. Technol. 2013, 34, 375–382. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, J.X. An Analytical Design Methodology for an Annular Combustor. Int. J. Comput. Fluid Dyn. 1995, 5, 231–243. [Google Scholar] [CrossRef]
- Hoffmann, N.; Markatos, N.C. Thermal Radiation Effects on Fires in Enclosures. Appl. Math. Model. 1988, 12, 129–140. [Google Scholar] [CrossRef]
- Amano, R.S. Development of a Turbulence Near-Wall Model and Its Application to Separated and Reattached Flows. Numer. Heat Transf. 1984, 7, 59–75. [Google Scholar] [CrossRef]
- Burdsall, E.A.; Canal, E., Jr.; Lyons, K.A. Core Compressor Exit Stage Study-I Aerodynamic and Mechanical Design; NASA Lewis Research Center: Cleveland, OH, USA, 1979.
- Behlke, R.F.; Burdsall, E.A.; Canal, E., Jr.; Korn, N.D. Core Compressor Exit Stage Study-II Final Report; NASA Lewis Research Center: Cleveland, OH, USA, 1979.
- Timko, L.P. Energy Efficient Engine High Pressure Turbine Component Test Performance Report; NASA Lewis Research Center: Cleveland, OH, USA, 1990.
- Kurzke, J.; Halliwell, I. Propulsion and Power: An Exploration of Gas Turbine Performance Modeling, 1st ed.; Springer International Publish: Cham, Switzerland, 2018; pp. 213–247. [Google Scholar] [CrossRef]


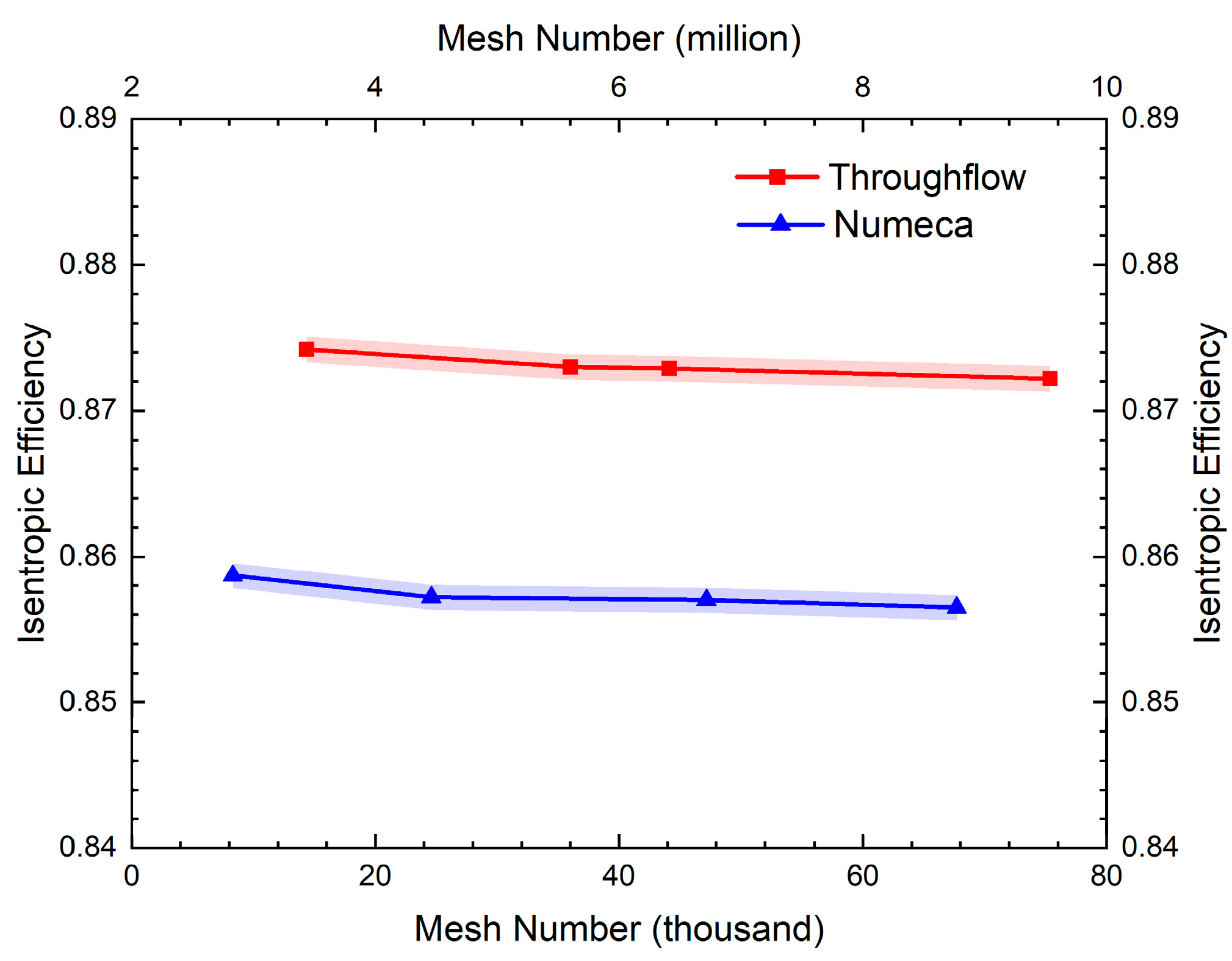
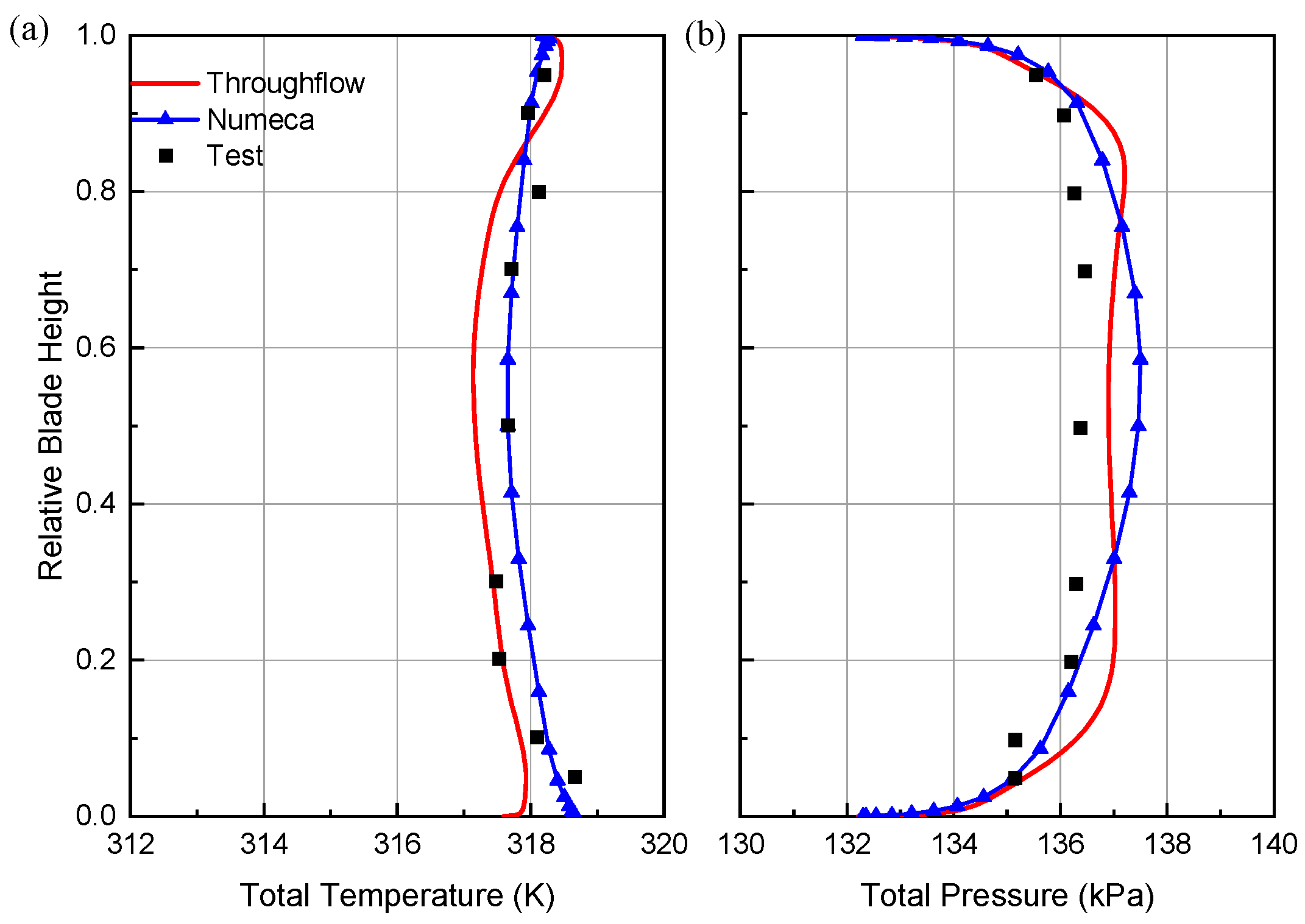
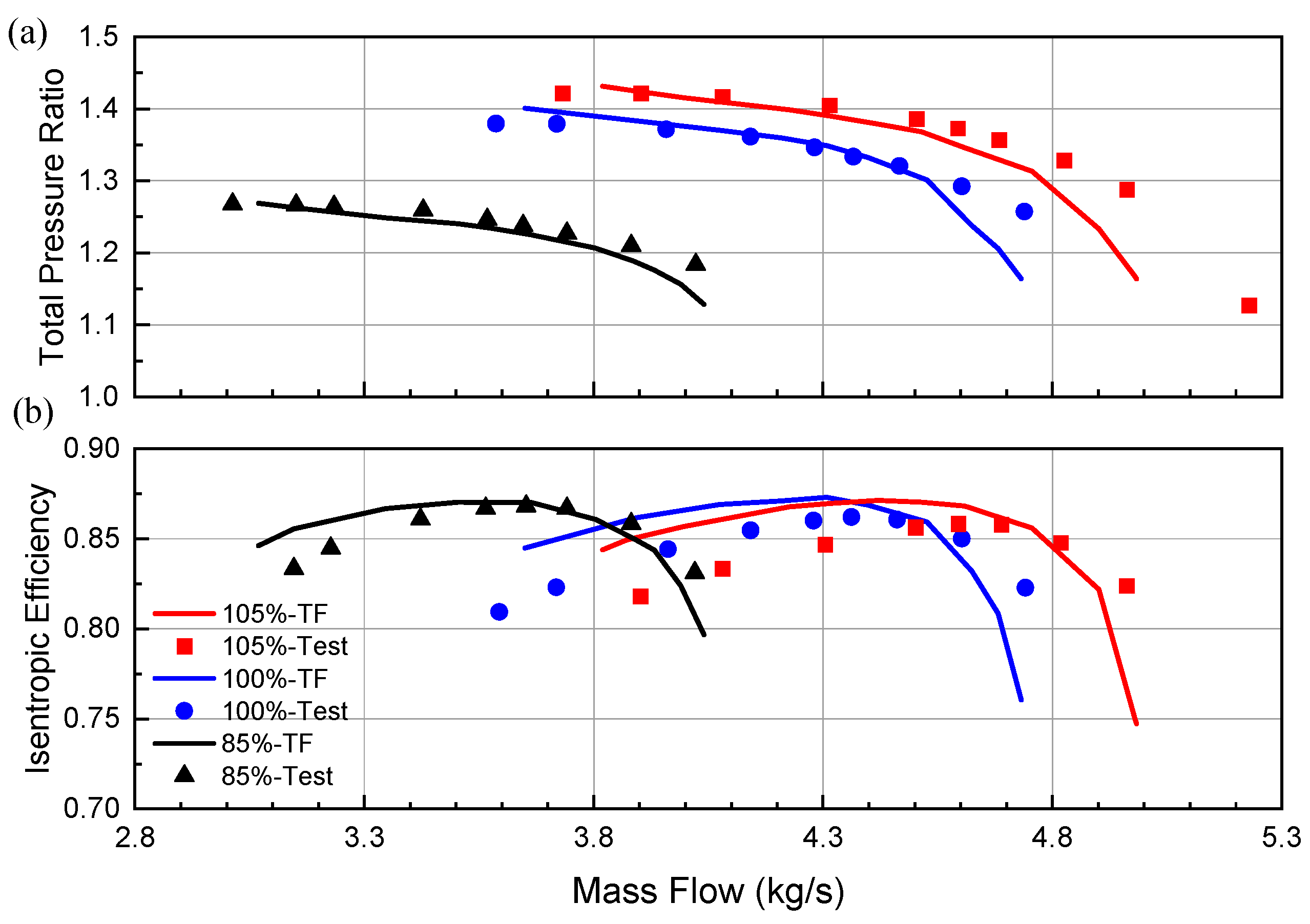

| Parameter | Experiment [46] | Throughflow | Numeca |
|---|---|---|---|
| Mass flow (kg/s) | 4.28 | 4.308 | 4.307 |
| Total pressure ratio | 1.346 | 1.349 | 1.347 |
| Isentropic efficiency | 0.861 | 0.873 | 0.8572 |
| Total temperature ratio | / | 1.102 | 1.1036 |
| Mass Flow (kg/s) | Expansion Ratio | Isentropic Efficiency | |
|---|---|---|---|
| Throughflow | 11.91 | 4.944 | 0.9317 |
| Numeca | 12.01 | 4.938 | 0.9213 |
| Error (%) | 0.8 | 0.2 | 1.16 |
| Zone | Cell Count |
|---|---|
| Compressor | 507 × 41 |
| Combustor | 41 × 41 |
| Turbine | 525 × 41 |
| Working Condition | Engine Speed |
|---|---|
| Maximum emergency | 1.005 |
| Maximum power rating | 1.0 |
| Intermediate emergency | 0.985 |
| Maximum continuous condition | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Ma, A.; Zhang, T.; Ge, N.; Huang, X. A Performance Simulation Methodology for a Whole Turboshaft Engine Based on Throughflow Modelling. Energies 2024, 17, 494. https://doi.org/10.3390/en17020494
Zhang S, Ma A, Zhang T, Ge N, Huang X. A Performance Simulation Methodology for a Whole Turboshaft Engine Based on Throughflow Modelling. Energies. 2024; 17(2):494. https://doi.org/10.3390/en17020494
Chicago/Turabian StyleZhang, Shuo, Aotian Ma, Teng Zhang, Ning Ge, and Xing Huang. 2024. "A Performance Simulation Methodology for a Whole Turboshaft Engine Based on Throughflow Modelling" Energies 17, no. 2: 494. https://doi.org/10.3390/en17020494
APA StyleZhang, S., Ma, A., Zhang, T., Ge, N., & Huang, X. (2024). A Performance Simulation Methodology for a Whole Turboshaft Engine Based on Throughflow Modelling. Energies, 17(2), 494. https://doi.org/10.3390/en17020494








