Direct Air Cooling of Pipe-Type Transmission Cable for Ampacity Enhancement: Simulations and Experiments
Abstract
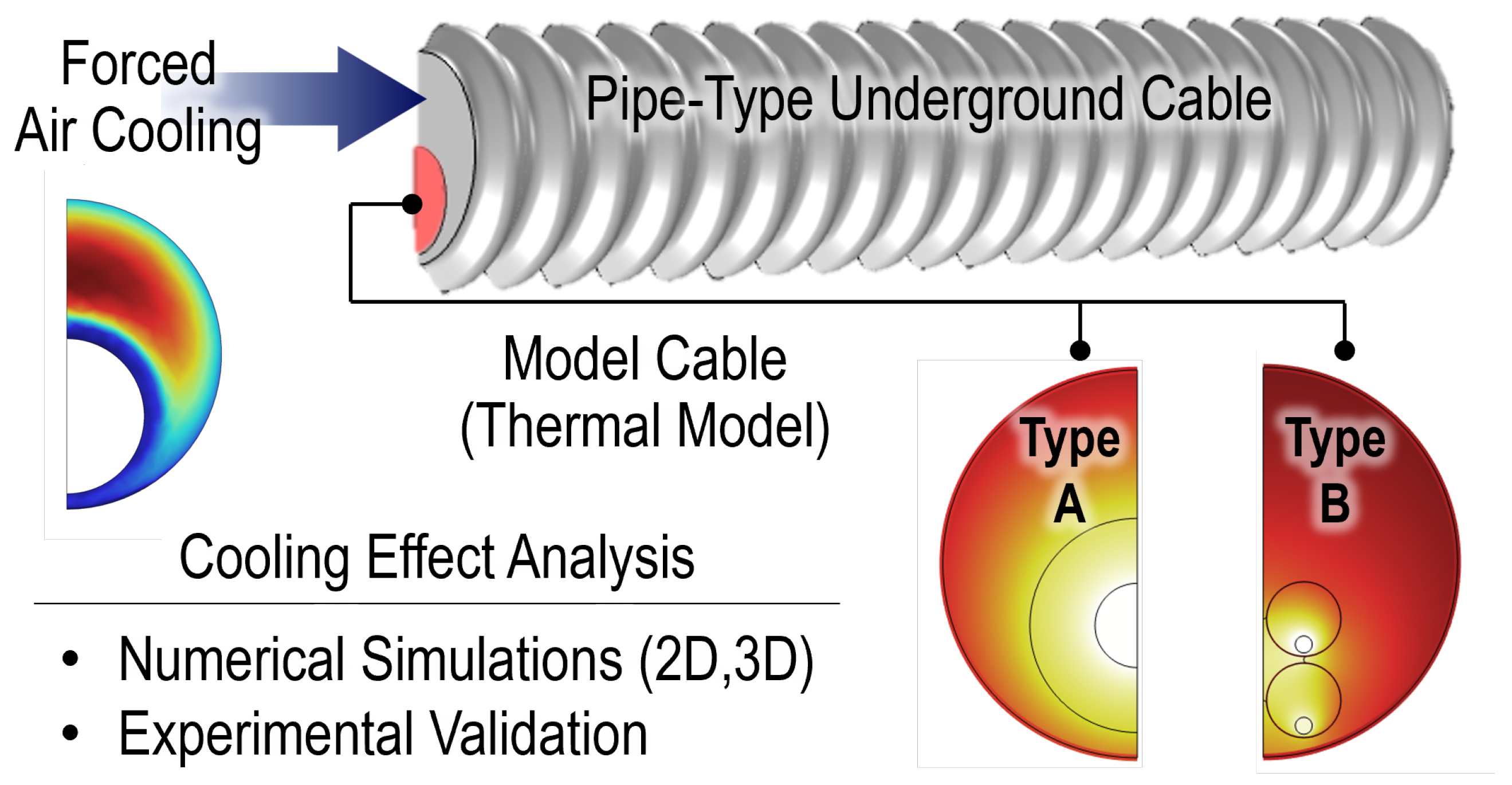
1. Introduction
2. Forced Air Cooling System
3. Numerical Simulations
3.1. Modeling and Simulation Details
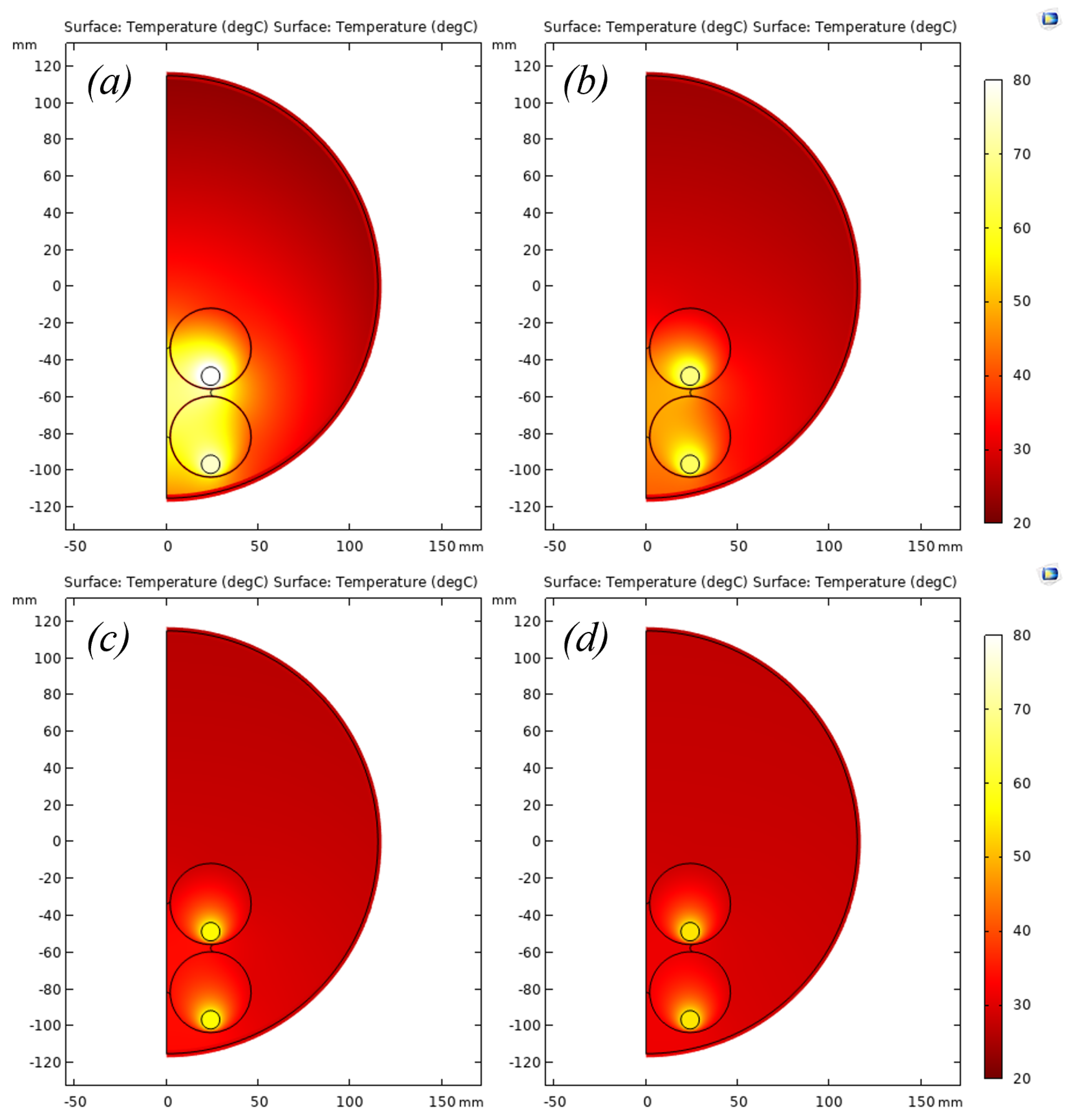
3.2. Simulation Result and Discussion
4. Experimental Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kwasiborska, A.; Stelmach, A.; Jabłońska, I. Quantitative and Comparative Analysis of Energy Consumption in Urban Logistics Using Unmanned Aerial Vehicles and Selected Means of Transport. Energies 2023, 16, 6467. [Google Scholar] [CrossRef]
- Lai, C.M.; Teh, J. Comprehensive review of the dynamic thermal rating system for sustainable electrical power systems. Energy Rep. 2022, 8, 3263–3288. [Google Scholar]
- Juan, A.A.; Ammouriova, M.; Tsertsvadze, V.; Osorio, C.; Fuster, N.; Ahsini, Y. Promoting Energy Efficiency and Emissions Reduction in Urban Areas with Key Performance Indicators and Data Analytics. Energies 2023, 16, 7195. [Google Scholar]
- Xu, X.B.; Liu, G. Investigation of the magnetic field produced by unbalanced phase current in an underground three-phase pipe-type cable. Electr. Power Syst. Res. 2002, 62, 153–160. [Google Scholar] [CrossRef]
- Li, B.; Ding, Y.; Du, Y.; Chen, M. Stable thin-wire model of buried pipe-type power distribution cables for 3D FDTD transient simulation. IET Gener. Transm. Distrib. 2020, 14, 6168–6178. [Google Scholar] [CrossRef]
- Brignone, M.; Mestriner, D.; Molfino, P.; Nervi, M.; Marzinotto, M.; Patti, S. The Mitigation of Interference on Underground Power Lines Caused by the HVDC Electrode. Energies 2023, 16, 7769. [Google Scholar] [CrossRef]
- De León, F. Major factors affecting cable ampacity. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; pp. 1–6. [Google Scholar]
- Xiao, R.; Liang, Y.; Fu, C.; Cheng, Y. Rapid calculation model for transient temperature rise of complex direct buried cable cores. Energy Rep. 2023, 9, 306–313. [Google Scholar] [CrossRef]
- Ratchapan, R.; Kongjeen, Y.; Plangklang, B. Ampacity Analysis of Low Voltage Underground Cables in Different Conduits. In Proceedings of the 2021 9th International Electrical Engineering Congress (iEECON), Pattaya, Thailand, 10–12 March 2021; pp. 25–28. [Google Scholar]
- Al-Dulaimi, A.A.; Güneşer, M.T.; Hameed, A.A. Investigation of thermal modeling for underground cable ampacity under different conditions of distances and depths. In Proceedings of the 2021 5th International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 21–23 October 2021; pp. 654–659. [Google Scholar]
- Ocłoń, P.; Pobędza, J.; Walczak, P.; Cisek, P.; Vallati, A. Experimental validation of a heat transfer model in underground power cable systems. Energies 2020, 13, 1747. [Google Scholar] [CrossRef]
- Xu, X.; Yuan, Q.; Sun, X.; Hu, D.; Wang, J. Simulation analysis of carrying capacity of tunnel cable in different laying ways. Int. J. Heat Mass Transf. 2019, 130, 455–459. [Google Scholar]
- Che, C.; Yan, B.; Fu, C.; Li, G.; Qin, C.; Liu, L. Improvement of cable current carrying capacity using COMSOL software. Energy Rep. 2022, 8, 931–942. [Google Scholar]
- Kim, J.G.; Sohn, S.H.; Lim, J.H.; Shim, M.J.; Lee, M. Numerical study on the ampacity enhancement of pipe-type underground transmission cable through the thermal interface material. Trans. Korean Soc. Mech. Eng. 2024, 48. [Google Scholar]
- Hayashi, M.; Uchida, K.; Kumai, W.; Sanjo, K.; Mitani, M.; Ichiyanagi, N.; Goto, T. Development of water pipe cooling system for power cables in tunnels. IEEE Trans. Power Deliv. 1989, 4, 863–872. [Google Scholar] [CrossRef]
- Kumai, W.; Hashimoto, I.; Ohsawa, S.; Mitani, M.; Matsuda, Y. Completion of high-efficiency water pipe cooling system for underground transmission line. IEEE Trans. Power Deliv. 1994, 9, 585–590. [Google Scholar]
- Joyce, R.; Lloyd, S. Indirect pipe water cooling study for a 220 kV underground XLPE cable system in New Zealand. In Proceedings of the International Conference on Insulated Power Cables, Paris, France, 21–25 June 2015; pp. 1–6. [Google Scholar]
- Wei, Y.; Liu, M.; Li, X.; Li, G.; Li, N.; Hao, C.; Lei, Q. Effect of temperature on electric-thermal properties of semi-conductive shielding layer and insulation layer for high-voltage cable. High Volt. 2021, 6, 805–812. [Google Scholar]
- Berger, S.A.; Talbot, L.; Yao, L.S. Flow in curved pipes. Annu. Rev. Fluid Mech. 1983, 15, 461–512. [Google Scholar]
- Farshad, F.F.; Rieke, H.H. Surface-roughness design values for modern pipes. SPE Drill. Complet. 2006, 21, 212–215. [Google Scholar] [CrossRef]
- Konrad, K. Dense-phase pneumatic conveying through long pipelines: Effect of significantly compressible air flow on pressure drop. Powder Technol. 1986, 48, 193–203. [Google Scholar] [CrossRef]
- Lee, M.; Zhu, Y.; Li, L.K.B.; Gupta, V. System identification of a low-density jet via its noise-induced dynamics. J. Fluid Mech. 2019, 862, 200–215. [Google Scholar]
- Park, S.; Lee, M. A semi-supervised framework for analyzing the potential core of a low-density jet. Flow Meas. Instrum. 2024, 95, 102516. [Google Scholar] [CrossRef]
- Olsen, R.; Anders, G.J.; Holboell, J.; Gudmundsdóttir, U.S. Modelling of dynamic transmission cable temperature considering soil-specific heat, thermal resistivity, and precipitation. IEEE Trans. Power Deliv. 2013, 28, 1909–1917. [Google Scholar] [CrossRef]
- Ocłoń, P.; Cisek, P.; Pilarczyk, M.; Taler, D. Numerical simulation of heat dissipation processes in underground power cable system situated in thermal backfill and buried in a multilayered soil. Energy Convers. Manag. 2015, 95, 352–370. [Google Scholar] [CrossRef]








| Item | Material | Diameter (in) | Thickness | Thermal Conductivity |
|---|---|---|---|---|
| Conductor (Type A) | Copper | 50 mm | - | 400 W/m·K |
| Conductor (Type B) | Copper | 5 mm | - | 400 W/m·K |
| Inner Pipe (Type A) | PVC | 127 mm | 2.0 mm | 0.4 W/m·K |
| Inner Pipe (Type B) | PVC | 44 mm | 1.0 mm | 0.4 W/m·K |
| Insulator | XLPE | 50 mm | 38.5 mm | 0.28 W/m·K |
| Outer Pipe | PVC | 230 mm | 4 mm | 0.4 W/m·K |
| Metallic Sheath * | Al | 98 mm | 2.6 mm | 237 W/m·K |
| Inner SC Layer * | Polymer | 55 mm | 2.0 mm | 0.60–0.85 W/m·K |
| Outer SC Layer * | Polymer | 80 mm | 1.0 mm | 0.60–0.85 W/m·K |
| q | I | T | |
|---|---|---|---|
| 0 m/s | 18.67 W/m (100%) | 100% | 41.5 C |
| 1 m/s | 23.93 W/m (128%) | 113% | 36.8 C |
| 5 m/s | 29.68 W/m (159%) | 126% | 34.2 C |
| 10 m/s | 30.92 W/m (165%) | 128% | 34.1 C |
| q | I | T | |
|---|---|---|---|
| 0 m/s | 14.01 W/m (100%) | 100% | 34.4 C |
| 1 m/s | 18.12 W/m (129%) | 114% | 30.8 C |
| 5 m/s | 22.54 W/m (161%) | 127% | 30.1 C |
| 10 m/s | 23.59 W/m (163%) | 128% | 30.3 C |
| L | ||
|---|---|---|
| 20 C | 0 m/s (natural) | 11.1 m |
| 1 m/s (forced) | 11.8 m | |
| 5 m/s (forced) | 10.3 m | |
| 10 C | 1 m/s (forced) | 40.2 m |
| 5 m/s (forced) | 75.0 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.-K.; Kang, Y.-W.; Jo, H.-R.; Kim, J.G.; Lee, M. Direct Air Cooling of Pipe-Type Transmission Cable for Ampacity Enhancement: Simulations and Experiments. Energies 2024, 17, 478. https://doi.org/10.3390/en17020478
Kim D-K, Kang Y-W, Jo H-R, Kim JG, Lee M. Direct Air Cooling of Pipe-Type Transmission Cable for Ampacity Enhancement: Simulations and Experiments. Energies. 2024; 17(2):478. https://doi.org/10.3390/en17020478
Chicago/Turabian StyleKim, Dong-Kyu, Yeon-Woog Kang, Hye-Rin Jo, Jin Geon Kim, and Minwoo Lee. 2024. "Direct Air Cooling of Pipe-Type Transmission Cable for Ampacity Enhancement: Simulations and Experiments" Energies 17, no. 2: 478. https://doi.org/10.3390/en17020478
APA StyleKim, D.-K., Kang, Y.-W., Jo, H.-R., Kim, J. G., & Lee, M. (2024). Direct Air Cooling of Pipe-Type Transmission Cable for Ampacity Enhancement: Simulations and Experiments. Energies, 17(2), 478. https://doi.org/10.3390/en17020478






