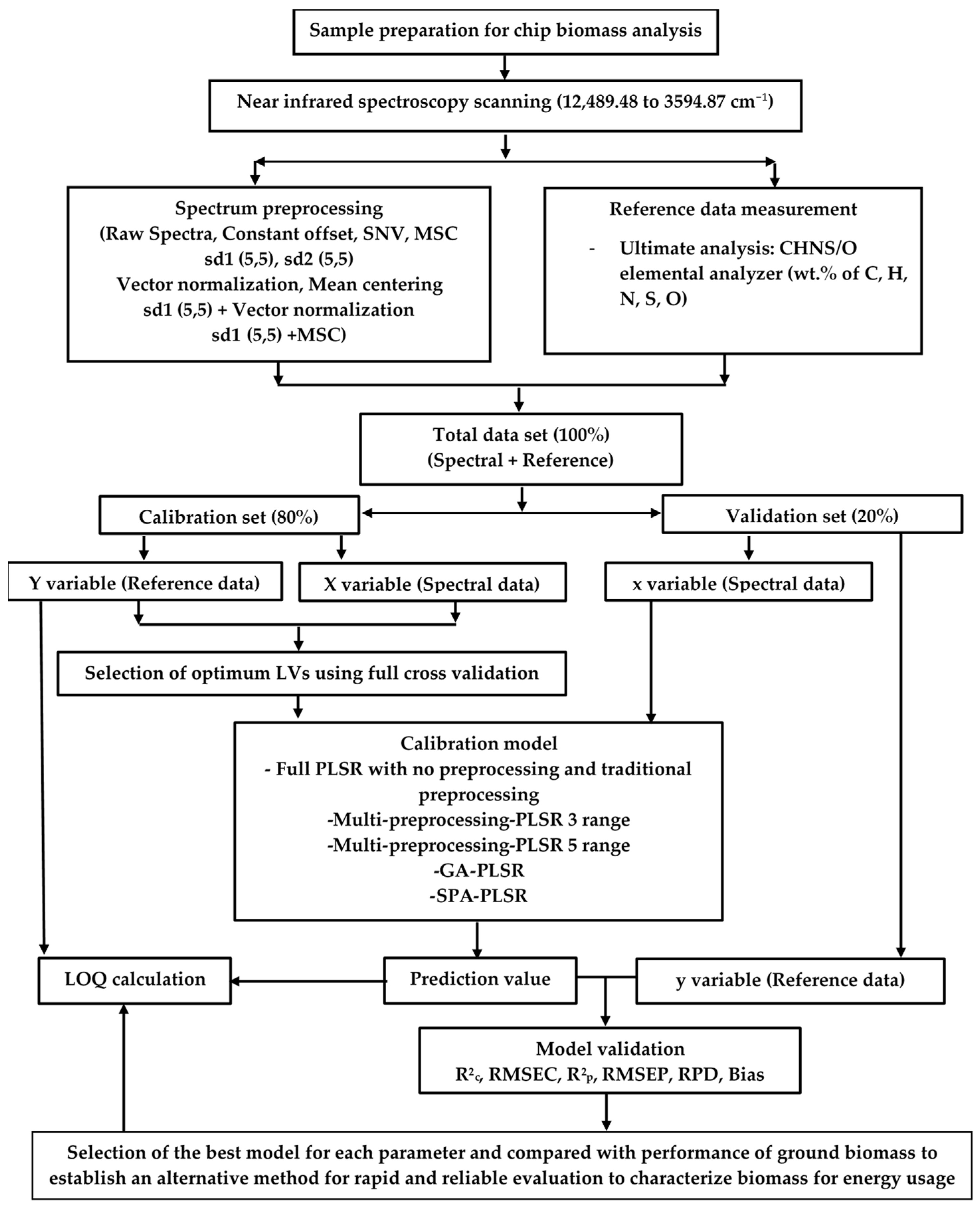
1. Introduction
The world is undergoing a significant transition away from fossil fuels, embracing modern renewable energy technologies to meet its escalating energy needs and demands. Bioenergy, derived from sources such as woody biomass, agricultural residues, and organic materials and waste, is pivotal in this paradigm shift, constituting the largest share (two–thirds) of global renewable energy utilization [
1]. It is anticipated that bioenergy will continue to have a decisive share in future net zero emission scenarios and that its contribution to energy supply will further increase. This transition underscores the growing significance of biomass energy within the global energy landscape. However, it is worth noting that billions of people still rely on the inefficient use of traditional biomass for cooking and heating [
1]. The combustion of biomass produces air pollutants similar to those emitted by fossil fuels, with the exception of sulfur oxides [
2]. Furthermore, research has shown that the health impacts attributed to emissions from biomass and wood combustion can be more harmful than those from fossil fuels [
3]. These emissions primarily result from incomplete biomass combustion and the release of solid particulate matter.
The adoption of woody biomass and non-wood biomass, such as agricultural residues, coupled with efficient combustion energy technologies, holds the potential to substantially reduce harmful emissions into the atmosphere while increasing its contribution to energy supply, making it a viable alternative to fossil fuels. Due to efficiency increase as compared to traditional biomass use, it is an important cornerstone of future scenarios. Despite significant investments in the research and development of biomass energy technologies, a knowledge gap persists, particularly concerning efficient, low-cost determination of biomass properties, including its elemental compositions (carbon (C), hydrogen (H), nitrogen (N), oxygen (O), sulfur (S), and others). During inefficient and incomplete combustion, harmful pollutants such as carbon monoxide, sulfur oxides (SOx), nitrogen oxides (NOx), along with particulate matter (PM
2.5 and PM
10) are continuously released into the environment as smoke, posing significant health risks through indoor and outdoor exposure, with women and children being the most vulnerable [
4,
5,
6].
The elemental composition of biomass has a profound impact on combustion efficiency and the emission levels released into the environment. These emissions, in turn, carry significant consequences for both the energy industry and the natural surroundings. Energy release during biomass combustion correlates positively with carbon and hydrogen contents, as they are the primary contributors to its energy value [
7]. High carbon content is desirable for energy production [
8], and hydrogen’s high energy content makes it valuable [
9]. During combustion, oxygen reacts with carbon and hydrogen, reducing the available energy in biomass. Elevated oxygen and nitrogen contents decrease the calorific value, thereby reducing energy potential [
10]. Nitrogen and sulfur are undesirable elements in biomass due to their contribution to the formation of harmful NOx and sulfur dioxide [
11,
12]. To minimize environmental impact and ensure sustainable operation and maintenance of combustion systems, low sulfur content in biomass is preferred [
12]. Hence, it is crucial to rapidly, accurately, and non-invasively assess the elemental composition of biomass, including C, N, O, H, and S. This assessment is essential for understanding biomass elemental composition and the potential emissions risks during energy production.
In our previous research [
13], an investigation was conducted into the application of NIR spectroscopy (NIRS) for the comprehensive analysis of the ultimate analysis parameters of ground biomass intended for energy utilization. The study concludes that NIRS offers a reliable and non-destructive alternative method for rapidly assessing the elemental composition of ground biomass for energy-related purposes. Despite the valuable findings from previous research, these findings primarily served academic and research institutions. However, biomass normally is made into pellet form for export and to increase energy density where grinding is necessary before making pellets. Woodchips are especially useful, as they are easy to use, and sometimes, ground wood is not suitable for power operations due to the high cost and length of time necessary for sample preparation; therefore, it is a popular source of energy for power plants because of low preparation costs. Meanwhile, woodchip quality could be more effectively examined to achieve higher levels of plant efficiency [
14]. Hence, this study aims to improve the applicability of NIR spectroscopy to assess the ultimate analysis parameters of chipped biomass, i.e., biomass with particle sizes commonly found in industrial applications. In consequence, this research outcome may directly benefit traders and energy companies, facilitating the utilization of research outcomes without the need for extensive biomass preparation such as grinding.
The data structure of samples used for model development in this present work was in two forms, i.e., non-wood and wood samples. As reported, the non-wood and wood species were different in their lignocellulosic constituents. Non-wood material of agricultural waste compost of lignin, holocellulose, α-cellulose, pentosan, and ash [
15]. For example, agricultural residues, such as hemp and sugarcane bagasse, contained higher concentrations of cellulose and lower levels of recalcitrant lignin when compared to the average woody biomass [
16,
17]. However, Hawanis et al. [
18] reported that non-wood contained lower cellulose and lignin while wood contained higher [
19,
20,
21]. Therefore, incorporating a wider range of ultimate analysis parameters (C, H, N, O, and S) as reference values will enhance the model robustness for prediction. Previous studies have strongly correlated ultimate analysis parameters to higher heating values in biomass [
22]. Hence, by predicting the ultimate analysis parameters and leveraging these correlations, the fuel heating value can be characterized. This study specifically investigated the effect of combined non-wood and wood spectra from biomass chips on rapidly predicting ultimate analysis parameters using NIR spectroscopy (NIRS).
The volume of available published studies is limited in which wood and non-wood biomasses are characterized concurrently. Generally, only one specific species of biomass was used for prediction modeling, and the determination of ultimate analysis constituents by NIRS was rarely reported. Only two reports were found, including Posom and Sirisomboon [
23], who optimized the PLS models using NIR spectra of 80 bamboo chip samples for evaluation of C, H, N, S, and O content. The models showed the coefficient of determination of prediction set (R
2P) and the ratio of prediction to deviation (RPD) of 0.803 and 2.31 for C; 0.856 and 2.65 for H; 0.973 and 6.6 for N; 0.785 and 2.19 for S; and 0.522 and 1.46 for O, respectively. Similarly, the models developed by Zhang et al. [
24] used 100 accessions of sorghum biomass with R
2P of 0.96 for wt.% of C, 0.87 for wt.% of H, 0.86 for wt.% of N, and 0.83 for wt.% of O.
There were two reports found in the available database that developed a model for two similar species to evaluate ultimate analysis parameters, C, H, N, O, and S. A total of 222 rice straw and wheat straw, collected from 24 provinces of China, were used for NIRS calibration and validation in this study where R
2P and standard error of predictions (SEP) of independent validation were, respectively, 0.97 and 0.37% for C, 0.77 and 0.17% for H, and 0.87 and 0.10% for N [
25]. Saha et al. [
26] developed models by using 276 wood chip ground samples of pine trees of two species (Loblolly (
Pinus taeda) and slash (
Pinus elliottii)), where the biomass spectra ranged from 400 to 2498 nm at 2 nm intervals. The samples were a mix of bark, branch, needle, wood, or whole tree biomass. The prediction results show for C (sample number (n) = 43; coefficient of R
2P = 0.90; RPD = 3.14; ratio of prediction to interquartile (RPIQ) = 3.23); for N (n = 44; R
2P = 0.95; RPD = 4.33; RPIQ = 5.96); and for S (n = 42; R
2P = 0.93; RPD = 3.67; RPIQ = 3.24).
There were two reports of our group contributed to the research results of NIR prediction models for ultimate analysis parameters of the non-wood and wood samples, including Pitak et al. [
27] who developed the PLS regression using the spectra obtained by line-scan NIR hyperspectral imager in which the most effective model for the prediction of C, H, and N content of 160 non-wood and wood biomass pellets including filter cake (15 pellets),
Leucaena leucocepphala (10 pellets), bamboo (15 pellets), cassava rhizome (15 pellets), bagasse (15 pellets), sugarcane leaves (15 pellets), straw (15 pellets), rice husk (15 pellets), eucalyptus bark (15 pellets), napier grass (15 pellets), and corn cob (15 pellets) developed using iGA wavelength selection and standard normal variate (SNV) spectral pretreatment and provided the highest accuracy with R
2Pp and SEP of 0.83 and 1.33% for C; 0.84 and 0.17% for H and 0.90 and 0.098% for N; respectively. The second report was contributed by Shrestha et al. [
13], where the ground non-wood and wood samples spectra, which were 110 samples of agricultural residues and 90 samples of fast-growing trees, were used to develop the PLSR models combined with multi-preprocessing methods for ultimate analysis showed R
2P and RPD for C of 0.7217 and 1.9, for N of 0.8410 and 2.7, for H of 0.7678 and 2.1, and for O of 0.6289 and 1.7, respectively.
The main objectives of this research include:
- (1)
Develop PLSR models using NIR raw spectra, traditional preprocessing, MP 5-range, MP 3-range, GA, and SPA for assessing chip biomass properties for energy usage by employing NIRS while the spectra of the biomass were from non-wood (agricultural residue and bamboo) and wood (fast growing trees) samples.
- (2)
Compare the performance of the PLSR models based on R2C, RMSEP, R2P, RMSEP, RPD, and bias.
- (3)
Study the effect of combined non-wood and wood species in model development on model performance by scatter plot analysis.
- (4)
Select the better performing PLSR-based model for each ultimate analysis parameter, compared with the performance of the ground biomass for rapidly assessing biomass properties for energy usage.
- (5)
Determine the limit of quantification (LOQ) value of the proposed model calibration set for each ultimate analysis parameter in chip biomass.
3. Results and Discussion
Table 1 shows the number of non-wood samples and wood samples in the calibration set and validation set. The wood sample number is about 33–35% of the total sample number; hence, the non-wood sample number is 65–67%. Out of 120 samples, the number of outlier samples can be evaluated by the data in
Table 1.
Table 2 presents statistical data for the ultimate analysis parameters of chip biomass obtained using CHNS/O elemental analyzer (Thermo Scientific
TM FLASH 2000). This data was used in both the calibration and prediction sets for model development. S content in the chip biomass was not detected, possibly due to its very low content falling below the detection threshold. Therefore, a PLSR-based model for S content in the chip biomass was not developed in this study. The wt.% of O is calculated using Equation (1).
Table 3 shows the results of the PLSR-based model for ultimate analysis (wt.%) of chip biomass, where the bolded model shows the best performance. However, it is essential to consider the recommendation provided by Williams et al. [
34], where with an R
2P value between 0.66–0.81, the model can be used for rough screening and other suitable calibration purposes. Therefore, C, O, and N models were. For the H model, according to Williams guideline [
34], a model with an R
2P value between 0.50–0.64 is only suitable for very rough screening. Likewise, every model of biomass chips for ultimate analysis parameters was in alignment with the recommendation from Zornoza et al. [
35], in which any model with an RPD value below 2 was deemed insufficient for any application.
3.1. wt.% of C
Table 3 presents the results of the PLSR-based model within the full wavenumber range of 3594.87–12,489.48 cm
−1 for the wt.% C of chip biomass, with the best–performing model highlighted in bold.
The model, developed using GA–PLSR with spectrum preprocessing involving the sd2, a gap, and segments of five each, along with nine LVs, provided better results. It achieved R2C, RMSEC, R2P, RMSEP, RPD, and bias values of 0.8078, 0.9320 wt.%, 0.6954, 1.1252 wt.%, 1.8, and 0.0053 wt.%, respectively. By determining RMSEP, these results represent a 6.8566% improvement in the model performance compared to Full-PLSR. Utilizing Equation (3), the LOQ value was calculated as 9.3724 wt.% for C. Notably, the LOQ value is lower than the minimum wt.% C value used during model development, indicating that the model exhibits high sensitivity and can quantify wt.% C starting from 9.3724 wt.%.
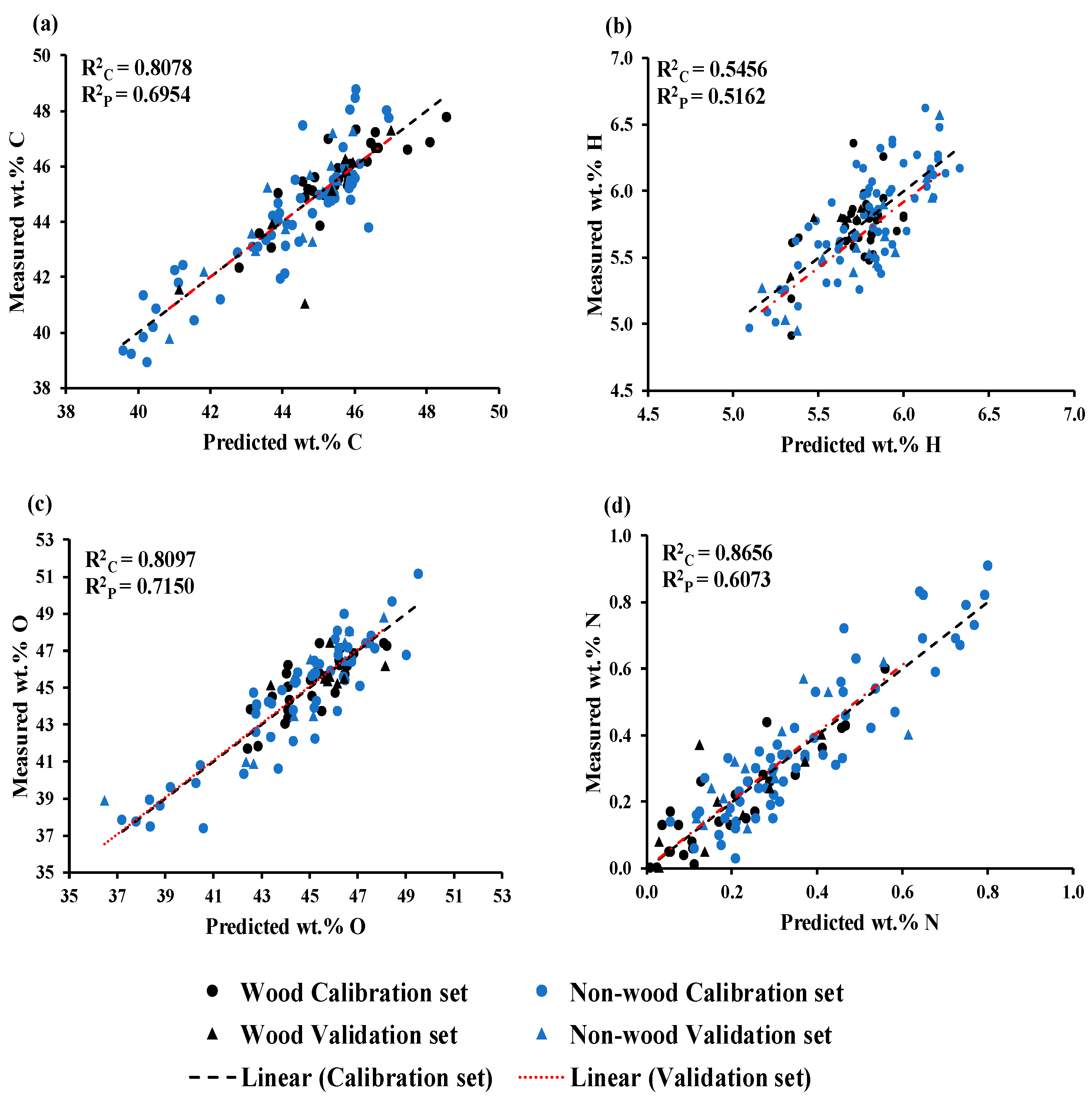
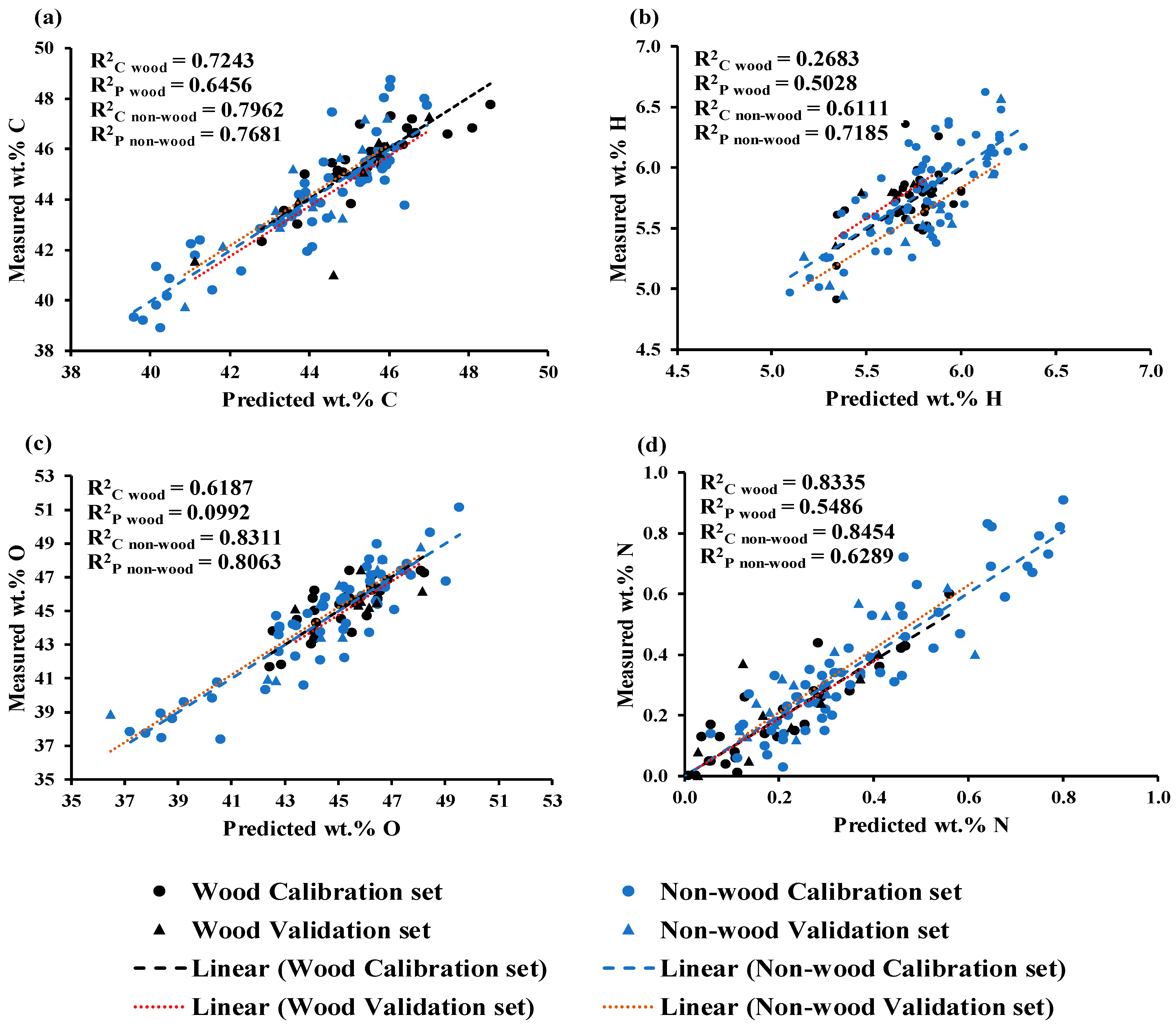
Figure 2a shows a scatter plot comparing the predicted and measured wt.% of C, which was obtained using GA–PLSR. The trend line for the prediction set and calibration set overlap, indicating the same slope. The slope shows the rate of change of Y (measured value) as a function of the rate of change of X (predicted values) [
34] or vice versa, hence indicating that predicted values of both sets of data have changed with the same rate and this characteristic is same for the models for O and N shown in
Figure 2c,d.
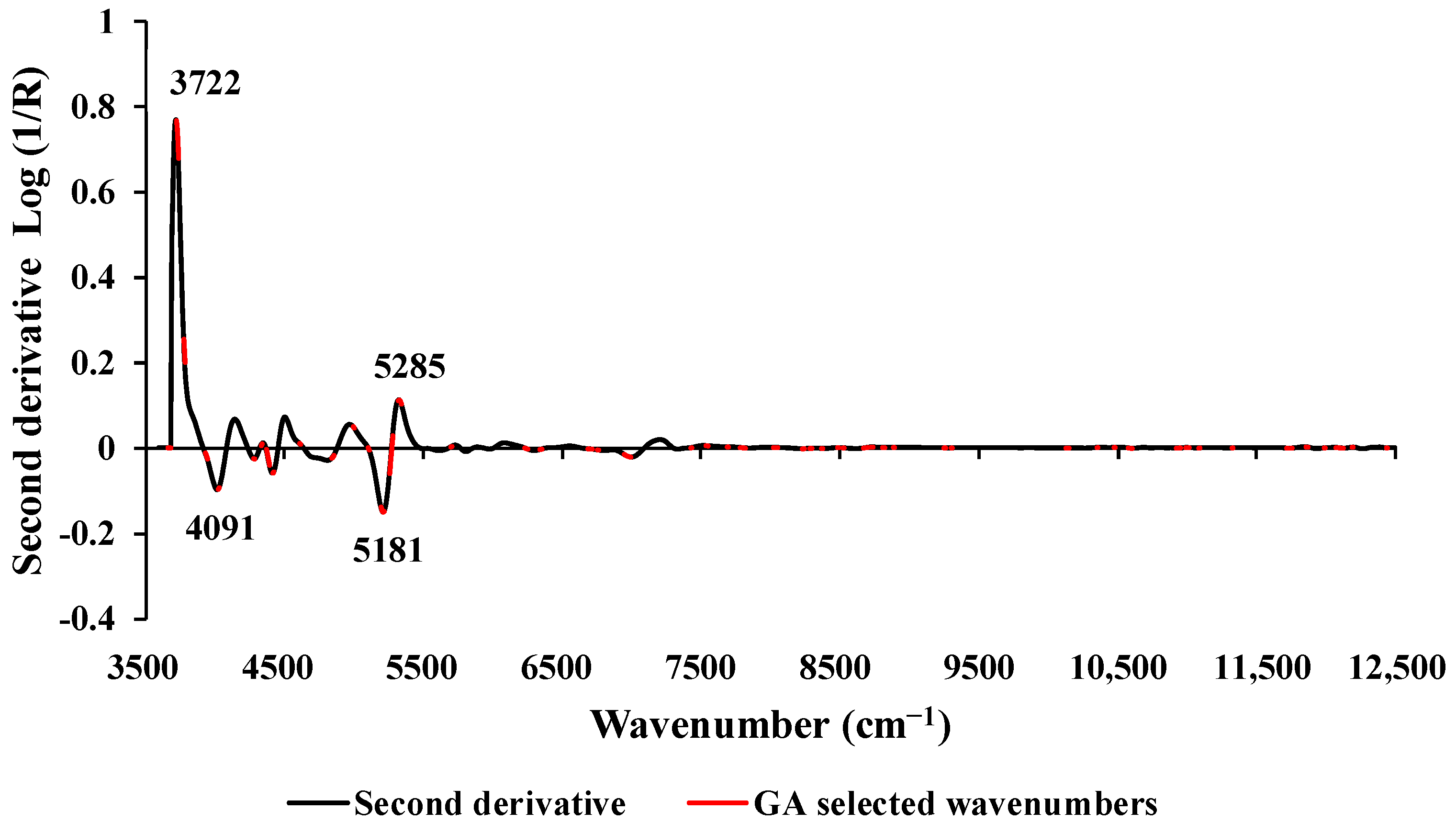
Figure 3 displays the average sd2 absorbance values obtained after preprocessing, highlighting 306 selected wavenumbers (marked in red) identified through GA. These wavenumbers fall within the full spectral range of 3594.87–12,489.48 cm
−1. Peaks were observed at 3722, 4091, 5181, and 5285 cm
−1, all of which might have the potential to enhance the model performance. The wavenumbers 3722 cm
−1 and 4091 cm
−1 are associated with the C–H aromatic functional group, specifically the C–H aryl material type [
36]. The peak at 5181 cm
−1 corresponds to a combination of O–H stretching and HOH bending, indicative of polysaccharides [
36]. Similarly, the peak at 5285 cm
−1 is associated with the functional group of O–H hydrogen bonding between water and exposed polyvinyl alcohol OH groups [
36].
Previous studies by Zhang et al. [
24] and Posom and Sirisomboon [
23] have demonstrated that vibrational bands related to C–H aromatic, C–H stretching, N–H stretching, N–H deformation, O–H stretching, HOH bending, O–H hydrogen bonding, and similar factors play a crucial role in predicting the wt.% of C in various biomass varieties. These findings align with the vibration bands observed in our study, providing support for our results and suggesting that these selected peaks likely have a significant influence on the model performance.
3.2. wt.% of H
The model developed using GA–PLSR with vector normalization as preprocessing showed the best performance with 11 LVs (
Table 3). It selected 67 important wavenumbers using GA. The model performance, in terms of R
2C, RMSEC, R
2P, RMSEP, RPD, and bias values, was 0.5456, 0.02336 wt.%, 0.5162, 0.2322 wt.%, 1.5, and −0.0781 wt.%, respectively. Compared with Full-PLSR, the GA improved the PLSR model accuracy by 1.6743%. The LOQ value was calculated as 2.3484 wt.%, which is lower than the minimum reference value used for the model development. This suggests that the selected model is sensitive and can sensitively quantify H from 2.3484 wt.%.
Figure 2b displays a scatter plot comparing the predicted and measured wt.% of H, which was obtained using GA–PLSR. It is clear that the trend line for the prediction set exhibits an offset in relation to the trend line of the calibration set and the 45-degree line. This offset raises concerns about the model constant bias along the range of the data, indicating the overestimating model.
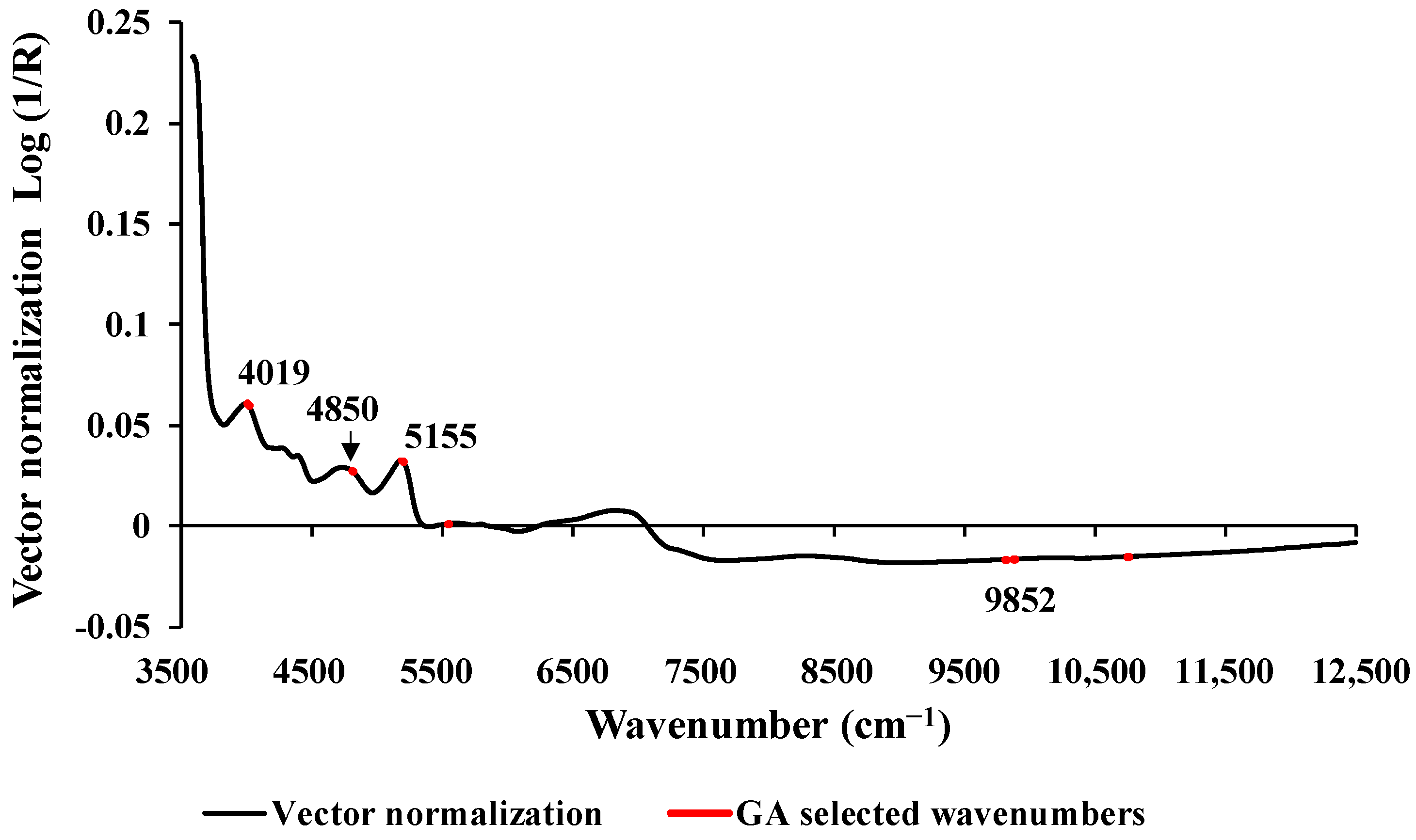
Figure 4 displays the average absorbance values within the range of 3594.87–12,489.48 cm
−1. These values were obtained after preprocessing using vector normalization and highlight 67 selected wavenumbers, marked in red, which were identified using GA. Significant peaks were observed at the wavenumbers 4019, 4850, 5155, and 9852 cm
−1, respectively, and these may have an influence on the model performance. The peak at 4019 cm
−1 is associated with the spectra–structure combination of C–H stretching and C–C stretching, with the material type being cellulose [
36]. The peak at 4850 cm
−1 corresponds to the functional group of N–H combination bands found in secondary amides within proteins [
36]. The peak at 5155 cm
−1 is related to the combination of O–H stretching and HOH bending, with the material type being water [
36]. Finally, the peak at 9852 cm
−1 is associated with the second overtone of the fundamental stretching band of N–H asymmetric stretching, and the material type is aromatic amine [
36].
In comparison to previous studies conducted by Shrestha et al. [
13], Zhang et al. [
24], and Posom and Sirisomboon [
23] that focused on measuring the wt.% of H in biomass using NIRS, our study discovered similar peaks within the range of 4000–9900 cm
−1 and vibration bands such as O–H stretching, HOH bending, C–H stretching, and C–C stretching. Therefore, our study findings align with these earlier studies on this specific aspect. However, when evaluating the overall performance of various PLSR-based models, this study suggests that the wt.% of H was not sufficiently explained by the vibration of those mentioned bonds.
3.3. wt.% of O
Assuming that the S content in chip biomass is negligible, as its wt.% is too low to be detected by the instrument, we calculated the wt.% of O in the chip biomass for 120 samples using Equation (1). The wt.% of ash content for each biomass was determined using a TGA.
Table 3 presents the optimal results from five different types of PLSR-based models. The most effective model was developed using the MP PLSR 5-range method, incorporating a spectral preprocessing combination set of 2, 5, 2, 1, and 5, which corresponded to the following ranges: 3625.72–5392.30 cm
−1 with SNV, 5400.02–7166.59 cm
−1 with the sd2, 7174.31–8940.89 cm
−1 with SNV, 8948.60–10,715 cm
−1 with raw spectra, and 10,722.9–12,489.48 cm
−1 with the sd2. This model employed 15 LVs.
Figure 2c illustrates the scatter plot comparing measured versus predicted wt.% of O obtained from the MP PLSR 5-range method. This method yielded R
2C of 0.8097, RMSEC of 1.2366 wt.%, R
2P of 0.7150, RMSEP of 1.3088 wt.%, RPD of 1.9, and a bias of 0.0733 wt.%. Compared with Full-PLSR method performance, the MP PLSR 5-range method significantly improved the model accuracy by 11.4913%. The LOQ value for wt.% of O was calculated as 12.4424 wt.%, which is lower than the minimum wt.% of O used during model development. This indicates that the model is highly sensitive and can quantify O content in chip biomass from 12.4424 wt.%.
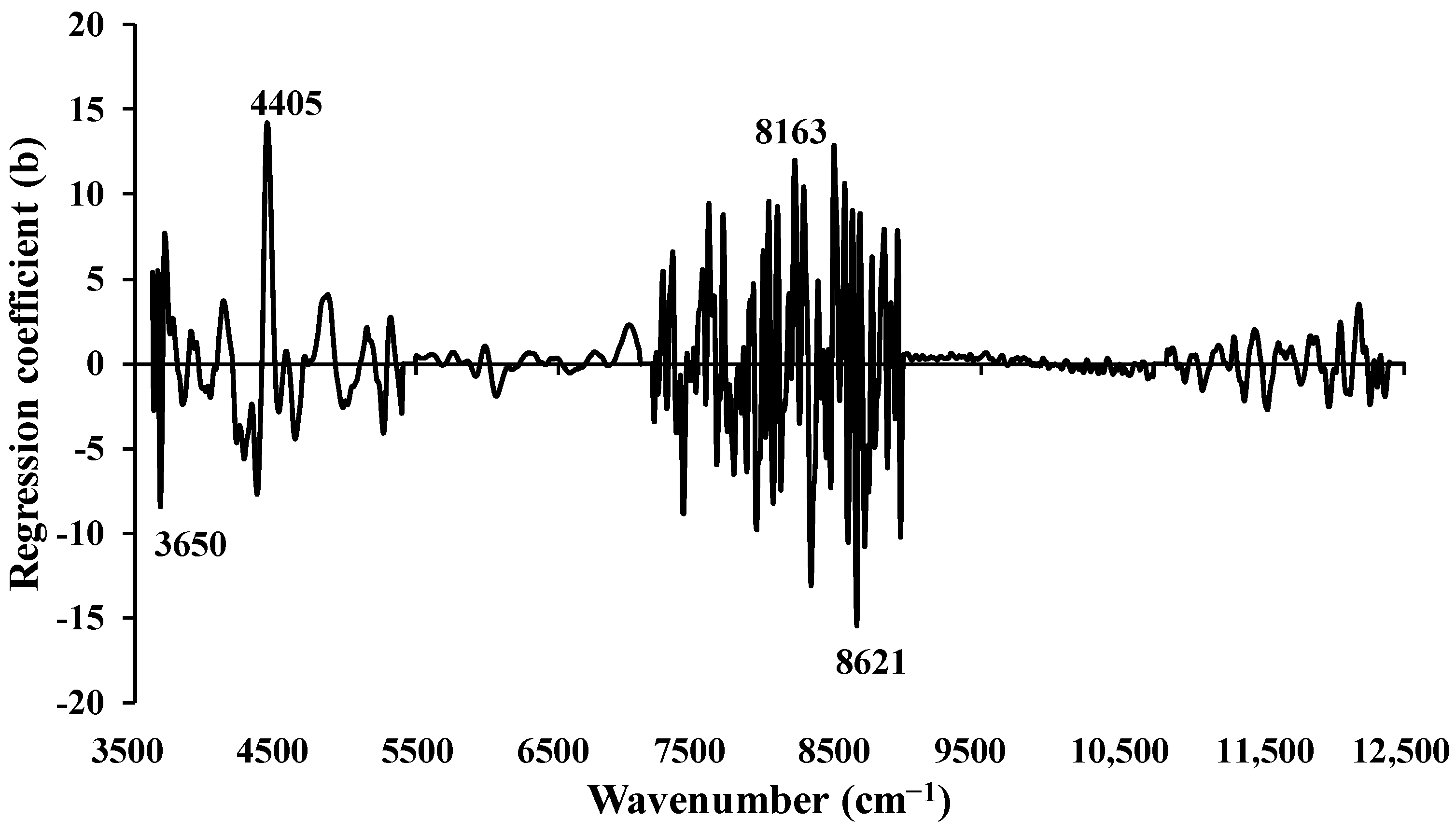
Figure 5 displays the regression coefficient plot for wt.% of O content in chip biomass obtained from the MP PLSR 5-range method. Several notable peaks were observed at 3650, 4405, 8163, and 8621 cm
−1, each potentially exerting a significant influence on the model performance. Specifically, the peak at 3650 cm
−1 corresponds to the O–H functional group found in the primary alcohols, characterized by the fundamental stretching vibrational absorption band of O–H [
36]. The peak at 4405 cm
−1 represents the combination of O–H stretching and C–O stretching, with cellulose as the material type [
36]. The peaks at 8163 cm
−1 and 8621 cm
−1 are associated with the second overtone of the fundamental stretching band of C–H and the fourth overtone of the fundamental stretching band of C=O, respectively, which are typically found in hydrocarbons and aliphatic compounds [
36].
When compared with previous studies on wt.% of O in biomass, such as those by Shrestha et al. [
13], Zhang et al. [
24], and Posom and Sirisomboon [
23], this study reveals some contradictory peaks. However, the vibrational bands, such as O–H from primary alcohol, C=O stretching, and C–H stretching, among others, were similar. These findings supports the research result of this study, suggesting that the significant peaks observed in this study have an impact on the development of the model for assessing wt.% of O in chip biomass.
3.4. wt.% of N
The best model for rapid prediction of wt.% of N was obtained using the MP PLSR 3-range method with a spectral preprocessing combination set of 4, 0, and 0 (
Table 3). This set corresponds to the sd1 from 3594.87 to 5492.59 cm
−1 and zero absorbance from 7498.314 to 12,489.48 cm
−1.
Figure 2d illustrates the scatter plot of measured versus predicted wt.% of N content in the chip biomass, obtained from the MP PLSR 3-range method with 15 LVs. The best–performing model achieved an R
2C of 0.8656, RMSEC of 0.0820 wt.%, R
2P of 0.6073, RMSEP of 0.1008 wt.%, RPD of 1.6, and a bias of 0.0191 wt.%. These results indicate that within the range 3594.87–5492.59 cm
−1 (refer
Figure 6), by effectively correcting baseline shifts and assigning zero absorbance value within the remaining wavenumber range, the model performance is enhanced. Compared with Full-PLSR using RMSEP value, the MP PLSR 3-range method improved the model performance by 2.5473%. However, based on R
2C and R
2P values, the selected model indicates overfitting. This suggests that our model fits the training data too closely, and too much less accurate in prediction the validation set. This was discussing in
Section 5 Comparison of Model Performance between Using Chipped and Ground Biomass Spectra by refer to Cawley and Talbot [
37].
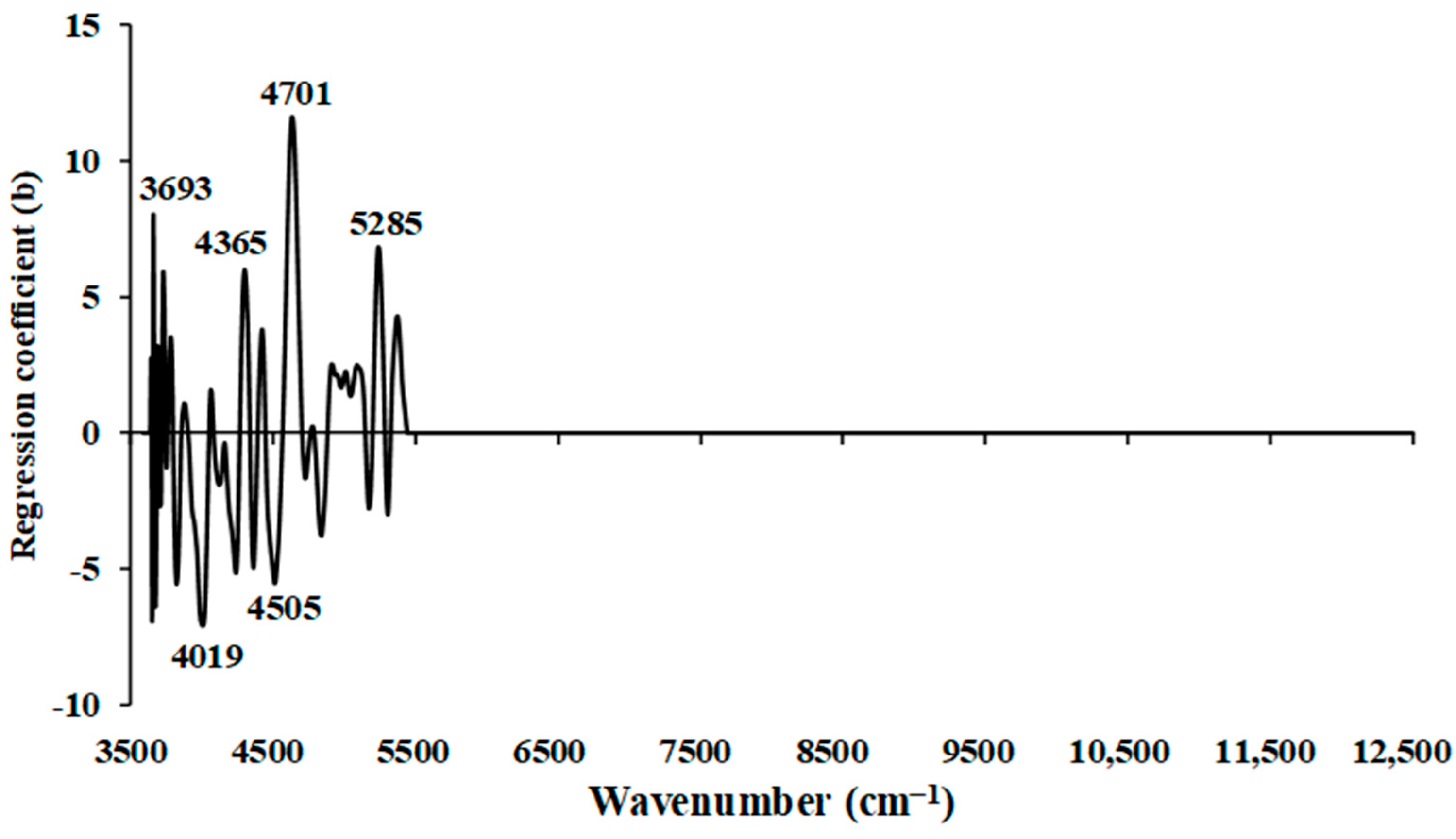
Figure 6 illustrates the regression coefficient plot for the wt.% of N in chip biomass, obtained using the multi-preprocessing PLSR 3-range method. Significant peaks that could potentially influence the model performance were observed within the wavenumber range of 3594.87–5492.59 cm
−1 only. These significant peaks were noticed at wavenumbers 3693, 4019, 4365, 4505, 4701, and 5285 cm
−1. Specifically, the peak at 3693 cm
−1 is associated with the function group of C–H aromatic C–H bands, characterized by the material type C–H aryl. At 4019 cm
−1, the peak represents functional groups with a combination of C–H stretching and C–C stretching from cellulose [
36]. The peak at 4365 cm
−1 corresponds to CONH
2, specifically due to C=O bonded to the N–H of the peptide link termed the α–helix structure [
36]. The peak at 4505 cm
−1 is associated with the N–H combination band [
36]. Similarly, the peak at 4701 cm
−1 corresponds to the function group of N–H/C=O combination from polyamide II [
36]. Lastly, the peaks at 5285 cm
−1 are associated with O–H hydrogen bonding between water and exposed polyvinyl alcohol OH [
36]. These peaks are crucial in understanding the composition of the chip biomass and are important for model development and analysis. Furthermore, in the range of 7498.314–12,489.48 cm
−1, the regression coefficient value equals zero. This indicates an insufficient linear relationship between the dependent (spectral information) and independent (reference value) variables in this range, and it does not significantly contribute to the predictive model for the prediction of wt.% of N.
The previous study conducted by Posom and Sirisomboon [
23], which aimed to evaluate the wt.% of N in bamboo, also revealed significant peaks within the range of 4424 to 6920 cm
−1. Similarly, Shrestha et al. [
13] conducted a study on wt.% of N in ground biomass from the same source and exhibited important peaks within a similar range, specifically within 4019 to 6711 cm
−1. This finding aligns with the results of our study, providing additional support for our research. It is noteworthy that in both studies, common vibrational bands, such as N–H stretching, C=O stretching, C–H stretching, C–C stretching, aromatic C–H, and O–H bonds between water and alcohol, among others, were identified. This consistency in vibration bonds reinforces our study findings and suggests that these specific peaks likely play a crucial role in influencing the model performance.
4. Effect of Non-Wood and Wood Samples on Model Performance
Table 4 shows the reference values of wt.% of C, H, N, and O of non-wood and wood samples in calibration and validation sets. From
Figure 2 and
Table 4, it is obvious that the range of every element content is wider after the two sets were combined for modeling. Therefore, the models can now be regarded as more robust models than only one set was used. From
Figure 2a,c, the range of wt.% of C and O of wood samples was narrower than those of the non-wood samples which were extended more to the lower wt%.
Figure 2d illustrates the opposite way, where the value range of N of wood samples was lower and narrower than those of the non-wood samples. Therefore, models for wt% of C, O, and N had better performance than that of the H model. The wood sample reference values of H were grouped together and more or less had the same range as the range of non-wood samples. (
Figure 2b).
The literature shows that the one species model of non-wood, which were bamboo wood chips [
23] and sorghum [
24] for evaluation of ultimate analysis parameters, C, H, N, O, and S had better performance than our combined non-wood and wood models as the results described in the introduction of this manuscript. Similarly, the two similar species of rice straw and wheat straw model [
25] and the pine tree of two species (Loblolly (
Pinus taeda) and slash (
Pinus elliottii)) model [
26] indicated better prediction performance, though they were homogeneous ground samples which might make their model performance better than the chip ones due to less scattering problem. Shrestha et al. [
13] worked with ground samples of the same batch of non-wood and wood samples. Spectra from this experiment showed better R
2P and RPD for C, N, H, and O, which is claimed to be due to the same merit of homogeneous samples.
Using larger biomass particle sizes, Pitak et al. [
27] combined the non-wood and wood biomass pellet NIR spectra obtained by averaging every pixel spectrum of the pellets from a hyperspectral image (HSI). This approach provided better performance in predicting elements from the ultimate analysis than our model, i.e., in-detail data collection by the HSI leads to significant improvements.
Figure 7 shows the scatter plots of the highest performance models in this study in predicting the C, H, O, and N content of the wood and non-wood samples, which is the same as
Figure 2, but the difference is
Figure 7 shows the simple regression lines of each group of non-wood and wood samples both for calibration set and prediction set. For better vision,
Table 5 shows the numeric data of R
2, slope, and intercept calculated from the scatter plots of wood and non-wood calibration and prediction sets. Williams et al. explained that the slope of the trend line plotted between Y (measured value) and X (NIR predicted value) indicated the rate of change of Y as a function of the rate of change of X [
34]. The intercept of different species illustrated the same trend as slope interpretation, especially when the slope is more than 1, the intercept was with a minus sign, and if less than 1, the intercept was with a plus sign. While the slope was 1, the intercept was low, close to zero, and when the slope was more or less than 1, the intercept was high, far from zero.
The perfect relationship between the reference values and the predicted values is when the correlation coefficient (R) and slope are equal to 1 and the intercept is equal to zero [
34].
From
Table 5, for the C model, the non-wood samples contributed slightly more merit on calibration model performance than wood samples for more R the slope was closer to 1, and the intercept was closer to zero. But the prediction set of non-wood provided a steeper slope and intercepted far more from zero.
By the same way of interpretation, the model for H obtained more merit from non-wood samples, while for the wood samples, the R of the trend line was very low, the slope was far from 1, and the intercept was slightly far from zero. The incongruous trend lines of both sets makes the overall performance of the model worse as shown in
Table 3.
For the N model, the wood and non-wood calibration set samples more or less had the same trend line characteristics, which supplement the good calibration model performance, though the prediction sample set of both biomass species trend line characteristics shows less R and slope far from 1 led to overfit calibration models of both biomass groups (
Table 5).
For the O model, the non-wood group had better trend line characteristics and contributed good merit to the model, while the poorer trend line characteristics of the wood group made the overall model inferior but by a small portion because the number of samples in the non-wood group was much more (
Table 5). By the strong merit of the non-wood group, the overall model performance for O prediction was fairly acceptable (
Table 3).
Table 6,
Table 7,
Table 8 and
Table 9 show the trend line characteristics, including R
2, slope, and intercept of each specific plant of wood and non-wood samples used in the optimized models for evaluation of C, N, H, and O, respectively. It was observed that most of the R
2P of every plant was equaled to 1 for the samples of those plants in the optimized model, with only two samples connected to a straight line. Therefore, we ignored interpreting of the trend line characteristics of the prediction set, and only the R
2C, slope, and intercept of the calibration set will be interpreted. As indicated by Williams et al. [
34], when the R approached 1 and the slope approached 1 and the intercept approached zero, the model approached excellence. Therefore, to include different species in a model, the species have to be not only in the different values of the constituents to make a wider range for a robust model, but also they must provide the characteristic of the same rate of change of NIR predicted values with the measured values (same slope and slope should approach 1, and intercept is same (no gap) and approached zero). As expected, the trend of R
2, slope, and intercept of different species were not the same for their different characteristics. However, in some species whose characteristics were similar, the trends were common supported the each other but might positively or negatively to the prediction performace of the model.
From
Table 6,
Table 7,
Table 8 and
Table 9, as expected, the intercept of different species illustrated the same trend as slope interpretation, especially when, by the fact, the slope is more than 1 the intercept was with minus sign, and if less than 1 the intercept was with plus sign. While the slope was 1, the intercept was low, closer to zero, and when the slope was more or less than 1, the intercept was high, far from zero.
Therefore, the following were the effects of specific species on the performance of the optimized models interpreted by scatter plot analysis using the R2 and slope of the trend line of the specific plant in the model developed.
For C (
Table 6), by R
2C interpretation, most non-wood species (agricultural waste) except bagasse and bamboo show unacceptable trend lines compared to wood species samples except pines. Therefore, including the mentioned non-wood species caused a poor effect on the C model. By interpretation of slope, there were three groups of slope (by value round up), i.e., 1 including Eucalyptus, Alnus and Bombax in wood species and corn cob, corn shell, rice husk, and bamboo in non-wood species, less than 1 including pine in wood specie, and more than 1 including corn stover and bagasse indicating unequal slope of different species in the same optimized model show the effect of specific species on model performance. These can be summarized that for the model to be better, pine and corn stover should not be included in modeling for C prediction.
By the same way of interpretation, from
Table 7, the optimized model for N, pine, and bagasse should not be included; from
Table 8, for H, pine, Alnus, corn shell, and bagasse should not be included; and from
Table 9, for O, pine should not be included for better performance of the models. These were due to the poor R and slope of the eliminated species, which were not in accordance with the other species.
These results show that the different species affected the model performance of each parameter prediction in a different manner, and by scatter plot analysis, which of these species were affecting the model negatively and how to improve the model performance were indicated.
5. Comparison of Model Performance between Using Chipped and Ground Biomass Spectra
In this section, the model performance of chipped biomass for ultimate analysis parameters to the model of ground biomass [
13] derived from the same sample varieties is compared. The comparison is based on the metrics R
2C, RMSEC, R
2P, RMSEP, and RPD. The results demonstrate that chipped biomass generally performs less effectively in these models compared to ground biomass, except for wt.% of O.
For wt.% of C and wt.% of H, both chipped and ground biomass models demonstrated better performance when employing the GA–PLSR model. This outcome aligns with expectations, as GA optimizes feature selection to maximize fitness, while PLSR maximizes covariance between absorbance values and areas of interest.
For wt.% of C, the GA–PLSR model applied to ground biomass yielded an R
2C of 0.7851, RMSEC of 0.9753 wt.%, R
2P of 0.7217, RMSEP of 0.9740 wt.%, and RPD of 1.93 [
13]. In contrast, the model applied to chipped biomass performed less effectively (
Table 2). Therefore, it is recommended to adopt the GA–PLSR model with sd2 preprocessing on ground biomass when evaluating wt.% of C.
Similarly, the GA–PLSR model applied to ground biomass outperforms that of chipped biomass for wt.% of H. Ground biomass yielded an R
2C of 0.8814, RMSEC of 0.1041 wt.%, R
2P of 0.7678, RMSEP of 0.1434 wt.%, and RPD of 2.14 [
13], whereas chipped biomass lagged behind (
Table 2). Hence, for wt.% of H, the GA–PLSR model with spectral preprocessing from SNV on ground biomass is recommended.
Regarding wt.% of N, the MP PLSR 5-range method exhibited superior model performance on ground biomass, as evidenced by R
2C, RMSEC, R
2P, RMSEP, and RPD values of 0.8682, 0.0675 wt.%, 0.8410, 0.0973 wt.%, and 2.65, respectively [
13], when compared to chipped biomass performance obtained from the MP PLSR 3-range method (
Table 2). This underscores the suitability of ground biomass for evaluating wt.% of N.
Surprisingly, in contrast, for wt.% of O, the model derived from chipped biomass excelled, despite both models utilizing the MP PLSR 5-range method. In the ground biomass, R
2C, RMSEC, R
2P, RMSEP, and RPD values were 0.6674, 1.4461wt.%, 0.6289, 1.5275 wt.%, and 1.71, respectively [
13], which fell short of chipped biomass results. Hence, it is recommended to adopt the MP PLSR-5 range method with the preprocessing combination set of 2, 5, 2, 1, and 5 for assessing wt.% of O in chipped biomass. This could be due to ash determination, where ash directly influences %O determination based on Equation (1). Also, ash is typically accumulating in small particles, i.e., the time of grinding in conjunction with subsampling can have an influence on ash determination.
All the above comparisons and findings underscore the importance of selecting the appropriate PLSR-based model for precise analysis of ultimate analysis parameters, depending on the specific parameter of interest. There could be several factors that contribute to the lower performance of the chipped biomass model, which can be addressed to improve the model performance. The key contributing factor to this performance difference is obviously the particle size of the biomass samples. Chipped biomass typically consists of larger and different sizes of particles, leading to increased scattering of NIR light during sample scanning. Consequently, the spectra generated from chipped biomass can be of lower quality, resulting in weaker correlations between spectral data and reference data [
38]. Additionally, ground biomass exhibits a more compact and uniform sample structure, reducing the likelihood of NIR light leakage during scanning. Another significant factor affecting the lower model performance is the moisture content in biomass samples. Chipped biomass often contains higher moisture levels, and water has the property of absorbing NIR light in the near-infrared region [
39]. This NIR absorption interferes with the measurements and can introduce inaccuracies, particularly for elements like C, H, O, and N.
In the chipped biomass models, it is evident that the performance of the prediction set consistently lags behind that of the calibration set. This suggests that the model closely overfits the calibration data, capturing both valuable information and noise or random variations [
40]. In the machine learning context, Cawley and Talbot [
37] emphasized that overfitting in model selection is likely to be most severe when the sample size is small and the number of hyperparameters to be tuned is relatively large [
41]. In our case, the number of latent variables of the best models was high.
Consequently, when new samples are introduced into the prediction set, the model may struggle to generalize and provide accurate predictions. Furthermore, the presence of outliers in the prediction set, which were not accounted for in the calibration set, can further negatively impact the model performance [
42].
The performance of ground biomass is better compared to chipped biomass due to several factors. Ground biomass allows for better sample homogenization, ensuring uniformity and consistent composition. Additionally, it offers more control over sample thickness, as chips may vary in thickness, affecting accuracy. Moreover, ground samples reduce light-scattering effects and enable improved penetration of the NIRS signal, allowing for precise and accurate logging of spectral information.
6. Conclusions
In this study, PLSR-based models were developed and compared using FT–NIRS to analyze the ultimate analysis parameters of combined non-wood and wood chip biomass, specifically focusing on wt.% of C, H, O, and N content. All chipped biomass samples were scanned within 3594.87–12,489.48 cm−1 on the diffuse reflectance with sphere macro sample rotating mode, with a particular emphasis on their suitability for energy application. The model with the optimum performance was selected based on trade-off parameters of R2C, RMSEC, R2P, RMSEP, RPD, and bias.
The optimum model performance analysis reveals that the model selected for predicting the wt.% of C, H, N, and O in chipped biomass is suitable primarily for initial rough screening. It is recommended to adopt the multi–preprocessing PLSR 5-range method chipped biomass model for wt.% of O content analysis as an alternative method for rapid assessment. However, for the evaluation of wt.% of C, H, and N content, the chipped biomass model performance falls short of the model developed for ground biomass by Shrestha et al. [
13]. Thus, it is advisable to use the chipped biomass model solely for initial screening before biomass trading. For a more comprehensive and accurate analysis, it is recommended to grind the chip biomass samples within the range of 0.01 to 3080 µm and employ the GA–PLSR model with sd1 for wt.% of C, GA–PLSR with SNV for wt.% of H, and the MP PLSR 5-range method with combination set of 4, 4, 5, 3, and 4 for wt.% of N, as developed by Shrestha et al. [
13]. The LOQ values for C, H, and O were below the model minimum reference value, demonstrating high model sensitivity. However, the LOQ value for N exceeds the minimum reference value, indicating the model detection limit to the minimum value in the calibration sample set range.
By analysis of scatter plots of measured constituent and NIR predicted constituent, the effect of including different biomass species (non-wood and wood species) in the modeling samples was studied. It was concluded that to include different species in a model, the species had to be not only in the different values of the constituents to be predicted to make a wider range for a robust model, but also the different sample species must provide the same rate of change of NIR predicted values with the measured values in the scatter plot (same slope and slope approached to 1, and intercept is same (no gap) and approached zero) for the high-performance model if R is approached to one. The results show that the different species affected the model performance of each parameter prediction in a different manner, and by scatter plot analysis, which of the species affecting the model negatively were identified and dictated how to improve the model performance.
To ensure the model robustness and reliability, it is crucial to expand it by incorporating a wider array of representative non-wood and wood species biomass samples, but the different species must provide the same rate of change of NIR predicted values with the measured values in the scatter plot. Validation and updation using additional unknown samples of the same species are essential for the model effective applicability. Furthermore, exploring alternative machine learning algorithms alongside the recommended model could enhance its practicability. These steps will contribute to not just a more comprehensive and versatile model but also increase its ability for real-world application and improve its overall reliability.