Site Selection and Capacity Determination of Electric Hydrogen Charging Integrated Station Based on Voronoi Diagram and Particle Swarm Algorithm
Abstract
1. Introduction
- (1)
- The OD travel matrix is used to portray the transportation demand, and then Dijkstra’s algorithm is used to plan the shortest driving paths of the vehicles to calculate the electric energy demand of EVs and the hydrogen energy demand of HFCVs.
- (2)
- The Voronoi diagram is used to divide the service area of each EHCIS site and determine the equipment capacity of the EHCIS.
- (3)
- Finally, simulation planning using the city of Sioux Falls and the IEEE33 network ensures stable operation of the grid while meeting the energy demand of EVs and HFCVs.
2. Framework for the Operation of EHCIS
3. Automotive Electric Hydrogen Demand Model
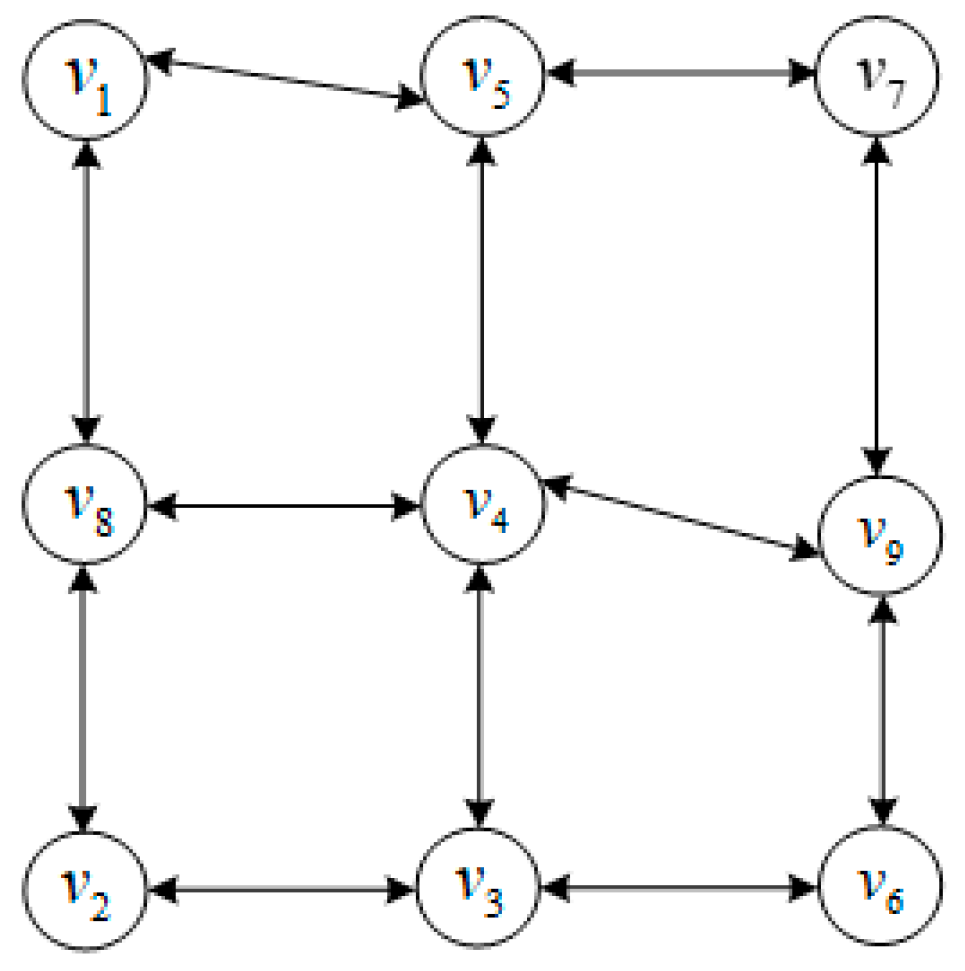
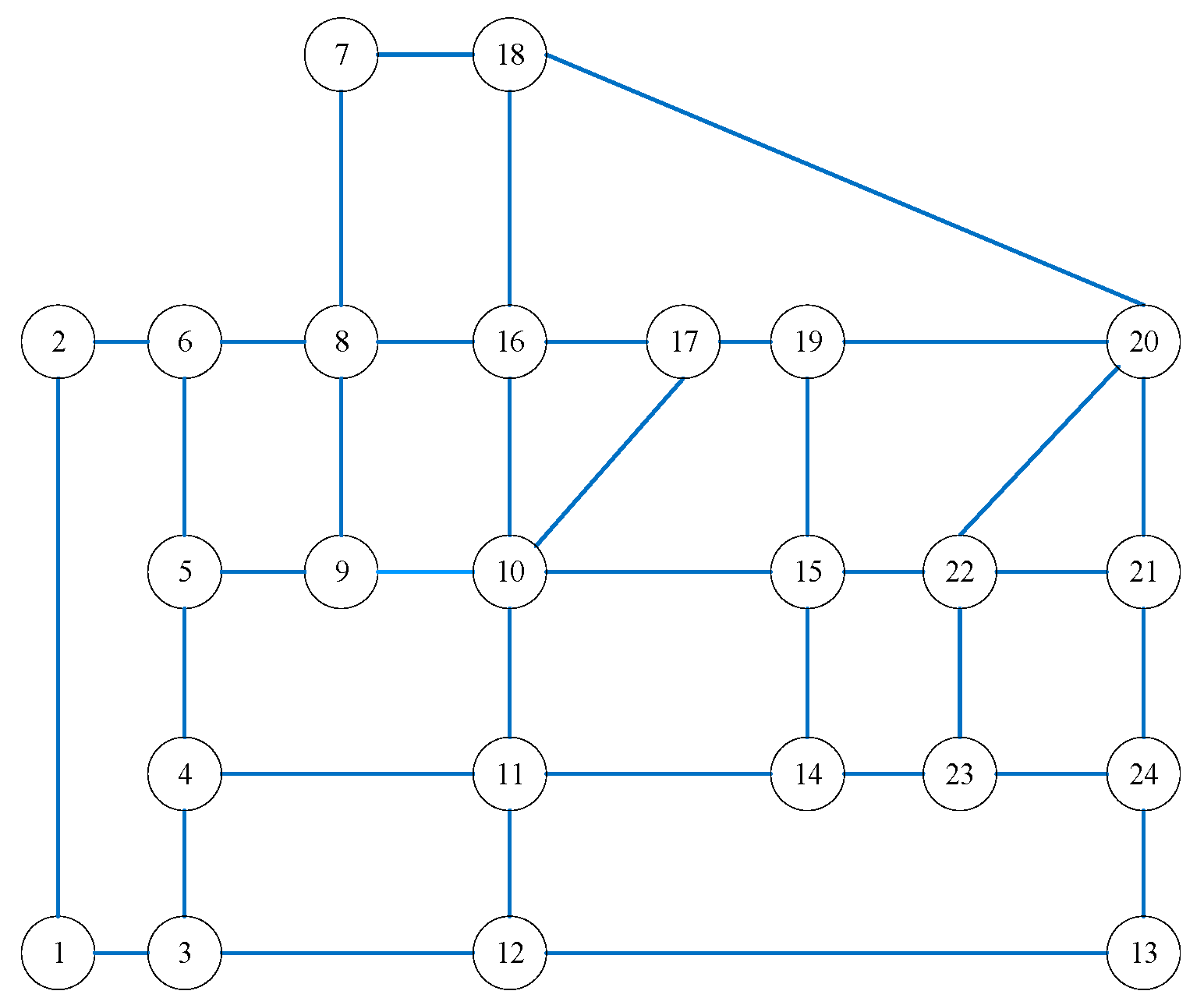
3.1. Transportation Network Model
3.2. New Energy Vehicle Charging and Hydrogen Injection
3.2.1. Road Resistance Function
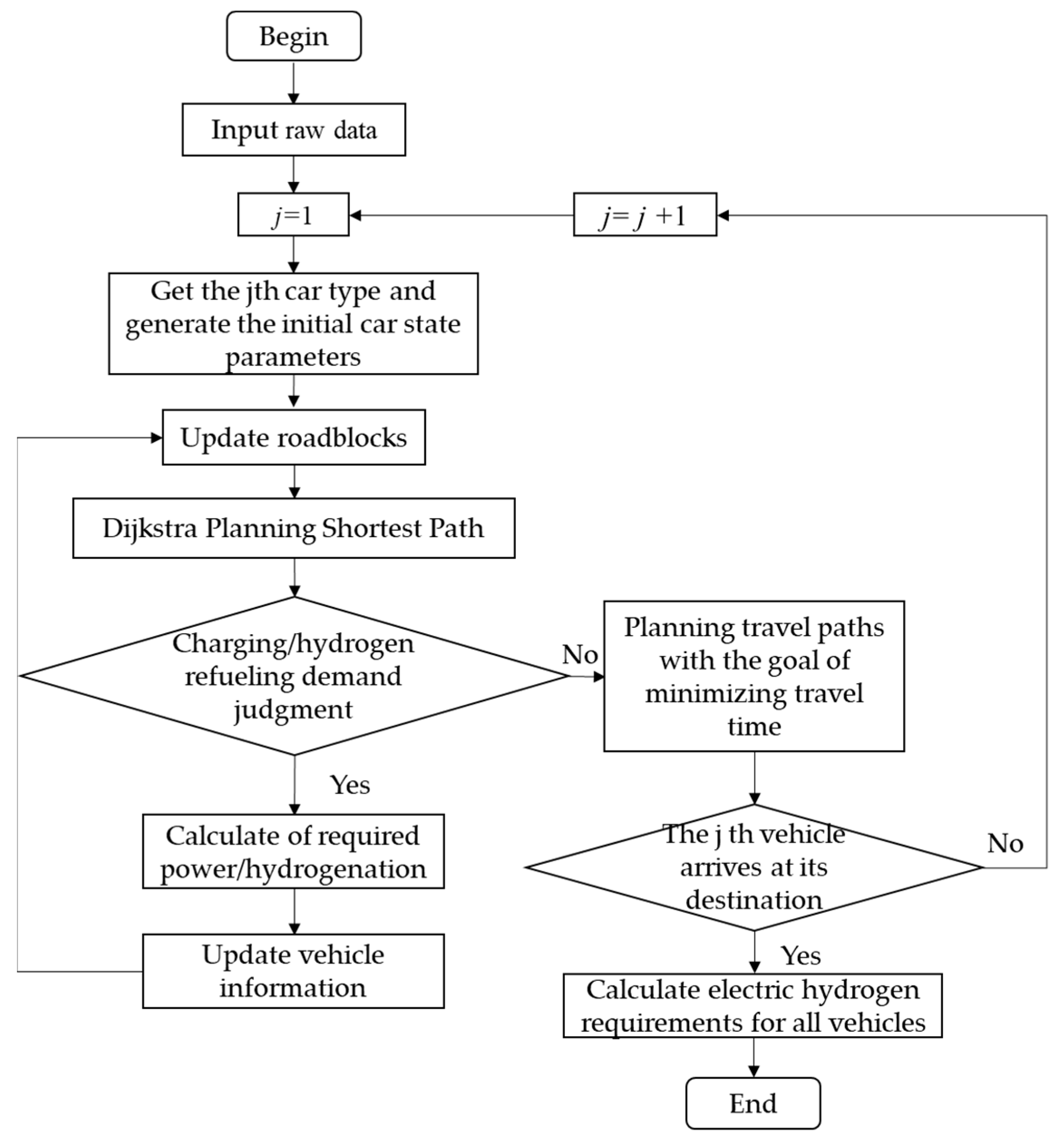
3.2.2. Vehicle Path Planning
3.2.3. EV Electricity Demand and HFCV Hydrogen Demand Calculation
4. Site Selection for Capacity Determination Based on Voronoi Diagram with Particle Swarm Algorithm
4.1. The Steps for Selecting the Initial Site for EHCIS
- (1)
- Calculate the electric and hydrogen energy demand of automobiles at each transportation node;
- (2)
- Randomly generate N EHCIS site coordinates in the planning area and compile them as the initial particle X;
- (3)
- Generate a Voronoi diagram [31] with each initial station site as a growth kernel, and the area formed by the growth is the service area of each charging station;
- (4)
- Using the investment and construction cost of the EHCIS and the user’s refueling loss cost as the site selection and capacity model, the particle swarm algorithm determines the optimal site distribution.
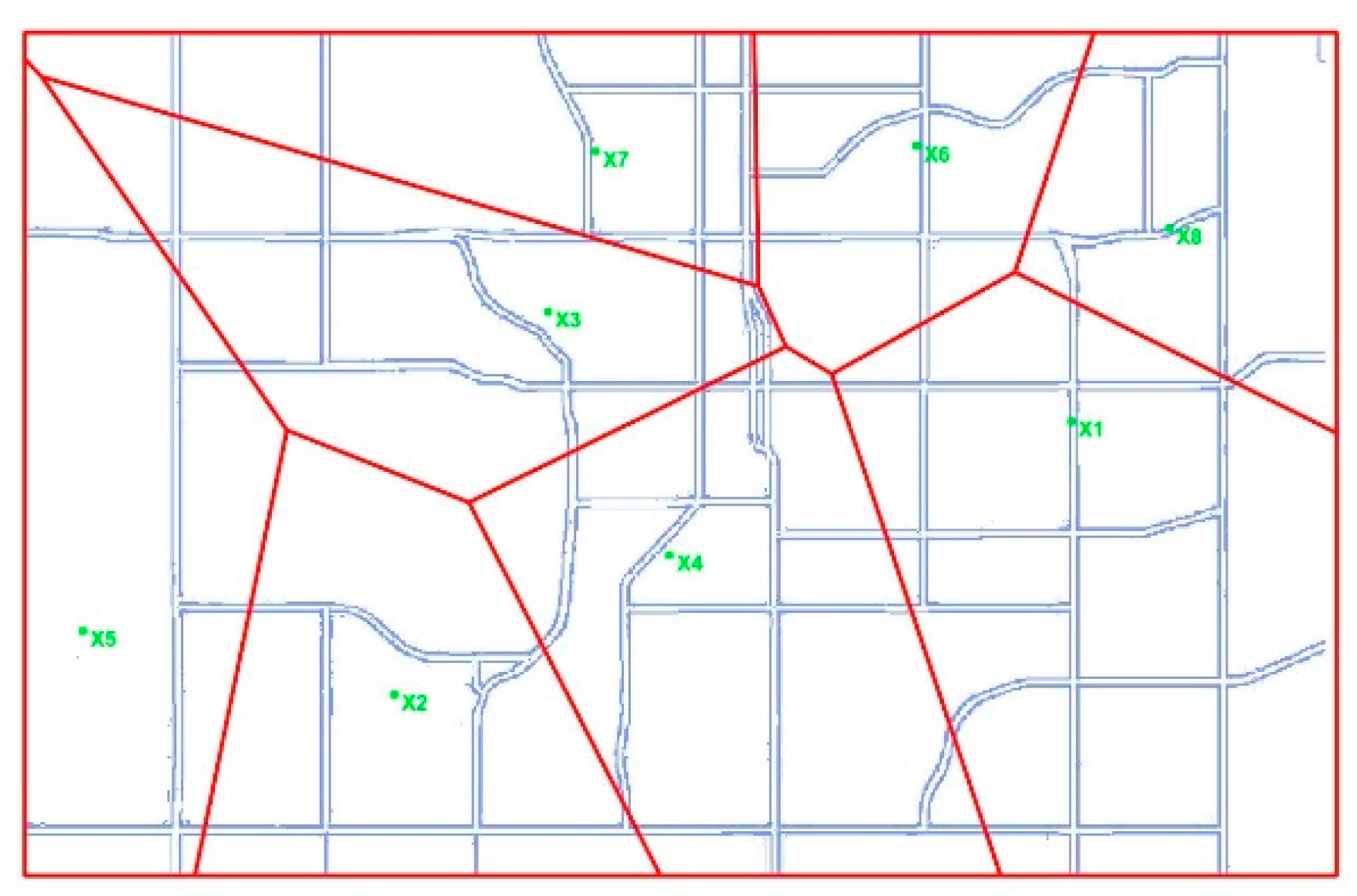
4.2. Voronoi Diagram Based on the Division of the Scope of Service of the Electric Hydrogen Refueling Integrated Station
5. Siting and Capacity Modeling of an EHCIS
5.1. Objective Function
5.2. Determination of the Number of Hydrogen Dispensers for Charging Piles at EHCIS
5.3. Constraints
5.4. Improved Particle Swarm Optimization Algorithm
5.4.1. Weighting Update Strategy
5.4.2. Solution Process
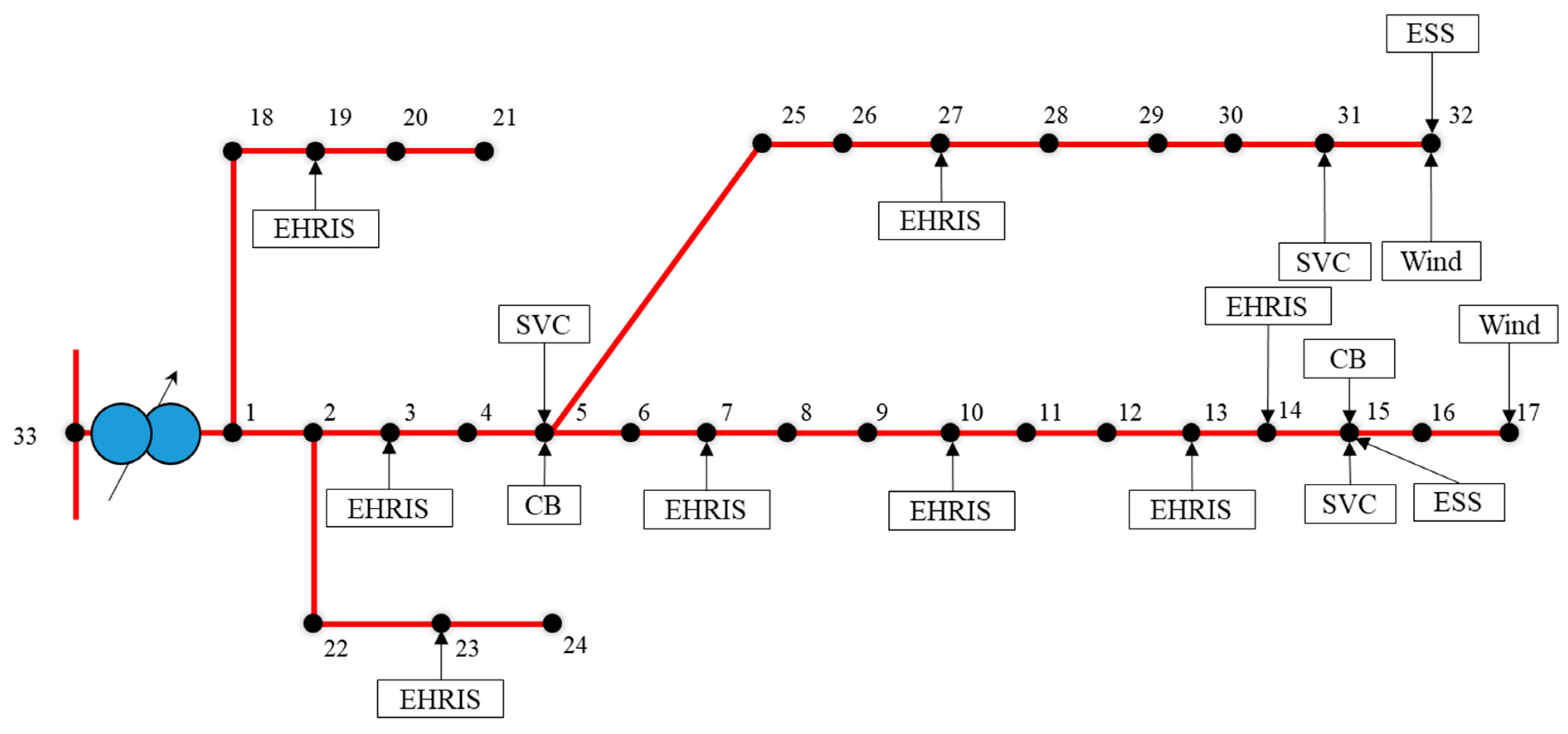
5.5. Grid Planning for Combined Electric Hydrogen Charging Station
6. Active Management Element Modeling
6.1. OLTC Modeling
6.2. Modeling of Reactive Power Regulation Devices
6.3. Modeling of Energy Storage Systems
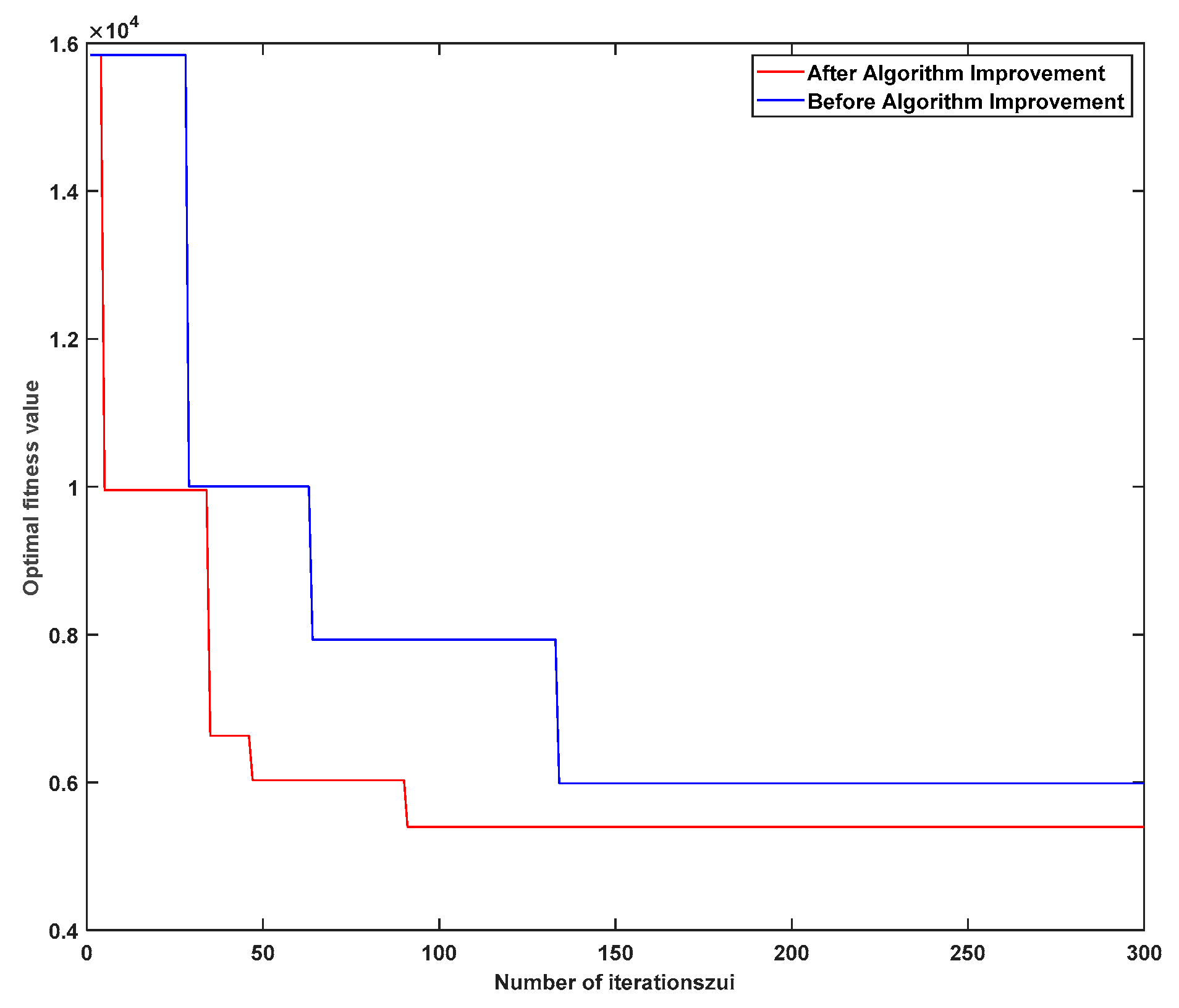
7. Algorithm Analysis
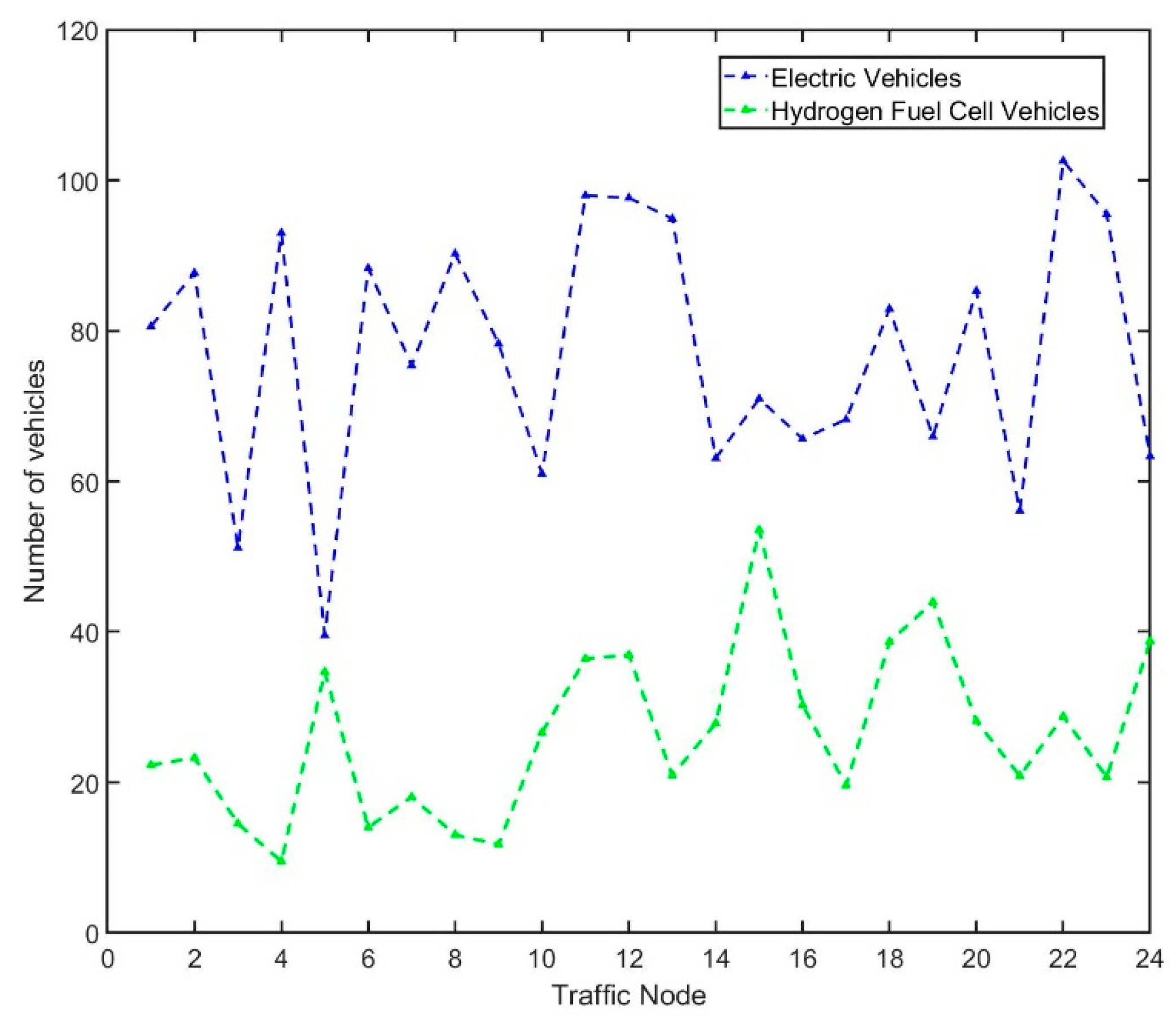
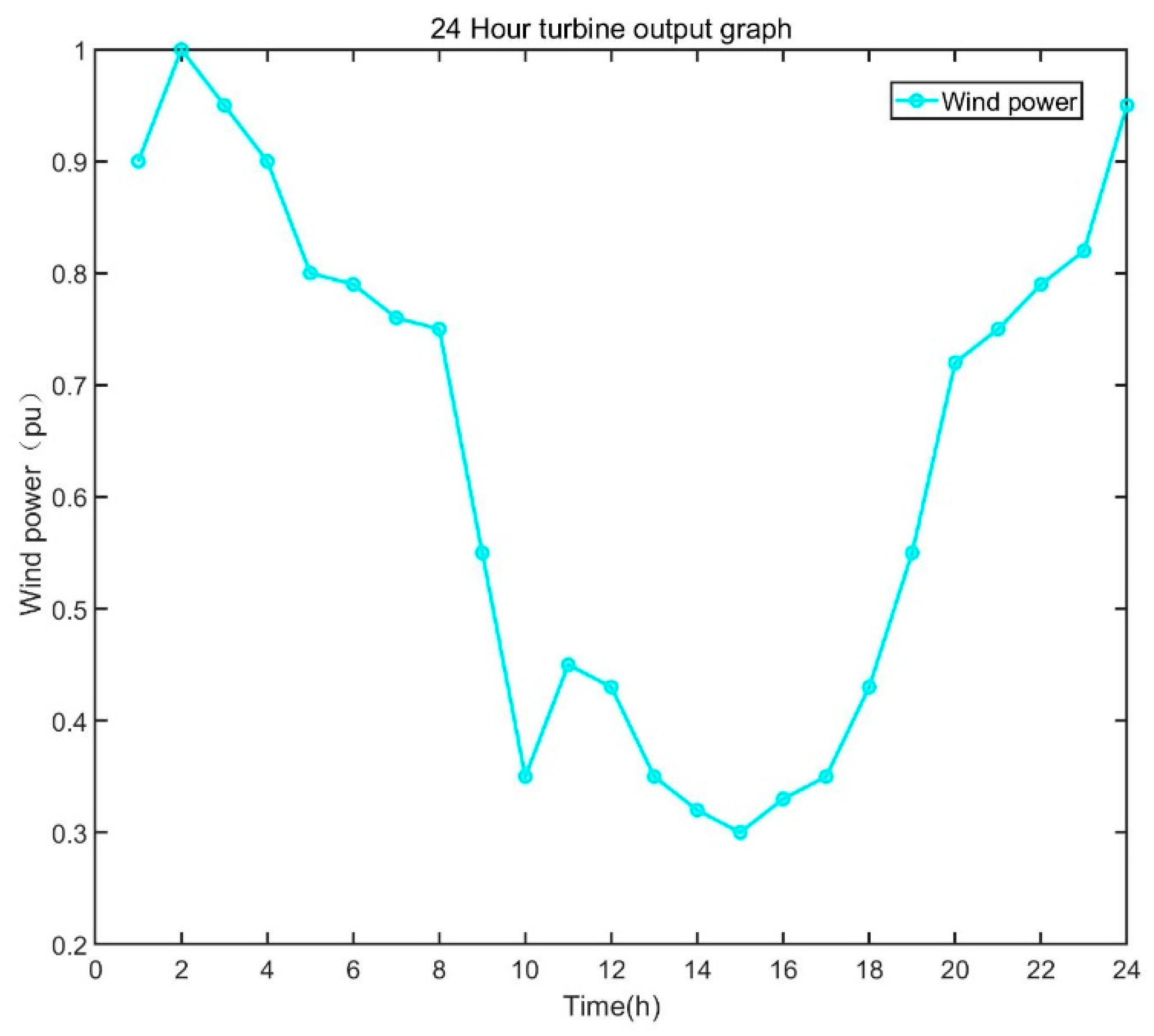
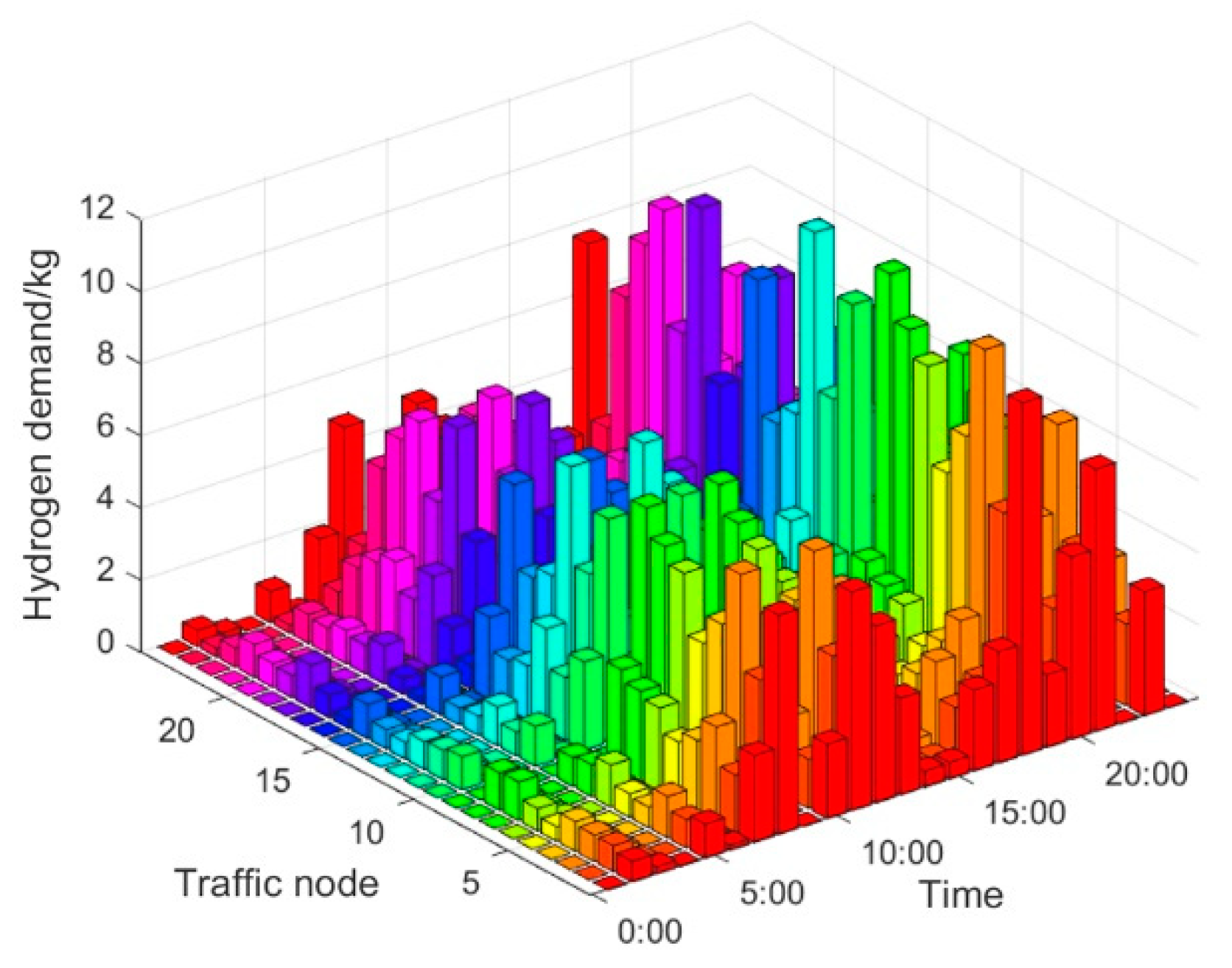
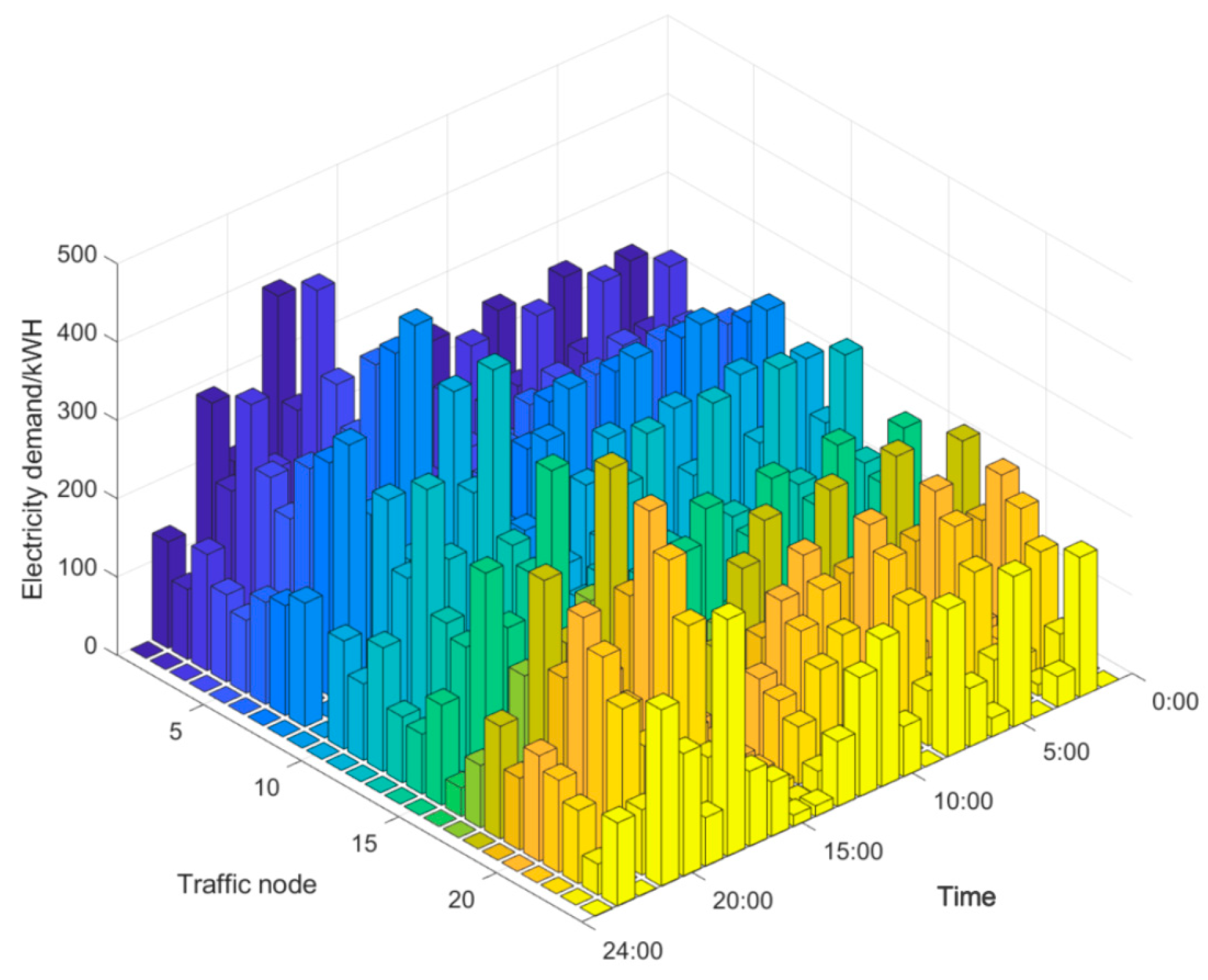
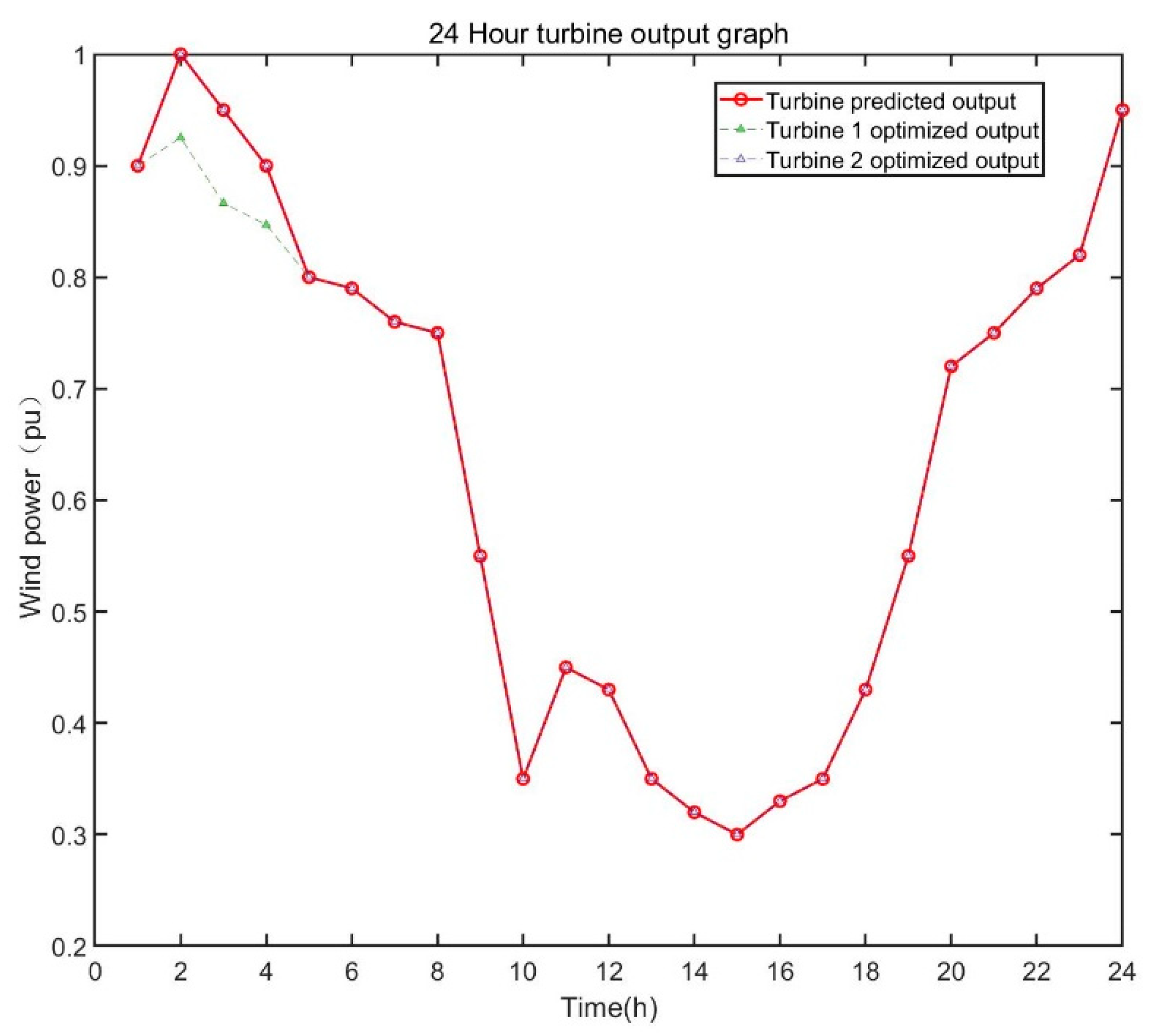
7.1. Electricity-Hydrogen Demand Calculations
7.2. Simulation Results
- (1)
- Time complexity:
- (2)
- Space complexity:
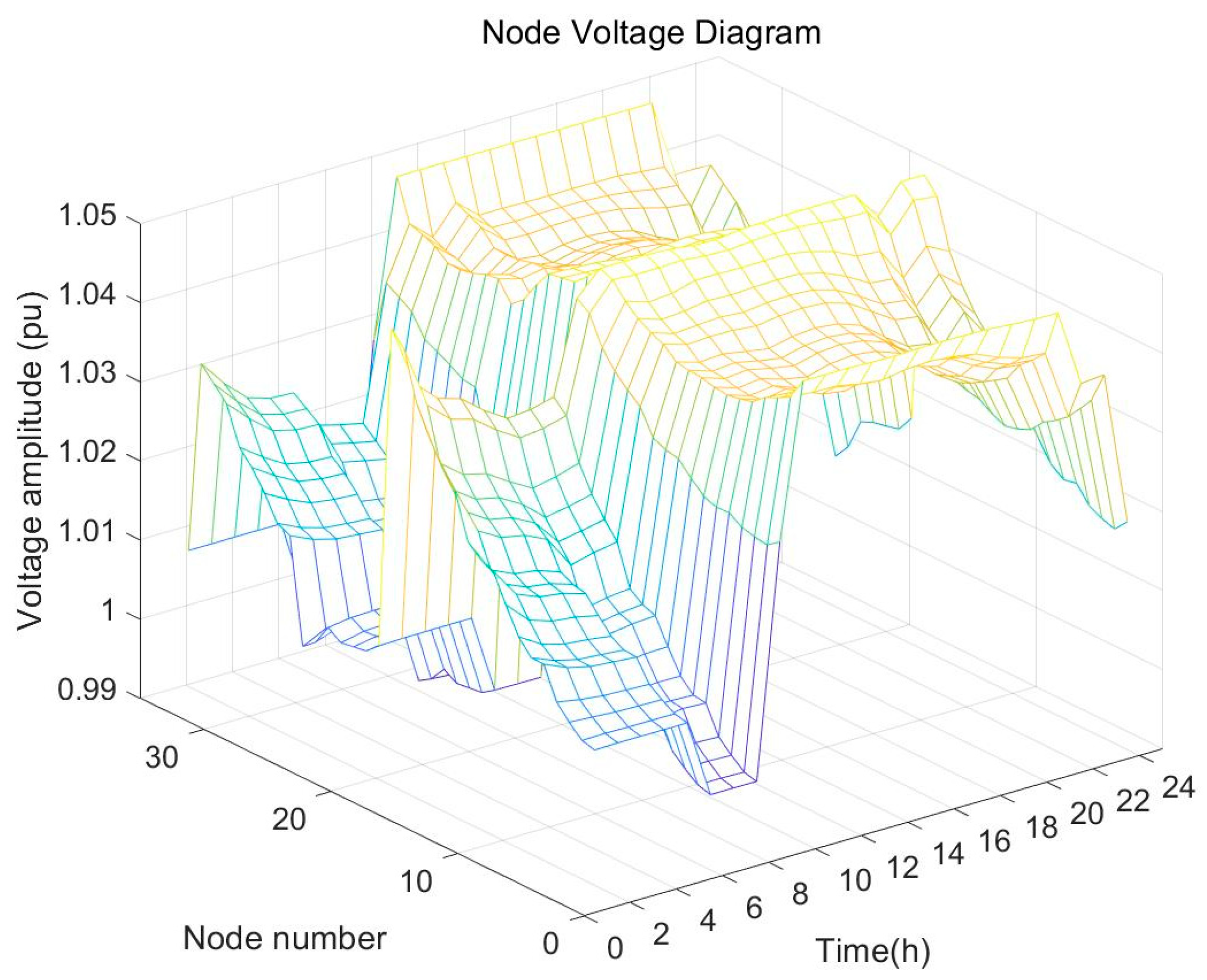
7.3. Integrated Distribution Network Planning
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Peak Period | Level Period | Valley Period | |
|---|---|---|---|
| Time | (12:00–15:00) (20:00–23:00) | (9:00–12:00) (15:00–20:00) (23:00–0:00) | (0:00–9:00) |
| price of electricity (¥/kWh) | 0.56 | 0.39 | 0.30 |
| Nodes | Unit Capacity/Mvar | Quantities |
|---|---|---|
| 5, 31 | 0.01 | 5 |
| Nodes | Limit of Power/MW | Limit of Capacity/(MW·h) | Charging Efficiency | Discharging Efficiency |
|---|---|---|---|---|
| 15, 32 | 0.3 | 1.5 | 0.9 | 1.11 |
| Nodes | Compensation Coverage |
|---|---|
| 5, 15, 31 | [−0.1, 0.3] |
References
- Mahmud, N.; Zahedi, A.J.R.; Reviews, S.E. Review of control strategies for voltage regulation of the smart distribution network with high penetration of renewable distributed generation. Renew. Sustain. Energy Rev. 2016, 64, 582–595. [Google Scholar] [CrossRef]
- Manoharan, Y.; Hosseini, S.E.; Butler, B.; Alzhahrani, H.; Senior, B.T.F.; Ashuri, T.; Krohn, J. Hydrogen fuel cell vehicles; Current status and future prospect. Appl. Sci. 2019, 9, 2296. [Google Scholar] [CrossRef]
- Xu, H.; Miao, S.; Zhang, C.; Shi, D. Optimal placement of charging infrastructures for large-scale integration of pure electric vehicles into grid. Int. J. Electr. Power Energy Syst. 2013, 53, 159–165. [Google Scholar] [CrossRef]
- Su, S. Method of Location and Capacity Determination of Intelligent Charging Pile Based on Recurrent Neural Network. World Electr. Veh. J. 2022, 13, 186. [Google Scholar] [CrossRef]
- Awasthi, A.; Venkitusamy, K.; Padmanaban, S.; Selvamuthukumaran, R.; Blaabjerg, F.; Singh, A.K. Optimal planning of electric vehicle charging station at the distribution system using hybrid optimization algorithm. Energy 2017, 133, 70–78. [Google Scholar] [CrossRef]
- Yang, G.; Jiang, Y.; You, S. Planning and operation of a hydrogen supply chain network based on the off-grid wind-hydrogen coupling system. Int. J. Hydrogen Energy 2020, 45, 20721–20739. [Google Scholar] [CrossRef]
- Sun, H.; He, C.; Wang, H.; Zhang, Y.; Lv, S.; Xu, Y. Hydrogen station siting optimization based on multi-source hydrogen supply and life cycle cost. Int. J. Hydrogen Energy 2017, 42, 23952–23965. [Google Scholar] [CrossRef]
- Kuby, M.; Lines, L.; Schultz, R.; Xie, Z.; Kim, J.-G.; Lim, S. Optimization of hydrogen stations in Florida using the flow-refueling location model. Int. J. Hydrogen Energy 2009, 34, 6045–6064. [Google Scholar] [CrossRef]
- Gu, J.; Wang, C.; Xie, D. Research on optimal operation of electricity-hydrogen integrated station in electricity market environment. J. Electr. Power Sci. Technol. 2022, 37, 130–139. [Google Scholar]
- Gao, C.; Wang, W.; Chen, T. Capacity Planning of Electric-hydrogen Integrated Energy Station Based on Reversible Solid Oxide Battery. Proc. Chin. Soc. Electr. Eng. 2022, 42, 6155–6169. [Google Scholar] [CrossRef]
- LeBlanc, L.J.; Morlok, E.K.; Pierskalla, W.P. An efficient approach to solving the road network equilibrium traffic assignment problem. Transp. Res. 1975, 9, 309–318. [Google Scholar] [CrossRef]
- Cervero, D.; Fotopoulou, M.; Muñoz-Cruzado, J.; Rakopoulos, D.; Stergiopoulos, F.; Nikolopoulos, N.; Voutetakis, S.; Sanz, J.F. Solid State Transformers: A Critical Review of Projects with Relevant Prototypes and Demonstrators. Electronics 2023, 12, 931. [Google Scholar] [CrossRef]
- Alba, J.M.-C.; Fuertes, J.B.; Gomez, A.M.M.; Osorio, J.F.S.; Puyal, E.L. 50-kW Modular V2G SiC Charger Station in Energy Island Microgrids: A Real Use-Case in Madeira Island. In Proceedings of the PCIM Europe 2022; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 10–12 May 2022; pp. 1–9. [Google Scholar]
- Biya, T.S.; Sindhu, M.R. Design and Power Management of Solar Powered Electric Vehicle Charging Station with Energy Storage System. In Proceedings of the 2019 3rd International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 12–14 June 2019; pp. 815–820. [Google Scholar]
- Chen, M.; Lu, H.; Chang, X.; Liao, H. An optimization on an integrated energy system of combined heat and power, carbon capture system and power to gas by considering flexible load. Energy 2023, 273, 127203. [Google Scholar] [CrossRef]
- Xue, P.; Zhao, B.; Zhang, L.; Deng, M.; Liu, J.; Huang, Y.; He, Z. Planning Method for Electric Vehicle Charging Station Considering Reliability Constraint. In Proceedings of the 2023 Panda Forum on Power and Energy (PandaFPE), Chengdu, China, 27–30 April 2023; pp. 1557–1561. [Google Scholar]
- Chen, Z.; Chen, Y.; Che, S. Framework of Integrated Charging Station for Renewable Energy Vehicle and Energy Optimal Dispatching Method. Autom. Electr. Power Syst. 2019, 43, 41–49. [Google Scholar] [CrossRef]
- Chen, L.; Yang, F.; Xing, Q.; Wu, S.; Wang, R.; Chen, J. Spatial-temporal distribution prediction of charging load for electric vehicles based on dynamic traffic information. In Proceedings of the 4th IEEE Conference on Energy Internet and Energy System Integration, EI2 2020, Wuhan, China, 30 October–1 November 2020; pp. 1269–1274. [Google Scholar]
- Abdelouadoud, S.Y.; Girard, R.; Neirac, F.-P.; Guiot, T. Optimal power flow of a distribution system based on increasingly tight cutting planes added to a second order cone relaxation. Int. J. Electr. Power Energy Syst. 2015, 69, 9–17. [Google Scholar] [CrossRef]
- Yuan, T.; Ji, L.; Tian, X.; Li, G. Synergistic Optimal Operation of Electricity-Hydrogen Systems Considering Hydrogen Refueling Loads for Fuel Cell Vehicles. Autom. Electr. Power Syst. 2023, 47, 16–25. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Y.; Figueiredo, A. Charging load forecasting of electric vehicles based on multi-source information fusion and its influence on distribution network. Electr. Power Autom. Equip. 2018, 38, 1–10. [Google Scholar] [CrossRef]
- Iliopoulou, C.; Kampitakis, E.; Kepaptsoglou, K.; Vlahogianni, E.I. Dynamic traffic-aware auction-based signal control under vehicle to infrastructure communication. Phys. A Stat. Mech. Its Appl. 2022, 608, 128258. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Qian, W.; Hu, K.; Zhou, X.; Li, X. Spatio-temporal dynamic load forecasting of charging pile based on spatio-temporal neural network. Shaanxi Electr. Power 2019, 47, 50–54. [Google Scholar]
- Zheng, Y.; Feng, L.I.; Dong, J. Optimal dispatch strategy of spatio-temporal flexibility for electric vehicle charging and discharging in vehicle-road-grid mode. Autom. Electr. Power Syst. 2022, 46, 88–97. [Google Scholar]
- Zhang, L.; Xu, C.; Wang, L.; Li, J.; Chen, X.; Yang, X.; Shi, Y. OD matrix based spatiotemporal distribution of EV charging load prediction. Power Syst. Prot. Control 2021, 49, 82–91. [Google Scholar] [CrossRef]
- Zu, S.; Sun, L. Research on location planning of urban charging stations and battery-swapping stations for electric vehicles. Energy Rep. 2022, 8, 508–522. [Google Scholar] [CrossRef]
- Huang, C.-Y.; Lai, C.-Y.; Cheng, K.-T. CHAPTER 4—Fundamentals of algorithms. In Electronic Design Automation; Wang, L.-T., Chang, Y.-W., Cheng, K.-T., Eds.; Morgan Kaufmann: Boston, MA, USA, 2009; pp. 173–234. [Google Scholar]
- Yen, J.Y. An algorithm for finding shortest routes from all source nodes to a given destination in general networks. Q. Appl. Math. 1970, 27, 526–530. [Google Scholar] [CrossRef]
- Yu, T.; Ma, J. A review of the link traffic time estimation of urban traffic. In Proceedings of the 2016 IEEE International Conference on Intelligent Transportation Engineering, ICITE 2016, Singapore, 20–22 August 2016; pp. 123–127. [Google Scholar]
- Shao, C.; Li, X.; Qian, T.; Wang, X.; Wang, X. Simulation of EV Fast Charging Load Based on Traffic Equilibrium. Proc. Chin. Soc. Electr. Eng. 2021, 41, 1368–1376. [Google Scholar] [CrossRef]
- Othman, A.M.; Gabbar, H.A.; Pino, F.; Repetto, M. Optimal electrical fast charging stations by enhanced descent gradient and Voronoi diagram. Comput. Electr. Eng. 2020, 83, 106574. [Google Scholar] [CrossRef]
- Alreni, A.; Momcheva, G.; Pavlov, S. Voronoi Diagrams and Perlin Noise for Simulation of Irregular Artefacts in Microscope Scans. In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (Bioimaging), Vol 2, Online, 9–11 February 2022; SCITEPRESS: Setúbal, Portugal, 2022; pp. 117–122. [Google Scholar] [CrossRef]
- Li, Y.; Cui, F.; Li, L. An integrated optimization model for the location of hydrogen refueling stations. Int. J. Hydrogen Energy 2018, 43, 19636–19649. [Google Scholar] [CrossRef]
- Yang, G.; Jiang, Y. Siting and sizing of the hydrogen refueling stations with on-site water electrolysis hydrogen production based on robust regret. Int. J. Energy Res. 2020, 44, 8340–8361. [Google Scholar] [CrossRef]
- Cao, F.; Meng, Q.; Miao, P.; Li, Y. Optimal substation planning based on improved weighted voronoi diagram and genetic algorithm. Power Syst. Technol. 2015, 39, 511–516. [Google Scholar] [CrossRef]
- Hou, H.; Tang, J.; Wang, Y.; Xia, X.; Wang, F.; Hu, P.; Xie, C. Layout planning of electric vehicle charging stations in urban areas. Power Syst. Prot. Control 2022, 50, 181–187. [Google Scholar] [CrossRef]
- Yan, G.; Liu, H.; Han, N.; Chen, S.; Yu, D. An Optimization Method for Location and Capacity Determination of Charging Stations Considering Spatial and Temporal Distribution of Electric Vehicles. Proc. Chin. Soc. Electr. Eng. 2021, 41, 6271–6283. [Google Scholar] [CrossRef]
- Liu, F. Design of Human Motion Training Motion Capture Model Based on Improved PSO Algorithm. In Proceedings of the 1st IEEE International Conference on Applied Intelligence and Sustainable Computing, ICAISC 2023, Dharwad, India, 16–17 June 2023. [Google Scholar]
- Choulli, I.; Elyaqouti, M.; Arjdal, E.; Ben Hmamou, D.; Saadaoui, D.; Lidaighbi, S.; Elhammoudy, A.; Abazine, I. Hybrid optimization based on the analytical approach and the particle swarm optimization algorithm (Ana-PSO) for the extraction of single and double diode models parameters. Energy 2023, 283, 129043. [Google Scholar] [CrossRef]
- Gao, H.; Liu, J.; Shen, X.; Xu, R. Optimal Power Flow Research in Active Distribution Network and Its Application Examples. Proc. Chin. Soc. Electr. Eng. 2017, 37, 1634–1644. [Google Scholar] [CrossRef]
- Low, S.H. Convex relaxation of optimal power flow—Part i: Formulations and equivalence. IEEE Trans. Control Netw. Syst. 2014, 1, 15–27. [Google Scholar] [CrossRef]
- Song, Z.; Hu, Y.; Guo, H.; Ma, J.; Song, B.; Xu, M.; Liu, Z. Optimal Design Method for the Partitioning of OLTC-Inverter Control Parameters in Distribution Stations with High-proportion Residential Photovoltaics. In Proceedings of the 2022 International Conference on Innovations and Development of Information Technologies and Robotics, IDITR 2022, Chengdu, China, 27–29 May 2022; pp. 43–49. [Google Scholar]
- Dabaghi-Zarandi, F.; Behjat, V.; Gauvin, M.; Picher, P.; Ezzaidi, H.; Fofana, I. Power Transformers OLTC Condition Monitoring Based on Feature Extraction from Vibro-Acoustic Signals: Main Peaks and Euclidean Distance. Sensors 2023, 23, 7020. [Google Scholar] [CrossRef]
- Huang, J.; Geng, Y.; Jin, Q.; Chen, X.; Yan, J.; Geng, Y. The Influence of the Dispersion in Pre-arcing Time of Vacuum Circuit Breakers on the Controlled Switching of Capacitor Banks. In Proceedings of the 6th International Conference on Electric Power Equipment—Switching Technology, ICEPE-ST 2022, Seoul, Republic of Korea, 15–18 March 2022; pp. 206–211. [Google Scholar]
- Zein, H.; Saodah, S.; Utami, S.; Wachjoe, C.K. Static VAR Compensation Capacity for Bus Voltage Setting in Electric Power Systems. In Proceedings of the 4th International Conference on Technology and Policy in Energy and Electric Power, ICT-PEP 2022, Jakarta, Indonesia, 18–20 October 2022; pp. 1–6. [Google Scholar]
- Liu, S.; Wei, C.; Wang, H.; Yang, W.; Zhang, J.; Wang, Z.; Zhao, W.; Lee, P.S.; Cai, G. Processable nanoarchitectonics of two-dimensional metallo-supramolecular polymer for electrochromic energy storage devices with high coloration efficiency and stability. Nano Energy 2023, 110, 108337. [Google Scholar] [CrossRef]
- Qian, Y.; Lyu, Z.; Zhang, Q.; Lee, T.H.; Kang, T.K.; Sohn, M.; Shen, L.; Kim, D.H.; Kang, D.J. High-Performance Flexible Energy Storage Devices Based on Graphene Decorated with Flower-Shaped MoS2 Heterostructures. Micromachines 2023, 14, 297. [Google Scholar] [CrossRef] [PubMed]
- Jin, B.; Liu, Z.; Liao, Y. Exploring the Impact of Regional Integrated Energy Systems Performance by Energy Storage Devices Based on a Bi-Level Dynamic Optimization Model. Energies 2023, 16, 2629. [Google Scholar] [CrossRef]
- Zhou, L.; Peng, W.; Ma, L.; Yu, W. Orderly Charging and Discharging Scheduling of DC V2G Charging Pile Considering Load Balance of Electricity Reticulation. In Proceedings of the 1st IEEE International Conference on Applied Intelligence and Sustainable Computing, ICAISC 2023, Dharwad, India, 16–17 June 2023. [Google Scholar]
- Jiang, Y.; Yang, G.; Zhu, Z. Wind-Hydrogen-Electricity Coupled Network Planning Considering Traffic Flow Capture. Autom. Electr. Power Syst. 2021, 45, 19–28. [Google Scholar] [CrossRef]
- Kashem, M.A.; Ganapathy, V.; Jasmon, G.B.; Buhari, M.I. A novel method for loss minimization in distribution networks. In DRPT2000. International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Proceedings (Cat. No.00EX382); IEEE: Piscataway, NJ, USA, 2000; pp. 251–256. [Google Scholar]
- Song, Y.; Hu, X. Learning-based demand-supply-coupled charging station location problem for electric vehicle demand management. Transp. Res. Part D Transp. Environ. 2023, 125, 103975. [Google Scholar] [CrossRef]
- Wang, M.; Dong, X.; Zhai, Y. Optimal Configuration of the Integrated Charging Station for PV and Hydrogen Storage. Energies 2021, 14, 7087. [Google Scholar] [CrossRef]


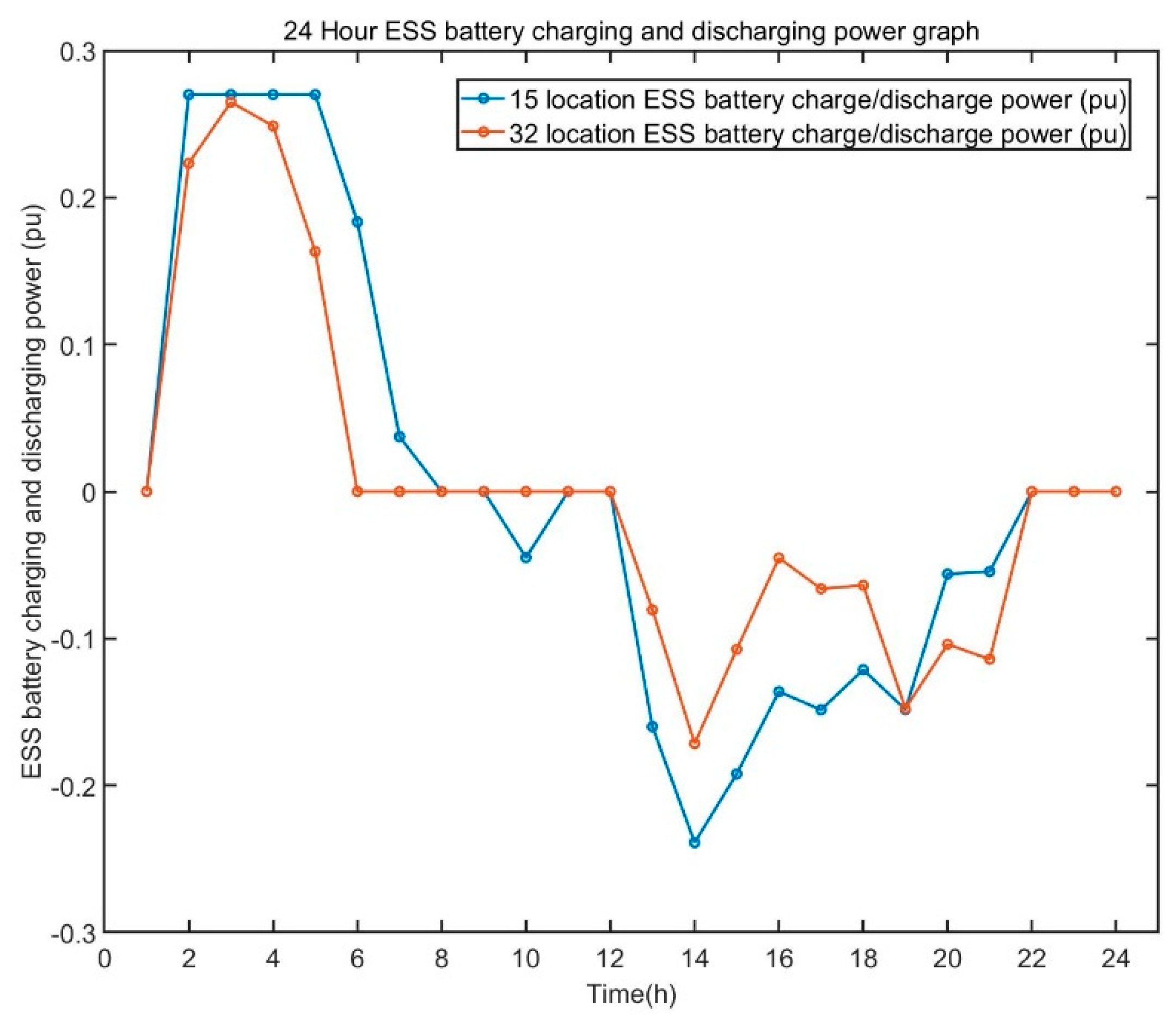

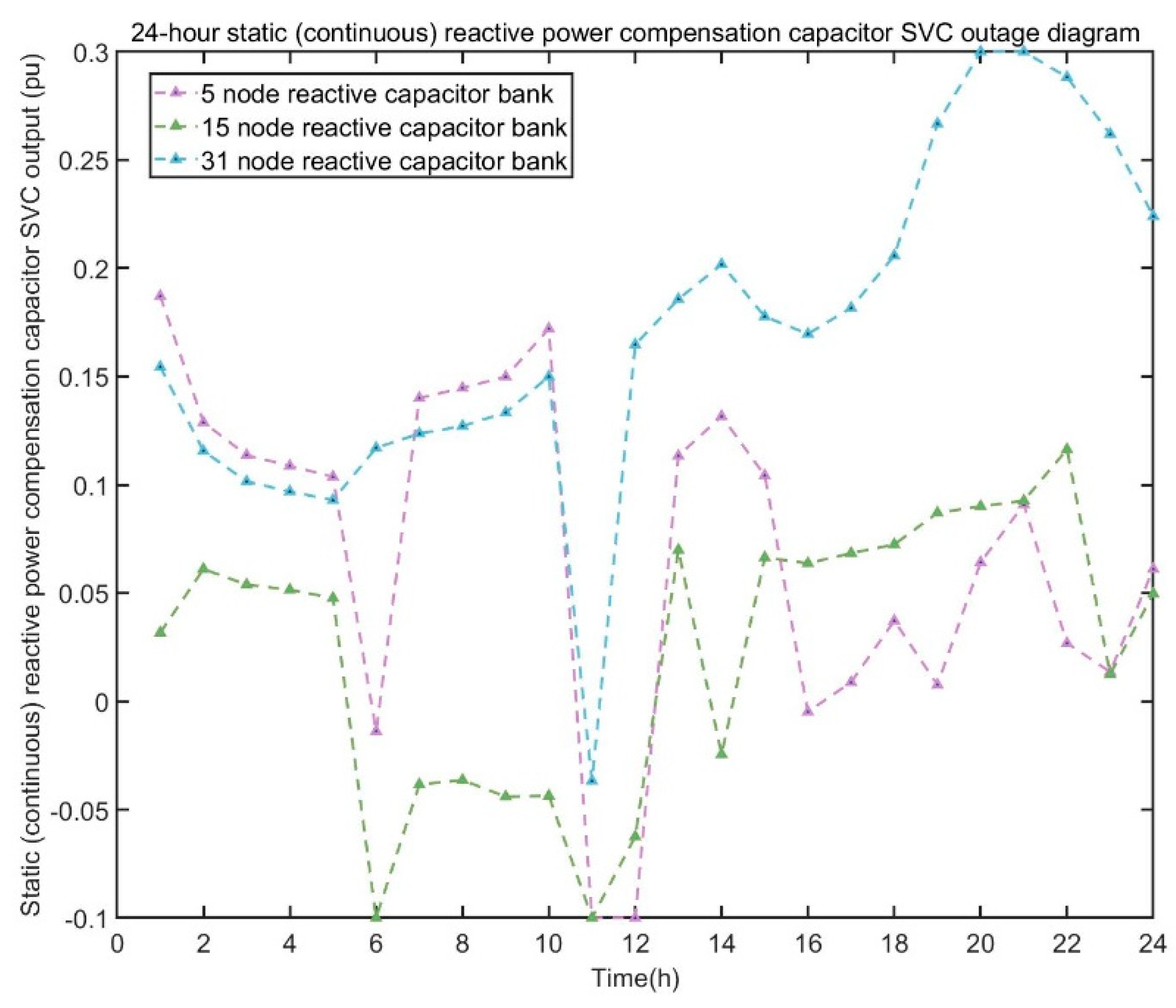
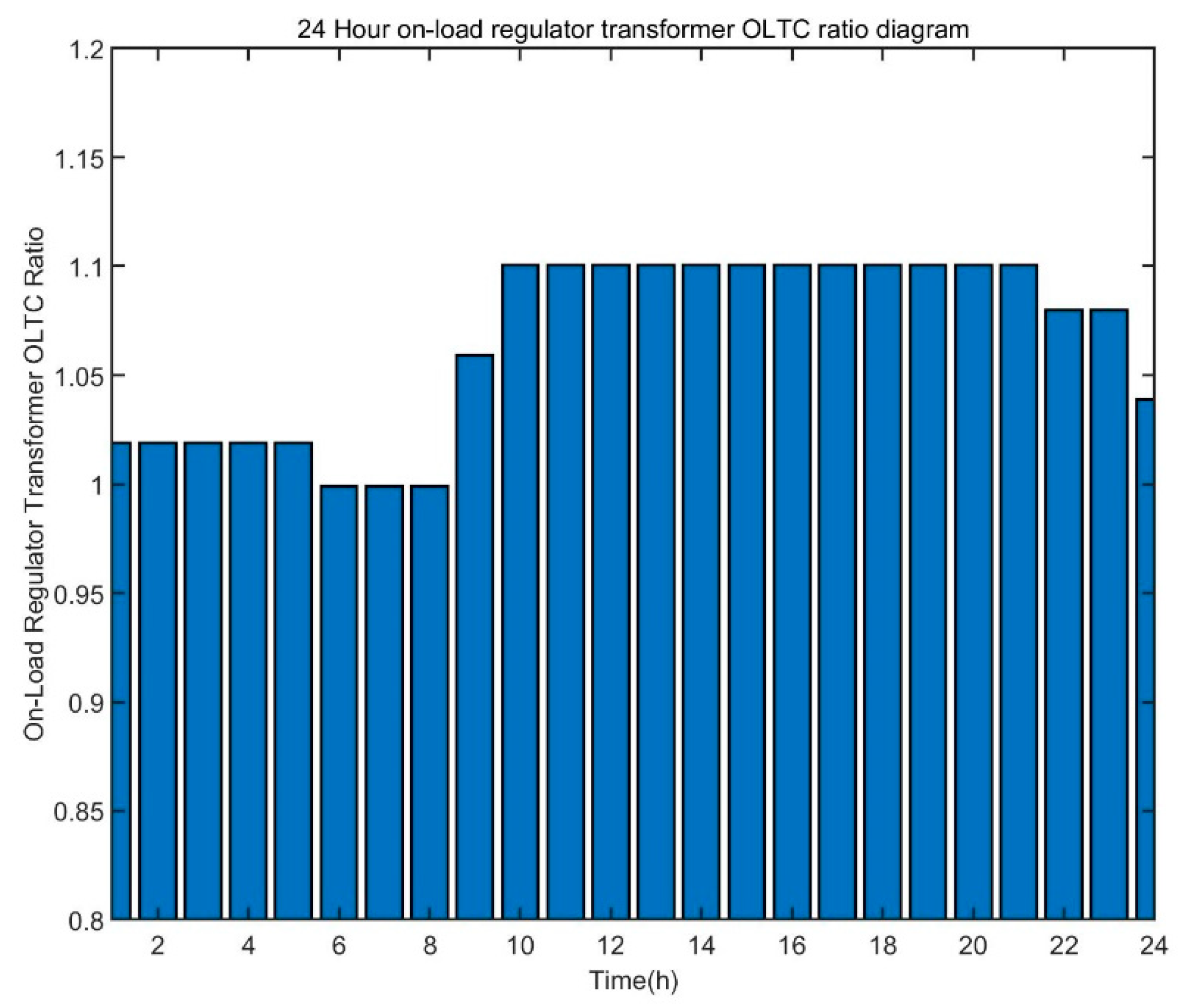
| Parameter | Explanation | Parameter | Explanation |
|---|---|---|---|
| EV Starting Point | EV travel time | ||
| EV Endpoints | Position of the EV at time t | ||
| EV Capacity | Initial power of EV | ||
| Amount of power remaining in the EV at time t | Consumption per kilometer Electricity consumption | ||
| HFCV starting point | HFCV endpoint | ||
| HFCV position at time t | HFCV position at time t | ||
| HFCV hydrogen content | Initial hydrogen for hydrogen | ||
| Amount of hydrogen remaining in the HFCV at time t | Hydrogen consumption per kilometer |
| Quantities | C1 (×106 ¥) | C2 (×106 ¥) | C3 (×106 ¥) | C4 (×106 ¥) | C (×106 ¥) |
|---|---|---|---|---|---|
| 7 | 5063.76 | 253.19 | 39.7 | 42.83 | 5379.48 |
| 8 | 5083.92 | 254.19 | 38.38 | 22.08 | 5398.57 |
| 9 | 5115.72 | 255.78 | 38.18 | 22.34 | 5432.02 |
| 10 | 5153.09 | 257.65 | 37.43 | 21.8 | 5469.97 |
| EHCIS Number | Number of Charging Piles | Number of Electrolytic Tanks | Hydrogen Storage Tank Capacity/(kg) | Number of Hydrogen Injectors |
|---|---|---|---|---|
| X1 | 17 | 97 | 7.9 | 1 |
| X2 | 10 | 96 | 7.6 | 1 |
| X3 | 13 | 136 | 11.2 | 1 |
| X4 | 23 | 298 | 20.1 | 1 |
| X5 | 2 | 19 | 1.46 | 1 |
| X6 | 14 | 132 | 10.1 | 1 |
| X7 | 27 | 199 | 19.4 | 1 |
| X8 | 1 | 7 | 0.54 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, X.; Yang, H.; Ge, Y.; Yuan, T. Site Selection and Capacity Determination of Electric Hydrogen Charging Integrated Station Based on Voronoi Diagram and Particle Swarm Algorithm. Energies 2024, 17, 418. https://doi.org/10.3390/en17020418
Tian X, Yang H, Ge Y, Yuan T. Site Selection and Capacity Determination of Electric Hydrogen Charging Integrated Station Based on Voronoi Diagram and Particle Swarm Algorithm. Energies. 2024; 17(2):418. https://doi.org/10.3390/en17020418
Chicago/Turabian StyleTian, Xueqin, Heng Yang, Yangyang Ge, and Tiejiang Yuan. 2024. "Site Selection and Capacity Determination of Electric Hydrogen Charging Integrated Station Based on Voronoi Diagram and Particle Swarm Algorithm" Energies 17, no. 2: 418. https://doi.org/10.3390/en17020418
APA StyleTian, X., Yang, H., Ge, Y., & Yuan, T. (2024). Site Selection and Capacity Determination of Electric Hydrogen Charging Integrated Station Based on Voronoi Diagram and Particle Swarm Algorithm. Energies, 17(2), 418. https://doi.org/10.3390/en17020418






