Wind Turbine Damage Equivalent Load Assessment Using Gaussian Process Regression Combining Measurement and Synthetic Data
Abstract
1. Introduction
1.1. Motivation
1.2. Objective
- Create a database of synthetic DEL based on publicly available turbine models with SCADA wind measurements as input.
- Develop a probabilistic model based on the database that represents the distribution of the descriptive statistics and DEL at varying wind speeds.
- Validate the probabilistic model by contrasting its output with the limited available measurements.
1.3. Paper Outline
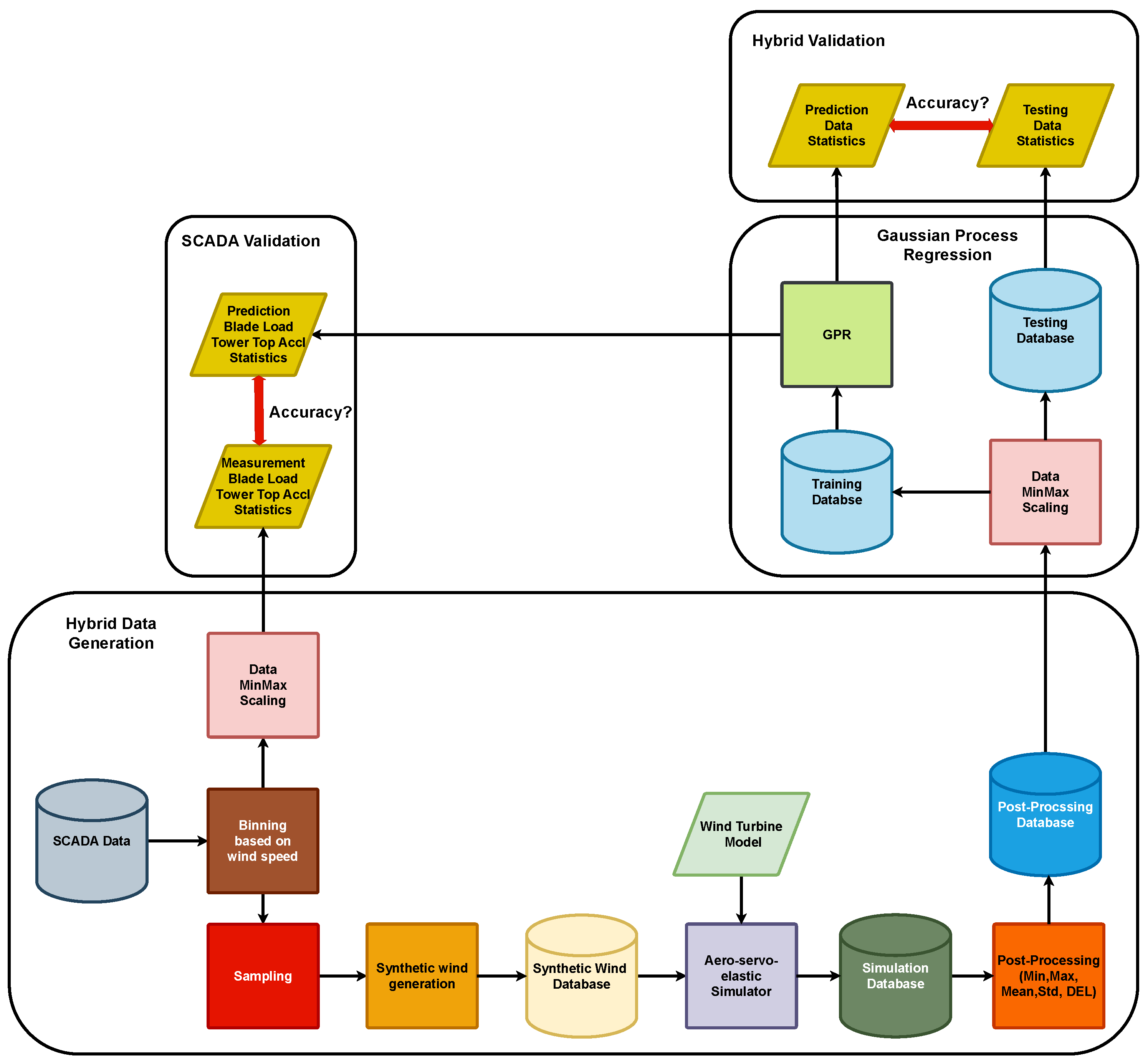
2. Methods
2.1. Supervisory Control and Data Acquisition Measurement, Binning, and Scaling
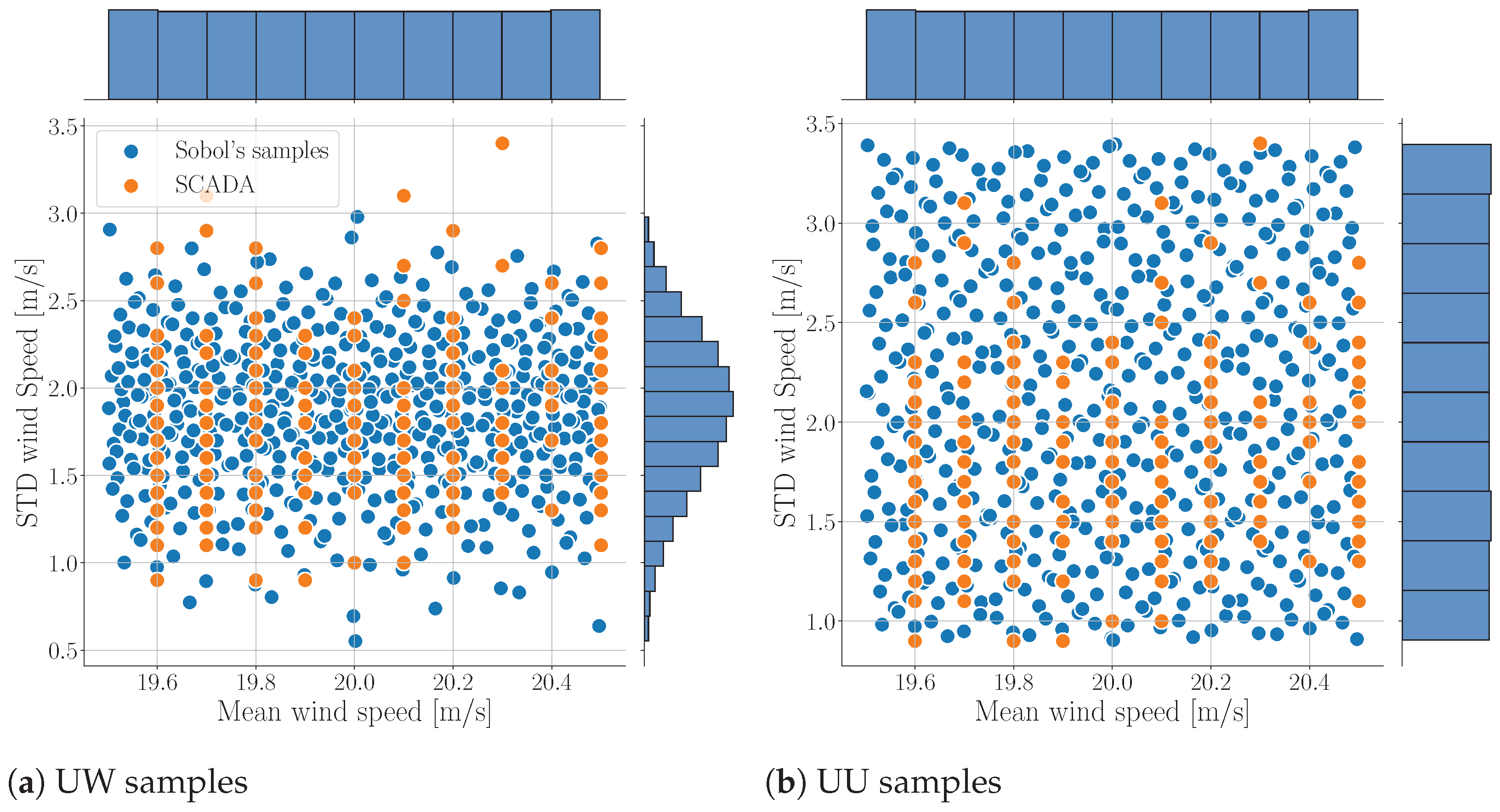
2.2. Joint Distributions and Sampling
2.3. Synthetic Wind Generation, Wind Turbine Models, and Aero-Servo-Elastic Simulations
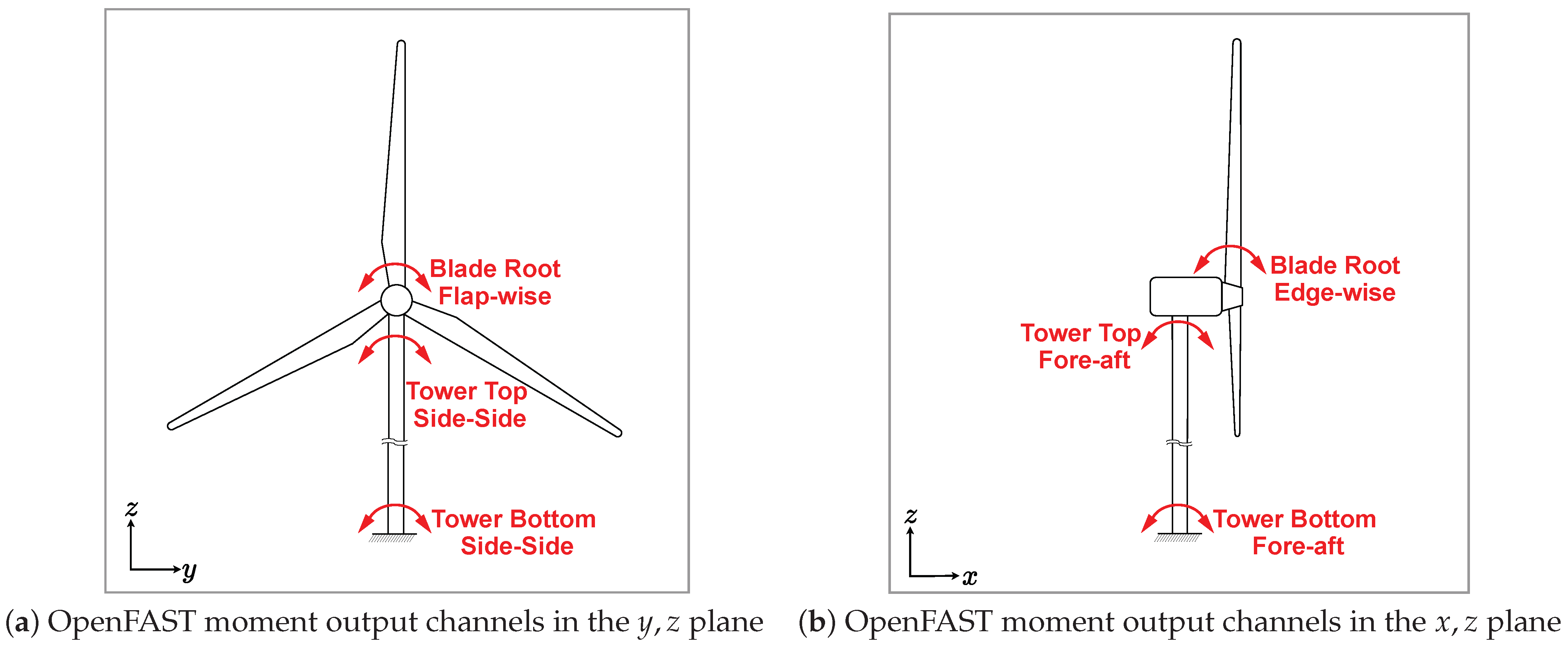
2.4. Post-Processing Database
2.5. Gaussian Process Regression
2.6. Measurement Statistics and Error Metrics
3. Results and Discussion
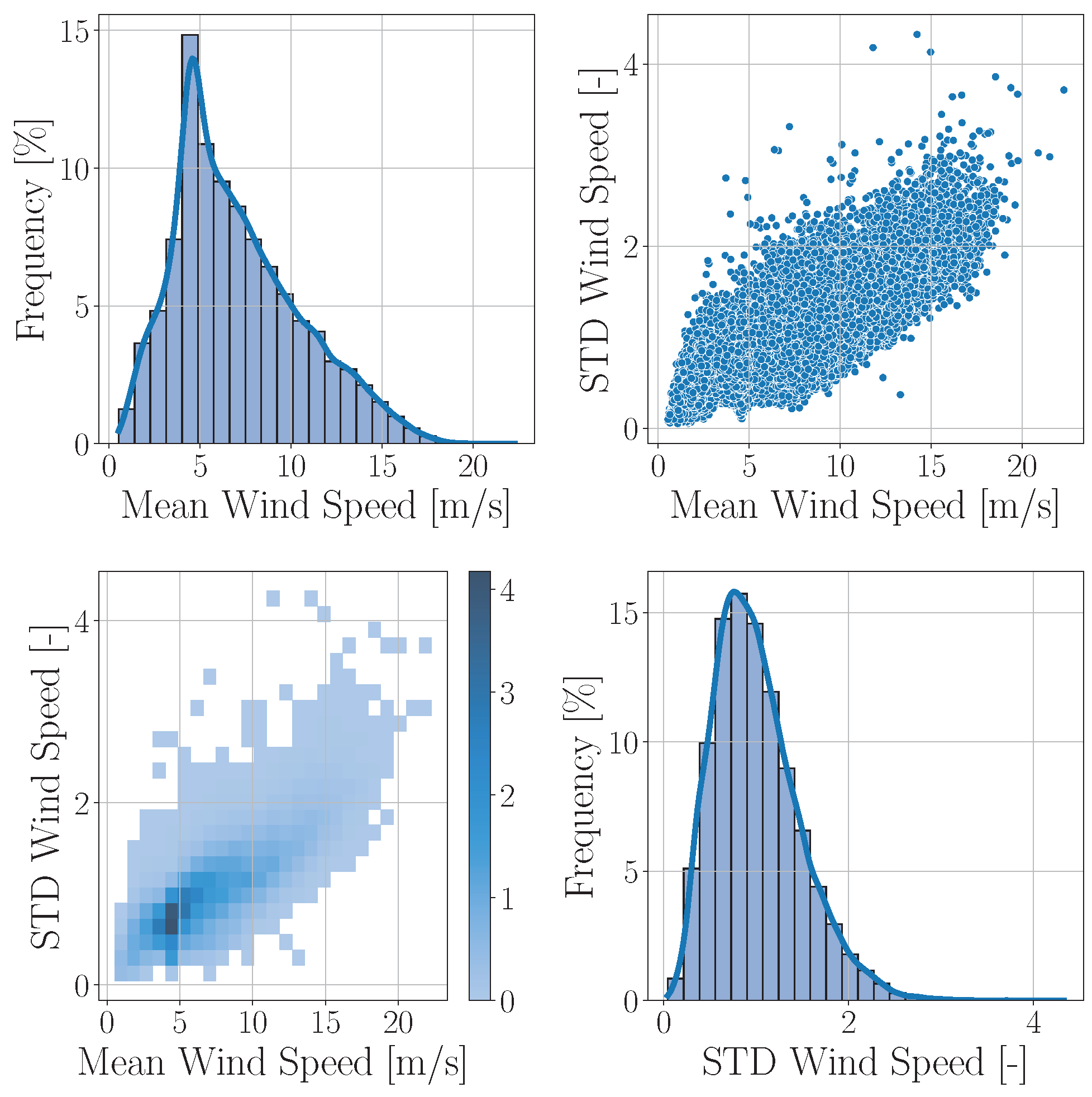
3.1. SCADA Measurement
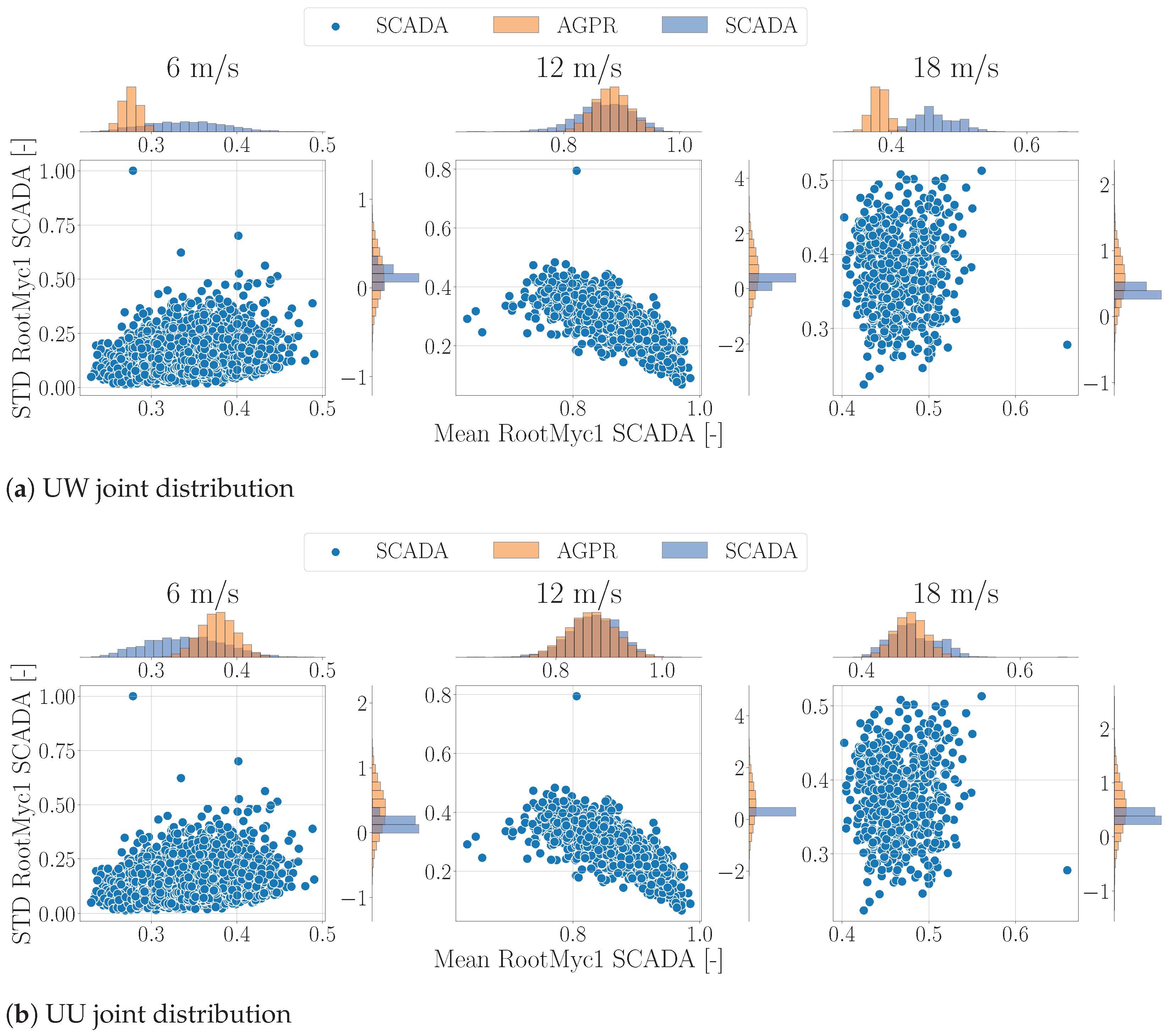
3.2. Joint Distributions and Sampling
3.3. TurbSim and OpenFAST Output
3.4. AGPR Training and Testing
3.5. Wind Turbine Model Verification
3.6. AGPR Testing Results—Hybrid Simulations
3.7. AGPR Testing Results—SCADA Measurement
3.8. How Can We Use This Model?
4. Conclusions
4.1. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ciang, C.C.; Lee, J.R.; Bang, H.J. Structural Health Monitoring for a Wind Turbine System: A Review of Damage Detection Methods. Meas. Sci. Technol. 2008, 19, 122001. [Google Scholar] [CrossRef]
- Martinez-Luengo, M.; Kolios, A.; Wang, L. Structural Health Monitoring of Offshore Wind Turbines: A Review through the Statistical Pattern Recognition Paradigm. Renew. Sustain. Energy Rev. 2016, 64, 91–105. [Google Scholar] [CrossRef]
- Yang, W.; Tavner, P.J.; Crabtree, C.J.; Feng, Y.; Qiu, Y. Wind Turbine Condition Monitoring: Technical and Commercial Challenges. Wind Energy 2014, 17, 673–693. [Google Scholar] [CrossRef]
- Tchakoua, P.; Wamkeue, R.; Ouhrouche, M.; Slaoui-Hasnaoui, F.; Tameghe, T.A.; Ekemb, G. Wind Turbine Condition Monitoring: State-of-the-Art Review, New Trends, and Future Challenges. Energies 2014, 7, 2595–2630. [Google Scholar] [CrossRef]
- Leahy, K.; Gallagher, C.; O’Donovan, P.; O’Sullivan, D.T.J. Issues with Data Quality for Wind Turbine Condition Monitoring and Reliability Analyses. Energies 2019, 12, 201. [Google Scholar] [CrossRef]
- Badrzadeh, B.; Bradt, M.; Castillo, N.; Janakiraman, R.; Kennedy, R.; Klein, S.; Smith, T.; Vargas, L. Wind Power Plant SCADA and Controls. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Marti-Puig, P.; Blanco-M., A.; Serra-Serra, M.; Solé-Casals, J. Wind Turbine Prognosis Models Based on SCADA Data and Extreme Learning Machines. Appl. Sci. 2021, 11, 590. [Google Scholar] [CrossRef]
- Tautz-Weinert, J.; Watson, S.J. Using SCADA Data for Wind Turbine Condition Monitoring—A Review. IET Renew. Power Gener. 2017, 11, 382–394. [Google Scholar] [CrossRef]
- Toft, H.S.; Svenningsen, L.; Moser, W.; Sørensen, J.D.; Thøgersen, M.L. Assessment of Wind Turbine Structural Integrity Using Response Surface Methodology. Eng. Struct. 2016, 106, 471–483. [Google Scholar] [CrossRef]
- Stewart, G. Design Load Analysis of Two Floating Offshore Wind Turbine Concepts. Doctoral Dissertation, University of Massachusetts Amherst, Amherst, MA, USA, 2016. [Google Scholar] [CrossRef]
- Teixeira, R.; O’Connor, A.; Nogal, M.; Krishnan, N.; Nichols, J. Analysis of the Design of Experiments of Offshore Wind Turbine Fatigue Reliability Design with Kriging Surfaces. Procedia Struct. Integr. 2017, 5, 951–958. [Google Scholar] [CrossRef]
- Müller, K.; Dazer, M.; Cheng, P.W. Damage Assessment of Floating Offshore Wind Turbines Using Response Surface Modeling. Energy Procedia 2017, 137, 119–133. [Google Scholar] [CrossRef]
- Müller, K.; Cheng, P.W. Application of a Monte Carlo Procedure for Probabilistic Fatigue Design of Floating Offshore Wind Turbines. Wind Energy Sci. 2018, 3, 149–162. [Google Scholar] [CrossRef]
- Dimitrov, N.; Kelly, M.C.; Vignaroli, A.; Berg, J. From Wind to Loads: Wind Turbine Site-Specific Load Estimation with Surrogate Models Trained on High-Fidelity Load Databases. Wind Energy Sci. 2018, 3, 767–790. [Google Scholar] [CrossRef]
- Haghi, R.; Crawford, C. Surrogate Models for the Blade Element Momentum Aerodynamic Model Using Non-Intrusive Polynomial Chaos Expansions. Wind Energy Sci. 2022, 7, 1289–1304. [Google Scholar] [CrossRef]
- Schröder, L.; Dimitrov, N.K.; Verelst, D.R. A Surrogate Model Approach for Associating Wind Farm Load Variations with Turbine Failures. Wind Energy Sci. 2020, 5, 1007–1022. [Google Scholar] [CrossRef]
- Dimitrov, N.; Göçmen, T. Virtual Sensors for Wind Turbines with Machine Learning-Based Time Series Models. Wind Energy 2022, 25, 1626–1645. [Google Scholar] [CrossRef]
- Maldonado-Correa, J.; Martín-Martínez, S.; Artigao, E.; Gómez-Lázaro, E. Using SCADA Data for Wind Turbine Condition Monitoring: A Systematic Literature Review. Energies 2020, 13, 3132. [Google Scholar] [CrossRef]
- Gonzalez, E.; Stephen, B.; Infield, D.; Melero, J.J. Using High-Frequency SCADA Data for Wind Turbine Performance Monitoring: A Sensitivity Study. Renew. Energy 2019, 131, 841–853. [Google Scholar] [CrossRef]
- Gray, C.S.; Watson, S.J. Physics of Failure Approach to Wind Turbine Condition Based Maintenance. Wind Energy 2010, 13, 395–405. [Google Scholar] [CrossRef]
- Galinos, C.; Dimitrov, N.; Larsen, T.J.; Natarajan, A.; Hansen, K.S. Mapping Wind Farm Loads and Power Production—A Case Study on Horns Rev 1. J. Phys. Conf. Ser. 2016, 753, 032010. [Google Scholar] [CrossRef]
- Alvarez, E.J.; Ribaric, A.P. An Improved-Accuracy Method for Fatigue Load Analysis of Wind Turbine Gearbox Based on SCADA. Renew. Energy 2018, 115, 391–399. [Google Scholar] [CrossRef]
- Remigius, W.D.; Natarajan, A. Identification of Wind Turbine Main-Shaft Torsional Loads from High-Frequency SCADA (Supervisory Control and Data Acquisition) Measurements Using an Inverse-Problem Approach. Wind Energy Sci. 2021, 6, 1401–1412. [Google Scholar] [CrossRef]
- Pandit, R.; Astolfi, D.; Hong, J.; Infield, D.; Santos, M. SCADA Data for Wind Turbine Data-Driven Condition/Performance Monitoring: A Review on State-of-Art, Challenges and Future Trends. Wind Eng. 2023, 47, 422–441. [Google Scholar] [CrossRef]
- Vera-Tudela, L.; Kühn, M. Analysing Wind Turbine Fatigue Load Prediction: The Impact of Wind Farm Flow Conditions. Renew. Energy 2017, 107, 352–360. [Google Scholar] [CrossRef]
- Natarajan, A.; Bergami, L. Determination of Wind Farm Life Consumption in Complex Terrain Using Ten-Minute SCADA Measurements. J. Phys. Conf. Ser. 2020, 1618, 022013. [Google Scholar] [CrossRef]
- Mylonas, C.; Abdallah, I.; Chatzi, E. Conditional Variational Autoencoders for Probabilistic Wind Turbine Blade Fatigue Estimation Using Supervisory, Control, and Data Acquisition Data. Wind Energy 2021, 24, 1122–1139. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar] [CrossRef]
- Pandit, R.K.; Infield, D. SCADA-based Wind Turbine Anomaly Detection Using Gaussian Process Models for Wind Turbine Condition Monitoring Purposes. IET Renew. Power Gener. 2018, 12, 1249–1255. [Google Scholar] [CrossRef]
- Li, Y.; Liu, S.; Shu, L. Wind Turbine Fault Diagnosis Based on Gaussian Process Classifiers Applied to Operational Data. Renew. Energy 2019, 134, 357–366. [Google Scholar] [CrossRef]
- Herp, J.; Ramezani, M.H.; Bach-Andersen, M.; Pedersen, N.L.; Nadimi, E.S. Bayesian State Prediction of Wind Turbine Bearing Failure. Renew. Energy 2018, 116, 164–172. [Google Scholar] [CrossRef]
- Avendaño-Valencia, L.D.; Abdallah, I.; Chatzi, E. Virtual Fatigue Diagnostics of Wake-Affected Wind Turbine via Gaussian Process Regression. Renew. Energy 2021, 170, 539–561. [Google Scholar] [CrossRef]
- Wilkie, D.; Galasso, C. Gaussian Process Regression for Fatigue Reliability Analysis of Offshore Wind Turbines. Struct. Saf. 2021, 88, 102020. [Google Scholar] [CrossRef]
- Singh, D.; Dwight, R.P.; Laugesen, K.; Beaudet, L.; Viré, A. Probabilistic Surrogate Modeling of Offshore Wind-Turbine Loads with Chained Gaussian Processes. J. Phys. Conf. Ser. 2022, 2265, 032070. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Feature Engineering and Selection: A Practical Approach for Predictive Models; CRC Press: Bocca Raton, FL, USA, 2020; Available online: http://www.feat.engineering/ (accessed on 15 September 2023).
- Daley, R. Atmospheric Data Analysis; Number 2; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Sobol’, I.M. On the Distribution of Points in a Cube and the Approximate Evaluation of Integrals. USSR Comput. Math. Math. Phys. 1967, 7, 86–112. [Google Scholar] [CrossRef]
- Kucherenko, S.; Albrecht, D.; Saltelli, A. Exploring Multi-Dimensional Spaces: A Comparison of Latin Hypercube and Quasi Monte Carlo Sampling Techniques. arXiv 2015, arXiv:1505.02350. [Google Scholar]
- Renardy, M.; Joslyn, L.R.; Millar, J.A.; Kirschner, D.E. To Sobol or Not to Sobol? The Effects of Sampling Schemes in Systems Biology Applications. Math. Biosci. 2021, 337, 108593. [Google Scholar] [CrossRef] [PubMed]
- Jonkman, B.J.; Buhl, M.L., Jr. TurbSim User’s Guide: Version 1.50; Technical Report NREL/TP–500-46198; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009. Available online: https://www.nrel.gov/docs/fy09osti/46198.pdf (accessed on 15 September 2023).
- Jonkman, B.; Mudafort, R.M.; Platt, A.; Branlard, E.; Sprague, M.; Jjonkman; HaymanConsulting; Hall, M.; Vijayakumar, G.; Buhl, M.; et al. OpenFAST/openfast: OpenFAST v3.3.0. Zenodo, 28 October 2022. Available online: https://zenodo.org/records/7262094 (accessed on 15 September 2023).
- IEC 61400-1:2019; Wind Energy Generation Systems—Part 1: Design Requirements. International Electrotechnical Commission: Geneva, Switzerland, 2019.
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009.
- Rinker, J.; Dykes, K. WindPACT Reference Wind Turbines; Technical Report NREL/TP–5000-67667, 1432194; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2018. [CrossRef]
- Bortolotti, P.; Tarres, H.C.; Dykes, K.; Merz, K.; Sethuraman, L.; Verelst, D.; Zahle, F. IEA Wind Task 37 on Systems Engineering in Wind Energy—WP2.1 Reference Wind Turbines; Technical Report; International Energy Agency: Paris, France, 2019. [Google Scholar]
- Quon, E. NREL/Openfast-Turbine-Models: A Repository of OpenFAST Turbine Models Developed by NREL Researchers. 2021. GitHub Repository. Available online: https://github.com/NREL/openfast-turbine-models/tree/master (accessed on 15 September 2023).
- Thomsen, K. The Statistical Variation of Wind Turbine Fatigue Loads; Number 1063 in Risø-R; Risø National Laboratory: Roskilde, Denmark, 1998.
- Stiesdal, H. Rotor Loadings on the BONUS 450 kW Turbine. J. Wind Eng. Ind. Aerodyn. 1992, 39, 303–315. [Google Scholar] [CrossRef]
- Matsuishi, M.; Endo, T. Fatigue of metals subjected to varying stress. Jpn. Soc. Mech. Eng. Fukuoka Jpn. 1968, 68, 37–40. [Google Scholar]
- Quiñonero-Candela, J.; Rasmussen, C.E.; Williams, C.K.I. Approximation Methods for Gaussian Process Regression. In Large-Scale Kernel Machines; Bottou, L., Chapelle, O., DeCoste, D., Weston, J., Eds.; The MIT Press: Cambridge, MA, USA, 2007; pp. 203–224. [Google Scholar] [CrossRef]
- Kersting, K.; Plagemann, C.; Pfaff, P.; Burgard, W. Most Likely Heteroscedastic Gaussian Process Regression. In Proceedings of the 24th International Conference on Machine Learning, Corvalis, OR, USA, 20–24 June 2007; pp. 393–400. [Google Scholar] [CrossRef]
- Jankowiak, M.; Pleiss, G.; Gardner, J. Parametric Gaussian Process Regressors. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 4702–4712. [Google Scholar]
- Hensman, J.; Matthews, A.; Ghahramani, Z. Scalable Variational Gaussian Process Classification. In Proceedings of the Eighteenth International Conference on Artificial Intelligence and Statistics, San Diego, CA, USA, 9–12 May 2015; pp. 351–360. [Google Scholar]
- Gardner, J.; Pleiss, G.; Weinberger, K.Q.; Bindel, D.; Wilson, A.G. GPyTorch: Blackbox Matrix-Matrix Gaussian Process Inference with GPU Acceleration. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; Volume 31. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Owen, A.B. On Dropping the First Sobol’ Point. arXiv 2021, arXiv:2008.08051. [Google Scholar]
- Jonkman, J.M.; Buhl, M.L., Jr. Fast User’s Guide-Updated August 2005; Technical Report NREL/TP–500-38230; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2005. Available online: https://www.nrel.gov/docs/fy06osti/38230.pdf (accessed on 15 September 2023).
- Branlard, E. pyfast. 2023. GitHub Repository. Available online: https://github.com/OpenFAST/python-toolbox (accessed on 15 September 2023).
- Lever, J.; Krzywinski, M.; Altman, N. Model Selection and Overfitting. Nat. Methods 2016, 13, 703–704. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems, Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
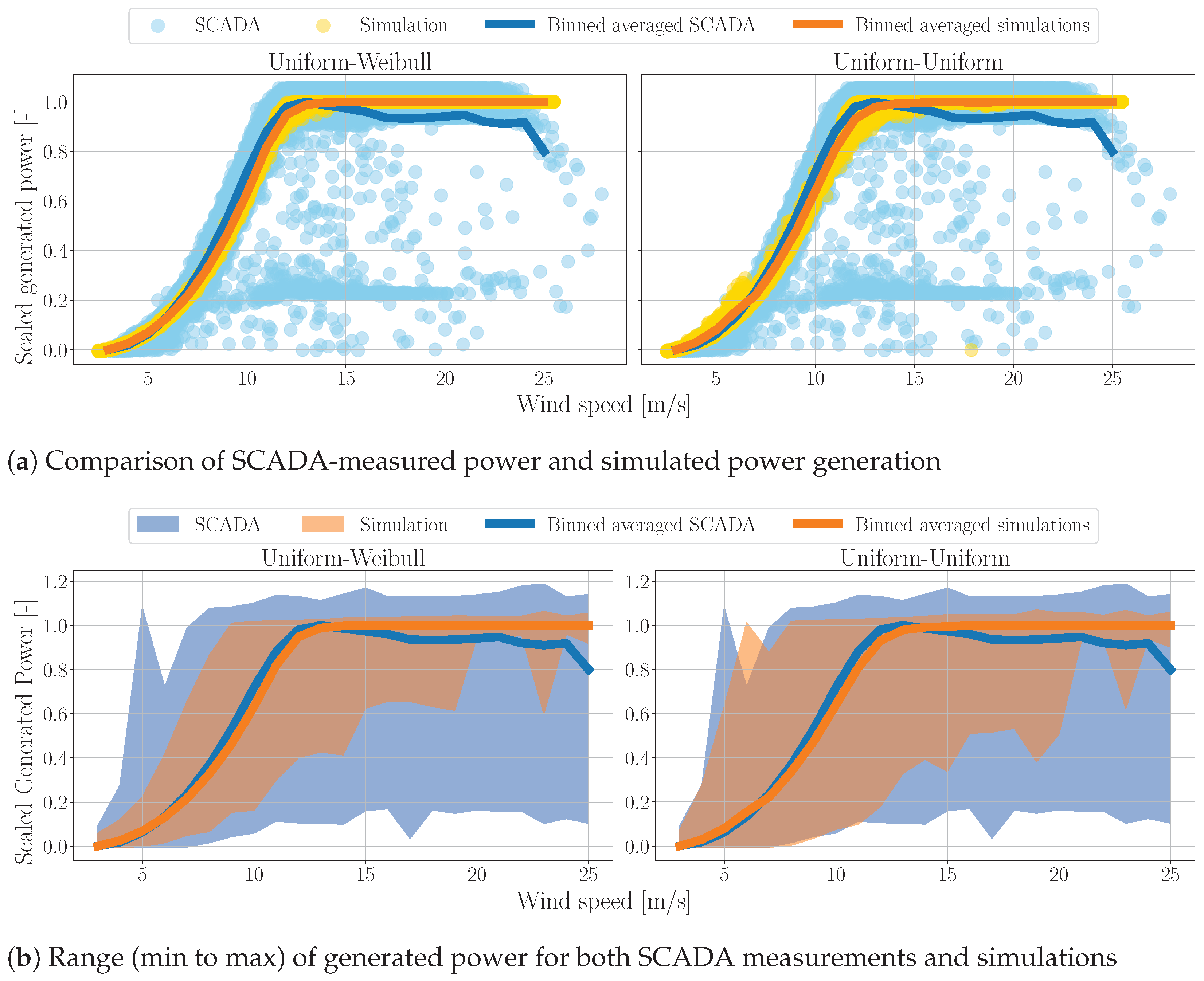
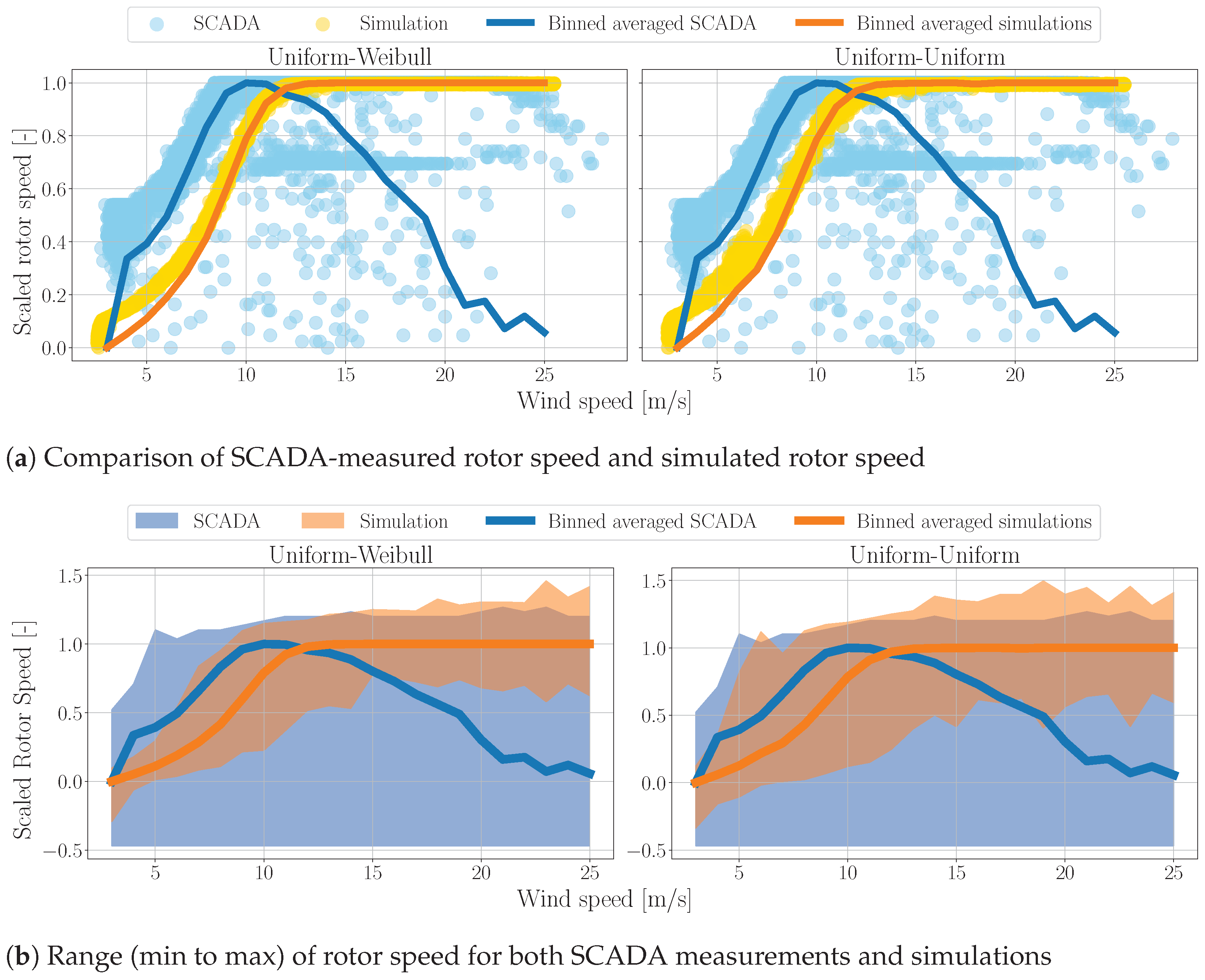
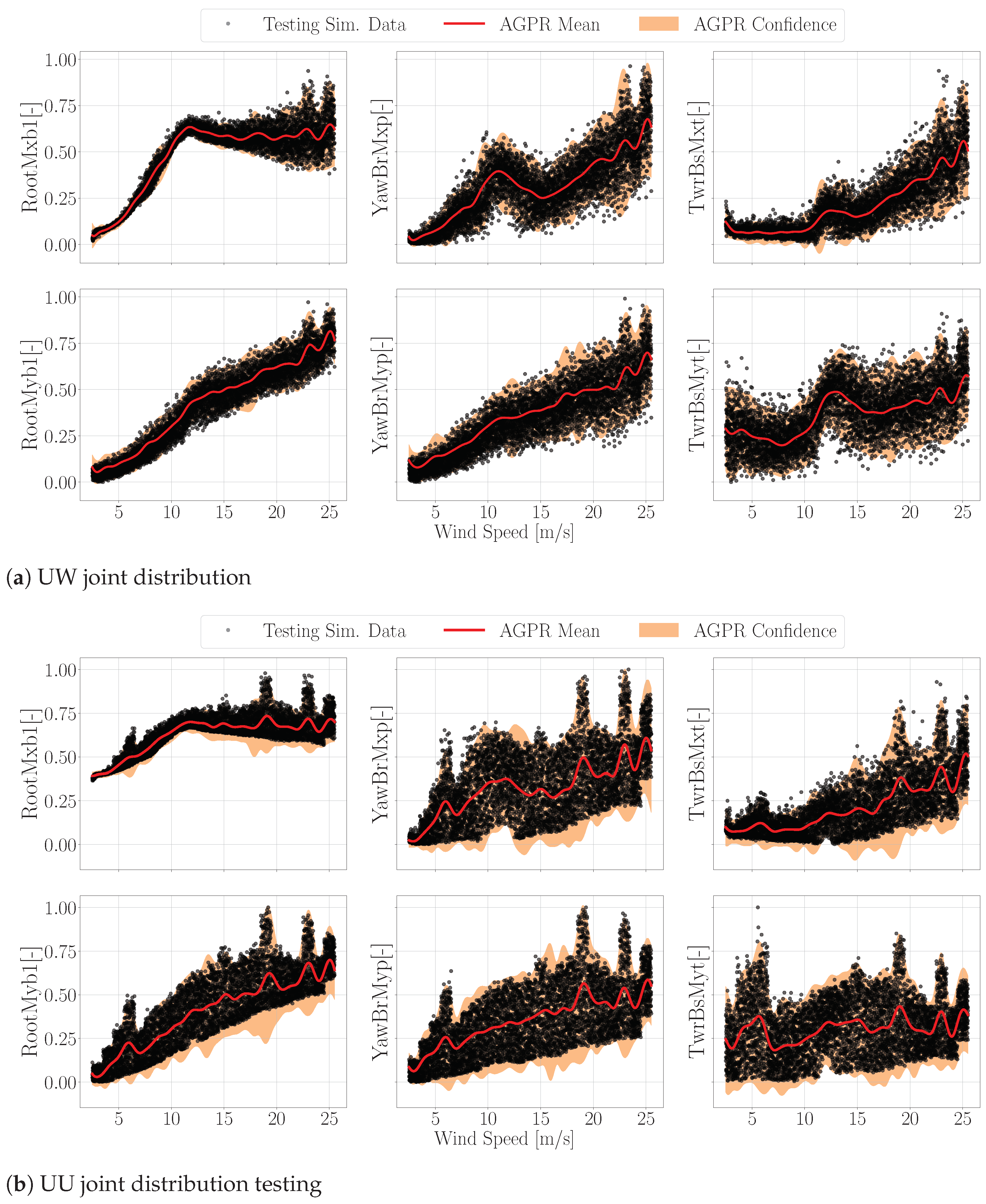
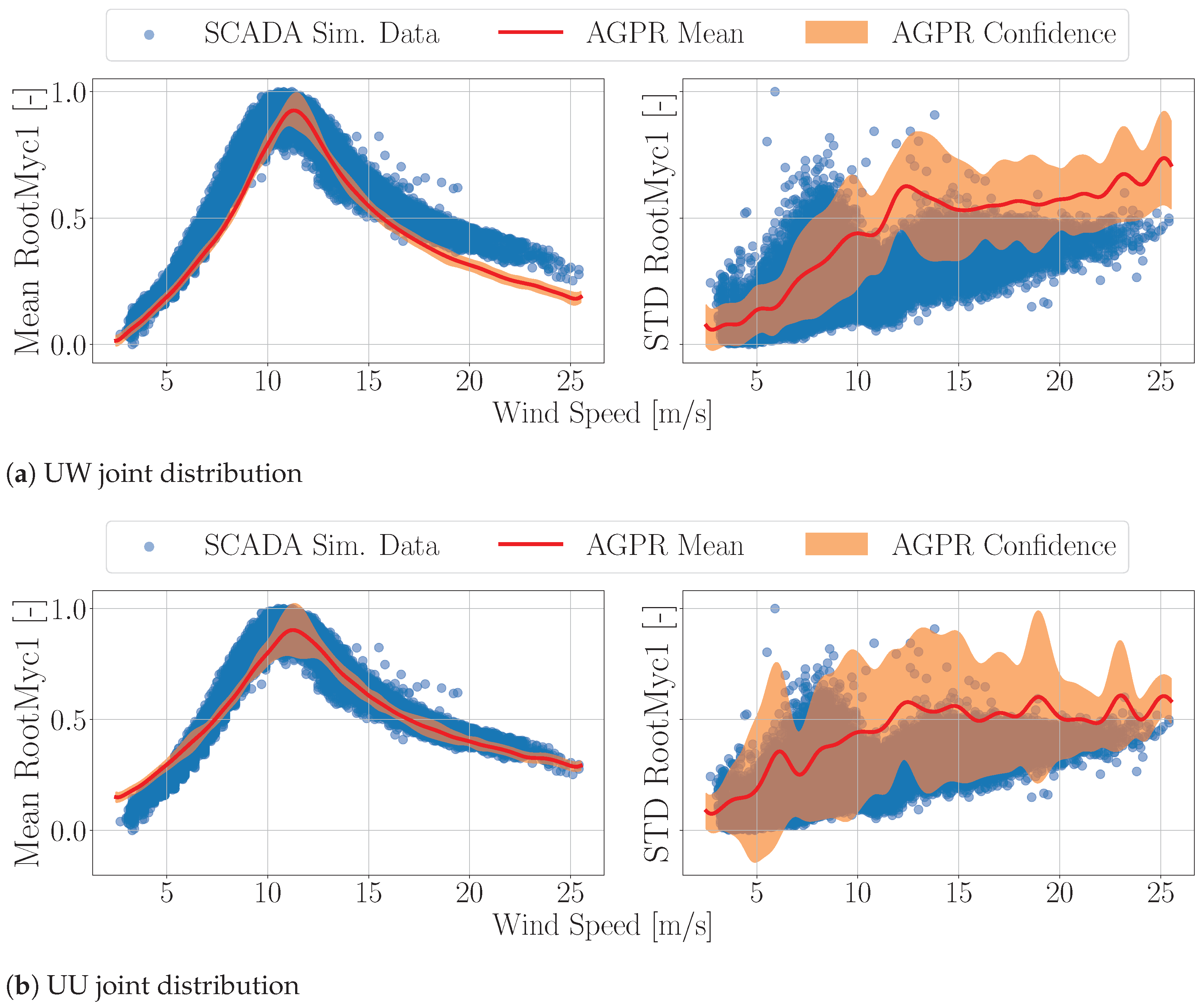


| Datafield | Unit | 10-min Avg | 10-min STD | 10-min Min | 10-min Max |
|---|---|---|---|---|---|
| Power | [kW] | ✓ | - | ✓ | ✓ |
| Rotor Speed | [rpm] | ✓ | - | ✓ | ✓ |
| OFP blade load | [Nm] | ✓ | ✓ | ✓ | ✓ |
| TT Res. accel. | [mm/s2] | ✓ | ✓ | ✓ | ✓ |
| OpenFAST Channel Label | Adopted Name | Post-Processing | Unit |
|---|---|---|---|
| GenPwr | Power Output | 10-min mean | [kW] |
| RtSpeed | Rotor Speed | 10-min mean | [kW] |
| RootMyc1 | Out-of-plane BR moment | 10-min mean | [kNm] |
| YawBrTAxp | TT fore-aft acceleration | 10-min mean | [m/s2] |
| YawBrTAyp | TT side-side acceleration | 10-min mean | [m/s2] |
| YawBrTAccl | TT resultant acceleration | 10-min mean | [m/s2] |
| RootMxb1 | Edge-wise BR moment | DEL | [kNm] |
| RootMyb1 | Flap-wise BR moment | DEL | [kNm] |
| YawBrMxp | TT side-side | DEL | [kNm] |
| YawBrMyp | TT fore-aft | DEL | [kNm] |
| TwrBsMxt | TB side-side | DEL | [kNm] |
| TwrBsMyt | TB fore-aft | DEL | [kNm] |
| DEL | 10 min Mean | Reference | |
|---|---|---|---|
| Model class | Approximate GP | Approximate GP | [50] |
| Kernel (length scale) | RBF Kernel (0.7) | RBF Kernel (0.7) | [28] |
| Marginal likelihood class | PLL | PLL | [52] |
| Variational distribution | Cholesky | Cholesky | [54] |
| Training dataset size | 5888 | 11,776 | - |
| Number of inducing points | 64 | 64 | - |
| Number of iterations | 500 | 500 | - |
| Wind Speed [m/s] | Uniform-Weibull [%] | Uniform-Uniform [%] |
|---|---|---|
| 3 | 0 | 0 |
| 5 | 8.63 | 26.86 |
| 10 | −11.99 | −10.97 |
| 15 | 2.65 | 2.17 |
| 20 | 6.20 | 6.20 |
| 25 | 25.03 | 25.02 |
| UW [-] | UU [-] | ||||||
|---|---|---|---|---|---|---|---|
| Channels | 6 m/s | 12 m/s | 18 m/s | 6 m/s | 12 m/s | 18 m/s | |
| RootMxb1 | 0.029 | 0.000 | 0.024 | 0.002 | 0.004 | 0.042 | |
| RootMyb1 | 0.010 | 0.009 | 0.014 | 0.003 | 0.001 | 0.005 | |
| YawBrMxp | 0.043 | 0.013 | 0.001 | 0.002 | 0.005 | 0.024 | |
| YawBrMyp | 0.004 | 0.007 | 0.020 | 0.003 | 0.001 | 0.013 | |
| TwrBsMxt | 0.009 | 0.025 | 0.005 | 0.001 | 0.000 | 0.003 | |
| TwrBsMyt | 0.002 | 0.000 | 0.011 | 0.005 | 0.004 | 0.001 |
| UW [-] | UU [-] | ||||||
|---|---|---|---|---|---|---|---|
| Data Field | 6 m/s | 12 m/s | 18 m/s | 6 m/s | 12 m/s | 18 m/s | |
| OFP BR Moment mean | 1.783 | 0.160 | 9.317 | 0.701 | 0.032 | 0.184 | |
| OFP BR Moment STD | 3.006 | 5.556 | 5.736 | 3.683 | 6.196 | 5.487 | |
| TT Res. accl. mean | 1.680 | 0.253 | 0.915 | 5.358 | 0.889 | 1.539 | |
| TT Res. accl. STD | 2.363 | 0.252 | 0.625 | 5.511 | 1.619 | 2.884 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haghi, R.; Stagg, C.; Crawford, C. Wind Turbine Damage Equivalent Load Assessment Using Gaussian Process Regression Combining Measurement and Synthetic Data. Energies 2024, 17, 346. https://doi.org/10.3390/en17020346
Haghi R, Stagg C, Crawford C. Wind Turbine Damage Equivalent Load Assessment Using Gaussian Process Regression Combining Measurement and Synthetic Data. Energies. 2024; 17(2):346. https://doi.org/10.3390/en17020346
Chicago/Turabian StyleHaghi, Rad, Cassidy Stagg, and Curran Crawford. 2024. "Wind Turbine Damage Equivalent Load Assessment Using Gaussian Process Regression Combining Measurement and Synthetic Data" Energies 17, no. 2: 346. https://doi.org/10.3390/en17020346
APA StyleHaghi, R., Stagg, C., & Crawford, C. (2024). Wind Turbine Damage Equivalent Load Assessment Using Gaussian Process Regression Combining Measurement and Synthetic Data. Energies, 17(2), 346. https://doi.org/10.3390/en17020346








