Experimental and Numerical Study of the Laminar Burning Velocity of Biogas–Ammonia–Air Premixed Flames
Abstract
1. Introduction
2. Materials and Methods
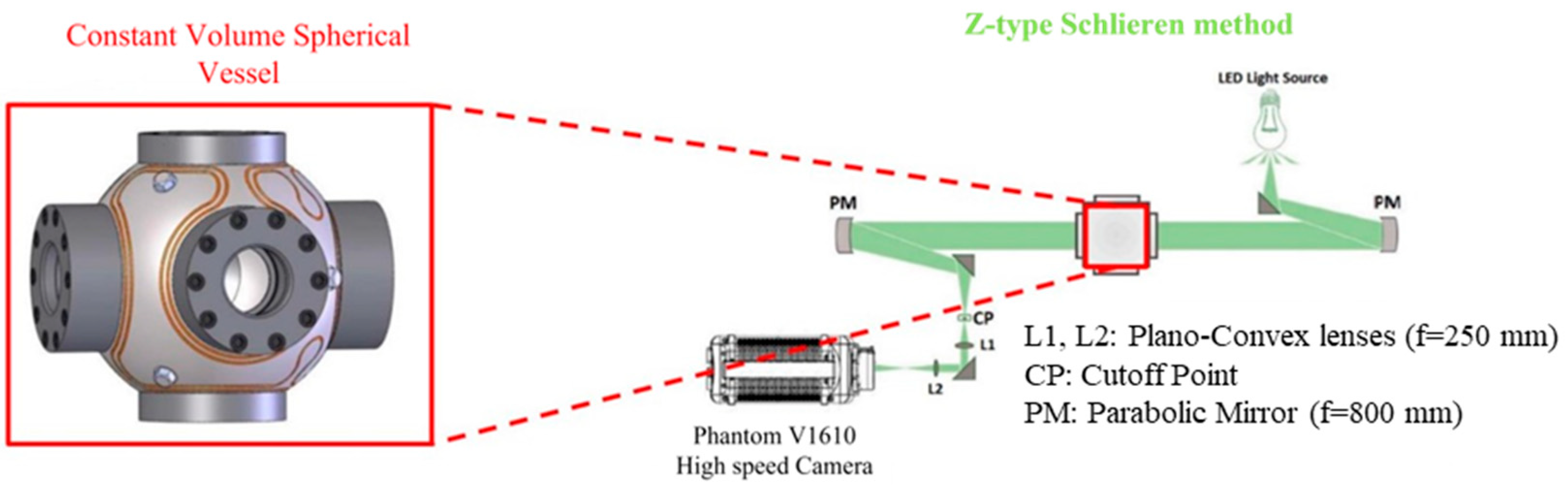
2.1. Laminar Flame Speed Measurment
2.2. Kinetics Simulation Setup
3. Results
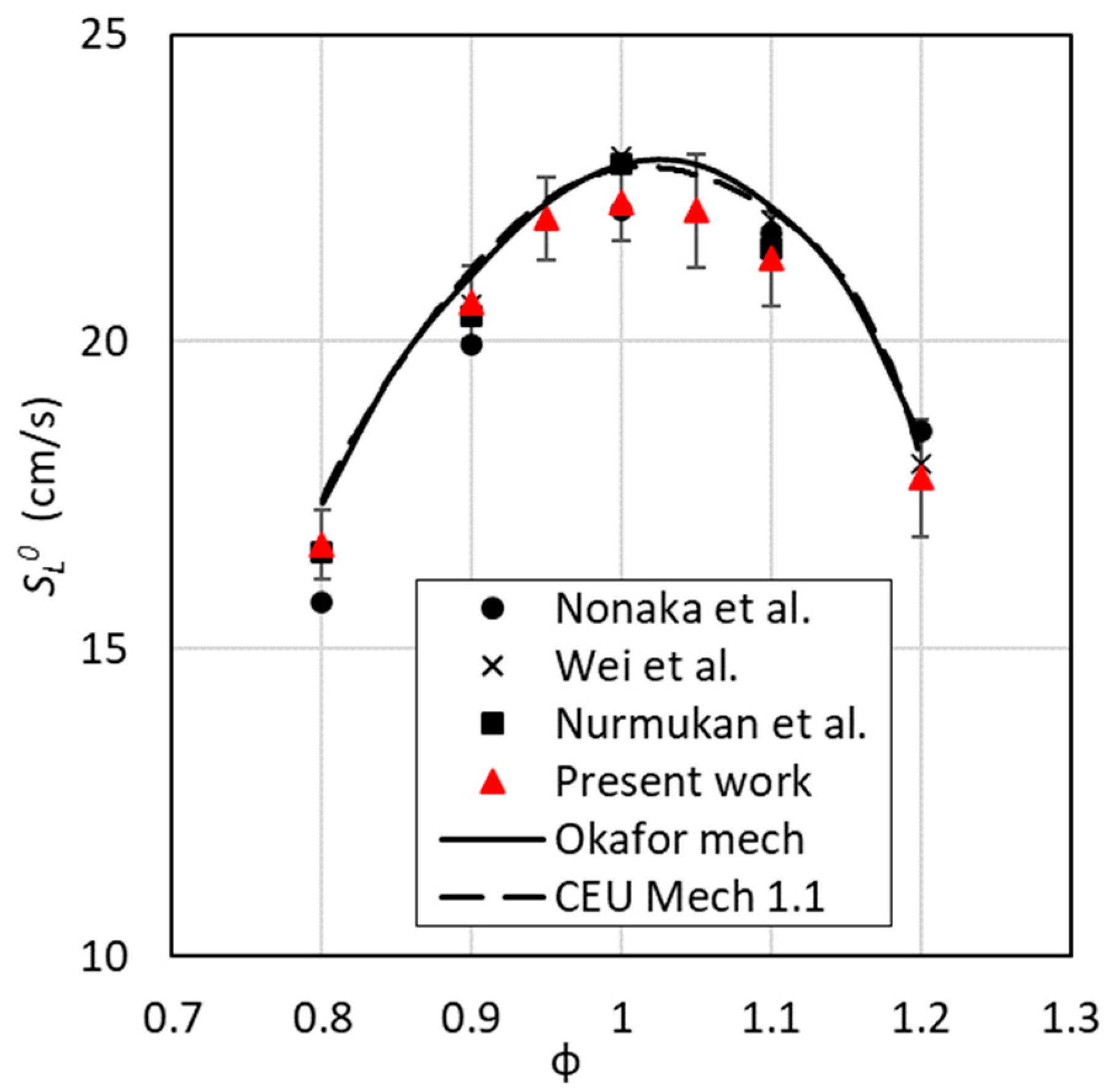
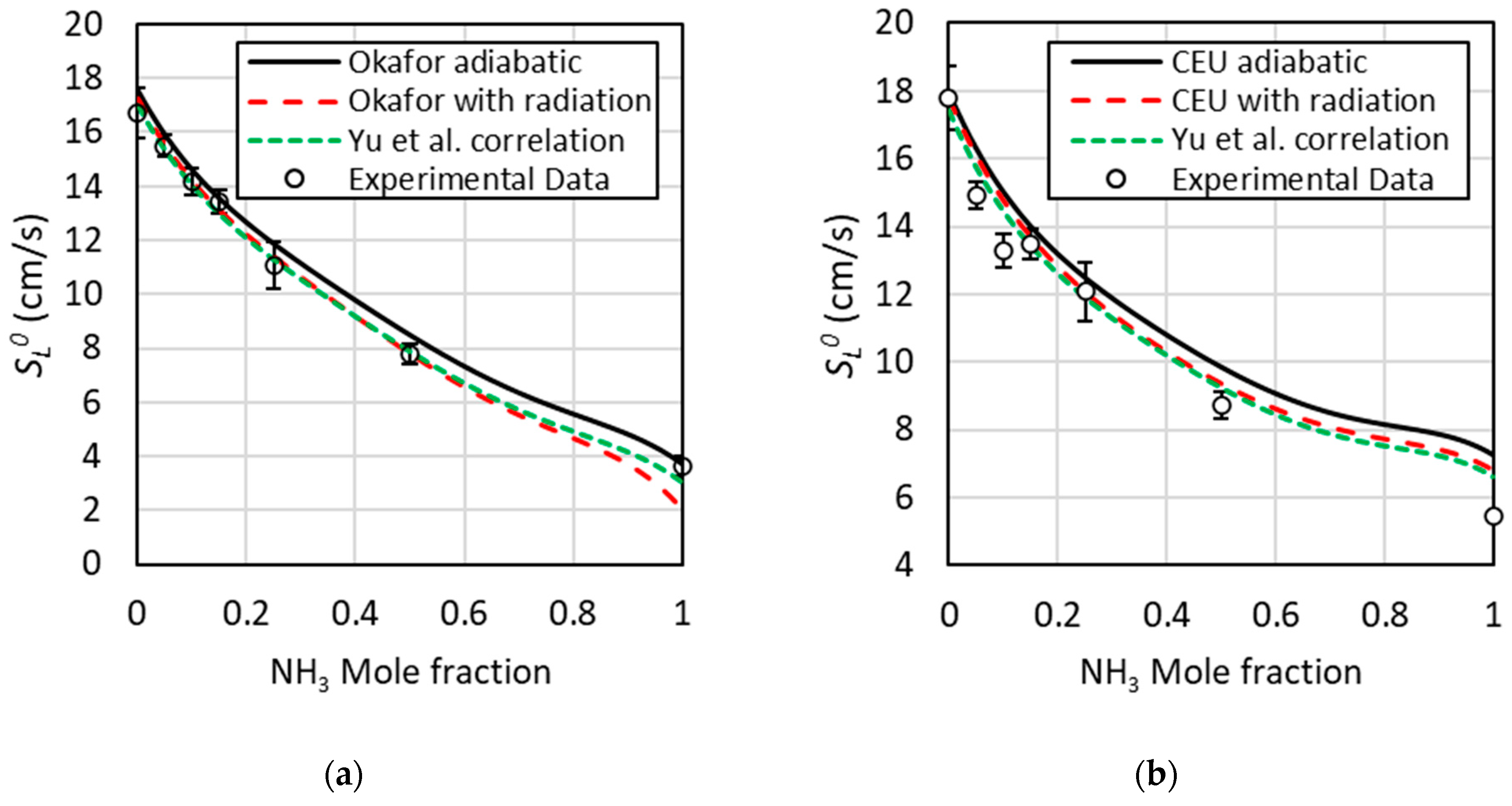
3.1. Mechanisms Validation
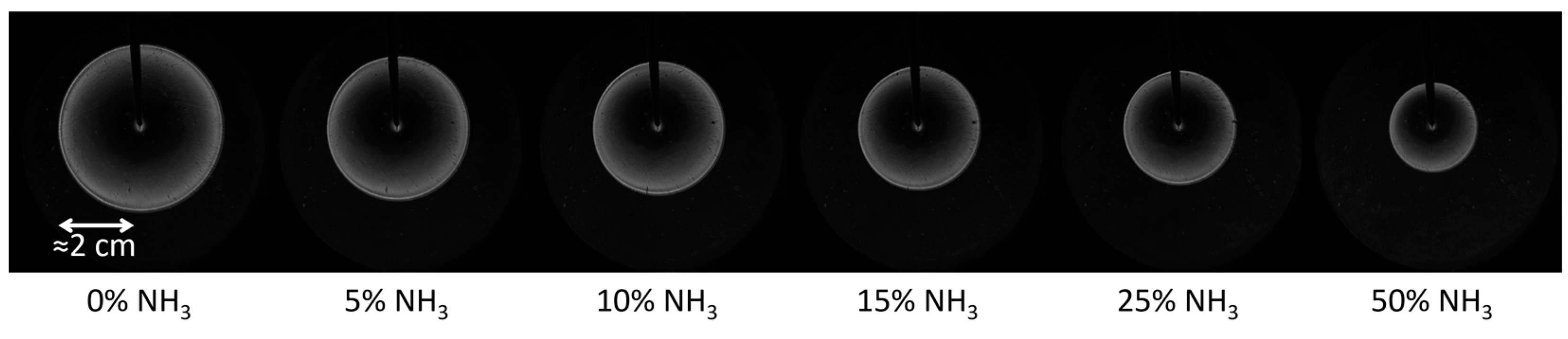
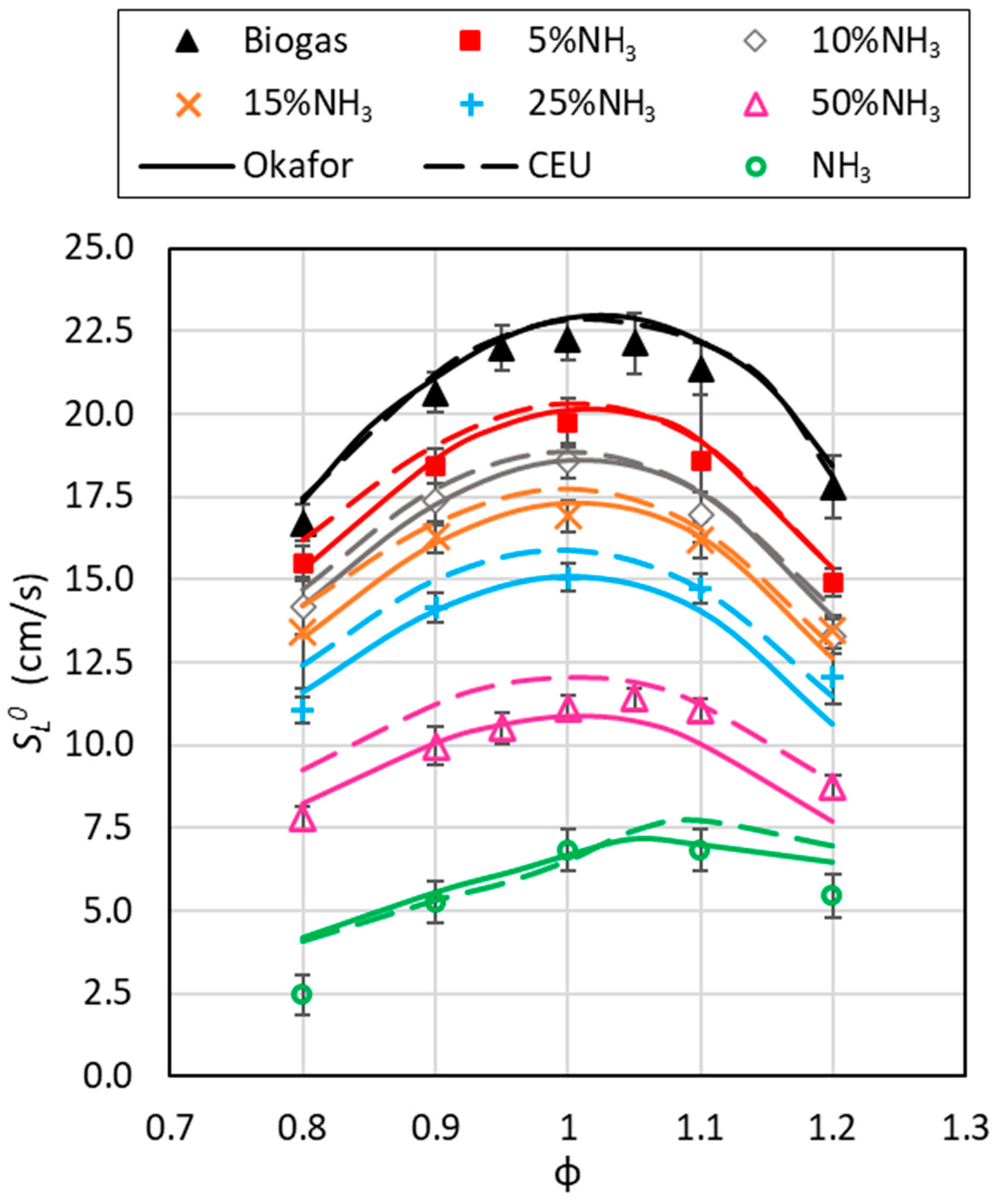
3.2. Experimental Laminar Burning Velocities
3.3. Markstein Lengths
3.4. Radiative Heat Losses
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Scarlat, N.; Dallemand, J.; Taylor, N.; Banja, M. Brief on Biomass for Energy in the European Union; Publications Office of the European Union: Luxembourg, 2019; pp. 1–8. [Google Scholar]
- Calbry-Muzyka, A.; Madi, H.; Rüsch-Pfund, F.; Gandiglio, M.; Biollaz, S. Biogas Composition from Agricultural Sources and Organic Fraction of Municipal Solid Waste. Renew. Energy 2022, 181, 1000–1007. [Google Scholar] [CrossRef]
- Wagner, A.O.; Hohlbrugger, P.; Lins, P.; Illmer, P. Effects of Different Nitrogen Sources on the Biogas Production—A Lab-Scale Investigation. Microbiol. Res. 2012, 167, 630–636. [Google Scholar] [CrossRef] [PubMed]
- Feiz, R.; Johansson, M.; Lindkvist, E.; Moestedt, J.; Påledal, S.N.; Svensson, N. Key Performance Indicators for Biogas Production—Methodological Insights on the Life-Cycle Analysis of Biogas Production from Source-Separated Food Waste. Energy 2020, 200, 117462. [Google Scholar] [CrossRef]
- Lhuillier, C.; Brequigny, P.; Lamoureux, N.; Contino, F.; Mounaïm-Rousselle, C. Experimental Investigation on Laminar Burning Velocities of Ammonia/Hydrogen/Air Mixtures at Elevated Temperatures. Fuel 2020, 263, 116653. [Google Scholar] [CrossRef]
- Grannell, S.M.; Assanis, D.N.; Bohac, S.V.; Gillespie, D.E. The Fuel Mix Limits and Efficiency of a Stoichiometric, Ammonia, and Gasoline Dual Fueled Spark Ignition Engine. J. Eng. Gas Turbines Power 2008, 130, 042802. [Google Scholar] [CrossRef]
- Mørch, C.S.; Bjerre, A.; Gøttrup, M.P.; Sorenson, S.C.; Schramm, J. Ammonia/Hydrogen Mixtures in an SI-Engine: Engine Performance and Analysis of a Proposed Fuel System. Fuel 2011, 90, 854–864. [Google Scholar] [CrossRef]
- Westlye, F.R.; Ivarsson, A.; Schramm, J. Experimental Investigation of Nitrogen Based Emissions from an Ammonia Fueled SI-Engine. Fuel 2013, 111, 239–247. [Google Scholar] [CrossRef]
- Koch, E. Ammonia as a Fuel for Motor Buses. J. Inst. Pet. 1949, 31, 21–32. [Google Scholar]
- Nonaka, H.O.B.; Pereira, F.M. Experimental and Numerical Study of CO2 Content Effects on the Laminar Burning Velocity of Biogas. Fuel 2016, 182, 382–390. [Google Scholar] [CrossRef]
- Hinton, N.; Stone, R. Laminar Burning Velocity Measurements of Methane and Carbon Dioxide Mixtures (Biogas) over Wide Ranging Temperatures and Pressures. Fuel 2014, 116, 743–750. [Google Scholar] [CrossRef]
- Wei, Z.; Zhen, H.; Fu, J.; Leung, C.; Cheung, C.; Huang, Z. Experimental and Numerical Study on the Laminar Burning Velocity of Hydrogen Enriched Biogas Mixture. Int. J. Hydrogen Energy 2019, 44, 22240–22249. [Google Scholar] [CrossRef]
- Hayakawa, A.; Goto, T.; Mimoto, R.; Arakawa, Y.; Kudo, T.; Kobayashi, H. Laminar Burning Velocity and Markstein Length of Ammonia/Air Premixed Flames at Various Pressures. Fuel 2015, 159, 98–106. [Google Scholar] [CrossRef]
- Kanoshima, R.; Hayakawa, A.; Kudo, T.; Okafor, E.C.; Colson, S.; Ichikawa, A.; Kudo, T.; Kobayashi, H. Effects of Initial Mixture Temperature and Pressure on Laminar Burning Velocity and Markstein Length of Ammonia/Air Premixed Laminar Flames. Fuel 2022, 310, 122149. [Google Scholar] [CrossRef]
- Zitouni, S.-E.; Brequigny, P.; Mounaїm-Rousselle, C. Influence of Hydrogen and Methane Addition in Laminar Ammonia Premixed Flame on Burning Velocity, Lewis Number and Markstein Length. Combust. Flame 2023, 253, 112786. [Google Scholar] [CrossRef]
- Mong, G.R.; Chiong, M.-C.; Chong, C.T.; Ng, J.-H.; Mashruk, S.; Tran, M.-V.; Lee, K.M.; Samiran, N.A.; Wong, K.Y.; Valera-Medina, A. Fuel-Lean Ammonia/Biogas Combustion Characteristics under the Reacting Swirl Flow Conditions. Fuel 2023, 331, 125983. [Google Scholar] [CrossRef]
- Shu, T.; Xue, Y.; Zhou, Z.; Ren, Z. An Experimental Study of Laminar Ammonia/Methane/Air Premixed Flames Using Expanding Spherical Flames. Fuel 2021, 290, 120003. [Google Scholar] [CrossRef]
- Okafor, E.C.; Naito, Y.; Colson, S.; Ichikawa, A.; Kudo, T.; Hayakawa, A.; Kobayashi, H. Experimental and Numerical Study of the Laminar Burning Velocity of CH4–NH3–Air Premixed Flames. Combust. Flame 2018, 187, 185–198. [Google Scholar] [CrossRef]
- Okafor, E.C.; Naito, Y.; Colson, S.; Ichikawa, A.; Kudo, T.; Hayakawa, A.; Kobayashi, H. Measurement and Modelling of the Laminar Burning Velocity of Methane-Ammonia-Air Flames at High Pressures Using a Reduced Reaction Mechanism. Combust. Flame 2019, 204, 162–175. [Google Scholar] [CrossRef]
- Han, X.; Wang, Z.; Costa, M.; Sun, Z.; He, Y.; Cen, K. Experimental and Kinetic Modeling Study of Laminar Burning Velocities of NH3/Air, NH3/H2/Air, NH3/CO/Air and NH3/CH4/Air Premixed Flames. Combust. Flame 2019, 206, 214–226. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Z.; Chen, C.; Elbaz, A.M.; Sun, Z.; Roberts, W.L. Applying Heat Flux Method to Laminar Burning Velocity Measurements of NH3/CH4/Air at Elevated Pressures and Kinetic Modeling Study. Combust. Flame 2022, 236, 111788. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the Uncertainties in Experimental Results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]
- Chi, C.; Han, W.; Thévenin, D. Effects of Molecular Diffusion Modeling on Turbulent Premixed NH3/H2/Air Flames. Proc. Combust. Inst. 2022, 17, 1–10. [Google Scholar] [CrossRef]
- Ben Zenou, J.; Vicquelin, R. Acceleration of Premixed H2-Air-Steam Flames When Accounting for Thermal Radiation. Combust. Flame 2023, 258, 113068. [Google Scholar] [CrossRef]
- Lapalme, D.; Halter, F.; Mounaïm-Rousselle, C.; Seers, P. Characterization of Thermodiffusive and Hydrodynamic Mechanisms on the Cellular Instability of Syngas Fuel Blended with CH4 or CO2. Combust. Flame 2018, 193, 481–490. [Google Scholar] [CrossRef]
- Shrestha, K.P.; Seidel, L.; Zeuch, T.; Mauss, F. Detailed Kinetic Mechanism for the Oxidation of Ammonia Including the Formation and Reduction of Nitrogen Oxides. Energy Fuels 2018, 32, 10202–10217. [Google Scholar] [CrossRef]
- University of California at San Diego Chemical-Kinetic Mechanisms for Combustion Applications”, San Diego Mechanism Web Page. Available online: http://web.eng.ucsd.edu/mae/groups/combustion/mechanism.html (accessed on 27 November 2023).
- Nurmukan, D.; Chen, T.J.M.; Hung, Y.M.; Ismadi, M.Z.; Chong, C.T.; Tran, M.V. Enhancement of Biogas/Air Combustion by Hydrogen Addition at Elevated Temperatures. Int. J. Energy Res. 2020, 44, 1519–1534. [Google Scholar] [CrossRef]
- Chen, Z. On the Extraction of Laminar Flame Speed and Markstein Length from Outwardly Propagating Spherical Flames. Combust. Flame 2011, 158, 291–300. [Google Scholar] [CrossRef]
- Bouvet, N.; Halter, F.; Chauveau, C.; Yoon, Y. On the Effective Lewis Number Formulations for Lean Hydrogen/Hydrocarbon/Air Mixtures. Int. J. Hydrogen Energy 2013, 38, 5949–5960. [Google Scholar] [CrossRef]
- Zitouni, S.; Pugh, D.; Crayford, A.; Bowen, P.J.; Runyon, J. Lewis Number Effects on Lean Premixed Combustion Characteristics of Multi-Component Fuel Blends. Combust. Flame 2022, 238, 111932. [Google Scholar] [CrossRef]
- Vieira, M.C.d.J.; Figueira da Silva, L.F. Flame Flashback Critical Damköhler Number for CO2 Diluted CH4 and C3H8 Mixtures with Air. Flow, Turbul. Combust. 2023, 110, 377–393. [Google Scholar] [CrossRef]
- Chen, Z.; Qin, X.; Xu, B.; Ju, Y.; Liu, F. Studies of Radiation Absorption on Flame Speed and Flammability Limit of CO2 Diluted Methane Flames at Elevated Pressures. Proc. Combust. Inst. 2007, 31, 2693–2700. [Google Scholar] [CrossRef]
- Yu, H.; Han, W.; Santner, J.; Gou, X.; Sohn, C.H.; Ju, Y.; Chen, Z. Radiation-Induced Uncertainty in Laminar Flame Speed Measured from Propagating Spherical Flames. Combust. Flame 2014, 161, 2815–2824. [Google Scholar] [CrossRef]




| Mechanism | Type | Number of Species | Number of Reactions |
|---|---|---|---|
| Okafor [18] (2018) | Reduced | 42 | 130 |
| Shrestha [26] (2018) | Detailed | 125 | 1090 |
| CEU-NH3-Mech-1.1 [21] (2022) | Detailed | 91 | 444 |
| San Diego [27] | Reduced | 69 | 311 |
| φ | 1 atm 298 K [21] | 1 atm 298 K [22] | 3 atm 298 K [22] | 5 atm 298 K [22] | 1 atm 298 K [18] | 5 atm 298 K [18] | 3 bar 298 K [20] | 5 bar 298 K [20] | Min | Max | Avg. | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| %NH3 | %NH3 | %NH3 | %NH3 | %NH3 | %NH3 | %NH3 | %NH3 | ||||||||||||||||||||
| 20 | 40 | 60 | 20 | 40 | 60 | 20 | 40 | 60 | 20 | 40 | 60 | 10 | 50 | 90 | 10 | 50 | 90 | 22 | 39 | 52 | 22 | 39 | 52 | ||||
| 0.7 | 0.0% | 1.0% | 0.9% | 7.1% | 10.3% | 15.3% | 15.3% | 24.4% | 19.1% | 21.5% | 0.0% | 24.4% | 11.5% | ||||||||||||||
| 0.8 | 1.6% | 2.5% | 4.2% | 5.2% | 7.0% | 12.5% | 6.9% | 11.4% | 10.9% | 8.2% | 13.6% | 14.1% | 4.8% | 9.3% | 9.8% | 23.0% | 11.2% | 6.0% | 7.8% | 7.6% | 1.9% | 4.3% | 7.3% | 1.6% | 23.0% | 8.3% | |
| 0.9 | 1.9% | 3.6% | 5.4% | 4.4% | 5.3% | 9.7% | 5.6% | 8.4% | 8.1% | 7.0% | 7.5% | 5.4% | 5.3% | 6.4% | 17.0% | 1.3% | 0.5% | 2.3% | 3.9% | 1.4% | 5.4% | 0.5% | 17.0% | 5.5% | |||
| 1 | 1.4% | 3.5% | 5.4% | 3.6% | 3.5% | 5.7% | 5.2% | 8.2% | 9.8% | 5.8% | 7.3% | 4.9% | 3.0% | 0.1% | 13.4% | 3.0% | 0.9% | 13.7% | 0.1% | 0.8% | 0.6% | 3.9% | 2.0% | 1.9% | 0.1% | 13.7% | 4.5% |
| 1.1 | 0.5% | 3.1% | 3.6% | 2.3% | 1.1% | 1.1% | 3.3% | 8.0% | 9.6% | 0.4% | 3.5% | 1.4% | 1.1% | 3.3% | 0.8% | 7.8% | 0.6% | 2.5% | 1.6% | 2.8% | 2.2% | 2.3% | 0.4% | 9.6% | 2.9% | ||
| 1.2 | 0.3% | 3.0% | 3.2% | 1.0% | 0.5% | 2.2% | 9.3% | 15.0% | 9.0% | 3.9% | 4.0% | 7.7% | 3.0% | 5.8% | 14.1% | 5.7% | 3.0% | 0.8% | 6.6% | 7.7% | 3.4% | 8.6% | 4.9% | 2.0% | 0.3% | 15.0% | 5.2% |
| 1.3 | 5.6% | 0.1% | 4.4% | 0.7% | 0.4% | 6.7% | 11.8% | 6.7% | 5.1% | 0.6% | 10.0% | 35.8% | 9.7% | 5.3% | 38.6% | 2.9% | 8.1% | 0.6% | 1.9% | 2.1% | 6.3% | 10.8% | 0.1% | 38.6% | 7.9% | ||
| φ | 1 atm 298 K [21] | 1 atm 298 K [22] | 3 atm 298 K [22] | 5 atm 298 K [22] | 1 atm 298 K [18] | 5 atm 298 K [18] | 3 bar 298 K [20] | 5 bar 298 K [20] | Min | Max | Avg. | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| %NH3 | %NH3 | %NH3 | %NH3 | %NH3 | %NH3 | %NH3 | %NH3 | ||||||||||||||||||||
| 20 | 40 | 60 | 20 | 40 | 60 | 20 | 40 | 60 | 20 | 40 | 60 | 10 | 50 | 90 | 10 | 50 | 90 | 22 | 39 | 52 | 22 | 39 | 52 | ||||
| 0.7 | 15.9% | 13.4% | 7.7% | 3.6% | 4.3% | 0.6% | 13.9% | 35.6% | 34.1% | 0.6% | 35.6% | 14.3% | |||||||||||||||
| 0.8 | 12.2% | 10.5% | 8.1% | 5.5% | 3.3% | 2.4% | 7.5% | 1.0% | 5.5% | 10.0% | 17.1% | 19.9% | 2.9% | 18.3% | 32.1% | 3.0% | 17.8% | 19.0% | 15.0% | 12.4% | 14.3% | 14.7% | 1.0% | 32.1% | 11.5% | ||
| 0.9 | 7.0% | 6.1% | 1.5% | 4.3% | 4.3% | 5.9% | 0.8% | 2.9% | 5.9% | 3.7% | 2.9% | 3.0% | 12.5% | 15.1% | 3.4% | 10.0% | 6.8% | 6.7% | 6.7% | 0.6% | 3.1% | 9.3% | 0.6% | 15.1% | 5.6% | ||
| 1 | 4.9% | 2.0% | 4.0% | 2.5% | 2.0% | 4.3% | 5.9% | 7.7% | 9.0% | 10.3% | 8.3% | 4.1% | 5.9% | 4.1% | 1.1% | 10.6% | 0.8% | 13.3% | 1.1% | 0.2% | 1.3% | 8.0% | 3.2% | 2.7% | 0.2% | 13.3% | 4.9% |
| 1.1 | 1.8% | 0.3% | 1.8% | 0.0% | 2.5% | 0.8% | 10.5% | 9.5% | 4.7% | 11.0% | 4.4% | 10.9% | 2.2% | 0.2% | 4.7% | 7.3% | 4.5% | 0.6% | 12.2% | 3.6% | 1.5% | 0.0% | 12.2% | 4.5% | |||
| 1.2 | 3.5% | 1.5% | 5.0% | 4.7% | 1.1% | 10.8% | 17.4% | 11.9% | 4.8% | 12.3% | 1.4% | 26.2% | 8.7% | 2.0% | 28.6% | 20.8% | 15.2% | 20.9% | 13.1% | 5.1% | 7.2% | 15.3% | 0.4% | 10.7% | 0.4% | 28.6% | 10.3% |
| 1.3 | 0.1% | 5.7% | 20.6% | 5.8% | 5.2% | 23.3% | 12.7% | 2.2% | 26.5% | 0.3% | 21.2% | 64.0% | 19.5% | 4.8% | 62.7% | 7.5% | 9.1% | 18.5% | 1.1% | 16.4% | 30.1% | 0.1% | 64.0% | 17.0% | |||
| φ | 1 atm 298 K [21] | 1 atm 298 K [22] | 3 atm 298 K [22] | 5 atm 298 K [22] | 1 atm 298 K [18] | 5 atm 298 K [18] | 3 bar 298 K [20] | 5 bar 298 K [20] | Min | Max | Avg. | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| %NH3 | %NH3 | %NH3 | %NH3 | %NH3 | %NH3 | %NH3 | %NH3 | ||||||||||||||||||||
| 20 | 40 | 60 | 20 | 40 | 60 | 20 | 40 | 60 | 20 | 40 | 60 | 10 | 50 | 90 | 10 | 50 | 90 | 22 | 39 | 52 | 22 | 39 | 52 | ||||
| 0.7 | 4.3% | 6.9% | 9.2% | 3.1% | 1.9% | 5.5% | 2.8% | 14.8% | 22.1% | 33.0% | 1.9% | 33.0% | 10.3% | ||||||||||||||
| 0.8 | 2.5% | 5.7% | 7.6% | 1.3% | 0.9% | 1.6% | 0.4% | 2.1% | 1.5% | 1.3% | 4.1% | 7.3% | 8.0% | 19.1% | 19.7% | 35.3% | 4.0% | 14.5% | 18.9% | 19.5% | 13.0% | 15.8% | 17.7% | 0.4% | 35.3% | 9.7% | |
| 0.9 | 1.5% | 3.0% | 5.2% | 1.1% | 1.2% | 0.4% | 0.5% | 0.2% | 1.0% | 0.7% | 0.6% | 1.4% | 8.1% | 16.2% | 10.3% | 8.1% | 10.0% | 12.6% | 2.9% | 7.1% | 14.3% | 0.2% | 16.2% | 5.1% | |||
| 1 | 1.0% | 2.1% | 4.4% | 1.3% | 2.1% | 4.1% | 2.3% | 1.8% | 1.4% | 1.9% | 1.3% | 1.7% | 4.8% | 7.6% | 18.4% | 1.5% | 8.1% | 10.0% | 3.5% | 5.9% | 9.5% | 0.4% | 4.3% | 10.0% | 0.4% | 18.4% | 4.6% |
| 1.1 | 1.3% | 1.9% | 7.3% | 0.5% | 4.1% | 10.1% | 0.4% | 0.1% | 2.9% | 2.0% | 4.7% | 12.7% | 0.2% | 4.5% | 11.1% | 18.4% | 2.9% | 4.6% | 10.3% | 0.2% | 4.9% | 7.6% | 0.1% | 18.4% | 5.1% | ||
| 1.2 | 3.6% | 5.9% | 13.8% | 2.3% | 8.7% | 20.1% | 2.8% | 2.7% | 6.3% | 1.9% | 7.0% | 21.4% | 0.7% | 7.8% | 28.6% | 3.3% | 15.9% | 7.1% | 0.6% | 5.4% | 11.7% | 2.4% | 6.0% | 10.4% | 0.6% | 28.6% | 8.2% |
| 1.3 | 15.7% | 15.4% | 18.1% | 8.9% | 14.9% | 20.8% | 3.9% | 2.4% | 14.4% | 4.5% | 15.3% | 44.0% | 3.9% | 8.2% | 50.4% | 8.3% | 1.0% | 8.4% | 11.1% | 1.9% | 11.5% | 17.1% | 1.0% | 50.4% | 13.6% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brequigny, P.; Soulé, A.; Mounaïm-Rousselle, C.; Dayma, G.; Halter, F. Experimental and Numerical Study of the Laminar Burning Velocity of Biogas–Ammonia–Air Premixed Flames. Energies 2024, 17, 319. https://doi.org/10.3390/en17020319
Brequigny P, Soulé A, Mounaïm-Rousselle C, Dayma G, Halter F. Experimental and Numerical Study of the Laminar Burning Velocity of Biogas–Ammonia–Air Premixed Flames. Energies. 2024; 17(2):319. https://doi.org/10.3390/en17020319
Chicago/Turabian StyleBrequigny, Pierre, Adnane Soulé, Christine Mounaïm-Rousselle, Guillaume Dayma, and Fabien Halter. 2024. "Experimental and Numerical Study of the Laminar Burning Velocity of Biogas–Ammonia–Air Premixed Flames" Energies 17, no. 2: 319. https://doi.org/10.3390/en17020319
APA StyleBrequigny, P., Soulé, A., Mounaïm-Rousselle, C., Dayma, G., & Halter, F. (2024). Experimental and Numerical Study of the Laminar Burning Velocity of Biogas–Ammonia–Air Premixed Flames. Energies, 17(2), 319. https://doi.org/10.3390/en17020319








