Next Article in Journal
Wildfire-Induced Risk Assessment to Enable Resilient and Sustainable Electric Power Grid
Next Article in Special Issue
Heat Convection in a Channel-Opened Cavity with Two Heated Sources and Baffle
Previous Article in Journal
Fault Detection and Prediction for Power Transformers Using Fuzzy Logic and Neural Networks
Previous Article in Special Issue
Experimental Tests of Conduction/Convection Heat Transfer in Very High Porosity Foams with Lattice Structures, Immersed in Different Fluids
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 17
Issue 2
10.3390/en17020295
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Steady- and Transient-State CFD Simulations of a Modified Barra–Costantini Solar System in Comparison with a Traditional Trombe–Michel Wall

by
Sandra Corasaniti
*,
Luca Manni
,
Ivano Petracci
and
Michele Potenza
Department of Industrial Engineering, University of Rome “Tor Vergata”, Via del Politecnico n.1, 00133 Rome, Italy
*
Author to whom correspondence should be addressed.
Energies 2024, 17(2), 295; https://doi.org/10.3390/en17020295
Submission received: 1 October 2023 / Revised: 26 December 2023 / Accepted: 28 December 2023 / Published: 7 January 2024
(This article belongs to the Special Issue New Challenges in Heat Transfer Enhancement)
Browse Figures
Versions Notes

Abstract

:
Passive solar systems are one of most important strategies to reduce the heating loads of buildings. The Trombe–Michel (TM) wall and its variants are some of the better-known structures in the field of solar systems. An alternative to the TM wall is the Barra–Costantini (BC) system. In the present paper, CFD numerical simulations, both in steady and transient states, of modified BC and TM walls were carried out in the winter season. Different interspace thicknesses were simulated in order to evaluate their effects on the temperature field and air velocity, and the numerical results were compared among them. It was found that the BC system offers greater hot air flow compared with the TM wall; the mass flow rate increased up to 43% in the BC system and up 28% in the TM system when the interlayer thickness was increased by 500%. The transient simulations (100 h simulated) demonstrated that the dynamic response of the BC wall was shorter than that of the TM wall, even when the TM wall was simulated with initial thermal conditions that were more advantageous than those for the BC wall. The BC system reached a periodic stabilized regime within 24 h, whereas the TM system failed to stabilize in 100 h. The results show that for both TM and BC structures, the interlayer thickness scarcely influenced the temperature of the environment reached (the temperature peak increased up to 3–4% as the interlayer thickness was increased by 500%), while larger air speed changes were observed in the BC system in the transient state compared with the TM system. Thus, in the TM system, the outlet air velocity was practically constant as the interlayer thickness was increased; in contrast, the outlet velocity peak increased up to 50% in the BC system. Moreover, the BC wall presented a quicker response to satisfy the ambient thermal loads.

1. Introduction

Energy consumption in buildings accounts for 30–40% of the total world energy consumption [1]. With the enhancement of the energy efficiency of buildings, it is possible to maintain the same comfort conditions using fewer resources, which is of primary importance in terms of environmental sustainability and fighting global warming. To achieve these objectives, various strategies have been implemented. In recent years, the use of renewable energy in buildings, such as solar energy, geothermal energy, and wind energy, has helped to reduce the use of fossil fuels. Other techniques are used to reduce the energy load required by buildings, such as the application of thermal coats (e.g., the plants described in [2]), the construction of massive walls, and the application of phase-change materials (PCMs) positioned in strategic areas of the wall [3]. Passive solar systems are another solution to reducing the energy load in buildings, and these systems function by exploiting solar radiation to heat buildings [4]. Passive systems can be integrated with photovoltaic modules to obtain a multi-purpose system [5,6,7]. Among these passive systems, the best-known and most analyzed realization is the TM wall, first proposed by Felix Trombe and Jacques Michel in the 1960s. The principle of the TM wall, in its winter operation, is to accumulate heat from solar radiation and transfer it to the internal environment [8]. The system consists of a layer of glass, an interspace region (a cavity), and a massive wall. The heat stored in the massive wall during the sunny hours guarantees internal comfort even at night. In fact, solar radiation crosses the glass and is absorbed by the massive wall surface (usually blackened to increase the absorption). This solar energy is converted into thermal energy, transferred by conduction through the wall, and transferred finally to the environment by convection and radiation. The thermal capacity of the massive wall produces delayed heating, so the environment can be heated even during the night [9]. To achieve this, the heat stored in the massive wall heats the air present in the cavity interlayer, and the vents located in the lower and upper parts of the wall promote convective circulation that involves the entire environment. The hot air flows into the environment through the upper vents and replaces the cold air exiting from the lower vents. During daylight hours, heating of the environment is mainly achieved by air circulation, while at night, the thermal delay produced by the massive wall contributes to heating. The TM wall, in its basic version, has several advantages: ease of design, lower cost, and zero operating costs. But it has drawbacks also: it has a low thermal resistance, an inverse thermosiphon effect, and an unsightly appearance [10]. In the scientific literature, several variations of the basic configuration of the TM wall can be found, such as the composite TM wall (TM–Michel wall), water TM wall, zigzag TM wall, solar transwall, fluidized TM, photovoltaic TM, and TM wall with PCM [11].
The BC system is one among the many variants of the TM wall. This system was born in Italy in the 1970s and can be seen as a very efficient modification of the TM system [12]. The BC system consists of a glass layer, a cavity, a massive wall, and, different from the TM wall, an absorber (a thin blackened metal plate) placed in the cavity. The operating principle of the BC system is similar to that of the TM system. In the BC system, the relatively low heat capacity of the metal absorber increases the heating speed of the internal air. In addition, the massive wall is covered with a layer of insulation on the south side, the side which interfaces with the cavity, so a further higher heat transfer to the cavity is obtained.
Overall, the heat storage of the massive wall in the BC system presents slower dynamics and lower temperature peaks in comparison with the TM system.
In [13], the authors evaluated the thermal performance of a TM wall with a venetian blind simulated through CFD modelling, with the goal of calculating the induced airflow and the heat transferred. They analyzed the effects of varying several parameters, such as the position and deflection angle of the venetian blind.
An up-to-date and comprehensive overview [14] reports a summary of the recent developments, which include the insertion of latent heat storage components. As a result of the stored energy, these systems turn out to be particularly efficient devices.
In [15], numerical simulations were carried out to analyze the energy performance of TM walls in different Mediterranean climates; the effect of parameters such as the thermal mass, vent dimensions, and channel width were evaluated in transient-regime simulations.
In [16], the authors numerically studied the effect of fins on the performance of a TM system. The insertion of fins in the interlayer allows both higher outlet temperatures and efficiency, especially as the height of the fins increases.
The above-mentioned review indicates the different approaches used to study the behavior of passive systems, such as experimental [17], analytical [18], electrical analogy [19], or numerical [20,21,22]. However, the numerical approach to the parametric study of these kinds of problems is more convenient and is predominantly adopted. In contrast, the construction of laboratory models turns out to be more difficult and expensive. Analytical calculations are easily solved for simple configurations, but they cannot evaluate the temperature, velocity, or pressure fields in complex structures. Thus, the numerical procedure becomes preferable for broad studies involving more parameter changes or when large numbers of experiments must be carried out.
Different types of numerical simulations can be used. A complete description of the wall geometry and structure can only be conducted through 3D simulations [23,24,25,26], but some simpler assumptions can be introduced, such as 2D geometries [27,28,29] or stand-alone models [30,31]. As a consequence, these simplified models require less computer time and costs [32].
Thus, in the present paper, 2D and stand-alone numerical simulations of a modified BC system in the winter season were carried out, and the results were compared with a traditional TM wall. Both steady-state and transient conditions were studied. The dynamic simulations covered a time of five days, so it was estimated how the periodic stationary regime during the progression of cycles evolves. Among all the system parameters, special attention was given to the cavity wideness (ranging from 10 cm to 50 cm), because it generally influences the temperature field, air velocity, and thermal efficiency. This is the reason why the present study was carried out to specifically test the influence of the interlayer thickness on the most meaningful parameters determining the behavior of the solar system, i.e., the mass flow rate and temperature of the mass flow rate introduced in ambient conditions.
Many numerical CFD analyses of TM solar systems in stabilized periodic regimes are present in the literature, but analogue calculations in the transient state are missing.
Also, studies on BC systems are lacking, both theoretical and experimental. Steady-state analyses are clearly sufficient to give evidence for the differences between the classic TM system and the BC variant, but these simulations cannot determine how much time the passive solar system takes to becomes stabilized. So, transient simulations are especially suited to compare the dynamics of a classical TM system with the BC variant. In fact, in the BC system, the absorber and the massive wall insulation are specially added to reduce the transient duration. The quantification of such effects is solely the purpose of the dynamic simulations.

2. Materials and Methods

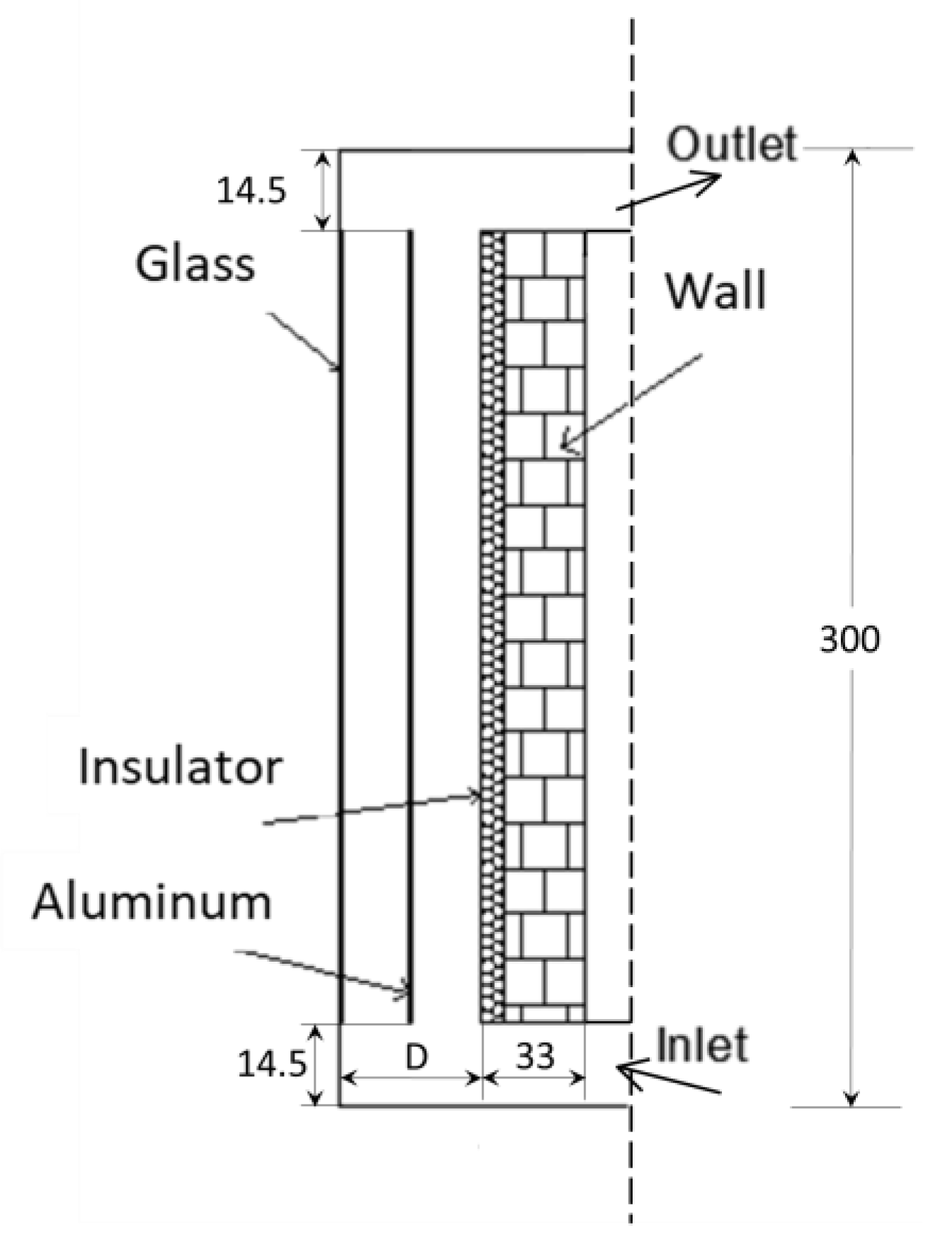
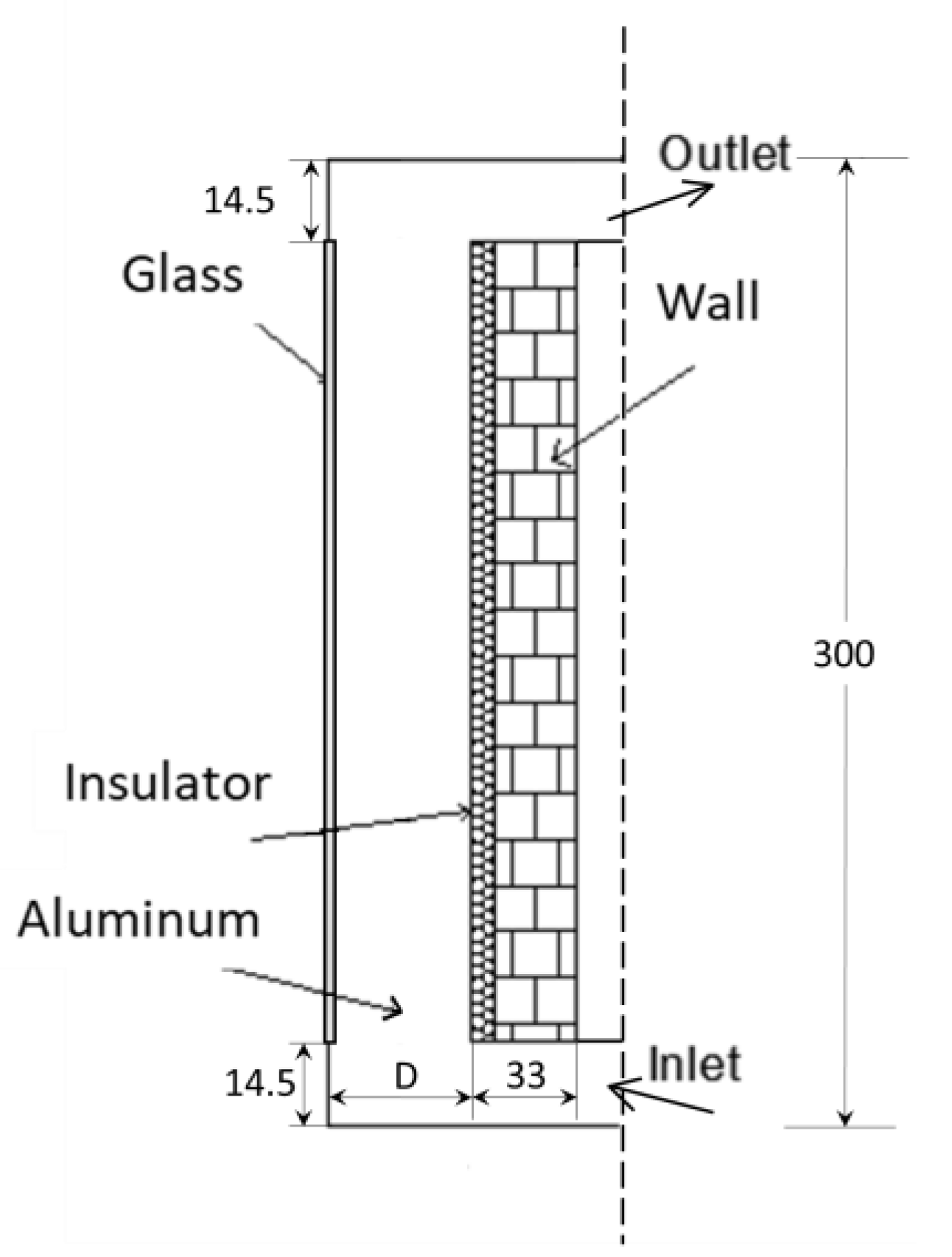
2.1. Steady State

Two structures were simulated in the steady-state regime with a stand-alone method: a modified BC system (Figure 1) and a traditional TM wall (Figure 2). The BC system in its basic version includes an upper channel that runs through the whole environment that requires heating. The present analysis did not include this channel, because in the stand-alone method, only the wall was considered, neglecting the remaining environment.
The TM wall consists of glass, a cavity, and a massive wall. In the modified BC system, a 2 mm thick blackened aluminum sheet is inserted in the center of the layer to increase the absorption of solar radiation. The massive wall (2.71 m high and 0.33 m thick) presents an 8 cm thick layer of insulation on its south side facing the cavity. The inlet and outlet vents are 14.5 cm wide. The following interlayer thicknesses were chosen as the model’s variable parameter: 10, 12, 16, 20, 22.5, 25, 30, 40, and 50 cm. The results of these structures were compared with those obtained with the traditional TM wall with the same dimensions.

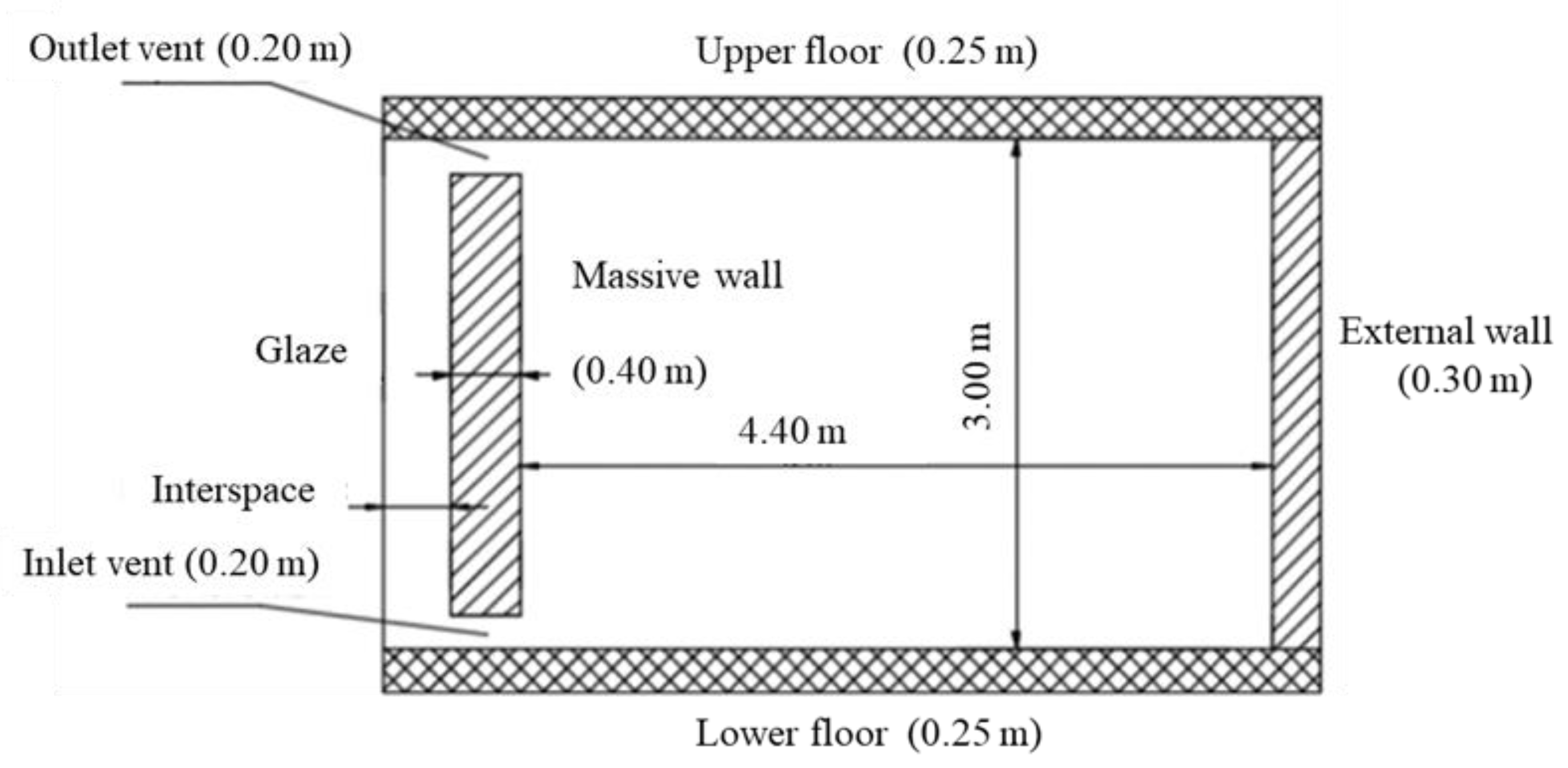
2.2. Transient State

Also, in transient conditions, 2D simulations of a modified BC system and a traditional TM wall were carried out. In this case, the entire environment to heat was considered, i.e., a room that was 4.4 m long and 3 m high. The thicknesses of the floor and ceiling were 0.25 m, the north wall was 0.3 m thick, and the massive wall was 0.4 m thick and 2.6 m high. Among all the thicknesses simulated in the steady-state conditions, only three were applied in the transient state: 0.1, 0.2, and 0.5 m. In fact, the steady-state simulations already demonstrated that the thickness of the cavity did not significantly influence the computed quantities of interest (i.e., temperature). The width of the air inlet and outlet vents was 0.2 m, and the thickness of the aluminum absorbing sheet was 2 mm. Figure 3 and Figure 4 show the TM and BC structures, respectively.

3. Numerical Methods

The equations of the model describing the TM and BC walls and the behavior of the environment are reported in Appendix A.1, and the turbulence model used is shown in Appendix A.2.

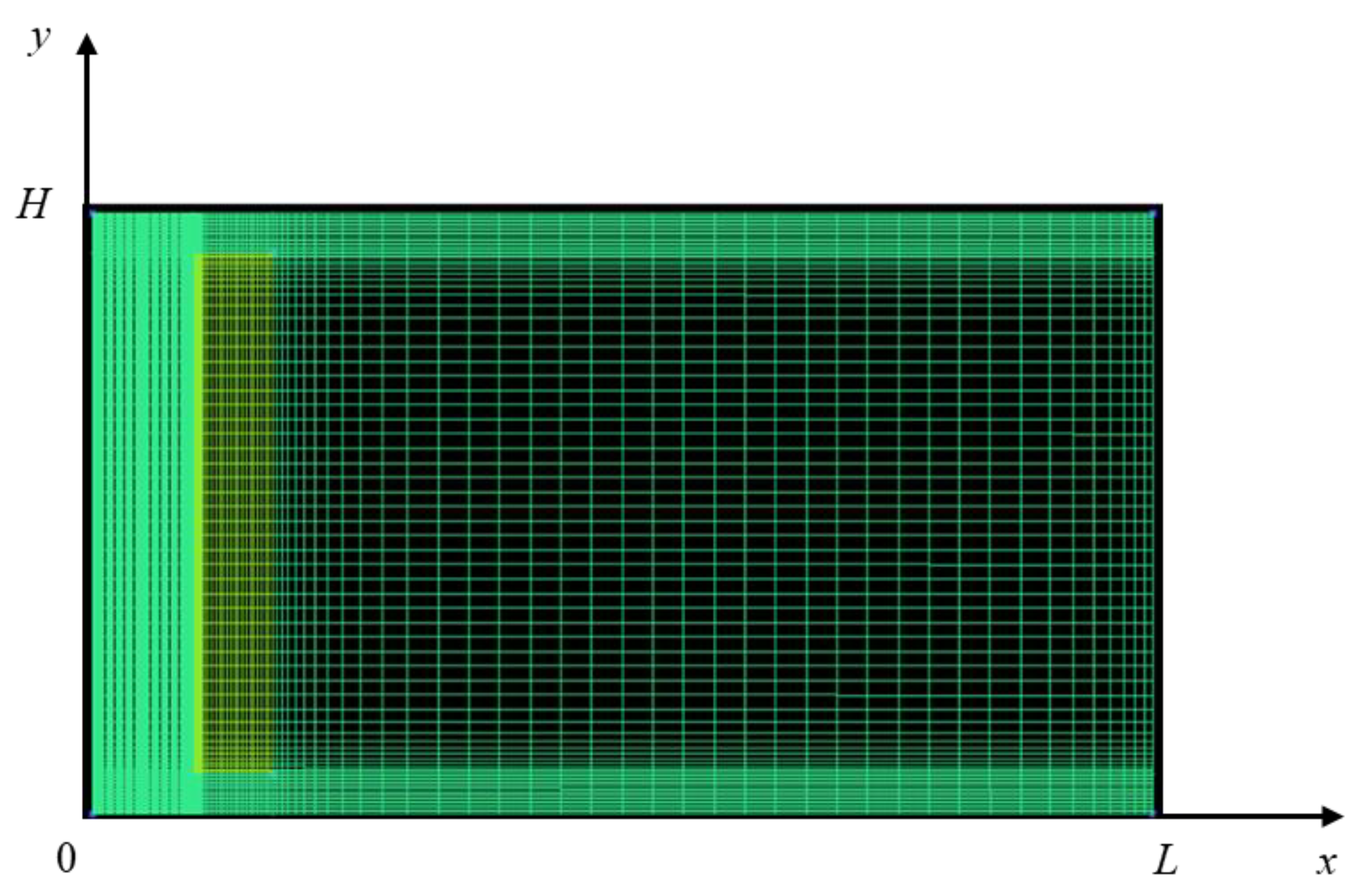
3.1. Computational Domain

The computational domain was discretized, keeping into account the need to compute the boundary layer without a wall function, as required by the k-ω SST turbulence model (par. A.2). Given the first cell height, the rest of the domain was discretized by means of a structured grid, with a growth rate of 1.1, a skewness below 0.6, and an aspect ratio below 5, with the thickness of the first mesh element that leads to y+ near 1 being close to the wall.
As regards to the temporal discretization, the use of a semi-implicit method does not require the Courant number to be kept below unity; therefore, another procedure was used to evaluate the time step size.
The solution was initialized with gravity acceleration set to 0.00981 m/s2, corresponding to a Rayleigh number of 0.8·107 indicative of a laminar flow regime. Then, steady-state conditions were simulated, and the time constant was estimated from the solution of the following [33]:
τ * = L U ∼ L 2 α Pr ⋅ Ra − 1 / 2 = L g β Δ T L
where L and U are the length and velocity scales, respectively. The time step adopted was calculated from the following initial value:
Δ t = τ * 4 ∼ 0.5 s
which was then increased until the solver reached convergence in 100 iterations per time step. So, Δt = 5 s was obtained.

3.2. Steady-State Simulations

The structures shown in Section 2.1 were simulated in steady-state conditions during the winter season using the commercial software ANSYS 15.0. This software provides the tools necessary for the different phases of the numerical analysis: geometry description, mesh generation (ICEM), and solver (Fluent). The simulated structures had a 2D geometry, discretized with a structured mesh made of quadrangular elements. The growth ratio of the mesh was set at 1.1. Figure 5 shows the details of the mesh.
The choice of the k-ω SST model was made due to its superiority with respect to other models, especially in terms of concerns regarding numerical stability. Furthermore, it was not damped in the region near the wall, resulting in a heat transfer between the air and the solid surface that was not numerically affected by the boundary layer (laminar sub-layer), which was computed using the wall function.
The boundary conditions for the modified BC structure were as follows: ∂ T ∂ x j x = D = 0 on the massive wall (adiabaticity); T = 288 K in x = 0 (glass temperature); heat power generation per unit volume inside the absorber to simulate the solar radiation equal to q ⃛ = 75,000 W/m3 for BC and q ¨ = 150 W/m2 applied in x = D; and inlet air temperature of 293 K.
The boundary conditions of the TM wall were assumed to be the same as the BC system. Table 1 shows the thermophysical properties of the materials used for both the steady- and transient-state conditions. The steady-state conditions used only the first two rows of the list in Table 1.

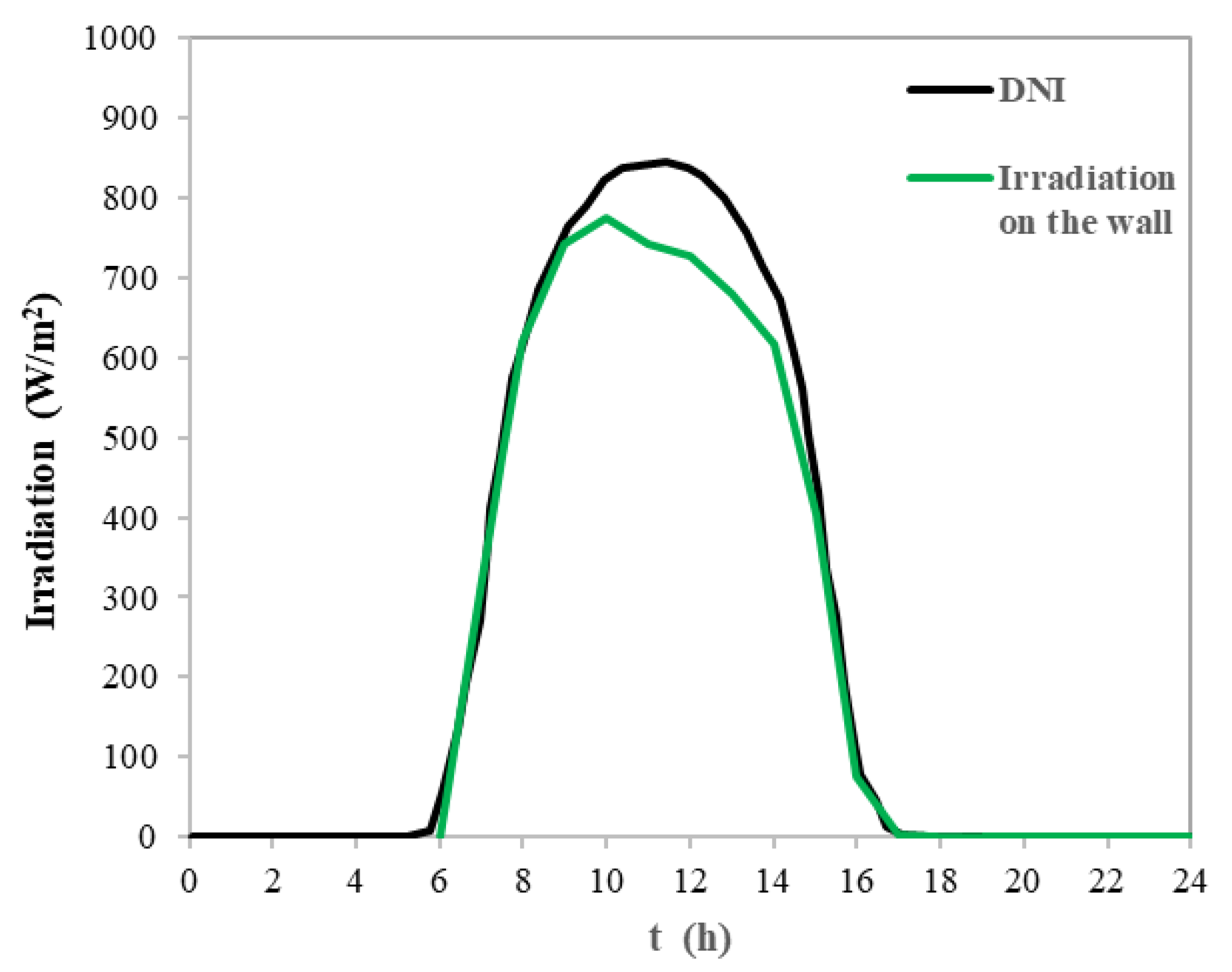
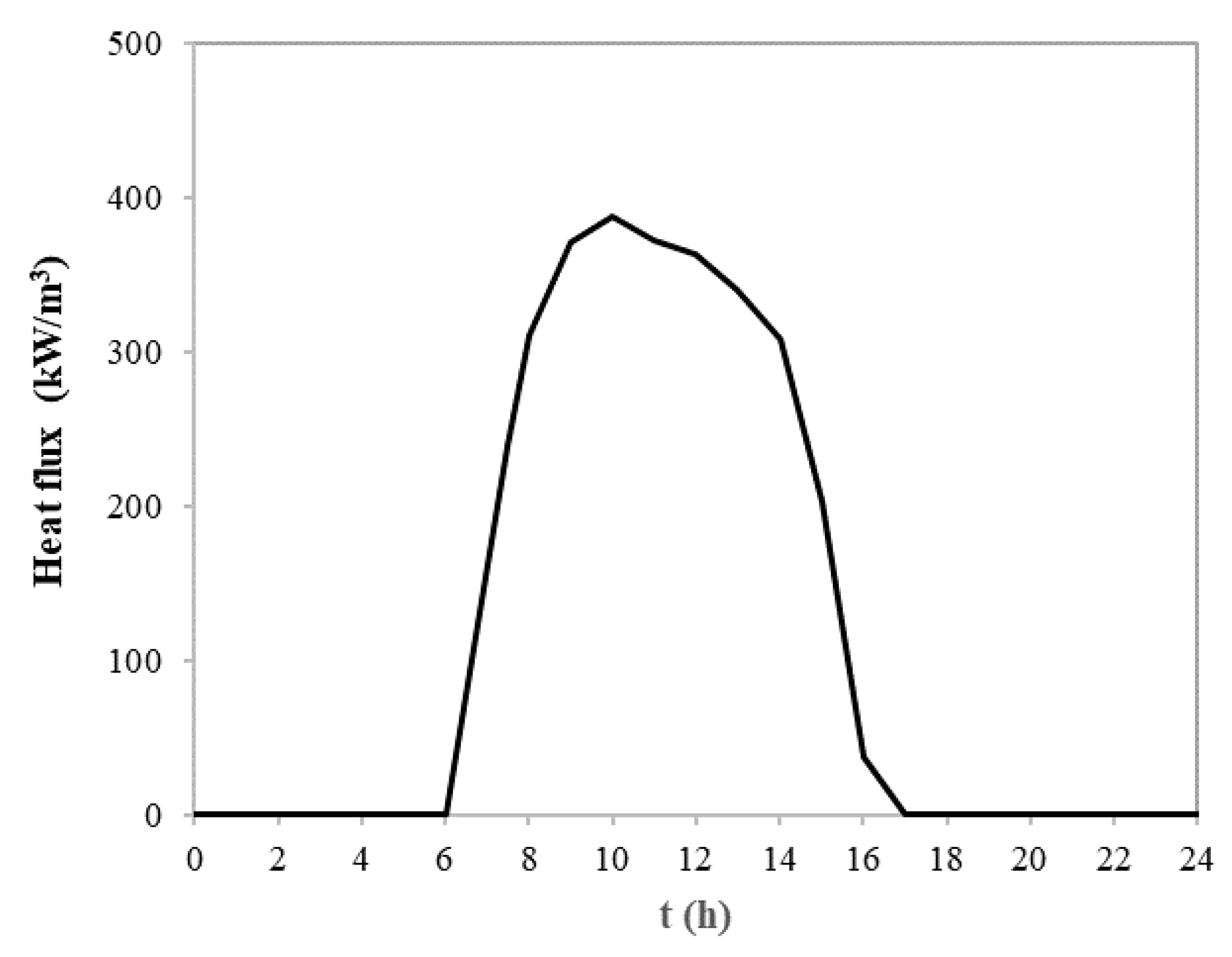
3.3. Transient-State Simulations

The dynamic behavior of the structures was simulated over five consecutive winter days. Again, ANSYS 15.0 was used for these simulations. Two-dimensional geometry and the mesh growth ratio were set to be the same as in the steady-state simulation. Figure 6 shows the geometry and the relative mesh.
The solar radiation intensity was obtained from the direct normal irradiation values in the city of Rome. To calculate the effective irradiation on the glass surface, the direct radiation was multiplied by the cosine of the solar height, as supplied by the website www.sunearthtools.com. Figure 7 shows the direct solar intensity and the effective irradiation during the simulated hours, while Figure 8 shows the heat flux generated per unit volume in 24 h for the BC wall. The heat flux reported in Figure 8 was assumed to be the same for all the simulated five days (120 h).
The boundary conditions chosen for the modified BC structure were as follows: imposed temperature of T = 283 K on y = H (the ceiling), on y = 0 (floor), and on x = L (north wall); adiabaticity on the southern surface of the massive wall; T = 278 K on x = 0 (glass temperature); and heat power generation on the absorber changing with time to simulate the variable solar radiation ( q ⃛ = q ⃛ ( t ) ) for the BC system (Figure 8) and q ¨ = q ¨ t in x = D for the TM system (Figure 7).
The same boundary conditions (Figure 7) were set for the TM wall, where only the adiabaticity of the southern surface of the massive wall was removed, which was only present in the BC system due to the presence of an insulator on the massive wall.
Different initial conditions were set for the two structures: T = 12 °C for t = 0 s on all of the air domain for the modified BC wall and T = 20 °C for t = 0 s on all of the air domain for the TM wall.
Again, the k-ω model was adopted as a turbulence model. The air was assumed to be incompressible according to the Boussinesq hypothesis.

4. Results

The simulation results for the steady- and transient-state conditions of the modified BC and TM walls are shown below.

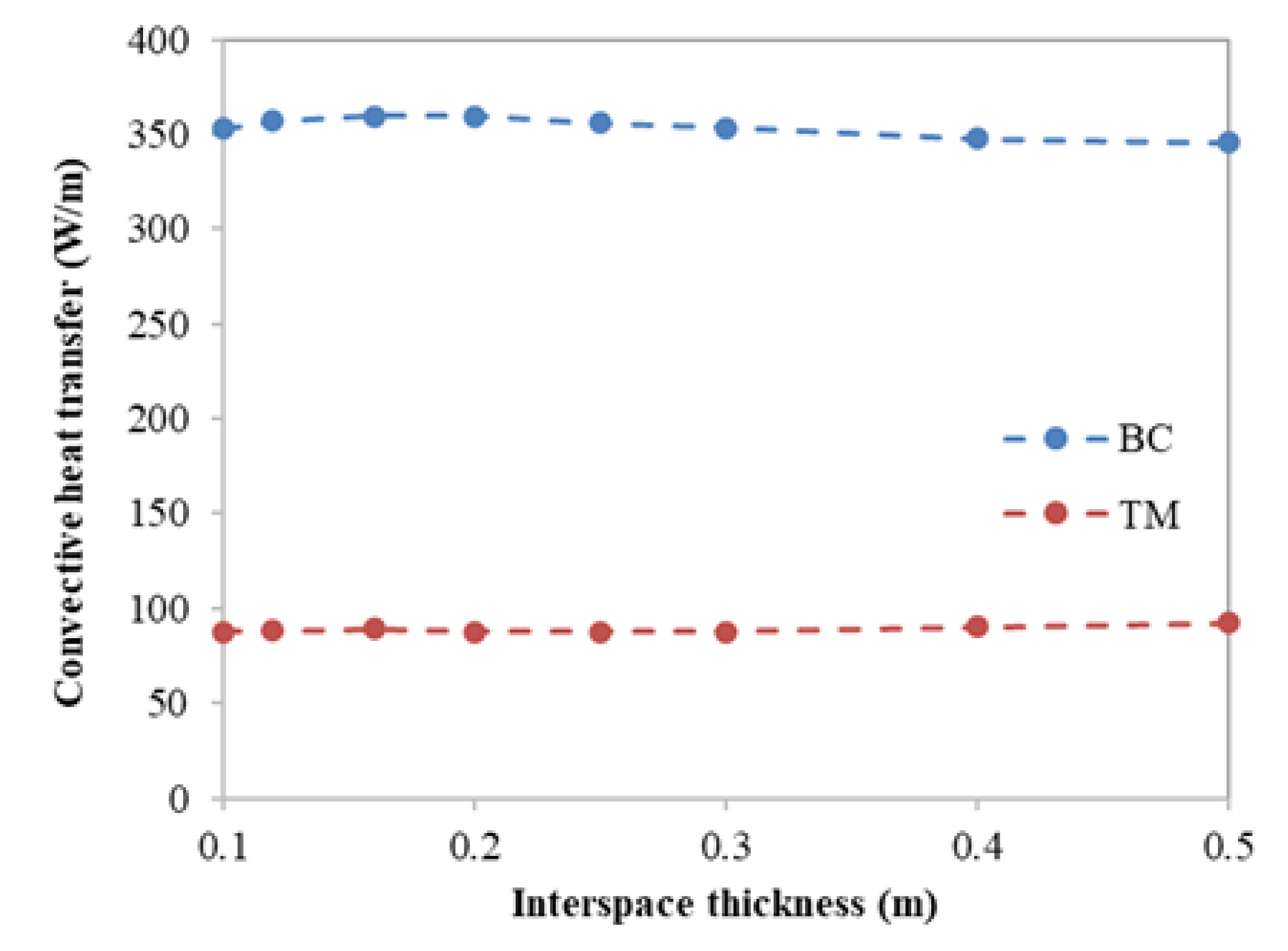
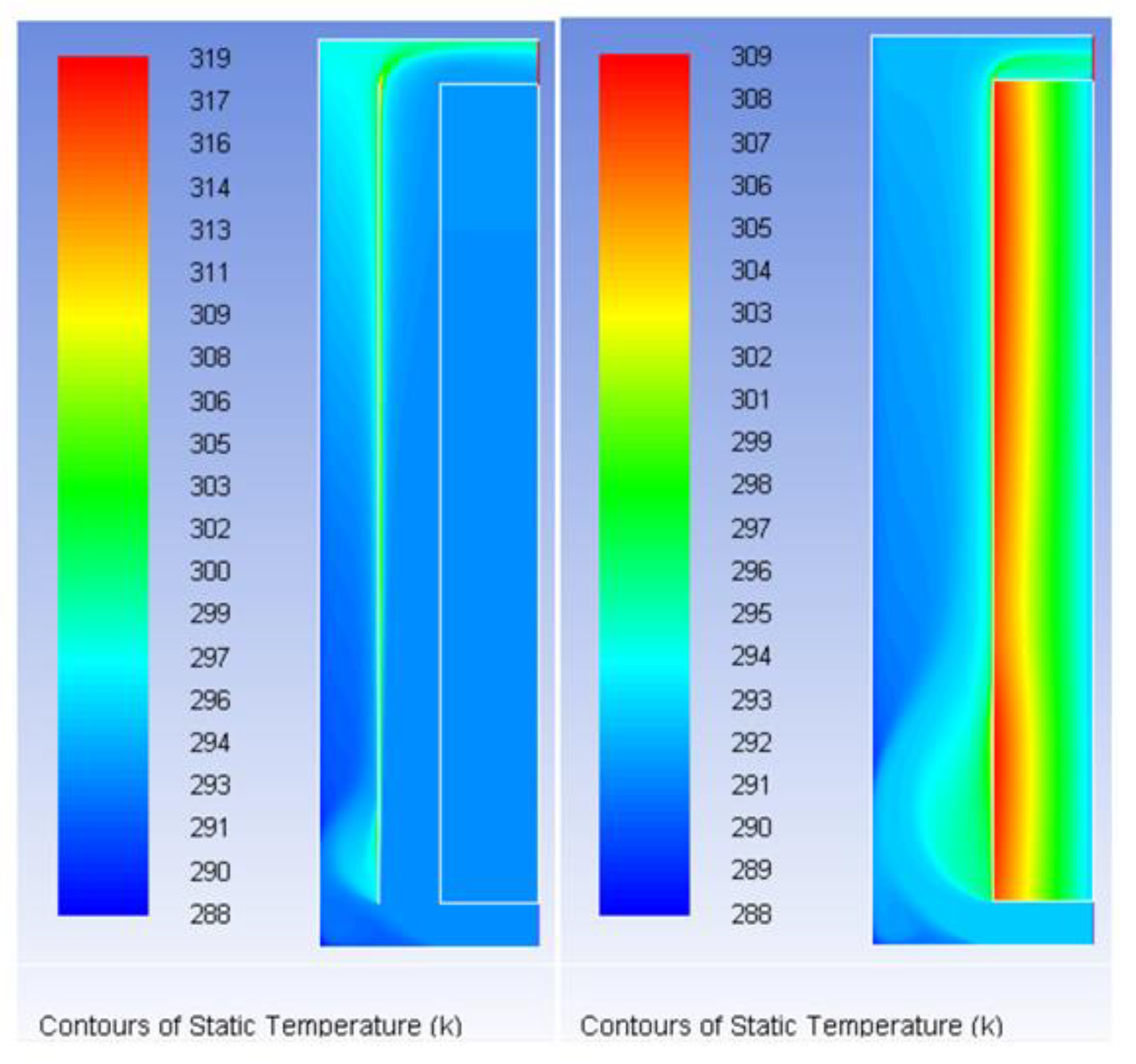
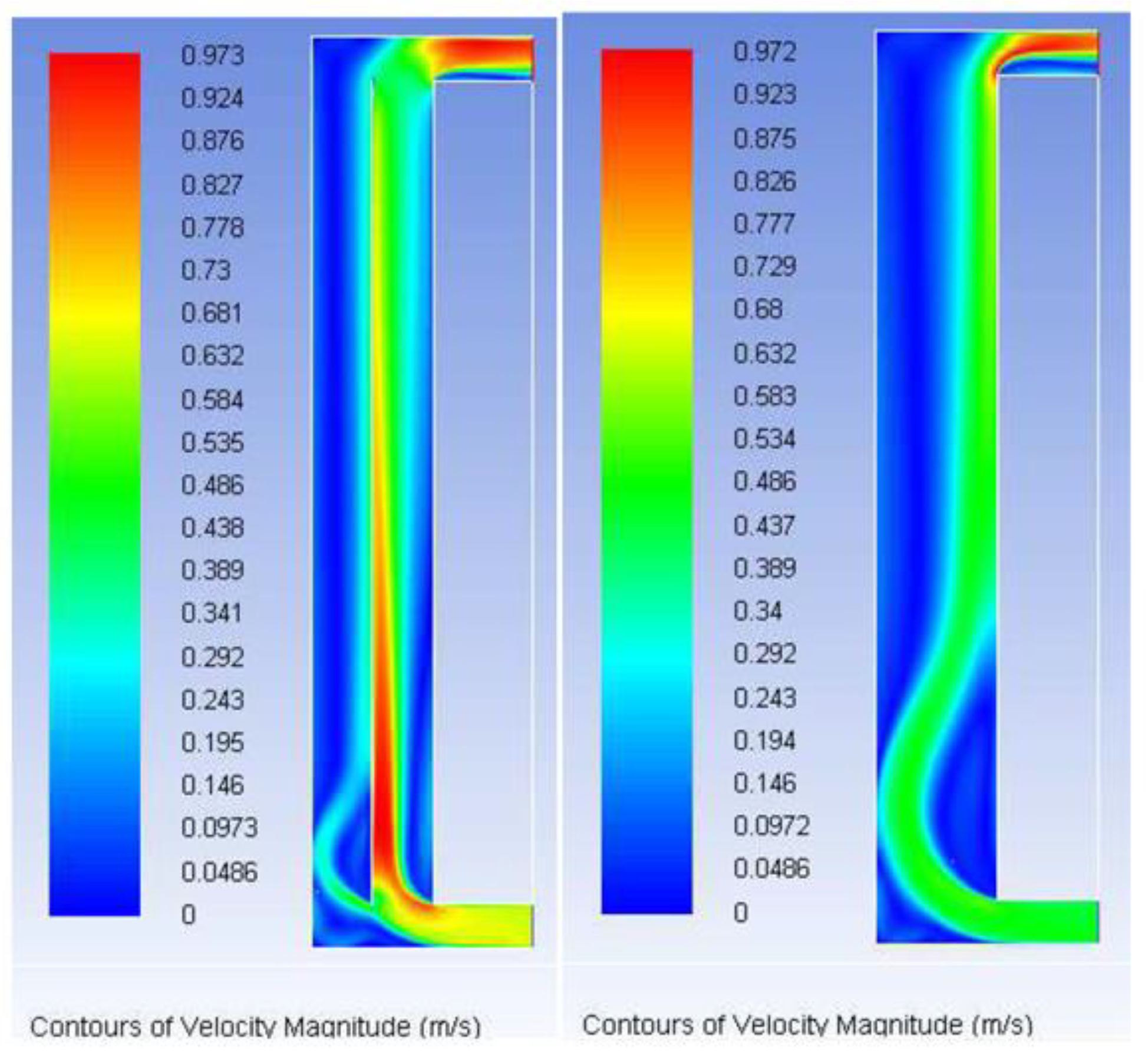
4.1. Steady State

Figure 9 shows the trends of the air temperature exiting from the interspaces of both the modified BC and TM walls as a function of the thickness of these spaces. The outlet temperature of the modified BC wall decreased from 24.5 to 22.9 °C as the layer thickness changed from 10 to 50 cm, while it remained almost constant (21 °C) in the TM wall.
These results agree with those reported in [27]; it can be noted that as the thickness of the cavity decreased, the air temperature increased until it approached the wall temperature. Consequently, the flow rate of hot air decreased (Figure 10). This effect was more evident in the BC system due to the insulation of the massive wall and the presence of the absorber. In fact, this resulted in the air being heated more than with the TM system due to the negligible heat capacity of the absorber.
Figure 10 shows how the thickness of the interspace influenced the air mass flow rate. The BC wall increased the exit mass flow rate from 0.067 to 0.119 kg/s (43%) as the interspace increased from 10 to 50 cm. On the contrary, the same two values of the interlayer thickness produced an increase in the mass flow rate in the TM wall of only 28%, from 0.0583 to 0.0811 kg/s m.
Figure 11 shows that the convection heat transfer was practically independent of the thickness of the cavity in both systems. This was due to the temperature increase observed when the thickness of the cavity decreased. This was compensated by a decrease in the flow rate, which consequently produced an almost constant convective heat flow. It is evident that the average convection heat transfer of the BC system (Figure 11) was four times that of the TM system, which was because of the BC insulated wall. Thus, the whole thermal power received by the sun was transmitted by free convection in the BC system. On the contrary, in the TM system, the thermal power was transmitted by convection in the cavity and by conduction within the massive wall.
In Figure 12 and Figure 13, comparisons of the temperature and velocity fields produced in the two systems are reported for the case of a 40 cm thick interlayer. As expected, the temperature of the massive BC wall was practically uniform. On the contrary, in the TM system, a 10 °C gradient was present. Figure 13 shows the streamlines generated in the two structures. In the BC system, a flow division into two parts and an air acceleration was clearly evident, both due to the absorber.

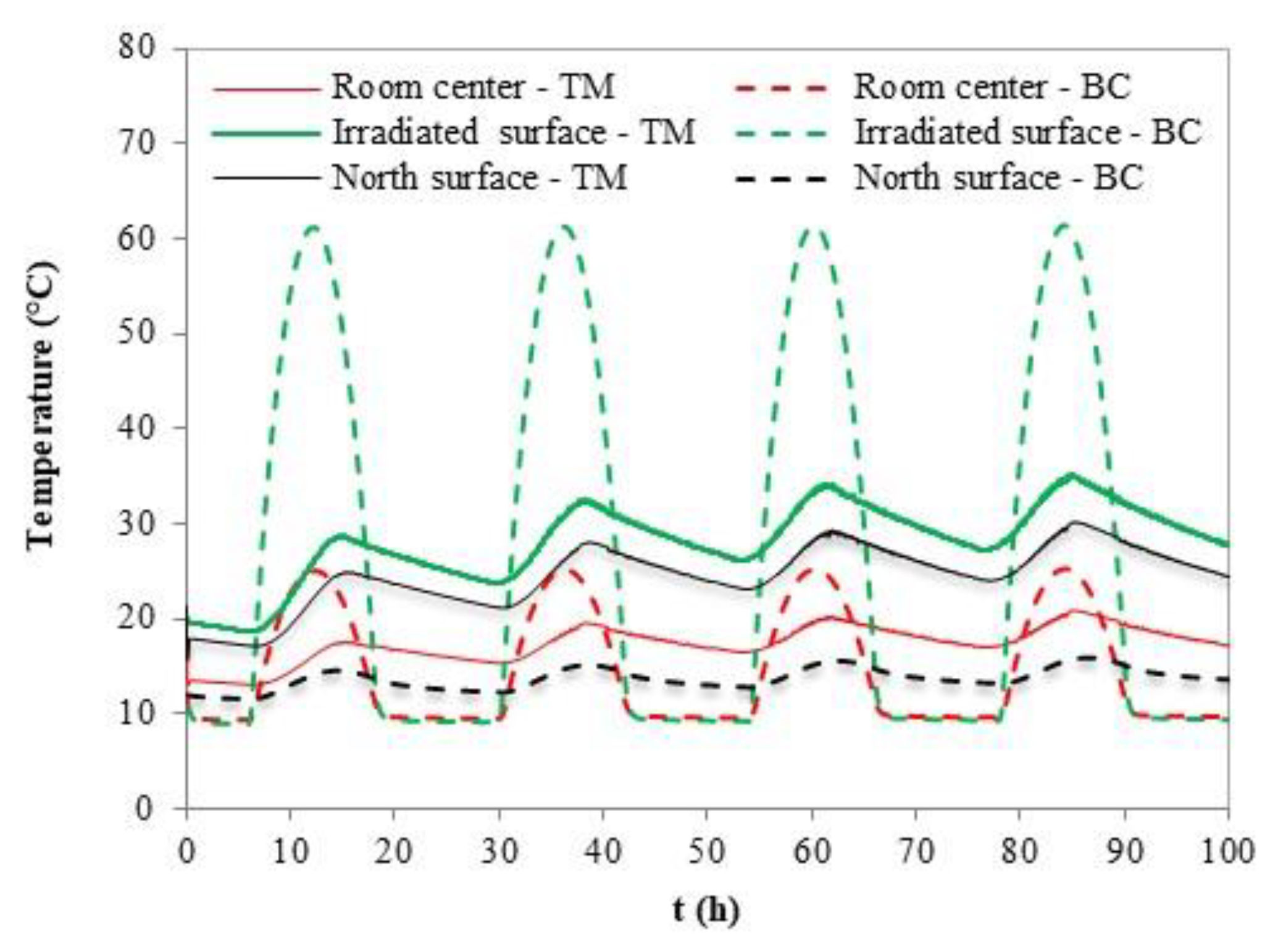
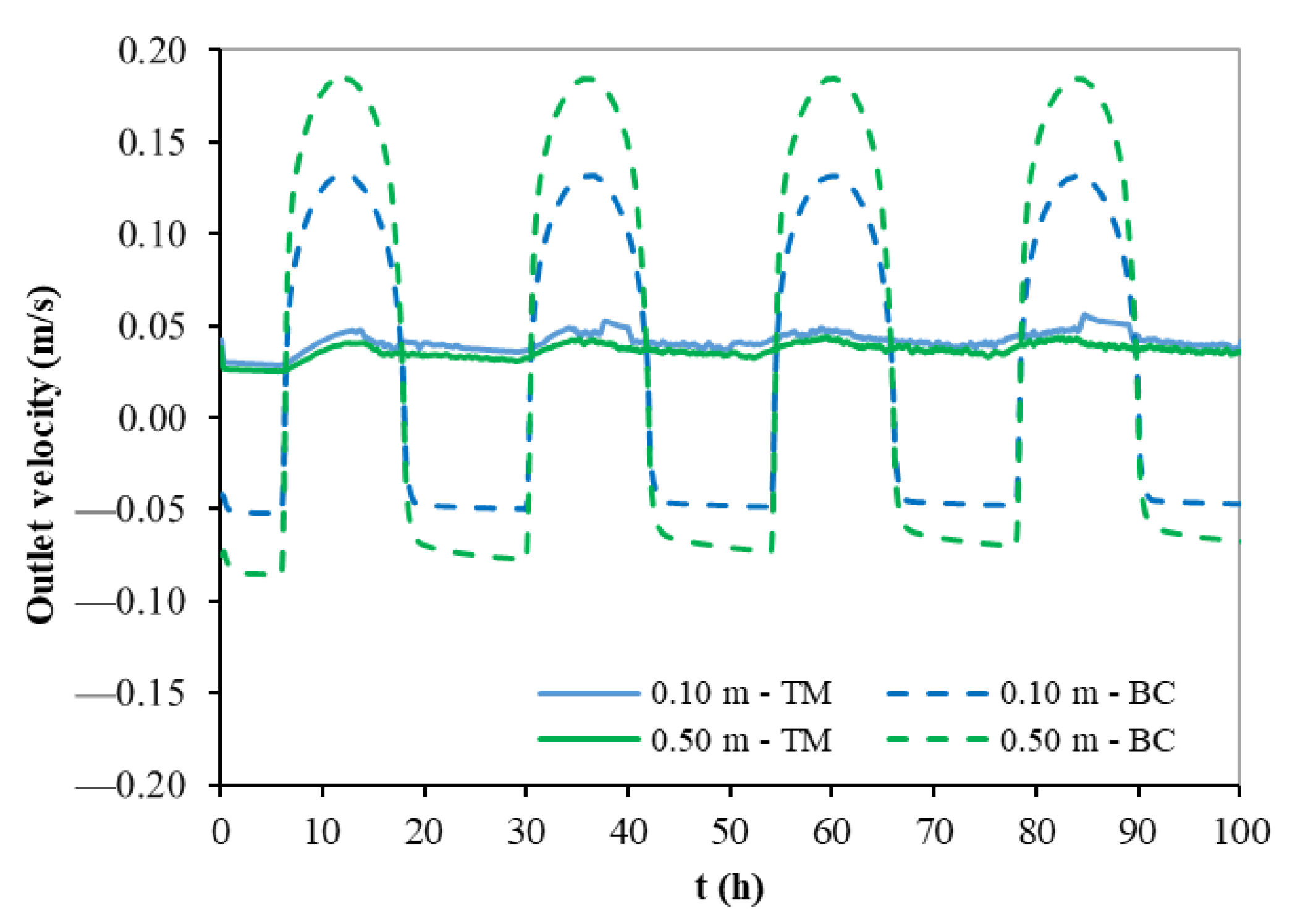
4.2. Transient Regime Results

Figure 14 shows the temperature trends of the modified BC system and the TM wall in the center of the room, on the north surface of the massive wall, and on the irradiated surface when the interlayer was 10 cm thick. When irradiation did not impinge on the system, such as, e.g., during non-sunny hours, the temperature in the center of the room behind the BC wall was lower than that with the TM wall, which was likely due to the vents being always opened in the simulations; in fact, during the night, the air motion inverts its direction (see Figure 16), thus cooling the room. The results show that the BC system presented a higher temperature oscillation in the center of the room (about 15 °C in the BC case compared to 4 °C in the TM case). Thus, the simulations with the vents being always open produced worse comfort conditions. In the real situation with the vents being closed in the night-time hours, the temperature oscillations were clearly lower, thus providing major comfort.
The dynamic response of the BC system was much shorter than the TM one, as evidenced by the results shown in Figure 14. In fact, the BC system already overcame the transient state within the first 24 h, while the TM system presented a continuous temperature increase even throughout the five days. These results agree with those reported in case 1 of [12].
Figure 15 shows how the same temperature changed with three different interspace thicknesses (10, 20, and 50 cm). It is evident that the thickness of the cavity did not produce significant changes both in the phase and intensity of the temperature response in the modified BC system and TM system. The minimum high-temperature peak (25.02 °C) happened in the first day for the 10 cm thick interspace, and the maximum (26.09 °C) occurred in the fifth day for the 50 cm thick interspace. That is, a 500% increase in the thickness produced only a 4% increase in the maximum temperature.
Figure 16 shows the trends of the outlet air velocity for different values of the interspace thickness. It is evident that the thickness of the cavity significantly influenced the air speed, and consequently the air mass flow rate, in the modified BC wall. During non-sunny hours, the velocity of the air changed its direction, activating a reverse thermosiphon effect. The BC system is equipped with valves that prevent this motion inversion. Also, this procedure was simulated in the calculations, that is, the air velocity was mirrored when it changed its direction.

5. Conclusions

The simulations of a modified BC system were carried out in steady and transient conditions and compared with the behavior of a traditional TM wall. The thickness of the cavity was varied to evaluate its influence on the air velocity and temperature of the ambient space that required heating. The following conclusions can be drawn from both simulations, both in steady and transient states.
1—The thickness of the cavity did not significantly influence the air temperatures of both structures.
2—The temperature peak increased up to 3–4% as the cavity thickness increased by 500%.
3—On the contrary, the thickness of the interspace significantly affected the flow of air injected in the modified BC structure, while it had a negligible effect on the TM system. This last result confirms the better performances of the BC structure, as characterized by a higher convection heat transfer efficiency because of the vents changing the air direction.
4—The insulation of the massive BC wall increased the heat supplied to the room cavity and produced a faster air heating. This allowed the BC structure to quicker respond to transient states. This effect was evident in the dynamic simulations in the center of the BC room, where an almost perfect stabilized periodic trend starting from the first day was observed. On the contrary, the traditional TM structure did not reach a stabilized periodic regime until the end of the five-day simulation. The BC system could then be used to heat rooms even farther away from the massive wall thanks to the higher mass flow rates supplied. The same could not be obtained in the traditional TM structure.

Author Contributions

Conceptualization, S.C., L.M., I.P. and M.P.; methodology, S.C., L.M., I.P. and M.P.; software, S.C., L.M., I.P. and M.P.; validation, S.C., L.M., I.P. and M.P; formal analysis, S.C., L.M., I.P. and M.P.; investigation, S.C., L.M., I.P. and M.P.; resources S.C., L.M., I.P. and M.P.; data curation, S.C., L.M., I.P. and M.P.; writing—original draft preparation S.C., L.M., I.P. and M.P.; writing—review and editing, S.C., L.M., I.P. and M.P.; visualization, S.C., L.M., I.P. and M.P.; supervision, S.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Appendix A.1. Governing Equations

Even if a buoyancy-driven flow should be theoretically treated as a compressible flow, in many natural-convection flows, a faster convergence can be achieved through the Boussinesq approximation. This model handles density as a constant value in all the solved equations, only adding a buoyancy term in the momentum equation:
ρ − ρ 0 g ≈ ρ 0 g β T − T 0
where ρ0 is the (constant) density of the undisturbed flow, T0 is the operating temperature, and β is the thermal expansion coefficient. Equation (A1) is derived from the Boussinesq approximation:
ρ = ρ 0 1 − β   Δ T
which eliminates ρ from the buoyancy term. This approximation is accurate as long as the changes in actual density are small, that is, when
β T − T 0 ≪ 1
This assumption is judged to be reasonable for the considered problem, and with it, the flow can be considered incompressible. Therefore, the governing equations for an incompressible Newtonian fluid are the continuity, the momentum, and the energy equations, generally known as the Navier–Stokes equations (NS). Whether the flow is turbulent or not, these equations can be written using the Einstein summation convention as follows:
∂ u i ∂ x i = 0
∂ u i ∂ t + u j ∂ 2 u i ∂ x j ∂ x j + T − T 0 T 0 g i = 0
∂ T ∂ t + u j ∂ T ∂ x j = λ ρ 0 c p ∂ 2 T ∂ x j ∂ x j + q ⃛ ρ 0 c p
where xi is the i-th coordinate, ui is the i-th instantaneous velocity component, written in a Cartesian reference system, p is the instantaneous static pressure, ρ0 is the density of the fluid, ν is the kinematic viscosity, T0 is the reference temperature for the calculation of the density variations, and T is the temperature. The effects of pressure work, kinetic energy, and viscous dissipation are neglected in the energy Equation (A6). cp is the specific heat at constant pressure, λ is the thermal conductivity, and q ⃛ is the heat generation per unit volume.
These equations can be only solved numerically for laminar flows. In order to check if this is the case, the Rayleigh number, defined as follows:
Ra = g β Δ T L 3 ρ μ α
must be calculated, with g being gravity acceleration, ΔT being the temperature difference between the hot and cold sides, ρ being the density, μ being the dynamic viscosity, and α being the thermal diffusivity.
In the present work, the Rayleigh number, based on the length of the surface heated by solar radiation, was approximately 0.8·1010, well beyond the 108 threshold, which is generally accepted as the limit of laminar flow. From this, the need to solve the NS equations considering turbulence is derived.
The so-called RANS approach, based on the RANS equations (Reynolds-averaged Navier–Stokes), consists of decomposing each instantaneous time-dependent variable into three components: long-time-averaged, periodic, and random turbulent [33]:
u i ( t ) = u ^ i + u ˜ i ( t ) + u ' i ( t )
p i ( t ) = p ^ i + p ˜ i ( t ) + p ' i ( t )
T i ( t ) = T ^ i + T ˜ i + T ' i ( t )
where, for instance, u ^ i denotes the long-time-averaged velocity component, u ˜ i is the periodic component, and u ' i is the turbulent component. The same notation is used for the pressure and temperature.
In the URANS equations, phase-averaged variables are present, which correspond to the sum of the long-time-averaged and periodic components:
U i ( t ) = u ^ i + u ˜ i ( t )
P i ( t ) = p ^ i + p ˜ i ( t )
T i ( t ) = T ^ i + T ˜ i
Here, the upper-case letter denotes the coherent (or phase-averaged) component of the quantity. Substituting these decomposed variables into the Navier–Stokes equations and performing an ensemble-average, the URANS equations are finally obtained:
∂ U i ∂ x i = 0
∂ U i ∂ t + U j ∂ U i ∂ x j = − 1 ρ ∂ P ∂ x i + ∂ ∂ x j ν ∂ U i ∂ x j − u i ' u j ' ¯ − g
∂ T ∂ t + U j ∂ T ∂ x j = ∂ ∂ x j λ + λ t ρ 0 c p ∂ T ∂ x j − u j ' T ' ¯ + q ⃛ ρ 0 c p
The operation of averaging and deriving can be temporarily inverted. Moreover, the average of the turbulent quantity is identically zero by definition. Consequently, all the products of the fluctuating and phase-averaged components disappear in the ensemble-averaging operation, beside the terms u i ′ u j ′ ¯ . These terms can be expressed as τ i j = − ρ u i ′ u j ′ ¯ and can be seen as the apparent stresses added by turbulent fluctuations to the mean flow field, so they are also called the Reynolds stresses. These terms are the only difference between the NS and URANS equations. In average motion, the non-linearity of the instantaneous fluctuations introduces new unknown quantities, i.e., the six terms of the Reynolds stresses tensor. The averaged equations do not contain any information about these terms; therefore, they need additional equations, i.e., the so-called turbulence closure problem equations. It should be noted that in order to consider the increased diffusion of thermal energy due to turbulent viscosity, the apparent thermal conductivity given by the sum of the thermal conductivity and its turbulent component, λt, is introduced as λeff = λ + λt.
The temperature field in the solid volume is calculated from the basic heat transfer equation:
∂ T ∂ t = ∂ ∂ x j λ s o l i d ρ s o l i d c p , s o l i d ∂ T ∂ x j + q ⃛ ρ s o l i d c p , s o l i d
where q ⃛ is the generic heat-generated power per unit volume. This term is used to simulate the effect of solar radiation and is only different from 0 in the BC absorber.
The most popular approach to the solution of RANS equations is the turbulent viscosity assumption introduced by Boussinesq [34]. This is based on relating the Reynolds stresses to the mean flow rate of the strain tensor through a linear constitutive relationship. It can be expressed as follows:
− u i ' u j ' ¯ = 2 ν T S i j − 2 3 k δ i j
where νT is the so-called turbulent viscosity (or eddy viscosity), k is the turbulent kinetic energy, and
S i j = 1 2 ∂ U i ∂ x j + ∂ U j ∂ x i − 1 3 ∂ U k ∂ x k δ i j
is the mean strain rate. It should be noted that its second term, 1 3 ∂ U k ∂ x k δ i j , is identically zero for incompressible flows. This linear Equation (A19) is the basis of the linear eddy viscosity models (EVMs). The reasonably accurate results are coupled with modest computational costs and make this approach the one most used in fluid dynamics calculations.
The apparent turbulent heat flux is thus written using this eddy viscosity term:
− u j ' T ' = ν T Pr T ∂ T ∂ x j
where PrT is the turbulent Prantdl number, which can be the result of a model (e.g., the Kays–Crawford model) or can be assumed as a constant.

Appendix A.2. Turbulence Modeling

The turbulence model used in the present work is the k-ω shear stress transport (SST) turbulence model [35]. It consists of a two-equation, linear eddy viscosity model, which has been extensively tested in the literature, showing good predictions even for separated flows. The k-ω SST turbulence model is a hybrid model combining Wilcox’s k-ω [36,37] and the standard k-ε turbulence models. The former, enabled inside the boundary layer, allows the model to be used all the way down to the wall without a wall function, whereas the latter gives robustness with respect to the free stream conditions.
The transport equations defining k and ω are as follows:
∂ k ∂ t + U j ∂ k ∂ x j = P k − β * k ω + ∂ ∂ x j ν + σ k ν T ∂ k ∂ x j
∂ ω ∂ t + U j ∂ ω ∂ x j = α S 2 − β ω 2 + ∂ ∂ x j ν + σ ω ν T ∂ ω ∂ x j + 2 1 + F 1 σ ω 2 1 ω ∂ k ∂ x i ∂ ω ∂ x i
where the turbulent viscosity is expressed as:
ν T = a 1 k max a 1 ω , S F 2
where S is the strain rate, and F1 and F2 are the blending functions, which are 1 inside the boundary layer and 0 in the free stream, as defined by the following expression:
F 1 = tanh min max k β * ω   y ' , 500 ν y 2 ω , 4 σ ω 2 k C D k ω y 2
F 2 = tanh max 2 k β * ω y ' , 500   ν y 2 ω 2
where CDkω can be written as follows:
C D k ω = max 2 ρ σ ω 2 1 ω ∂ k ∂ x i ∂ ω ∂ x i , 10 − 10
where σk and σkω are the turbulent Prandtl numbers for k and ω, respectively, and are obtained using the blending functions F 1 and F 2 .
The term Pk in the k transport equation is the production limiter:
P k = min τ i j ∂ U i ∂ x j , 10 β * k ω
This term avoids excessive turbulent kinetic energy near stagnation points, such as the leading edge of an airfoil. However, it is well known that the k-ω SST turbulence model predicts too large turbulence levels in large-normal-strain zones (i.e., stagnation and acceleration regions), although this over prediction is moderate in comparison with the normal k-ε turbulence model. The other coefficients are as follows:
α 1 = 5 9   ;   α 2 = 0.44   ;   β 1 = 3 40   ;   β 2 = 0.0828   ;   β * = 9 100 σ k 1 = 0.85   ;   σ k 2 = 1   ;   σ ω 1 = 0.5   ;   σ ω 2 = 0.856
The constants βi, σk, and σω are computed by a blend from the corresponding constants via the following equation:
ϕ = F 1 ϕ 1 + 1 − F 1 ϕ 2
The turbulent Prandtl number, PrT, is equal to 0.85.
The SIMPLE algorithm (semi-implicit method for pressure-linked equations) was used for solving the above set of equations.

References

  1. Bellos, E.; Tzivanidis, C.; Zisopoulou, E.; Mitsopoulos, G.; Antonopoulos, K.A. An innovative Trombe wall as a passive heating system for a building in Athens—A comparison with the conventional Trombe wall and the insulated wall. Energy Build. 2016, 133, 754–769. [Google Scholar] [CrossRef]
  2. Perini, K.; Ottelé, M.; Fraaij, A.L.A.; Haas, E.M.; Raiteri, R. Vertical greening systems and the effect on air flow and temperature on the building envelope. Build. Environ. 2011, 46, 2287–2294. [Google Scholar] [CrossRef]
  3. Lichołai, L.; Starakiewicz, A.; Krasoń, J.; Miąsik, P. The Influence of Glazing on the Functioning of a Trombe Wall Containing a Phase Change Material. Energies 2021, 14, 5243. [Google Scholar] [CrossRef]
  4. Bruno, R.; Bevilacqua, P.; Cirone, D.; Perrella, S.; Rollo, A. A Calibration of the Solar Load Ratio Method to Determine the Heat Gain in PV-Trombe Walls. Energies 2022, 15, 328. [Google Scholar] [CrossRef]
  5. Abdullah, A.A.; Attulla, F.S.; Ahmed, O.K.; Algburi, S. Effect of cooling method on the performance of PV/Trombe wall: Experimental assessment. Therm. Sci. Eng. Prog. 2022, 30, 101273. [Google Scholar] [CrossRef]
  6. Jie, J.; Hua, Y.; Wei, H.; Gang, P.; Jianping, L.; Bin, J. Modeling of a novel Trombe wall with PV cells. Build. Environ. 2007, 42, 1544–1552. [Google Scholar] [CrossRef]
  7. Jie, J.; Hua, Y.; Gang, P.; Bin, J.; Wei, H. Study of PV-Trombe wall assisted with DC fan. Build. Environ. 2007, 42, 3529–3539. [Google Scholar] [CrossRef]
  8. Zhu, Y.; Zhang, T.; Ma, Q.; Fukuda, H. Thermal Performance and Optimizing of Composite Trombe Wall with Temperature-Controlled DC Fan in Winter. Sustainability 2022, 14, 3080. [Google Scholar] [CrossRef]
  9. Yilmaz, Z.; Kundakci, A.B. An approach for energy conscious renovation of residential buildings in Istanbul by Trombe wall system. Build. Environ. 2008, 43, 508–517. [Google Scholar] [CrossRef]
  10. Wang, X.; Xi, Q.; Ma, Q. A review of current work in research of Trombe walls. In Proceedings of the 2021 3rd International Conference on Civil Architecture and Energy Science (CAES 2021), Hangzhou, China, 19–21 March 2021; Volume 248, p. 03025. [Google Scholar] [CrossRef]
  11. Omara, A.A.M.; Abuelnuor, A.A.A. Trombe walls with phase change materials: A review. Energy Storage 2020, 2, e123. [Google Scholar] [CrossRef]
  12. Saadi, S.; Chaker, A.; Boubekri, M. Study of two new configurations of the Barra-Costantini system with sunspot modelling. Appl. Therm. Eng. 2020, 173, 115221. [Google Scholar] [CrossRef]
  13. Hong, X.; Leung, M.K.H.; He, W. Thermal behaviour of Trombe wall venetian blind in summer and transition seasons. Energy Procedia 2019, 158, 1059–1064. [Google Scholar] [CrossRef]
  14. Xiong, Q.; Alshehri, H.M.; Monfaredi, R.; Tayebi, T.; Majdoub, F.; Hajjar, A.; Delpisheh, M.; Izadi, M. Application of phase change material in improving Trombe wall efficiency: An up-to-date and comprehensive overview. Energy Build. 2022, 258, 111824. [Google Scholar] [CrossRef]
  15. Simoes, N.; Manaia, M.; Simoes, I. Energy performance of solar and Trombe walls in Mediterranean climates. Energy 2021, 234, 121197. [Google Scholar] [CrossRef]
  16. Wu, S.Y.; Yan, R.R.; Xiao, L. Numerically predicting the effect of fin on solar Trombe wall performance. Sustain. Energy Technol. Assess. 2022, 52, 102012. [Google Scholar] [CrossRef]
  17. Szyszka, J. Simulation of modified Trombe wall. In Proceedings of the SOLINA 2018—VII Conference SOLINA Sustainable Development: Architecture—Building Construction—Environmental Engineering and Protection Innovative Energy-Efficient Technologies—Utilization of Renewable Energy Sources, Solina, Poland, 19–23 June 2018; Volume 49, p. 00114. [Google Scholar] [CrossRef]
  18. Baxevanou, C.; Fidaros, D.; Tsangrassoulis, A. Analytical model for the simulation of Trombe wall operation with heat storage. Green Energy Sustain. 2021, 1, 0007. [Google Scholar] [CrossRef]
  19. Imessad, K.; Messaoudene, N.A.; Belhamel, M. Performances of the Barra–Costantini passive heating system under Algerian climate conditions. Renew. Energy 2004, 29, 357–367. [Google Scholar] [CrossRef]
  20. Zhang, L.; Dong, J.; Sun, S.; Chen, Z. Numerical simulation and sensitivity analysis on an improved Trombe wall. Sustain. Energy Technol. Assess. 2021, 43, 100941. [Google Scholar] [CrossRef]
  21. Corasaniti, S.; Manni, L.; Russo, F.; Gori, F. Numerical simulation of modified Trombe-Michel Walls with exergy and energy analysis. Int. Commun. Heat Mass Transf. 2017, 88, 269–276. [Google Scholar] [CrossRef]
  22. Hong, T.; Chou, S.K.; Bong, T.Y. Building simulation: An overview of developments and information sources. Build. Environ. 2000, 35, 347–361. [Google Scholar] [CrossRef]
  23. Albaqawy, G.; Mesloub, A.; Kolsi, L. CFD investigation of effect of nanofluids filled Trombe wall on 3D convective heat transfer. J. Cent. South Univ. 2021, 28, 3569–3579. [Google Scholar] [CrossRef]
  24. Hong, X.; He, W.; Hu, Z.; Wang, C.; Ji, J. Three-dimensional simulation on the thermal performance of a novel Trombe wall with venetian blind structure. Energy Build. 2015, 89, 32–38. [Google Scholar] [CrossRef]
  25. Long, J.; Jiang, M.; Lu, J.; Du, A. Vertical temperature distribution characteristics and adjustment methods of a Trombe wall. Build. Environ. 2019, 165, 106386. [Google Scholar] [CrossRef]
  26. Błotny, J.; Nems, M. Analysis of the Impact of the Construction of a Trombe Wall on the Thermal Comfort in a Building Located in Wrocław, Poland. Atmosphere 2019, 10, 761. [Google Scholar] [CrossRef]
  27. Zamora, B.; Kaiser, A.S. Thermal and dynamic optimization of the convective flow in Trombe Wall shaped channels by numerical investigation. Heat Mass Transf. 2009, 45, 1393–1407. [Google Scholar] [CrossRef]
  28. Koyunbaba, B.K.; Yilmaz, Z. The comparison of Trombe wall systems with single glass, double glass and PV panels. Renew. Energy 2012, 45, 111e118. [Google Scholar] [CrossRef]
  29. Hong, X.; Leungb, M.K.H.; He, W. Effective use of venetian blind in Trombe wall for solar space conditioning control. Appl. Energy 2019, 250, 452–460. [Google Scholar] [CrossRef]
  30. Hu, Z.; Wei He, W.; Hu, D.; Lv, S.L.; Jie, J.J.; Chen, H.; Ma, J. Design, construction and performance testing of a PV blind-integrated Trombe wall module. Appl. Energy 2017, 203, 643–656. [Google Scholar] [CrossRef]
  31. Yu, B.; He, W.; Li, N.; Zhou, F.; Shen, Z.; Chen, H.; Gang Xu, G. Experiments and kinetics of solar PCO for indoor air purification in PCO/TW system. Build. Environ. 2017, 115, 130e146. [Google Scholar] [CrossRef]
  32. Wang, D.; Hu, L.; Du, H.; Liu, Y.; Huang, J.; Xu, Y.; Liu, J. Classification, experimental assessment, modeling methods and evaluation metrics of Trombe walls. Renew. Sustain. Energy Rev. 2020, 124, 109772. [Google Scholar] [CrossRef]
  33. Bejan, A. Convection Heat Transfer; John Wiley and Sons: New York, NY, USA, 1984. [Google Scholar]
  34. Hussain AK, M.F.; Reynolds, W.C. The mechanics of an organized wave in turbulent shear flow. J. Fluid Mech. 1970, 41, 241–258. [Google Scholar] [CrossRef]
  35. Boussinesq, J. Essai sur la theorie des eaux courantes. Memoires presents par divers savants a l’. Acad. Des Sci. 1877, XXIII, 1–680. [Google Scholar]
  36. Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
  37. Wilcox, D.C. Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
Energies 17 00295 g001
Figure 1. Modified BC structure (sizes are in cm).
Figure 1. Modified BC structure (sizes are in cm).
Energies 17 00295 g001
Energies 17 00295 g002
Figure 2. TM wall structure (sizes are in cm).
Figure 2. TM wall structure (sizes are in cm).
Energies 17 00295 g002
Energies 17 00295 g003
Figure 3. TM wall simulated in transient state.
Figure 3. TM wall simulated in transient state.
Energies 17 00295 g003
Energies 17 00295 g004
Figure 4. Modified BC wall simulated in transient state.
Figure 4. Modified BC wall simulated in transient state.
Energies 17 00295 g004
Energies 17 00295 g005
Figure 5. Details of the mesh of the modified BC structure simulated in steady-state conditions: (a) entire wall structure; (b) sample of a corner.
Figure 5. Details of the mesh of the modified BC structure simulated in steady-state conditions: (a) entire wall structure; (b) sample of a corner.
Energies 17 00295 g005
Energies 17 00295 g006
Figure 6. Geometry and mesh of the modified BC system used to simulate the transient-state conditions.
Figure 6. Geometry and mesh of the modified BC system used to simulate the transient-state conditions.
Energies 17 00295 g006
Energies 17 00295 g007
Figure 7. Direct normal irradiation (DNI) (black line) and effective irradiation (green line) for a typical winter day in Rome.
Figure 7. Direct normal irradiation (DNI) (black line) and effective irradiation (green line) for a typical winter day in Rome.
Energies 17 00295 g007
Energies 17 00295 g008
Figure 8. Heat flux generated per unit volume in 24 h for BC wall.
Figure 8. Heat flux generated per unit volume in 24 h for BC wall.
Energies 17 00295 g008
Energies 17 00295 g009
Figure 9. Outlet air temperature as a function of the thickness for modified BC wall and TM wall.
Figure 9. Outlet air temperature as a function of the thickness for modified BC wall and TM wall.
Energies 17 00295 g009
Energies 17 00295 g010
Figure 10. Exit mass flow rate as a function of the thickness in modified BC and TM walls.
Figure 10. Exit mass flow rate as a function of the thickness in modified BC and TM walls.
Energies 17 00295 g010
Energies 17 00295 g011
Figure 11. Convective heat flux as a function of the thickness for modified BC wall and TM wall.
Figure 11. Convective heat flux as a function of the thickness for modified BC wall and TM wall.
Energies 17 00295 g011
Energies 17 00295 g012
Figure 12. Temperature field of modified BC wall (left) and TM wall (right) for interspace of 0.40 m.
Figure 12. Temperature field of modified BC wall (left) and TM wall (right) for interspace of 0.40 m.
Energies 17 00295 g012
Energies 17 00295 g013
Figure 13. Velocity field of modified BC wall (left) and TM wall (right) for interspace of 0.40 m.
Figure 13. Velocity field of modified BC wall (left) and TM wall (right) for interspace of 0.40 m.
Energies 17 00295 g013
Energies 17 00295 g014
Figure 14. Temperature trend of modified BC wall and TM wall in the center of the room, irradiated surface, and north surface of massive wall for interspace of 0.10 m.
Figure 14. Temperature trend of modified BC wall and TM wall in the center of the room, irradiated surface, and north surface of massive wall for interspace of 0.10 m.
Energies 17 00295 g014
Energies 17 00295 g015
Figure 15. Temperature trend of modified BC wall and TM wall in the center of the room for different values of interspace thickness (a) and a detail between 70 and 90 h (b).
Figure 15. Temperature trend of modified BC wall and TM wall in the center of the room for different values of interspace thickness (a) and a detail between 70 and 90 h (b).
Energies 17 00295 g015
Energies 17 00295 g016
Figure 16. Outlet air velocity of modified BC wall and TM wall.
Figure 16. Outlet air velocity of modified BC wall and TM wall.
Energies 17 00295 g016
Table 1. Thermophysical properties of materials.
Table 1. Thermophysical properties of materials.
Density
kg/m3		Thermal Conductivity
W/(m K)		Specific Heat
J/(kg K)
Air1.2250.02421006
Aluminum absorber2719202.4871
Concrete18001.6880
Hollow bricks8500.2511000
Glass25000.8670
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Corasaniti, S.; Manni, L.; Petracci, I.; Potenza, M. Steady- and Transient-State CFD Simulations of a Modified Barra–Costantini Solar System in Comparison with a Traditional Trombe–Michel Wall. Energies 2024, 17, 295. https://doi.org/10.3390/en17020295

AMA Style

Corasaniti S, Manni L, Petracci I, Potenza M. Steady- and Transient-State CFD Simulations of a Modified Barra–Costantini Solar System in Comparison with a Traditional Trombe–Michel Wall. Energies. 2024; 17(2):295. https://doi.org/10.3390/en17020295

Chicago/Turabian Style

Corasaniti, Sandra, Luca Manni, Ivano Petracci, and Michele Potenza. 2024. "Steady- and Transient-State CFD Simulations of a Modified Barra–Costantini Solar System in Comparison with a Traditional Trombe–Michel Wall" Energies 17, no. 2: 295. https://doi.org/10.3390/en17020295

APA Style

Corasaniti, S., Manni, L., Petracci, I., & Potenza, M. (2024). Steady- and Transient-State CFD Simulations of a Modified Barra–Costantini Solar System in Comparison with a Traditional Trombe–Michel Wall. Energies, 17(2), 295. https://doi.org/10.3390/en17020295

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop