A Lyapunov Theory-Based SEIG–STATCOM Voltage Regulation Control Strategy
Abstract
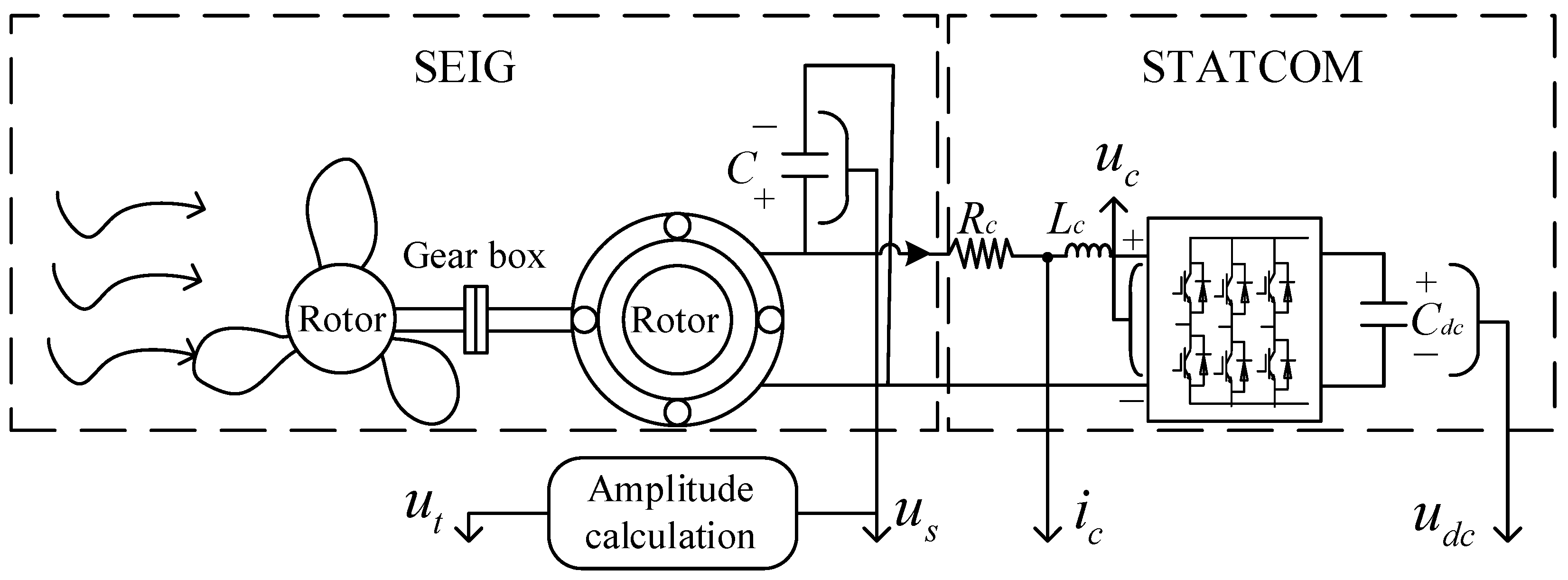
1. Introduction
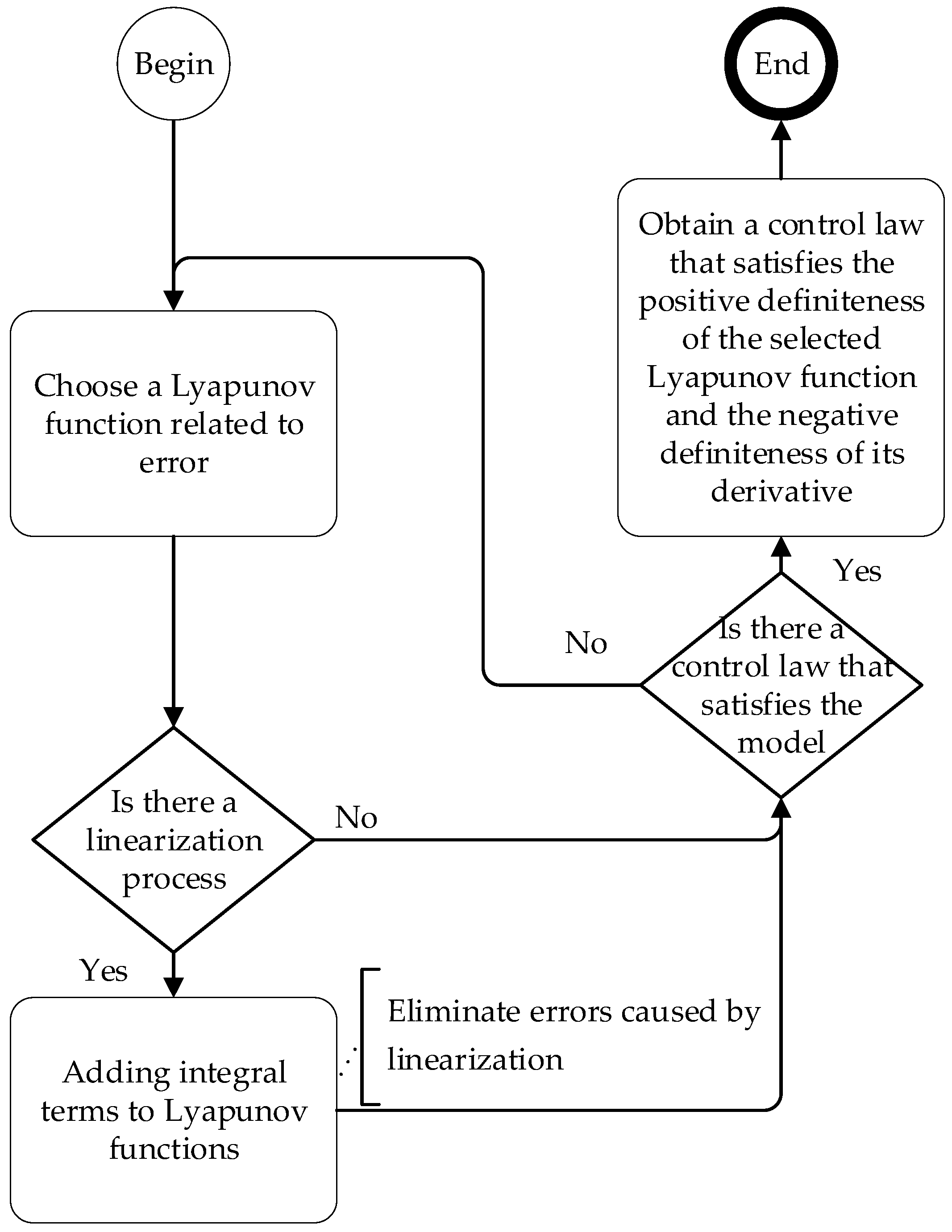
2. LBC Design
- (i)
- , for all
- (ii)
- for all .
- (i)
- Stable (in sense of A.M. Lyapunov), if for any neighborhood of u there exists a neighborhood (i.e., not necessarily the same neighborhood) of the same point, such that for all (a certain value of u) ;
- (ii)
- Asymptotically stable (in sense of A.M. Lyapunov), if it is stable and for any point v in some neighborhood of u, for .
- (i)
- V(u) = 0
- (ii)
- . Here, φ is strictly increasing continuous function such that φ(0) = 0 and φ(r) > 0 for ; this indicates the point u is stable.
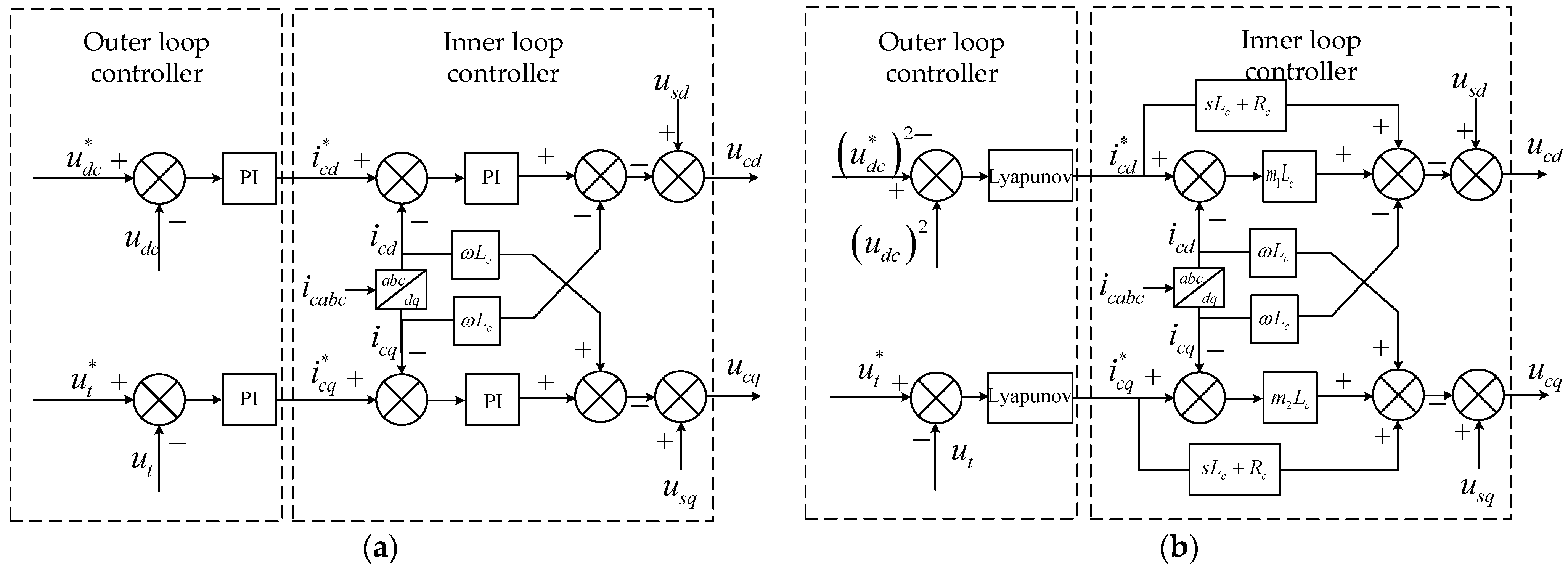
2.1. Design of the d-Axis Voltage Controller
2.2. Design of the q-Axis Voltage Controller
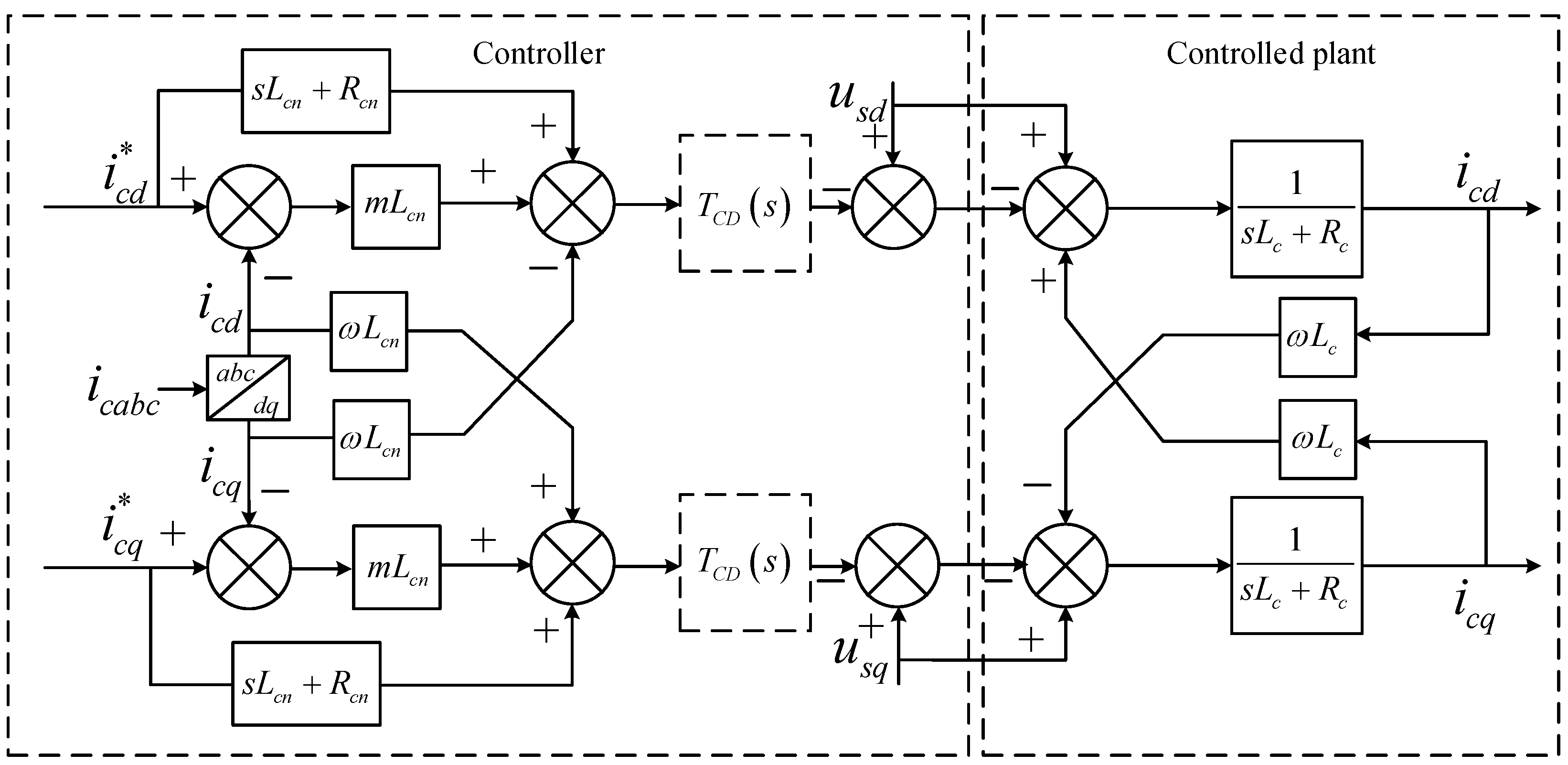
2.3. Design of the Current Controller
3. Results
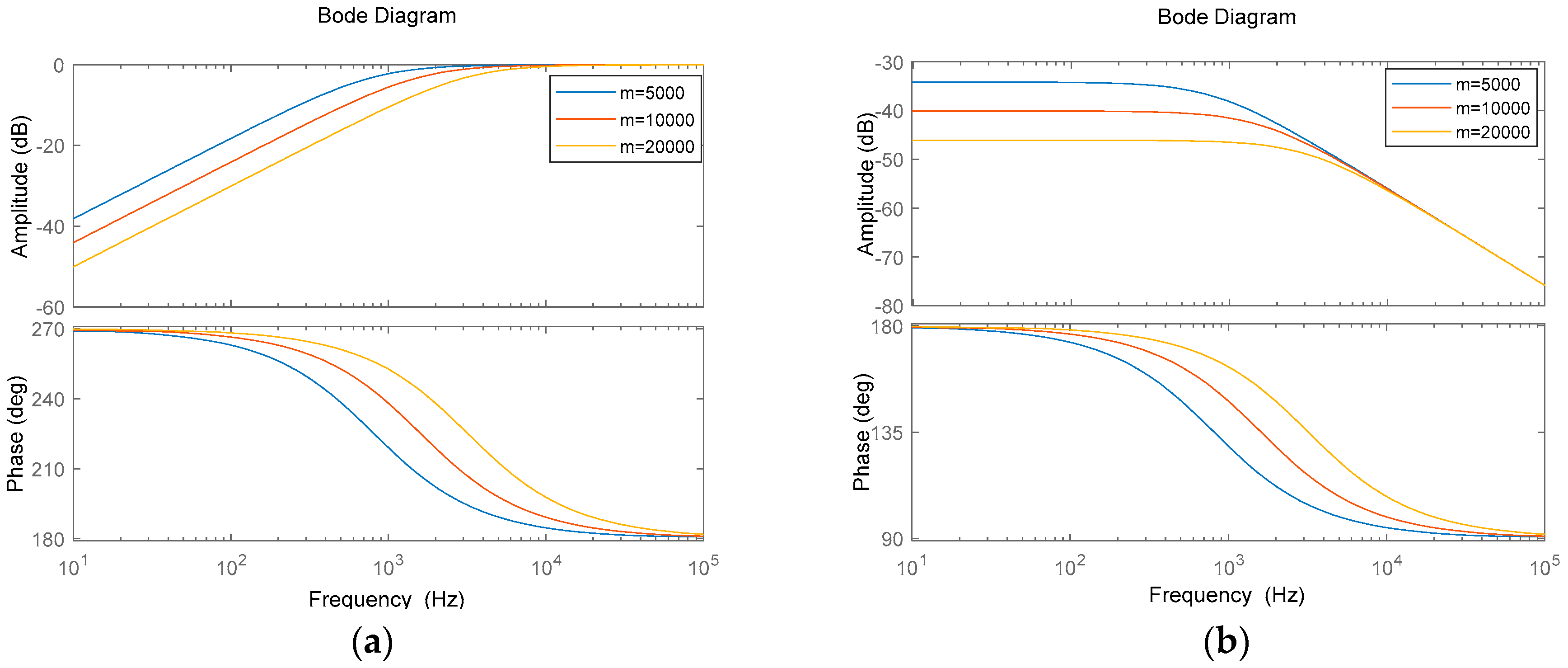
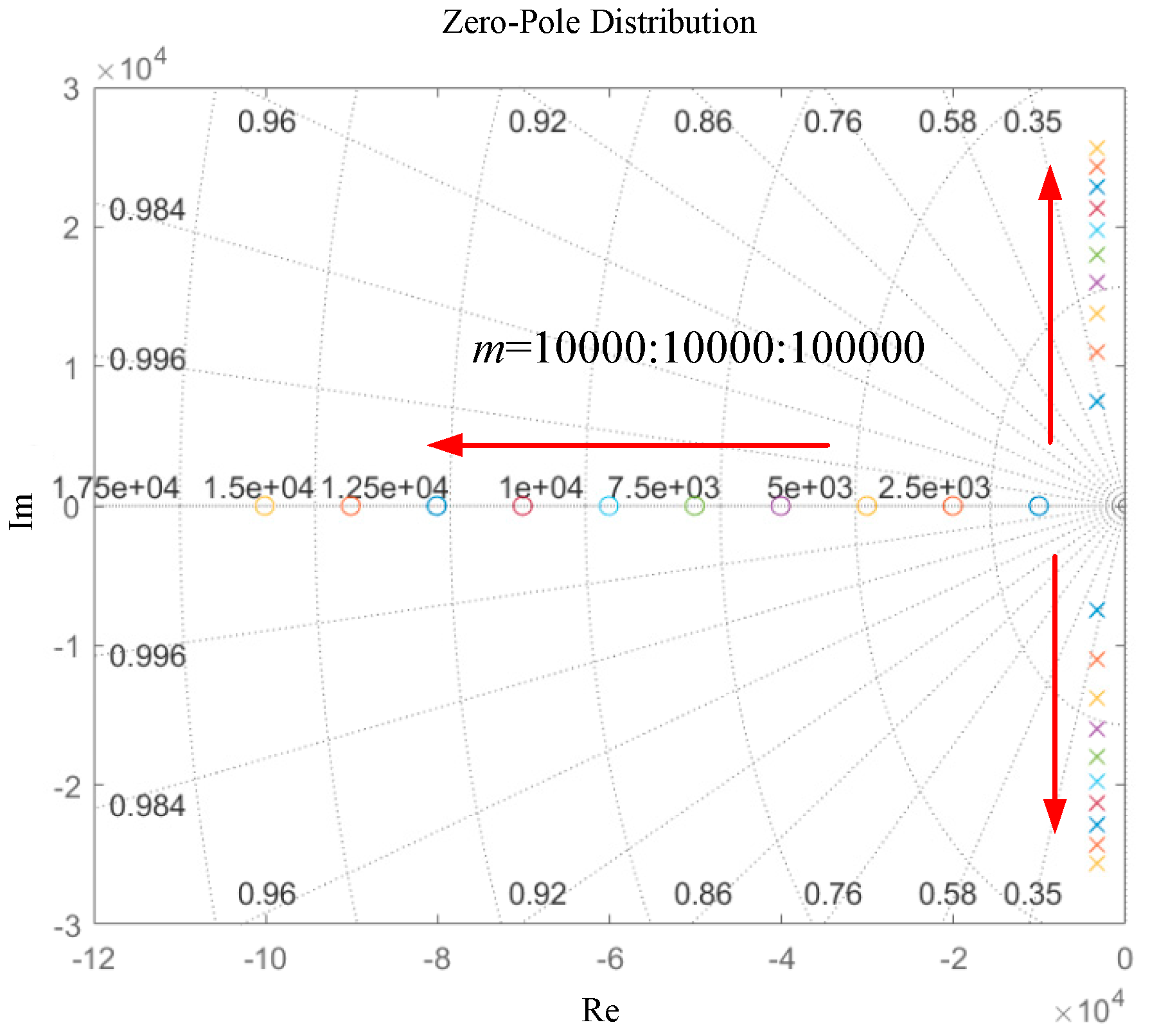
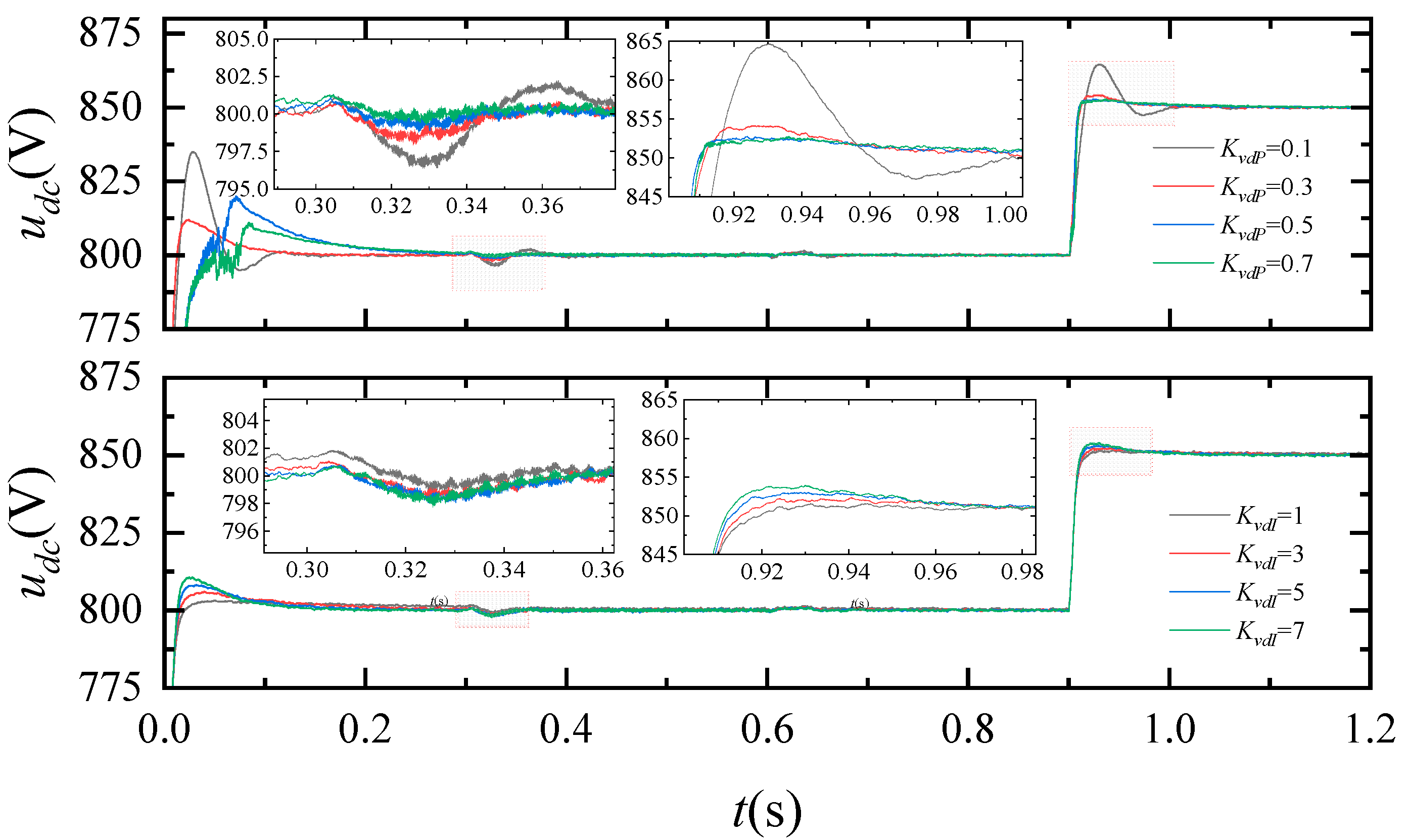
3.1. Analysis of the Controller
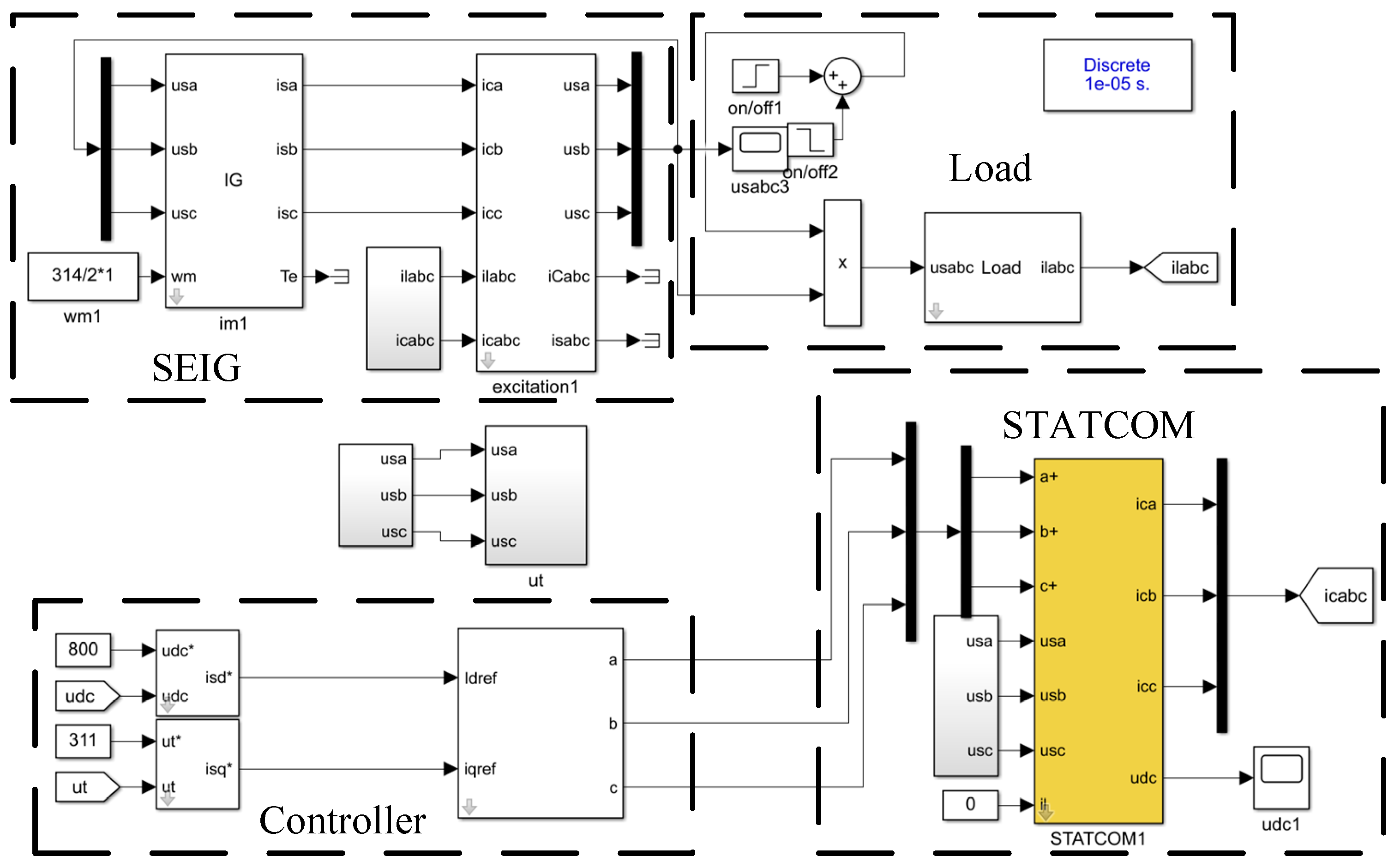
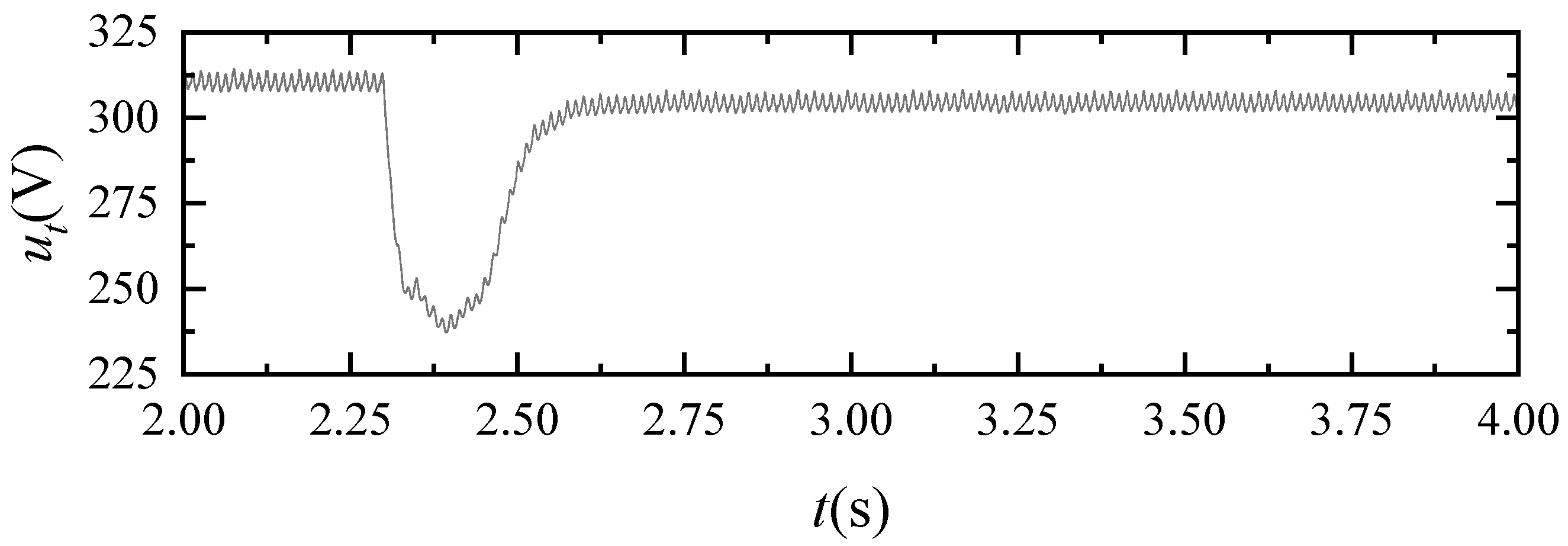
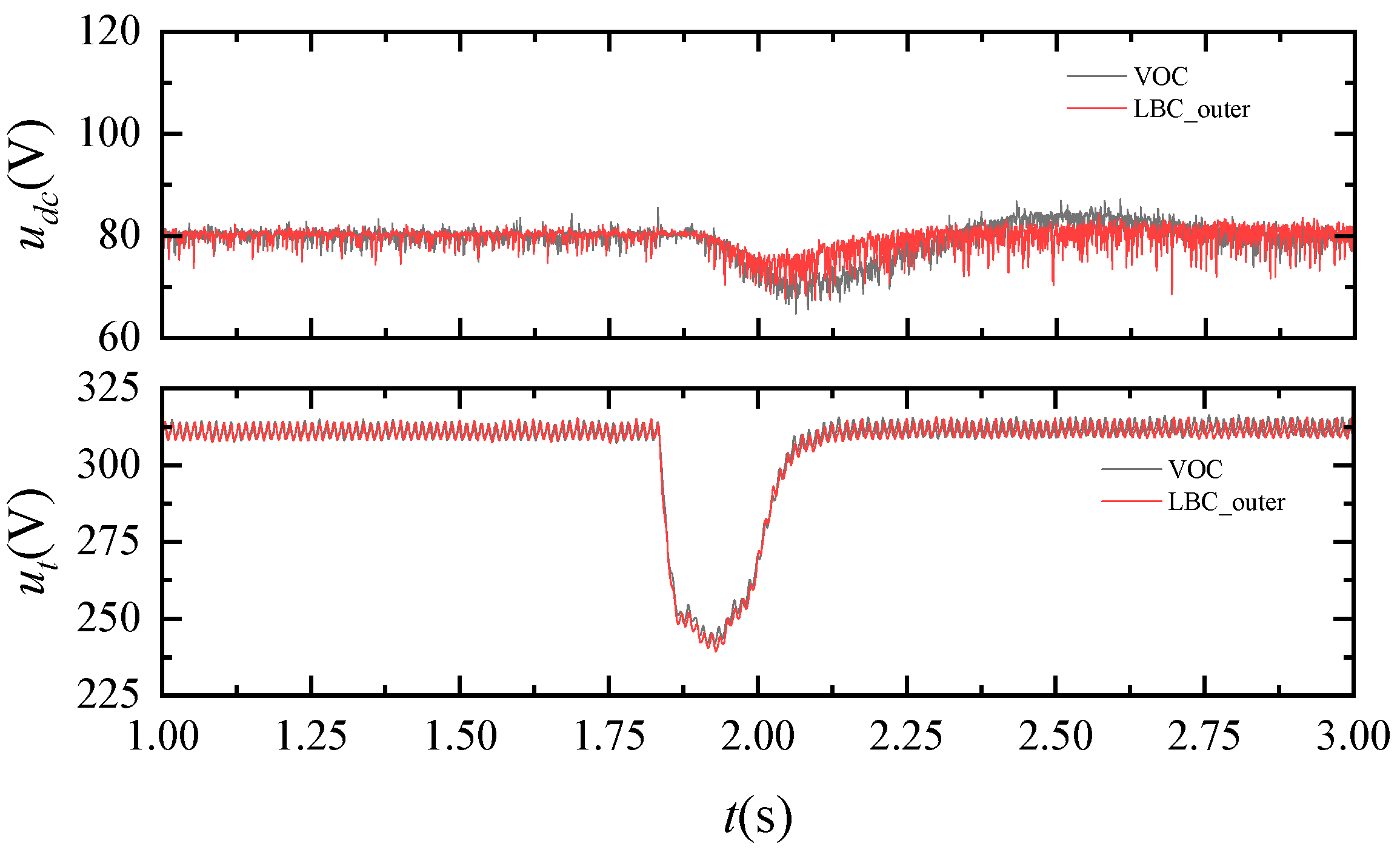
3.2. Simulation Results
- PI (outer) + LBC (inner);
- LBC (outer) + PI (inner);
- The traditional approach VOC: PI (outer) + PI (inner).
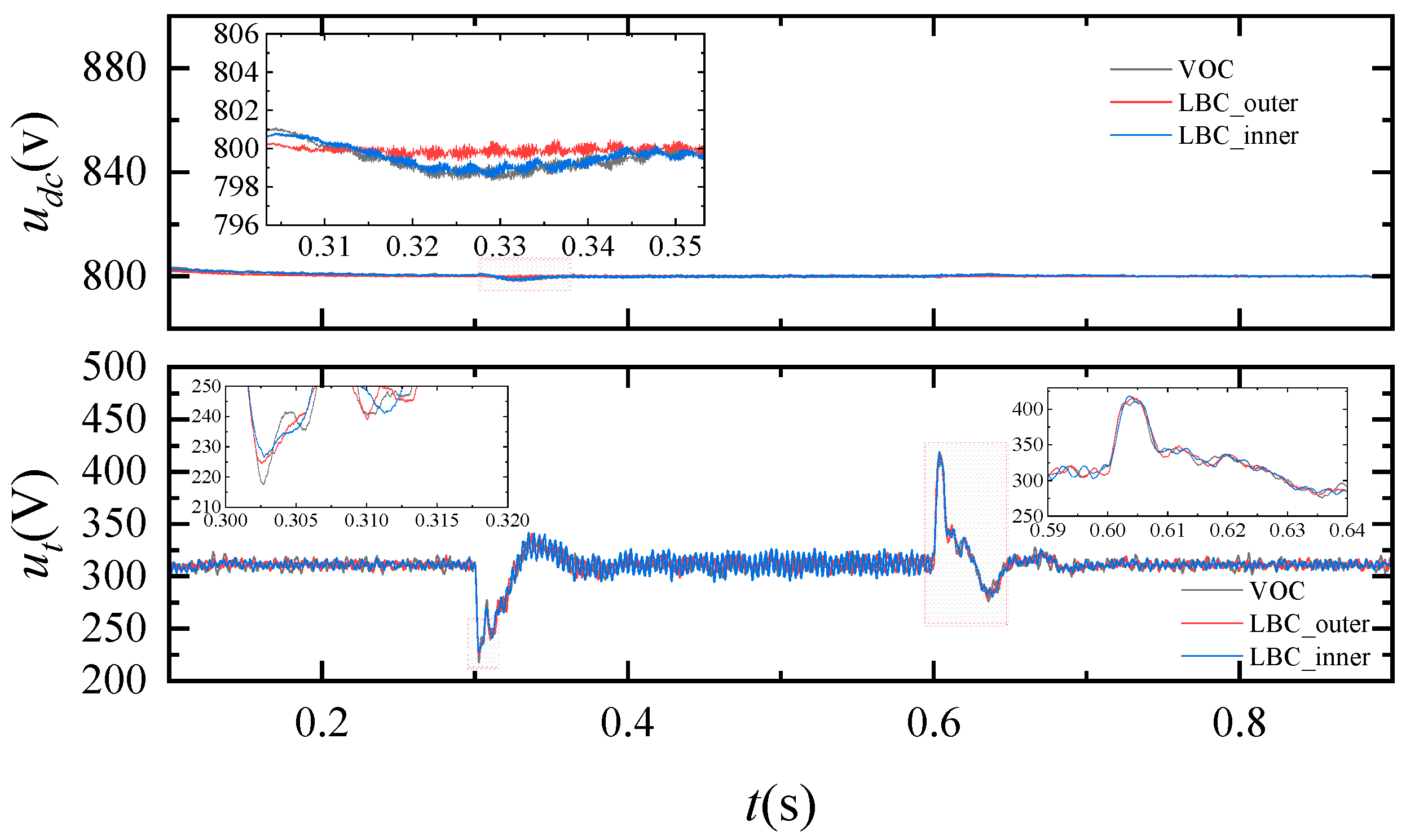
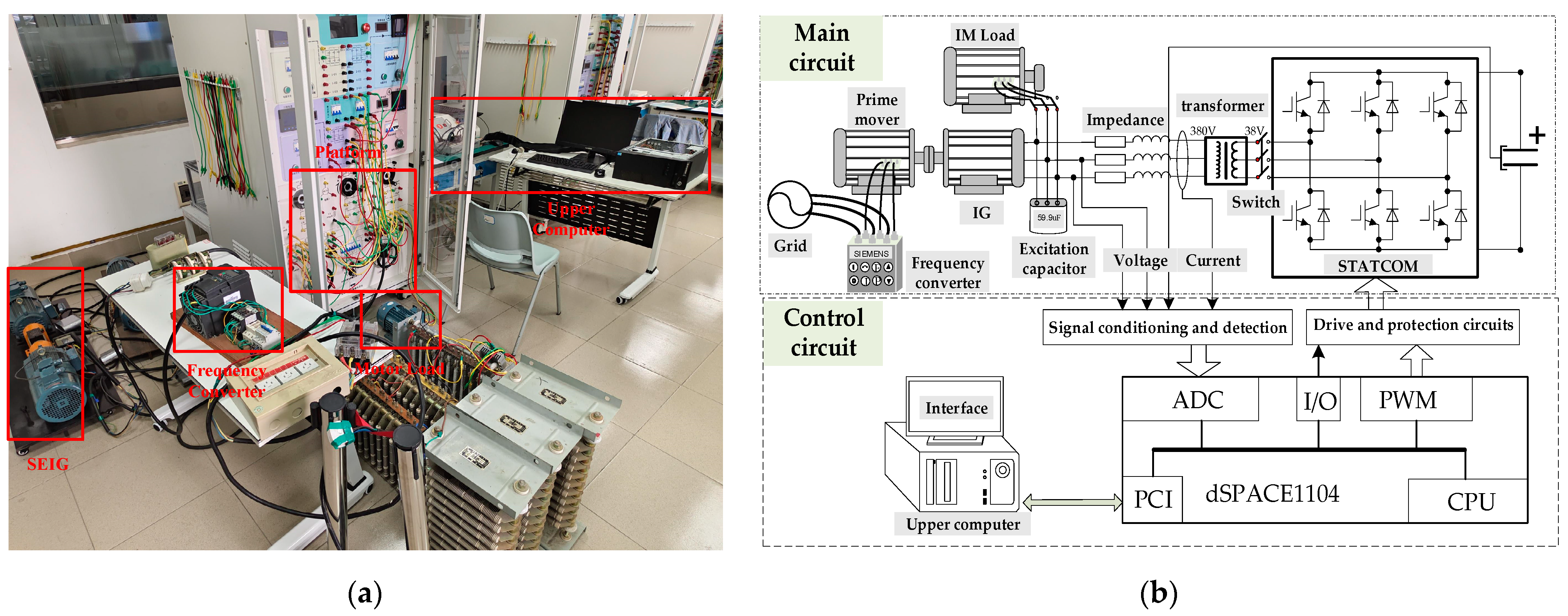
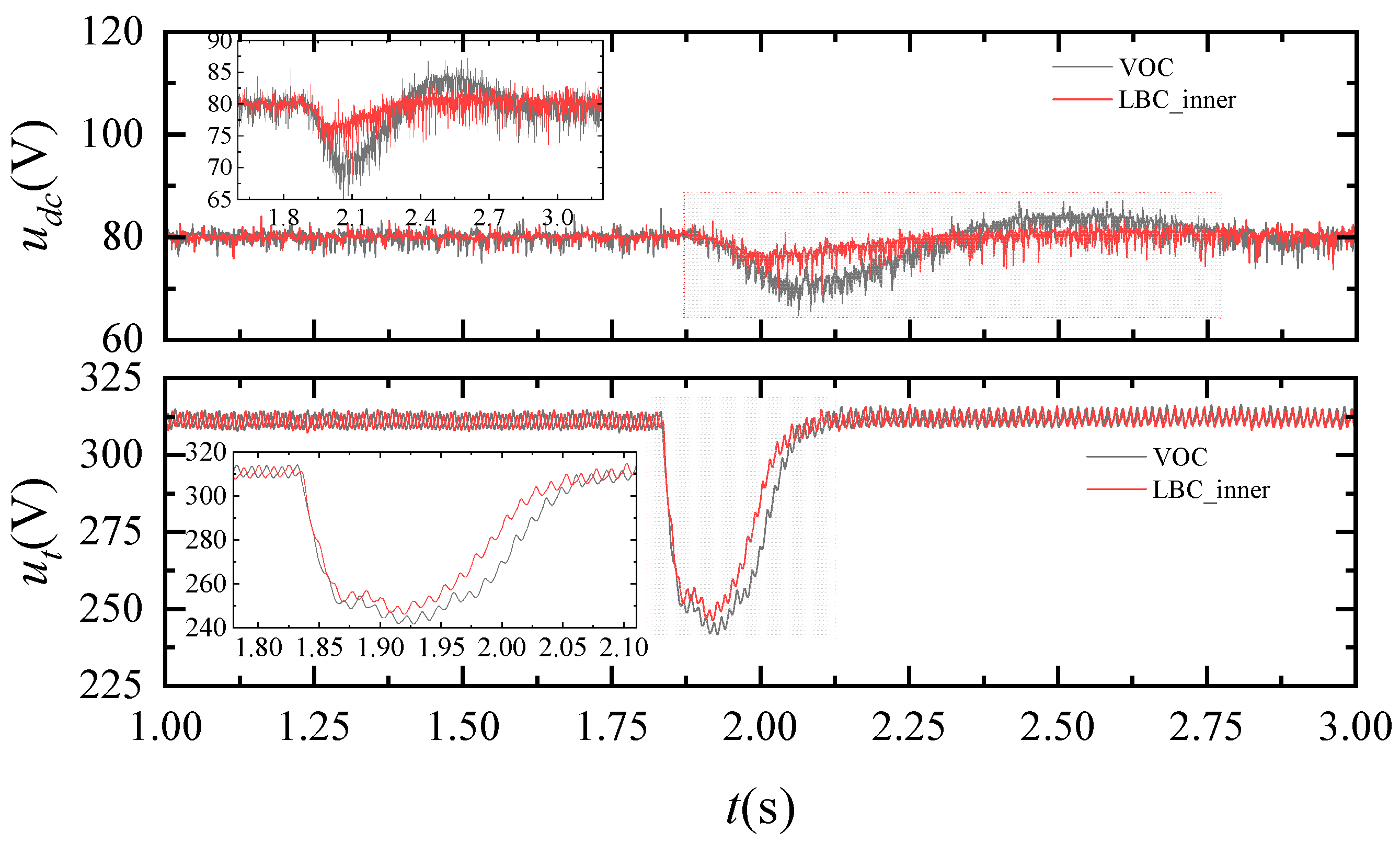
3.3. Experiment Results
4. Conclusions
- (1)
- The proposed LBC (outer loop on d-axis) achieves linearized voltage control with a quadratic outer loop structure; LBC (outer loop on q-axis) provides theoretical support for obtaining the q-axis reference current through proportional integration of the terminal voltage error.
- (2)
- A transfer function analysis was conducted on the inner loop of the proposed method, demonstrating its effectiveness in achieving decoupling and current tracking.
- (3)
- SEIG connected to STATCOM effectively improves voltage regulation capability and shortened the process of the transient by about 3.1 ms. Compared to traditional VOC, the outer loop LBC has an effect on shortening the transient processes of DC voltage by about 9.4 ms and the inner loop LBC has an effect on shortening the transient processes of both AC and DC voltages by about 2.6 ms and 8.7 ms, respectively. The simulation and experiment results show that the proposed LBC outperforms traditional methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Classification | Symbol | Quantity |
| Measured value | Rc | The actual line resistance of SEIG–STATCOM |
| Measured value | Lc | The actual line inductance of SEIG–STATCOM |
| Known value | Rcn | The nominal line resistance of SEIG–STATCOM |
| Known value | Lcn | The nominal line inductance of SEIG–STATCOM |
| Measured value | Cdc | The capacitance of DC side capacitor |
| Defined variable | Sd, Sq | The switching function on dq-axis |
| Known value | ω | The synchronously rotating angle speed |
| Measured value | udc | The voltage of DC side |
| Measured value | ut | The voltage amplitude of PCC |
| Measured value | usd, usq | The voltages of PCC on dq-axis |
| Known value | ucd, ucq | The output voltages of STATCOM on dq-axis |
| Measured value | icd, icq | The currents of STATCOM on dq-axis |
| Known value | (·)* | The reference value of a certain value |
| Measured value | uDC | uDC = (udc)2 |
| Defined variable | VDC | The Lyapunov function of the outer loop on d-axis |
| Defined variable | Vt | The Lyapunov function of the outer loop on q-axis |
| Defined variable | V | The Lyapunov function of the inner loop |
| Defined variable | edc | The error of DC voltage |
| Defined variable | eDC | The error of DC voltage’ square |
| Defined variable | et | The error of PCC voltage |
| Defined variable | e | The error of current |
| Measured value | Xc | The inductive reactance of SEIG–STATCOM |
| Measured value | U | The effective value of the line-to-line voltage |
| Measured value | P, Q | The active and reactive power consumed |
| Known value | τCD | The equivalent time constant of control loop |
| Control parameters | KvdP, KvqP | The voltage loop proportional gain on dq-axis |
| Control parameters | KvdI, KvqI | The voltage loop integral gain on dq-axis |
| Control parameters | KiP, KiI | The current loop proportional and integral gain |
| Control parameters | K1, K2 | The voltage loop virtual coefficient on d-axis |
| Control parameters | K3, K4 | The voltage loop virtual coefficient on q-axis |
| Control parameters | m1, m2 | The current loop virtual coefficient on dq-axis |
References
- Østergaard, P.A.; Duic, N.; Noorollahi, Y.; Kalogirou, S.A. Recent advances in renewable energy technology for the energy transition. Renew. Energy 2021, 179, 877–884. [Google Scholar] [CrossRef]
- Wei, Y.; Kang, L.; Huang, Z.; Li, Z. A magnetic energy recovery switch based terminal voltage regulator for the three-phase self-excited induction generators in renewable energy systems. J. Power Electron. 2015, 15, 1305–1317. [Google Scholar] [CrossRef][Green Version]
- Krishna, V.M.; Sandeep, V.; Murthy, S.; Yadlapati, K. Experimental investigation on performance comparison of self excited induction generator and permanent magnet synchronous generator for small scale renewable energy applications. Renew. Energy 2022, 195, 431–441. [Google Scholar] [CrossRef]
- Calgan, H.; Demirtas, M. A robust LQR-FOPIλDµ controller design for output voltage regulation of stand-alone self-excited induction generator. Electr. Power Syst. Res. 2021, 196, 107175. [Google Scholar] [CrossRef]
- Krishna, V.M.; Sandeep, V.; Narendra, B.; Prasad, K. Experimental study on self-excited induction generator for small-scale isolated rural electricity applications. Results Eng. 2023, 18, 101182. [Google Scholar] [CrossRef]
- Singh, B.; Murthy, S.S.; Chilipi, R.S.R. STATCOM-based controller for a three-phase SEIG feeding single-phase loads. IEEE Trans. Energy Convers. 2014, 29, 320–331. [Google Scholar]
- Wang, H.; Wu, X.; You, R.; Li, J. Modeling and analysis of SEIG-STATCOM systems based on the magnitude-phase dynamic method. J. Power Electron. 2018, 18, 944–953. [Google Scholar]
- Saidur, R. A review on electrical motors energy use and energy savings. Renew. Sustain. Energy Rev. 2010, 14, 877–898. [Google Scholar] [CrossRef]
- Prakash, S.B.; Sagar, M.P. Fuzzy Logic Controlled Based STATCOM to Compensate Loads for SEIG System. Int. J. Sci. Eng. Technol. Res. 2016, 5, 4048–4054. [Google Scholar]
- Xia, Y.; Peng, Y.; Yang, P.; Yu, M.; Wei, W. Distributed coordination control for multiple bidirectional power converters in a hybrid AC/DC microgrid. IEEE Trans. Power Electron. 2016, 32, 4949–4959. [Google Scholar] [CrossRef]
- Dyanamina, G.; Kakodia, S.K. SEIG voltage regulation with STATCOM Regulator using Fuzzy logic controller. In Proceedings of the 2021 International Conference on Sustainable Energy and Future Electric Transportation (SEFET), Hyderabad, India, 21–23 January 2021; pp. 1–6. [Google Scholar]
- Ansari, J.; Abbasi, A.R.; Heydari, M.H.; Avazzadeh, Z. Simultaneous design of fuzzy PSS and fuzzy STATCOM controllers for power system stability enhancement. Alex. Eng. J. 2022, 61, 2841–2850. [Google Scholar] [CrossRef]
- Das, M.; Giribabu, D. ANFIS controller based STATCOM regulator for self excited induction generator. In Proceedings of the 2016 IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar]
- Singh, P.D.; Gao, S. Clean and sustainable micro hydro power generation using parallel variable asynchronous generators controlled by AC-DC-AC converter and fuzzy PSO/PI D-STATCOM for remote areas. Sustain. Cities Soc. 2022, 77, 103527. [Google Scholar] [CrossRef]
- Mokhtari, M.; Zouggar, S.; M’sirdi, N.K.; Elhafyani, M. Sliding Mode & Single Input Fuzzy Logic Controllers for Voltage Regulation Of an Asynchronous Wind Turbine Using STATCOM. IFAC-PapersOnLine 2020, 53, 12803–12808. [Google Scholar]
- Oliveira, T.R.; Hsu, L.; Nunes, E.V.L. Smooth sliding control to overcome chattering arising in classical SMC and super-twisting algorithm in the presence of unmodeled dynamics. J. Frankl. Inst. 2022, 359, 1235–1256. [Google Scholar] [CrossRef]
- Furat, M. Chattering attenuation analysis in variable structure control for automatic voltage regulator with input constraints. Eng. Sci. Technol. Int. J. 2023, 45, 101499. [Google Scholar] [CrossRef]
- Ullah, M.F.; Hanif, A. Power quality improvement in distribution system using distribution static compensator with super twisting sliding mode control. Int. Trans. Electr. Energy Syst. 2021, 31, e12997. [Google Scholar] [CrossRef]
- Sefa, I.; Ozdemir, S.; Komurcugil, H.; Altin, N. An enhanced Lyapunov-function based control scheme for three-phase grid-tied VSI with LCL filter. IEEE Trans. Sustain. Energy 2018, 10, 504–513. [Google Scholar] [CrossRef]
- Rahmani, S.; Hamadi, A.; Al-Haddad, K. A Lyapunov-function-based control for a three-phase shunt hybrid active filter. IEEE Trans. Ind. Electron. 2011, 59, 1418–1429. [Google Scholar] [CrossRef]
- Dasgupta, S.; Mohan, S.N.; Sahoo, S.K.; Panda, S.K. Lyapunov function-based current controller to control active and reactive power flow from a renewable energy source to a generalized three-phase microgrid system. IEEE Trans. Ind. Electron. 2012, 60, 799–813. [Google Scholar] [CrossRef]
- Bayhan, S.; Seyedalipour, S.S.; Komurcugil, H.; Abu-Rub, H. Lyapunov energy function based control method for three-phase UPS inverters with output voltage feedback loops. IEEE Access 2019, 7, 113699–113711. [Google Scholar] [CrossRef]
- Beheshti, N.; Rezanejad, M.; Mehrasa, M. Linearized control technique with Lyapunov function-based compensators for MMC-based HVDC system under load variation and fault condition. Int. J. Electr. Power Energy Syst. 2021, 124, 106333. [Google Scholar] [CrossRef]
- He, J.; Zhang, X.; Ma, H.; Cai, C. Lyapunov-based large-signal control of three-phase stand-alone inverters with inherent dual control loops and load disturbance adaptivity. IEEE Trans. Ind. Electron. 2020, 68, 8391–8401. [Google Scholar] [CrossRef]
- Blasko, V.; Kaura, V. A new mathematical model and control of a three-phase AC-DC voltage source converter. IEEE Trans. Power Electron. 1997, 12, 116–123. [Google Scholar] [CrossRef]
- Harnefors, L.; Wang, X.; Chou, S.-F.; Bongiorno, M.; Hinkkanen, M.; Routimo, M. Asymmetric complex-vector models with application to VSC–grid interaction. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1911–1921. [Google Scholar] [CrossRef]
- Wu, L.; Li, J.; Lu, Y.; Yang, K.; He, K.; Chen, H.; Chen, Z. Design of complex vector controller for high-power induction machine drive. IEEE Trans. Transp. Electrif. 2023, 10, 1816–1826. [Google Scholar] [CrossRef]
- Xiao, Q.; Tang, F.; Xin, Z.; Zhou, J.; Chen, P.; Loh, P.C. Large time-delay decoupling and correction in synchronous complex-vector frame. IET Power Electron. 2019, 12, 254–266. [Google Scholar] [CrossRef]
- Moskvicheva, P.O.; Semenova, I.N. The Lyapunov stability of the Cauchy-Dirichlet problem for the generalized Hoff equation. Весmнuк Южнo-Уpaльcкoгo Гocyдapcmвeннoгo Унuвepcumema. Cepuя Mameмamuчecкoe Moдeлupoвaнue И Пpoгpaммupoвaнue 2014, 7, 126–131. [Google Scholar] [CrossRef]
- Varshney, L.; Vardhan, A.S.S.; Vardhan, A.S.S.; Kumar, S.; Saket, R.; Sanjeevikumar, P. Performance characteristics and reliability assessment of self-excited induction generator for wind power generation. IET Renew. Power Gener. 2021, 15, 1927–1942. [Google Scholar] [CrossRef]
- Xu, Y.; Li, F. Adaptive PI control of STATCOM for voltage regulation. IEEE Trans. Power Deliv. 2014, 29, 1002–1011. [Google Scholar] [CrossRef]
| SEIG Parameters | Value |
|---|---|
| Pole pairs | 2 |
| Excitation capacitor C/μF | 47 |
| Stator resistance Rs/Ω | 3.383 |
| Stator inductance Ls/mH | 8.479 |
| Rotor resistance Rr/Ω | 2.973 |
| Rotor inductance Lr/mH | 8.479 |
| Rated speed ω/ | 1430 |
| AC induction motor load parameters | |
| Rated capacity P/kW | 1.1 |
| Rated speed ω/ | 1425 |
| STATCOM parameters | |
| DC capacitor Cdc/mF | 5 |
| line inductance Lc/mH | 5 |
| line resistance Rc/Ω | 0.5 |
| DC voltage reference udc*/V | 800 |
| AC voltage reference ut*/V | 311 |
| Controller parameters | |
| d-axis voltage loop proportional gain KvdP | 0.2 |
| q-axis voltage loop proportional gain KvqP | 0.002 |
| d-axis voltage loop integral gain KvdI | 8 |
| q-axis voltage loop integral gain KvqI | 15 |
| Current loop proportional gain KiP | 65.8 |
| Current loop integral gain KiI | 6580 |
| d-axis voltage virtual coefficient K1, K2 | 200, 4000 |
| q-axis voltage virtual coefficient K3, K4 | 0.012, 28,260 |
| Current loop virtual coefficient m1, m2 | 40,000 |
| Sampling frequency fsa | 10 kHz |
| Switching frequency fsw | 10 kHz |
| STATCOM Parameters | |
|---|---|
| DC capacitor Cdc/mF | 5 |
| Line inductance Lc/mH | 5 |
| Line resistance Rc/Ω | 0.01 |
| DC voltage reference udc*/V | 80 |
| AC voltage reference ut*/V | 311 |
| Controller parameters | |
| d-axis voltage loop proportional gain KvdP | 0.2 |
| q-axis voltage loop proportional gain KvqP | 0.2 |
| d-axis voltage loop integral gain KvdI | 5 |
| q-axis voltage loop integral gain KvqI | 8 |
| Current loop proportional gain KiP | 30 |
| Current loop integral gain KiI | 60 |
| d-axis voltage virtual coefficient K1, K2 | 100, 2000 |
| q-axis voltage virtual coefficient K3, K4 | 1.2, 15,000 |
| Current loop virtual coefficient m1, m2 | 4000 |
| Controller | Voltage Dip (V) | Transient Time (ms) | ||
|---|---|---|---|---|
| DC Side | AC Side | DC Side | AC Side | |
| Without STATCOM | 73.78 | 32.0 | ||
| VOC | 11.17 | 69.24 | 44.7 | 28.9 |
| LB (Inner controller) | 5.79 | 64.65 | 36.0 | 26.5 |
| LB (Outer controller) | 5.28 | 73.69 | 35.3 | 28.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Gong, P.; Lu, Z. A Lyapunov Theory-Based SEIG–STATCOM Voltage Regulation Control Strategy. Energies 2024, 17, 4992. https://doi.org/10.3390/en17194992
Zhang Z, Gong P, Lu Z. A Lyapunov Theory-Based SEIG–STATCOM Voltage Regulation Control Strategy. Energies. 2024; 17(19):4992. https://doi.org/10.3390/en17194992
Chicago/Turabian StyleZhang, Zeyu, Pingping Gong, and Ziguang Lu. 2024. "A Lyapunov Theory-Based SEIG–STATCOM Voltage Regulation Control Strategy" Energies 17, no. 19: 4992. https://doi.org/10.3390/en17194992
APA StyleZhang, Z., Gong, P., & Lu, Z. (2024). A Lyapunov Theory-Based SEIG–STATCOM Voltage Regulation Control Strategy. Energies, 17(19), 4992. https://doi.org/10.3390/en17194992






