1. Introduction
The water consumption rate of power generation is the ratio of a hydropower station’s quotative flow Q to its output P in m3/(s · kW), or the ratio of hydropower station’s quotative water W to its power generation E in m3/(kWh), which is an important index of a hydropower station’s economic operation and is the key concern of a hydropower station’s water conservation and efficiency work. The study of the water consumption rate of power generation has important theoretical significance and practical application value for improving the operating efficiency of units, guiding the economic operation of hydropower stations and improving the utilization rate of hydropower resources in basins. Currently, there have been some studies on the definition and influencing factors of the water consumption rate of hydropower stations, and many scholars use this index to optimize the operation of hydropower stations.
The goal of a hydropower station is to produce more output with the same amount of water, that is, the minimum water consumption rate. However, the calculation methods of the water consumption rate are not unified. Different scholars have given specific calculation methods under different conditions. Bakke et al. [
1] improved a conceptual framework of water consumption in order to calculate the water footprint from hydropower projects. Tu et al. [
2] introduced the standard water consumption rate and proposed a method for calculating and assessing the long-term average water consumption rate of the cascade hydropower station in a study on improving the assessment method of the water consumption rate in hydropower stations. Wu [
3] proposed to use the relative water consumption rate for power generation, i.e., the ratio of the actual water consumption rate during the assessment period to the assessment-calculated water consumption rate for power generation as the assessment index of the daily regulation of hydropower plants. However, the above studies give the calculation method of the water consumption rate based on the actual operating conditions and operating data. These studies can measure the operating efficiency in a certain period, but they did not find the rules of water the consumption rate under different conditions and cannot be used to guide the operation of hydropower stations.
In addition, the influencing factors of the water consumption rate are also the focus of research. For example, Sun et al. [
4], Yu et al. [
5], Hou [
6], and Zhou et al. [
7] all carried out some research and analyses on the influencing factors of the water consumption rate. Based on the actual operation data and actual operation conditions of hydropower stations, they summarized some influencing factors of the water consumption rate, but did not deeply explore how the water consumption rate changes with the changes in these influencing factors, that is, they did not systematically summarize the change law of the water consumption rate. And since some of the factors they summarize, such as upstream maintenance work, are based on specific hydropower stations and are under certain limitations, it is difficult to extend to other hydropower stations.
Based on the definition and influencing factors of the water consumption rate, the water consumption rate is used as an indicator of economic operation to solve the optimization problem. Zhao [
8] established a dynamic planning model based on the rate of water consumption to carry out a study on the optimal scheduling of reservoirs of the Liangjiang hydropower station. Bu [
9] studied the joint application of the water consumption rate curve and the water balance equation in the power generation plan of the Taoyuan hydropower station, and proposed measures to improve the water consumption rate. However, this paper uses the correlation between the water consumption rate and gross head to calculate the water consumption rate, and the calculation result is not rigorous enough. Shi [
10], in the study of reservoir optimal dispatching based on the dynamic analysis of the water consumption rate in the dry period of the Ludila hydropower station, comprehensively analyzed the relationship between the water consumption rate and various variables, and transformed the problem of the optimal dispatching of reservoirs into a problem dealing with the correlation between power generation plans and the water consumption rate. Lei et al. [
11] established the mathematical model of the water consumption rate of Longtan hydropower station to achieve the aim of energy saving and consumption reduction. Wu, Y. et al. [
12] developed a short-term load distribution (SLD) model considering complicated hydraulic and electricity constraints. The results show that the developed model reduces water consumption by 4.02, 4.70, 5.79, and 5.28% compared to the constant proportional distribution model and the real operation. In the above studies, the water consumption rate is often used as an indicator; however, due to the complexity of the calculation process of the water consumption rate, it is often estimated, resulting in a lack of rigor.
The study of the water consumption rate is a vital work of hydropower stations but the water consumption rate calculated on the basis of actual operation data is difficult in systematically reflecting the change law of the water consumption rate, and it cannot be used to guide the real-time operation decisions of hydropower stations. In this paper, based on the unit flow characteristic curve, the flow–head loss curve of the unit, and the relationship curve of the hydropower station’s flow–tail water level are used to deduce the water consumption change curve of the cascade hydropower station with the hydropower station’s water level as the reference. The water consumption change law of the single unit, the multi-unit, the hydropower station, and the cascade hydropower station are found. These laws can be used to guide the economic operation of hydropower stations and improve the utilization rate of hydropower resources in basins.
2. Research Objects
Located in the lower reaches of the Jinsha River on the border between Yunnan and Sichuan Provinces in China, hydropower station A is a giant hydropower station that mainly generates electricity and also has the comprehensive benefits of sand blocking, flood control, and the improvement of downstream navigation, and it is the upstream hydropower station in the cascade hydropower stations of this study. With a normal water level of 600 m, the reservoir has a total capacity of 12.67 billion cubic meters, a regulated storage capacity of 6.46 billion cubic meters, and a flood control capacity of 4.65 billion cubic meters. The hub project consists of a barrage dam, a diversion power generation building, flood discharge, and an energy dissipation building. The barrage dam adopts a concrete double-curved arch dam with a crest elevation of 610 m, a crest length of 700 m, and a maximum dam height of 278 m. The left and right banks are arranged with underground plants, each installed with nine sets of hydroelectric generating units with a capacity of 700,000 kW, with a total installed capacity of 12.6 million kW and a multi-year average generating capacity of 57.12 billion kWh.
Hydropower station B is located about 196 km downstream of hydropower station A; it is a giant hydropower station that mainly generates electricity and takes flood control, sand retaining, irrigation, navigation, and other comprehensive benefits into consideration. The normal water level is 380 m, the total reservoir capacity is 5.185 billion cubic meters, and the regulated storage capacity is 905 million cubic meters; the hydropower station is installed with eight sets of hydroelectric turbine generators of 750,000 kW capacity. The total installed capacity is 6 million kW and the average power generation for many years is 30.13 billion kW per hour. The relative position map of the research hydropower stations A and B is shown in
Figure 1.
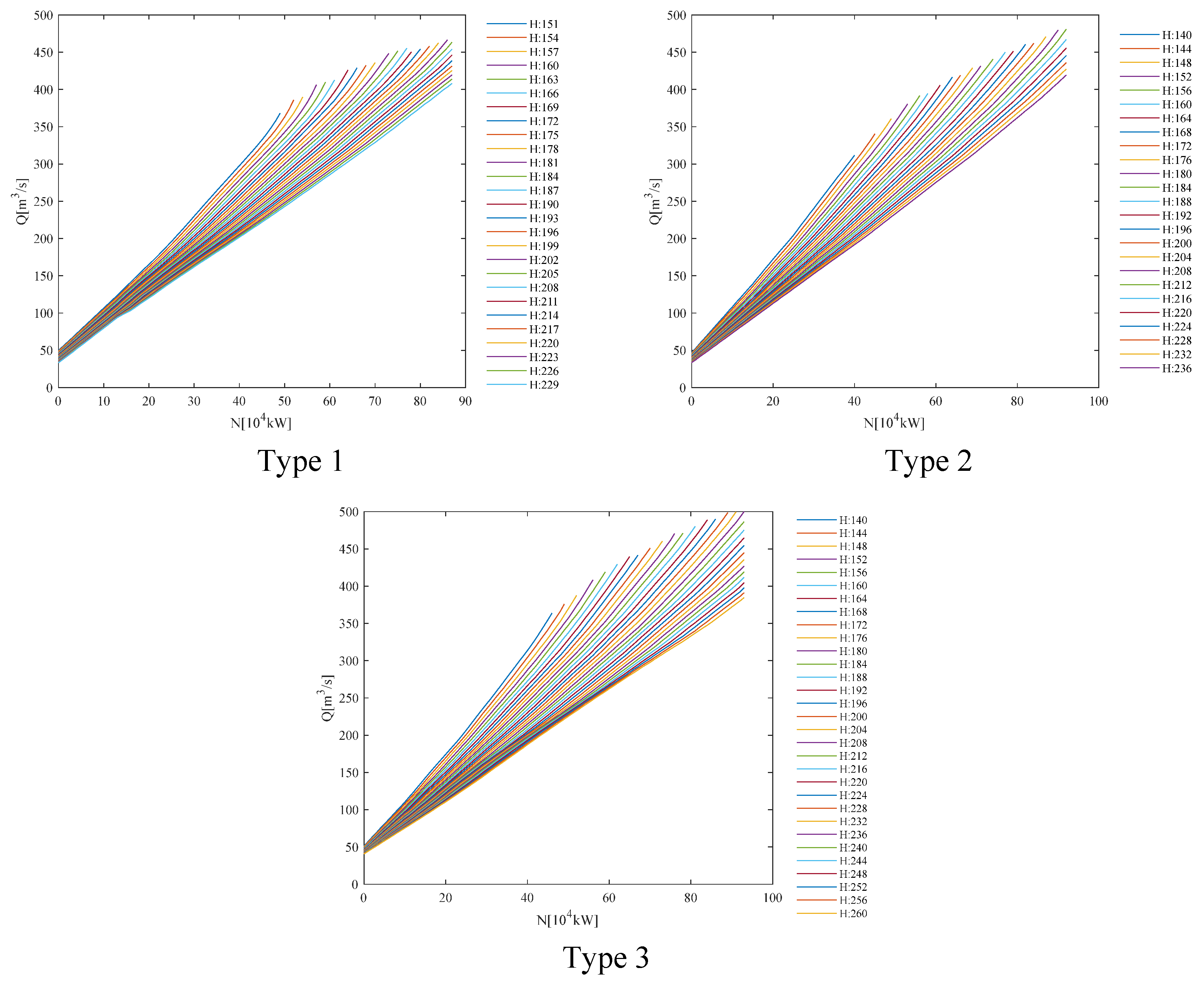
Each unit of a hydropower station has a unit flow characteristic curve given by the manufacturer, which characterizes the relationship between the unit flow and output at each net head, also known as the NHQ relationship curve.
There are 18 hydro generator units installed in hydropower station A, with three types. Units no. 1–6 are of the same type, units no. 7–9 are of the same type, and units no. 10–18 are of the same type, and the flow characteristic curves of the three types of units are shown in
Figure 2. The meaning of H in the figure is the net head.
Hydropower station B has eight units, of which units no. 1–4 are of the same type and units no. 5–8 are of the same type, and their flow characteristic curves are shown in
Figure 3.
3. Calculation of the Characteristic Curve of Water Consumption Rate for a Hydropower Station with Water Level as a Parameter
3.1. Calculation of the Characteristic Curve of Water Consumption Rate for a Single Unit
3.1.1. Plotting Relationship Curves of Flow–Gross Head–Output
Since the units of A and B hydropower stations are distributed side by side, in the process of power generation, the power generation flow of each unit of the same station may be different, i.e., the net head is different. While the gross head is the difference between the upstream water level and the downstream water level, which is the same, to better solve the output characteristics in the case of multi-unit stations, the net head of the unit characteristic curve is converted into the gross head to be calculated, in which the relationship between the unit’s net head and the gross head is as follows:
where H
gross is the hydropower station’s gross head; H is the net head; and ΔH is the head loss in the diversion system.
Therefore, the net head of the unit is added to the head loss at the corresponding flow in the relationship curve output–net head–flow (NHQ) for a unit to obtain the relationship curve output–gross head–flow (NHgrossQ) for a unit.
3.1.2. Calculation of Characteristic Curve of Water Consumption Rate with the Gross Head as a Parameter
The water consumption rate is the amount of water consumed by a hydropower station for each unit of electricity generated, which is calculated as follows:
where μ is the integrated water consumption rate, m
3/(kWh); E is the total amount of power generation, kWh; W is the total amount of water generated, m
3; N is the power station output, kW; Q is the power generation flow, m
3/s; and C is the unit conversion factor.
From Equation (2), it can be seen that a set of determined flow and output data can determine a value of the water consumption rate, and for a single type of unit, the characteristic curve or characteristic curve can be derived from the unit’s NHgrossQ characteristic curve data, i.e., the flow–gross head–water consumption rate characteristic curve or the output–gross head–water consumption rate characteristic curve.
3.2. Plotting Characteristic Curve of Flow–Gross Head–Optimal Output for Multi-Unit Stations
3.2.1. Curve Plotting Method—The Mirror Vertical Shift Method
When two units are combined at a given gross head, a given generation flow is distributed among the two units to find the flow distribution scheme that maximizes the total generation output of the two units, i.e., the flow distribution scheme of the units at the optimal output. This process can be deduced by the mirror vertical shift method with the following steps:
Firstly, the relationship curves of output–gross head–flow (NHgrossQ) of the two units are organized into graphs whose horizontal coordinate is the value of output force, the vertical coordinate is the value of flow, and the scales of horizontal and vertical coordinate axes are the same.
Extract the graphs of the flow–output relationship between the two units at the same gross head separately and invert the graph of the second unit on the graph of the first unit.
Vertically move the power characteristic curve of the second unit, so that the longitudinal coordinates of the flow data are partially overlapped; it can be found that the sum of the flow values at each point is the same in the overlapped part. Plot several horizontal lines in the range of the overlapped part so that they intersect two curves, respectively. The sum of the coordinate values N
1 and N
2 corresponding to the intersections is the value of the total output of two units. As shown in
Figure 4, the curve of the change in the total output can be plotted in the range of the overlap. The maximum output value on the curve is the optimal output N
i,max that can be issued by the two units when the flow sum is Q. Record the flow and output value of each unit at the maximum output.
- 4.
Move the graph of the second unit up and down to obtain the optimal output N1,max, N2,max…Nn,max corresponding to different flow sums Q1, Q2, Q3,…Qn of the two units, and then obtain the combination of the two units under the gross head. Then, obtain the optimal output–gross head–flow relationship curve for the combination of two units under this gross head.
- 5.
Perform the same calculation for each gross head Hgross,1, Hgross,2…Hgross,n to obtain the optimal output–gross head–flow relationship curve cluster in the case of the combination of two units.
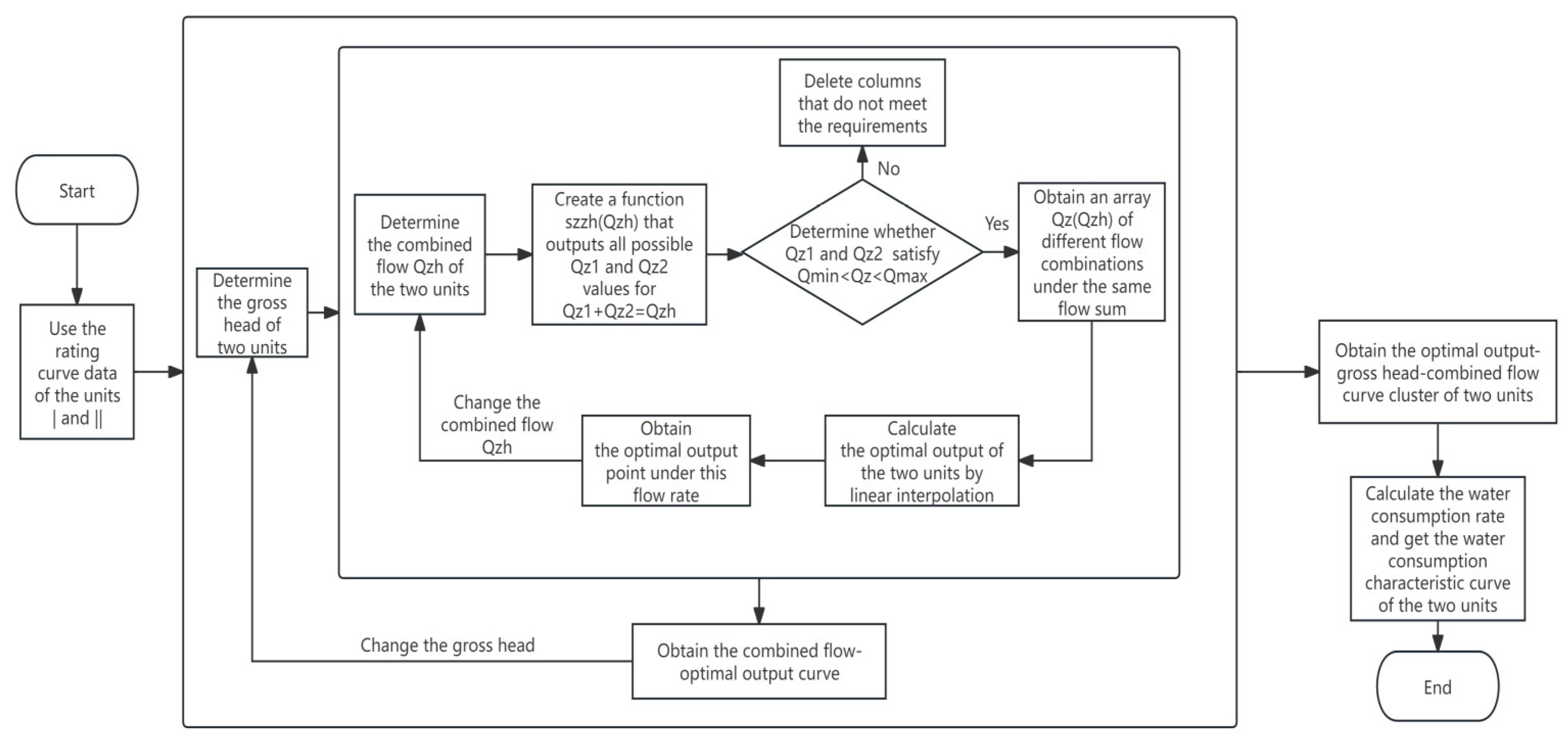
3.2.2. Determination of Joint Operation Curve of Two Units Based on the Mirror Vertical Shift Method
The specific implementation idea of the multi-unit joint operation algorithm based on the mirror vertical shift method is as follows:
Based on the relationship curve of flow–net head–output for the unit and the relationship curve of flow–head loss for the unit, the head loss is calculated by interpolation. Then, add it to the net head to obtain the flow–gross head–output relationship data.
Fit the relationship curves of flow–output under an equal gross head Hm to obtain the flow–gross head–output relationship data for the two units.
Obtain the relationship curve of flow–gross-head–output when two units are combined. Firstly, determine the gross head Hgross and the combined flow Qzh of the two units, then interpolate the total output N12 corresponding to different flow combinations to find the optimal output N12,max. Secondly, change the combined flow Qzh to obtain the corresponding optimal output. Thirdly, plot the data above into a curve. Finally, change the gross head Hgross and obtain the combined flow–optimal output curve under different gross head conditions, and then obtain the combination of optimal combined flow–gross head–output curve clusters.
Since the water consumption rate is uniquely determined by the flow and output, the relationship curve cluster of flow–gross head–optimal output for two units is converted into the relationship curve cluster of water consumption rate–gross head–combined flow for two units, i.e., the characteristic curve of the water consumption rate for the hydropower station.
The workflow of the two units’ combined work operation model based on the mirror vertical shift method is shown in
Figure 5.
3.2.3. Determination of Joint Operation Curve of Multi-Unit Stations Based on the Mirror Vertical Shift Method
First of all, merge the curve cluster of optimal output–gross head–flow for the combination of two units into one virtual unit’s curve. Then, apply the mirror vertical shift method to calculate the curve cluster of flow–gross head–optimal output after adding one unit. After that, merge the curve cluster of flow–gross head–optimal output for the combination of three units into one virtual unit’s curve, and apply the mirror vertical shift method to calculate the curve cluster of flow–gross head–optimal output after adding one unit, and so on until all available unit combinations of the hydropower station are obtained.
The units added to the calculation are all available units of the hydropower station. The use of this calculation method will not be affected when some units are repaired or broken down.
3.3. Calculation of Water Consumption Rate Characteristics of Hydropower Station Based on Station Water Level
3.3.1. Relationship between Gross Head and Water Level of Hydropower Station
The formula for calculating the gross head of a hydropower station is
where H
gross is the gross head of the hydropower station, Z
up is the upstream water level of the reservoir, and Z
down is the tail water level of the reservoir. The tail water level of the reservoir can be obtained from the outflow Q
out by checking the relationship curve of reservoir outflow–tail water level. Therefore, when the outflow and the gross head of the reservoir are known, the upstream water level of the hydropower station can be determined.
3.3.2. Calculation of the Curve of Water Consumption Rate Characteristic for Hydropower Station
Applying the obtained curve cluster of outflow–gross head–optimal output relationship curves for hydropower stations, the curve cluster of outflow–water level–optimal output relationship curves for hydropower stations are obtained based on the property that the gross head is uniquely determined by the water level and the outflow of the hydropower station; then, as the water consumption rate is uniquely determined by the outflow and output, calculate the relationship curve cluster of outflow–water level–water consumption rate and the relationship curve cluster of output–station water level–water consumption rate.
4. Results of the Characteristic Curve of Water Consumption Rate of Hydropower Station with Water Level as a Covariant Variable
4.1. Hydropower Station A
The water consumption rate characteristic of hydropower station A was calculated by applying the previous calculation method.
Figure 6 and
Figure 7 show the results of the characteristic curve of the water consumption rate for unit 1 and twin units 1 and 2 of hydropower station A, respectively. The legends in
Figure 6 and
Figure 7 indicate the gross head in meters (note that the Hg in all the figures below represents the meaning of H
gross in this article—gross head).
The changing pattern of the water consumption rate of each unit of hydropower station A is similar to that of
Figure 6. The changing trend in the water consumption rate under each gross head is basically the same, decreasing with the increase in flow and decreasing with the increase in the gross head. When the flow is small, the water consumption rate decreases faster. With the increase in flow, the water consumption rate decreases slower. When the flow increases to a certain value and the gross head is small, the water consumption rate starts to increase slowly again.
As can be seen in
Figure 7, the characteristic curve of the water consumption rate for the combination of two units shows a slow and smooth decreasing trend. When the gross head is certain, the water consumption rate firstly decreases with the increase in flow; when the flow is small, the water consumption rate decreases faster, and then the water consumption rate decreases slower. When the flow is certain, the water consumption rate decreases with the increase in the gross head. When the flow is around 350 m
3/s, there is a small fluctuation in the bottom curve, which is the result when converting from one unit of work to two units of work.
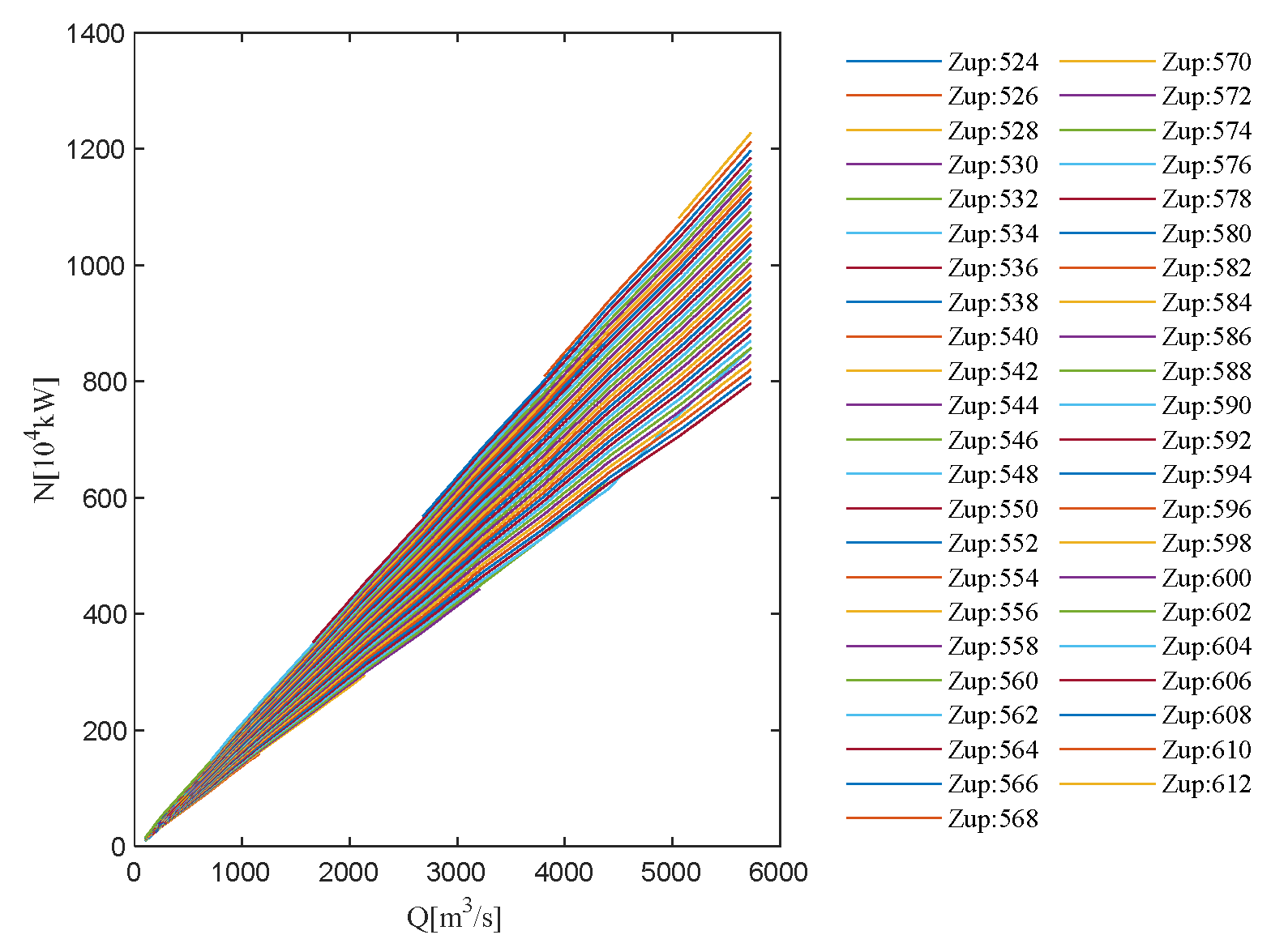
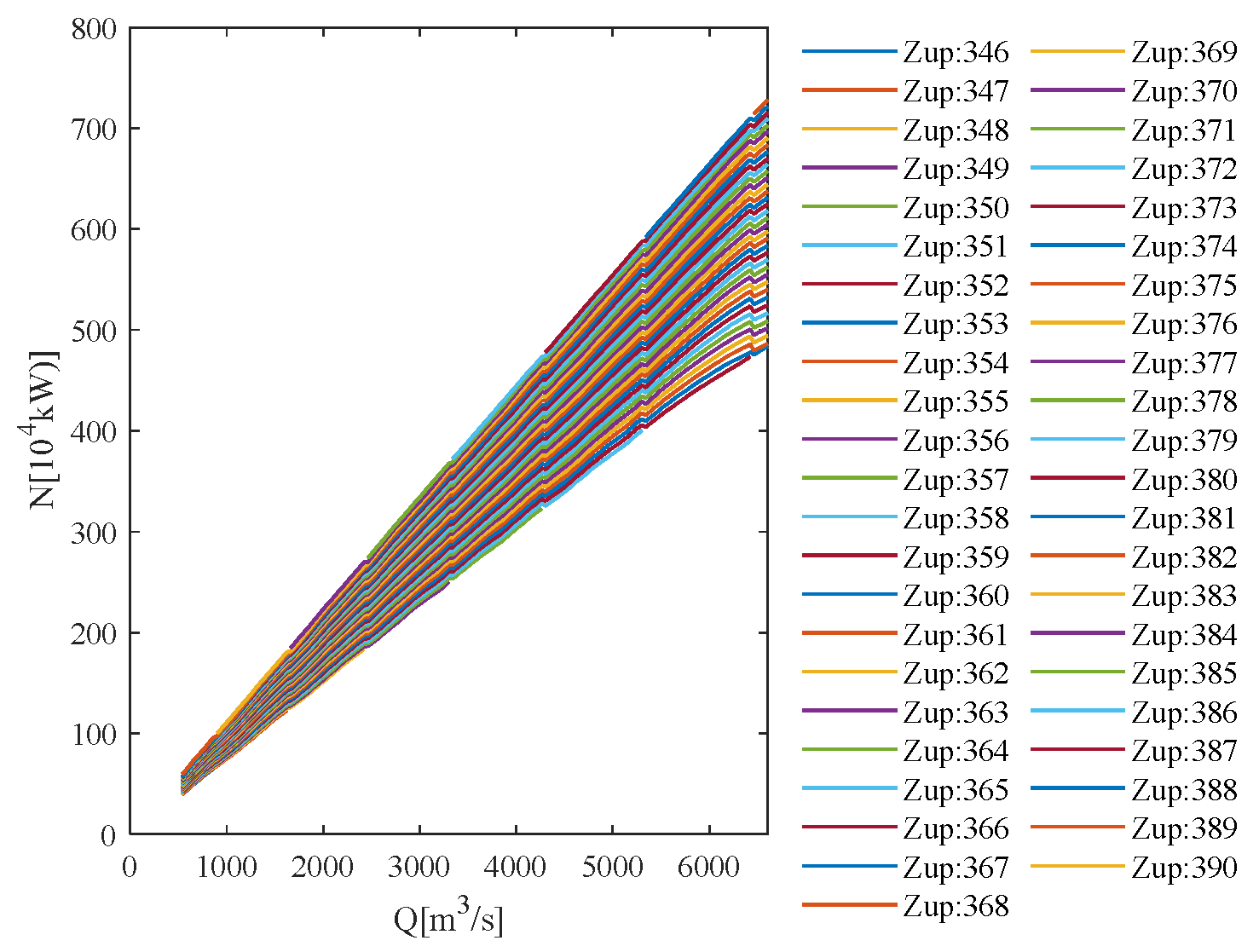
The characteristic curve and water consumption rate characteristic curve of hydropower station A are shown in
Figure 8 and
Figure 9. Since the return water from reservoir B downstream of reservoir A may have a top-supporting effect on the tailwater level of reservoir A, the relationship curve of outflow–water level–optimal output and the relationship curve of outflow–water level–water consumption rate for hydropower station A when the water level of for hydropower station B is 370 m are shown in the figures. The legends in
Figure 8 and
Figure 9 indicate the water level in meters.
As can be seen in
Figure 8, the flow characteristic curve basically presents a linear upward trend. It can be seen from
Figure 9 that the water consumption rate characteristic curve decreases rapidly when the flow is small and tends to be gentle when the flow is large, showing a stepwise upward trend.
4.2. Hydropower Station B
Figure 10 and
Figure 11 show the results of the characteristic curve of the water consumption rate characteristic curves for unit 1 and twin units 1 and 2 of hydropower station B, respectively. The legends in
Figure 10 and
Figure 11 indicate the gross head in meters.
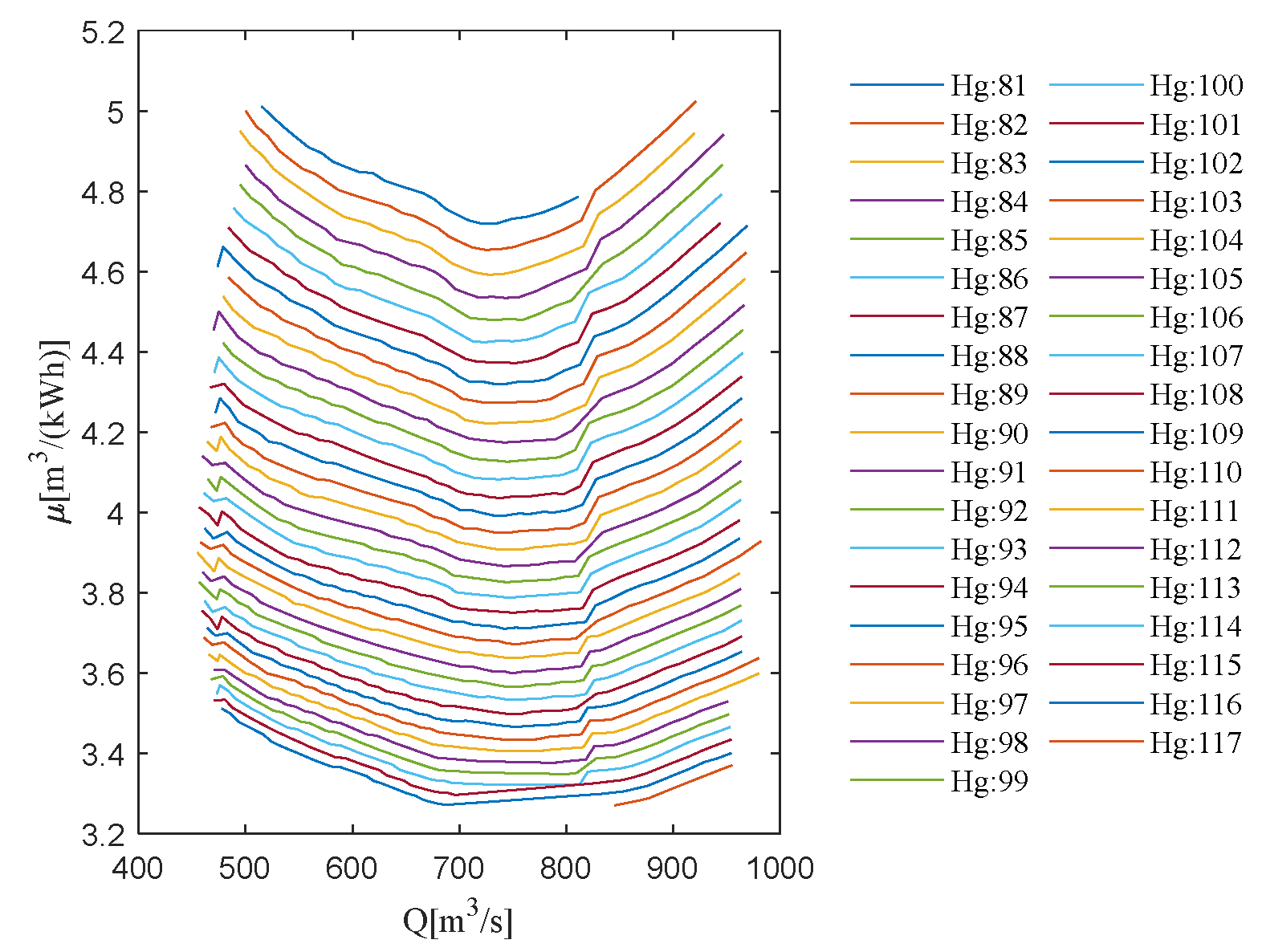
As can be seen in
Figure 10, the characteristic curve of the water consumption rate for a single unit of hydropower station B presents V-shaped change characteristics. When the gross head is certain, the water consumption rate of a single unit first decreases with the increase in flow. When the flow increases to a certain value, the water consumption rate starts to increase again, and the increase trend is more obvious. From
Figure 11, the characteristic curve of the water consumption rate for the combination of two units has an overall W-shaped trend, i.e., when the gross head is certain, the water consumption rate shows a decreasing–increasing–decreasing–increasing process with the increase in flow. When the flow is certain, the water consumption rate decreases with the increase in the gross head.
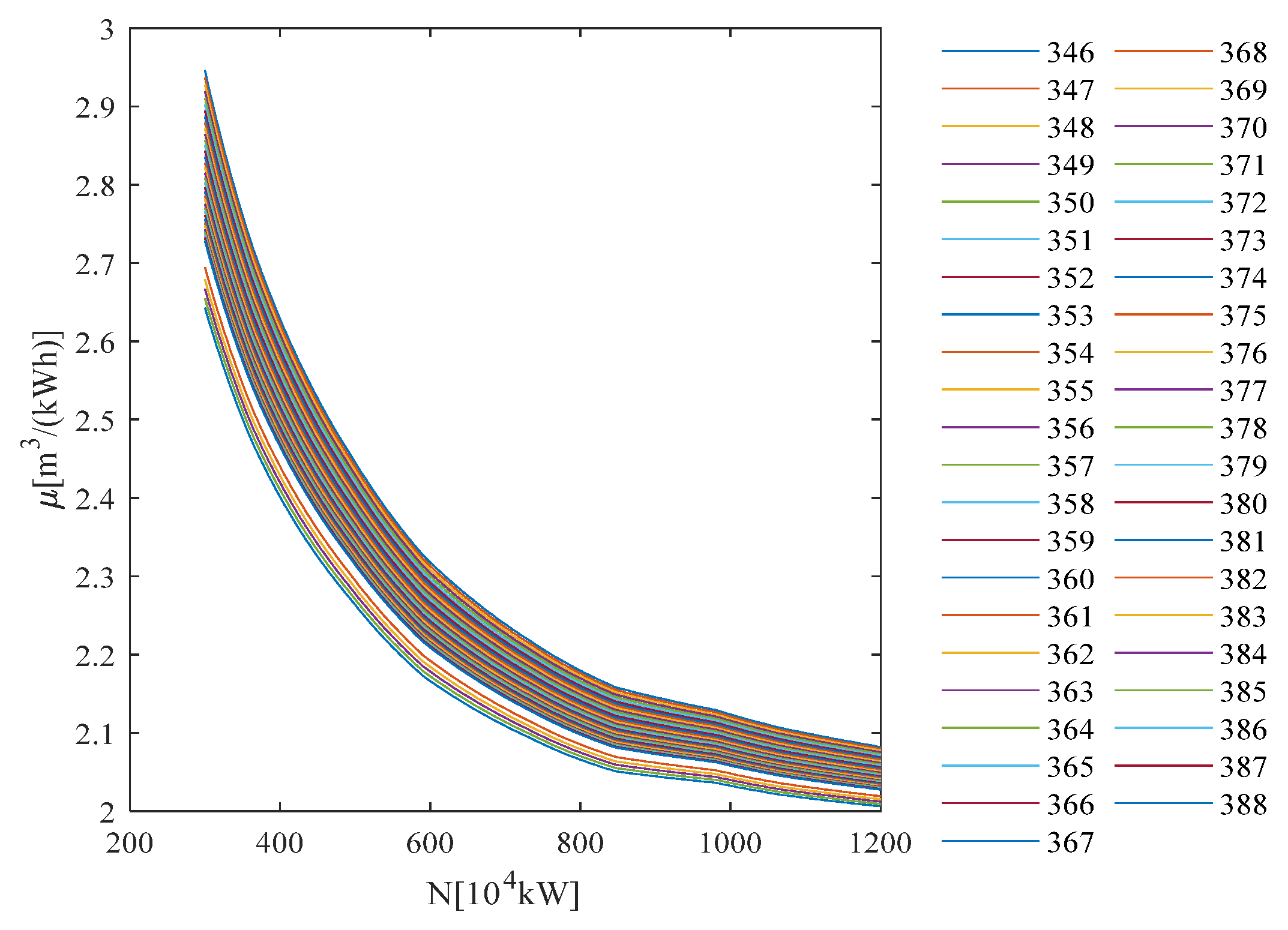
The characteristic curve and water consumption rate characteristic curve of hydropower station B are shown in
Figure 12 and
Figure 13. The legends in
Figure 12 and
Figure 13 indicate the water level in meters.
As can be seen in
Figure 12, at a certain water level, the optimal output of the hydropower station has a linear growth trend with the outflow, and the growth rate slows down with the increase in the outflow. As can be seen in
Figure 13, when the water level of the hydropower station is certain, the curve as a whole shows a stepwise upward trend with the increase in flow. When the flow is certain, the water consumption rate of the hydropower station decreases with the increase in the gross head.
5. Changing Pattern of Optimal Water Consumption Rate in Cascade Hydropower Station
5.1. Formula
Based on the characteristic curves of the water consumption rate of hydropower station A and hydropower station B, this section carries out the study on the changing pattern of the water consumption rate during the joint optimized operation of cascade hydropower stations.
When the water level of hydropower station A, the water level of hydropower station B, and the total output are given, it is possible to obtain the distribution of flow between the two hydropower stations at the time as the lowest rate of consumption, the distribution of output, and the rate of consumption at that time, thus realizing the economic operation of the cascade hydropower stations.
The water consumption rate of the cascade hydropower stations is characterized by the ratio of the total power generation flow of the cascade hydropower stations to the total output of power generation of the cascade hydropower stations [
13], and the formula for calculating the water consumption rate of the cascade hydropower stations is as follows:
where
is the total water consumption rate of the joint operation of cascade hydropower stations, m
3/(kWh);
is the power generation of the
ith hydropower station of the cascade hydropower stations, kWh;
is the power generation of water of the
ith hydropower station of the cascade hydropower stations, m
3;
is the output of the
ith hydropower station of the cascade hydropower stations, kW;
is the power generation flow of the
ith hydropower station of the cascade hydropower stations, m
3/s; and
C is the unit conversion constant.
When the total load of the cascade hydropower stations is given, under the consideration of the minimum outflow of each hydropower station, i.e., the outflow of A is not less than 1200 m3/s and the outflow of B is not less than 1700 m3/s, the load can be distributed among each hydropower station of the cascade hydropower stations. Thus, the distribution combination that minimizes the water consumption rate of the cascade hydropower stations must be found, i.e., the optimal water consumption rate under the total load of the cascade hydropower stations.
5.2. Calculation Steps
The steps for calculating the water consumption rate for the joint operation of cascade hydropower stations are as follows:
Calculate the relationship curve cluster of outflow–water level–optimal output for each single station.
Under the condition of the given total output of the cascade hydropower stations and the initial water level of each hydropower station, the curve of outflow–water level–optimal output for each hydropower station can be used to obtain the corresponding outflow under different output distributions. When the sum of outflow is the smallest, the water consumption rate is the smallest. Record the output distribution and flow distribution in this case.
Change the total output, obtain the results of the output of each power station of the cascade under different total outputs, and plot the total output of the cascade hydropower stations to the optimal water consumption rate under the conditions of the combination of water level at this time.
Change the water level and repeat the above calculations to obtain the optimal water consumption rate–different water level combinations–the total output of the cascade hydropower stations relationship curve clusters under the conditions of different combinations of water levels.
5.3. Calculation Result
Taking A–B cascade hydropower stations as an example, the calculation of the characteristic curve of the optimal water consumption rate of the calculated cascade was carried out according to the above steps. When the water level of hydropower station A is 540 m and the water level of hydropower station B is 370 m, the relationship curve of total output–optimal water consumption rate for the cascade hydropower stations is obtained, as shown in
Figure 14. The results of the optimal water consumption rate of the cascade hydropower stations in several typical cases are shown in
Table 1.
It can be seen from the graph that as the output increases, the water consumption rate becomes lower and lower, and finally stabilizes. The specific output distribution is shown in
Table 1. Three sets of examples are given in the table, meaning that when a total output value is determined, the output distribution scheme of the two hydropower stations can be output when the cascade water consumption rate is optimal, including the flow and gross head under the output. For example, when the total output is 558 × 10
4 kW, the optimal water consumption rate at this time is 2.7148 m
3/kWh, in which the output of hydropower station A is 267 × 10
4 kW and that of hydropower station B is 291 × 10
4 kW. Similarly, the corresponding flow and gross head under this scheme can be obtained.
Figure 15 shows the relationship curve cluster of total output–A–B joint optimal water consumption rate for hydropower station A with a water level of 580 m and for hydropower station B with different water levels. The legend in
Figure 15 indicates hydropower station B’s water level in meters.
From
Figure 15, it can be seen that the optimal water consumption rate decreases with the increase in the total output of the cascade hydropower stations. The optimal water consumption rate of the cascade hydropower stations decreases with the increase in the water level of B in the case of the same water level of A and the total output.
6. Conclusions
In this paper, from the relationship curve of output–head–flow of the unit for hydropower stations, the relationship curve of output–gross head–flow is calculated and the power characteristic curve of unit combination with the gross head as the parameter is put forward. Then, the calculation method of the characteristic curve of the water consumption rate for hydropower stations with their water level as the parameter is established. Finally, the relationship between the change in the water consumption rate of hydropower stations under different conditions of water levels, flow, output, etc., was obtained. At the same time, the optimal water consumption rate changing pattern of cascade hydropower stations under the given various total output conditions was studied. The following conclusions were obtained:
The changing pattern of the water consumption rate of a single unit is as follows: when the gross head is certain, the water consumption rate decreases with the increase in flow when the flow is small; when the flow increases to a certain value, the water consumption rate starts to increase slowly. The changing pattern of the water consumption rate of the hydropower stations is as follows: when the gross head is certain, hydropower station ’s water consumption rate with the increase in outflow shows slight fluctuations and an increasing trend. The changing pattern of the optimal water consumption rate of cascade hydropower stations is as follows: with the increase in the water level of each hydropower station, the optimal water consumption rate becomes smaller, and with the increase in total output, the optimal water consumption rate shows a smooth decline—first a fast decline, then the rate slows down.
The calculation method of the characteristic curve of the water consumption rate proposed in this research can be extended to other cascade hydropower stations. The results of the water consumption rate changing pattern are clear and intuitive, which is of great significance to understanding the characteristics of the water consumption rate of hydropower stations, applying the characteristics to carry out the economic operation of hydropower stations and promote the improvement of hydropower station power generation efficiency. It can be used as a reference for important decision-making in the economic operation of hydropower stations and cascade hydropower stations.
Author Contributions
Conceptualization, X.A. and X.Z.; methodology, F.L.; software, F.L. and J.Z.; validation, X.A., X.Z. and F.L.; formal analysis, X.A. and X.Z.; investigation, X.A.; resources, F.L.; data curation, X.A.; writing—original draft preparation, X.A. and X.Z.; writing—review and editing, X.A. and F.L.; visualization, X.Z.; supervision, F.L.; project administration, X.A.; funding acquisition, R.G., X.L. and M.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Open Research Fund of Hubei Key Laboratory of Intelligent Yangtze and Hydroelectric Science, China Yangtze Power Co., Ltd., grant number 242202000916, the Natural Science Foundation of Hubei Province Innovation and Development Joint Fund Project, grant number 2022CFD169, and the National Natural Science Foundation of China, grant number 51979198, 52279024.
Data Availability Statement
Restrictions apply to the availability of these data. Data were obtained from [China Yangtze Power Co., Ltd.] and are available [from the authors] with the permission of [China Yangtze Power Co., Ltd.].
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. Renwei Guo, Xiao Li, Mian Wang are employees of China Yangtze Power Co., Ltd., who provided funding and technical support for the work. The funder had no role in the design of the study; in the collection, analysis, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
References
- Bakken, T.H.; Killingtveit, Å.; Engeland, K.; Alfredsen, K.; Harby, A. Water consumption from hydropower plants–review of published estimates and an assessment of the concept. Hydrol. Earth Syst. Sci. 2013, 17, 3983–4000. [Google Scholar] [CrossRef]
- Tu, Q.; Cai, J. New and improved assessment method of water consumption rate of hydropower plant. Water Resour. Power 2013, 31, 32–34. (In Chinese) [Google Scholar]
- Wu, S. Research on assessment method of water-saving generation increase of hydropower station with daily regulation performance. Distrib. Energy 2019, 4, 22–26. (In Chinese) [Google Scholar]
- Sun, F.; Li, X. Research on optimal scheduling strategy of Pankou and Xiaoxuan reservoirs. Hydropower New Energy 2016, 4, 9–12. (In Chinese) [Google Scholar]
- Yu, Y.; Wang, G. Analysis and improvement measures of increasing water consumption rate of large hydropower station during dry period. Hydropower Pumped Storage 2017, 3, 71–74. (In Chinese) [Google Scholar]
- Hou, G. Analysis of Main influencing factors and countermeasures of comprehensive water consumption rate in Silin Power Plant. Huadian Technol. 2018, 40, 68–69+79–80. (In Chinese) [Google Scholar]
- Zhou, J.; Feng, H. Analysis of influencing factors and countermeasures of water consumption rate of a cascade hydropower station in Wujiang River. Hongshui River 2021, 40, 135–137+147. (In Chinese) [Google Scholar]
- Zhao, J. Reservoir optimization of hydropower station based on dynamic programming model of water consumption rate. Jilin Water Resour. 2014, 8, 24–26+29. (In Chinese) [Google Scholar]
- Bai, F. Joint application of water consumption rate curve and water balance equation in power generation planning of Taoyuan Hydropower Station. Hydropower Pumped Storage 2020, 6, 73–76. (In Chinese) [Google Scholar]
- Shi, J. Reservoir optimal operation based on dynamic analysis of water consumption rate of Ludila Hydropower Station during dry season. Yunnan Water Power 2022, 38, 12–15. (In Chinese) [Google Scholar]
- Lei, X.; Yin, A. An Analysis on the Water Consumption Rate of LongTan Hydropower Station with Properties of Water Energy. Adv. Mater. Res. 2013, 648, 218–222. [Google Scholar] [CrossRef]
- Wu, Y.; Liao, S.; Liu, B.; Cheng, C.; Zhao, H.; Fang, Z.; Lu, J. Short-term load distribution model for cascade giant hydropower stations with complex hydraulic and electrical connections. Renew. Energy 2024, 232, 121067. [Google Scholar] [CrossRef]
- Enterprise Standard Q/CSG1204020-2016; Specifications for economic operation indicators of hydropower in China Southern Power Grid. China Southern Power Grid Co., Ltd.: Guangzhou, China, 2024. Available online: https://www.docin.com/p-2413212820.html (accessed on 3 April 2024).
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).