Abstract
This study presents a comprehensive experimental investigation of the mechanical response of the jellyroll and complete Li-ion 18650 Nickel–Cobalt–Alumina (NCA) battery under axial compression, highlighting the effects of strain rate and state-of-charge (SOC). The jellyroll was subjected to both static (1 mm/min) and dynamic (10–30 m/s) axial compression using a Split-Hopkinson Pressure Bar (SHPB). A key innovation of this work is the investigation of the role of electrolytes under both static and dynamic conditions, revealing their significant impact on stress and strain behavior due to hydrostatic pressure. Additionally, the complete NCA battery was tested under various SOC levels (0–75%) using flat plate compression. The results demonstrate the jellyroll’s sensitivity to strain rate, with increased stress responses at higher loading speeds. Furthermore, the inclusion of electrolytes markedly amplified the stress and strain response. The Fu-Chang model was successfully employed to numerically replicate the observed static and dynamic behaviors. Critically, the full battery tests revealed a negative correlation between voltage cutoff and SOC, with the risk of fire and explosion increasing at higher SOC levels. This research provides novel insights into the safety and mechanical resilience of Li-ion batteries under compression.
1. Introduction
There has been a remarkable increase in the usage of Li-ion batteries in the last decade, with applications ranging from the power source of the smartphone to powering the modern electric vehicle. By 2017, there were around two million units of electric vehicles worldwide, and this is predicted to reach 130 million in 2030, not to mention the steady rise in battery capacity each year and the pressure to cut carbon emissions to reduce global warming that could further increase demand in the future [1]. However, using Li-ion batteries as the power source, especially for electric vehicles, raises safety concerns since Li-ion batteries pose a hazardous risk when damaged.
Similar to a vehicle with an internal combustion engine, the electric vehicle is not accident-proof. In fact, several recorded accidents involving electric vehicles tend to be more destructive as the Li-ion battery reacts more violently when damaged during the accident. Several of the recorded accidents followed by fire or explosion were due to crashes and collisions [2,3,4,5], while others happened during charging [6,7,8], and some happened when the car was parked [9,10,11]. An explosion or fire, especially caused by a collision or crash, happens due to thermal runaway, triggered when the battery is damaged, followed by an internal short-circuit.
There are numerous studies regarding the characterization and failure assessment of the battery and studies regarding the safety and protection of the battery. Some of the reported studies are related to the characterization of the battery components, such as the separator [12,13], anode, and cathode [14,15,16], and the casing of the battery [17]. Attempts to study and model the jellyroll of the battery have also been made [18,19,20]. Currently, a limited number of reported studies focus on the battery’s mechanical response during dynamic loading, such as impact loading. Several that have been reported are related to the pouch and elliptical battery [21], battery pack [22], and cylindrical 18650 battery with lateral compression and 3-point bending load [23,24]. The currently available reports and results are mainly in the low-strain rate or low-speed regime for component characterization. The high-speed test on the battery mainly focuses on investigating the failure mechanism of the battery or battery pack and its force-displacement response. Currently, there is no study regarding the characterization and mechanical response of the battery component at high-speed loading.
There are two main objectives of this research. The first objective is to characterize the mechanical properties of the jellyroll of the 18650 NCA battery through experimentation of the jellyroll on several variations and to build a homogenized numerical model that could reproduce the stress–strain results of the experiments. NCA 18650 is chosen for this study due to its widespread usage, especially for electric vehicle applications, and its high energy density, which is around twice that of Li-Po. The variations in the experiments are the variation of the loading speed and the variation of the specimen condition, which includes the usage of electrolytes, aluminum cover, specimen length-to-diameter (L/D) ratio, specimen cut position, and production batch. These variations are performed to measure the sensitivity of the jellyroll to the strain rate, electrolyte usage, location, production batch, and dimension in terms of the stress–strain response.
The second main objective is to study and report the failure characteristics of the complete 18650 NCA battery when subjected to static and dynamic axial compression. The failure characteristics are determined through measurement of the force, displacement, and voltage of the battery.
2. Research Methodology
Several parameters were varied to measure their effects on the stress–strain response of the Li-ion NCA 18650 jellyroll. The experiment and the simulation performed are divided into two main categories based on the subjected loading: static and dynamic compression. For the dynamic compression, four different loading speeds, 10 m/s, 15 m/s, 20 m/s, and 30 m/s are used to measure the sensitivity of the jellyroll to strain rate compared to the static compression. Two different materials, AISI 4340 and PMMA, are compared and used for the SHPB as an estimator of the jellyroll’s impedance since the exact value of the jellyroll’s impedance is not known, and only the approximation can be obtained using Equation (1).
where Z is specimen impedance, E is specimen Young’s modulus, and σ is specimen density.
For the specimen used in static and dynamic compression, the dimensions of the specimen are based on the constraint of the SHPB. The one-dimensionality of the strain wave can be ensured by setting the ratio of the length and diameter (L/D) of the specimen in the range of 0.8–1 [25]. The effect of L/D on the stress–strain response can be shown by varying the specimen’s L/D, where the ratios of 0.5, 0.8, 1.0, 1.2, and 1.5 are tested. Since the diameter of the specimen is already fixed by the producer, the only parameter that changes is the specimen’s length. Since the length of the specimen used in the test is shorter than the original length, the effect of the chosen section of the jellyroll is studied in this research. Variation of the production batch of the jellyroll is also investigated to check if the inconsistency in production could affect the result. For the wet specimen, the specimen is covered by aluminum foil to contain the electrolyte inside. The static test on the jellyroll specimen using aluminum cover without electrolyte is performed to ensure the aluminum cover does not affect the result of the test significantly.
For the dynamic compression test, the Split-Hopkinson Pressure Bar is used to obtain the stress–strain curve of the jellyroll. The stress–strain curve of the material is calculated based on the measured strain wave on the incident bar and the transmitter bar. Assuming all the bars and the specimen have similar impedance, and the bars have similar cross-sectional areas, then the stress and the strain of the material can be calculated using Equations (2)–(4).
where E is Young’s modulus, A is the specimen cross-sectional area, A0 is the cross-section of the bar, C is the elastic wave speed velocity in the bar, and LSP is the length of the specimen.
2.1. Experiment Setup
2.1.1. Jellyroll Compression
The static compression test was performed using Instron 8800 MT (Instron, Norwood, MA, USA) with a 25 kN load cell. The specimen is subjected to a constant compression rate of 1 mm/min to ensure that the static loading condition is achieved. The test is repeated three to four times for each of the dry specimens, dry-covered specimens, and wet specimens.
The dynamic compression is performed using a Split-Hopkinson Bar setup, which comprises the impactor bar, the incident bar, and the transmitter bar. The specimen is put in between the incident and the transmitter bar. For this experiment, a high-speed camera is also used to observe the compression and rebound of the specimen and to measure the speed of the impactor bar. The setup of the experiment is shown in Figure 1. The specimen is tested at four loading speeds—10 m/s, 15 m/s, 20 m/s, and 30 m/s—to measure the material’s strain rate and observe the effect of the strain rate on the specimen’s stress–strain response.

Figure 1.
Experiment setup for dynamic compression using SHPB.
Two materials are tested to find the material with the same impedance as the specimen: AISI 4340 and Polymethyl methacrylate (PMMA). The reasons for choosing these materials are, first, because both materials represent both extremes on the impedance range where AISI 4340 is high-strength steel with high impedance and PMMA is a polymer with low impedance and, second, both materials with the required length and straightness are easy to find on the market. Testing on both ends would help to determine the approximate value of the specimen’s impedance and the result could aid in determining other materials as candidates for the bar material should another iteration of the experiment be conducted.
The Li-ion NCA 18650 jellyroll was sourced from a battery jellyroll producer. The jellyroll is cut using a lathe machine to obtain the desired specimen dimension for the dry specimen, as shown in Figure 2. Before the cutting process, the protruding metal tab is removed, and then the jellyroll is wrapped with a layer of cellophane tape to ensure that the jellyroll will not disintegrate during the cutting process. Since the length of the specimen used is constrained by the limitation of the SHPB test, two sections of the specimen will be tested in the static test, the midsection and sidecut, as shown in Figure 2.

Figure 2.
(a) Jellyroll midsection specimen used in the dry static and dynamic tests, (b) specimen used for wet static and dynamic compression tests. (c) Highlight of the sidecut and midsection used in the test.
Preparation of the wetted specimen is performed initially by cutting the jellyroll in a similar manner to the dry specimen. Afterward, the cut specimen is wetted with electrolyte and then covered with aluminum foil. This process is performed inside an airtight glovebox filled with inert gas. Inside the glove box, two rectangular aluminum foils are bonded on their three sides using a vacuum thermal laminator. Then, the specimen is inserted into the aluminum foil from the remaining unbonded side. The specimen is oriented so that the flat plane of the cut specimen is oriented parallel to the normal direction of the aluminum foil surface. The specimen is then wetted using 0.89 cc of LiPF6. The cover’s opening is then sealed using the vacuum thermal laminator. The result is shown in Figure 2.
2.1.2. Battery Compression
The experiments are performed in two loading conditions: static loading condition and dynamic loading condition. For the static loading condition, the battery is compressed with a loading speed of 1 mm/min with SOC varied at 0%, 25%, 50%, and 75%, with as many as three repetitions for each SOC using Instron 8800 MT (Instron, Norwood, MA, USA) with a 25 kN load cell. For the dynamic loading condition or drop-weight test, the battery is impacted axially by a flat impactor with a total mass of 32 kg at dropping heights of 0.5 m and 1 m. The SOC used in the drop-weight test are 0%, 25%, and 50%, with three repetitions for each SOC. The SOC above 75% for the static compression test and the SOC above 50% were not used in the test due to safety reasons as the limitation of the testing location and the readily available equipment do not allow a more extreme testing condition to be conducted.
Three parameters are measured in both static and dynamic tests: force, displacement, and battery voltage. In the static compression test, the force and the displacement are measured directly from the sensors of the UTM, and the voltage is measured using a 100 kHz voltage recorder, which continuously measures the voltage of the battery during the testing. For the dynamic test, the force is measured using a 44 kN Piezoelectric load cell, the displacement is measured from a video recorded by a high-speed camera, and the voltage is measured using the 100 kHz voltage recorder. The testing setup for static and dynamic compression is shown in Figure 3.
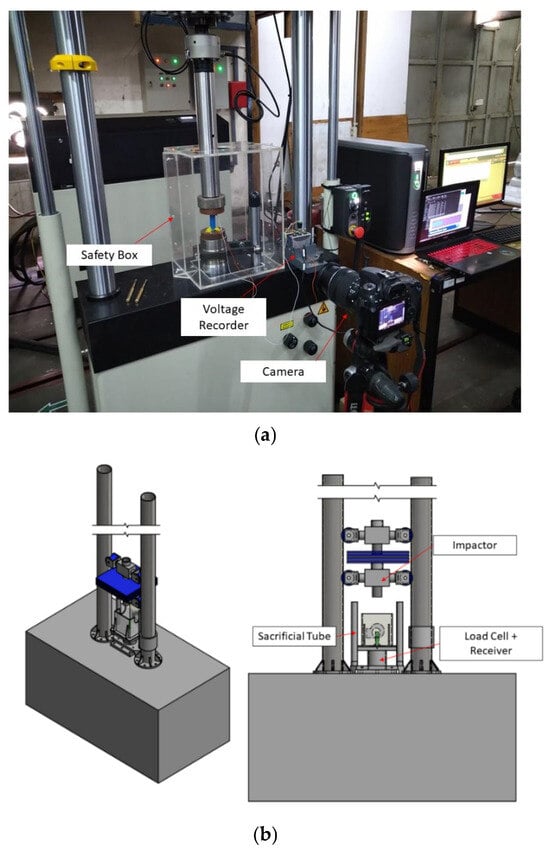
Figure 3.
Experimental setup for (a) Li-ion battery static compression test and (b) Li-ion dynamic compression test.
2.2. Numerical Model
The numerical models of each of the static and dynamic compressions were made using LS-DYNA ver. 2021 to simulate the stress–strain response obtained from the experiment. The dimensions of the bars and the specimen used in the simulation are tabulated in Table 1. For the static simulation, the bars are replaced with a flat plate to replicate the puncher and the static plate, as shown in Figure 4. The bars, the plates, and the specimen are modeled using solid elements.

Table 1.
The dimensions of the bars and the specimen used in the simulation.
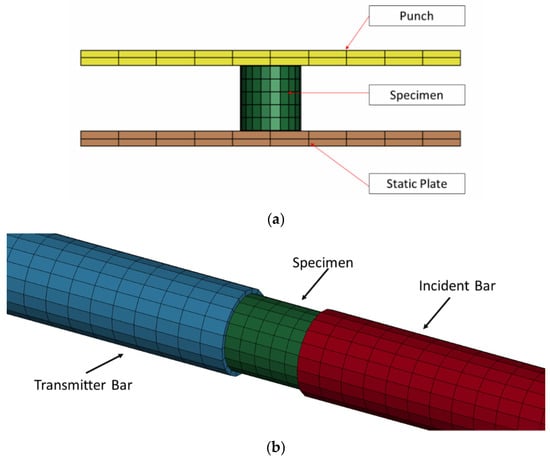
Figure 4.
(a) Numerical model for the static compression test using the static plate and punch, and (b) numerical model for the SHPB test showing the specimen, incident bar, and transmitter bar.
The MAT 83 Fu-Chang material model is used for the static and dynamic compression simulation to model the Li-ion NCA 18650 jellyroll material. Fu-Chang foam is used to model a foam with a very low Poisson ratio, where it has been reported that compression on the battery jellyroll has zero Poisson ratio [26]. The strain rate effect of the material is obtained from the interpolation of the inputted stress–strain curves at varying strain rates. The Fu-Chang material model is formulated by dividing the strain as the sum of the linear and nonlinear parts. The deformation strain rate can be assumed as the sum of the linear deformation strain rate and the nonlinear deformation strain rate. The nonlinear strain rate is the function of stress and state variables, which is shown in Equation (5).
where is the nonlinear deformation strain rate, S is the state variable, is the stress, and D0, c0, and n0 are the material constants. If D0 is equal to 0 or c0 is reaching infinity, the nonlinear strain rate vanishes.
The state variable term can be expanded as shown in Equations (6)–(9)
where c1, c2, c3, c4, n1, n2, n3, and aij are the material constants, R is the rate coefficient, P is the strain power, and W is the work done. The scalar stress and the strain rate can be formulated as shown in Equations (10)–(12).
The input for the material models is obtained by iteration to obtain the optimal result that could fit the experimental result. The input value is tabulated in Table 2.

Table 2.
Material inputs for the dynamic compression simulation for dry and wet specimens.
For the bars, the elastic material model is used to represent the mechanical behavior of the bars. The selection of the elastic material is used to ensure that only the elastic strain wave generated by the bar and the observation of the experiments have shown that no plastic deformation occurs on the bar. PMMA is chosen as the material with a density of 1190 kg/m3, Poisson ratio of 0.34, and Young’s modulus of 5.7 GPa.
3. Results
3.1. Experimental Result
3.1.1. Static Jellyroll Compression Experiment
The static compression test is used as the basis to determine the factors that will be important for determining the specimen setup for the dynamic compression test. These parameters are the location of the section cut, the effect of the aluminum cover on the stress–strain result, and the effect of the electrolyte.
Figure 5a shows the average stress–strain results of compressed specimens cut on their midsection and on their sidecut. The results on both cuts show that the jellyroll exhibits a behavior similar to a foam that is pointed by the existence of a plateau region after they reach the yield point and then followed by a densification region, which is indicated by the exponentially rising stress. A similar result was also reported for pouch batteries but with zero plateau stress and a very low Poisson ratio [26]. The average yield point of the sidecut specimens is around 29 MPa, which is higher than the average yield point of the midsection specimens at around 17–20 MPa. This is due to the leftover metal strip that cannot be removed without damaging the connection between the metal strip and the jellyroll.
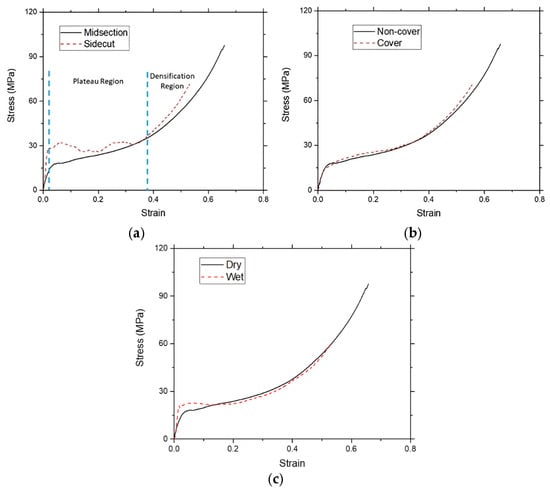
Figure 5.
(a) Average stress–strain response for midsection and sidecut jellyroll on static compression, (b) dry jellyroll with aluminum cover and non-covered jellyroll, (c) and wetted and dry jellyroll. The plateau region is marked when the material reaches the yield point. The densification region is marked when the stress increases exponentially.
The leftover metal strip would add additional stiffness to the jellyroll as it helps to resist the buckling of the electrodes during the compression. The erratic plateau region on the sidecut specimen is due to the non-uniformity of the applied load during the rolling of the jellyroll in the manufacturing process, which produces a relatively uniform roll on the midsection area but is slightly loose on the sidecut area. The looseness of the roll on the sidecut specimen would allow multiple buckling on the loose area, thus creating erratic stress behavior in the plateau region. Since the midsection specimen shows a lower stress response, which indicates a weaker position compared to the sidecut, and a more consistent stress–strain result compared to the sidecut, the midsection is chosen for the dynamic compression test.
The effect of the aluminum foil cover on the result is shown in Figure 5b, which shows the average stress–strain results of the dry specimen without an aluminum cover and the one with an aluminum cover. The results clearly illustrate that the aluminum cover does not have any significant impact on the stress–strain results. Thus, the usage of an aluminum cover for the wet specimen for the dynamic test will not affect the test results.
The effect of the electrolyte usage is also shown in Figure 5c. For this test, the midsection of the jellyroll is used as the specimen. The addition of electrolytes increases the yield point of the jellyroll. This increase is due to the hydrostatic pressure given by the electrolyte inside the wetted specimen. A similar response on a pouch battery was already reported, where pouch battery was reported to show an increase in stress response when the electrolyte was added [21].
An interesting phenomenon is shown where the stress–strain response of the wetted material is similar to the one from the dry specimen at a strain value of 0.15, where the densification process starts to happen. The plausible explanation for this is that the electrolyte is already pushed out of the jellyroll from the compression and forced to fill the crevices in the aluminum foil and no longer exerts hydrostatic pressure. Without additional hydrostatic pressure, the only loaded component is the jellyroll, and this might explain why the stress response of the wet specimen on the densification region is similar to the stress response of the dry specimen.
3.1.2. Dynamic Jellyroll Compression Experiment
The dynamic compression test using SHPB is performed to measure the sensitivity of the material due to strain rate. The first test performed in this research is to determine which bar material should be used for the SHPB module. Figure 6 shows the strain wave results of the SHPB test using AISI 4340 and PMMA as the bar material.
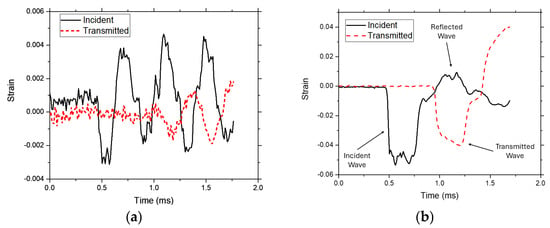
Figure 6.
Strain wave results of the (a) AISI 4340 and (b) PMMA bars.
A measure to determine which material is proper for the test is to locate where the transmitted wave is located compared to the location of the incident and the reflected wave. For the one-dimensional wave equation given to be applicable, the bar should have a similar impedance to the specimen. If the impedance of the bar is similar to or close to the impedance of the specimen, then the transmitted wave should appear at the same time as the first reflected wave is recorded, assuming the transmitter and the incident bar have the same length. From Figure 6, it is shown that the PMMA bar has the closest impedance to the specimen, where the transmitted wave appears approximately at the same time as the reflected wave. For the AISI 4340, it can be seen that the transmitted wave appears at the same time as the second reflected wave, which indicates that the bar impedance does not match the impedance of the specimen. From this result, the PMMA bar is used for the rest of the dynamic test.
The specimen L/D is known to affect the stress–strain result by the effect of the radial inertia during the compression of the material [27]. Thus, it is important to perform a check on this parameter before testing the material. Figure 7 shows the average stress–strain results from the specimen with values in the range of 0.5 and 1.5 for its L/D value. It is shown that the peak stresses of specimens with L/D of 0.5, 1.0, and 1.2 are similar, while specimens with L/D values of 0.8 and 1.5 experienced a slight increase in peak stress, with the difference between the lowest peak and the highest peak stress at around 2–3 MPa. Since there is no general pattern that can be seen from the peak stress of the component and the L/D value, and the variation of the peak stress is in the range of 10–15%, it is safe to conclude that the peak stress is relatively similar and the variations are due to the other factors such as small inconsistencies in the production rather than the L/D value of the specimen itself. Similar results are also reported where the testing of the material with the L/D ratio between 0.1 and 0.4 would result in a relatively similar stress–strain response [28].
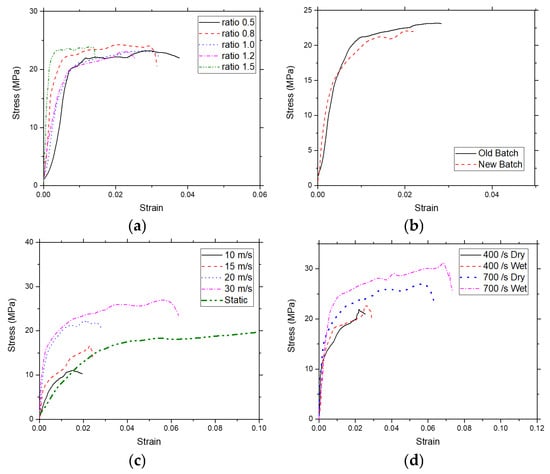
Figure 7.
(a) Average stress–strain results of the jellyroll with different specimen L/D ratio, (b) different production batch, (c) different loading speed in comparison with static compression test, and (d) different loading speed with dry and wet specimen.
It is also worth noting that specimens with lower L/D values have longer strains than the specimens with higher L/D values. One possible explanation for this phenomenon is that if all specimens experience the same deformation length, then the specimen with a shorter initial length will have a larger strain compared with the specimen with a longer initial length. Since the diameter is fixed, the specimen with a lower L/D has a lower initial length than the specimen with a higher L/D value; thus, the specimen with a lower L/D value will have a bigger strain value compared to the specimen with a higher L/D value with the same deformation length on all L/D values. From the results, a ratio of 1.0 is chosen as it will not affect the stress, and it is also deformed long enough to be consistent for the remainder of the test.
For the effect of the production batch on the stress–strain result, the test is performed with the same loading speed at 20 m/s, the same L/D value, and using a dry specimen. Figure 7b shows the stress–strain response from specimens with different production batches. There is no significant variance in the stress response from both batches. The noticeable difference is from the strain at the unloading phase, where the old batch’s specimen has a slightly longer strain than the newer batch. This difference has no major impact as the strain at the unloading phase is commonly not used unless there is an interesting phenomenon that occurs in that region. Thus, the difference in production batch has no immediate major impact on the stress-strain result.
Compression of the jellyroll at different loading speeds is expected to have varying results on the measured stress and strain, as shown in Figure 7c. From the results, it is clear the stress response increases with the increase in the applied loading speed, from which it can be concluded that the jellyroll is strain-rate sensitive. Comparing the dynamic compression results with the static compression results shows an interesting founding where the results from compression with speeds of 10 m/s and 15 m/s are lower than the static results. This result could be due to the lack of compressive energy generated from the loading speeds of 10 m/s and 15 m/s. Due to this result, only loading speeds of 20 m/s and 30 m/s are used for the wet and dry specimen comparisons. The measured strain rates at loading speeds of 20 m/s and 30 m/s are around 400/s and 700/s, respectively.
For the comparison of the wet and dry specimens, the static test shows that the addition of electrolytes increases the stress response of the jellyroll. A similar phenomenon also occurs on the dynamic compression test, where there is an increase in the stress response at the wetted specimen, as shown in Figure 7d. The increase in the stress response is due to the addition of the electrolyte which fills the porous bodies of the jellyroll components. The trapped electrolyte can explain the strain-rate effect on the wetted specimen in the porous bodies of the jellyroll. The electrolyte is trapped due to inadequate time for electrolyte to flow out of the jellyroll.
An interesting phenomenon occurred during the compressing process of the jellyroll. From Figure 8, it is shown that the specimen does not retain its maximum deformation. In Figure 8b, the compression buckling is visible on the surface of the jellyroll as indicated by the reflected light. However, in Figure 8c, the surface of the specimen does not show any buckling on the surface, which indicates that there is an unloading process immediately after the maximum compression is over. This process would create a slightly longer strain wave during the decompression stage, as shown in Section 3.2.2.

Figure 8.
Compression of the jellyroll captured from the high-speed camera: (a) initial state, (b) maximum compression, (c) end of the compression. Note that the rebounding of the specimen is visible.
3.1.3. Static Battery Compression
There are a total of 12 specimens tested on the static compression test on their own respective SOC. The failure of the battery is mostly determined from the onset of the occurrence of the short circuit on the battery. The results of the static axial compression test on SOC 0%, 25%, 50%, and 75% are shown in Figure 9. The results obtained from the test are quite similar to the results reported on the static axial compression test on the LCO battery [19], where the first 2 mm of the deformation is dominated by the deformation of the top section of the shell casing. The difference is the point of the short-circuit or voltage cutoff is slightly higher in this test than the one reported. The average peak load and average voltage cutoff are tabulated in Table 3.
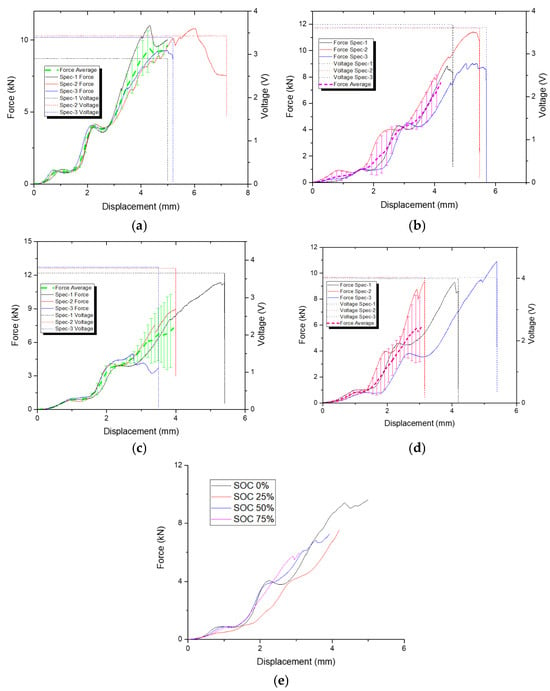
Figure 9.
Force, displacement, and voltage curves from the static compression test at (a) 0% SOC, (b) 25% SOC, (c) 50% SOC, and (d) 75% SOC. (e) Comparison of the force–displacement responses at different SOC values.

Table 3.
Experiment results for static battery compression on 0%, 25%, 50%, and 75% SOC with variation of loading condition (static, drop weight 0.5 m and 1 m).
The average voltage cutoff data shows that higher SOC correlates with lower voltage cutoff, which indicates the sensitivity of the battery to the SOC. The voltage cutoff occurs when the internal layers of the battery jellyroll have been compromised, causing an internal short circuit. One of the possible reasons is that the separator was damaged during the test. It has been reported that an increase in SOC could reduce the integrity of the separator due to thermal runaway melting the separator and short-circuits tend to happen faster at higher SOC [29]. The reduction in the failure strain of the separator due to the increase in battery SOC could explain the decrease in the voltage cutoff deformation in the static test. It is not feasible to judge how the battery SOC affects the peak load as the short-circuit process also affects the internal structure of the battery and in the high SOC cases (SOC > 50%), the battery tends to be combusted or exploded, which in turn compromises the structural integrity of the battery. However, it is possible to evaluate the general force–displacement of the battery as shown in Figure 9e where SOC does not seem to affect the overall force–displacement response of the battery in static axial compression.
The failure mode of the specimen at its respective SOC is shown in Figure 10. Compression of the battery at 0% SOC would only cause the battery to deform with a noticeable increase in the temperature of the battery, while increasing the SOC would cause a more violent effect. Explosion starts to occur at 25% SOC where the metal casing is violently ruptured due to the increase in the internal pressure inside the battery, but no fire is produced at this SOC. Fire starts to occur at 50% SOC, where the plastic covering is shown to be melted. The fire occurs after the explosion occurs, exposing the inside of the battery to atmospheric conditions, which leads to the combustion of the internal components of the battery due to the chemical interaction between the air and the inside of the battery. Increasing the SOC further would make the reaction more violent, as shown by the battery state at 75% SOC, where the opening of the metal casing is much wider and the flame produced is more sustained than the one produced by the 50% SOC battery.

Figure 10.
State of the battery (a) before test and at (b) 0% SOC, (c) 25% SOC, (d) 50% SOC, and (e) 75% SOC.
3.1.4. Dynamic Battery Compression
The dynamic compression test using a drop-weight testing apparatus is performed on 12 specimens at the specified drop heights and SOC. Similar to the static test, the failure point of the specimen is determined at its voltage cutoff or the onset of the short circuit. Figure 11 shows the force–displacement–voltage curves obtained from each of the specimens and the corresponding average. In the case of dynamic tests, evaluation of the peak load is feasible since fire or explosion does not occur instantaneously but rather a couple of seconds after the impactor is already in a resting position. Hence, the battery component is not compromised even though the short-circuit occurred during the impact based on the data captured by the voltage recorder. The comparison of varying SOC at similar drop heights shows the increase in the measured peak force with the increase in the battery SOC as the same result is also shown in Table 3. A possible explanation for this phenomenon is that a charged battery would have an increase in the volume of the anode layer due to the insertion of the Li+ ion in the anode layer and this process also increases the stiffness of the anode layer [30]. The volumetric expansion of the electrode could increase the force response as the expansion of the electrode is restricted in a cylindrical casing. The same phenomenon is observed in the pouch casing as the nominal stress on the wet battery pouch increases with velocity due to the increase in the pore pressure [31] and combined with the stiffness of the steel casing that prevents expansion of the electrolyte. Comparison of the force–displacement curve at various loading speeds shows that the general trend of the peak load increases with the increase in the loading speed. The increase in the momentum and the strain rate effect of the steel casing and the jellyroll could explain the increase in the peak load due to the compression.
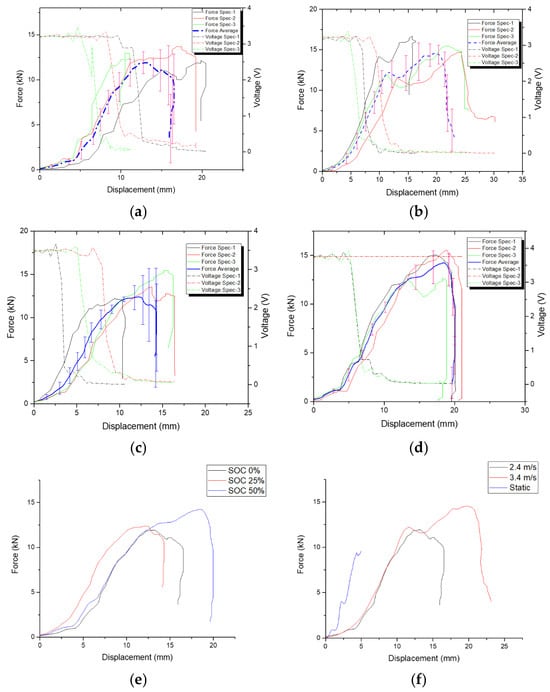
Figure 11.
Force, displacement, and voltage curves from dynamic compression test on (a) 0% SOC, 0.5 m, (b) 0% SOC, 1 m, (c) 25% SOC, 0.5 m, (d) 50% SOC, 0.5. (e) Comparison of average force–displacement responses with variations in SOC. (f) Comparison of average force–displacement response with variations in loading speed at 0% SOC.
The average voltage cutoff displacement tends to decrease with the increase in the SOC as shown in Table 3. What caused the increase in the average cutoff voltage displacement at 50% SOC is still inconclusive. The current possible explanation for this phenomenon is that the unevenness of the testing apparatus might cause the battery to be slightly tilted, causing the load to be off-center. The battery in Figure 10d is shown to be slightly curved on the bottom, which is indicative of off-center compression.
3.2. Numerical Results
3.2.1. Static Experiment
The static compression simulation of the jellyroll is conducted using a homogenized foam model implementing the MAT-83 Fu-Chang foam material model in LS-DYNA. The comparisons of the simulation and experimental results are shown in Figure 12. It is shown that the numerical model could adequately follow the experimental results on the initial elastic compression and the plateau stress region. However, the model could not model the behavior of the densification region adequately, especially for the dry experiment results.
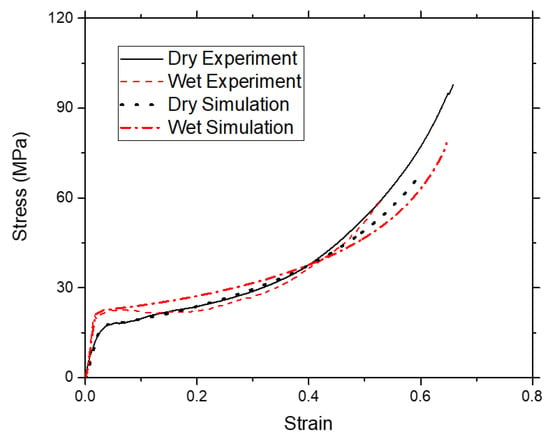
Figure 12.
Simulation results of the Fu-Chang foam compared with dry and wetted specimen static test results.
Further iteration and tuning of the model are still necessary to perfectly capture the response in the transition from plateau stress to densification area, as this area might require modeling the fluid flow inside the jellyroll.
3.2.2. Dynamic Experiment
For the dynamic simulation, the cases that will be simulated are the impact speeds of 20 m/s and 30 m/s, which correspond to the strain rates of around 400/s and 700/s from the experiment results. The selection of these strain rate values for the simulation is because the experiment results at loading speeds of 10 m/s and 15 m/s are below the stress–strain results from the static compression test.
The Fu-Chang model is also used to model the stress–strain response of the jellyroll in wet and dry conditions at the strain rates of 400/s and 700/s. Figure 13 shows the comparison between the simulation and the experiment results. The simulation results are well correlated with the average of the experiment results in both wet and dry conditions at two strain rate values using the material input given in Table 2.
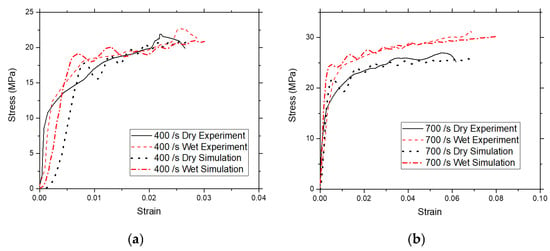
Figure 13.
Stress–strain results of the Fu-Chang foam compared with the average SHPB test results at strain rates of (a) 400/s and (b) 700/s.
The rebounding effect of the specimen after the dynamic compression using the SHPB would lengthen the strain response after peak compression. The added strain due to the unloading of the jellyroll can be modeled using the Fu-Chang foam by simply adjusting the shape and the hysteretic unloading factor (HU) of the material model. The effect on the specimen’s final deformation by varying the shape and the hysteretic unloading was also recorded. The specimen’s unloading behavior during the experiment could be simulated, as shown in Figure 14, in correlation with the results in Figure 15. The results of the base model show that the specimen retains its deformation since the front and rear surfaces have different displacements. For models with HU of 0 and 1, the displacement of the front side of the specimen gets closer to the displacement of the rear side, which indicates a rebounding phenomenon of the specimen after compression.
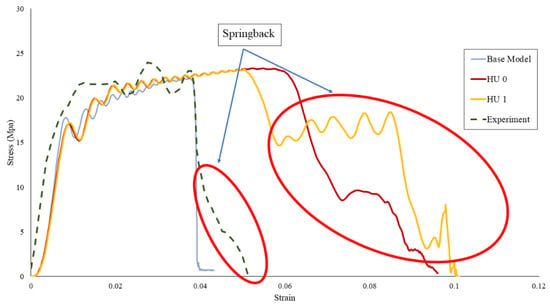
Figure 14.
Comparison of the experimental results with the numerical simulations with variation in hysteretic unloading (HU) on the Fu-Chang material model.
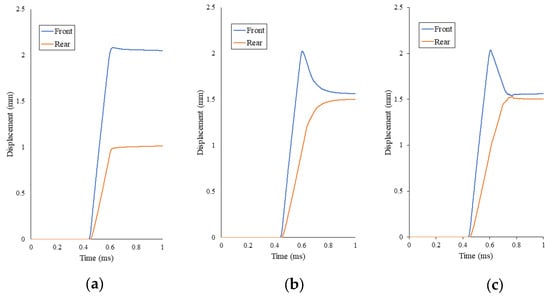
Figure 15.
Measurement of the displacement on the top and the bottom ends of the jellyroll model (a) base model, (b) HU = 0, (c) HU = 1.
4. Conclusions
This research investigates the stress–strain behavior of jellyrolls and complete NCA batteries under static and dynamic axial compression, with variations in electrolyte application and aluminum foil coverings. A homogenized numerical model was developed using the experimental data.
In the static tests, jellyrolls exhibited foam-like behavior with lower plateau stress in the midsection. The aluminum foil covering did not affect the stress–strain results, but the addition of electrolytes increased stress due to hydrostatic pressure. In dynamic tests, the length-to-diameter ratio influenced strain but not stress, and the manufacturing process was consistent across batches. Jellyrolls were sensitive to strain rate, but lower loading speeds (10–15 m/s) produced less compression than static conditions. Electrolytes again increased stress and strain responses.
For the complete battery tests, both static and dynamic compression showed decreasing voltage cutoff displacement. Higher SOC levels increased peak load and caused more violent failure modes, ranging from temperature rise at 0% SOC to explosions at 75% SOC.
Numerical simulations using the Fu-Chang foam model successfully captured both static and dynamic behaviors, including rebounding effects. Further research is needed to refine the model, study lateral responses, and explore voltage cutoff displacement at 50% SOC.
Future study and research might include further investigation of the mechanical characteristics of the jellyroll at higher speeds, variation of loading position of the jellyroll, and investigation of other types of batteries, such as NCM, Li-ion batteries such as Mn-Fe [32], or Li-sulfur [33].
Author Contributions
Conceptualization, S.P.S.; methodology, S.P.S. and H.F.; validation, S.P.S. and H.F.; formal analysis, H.F.; investigation, H.F.; resources, S.P.S.; data curation, H.F.; writing—original draft preparation, H.F.; writing—review and editing, S.P.S.; visualization, H.F.; supervision, S.P.S.; project administration, S.P.S.; funding acquisition, S.P.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded through the Research, Community Service, and Innovation ITB (P2MI) program of the Institute For Research And Community Service (LPPM) Institut Teknologi Bandung.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
This research is funded and supported by the Research, Community Service, and Innovation ITB (P2MI) program of the Institute For Research And Community Service (LPPM) Institut Teknologi Bandung. Thanks are due to the Research Center for Nanoscience and Nanotechnology (RCNN) and the National Center for Sustainable Transportation Technology (NCSTT), UNS Center for Energy Storage Technology.
Conflicts of Interest
All of the authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- International Energy Agency. Global EV Outlook 2018; International Energy Agency: Paris, France, 2018; 143p. [Google Scholar]
- Jensen, C. Chevy Volt Fire Prompts Federal Investigation into Lithium-Ion Batteries. 2011. Available online: https://wheels.blogs.nytimes.com/2011/11/11/chevy-volt-fire-prompts-federal-investigation-into-lithium-ion-batteries/ (accessed on 20 February 2019).
- ABC7. Tesla Driver Killed in Fiery Crash on Highway 101 in Mountain View Identified; ABC7: San Francisco, CA, USA, 2018. [Google Scholar]
- Kuzin, V. The Details of the Tesla Electric Car Fire in Moscow Have Been Published. 2019. Available online: https://4pda.to/2019/08/12/360223/ (accessed on 21 February 2019).
- Mendoza, A. Tesla Slams into Lake Forest Garage, Severely Damaging It and Sparking a Fire. 2017. Available online: https://www.ocregister.com/2017/08/25/tesla-slams-into-lake-forest-garage-severely-damaging-it-and-sparking-a-fire/ (accessed on 20 February 2019).
- Sean, G. Everything We Know about the Chevy Bolt EV Fires. 2021. Available online: https://electrek.co/2021/07/28/everything-we-know-about-the-chevy-bolt-ev-fires/ (accessed on 20 February 2019).
- Fred, L. Tesla Vehicle Caught on Fire While Plugged in at Supercharger Station. 2019. Available online: https://electrek.co/2019/06/01/tesla-fire-supercharger/ (accessed on 20 February 2019).
- Porsche Catches Fire While Charging. 2018. Available online: https://www.bangkokpost.com/thailand/general/1429518/porsche-catches-fire-while-charging (accessed on 20 February 2019).
- Tesla Car Catches Fire in Hong Kong Parking Lot: Media. 2019. Available online: https://www.reuters.com/article/technology/tesla-car-catches-fire-in-hong-kong-parking-lot-media-idUSKCN1SK0EO/ (accessed on 20 February 2019).
- Lambert, F. Porsche Taycan Caught on Fire—Burning down a Garage in Florida. 2020. Available online: https://electrek.co/2020/02/17/porsche-taycan-fire-burning-garage-florida/ (accessed on 20 February 2019).
- Cori-Manocchio, V. Electric Car Catches Fire and Explodes in Île-Bizard Garage. 2019. Available online: https://www.cbc.ca/news/canada/montreal/electric-car-catches-fire-and-explodes-in-%C3%AEle-bizard-garage-1.5227665 (accessed on 22 February 2019).
- Sheidaei, A.; Xiao, X.; Huang, X.; Hitt, J. Mechanical Behavior of a Battery Separator in Electrolyte Solutions. J. Power Sources 2011, 196, 8728–8734. [Google Scholar] [CrossRef]
- Kalnaus, S.; Wang, Y.; Turner, J.A. Mechanical Behavior and Failure Mechanisms of Li-Ion Battery Separators. J. Power Sources 2017, 348, 255–263. [Google Scholar] [CrossRef]
- Sahraei, E.; Bosco, E.; Dixon, B.; Lai, B. Microscale Failure Mechanisms Leading to Internal Short Circuit in Li-Ion Batteries under Complex Loading Scenarios. J. Power Sources 2016, 319, 56–65. [Google Scholar] [CrossRef]
- Wang, L.; Yin, S.; Zhang, C.; Huan, Y.; Xu, J. Mechanical Characterization and Modeling for Anodes and Cathodes in Lithium-Ion Batteries. J. Power Sources 2018, 392, 265–273. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, J.; Cao, L.; Wu, Z.; Santhanagopalan, S. Constitutive Behavior and Progressive Mechanical Failure of Electrodes in Lithium-Ion Batteries. J. Power Sources 2017, 357, 126–137. [Google Scholar] [CrossRef]
- Zhang, X.; Wierzbicki, T. Characterization of Plasticity and Fracture of Shell Casing of Lithium-Ion Cylindrical Battery. J. Power Sources 2015, 280, 47–56. [Google Scholar] [CrossRef]
- Sahraei, E.; Campbell, J.; Wierzbicki, T. Modeling and Short Circuit Detection of 18650 Li-Ion Cells under Mechanical Abuse Conditions. J. Power Sources 2012, 220, 360–372. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, X.; Sahraei, E.; Wierzbicki, T. Deformation and Failure Mechanisms of 18650 Battery Cells under Axial Compres-Sion. J. Power Sources 2016, 336, 332–340. [Google Scholar] [CrossRef]
- Kisters, T.; Gilaki, M.; Nau, S.; Sahraei, E. Modeling of Dynamic Mechanical Response of Li-Ion Cells with Homogenized Elec-Trolyte-Solid Interactions. J. Energy Storage 2022, 49, 104069. [Google Scholar] [CrossRef]
- Kisters, T.; Sahraei, E.; Wierzbicki, T. Dynamic Impact Tests on Lithium-Ion Cells. Int. J. Impact Eng. 2017, 108, 205–216. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, G.; Zhou, Q.; Shi, X.; Shi, F. Failure Behaviours of 100% SOC Lithium-Ion Battery Modules under Different Impact Loading Conditions. Eng. Fail. Anal. 2017, 82, 149–160. [Google Scholar] [CrossRef]
- Xu, J.; Liu, B.; Wang, X.; Hu, D. Computational Model of 18650 Lithium-Ion Battery with Coupled Strain Rate and SOC Depend-Encies. Appl. Energy 2016, 172, 180–189. [Google Scholar] [CrossRef]
- Spielbauer, M.; Berg, P.; Ringat, M.; Bohlen, O.; Jossen, A. Experimental Study of the Impedance Behavior of 18650 Lithium-Ion Battery Cells under Deforming Mechanical Abuse. J. Energy Storage 2019, 26, 101039. [Google Scholar] [CrossRef]
- Afdhal. Development fof Split Hopkinson Pressure Bar to Measure Mechanical Properties of Material at High Strain Rates; Institut Teknologi Bandung: Bandung, Indonesia, 2015. [Google Scholar]
- Sahraei, E.; Hill, R.; Wierzbicki, T. Calibration and Finite Element Simulation of Pouch Lithium-Ion Batteries for Mechanical Integrity. J. Power Sources 2012, 201, 307–321. [Google Scholar] [CrossRef]
- Chen, W.W.; Song, B. Split Hopkinson (Kolsky) Bar: Design, Testing and Applications; Springer: New York, NY, USA, 2011. [Google Scholar]
- Pankow, M.; Attard, C.; Waas, A.M. Specimen Size and Shape Effect in Split Hopkinson Pressure Bar Testing. J. Strain Anal. Eng. Des. 2009, 44, 689–698. [Google Scholar] [CrossRef]
- Sheikh, M.; Elmarakbi, A.; Elkady, M. Thermal Runaway Detection of Cylindrical 18650 Lithium-Ion Battery under Quasi-Static Loading Conditions. J. Power Sources 2017, 370, 61–70. [Google Scholar] [CrossRef]
- Jia, Y.; Yin, S.; Liu, B.; Zhao, H.; Yu, H.; Li, J.; Xu, J. Unlocking the Coupling Mechanical-Electrochemical Behavior of Lithium-Ion Battery upon Dynamic Mechanical Loading. Energy 2019, 166, 951–960. [Google Scholar] [CrossRef]
- Zhu, J.; Luo, H.; Li, W.; Gao, T.; Xia, Y.; Wierzbicki, T. Mechanism of Strengthening of Battery Resistance under Dynamic Loading. Int. J. Impact Eng. 2019, 131, 78–84. [Google Scholar] [CrossRef]
- Fan, L.; Guo, X.; Li, W. Rational Design of Prussian Blue Analogue-Derived Manganese-Iron Oxides-Based Hybrids as High-Performance Li-Ion-Battery Anodes. Chin. Chem. Lett. 2023, 34, 107447. [Google Scholar] [CrossRef]
- Du, M.; Geng, P.; Jiang, X. High-Entropy Prussian Blue Analogues and Their Oxide Family as Sulfur Hosts for Lithium-Sulfur Batteries. Angew. Chem. Int. Ed. 2022, 61, e202209350. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).