1. Introduction
Buildings are responsible for approximately 40% of energy consumption and 36% of greenhouse gas emissions in the European Union, making them the single largest energy consumer [
1].
In order to improve their energy efficiency and overall sustainability, many efforts are made to understand, model, and forecast their energy consumption, both thermal and electrical. Historically, the initial attempts relied on engineering software packages, e.g., Energy Plus, to model energy consumption in buildings. Despite the considerable software setup time and data used regarding the structural, geometrical and material characteristics of the buildings, the results are not usually as valuable as would be expected. This is due to the hurdles in estimating anthropic loads, behaviors, and nonlinearities that affect energy consumption. As a more efficient and effective alternative, data-driven approaches to modeling and forecasting the energy consumption of buildings are explored: smart meters and bills are utilized to capture energy consumption data, which are fed into machine learning algorithms to infer the complex relationships between energy consumption and other variables, such as weather, degree-days, timestamp features, and building characteristics. While the literature regarding data-driven forecasting techniques is growing quickly, few studies actually investigate what is the most important set of variables that may be correlated with building energy needs and their dynamics. This is a critical element for forecasting building energy needs as it has an impact both on the economic and financial aspects of resource allocation in building management and on the environmental consequences for the surrounding communities. In addition to this, despite the extensive efforts and studies, the topic is far from reaching state of the art. This is mainly due to the inherent complexities that arise from the variabilities and interactions characterizing each building envelope and from the vast amount of data needed to achieve good forecasting performance.
In this sense, the development of artificial intelligence algorithms (e.g., machine learning and deep learning) has made it possible to improve performance and forecasting even when there is significant uncertainty that is difficult to model through sets of equations or to investigate without an adequate set of measurement tools. The abundance of data, in fact, has made it possible to develop increasingly sophisticated and high-performance models and algorithms under ordinary and easily reproducible conditions. At the same time, this constitutes an element of weakness in all circumstances that are difficult to reproduce or predict (e.g., COVID-19 and its impact on building consumption) or, more simply, when there is a lack of data (e.g., due to a breakdown or maintenance activities).
The vast quantity of data generally required for artificial intelligence-based models is particularly critical, especially in cases where the building under investigation lacks a historical dataset from an adequate monitoring system to train the model and achieve a sufficient level of generalization to predict situations outside the training set.
In this work, a similitude approach based on machine learning methods is explored for building energy consumption modeling and forecasting to overcome the hurdles mentioned above. Different data-driven modeling approaches deriving from artificial intelligence are considered. As highlighted by the literature review, each approach has its strengths and limitations, and there is no clear winner among those available. Therefore, a set of algorithms is introduced to address the complexities and uncertainties associated with building energy consumption.
The case study focuses on Ca’ Foncello Hospital in Treviso, Italy (i.e., the building for which the energy demands are considered known and used for training) and Sant’Anna Hospital in Ferrara, Italy (i.e., the building for which the energy demands are considered unknown and used for testing). The energy demands of these hospitals, including heating, cooling, electricity, and steam, are analyzed using data collected from the building management systems. The algorithm developed in this project incorporates automatic preprocessing steps, such as data cleaning and normalization, and hyperparameter optimization of ensemble methods. These methods combine multiple models to improve predictive performance. The remainder of the paper is outlined as follows.
Section 2 presents an overview of the available methods for forecasting building energy needs, with a particular focus on artificial intelligence-based tools.
Section 3 describes the methodology that enables the utilization of data from a known structure to estimate the unknown energy needs of another structure, adopting easily and economically obtainable variables.
Section 4 outlines the case studies in detail, while in
Section 5, the results are reported, and the final conclusions are drawn in
Section 6. The primary novel contributions of this research pertain to (i) the employment of a similitude criteria, (ii) data cleaning based on plant technical specifications rather than statistical analysis, (iii) an innovative methodology for time series analysis, and (iv) the incorporation of an automated optimization procedure for the parameters of the forecasting techniques employed.
2. Literature Review
2.1. Methods for Building Energy Forecasting
Building energy consumption modeling and forecasting is a challenging task due its many variables, such as weather conditions, building envelope features, anthropic factors (e.g., behavior and occupancy), lighting, electrical equipment, and HVAC performance [
2]. For this reason, numerous techniques were developed, adapted and used in recent research. The literature suggests the following unifying nomenclature in modeling processes, without considering any particular building type, energy end-use distinctions, or building scale applications [
3,
4]:
White-box approaches: These models use a transparent process based on solving first-principle equations to describe the energy behavior of buildings. Physics-based modeling was introduced with different names, such as “engineering models” [
4]. As reported above, the development of white-box models for an entire building would require a remarkable amount of time to set the physical properties and characteristics. This is only made possible by a collection of detailed information in order to ensure the sufficient accuracy of building energy models (BEMs). To speed up the simulation time, it is common to make use of representative buildings, called archetypes, for the simulation: these are usually developed after an accurate identification of the most common characteristics of different groups of analogous buildings [
5]. This method analyzes portions of the buildings, producing detailed BEMs, which still preserve the ability to characterize the energy performance of the whole building portfolio with the desired level of accuracy. Moreover, it allows the accurate creation of benchmarking models at a local level through a classification process. Ultimately, another considerable benefit of this approach is the assessment of retrofit interventions by what-if scenarios [
6]. However, to date, this kind of representation has required dedicated simulation engines and large amounts of data to correctly represent the buildings of a given portfolio, making the benefits listed above only potential and not real.
Black-box approaches: These models use building data analysis and data mining tools to predict and forecast energy consumption at a more complex scale than single building level [
4]. They are widely used for prediction and forecasting of energy use based on the selection of hierarchically important inputs [
7,
8]. The most widespread black-box approaches for prediction and forecasting at a building level are as follows [
9]: simple regression model (SRM), multiple linear regression (MLR), decision trees (DT), artificial neural networks (ANN), and support vector machine (SVM). All of the above rely on the availability of prior data to forecast energy consumption. In addition, data-driven approaches based on machine learning are used to select and identify the archetypes of the main building categories [
10]. Nevertheless, these methods are not employed to carry out building energy demand forecasting both in the short- and long-term.
Grey-box approaches: These models have a hybrid structure combining first-principle physics and data-driven approaches. As expected, they share some advantages and limitations of white- and black-box models. In the recent literature, hybrid modeling presents two main orientations. Some examples use data-driven methods to optimize specific parameters of white-box models [
11], while others combine a Gaussian process with a resistance–capacitance lumped model to predict and adjust the error of the physics-based model. Finally, another way to combine data-driven and physics-based models is to replace parts of the latter with machine learning algorithms, for instance with the aim of representing energy equipment load demand [
3,
12].
To the best of the authors’ knowledge, none of the articles shows a clear winner among all the available algorithms. This is especially true concerning situations in which the building data and features are unknown and it is challenging to find similarities. Since the main interest is the implementation of real use cases where execution time is crucial and cost-effectiveness drives the whole process, the paper at hand is focused on data-driven approaches. It proposes a method for predicting the energy needs of buildings, applying similitude criteria for verifying the results, or making predictions in the absence of historical data.
2.2. Machine Learning Algorithms
Among the artificial intelligence tools available in the literature, data-driven models are simple and consist of two distinct and iteratively subsequent phases: learning and validation. The learning process starts with carefully selecting all the parameters and modifying them through subsequent validation, namely, systematically comparing between the model outputs and the historical data. Once the error is lower than the required threshold, the data-driven model is deemed validated and, consequently, qualified for practical applications with new input data [
13].
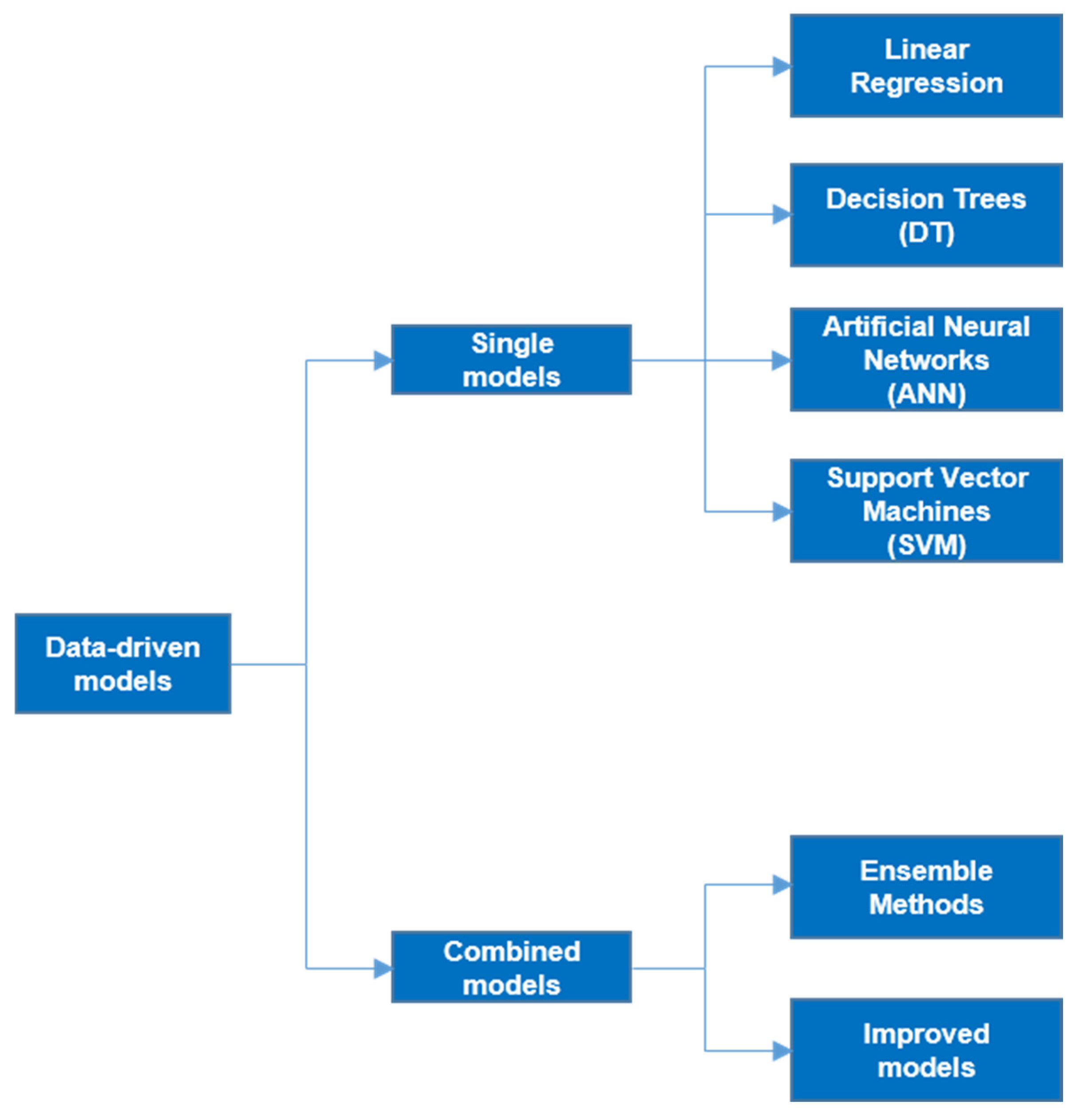
Due to the low costs and limited requirements for expensive equipment or audit activity, data-driven approaches are widely applied in several fields (e.g., medical diagnosis, political campaigns, commerce). Recently, their use has been extended to the building sector in order to estimate building energy demands or profile energy consumption patterns. The most widespread methods are grouped in
Figure 1.
2.2.1. Single Models
Statistical regression or linear regression (LR) is the easiest and fastest to implement among the methods mentioned above. It is a straightforward and simple approach for predicting building energy consumption: in more detail, it is mainly used during early studies to predict the average consumption over a long period of time. However, compared with other approaches, such as ANN or SVM, the regression models require vast historical datasets for training, and their accuracy for short-term prediction is poor. It is also challenging to select a good set of predictors and an appropriate time scale to achieve a good building energy consumption correlation under a wide range of environmental and weather conditions. In addition to this, unforeseen correlations among the selected variables may result in an unpredictable level of accuracy in the regression outputs [
2]. The main applications concern their use for administrative buildings [
14] and the design of new buildings [
15].
In the last few years, researchers have proposed modifications for statistical regression aimed at solving inaccuracy issues, claiming in most cases better results than the ANN models. However, the authors consider the tool validated for simple buildings, such as those of the tertiary sector, and in climatic zones characterized by small temperature ranges [
16]. Nevertheless, in most cases, statistical regression is adopted to estimate the important parameters needed for characterizing building energy performance, designing, tracing, and analyzing building thermal behavior [
17], or drafting heat control strategies for energy saving [
18].
Another data-driven approach for building energy forecasting is a decision tree model [
19]: it is a flowchart-like structure in which each internal node represents a test on an attribute, each branch represents the outcome of the test, and each leaf node represents a class label, each assigned after computing all attributes. The topmost node of DT is known as the root node where the input data are split into different groups based on some predictor variables predefined as splitting criteria. These split data form sub-nodes as branches emanating from the root node. The data on the sub-nodes undergoes either further or no splits: in the former case, a subsequent data split is conducted to form new subgroups as child branches emanated graphically at the next level, whereas the latter are called leaf nodes and the corresponding data groups at those levels are their final outputs. DT are versatile data-driven techniques applicable to early design and post-occupancy studies. Their predictive accuracy is comparable to ANNs and SVM. However, DT offers the distinct advantage of being interpretable while maintaining reasonable implementation and operational complexity, at least for less complex use cases, such as residential dwellings, as studied by Tsanas and Xifara [
20]. As for the limitations of this approach, apart from being mostly applied in noncomplex applications, such as buildings in residential areas, it is usually unstable in the presence of noisy or nonlinear data [
21].
An additional machine learning algorithm widely used in building energy forecasting is ANNs, which are biologically inspired computational networks attempting to mimic how the human brain processes information [
22]. One of the primary ANN design objectives is to implement suitable modifications that enable it to absorb features of each scenario. The three components that determine the behavior of an ANN are as follows:
Architecture: the number and positions of neurons/layers and the connection pattern between them;
Learning algorithm: that is the iterative methodology for minimizing the error;
Activation functions: the element that enables the nonlinear operations of ANNs.
Regarding the first point, architecture consists of a set of neurons, each representing a node, which are connected to other nodes through links corresponding to biological axon–synapse–dendrite connections. Finally, each link has a weight, determining to what extent one node influences another [
23]. The networks constitute a directed weighted graph. Each artificial neuron of the ANN can be considered as a mathematical function chaining the outputs to the inputs through a (linear) transfer function and a (nonlinear) activation function. Among the various types of ANNs, multilayer perceptrons with backpropagation learning algorithms are widely used in these applications. Due to their ability to model and reproduce nonlinear phenomena and processes, fault tolerance, robustness, and noise immunity, ANNs have been successfully applied in many disciplines and cases. Specific attention has been dedicated to forecasting building energy demands, in particular, in tertiary [
24], residential [
25], and educational buildings [
26]. In fact, they provide a flexible way to handle regression and classification problems without explicitly specifying any relationships between the input and output variables. This is a positive feature, considering that buildings exhibit predominantly nonlinear dynamics and highly complex input–output relationships. On the other hand, it must be pointed out that the architecture choice and learning rate optimization process still rely on ad hoc methods: this implies that ANNs are case-dependent and have to be designed and validated each time for every different application. Thus, in building contexts, ANNs cannot effectively handle tasks requiring the prediction of unforeseen events.
It is also worth mentioning another category of data-driven methods, namely, long short-term memory (LSTM) models, which have been employed for instance to forecast heat loads in multi-floor buildings [
27] or to reproduce general electricity consumption data for an operating year [
28]. LSTM models are mainly based on neural networks and allow for long-term prediction. Nonetheless, no study has used them in combination with similitude methods.
Last, in the list of machine learning methods in the literature regarding building energy need forecasting, originally designed to solve pattern recognition problems, the support vector method has evolved over the years and has become a tool for solving multidimensional function estimation problems. Nowadays, this method has been widely applied to solve regression problems and estimate an underlying relationship among nonlinear inputs to the continuous real-valued target. In particular, the support vector machine used for regression is called support vector regression (SVR) [
13]. SVR has been implemented with various time steps, input variables, and real or simulated data. Despite competitive forecasting performance and flexibility, SVR suffers from a major drawback: the challenging and critical process of parameter calibration significantly affects prediction accuracy. For instance, accurately determining the kernel function is problematic yet crucial. Consequently, optimizing the SVR parameters has become a key challenge in building energy studies [
29]. Furthermore, in standard SVR, the training process has O(n
3) time and O(n
2) space complexities where n is the training dataset size, rendering it computationally infeasible for very large datasets, i.e., high-frequency or long-term forecasting, as Li and Hu demonstrated in their studies [
30].
The main applications of the model aimed to forecast the combined cooling and heating energy demand in residential low energy buildings [
31], the electrical load of an office building at the university [
32], and the day-ahead electrical consumption of an office building [
33]. In more detail, the last two case studies performed a comparison of SVR with ANNs, and the former results outperformed the latter in all the metrics.
2.2.2. Combined Models
Combined modeling techniques emphasize the optimization of forecasting methods to enhance prediction accuracy. The combined modeling framework either pairs them with optimization techniques (improved models) or combines multiple individual algorithms (ensemble models). In the literature, improved models are a combination of single models and optimization techniques [
3]. The former are mainly ANN [
34] and SVR [
35], already mentioned above, while the latter are mainly genetic algorithm [
36], differential evolution [
37], and particle swarm optimization [
38]. These improved models have all been tested on residential or tertiary buildings, but none of them has succeeded in the simultaneous investigation of heating, cooling, and electrical energy needs in complex applications. Furthermore, their application mainly relates to short-term forecasting, namely, from half an hour to a day ahead, with a ratio of training data needed for each forecasted data of around 250:1, even for the most advanced techniques [
35]. This is, once more, a critical aspect for new buildings or if monitoring systems are absent.
Conversely, in statistics and machine learning, ensemble methods combine multiple learning algorithms to achieve a better predictive performance than that obtained with any single method [
39]: the main hypothesis supporting this class of tools is that combining multiple models together can often produce a much more powerful and flexible model [
40]. In fact, most of the times, basic models perform poorly because of high bias or too high variance. Although a good degree of freedom is desirable to resolve the underlying complexity of data, it should be limited so as to avoid high variance and achieve robustness [
40]: this is a well-known bias–variance trade-off.
In addition to this valuable variety of algorithms, ensemble learning methods also present an interesting set of underlying benefits and reasons why they may be preferred, such as robustness, small volumes of training data needed, manageable complex decision boundaries, and data fusion [
39]. In order to set up an ensemble learning method, the first step is to select the base models that have to be aggregated. In the literature, an ensemble model is called homogeneous when it takes a single base learning algorithm, and weak learners (i.e., algorithms that perform slightly better than random guessing for a given problem) are trained in different ways. Vice versa, other ensemble learning methods use different kinds of base learning algorithms: hence, heterogeneous weak learners are combined into a so-called heterogeneous ensemble model. The choice of weak learners must be coherent with the model aggregating process: if base models are characterized by a low bias and high variance, the chosen aggregating method must tend to reduce variance, and vice versa [
40]. Common types of ensembles used for regression problems regarding building energy needs are bootstrap aggregating (bagging) type [
41], namely, random forest, and extremely randomized trees (also known as extra trees). Random forest regressor and extremely randomized trees are ensemble learning methods that combine multiple decision trees to improve predictive performance and reduce overfitting. While both techniques leverage tree-based models and aggregation strategies, they differ in their approach to introducing randomness and constructing individual trees.
Random forest regressor employs bootstrap sampling where each tree is trained on a randomly drawn subset of the original training data with replacement. Additionally, it incorporates feature subsampling, randomly selecting a subset of features for splitting at each node. In contrast, extremely randomized trees do not utilize bootstrap sampling but instead train each tree on the entire training set. Furthermore, they introduce randomness by randomly selecting both the subset of features and the split point for each feature at each node, rather than finding the optimal split based on impurity measures.
The additional randomization in extremely randomized trees can lead to increased diversity and reduced correlation among the individual trees, potentially enhancing generalization performance. However, this increased randomness may also increase the risk of overfitting if the ensemble size is not appropriately controlled. Both methods have proven effective in various domains, handling high-dimensional data, nonlinear relationships, and missing values, making them promising tools for regression tasks in scientific applications. In more detail, tree-based ensemble models have been successfully applied in many fields and practical applications, but their full potential has not yet been explored in building energy applications. The literature cites their capability in the residential [
42] and tertiary sectors [
43], mainly for short-term forecasting, while more complex buildings and longer timeframes remain unexplored.
Overall, the aforementioned data-driven approaches and their potential use in building energy demand forecasting, with advantages, limitations, and case studies, are summarized in
Table 1.
2.3. Research Gap
The literature review has highlighted that a wide range of solutions are available for forecasting the energy needs of a building. Indeed, the choice between single models and combined models highly depends on the type of forecast and on the specific requirements of the case study. Looking for the best model or algorithm for each application is far from being a real artificial intelligence approach since it always relies on human setup and skills. Furthermore, it must be pointed out that, usually, a good approach today might not be as good in the future, so there is no sense in looking for the best global model and best algorithm for a case-based situation. In addition to this, many self-claimed artificial intelligence models may be weak in terms of how they adapt to unfavorable contexts, such as lack of data. Every mentioned algorithm relies only on monitoring data, which makes them useless if the monitoring system is unavailable. Moreover, they are not robust enough to manage unforeseen circumstances because of too intrusive statistical-based data-cleaning approaches, case-based models, and time-consuming hyperparameter optimization algorithms.
For all these reasons, it is believed that the most appropriate approach is to equip the algorithm with a set of models (e.g., combined models) and optimization tools that can deal with different events that it might face, predicting the building energy demand with adequate accuracy and precision. Furthermore, this approach can prove useful when there is a lack of data.
In addition, to the best of the authors’ knowledge, there is no other literature that deals with data scarcity using similitude techniques combined with data-driven approaches.
The paper at hand aims to help fill this gap by introducing and demonstrating a novel approach with the following features:
A similitude criteria, which allows for the use of historical data from similar buildings to train the model and to overcome the lack of data issue;
An automatic data preprocessing and hyperparameter optimization, which further improves the combined model performance and frees the model development from human skills;
A methodology that will allow for the automatic comparison of different data-driven models and the selection of the most suitable model based on performance evaluation metrics that can be modified according to specific needs.
3. Materials and Methods
The first step to overcome the research gap highlighted in
Section 2.3, especially when the there is a lack of data in forecasting building energy needs, is the similitude approach. This consists of identifying a structure that is similar to the building under investigation and for which it is possible to derive possible demand profiles and the information needed. To do this, the work at hand proposes a detailed procedure represented in
Figure 2. First, criteria are established to trace similar structures, even when a substantial database of information is not available for the target building. In more detail, this work aims to provide a codified and usable set of criteria and operating methods, usually shared by professionals, of which little or nothing can be found in the literature and which are often learned experientially. A similar structure or a possible demand profile must be identified based on available consumption information. This historical series must be representative of the phenomenon under analysis; thus, in the preprocessing phase, it must be cleaned of the outliers that negatively influence the results. Afterwards, the best performing model and the set of most correlated variables must be selected and the predictive phase of the model begins.
3.1. Similitude Criteria
The steps of the algorithm outlined in
Figure 2 replicate those typically taken when investigating the energy performance of a building (as described, for example, in the UNI CEI EN 16247-1 standard regarding energy audits). In particular, to establish similitude between two buildings, it is necessary to investigate the following variables:
Intended use;
Climate zone;
Year of construction;
Geometric factors (volumes, surfaces, number of floors above ground);
Ratios between energy needs;
Beds (in the case of hospital facilities).
The criterion underlying the choice of the set of variables mentioned above is that similar structures will have similar energy needs. In this regard, the intended use typically influences the shape of the demand profiles on different time scales, whether short, medium, or long term. The climate zone typically affects the magnitude of the needs, especially heating and cooling. The year of construction, on the other hand, is generally correlated with the construction criteria adopted and, consequently, with the energy class and energy losses of the building (recently constructed buildings, in particular, must meet specific requirements, as stated in European Directive 2010/31/EU). Geometric factors, such as volumes and surfaces, affect both the definition of comfort-related needs and energy losses to the outside. Finally, in the case of hospital structures, the number of beds is typically an indicator of technological intensity compared with other structures with the same intended use: in particular, a low number of beds with the same surface area indicates a high level of technological intensity due, for example, to a high incidence of intensive care, resuscitation, or long-term care units.
In this particular case, it is important to note that the procedure has been applied to the hospital facilities although it remains general in its layout and is, therefore, applicable to any category of building. In such case, the right similitude metrics must be identified for each class of building use. For instance, in the case of tertiary buildings, the metrics might relate to hours of being open to the public or the area available per employee, while in the case of university buildings, they might relate to the number of students enrolled in addition to opening hours.
First, a set of buildings is identified according to the end use. Then, for this set of buildings, the characteristics are checked to verify whether they can be considered in similitude with each other. In this regard, the various requirements are analyzed and the quantities influencing their behavior and, consequently, their profiles are determined.
Heating is known to be influenced by volume and degree-days in winter and cooling by surface areas and degree-days in summer. To these two elements, a third element of similitude is added, which gives information about the level of service offered within the facility: for hospital facilities, it is derived from the ratio between the total surface area and number of beds as more advanced facilities offer more space to their residents. The same applies to electricity and steam consumption, which are usually related to the intensity of care provided and the number of hospitalized patients the facility can accommodate. In general, each requirement of the i-th facility is assumed to be a function of a combinations of parameters, as reported in the following equations:
where
HD,
CD,
ED, and
SD are the heating, cooling, electricity, and steam demand, respectively;
V and
S are the volume and heated surface of the structure;
B is the number of beds in the hospital; and
HDD and
CDD are the heating degree-days and cooling degree-days, respectively. Hence, the i-th structure scaled with respect to the j-th structure results in:
where
Thus, the i-th structure can be held in similitude with the j-th structure if
Once this step is completed, the j-th building can be assumed similar to the i-th building. The creation of the raw dataset requires, at this point, that the data of the j-th structure (with unknown consumption) are simply linked to those of the i-th structure (with known consumption).
3.2. Preprocessing
3.2.1. Data Cleaning
Once the initial dataset is established, data cleaning represents a necessary step in any strategy, model, and algorithm for predicting the energy needs of a building for many (if not all) real-world applications where numerous situations and circumstances can affect the continuity and performance of the data collection systems and, consequently, the quality of the data. This happens, for example, when scheduled routine maintenance operations must be performed and it is necessary to power off the interested portion of the system for safety reasons.
Data preprocessing is a crucial step to ensure the quality and usability of the available data for training the machine learning models. The primary objective is to prepare a dataset that enables the model to learn meaningful correlations between input and output variables, while maintaining the ability to generalize and accurately predict unseen events. In order to correctly address the training process toward a robust model, the preprocessing phase must address the following key aspects:
Outlier removal: Anomalous or extreme values can distort the learning process and lead to inaccurate results. Identifying and handling outliers through techniques such as removal or replacement is essential.
Missing value imputation: Datasets may contain missing or incomplete data points, which need to be addressed through appropriate methods such as statistical imputation or learning-based estimation.
Handling extreme values: Excessively high or low values can negatively impact model performance. Techniques such as normalization or clipping can be employed to mitigate the influence of extreme values.
Bias correction: Systematic biases or distortions in the data can skew the model training. Identifying and correcting biases through techniques such as data sampling or weighting is crucial.
Temporal dependency removal: If the data exhibit temporal dependencies or correlations between instances, randomization or shuffling techniques may be necessary to ensure the model learns generalizable patterns.
For all of these reasons, the adopted data cleaning approach can be considered as technical- and engineering-based. It allows for the isolation of outliers based on objective criteria and maintains the ability to monitor the occurrence of any anomalous phenomena. The approach involves data cleaning based on the actual technical constraints of the power plant of the building. This includes identifying the component that imposes the slowest load ramp as all other components need to adapt to it. Additionally, if each component has its own autonomous or interconnected control system, it typically imposes load variations within the limits set by the constructors, preventing too rapid ramp-ups or ramp-downs.
The refinement of the data cleaning algorithm necessitates the study of plant patterns and, consequently, the identification of the ‘weak’ elements in the supply chain for each of the energy vectors being forecasted. Specifically, for each of these, the element with the lowest ascent/descent ramp is identified as it is technically more vulnerable to stress from load variations, and this limit is set as a threshold for identifying potential outliers.
Regarding the choice of limit values, the literature mentions those concerning fire tube boilers, cogeneration engines [
44], absorption chillers [
45,
46], electrically powered refrigeration units and heat pumps [
47], and electrical distribution [
48], as reported in
Table 2. These limits are implemented in the proposed method.
It can be noted that the plants that require the most attention are thermal plants due to the high thermal excursions that can range from at least 50 °C during startup/shutdown to 10 °C during operation, unlike those refrigeration plants that are around 10 °C during startup/shutdown and up to about 5 °C during operation. As for the electrical plants, they typically present very steep ascent or descent rates as the utilities can be powered or depowered simply by turning a switch on and off. In this regard, the slowest utilities are represented by the refrigeration units; thus, the acceptable ascent and descent ramps of the electrical utilities are considered equal to those of the refrigeration units.
It is also worth noting that, typically, the most stressful and critical part for a plant is the startup phase where the imposed stress can be excessive compared with the structural capacities of the plant itself, causing fatigue in the materials or even failures. On the contrary, the shutdown phase is less critical; indeed, it is essentially impossible to impose a descent ramp on the plant as even if everything is turned off, the decrease in its operating temperatures is linked to the dissipation rates (e.g., usually around 2%/hour for plants of the sizes being studied). The only exception is represented by electrical plants, to which the above reasoning applies. In light of these considerations, for all of the energy vectors analyzed, it is decided to impose equal values between the ascent and descent ramp of the plant as acceptable limit thresholds, taking the former as a reference as it is more conservative and technically more binding than the latter.
3.2.2. Data Normalization
Following the data cleaning stage, the acquired dataset undergoes min-max normalization. This is performed to mitigate the potential for variables to exert disproportionate statistical influence due to their large magnitudes or ranges of variation, rather than their actual correlation with the target variables. Then, the final step needed before proceeding with training the machine learning model consists of splitting the dataset into the training set and the test set. For this part, the known building dataset is chosen as the training set, and the unknown building dataset as the test set. This way, the sizes of the training set and the test set are decided, and consequently, so is their ratio.
3.2.3. Data Shuffling
Prior to training the model itself, the dataset undergoes a crucial preprocessing step known as “data shuffling”: this process involves randomly reordering the sequence of data points within the dataset, without mixing the training data with the test data, in order to effectively break any inherent patterns or correlations that may exist due to the original order in which the data were collected or arranged. The rationale behind data shuffling is twofold. First, it mitigates potential biases that could arise from the specific order of the data points, ensuring that the model learns from a diverse and representative sample of the entire dataset. Second, it introduces a degree of independence between consecutive samples, which is a desirable property for many statistical and machine learning algorithms, particularly those employing stochastic optimization techniques. In the context of this study, data shuffling plays a pivotal role in the training process of the proposed models. The dataset is divided into smaller batches for computational efficiency, and shuffling ensures that each batch contains a random and diverse subset of the entire dataset. In such a way, the model becomes more robust and generalizable.
Furthermore, the use of optimization algorithms for hyperparameter tuning necessitates data shuffling. In more detail, by shuffling the data before dividing them into batches, it is ensured that the batches used for training are truly random and independent, preventing the models from being overly influenced by any specific subset of the data. However, shuffling is not universally applied, particularly for time series data or online learning scenarios where temporal dependencies must be preserved. In this specific application, it is not of interest to reproduce specific time series but rather to correlate input variables with output variables as much as possible. Therefore, shuffling proves to be an excellent tool to reduce the interference of negative phenomena on the training of the model and, at the same time, amplify its benefits, thus increasing its performance.
The data shuffling process is performed using the built-in functions provided by the respective machine learning libraries, ensuring a consistent and reproducible approach across all experiments.
3.3. Machine Learning Model and Variables Selection
After the preprocessing phase, the algorithm selects the most significant variables for each model and the target variables, ranking them by importance based on their contribution to maximizing the chosen metric. It employs a progressive scoring system, utilizing only the highly correlated variables or incorporating additional variables if they enhance the metric, and it aims to optimize the model performance while mitigating overfitting issues.
Once the variables are identified, the machine learning model for forecasting is selected and tuned. As mentioned above, a single model alone is not sufficient to handle the intrinsic complexity of the problems faced; therefore, employing an ensemble method is a rational choice. It is decided to discard the random forest algorithm because its ‘greedy’ approach means that it can be misled by trends that are not clearly identifiable or that could be generated in some way by the data shuffling. Therefore, it is decided to employ the extremely randomized trees regressor as it adopts a random tree-splitting criterion and not the one based on error minimization, which could, in some way, penalize the degree of correlation among input and output variables, also known as the coefficient of determination R2.
3.3.1. Hyperparameter Optimizer
In parallel with the selection of the right machine learning model for the considered application, hyperparameters are pivotal elements that govern the training process and the performance of a model. They are fixed features that cannot be learned from the training process itself, but rather, they must be defined prior to training and essentially control the overarching behavior of a machine learning algorithm, influencing its complexity and capacity to learn. The importance of tuning these hyperparameters cannot be underrated, particularly in ensemble methods where multiple base models are combined: in these methods, hyperparameters can control the number of base models, their type, and how they are combined, thereby directly impacting the bias–variance trade-off and overall predictive performance of the model.
The possible sets of hyperparameters are potentially infinite. To deal with this challenge, an automatic approach through a Bayesian optimizer is adopted instead of typical manual approaches or methods based on brute force. This is among the major steps of this article because machine learning algorithms often rely on data science expertise in order to tune the hyperparameters or to choose the believed best optimization algorithm.
The Bayesian optimizer is selected because of its step-wise approach and its features that make it effective in noisy search spaces as it could be in a multi-variable environment for forecasting building energy needs. One of the main advantages of this method, in fact, is its remarkable efficiency and ability to handle search spaces characterized by high noise and a considerable number of dimensions.
In particular, the transfer of the results from one step to another allows for the optimization algorithm to proceed in a so-called informed manner, which avoids wasting time calculating the hyperparameters that are already known to be unpromising upstream. In addition, it allows for effective management of noisy search spaces with a large number of dimensions, while the use of a surrogate model of the objective function significantly reduces the computational time [
49].
3.3.2. Model Training
In addition to hyperparameter optimization, k-fold cross-validation in the model training is implemented. This resampling technique partitions the training set and the test set into a number of equal-sized folds where one test fold is used for validation, and the remaining training folds are used for training. Cross-validation is then repeated with each fold serving as the validation set once: this process mitigates overfitting by providing a more reliable estimate of the model performance on unseen data. By training and evaluating different subsets, potential unusual patterns in the training data are accounted for, ensuring a robust assessment of generalization ability. In these experiments, a number of folds equal to 10 is adopted as it is a common value that balances computational efficiency and reliable performance estimation. The dataset is therefore randomly partitioned into 10 folds, and the models are trained and evaluated 10 times, with each test fold serving as the validation set once. Then, performance metrics are averaged across all folds. The cross-validation procedure is implemented using the scikit-learn library in Python (Version 3.12), ensuring a consistent and reproducible approach.
4. Case Study
In addition, Sant’Anna Hospital (
Figure 3), located near the city of Ferrara in the Emilia-Romagna region of northern Italy, serves as the case study for this work: with approximately 900 beds, the hospital handles over 27,000 hospitalizations annually [
50]. According to the criteria presented in
Section 3, the facility identified as similar is Ca’ Foncello Hospital in Treviso (
Figure 4), with its 862 beds, an annual number of hospitalizations of 37,000, similar categories of energy needs, and a total area of 167,000 square meters [
51].
These structures were selected among the hospital sites for which data are available because they present a similitude based on the criteria explained previously.
Both hospitals require heating, cooling, and electricity, as well as high-temperature energy for steam production, which is utilized for various special utilities such as the sterilization department and laundry. The steam demand is excluded from the current article because no real-time data are available. The annual demands for these energy sources in 2023, normalized with respect to electricity for confidentiality purposes, are presented in
Table 3. Moreover, the table reports the ratio between the energy needs of Ca’ Foncello scaled according to Equations (13)–(16) and Sant’Anna, confirming the similitude of the facilities.
For both hospital facilities, it is chosen to use post-COVID-19 annual data as references. This decision allows for the algorithm performance to be tested in the presence of unforeseen events such as the COVID-19 pandemic, which had a significant impact on energy consumption due to the high number of hospitalizations during that period.
The data are collected hourly for each energy need by the building management system through meters installed in the substations. Higher frequencies are available, but no relevant gains are detected in using them. In addition, it is important to show the applicability of the proposed method in the presence of standard datasets, which are generally hourly.
Both hospitals exhibit a similar distribution of needs, particularly in terms of heating, while cooling and electrical needs appear at first glance to be slightly higher in Ca’ Foncello Hospital. However, it should be noted that both are roughly balanced in their respective structures, indicating an incidence of surfaces (and therefore volumes) with high intensity of care that is equivalent between the two hospitals.
Simulation Setup
In this section, information regarding the setup of the simulations is provided. The first step involves setting the optimal thresholds for data cleaning, with the aim of having sufficiently clean data for the simulations. For the ascent and descent ramps of the needs, the values set in
Table 4 are adopted, based on the plants serving each demand (
Section 3.2).
The latter constraints are set equal to the former to reduce the possibility of outliers as they are more restrictive. The adopted values are the result of analyses conducted with the operational staff and are significantly steeper than what is stated in the literature. This approach is taken to avoid the excessive cleaning of the data, which could eliminate valid data, and to ensure that the algorithm is trained on situations that are not always perfectly linear. Instead, the algorithm is designed to recognize and account for potentially anomalous situations or those representative of the actual management of the plant and its real limits.
Once the final dataset is ready, it is used to complete the hyperparameter tuning phase. The R
2 metric is chosen for the optimization of the hyperparameters of the model, while the results are compared through the adjusted coefficient of determination, referred to as adjusted R
2 (i.e., tuned with the number of variables). The searches are carried out through the solution space shown in
Table 5.
Regarding the choice of the hyperparameter optimization algorithm for machine learning models, some thresholds are chosen in order to correctly address the optimization process. In detail, a minimum and maximum value of adjusted R
2 are considered in order to avoid underfitting and overfitting, respectively, while maximum iterations and execution time are set in order to avoid any kind of inefficient use of computational resources. The exact values considered for each one of them are reported in
Table 6.
Among these, the metrics given the most consideration are the adjusted R2 and the execution time: the former, as is well known, represents the goodness-of-fit index of the model and its related variables to the observed phenomenon, while the latter is useful for evaluating the feasibility of implementation in real-world applications where there are time constraints for updating the models and their respective results.
5. Results
In this section, the results achieved for the different parts of the presented algorithm are reported. First, the data cleaning output, with the pre- and post-cleaning situation, highlights how the data are improved and less affected by outliers. Subsequently, the optimal hyperparameter set, the execution time required to reach the most performing solution, and the value of the optimization metric are presented. Finally, the results of the simulations for each of the energy demands under investigation are reported, with reference to the results of the target structure corresponding to Sant’Anna Hospital.
5.1. Preprocessing
The application of the thresholds indicated in the previous section results in the reduction in the data quantities reported in
Table 7. As can be observed from the reported values, the presence of potentially ‘dirty’ data is a non-negligible factor when dealing with real-world cases. Additionally, the data most affected by this circumstance are precisely those related to heating and cooling demands as the respective equipment, plant components, and distribution systems are subject to the most frequent maintenance operations, compared with, for example, the electrical systems. In particular, the most common issue encountered was the presence of gaps or ‘NaN’ values due to interruptions in the power supply to the meters during the maintenance of the affected plant components. Consequently, since the meters record cumulative values, upon resumption of operation, they generated ‘spikes’ resulting from the difference between the last value transmitted before the interruption of power and the value upon resuming operation.
It is finally worth highlighting that, contrary to conventional data-driven approaches, this method does not present a dataset that has to be divided into a training set and a test set. The former is instead entirely related to the known structure (Ca’ Foncello Hospital in this case study), while the latter is related to the entire dataset of the unknown structure (Sant’Anna Hospital in this case study).
5.2. Optimization
The hyperparameter optimization process yielded the results listed in
Table 8. From a comparison of the hyperparameters, it is observed that the thermal and cooling energy demands require significantly less computational effort compared with the electrical energy demand despite the larger volume of data available for the latter during the training phase.
5.3. Simulations
Once the data are cleaned and the hyperparameters optimized, the next step involves running simulations for each of the energy demand forecasting targets. Among the first results investigated, there is the feature importance, which is the score of each input variable according to its importance in improving model performance and, consequently, its correlation with the output variable. The results are listed in
Table 9, from which it is evident that heating and cooling requirements are mostly influenced by the outside temperature and the month in which this occurs.
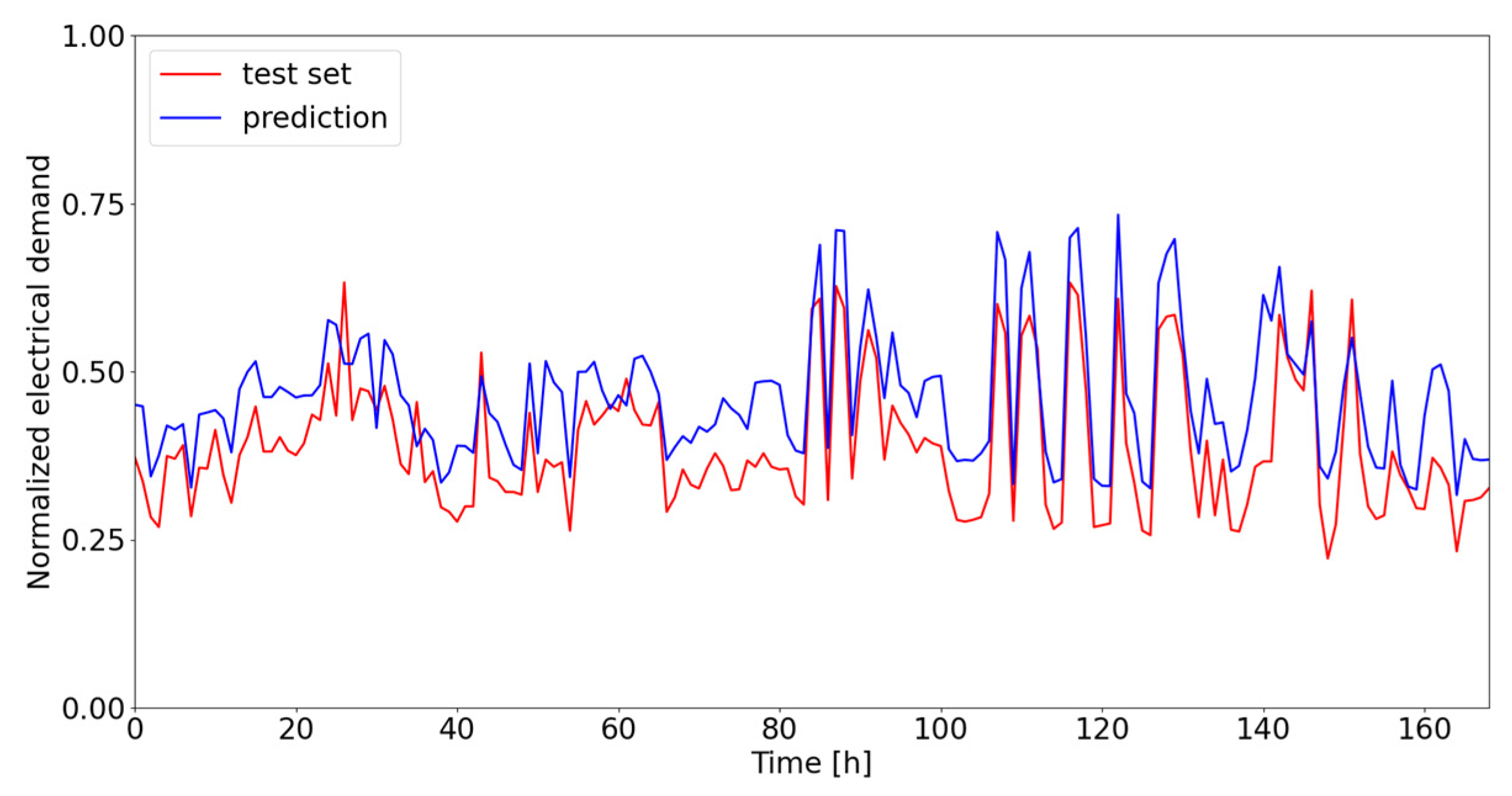
The same applies to electricity requirements, which could also indicate the presence of portable or split system-type equipment. The weights of the other variables are aligned with each other with respect to the three requirements, assuming greater or lesser importance depending on the requirement to be forecasted: for example, relative humidity is between 2 and 3 times more important in forecasting refrigeration and electricity requirements, which could be related to dehumidification and the incidence of latent heat. Similarly, the time at which the energy demand arises is of great importance in the case of electrical energy where the time, day, year, and day of the week are relevant. Conversely, the characteristics of the building, such as its geometric factors, intended use, and the level of service offered (e.g., beds) have a greater influence on the heating and electricity requirements than the refrigeration requirements. Indeed, heating and electricity requirements are more closely linked to the actual use of the structure and its spaces. On the contrary, cooling requirements are usually more related to environments characterized by continuous use and constant temperatures throughout the year, such as surgery blocks and intensive care units.
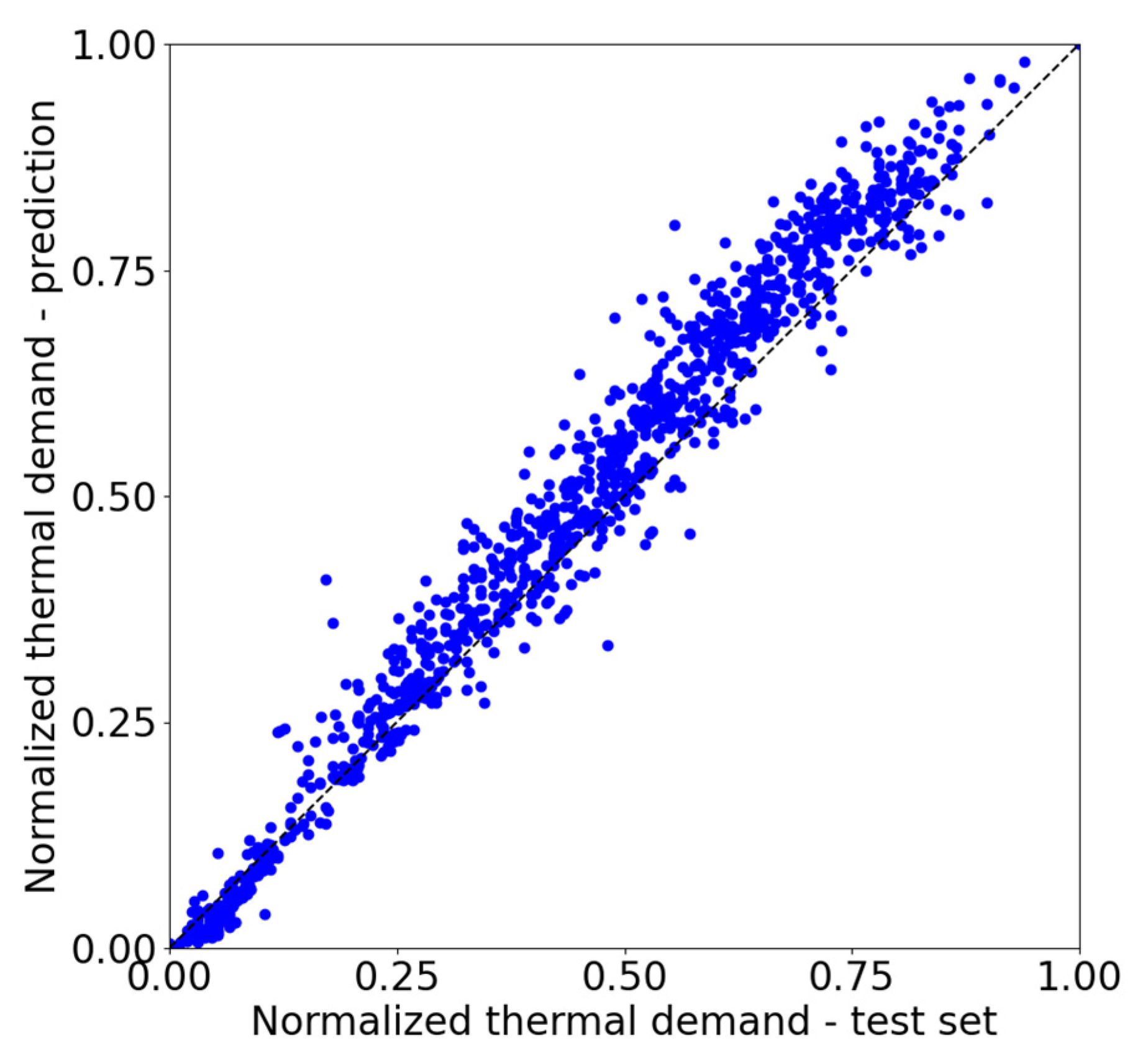
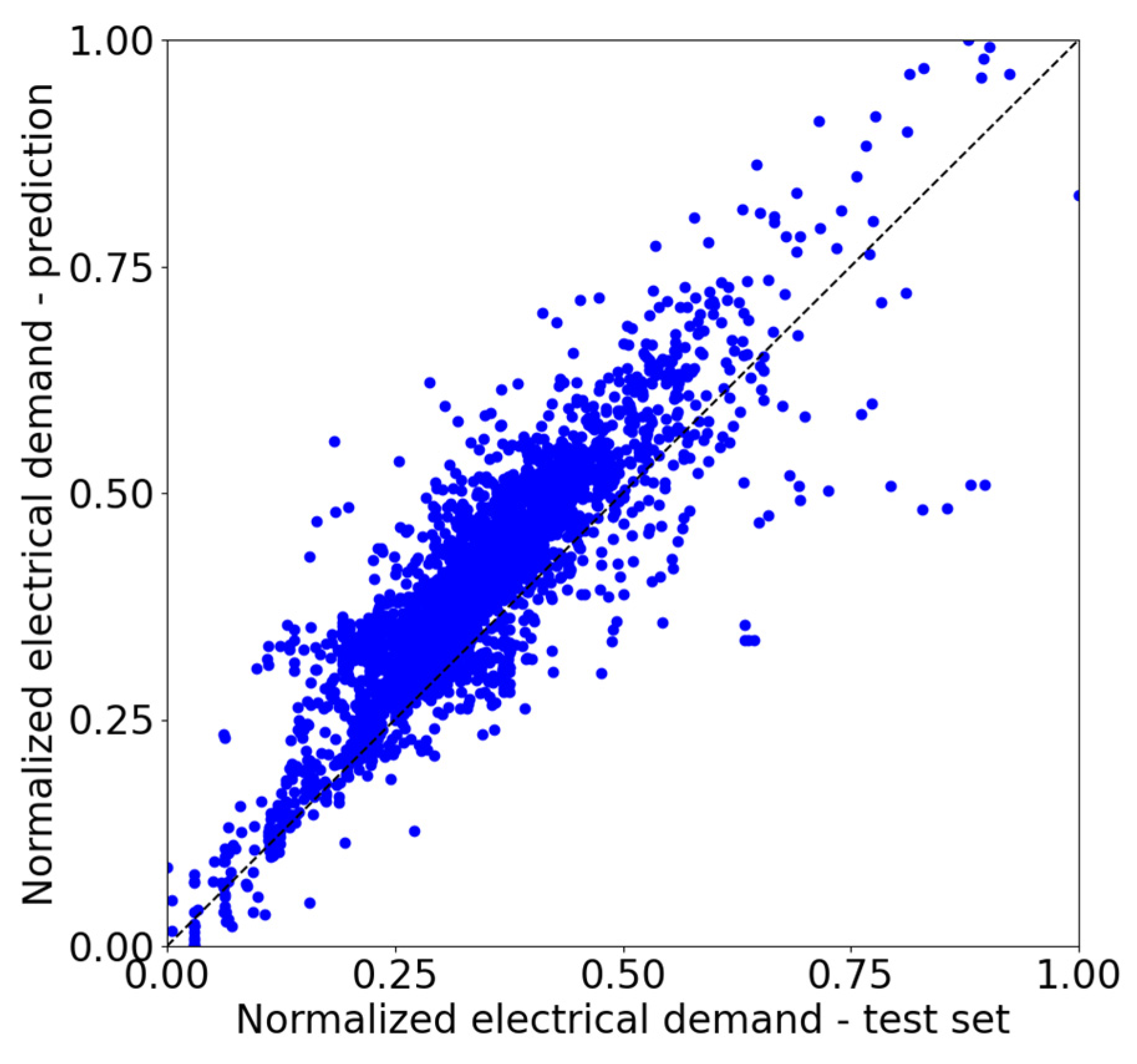
With regard to the prediction accuracy, the main metrics are reported in
Table 10, and the data predicted vs. data test set diagrams are provided in
Figure 5,
Figure 6 and
Figure 7 where the results can be compared.
When comparing results in
Table 8 with those in
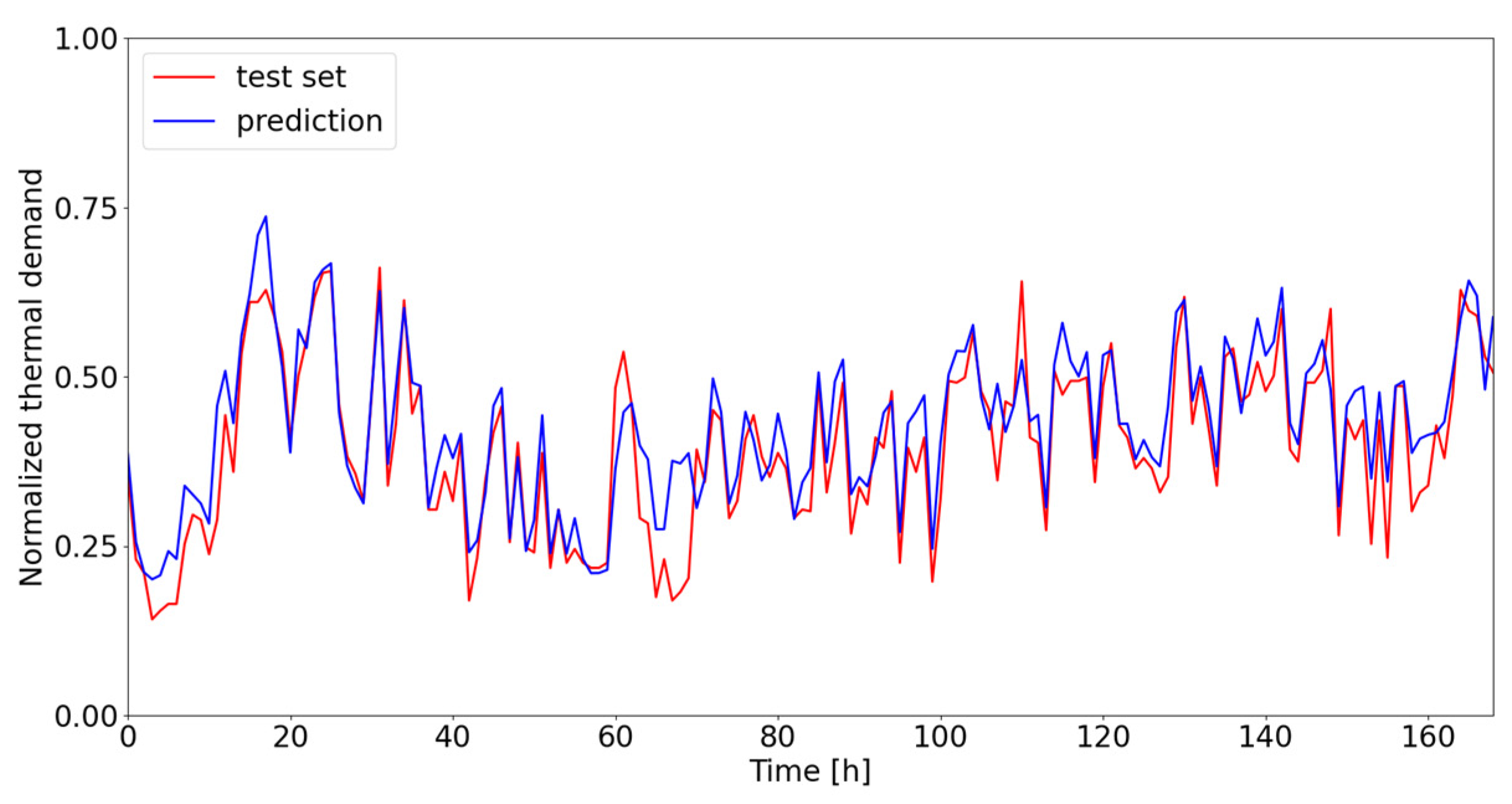
Table 10, it can be observed how electricity forecasting requires more features to reach acceptable thresholds, compared with heating and cooling: this is mainly due to the sudden and unpredictable load variations that can occur, e.g., sudden switching on or off of high-energy consuming utilities (in surgery rooms), as well as the fact that electrical systems are characterized by low inertia, unlike other demand categories. As a matter of fact, heating shows short calculation times and less computational effort when compared wih the other needs. Cooling shows the lowest accuracy and highest execution time.
From
Figure 5,
Figure 6 and
Figure 7, it can be seen how the heating prediction model tends to underestimate the real need when it is low (namely, the start and the end of the heating season and the summer period for domestic hot water), while there is a dispersion in the middle of the period and good prediction accuracy close to the nominal heating load.
The case of cooling is quite similar as the model tends to overestimate the real energy needs close to the nominal load. Residual dispersion is more or less constant in the whole range of loads, slightly increasing at low cooling loads. The electrical need is the least accurate among the three.
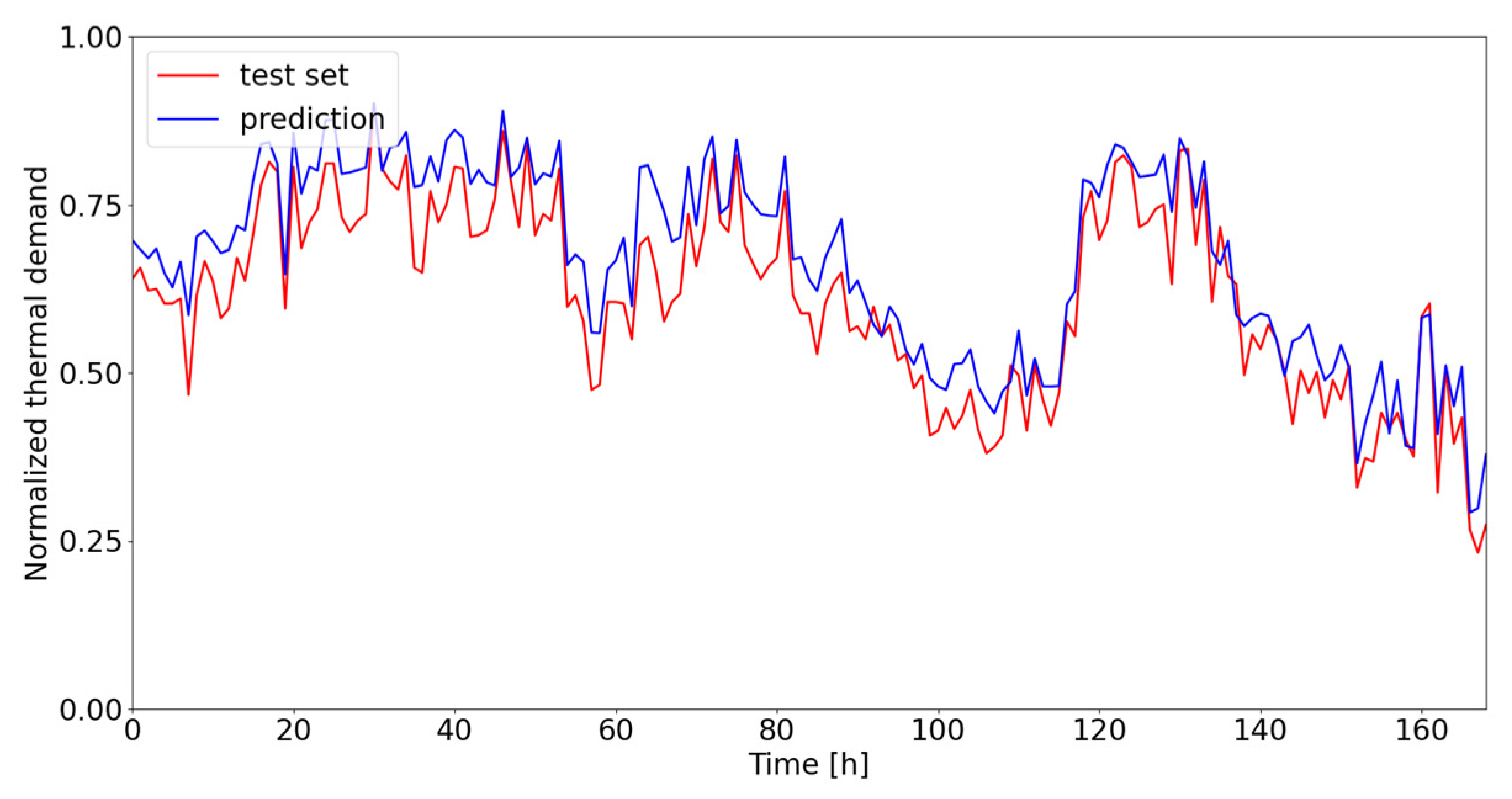
There is a trend in overestimating the real electrical needs in the whole range of loads, with a light improvement close to the nominal loads. However, all these considerations result in a good prediction of load profiles for all three energy needs as can be observed from
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12,
Figure 13,
Figure 14,
Figure 15 and
Figure 16. In more detail, the actual profiles are compared with those predicted by the algorithm for three weeks, each representative of a period of the year: in particular, winter, autumn/spring (as intermediate seasons), and summer are considered.
As can be seen from
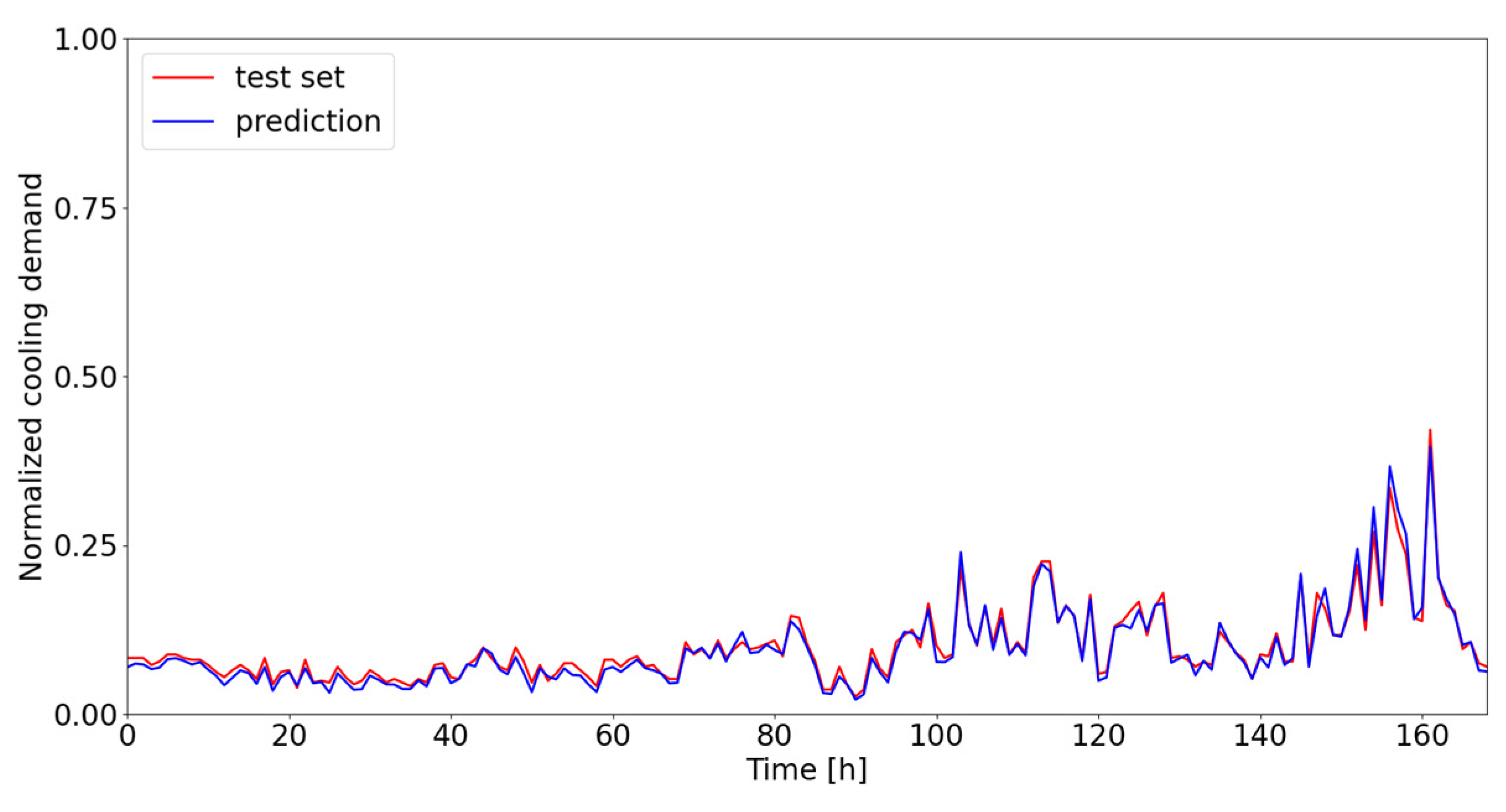
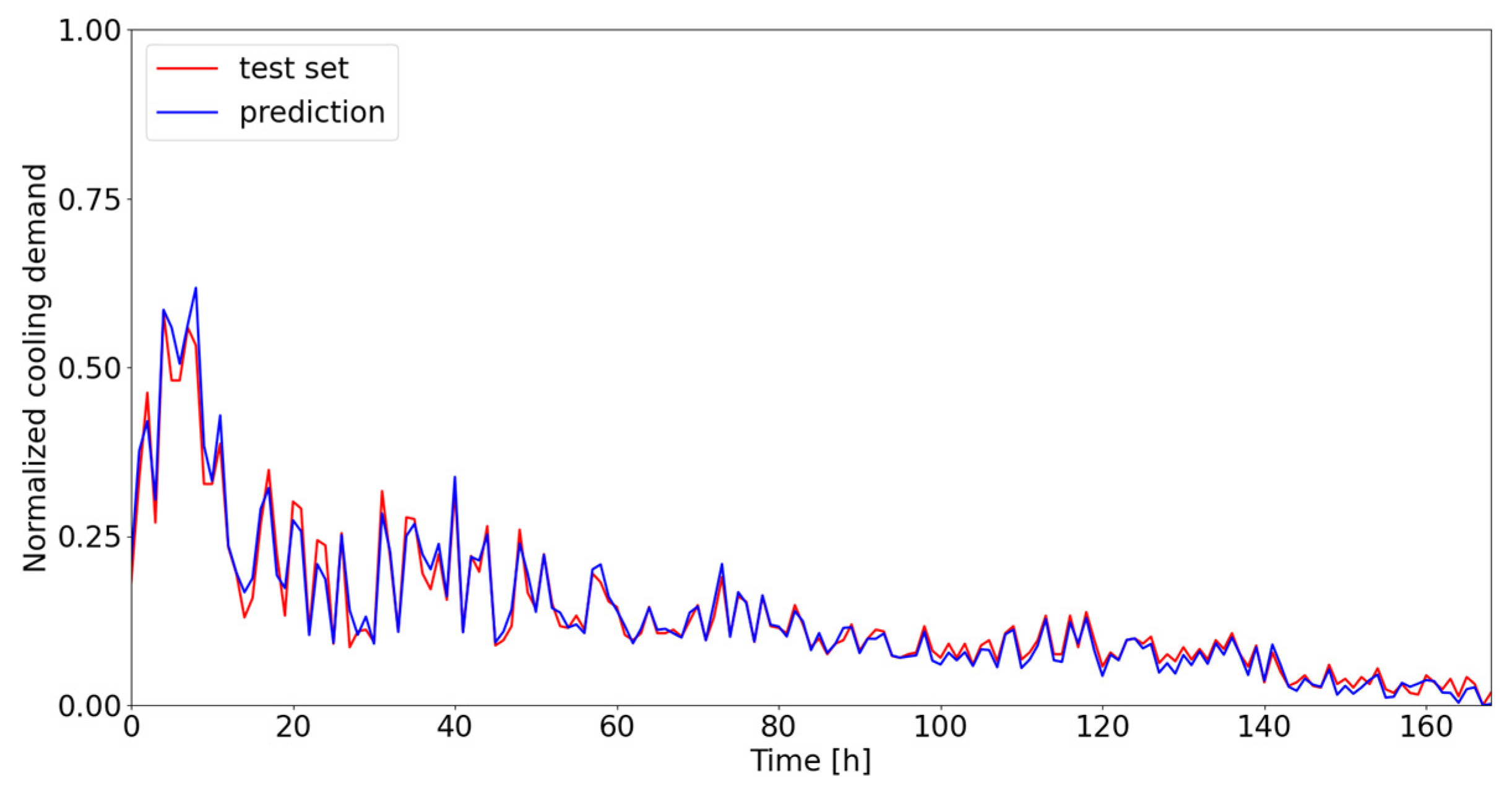
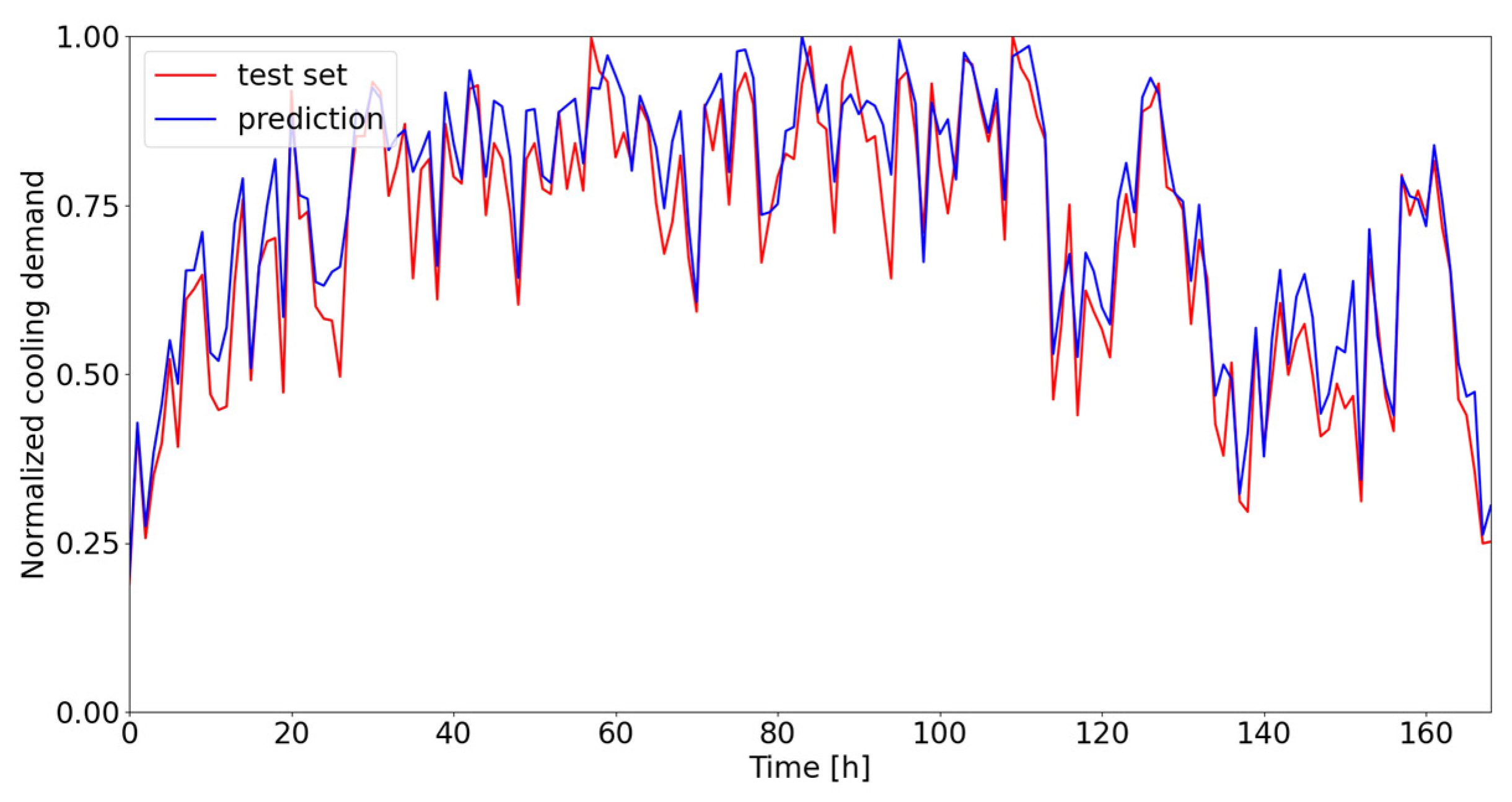
Figure 8, the thermal energy demand profile is reproduced fairly faithfully if one sets aside the tendency to overestimate or underestimate actual values at certain times of the year. This is probably attributable to the data cleaning criteria set in the preprocessing phase. It is interesting to note that the developed models exhibit lower predictive accuracy in the case of descending plant ramps, while the ascending ramps are mostly predicted correctly. The above is probably even more evident when looking at cooling energy requirements. In this case in particular, the profiles are reproduced even better, with no doubt due to the greater regularity of the profiles during the various periods of the year compared with the thermal profiles. Moreover, it can be observed that, at the ‘valleys’, the model tends to overestimate the actual demand, while the ‘peaks’ are reproduced well in almost all cases.
The model for forecasting electricity demand shows good reproduction of the profiles although there is a tendency to underestimate their true value during the summer season. In particular, load variations are also identified, although there are limitations in their actual reproduction, probably due to the criteria for cleaning the data.
6. Conclusions
The article presented a method for predicting the energy needs of a complex system for which they are not known beforehand. In particular, the proposed methodology concentrated on complex buildings characterized by high energy requirements. The study and validation of the method were carried out on two hospital structures, specifically Ca’ Foncello Hospital in Treviso and Sant’Anna Hospital in Ferrara. The method first involved the identification of a building similar to the building under investigation (in this case Ca’ Foncello Hospital was considered similar to Sant’Anna Hospital), of which as much information as possible was available and from which the starting dataset could be obtained. This dataset, once suitably cleaned on the basis of technical plant constraints, allowed for the set of models and the related hyperparameter optimization algorithm to be trained in a timeframe compatible with that of the management of the plants called upon to meet these requirements. For all the energy needs investigated at the two facilities, the performance evaluation metrics were met, with adjusted R2 greater than 0.7, prediction errors less than 10%, and run times less than a minute, all using training set/test set ratios of 3:1 to 12:1.
The findings from this research have significant potential to contribute to advancements in energy efficiency and management practices across the energy sector. By developing an enhanced understanding of the mechanisms that drive energy needs, the key variables influencing these needs, and the processes governing energy usage similarities, this work enables more rapid forecasting of building energy requirements from the outset. This allows for the timely implementation of measures aimed at evaluating and improving overall efficiency, as well as conducting insightful what-if scenario analyses to deepen the understanding of the energy profile of the facility without relying on time-consuming simulations.
The implementation of an automated algorithm capable of replicating the manual steps typically undertaken when investigating building energy needs can effectively streamline this process while reducing errors associated with building selection. The data cleaning process, grounded in technical constraints, proved highly effective in enhancing the robustness of the algorithm by selectively utilizing data deemed realistic, even if it deviates from the median values. This approach further minimizes the amount of data required to accomplish the task successfully, enabling a similitude approach. Moreover, the incorporation of an optimizer, coupled with hyperparameter tuning, data shuffling, and cross-validation techniques, rendered the entire process more resilient to any changes or anomalies that may arise. The implementation of ensemble methods facilitated rapid execution times, even when handling large datasets, while reproducing load profiles with acceptable accuracy.
Collectively, these findings pave the way for more efficient and effective energy management strategies, potentially yielding significant economic and environmental benefits across the energy sector.
Future developments include extending, testing, and validating the methodology for a larger pool of complex systems and buildings, with similar or additional uses as in the case study, as well as identifying improvements to further reduce the amount of data required for training.
Author Contributions
Conceptualization, A.V.; methodology, A.V.; software, A.V.; investigation, A.V.; writing—original draft preparation, A.V. and C.S.; writing—review and editing, A.V., A.G., M.M., and C.S.; visualization, A.V.; supervision, A.G. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
This work was co-authored by a researcher with a research contract co-funded by the European Union—PON Ricerca e Innovazione 2014–2020 (according to Italian legislation: art. 24, comma 3, lett. a), della Legge 30 dicembre 2010, n. 240 e s.m.i. e del D.M. 10 agosto 2021 n. 1062).
Conflicts of Interest
Author Andrea Vieri was employed by the company Siram Veolia. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
| B | Number of beds [-] |
| CD | Cooling demand [kWh] |
| CDD | Cooling degree-days [°C d] |
| ED | Electricity demand [kWh] |
| HD | Heating demand [kWh] |
| HDD | Heating degree-days [°C d] |
| k | Scaling coefficient [-] |
| S | Surface [m2] |
| SD | Steam demand [kWh] |
| V | Volume [m3] |
| Acronyms |
| ANN | Artificial neural network |
| BEM | Building energy model |
| DT | Decision tree |
| LR | Linear regression |
| LSTM | Long short-term memory |
| MAPE | Mean absolute percentage error |
| MLR | Multiple linear regression |
| RMAE | Root mean absolute error |
| RMSE | Root mean square error |
| SRM | Simple regression model |
| SVM | Support vector machine |
| SVR | Support vector regression |
References
- European Commission. The Energy Performance of Buildings Directive; European Commission: Brussels, Belgium, 2019. [Google Scholar]
- Zhao, H.; Magoulès, F. A review on the prediction of building energy consumption. Renew. Sustain. Energy Rev. 2012, 16, 3586–3592. [Google Scholar] [CrossRef]
- Bourdeau, M.; Qiang Zhai, X.; Nefzaoui, E.; Guo, X.; Chatellier, P. Modeling and forecasting building energy consumption: A review of data-driven techniques. Sustain. Cities Soc. 2019, 48, 101533. [Google Scholar] [CrossRef]
- Tardioli, G.; Kerrigan, R.; Oates, M.; James, O.D.; Finn, D. Data driven approaches for prediction of building energy consumption at urban level. Energy Procedia 2015, 78, 3378–3383. [Google Scholar] [CrossRef]
- Ballarini, I.; Corgnati, S.P.; Corrado, V.; Talà, N. Improving energy modeling of large building stock through the development of archetype buildings. In Proceedings of the 12th Conference of the International Building Performance Simulation Association (IBPSA), Sydney, Australia, 14–16 November 2011; pp. 14–16. [Google Scholar]
- Ballarini, I.; Corgnati, S.P.; Corrado, V. Use of reference buildings to assess the energy saving potentials of the residential building stock: The experience of TABULA project. Energy Policy 2014, 68, 273–284. [Google Scholar] [CrossRef]
- Ahmad, A.S.; Hassan, M.Y.; Abdullah, M.P.; Rahman, H.A.; Hussin, F.; Abdullah, H.; Saidur, R. A review on applications of ANN and SVM for building electrical energy. Renew. Sustain. Energy Rev. 2014, 33, 102–109. [Google Scholar] [CrossRef]
- Dong, B.; Cao, C.; Lee, S.E. Applying support vector machines to predict building energy consumption in tropical region. Energy Build. 2005, 37, 545–553. [Google Scholar] [CrossRef]
- Swan, L.G.; Ugursal, V.I. Modeling of end-use energy consumption in the residential sector: A review of modeling techniques. Renew. Sustain. Energy Rev. 2009, 13, 1819–1835. [Google Scholar] [CrossRef]
- Shen, P.; Wang, H. Archetype building energy modeling approaches and applications: A review. Renew. Sustain. Energy Rev. 2024, 199, 114478. [Google Scholar] [CrossRef]
- Siddharth, V.; Ramakrishna, P.V.; Geetha, T.; Sivasubramaniam, A. Automatic generation of energy conservation measures in buildings using genetic algorithms. Energy Build. 2011, 43, 2718–2726. [Google Scholar] [CrossRef]
- Kim, E.J.; Plessis, G.; Hubert, J.L.; Roux, J.J. Urban energy simulation: Simplification and reduction of building envelope models. Energy Build. 2014, 84, 193–202. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, X.; Shi, Y.; Xia, L.; Pan, S.; Wu, J.; Han, M.; Zhao, X. A review of data-driven approaches for prediction and classification of building energy consumption. Renew. Sustain. Energy Rev. 2018, 82, 1027–1047. [Google Scholar] [CrossRef]
- Amber, K.P.; Aslam, M.W.; Mahmood, A.; Kousar, A.; Younis, M.Y.; Akbar, B.; Qadar Chaudhary, G.; Hussain, S.K. Energy consumption forecasting for university sector buildings. Energies 2017, 10, 1579. [Google Scholar] [CrossRef]
- Pulido-Arcas, J.A.; Pérez-Fargallo, A.; Rubio-Bellido, C. Multivariable regression analysis to assess energy consumption and CO2 emissions in the early stages of offices design in Chile. Energy Build. 2016, 133, 738–756. [Google Scholar] [CrossRef]
- Li, Z.; Huang, G. Re-evaluation of building cooling load prediction models for use in humid subtropical area. Energy Build. 2013, 62, 442–449. [Google Scholar] [CrossRef]
- Mejri, O.; Barrio, E.P.D.; Ghrab-Morcos, N. Energy performance assessment of occupied buildings using model identification techniques. Energy Build. 2011, 43, 285–299. [Google Scholar] [CrossRef]
- Wauman, B.; Breesch, H.; Saelens, D. Evaluation of the accuracy of the implementation of dynamic effects in the quasi steady-state calculation method for school buildings. Energy Build. 2013, 65, 173–184. [Google Scholar] [CrossRef]
- Yu, Z.; Haghighat, F.; Fung, B.C.; Yoshino, H. A decision tree method for building energy demand modeling. Energy Build. 2010, 10, 1637–1646. [Google Scholar] [CrossRef]
- Tsanas, A.; Xifara, A. Accurate quantitative estimation of energy performance of residential buildings using statistical machine learning tools. Energy Build. 2012, 49, 560–567. [Google Scholar] [CrossRef]
- Tso, G.K.; Yau, K.K. Predicting electricity energy consumption: A comparison of regression analysis, decision tree and neural networks. Energy 2007, 32, 1761–1768. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; McClelland, J.L. Parallel Distributed Processing: Explorations in the Microstructure of Cognition; Foundations; MIT Press: Cambridge, MA, USA, 1986; Volume 1. [Google Scholar]
- Shoham, R.; Permuter, H. Amended Cross-Entropy Cost: An Approach for Encouraging Diversity in Classification Enemble (Brief Announcement). Lect. Notes Comput. Sci. 2019, 11527, 202–207. [Google Scholar]
- Ahmad, M.W.; Mourshed, M.; Rezgui, Y. Trees vs Neurons: Comparison between random forest and ANN for high-resolution prediction of building energy consumption. Energy Build. 2017, 147, 77–89. [Google Scholar] [CrossRef]
- Marino, D.L.; Amarasinghe, K.; Manic, M. Building energy load forecasting using deep neural networks. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 24–27 October 2016; IEEE: New York, NY, USA, 2016; pp. 7046–7051. [Google Scholar]
- Fan, C.; Wang, J.; Gang, W.; Li, S. Assessment of deep recurrent neural network-based strategies for short-term building energy predictions. Appl. Energy 2019, 236, 700–710. [Google Scholar] [CrossRef]
- Wang, Y.; Zhan, C.; Li, G.; Zhang, D.; Han, X. Physics-guided LSTM model for heat load prediction of buildings. Energy Build. 2023, 294, 113169. [Google Scholar] [CrossRef]
- Somu, N.; MR, G.R.; Ramamritham, K. A deep learning framework for building energy consumption forecast. Renew. Sustain. Energy Rev. 2021, 137, 110591. [Google Scholar] [CrossRef]
- Chen, X.; Yang, H. Integrated energy performance optimization of a passively designed high-rise residential building in different climatic zones of China. Appl. Energy 2018, 215, 145–158. [Google Scholar] [CrossRef]
- Li, B.; Wang, Q.; Hu, J. A fast SVM training method for very large datasets. In Proceedings of the 2009 International Joint Conference on Neural Networks, Atlanta, GA, USA, 14–19 June 2009; pp. 1784–1789. [Google Scholar]
- Paudel, S.; Elmitri, M.; Couturier, S.; Nguyen, P.H.; Kamphuis, R.; Lacarrière, B.; Le Corre, O. A relevant data selection method for energy consumption prediction of low energy building based on support vector machine. Energy Build. 2019, 138, 240–256. [Google Scholar] [CrossRef]
- Massana, J.; Pous, C.; Burgas, L.; Melendez, J.; Colomer, J. Short-term load forecasting in a non-residential building contrasting models and attributes. Energy Build. 2015, 92, 322–330. [Google Scholar] [CrossRef]
- Fu, Y.; Li, Z.; Zhang, H.; Xu, P. Using support vector machine to predict next day electricity load of public buildings with sub-metering devices. Procedia Eng. 2015, 121, 1016–1022. [Google Scholar] [CrossRef]
- Castelli, M.; Trujillo, L.; Vanneschi, L.; Popovič, A. Prediction of energy performance of residential buildings: A genetic programming approach. Energy Build. 2015, 102, 67–74. [Google Scholar] [CrossRef]
- Zhang, F.; Deb, C.; Lee, S.E.; Yang, J.; Shah, K.W. Time series forecasting for building energy consumption using weighted Support Vector Regression with differential evolution optimization technique. Energy Build. 2016, 126, 94–103. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms; The MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95 International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Polikar, R. Ensemble Based Systems in Decision Making. IEEE Circuits Syst. Mag. 2006, 6, 21–45. [Google Scholar] [CrossRef]
- Rocca, J. Ensemble Methods: Bagging, Boosting and Stacking. Understanding the Key Concepts of Ensemble Learning. Towards Data Science. 23 April 2019. Available online: https://towardsdatascience.com/ensemble-methods-bagging-boosting-and-stacking-c9214a10a205 (accessed on 25 September 2024).
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Papadopoulos, S.; Azar, E.; Woon, W.L.; Kontokosta, C.E. Evaluation of tree-based ensemble learning algorithms for building energy energy performance estimation. J. Build. Perform. Simul. 2017, 11, 1–11. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Zeng, R.; Srinivasan, R.S.; Ahrentzen, S. Random Forest based Hourly Building Energy Prediction. Energy Build. 2018, 171, 11–25. [Google Scholar] [CrossRef]
- Salman, C.A.; Li, H.; Li, P.; Yan, J. Improve the flexibility provided by combined heat and power plants (CHPs)—A review of potential technologies. E-Prime-Adv. Electr. Eng. Electron. Energy 2021, 1, 100023. [Google Scholar] [CrossRef]
- Abushamah, H.A.S.; Burian, O.; Škoda, R. Design and Operation Optimization of a Nuclear Heat-Driven District Cooling System. Int. J. Energy Res. 2023, 1, 7880842. [Google Scholar] [CrossRef]
- York. YHAU-CL/CH Single Effect Hot Water Absorption Chiller (Mod A) 30 ton to 2000 ton, 105 kW to 7034 kW; York: York, UK, 2023; Available online: https://docs.johnsoncontrols.com/chillers/api/khub/documents/v0s5_zvbFvXiMABui_Vp9w/content (accessed on 25 September 2024).
- Hovenga, N. Dynamic Characteristics of Industrial Heat Pump Operation—A Modeling Study. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 9 July 2021. [Google Scholar]
- Tadie, A.T.; Guo, Z.; Xu, Y. Hybrid model-based BESS sizing and control for wind energy ramp rate control. Energies 2022, 15, 9244. [Google Scholar] [CrossRef]
- Bergstra, J.; Yamins, D.; Cox, D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; Volume 28, pp. 115–123. [Google Scholar]
- Gambarotta, A.; Malabarba, R.; Morini, M.; Randazzo, G.; Rossi, M.; Saletti, C.; Vieri, A. Demonstrating a smart controller in a hospital integrated energy system. Smart Energy 2023, 12, 100120. [Google Scholar] [CrossRef]
- Azienda ULSS n.2 Marca Trevigiana. Deliberazione del Direttore Generale n.1348 del 28/06/2024. Available online: https://www.aulss2.veneto.it/mys/apridoc/iddoc/7561 (accessed on 25 September 2024).
Figure 1.
Main data-driven models according to the literature.
Figure 1.
Main data-driven models according to the literature.
Figure 2.
Block diagram of the proposed algorithm.
Figure 2.
Block diagram of the proposed algorithm.
Figure 3.
Sant’Anna Hospital in Ferrara.
Figure 3.
Sant’Anna Hospital in Ferrara.
Figure 4.
Ca’ Foncello Hospital in Treviso.
Figure 4.
Ca’ Foncello Hospital in Treviso.
Figure 5.
Predicted vs. test set results for thermal needs.
Figure 5.
Predicted vs. test set results for thermal needs.
Figure 6.
Predicted vs. test set results for cooling needs.
Figure 6.
Predicted vs. test set results for cooling needs.
Figure 7.
Predicted vs. test set results for electrical needs.
Figure 7.
Predicted vs. test set results for electrical needs.
Figure 8.
Thermal energy needs predicted (blue) vs. real (red)—winter week.
Figure 8.
Thermal energy needs predicted (blue) vs. real (red)—winter week.
Figure 9.
Thermal energy needs predicted (blue) vs. real (red)—intermediate season week.
Figure 9.
Thermal energy needs predicted (blue) vs. real (red)—intermediate season week.
Figure 10.
Thermal energy needs predicted (blue) vs. real (red)—summer week.
Figure 10.
Thermal energy needs predicted (blue) vs. real (red)—summer week.
Figure 11.
Cooling energy needs predicted (blue) vs. real (red)—winter week.
Figure 11.
Cooling energy needs predicted (blue) vs. real (red)—winter week.
Figure 12.
Cooling energy needs predicted (blue) vs. real (red)—intermediate season week.
Figure 12.
Cooling energy needs predicted (blue) vs. real (red)—intermediate season week.
Figure 13.
Cooling energy needs predicted (blue) vs. real (red)—summer week.
Figure 13.
Cooling energy needs predicted (blue) vs. real (red)—summer week.
Figure 14.
Electrical energy needs predicted (blue) vs. real (red)—winter week.
Figure 14.
Electrical energy needs predicted (blue) vs. real (red)—winter week.
Figure 15.
Electrical energy needs predicted (blue) vs. real (red)—intermediate season week.
Figure 15.
Electrical energy needs predicted (blue) vs. real (red)—intermediate season week.
Figure 16.
Electrical energy needs predicted (blue) vs. real (red)—summer week.
Figure 16.
Electrical energy needs predicted (blue) vs. real (red)—summer week.
Table 1.
Data-driven approaches for forecasting building energy demand.
Table 1.
Data-driven approaches for forecasting building energy demand.
| Method | Advantages | Disadvantages | Reference | Use Case |
|---|
| LR | Easy and fast | Potentially inaccurate in short-term forecasting | [14] | University buildings, electricity demand |
| [15] | Office, heating and cooling demand |
| [16] | Office, cooling demand |
| [17] | Office, heating and electricity demand |
| [18] | School, heating and cooling demand |
| DT | Flexible and interpretable | Instable with noise and outliers, not good for nonlinear data | [19] | Residential households, heating, cooling, electricity demand |
| [20] | Residential buildings, heating and cooling demand |
| [21] | Residential buildings, electricity demand |
| ANN | Highly flexible and adaptable | Case-dependent, subject to overfitting | [24] | Tertiary buildings, electricity demand |
| [25] | Residential buildings, electricity demand |
| [26] | Educational buildings, cooling demand |
| SVM | Able to manage large and complex datasets, effective with high dimensional features, robust | Complex to set up, computationally expensive, sensitive to hyperparameters | [31] | Residential buildings, heating and cooling demand |
| [32] | University office building, electric demand |
| [33] | Office building, electrical demand |
| Improved models | Highly accurate, increased automation, able to handle complex tasks | Requires high computational resources and high quantity of data to train a model, complex | [34] | Residential buildings, heating and cooling demand |
| [35] | Office and campus, electricity demand |
| Ensemble models | Robust, versatile, easy to implement | Hard to interpret, computationally expensive, complex | [42] | Residential buildings, heating and cooling demand |
| [43] | Institutional buildings, electricity demand |
Table 2.
Ramp limits of different types of power plant.
Table 2.
Ramp limits of different types of power plant.
| | Gas Boiler [44] | CHPs [44] | Electrical Chillers/Heat Pumps [47] |
|---|
| Power capacity (MW) | Up to 300 MW | 0.01–20 | 0.08–6.00 |
| Operation range (%) | 16–100 | 30–100 | 50–100 |
| Ramp rate (%power/min) | 4–6 | 20–50 | 10–20 |
| | Absorption Chiller [45,46] | Electric Grid [48] |
| Power capacity (MW) | 0.1–7.0 | --- |
| Operation range (%) | 20–100 | --- |
| Ramp rate (%power/min) | 10–20 | 1–10 |
Table 3.
Normalized annual energy demands of the hospitals for 2023.
Table 3.
Normalized annual energy demands of the hospitals for 2023.
| | Heat | Cold | Electricity | Steam |
|---|
| Sant’Anna Hospital | 0.761 | 0.226 | 1 | 0.176 |
| Ca’ Foncello Hospital | 0.863 | 0.873 | 1 | 0.353 |
| Scaled Ca’ Foncello/Sant’Anna | 0.966 | 1.01 | 1 | 0.999 |
Table 4.
Data cleaning preprocessing thresholds.
Table 4.
Data cleaning preprocessing thresholds.
| | Heat | Cold | Electricity |
|---|
| Ramp-up threshold (%/min) | 8.5 | 8.5 | 8.5 |
| Ramp-down threshold (%/min) | 2 | 2 | 2 |
Table 5.
Extra trees hyperparameter search space.
Table 5.
Extra trees hyperparameter search space.
| Hyperparameter | Range |
|---|
| Estimators | 10–1000 |
| Maximum depth | 1–110 |
| Minimum sample split | 2–10 |
| Minimum sample leaf | 1–4 |
| Maximum features | 0.1–0.99 |
Table 6.
Metrics thresholds.
Table 6.
Metrics thresholds.
| Metric | Threshold |
|---|
| Adjusted R2 minimum | 0.7 |
| Adjusted R2 maximum | 0.95 |
| Maximum iterations | 100 |
| Time of execution [s] | 900 |
Table 7.
Number of timestamps before and after the preprocessing phase.
Table 7.
Number of timestamps before and after the preprocessing phase.
| | | Heat | Cold | Electricity |
|---|
| Raw dataset | Training set | 23,064 | 23,064 | 23,064 |
| Test set | 8760 | 8760 | 8760 |
| Preprocessed dataset | Training set | 7319 | 10,407 | 16,590 |
| Test set | 1219 | 867 | 5529 |
| Training/Test data ratio | | 6:1 | 12:1 | 3:1 |
Table 8.
Results of the hyperparameter optimization.
Table 8.
Results of the hyperparameter optimization.
| Model | Estimators | Maximum Depth | Minimum Sample Split | Minimum Sample Leaf | Maximum Features |
|---|
| Heat | 600 | 30 | 9 | 3 | 0.4 |
| Cold | 639 | 38 | 2 | 1 | 0.38 |
| Electricity | 613 | 31 | 9 | 2 | 0.7 |
Table 9.
Feature importance.
Table 9.
Feature importance.
| Feature | Score |
|---|
| | Heat | Cold | Electrical |
|---|
| External temperature | 0.58221 | 0.71237 | 0.13436 |
| Month | 0.16216 | 0.14422 | 0.19411 |
| Relative humidity | 0.0186 | 0.03491 | 0.04598 |
| Hour | 0.02218 | 0.02659 | 0.05992 |
| Day | 0.01768 | 0.01432 | 0.11383 |
| Year | 0.04018 | 0.05717 | 0.25475 |
| Weekday | 0.00797 | 0.00654 | 0.06408 |
| Volume | 0.05041 | 0.00138 | 0.04059 |
| Surface | 0.05419 | 0.00116 | 0.05254 |
| Number of beds | 0.04441 | 0.00133 | 0.03984 |
Table 10.
Metrics results.
Table 10.
Metrics results.
Energy
Need | RMAE | RMSE | MAPE
[%] | Adjusted R2 | Execution Time [s] |
|---|
| Heat | 0.1781 | 0.2291 | 9.39 | 0.9422 | 1.253 |
| Cold | 0.1049 | 0.1893 | 9.68 | 0.9421 | 56.89 |
| Electrical | 0.2931 | 0.4700 | 9.05 | 0.7487 | 35.72 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).