Two-Layer Optimal Scheduling and Economic Analysis of Composite Energy Storage with Thermal Power Deep Regulation Considering Uncertainty of Source and Load

Abstract

A two-layer scheduling method of energy storage that considers the uncertainty of both source and load is proposed to coordinate thermal power with composite energy storage to participate in the peak regulation of power systems. Firstly, considering the characteristics of thermal power deep peak regulation, a cost model of thermal power deep peak regulation is constructed and fuzzy parameters are used to manage the uncertainty of wind, photovoltaics, and load. Secondly, based on the peaking characteristics and operating costs of composite energy storage, a two-layer optimal scheduling model of energy storage is constructed. The upper layer takes pumped storage as the optimization goal to improve net load fluctuation and the optimal peak load benefit; the lower layer takes the system’s total peak load cost as the optimization goal and obtains a day-before scheduling plan for the energy storage system, using an improved gray wolf algorithm to process it. Finally, we verify the effectiveness of the proposed strategy based on an IEEE 39-node system.

1. Introduction

In order to achieve the strategic goal of “carbon peak and carbon neutrality”, new energy generation, mainly wind power and photovoltaics, has grown rapidly [1,2]. The increase of new energy capacity makes peak regulation more difficult. How to satisfy the increasing demand for peak regulation has become an important issue that needs to be solved urgently. At present, China’s power system is still predominantly reliant on thermal power, and the thermal power units with a large capacity usually have the ability to perform deep peak regulation. However, frequent deep peak regulation in thermal power units increases their operation cost and impacts the economy [3]. Therefore, it is necessary to adopt other power sources for peak regulation.

Energy storage is one of the most important power sources for peak regulation due to its characteristic of energy shifting [4]. Among storage methods, pumped storage is the most mature energy storage technology. It is widely used in power grid peak regulation and frequency modulation [5,6,7]. In the research field of pumped storage participating in peak regulation, reference [8] proposes a two-layer optimization scheduling strategy and compares the peak regulation effect and economics of three different pumped storage scheduling strategies, obtaining an optimal pumped storage scheduling scheme. Reference [9] designs a variable time period control method for a system containing a pumped storage power station; that is, it reduces the scheduling step size when the load changes dramatically and increases the scheduling step size when the load changes gently. It is verified that this strategy can improve the scheduling accuracy of thermal power units. Reference [10] establishes a coordinated operation model of wind power and pumped storage based on the operation characteristics of pumped storage power stations. It takes the minimum wind abandonment volume of the system as the optimization goal to optimize the coordinated operation of the wind power and pumped storage. To verify the effect of pumped storage on reducing wind curtailment, reference [11] studies the multi-objective, safety-constrained, dynamic optimal scheduling problem of a power system with multiple wind farms and pumped storage power stations. It solves the multi-objective problem in the system containing wind power and pumped storage and gives the optimal scheduling scheme. Although pumped storage can effectively relieve the peak regulation pressure of the system, the development of pumped storage is still limited due to the limitations of natural resources such as site selection.

As an energy storage technology secondary to pumped storage, battery storage has developed rapidly in recent years [12,13,14,15,16]. In the research field of battery storage participation in peak regulation, reference [17] proposes a three-layer scheduling scheme of battery energy storage combined with thermal power peak regulation. The objective function considers the cost of the thermal power unit’s deep peak regulation. The simulation results show that the participation of battery storage improved the economics of the system. Reference [18] considers the optimal energy abandonment rate, proposing a two-layer optimal scheduling model of a combined system containing wind power, photovoltaics, energy storage, and thermal power, exploring the influence of reasonable abandonment on the difficulty and economics of power grid peak regulation. Reference [19] describes the uncertainty of the output of wind power and photovoltaics, establishing a multi-objective optimal scheduling model for the landscape storage system, and solves it by using a hybrid intelligent algorithm; it can solve high-dimensional uncertain programming problems well, its convergence speed is fast, and its global and local searching ability is outstanding. Reference [20] improves the cost and efficiency model of battery storage and analyzes the changes of various costs and benefits of the system after the participation of battery storage. It can scientifically reflect the actual cost and real value of energy storage participating in frequency modulation and peak regulation and also provide a reference for the formulation of an auxiliary service market mechanism.

All the above research focuses on the analysis of a single type of energy storage assisting thermal power in peak regulation. In the research field of hybrid energy storage participating in peak regulation, reference [21] proposes a coordinated optimization operation model of composite energy storage to make full use of the advantages of different forms of energy storage in terms of capacity and output response speed to improve the output characteristics of wind power. Reference [22] uses a ladder-type carbon trading mechanism, building an optimal scheduling model based on carbon trading, including battery energy and pumped storage to improve the utilization rate of the photovoltaic power generation in the system so as to realize the low-carbon economic scheduling of the system. Reference [23] analyzes the output characteristics of two kinds of energy storage power stations and their interaction with the multi-time scale characteristics of demand response resources to realize the formulation of a day-ahead scheduling plan and restrains the uncertainty of new energy prediction and load prediction to a certain extent through intra-day rolling and real-time correction.

The above studies analyze the issue on different time scales. Although the accuracy of energy storage scheduling has been improved to a certain extent, the flexibility of energy storage is not fully utilized. Meanwhile, the above research lacks consideration of the coordination between different types of energy storage and the impact of thermal power deep peak regulation on power systems’ economics.

Based on the above analysis, this paper takes a composite energy storage system composed of battery storage and pumped storage as an example, considering the deep peak regulation cost of thermal power units, the investment cost and operating cost of composite energy storage, and also considers the uncertainty of wind power, photovoltaics, and load, building a double-layer optimization scheduling model for thermal power and composite energy storage’s participation in peak regulation with fuzzy opportunity constraints. The optimal objective of the upper-layer scheduling is to smooth the net load fluctuation of pumped storage to the minimum and to obtain the best benefit of pumped storage. The optimal objective of the lower-layer scheduling is to minimize the total peak regulation cost and optimize the output of the thermal power units and composite energy storage in each period. Based on the typical daily data, the influence of thermal power deep peak regulation and composite energy storage on peak regulation, and their economic benefit, are discussed. This provides an important reference for the development and planning of peak regulation resources in the power grid.

2. Thermal Power Deep Peak Regulation Process and Cost Model

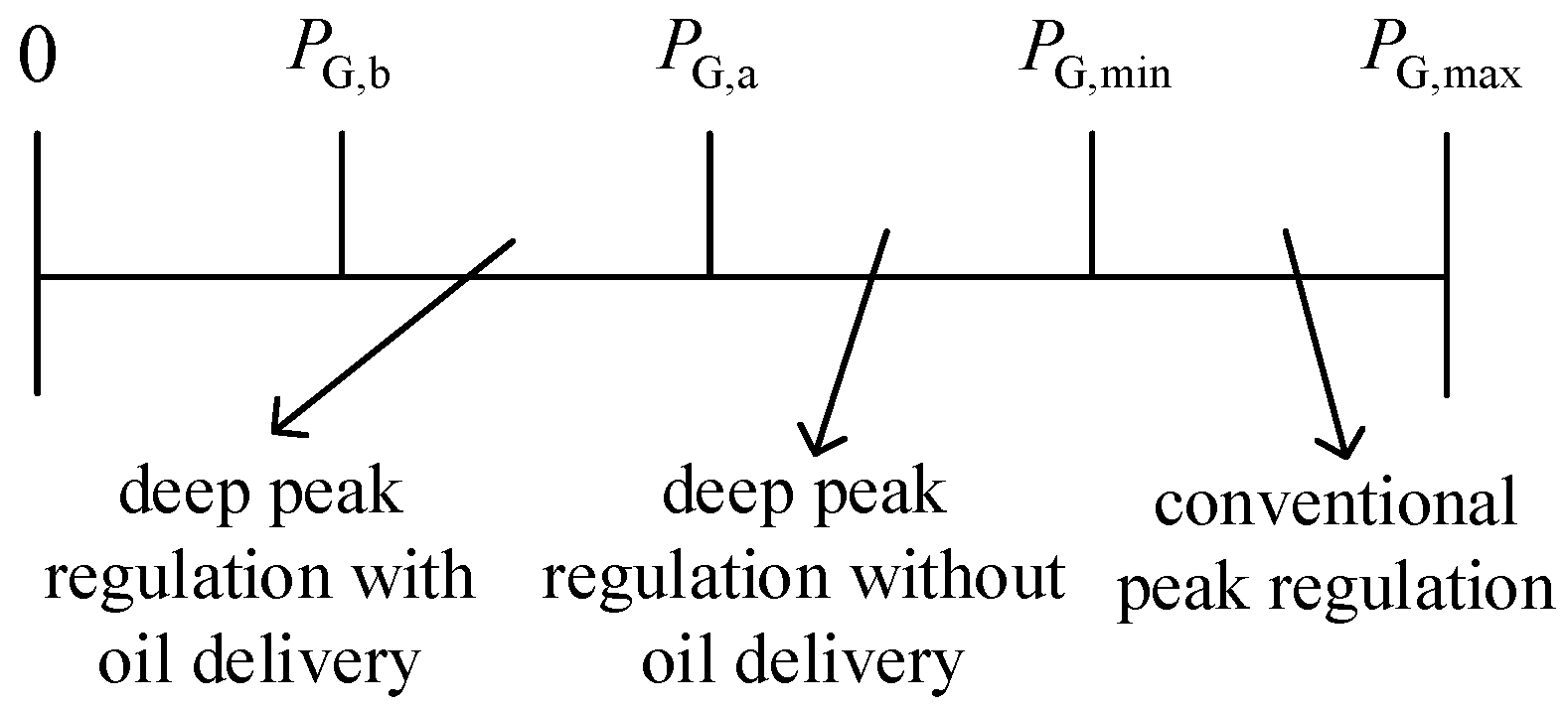
According to the characteristics and combustion medium status of thermal power, the operation process is usually divided into three stages: conventional peak regulation, deep peak regulation without oil delivery, and deep peak regulation with oil delivery, as seen in Figure 1.

In the figure, P_G,max is the maximum output of the thermal power; P_G,min is the lowest output of the thermal power in the conventional peaking stage; P_G,a is the lowest output of the thermal power in the deep peak regulation stage without oil delivery; and P_G,b is the lowest output of the thermal power in the deep peak regulation stage with oil delivery.

There are many factors affecting the peak regulation cost of thermal power, but it mainly includes three aspects: coal consumption cost, unit loss cost, and deep regulation cost with oil delivery [8].

(1)

Coal consumption cost

The coal consumption cost is generally expressed by the coal consumption characteristics. The coal consumption cost of the thermal power units (i) at time t is calculated as follows:

$$C_{G,i,t}^1=(a_i{P}_{G,i,t}^2+b_i{P}_{G,i,t}+c_i)C_{coal}$$

(1)

In the formula, P_G,i,t is the active power output of the thermal power units (i) at time t; a_i, b_i, and c_i are the coefficients of the unit consumption characteristic function, related to unit type, boiler type, and coal quality, respectively; and C_coal is the current quarterly price of coal.

(2)

Unit loss cost

When the unit runs in the deep peak regulation stage, it will produce wear and tear and also increase the additional cost depletions. The consumption cost of the thermal power unit’s (i) loss at time t can be expressed as follows:

$$C_{G,i,t}^2=d\tau C_{unit,i}$$

(2)

$$d={\displaystyle \frac{1}{2N_f(P_{G,i,t}-P_{G,i,t-1})}}$$

(3)

In the formula, d is the unit loss rate; N_f (P_G,i,t − P_G,i,t−1) is the cycle of rotor cracking at time t; C_unit,i is the actual purchase cost of the units (i); and τ is the loss coefficient.

(3)

Deep regulation cost with oil

When the unit is running in the stage of deep peak regulation with oil delivery, it is necessary to inject fuel to maintain the stability of the boiler and water circulation system. The oil cost of the thermal power units (i) at time t is calculated as follows:

$$C_{G,i,t}^3=Q_{i,t}{C}_{oil}$$

(4)

In the formula, Q_i,t is the fuel consumption at the stage of the thermal power units (i) at time t; and C_oil is the current quarter’s oil price.

In conclusion, the operation cost model of the thermal power units (i) at time t can be expressed as the following segment functions:

$$C_{G,i,t}=\{\begin{array}{l}{C}_{G,i,t}^1,\begin{array}{l}\hfill \end{array}\begin{array}{l}\hfill \end{array}\begin{array}{l}\hfill \end{array}\begin{array}{l}\hfill \end{array}\begin{array}{l}\hfill \end{array}\begin{array}{l}\hfill \end{array}\begin{array}{l}\hfill \end{array}\begin{array}{l}\hfill \end{array}{P}_{G,i,\min }\le P_{G,i,t}<P_{G,i,\max }\hfill \\ C_{G,i,t}^1+C_{G,i,t}^2,\begin{array}{l}\hfill \end{array}\begin{array}{l}\hfill \end{array}\begin{array}{l}\hfill \end{array}\begin{array}{l}\hfill \end{array}{P}_{G,i,a}\le P_{G,i,t}<P_{G,i,\min }\hfill \\ C_{G,i,t}^1+C_{G,i,t}^2+C_{G,i,t}^3,P_{G,i,b}\le P_{G,i,t}<P_{G,i,a}\hfill \end{array}$$

(5)

In the formula, P_G,i,max, P_G,i,min, P_G,i,a, and P_G,i,b represent the maximum output of the thermal power units (i), the minimum output of the conventional peak regulation stage, the minimum output in the deep peak regulation stage without oil delivery, and the minimum output in the oil deep peak regulation stage with oil delivery, respectively.

3. Energy Storage Coordination Optimization Scheduling Model with Fuzzy Chance Constraint

3.1. Uncertainty of Source and Load

As new energy and load possesses a high degree of randomness, there will be some errors in the day-ahead prediction results. To ensure the power system’s stable operation, the power sector usually needs to take the uncertain factors into account when arranging the day-ahead dispatching plan. Because the system power balance and rotation reserve constraints contain uncertain variables, the power balance under certain conditions is no longer applicable.

In this paper, the fuzzy opportunity constraint method is used to deal with the uncertainty problem. The system power balance and the rotational alternate inequality equilibrium constraint are relaxed to the power constraint equilibrium under a certain confidence level, so that the possibility of the equilibrium constraint is not less than the confidence level.

Fuzzy parameters are used to deal with the uncertainty of wind power, photovoltaics, and load [24,25]. In the process of solving fuzzy chance-constrained programming, the fuzzy parameters are transformed into clear equivalences. Then, the problem can be solved according to the power balance equation under certain conditions.

The fuzzy parameters are mainly divided into triangular fuzzy numbers and trapezoidal fuzzy numbers. The membership degree of triangular fuzzy number increases first and then decreases, which is suitable for describing well-defined nearby ranges, but only allows a certain point to have the largest membership degree. The membership degree of the trapezoid fuzzy number increases for a period of time and then decreases, which can maintain the maximum membership degree for a period of time, which is suitable for the scenario in this paper. Therefore, trapezoidal fuzzy numbers are used to describe the uncertainty of wind power, photovoltaics, and load. Wind power, photovoltaics, and load day-ahead forecast results are used as fuzzy parameters, and the expression is as follows:

$$\{\begin{array}{l}{\tilde{P}}_{W,t}=P_{W,t}^{pre}(w_1,w_2,w_3,w_4)\hfill \\ {\tilde{P}}_{V,t}=P_{V,t}^{pre}(v_1,v_2,v_3,v_4)\hfill \\ {\tilde{P}}_{L,t}=P_{L,t}^{pre}(l_1,l_2,l_3,l_4)\hfill \end{array}$$

(6)

In the formula, ${\tilde{P}}_{W,t}$, ${\tilde{P}}_{V,t}$, and ${\tilde{P}}_{L,t}$ represent the fuzzy parameters of wind power, photovoltaics, and load, respectively; $P_{W,t}^{pre}$, $P_{V,t}^{pre}$, and $P_{L,t}^{pre}$ represent the day’s predicted values of wind power, photovoltaics, and load, respectively; w_i, v_i, and l_i are the corresponding proportional coefficients (i = 1, 2, 3, 4), whose values are generally determined by the historical data.

Since trapezoidal fuzzy parameters cannot be directly applied to the formula’s calculations, the trapezoidal fuzzy parameters need to be numerically equivalent, and the equivalent formula is as follows:

$$\{\begin{array}{l}{\tilde{P}}_{W,t}=P_{W,t}^{pre}={\displaystyle \frac{1-\alpha }{2}}(w_1+w_2)+{\displaystyle \frac{\alpha }{2}}(w_3+w_4)\hfill \\ {\tilde{P}}_{V,t}=P_{V,t}^{pre}={\displaystyle \frac{1-\alpha }{2}}(v_1+v_2)+{\displaystyle \frac{\alpha }{2}}(v_3+v_4)\hfill \\ {\tilde{P}}_{L,t}=P_{L,t}^{pre}={\displaystyle \frac{1-\alpha }{2}}(l_1+l_2)+{\displaystyle \frac{\alpha }{2}}(l_3+l_4)\hfill \end{array}$$

(7)

In the formula, α is the constraint that meets the confidence level of the rotation standby.

3.2. The Upper-Layer Scheduling Model

Pumped storage has the characteristics of large capacity and long-term operation, and mainly plays the important role of peak shifting and valley filling in the peak regulation process of the power grid [26,27,28] in order to reduce the frequency and amplitude of the output of thermal power. Therefore, the upper-layer dispatching adopts pumped storage energy to stabilize the net load fluctuation, giving consideration to both the peak regulation effect and operation economy. Pumped storage smooths net load fluctuations to the minimum and maximizes the benefit of the pumped storage, and then obtains the plan of the pumped storage’s start–stop and output.

3.2.1. Objective Function

In this stage, the goal is to minimize the fluctuation of the net load via pumped storage and achieve the maximum benefit of pumped storage, and the expression is as follows:

$$F_1=\min [p{\displaystyle \frac{f_1}{f_1^{\ast }}}-(1-p){\displaystyle \frac{f_2}{f_2^{\ast }}}]$$

(8)

$$f_1=\min {\displaystyle \frac{1}{T}}{\displaystyle \sum _{t=1}^T{[(P_{JL,t}-P_{H,t})-\frac{1}{T}{\displaystyle \sum _{t=1}^T{P}_{JL,t}}]}^2}$$

(9)

$$f_2=\max {\displaystyle \sum _{t=1}^T(G_{H,t}-C_{H,t})}$$

(10)

$$P_{JL,t}=P_{L,t}^{pre}-P_{W,t}^{pre}-P_{V,t}^{pre}$$

(11)

In the formulas, $f_1^{\ast }$ and $f_2^{\ast }$ represent the base values of two targets, respectively; p is the weight coefficient, and p is 0.5 (the weight of two objective functions in half is taken as an example); P_H,t is the output of the pumped storage power station at time t (P_H,t > 0 represents the power generation condition, P_H,t < 0 represents the pumping working condition); P_JL,t is the net load forecast value at time t; G_H,t is the operation benefit of the pumped storage power station at time t; C_H,t is the operation cost of the pumped storage power station at time t; and T is the total dispatching time.

(1)

Pumped storage energy benefit model

During the operation of the pumped storage power station, the main benefit is the electricity benefit, which is expressed as follows:

$$G_{H,t}=(P_{H,t}^g-P_{H,t}^p)\mathrm{\Delta }t{C}_{price,t}$$

(12)

In the formula, $P_{H,t}^g$ and $P_{H,t}^p$ represent the generation power and pumping power of power station at time t, respectively; C_price,t is the electricity price for the peak and valley period; and t is the dispatching time interval.

(2)

Pumped storage energy cost model

There are many factors affecting the operation costs in a pumped storage power station. This paper mainly discusses the investment cost and the operation loss cost. The investment cost is mainly determined by the rated power and rated capacity of the energy storage power station put into operation [29]. The operation loss cost is mainly determined by the operating power of the pumped storage power station. The operation cost of pumped storage at time t can be expressed as follows:

$$C_{H,t}={\displaystyle \frac{(C_{H,P}{P}_{HN}+C_{H,E}{E}_{HN})}{365\cdot T}}{\displaystyle \frac{r{(1+r)}^{T_H}}{{(1+r)}^{T_H}-1}}+k_p(Z_t^p{P}_{H,t}^p+Z_t^g{P}_{H,t}^g)$$

(13)

In the formula, C_H,P is the construction cost per unit of power of the station; C_H,E is the construction cost per unit of capacity; P_HN and E_HN represent the rated power and rated capacity (MWh), respectively; $Z_t^g$ and $Z_t^p$ represent the operating conditions of the pumped storage power station at time t ($Z_t^g$ and $Z_t^p$ are set to 1 for the generating and pumping condition, and 0 for the static condition), respectively; k_p is the operating loss coefficient; T_H is the service life of the pumped storage power station project, which in this paper is taken as 40 years; and r is the discount rate, taken as 8%.

3.2.2. Constrains

The upper dispatching constraints are mainly the pumped storage power station’s constraints, including unit output constraints and reservoir water balance constraints.

(1)

Constrains of unit output

$$\{\begin{array}{l}{Y}_{j,t}^g{P}_{H,j,\min }^g\le P_{H,j,t}^g\le Y_{j,t}^g{P}_{H,j,\max }^g\hfill \\ Y_{j,t}^p{P}_{H,j,\min }^p\le P_{H,j,t}^p\le Y_{j,t}^p{P}_{H,j,\max }^p\hfill \end{array}$$

(14)

In the above formula, $P_{H,j,\max }^g$ and $P_{H,j,\min }^g$ represent the maximum and minimum output under the generating condition of the pumped storage units (j), respectively; $P_{H,j,\max }^p$ and $P_{H,j,\min }^p$ represent the maximum and minimum output under the pumping condition of the pumped storage units (j), respectively; and $Y_{j,t}^g$ and $Y_{j,t}^p$ represent the operating condition of the pumped storage units (j) at time t (1 means that the unit is in the generating or pumping condition, and 0 is the static condition), respectively.

(2)

Constrains of water yield balance

$$\{\begin{array}{l}\begin{array}{l}{E}_{H,\min }\le E_{H,t}\le E_{H,\max }\\ E_{H,0}=E_{H,\mathrm{end}}\end{array}\hfill \\ E_{H,t}-E_{H,t-1}=({\eta }_p{\displaystyle \sum _{j=1}^J{Y}_{j,t}^p{P}_{H,j,t}^p}-{\displaystyle \sum _{j=1}^J{Y}_{j,t}^g{P}_{H,j,t}^g}/{\eta }_g)\mathrm{\Delta }t\hfill \end{array}$$

(15)

In the above formula, E_H,t is the upstream reservoir capacity at time t; E_H,max and E_H,min represent the maximum and minimum value of the upstream reservoir capacity, respectively; E_H,0 and E_H,end represent the beginning and end values of the reservoir capacity, respectively; and η_g and η_p represent the generating and pumping efficiency, respectively.

3.3. The Lower-Layer Scheduling Model

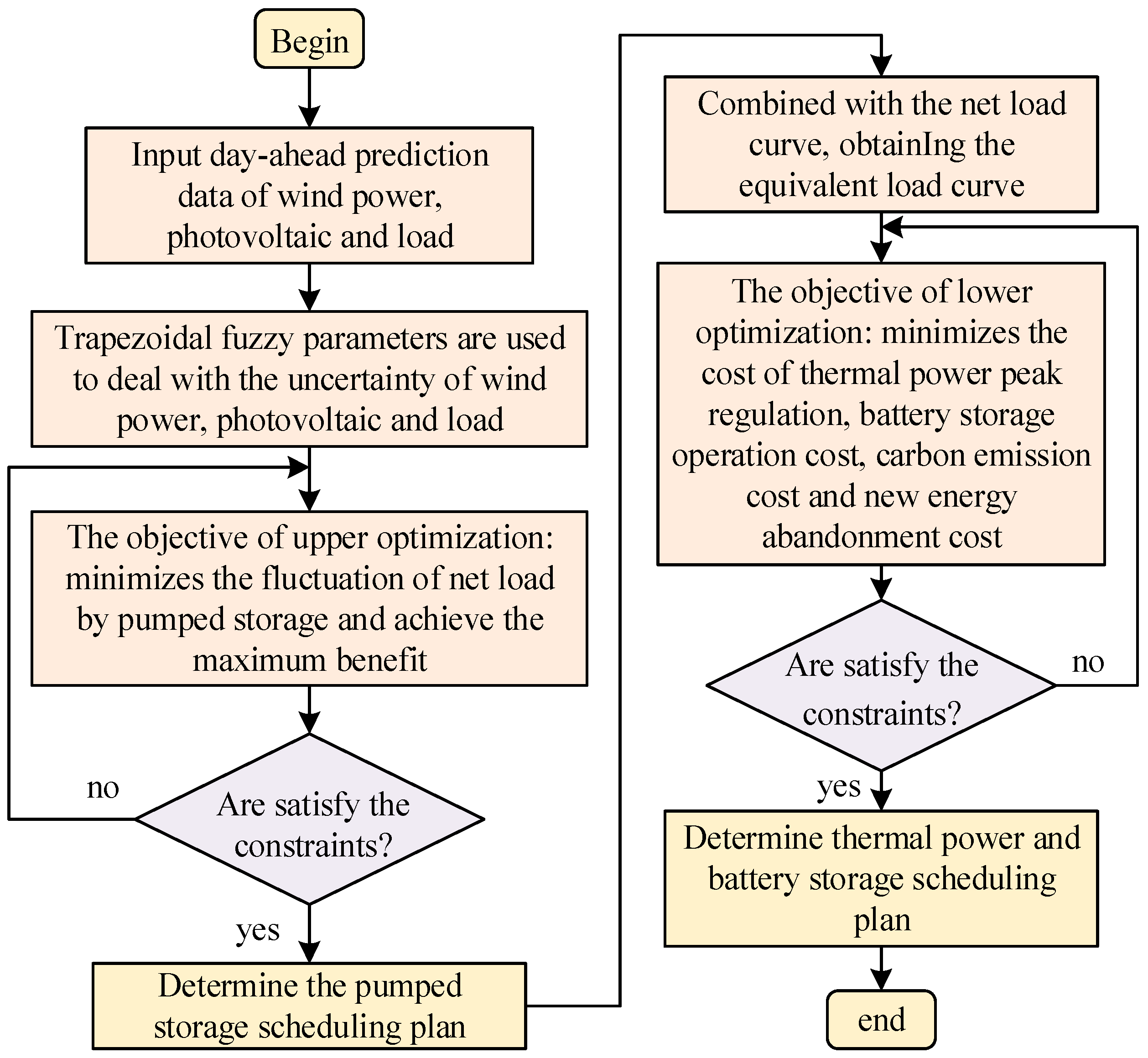
The upper-layer scheduling obtains the scheduling plan of the pumped storage, combined with the net load curve, and then obtains the equivalent load curve and passes to the lower level. The lower dispatching considers that thermal power and battery storage participate in the peak regulation, with the minimum total peak regulation cost of the system as the optimization objective, and then solves the output plan for the thermal power and battery storage.

3.3.1. Objective Function

In this stage, the optimization goal is to minimize the total peak regulation cost of the system. In the target function, the operating cost of thermal power, the operating cost of battery storage, the carbon emission cost, and the penalty cost of new energy abandonment are considered. The expressions are as follows:

$$F_2=\min (C_1+C_2+C_3+C_4)$$

(16)

In the formula, C₁ is the operating cost of thermal power; C₂ is the operating cost of battery storage; C₃ is the carbon emission cost; and C₄ is the penalty cost of wind power and photovoltaic abandonment.

(1)

Peak regulation cost of thermal power unit

In addition to fuel consumption and deep peak regulation loss during the operation process of thermal power, additional fuel use during the start–stop process will accelerate the loss of the unit, so the start–stop cost of the thermal power units (i) at time t can be expressed as follows:

$$C_{G,i,t}^{\mathrm{T}}=X_{i,t}(1-X_{i,t-1})C_{G,i,on}+X_{i,t-1}(1-X_{i,t})C_{G,i,off}$$

(17)

In the formula, X_i,t is the operating status of the thermal power units (i) at time t (X_i,t takes 1 as the operation state, and X_i,t takes 0 as the downtime state); and C_G,i,on and C_G,i,off represent the startup cost and stop cost of the thermal power units (i), respectively.

On the basis of the above analysis, the total peak regulation cost of thermal power can be expressed as follows:

$$C_1={\displaystyle \sum _{i=1}^I{\displaystyle \sum _{t=1}^T{C}_{G,i,t}}}+{\displaystyle \sum _{i=1}^I{\displaystyle \sum _{t=1}^T{C}_{G,i,t}^T}}$$

(18)

(2)

Operating cost of battery storage

Similar to pumped storage, the cost of battery storage also considers the investment cost and operating loss cost. The expression is as follows:

$$C_2={\displaystyle \sum _{t=1}^T[\frac{(C_{B,P}{P}_{BN}+C_{B,E}{E}_{BN})}{365\cdot T}\frac{r{(1+r)}^{T_B}}{{(1+r)}^{T_B}-1}+}\begin{array}{c}{k}_B|({\mu }_t^c+{\mu }_t^d)P_{B,t}|]\end{array}$$

(19)

In the formula, P_BN is the rated power for the battery storage; E_BN is the rated capacity of the battery storage; C_B,P and C_B,E represent the per power construction cost and per capacity construction cost of the battery storage, respectively; P_B,t is the output of battery storage at time t (P_B,t > 0 represents the discharge state, P_B,t < 0 represents the charging state); ${\mu }_t^d$ and ${\mu }_t^c$ are the charging mark and discharge mark of the battery storage at time t (for ${\mu }_t^d$ and ${\mu }_t^c$, 1 represents the discharging and charging state, and 0 represents the idle state), respectively; k_B is the operating loss coefficient; and T_B is the service life of the battery storage project, which in this paper is taken as 10 years.

(3)

Carbon emission cost

$$C_3=C_C[{\displaystyle \sum _{i=1}^I{\displaystyle \sum _{t=1}^T{K}_C{P}_{G,i,t}}}-\lambda {\displaystyle \sum _{i=1}^I{\displaystyle \sum _{t=1}^T{P}_{G,i,t}}}]$$

(20)

In the above formula, C_C is the trading price for carbon emissions; K_C is the carbon emissions of thermal power; and λ is the carbon emission quota of thermal power.

(4)

Penalty cost of new energy abandonment

$$C_4={\displaystyle \sum _{t=1}^T[K_W(P_{W,t}^{pre}-P_{W,t})+K_V(P_{V,t}^{pre}-P_{V,t})]}$$

(21)

In the above formula, K_W is the penalty coefficient of wind power abandonment; K_V is the penalty coefficient of photovoltaic abandonment; and P_W,t and P_V,t are the actual output of wind power and photovoltaic scheduling at time t, respectively.

3.3.2. Constrains

The lower-layer scheduling constraints include power balance constraints and thermal power- and battery storage-related constraints. The specific expressions are as follows:

(1)

Power balance constraints

$$P_{L,t}^{pre}={\displaystyle \sum _{i=1}^I{P}_{G,i,t}}+P_{H,t}+P_{B,t}+P_{W,t}+P_{V,t}$$

(22)

(2)

Output constraints of thermal power units

$$X_{i,t}{P}_{G,i,\min }\le P_{G,i,t}\le X_{i,t}{P}_{G,i,\max }$$

(23)

(3)

Climbing constraints of thermal power units

$$-V_{G,i}\le P_{G,i,t}-P_{G,i,t-1}\le V_{G,i}$$

(24)

In the formula, V_G,i is the maximum climbing rate of the thermal power units (i).

(4)

Minimum start and stop time limit of thermal power units

$$\{\begin{array}{l}(X_{i,t-1}-X_{i,t})(T_{G,i,t-1}^{on}-T_{G,i,on})\ge 0\hfill \\ (X_{i,t}-X_{i,t-1})(T_{G,i,t-1}^{off}-T_{G,i,off})\ge 0\hfill \end{array}$$

(25)

In the above formula, T_G,i,on is the minimum continuous operation time of the thermal power units (i); T_G,i,off is the minimum continuous stop time of the thermal power units (i); $T_{G,i,t-1}^{on}$ is the continuous operation time of the thermal power units (i) during time t; and $T_{G,i,t-1}^{off}$ is the continuous stop time of the thermal power units (i) during time t.

(5)

Constraints of positive and negative rotation standby

$$\{\begin{array}{l}\mathrm{Pr}\{{\displaystyle \sum _{i=1}^I[P_{G,i,t}+X_{i,t}(P_{G,i,\max }-P_{G,i,t})]}+P_{H,t}+P_{B,t}+{\tilde{P}}_{W,t}+{\tilde{P}}_{V,t}\ge {\tilde{P}}_{L,t}\}\ge \alpha \hfill \\ \mathrm{Pr}\{{\displaystyle \sum _{i=1}^I[P_{G,i,t}+X_{i,t}(P_{G,i,t}-P_{G,i,\min })]}+P_{H,t}+P_{B,t}+{\tilde{P}}_{W,t}+{\tilde{P}}_{V,t}\ge {\tilde{P}}_{L,t}\}\ge \alpha \hfill \end{array}$$

(26)

In the above formula, Pr{∙} is the confidence level; and α is 0.95.

(6)

Constraints of battery storage

This mainly includes the charge and discharge power constraints, charge state constraint, daily clearing constraint, and power balance constraint. The expression is as follows:

$$\{\begin{array}{l}-P_{BN}\le P_{B,t}\le P_{BN}\hfill \\ S_{SOC,\min }\le S_{SOC,t}\le S_{SOC,\max }\hfill \\ S_{SOC,0}=S_{SOC,\mathrm{end}}\hfill \\ S_{SOC,t}={\displaystyle \frac{E_{B,t}}{E_{BN}}}\hfill \\ S_{SOC,t}-S_{SOC,t-1}={\displaystyle \frac{\mathrm{\Delta }t}{E_{BN}}}({\mu }_t^c{P}_{B,t}{\eta }_c-{\displaystyle \frac{{\mu }_t^d{P}_{B,t}}{{\eta }_d}})\hfill \\ {\mu }_t^c+{\mu }_t^d\le 1\hfill \end{array}$$

(27)

In the formula, S_SOC,t is the state of charge at time t; S_SOC,max and S_SOC,min represent the maximum and minimum values of the state of charge, respectively; S_SOC,0 and S_SOC,end represent the initial and end values of the state of charge, respectively; E_B,t is the battery capacity at time t; and η_c and η_d represent the charge and discharge efficiency, respectively.

Through the two-layer scheduling scheme, the characteristics of battery storage and pumped storage and the deep peak regulation of thermal power units are fully utilized to achieve coordinated operation. The peak regulation-balancing scheduling process of the thermal power and composite energy storage is shown in Figure 2.

4. Solution Based on an Improved Grey Wolf Algorithm

The grey wolf optimization algorithm has few parameters and a simple structure and is easy to implement. However, the location update of the traditional grey wolf optimization algorithm is only guided by the α wolf, its ability to perform global exploration is weak, and it is easy to fall into the local optimal solution [30]. The two-layer scheduling model belongs to the mixed integer nonlinear programming model because of the existence of the nonlinear term. The solution result of the unconstrained optimization problem depends too much on the selection of the initial value, and it is easy to fall into the local optimal convergence.

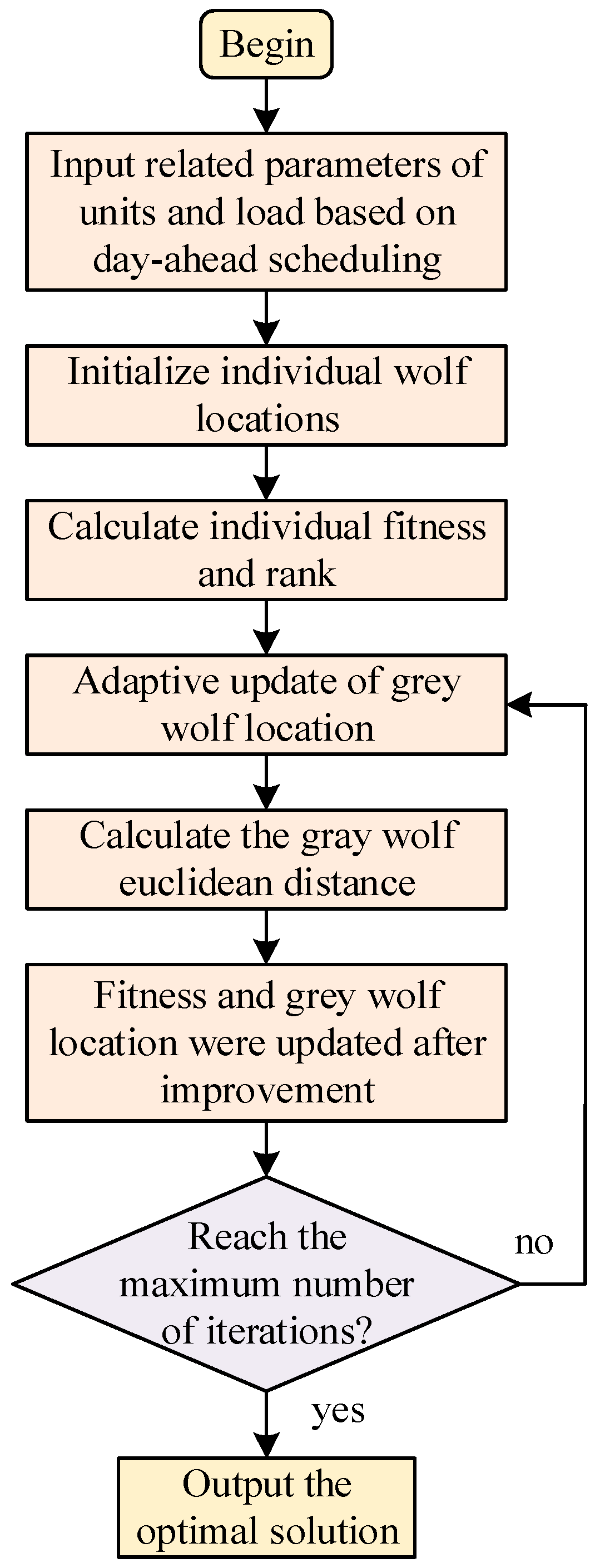
Therefore, this paper improves the traditional grey wolf optimization algorithm and uses an improved grey wolf optimization algorithm to solve the two-layer scheduling model. The specific improvement measures are as follows:

(1)

Convergence factor update: the change of the convergence factor α will have a significant impact on the algorithm. In the traditional algorithm, the convergence factor α is a linear change, while the convergence process of the algorithm is mostly non-linear. Therefore, in order to improve the searching ability of the algorithm, a sine adjustable convergence factor α update method is proposed, expressing the following:

$$a=2\left[1-\sin {({\displaystyle \frac{t\pi }{2t_{\max }}})}^m\right]$$

(28)

In the formula, t is the number of current iterations; t_max is the maximum number of iterations; and m is the adjustment factor.

From (28), the decline rate of the convergence factor α is slow in the early iteration, which improves the global optimization ability of the algorithm, which is beneficial to improving the convergence rate. After testing, we know that when m is greater than 2, the algorithm has good optimization accuracy, taking m = 3.

(2)

Location update: In the actual optimization process of the algorithm, the α wolf is more likely to be the optimal solution. Therefore, in this paper, in the gray wolf location update process, the weight of the wolf is gradually increased, and the updated expression of the grey wolf location is as follows:

$$\overrightarrow{X}(t+1)={\displaystyle \frac{t}{t_{\max }}}\sin ({\displaystyle \frac{t\pi }{2t_{\max }}}){\overrightarrow{X}}_1+(1-{\displaystyle \frac{t}{t_{\max }}}){\displaystyle \frac{{\overrightarrow{X}}_1+{\overrightarrow{X}}_2+{\overrightarrow{X}}_3}{3}}$$

(29)

In the formula, $\overrightarrow{X}(t+1)$ is the direction vector of the next movement of the gray wolf; and ${\overrightarrow{X}}_1$, ${\overrightarrow{X}}_2$, and ${\overrightarrow{X}}_3$ are the vectors corresponding to the positions of the wolf α, wolf β, and wolf δ, respectively.

(3)

Dynamic weight adjustment: The traditional grey wolf algorithm using the average method cannot reflect the importance of individual wolves. To accelerate the convergence speed of the algorithm, it is necessary to dynamically adjust the weight ratio of wolf α, wolf β, and wolf δ. In this paper, we use the improved proportional weight of the Euclidean type of grey wolf distance, and the improved position expression of the grey wolves is:

$$\overrightarrow{X}(t+1)={\displaystyle \frac{t}{t_{\max }}}\sin ({\displaystyle \frac{t\pi }{2t_{\max }}}){\overrightarrow{X}}_1+(1-{\displaystyle \frac{t}{t_{\max }}}){\displaystyle \frac{A_1{\overrightarrow{X}}_1+A_2{\overrightarrow{X}}_2+A_3{\overrightarrow{X}}_3}{3}}$$

(30)

$$\{\begin{array}{c}{A}_1={\displaystyle \frac{\left|{\overrightarrow{X}}_1\right|}{\left|{\overrightarrow{X}}_1\right|+\left|{\overrightarrow{X}}_2\right|+\left|{\overrightarrow{X}}_3\right|}}\\ A_2={\displaystyle \frac{\left|{\overrightarrow{X}}_2\right|}{\left|{\overrightarrow{X}}_1\right|+\left|{\overrightarrow{X}}_2\right|+\left|{\overrightarrow{X}}_3\right|}}\\ A_3={\displaystyle \frac{\left|{\overrightarrow{X}}_3\right|}{\left|{\overrightarrow{X}}_1\right|+\left|{\overrightarrow{X}}_2\right|+\left|{\overrightarrow{X}}_3\right|}}\end{array}$$

(31)

The above measures mainly improve the convergence factor, position, and weight of the grey wolf algorithm and uses the improved grey wolf optimization algorithm to deal with the two-layer scheduling model. The specific solution process is shown in Figure 3.

5. Example Analysis

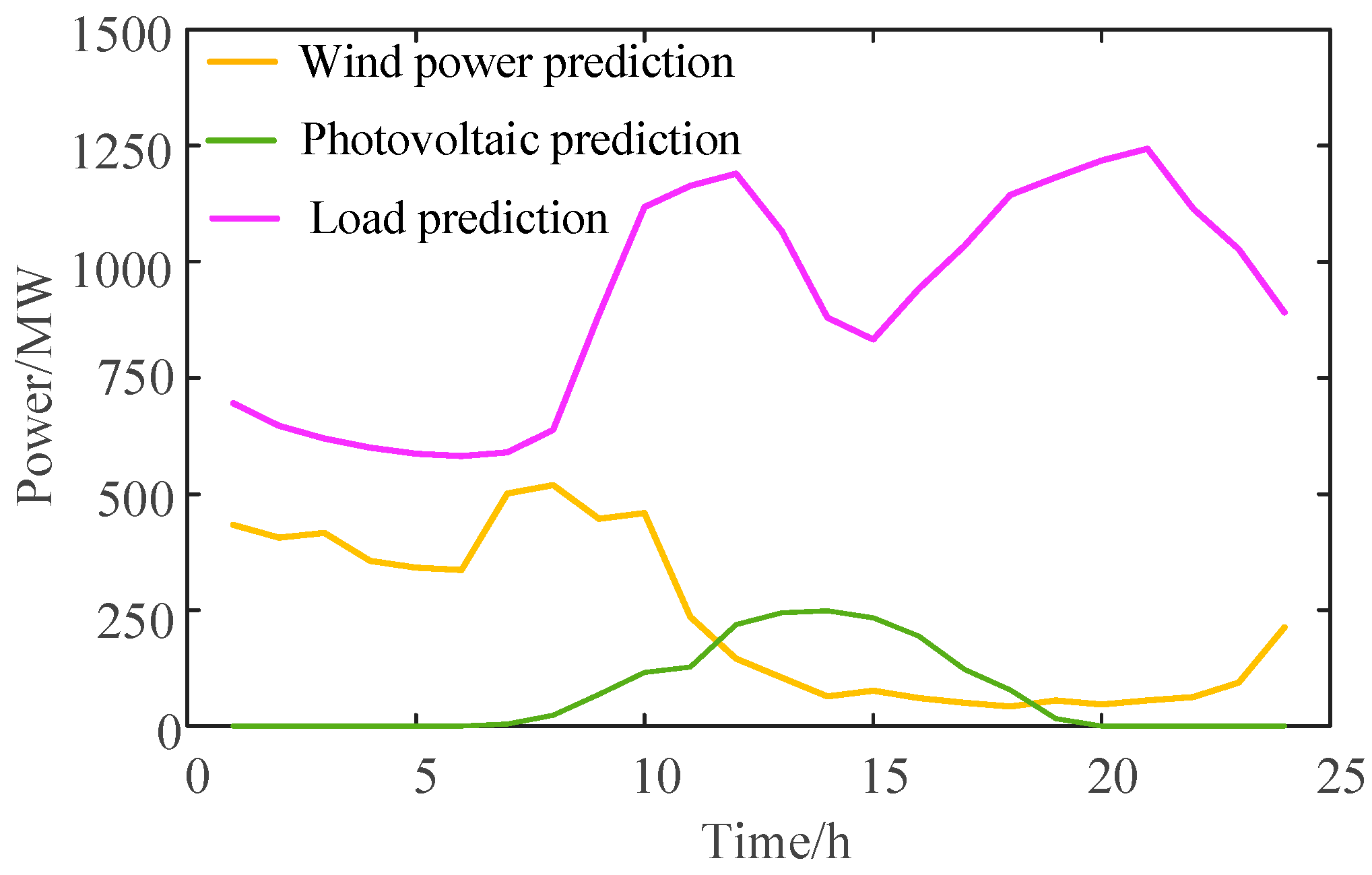
In this paper, an IEEE 39-node system is used for analysis, and the access position of each unit is shown in Figure 4. The capacity of the wind farm and the photovoltaic power station is 600 MW and 300 MW, respectively; the capacity of pumped storage station is 200 MW (including four units); only thermal power units (G1 and G2) above 300 MW have deep peak regulation, and the minimum output of thermal power unit in the conventional peak regulation stage, the minimum output without oil delivery, and minimum output with oil delivery in the deep peak regulation stage are set to 60%, 45%, and 30% of the maximum output, respectively. Other thermal power units (G3–G6) only participate in the conventional peak regulation; the scheduling cycle is 24 h and the time scale is 1 h; a typical daily datapoint is selected for the research. The original load and wind and the photovoltaic forecast curves are shown in Figure 5, the parameters of each thermal power unit are shown in

Table 1. Parameters of thermal power unit.

Unit	PG,max (MW)	PG,min (MW)	VG (MW/h)	τ	a (t/MW2)	b (t/MW)	c (t)	TG,on/TG,off (h)	CG,on (CNY/Time)	CG,off (CNY/Time)	KC (t/MW∙h)
G1	350	105	150	1.2	0.000182	0.25742	8.5486	2	24,000	15,000	0.92
G2	300	90	120	1.2	0.000162	0.23675	7.3785	2	24,000	15,000	0.96
G3	250	150	100	—	0.000147	0.22543	4.8268	2	18,000	10,000	1.04
G4	200	120	100	—	0.000124	0.24687	4.5764	2	18,000	10,000	1.04
G5	120	72	50	—	0.000098	0.21775	6.4785	2	10,000	5000	1.12
G6	80	48	50	—	0.000065	0.21458	3.8676	2	10,000	5000	1.14

, and the composite energy storage and other parameters are shown in

Table 2. Parameters of pumped storage station.

Unit	${\mathit{P}}_{\mathbf{HN}}^{\mathbf{g}}$ (MW)	${\mathit{P}}_{\mathbf{HN}}^{\mathbf{p}}$ (MW)	EHN (MW∙h)	ηg (%)	ηp (%)	kP (CNY/MW∙h)	EH,0 (MW∙h)	EH,max (MW∙h)	EH,min (MW∙h)	CH,P (CNY/MW)	CH,E (CNY/MW∙h)
1–4	4 × 50	4 × 50	2000	90	85	3.4	200	1800	200	1.5 × 106	0.25 × 106

,

Table 3. Parameters of battery storage.

PBN (MW)	EBN (MW∙h)	ηd (%)	ηc (%)	kB (CNY/MW∙h)	SOC0 (%)	SOCmax (%)	SOCmin (%)	CB,P (CNY/MW)	CB,E (CNY/MW∙h)
50	200	95	95	65	10	90	10	5 × 105	2.5 × 106

,

Table 4. Membership parameters.

Name	w1	w2	w3	w4	v1	v2	v3	v4	l1	l2	l3	l4
value	0.8	0.92	1.08	1.2	0.75	0.9	1.1	1.25	0.9	0.95	1.05	1.1

and

Table 5. Other parameters.

Name	Coil (CNY/t)	Ccoal (CNY/t)	CC (CNY/t)	KW (CNY/MW∙h)	KV (CNY/MW∙h)	λ (t/MW∙h)
value	6200	700	80	600	600	0.7

.

5.1. Analysis of Example Results

In order to reflect the function of the coordinated operation of composite energy storage in improving the peak regulation effect and economy, three other scheduling schemes are set up for comparative analysis.

(1)

Scheme 1: Composite energy storage does not participate in peak regulation, and only thermal power units participate in peak regulation, with the lowest total peak regulation cost of the system as the optimization goal;

(2)

Scheme 2: Only including the pumped storage station, the double-layer scheduling scheme is adopted, and only the thermal power units participate in peak regulation;

(3)

Scheme 3: Including composite energy storage, using double-layer scheduling scheme, thermal power units only participate in conventional peak regulation;

(4)

Scheme of this paper: including composite energy storage, using a double-layer scheduling scheme.

5.1.1. Analysis of the Scheduling Results

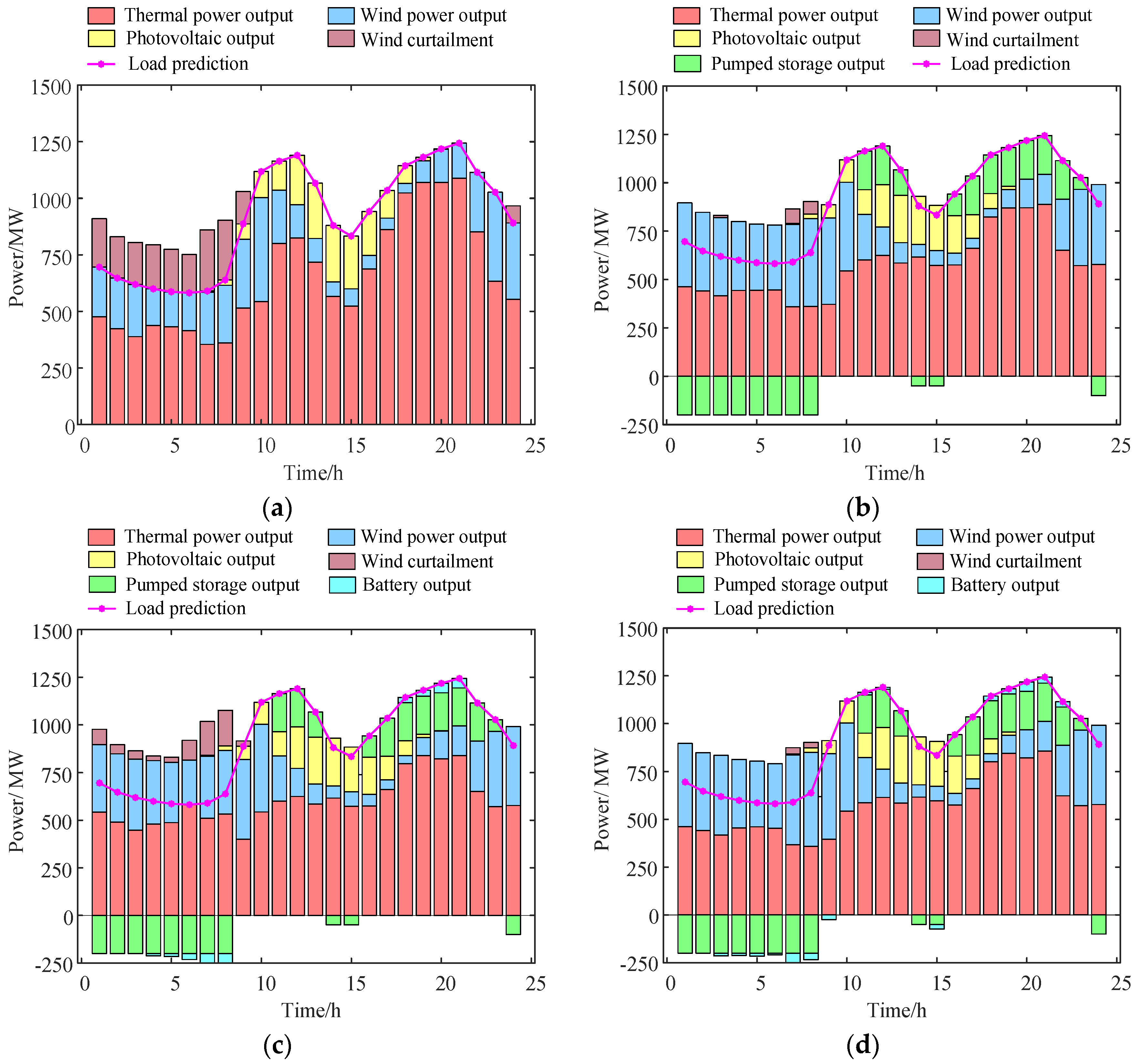
The improved grey wolf algorithm is used to solve the two-layer scheduling model, and the system optimization scheduling results and peak regulation effect index under each scheme are shown in Figure 6 and

Table 6. Index of system peak shaving under each scheme.

Peak Regulation Index	Net Load Standard Deviation/MW	Net Load Peak–Valley Difference/MW	Wind Abandonment Rate/%
Scheme 1	432.78	733.8	29.19
Scheme 2	186.45	529.46	2.35
Scheme 3	111.05	437.92	11.17
This scheme	174.98	497.07	0.96

, respectively.

Because only the thermal power units participate in the peak regulation in scheme 1, the output of the thermal power units changes greatly, resulting in the frequent operation of the unit in the deep peak regulation stage and an increase of the start and stop times. There is serious wind abandonment in the low-load period, and the wind abandonment rate reaches 29.19%. Scheme 2 is based on scheme 1 with the addition of pumped storage, and in Figure 6b it can be seen that pumping mainly occurs during the low load period, and generating during the peak load period, having the effect of shaving peaks and filling valleys. The output fluctuation of the thermal power units decreases significantly, the net load peak–valley difference and net load standard deviation increase by 204.34 MW and 246.33 MW, respectively, and the wind power on the grid increases. The thermal power units in scheme 3 only participate in conventional peak regulation. Although the peak valley difference of the net load and the standard deviation of net load are optimal, the wind abandonment rate is still large. In this paper, the wind abandonment rate of this scheme is better than the other three schemes, but compared with scheme 2, the improvement is not obvious. Because the battery storage capacity is smaller than that of pumped storage, and cannot be in the charging or discharging state for a long time, the abandonment rate of new energy is only increased by 1.39%. Through the double-layer optimization scheduling, the pressure of thermal power participating in peak regulation is greatly alleviated, the wind abandonment is significantly reduced, and the utilization rate of composite energy storage is also improved.

5.1.2. Analysis of Peak Regulation Cost and Benefit

The peak regulation cost and total cost under different schemes are shown in

Table 7. The comparison of the cost of system peak shaving under each scheme.

Cost/CNY	Coal Consumption Cost	Deep Peak Regulation Loss Cost	Deep Peak Regulation Oil Cost	Start–Stop Cost	Carbon Emission Cost	New Energy Abandonment Cost	Total Peaking Cost
Scheme 1	2,965,600	201,600	139,500	112,000	372,500	1,132,100	4,923,300
Scheme 2	3,061,800	120,800	0	66,000	304,000	91,300	3,643,900
Scheme 3	3,150,900	0	0	86,000	327,900	433,200	3,998,000
This scheme	3,044,000	88,200	0	66,000	301,400	37,400	3,537,000

. It can be showed that, lacking energy storage, the thermal power units operate in the deep regulation state for a long time, which not only increases the loss of units but also increases the deep regulation cost of the units and the penalty for new energy power abandonment, and the total peak regulation cost is the highest. The total peak regulation cost in scheme 2 is reduced by 25.98% compared to scheme 1, and the new energy power abandonment cost and thermal power units’ deep peak regulation cost are greatly reduced by 91.93% and 64.58%, respectively, showing that pumped storage can effectively reduce the time units are in the deep peak regulation period, increasing the new energy power on the grid, but also reducing the output of thermal power in the peak load period, reducing the carbon emissions of the thermal power units. Due to the fact that the thermal power units do not participate in deep peak regulation in scheme 3, although the loss of the thermal power units and the deep regulation cost is reduced, when the down margin is insufficient, the system can only carry out the work via start–stop peak regulation or wind power and photovoltaic abandonment, resulting in an increase of the start and stop times of the units and the new energy abandonment rate; thus, the total peak regulation cost of the system is increased by CNY 354,100 compared with scheme 2. This paper scheme considering the function of pumped storage and battery storage, the system regulated capacity increasing, helping to alleviate the pressure of deep peak regulation of thermal power units and promoting the offset of new energy, the total peak regulation cost saved CNY 1,386,300, CNY 106,900, and CNY 461,000, respectively, compared with scheme 1, scheme 2, and scheme 3, the system economic improvement effect is the best.

Analyzing the peak regulation revenue of the system, the on-grid price of thermal power is CNY 375/(MWh), and on grid price of the composite energy storage should be formulated according to the peak and valley load period. The peak and valley price of each period is shown in

Table 8. Time-of-use electricity price.

Price/(CNY/MWh)	Time Frame	Peak–Valley Regime
500	00:00–09:00, 23:00–24:00	valley period
700	12:00–16:00, 21:00–23:00	Parallel period
1000	09:00–12:00, 16:00–21:00	peak period

. The revenue situation of the system peak regulation under each scheme is shown in

Table 9. Comparison of the benefits of system under each scheme.

Cost and Income/CNY	Thermal Power Income	Pumped Storage Cost	Pumped Storage Income	Pumped Storage Net Income	Battery Storage Cost	Battery Storage Income	Battery Storage Net Income
Scheme 1	5,857,100	—	—	—	—	—	—
Scheme 2	5,167,200	196,400	833,500	637,100	—	—	—
Scheme 3	5,380,900	196,400	833,500	637,100	235,100	80,000	−155,100
This scheme	5,133,500	196,400	833,500	637,100	238,200	78,800	−159,400

.

In the upper-layer scheduling, the pumped storage is used to smooth the fluctuation of net load. Under the condition of the same net load curves before the day, the pumped storage scheduling plan is the same. Therefore, the benefits of pumped storage in scheme 2 and scheme 3 are the same. The income of thermal power in scheme 1 is higher than that of the other schemes, but the excess income cannot compensate for the increased peak regulation cost, and the economy is poor. Compared with scheme 1, the total peak regulation cost of scheme 2 is reduced by CNY 1,279,400, bringing the net income generated by pumped storage to CNY 637,100, and the system economy is significantly improved. Although the income of the thermal power and the net income of the battery storage are slightly improved compared with this paper’s scheme, the conventional peak regulation of the thermal power units leads to a large amount of wind abandonment, which cannot compensate for the increase in the peak regulation cost of the system, and the economic benefit is not as good as that of this paper’s scheme. In this paper’s scheme, the income of the thermal power is similar to that of scheme 2. Although the total peak regulation cost is reduced by CNY 106,900, the net income of the battery storage is CNY −159,400, and the overall benefit is slightly lower than that of scheme 2.

In summary, the scheme of this paper is better than scheme 1 and scheme 3, and is slightly worse than scheme 2 in terms of peak regulation economics. It is improved compared with other three schemes in terms of its new energy abandonment rate. At the same time, due to its own characteristics of low cost and large capacity, both in the aspect of peak regulation efficiency and peak regulation benefits, pumped storage is better than battery storage.

5.2. Analysis of Composite Energy Storage Capacity

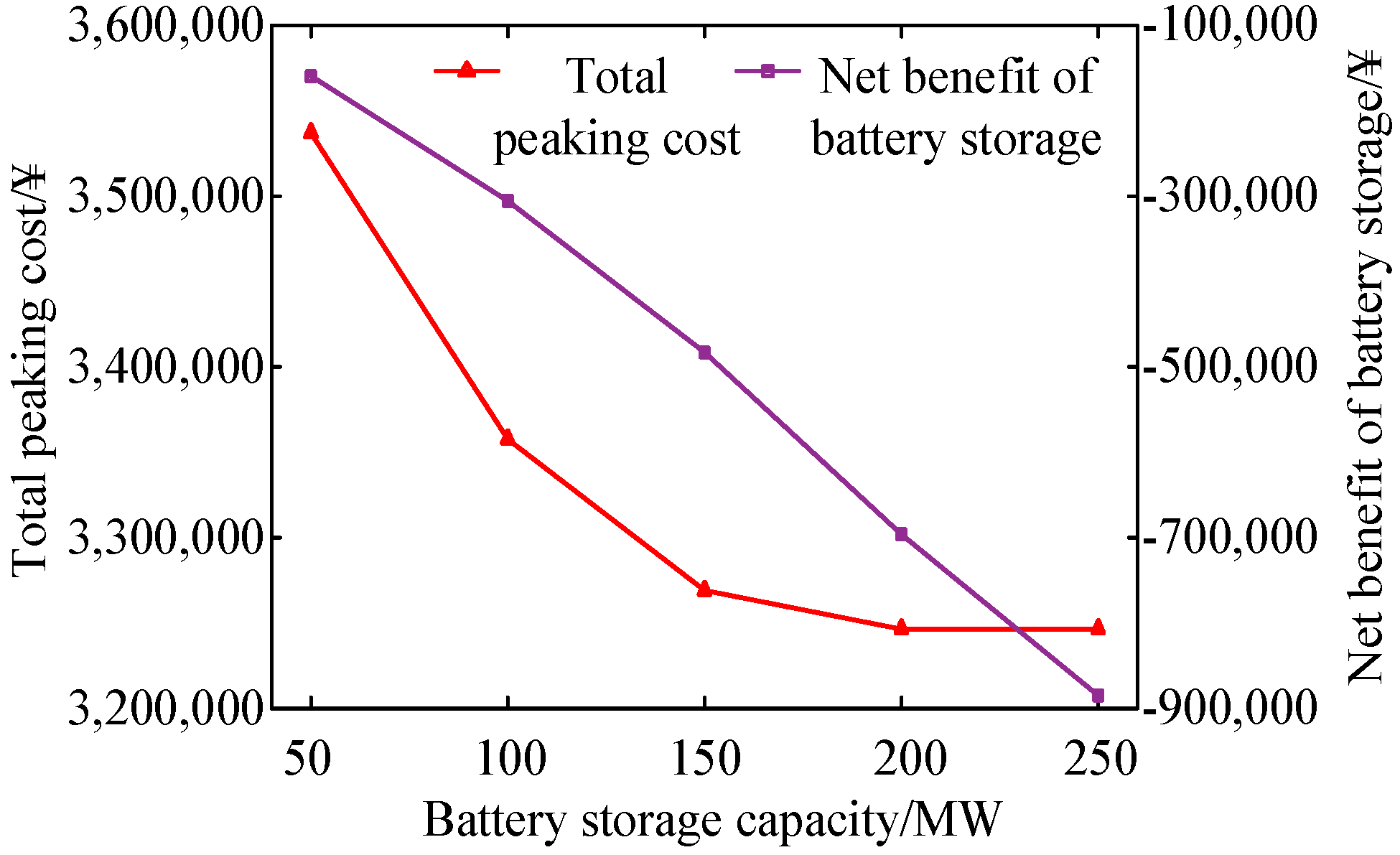
An energy storage device with a large capacity can better offset the fluctuation of new energy and improve the rotating reserve margin of thermal power units, but the operating cost of energy storage will also increase. Too large an energy storage capacity not only does not bring additional revenue, but also reduces the benefits of the system. Therefore, based on the two-layer scheduling scheme with composite energy storage, this paper compares the influence of the economics of battery energy storage and pumped storage on energy systems while keeping other parameters unchanged. 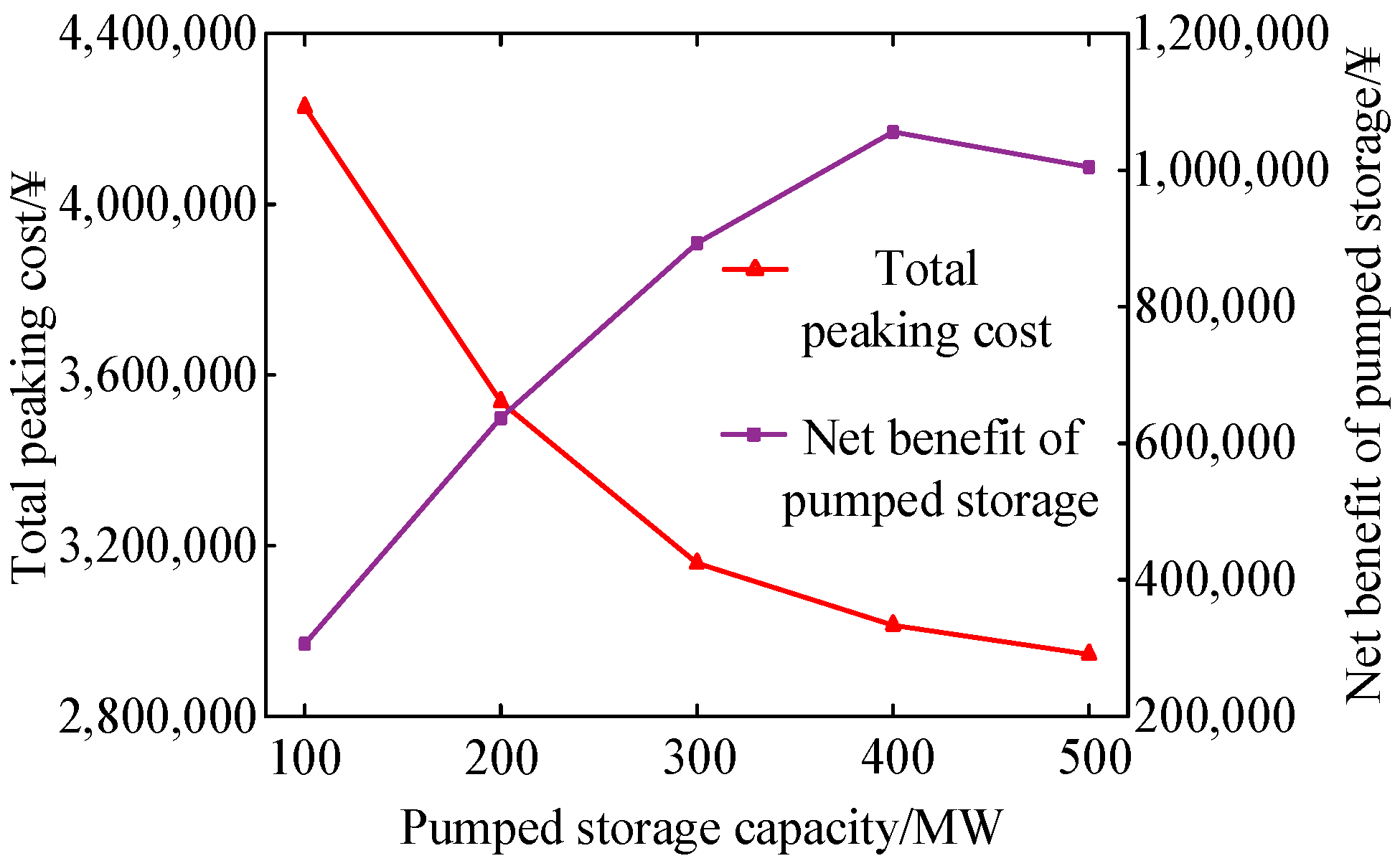Figure 7 shows the change of the total peak regulation cost and the net income of battery storage under the installation of battery storage with different capacities. The changes of the total peak regulation cost and the net revenue of the system under different pumped storage capacities are shown in Figure 8.

As can be seen from Figure 7, the operating cost of battery energy storage is greater than its income. With the increase of capacity, the loss increases, and it also reduces the output change range and start and stop times of thermal power units. The operating cost of thermal power is reduced, and the total cost of peaking decreases. Therefore, when equipped with a certain capacity of battery storage, the peak regulation cost saved by the system can make up for the loss caused by it. When the capacity reaches 150 MW or above, the cost of battery storage increases, the demand of the system is no longer increased, and the total peak adjustment cost is no longer reduced. The loss is larger than the peak regulation cost saved by the system, and the economic benefits of the system begin to decrease.

As seen from Figure 8, with the increase of the scale of pumped storage, the increase of pumping power improves the absorption ability of new energy and also reduces the output of thermal power in the peak load period, so as to reduce the abandonment rate and carbon emissions and continuously reduce the total peak regulation cost. With the increase of pumped storage capacity, the increased benefit of pumped storage is bigger than the increase of its operating cost, so the net income is constantly increasing. When the pumped storage capacity increases to a certain extent, the demand for the system reaches saturation, and the wind power and photovoltaic abandonment rate, carbon emissions, and total peak regulation cost all tend to be stable. However, the operating cost of pumped storage still increases, and the net income decreases.

5.3. Influence Analysis of Different Confidence Levels

This section discusses the effects of different confidence levels on scheduling results. Taking the scheduling model in this paper as an example,

Table 10. Scheduling results of the scheme in this paper under different confidence levels.

Confidence Level α	Reserve Capacity/MW	Wind Abandonment Rate/%	Total Peaking Cost/CNY
0.7	1729.3	13.78	3,145,000
0.75	1953.8	10.02	3,213,000
0.8	2114.6	7.85	3,323,000
0.85	2297.8	5.18	3,406,000
0.9	2451.4	2.44	3,493,000
0.95	2644.7	0.96	3,537,000

shows the system scheduling results when the confidence level changes from 0.7 to 0.95.

As can be seen from Table 10, with the increase of α, the wind abandonment rate decreases, the reserve capacity increases by 915.4 MW, and the total peak regulation cost also increases from CNY 3,145,000 to CNY 3,537,000. The main reason is that the confidence level is reduced, which reduces the on-grid power of wind power and photovoltaics, and thus increases the wind abandonment rate. In order to fill the power shortage, the output of the thermal power units increases, and the total peak regulation cost of the system increases.

Through the above analysis, it can be seen that the higher the confidence level, the higher the cost of input, the security of the reserve capacity is increased, and the economy is reduced. Therefore, when making actual decisions, the data of wind power, photovoltaics, and load output at different confidence levels can be analyzed to select the economically optimal scheduling scheme under a certain confidence level.

5.4. Comparative Analysis of the Solution Algorithm

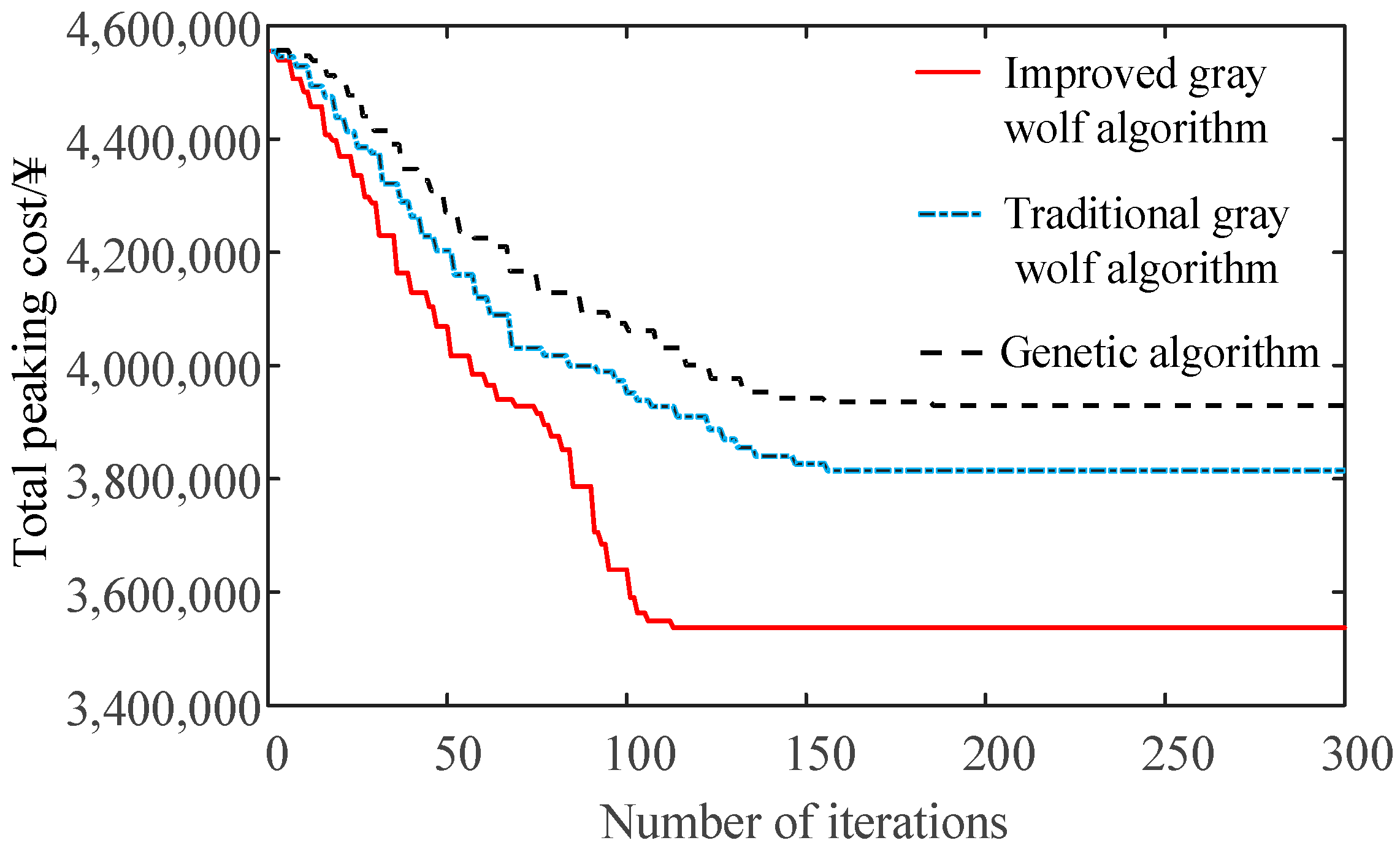
In order to verify the advantages of the improved grey wolf algorithm in the solution accuracy and convergence speed, the improved gray wolf algorithm, traditional gray wolf algorithm, and a genetic algorithm are compared and analyzed respectively. All population sizes were set to 30, and the maximum number of iterations was 500. Using three algorithms to solve the day-ahead scheduling model respectively, the optimization process is shown in Figure 9.

As can be seen from Figure 9, the total peak regulation cost of the genetic algorithm converged to CNY 3,927,800 after it iterated 184 times, and the traditional grey wolf algorithm converged to CNY 3,814,600 after it iterated 156 times, while the improved grey wolf algorithm converged to CNY 3,537,000 after it iterated 113 times. Compared to the traditional grey wolf algorithm, the convergence speed of the improved grey wolf algorithm increased by 27.56%, and the total peak regulation cost of the system after optimization was reduced by 7.28%. In conclusion, the improved grey wolf algorithm has more advantages in solving the day-ahead scheduling model and is even more advantageous in this paper, and its solution performance is better than other two algorithms.

6. Conclusions

In the context of a new power system, in order to further study the influence of composite energy storage and thermal power deep peak regulation on the peak regulation capacity and economics of the system, this paper analyzes a scheme based on two-layer optimization scheduling. The uncertainty of the system is described by setting the confidence level, and the conclusions are as follows:

(1)

Compared with three other schemes, the new energy power abandonment rate of composite energy storage participating in peak regulation is the best. The wind curtailment rate is 0.96%; although the net load peak–valley difference and net load standard deviation are the lowest in scheme 3, the wind curtailment rate is larger, and the total peak regulation cost is higher than the scheme in this paper, at CNY 461,000. After comprehensively considering the cost of composite energy storage, the scheduling scheme only containing pumped storage has the best benefit: the net income is higher than the scheme of this paper, at CNY 86,200

(2)

The net income of scheme 2 and scheme of this paper are higher than scheme 3, at CNY 295,500 and CNY 209,300, respectively. Proper deep peak regulation of thermal power units can not only improve the absorption of new energy and have certain economic benefits; when the capacity of energy storage reaches 150 MW or the capacity of pumped storage reaches 400 MW, the net income of the system will reduce, which is not conducive to the economic operation of the system. An energy storage device with appropriate capacity can achieve the optimal overall economic benefit for the system.

(3)

From the perspective of peak regulation benefit, it can be seen that pumped storage is the primary choice. When the development of pumped storage reaches the upper limit, the capacity transformation of deep peak regulation of thermal power units and the development of battery storage are an important way to excavate the peak regulation resources of the power grid.

(4)

Compared with the genetic algorithm and the traditional grey wolf algorithm, the optimization result of the improved grey wolf algorithm model is better, and the solution efficiency is higher.