The Operation Strategy of a Multi-Microgrid Considering the Interaction of Different Subjects’ Interests

Abstract

As the share of renewable energy generation continues to increase, the new-type power system exhibits the characteristics of coordinated operation between the main grid, distribution networks, and microgrids. The microgrid is primarily concerned with achieving self-balancing between power sources, the network, loads, and storage. In decentralized multi-microgrid (MMG) access scenarios, the aggregation of distributed energy within a region enables the unified optimization of scheduling, which improves regional energy self-sufficiency while mitigating the impact and risks of distributed energy on grid operations. However, the cooperative operation of MMGs involves interactions among various stakeholders, and the absence of a reasonable operational mechanism can result in low energy utilization, uneven resource allocation, and other issues. Thus, designing an effective MMG operation strategy that balances the interests of all stakeholders has become a key area of focus in the industry. This paper examines the definition and structure of MMGs, analyzes their current operational challenges, compiles existing research methods and practical experiences, explores synergistic operational mechanisms and strategies for MMGs under different transaction models, and puts forward prospects for future research directions.

1. Introduction

The global energy crisis is increasingly becoming a problem due to the overexploitation of fossil resources, long-term dependence, and the imbalance between supply and demand. Against this backdrop, renewable energy technologies such as photovoltaic and wind power have developed rapidly. However, the rapid expansion of renewable energy has significantly impacted the power grid, forcing the traditional distribution network to transform from a passive, non-powered network into an active network integrated with distributed generation. This transformation has not only overturned the original balance between power supply and consumption but also triggered frequent voltage fluctuations while intensifying the changes in power flow in the main distribution network, posing unprecedented challenges to the stable operation of the grid [1]. Microgrid technology is a promising solution to address these challenges. A microgrid is a small-scale power generation and distribution system that includes distributed energy sources, energy storage devices, conversion technologies, loads, monitoring, and protection systems. It is designed to improve the efficiency of distributed energy utilization, enhance regional energy self-sufficiency, and reduce the grid’s load [2,3]. However, the energy imbalance in time and space limits the dispatch capability of individual microgrids. Therefore, this paper explores the cooperative operation of multiple microgrids to significantly increase local consumption of renewable energy and reduce its impact on the grid through energy interactions between microgrids.

In research on microgrid-related topics, model accuracy directly affects the conclusions, making refined modeling critical. Ref. [4] proposed a mechanistic model for multiple devices in a microgrid system, formulated management and scheduling strategies, and tested system operation under different conditions through three application scenarios. Ref. [5] introduced a three-layer information–physical fusion modeling framework, which consists of a physical equipment layer, a control decision layer, and a system optimization layer. This approach uses state machines, multivariate groups, and optimization objectives to establish models at each layer, revealing the control and operation mechanisms of the microgrid system under optimization goals.

To enhance the efficiency of cooperative operations among multiple microgrids and ensure active participation in joint scheduling, a rational joint operation strategy is needed. In [6], source–load–storage coordination and full-time co-optimization both inside and outside the microgrid were considered. Demand response and economic energy storage scheduling were introduced to enhance the self-coordination and self-balancing capabilities of different resources within the microgrid. Ref. [7] proposed a strategy to improve grid-connected MMG systems by leasing shared energy storage (SES) and forming a collaborative microgrid consortium (MGCO). This approach optimizes storage utilization, reduces load fluctuations, integrates renewable energy, and fairly distributes the benefits of cooperation. Ref. [8] proposed a distributed electricity–gas–heat energy sharing mechanism based on the sharing economy, establishing an integrated energy system centered on an energy hub. Through the Stackelberg model, system operators’ and users’ benefits and comfort are optimized, while privacy is protected using distributed algorithms. In addition, Ref. [9] proposed a Nash bargaining-based distributed low-carbon optimal operation strategy for a MMG-integrated energy system, achieving game equilibrium through a distributed solution method.

In recent years, various methods have been employed to solve the optimization problem of cooperative operation among multiple microgrids. For example, [10] constructed a game model involving operators, producers, and consumers using master–slave game theory. By integrating optimization algorithms, this approach demonstrated its advantages in enhancing revenue and optimizing system load. Ref. [11] presented a two-tier, two-stage robust optimal dispatch model for AC/DC hybrid MMGs, dividing the system into utility and supply tiers. This model achieves robust optimization by considering uncertainties at each tier and introduces power constraints and deviation penalty mechanisms for interacting lines to enable cooperative scheduling between the two layers. Ref. [12] explored various applications of artificial intelligence (AI) techniques in microgrids, including energy management, load and generation forecasting, protection, power electronic control, and cybersecurity. AI, through methods such as machine learning, artificial neural networks, fuzzy logic, and support vector machines, addresses challenges in microgrid design and implementation, improving the efficiency, stability, security, and reliability of the system.

Several review articles focus on MMGs. For instance, Ref. [13] discusses energy management systems in interconnected MMGs, outlining their topology, the objectives of the energy management system, and optimal scheduling algorithms. Ref. [14] synthesized the characteristics, architecture, application scenarios, and control mechanisms of MMG systems by utilizing power electronics, control theory, optimization algorithms, and information and communication technologies. Ref. [15] explored key technologies such as network topology, energy scheduling, operational control strategies, and stability analyses in MMG systems. Ref. [16] introduced emerging communication technologies for information monitoring and interaction among microgrids and further investigated the energy scheduling and control strategies of microgrid clusters. Most of the above studies focus on the energy management and control strategies of MMGs, without sufficiently considering the interaction of interests among different stakeholders in MMG systems. To address this research gap, this paper explores the interactions of interests among multiple microgrids and stakeholders from three aspects: operational framework, operational mechanisms, and research methods.

First, the operational framework provides the structural foundation for these interactions, determining the modes of interaction and the division of responsibilities and rights among stakeholders. A well-designed framework is crucial for ensuring efficient coordination among microgrids.

Second, operational mechanisms are the core drivers of resource optimization and market participation. Effective transaction mechanisms can significantly facilitate energy scheduling among microgrids, ensure supply–demand balance, and enhance overall market efficiency.

Finally, research methods offer theoretical and practical tools for addressing complex interaction issues. Through a detailed analysis of the operational framework, mechanisms, and research methods, this paper aims to provide comprehensive theoretical guidance for future research on MMG and multi-stakeholder transactions.

This paper is organized as follows: Section 2 introduces a framework model for the cooperative operation of multi-microgrids; Section 3 describes transaction mechanisms and operational modes for cooperative multi-microgrid systems; Section 4 summarizes the current mainstream research methodologies for multi-microgrid systems; Section 5 presents an outlook for future research in this field; and Section 6 concludes the paper.

2. Operational Frameworks

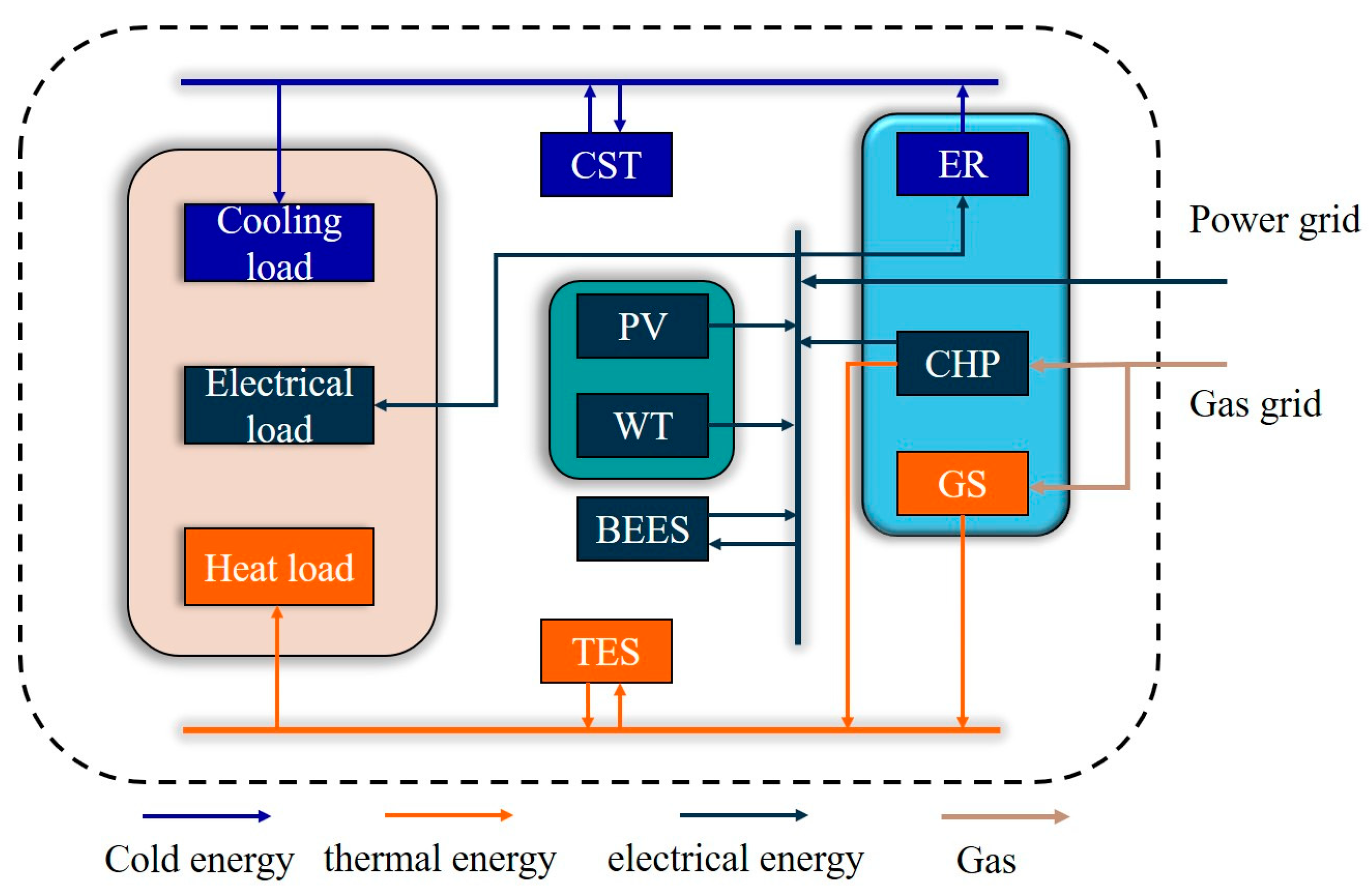
2.1. Operation Framework Diagram of a Single Microgrid

A microgrid typically refers to a regional energy system that includes distributed power generation, various types of loads, energy storage devices, and energy conversion units. It is designed to achieve a certain degree of regional energy self-sufficiency through multi-energy complementarity, as illustrated in Figure 1.

As shown in Figure 1, microgrids usually incorporate renewable energy generation devices such as photovoltaic (PV) panels and wind turbines (WT). Additionally, they accommodate multiple types of loads, including electrical, thermal, and cooling loads. Microgrids also contain various energy conversion units and energy storage devices, such as gas boilers (GB), combined heat and power (CHP) systems, and electric refrigeration (ER) equipment. The energy storage devices in microgrids can store energy in several forms, including electricity, cooling, and heat.

A microgrid functions as a small-scale energy system connected to the external power grid and gas network, purchasing electricity and natural gas from these external sources. The multiple forms of energy and loads within the microgrid are interconnected through their respective busbars. Natural gas is used to generate both electricity and heat via the CHP unit. Electricity purchased from the grid, electricity generated from renewable sources, and electricity produced by CHP systems all converge at the busbars, which are connected to various electrical loads. The system maintains an internal balance of electrical energy by optimally managing the charging and discharging of the battery storage system.

Thermal energy is primarily generated by the CHP and GB units, which convert natural gas into heat. This heat is transported to the thermal energy bus, where the optimal scheduling of thermal energy storage tanks (TES) ensures an effective balancing of local thermal loads. Cold energy is primarily supplied through ER systems, which are connected to the electrical bus. These systems convert electricity into cold energy, which is stored in cold energy storage tanks (CST) and distributed via the cold energy bus to meet local cooling demands. When local energy resources exceed demand, energy can be stored using ER and CST to enhance overall energy utilization [17,18,19,20].

2.2. Multi-Microgrid Centralized Cooperative Operation Framework

As shown in Figure 2, within the MMG centralized operation framework, the upper-level leader acts as an intermediary for multiple microgrids in conducting transactions with the distribution grid. There is no direct interconnection between the microgrids for energy or data exchange, so transactions between microgrids must occur indirectly through the leader. Each microgrid maintains an independent energy management system (EMS) to optimize local loads and calculate energy surpluses or deficits, which are then communicated to the upper-level EMS. The upper-level leader consolidates the energy surpluses and deficits of all microgrids via the energy bus and coordinates and optimizes them to ensure power balance. If the user group cannot achieve energy self-balancing, it must purchase or sell energy from the distribution grid to maintain balance on the bus. In this structure, the leader, acting as an energy hub, typically possesses energy regulation capabilities, such as energy storage and conversion devices, enabling the joint scheduling of multiple microgrids. The benefits of this framework include its structural simplicity and increased grid stability, though it also results in the greater dependency of each microgrid on the operator and lower interaction efficiency [21,22].

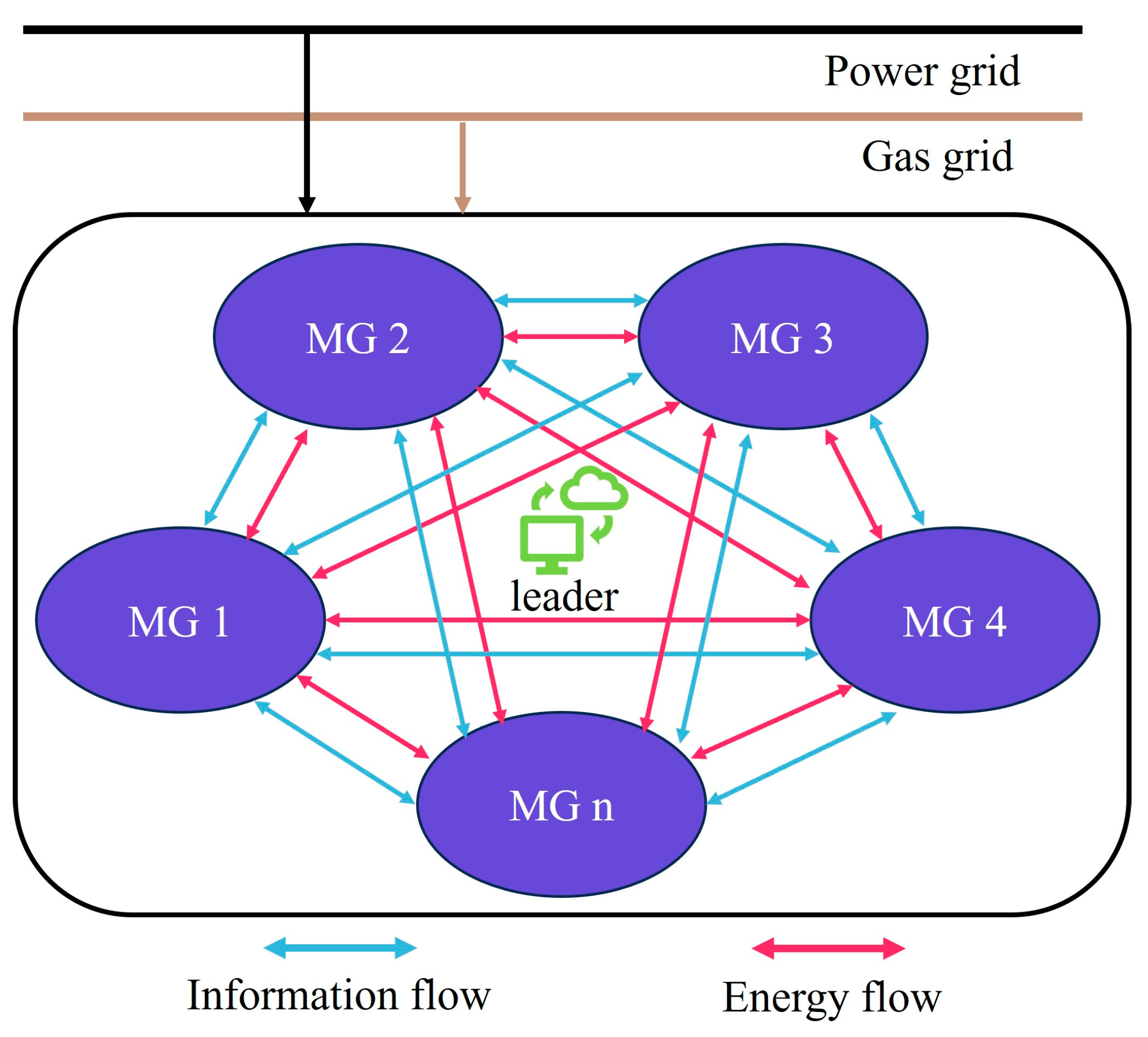
2.3. Multi-Microgrid Distributed Cooperative Operation Framework

As shown in Figure 3, in the distributed cooperative operation framework of MMGs, each microgrid is interconnected via energy and data transmission lines, forming an energy-information network. These microgrids can exchange information on power consumption and energy transmission among themselves. Under this framework, each microgrid can not only optimize and manage its local energy system independently but also share resources and scheduling information with other microgrids, achieving more efficient energy utilization and a more stable system operation.

In the case of local power surpluses or shortages, microgrids support each other through energy transmission lines, reducing dependency on external grids and enhancing the system’s self-balancing capability. Data transmission lines allow microgrids to share real-time information on electricity consumption, energy demand, and supply conditions, making the entire market more open and transparent. Within this model, the role of the leader shifts from acting as a trading agent to focusing on coordination and supervision, ensuring orderly trading and network security.

The distributed cooperative operation mode of MMGs offers high flexibility, allowing for direct energy trading between any two microgrids, which significantly improves trading efficiency. However, the downside of this model is its more complex network structure, increased information density, and higher overall system operation costs [23,24].

3. Operating Model

The operation of an MMG system involves interactions among various stakeholders, and the development of a well-designed trading mechanism can encourage their active participation in transactions, significantly improving transaction efficiency and enhancing the overall economic performance of the system. This paper discusses the impact of demand-side response, shared energy storage, peer-to-peer (P2P) trading, and carbon trading on the operation of the system.

3.1. Demand-Side Response

Demand-side response (DSR) refers to the actions taken by electricity users to adjust their consumption patterns in response to the needs of the distribution system, in exchange for financial incentives. This interaction typically occurs between electricity consumers and distribution network operators but can also take place in other scenarios. A DSR helps to balance peak and off-peak demand, enhance the flexibility of the power system, ensure the safe and stable operation of the grid, and promote the integration of renewable energy sources. MMG systems contain various flexible resources, such as distributed generation, energy storage devices, energy conversion equipment, and controllable loads, making them a key source of demand-side flexibility for the power system [25].

A DSR is generally categorized into price-based and incentive-based models. Price-based demand response encourages users to modify their consumption patterns through time-of-use pricing to meet the grid’s peak-shaving needs. Incentive-based demand response involves network operators issuing specific peak-shaving requests, offering corresponding compensation, and signing contracts to ensure an effective response—essentially engaging in direct energy block transactions [26,27].

In microgrids, network operators can send real-time price signals or load adjustment requests to users through smart meters and other devices. Upon receiving these signals, users can respond by adjusting controllable loads (e.g., air conditioning, electric vehicle charging) or utilizing distributed energy resources and storage systems. By flexibly adjusting their electricity consumption, users can reduce power consumption during peak periods or increase it during off-peak periods, earning financial incentives or reducing their electricity bills while alleviating stress on the grid.

The interests of each participant in a microgrid vary, and implementing different demand response strategies tailored to different types of microgrids is crucial for encouraging user participation in demand-side response programs [28,29]. To address this, response programs can be tailored to the load profiles of different users. For instance, price-based demand response programs, which use the electricity tariff elasticity matrix, can be applied to users sensitive to price changes, while incentive-based programs are suitable for users who respond better to direct financial compensation [30]. Combining these two approaches can yield more effective demand response results. Specifically, distribution network operators can guide microgrid clusters to adjust their energy usage by setting time-of-use tariffs. The microgrid cluster then adjusts its energy usage based on these tariffs and communicates the revised program to the distribution grid operator. If a gap remains between the actual and desired response, the shortfall can be addressed through energy block bidding, thereby minimizing overall system operation costs by integrating both response methods.

There are various energy demands, such as cooling, heating, and power, in the microgrid, so multi-energy coupling demand response can be considered, such as incentive-based thermal load demand response and cooling load demand response that takes into account comfort levels [31]. Additionally, in scenarios such as trading markets based on energy supply–demand ratio pricing strategies, users can adjust their energy use to influence the supply–demand ratio, which in turn affects energy trading prices and optimizes energy costs [32].

In conclusion, microgrid clusters possess significant dispatch potential and are key participants in the demand-side response market. With advancements in renewable energy generation technologies and MMG cooperative control, the future power system will evolve towards greater flexibility, intelligence, and low carbonization.

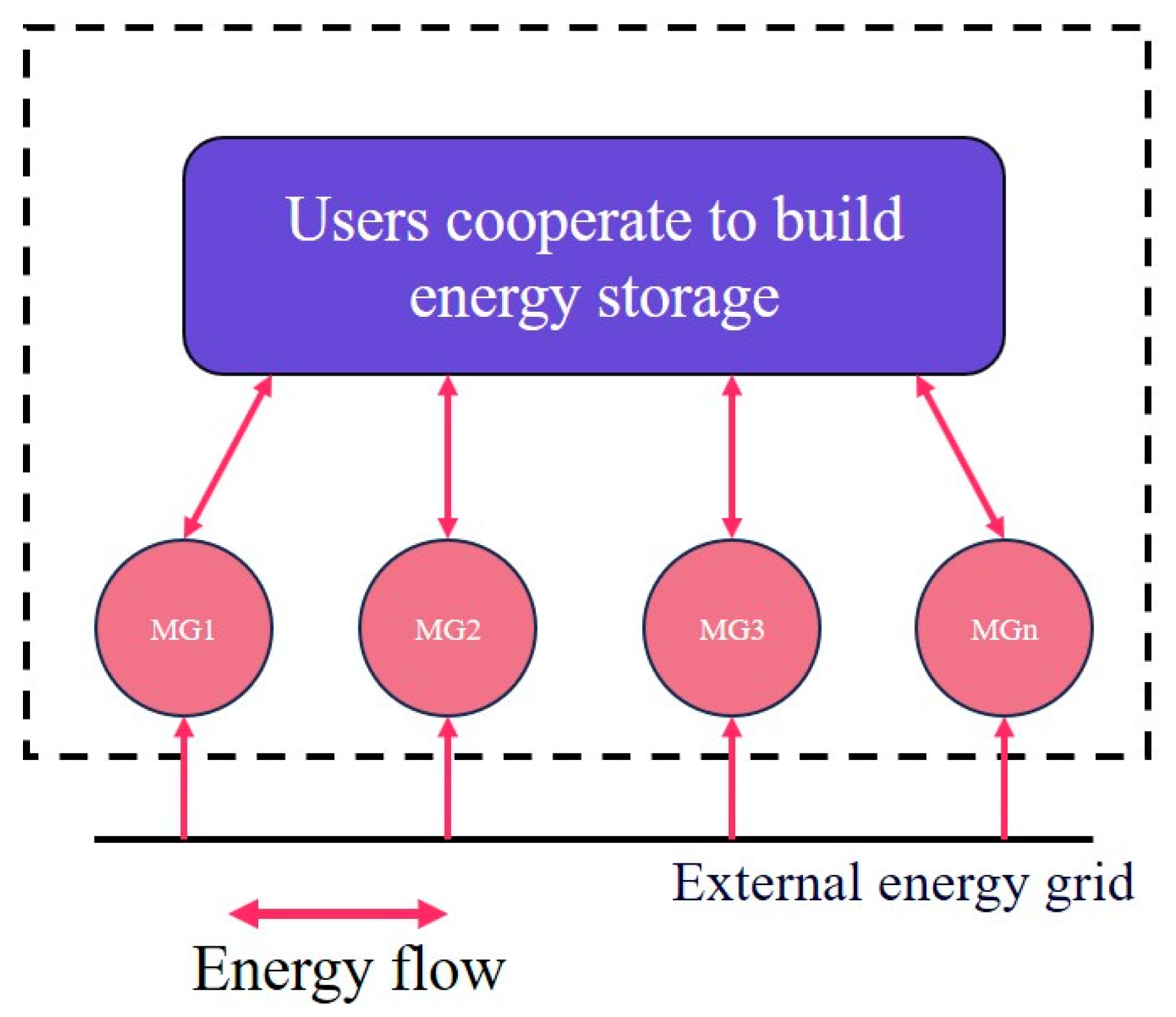
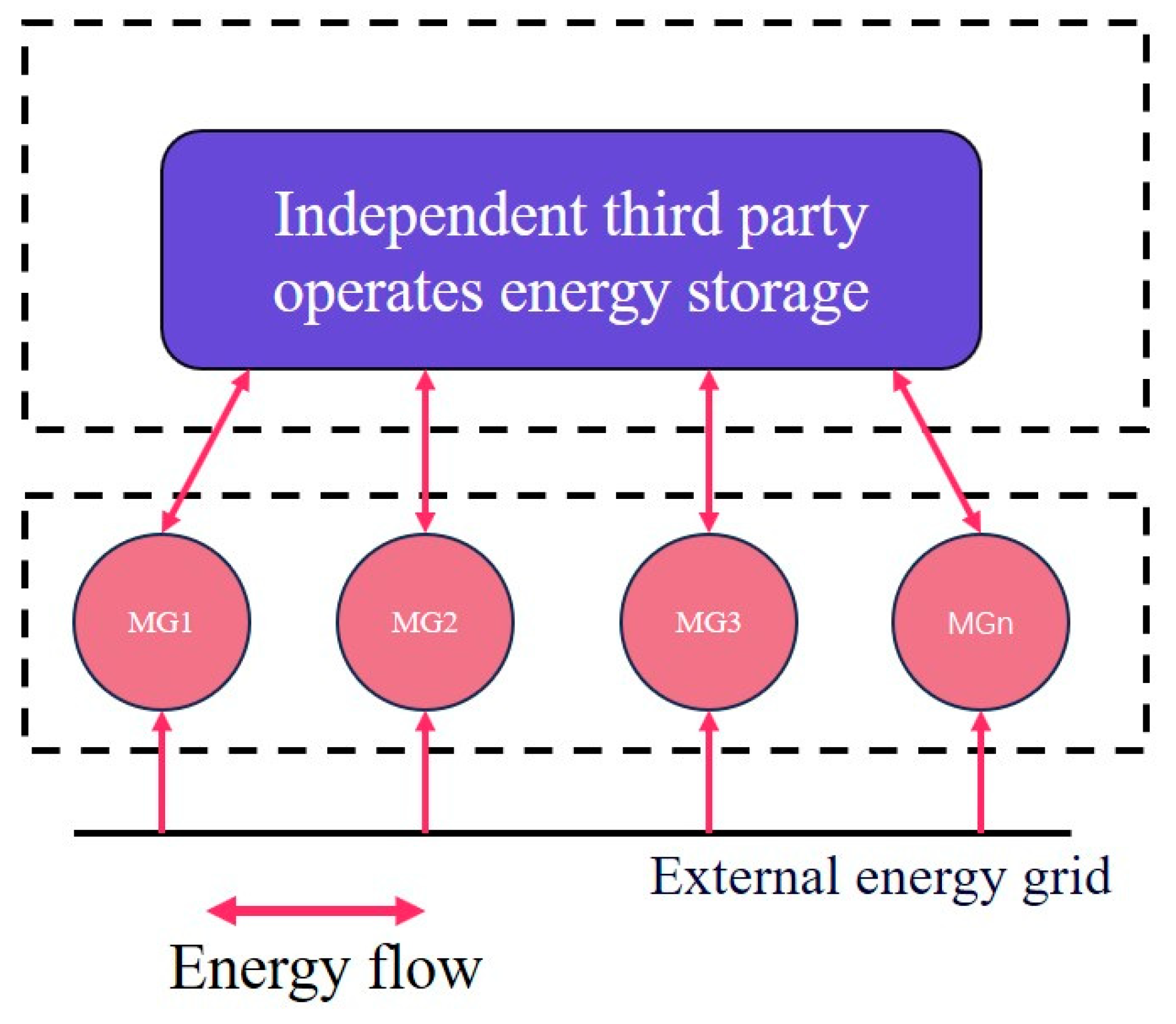
3.2. Shared Energy Storage

In recent years, amidst the booming development of the sharing economy, shared energy storage, as an emerging energy management model, has garnered increasing attention. Its core concept lies in connecting multiple users to a centralized energy storage system, thereby realizing energy sharing and optimized scheduling within a regional scope [33]. Shared energy storage not only enables the storage of surplus renewable energy generated by users, enhancing the utilization rate of renewable energy, but also allows for the storage of low-cost power during off-peak hours and its subsequent release during peak hours, achieving peak shaving and valley filling while simultaneously reaping economic benefits. More importantly, this model contributes to breaking down the isolation of traditional household energy storage, fostering greater coordination in energy use and enhancing overall efficiency [34]. In MMG systems, individual microgrids may possess varying electricity loads, renewable energy generation capacities, and electricity pricing strategies. Shared energy storage can function as a “regulator”, connecting multiple microgrids and enabling better collaborative optimization and resource scheduling [35].

The shared energy storage service model primarily includes two approaches: capacity sharing and energy sharing. In capacity sharing, multiple microgrid users share the capacity of a centralized energy storage device. Each user reserves a certain amount of storage capacity according to their needs and pays for the reserved capacity, which is typically proportional to the amount reserved [36]. In energy sharing, users share the energy from the storage device over a specified period, with fees based on the actual amount of energy used rather than the reserved capacity. In practice, combining capacity and energy sharing modes can leverage their respective advantages to meet diverse user needs. For example, a microgrid user might reserve a specific amount of storage capacity for basic needs and participate in energy sharing to gain additional economic benefits. This combined approach can enhance resource utilization and offer more flexible energy management. Currently, there are two main types of shared energy storage operation modes [37].

In the shared energy storage operation model depicted in Figure 4, microgrids within a region form a cooperative alliance to jointly invest in and operate the shared energy storage system. This model requires careful consideration of cost sharing and profit distribution issues [38]. Ref. [39] proposes a cost-sharing strategy based on generalized Nash bargaining, which accounts for users’ complementary contributions and incorporates these into the evaluation of bargaining power, thereby maximizing fairness in cost sharing. Ref. [40] introduces a profit-sharing method based on the kernel method, which aims to identify an optimal benefit-sharing scheme among all solutions that meet rationality criteria, achieved through linear programming.

In the model illustrated in Figure 5, a third party independently invests in shared energy storage and connects all microgrid users in the region. In this model, the shared energy storage operator provides services to each user through energy trading and capacity leasing to generate profits. Ref. [41] presents a personalized pricing strategy tailored to the price sensitivity of users, which can significantly increase energy storage utilization and reduce costs for users. In the integrated energy microgrid scenario, Ref. [42] proposes a multi-energy coupled shared energy storage plant established by an operator, offering storage capacity leasing services for power, cooling, and heat to microgrid users. This approach facilitates multi-energy interactions among microgrids and prevents individual microgrid users from having to build separate energy storage systems, thus reducing overall system operating costs. In terms of operators’ business strategies, Ref. [43] proposes a credit-based energy storage sharing model. This model adopts a cost-based capacity sharing pricing strategy when the user’s credit is positive and switches to a demand-based energy sharing pricing strategy when the user’s credit is negative. This hybrid strategy effectively increases the net profit of shared energy storage operators.

The primary function of shared energy storage is to balance energy supply and demand both temporally and spatially, promoting energy complementarity between microgrids and mitigating the impact of renewable energy fluctuations on the distribution grid. Through proper configuration and management, the shared energy storage system can regulate the imbalance between energy supply and demand, enhance energy utilization efficiency, reduce waste, and thereby improve the stability and reliability of the power grid. This mechanism not only supports the large-scale deployment of renewable energy but also establishes a solid foundation for the synergistic operation of microgrids and distributed energy systems.

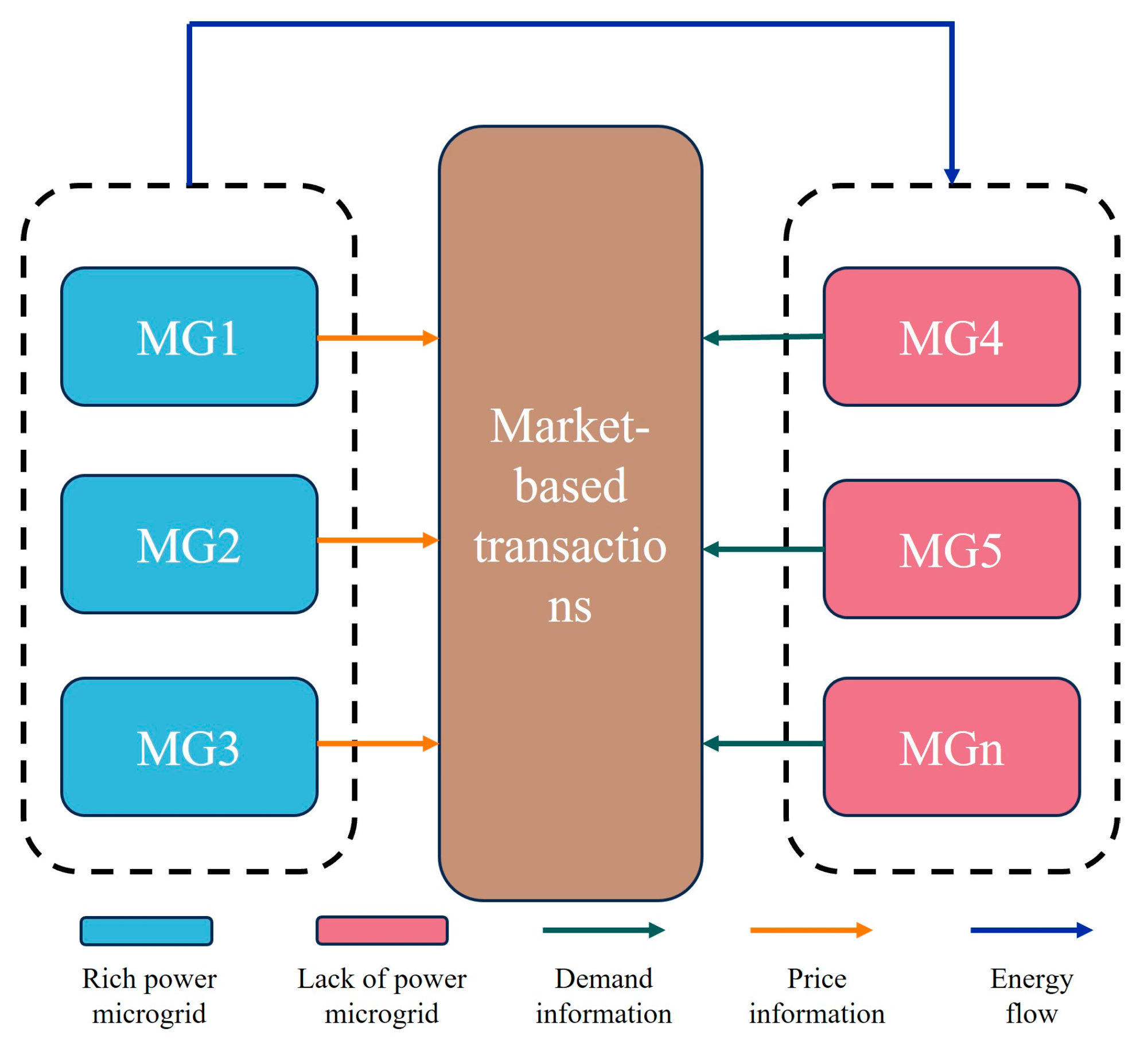
3.3. Peer-to-Peer Trading

Due to the varying penetration rates of renewable energy in different microgrids, power-rich and power-deficient microgrids often emerge within the microgrid cluster. To maintain a power balance between these microgrids, an efficient energy trading mechanism is essential. P2P transactions involve the direct exchange of assets between individuals without intermediaries, with the transaction organizer only charging a service fee. This mode of transaction can effectively reduce costs and improve efficiency, and it has been widely adopted for energy interactions within microgrid clusters. The two primary operational modes of P2P transactions are as follows:

As illustrated in Figure 6 and Figure 7, there are two main P2P transaction models in the current market:

[1]

Centralized Pricing P2P Transaction Model [44]: In this model, users report their needs to a central platform, which sets the prices based on the collected data. Examples include platforms like Didi and Uber.

[2]

Fully Market-Based P2P Trading Model [45]: In this model, the P2P trading center merely provides a platform to facilitate transactions and does not participate in setting transaction prices. Energy prices are negotiated directly among users, similar to platforms like eBay and TaoBao.

Figure 6. Centralized pricing model for P2P transactions.

Figure 6. Centralized pricing model for P2P transactions.

Figure 7. Fully market-oriented P2P transaction model.

Figure 7. Fully market-oriented P2P transaction model.

Both transaction models have their respective advantages and disadvantages. The centralized pricing model simplifies end-to-end transactions and facilitates computation but may overlook individual user preferences. Conversely, the fully market-based model can maximize users’ differentiated benefits but involves greater transaction complexity and computational difficulty.

Under the centralized pricing model, different types of microgrids must be modeled precisely due to their varying energy preferences [46]. Researchers have proposed a P2P transaction pricing strategy based on user energy preferences. This strategy categorizes energy sources according to user preferences (e.g., generation technology, user reputation, economic factors) and integrates these preferences into the user’s utility function. Users who select energy types that match their preferences see increased revenue [44]. This model effectively addresses personalized user needs and promotes fairness in energy trading. Additionally, the supply-and-demand relationship significantly influences energy trading prices. Some studies have proposed a multi-microgrid P2P transaction pricing strategy based on the energy supply–demand ratio, establishing an internal pricing model accordingly. Users can adjust their energy plans to alter the supply–demand ratio, thereby affecting the internal transaction price. Compared to traditional contract pricing models, the supply–demand ratio-based pricing model better guides users in optimizing their electricity consumption and encourages local consumption of renewable energy [47].

In the fully marketized trading model, there are two main operational modes: the cooperative alliance mode [48] and the free competition mode [49]. In the cooperative alliance mode, each sub-microgrid optimizes its own objectives while considering the interests of the entire alliance. In contrast, the free competition mode focuses solely on each sub-microgrid’s own optimization goals, aiming to maximize individual interests.

In the cooperative alliance model, a contribution-based cooperative strategy for multiple microgrids has been proposed. This strategy uses a nonlinear energy-sharing mapping approach to assess the electrical energy contributions of microgrid users and distributes the total profit of the alliance according to these contributions [50]. In a free competition scenario, Ref. [51] introduced a multi-microgrid P2P trading model based on a multi-party bidding mechanism. In this model, power-deficit microgrids post their power demands and desired transaction prices online, multiple power-rich microgrids submit bids, and the power-deficit microgrids select a power-rich microgrid for the transaction based on their optimization objectives. This multi-party bidding scheme better reflects individual rational choices.

Other research has explored financial attributes of energy. For example, Ref. [52] developed a P2P trading model combining equity trading with energy trading and proposed the concept of group producers and sellers. Users share distributed energy sources and storage devices through equity allocation, trading power generation, and storage capacity via equity transfer. This approach enhances user participation in energy trading and promotes renewable energy consumption. Additionally, Ref. [53] suggests a P2P trading network charging strategy that includes network loss costs and network blocking costs, making the P2P trading model more reflective of real-world conditions.

3.4. Carbon Trade

Since the Industrial Revolution, the world’s heavy dependence on traditional fossil fuels, such as coal, oil, and natural gas, has significantly increased greenhouse gas emissions, leading to global warming. From the mid-20th century onward, global warming has gradually attracted widespread attention from various nations. In response to this challenge, several international climate agreements have been established, including the Kyoto Protocol and the Paris Agreement. These agreements set emission reduction targets for industrialized countries and introduced mechanisms like the Clean Development Mechanism (CDM), Joint Implementation (JI), and International Emission Trading (IET), which laid the groundwork for the development of carbon trading systems [54].

Carbon trading refers to the market-based exchange of carbon dioxide emission rights. Its core principle is to set an overall cap on carbon emissions and then distribute allowances to carbon users based on specific allocation rules. If a user’s actual emissions are lower than their allotted quota, the surplus can be sold to those who exceed their limit, thereby enabling the trading of carbon emission rights. Currently, the most commonly used method for allocating carbon quotas in the industry is the baseline approach, in which carbon emission allowances are determined by historical energy use and industry averages. Common methods for calculating carbon emissions include direct measurement, model-based calculation, and the emission factor approach. The emission factor method, proposed by the Intergovernmental Panel on Climate Change (IPCC), is widely adopted due to its data usability [55,56].

As thermal power generation continues to be the primary source of carbon emissions, microgrids that integrate significant amounts of renewable energy naturally hold an advantage in reducing emissions. Compared with traditional power systems, microgrids can provide the same or more energy supply with lower carbon emissions, giving them a competitive advantage in the carbon trading market. Users facing high emission reduction costs can purchase carbon allowances to compensate for their unattainable reduction targets. For governments, the carbon trading mechanism incentivizes society as a whole to lower emissions, helping achieve reduction targets and promoting a green economic transformation.

Currently, extensive research has been conducted in the field of MMG carbon trading. Regarding carbon quotas, Ref. [57] proposes a cross-regional electricity cooperation model based on carbon quotas. It introduces the concept of shared responsibility, compares the effects of the producer responsibility system and the shared responsibility system on cross-regional electricity cooperation, and demonstrates that the shared responsibility system is more effective. Furthermore, it examines the impact of different carbon quota systems on the benefits of cooperation. In terms of carbon emission reduction, Ref. [58] proposes a cooperative scheduling model for MMGs that includes power-to-gas (P2G) and carbon capture and storage (CCS). CCS technology captures carbon dioxide directly from the air and stores it in liquid or solid form for use in the P2G process. P2G occurs in two phases: first, the power-to-hydrogen (P2H) system converts electricity into hydrogen. Then, the hydrogen reacts with the carbon dioxide captured via CCS in a methanation reactor to produce natural gas. This significantly reduces system emissions and enhances the competitiveness of microgrids in the carbon market. In terms of carbon accounting, Ref. [59] proposes a cooperative low-carbon economic dispatch strategy for MMGs considering carbon accounting and profit distribution. An energy–carbon coupled carbon emission accounting model is constructed, which not only considers the carbon transfer generated in energy transactions but also incorporates the environmental benefits brought about by carbon emission reductions into the profit distribution evaluation system. This model can not only accurately account for the system’s carbon emissions but also fairly distribute cooperative profits based on the comprehensive contributions of participants in terms of energy and carbon emission reductions.

In terms of carbon trading, Ref. [60] proposes a tiered pricing method for P2P carbon trading in large-scale interconnected microgrids, where carbon emissions are divided into multiple tiers and higher emissions correspond to higher trading prices. Compared to fixed carbon pricing, this tiered approach more effectively incentivizes users to reduce their carbon emissions. Ref. [61] suggests a decentralized microgrid model combined with carbon emission trading, integrating power and carbon trading while accounting for both individual and overall carbon emission limits. This method optimizes resource allocation and effectively controls system-wide carbon emissions. Ref. [62] introduces an MMG trading model that considers energy, green certificates, and carbon coupling. It establishes a cooperative sharing framework within microgrid clusters and implements an internal pricing mechanism based on the elasticity of the supply–demand ratio, balancing the low-carbon and economic aspects of microgrid cluster operations.

In summary, the carbon trading mechanism provides significant economic incentives for multi-microgrids to reduce carbon emissions. By integrating renewable energy technologies, various energy conversion, and storage methods, microgrids exhibit notable advantages in the carbon trading market. Furthermore, the innovative model combining carbon trading with MMG transactions effectively enhances resource utilization efficiency and carbon emission reduction effects, providing crucial support for promoting green transformation across society. The carbon trading system not only strengthens the competitiveness of microgrids but also offers a practical path to achieving global climate goals and the low-carbon development of energy systems [63].

4. Research Methodology

The cooperative operation of MMGs involves several issues, including the balanced distribution of benefits, the protection of personal information, and the management of uncertainty risks. To address these concerns, this chapter introduces the corresponding research methods for each.

4.1. Equilibrium Distribution of Benefits Problem—Game Theory

In the study of MMG transactions, the competition and cooperation between multiple agents present a high level of complexity. Each microgrid acts as an independent decision-maker, inevitably leading to conflicts of interest during power trading and resource allocation. Under such circumstances, how to coordinate the behavior of these agents, optimize resource allocation, and ensure fairness and efficiency in transactions becomes a crucial issue that needs to be addressed.

Game theory plays an irreplaceable role in resolving these issues. First, game theory can effectively analyze the strategic choices and mutual influences among multiple agents, depicting the dynamics of competition and cooperation between them. Second, by designing appropriate incentive mechanisms, game theory can facilitate coordination among agents, achieving the maximization of overall benefits. In terms of market mechanism design, game theory provides theoretical support for constructing fair and efficient transaction mechanisms and price formation mechanisms.

In multi-agent transaction problems, non-cooperative games [64], cooperative games [65], and Stackelberg games [66] are the three most commonly used game models. Starting from the optimal decision-making problem of a single microgrid, the optimal decision of an individual agent typically falls within the domain of operation research, and its optimization model can be represented as follows:

$$\begin{array}{cc}\hfill \min :& f(x)\hfill \\ \hfill s.t& Ax=0\hfill \\ & Bx<0\hfill \end{array}$$

(1)

Here, $f(x)$ represents the optimization objective, $x$ is a set of strategies, and the equality and inequality constraints limit the range of $x$, forming a feasible strategy set. The above equation introduces the three essential elements of a game: decision-makers, optimization objectives, and strategy sets.

Further discussing multi-agent decision-making problems, in a multi-agent decision problem where conflicts of interest exist among agents, if each agent makes decisions based solely on its own known information and considers only its own interests, a non-cooperative game problem can be formed. In a non-cooperative game problem, let the set of participants consisting of n agents be denoted as P = {$p_1$,$p_2$……$p_n$}, and let the strategy space of a single agent be denoted as z = {$s_1$,$s_2$……$s_k$}. Then, the strategy set of multiple agents is S = {$z_1$,$z_2$……$z_n$}, and similarly, the set of optimization objectives for multiple agents is F = {$f_1$,$f_2$……$f_n$}.

When none of the agents in the set can benefit by unilaterally changing its own strategy, the non-cooperative game model is said to have reached a Nash equilibrium, denoted as $S^{*}$. For any $s_i^{*}$ in $S^{*}$, the following relationship holds [67]:

$$f_i(s_i^{*},s_{-i}^{*})\ge f_i(s_i,s_{-i}^{*}),\forall s_i\in z_i$$

(2)

In the equation, $s_{-i}$ represents the strategies of all other agents except for $s_i$.

In a non-cooperative game, participants often focus solely on maximizing their own interests. However, in a cooperative game, participants can negotiate and cooperate to pursue the maximization of collective benefits, making the total gain of all participants greater than the sum of their individual gains when acting alone. The cooperative game model can be represented as follows: let a cooperative coalition be M = {$m_1$, $m_2$……$m_n$}, and let the payoff distributed to each agent in the coalition be denoted as C = {$c_1$,$c_2$……$c_n$}. A characteristic function v(x) is defined to calculate the payoff of both the coalition and individual agents. A cooperative game must satisfy the following conditions [68]:

[1]

Individual Rationality Condition: The payoff allocated to each individual after joining the coalition must not be less than the payoff the individual would have received by acting alone. This can be expressed as follows:

$$c_i\ge v(m_i),\forall i\in N$$

(3)

[2]

Collective Rationality Condition: The total revenue of the cooperative alliance should not be less than the sum of the revenues of each individual operating independently, expressed as follows:

$${\displaystyle \sum _{i=1}^N{c}_i}\ge {\displaystyle \sum _{i=1}^{N}v(m_i)},\forall i\in N$$

(4)

In multi-agent game theory, there is a class of multi-stage decision problems where the decisions made by various participants influence one another and follow a certain sequence. Participants who make decisions first typically hold an advantage or a leadership position, allowing them to set strategies or rules. These participants are called leaders in the game, while those who make decisions later, based on the leaders’ strategies or rules, are referred to as followers. This type of model is known as a Stackelberg game model and is often used in games involving participants at different hierarchical levels. For example, in the context of MMG transactions, microgrid operators typically act as price setters, positioned at the upper level of the game model. Microgrid users, in turn, respond to the prices set by the operators, formulating their energy consumption strategies at the lower level. The decisions between the two levels are mutually influential, and both parties continually adjust their strategies until neither can improve their benefits through unilateral changes, reaching what is known as the equilibrium of the Stackelberg game.

When dealing with complex multi-agent game problems involving multiple levels and diverse interest relationships, a single game model may no longer be sufficient to describe the interactions. A combination of different game models can yield better results. For instance, in a game involving multiple microgrid users and operators, a multi-leader multi-follower Stackelberg game model can be constructed from the perspective of decision-making sequences. Furthermore, there may also be interest relationships among participants at the same level. Microgrid users at the lower level often aim to minimize their energy costs, with a shared objective of maximizing collective benefits, making a cooperative game model suitable for this layer. Meanwhile, multiple operators at the upper level are in competition for limited user resources, where conflicts of interest are more pronounced, making a non-cooperative game model more appropriate. In summary, when constructing a game model for specific scenarios, it is essential to consider both the hierarchical and interest relationships among participants to create the most suitable hybrid game model. The relevant applications of game theory in the coordinated operation of MMGs are shown in

Table 1. The application of game theory in the problem of multi-microgrid collaborative operation.

Document Number	Non-Cooperative Game	Cooperative Game	Stackelberg Game
[64,69,70,71,72,73]	✓
[68,74,75,76,77]		✓
[78,79,80,81,82,83]			✓

.

4.2. Personal Information Protection Issues—Blockchain Technology

In the distributed and cooperative operation of multiple microgrids, ensuring the accuracy and privacy of information is crucial due to the complex information network formed through their interconnection. Blockchain technology, which relies on cryptographic principles and distributed computing, provides a solution for data storage, transmission, and verification. Its core feature is the linking of data into an ever-growing chain of blocks, each containing transaction information for a specific time period, with cryptographic methods ensuring data security and integrity. Key features of blockchain include decentralization, transparency, security, and immutability. Decentralization eliminates the need for a central administrator, with all participants collaborating to maintain the network. Transparency ensures that all transactions and data records are openly visible, while security and immutability are achieved because each block contains the hash value of the previous block, making any tampering immediately noticeable to other nodes [84].

Blockchain technology plays a crucial role in MMG transactions, as outlined below:

[1]

Security: Blockchain ensures transaction security by recording each energy transaction on the blockchain and encrypting it with cryptographic methods, making the data resistant to tampering or forgery.

[2]

Immediate Settlement: Blockchain facilitates immediate transaction settlement and clearing. As transaction records are updated and shared in near real time, energy transactions between microgrids can be settled swiftly, reducing time and management costs.

[3]

Smart Contracts: Blockchain’s smart contract functionality offers enhanced transaction flexibility and automation. These pre-programmed contracts automatically execute based on predefined conditions, such as dynamically adjusting energy trading strategies based on market prices or allocating energy resources according to environmental conditions.

Blockchain technology has seen widespread application in multi-microgrid P2P transaction scenarios. In terms of data recording, Ref. [85] introduces a mechanism that utilizes proof of work (PoW), where the node that completes the workload first is responsible for packing and creating a new block. Homomorphic encryption and the Practical Byzantine Fault Tolerance (PBFT) consensus mechanism, as discussed in [86], effectively ensure data privacy and security. Additionally, Ref. [87] explores replacing the original fragile communication scheme with blockchain technology, thereby mitigating the impact of Forged Data Injection Attacks (FDIA). Ref. [88] employs the concept of mining to incentivize users to sell surplus power to meet system power demand. Users compete for mining eligibility with their surplus power, and those who qualify must pledge their surplus power to receive rewards. The reward is proportional to the contribution, and if the current miner cannot balance the demand, a secondary miner is selected until the system achieves power balance. To enhance trust between microgrids, Ref. [89] proposes a random information transfer mechanism based on blockchain smart contracts, which replaces the traditional fixed communication topology and helps prevent collusion.

Overall, blockchain technology offers a robust solution for secure transactions and information management in MMG systems through its decentralized, encrypted, and smart contract features, demonstrating broad potential in energy management and communication security [90].

4.3. Uncertainty Risk Problem—Robust Optimization

Uncertainty has a significant impact on MMG transactions, including fluctuations in renewable energy supply, changes in market prices, uncertainty in user load demand, and equipment failures. These factors lead to supply–demand imbalances, unpredictable transaction profits, and low energy utilization efficiency. In recent years, extensive research has been conducted to address uncertainty, primarily focusing on stochastic optimization, robust optimization, and distributed robust optimization.

Consider an optimization problem where the decision variable is p and the uncertainty variable is d, with the profit function denoted as $f(p,d)$. Both the user’s decision and the uncertainty variable influence the user’s final profit, making it impossible to maximize the profit by optimizing a single variable. If the value of the uncertainty variable, denoted as $d^{*}$, could be known in advance, the problem would transform into a deterministic optimization problem:

$$\underset{p}{\max } f(p,d^{*})$$

(5)

This is easy to calculate, but in most cases, the uncertainty variable d is unknown. If the distribution of d is denoted as m, the problem then transforms into a stochastic optimization (SO) problem. SO can be solved by calculating the expected value of the uncertainty variable:

$$\underset{p}{\max } E_m(f(p,d))$$

(6)

If the distribution of d is also unknown and only a range of possible distributions exists, robust optimization (RO) can be used for solving the problem. The core idea of RO is to find the worst-case distribution within the range of possible distributions and determine the optimal decision under this worst-case scenario [91]. Since this decision is still applicable under the worst-case distribution, it is considered to be applicable under all possible distributions. Denote a possible distribution as q and the set of possible distributions as Q. The optimization problem can be formulated as follows:

$$\underset{p}{\max } \underset{q\in Q}{\min } E_q(f(p,d))$$

(7)

However, decisions made using RO can be overly conservative, sacrificing too much economic efficiency for stability, and such extreme distributions are generally unlikely in real situations. To balance both stability and economic efficiency, some researchers have proposed using distributionally robust optimization (DRO) [92]. In DRO problems, the distribution of d remains unknown, but methods can be used to describe the distribution trends of d, such as moment-based fuzzy sets, distribution distance-based fuzzy sets [93,94], and distribution feature-based fuzzy sets [95]. Denote a moment-based fuzzy set as I, where I is a proper subset of Q. The DRO optimization problem can be expressed as follows:

$$\underset{p}{\max } \underset{q\in I}{\min } E_q(f(p,d)),I\in Q$$

(8)

From the above expression, it can be seen that compared to robust optimization problems, DRO problems eliminate some distributions with very low probabilities while ensuring the economic efficiency and stability of the system.

Through stochastic optimization, robust optimization, and distributionally robust optimization, MMG transactions can achieve higher robustness in dealing with uncertainties. In specific scenarios, the choice of the optimization method should be based on robustness requirements and data availability. For instance, if the distribution information of the uncertainty variable is fully known, stochastic optimization should be preferred. If the system has very high robustness requirements, such as in scenarios with significant risks, like extreme weather or equipment failures, robust optimization should be used. If the uncertainty variable information is unknown but the system does not require absolute robustness, distributionally robust optimization can be considered to balance economic efficiency and robustness. The relevant applications of these three uncertainty optimization methods in the coordinated operation of MMGs are presented in

Table 2. Application of uncertainty optimization methods in microgrid operation issues.

Document Number	SO	RO	DRO
[78,96,97,98,99,100]	✓
[101,102,103,104,105]		✓
[106,107,108,109]			✓

.

5. Future Outlook

In the field of research on interactions of interests among multiple microgrids and stakeholders, although significant progress has been made, there are still numerous challenges and opportunities ahead.

First, regarding the collaborative operation framework of microgrids, system scalability could be a challenging issue. As the number of microgrids and trading entities increases, existing centralized and decentralized frameworks may struggle to handle the vast amount of information and energy flows generated during transactions, potentially leading to information congestion and network bottlenecks. Therefore, developing more flexible and scalable operational frameworks will be a major research direction in the future.

Second, the design of operational mechanisms still needs further optimization. Current mechanisms may not fully account for the complex interests among stakeholders and the dynamic changes in the market environment. Future research should focus on designing more adaptive operational mechanisms that maintain incentive compatibility under varying market conditions, promote cooperation, and ensure fair trading. Additionally, mechanisms such as P2P trading and carbon trading face technical and policy barriers related to large-scale deployment, which require further exploration.

Lastly, in terms of research methods, uncertainty and risk management will be key areas of focus. Current research may not be comprehensive enough in uncertainty modeling. Many existing models might only consider a single uncertainty factor, such as energy supply–demand fluctuations, while neglecting the interactive effects of other uncertainties, like market price volatility and policy changes. This limitation may prevent models from accurately reflecting the complex situations encountered in actual operations, potentially leading to suboptimal decision support. Designing more comprehensive and integrated uncertainty modeling methods will be crucial for future research. Moreover, incorporating advanced artificial intelligence and machine learning technologies into the prediction and optimization processes of MMG transactions could further enhance the system’s level of intelligence.

6. Conclusions

The paper provides a comprehensive discussion on the collaborative operation model of multiple microgrids from three aspects: the operational framework, operational mechanisms, and research methods. In terms of the operational framework, the paper starts with the framework of a single microgrid, introducing both centralized and decentralized operational models. It analyzes the operational modes and advantages and disadvantages of each model. Regarding operational mechanisms, the paper covers four main mechanisms: demand response, shared energy storage, P2P trading, and carbon trading. It delves into the interactions of interests among different stakeholders within these mechanisms. In terms of research methods, the paper addresses core issues in MMG and multi-stakeholder transactions, such as resource allocation, efficient information transmission, and uncertainty risk. It discusses three research methods—game theory, blockchain, and robust optimization—and explores their applications in enhancing system stability and transaction efficiency. Finally, the paper offers an outlook on future research based on the current state of the field.

In summary, the paper thoroughly examines the current research status and future prospects of MMG collaborative operation and multi-stakeholder transactions from the perspective of interest interactions. The work aims to provide theoretical guidance for addressing the issues of interest interactions among multiple microgrids and stakeholders, exploring market-based approaches to energy trading, and advancing the optimization and innovation of energy utilization patterns.