Abstract
Harmonics in the power grid contribute to increased power losses in both the core and windings of power transformers. These losses lead to abnormal rises in temperature causing overheating and reduce the efficiency of the transformer. If the losses and temperature exceed the values set during the design stage for linear load conditions, it can damage the transformer’s insulating materials and shorten its lifespan. To assess the thermal impact of power system harmonics on transformers under steady-state and transient conditions, the rated losses and harmonic losses of the transformer are calculated. These losses are then inputted into a developed thermal 3D finite element method (FEM) performance model to determine the temperature distribution of transformer components. The numerical results from the thermal model will be compared with data from a Hyundai test report and real measurements from Egypt’s Kureimat power plant, specifically a 750 MW combined cycle power plant. The thermal modeling is focused on a step-up (16.5/240 kV), 240 ± 4 × 2.5%, 180/240/300 MVA power transformer operating in ONAN, ONAF1, and ONAF2 modes. This paper shows that the developed model aligns closely with actual measurements and the HYUNDAI test report. The loss calculations reveal that the discrepancy in total losses, with and without accounting for harmonics, becomes more pronounced as the load increases. Using this model, the presence of grid harmonics results in a higher temperature distribution across transformer components, leading to an increase in the hot spot temperature.
1. Introduction
In electrical power systems, the power transformer stands out as the most costly and significant element. To counteract the elevated losses caused by harmonic currents, the transformer must undergo thermal expansion. Nowadays, the use of non-linear loads places additional strain on supply transformers, leading to increased inherent losses that can reinforce machine aging or lead to failure [1].
Transformers are usually designed to operate at their specified frequency under a linear load. However, when a non-linear load is present, it generates harmonic currents [2]. The presence of harmonic currents elevates losses in both the winding and the structure of the transformer, while harmonic voltages contribute to losses in the magnetic core. The skin effects result in increased heat dissipation in the windings, leading to losses such as harmonic losses, eddy currents, core losses, and the square of the rms current.
Harmonic distortion primarily impacts transformer losses, including ohmic, eddy, and stray losses influenced by harmonic current loads. Previous research has explored the effects of harmonics on power transformer losses over time [3,4], yet these efforts often overlooked harmonics requirements.
To enhance clarity, it is important to include information on harmonic content in terms of Total Harmonic Distortion (THD), as well as the characteristics of harmonic sources. THD is a measure of the distortion of the voltage or current waveform caused by the presence of harmonic frequencies. It quantifies how much of the signal is made up of harmonics as a percentage of the fundamental frequency. A high THD indicates significant harmonic distortion, which leads to increased eddy currents and higher transformer losses, especially in the windings and core.
Harmonic Sources include industrial equipment such as variable speed drives, uninterruptible power supplies (UPS), electric arc furnaces, and power electronic devices. Each harmonic source has unique characteristics that determine the magnitude and order of harmonics they produce. For instance, VFDs often introduce lower-order harmonics (e.g., 5th, 7th), while UPS systems can generate a wider spectrum of harmonics.
Understanding the nature of the harmonics impacting the transformer—both the frequency spectrum and amplitude—provides valuable insights into the impact on transformer thermal performance. Harmonics can lead to increased I2R losses, heating, and reduced transformer lifespan. Furthermore, harmonics raise the eddy current losses in transformer cores and windings, exacerbating temperature rise and potentially requiring more robust cooling mechanisms.
As Total Harmonic Distortion (THD) rises, transformer losses increase, leading to higher temperatures and reduced performance [5,6]. Ref. [7] experimentally measured harmonic current distortion and calculated transformer efficiency under nonlinear loads, showing that efficiency improves as THD decreases. Additionally, non-sinusoidal voltages cause extra core losses, but these are less impactful compared to THD-induced load losses. Ref. [8] found that eddy current and resistance losses in transformer windings increase exponentially with higher frequency, leading to an exponential rise in winding hot-spot temperature. The influence of higher harmonics on transformer losses was further examined in Ref. [9], determining the no-load losses for various harmonic voltages and currents, along with their phase values. Ref. [10] quantitatively evaluated the non-sinusoidal steady-state operation of transformers by examining loss distribution and found that nonlinear loads cause significant distortion in electric current waveforms. This results in extra losses and thermal stress in the power system, raising the transformer’s hot-spot temperature, which may degrade insulation and shorten transformer life. Ref. [11] concluded that the impact of harmonics from residential loads on a transformer is proportional to the square of the transformer current’s THD. Finally, Ref. [12] analyzed how harmonic currents affect winding resistance, eddy current, and stray losses, revealing that higher harmonic distortion and frequency cause faster load loss increases.
Recent studies focusing on the behavior of power loss due to nonlinear loads and challenges in low power quality have become more prominent with the rise of the smart grid concept. Investigating the impact of nonlinear loads on transformers has become a key area of research [13,14,15,16,17,18]. Much attention has been directed towards assessing how voltage and current harmonics affect power transformers [19].
Notably, there has been a lack of comprehensive studies on temperature distribution methodology within power transformers to examine the impact of grid harmonics using thermal models.
In the paper recently published by the authors [20], a thermal model was developed and validated against experimental results to investigate the temperature distribution inside a three-phase oil-insulated power transformer. The finite-element technique was used to obtain the steady-state temperature distribution and the transient temperature distribution at fixed time intervals at any specified location within this kind of transformer.
Therefore, in this paper, the 3D thermal model is used and tailored to carry out the harmonic impacts on the transformer thermal performance in both steady-state and transient conditions over 24 h with actual loads. Harmonic losses were evaluated for different loads (180 MVA/240 MVA/300 MVA), comparing losses (copper, eddy current, and stray losses) with and without considering harmonics based on the transformer’s loading. Additionally, the model determined temperature distribution and identified hot spots within the power transformer.
In this study, the focus is on modeling a Generation Transformer (180/240/300) MVA with specifications of (16.5/240 KV), situated at the Kureimat Power Plant (750 MW—Combined Cycle) in Egypt. The aim is to create a 3D thermal model using Finite Element Method (FEM) based on the fundamental heat transfer principles in ANSYS. The objectives outlined in this paper are as follows:
- Validate the model’s accuracy by comparing temperature distributions against a HAUNDAI test report’s data, specifically focusing on linear loads and disregarding grid harmonics.
- Analyze the 3D model considering the impact of grid harmonics (nonlinear load) by calculating harmonic losses, incorporating these losses into the model, and comparing results with measured temperatures of the Generation Transformer (300 MVA, 16.5/240 KV) at Kureimat Power Plant.
- Investigate the effects of varying transformer loads on ohmic, eddy current, and other stray losses concerning grid harmonics.
- Generate transient simulations to observe temperature variations in transformer components over time, considering harmonics induced by actual loads, with simulations running for 24 h under variable loads.
- Utilize a pyrometer measuring device to verify the modeled tank temperature against calculated values.
2. Methodology
The methodology employs ANSYS 19 software to develop a 3D model of a power transformer using the Finite Element Method (FEM). This transformer is a three-phase oil-immersed unit connected to a turbo generator, designed to step up the voltage from 16.5 kV to a transmission level of 220 kV using a Delta-Star Connection. The methodology for analyzing the impact of grid harmonics on the model’s thermal performance involves the following steps:
- Creating a 3D thermal model with ANSYS software, based on the actual dimensions and geometry of the transformer [21]. The transformer structure includes components such as the external tank, insulating oil, iron core, and copper windings (HV and LV).
- Calculating transformer losses in two scenarios:
- Without considering harmonic measurements for three different loads (300, 240, and 180 MVA at full load).
- Considering the harmonic losses by using current harmonic measurements and substituting them into loss factors equations to determine the I2R, eddy current losses, and other stray losses at different loads (180, 240, and 300 MVA).
- Applying these losses as inputs to the model so the ANSYS model can calculate the temperature distribution based on these losses.
- Analyzing the temperature distribution within the transformer under different load conditions using the models.
- Verifying the accuracy of the FEM model predictions using the test report from Hyundai.
- Comparing the temperature distribution results from the FEM analysis in both scenarios to evaluate the effect of grid harmonics.
- The pyrometer device is used for measuring the transformer tank temperature for several points and compared with the calculated value.
In this study, Finite Element Method (FEM) is a powerful tool used for analyzing temperature distribution in complex structures like power transformers. Here are some advantages of using FEM over Computational Fluid Dynamics (CFD) Simulation Software for example:
- ▪
- Accuracy in Solid Structures: FEM is particularly well-suited for analyzing the temperature distribution in solid structures. Power transformers have complex solid geometries, and FEM can provide highly accurate results for heat conduction within these solids.
- ▪
- Mesh Flexibility: FEM allows for greater flexibility in meshing complex geometries. It can easily handle irregular shapes and varying material properties, which are common in power transformers.
- ▪
- Integration with Structural Analysis: FEM is often integrated with structural analysis tools. This allows for simultaneous analysis of thermal and mechanical stresses, providing a comprehensive understanding of the transformer’s behavior under different operating conditions.
- ▪
- Efficiency in Solving Equations: FEM uses variation methods to minimize error and efficiently solve the governing equations for heat transfer. This can be computationally less intensive compared to CFD, which often involves solving complex fluid flow equations alongside heat transfer.
- ▪
- Simplicity for Steady-State Problems: For steady-state thermal analysis, FEM can be simpler to set up and solve compared to CFD, which requires detailed modeling of fluid flow and turbulence, which can be unnecessary if the primary concern is heat conduction in solids.
- ▪
- Reduced Computational Resources: FEM generally requires fewer computational resources for thermal analysis in solids compared to CFD, which can be highly demanding due to the need to resolve fluid flow fields and their interactions with heat transfer.
3. Transformer Losses under Harmonic Conditions
The increase in non-linear loads over recent years has led to a deviation from sinusoidal load currents. This non-sinusoidal current causes the transformer to experience higher losses and temperatures.
The losses in transformers are categorized into two main types: PNL iron core losses and PLL load losses, which encompass winding losses and stray losses [22].
The load loss PLL can be calculated using Equation (2) and includes the following components: P, which represents ohmic current losses in windings, PEC, which stands for eddy losses in windings, and POSL, referring to other stray losses caused by structures other than windings [23].
There is currently no test method available to distinguish between winding eddy losses and stray losses in structural components. Total stray losses (PTSL) are determined by subtracting the load losses measured during the impedance test from the ohmic current losses.
3.1. Ohmic Current Losses
The calculation involves monitoring the increase in winding current caused by the harmonic component. As the load current increases, so do these losses. Equation (4) details the ohmic loss in the winding under harmonic conditions [23].
where
- R: winding resistance
- Ih: rms current at harmonic (h)
- h: harmonic order.
3.2. Eddy Current Loss in the Windings
The eddy current loss of windings is proportional to the square of current and the square of harmonic frequency in harmonic conditions. In Equation (5), it represents a fraction involving the square of the current and the harmonic frequency in the harmonic state [23].
where PEC-R is rated eddy current loss of windings, Ih is the current related hth harmonics, IR is rated load current, and h is the order of harmonics. Also, the harmonic loss factor for eddy current loss of winding can be expressed as follows [23]:
3.3. Other Stray Losses
Because of the relationship between electromagnetic flux and conductor, voltage is induced in the conductor, causing eddy currents to flow, which raises the temperature and causes loss. Another type of stray loss is a portion of the eddy current loss generated in the structural components of the transformer, excluding the windings [23,24]. Various factors contribute to this, such as the size of the core, the voltage class of the transformer, the construction materials used in the tank structure, and the clamps [25].
POSL-R is the other stray losses at rated sinusoidal load and POSL is the corresponding losses under non-sinusoidal loads.
The loss factor for other stray losses:
Under non-sinusoidal currents, it is only necessary to multiply the rated other stray loss by harmonic loss factor FHL-STR.
Therefore, when dealing with nonlinear currents, the harmonic loss factor is increased by the ohmic loss, eddy current, and other stray losses. In the presence of harmonics, the FHL-STR factor increases other stray losses, the FHL factor increases eddy current loss, and the I2R loss factor increases I2R loss.
4. Estimating and Analyzing Harmonic Loads’ Transformer Losses and Capacity
The study involves calculating losses for three different loads (300, 240, and 180 MVA at full load), considering the influence of grid harmonics. This calculation relies on the computation of harmonic loss factors, based on the harmonic scaling data provided in Table 1. Subsequently, Table 2, Table 3 and Table 4 facilitate the calculation of corrected eddy current loss and other incidental losses.

Table 1.
Measured values of harmonic currents.

Table 2.
Losses at full load (300 MVA).

Table 3.
Losses at load (240 MVA).

Table 4.
Losses at load (180 MVA).
The calculation is based on actual measured harmonic currents at the transformer’s LV terminals when the LV side is supplied with a rated voltage of 16.5 kV and a frequency of 50 Hz. The harmonic currents considered (measured) in relation to the 1st harmonic current are indicated in the tables reported in [21].
For determining eddy currents and other stray losses, one can refer to the International Standard Recommendations [19] applicable to oil-filled distribution transformers as shown in Equation (9). The total stray losses for the transformer under consideration are documented in the Hyundai test report [21] for each load condition.
5. The Thermal Model for the Transformer
The distribution losses of the model are determined using the transformer loss equations provided in Section 3 of the article, based on the data from the Hyundai Test Report (Technical Documentation) [21]. The calculated loss values for the transformer, as shown in Table 2, Table 3 and Table 4, are applied to the thermal model according to each specific case.
Before using the power transformer model to evaluate harmonic impacts, it is essential to confirm its accuracy. The fundamental assumptions for the proposed thermal model of this transformer type include the uniform distribution of heat generated per unit volume per unit time within the iron core and the insulation at the tank base. The winding configuration, arrangement, and cooling method greatly influence the complex heat distribution within the windings. To simplify the analysis, winding insulation is excluded due to its lower dielectric loss compared to copper losses in conductors. Ambient temperature measurements are consistently considered, and the thermo-physical properties of transformer materials and oil, which vary with temperature, are detailed in [26]. Only ¼ of the transformer was modeled, as shown in Figure 1, due to the symmetry on the x and y axes of the transformer. This simplification reduces computation time.
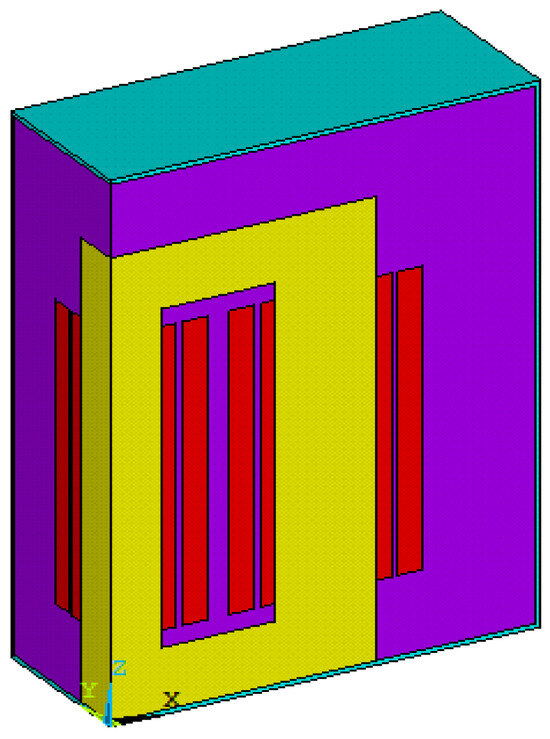
Figure 1.
3D Simulation model.
The heat produced by transformer losses leads to a rise in temperature. When the winding temperature is below 65 °C, the cooling mode is Oil-Natural Air-Natural (ONAN). However, if the winding temperature exceeds 65 °C, the cooling system employs both air force and natural oil cooling. The first set of fans (ONAF1), consisting of 10 fans (five on each side), operates initially. When the coil temperature surpasses 75 °C, the second set of fans (ONAF2) activates, with 10 fans operating on each side. The heat varies with environmental changes, and these cooling modes, along with their respective parameters and limits, are summarized as follows:
- Heat is transferred through thermal conduction from the inner part of the core or windings and spreads to the oiled surface outside and by the same conduction mechanism through the transformer tank wall.
The conduction heat transfer mode is ruled by Fourier’s law, which is stated as follows:
k is the thermal conductivity for the materials used in the core and windings, and ∇T is the rate of temperature change over a distance in the direction of heat flow (°C/m).
- 2.
- Convection is responsible for moving heat from the external parts of the core and windings to the insulating oil, then from the oil to the inside walls of the tank, and finally from the tank’s outer surfaces to the air around it.
In the proposed model, the type of convective heat transfer whether natural or forced depends on the load level. The temperature of transformer windings is controlled by the load and influences the cooling mechanism.
The mathematical expression for the convective boundary condition in isotropic (three-dimensional) systems is derived by considering the energy balance on the specified surface, as outlined in Ref. [27].
According to traditional Nusselt number correlations, the heat transfer coefficient is defined as follows:
The average Nusselt number is calculated for both natural and forced convection scenarios, involving heat exchange between the outer surfaces of the iron core, the LV and HV windings, and the fluid surrounding them. This includes the heat transfer between the oil and the inner surface of the tank and, finally, between the outer surface of the tank and the surrounding air:
For free convection for vertical plates in laminar and turbulent flow with uniform wall temperature, Equation (13) is utilized.
However, the average Nusselt number for free convection on a horizontal plate relies on two factors: whether the surface is pointing up or down, and whether the temperature of the plate surface is higher or lower than that of the surrounding fluid [27].
With the heated surface facing upward:
With the heated surface facing downward:
The Rayleigh number (Ra), Grashof number (Gr), and Prandtl number (Pr), among other dimensionless parameters of free convection, are described in [27].
The Reynolds number (Re) determines whether laminar or turbulent flow occurs over a flat plate in forced convection [27].
If the Reynolds number is fewer than 5 × 105, the Nusselt number for laminar flow along a flat plate is specified by [27]:
However, if the Reynolds number is larger than 5 × 105, for turbulent flow along a flat plate, the Nusselt number is provided by [27]:
- 3.
- The temperature difference between the active components (core and windings) and the outer surfaces of the tank leads to radiation heat transfer between them and from the tank’s exterior to the area immediately surrounding the transformer.
To establish the mathematical representation of the radiation boundary condition in three dimensions, an energy balance is applied at the surface, as referenced in [27,28].
The term of z is reduced for the two-dimension model. The process to estimate the view factor between surfaces is implemented by the following integration [28].
A line of length R connects the elemental areas on surfaces dAi and dAj, forming the polar angles θi and θj, respectively. The elemental areas’ positions on Ai and Ai affect the values of R, θi, and θj.
The 3D geometry of the transformer model, depicted in Figure 2, is constructed and simulated using Finite Element Method ANSYS 19 software. The outcomes were obtained by solving the governing heat transfer equation, represented below as Equation (20):
where T is the temperature (K), x, y, and z are spatial variables (m), while K, q’, ρ, c, and t are, respectively, the thermal conductivity in (W/m·K), the heat transfer rate (W/m3), the density (kg/m3), the specific heat (J/kg·K), and the time (s).
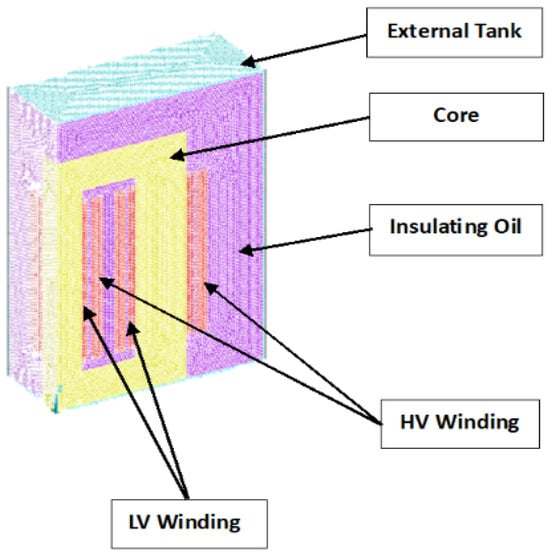
Figure 2.
Schematic of transformer with elements layout for finite element formulation for 3D model.
6. Results and Analysis
6.1. Variation of Transformer Losses with Harmonics
The results from Table 2, Table 3 and Table 4 reveal that as the transformer operates at higher loads, the losses due to harmonics increase compared to losses without considering harmonics. Specifically, when the transformer is fully loaded at 300 MVA, the harmonic losses are 1.46 times greater than losses without harmonics; at 240 MVA load, the ratio is 1.47; and at 180 MVA load, it is 1.47 times larger.
Furthermore, Table 2, Table 3 and Table 4 illustrate that the difference in total losses with and without accounting for harmonics becomes more significant with increasing load. This difference is quantified as 114 KW, 203 KW, and 313 KW at loads of 180, 240, and 300 MVA, respectively.
Figure 3, Figure 4 and Figure 5 provide a visual comparison of losses with and without considering harmonics, depending on the transformer’s load. Notably, the impact of harmonics is most pronounced in eddy-current losses, which also exhibit the highest harmonic loss factor according to Table 3, Table 4 and Table 5.
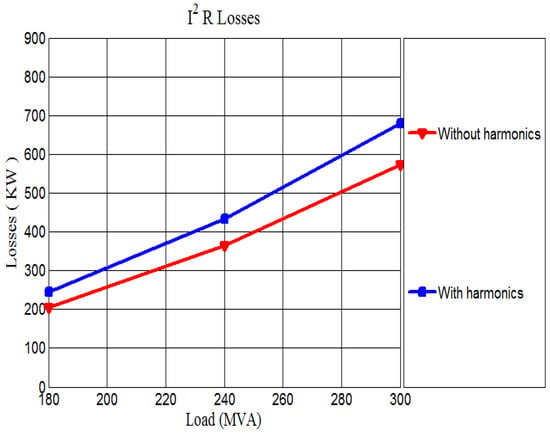
Figure 3.
Influence of harmonics on I2R losses.
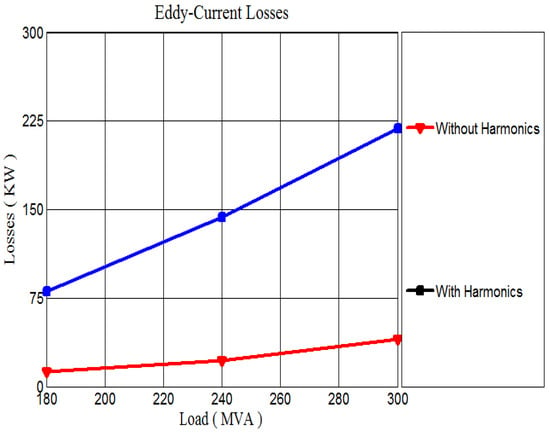
Figure 4.
Influence of harmonics on eddy-current losses.
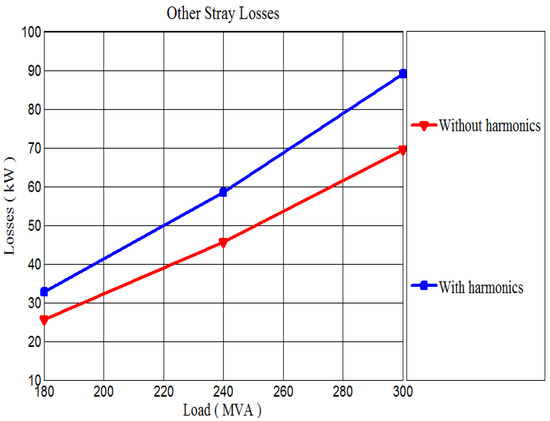
Figure 5.
Influence of harmonics on other stray losses.

Table 5.
The comparison between results of calculation values.
6.2. The Model Accuracy
In a power transformer, temperature distribution is a critical aspect of its thermal performance and lifespan. The temperature inside a transformer varies spatially, and the distribution depends on factors such as the transformer’s design, loading conditions, cooling methods, and the heat generated by electrical losses.
- Detailed Temperature Profile:
- Core and Windings: Highest temperatures due to direct heat generation.
- Oil: The heat is transferred from the core and windings to the cooling fluid. Oil closer to the windings will be warmer, and as it rises, it transfers heat to the outer walls.
- Outer Tank: Assumed to be close to ambient temperature, with a temperature gradient from the interior (hotter) to the exterior (cooler).
The aim of these simulations is to develop a highly accurate model for assessing the impact of grid harmonics on transformers under various loads. Model precision is achieved by subjecting it to a 240 MVA load and comparing its calculated values with those from the test report [21]. Additionally, a pyrometer device is utilized in this study to gauge tank temperature and compare it with the thermal model’s calculations.
Figure 6 displays a contour plot depicting the nodal temperature distribution of the power transformer under load (240 MVA) and ambient temperature (20.6 °C). Notably, the highest temperature is recorded at 56.83 °C for the HV winding and 57.71 °C for the core. The LV winding and core register the highest temperatures overall. According to the HYUNDAI test report, the average measured temperature for the LV winding is 56.09 °C and for the HV winding is 55.04 °C [21]. In contrast, the calculated temperature distribution from the model yields an average of 56.48 °C for the LV winding and 55.92 °C for the HV winding.
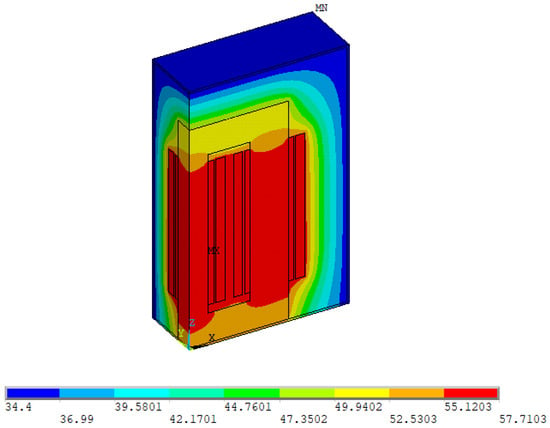
Figure 6.
Calculated temperature distribution of transformer at 240 MVA without grid harmonic.
By comparing the calculated temperatures of the LV and HV windings with the results from the HYUNDAI test report, the Mean Absolute Percentage Error (MAPE) is found to be 0.7% and 1.6%, respectively. This indicates a good match between the test data and the calculated values, especially concerning temperature levels and the points of maximum heat. Additionally, a pyrometer is used to check the tank temperature, with measurements taken from multiple locations yielding an average of 36.1 °C, which closely aligns with the calculated average tank temperature of 35.69 °C.
6.3. Effect of Grid Harmonics in Steady-State Performance
The effects of harmonics on transformers have been investigated across three different loads: 180, 240, and 300 MVA. The thermal model is simulated using corrected losses, which are derived from grid harmonics calculated at these loads (as detailed in Table 2, Table 3 and Table 4). These corrected losses serve as inputs for the 3D thermal model, which then analyzes the model’s thermal behavior, resulting in nodal temperatures.
The calculation of corrected losses for the transformer is load-dependent and varies based on the losses factor and type of losses. By incorporating harmonics measurements from Table 1 at each load, the corrected losses are computed and presented in Table 2, Table 3 and Table 4.
These corrected losses, specific to each load, are utilized as inputs for the model. Once the model reaches a steady state, the nodal temperatures are obtained, as depicted in Figure 7, Figure 8 and Figure 9.

Figure 7.
Transformer temperature spreading at full load (300 MVA) was calculated with grid harmonics.
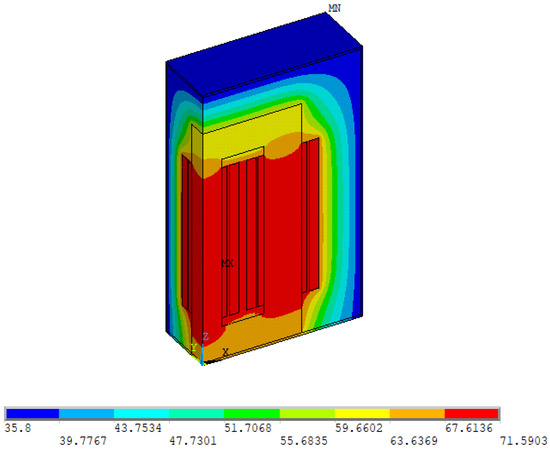
Figure 8.
Transformer temperature spreading at 240 MVA was calculated with the grid harmonic.

Figure 9.
Transformer temperature spreading at 180 MVA was calculated with the grid harmonic.
The modeling process considers ambient temperatures consistent with those used for models without harmonics. For instance, the model at 300 MVA load is computed at an ambient temperature of 24.3 °C; at 240 MVA load, it is at 20.6 °C; and at 180 MVA load, it is at 16 °C.
It is evident that under linear load conditions (180 MVA), the transformer’s maximum temperature is calculated at 54.35 °C. When subjected to non-linear load conditions, this temperature rises by 4.54 °C, reaching 71.59 °C for 240 MVA load and 87.36 °C for 300 MVA load. The impact of grid harmonics is notable, particularly in 300 MVA load, where the hotspot temperature rises by more than 19.08 °C above the calculated value.
Table 5 provides a comparison of the calculated maximum temperature values for the power transformer’s LV winding under three different loads in two cases (with and without harmonics).
The precision of the thermal model in assessing the impact of harmonics is demonstrated by its close alignment with the measured values across various loads, as illustrated in Table 5.
6.4. Transient Performance
Harmonic-induced losses play a significant role in shaping the system’s dynamic behavior. When harmonics are present in a transformer’s operation, they cause additional losses that differ from conventional losses under purely sinusoidal conditions. The key types of losses induced by harmonics include Copper Losses, Iron (Core) Losses, and Stray Losses.
Harmonic-induced losses directly impact the thermal performance of transformers. The additional losses result in extra heat generation, which can affect the following: Winding Temperature Rise, Core Heating, and Thermal Time Constant.
The dynamic nature of transformer operation, especially under varying load conditions, introduces complexity to thermal performance analysis. Harmonics may not be present continuously but could fluctuate depending on load profiles. Thus, the transient response of the transformer, characterized by the following, becomes important: Load Cycling, Thermal Overshoot, and Hot Spot Formation.
In conclusion, understanding the transient behavior of transformers, especially under harmonic conditions, is vital for ensuring reliable operation and longevity. Harmonics introduce additional losses that increase the thermal stress on the transformer, impacting both short-term performance and long-term durability. Advanced thermal modeling and simulation that take these dynamic factors into account can provide better insights and improve transformer design for harmonic-rich environments.
The thermal model incorporates harmonic losses and is validated by comparing the estimated temperature of the transformer with actual measured temperatures recorded over a 24 h period under real load conditions. This process involves calculating corrected losses for each load throughout the day and using these values to feed the thermal model.
Figure 10 and Figure 11 display the normal load cycle of the system and ambient temperature, respectively, across 24 h. By monitoring the highest temperature point on the transformer’s LV winding over the course of a day, the accuracy of the thermal model is confirmed. Figure 12 presents a comparison between the measured and estimated values of the highest temperature reached on the LV winding.
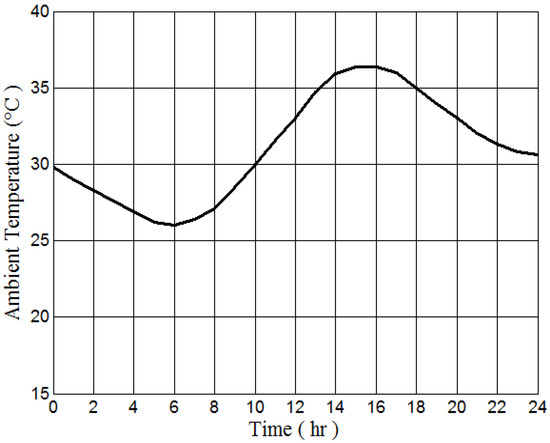
Figure 10.
Time change of ambient temperatures.
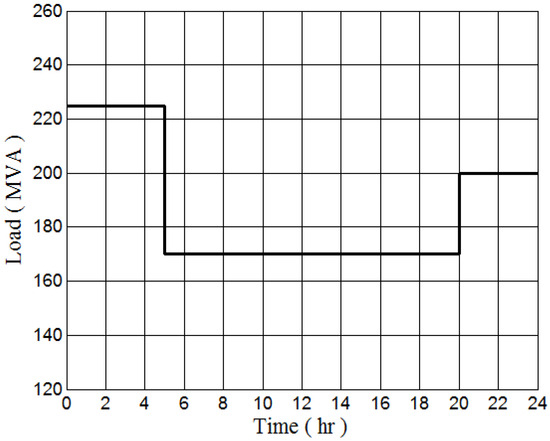
Figure 11.
Actual load over 24 h.
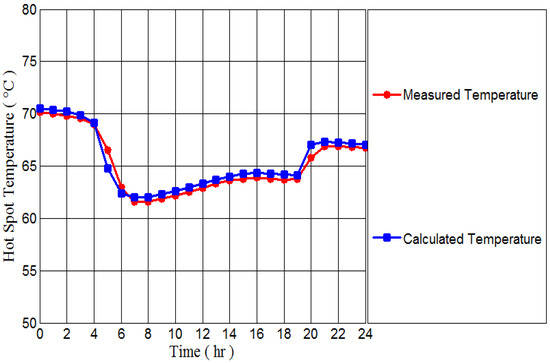
Figure 12.
Comparison between calculated and measured hottest temperature.
The recorded data from the 24 h period were taken in September during the autumn season because the temperature is average in Egypt, with ambient temperatures ranging from 26 °C (minimum) to 36.4 °C (maximum).
As indicated in Figure 11, the transformer operated at a load of 225 MVA for the initial four hours at an ambient temperature of 29.8 °C. Notably, there is a significant increase in the highest spot temperature during this period. Although the load remains constant at 225 MVA, the temperature at which it reaches its peak varies with ambient temperature and decreases as the ambient temperature decreases.
The transformer’s load is decreased to 170 MVA, which is the minimum load required for normal operation, at 5 o’clock in accordance with grid requirements. This reduction in load leads to a noticeable decrease in component temperatures, resulting in a decrease in the hottest temperature, as depicted in Figure 12. Initially, when the load is reduced at 5 o’clock, it takes time for the measured temperature of the hottest point to stabilize, leading to a 1.78 °C difference between the calculated and measured values at that moment.
From 5 o’clock to 20 o’clock, the transformer load remains constant, during which time the ambient temperature significantly impacts the component temperatures and the hottest point. Figure 10 shows a clear increase in ambient temperature starting at 6 o’clock, peaking at 16 o’clock. Consequently, as the ambient temperature rises, so does the hottest temperature, as shown in Figure 12.
At 20 o’clock, the load is increased from 170 MVA to 200 MVA. This change results in a 1.3 °C difference between the calculated and measured values initially, as the measured value takes time to stabilize. However, after this point, the calculated temperature aligns closely with the measured temperature, with the hottest temperature depending on the ambient temperature.
The established model demonstrates a strong agreement between the measured and calculated values based on the transformer’s load and the ambient temperature.
6.5. Practical Implications of Harmonics on Transformer Design
Harmonics have a substantial impact on transformer performance, leading to higher losses, overloading, insulation stress, core saturation, voltage distortion and poor power quality, vibration and noise, and maintenance issues. Proper design and operational adjustments are essential to mitigate these effects and ensure reliable transformer performance in harmonic-rich environments.
Transformers in harmonic-rich environments need to be designed with special considerations such as:
- De-rating the transformer to account for increased losses and heat generation.
- Use of larger cores or improved core materials to prevent saturation.
- Enhanced cooling systems to manage higher temperatures.
- K-rated transformers that are designed to handle harmonics without excessive heating.
7. Conclusions
This paper presents a 3D simulation model for a 300 MVA generation transformer to demonstrate the impact of grid harmonics on its thermal performance. The model calculates and integrates harmonic losses due to nonlinear grid loads at various load levels, considering both steady-state and transient conditions over a 24 h period with time-varying loads. Different loading factors are analyzed to evaluate the thermal effects on the transformer operating at specific power levels.
The calculated results are compared with actual measurements and the HYUNDAI test report, showing satisfactory correlations. The study examines the effects of varying transformer loads on ohmic, eddy current, and other stray losses related to grid harmonics, highlighting that eddy-current losses exhibit the highest harmonic loss factor and are most affected by harmonics.
The loss calculations indicate that the difference in total losses with and without considering harmonics becomes more significant with increasing load, quantified as 114 KW, 203 KW, and 313 KW at loads of 180, 240, and 300 MVA, respectively. The simulation model shows that grid harmonics increase temperature distribution inside the transformer, causing the hot spot temperature to rise. Under linear load conditions, the hot spot temperatures are 54.35 °C, 57.71 °C, and 68.28 °C at loads of 180, 240, and 300 MVA, respectively. However, with harmonic loads, these temperatures increase to 58.89 °C, 71.59 °C, and 87.36 °C for the same loads.
Therefore, the presence of grid harmonics raises the hot spot temperature, potentially damaging winding insulation over the extended operation, adversely affecting the reliability of the generator system and grid efficiency. Thus, it is crucial to consider the transformer’s capacity to mitigate issues related to harmonic load currents.
It is obvious based on the present investigation that assessing the thermal behavior in the presence of harmonics offers a more realistic representation of actual operating conditions.
Author Contributions
Methodology, M.S.S. and M.B.E.; Software, M.S.S.; Validation, M.B.E. and J.S.; Formal analysis, J.S.; Investigation, M.B.E.; Resources, M.S.S.; Writing—original draft, M.S.S.; Supervision, M.B.E. and J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sinvula, R.; Abo-Al-Ez, K.M.; Kahn, M.T. A Proposed Power Transformers Failure Assessment Method for Resolving Harmonic Distortion Problem. In Proceedings of the 2021 IEEE PES/IAS PowerAfrica, Nairobi, Kenya, 23–27 August 2021; pp. 1–5. [Google Scholar]
- Makarov, S.N.; Emanuel, A.E. Corrected Harmonic Loss Factor for Transformers supplying Non-sinusoidal Load current. In Proceedings of the IEEE 9th International Conference on Harmonics and Power Quality, Orlando, FL, USA, 1–4 October 2000; Volume 1, pp. 87–90. [Google Scholar]
- Marzband, M.; Shaikholeslami, A. A program for harmonic modeling of distribution network transformers and determination of loss in the transformers and the amount of decrease of their life. In Proceedings of the International Conference on Power Electronics, Drives and Energy Systems, PEDES’06, New Delhi, India, 12–15 December 2006; pp. 1–6. [Google Scholar]
- Elmoudi, A.; Lehtonen, M.; Nordman, H. Effect of harmonics on transformers loss of life. In Proceedings of the Conference Record of the 2006 IEEE International Symposium on Electrical Insulation, Espoo, Finland, 11–14 June 2006; pp. 408–411. [Google Scholar]
- Shareghi, M.; Phung, B.T.; Naderi, M.S.; Blackburn, T.R.; Ambikairajah, E. Effects of Current and Voltage Harmonics on Distribution Transformer Losses. In Proceedings of the 2012 IEEE International Conference on Condition Monitoring and Diagnosis, Bali, Indonesia, 23–27 September 2012. [Google Scholar]
- Dursun, K.; Rahmanov, N. Harmonic load losses in power transformer windings using Finite Element methods. In Proceedings of the Eurocon 2013, Zagreb, Croatia, 1–4 July 2013; pp. 1526–1530. [Google Scholar]
- Soh, T.L.G.; Said, D.M.; Ahmad, N.; Nor, K.M.; Salim, F. Experimental Study on the Impact of Harmonics on Transformer. In Proceedings of the IEEE 7th International Power Engineering and Optimization Conference (PEOCO2013), Langkawi, Malaysia, 3–4 June 2013. [Google Scholar]
- Wu, J.; Liu, C.; Zhang, X.; Hao, J.; Sun, J.; Li, Z. Influence of Harmonic Current on the Winding Loss and Temperature Distribution of AC Transformer. In Proceedings of the 2021 6th Asia Conference on Power and Electrical Engineering, Chongqing, China, 8–11 April 2021. [Google Scholar]
- Zvada, P.; Ilinykh, M.; Zvezdilin, R.; Daria, T. Investigation of the influence of non-sinusoidal voltage and currents on electricity losses in a power transformer. In Proceedings of the 2022 5th International Youth Scientific and Technical Conference on Relay Protection and Automation, Moscow, Russia, 20–21 October 2022. [Google Scholar]
- Cazacu, E.; Petrescu, L.; Ioniğă, V. Losses and Temperature Rise within Power Transformers Subjected to Distorted Currents. In Proceedings of the 14-th International Conference on Electrical Machines, Drives, and Power Systems, Sofia, Bulgaria, 1–3 June 2017. [Google Scholar]
- Bagheri, P.; Xu, W.; Shaloudegi, K. New indices to evaluate the impact of harmonic currents on power transformers. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; pp. 1–6. [Google Scholar]
- Wan, D.; You, K.; Zhou, H.; Qi, F.; Peng, S.; Peng, T. Study on Harmonic Load Loss Calculation Method of Oil-Paper Insulated Distribution Power Transmission Equipment. In Proceedings of the 3rd IEEE conference on Energy Internet and Energy System Integration, Changsha, China, 8–10 November 2019. [Google Scholar]
- Akbari, E.; Seyyedi, A.Z.G. Multi-functional voltage and current based enhancement of power quality in grid-connected microgrids considering harmonics. Heliyon 2024, 10, e26008. [Google Scholar] [CrossRef] [PubMed]
- Plienis, M.; Deveikis, T.; Jonaitis, A.; Gudžius, S.; Konstantinavi, I.; Putnaite, D. Improved Methodology for Power Transformer Loss Evaluation: Algorithm Refinement and Resonance Risk Analysis. Energies 2023, 16, 7837. [Google Scholar] [CrossRef]
- Thango, B.A.; Bokoro, P.N. A Novel Approach to Predict Transformer Temperature Rise under Harmonic Load Current Conditions. Energies 2022, 15, 2769. [Google Scholar] [CrossRef]
- Badri, J.A.; Riba, J.R.; Garcia, A.; Trujillo, S.; Marzàbal, A. Transformer modelling considering power losses using an inverse Jiles-Atherton approach. Int. J. Electr. Power Energy Syst. 2023, 154, 109461. [Google Scholar] [CrossRef]
- Rustemli, S.; Satici, M.A.; Sahin, G.; van Sark, W. Investigation of harmonics analysis power system due to non-linear loads on the electrical energy quality results. Energy Rep. 2023, 10, 4704–4732. [Google Scholar] [CrossRef]
- Altun, H.; Sünter, S.; Aydoğmuş, Ö. Modeling and analysis of a single-phase core-type transformer under inrush current and nonlinear load conditions. Electr. Eng. 2021, 103, 2961–2972. [Google Scholar] [CrossRef]
- IEEE Std C57.110-2008; IEEE Recommended Practice for Establishing Liquid-Filled and Dry-Type Power and Distribution Transformer Capability When Supplying Nonsinusoidal Load Currents. IEEE Power Engineering Society: Piscataway, NJ, USA, 2008.
- Seddik, M.S.; Shazly, J.; Eteiba, M.B. Thermal Analysis of Power Transformer Using 2D and 3D Finite Element Method. Energies 2024, 17, 3203. [Google Scholar] [CrossRef]
- Manual Manufacturer, Technical Documentation for Hyundai Test Report; Serial number: 52579T10017-001& 002; Hyundai B/D: Seoul, Republic of Korea, 2006.
- Jayasinghe, N.R.; Lucas, J.R.; Perera, K.B.I.M. Power System Harmonic Effects on Distribution Transformer and New Design considerations for K Factor transformers. In Proceedings of the IEEE Sri Lanka Annual Sessions, Colombo, Sri Lanka, September 2003. [Google Scholar]
- IEEE Std C57.110-2018; IEEE Recommended Practice for Establishing Liquid Immersed and Dry-Type Power and Distribution Transformer Capability when Supplying Nonsinusoidal Load Currents. IEEE Power Engineering Society: Piscataway, NJ, USA, 2018.
- Olivares, J.C.; Escarela-Perez, R.; Kulkarni, S.V.; De Leon, F.; Venegas-Vega, M.A. 2D Finiteelement determination of tank wall losses in padmounted transformers. Electr. Power Syst. Res. 2004, 71, 179–185. [Google Scholar] [CrossRef]
- Radmehr, M.; Farhangi, S.; Nasiri, A. Effect of Power Quality Distortion on Electrical Drives and Transformer Life in Paper Industries: Simulation and Real Time Measurements. In Proceedings of the Pulp and Paper Industry Technical Conference, Appleton, WI, USA, 18–23 June 2006; pp. 1–9. [Google Scholar]
- Lienhard, J.H. A Heat Transfer Textbook, 3rd ed.; Phlogiston Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Ozisik, M.N. Heat Transfer a Basic Approach; McGrawHill: New York, NY, USA, 1985. [Google Scholar]
- von Böckh, P.; Wetzel, T. Heat Transfer (Basics and Practice); Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2012. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).