1. Introduction
In recent decades, the population growth and socio-economic development of countries have led to a worldwide trend characterized by increasing energy demand, primarily dominated by fossil fuels (natural gas, oil, coal) [
1,
2]. However, the global energy dependence on fossil fuels has adverse effects on the environment, including global warming associated with the excessive emission of greenhouse gases (GHGs) [
3]. Structural changes in how energy is produced and consumed are necessary to meet the current high energy demand and mitigate the increase in emissions (GHGs) that detrimentally impact climatic conditions. Renewable energies are regarded as an opportunity for a global energy transition from fossil fuels to clean and sustainable energy sources (hydropower, wind, photovoltaic solar, geothermal, biomass). Therefore, governments, in collaboration with international organizations, have begun to formulate decisive actions in the field of energy and climate change, aiming to meet current demands without jeopardizing future generations [
4]. Energy production from renewable sources offers various options, such as hydropower. This form of energy is based on the transformation of hydraulic energy into electricity and consists of potential and kinetic energy. Potential energy can be extracted through dams or water flows at a certain height, while kinetic energy is related to water velocity [
4]. The devices that convert potential energy into mechanical and electrical energy through an electrical generator are called hydraulic turbines, with the most well-known being the Pelton, Kaplan, and Francis turbines [
5]. Additionally, kinetic energy has a less explored hydropower potential and can be harnessed by unconventional hydraulic turbines such as hydrokinetic turbines (HKT) in natural water currents found in oceans, rivers, and low-flow canals, where conventional turbines are less viable [
6]. Compared to a conventional hydropower plant, the energy produced by HKT is not very high; however, hydrokinetic technology has gained significant momentum. Unlike conventional hydropower plants, there is no need for the construction of civil works (dams, reservoirs, canals, and load tunnels), which have a considerable economic cost and generate significant environmental and social impact in their implementation [
7,
8,
9].
There are different types of HKT, and a general classification is based on the orientation of the turbine’s axis of rotation and the flow direction, resulting in the following two types: (a) axial flow turbines (HAHT) and (b) cross-flow turbines (VAHT) [
7]. In a HAHT, the turbine’s axis of rotation is generally aligned with the flow direction. In contrast, in a VAHT, the axis of rotation is orthogonal to the flow direction. VAHTs have advantages in terms of the implementation and use of conventional turbines, such as the ability to self-start in shallow waters, low manufacturing costs, and ease of operation and maintenance, as they mainly consist of a generator group installed on the riverbed [
7,
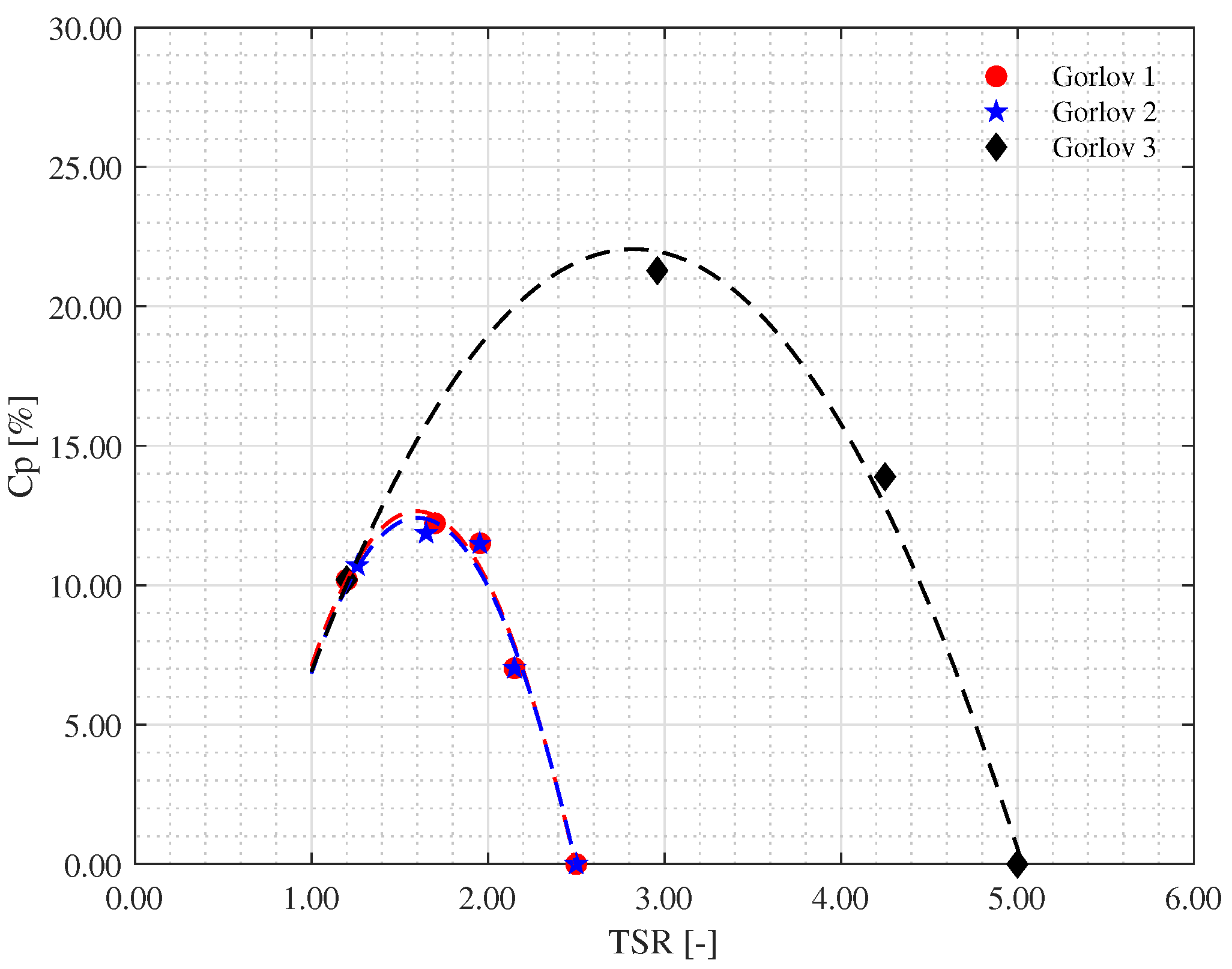
10]. Among the various types of VAHT rotors, the following three are primarily distinguished: Darrieus and its variations, Savonius, and Gorlov. The Gorlov-type HKT stands out in its class due to its ability to self-start in low-speed currents and its better torque stability, increasing its efficiency and reducing intermittency in the generation of electrical energy [
11].
An alternative for harnessing hydropower potential through hydrokinetic technology is provided by systems known as hydrokinetic arrays or farms. These systems are equipped with a certain number of turbines, which can be VAHT or HAHT [
12], and are considered a promising means to generate energy economically and ecologically in almost any location with water flows, allowing for a reduction in energy dependence on fossil fuels in a context of increasing resource scarcity [
7]. However, the implementation of hydrokinetic arrays or farms in rivers faces pending tasks, such as the development of methodologies to define the location and arrangement of the turbines within the array. The passage of fluid through the turbine generates a downstream turbulence region known as the fluid wake; thus, the spacing between turbines plays a significant role [
13]. The wake length and the available space for installation will influence the number of turbines to be installed, the amount of captured energy, and, in turn, the overall viability of the hydrokinetic system for energy production.
There are specific cases around the world where hydrokinetic farms of various capacities have been implemented, most of them in the United States and Asia: a power unit consisting of six HAHT turbines in the city of Hastings, Minnesota, USA, with a capacity of 100 kW [
14]; an energy unit consisting of two HKT turbines in the Chilla canal, India, with a capacity of 50 kW [
15]. In South America, there are no reports of studies or the developments of Gorlov-type HKT arrays. Research in Brazil focuses on the implementation of HAHT and simplified turbines using the actuator disk model [
13].
The available information on the specialized design, optimization, and implementation of hydrokinetic arrays or farms is somewhat scattered and primarily focused on very specific cases: (a) systems equipped with a single turbine and (b) arrays or farms equipped with HAHT, based on wind farm models [
16]. This study stands out as a pioneering effort, as it specifically addresses the design and optimization of a Gorlov-type VAHT array, an area that has not been extensively explored before.
In recent studies, Cacciali et al. [
17] introduced a multi-array tool for evaluating turbine arrays in mild slope hydropower canals, providing reliable power output estimates by modeling hydraulic transitions. The tool integrates a 1-D channel model with a Double Multiple Streamtube code and wake sub-models to optimize array power. Results show that power output scales linearly for up to five arrays, while water depth variation follows a power law from the downstream array towards upstream, independent of plant size.
Okulov et al. [
18] presented an experiment on the interference of multiple horizontal-axis hydro turbines arranged in a line array. This was the first time turbine output has been optimized by adjusting operating conditions. The results show that power decreases significantly for the second turbine but then increases and stabilizes for the third and subsequent turbines, contradicting early theoretical predictions of continual performance decline. This stabilization suggests that line arrays of hydro turbines, similar to wind farms, could be effectively used in rivers. The study highlights the benefits of line arrays for river power extraction, such as reduced environmental impact and continued navigation, but emphasizes the need for further research on power stabilization, array configurations, and blockage effects.
Multiple hydrokinetic turbines in three array configurations were analyzed by Riglin et al. [
19], using Reynolds-averaged Navier–Stokes equations. The simulations were performed on existing turbines operating at an optimal power coefficient of 0.43. Mechanical power was predicted for adjacent turbines at various lateral separations, and a two-by-two turbine array was studied to simulate a hydro-farm. At a lateral separation of 0.5
D, turbines achieved 86% of the peak power of a single turbine. Interaction effects were minimal at separations greater than 2.5
D. However, downstream turbines experienced significant performance reductions within 6
D longitudinal spacing, performing around 20% or less compared to a single turbine. These results align with experimental findings.
dos Santos et al. [
13] introduced a methodology for assessing the length of hydrokinetic rotor wakes in natural channels using computational fluid dynamics techniques and the actuator disk model. Applied to a segment of the Brazilian Amazon River with real field data on velocity, curvature, and geometry, the wake length was found to be between seven and nine diameters, depending on the turbine’s operating point. Additionally, an evaluation of a three-turbine hydrokinetic setup yielded an electrical power output of 18.3 kW.
The goal of this research work is to advance knowledge in the field of renewable energy by proposing a novel approach for the design and optimization of Gorlov-type VAHT arrays for energy generation. This includes utilizing numerical simulations in computational fluid dynamics (CFD) software, conducting experimental tests, and employing a response surface methodology to achieve an efficient system with low manufacturing and maintenance costs.
This study represents a significant innovation, particularly concerning Gorlov-type hydrokinetic arrays. The combination of advanced simulation techniques and experimental validation ensures that the findings are not only theoretically robust but also practically applicable. By addressing a gap in the current research landscape, this study provides valuable insights for future developments in hydrokinetic energy and could guide large-scale implementations in regions with untapped hydrokinetic potential. The innovative approach and focus on optimization contribute to the growing body of knowledge in renewable energy technologies, positioning this research as a crucial step toward sustainable energy solutions.
4. Conclusions
The theoretical considerations for designing and developing an energy generation system using Gorlov vertical-axis hydrokinetic turbines (VAHTs) in a hydrokinetic array or farm configuration were thoroughly reviewed. The main conclusions were the following:
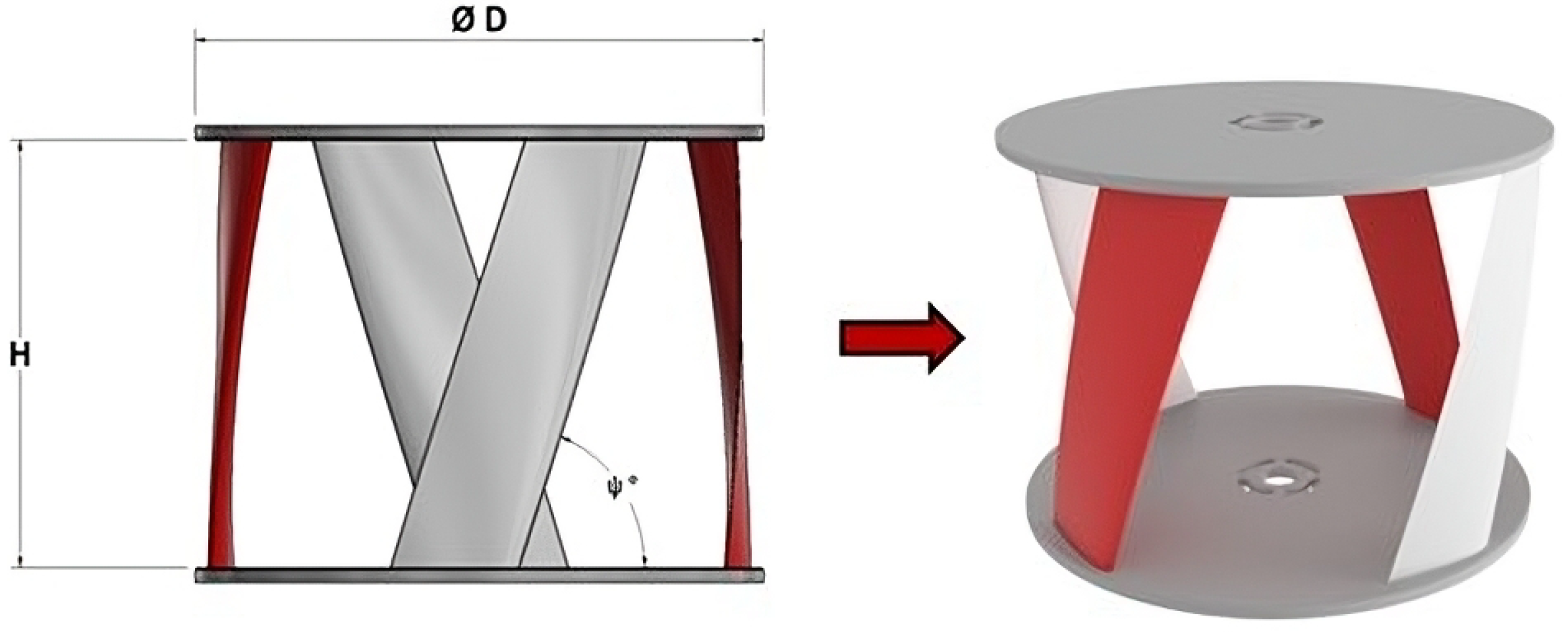
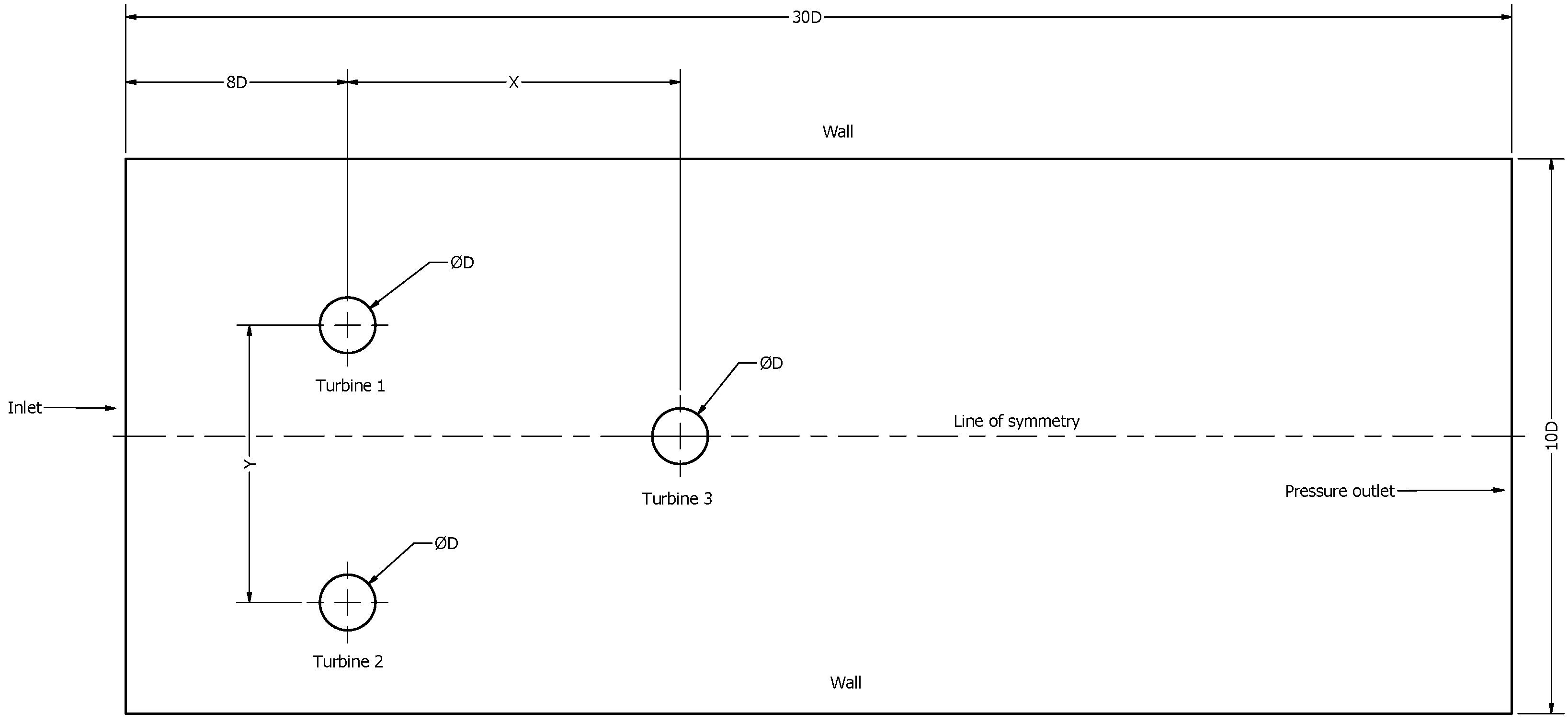
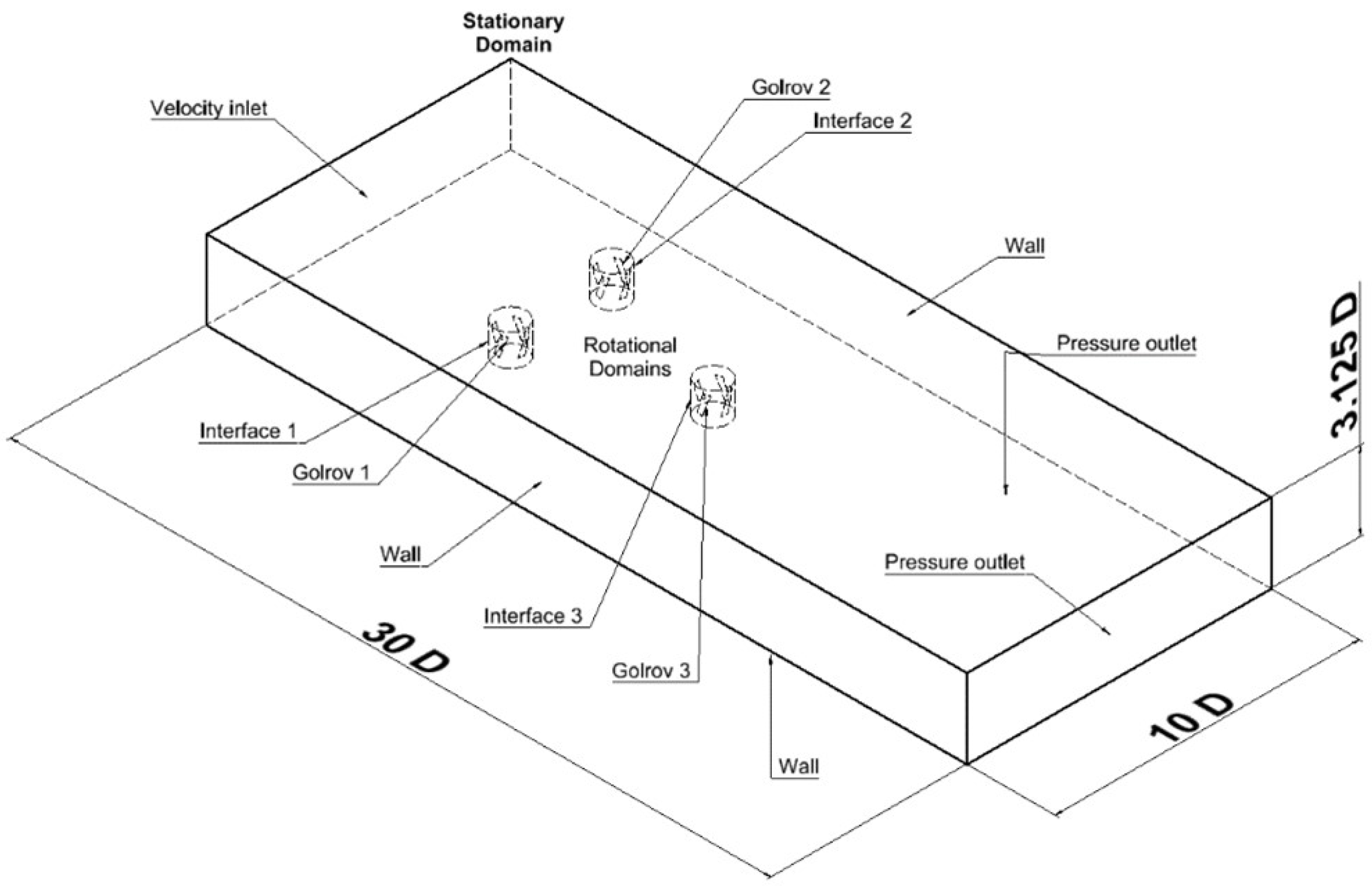
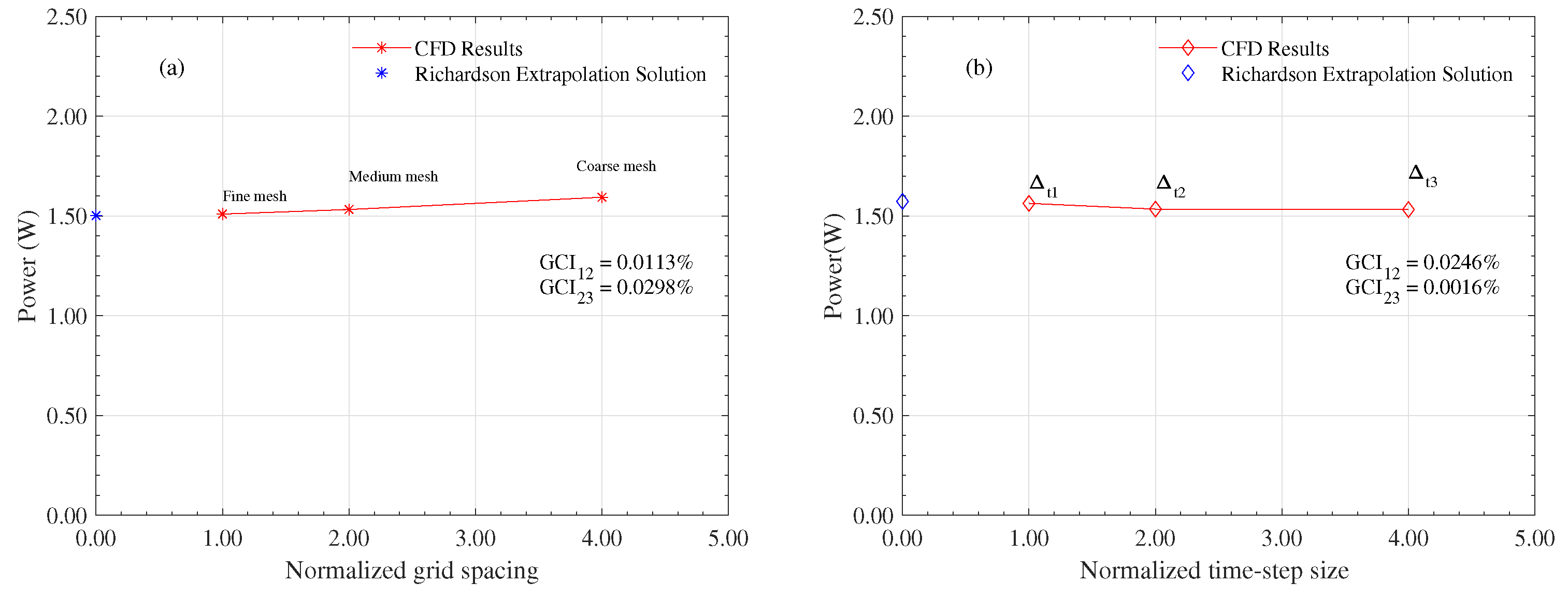
The experimental design employed was a factorial design, analyzing two factors at three levels of variation, resulting in nine treatments or experimental units. These nine treatments were numerically simulated using ANSYS software, specifically within the ANSYS-Fluent environment, utilizing the 6-DOF tool to analyze the fluid dynamic behavior of three Gorlov-type hydrokinetic turbines in a Triframe configuration.
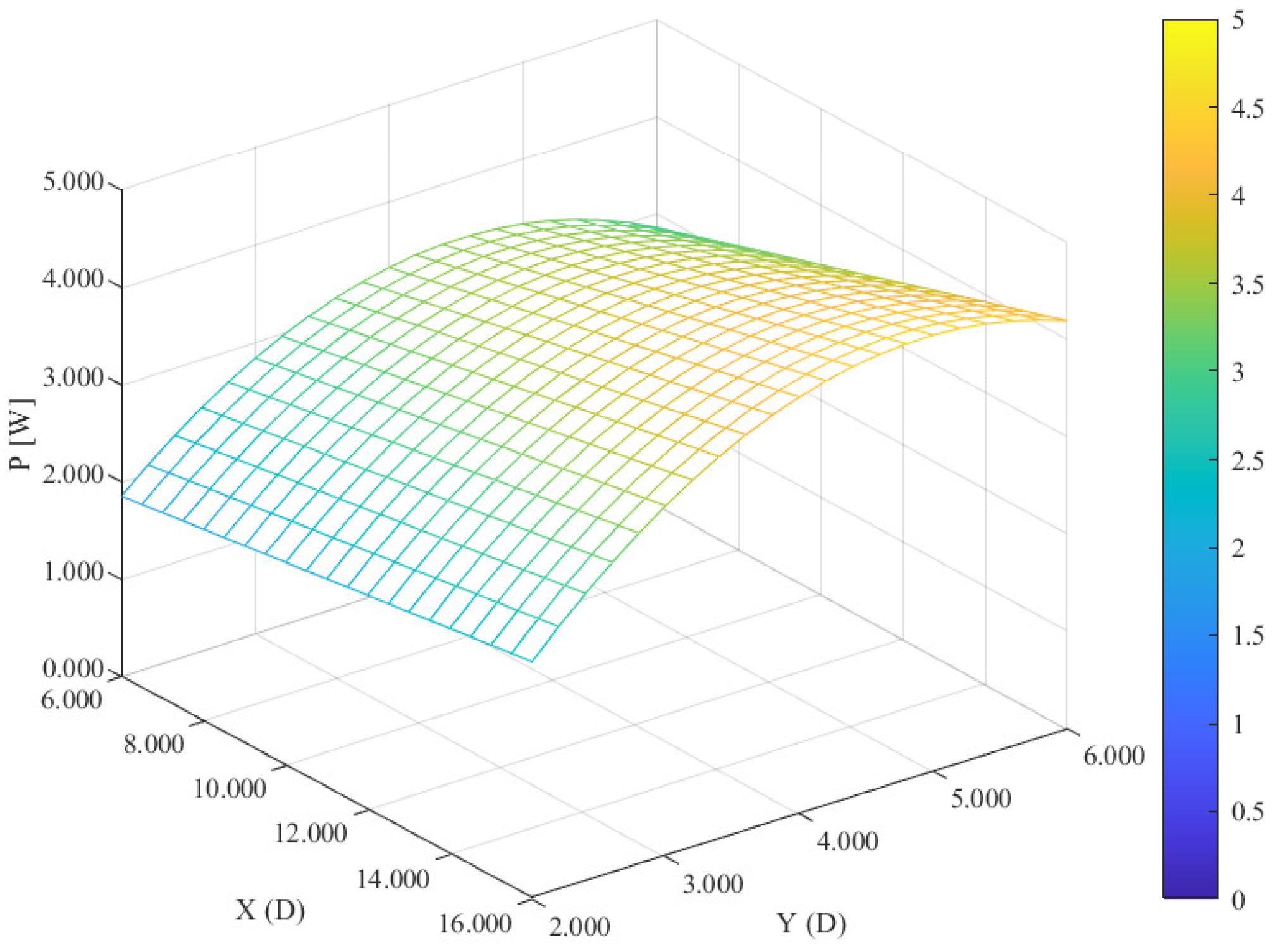
The optimization process was conducted using response surface methodology (RSM), with a detailed validation of treatments that yielded optimal values. The separation distance between rotors, both along (X) and across (Y) the fluid flow direction, significantly impacted the total power generated by the hydrokinetic array (P).
The optimal values for these factors, expressed in terms of the turbine diameter D, were found to be for X and for Y, resulting in a power output of 4.4076 W, representing a 2.809% increase compared to experimental unit 7, which had reported the highest power output in the initial experimental matrix.
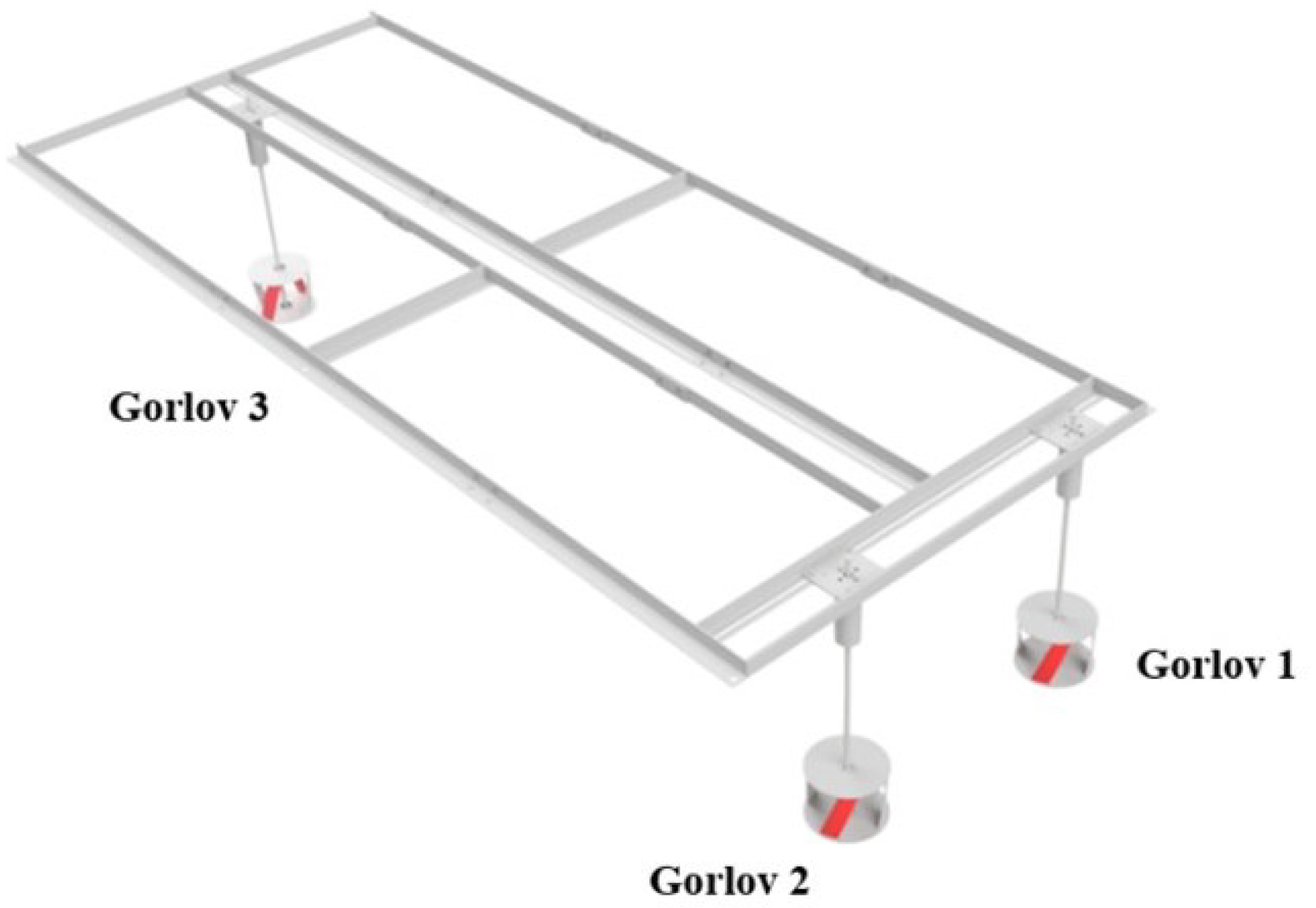
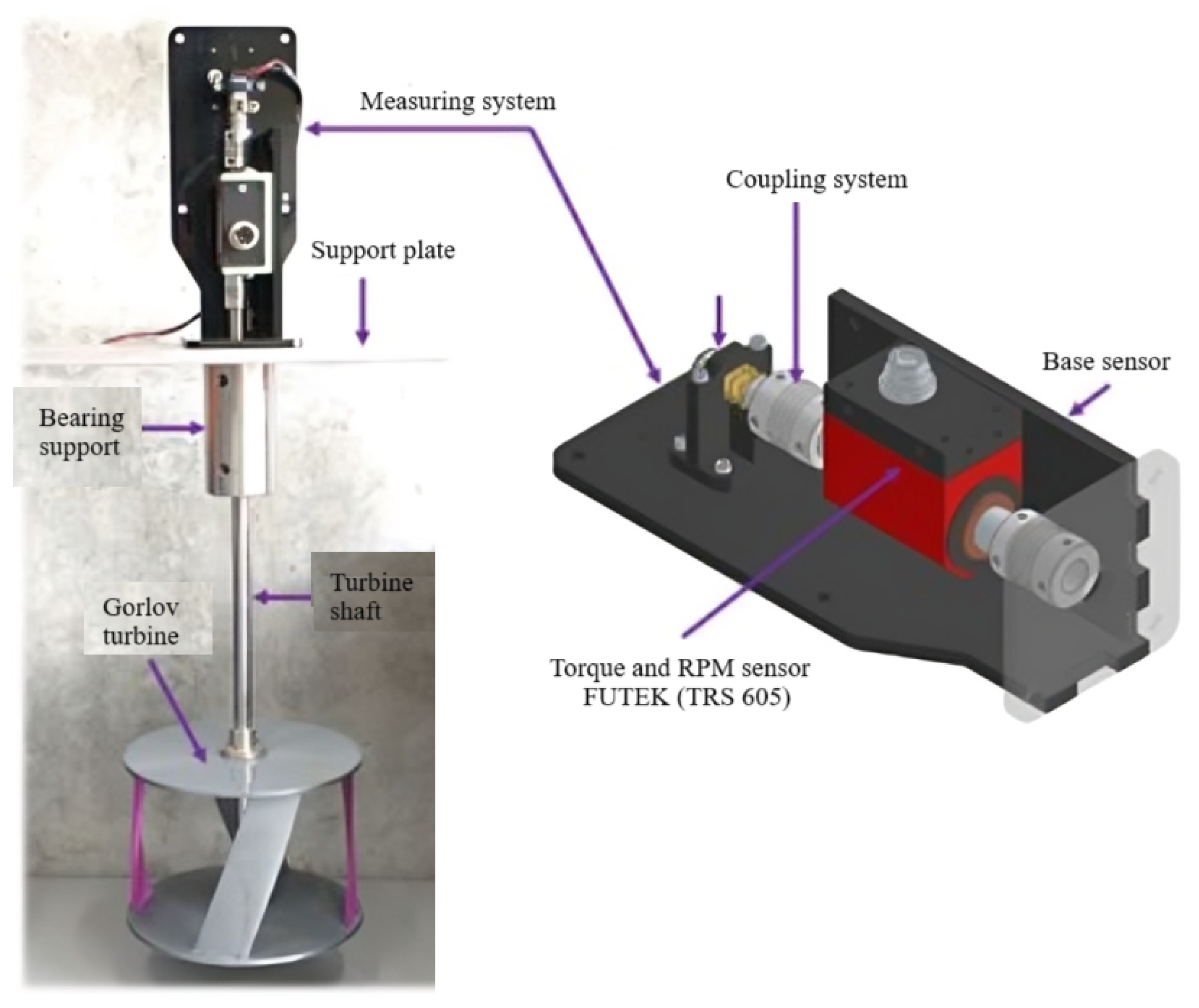
The method of 3D printing was utilized to create three scale models of the Gorlov VAHTs used in the hydrokinetic array. A support structure was also designed to maintain the three rotors in their optimal configuration. The experimental setup was conducted in the Tempranos stream, near Retiro, Antioquia, due to the array’s size. The installation included the rotors, support structure, and measurement instruments to evaluate the system’s performance in terms of and .
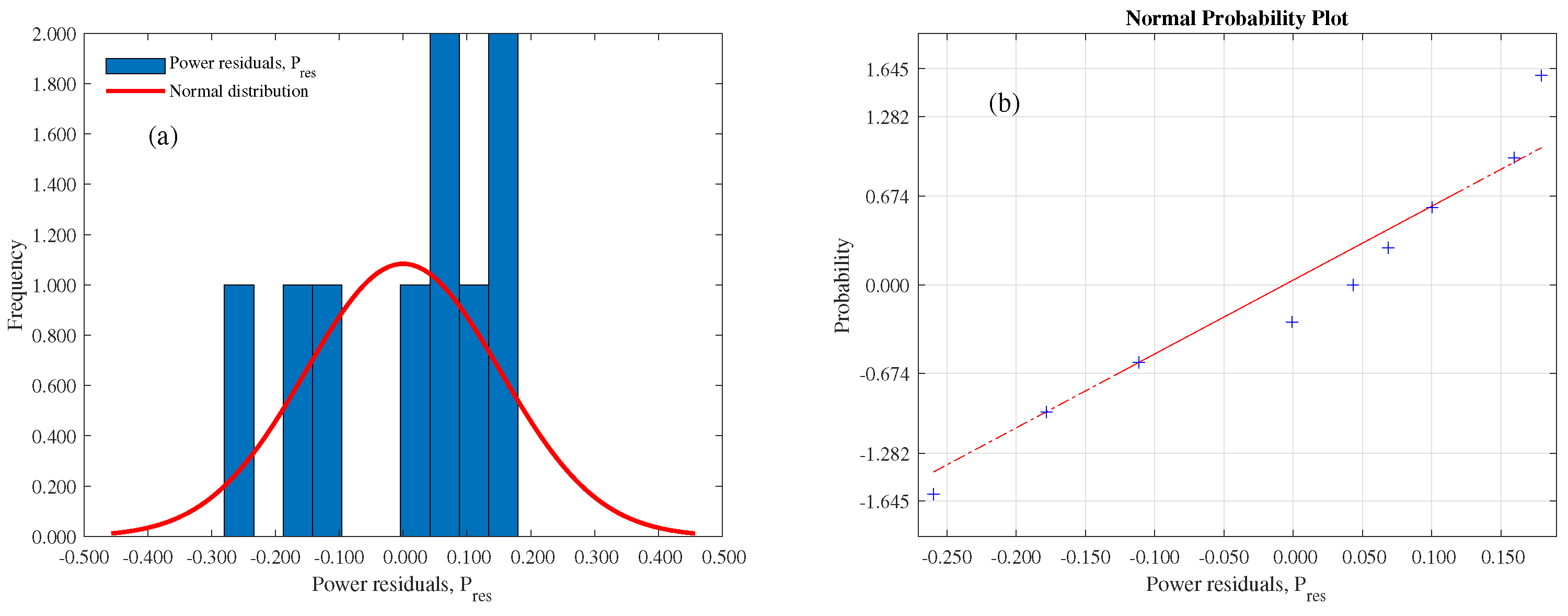
Numerical and experimental approaches are essential for developing devices and systems that harness renewable resources. Numerical simulation, combined with response surface methodology (RSM), offers an efficient alternative for optimization processes that would otherwise be prohibitively expensive due to the multitude of resulting treatments. However, numerical simulations must be validated by experimental results to account for and quantify the negative effects of variables not included in the numerical models due to time constraints and high computational costs.
Future research on Gorlov vertical-axis hydrokinetic turbines (VAHTs) should start with investigating various array configurations and rotor arrangements beyond the current Triframe setup to further optimize power generation and spatial efficiency. To validate these designs in real-world scenarios, field tests of larger-scale hydrokinetic arrays in diverse environmental conditions are essential. Additionally, integrating VAHTs with energy storage systems could help manage energy production and ensure a consistent energy supply. It is also important to study the effects of varying environmental conditions, such as water flow rates, sediment loads, and seasonal variations, on the performance and longevity of VAHTs. Improvements in measurement and data collection methods are also needed to better assess rotor design parameters, including variations in blade shape, material, and construction methods. Lastly, implementing long-term monitoring programs will help study the reliability and performance of VAHTs over extended periods, identifying potential areas for further improvement.