Abstract
The rapid development of electric vehicles (EVs) has brought great challenges to the power grid, so improving the EV load prediction accuracy is crucial to the safe operation of the power grid. Aiming at the problem of insufficient consideration of spatial dimension information in the current EV charging load forecasting research, this study proposes a forecasting method that considers spatio-temporal node importance information. The improved PageRank algorithm is used to carry out the importance degree calculation of the load nodes based on the historical load information and the geographic location information of the charging station nodes, and the spatio-temporal features are initially extracted. In addition, the attention mechanism and convolutional network techniques are also utilized to further mine the spatio-temporal feature information to improve the prediction accuracy. The results on a charging station load dataset within a city in the Hebei South Network show that the model in this study can effectively handle the task of forecasting large fluctuations and long time series of charging loads and improve the forecasting accuracy.
1. Introduction
With the growth of global energy demand and the aggravation of environmental problems, new energy vehicles have attracted much attention and promotion as a solution for sustainable development in the field of transportation [1]. Since 2016, the number of electric vehicles (EVs) in China has been climbing year by year and is expected to exceed 80 million in 2030 [2], but the charging demand of electric vehicle users presents randomness, and the large amount of random loads it generates will bring great challenges to the power grid [3], especially in terms of the balance of power supply and demand, grid stability, and economic feasibility [4]. But at the same time, EVs can also be used as distributed energy storage devices to provide vehicle-to-grid (V2G) services to alleviate grid overload and benefit the power system [5]. In addition, EVs can also be included in the optimal scheduling of the carbon market to improve the economic feasibility of China’s low-carbon transition through the optimal scheduling of EV charging [6]. Therefore, constructing effective prediction models to accurately predict EV charging loads and optimize V2G dispatching strategies is crucial to promote the synergistic development of EVs and power grids.
The current EV charging load prediction research can be summarized into two main categories: mechanistic model-driven methods and artificial intelligence-based data-driven methods [7]. Mechanistic model-driven methods model the spatial and temporal distribution characteristics of charging loads to reflect the travel patterns of users or vehicles in a certain area and time period [8]. Reference [9] analyzes the charging history data by clustering based on user characteristics and gives the corresponding probability distribution function, which allows the prediction of the primary charging time of an electric vehicle and the load of the charging station. The authors in [10] used Monte Carlo method to simulate the travel habits of different EV types by considering the initial charging time, battery parameters, charging efficiency and other influencing factors, so as to perform EV load prediction. In [11], the authors analyze the travel laws of EVs by counting users’ travel habits, combining the user travel chain and Markov process, and establish the charging load prediction model under the two conditions of charging at home and charging on the go for electric vehicles, respectively. Reference [12], based on the Monte Carlo method, comprehensively considered the charging cost, time cost, path, and other factors to study the EV user decision-making problem under the condition of insufficient battery power, so as to obtain the spatio-temporal distribution law of charging load. The authors in [13] classify EVs into four categories, namely private EVs, electric cabs, electric buses, and official EVs, and predict the additional load generated by EV charging in the medium to long term by constructing a probabilistic model of EV charging and a predictive model of future EV ownership.
Artificial intelligence-based data-driven methods use artificial intelligence techniques such as machine learning and deep learning as a means to mine the features in the data by analyzing and predicting the historical EV charging load data [14]. In [15], the authors construct an EV charging load model based on ConvLSTM and BiConvLSTM by mining the spatial and temporal distribution characteristics of charging station energy consumption, so as to perform load prediction. Reference [16] used a recurrent neural network (LSTM, GRU) as the basis, combined with various machine learning models, and utilized the historical load information of charging stations for EV load prediction. The authors of [17] introduced a new prediction method based on a nonlinear autoregressive (NAR) neural network. The Levenberg–Marquardt (LM) neural network was selected as the learning object, and a recursive prediction method was used to predict the medium- and long-term clock deviation, thus improving the prediction accuracy of EV charging load. Reference [18] used a Bayesian deep neural network to predict the load of EV charging stations. The Long Short-Term Memory (LSTM) network and Bayesian probability theory are organically integrated to solve the uncertainty problem in load prediction.
The mechanistic model-driven method is more general and interpretable [19], but it is difficult to comprehensively consider various influencing factors in the model construction process. In contrast, the data-driven prediction method based on artificial intelligence uses real load data when constructing the prediction model [20], and the prediction results are much closer to the real values, so the data-driven method is gradually gaining importance.
However, most of the current research focuses more on the influence of the time dimension, and when mining the spatial dimension information, artificial intelligence methods are mostly used to extract it from the load data, and there is insufficient consideration of the influence of the actual traffic geographic information on the charging load. In summary, how to reasonably construct the transportation network model and fully consider the influence of spatial dimension information in the spatio-temporal distribution prediction of EV charging load still needs further research.
Aiming at the above problems, this study proposes an EV charging load prediction model considering spatio-temporal node importance information, which takes into account the actual transportation network information, and generates a spatio-temporal graph of load information considering node importance by combining the load information to learn the potential spatio-temporal dynamic features. Then, the spatio-temporal graph of information is combined with the spatio-temporal attention layer, and the spatio-temporal feature information is further extracted. Further, the extracted features are input to a graph convolutional neural network (GCN) to obtain spatial dependencies from the neighborhood. Finally, the temporal dependencies are obtained from the neighboring time using dilated causal convolution, which enhances the model’s ability to capture long-term dependencies, captures spatio-temporal couplings, and improves the charging load prediction accuracy.
2. Methodology
2.1. Prediction Model
The EV charging load prediction model proposed in this study considering the spatio-temporal node importance information is shown in Figure 1.
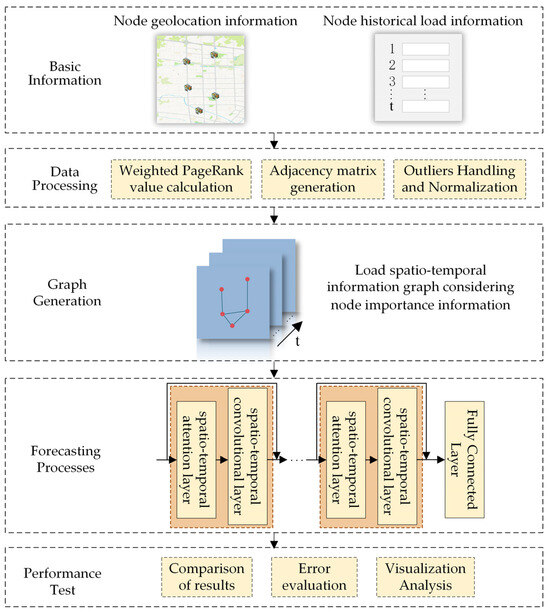
Figure 1.
Flowchart of load forecasting considering node spatio-temporal importance information.
The basic process of forecasting can be divided into the following steps:
- (1)
- In each time slice, the importance degree of each charging station node is calculated based on the historical load information and the actual traffic geographic location information of the node, so as to obtain a dynamic spatio-temporal importance degree information of the node, and initially excavate the spatio-temporal correlation characteristics of the charging load.
- (2)
- Combine the spatio-temporal importance information of each charging station node in each time slice with the corresponding historical load data to form a node feature vector containing multi-dimensional features, and construct the connection relationship between nodes, according to the geographic location information of the nodes, to generate a load spatio-temporal information graph that comprehensively considers the importance information of the nodes.
- (3)
- Input the spatio-temporal information graph to the spatio-temporal attention layer, calculate the degree of association of each load node with other nodes at the current moment through the attention mechanism [21], and dynamically adjust the feature weights to improve the model’s attention to the important nodes.
- (4)
- Utilize spatio-temporal convolutional network to perform convolution operation on the output results of spatio-temporal attention layer to further capture the local patterns in time and space, and improve the model’s ability to extract complex spatio-temporal features.
- (5)
- Integrate the output results of the spatio-temporal convolutional layer through the fully connected layer to generate the final prediction results, i.e., map the high-dimensional feature vectors to the output space through the fully connected layer to output the predicted charging load values.
2.2. Spatio-Temporal Feature Extraction Layer
2.2.1. Data Preprocessing
Due to the randomness of the user’s behavior in going to the charging station, the charging load of the station shows high uncertainty. By analyzing and studying the load characteristics of the dataset, the effects of spatio-temporal factors on the charging loads of EV charging stations are considered and used together with historical charging loads as input features.
In addition, charging load data collected from charging stations often contain some null values, and while the EV charging load data have a certain periodicity, the load data have a high degree of consistency at similar date types. Therefore, for the missing load data xt at time t, it can be filled with the average load data of the same time period for the rest of the days in the same week, and the filling expression is as follows.
where xt is the filling data at the missing time t; k denotes the number of vacant days in a week; d is the number of remaining days in a week excluding the day of the vacant value, which is usually 6; and xdt denotes the load data for the remaining days at time t.
Moreover, this study uses an undirected graph to represent the topology of charging stations, which can be expressed as G = (Vt, Et, At), where Vt represents the set of nodes of charging stations and |V| = N is the number of nodes, Et represents the set of edges connecting two charging stations, and At ∈ RN×N is the adjacency matrix reflecting the connectivity between nodes inside the graph G.
This results in graph G, consisting of N charging station nodes, and the charging station data at any moment t can be viewed as a graph Xt, where Xt = [x1,t, x2,t, …, xN,t] denotes the historical eigenvalues of the N charging station nodes at moment t, and where xi,t = [xi,t,1, xi,t,2, …, xi,t,F] denotes the F eigenvalues of the i-th charging station node at time t.
Knowing the spatial distribution map G of the charging stations and the data collected during Th consecutive historical time steps, the objective of the EV charging load forecasting task; i.e., to predict the future Tp time steps, can be expressed as:
where f is the EV charging load prediction model.
In addition, this study introduces an attention mechanism to mine the spatio-temporal characteristics of the load information, and in order to formulate the attention operation, the slice representation is used here; i.e., for a tensor χ ∈ RN×F×T, the slice at moment t is X::t ∈ RN×F.
2.2.2. Spatio-Temporal Node Importance
The drawback of most of the attention-based methods is that they share all the parameters of location and time intervals, so the node correlation only depends on the respective features. But the traffic correlation of different nodes at different times is different, and the degree of correlation between the loads of each charging station also varies. Therefore, considering various types of spatial correlations, the spatial PageRank weight values of the nodes considering the impact of loads are used for spatial feature learning to fully exploit the spatio-temporal features.
The PageRank algorithm [22] is an algorithm used to rank web pages with the aim of evaluating the importance of each web page by calculating the linking relationships between them. The calculation formula can be expressed as
where PR is the PageRank value of the requested web page; d is the damping factor, usually set to 0.85; Ti is the other web pages connected to the web page; PR(Ti) is the PageRank value of the web page Ti; and C(Ti) is the number of outgoing links of the web page Ti.
The PageRank algorithm can efficiently identify the most influential nodes in the network, so this study introduces it for the identification of key nodes in charging stations. Considering the characteristics of actual transportation network and charging station, there are some problems in applying the PageRank algorithm directly, so this study makes some modifications to it as follows:
- (1)
- The PageRank algorithm assigns the PR value of each node to all other nodes it points to equally, but in the network composed of charging station nodes, there are differences in the relationship between nodes, so it is necessary to assign the PR value based on specific relevance. Considering the influence of the geographic location of the charging stations on their importance, a weighted PageRank algorithm is used, where the weights of the edges reflect the distance between the charging stations.
- (2)
- The PageRank algorithm takes into account the number of outgoing links, i.e., the number of nodes pointing from one node to other nodes, in its calculations. But the actual transportation roads are well connected, and all the charging stations are reachable from each other; i.e., the influence of each charging station on other charging stations is bi-directional. So a weighted undirected graph is constructed for the actual calculations to take into account the bi-directional influence of each undirected edge on the connected nodes.
- (3)
- The charging station load information can reflect the actual usage of the charging station, which reflects the capacity and usage frequency of the charging station to a certain extent, so its influence on the importance of the charging station should also be considered when calculating the key nodes of the charging station.
In summary, based on the complex network theory [23], the charging stations and roads in the transportation network are equated into a weighted network graph, with the charging stations as nodes, and the road connectivity between the charging stations as edges. The PageRank value of the charging stations at a certain moment is
where Ti is other charging stations connected to that charging station, wij is the weight value of the edge between charging station Ti and that charging station, and ∑k∈n(Ti)wik is the sum of the weights of all the neighboring edges of charging station Ti.
In summary, the PageRank algorithm to find the spatio-temporal importance of nodes can be roughly divided into the following steps. Firstly, the load data are sliced by time. Secondly, within each time slice, the standardized charging station load data are combined with the traffic information using the improved algorithm, and the calculation of the PageRank value is dynamically adjusted according to the information of the load data as a way of reflecting the degree of importance of each charging station in the time period. Finally, the PageRank results of different time slices are summarized to analyze the dynamic importance of charging stations in the whole time period. This method takes the neglected spatial features into account and effectively integrates the spatio-temporal features, which can more comprehensively assess the relative importance of charging stations under different spatio-temporal conditions and improve the prediction accuracy.
2.2.3. Multi-Head Attention Mechanism
Differently from the traditional electric vehicle charging load prediction model that directly inputs the time series information of charging load into the model, this study constructs a spatio-temporal correlation feature extraction layer based on the multi-head attention mechanism. In the temporal attention layer, the multi-head attention mechanism is utilized to establish the coupling between long time series, and each attention head captures information from different subspaces separately to improve the expressive power of the model.
In the spatial dimension, the traffic conditions at different locations interact with each other, and the interactions between charging stations are also highly dynamic. Using the attention mechanism to adaptively capture the dynamic correlation between the charging station load nodes in the spatial dimension, and constructing the spatial attention matrix [24]
where χh = (X1, X2, …, XT) ∈ RN×F×T, Vs, bs ∈ RN×N, W1 ∈ RT, W2 ∈ RF×T, and W2 ∈ RF×T are the learnable parameters; σ denotes the sigmoid activation function that dynamically computes the attention matrix S based on the inputs of the layer; and Si,j denotes the strength of association between node i and node j. When performing graph convolution, the spatial attention matrix S′ ∈ RN×N is combined with the adjacency matrix A to implement dynamic adjustment of the influence weights between nodes.
In the temporal dimension, there is correlation between the load information of different time slices, and the same attention mechanism is used to adaptively assign different importance to the data:
where Ve, be ∈ RT×T, U1 ∈ RN, U2 ∈ RF×N, and U3 ∈ RF are learnable parameters. The normalized temporal attention matrix is directly applied to the inputs and the inputs are dynamically adjusted by merging the relevant information.
2.3. Spatio-Temporal Convolutional Layer
2.3.1. Spatial Convolutional Network
The spatio-temporal feature extraction module for charging load information captures and extracts the key information of the load information in both temporal and spatial dimensions, and the inputs after spatio-temporal feature extraction are fed into the spatio-temporal convolution module. In this study, the network composed of charging stations is essentially a graph structure, and the features of each node can be regarded as signals on the graph. In order to fully utilize the topological properties of each charging station in space, a graph convolutional neural network is used to directly process the signal at each time slice.
Here, the graph is represented by its corresponding Laplace matrix with the expression, and the nature of the graph structure can be obtained by analyzing the Laplace matrix and its eigenvalues. The Laplace matrix can be expressed as
where D is the degree matrix of the graph and A is the adjacency matrix of the graph.
The graph Fourier transform can be correspondingly expressed as follows:
where U is the matrix such that L = UΛUT and Λ denotes the eigenvector.
The corresponding graph convolution expression can be written as
where gθ is the eigenfunction about L.
However, the calculation of gθ requires the computation of Laplace matrix eigenvalues, which is complicated. In this study, we use Chebyshev polynomials for the approximation operation. Using Chebyshev polynomials as the kernel, we can reduce the eigenvalue matrix computation to L, thus skipping the eigenvalue computation step, denoted as follows:
Substituting the convolution expression gives
The Chebyshev graph convolution layer with the spatial attention mechanism is able to dynamically adjust the adjacency of the load information graph during the convolution operation by introducing a spatial attention matrix, thus better capturing the important information in the graph structure. Compared with the direct graph convolution operation, it can enhance the model’s ability to perceive important nodes and improve the effect of the convolution operation.
2.3.2. Temporal Convolutional Network
After obtaining the spatial dependencies of the load nodes from the neighborhood using graph convolutional network, temporal convolutional network is used to obtain the temporal dependencies from the proximity time. Causal convolution is often used as temporal convolution due to its characteristic of relying only on current and past inputs without involving future inputs. For a time series x(t), the output y(t) of the causal convolution depends only on x(t) and the previous inputs, i.e.,
where k is the size of the convolution kernel and w is the convolution kernel weight.
However, in the actual process of capturing long time dependencies, causal convolution requires more layers when spanning long time intervals, which increases the computational cost and memory usage; and multi-layer causal convolution also prolongs the training time and increases the complexity of the model. Therefore, in this study, we adopt the dilated causal convolution, which introduces an inflated rate d to increase the sensory field, so that the convolution kernel can capture features over a larger time range without increasing the size of the convolution kernel. The dilated causal convolution is defined as
Dilated causal convolution is able to capture dependencies over a long time horizon without significantly increasing the computational cost. In the processing of long time series forecasting tasks, the inflated causal convolution can enhance the model’s ability to capture the long-term dependencies of loads and improve the forecasting accuracy.
The mechanism of the model’s spatio-temporal attention and spatio-temporal convolutional layers is shown in Figure 2.
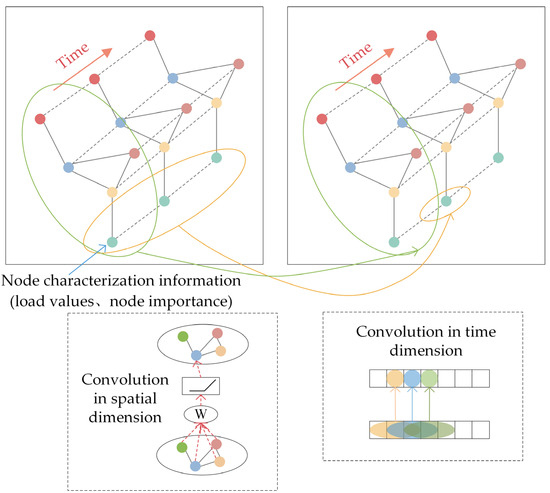
Figure 2.
Schematic of spatio-temporal attention and convolutional layers. The green lines represent the convolution in spatial dimension and the orange lines represent the convolution in time dimension.
3. Case Study
3.1. Data Preparation
In this study, five typical EV charging stations in a city in the Hebei South Network were selected for monitoring for a period of one month, and the charging load data were recorded every 15 min. The charging loads of the same charging station at different time points reflect its temporal dimension information, while the loads of different stations at the same time reflect its spatial dimension information.
The dataset is divided into training set, validation set, and test set according to the ratio of 7:2:1. In order to accelerate the convergence of the network loss function and improve the speed of model training, it is necessary to normalize the historical load data, and these three datasets are normalized with the mean and standard deviation of the training set, and the normalization formula is
where x is the sample data of the training set before normalization; x’ is the normalized value; and μ and σ are the mean and standard deviation of the sample data of the training set before normalization, respectively.
In addition, two evaluation indexes, mean absolute error (MAE) and rooted mean square error (RMSE), were selected to compare the prediction effects of different methods.
The hyperparameters were validated and confirmed several times, and were finally determined as follows: the batch size is 32, the learning rate is 0.004, the hidden unit is 64, the number of heads of multi-head attention is 2, and the number of fully connected layers is 1.
3.2. Result Analysis
3.2.1. Model Prediction Performance Comparison
In this study, six representative models are selected for comparison:
- (1)
- SVR (Support Vector Machine Regression): utilizes support vector machines for regression prediction;
- (2)
- LSTM (Long Short-Term Memory Network): a temporal recurrent neural network;
- (3)
- GCN (Graph Convolutional Neural Network): a neural network for processing graph-structured data, where feature updates at all nodes follow the same rules.
- (4)
- GAT (Graph Attention Network): introduces an attention mechanism based on GCN and assigns different attention weights according to different neighboring nodes.
- (5)
- DAGAT (Dynamic Adaptive Graph Attention Network) [25]: combines a multi-head attention mechanism with an adaptive correlation graph to capture spatio-temporally correlated features.
- (6)
- Graph WaveNet [26]: learning by adaptive dependency matrix and node embedding so as to capture spatio-temporal dependencies.
In addition, in order to further validate the effectiveness of the spatio-temporal node importance information as an input feature in this study’s method, i.e., the effectiveness of the improved PageRank algorithm, ablation experiments are also conducted. In this study, “Methodology of the study-A” denotes the prediction model in which the multi-head attention mechanism is not combined with spatio-temporal node importance information.
SVR-related setup parameters/values are given here: kernel function type is ‘rbf’, kernel function coefficient is 0.5, and penalty parameter is 10. In addition, other model parameters are shown in Table 1.

Table 1.
Parameters of the models.
The training prediction process is repeated 100 times for each model, respectively, and Table 2 shows the prediction results for the future 1 h (Tp = 4) in the case of an input length of 1 h (Th = 4).

Table 2.
Comparison of prediction errors of different models.
The following can be seen:
- (1)
- The method in this study has the best prediction effect. Compared with the second best prediction, the MAE and RMSE of this study’s method are reduced by 10.56% and 3.74%, respectively.
- (2)
- SVR and LSTM predict poorly, while GCN, GAT, DAGAT, and Graph WaveNet, which are graph-based models, are better than SVR and LSTM, which only consider temporal features, proving the importance of spatial dimension information for charging station load prediction.
- (3)
- GAT adds an attention mechanism to GCN so that nodes can assign different attention weights when aggregating neighbor information, thus flexibly dealing with the degree of influence of different neighbor nodes on the central node, and better mining the features in the load information, so the prediction effect is better than GCN; DAGAT adds a dynamic adaptive adjacency matrix to GAT, which can capture the important dynamic changes of nodes to better mine features and further improve the prediction performance; and Graph WaveNet, by developing a new adaptive dependency matrix and learning it through node embedding, can better capture the spatial dependency of the data, and its prediction effect is also better than the other models mentioned above. These observations also prove that fully considering the hidden information in the spatio-temporal dimension can significantly improve the load prediction effect.
- (4)
- The method in this study combines the advantages of each of the above models, and the prediction performance has been further improved. From the results of the ablation experiments, it can be seen that by combining the spatio-temporal node importance information computed through the improved PageRank algorithm with the attention mechanism, the MAE and RMSE of the model are reduced by 7.82% and 3.31%, respectively. And the model is able to more accurately capture spatio-temporal correlations and dynamic features in the charging load data, which improves the prediction performance. The results also demonstrate that, in addition to relying on deep learning methods to capture spatio-temporal coupling from raw load data, the method that takes into account the actual traffic geographic location information of charging stations and combines it with load information can maximize the mining of spatio-temporal features with the best prediction results.
The Graph WaveNet model, which has the best prediction performance among the comparison models, is selected for further comparison with this study’s model, and the load data of charging station No. 1 is selected to be displayed, and the coefficients of determination (R2) of the load curves obtained from the two methods are calculated separately, as shown in Figure 3. It is not difficult to see that the determination coefficient of the load curve obtained by this study’s method is closer to 1, which indicates that the prediction fitting of this study’s method is better. Moreover, as the charging load in the station fluctuates greatly, especially the load surge behavior, this study’s method has a high prediction accuracy, while the prediction effect of the Graph WaveNet is obviously much inferior, which further proves the effectiveness of this study’s prediction method.
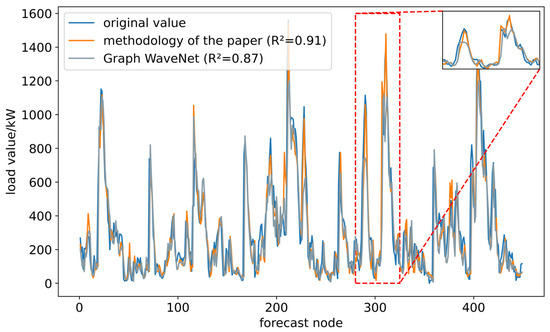
Figure 3.
Predicted results for charging station No. 1.
3.2.2. Input Duration Prediction Performance Comparison
The input length of 1 h, 6 h, 12 h, and 1 day are selected for prediction, respectively. At the same time, the time interval growth is 15 min so that the prediction length grows to 1 h, comparing the change in the prediction performance of this study’s method under different input time lengths, and the experimental results are shown in Table 3.

Table 3.
Variation in prediction performance for different input durations.
Usually, as the prediction time step increases, the prediction task will become more difficult. As can be seen from Table 3, for the first time point in the predicted future, the prediction error of the model increases with the increase in the input time length. However, with the increase in the prediction time length and the increase in the input time length, the change in the prediction error is getting smaller and smaller, and also shows a good prediction effect for the points with larger time spans, which proves that the longer the input time is, the more adequate the capture of spatio-temporal features is, and verifies that this study’s method’s consistent superiority under different prediction durations, especially when dealing with long time series tasks.
In addition, this study also analyzes the effect of model parameter changes on the prediction results. Considering that the change in the number of convolutional layers will have some impact on the model complexity and the feature extraction ability of the graph data, the changes in the prediction results under different spatio-temporal layers are analyzed, as shown in Figure 4. In order to compare the changes in prediction accuracy more intuitively, a baseline is added to the MAE and RMSE box plots, respectively.
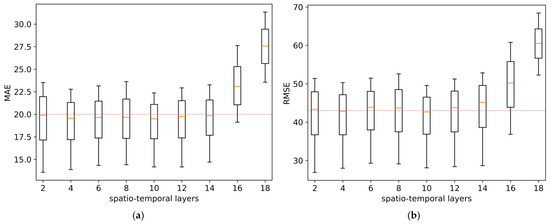
Figure 4.
(a) Effect of different spatio-temporal layers on MAE; (b) effect of different spatio-temporal layers on RMSE.
It is easy to see that when the number of spatio-temporal layers is 10, the box is flatter and the median error line is the lowest, indicating that the prediction accuracy is the highest at this time. In addition, it can also be seen from the figure that with the increase in the number of spatio-temporal layers, the prediction accuracy first improves and then decreases. This is because initially increasing the number of spatio-temporal layers helps the model to learn higher-level spatio-temporal feature representations from the original load map data. However, as the number of spatio-temporal layers continues to increase, the number of layers of the convolutional network also increases, and the complexity of the model increases, which may lead to overfitting, thus reducing the prediction accuracy. Therefore, an appropriate number of spatio-temporal layers needs to be selected, and 10 spatio-temporal layers are selected in this study.
4. Conclusions
Aiming at the deficiencies of current EV charging load prediction methods in mining complex dynamic spatio-temporal characteristics, this study combines the attention mechanism with the spatio-temporal importance of charging station nodes to generate a comprehensive feature representation with spatio-temporal correlation, so that the model can extract spatio-temporal feature information to the greatest extent possible. And then the extracted features are inputted into the graphical convolutional neural network and the inflated causal convolutional network to capture the spatial-temporal coupling relationship, which provides an in-depth understanding of the spatial interactions between charging station nodes and the dynamic changes in the time series, and improves the model’s perceptual ability and the accuracy of the prediction results.
Experimental studies show that the method proposed in this study achieves higher prediction accuracy compared with existing methods, and demonstrates more excellent prediction performance when dealing with large fluctuation situations of load data and long time series prediction tasks. Future studies will further explore the influence of spatial factors on load forecasting accuracy and continue to improve the forecasting accuracy based on this study.
Author Contributions
Conceptualization, S.H., X.Z. and H.Y.; methodology, S.H.; software, X.Z.; validation, S.H., X.Z. and, H.Y.; formal analysis, S.H.; investigation, X.Z.; resources, S.H., X.Z. and H.Y.; data curation, X.Z.; writing—original draft preparation, S.H., X.Z. and H.Y.; writing—review and editing, X.Z.; visualization, S.H., X.Z. and H.Y.; supervision, S.H.; project administration, S.H.; funding acquisition, S.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by State Grid Shanxi Electric Power Company: Research on fault type identification and localization technology of distribution network based on multi-dimensional features, grant number 5205M0230008.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ehsani, M.; Singh, K.V.; Bansal, H.O.; Mehrjardi, R.T. State of the Art and Trends in Electric and Hybrid Electric Vehicles. Proc. IEEE 2021, 109, 967–984. [Google Scholar] [CrossRef]
- Jiang, Z.; Xie, Y.; Gong, F.; Liu, S.; Fan, H.; Chen, X. Research on Planning of Connecting Large-Scale Electric Vehicle Charging Facilities to Distribution Network. In Proceedings of the 2023 IEEE 3rd International Conference on Data Science and Computer Application (ICDSCA), Dalian, China, 27–29 October 2023. [Google Scholar] [CrossRef]
- Zaboli, A.; Kasimalla, S.R.; Park, K.; Hong, Y.; Hong, J. A Comprehensive Review of Behind-the-Meter Distributed Energy Resources Load Forecasting: Models, Challenges, and Emerging Technologies. Energies 2024, 17, 2534. [Google Scholar] [CrossRef]
- Zheng, Y.; Niu, S.; Shang, Y.; Shao, Z.; Jian, L. Integrating plug-in electric vehicles into power grids: A comprehensive review on power interaction mode, scheduling methodology and mathematical foundation. Renew. Sustain. Energy Rev. 2019, 112, 424–439. [Google Scholar] [CrossRef]
- Zheng, Y.; Shao, Z.; Shang, Y.; Jian, L. Modeling the temporal and economic feasibility of electric vehicles providing vehicle-to-grid services in the electricity market under different charging scenarios. J. Energy Storage 2023, 68, 107579. [Google Scholar] [CrossRef]
- Lei, X.; Yu, H.; Yu, B.; Shao, Z.; Jian, L. Bridging electricity market and carbon emission market through electric vehicles: Optimal bidding strategy for distribution system operators to explore economic feasibility in China’s low-carbon transitions. Sustain. Cities Soc. 2023, 94, 104557. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Choi, D.-H. Distributionally Robust Model Predictive Control for Smart Electric Vehicle Charging Station with V2G/V2V Capability. IEEE Trans. Smart Grid 2023, 14, 4621–4633. [Google Scholar] [CrossRef]
- Jia, Z.; Li, J.; Zhang, X.; Zhang, R. Review on Optimization of Forecasting and Coordination Strategies for Electric Vehicle Charging. J. Mod. Power Syst. Clean Energy 2023, 11, 389–400. [Google Scholar] [CrossRef]
- Nespoli, A.; Ogliari, E.; Leva, S. User Behavior Clustering Based Method for EV Charging Forecast. IEEE Access 2023, 11, 6273–6283. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, Y.; Xu, G.; Cui, J.; Qing, D.; Zhu, X. Load forecasting of electric vehicles based on Monte Carlo method. In Proceedings of the 2020 5th International Conference on Mechanical. Control and Computer Engineering (ICMCCE), Harbin, China, 25–27 December 2020. [Google Scholar] [CrossRef]
- Liang, C.; Li, W. Electric Vehicle Charging Load Forecasting Model Considering Users’ Travel Rules. In Proceedings of the 2023 3rd New Energy and Energy Storage System Control Summit Forum (NEESSC), Mianyang, China, 26–28 September 2023. [Google Scholar] [CrossRef]
- Zhuang, Z.; Zheng, X.; Chen, Z.; Jin, T.; Li, Z. Load Forecast of Electric Vehicle Charging Station Considering Multi-Source Information and User Decision Modification. Energies 2022, 15, 7021. [Google Scholar] [CrossRef]
- Zheng, Y.; Shao, Z.; Zhang, Y.; Jian, L. A Sytematic Methodology for Mid-and-Long Term Electric Vehicle Charging Load Forecasting: The Case Study of Shenzhen, China. Sustain. Cities Soc. 2020, 56, 10204. [Google Scholar] [CrossRef]
- Tang, Z.; Hu, Q.; Cui, Y.; Rao, W.; Li, Y. Predicting Electric Vehicle Charging Load Using Graph Attention Networks and Autoformer. In Proceedings of the 2024 IEEE 4th International Conference on Power, Electronics and Computer Applications (ICPECA), Shenyang, China, 26–28 January 2024. [Google Scholar] [CrossRef]
- Mohammad, F.; Kang, D.-K.; Ahmed, M.A.; Kim, Y.-C. Energy Demand Load Forecasting for Electric Vehicle Charging Stations Network Based on ConvLSTM and BiConvLSTM Architectures. IEEE Access 2023, 11, 67350–67369. [Google Scholar] [CrossRef]
- Matrone, S.; Ogliari, E.; Nespoli, A.; Leva, S. Electric Vehicle Supply Equipment Day-Ahead Power Forecast Based on Deep Learning and the Attention Mechanism. IEEE Trans. Intell. Transp. 2024, 25, 9563–9571. [Google Scholar] [CrossRef]
- Zhao, Y.; Dong, J.; Fan, X.; Lin, X.; Tang, J.; Qian, B.; Zhang, F. Electric Vehicle Charging Load Prediction Method Based on Nonlinear Auto-Regressive Neural Networks. In Proceedings of the 2023 4th International Conference on Computer Engineering and Intelligent Control (ICCEIC), Guangzhou, China, 20–22 October 2023. [Google Scholar] [CrossRef]
- Zhou, D.; Guo, Z.; Xie, Y.; Hu, Y.; Jiang, D.; Feng, Y.; Liu, D. Using Bayesian Deep Learning for Electric Vehicle Charging Station Load Forecasting. Energies 2022, 15, 6195. [Google Scholar] [CrossRef]
- Zhang, X.; Chan, K.W.; Li, H.; Wang, H.; Qiu, J.; Wang, G. Deep-Learning-Based Probabilistic Forecasting of Electric Vehicle Charging Load With a Novel Queuing Model. IEEE Trans. Cybern. 2021, 51, 3157–3170. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Zhu, J.; Lan, J.; Li, S.; Wu, W.; Zhu, H. Optimal planning of electric vehicle battery centralized charging station based on EV load forecasting. IEEE Trans. Ind. Appl. 2022, 58, 6557–6575. [Google Scholar] [CrossRef]
- O’Donnell, J.; Su, W. Attention-Focused Machine Learning Method to Provide the Stochastic Load Forecasts Needed by Electric Utilities for the Evolving Electrical Distribution System. Energies 2023, 16, 5661. [Google Scholar] [CrossRef]
- Cheng, W.; Yang, B.; Zhang, R.; Wu, Q.; Zhu, B.; Liu, Z.; Xi, H.; Niu, K. Research on Key Node Identification Method of Transmission Network based on Improved PageRank Algorithm. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022. [Google Scholar] [CrossRef]
- Guo, S.; Miao, S.; Yin, H.; Wang, Z.; Han, J. Construction of Coupling Model and Evaluation of Node Importance for Electric Sensor Communication Network. In Proceedings of the 2020 IEEE 1st China International Youth Conference on Electrical Engineering (CIYCEE), Wuhan, China, 1–4 November 2020. [Google Scholar] [CrossRef]
- Guo, S.; Lin, Y.; Feng, N. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Beijing, China, 27 January–1 February 2019. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Liu, C.; Zhang, X.; Zhou, Y. Electric vehicle charging load prediction based on dynamic adaptive graph neural network. Autom. Electr. Power Syst. 2024, 48, 86–93. [Google Scholar] [CrossRef]
- Hu, B.; Zhang, P.; Huang, E.; Liu, J.; Xu, J.; Xing, Z. Graph WaveNet based charging load forecasting of electric vehicle. Autom. Electr. Power Syst. 2022, 46, 207–213. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).