The Role of Fully Coupled Computational Fluid Dynamics for Floating Wind Applications: A Review
Abstract
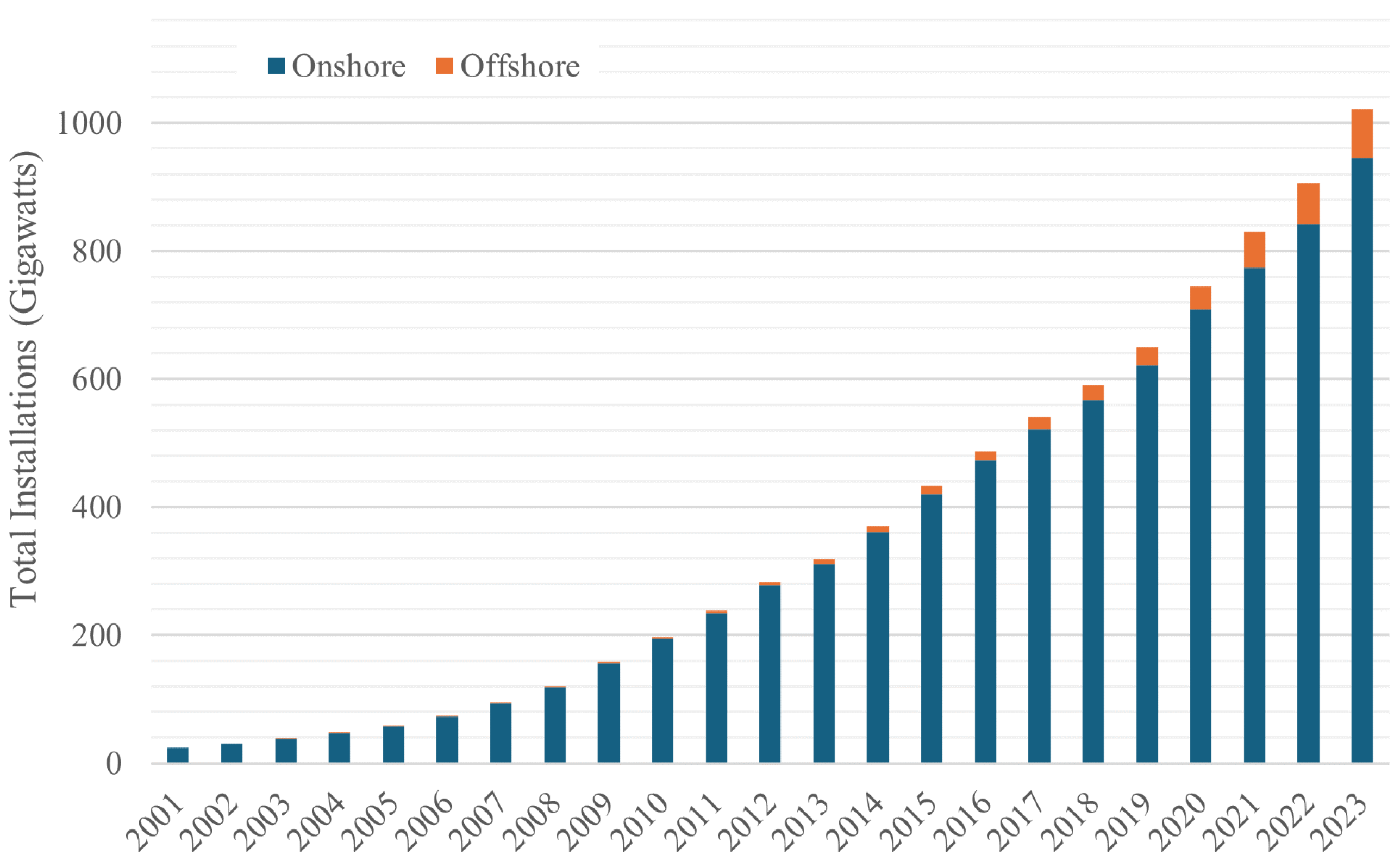
1. Introduction
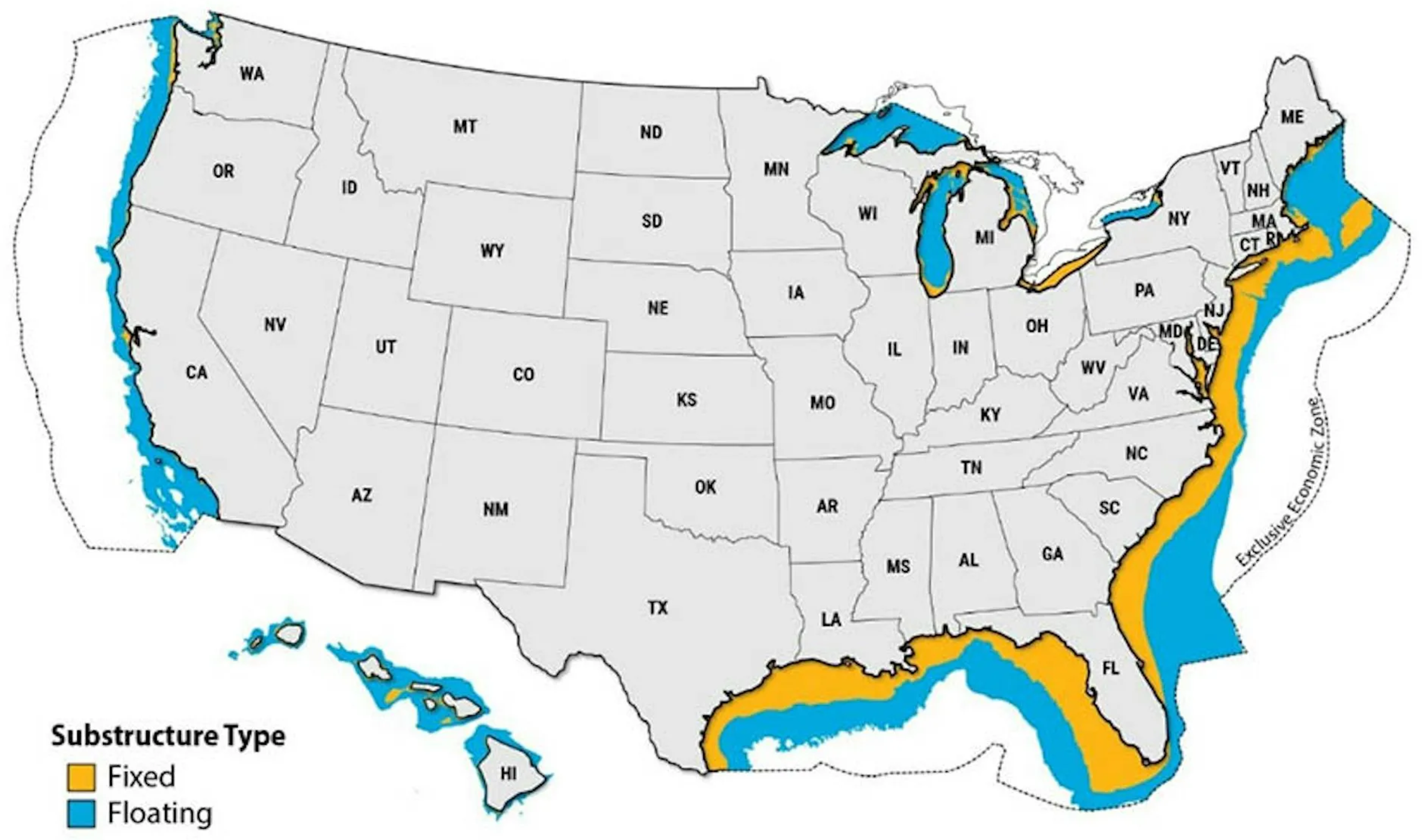
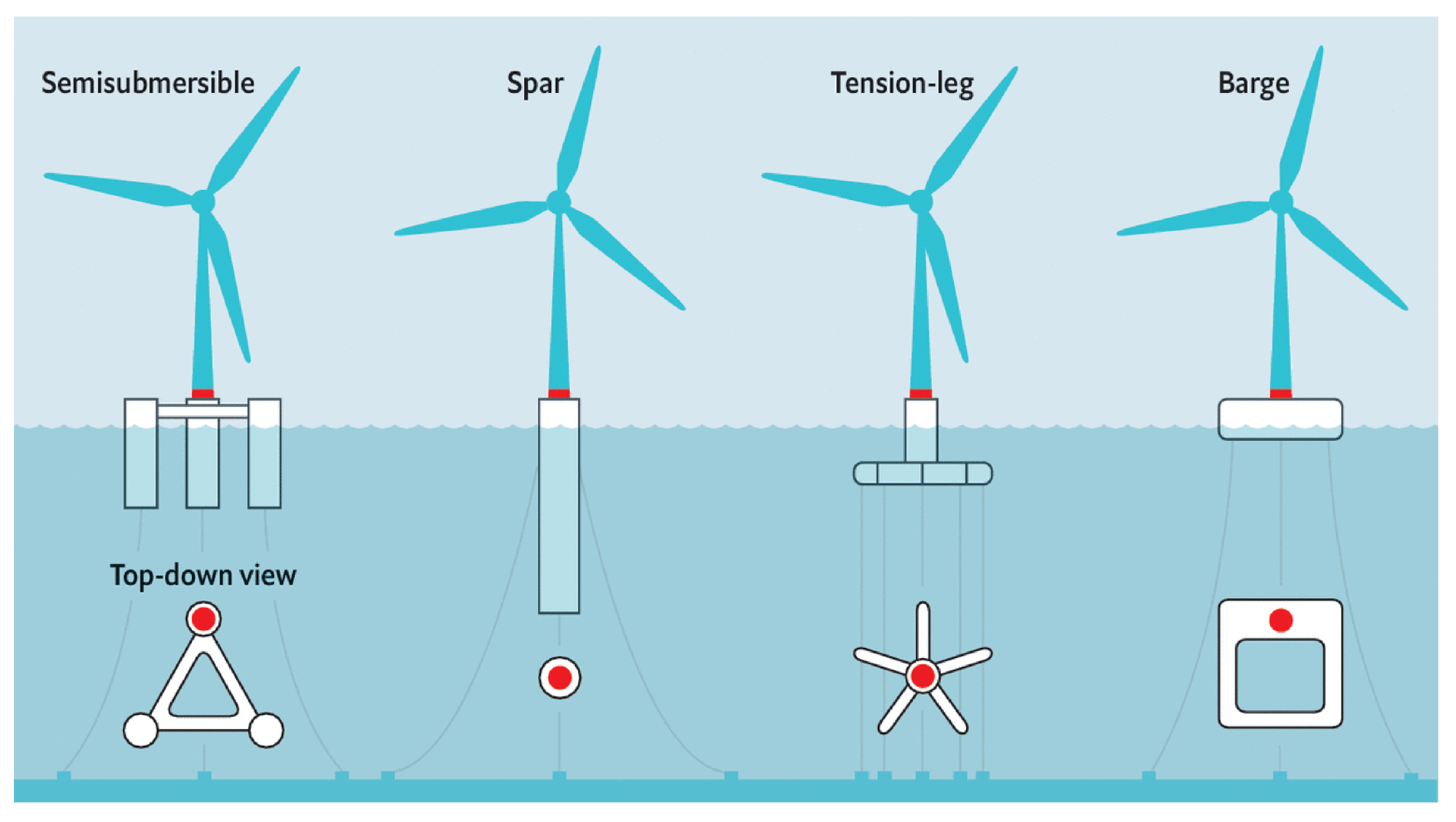
2. Floating Offshore Wind: Overview
3. Dynamic Challenges of FOWTs
3.1. Aerodynamic Contributions
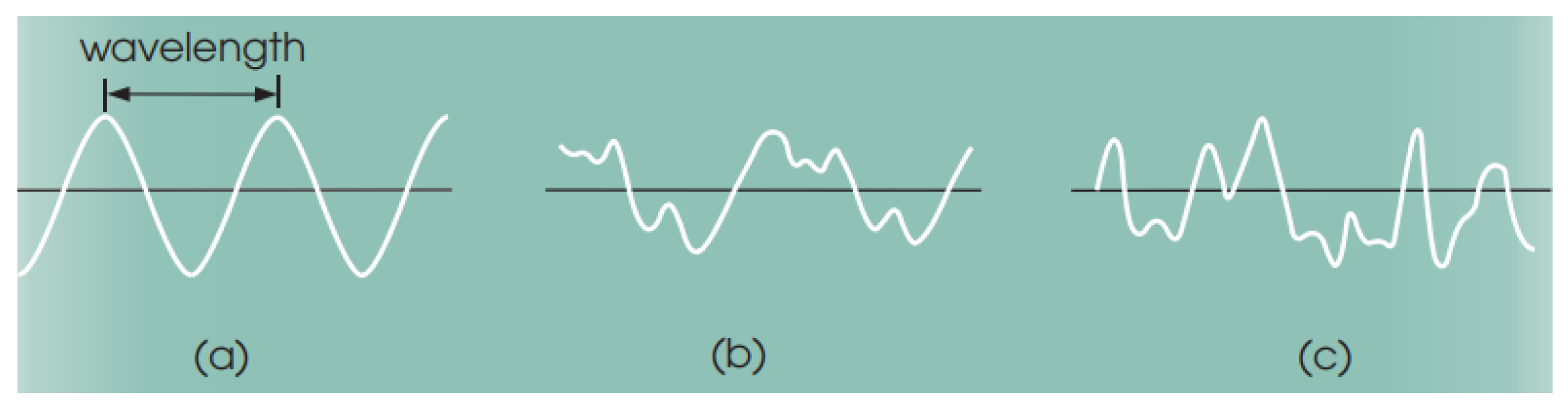
3.2. Hydrodynamic Contributions
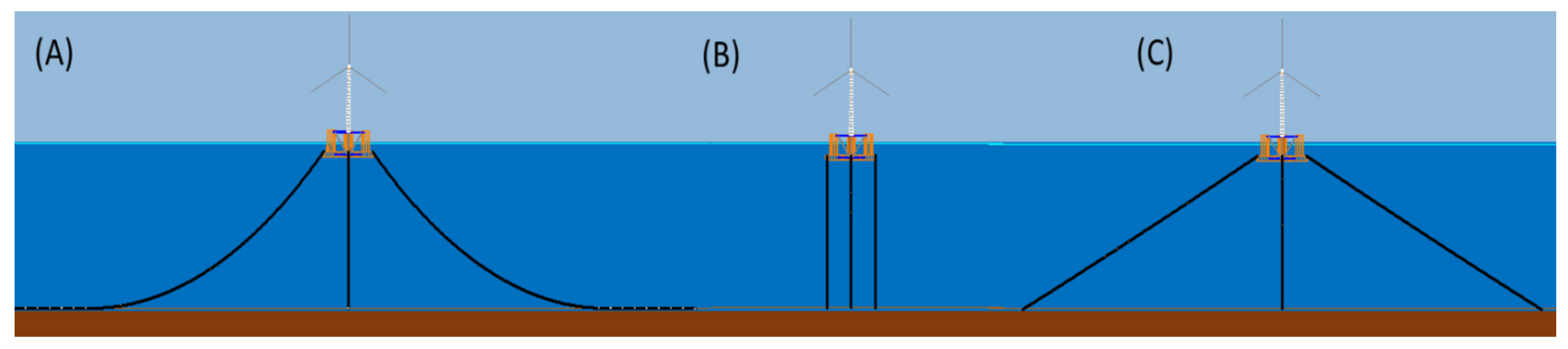
3.3. Restoring Systems
4. FOWT Modeling
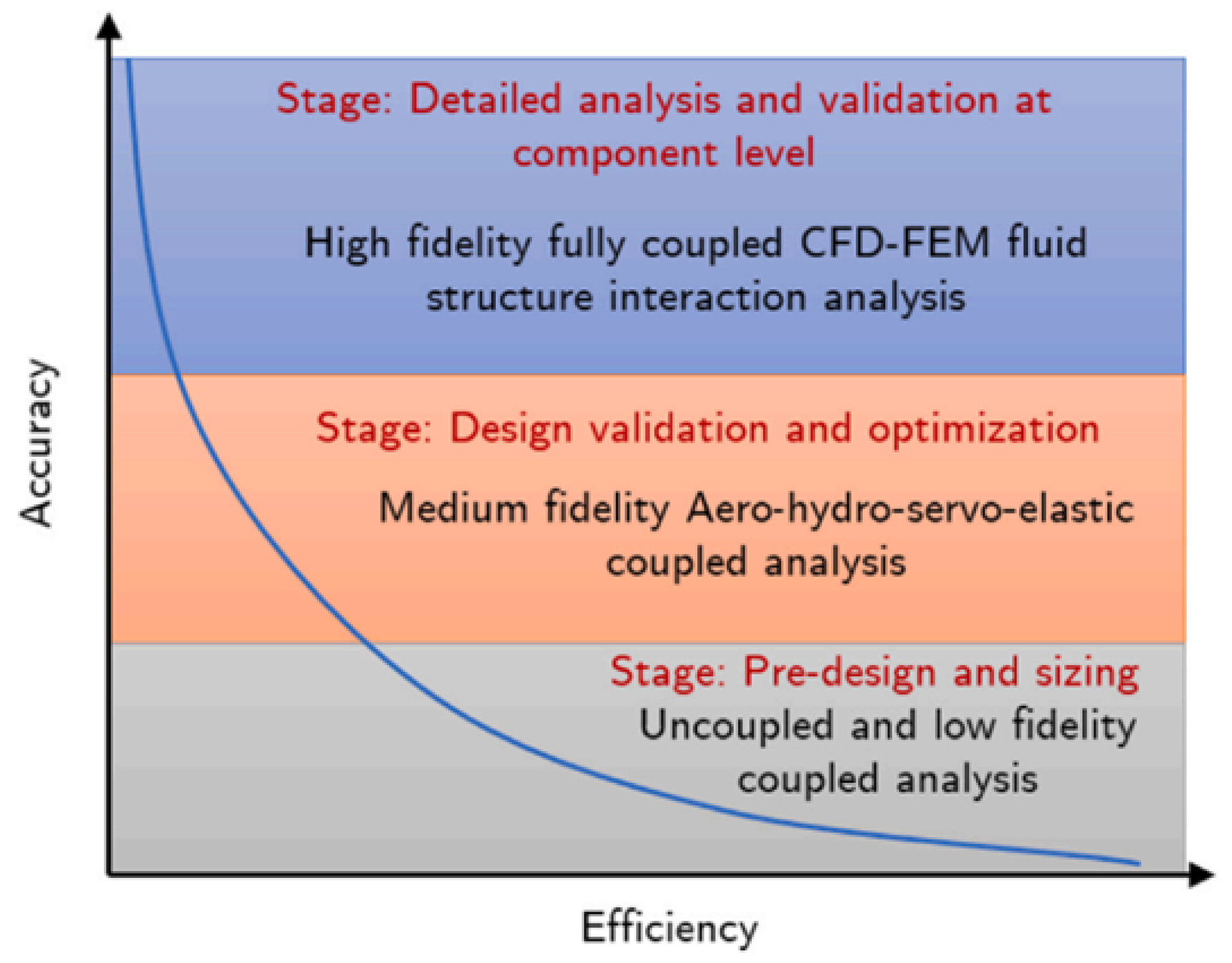
5. Fully Coupled CFD Approaches
5.1. Computational Methods
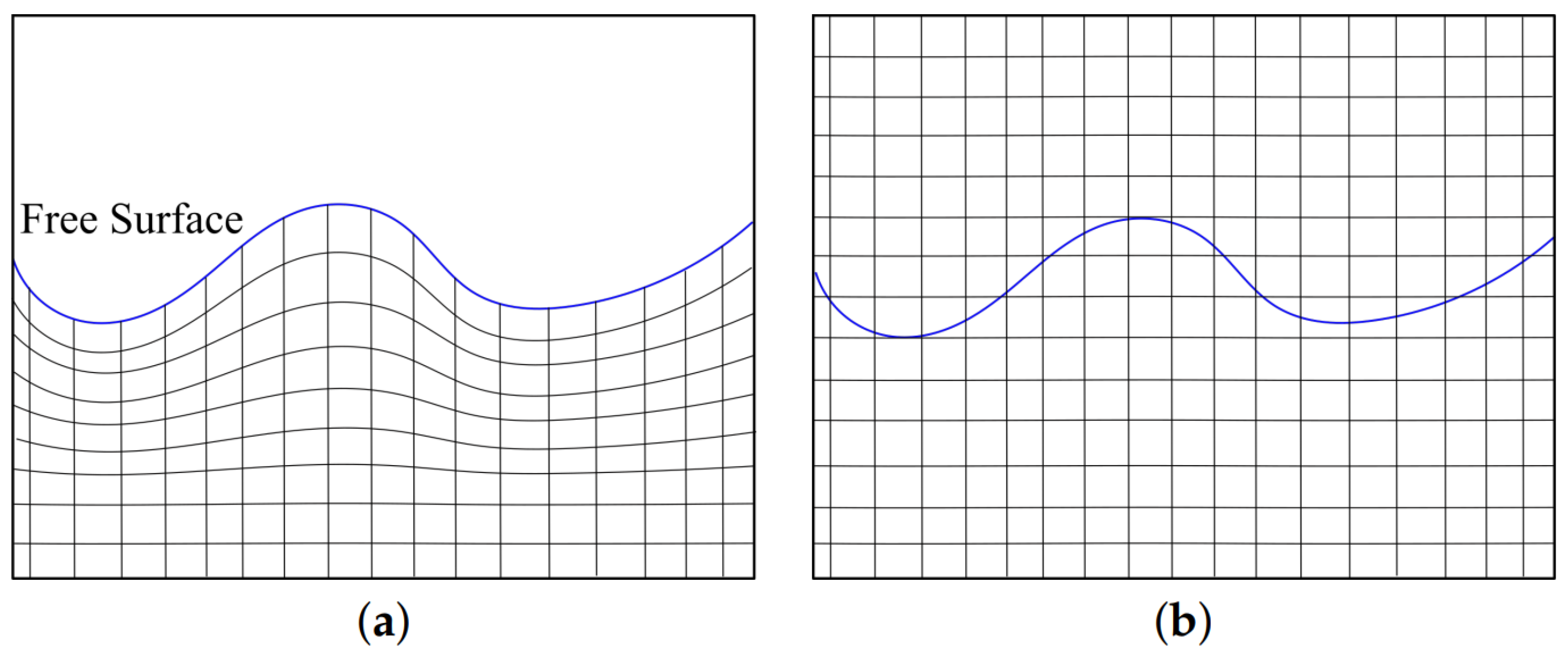
5.1.1. Geometry and Mesh Construction
5.1.2. Physics Definition
5.1.3. Solver Settings
6. Future Directions and Research Opportunities
6.1. Improving Model Accuracy
6.2. Increasing Computational Efficiency
6.3. Adapting to New Technological Advancements
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IPCC. 2023: Sections. In Climate Change 2023: Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023; pp. 35–115. [Google Scholar] [CrossRef]
- Veers, P.; Dykes, K.; Baranowski, R.; Bay, C.; Bortolotti, P.; Doubrawa, P.; MacDonald, S.; Rooney, S.; Bottasso, C.L.; Fleming, P.; et al. Grand Challenges Revisited: Wind Energy Research Needs for a Global Energy Transition; Technical report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2023. [Google Scholar]
- Stéphanie, B.; Araceli Fernandez, P.; Christophe, M.; Uwe, R.; Brent, W.; Laszlo, V.; Davide, D.; Thomas, S. Net Zero by 2050: A Roadmap for the Global Energy Sector; OECD Publishing: Paris, France, 2021. [Google Scholar]
- IRENA. Tracking COP28 Outcomes: Tripling Renewable Power Capacity by 2030; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2024. [Google Scholar]
- Shourangiz-Haghighi, A.; Haghnegahdar, M.A.; Wang, L.; Mussetta, M.; Kolios, A.; Lander, M. State of the art in the optimisation of wind turbine performance using CFD. Arch. Comput. Methods Eng. 2020, 27, 413–431. [Google Scholar] [CrossRef]
- Liu, T.; Tavner, P.; Feng, Y.; Qiu, Y. Review of recent offshore wind power developments in china. Wind Energy 2013, 16, 786–803. [Google Scholar] [CrossRef]
- Bazmi, A.A.; Zahedi, G. Sustainable energy systems: Role of optimization modeling techniques in power generation and supply—A review. Renew. Sustain. Energy Rev. 2011, 15, 3480–3500. [Google Scholar] [CrossRef]
- Lead Authors: Lee, J.; Zhao, F. GWEC Global Wind Report 2024; Global Wind Energy Council: Brussels, Belgium, 2024. [Google Scholar]
- Barooni, M.; Ashuri, T.; Velioglu Sogut, D.; Wood, S.; Ghaderpour Taleghani, S. Floating offshore wind turbines: Current status and future prospects. Energies 2022, 16, 2. [Google Scholar] [CrossRef]
- Asim, T.; Islam, S.Z.; Hemmati, A.; Khalid, M.S.U. A review of recent advancements in offshore wind turbine technology. Energies 2022, 15, 579. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, Q.; Incecik, A.; Peyrard, C.; Wan, D. Establishing a fully coupled CFD analysis tool for floating offshore wind turbines. Renew. Energy 2017, 112, 280–301. [Google Scholar] [CrossRef]
- Díaz, H.; Soares, C.G. Review of the current status, technology and future trends of offshore wind farms. Ocean Eng. 2020, 209, 107381. [Google Scholar] [CrossRef]
- Arapogianni, A.; Genachte, A.; Ochagavia, R.; Vergara, J.; Castell, D.; Tsouroukdissian, A.; Korbijn, J.; Bolleman, N.; Huera-Huarte, F.; Schuon, F.; et al. Deep Water—The Next Step for Offshore Wind Energy; European Wind Energy Association (EWEA): Brussels, Belgium, 2013; pp. 972–978. [Google Scholar]
- O’Kelly, B.; Arshad, M. Offshore wind turbine foundations–analysis and design. In Offshore Wind Farms; Elsevier: Amsterdam, The Netherlands, 2016; pp. 589–610. [Google Scholar]
- Zeng, X.; Shao, Y.; Feng, X.; Xu, K.; Jin, R.; Li, H. Nonlinear hydrodynamics of floating offshore wind turbines: A review. Renew. Sustain. Energy Rev. 2024, 191, 114092. [Google Scholar] [CrossRef]
- Wind Energy Technologies Office. Floating Offshore Wind Shot: Unlocking the Power of Floating Offshore Wind Energy. Energy Earthshots U.S. Department of Energy: Washington, DC, USA, 2022. [Google Scholar]
- Mills, S.B.; Bessette, D.; Smith, H. Exploring landowners’ post-construction changes in perceptions of wind energy in Michigan. Land Use Policy 2019, 82, 754–762. [Google Scholar] [CrossRef]
- Schallenberg-Rodríguez, J.; Montesdeoca, N.G. Spatial planning to estimate the offshore wind energy potential in coastal regions and islands. Practical case: The Canary Islands. Energy 2018, 143, 91–103. [Google Scholar] [CrossRef]
- Subbulakshmi, A.; Verma, M.; Keerthana, M.; Sasmal, S.; Harikrishna, P.; Kapuria, S. Recent advances in experimental and numerical methods for dynamic analysis of floating offshore wind turbines—An integrated review. Renew. Sustain. Energy Rev. 2022, 164, 112525. [Google Scholar] [CrossRef]
- Otter, A.; Murphy, J.; Pakrashi, V.; Robertson, A.; Desmond, C. A review of modelling techniques for floating offshore wind turbines. Wind Energy 2022, 25, 831–857. [Google Scholar] [CrossRef]
- Chen, P.; Chen, J.; Hu, Z. Review of experimental-numerical methodologies and challenges for floating offshore wind turbines. J. Mar. Sci. Appl. 2020, 19, 339–361. [Google Scholar] [CrossRef]
- Xu, S.; Xue, Y.; Zhao, W.; Wan, D. A Review of High-Fidelity Computational Fluid Dynamics for Floating Offshore Wind Turbines. J. Mar. Sci. Eng. 2022, 10, 1357. [Google Scholar] [CrossRef]
- Zhang, W.; Calderon-Sanchez, J.; Duque, D.; Souto-Iglesias, A. Computational Fluid Dynamics (CFD) applications in Floating Offshore Wind Turbine (FOWT) dynamics: A review. Appl. Ocean Res. 2024, 150, 104075. [Google Scholar] [CrossRef]
- Haider, R.; Li, X.; Shi, W.; Lin, Z.; Xiao, Q.; Zhao, H. Review of computational fluid dynamics in the design of floating offshore wind turbines. Energies 2024, 17, 4269. [Google Scholar] [CrossRef]
- Heronemus, W.E. Pollution-free energy from offshore winds. In Proceedings of the 8th Annual Conference and Exposition, Marine Technology Society, Washington, DC, USA, 11–13 September 1972. [Google Scholar]
- Stoddard, W. The Life and Work of Bill Heronemus, wind engineering pioneer. Wind Eng. 2002, 26, 335–341. [Google Scholar] [CrossRef]
- Butterfield, S.; Musial, W.; Jonkman, J.; Sclavounos, P. Engineering Challenges for Floating Offshore Wind Turbines; Technical report, National Renewable Energy Lab. (NREL): Golden, CO, USA, 2007. [Google Scholar]
- Edwards, E.C.; Holcombe, A.; Brown, S.; Ransley, E.; Hann, M.; Greaves, D. Trends in floating offshore wind platforms: A review of early-stage devices. Renew. Sustain. Energy Rev. 2024, 193, 114271. [Google Scholar] [CrossRef]
- Mei, X.; Xiong, M. Effects of second-order hydrodynamics on the dynamic responses and fatigue damage of a 15 MW floating offshore wind turbine. J. Mar. Sci. Eng. 2021, 9, 1232. [Google Scholar] [CrossRef]
- Castro-Santos, L.; Diaz-Casas, V. Floating Offshore Wind Farms; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Savenije, L.; Ashuri, T.; Bussel, G.; Staerdahl, J. Dynamic modeling of a spar-type floating offshore wind turbine. In Proceedings of the European Wind Energy Conference and Exhibition (EWEC), Warsaw, Poland, 20–23 April 2010; pp. 20–23. [Google Scholar]
- Equinor. Hywind Scotland. 2021. Available online: https://www.equinor.com/energy/hywind-scotland (accessed on 22 September 2024).
- Windplus. WindFloat Atlantic. 2020. Available online: www.windfloat-atlantic.com (accessed on 22 September 2024).
- Principle Power. Kincardine. 2021. Available online: www.principlepower.com/projects/kincardine-offshore-wind-farm (accessed on 22 September 2024).
- Equinor. Hywind Tampen. 2022. Available online: www.equinor.com/energy/hywind-tampen (accessed on 22 September 2024).
- Musial, W.; Spitsen, P.; Duffy, P.; Beiter, P.; Shields, M.; Mulas Hernando, D.; Hammond, R.; Marquis, M.; King, J.; Sathish, S. Offshore Wind Market Report: 2023 Edition; Technical report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2023. [Google Scholar]
- Hu, D.; Deng, L.; Zeng, L. Study on the aerodynamic performance of floating offshore wind turbine considering the tower shadow effect. Processes 2021, 9, 1047. [Google Scholar] [CrossRef]
- Cottura, L.; Caradonna, R.; Novo, R.; Ghigo, A.; Bracco, G.; Mattiazzo, G. Effect of pitching motion on production in a OFWT. J. Ocean Eng. Mar. Energy 2022, 8, 319–330. [Google Scholar] [CrossRef]
- Nielsen, F.G. Offshore Wind Energy: Environmental Conditions and Dynamics of Fixed and Floating Turbines; Cambridge University Press: Cambridge, UK, 2024. [Google Scholar]
- Cruz, J.; Atcheson, M. Floating Offshore Wind Energy: The Next Generation of Wind Energy; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Ranta, J.; Polojärvi, A. Limit mechanisms for ice loads on inclined structures: Local crushing. Mar. Struct. 2019, 67, 102633. [Google Scholar] [CrossRef]
- Sirnivas, S.; Musial, W.; Bailey, B.; Filippelli, M. Assessment of Offshore Wind System Design, Safety, and Operation Standards; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2014. [Google Scholar]
- Karimirad, M. Offshore Energy Structures: For Wind Power, Wave Energy and Hybrid Marine Platforms; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Leishman, J.G. Challenges in modelling the unsteady aerodynamics of wind turbines. Wind Energy Int. J. Prog. Appl. Wind Power Convers. Technol. 2002, 5, 85–132. [Google Scholar] [CrossRef]
- Huyer, S.A.; Simms, D.; Robinson, M.C. Unsteady aerodynamics associated with a horizontal-axis wind turbine. AIAA J. 1996, 34, 1410–1419. [Google Scholar] [CrossRef]
- Robinson, M.; Galbraith, R.; Shipley, D.; Miller, M. Unsteady aerodynamics of wind turbines. In Proceedings of the 33rd Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 1995; p. 526. [Google Scholar]
- Cai, Y.; Zhao, H.; Li, X.; Liu, Y. Effects of yawed inflow and blade-tower interaction on the aerodynamic and wake characteristics of a horizontal-axis wind turbine. Energy 2023, 264, 126246. [Google Scholar] [CrossRef]
- Chanprasert, W.; Sharma, R.; Cater, J.; Norris, S. Large Eddy Simulation of wind turbine wake interaction in directionally sheared inflows. Renew. Energy 2022, 201, 1096–1110. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Micallef, D. Wake interactions of two tandem floating offshore wind turbines: CFD analysis using actuator disc model. Renew. Energy 2021, 179, 859–876. [Google Scholar] [CrossRef]
- Zhou, Y.; Xiao, Q.; Liu, Y.; Incecik, A.; Peyrard, C.; Wan, D.; Pan, G.; Li, S. Exploring inflow wind condition on floating offshore wind turbine aerodynamic characterisation and platform motion prediction using blade resolved CFD simulation. Renew. Energy 2022, 182, 1060–1079. [Google Scholar] [CrossRef]
- Matha, D.; Schlipf, M.; Pereira, R.; Jonkman, J. Challenges in simulation of aerodynamics, hydrodynamics, and mooring-line dynamics of floating offshore wind turbines. In Proceedings of the 21st International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011; p. ISOPE–I. [Google Scholar]
- Sebastian, T.; Lackner, M. Characterization of the unsteady aerodynamics of offshore floating wind turbines. Wind Energy 2013, 16, 339–352. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.H. The platform pitching motion of floating offshore wind turbine: A preliminary unsteady aerodynamic analysis. J. Wind Eng. Ind. Aerodyn. 2015, 142, 65–81. [Google Scholar] [CrossRef]
- Lynn, P.A. Onshore and Offshore Wind Energy: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Williamson, C.H.; Govardhan, R. Vortex-induced vibrations. Annu. Rev. Fluid Mech. 2004, 36, 413–455. [Google Scholar] [CrossRef]
- Benitz, M.A.; Lackner, M.; Schmidt, D. Hydrodynamics of offshore structures with specific focus on wind energy applications. Renew. Sustain. Energy Rev. 2015, 44, 692–716. [Google Scholar] [CrossRef]
- Thiagarajan, K.; Dagher, H. A review of floating platform concepts for offshore wind energy generation. J. Offshore Mech. Arct. Eng. 2014, 136, 020903. [Google Scholar] [CrossRef]
- Sound and Sea Technology. Advanced Anchoring and Mooring Study; Technical Report; Oregon Wave Energy Trust (OWET): Portland, OR, USA, 2009. [Google Scholar]
- Rui, S.; Zhou, Z.; Gao, Z.; Jostad, H.P.; Wang, L.; Xu, H.; Guo, Z. A review on mooring lines and anchors of floating marine structures. Renew. Sustain. Energy Rev. 2024, 199, 114547. [Google Scholar] [CrossRef]
- Lamei, A.; Hayatdavoodi, M. On motion analysis and elastic response of floating offshore wind turbines. J. Ocean Eng. Mar. Energy 2020, 6, 71–90. [Google Scholar] [CrossRef]
- Robertson, A.; Jonkman, J.; Goupee, A.; Coulling, A.; Prowell, I.; Browning, J.; Masciola, M.; Molta, P. Summary of conclusions and recommendations drawn from the DeepCwind scaled floating offshore wind system test campaign. Am. Soc. Mech. Eng. Int. Conf. Offshore Mech. Arct. Eng. 2013, 55423, V008T09A053. [Google Scholar]
- Müller, K.; Sandner, F.; Bredmose, H.; Azcona, J.; Manjock, A.; Pereira, R. Improved Tank Test Procedures for Scaled Floating Offshore Wind Turbines; University of Stuttgart: Stuttgart, Germany, 2014. [Google Scholar]
- Stewart, G.; Muskulus, M. A review and comparison of floating offshore wind turbine model experiments. Energy Procedia 2016, 94, 227–231. [Google Scholar] [CrossRef]
- Gueydon, S.; Bayati, I.; De Ridder, E. Discussion of solutions for basin model tests of FOWTs in combined waves and wind. Ocean Eng. 2020, 209, 107288. [Google Scholar] [CrossRef]
- Edition, F.; Journée, J.; Massie, W. Offshore Hydromechanics; Delft University of Technology: Delft, The Netherlands, 2001. [Google Scholar]
- Barltrop, N.D.P. Floating Structures: A Guide for Design and Analysis; Energy Institute: London, UK, 1998. [Google Scholar]
- Yu, W.; Müller, K.; Lemmer, F. Qualification of innovative floating substructures for 10 MW wind turbines and water depths greater than 50 m. LIFES50 2018. [Google Scholar] [CrossRef]
- Hegseth, J.M.; Bachynski, E.E. A semi-analytical frequency domain model for efficient design evaluation of spar floating wind turbines. Mar. Struct. 2019, 64, 186–210. [Google Scholar] [CrossRef]
- Karimi, M.; Hall, M.; Buckham, B.; Crawford, C. A multi-objective design optimization approach for floating offshore wind turbine support structures. J. Ocean Eng. Mar. Energy 2017, 3, 69–87. [Google Scholar] [CrossRef]
- Pegalajar-Jurado, A.; Borg, M.; Bredmose, H. An efficient frequency-domain model for quick load analysis of floating offshore wind turbines. Wind Energy Sci. 2018, 3, 693–712. [Google Scholar] [CrossRef]
- Hall, M.; Housner, S.; Zalkind, D.; Bortolotti, P.; Ogden, D.; Barter, G. An open-source frequency-domain model for floating wind turbine design optimization. J. Physics Conf. Ser. 2022, 2265-4, 042020. [Google Scholar] [CrossRef]
- NREL. OpenFAST n.d. Available online: www.nrel.gov/wind/nwtc/openfast.html (accessed on 22 September 2024).
- Jonkman, J.M.; Wright, A.D.; Hayman, G.J.; Robertson, A.N. Full-system linearization for floating offshore wind turbines in OpenFAST. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, Madrid, Spain, 17–22 June 2018; Volume 51975, p. V001T01A028. [Google Scholar]
- DTU Wind. HAWC2 n.d. Available online: www.hawc2.dk (accessed on 22 September 2024).
- SINTEF Ocean. SIMA. n.d. Available online: www.sintef.no/en/software/sima (accessed on 22 September 2024).
- DNV. Bladed n.d. Available online: https://www.dnv.com/services/wind-turbine-design-software-bladed-3775 (accessed on 22 September 2024).
- Dassault Systems. SIMPACK Multibody System Simulation Software n.d. Available online: www.3ds.com/products/simulia/simpack/wind (accessed on 22 September 2024).
- Orcina. Orcaflex n.d. Available online: www.orcina.com/orcaflex (accessed on 22 September 2024).
- Wood Group. Flexcom n.d. Available online: www.woodplc.com/solutions/expertise/flexcom (accessed on 22 September 2024).
- OpenFOAM, The OpenFOAM Foundation. 2024. Available online: www.openfoam.org (accessed on 22 September 2024).
- OpenFOAM, OpenCFD Limited. 2024. Available online: www.openfoam.com (accessed on 22 September 2024).
- StarCCM+, Siemens Simcenter. 2024. Available online: https://plm.sw.siemens.com/en-US/simcenter/fluids-thermal-simulation/star-ccm/ (accessed on 22 September 2024).
- Ansys Fluent, Ansys. 2024. Available online: www.ansys.com/products/fluids/ansys-fluent (accessed on 22 September 2024).
- CONVERGE CFD Software, Convergent Science Inc. 2024. Available online: https://convergecfd.com (accessed on 22 September 2024).
- Helicopter Multi-Block Code. ARCHIE-WeSt. University of Glasgow. 2024. Available online: www.archie-west.ac.uk/projects/computational-fluid-dynamics/helicopter-multi-block-code/ (accessed on 22 September 2024).
- ReFRESCO, MARIN. 2024. Available online: www.marin.nl/en/about/facilities-and-tools/software/refresco (accessed on 22 September 2024).
- CFDShip-Iowa. The University of Iowa. Stern Lab. 2024. Available online: https://stern.lab.uiowa.edu/cfd-code (accessed on 22 September 2024).
- Van Bussel, G.J.W. The Aerodynamics of Horizontal axis Wind Turbine Rotors Explored with Asymptotic Expansion Methods. Ph.D. Thesis, Technische Universiteit Delft, Delft, The Netherlands, 1995. [Google Scholar]
- Glauert, H. Airplane Propellers. In Aerodynamic Theory; Springer: Berlin/Heidelberg, Germany, 1935. [Google Scholar]
- Fadaei, S.; Afagh, F.F.; Langlois, R.G. A survey of numerical simulation tools for offshore wind turbine systems. Wind 2024, 4, 1–24. [Google Scholar] [CrossRef]
- Cordle, A.; Jonkman, J. State of the art in floating wind turbine design tools. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011; ISOPE: Mountain View, CA, USA, 2011; p. ISOPE–I. [Google Scholar]
- Maali Amiri, M.; Shadman, M.; Estefen, S.F. A Review of Numerical and Physical Methods for Analyzing the Coupled Hydro–Aero–Structural Dynamics of Floating Wind Turbine Systems. J. Mar. Sci. Eng. 2024, 12, 392. [Google Scholar] [CrossRef]
- Jonkman, J.; Musial, W. Offshore Code Comparison Collaboration (OC3) for IEA Wind Task 23 Offshore Wind Technology and Deployment; Technical report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2010. [Google Scholar]
- COREWIND. WindCrete. 2024. Available online: www.windcrete.com (accessed on 22 September 2024).
- Molins, C.; Yagüe, A.; Trubat, P. Construction possibilities for monolithic concrete spar buoy serial production. J. Physics Conf. Ser. IOP 2018, 1104-1, 012020. [Google Scholar] [CrossRef]
- Mahfouz, M.Y.; Molins, C.; Trubat, P.; Hernández, S.; Vigara, F.; Pegalajar-Jurado, A.; Bredmose, H.; Salari, M. Response of the International Energy Agency (IEA) Wind 15 MW WindCrete and Activefloat floating wind turbines to wind and second-order waves. Wind Energy Sci. 2021, 6, 867–883. [Google Scholar] [CrossRef]
- Coulling, A.J.; Goupee, A.J.; Robertson, A.N.; Jonkman, J.M.; Dagher, H.J. Validation of a FAST semi-submersible floating wind turbine numerical model with DeepCwind test data. J. Renew. Sustain. Energy 2013, 5, 023116. [Google Scholar] [CrossRef]
- Robertson, A.; Jonkman, J.; Masciola, M.; Song, H.; Goupee, A.; Coulling, A.; Luan, C. Definition of the Semisubmersible Floating System for Phase II of OC4; Technical report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2014. [Google Scholar]
- Robertson, A.; Jonkman, J.; Wendt, F.; Goupee, A.; Dagher, H. Definition of the OC5 DeepCwind semisubmersible floating system. National Renewable Energy Laboratory, University of Maine 2016. Available online: https://a2e.energy.gov/api/datasets/oc5/oc5.phase2/files/oc5.phase2.model.definition-semisubmersible-floating-system-phase2-oc5-ver15.pdf (accessed on 22 September 2024).
- Robertson, A.N.; Wendt, F.; Jonkman, J.M.; Popko, W.; Dagher, H.; Gueydon, S.; Qvist, J.; Vittori, F.; Azcona, J.; Uzunoglu, E.; et al. OC5 project Phase II: Validation of global loads of the DeepCwind floating semisubmersible wind turbine. Energy Procedia 2017, 137, 38–57. [Google Scholar] [CrossRef]
- Wang, L.; Robertson, A.; Jonkman, J.; Kim, J.; Shen, Z.R.; Koop, A.; Borràs Nadal, A.; Shi, W.; Zeng, X.; Ransley, E.; et al. OC6 Phase Ia: CFD simulations of the free-decay motion of the DeepCwind semisubmersible. Energies 2022, 15, 389. [Google Scholar] [CrossRef]
- Bergua, R.; Robertson, A.; Jonkman, J.; Branlard, E.; Fontanella, A.; Belloli, M.; Schito, P.; Zasso, A.; Persico, G.; Sanvito, A.; et al. OC6 project Phase III: Validation of the aerodynamic loading on a wind turbine rotor undergoing large motion caused by a floating support structure. Wind Energy Sci. 2023, 8, 465–485. [Google Scholar] [CrossRef]
- Wiley, W.; Bergua, R.; Robertson, A.; Jonkman, J.; Wang, L.; Borg, M.; Fowler, M. Definition of the Stiesdal Offshore TetraSpar Floating Wind System for OC6 Phase IV; Technical report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2023. [Google Scholar]
- Allen, C.; Viscelli, A.; Dagher, H.; Goupee, A.; Gaertner, E.; Abbas, N.; Hall, M.; Barter, G. Definition of the UMaine VolturnUS-S Reference Platform Developed for the IEA Wind 15-Megawatt Offshore Reference Wind Turbine; Technical report; National Renewable Energy Lab. (NREL): Golden, CO, USA; University of Maine: Orono, ME, USA, 2020. [Google Scholar]
- Bachynski, E.E.; Moan, T. Design considerations for tension leg platform wind turbines. Mar. Struct. 2012, 29, 89–114. [Google Scholar] [CrossRef]
- Jonkman, J.M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine; Technical report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2007. [Google Scholar]
- Vijfhuizen, W. Design of a Wind and Wave Power Barge. Master’s Thesis, Department of Naval Architecture and Mechanical Engineering, Universities of Glasgow and Strathclyde, Glasgow, Scotland, 2006. [Google Scholar]
- Jonkman, J. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Hansen, M.H.; Blasques, J.P.A.A.; Gaunaa, M.; Natarajan, A. The DTU 10-MW reference wind turbine. In Proceedings of the Danish Wind Power Research 2013, Fredericia, Denmark, 27–28 May 2013. [Google Scholar]
- Gaertner, E.; Rinker, J.; Sethuraman, L.; Zahle, F.; Anderson, B.; Barter, G.; Abbas, N.; Meng, F.; Bortolotti, P.; Skrzypinski, W.; et al. Definition of the IEA 15-Megawatt Offshore Reference Wind Turbine; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2020. [Google Scholar]
- Zahle, F.; Barlas, T.; Lonbaek, K.; Bortolotti, P.; Zalkind, D.; Wang, L.; Labuschagne, C.; Sethuraman, L.; Barter, G. Definition of the IEA Wind 22-Megawatt Offshore Reference Wind Turbine; Technical report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2024. [Google Scholar]
- Ren, N.; Li, Y.; Ou, J. Coupled wind-wave time domain analysis of floating offshore wind turbine based on Computational Fluid Dynamics method. J. Renew. Sustain. Energy 2014, 6, 023106. [Google Scholar] [CrossRef]
- Quallen, S.; Xing, T. CFD simulation of a floating offshore wind turbine system using a variable-speed generator-torque controller. Renew. Energy 2016, 97, 230–242. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.H. Fully coupled aero-hydrodynamic analysis of a semi-submersible FOWT using a dynamic fluid body interaction approach. Renew. Energy 2016, 92, 244–261. [Google Scholar] [CrossRef]
- Leble, V.; Barakos, G. Demonstration of a coupled floating offshore wind turbine analysis with high-fidelity methods. J. Fluids Struct. 2016, 62, 272–293. [Google Scholar] [CrossRef]
- Li, P.; Wan, D.; Hu, C. Fully-coupled dynamic response of a semi-submerged floating wind turbine system in wind and waves. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–1 July 2016; ISOPE: Mountain View, CA, USA, 2016; p. ISOPE–I. [Google Scholar]
- Tran, T.T.; Kim, D.H. A CFD study of coupled aerodynamic-hydrodynamic loads on a semisubmersible floating offshore wind turbine. Wind Energy 2018, 21, 70–85. [Google Scholar] [CrossRef]
- Zhang, Y.; Kim, B. A fully coupled computational fluid dynamics method for analysis of semi-submersible floating offshore wind turbines under wind-wave excitation conditions based on OC5 data. Appl. Sci. 2018, 8, 2314. [Google Scholar] [CrossRef]
- Zhou, Y.; Xiao, Q.; Liu, Y.; Incecik, A.; Peyrard, C.; Li, S.; Pan, G. Numerical modelling of dynamic responses of a floating offshore wind turbine subject to focused waves. Energies 2019, 12, 3482. [Google Scholar] [CrossRef]
- Huang, Y.; Wan, D. Investigation of interference effects between wind turbine and spar-type floating platform under combined wind-wave excitation. Sustainability 2019, 12, 246. [Google Scholar] [CrossRef]
- Huang, Y.; Cheng, P.; Wan, D. Numerical analysis of a floating offshore wind turbine by coupled aero-hydrodynamic simulation. J. Mar. Sci. Appl. 2019, 18, 82–92. [Google Scholar] [CrossRef]
- Cheng, P.; Huang, Y.; Wan, D. A numerical model for fully coupled aero-hydrodynamic analysis of floating offshore wind turbine. Ocean Eng. 2019, 173, 183–196. [Google Scholar] [CrossRef]
- Zhou, Y.; Xiao, Q.; Peyrard, C.; Pan, G. Assessing focused wave applicability on a coupled aero-hydro-mooring FOWT system using CFD approach. Ocean Eng. 2021, 240, 109987. [Google Scholar] [CrossRef]
- Zheng, J.; Huang, Y.; Wan, D. Numerical Study of Coupled Aero-Hydrodynamics Performances of a Floating Offshore Wind Turbine with Heave Plate. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Rhodes, Greece, 20–25 June 2021; ISOPE: Mountain View, CA, USA, 2021; p. ISOPE–I. [Google Scholar]
- Xie, S.; Sadique, J. CFD Simulations of Two Tandem Semi-Submersible Floating Offshore Wind Turbines Using a Fully-Coupled Fluid-Structure-Interaction Simulation Methodology. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Hamburg, Germany, 5–10 June 2022; American Society of Mechanical Engineers: New York, NY, USA, 2022; Volume 86618, p. V001T01A006. [Google Scholar]
- Huang, H.; Liu, Q.; Yue, M.; Miao, W.; Wang, P.; Li, C. Fully coupled aero-hydrodynamic analysis of a biomimetic fractal semi-submersible floating offshore wind turbine under wind-wave excitation conditions. Renew. Energy 2023, 203, 280–300. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, W.; Wan, D. Wake interaction between two spar-type floating offshore wind turbines under different layouts. Phys. Fluids 2023, 35, 097102. [Google Scholar] [CrossRef]
- Yu, Z.; Zheng, X.; Yuan, Y. Analysis of the blade aeroelastic effect on the floating offshore wind turbine wake in a focusing wave with a hybrid model. Eng. Appl. Comput. Fluid Mech. 2023, 17, 2260470. [Google Scholar] [CrossRef]
- Yu, Z.; Ma, Q.; Zheng, X.; Liao, K.; Sun, H.; Khayyer, A. A hybrid numerical model for simulating aero-elastic-hydro-mooring-wake dynamic responses of floating offshore wind turbine. Ocean Eng. 2023, 268, 113050. [Google Scholar] [CrossRef]
- Feng, X.; Fang, J.; Lin, Y.; Chen, B.; Li, D.; Liu, H.; Gu, Y. Coupled aero-hydro-mooring dynamic analysis of floating offshore wind turbine under blade pitch motion. Phys. Fluids 2023, 35, 045131. [Google Scholar]
- Alkhabbaz, A.; Hamza, H.; Daabo, A.M.; Yang, H.S.; Yoon, M.; Koprulu, A.; Lee, Y.H. The aero-hydrodynamic interference impact on the NREL 5-MW floating wind turbine experiencing surge motion. Ocean Eng. 2024, 295, 116970. [Google Scholar] [CrossRef]
- Sadique, J.; Xie, S.; Shekhawat, Y.; Darling, H.; Schmidt, D. Numerical Assessment and Validation of Floating Offshore Wind Turbines in One Fully Coupled CFD Simulation. In Proceedings of the Offshore Technology Conference Asia, Kuala Lumpur, Malaysia, 27 February–1 March 2024; p. D031S037R001. [Google Scholar]
- Yu, Z.; Hu, Z.; Zheng, X.; Ma, Q.; Hao, H. Aeroelastic performance analysis of wind turbine in the wake with a new Elastic Actuator Line model. Water 2020, 12, 1233. [Google Scholar] [CrossRef]
- Santo, G.; Peeters, M.; Van Paepegem, W.; Degroote, J. Fluid–structure interaction simulations of a wind gust impacting on the blades of a large horizontal axis wind turbine. Energies 2020, 13, 509. [Google Scholar] [CrossRef]
- Miao, W.; Li, C.; Wang, Y.; Xiang, B.; Liu, Q.; Deng, Y. Study of adaptive blades in extreme environment using fluid–structure interaction method. J. Fluids Struct. 2019, 91, 102734. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics; Springer Nature Switzerland AG: Cham, Switzerland, 2020. [Google Scholar]
- OpenFOAM 2.1.0: Arbitrary Mesh Interface. The OpenFOAM Foundation. 2011. Available online: https://openfoam.org/release/2-1-0/ami (accessed on 22 September 2024).
- Muzaferija, S. Computation of free surface flows using interface-tracking and interface-capturing methods. In Nonlinear Water-Wave Interaction; Computational Mechanics Publications, WIT Press: Southamption, UK, 1998. [Google Scholar]
- Bertram, V. Practical Ship Hydrodynamics; Elsevier Ltd.: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Hou, G.; Wang, J.; Layton, A. Numerical methods for fluid-structure interaction—A review. Commun. Comput. Phys. 2012, 12, 337–377. [Google Scholar] [CrossRef]
- Davis, M.; Zarnick, E.E. Testing ship models in transient waves. In Proceedings of the 5th Symposium on Naval Hydrodynamics, Bergen, Norway, 10–12 September 1964; Volume 507. [Google Scholar]
- Windt, C.; Davidson, J.; Ringwood, J.V. High-fidelity numerical modelling of ocean wave energy systems: A review of computational fluid dynamics-based numerical wave tanks. Renew. Sustain. Energy Rev. 2018, 93, 610–630. [Google Scholar] [CrossRef]
- Windt, C.; Davidson, J.; Schmitt, P.; Ringwood, J.V. On the assessment of numerical wave makers in CFD simulations. J. Mar. Sci. Eng. 2019, 7, 47. [Google Scholar] [CrossRef]
- Jacobsen, N.G. waves2Foam Manual; Deltares, The Netherlands; Research Gate: Berlin, Germany, 2017; Volume 570. [Google Scholar]
- Alfonsi, G. Reynolds-averaged Navier–Stokes equations for turbulence modeling. In Applied Mechanics Reviews; American Society of Mechanical Engineers: New York City, USA, 2009; Volume 62, p. 040802. [Google Scholar]
- Bredberg, J. On Two-Equation Eddy-Viscosity Models; Department of Thermo and Fluid Dynamics, Chalmers University of Technology: Göteborg, Sweden, 2001. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Sanderse, B.; Van der Pijl, S.; Koren, B. Review of computational fluid dynamics for wind turbine wake aerodynamics. Wind Energy 2011, 14, 799–819. [Google Scholar] [CrossRef]
- de Oliveira, M.; Puraca, R.; Carmo, B. Blade-resolved numerical simulations of the NREL offshore 5 MW baseline wind turbine in full scale: A study of proper solver configuration and discretization strategies. Energy 2022, 254, 124368. [Google Scholar] [CrossRef]
- Wang, L.; Robertson, A.; Jonkman, J.; Yu, Y.H. Uncertainty assessment of CFD investigation of the nonlinear difference-frequency wave loads on a semisubmersible FOWT platform. Sustainability 2020, 13, 64. [Google Scholar] [CrossRef]
- Popko, W.; Vorpahl, F.; Zuga, A.; Kohlmeier, M.; Jonkman, J.; Robertson, A.; Larsen, T.J.; Yde, A.; Sætertrø, K.; Okstad, K.M.; et al. Offshore code comparison collaboration continuation (OC4), phase 1-results of coupled simulations of an offshore wind turbine with jacket support structure. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012; ISOPE: Mountain View, CA, USA, 2012; p. ISOPE–I. [Google Scholar]
- Robertson, A.; Jonkman, J.; Musial, W.; Vorpahl, F.; Popko, W. Offshore Code Comparison Collaboration, Continuation: Phase II Results of a Floating Semisubmersible Wind System; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2013. [Google Scholar]
- Robertson, A.N.; Wendt, F.F.; Jonkman, J.M.; Popko, W.; Vorpahl, F.; Stansberg, C.T.; Bachynski, E.E.; Bayati, I.; Beyer, F.; de Vaal, J.B.; et al. OC5 project phase I: Validation of hydrodynamic loading on a fixed cylinder. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Kona, HI, USA, 21–26 June 2015; ISOPE: Mountain View, CA, USA, 2015; p. ISOPE-I-15-116. [Google Scholar]
- Robertson, A.N.; Wendt, F.; Jonkman, J.M.; Popko, W.; Borg, M.; Bredmose, H.; Schlutter, F.; Qvist, J.; Bergua, R.; Harries, R.; et al. OC5 Project Phase Ib: Validation of hydrodynamic loading on a fixed, flexible cylinder for offshore wind applications. Energy Procedia 2016, 94, 82–101. [Google Scholar] [CrossRef]
- Popko, W.; Huhn, M.L.; Robertson, A.N.; Jonkman, J.M.; Wendt, F.; Müller, K.; Kretschmer, M.L.; Vorpahl, F.; Hagen, T.R.; Galinos, C.; et al. Verification of Numerical Offshore Wind Turbine Models Based on Full Scale Alpha Ventus Data within OC5 Phase III. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering-Volume 10: Ocean Renewable Energy, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Popko, W.; Robertson, A.; Jonkman, J.; Wendt, F.; Thomas, P.; Müller, K.; Kretschmer, M.; Ruud Hagen, T.; Galinos, C.; Le Dreff, J.B.; et al. Validation of numerical models of the offshore wind turbine from the alpha ventus wind farm against full-scale measurements within OC5 phase III. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Glasgow, UK, 9–14 June 2019; American Society of Mechanical Engineers: New York City, NY, USA, 2019; Volume 58899, p. V010T09A065. [Google Scholar]
- Robertson, A.N.; Gueydon, S.; Bachynski, E.; Wang, L.; Jonkman, J.; Alarcon, D.; Amet, E.; Beardsell, A.; Bonnet, P.; Boudet, B.; et al. OC6 Phase I: Investigating the underprediction of low-frequency hydrodynamic loads and responses of a floating wind turbine. J. Physics Conf. Ser. 2020, 1618-3, 032033. [Google Scholar] [CrossRef]
- Wang, L.; Robertson, A.; Jonkman, J.; Yu, Y.H.; Koop, A.; Borràs Nadal, A.; Li, H.; Bachynski-Polić, E.; Pinguet, R.; Shi, W.; et al. OC6 Phase Ib: Validation of the CFD predictions of difference-frequency wave excitation on a FOWT semisubmersible. Ocean Eng. 2021, 241, 110026. [Google Scholar] [CrossRef]
- Bergua, R.; Robertson, A.; Jonkman, J.; Platt, A.; Page, A.; Qvist, J.; Amet, E.; Cai, Z.; Han, H.; Beardsell, A.; et al. OC6 Phase II: Integration and verification of a new soil–structure interaction model for offshore wind design. Wind Energy 2022, 25, 793–810. [Google Scholar] [CrossRef]
- Cioni, S.; Papi, F.; Pagamonci, L.; Bianchini, A.; Ramos-García, N.; Pirrung, G.; Corniglion, R.; Lovera, A.; Galván, J.; Boisard, R.; et al. On the characteristics of the wake of a wind turbine undergoing large motions caused by a floating structure: An insight based on experiments and multi-fidelity simulations from the OC6 Phase III Project. Wind Energy Sci. Discuss. 2023, 2023, 1–37. [Google Scholar] [CrossRef]
- Bergua, R.; Robertson, A.; Jonkman, J.; Alarcón Fernández, D.; Trubat Casal, P. OC6 project Phase IV: Validation of numerical models for novel floating offshore wind support structures. Wind Energy Sci. 2024, 9, 1025–1051. [Google Scholar] [CrossRef]
- IEA Wind TCP Task 56. OC7 Project (Offshore Code Comparison Collaboration 7). IEA Wind TCP. 2024. Available online: https://iea-wind.org/task-56-oc7-project-offshore-code-comparison-collaboration-7 (accessed on 22 September 2024).
- Chitteth Ramachandran, R.; Desmond, C.; Judge, F.; Serraris, J.J.; Murphy, J. Floating wind turbines: Marine operations challenges and opportunities. Wind Energy Sci. 2022, 7, 903–924. [Google Scholar] [CrossRef]
- Panchigar, D.; Kar, K.; Shukla, S.; Mathew, R.M.; Chadha, U.; Selvaraj, S.K. Machine learning-based CFD simulations: A review, models, open threats, and future tactics. Neural Comput. Appl. 2022, 34, 21677–21700. [Google Scholar] [CrossRef]
- Kareem, A. Emerging frontiers in wind engineering: Computing, stochastics, machine learning and beyond. J. Wind Eng. Ind. Aerodyn. 2020, 206, 104320. [Google Scholar] [CrossRef]
- Wu, T.; Snaiki, R. Applications of machine learning to wind engineering. Front. Built Environ. 2022, 8, 811460. [Google Scholar] [CrossRef]
- Wang, H.; Cao, Y.; Huang, Z.; Liu, Y.; Hu, P.; Luo, X.; Song, Z.; Zhao, W.; Liu, J.; Sun, J.; et al. Recent Advances on Machine Learning for Computational Fluid Dynamics: A Survey. arXiv 2024, arXiv:2408.12171. [Google Scholar]
- Vinuesa, R.; Brunton, S.L. Enhancing computational fluid dynamics with machine learning. Nat. Comput. Sci. 2022, 2, 358–366. [Google Scholar] [CrossRef] [PubMed]
- Masoumi, M. Machine learning solutions for offshore wind farms: A review of applications and impacts. J. Mar. Sci. Eng. 2023, 11, 1855. [Google Scholar] [CrossRef]
- Eivazi, H.; Tahani, M.; Schlatter, P.; Vinuesa, R. Physics-informed neural networks for solving Reynolds-averaged Navier–Stokes equations. Phys. Fluids 2022, 34, 075117. [Google Scholar] [CrossRef]
- Kim, Y.; Choi, Y.; Widemann, D.; Zohdi, T. A fast and accurate physics-informed neural network reduced order model with shallow masked autoencoder. J. Comput. Phys. 2022, 451, 110841. [Google Scholar] [CrossRef]
- Eivazi, H.; Wang, Y.; Vinuesa, R. Physics-informed deep-learning applications to experimental fluid mechanics. Meas. Sci. Technol. 2024, 35, 075303. [Google Scholar] [CrossRef]
- Markidis, S. The old and the new: Can physics-informed deep-learning replace traditional linear solvers? Front. Big Data 2021, 4, 669097. [Google Scholar] [CrossRef]
- Kochkov, D.; Smith, J.A.; Alieva, A.; Wang, Q.; Brenner, M.P.; Hoyer, S. Machine learning–accelerated computational fluid dynamics. Proc. Natl. Acad. Sci. USA 2021, 118, e2101784118. [Google Scholar] [CrossRef]
- Després, B.; Jourdren, H. Machine learning design of volume of fluid schemes for compressible flows. J. Comput. Phys. 2020, 408, 109275. [Google Scholar] [CrossRef]
- Bar-Sinai, Y.; Hoyer, S.; Hickey, J.; Brenner, M.P. Learning data-driven discretizations for partial differential equations. Proc. Natl. Acad. Sci. USA 2019, 116, 15344–15349. [Google Scholar] [CrossRef]
- List, B.; Chen, L.W.; Thuerey, N. Learned turbulence modelling with differentiable fluid solvers: Physics-based loss functions and optimisation horizons. J. Fluid Mech. 2022, 949, A25. [Google Scholar] [CrossRef]
- Deshmukh, A.; Allison, J. Simultaneous structural and control system design for horizontal axis wind turbines. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013; p. 1533. [Google Scholar]
- Froese, G.; Ku, S.Y.; Kheirabadi, A.C.; Nagamune, R. Optimal layout design of floating offshore wind farms. Renew. Energy 2022, 190, 94–102. [Google Scholar] [CrossRef]
- Cao, L.; Ge, M.; Gao, X.; Du, B.; Li, B.; Huang, Z.; Liu, Y. Wind farm layout optimization to minimize the wake induced turbulence effect on wind turbines. Appl. Energy 2022, 323, 119599. [Google Scholar] [CrossRef]
- Lozon, E.; Hall, M. Coupled loads analysis of a novel shared-mooring floating wind farm. Appl. Energy 2023, 332, 120513. [Google Scholar] [CrossRef]
- Lopez-Olocco, T.; Liang, G.; Medina-Manuel, A.; Ynocente, L.S.; Jiang, Z.; Souto-Iglesias, A. Experimental comparison of a dual-spar floating wind farm with shared mooring against a single floating wind turbine under wave conditions. Eng. Struct. 2023, 292, 116475. [Google Scholar] [CrossRef]
- Micallef, D.; Rezaeiha, A. Floating offshore wind turbine aerodynamics: Trends and future challenges. Renew. Sustain. Energy Rev. 2021, 152, 111696. [Google Scholar] [CrossRef]
- Liang, Z.; Liu, H. Layout optimization of an offshore floating wind farm deployed with novel multi-turbine platforms with the self-adaptive property. Ocean Eng. 2023, 283, 115098. [Google Scholar] [CrossRef]
- Bashetty, S.; Ozcelik, S. Design and stability analysis of an offshore floating multi-turbine platform. In Proceedings of the 2020 IEEE Green Technologies Conference (GreenTech), Oklahoma City, OK, USA, 1–3 April 2020; IEEE: New York, NY, USA, 2020; pp. 184–189. [Google Scholar]
- Fenu, B.; Attanasio, V.; Casalone, P.; Novo, R.; Cervelli, G.; Bonfanti, M.; Sirigu, S.A.; Bracco, G.; Mattiazzo, G. Analysis of a gyroscopic-stabilized floating offshore hybrid wind-wave platform. J. Mar. Sci. Eng. 2020, 8, 439. [Google Scholar] [CrossRef]
- Ding, S.; Yan, S.; Han, D.; Ma, Q. Overview on hybrid wind-wave energy systems. In Proceedings of the 2015 International Conference on Applied Science and Engineering Innovation, Jinan, China, 30–31 August 2015; Atlantis Press: Dordrecht, The Netherlands, 2015; pp. 502–507. [Google Scholar]







| Author/Ref. | Year | Software | Ref. Turbine | Ref. Platform |
|---|---|---|---|---|
| Ren et al. [113] | 2014 | Ansys Fluent | NREL 5 MW | TLP |
| Quallen & Xing [114] | 2016 | CFDShip-Iowa | NREL 5 MW | OC3 Hywind Spar |
| Tran & Kim [115] | 2016 | STAR-CCM+ | NREL 5 MW | OC4 DeepCWind |
| Leble & Barakos [116] | 2016 | HMB2 | DTU 10 MW | WindFloat |
| Li et al. [117] | 2016 | OpenFOAM | NREL 5 MW | OC4 DeepCWind |
| Liu et al. [11] | 2017 | OpenFOAM | NREL 5 MW | OC4 DeepCWind |
| Tran & Kim [118] | 2018 | STAR-CCM+ | NREL 5 MW | OC4 DeepCWind |
| Ren et al. [113] | 2014 | Ansys Fluent | NREL 5 MW | TLP |
| Zhang & Kim [119] | 2018 | STAR-CCM+ | NREL 5 MW | OC4 DeepCWind |
| Zhou et al. [120] | 2019 | OpenFOAM | NREL 5 MW | OC4 DeepCWind |
| Huang et al. [121,122] | 2019 | OpenFOAM | NREL 5 MW | OC3 Hywind Spar |
| Cheng et al. [123] | 2019 | OpenFOAM | NREL 5 MW | OC4 DeepCWind |
| Zhou et al. [124] | 2021 | OpenFOAM | NREL 5 MW | OC4 DeepCWind |
| Zheng et al. [125] | 2021 | OpenFOAM | NREL 5 MW | OC3 Hywind Spar |
| Zhou et al. [51] | 2022 | OpenFOAM | NREL 5 MW | OC4 DeepCWind |
| Xie & Sadique [126] | 2022 | CONVERGE | NREL 5 MW | OC4 DeepCWind |
| Huang et al. [127] | 2023 | OpenFOAM | NREL 5 MW (×2) | OC3 Hywind Spar |
| Huang et al. [128] | 2023 | OpenFOAM | NREL 5 MW | Bionic Fractal Semi-Sub |
| Yu et al. [129,130] | 2023 | OpenFOAM | NREL 5 MW | OC4 DeepCWind |
| Feng et al. [131] | 2023 | STAR-CCM+ | NREL 5 MW | OC4 DeepCWind |
| Alkhabbaz et al. [132] | 2024 | STAR-CCM+ | NREL 5 MW | OC4 DeepCWind |
| Sadique et al. [133] | 2024 | CONVERGE | Siemens 3.6 MW | OC6 Stiesdal TetraSpar |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darling, H.; Schmidt, D.P. The Role of Fully Coupled Computational Fluid Dynamics for Floating Wind Applications: A Review. Energies 2024, 17, 4836. https://doi.org/10.3390/en17194836
Darling H, Schmidt DP. The Role of Fully Coupled Computational Fluid Dynamics for Floating Wind Applications: A Review. Energies. 2024; 17(19):4836. https://doi.org/10.3390/en17194836
Chicago/Turabian StyleDarling, Hannah, and David P. Schmidt. 2024. "The Role of Fully Coupled Computational Fluid Dynamics for Floating Wind Applications: A Review" Energies 17, no. 19: 4836. https://doi.org/10.3390/en17194836
APA StyleDarling, H., & Schmidt, D. P. (2024). The Role of Fully Coupled Computational Fluid Dynamics for Floating Wind Applications: A Review. Energies, 17(19), 4836. https://doi.org/10.3390/en17194836






