ADPA Optimization for Real-Time Energy Management Using Deep Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Establishment of Microgrid Real-Time Energy Management Control Model
2.2. Establishment of Microgrid REP Energy Management Control Model
2.2.1. Relationship between REP and Distribution Network Electricity Price
- (1)
- When plmin(t) ≥ ps(t) + pw(t) + pg(t), the distributed power generation in the microgrid is less, so that the rigid-load power demand of the microgrid cannot be met. At this time, the microgrid operator needs to charge the REP for the electricity purchased to supply the flexible-load users after meeting the rigid-load demand. Therefore, the value range of the pm(t) is as follows:
- (2)
- When plmin(t) ≤ ps(t) + pw(t) + pg(t), the distributed power generation in the microgrid can not only meet the rigid-load demand in the network but can also provide part of the remaining power to the flexible load in the network; however, it cannot fully meet the needs of the flexible load in the network. At this time, for the part that does not meet the demand for the flexible load, the microgrid operator must purchase electricity from the distribution network and charge the REP for the electricity supplied to the flexible-load user. Therefore, the value range of the pm(t) of the purchased electricity at this time is as follows:
2.2.2. Cost and Profit of REP
- (1)
- Distributed generation cost and energy storage conversion cost
- (2)
- The cost of purchasing electricity from the distribution network
- (3)
- REP profit
3. Results and Discussion
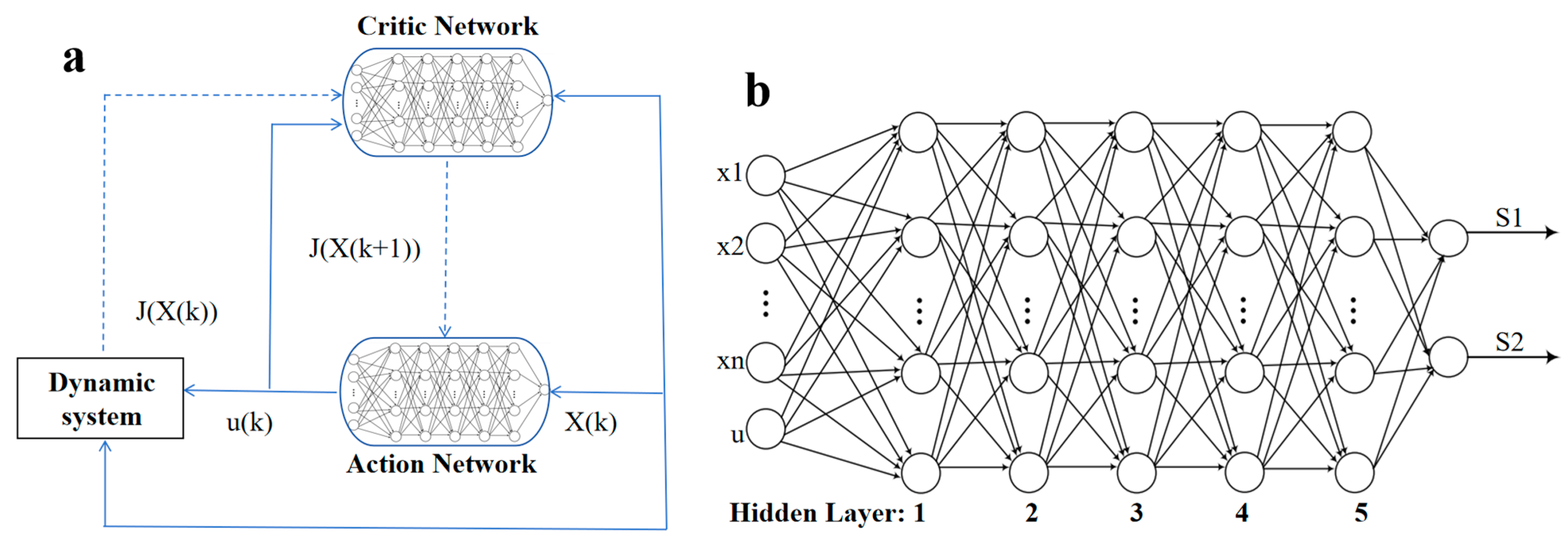
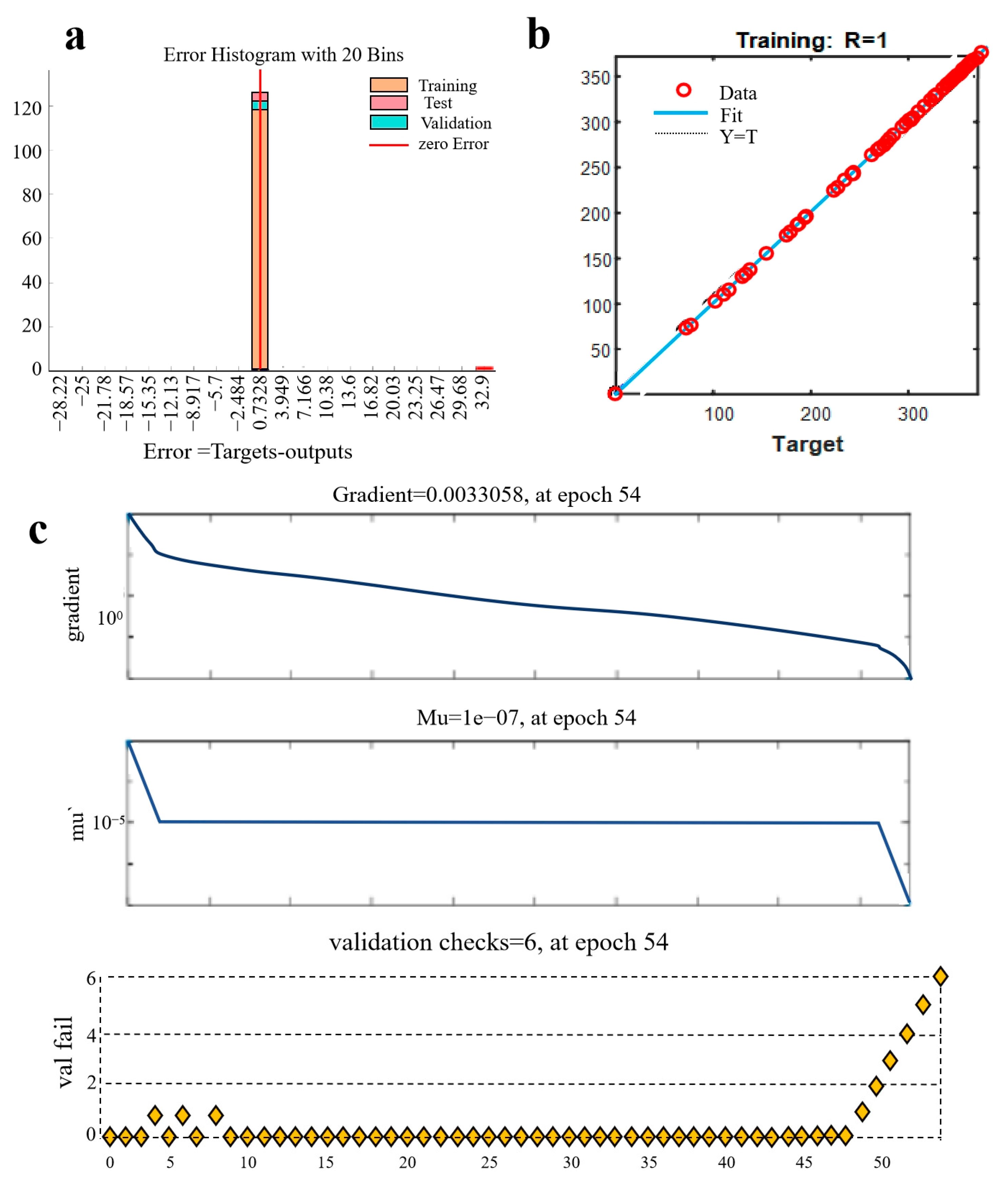
3.1. Deep Learning ADPA-REP Energy Management Strategy
| Algorithm 1. Parameter-setting program |
| INPUT: None OUTPUT: Fitness value (fx) BEGIN DEFINE global variables glo.aw=5; glo.bw=12; glo.kw=0; glo.ag=0.2; glo.ap=2.5; glo.bp=1; glo.kp=0; glo.as=1; glo.ks=0; glo.kexi=3.4; glo.fw=1; glo.fg=l; glo.fs=1:glo.fl=1; glo.fp=1; glo.k=2.5; glo.rl=0.45; CALCULATE plt plt=glo.pmax-glo.pwt-glo.pgt-glo.pst-glo.pxt; INITIALIZE rowRT rowRT=1; CALL fitness function to calculate fitness value fx=fitness2019_07_22_23 15_01(glo.pwt,glo.pgt,glo.pst,plt,rowRT) DEFINE fitness function fumction fx=fitness2019_07_22_23_15_01(pwt,pgt,pst,plt,rowRT) BEGIN DEFINE local variables cw=glo.aw.*pwt*pwt+glo.bw.*pwt+glo.kw; cs=glo.as.*pst*pst+glo.ks; cg=glo.ag.*pgt; cp=((glo.ap*plt)^2+glo.bp*plt+glo.kp)^(1/2); rrt=exp((glo.k*plt)/(glo.pmax-glo.pmin))*glo.rl; cl=plt*(glo.rl-rrt); CALCULATE fitness value fx=glo.fw,*cw+glo.fg.*cg+glo.fs.*cs+glo.fl.*cl+glo.fp*cp; RETURN fx End End |
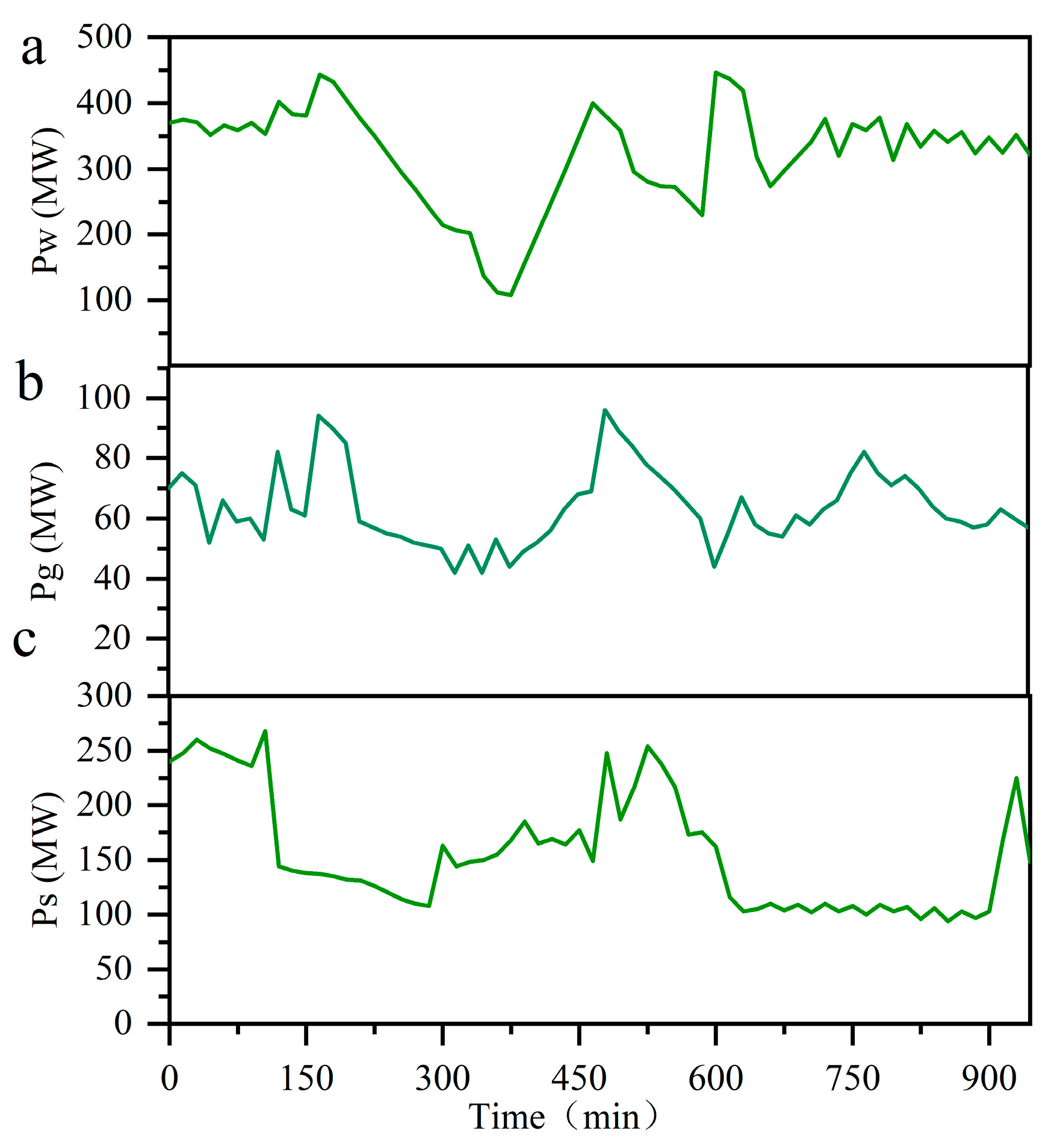
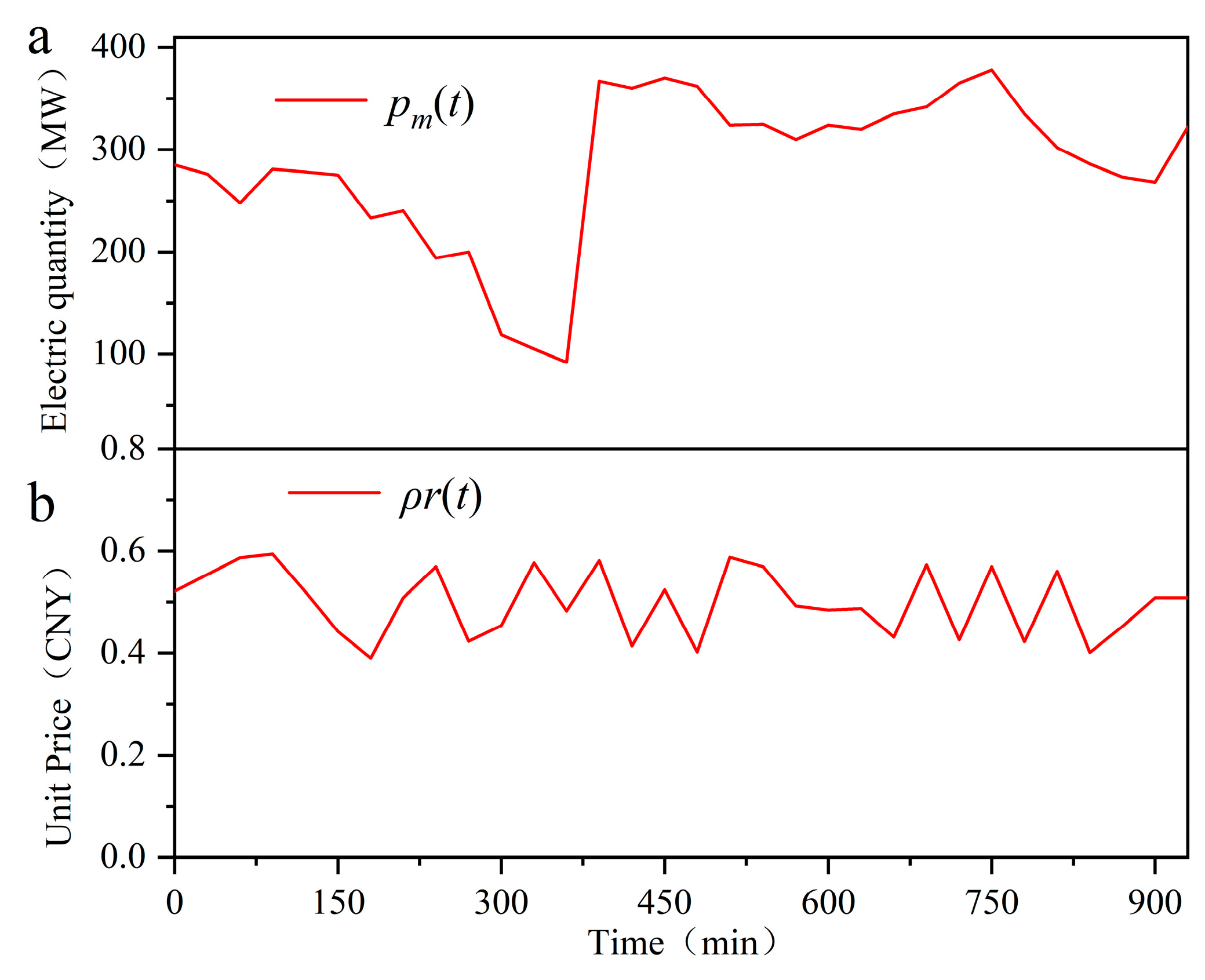
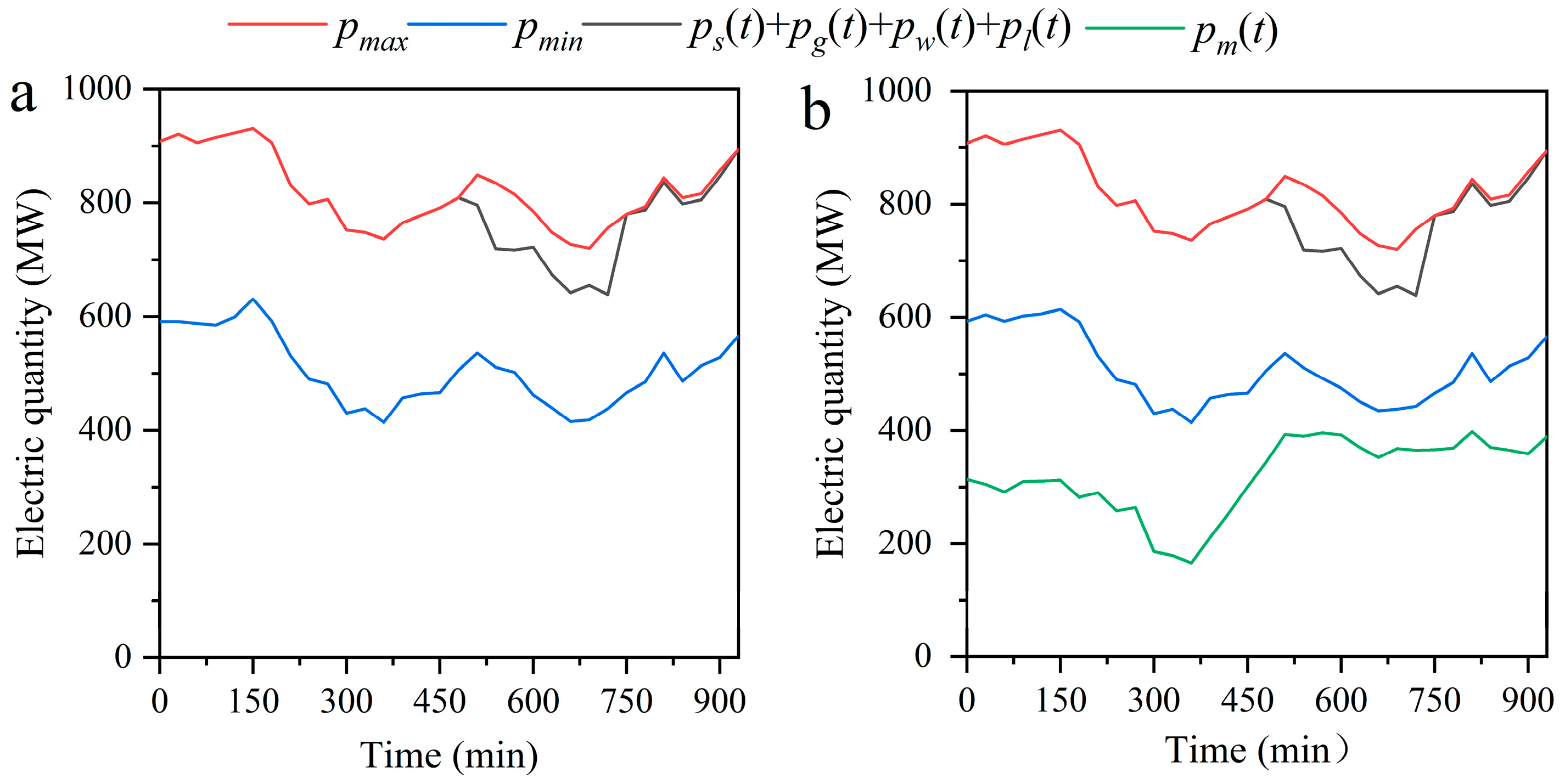
3.2. Simulation Case Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Katiraei, F.; Iravani, R.; Hatziargyriou, N.; Dimeas, A. Micro-grids management. IEEE Power Energy Mag. 2008, 6, 54–65. [Google Scholar] [CrossRef]
- Santhosh Krishna, B.V.; Pauline, S.; Sivakumar, S.; Palagan, C.A.; Talasila, V.; Krishna, M.M.S. Enhanced efficiency in smart grid energy systems through advanced AI-based thermal modeling. Therm. Sci. Eng. Prog. 2024, 53, 102765. [Google Scholar] [CrossRef]
- de Lima, T.D.; Lezama, F.; Soares, J.; Franco, J.F.; Vale, Z. Modern distribution system expansion planning considering new market designs: Review and future directions. Renew. Sustain. Energy Rev. 2024, 202, 114709. [Google Scholar] [CrossRef]
- Elsied, M.; Oukaour, A.; Gualous, H.; Brutto, O.A.L. Optimal economic and environment operation of micro-grid power systems. Energy Convers. Manag. 2016, 122, 182–194. [Google Scholar] [CrossRef]
- Huang, T.; Liu, D.-E. A self-learning scheme for residential energy system control and management. Neural Comput. Appl. 2013, 2, 259–269. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Y.; Li, R. Reinforcement learning based bilevel real-time pricing strategy for a smart grid with distributed energy resources. Appl. Soft Comput. 2024, 155, 111474. [Google Scholar] [CrossRef]
- Li, B.; Roche, R.; Paire, D.; Miraoui, A. A price decision approach for multiple multi-energy-supply microgrids considering demand response. Energy 2019, 167, 117–135. [Google Scholar] [CrossRef]
- Ali, R.; Cha, Y.-J. Subsurface damage detection of a steel bridge using deep learning and uncooled micro-bolometer. Constr. Build. Mater. 2019, 226, 376–387. [Google Scholar] [CrossRef]
- Li, D.; Channa, I.A.; Chen, X.; Dou, L.; Khokhar, S.; Ab Azar, N. A new deep learning method for classification of power quality disturbances using DWT-MRA in utility smart grid. Comput. Electr. Eng. 2024, 117, 109290. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Liu, Z.; Wang, Y. Model-free optimal controller design for continuous-time nonlinear systems by adaptive dynamic programming based on a precompensator. ISA Trans. 2015, 57, 63–70. [Google Scholar] [CrossRef]
- Liu, D.; Ha, M.; Xue, S. State of the Art of Adaptive Dynamic Programming and Reinforcement Learning. CAAI Artif. Intell. Res. 2022, 1, 93–110. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.; Liu, N. A two-stage energy management for heat-electricity integrated energy system considering dynamic pricing of Stackelberg game and operation strategy optimization. Energy 2022, 244, 122576. [Google Scholar] [CrossRef]
- Wu, N.; Wang, H. Deep learning adaptive dynamic programming for real time energy management and control strategy of micro-grid. J. Clean. Prod. 2018, 204, 1169–1177. [Google Scholar] [CrossRef]
- Ye, Y.; Yuan, Q.; Tang, Y.; Strbac, G. Decentralized Coordination Parameters Optimization in Microgrids Mitigating Demand Response Synchronization Effect of Flexible Loads. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2022, 42, 1748–1759. [Google Scholar]
- Turdybek, B.; Tostado-Véliz, M.; Mansouri, S.A.; Jordehi, A.R.; Jurado, F. A local electricity market mechanism for flexibility provision in industrial parks involving Heterogenous flexible loads. Appl. Energy 2024, 359, 122748. [Google Scholar] [CrossRef]
- Sun, S.; Dong, M.; Liang, B. Joint supply, demand, and energy storage management towards microgrid cost minimization. In Proceedings of the 2014 IEEE International Conference on Smart Grid Communications (SmartGridComm), Venice, Italy, 3–6 November 2014. [Google Scholar]
- Ullah, Z.; Wang, S.; Wu, G.; Xiao, M.; Lai, J.; Elkadeem, M.R. Advanced energy management strategy for microgrid using real-time monitoring interface. J. Energy Storage 2022, 52, 104814. [Google Scholar] [CrossRef]
- Cui, G.; Jia, Q.S.; Guan, X. Energy Management of Networked Microgrids With Real-Time Pricing by Reinforcement Learning. IEEE Trans. Smart Grid 2024, 15, 570–580. [Google Scholar] [CrossRef]
- Wu, N.; Wang, H.; Yin, L.; Yuan, X.; Leng, X. Application Conditions of Bounded Rationality and a Microgrid Energy Management Control Strategy Combining Real-Time Power Price and Demand-Side Response. IEEE Access 2020, 8, 227327–227339. [Google Scholar] [CrossRef]
- Bishwajit, D.; Gulshan, S.; Bokoro, P.N. Economic Management of Microgrid Using Flexible Non-Linear Load Models Based on Price-Based Demand Response Strategies. Results Eng. 2024, 102993. [Google Scholar] [CrossRef]
- He, Y.; Zhang, J. Real-time electricity pricing mechanism in China based on system dynamics. Energy Convers. Manag. 2015, 94, 394–405. [Google Scholar] [CrossRef]
- Wang, C.; Li, X. Optimization scheduling of microgrid comprehensive demand response load considering user satisfaction. Sci. Rep. 2024, 14, 16034. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Fan, R.; Yang, P.; Du, K.; Xu, X.; Chen, R. Research on floating real-time pricing strategy for microgrid operator in local energy market considering shared energy storage leasing. Appl. Energy 2024, 368, 123412. [Google Scholar] [CrossRef]
- Wesseh, P.K.; Lin, B. A time-of-use pricing model of the electricity market considering system flexibility. Energy Rep. 2022, 8, 1457–1470. [Google Scholar] [CrossRef]
- Fagundes, T.A.; Fuzato, G.H.F.; Magossi, R.F.Q.; Flores, M.A.B.; Vasquez, J.C.; Guerrero, J.M.; Machado, R.Q. Economic Operation Optimization Under Real-Time Pricing for an Energy Management System in a Redundancy-Based Microgrid. IEEE Trans. Ind. Electron. 2024, 71, 8872–8882. [Google Scholar] [CrossRef]
- Li, B.; Zhao, R.; Lu, J.; Xin, K.; Huang, J.; Lin, G.; Chen, J.; Pang, X. Energy management method for microgrids based on improved Stackelberg game real-time pricing model. Energy Rep. 2023, 9, 1247–1257. [Google Scholar] [CrossRef]
- Xiong, S.; Liu, D.; Chen, Y.; Zhang, Y.; Cai, X. A deep reinforcement learning approach based energy management strategy for home energy system considering the time-of-use price and real-time control of energy storage system. Energy Rep. 2024, 11, 3501–3508. [Google Scholar] [CrossRef]
- Jesus, L.; Fjo, D.R.; Bart, D.S. Forecasting spot electricity prices: Deep learning approaches and empirical comparison of traditional algorithms. Appl. Energy 2018, 221, 386–405. [Google Scholar]
- Guo, Z.; Xu, W.; Yan, Y.; Sun, M. How to realize the power demand side actively matching the supply side?—A virtual real-time electricity prices optimization model based on credit mechanism. Appl. Energy 2023, 343, 121223. [Google Scholar] [CrossRef]
- Jiang, J.; Kou, Y.; Bie, Z.; Li, G. Optimal Real-Time Pricing of Electricity Based on Demand Response. Energy Procedia 2019, 159, 304–308. [Google Scholar] [CrossRef]
- Singh, A.R.; Kumar, R.S.; Bajaj, M.; Khadse, C.B.; Zaitsev, I. Machine learning-based energy management and power forecasting in grid-connected microgrids with multiple distributed energy sources. Sci. Rep. 2024, 14, 19207. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, Z.; Huang, Y.; Wu, L.; Liu, C. ADPA Optimization for Real-Time Energy Management Using Deep Learning. Energies 2024, 17, 4821. https://doi.org/10.3390/en17194821
Wan Z, Huang Y, Wu L, Liu C. ADPA Optimization for Real-Time Energy Management Using Deep Learning. Energies. 2024; 17(19):4821. https://doi.org/10.3390/en17194821
Chicago/Turabian StyleWan, Zhengdong, Yan Huang, Liangzheng Wu, and Chengwei Liu. 2024. "ADPA Optimization for Real-Time Energy Management Using Deep Learning" Energies 17, no. 19: 4821. https://doi.org/10.3390/en17194821
APA StyleWan, Z., Huang, Y., Wu, L., & Liu, C. (2024). ADPA Optimization for Real-Time Energy Management Using Deep Learning. Energies, 17(19), 4821. https://doi.org/10.3390/en17194821



