Electric Vehicle Charging Load Prediction Based on Weight Fusion Spatial–Temporal Graph Convolutional Network
Abstract
1. Introduction
2. WSTGCN-Based Traffic Flow Prediction
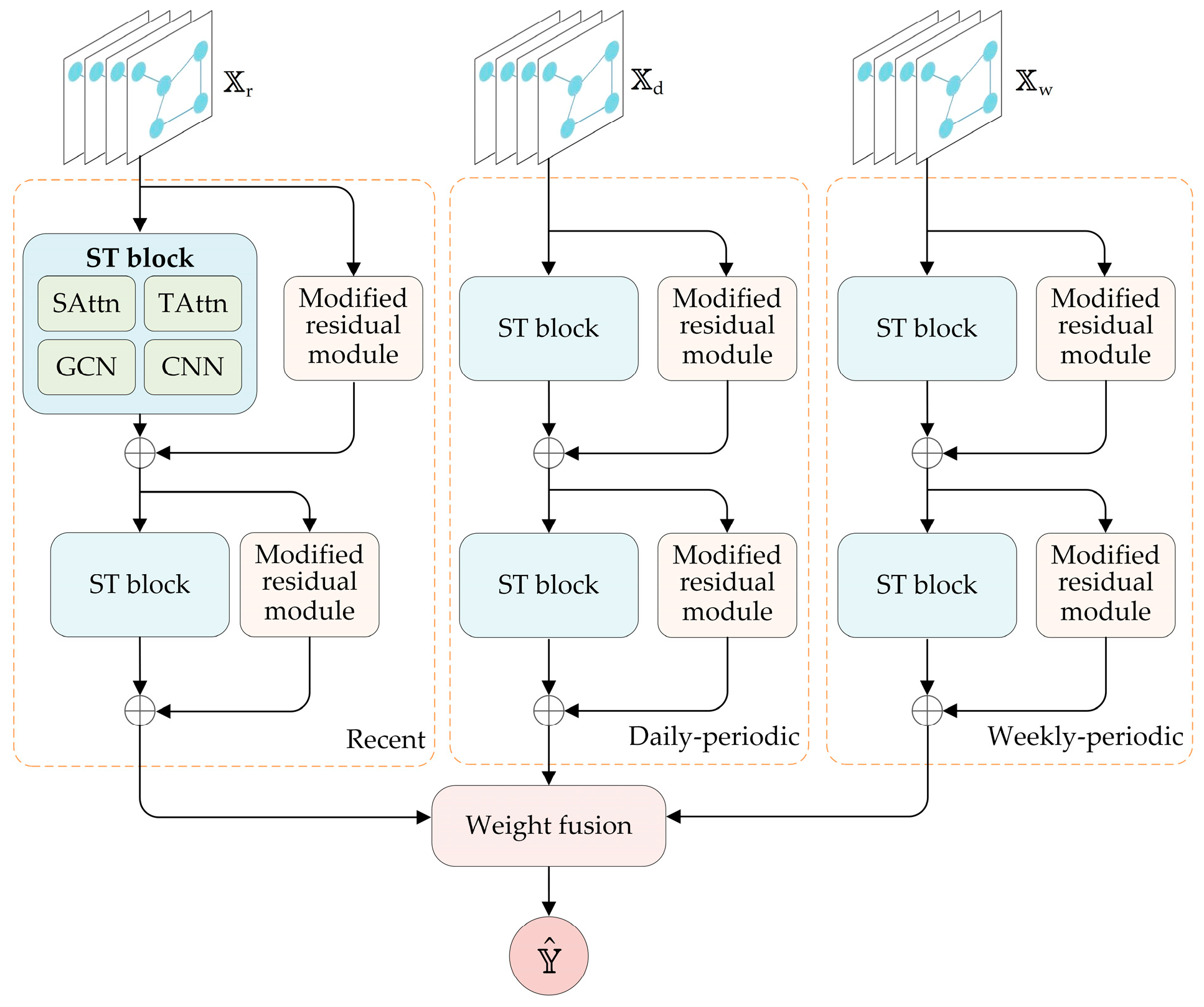
2.1. WSTGCN Framework
2.2. Periodic Components of WSTGCN
- (1)
- The recent component
- (2)
- The daily periodic component
- (3)
- The weekly periodic component
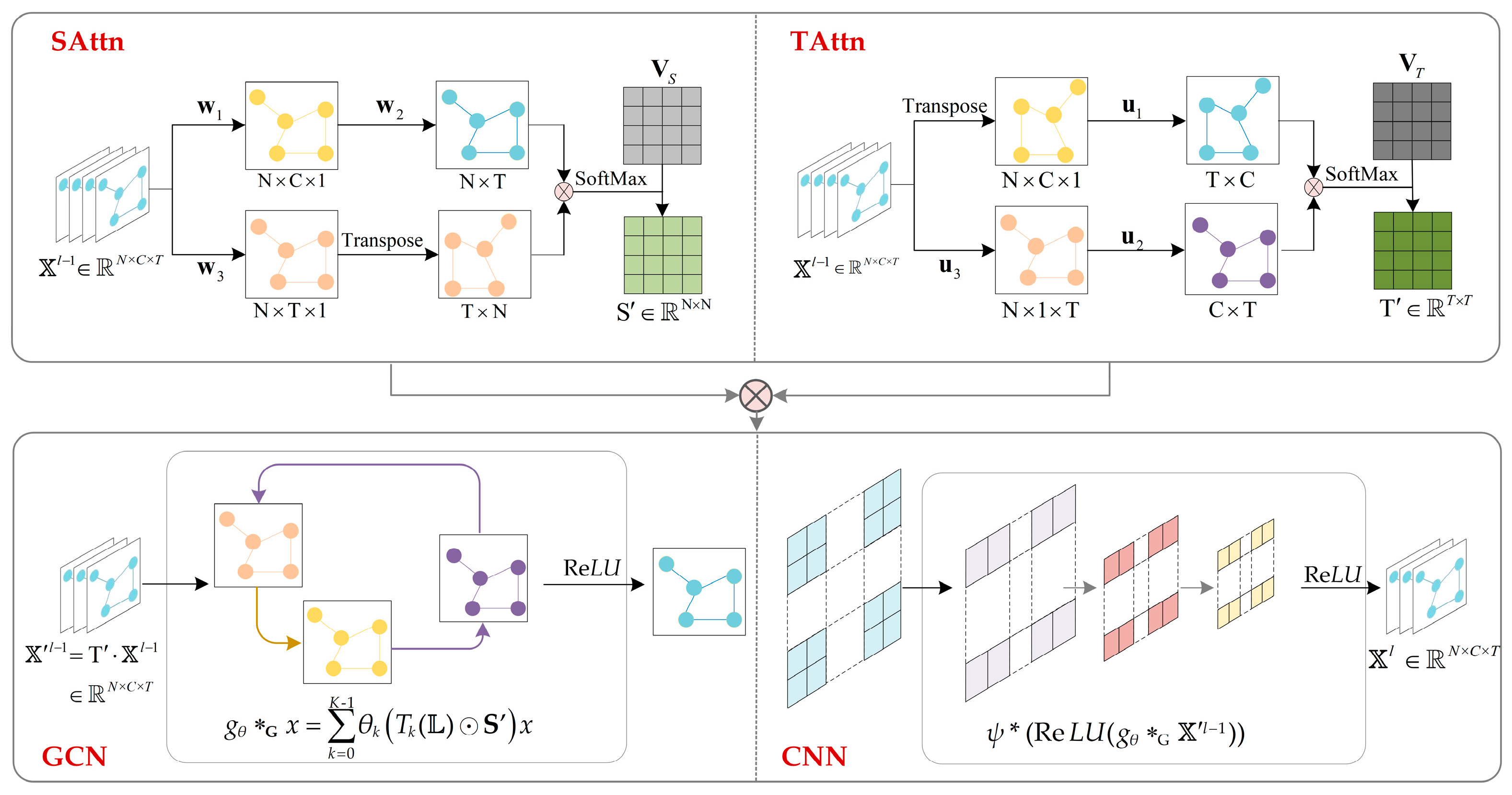
2.3. Spatial–Temporal Block of WSTGCN
- (1)
- Spatial–Temporal Attention Mechanism
- (2)
- Spatial–Temporal Convolutional Block
- (3)
- Modified Residual Module
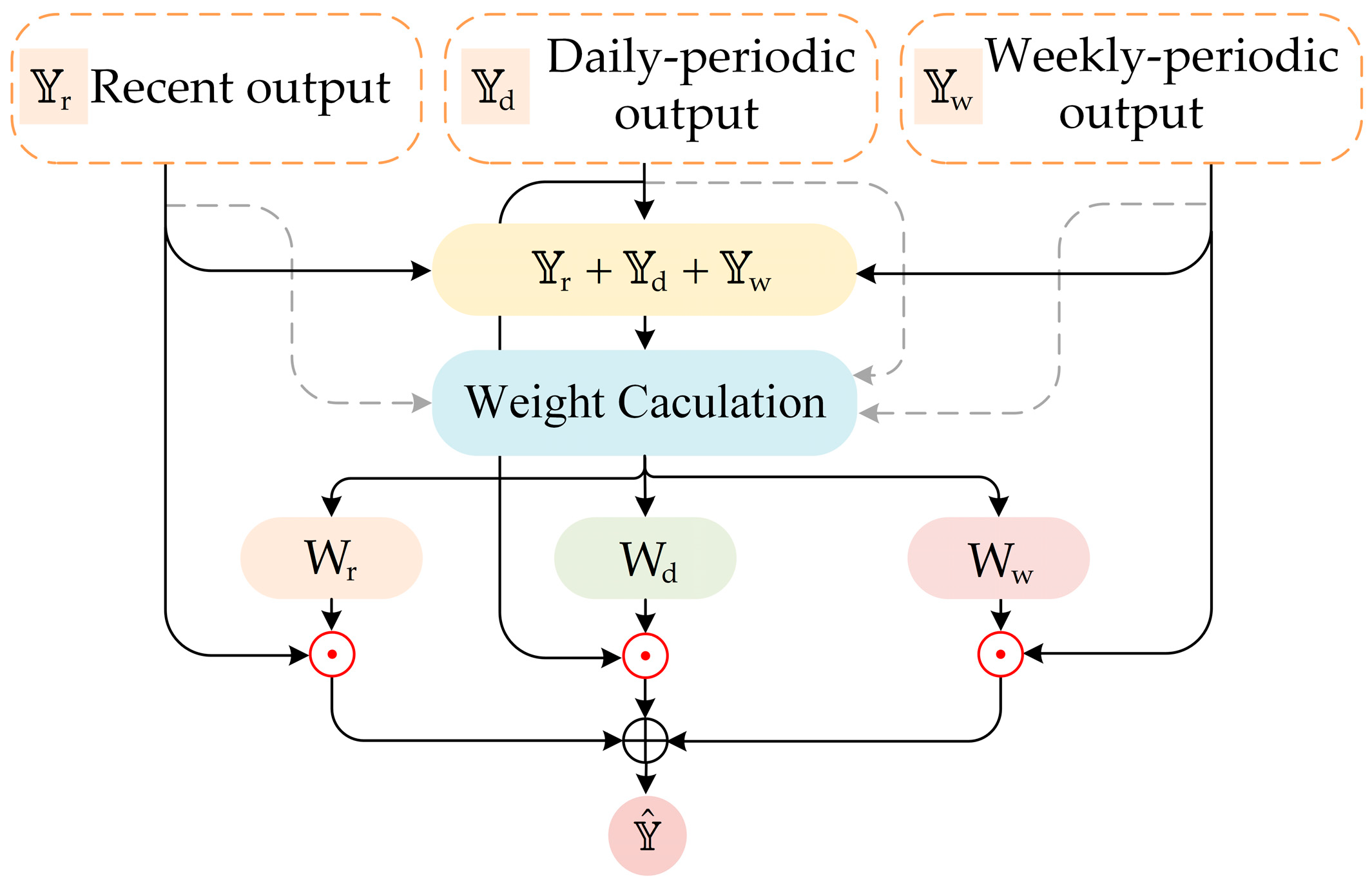
2.4. Weight Fusion Mechanism in WSTGCN
3. Electric Vehicle Charging Demand Modeling
3.1. Electric Vehicle Arrival Rate Estimation
3.2. Improved Queuing Model Considering Driver Behaviors
3.3. Markov Chain-Based Charging Process Analysis
4. Experiments
4.1. Performance Evaluation for the WSTGCN Model
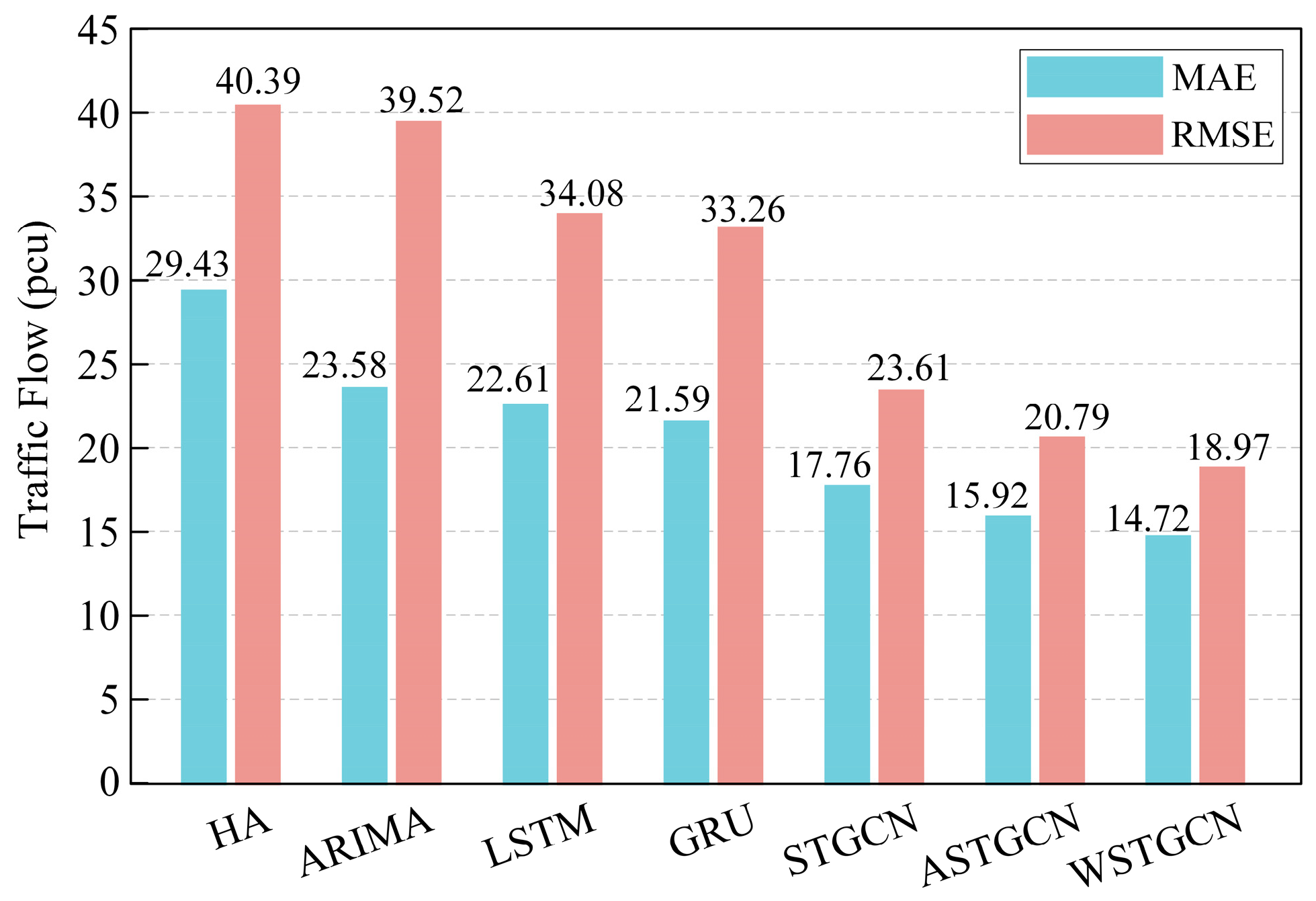
4.1.1. Prediction Accuracy Comparison
4.1.2. Ablation Study
4.1.3. Predicting Performance under Different Predicting Horizons
4.2. Charging Load Model Validation
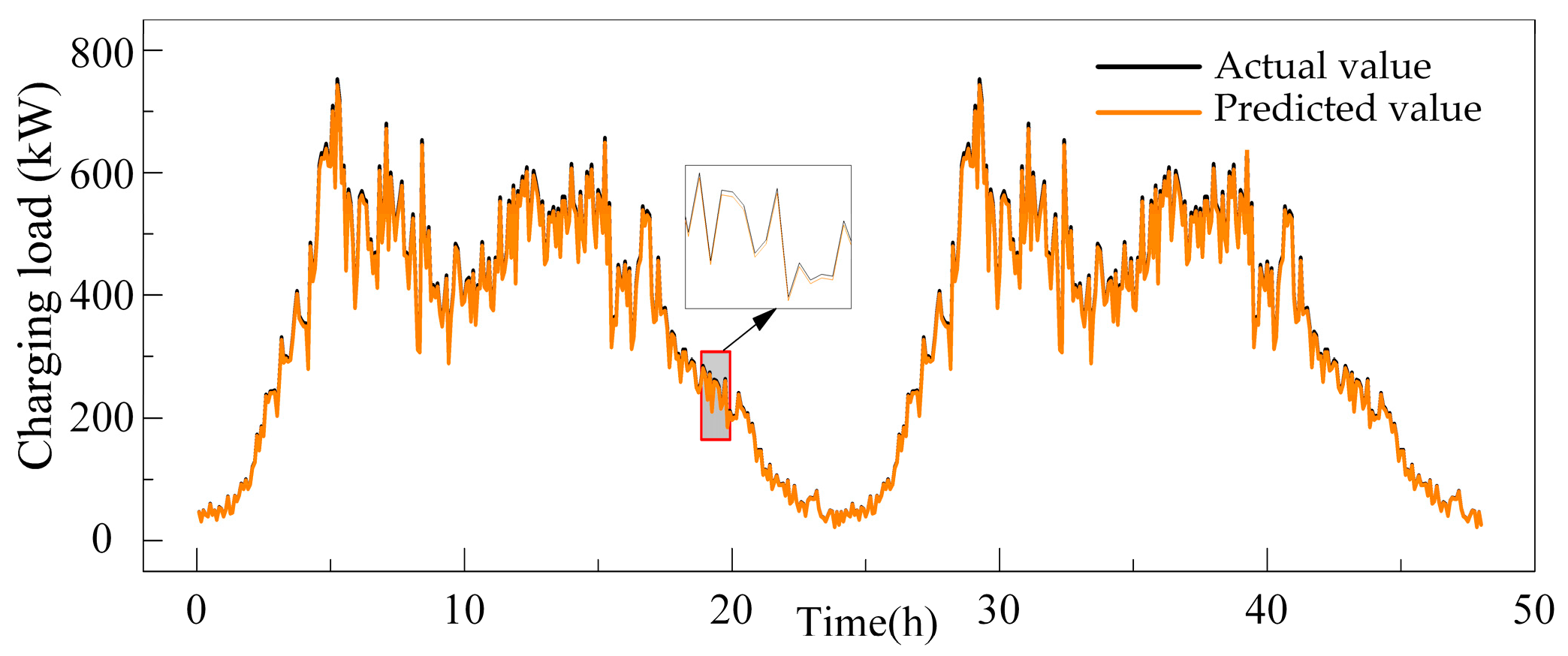
4.2.1. Charging Load Prediction Results
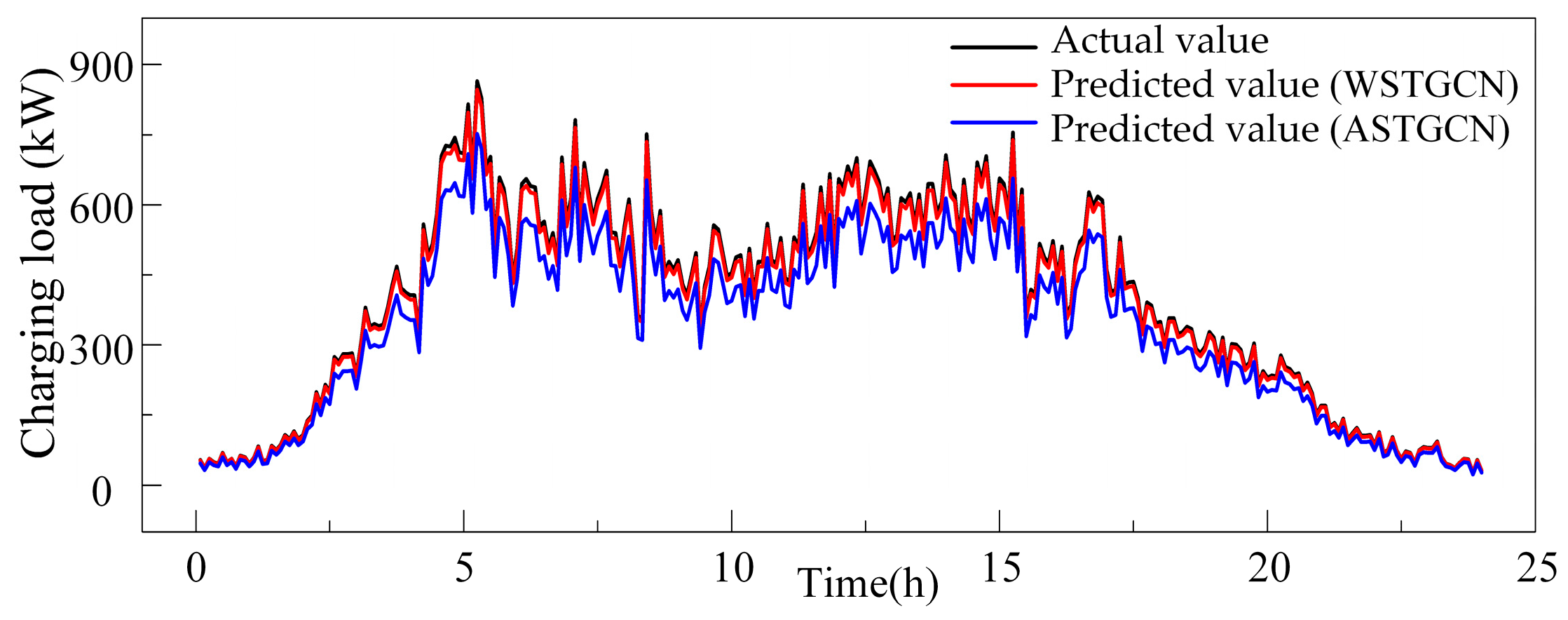
4.2.2. Impact of the WSTGCN Model
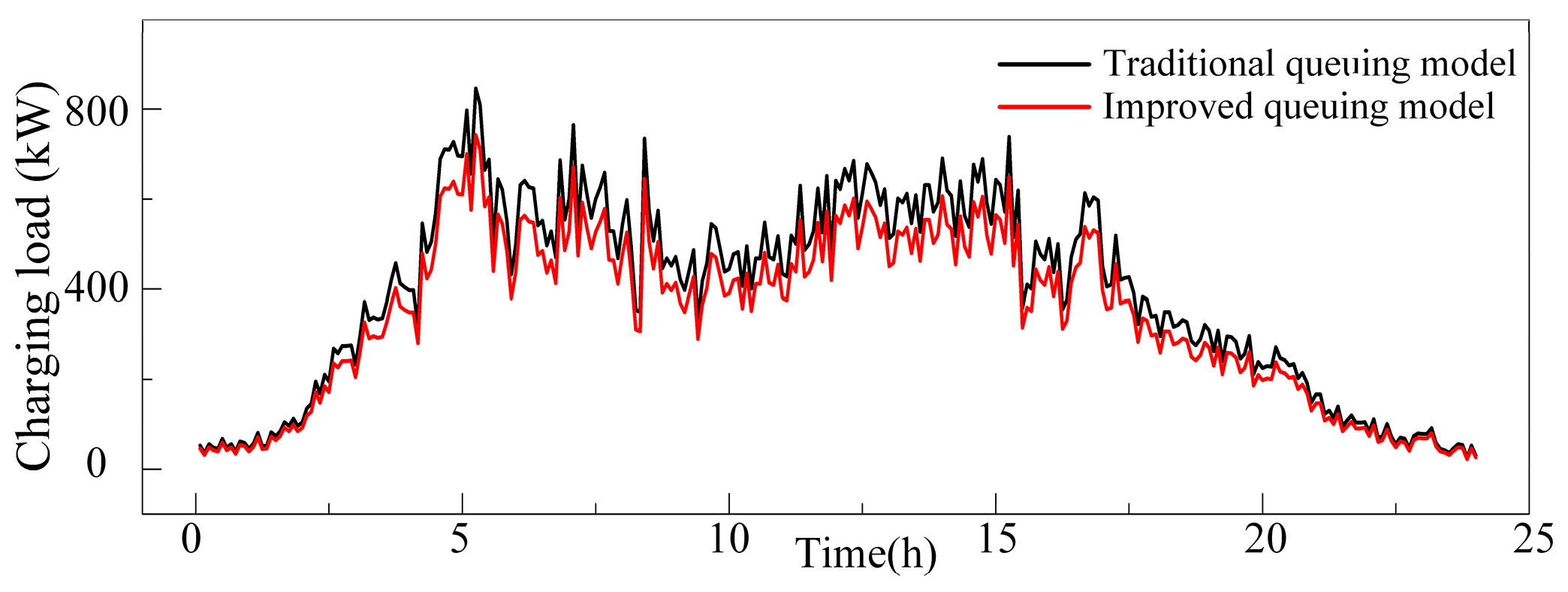
4.2.3. Impact of Improved Queuing Model
4.2.4. Sensitivity Analysis
4.2.5. Impact of FCS Scale on Service Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Amini, M.; Kargarian, A.; Karabasoglu, O. ARIMA-based decoupled time series forecasting of electric vehicle charging demand for stochastic power system operation. Electr. Power Syst. Res. 2016, 140, 378–390. [Google Scholar] [CrossRef]
- Louie, H.M. Time-series modeling of aggregated electric vehicle charging station load. Electr. Power Compon. Syst. 2017, 45, 1498–1511. [Google Scholar] [CrossRef]
- Akshay, K.C.; Grace, G.H.; Gunasekaran, K.; Samikannu, R. Power consumption prediction for electric vehicle charging stations and forecasting income. Sci. Rep. 2024, 14, 6497. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhuge, C.; Shao, C.; Wang, P.; Yang, X.; Wang, S. Short-term electric vehicle charging demand prediction: A deep learning approach. Appl. Energy 2023, 340, 121032. [Google Scholar] [CrossRef]
- Yi, Z.; Liu, X.; Wei, R.; Chen, X.; Dai, J. Electric vehicle charging demand forecasting using deep learning model. J. Intell. Transp. Syst. 2022, 26, 690–703. [Google Scholar] [CrossRef]
- Jahangir, H.; Gougheri, S.; Vatandoust, B.; Golkar, M.A.; Ahmadian, A.; Hajizadeh, A. Plug-in electric vehicle behavior modeling in energy market: A novel deep learning-based approach with clustering technique. IEEE Trans. Smart Grid 2020, 11, 4738–4748. [Google Scholar] [CrossRef]
- Sasidharan, M.; Kinattingal, S.; Simon, S. Comparative analysis of deep learning models for electric vehicle charging load forecasting. J. Inst. Eng. Ser. B 2023, 104, 105–113. [Google Scholar] [CrossRef]
- Dabbaghjamanesh, M.; Moeini, A.; Kavousi-Fard, A. Reinforcement learning-based load forecasting of electric vehicle charging station using Q-learning technique. IEEE Trans. Ind. Inf. 2021, 17, 4229–4237. [Google Scholar] [CrossRef]
- Mekkaoui, D.; Midoun, M.; Shen, Y. LA-RCNN: Luong attention-recurrent-convolutional neural network for EV charging load prediction. Appl. Intell. 2024, 54, 4352–4369. [Google Scholar] [CrossRef]
- Li, Y.; Huang, Y.; Zhang, M. Short-term load forecasting for electric vehicle charging station based on niche immunity lion algorithm and convolutional neural network. Energies 2018, 11, 1253. [Google Scholar] [CrossRef]
- Wang, S.; Chen, A.; Wang, P.; Zhuge, C. Predicting electric vehicle charging demand using a heterogeneous spatio-temporal graph convolutional network. Transp. Res. Part C Emerg. Technol. 2023, 153, 104205. [Google Scholar] [CrossRef]
- Su, S.; Li, Y.; Chen, Q.; Xia, M.; Yamashita, K.; Jurasz, J. Operating status prediction model at EV charging stations with fusing spatiotemporal graph convolutional network. IEEE Trans. Transp. Electrif. 2023, 9, 114–129. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, M.; Wei, Y.; Huang, X.; Gao, S. Multi-encoder spatio-temporal feature fusion network for electric vehicle charging load prediction. J. Intell. Robot. Syst. 2024, 110, 94. [Google Scholar] [CrossRef]
- Li, M.; Zhu, Z. Spatial-Temporal Fusion Graph Neural Networks for Traffic Flow Forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 4189–4196. [Google Scholar] [CrossRef]
- Li, F.; Feng, J.; Yan, H.; Jin, J.; Yang, F.; Sun, F.; Jin, D.; Li, Y. Dynamic graph convolutional recurrent network for traffic prediction: Benchmark and solution. ACM Trans. Knowl. Discov. Data 2023, 17, 1–21. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, C.; Rao, X.; Zhang, X.B.; Zhou, Y. Spatial-temporal load forecasting of electric vehicle charging stations based on graph neural network. J. Intell. Fuzzy Syst. 2024, 46, 821–836. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, W.; Bao, Y.; Gao, D.W.; Wang, Z.H. Load forecasting of electric vehicle charging stations: Attention-based spatiotemporal multi-graph convolutional networks. IEEE Trans. Smart Grid 2023, 15, 3016–3027. [Google Scholar] [CrossRef]
- Zhang, X.; Chan, K.W.; Li, H.; Wang, H.; Qiu, J.; Wang, G. Deep-learning-based probabilistic forecasting of electric vehicle charging load with a novel queuing model. IEEE Trans. Cybern. 2020, 51, 3157–3170. [Google Scholar] [CrossRef]
- Wu, T.; Ji, X.; Wang, G.; Liu, Y.; Yang, Q.; Bao, Z.; Peng, J. Hydrogen energy storage system for demand forecast error mitigation and voltage stabilization in a fast-charging station. IEEE Trans. Ind. Appl. 2021, 58, 2718–2727. [Google Scholar] [CrossRef]
- Arias, M.B.; Kim, M.; Bae, S. Prediction of electric vehicle charging-power demand in realistic urban traffic networks. Appl. Energy 2017, 195, 738–753. [Google Scholar] [CrossRef]
- Feng, J.; Chang, X.; Fan, Y.; Luo, W. Electric vehicle charging load prediction model considering traffic conditions and temperature. Processes 2023, 11, 2256. [Google Scholar] [CrossRef]
- Tang, S.; Mu, Y.; Zhou, Y.; Dong, X.; Jia, H. A spatial-temporal electric vehicle charging load forecasting method considering the coordination among the multiple charging behaviors. In Proceedings of the 2021 Power System and Green Energy Conference (PSGEC), Shanghai, China, 20–22 August 2021; pp. 629–634. [Google Scholar]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention-based spatial-temporal graph convolutional networks for traffic flow forecasting. Proc. AAAI Conf. Artif. Intell. 2019, 33, 922–929. [Google Scholar] [CrossRef]
- Williams, B.M.; Hoel, L.A. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: Theoretical basis and empirical results. J. Transp. Eng. 2003, 129, 664–672. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. arXiv 2014, arXiv:1409.3215. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.H.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. arXiv 2017, arXiv:1709.04875. [Google Scholar]
- Our World in Data. Number of New Cars Sold, by Type, World. Available online: https://ourworldindata.org/energy (accessed on 18 September 2024).
- IEA. Global Electric Car Stock, 2013–2023. Available online: https://www.iea.org/data-and-statistics/charts/global-electric-car-stock-2013-2023 (accessed on 18 September 2024).




| Predicting Horizon | Metrix | HA | ARIMA | LSTM | GRU | STGCN | ASTGCN | RSTGCN | WSTGCN |
|---|---|---|---|---|---|---|---|---|---|
| 15 min | MAE | 23.15 | 18.33 | 16.89 | 16.25 | 15.03 | 12.45 | 12.15 | 11.04 |
| RMSE | 35.96 | 29.49 | 26.72 | 25.91 | 20.12 | 18.69 | 18.24 | 16.54 | |
| 30 min | MAE | 26.54 | 19.77 | 19.93 | 19.47 | 16.85 | 14.51 | 14.16 | 13.25 |
| RMSE | 38.17 | 36.91 | 30.29 | 29.84 | 22.37 | 19.58 | 19.11 | 17.63 | |
| 1 h | MAE | 29.43 | 23.58 | 22.61 | 21.59 | 17.76 | 15.92 | 15.56 | 14.72 |
| RMSE | 40.39 | 39.32 | 34.08 | 33.26 | 23.61 | 20.79 | 20.36 | 18.97 |
| Traffic Flow Model | ASTGCN | WSTGCN |
|---|---|---|
| Charging model | Improved queuing model | |
| MAE | 15.32 | 9.01 |
| RMSE | 17.76 | 10.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Cong, H.; Zhou, H.; Wang, Z.; Wen, Z.; Zhang, X. Electric Vehicle Charging Load Prediction Based on Weight Fusion Spatial–Temporal Graph Convolutional Network. Energies 2024, 17, 4798. https://doi.org/10.3390/en17194798
Zhang J, Cong H, Zhou H, Wang Z, Wen Z, Zhang X. Electric Vehicle Charging Load Prediction Based on Weight Fusion Spatial–Temporal Graph Convolutional Network. Energies. 2024; 17(19):4798. https://doi.org/10.3390/en17194798
Chicago/Turabian StyleZhang, Jun, Huiluan Cong, Hui Zhou, Zhiqiang Wang, Ziyi Wen, and Xian Zhang. 2024. "Electric Vehicle Charging Load Prediction Based on Weight Fusion Spatial–Temporal Graph Convolutional Network" Energies 17, no. 19: 4798. https://doi.org/10.3390/en17194798
APA StyleZhang, J., Cong, H., Zhou, H., Wang, Z., Wen, Z., & Zhang, X. (2024). Electric Vehicle Charging Load Prediction Based on Weight Fusion Spatial–Temporal Graph Convolutional Network. Energies, 17(19), 4798. https://doi.org/10.3390/en17194798





