Minimum Risk Quantification Method for Error Threshold of Wind Farm Equivalent Model Based on Bayes Discriminant Criterion

Abstract

The error threshold is the cornerstone to balance the mathematical complexity and simulation speed of wind farm (WF) equivalent models, and can promote the standardization process of equivalent methodology. Due to differences in power system conditions and model evaluation standards in different countries, the form and indexes of error thresholds of WF equivalent models have not been unified yet. This paper proposes a theoretical method for quantifying the minimum risk of error threshold of WF equivalent models based on the Bayes discriminant criterion. Firstly, the Euclidean errors of WF equivalent models in different periods are quantified, and the probability density distributions of the errors are fitted by kernel density estimation. Secondly, the real-time weighted prior probability algorithm is used to obtain the prior probability of a valid WF equivalent model, and the different losses caused by the missed judgment and misjudgment of the model validity to power systems are taken into account. Thirdly, the minimum risk quantification model of error threshold is established based on the Bayes discriminant criterion, and the feasibility of the proposed method is verified by an actual WF with numerical examples. Compared with the existing error thresholds, the proposed error threshold can more quickly and accurately determine the validity of WF equivalent models.

1. Introduction

Renewable energy brings freshness, vitality, and opportunities to the power family, but also brings new challenges. To avoid the shortcomings, power system operators have carried out a large number of simulations [1]. At the same time, the accuracy of the simulation model and the credibility of the result analysis have also received common attention from the power science and engineering communities, especially for wind farm (WF) equivalent models, which have been widely used in the stability analysis, but the modeling methodology has originated from the consistency of the rotor swing curve of synchronous generators [2,3,4].

Unlike coal-fired power plants, the WF contains numerous small generators, and they have different operating conditions. For modeling WFs, the contradiction between model complexity and time-domain simulation speed is prominent [5,6]. As the final stage of simulation modeling work, model validation can increase the confidence of model developers and users. At present, the major wind power installation countries have stipulated different validation processes and requirements of wind power models in the form of guidelines, standards, or reports based on the operation and control characteristics of their own power systems. The German FGW TR 4 specifies the error thresholds for different periods in the dynamic response process, in which the error thresholds for the steady state period, the transient period, and the total period are 0.07 p.u., 0.2 p.u., and 0.15 p.u., respectively [7,8]. However, the adaptive time window division method and the validity discrimination process are too cumbersome for engineering applications. Spain’s PO 12.3 defines the time starting from 0.1 s before the fault and totaling 1 s as the time window for model validity, and stipulates that the wind power model will be considered valid if the percentage of sampling points with an equivalent error less than 10% exceeds 85% [9,10]. Due to the long-distance transmission in Australian power systems, the AEMO standard raises the percentage to 90% [11]. It should be noted that the model validation methods of Spain and Australia reflect their convention of focusing more on the fault period rather than the fault recovery period [12]. The Western Electricity Coordinating Council relies mainly on the subjective judgment of experienced engineers and does not give a mandatory quantitative index for the error threshold [13]. To expand the scope of application of international standards, the quantification-of-error thresholds in IEC 61400-27-2 are handed over to domestic power system operators or authoritative organizations [14]. China’s GB/T 36237-2023 does not involve the quantification-of-error thresholds [15], while NB/T 31053-2021 draws on the relevant indexes of FGW TR4 [16].

The core of the research on the error threshold of WF equivalent models lies in the quantification criteria. In other research fields, the most used threshold quantification method is based on the $3\delta$ criterion [17], but it is required that the data need to conform to the normal distribution. The threshold quantization method based on the minimum error probability criterion has a better effect [18], but this method has two significant shortcomings. On the one hand, the prior probability is not taken into account. Generally, the probabilities of WF equivalent models being valid and invalid are not equal and may have large differences. On the other hand, it does not consider the losses to power systems caused by wrong judgments. For the power system stability analysis, the loss caused by missed judgment and misjudgment of the model validity is markedly different.

The remainder of this paper is organized as follows. In Section 2, the equivalent modeling of WFs and error analysis methods are introduced. The quantitative model of minimum risk of equivalent error threshold of WFs based on the Bayes discriminant criterion is presented in detail in Section 3. The example analysis and conclusions are discussed in Section 4 and Section 5.

2. Equivalent Modeling of WFs and Error Analysis Methods

2.1. Single-Machine Equivalent Modeling Method for WFs

Except for the situations where one WF contains different types of wind turbines or has inconsistent control algorithms, a single-machine equivalent model (SEM) generally has the same behavior at the point of interconnection (POI) as a detailed model [13,19]. In addition, the SEM can maximize the excitation of equivalent errors, which is consistent with the intention of usually setting the fault point at the POI [20]. Therefore, this paper adopts the SEM; this means that the whole WF is aggregated into one equivalent machine for equivalent error analysis.

The SEM requires equivalent parameters of input wind speed, wind turbine, pad-transformer, and a collector system. The input wind speed is calculated according to the principle of equal wind energy captured before and after an equivalent value; the calculation of wind turbine and end-transformer is calculated by the capacity-weighted method; and the calculation of the collector system is based on the principle of equal power loss of the collector line before and after an equivalent value. The method for calculating the equivalent parameters is detailed in [12].

2.2. WF Equivalent Error Calculation

Compared with bias error, relative error and absolute value of relative error, the Euclidean error is the most reasonable measure to quantify the active and reactive power errors of the WF equivalent model [21]. To avoid the similar and single expression of error information in mean error measures, this paper further adopts a six-time window division method to quantify equivalent errors, as shown in Figure 1 [21]. The Euclidean error of each time window is calculated according to Equation (1).

$$e_{EE}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\left|Y_f(i)-Y(i)\right|}$$

(1)

where $Y_f(i)$ and $Y(i)$ are the active or reactive power of the detailed model and the SEM corresponding with the $i$ th sampling point, respectively, and $N$ is the total number of sampling points within one time window.

2.3. Probability Density Function of Equivalent Errors

Considering the uncertainty of input wind speed and fault disturbance, this paper selects kernel density estimation to fit the probability density distribution of equivalent errors of WFs [22]. Let $x_1,x_2,...,x_n$ represent the equivalent power error of WFs, then the kernel density function with respect to $x$ can be written as

$$\hat{f}(x)={\displaystyle \frac{1}{nh}}{\displaystyle \sum _{i=1}^{n}K(\frac{x-x_i}{h})}$$

(2)

where $\hat{f}(x)$ denotes the probability density function of the equivalent error of the WF, $K(x)$ denotes the kernel function, $h$ denotes the window width, and $n$ denotes the number of samples.

The window width $h$ is crucial for kernel density estimation. Currently, the insertion method based on a fixed window width is the most widely used and efficient window width selection method, which originates from the idea of least-square difference and obtains the optimal window width by minimizing the mean integral square error (MISE). The solution process is shown below.

$$MISE(\hat{f}(x))=E{{\displaystyle \int [\hat{f}(x)-f(x)]}}^{2}dx={{\displaystyle \int [E\hat{f}(x)-f(x)]}}^{2}dx+{\displaystyle \int Var\hat{f}}(x)dx$$

(3)

where the first term represents the integral of the square deviation between the expected value of $\hat{f}$ and the true value, and the second term represents the variance integral of the estimate. By solving and transforming Equation (3), the optimal window width $h_{*}$ can be determined, namely

$$h_{*}={\left[{\displaystyle \frac{{\displaystyle \int K{(t)}^{2}dt}}{{({\displaystyle \int t^2}K(t)dt)}^2{\displaystyle \int f^{″}{(x)}^{2}dx}}}\right]}^{{\displaystyle \frac{1}{5}}n-{\displaystyle \frac{1}{5}}}$$

(4)

3. Quantitative Model of Minimum Risk of Error Threshold of WF Equivalent Model

The $3\sigma$ criterion is the most commonly used threshold quantification method, but it requires the data to conform to a normal distribution. The threshold quantization method based on the minimum error probability is more effective, but it ignores the fact that the probabilities of model validity and invalidity are usually not equal and differ greatly. In addition, the impacts of missed judgment and misjudgment on power systems are not the same. The Bayes discriminant criterion can efficiently take into account a prior probability of WF equivalent error and a loss of wrong judgments, which can reduce the risk while improving the robustness of WF equivalent models.

3.1. The Bayes Discriminant Criterion and Mathematical Model

Assume that the prior probability of the WF equivalent model in the valid state is $q_{ok}$, and the prior probability of the invalid state is $q_{fault}$. The loss caused by the WF equivalent model’s missed judgment is $L(ok|fault)$, and the loss caused by misjudgment is $L(fault|ok)$. The Bayes discriminant function of the WF equivalent model is

$$W(x)={\displaystyle \frac{f_{ok}(x)}{f_{fault}(x)}},d={\displaystyle \frac{q_{fault}L(ok|fault)}{q_{ok}L(fault|ok)}}$$

(5)

The Bayes discriminant criterion is as follows:

$$\left\{\begin{array}{ll}x\in ok,& W(x)>d\\ x\in fault,& W(x)\le d\end{array}\right.$$

(6)

According to Equation (6), it is converted into an equation, which is

$${\displaystyle \frac{f_{ok}(x)}{f_{fault}(x)}}={\displaystyle \frac{q_{fault}L(ok|fault)}{q_{ok}L(fault|ok)}}$$

(7)

To solve Equation (7), the solution is the error threshold $Th$ of the WF equivalent model under the minimum risk. Based on $Th$, the validity of the WF equivalent model can be determined according to Equation (8).

$$\left\{\begin{array}{ll}x\in ok,& x<Th\\ x\in fault,& x\ge Th\end{array}\right.$$

(8)

3.2. Real-Time Weighted Prior Probability Algorithm

The Bayes discriminant criterion requires a prior probability of the equivalent error of WFs, and we adopt a real-time weighted solver algorithm to obtain the prior probability. The algorithm does not rely on prior knowledge and can adaptively adjust in real-time by measuring system parameters.

In the case of insufficient prior knowledge, let the prior probabilities of a valid and invalid WF equivalent model equal, i.e., $q_{ok}=q_{fault}=0.5$. Assuming the weighting coefficient $n=1$, it can be interpreted that the increase or decrease in the value of the prior probability at the current moment is completely dependent on the state of the previous moment, or that the increase or decrease in the value of the prior probability at the next moment is completely dependent on the state of the current moment, i.e.,

$$q_{i+1}(ok)=p_i(ok|s)$$

(9)

$$q_{i+1}(fault)=1-q_{i+1}(ok)$$

(10)

where $p_i(ok|s)$ represents the probability value that the state $s$, and the wind farm equivalent model is in a valid state at the time of monitoring.

According to the Bayes full probability model, there is a monitored state $s$ at the time $i$:

$$p_i(ok|s)={\displaystyle \frac{f_i(s|ok)\times q_i(ok)}{f_i(s|ok)\times q_i(ok)+f_i(s|fault)\times q_i(fault)}}$$

(11)

where $f_i(s|ok)$ (or $f_i(s|fault)$) represents the probability of monitoring state $s$ if the WF equivalent model is in a valid (invalid) state at the time.

The identity transformation of Equation (11) gives

$$p_i(ok|s)={\displaystyle \frac{1}{1+\frac{f_i(s|fault)}{f_i(s|ok)}\times \frac{q_i(fault)}{q_i(ok)}}}$$

(12)

Substituting $q_i(fault)=1-q_i(ok)$ into Equation (12) yields

$$p_i(ok|s)={\displaystyle \frac{1}{1+a_i\times b_i}}$$

(13)

where $a_i=1-{\displaystyle \frac{1}{q_i(ok)}},b_i={\displaystyle \frac{f_i(s_i|fault)}{f_i(s_i|ok)}}$.

What is discussed above is the real-time update algorithm of prior probability when $n=1$; when $n\ge 1$, it only needs to transform Equations (9) and (10) into

$$q_{i+1}(ok)={\displaystyle {\sum }_{j=0}^{n-1}{w}_j}{p}_{i-j}(ok|s)$$

(14)

$$q_{i+1}(fault)=1-q_{i+1}(ok)$$

(15)

where ${\displaystyle {\sum }_{j=0}^{n-1}{w}_j}=1$ and, under normal circumstances, $w_0>w_1>...>w_n,w_j$ represents the contribution factor of the prior probability of moment $(i-1)$ to moment $(i+1)$.

4. Example Analysis

An actual WF consists of $28\times 1.5$ MW doubly fed induction generators (DFIGs), which are connected to node 1 of the IEEE 39-node system. The network topology is shown in Figure A1. Based on the MATLAB/Simulink R2024a platform, the detailed model and SEM of the WF are built, in which the parameters of the detailed model are shown in

Table A1. Simulation parameters.

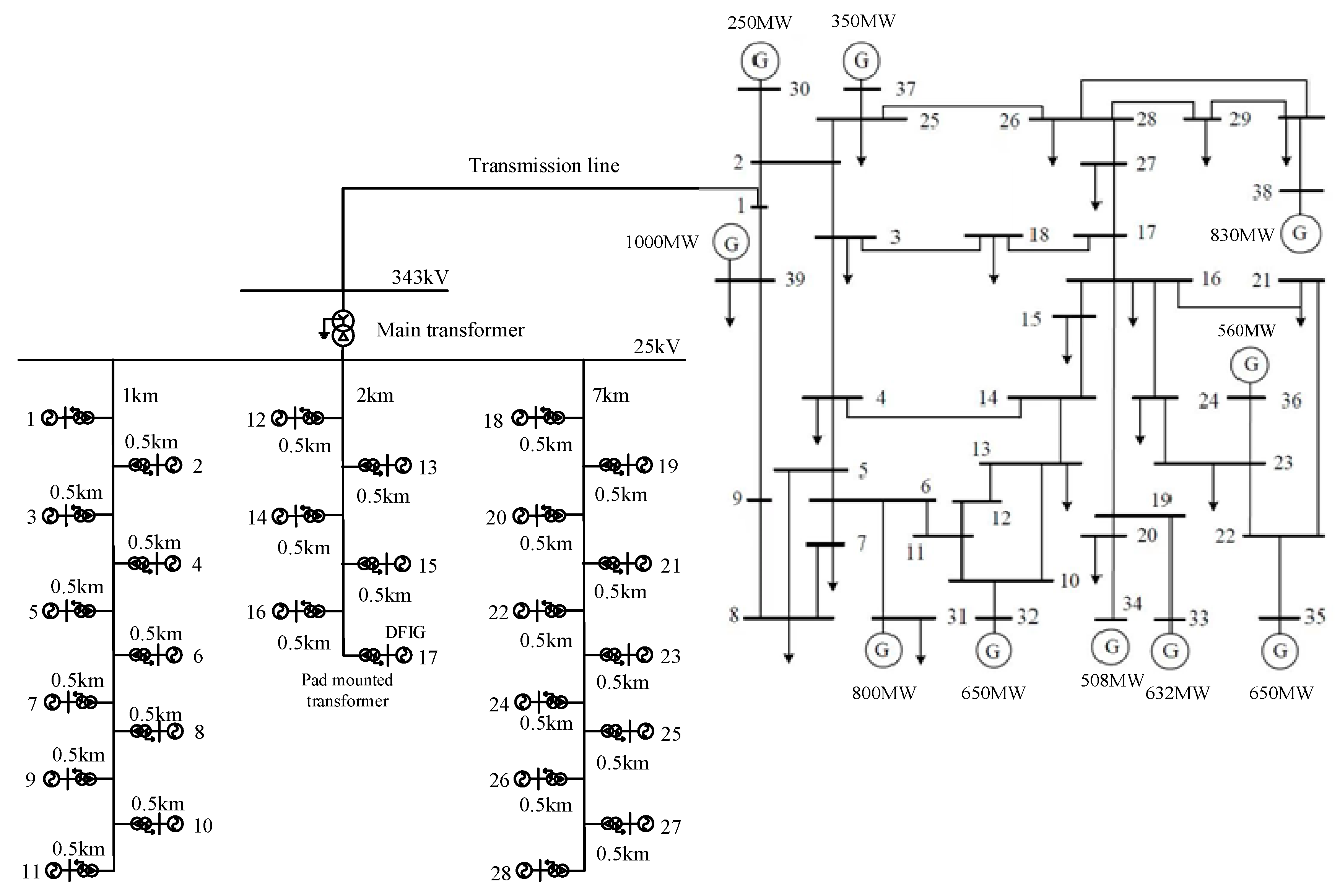
DFIG	Wind turbine
	Blade radius (m)	31	Stiffness coefficient of shafting (pu/rad)	1.11
	Inertial time constant (s)	4.32	Rated wind speed (m/s)	12.5
	Cut-in wind speed (m/s)	4	Cut-out wind speed (m/s)	22
	Doubly fed induction generator
	Rated power (MW)	1.5	Rated frequency (Hz)	50
	Rated voltage (kV)	0.575	Stator impedance (pu)	0.016 + j0.16
	Rotor impedance (pu)	0.023 + j0.18	Mutual impedance of stator and rotor (pu)	j2.9
	Power converter
	Rotor side converterRated capacity (MVA)	0.525	Network side converterRated capacity (MVA)	0.75
	Rated voltage of DC bus (kV)	1.15	DC side bus capacitance (F)	0.01
	Pry bar circuit input threshold (pu)	2	Pry bar circuit cut out threshold (pu)	0.35
	Pry resistance (pu)	0.1
Pad Mounted Transformer	Rated capacity (MVA)	1.75	Rated frequency (Hz)	50
	Rated ratio (kV)	25/0.575	Impedance (pu)	0.06
Main Transformer	Rated capacity (MVA)	150	Rated frequency (Hz)	50
	Rated ratio (kV)	343/25	Impedance (pu)	0.135
Cable Line	Unit resistance (Ω/km)	0.1153	Unit inductance (Ω/km)	j0.3297

. Parameters of the SEM are calculated according to Section 2.1, and the equivalent errors of the WF are calculated as described in Section 2.2. The voltage dip is realized by setting a short-circuit fault at the POI.

4.1. Determination of WF Equivalent Error Probability Density Function

Between the cut-in and cut-out wind speeds of the DFIG, 200 sets of input wind speeds of 28 DFIGs and 100 sets of input wind speeds of $28\times 2$ DFIGs are randomly generated. In total, 300 sets of voltage dips are randomly generated within the range of 0.1 to 0.9 p.u. A short-circuit fault occurs at 20 s, and the fault is cleared after 0.625 s. The power response curves at the POI are simulated based on the above data, and the equivalent errors are carried out according to Equation (1) with a 5 ms sample step.

According to Equation (2), the density functions of an equivalent error in six time windows are fitted, and then the probability density curves can be drawn. The active and reactive powers of time window 4 are shown in Figure 2 and Figure 3, respectively.

It can be seen that the kernel density estimation method based on a fixed window width can reflect the distribution characteristics of the frequency histogram of sample data, and the fitted probability density function curve is smooth, which is conducive to reducing the error of subsequent data processing.

4.2. Influence of Different Missed Judgment and Misjudgment Loss Ratio Thresholds

Due to the subjectivity of the selection of the loss ratio of missed judgment and misjudgment in the WF equivalent model validation, the loss ratios of missed judgment and misjudgment are set as 1, 10, 50, and 100 in turn. The error threshold of the WF equivalent models under each time window is quantified according to Equation (7), as shown in Figure 4 and Figure 5.

It can be seen that the error threshold of WF equivalent models under each time window shows a decreasing trend but has little change with the increase in the loss ratio of missed judgement and misjudgement of model validation. With the increase in the cost of missed judgment, the threshold quantification method based on minimum risk is more prone to misjudgment, and the error threshold is reduced in the validity criterion. According to the actual situation, the losses caused by missed judgment and misjudgment of the WF equivalent model validity are different. When the loss ratio is 1, the proportion of missed judgments will increase, and the losses caused to the system will also increase. With the increase in loss ratio, the equivalent error threshold of WFs will decrease, which is easy to cause misjudgment. Therefore, this paper sets the loss ratio of missed judgment and misjudgment of the equivalent WF validity as 10.

4.3. Determination of Equivalent Error Threshold for WFs

According to the minimum-risk Bayes threshold selection theory and the threshold discrimination criterion of Equation (7), threshold selection research is carried out to judge the validity of the WF equivalent models. Among them, the density function curve of an equivalent WF power error can be obtained through Section 4.1, and the prior probability of valid and invalid equivalent WF models can be obtained by real-time weighting algorithms. Based on Section 4.2, it is determined that the loss ratio of missed judgment and misjudgment of equivalent WF model validity is 10. The threshold quantization results of equivalent errors of WFs are shown in

Table 1. Active power equivalent error threshold of WFs.

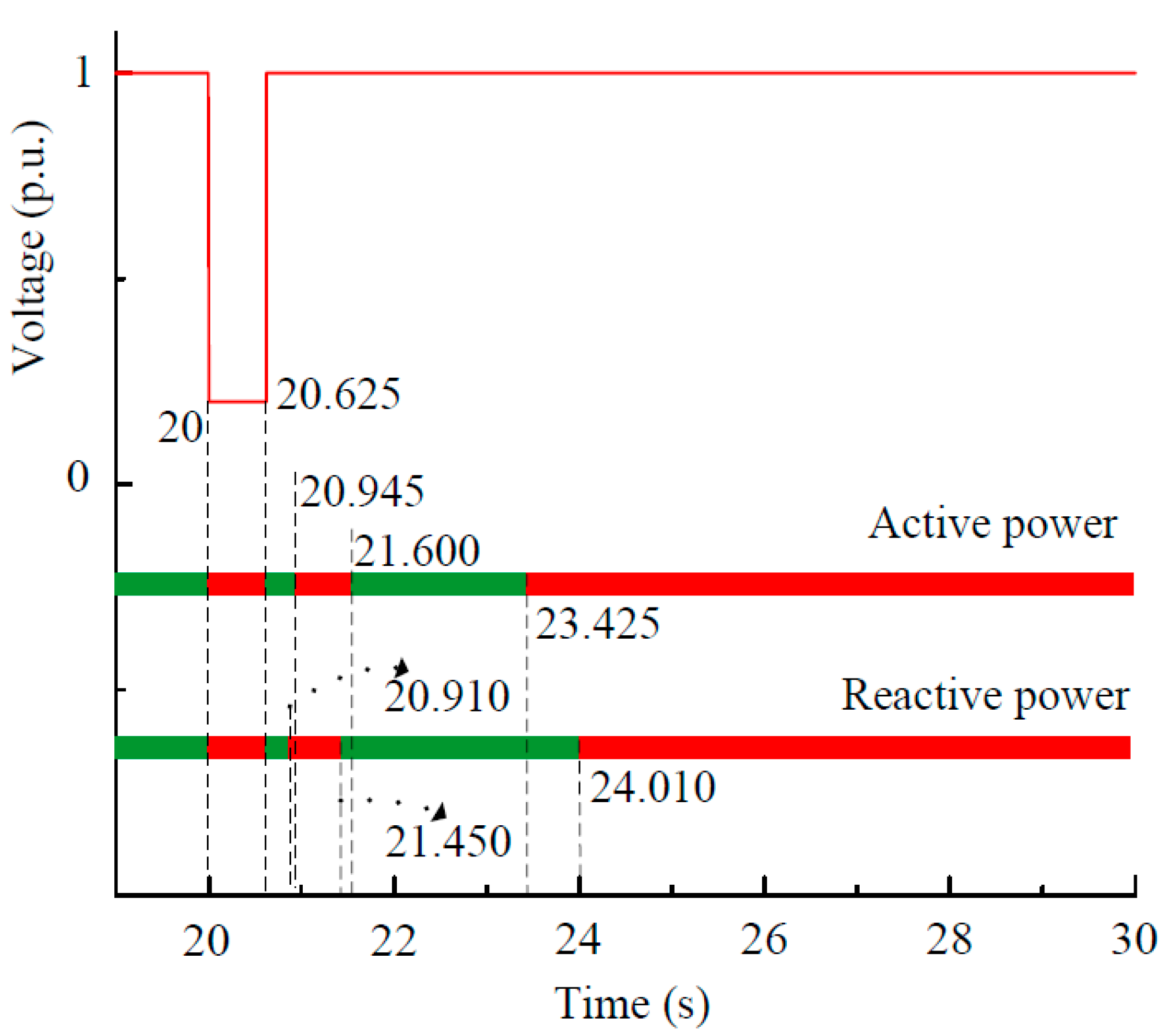
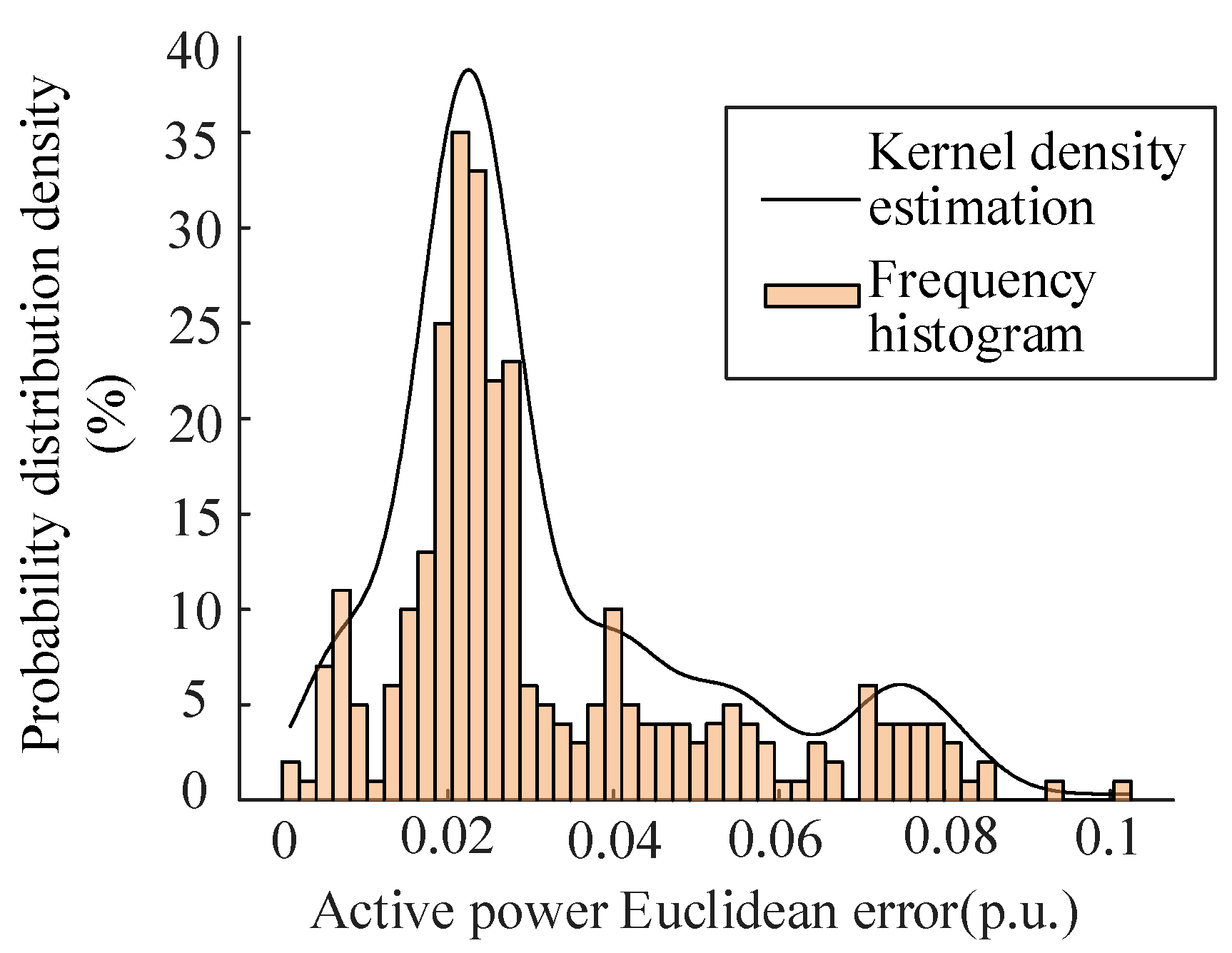
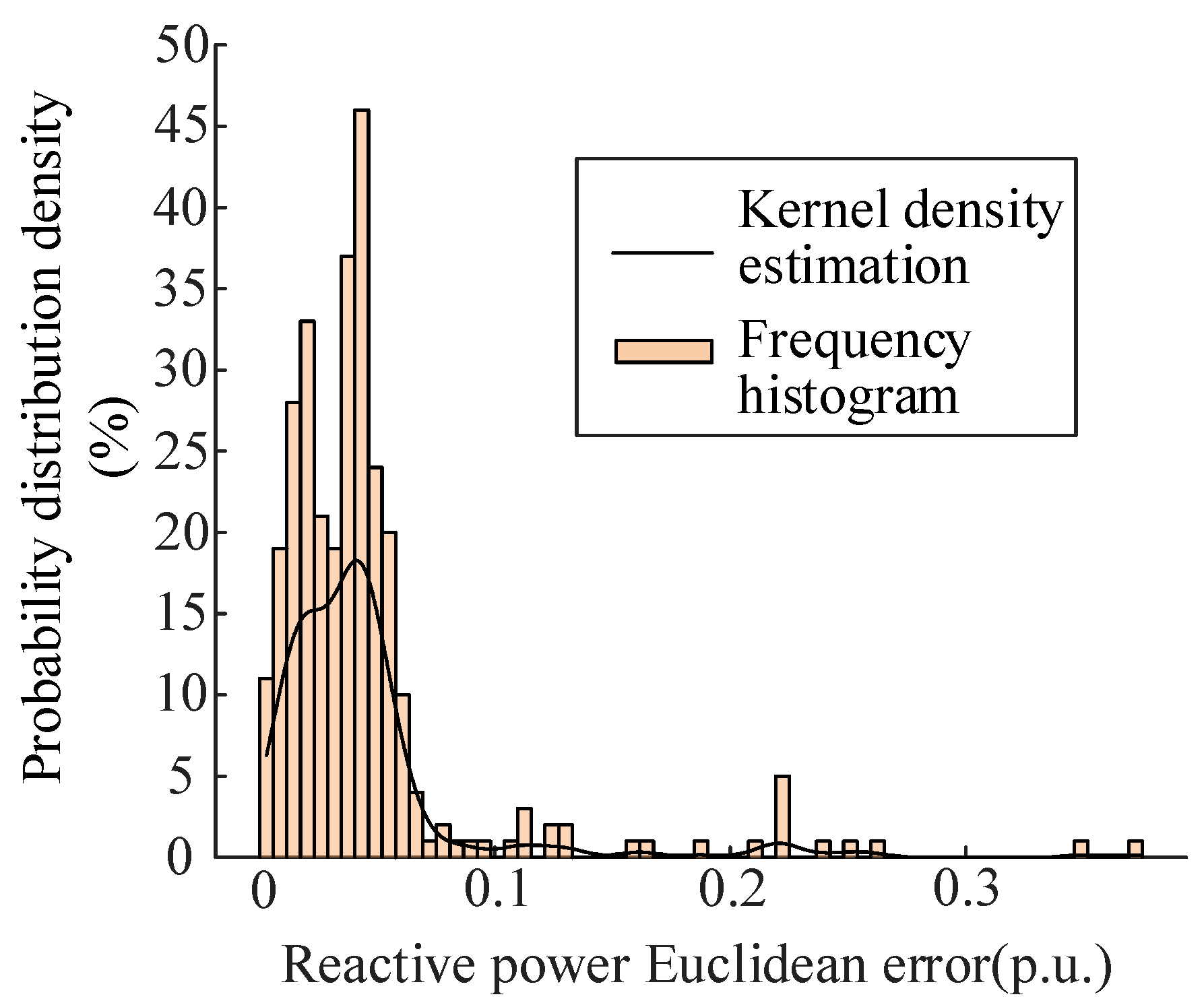
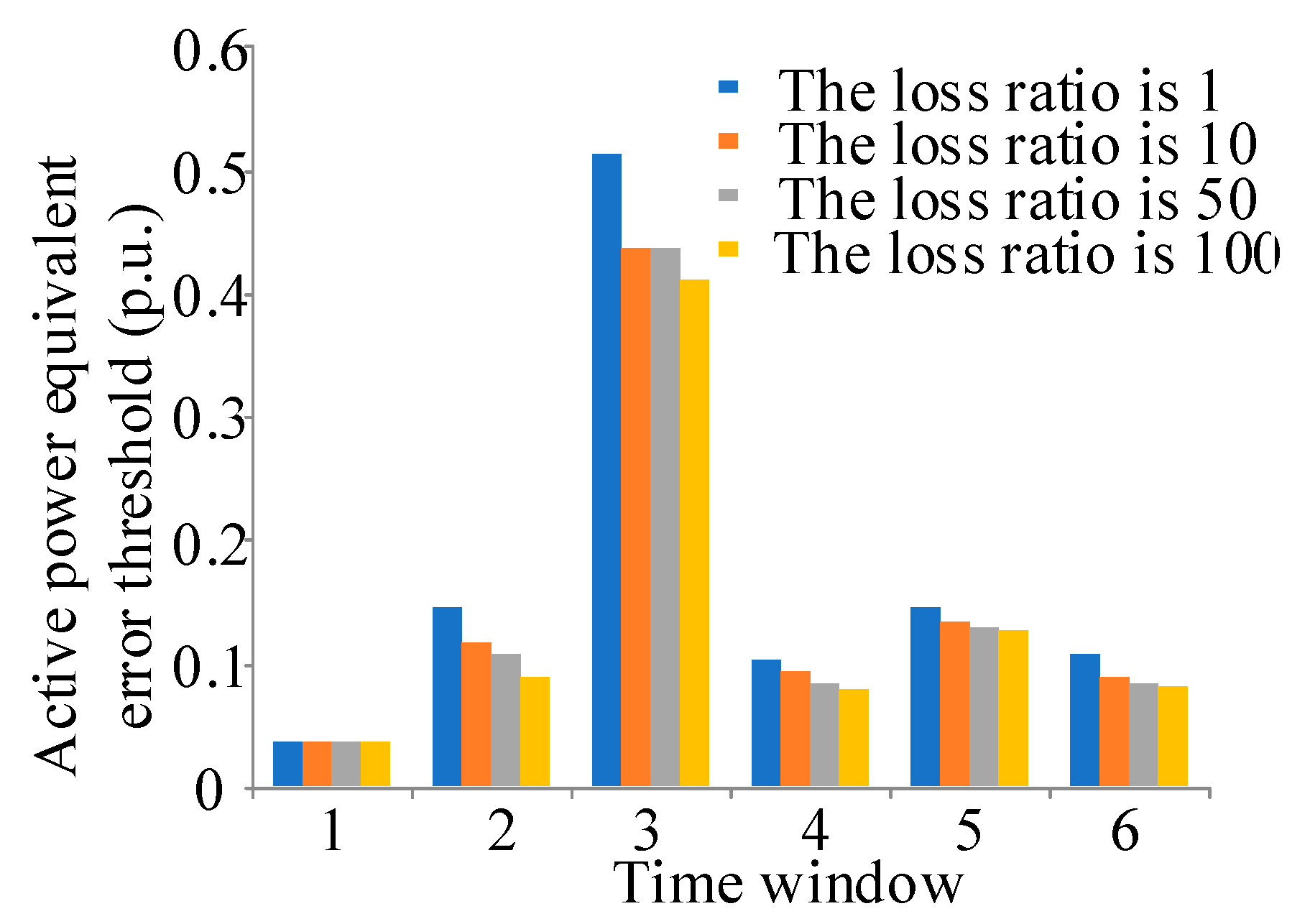
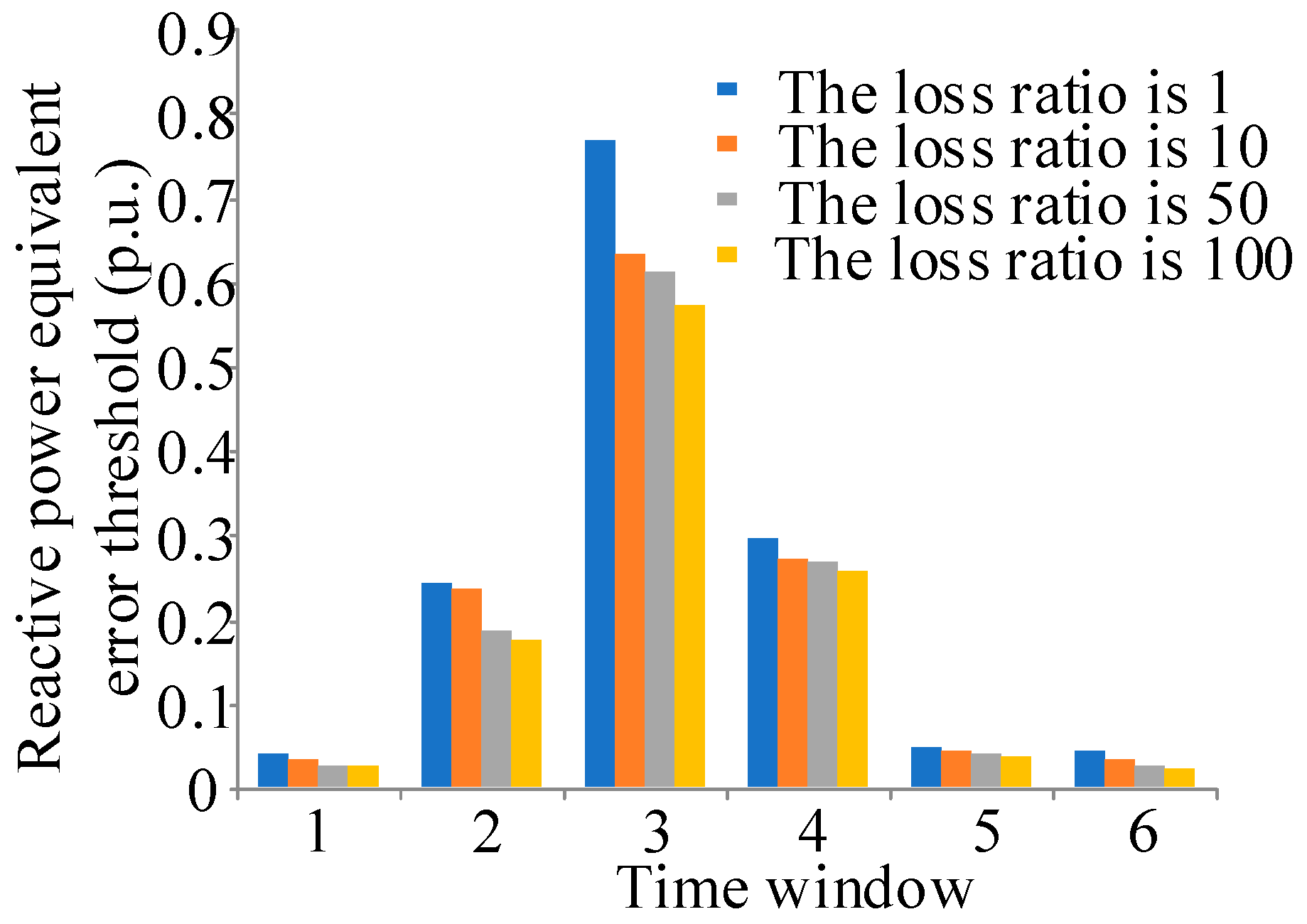
Active Time Window	1	2	3	4	5	6
Proposed method	0.0356	0.181	0.6525	0.1328	0.1322	0.0876
Minimum error probability criterion	0.0236	0.1462	0.2377	0.1025	0.0899	0.0535
3σ criterion	0.0387	0.1422	0.4753	0.1121	0.0944	0.06

and

Table 2. Reactive power equivalent error threshold of WFs.

Reactive Time Window	1	2	3	4	5	6
Proposed method	0.0316	0.2431	0.6335	0.2708	0.0447	0.0323
Minimum error probability criterion	0.0254	0.2219	0.5749	0.2257	0.0367	0.0218
3σ criterion	0.0384	0.2226	0.4508	0.1935	0.0591	0.0398

.

To shorten the discriminant time while ensuring the accuracy of the discriminant, this paper further distinguishes the main discriminant time window and the secondary discriminant time window. In total, 80 sets of test data are randomly generated within the input wind speed range of 4~22 m/s and voltage dip range of 0.1~0.9 p.u. Through preliminary observation of the test data, it is found that time window 1 and time window 2 are easy to cause misjudgment of the equivalent WF model validity, so the discrimination window is selected from the other four time windows. As a result, six typical discrimination combinations of time window are selected according to the test data and discrimination requirements, as shown in

Table 3. Threshold decision results under different validation time windows.

The Main Discriminant Time Window	Secondary Discriminant Time Window	Number of Wrong Judgments	Correct Rate/%
Window 3, 4	Window 5, 6	2	97.5
Window 5, 6	Window 3, 4	2	97.5
Window 3, 4	Window 5	2	97.5
Window 3, 4	Window 6	2	97.5
Window 3, 4	none	5	93.75
Window 5, 6	none	21	73.75

.

As can be seen from Table 3, when window 3 and window 4 are the main validation window and window 5 is the secondary validation window, the accuracy of discrimination is not only high but also the validation time of the equivalent WF models is shortened. The specific validation method is as follows: when the equivalent errors of windows 3 and 4 are lower than the given error threshold at the same time, the WF equivalent model is judged to be valid. When the equivalent errors of windows 3 and 4 are both higher than the given error threshold, it is also necessary to verify whether time window 5 meets the given error threshold. If it is less than the given error threshold, the WF equivalent model will be judged to be valid. Otherwise, it will be invalid.

4.4. Verification in Different Wind Speed Scenarios

To verify the validity of the proposed threshold quantization method of the WF equivalent models, four scenarios are selected, including random wind speed, rated wind speed, sub-synchronous speed, and super-synchronous speed. For each scenario, five sets of test data are generated in the voltage dip range of 0.2~0.9 p.u. In the random wind speed scenario, the input wind speeds are generated randomly in the range of 4 to 22 m/s. For the rated wind speed scenario, the input wind speeds are fixed at 12.5 m/s. The input wind speeds in the sub-synchronous and super-synchronous speed scenario are randomly generated within the range of 4~9.5 m/s and 9.6~22 m/s, respectively.

Table 4. Determination results of the WF equivalent model based on the proposed method.

Test Group Number	Time Window 3		Time Window 4		Time Window 5		Time Window 6		Decision Result
	Active Power	Reactive Power	Active Power	Reactive Power	Active Power	Reactive Power	Active Power	Reactive Power	3σ Criterion	Minimum Error Probability Criterion	Methodology of This Paper
1	0.0677	0.1248	0.0765	0.0634	0.0569	0.0683	0.0409	0.0942	right	right	right
2	0.5976	1.2545	0.0810	0.1642	0.1583	0.0249	0.1261	0.0633	right	right	right
3	1.3517	0.8261	0.3966	1.1961	0.1089	0.1610	0.1303	0.0305	wrong	wrong	right
4	0.6323	1.4061	1.4189	0.9739	1.3036	1.0969	1.2914	1.0548	right	right	right
5	2.0831	0.8932	1.4873	0.6725	1.3176	1.1206	1.2867	1.0569	right	right	right

,

Table 5. Determination results of WF equivalent model based on NB/T 31053-2021 in super-synchronous speed scenario.

Test Group Number	Pre-Failure Mean Absolute Deviation		Mean Absolute Deviation during Failure		Mean Absolute Deviation after Failure		Weighted Mean Absolute Deviation		Decision Result
	Active Power	Reactive Power	Active Power	Reactive Power	Active Power	Reactive Power	Active Power	Reactive Power
1	0.046	0.093	0.006	0.142	0.047	0.086	0.023	0.120	right
2	0.046	0.093	0.052	0.024	0.145	0.095	0.079	0.053	right
3	0.046	0.091	0.065	0.030	0.187	0.157	0.099	0.074	wrong
4	0.046	0.093	0.031	0.027	1.281	1.073	0.408	0.347	right
5	0.046	0.093	0.010	0.014	1.335	1.048	0.411	0.332	right

and

Table 6. Determination results of WF equivalent model based on Spanish PO 12.3 in super-synchronous speed scenario.

Test Group Number	Parameters	Error Sampling Point below 0.1 p.u./%	Decision Result
1	Active power	96.02	wrong
	Reactive power	17.91
2	Active power	74.13	wrong
	Reactive power	73.63
3	Active power	72.64	wrong
	Reactive power	75.12
4	Active power	74.13	right
	Reactive power	75.62
5	Active power	73.63	right
	Reactive power	73.63

list the quantitative analysis results of equivalent errors in the hyper-synchronous speed scenario, and Appendix B, Appendix C and Appendix D list the quantitative analysis results in the other three scenarios.

As shown in Table 4, Table 5, Table 6 and

Table 7. Different criteria determine the results under different wind speeds.

Criterion	Number of Misjudgments (Sample Number is 20)/Piece	False Judgment Rate/%	Correct Rate/%
Proposed method	0	0	100
3σ criterion	1	5	95
MPE criterion	1	5	95
NB/T 31053-2021	1	5	95
PO 12.3	12	60	40

, it can be seen that the error rate corresponding to the $3\sigma$ criterion and the minimum error probability criterion is 5%, while the error rate corresponding to Spanish PO 12.3 is 60%, which is much higher than other discrimination criteria. The reason why Spanish PO 12.3 is poor is that its model validity time is only set to 1 s (calculated from 0.1 s before the fault), while the time in the fault recovery stage is only 0.275 s. This paper finds that the fault recovery period has a great impact on the judgment results, resulting in a high error rate of this method. Therefore, this validation method has been gradually replaced. The error rate corresponding to NB/T 31053-2021 is also 5%, but the error threshold criterion has too many verification indexes, making the validity verification process complicated. The quantized error threshold of the method in this paper can not only reduce the error rate to 0 but can also be distinguished by focusing on the index comparison of the initial period of fault recovery (time windows 3 and 4), which is simpler and more efficient in the engineering application process.

5. Conclusions

To solve the problem of the model accuracy of WFs as a component in power systems, this paper puts forward a minimum risk quantification method of equivalent error thresholds of WFs based on the Bayes discriminant criterion, which integrates the probability difference between the valid and invalid equivalent WF models and the different losses caused by missed judgment and misjudgment of model validity into the error threshold quantification model. Through the analysis of simulation examples, the following conclusions are obtained:

(1)

In the case that prior knowledge cannot be obtained, the real-time weighted prior probability solving algorithm can update the probability of the validity of the WF equivalent models according to the dynamic data set, and solve the problem of prior distribution selection in the Bayes discrimination criterion.

(2)

The identification method of “error thresholds of the windows 3 and 4 are the main ones, and error threshold of the window 5 is the auxiliary one” can accurately and efficiently determine the validity of the WF equivalent model, and improve the engineering practical value of the threshold quantization results.

(3)

Compared with the error threshold of existing wind power models, the Bayes threshold quantization result oriented to minimum risk can more accurately determine the validity of WF equivalent models.

However, the main drawback of this paper is that it only considers the equivalent error of DFIG-based WFs using the single-machine equivalent modeling method. To expand the applicability of the error threshold, the equivalent errors of DFIG-based WFs with different turbine parameters, PMSG-based WFs and hybrid WFs with both DFIGs and PMSGs need to be analyzed in future works. In addition, the equivalent errors under different equivalent modeling methods might need to be discussed.