Co-Design of a Wind–Hydrogen System: The Effect of Varying Wind Turbine Types on Techno-Economic Parameters
Abstract
1. Introduction
2. Materials and Methods
2.1. WTG Cost Model
2.2. Wind Farm Optimizer (WIFO)
2.3. Hybrid Wind-Farm Design Environment (HyDE)
3. Results
3.1. Wind Farm Site and Wind Turbine Generators
3.2. WIFO Results
3.3. Wind–Hydrogen System
3.4. Wind–Hydrogen System under Market Conditions
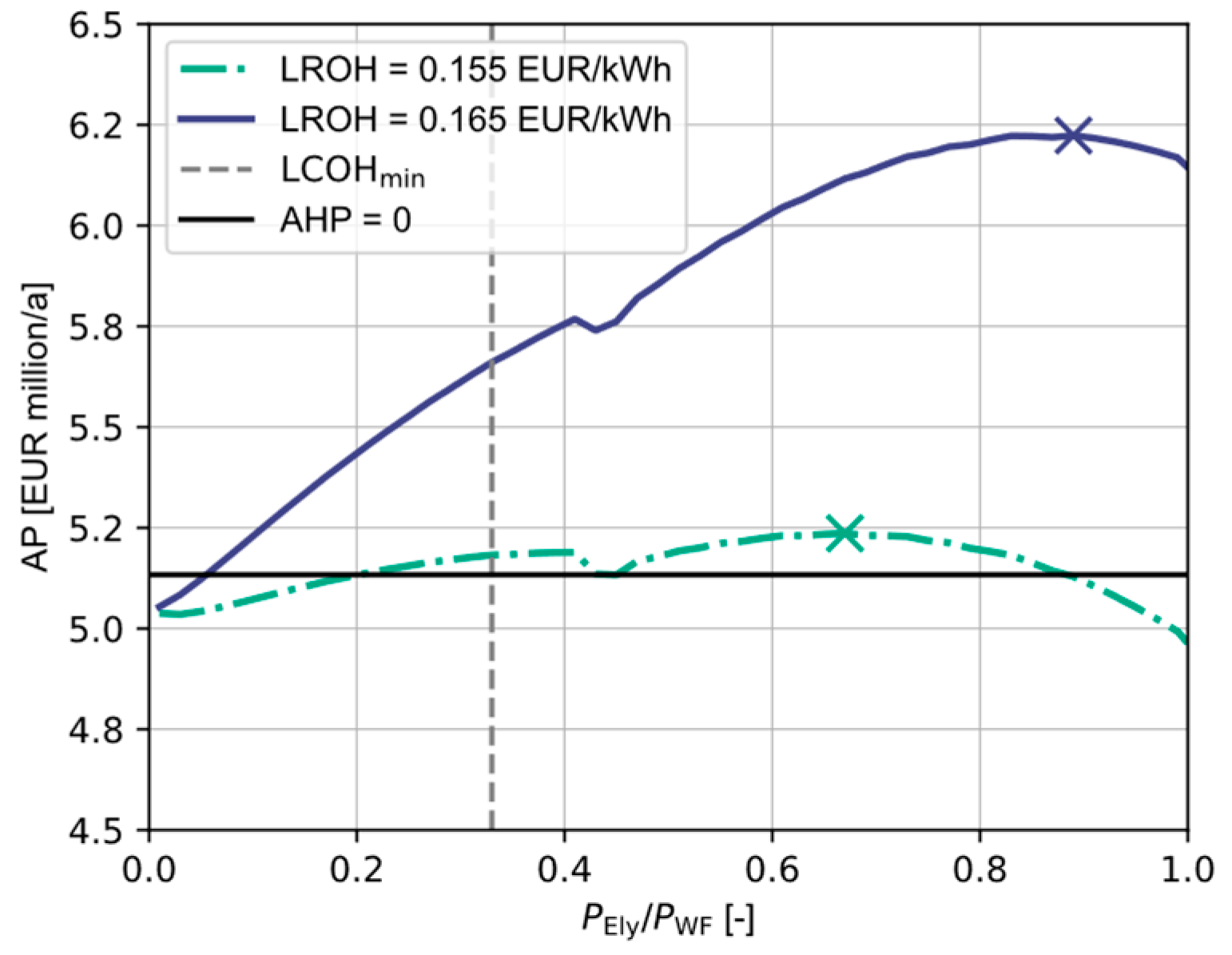
3.4.1. Effect of Varying LROH on the Optimal System Design
3.4.2. Effect of Varying WTGs on the Most Profitable Hybrid WF
3.4.3. Effect of Varying LROE on the Optimal System Design
4. Summary and Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Abbreviation | Abbreviation | ||
|---|---|---|---|
| AEL | Alkaline Electrolyzer | POD | Point Of Demand |
| AEP | Annual Energy Product | PV | Photovoltaic |
| AHP | Annual Hydrogen Product | PWF | rated WF Power |
| AP | Annual Profit | PWTG | rated Wind Turbine Generator Power |
| CAPEX | Capital Expenditures | RD | Rotor Diameter |
| cComponent | Component Cost | RES | Renewable Energy Sources |
| CFEly | Capacity Utilization Electrolyzer | TOTEX | Total Expenditures |
| ECHS | Electricity Consumption Hydrogen System | vcutin | cut in wind speed |
| FLH | Full-Load Hours | vcutout | cut out wind speed |
| H | Hub Height | WF | Wind Farm |
| HyDe | Hybrid Wind Farm Design Environment | WIFO | Wind Farm Optimizer |
| LCOE | Levelized Cost Of Electricity | WTG | Wind Turbine Generator |
| LCOH | Levelized Cost Of Hydrogen | 5MW100 | 5 MW WTG with 100 m H |
| LDC | Load Duration Curve | 5MW120 | 5 MW WTG with 120 m H |
| LROE | Levelized Revenue Of Electricity | 5MW140 | 5 MW WTG with 140 m H |
| LROH | Levelized Revenue Of Hydrogen | 7MW140 | 7 MW WTG with 140 m H |
| OPEX | Operational Expenditures | WF5MW100 | WF with 5 MW WTG with 100 m H |
| PEl/PWF | ratio PEly to PWF | WF5MW120 | WF with 5 MW WTG with 120 m H |
| PEly | rated Electrolyzer Power | WF5MW140 | WF with 5 MW WTG with 140 m H |
| PEMEL | Proton Exchange Membrane Electrolyzer | WF7MW140 | WF with 7 MW WTG with 140 m H |
| POCC | Point Of Common Coupling |
References
- IEA. Global Hydrogen Review 2021. 2021. Available online: https://www.iea.org/reports/global-hydrogen-review-2021 (accessed on 14 August 2024).
- European Commission. REPowerEU Plan. 2022. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=COM:2022:230:FIN (accessed on 15 August 2024).
- Odenweller, A.; George, J.; Müller, V.; Verpoort, P.; Gast, L.; Pfluger, B.; Ueckerdt, F. Wasserstoff und Die Energiekrise: Fünf Knackpunkte; Kopernikus-Projekt Ariadne Potsdam-Institut für Klimafolgenforschung (PIK): Potsdam, Germany, 2022. [Google Scholar]
- EERA. NeWindEERA: A New Research Programme for the European Wind Energy Sector. 2024. Available online: https://www.northwindresearch.no/wp-content/uploads/2024/03/NeWindEERA-Brochure-Final-Checked.pdf (accessed on 14 August 2024).
- Roscher, B. Multi-Dimensionale Windparkoptimierung in der Planungsphase: Multi-Dimensional Wind Farm Optimization in the Concept Phase, 1st ed; Verlagsgruppe Mainz GmbH: Aachen, Germany, 2020. [Google Scholar]
- Balasubramanian, K.; Thanikanti, S.B.; Subramaniam, U.; Sudhakar, N.; Sichilalu, S. A novel review on optimization techniques used in wind farm modelling. Renew. Energy Focus 2020, 35, 84–96. [Google Scholar] [CrossRef]
- Hofrichter, A.; Rank, D.; Heberl, M.; Sterner, M. Determination of the optimal power ratio between electrolysis and renewable energy to investigate the effects on the hydrogen production costs. Int. J. Hydrogen Energy 2023, 48, 1651–1663. [Google Scholar] [CrossRef]
- Grant, E.; Brunik, K.; King, J.; Clark, C.E. Hybrid power plant design for low-carbon hydrogen in the United States. J. Phys. Conf. Ser. 2024, 2767, 82019. [Google Scholar] [CrossRef]
- Ibagon, N.; Muñoz, P.; Correa, G. Techno economic analysis tool for the sizing and optimization of an off-grid hydrogen hub. J. Energy Storage 2023, 73, 108787. [Google Scholar] [CrossRef]
- Schnuelle, C.; Wassermann, T.; Fuhrlaender, D.; Zondervan, E. Dynamic hydrogen production from PV & wind direct electricity supply—Modeling and techno-economic assessment. Int. J. Hydrogen Energy 2020, 45, 29938–29952. [Google Scholar]
- Benalcazar, P.; Komorowska, A. Prospects of green hydrogen in Poland: A techno-economic analysis using a Monte Carlo approach. Int. J. Hydrogen Energy 2022, 47, 5779–5796. [Google Scholar] [CrossRef]
- Sens, L.; Piguel, Y.; Neuling, U.; Timmerberg, S.; Wilbrand, K.; Kaltschmitt, M. Cost minimized hydrogen from solar and wind—Production and supply in the European catchment area. Energy Convers. Manag. 2022, 265, 115742. [Google Scholar] [CrossRef]
- Reichartz, T.; Jacobs, G.; Rathmes, T.; Blickwedel, L.; Schelenz, R. Optimal position and distribution mode for on-site hydrogen electrolyzers in onshore wind farms for a minimal levelized cost of hydrogen (LCoH). Wind Energ. Sci. 2024, 9, 281–295. [Google Scholar] [CrossRef]
- Sens, L.; Neuling, U.; Kaltschmitt, M. Capital expenditure and levelized cost of electricity of photovoltaic plants and wind turbines—Development by 2050. Renew. Energy 2022, 185, 525–537. [Google Scholar] [CrossRef]
- Correa, G.; Volpe, F.; Marocco, P.; Muñoz, P.; Falagüerra, T.; Santarelli, M. Evaluation of levelized cost of hydrogen produced by wind electrolysis: Argentine and Italian production scenarios. J. Energy Storage 2022, 52, 105014. [Google Scholar] [CrossRef]
- Ajanovic, A.; Sayer, M.; Haas, R. The economics and the environmental benignity of different colors of hydrogen. Int. J. Hydrogen Energy 2022, 47, 24136–24154. [Google Scholar] [CrossRef]
- Reichartz, T.; Jacobs, G.; Oertmann, A.; Blickwedel, L.; Schelenz, R. Introducing a partial bottom-up model for onshore wind turbine CAPEX estimation. J. Phys. Conf. Ser. 2024, 2767, 52002. [Google Scholar] [CrossRef]
- Reichartz, T.; Jacobs, G.; Oertmann, A.; Blickwedel, L.; Schelenz, R. Supplement to: Introducing a bottom-up cost model for wind turbines—Model equations. Zenodo 2024. [Google Scholar] [CrossRef]
- Satymov, R.; Bogdanov, D.; Breyer, C. Global-local analysis of cost-optimal onshore wind turbine configurations considering wind classes and hub heights. Energy 2022, 256, 124629. [Google Scholar] [CrossRef]
- Wietschel, M.; Ullrich, S.J.; Markewitz, P.; Schulte, F.; Genoese, F. (Eds.) Energietechnologien der Zukunft: Erzeugung, Speicherung, Effizienz und Netze; Springer Vieweg: Wiesbaden, Germany, 2015. [Google Scholar]
- Wallasch, A.-K.; Lüers, S.; Heyken, M.; Rehfeld, K. Vorbereitung und Begleitung bei der Erstellung Eines Erfahrungsberichts Gemäß § 97 Erneuerbare-Energien-Gesetz: Teilvorhaben II e): Wind an Land. 2019. Available online: https://www.zsw-bw.de/uploads/media/deutsche-windguard-vorbereitung-begleitung-erfahrungsbericht-eeg.pdf (accessed on 26 August 2024).
- Kost, C.; Shammugan, S.; Fluri, V.; Peper, D.; Memar, A.; Schlegl, T. Stromgestehungskosten Erneuerbare Energien. 2021. Available online: https://www.ise.fraunhofer.de/content/dam/ise/de/documents/publications/studies/DE2021_ISE_Studie_Stromgestehungskosten_Erneuerbare_Energien.pdf (accessed on 26 August 2024).
- Brusca, S.; Lanzafame, R.; Famoso, F.; Galvagno, A.; Messina, M.; Mauro, S.; Prestipino, M. On the Wind Turbine Wake Mathematical Modelling. Energy Procedia 2018, 148, 202–209. [Google Scholar] [CrossRef]
- Schiebahn, S.; Grube, T.; Robinius, M.; Tietze, V.; Kumar, B.; Stolten, D. Power to gas: Technological overview, systems analysis and economic assessment for a case study in Germany. Int. J. Hydrogen Energy 2015, 40, 4285–4294. [Google Scholar] [CrossRef]
- Davoudi, S.; Khalili-Garakani, A.; Kashefi, K. Power-to-X for Renewable-Based Hybrid Energy Systems. In Whole Energy Systems: Bridging the Gap via Vector-Coupling Technologies; Vahidinasab, V., Mohammadi-Ivatloo, B., Eds.; Springer International Publishing: Cham, The Netherlands, 2022; pp. 23–40. [Google Scholar]
- Buttler, A.; Spliethoff, H. Current status of water electrolysis for energy storage, grid balancing and sector coupling via power-to-gas and power-to-liquids: A review. Renew. Sustain. Energy Rev. 2018, 82, 2440–2454. [Google Scholar] [CrossRef]
- Hermesmann, M.; Grübel, K.; Scherotzki, L.; Müller, T.E. Promising pathways: The geographic and energetic potential of power-to-x technologies based on regeneratively obtained hydrogen. Renew. Sustain. Energy Rev. 2021, 138, 110644. [Google Scholar] [CrossRef]
- Krishnan, S.; Corona, B.; Kramer, G.J.; Junginger, M.; Koning, V. Prospective LCA of alkaline and PEM electrolyser systems. Int. J. Hydrogen Energy 2024, 55, 26–41. [Google Scholar] [CrossRef]
- Koponen, J.; Kosonen, A.; Ruuskanen, V.; Huoman, K.; Niemelä, M.; Ahola, J. Control and energy efficiency of PEM water electrolyzers in renewable energy systems. Int. J. Hydrogen Energy 2017, 42, 29648–29660. [Google Scholar] [CrossRef]
- González, J.S.; Rodríguez, Á.G.; Mora, J.C.; Burgos Payán, M.; Santos, J.R. Overall design optimization of wind farms. Renew. Energy 2011, 36, 1973–1982. [Google Scholar] [CrossRef]
- Blickwedel, L.; Harzendorf, F.; Schelenz, R.; Jacobs, G. Future economic perspective and potential revenue of non-subsidized wind turbines in Germany. Wind Energ. Sci. 2021, 6, 177–190. [Google Scholar] [CrossRef]
- DeepL. DeepL: Translator Computer Software. 2024. Available online: https://www.deepl.com/de/translator (accessed on 4 September 2024).
- OpenAI. ChatGPT: Large Language Model. 2024. Available online: https://www.openai.com/chatgpt (accessed on 4 September 2024).
- DWD Climate Data Center (CDC). Historical Hourly Station Observations of Wind Speed and Wind Direction for Germany, Versionv006. 2018. Available online: https://opendata.dwd.de/climate_environment/CDC/observations_germany/climate/hourly/wind/historical/ (accessed on 22 May 2018).
- FNB Gas. 2024. Available online: https://fnb-gas.de/en/hydrogen-core-network/ (accessed on 6 August 2024).
- Bundesnetzagentur. Bundesnetzagentur—EEG-Förderung und-Fördersätze; 2024. Available online: https://www.bundesnetzagentur.de/DE/Fachthemen/ElektrizitaetundGas/ErneuerbareEnergien/EEG_Foerderung/start.html (accessed on 19 August 2024).
- Bhandari, R.; Shah, R.R. Hydrogen as energy carrier: Techno-economic assessment of decentralized hydrogen production in Germany. Renew. Energy 2021, 177, 915–931. [Google Scholar] [CrossRef]







| Parameter | 5 MW WTG | 7 MW WTG |
|---|---|---|
| PWTG (MW) | 5 | 7 |
| RD (m) | 185 | 162 |
| H (m) | 100/120/140 | 140 |
| Power density (W/m2) | 186 | 340 |
| vcutin (m/s) | 3 | 3 |
| vcutout (m/s) | 22 | 25 |
| CAPEXWTG (€/kW) 1 | 1251/1274/1297 | 931 |
| Parameter | 30 MW WF | 42 MW WF |
|---|---|---|
| WTG | 5MW100/5MW120/5MW140 | 7MW140 |
| CAPEXWF (Mio. €) | 53.16/53.85/54.53 | 60.98 |
| AEP (GW) | 171.28/178.36/181.49 | 216.57 |
| FLH (h) | 5709/5945/6050 | 5157 |
| LCOE (€ct./kWh) | 3.62/3.56/3.54 | 3.55 |
| Parameter | 30 MW WF | 42 MW WF |
|---|---|---|
| WTG | 5MW100/5MW120/5MW140 | 7MW140 |
| LCOHmin (€ct./kWh) | 11.22/11.06/11.00 | 11.08 |
| PEly (kW) 1 | 8700/9900/9900 | 9660 |
| CFEly (%) 1 | 84.3/84.3/84.8 | 83.8 |
| PEly/PWF (%) 1 | 29/33/33 | 23 |
| Distribution mode 1 | Diesel-LOHC 2 | Diesel-LOHC 2 |
| CAPEXEly (Mio. €) 1,3 | 14.04/15.76/15.78 | 15.40 |
| AHP (t/a) 1 | 1254/1425/1436 | 1384 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reichartz, T.; Jacobs, G.; Blickwedel, L.; Frings, D.; Schelenz, R. Co-Design of a Wind–Hydrogen System: The Effect of Varying Wind Turbine Types on Techno-Economic Parameters. Energies 2024, 17, 4710. https://doi.org/10.3390/en17184710
Reichartz T, Jacobs G, Blickwedel L, Frings D, Schelenz R. Co-Design of a Wind–Hydrogen System: The Effect of Varying Wind Turbine Types on Techno-Economic Parameters. Energies. 2024; 17(18):4710. https://doi.org/10.3390/en17184710
Chicago/Turabian StyleReichartz, Thorsten, Georg Jacobs, Lucas Blickwedel, Dustin Frings, and Ralf Schelenz. 2024. "Co-Design of a Wind–Hydrogen System: The Effect of Varying Wind Turbine Types on Techno-Economic Parameters" Energies 17, no. 18: 4710. https://doi.org/10.3390/en17184710
APA StyleReichartz, T., Jacobs, G., Blickwedel, L., Frings, D., & Schelenz, R. (2024). Co-Design of a Wind–Hydrogen System: The Effect of Varying Wind Turbine Types on Techno-Economic Parameters. Energies, 17(18), 4710. https://doi.org/10.3390/en17184710






