Heat Transfer of Crude Waxy Oil with Yield Stress in a Pipe
Abstract
1. Introduction
2. Heat Transfer Model
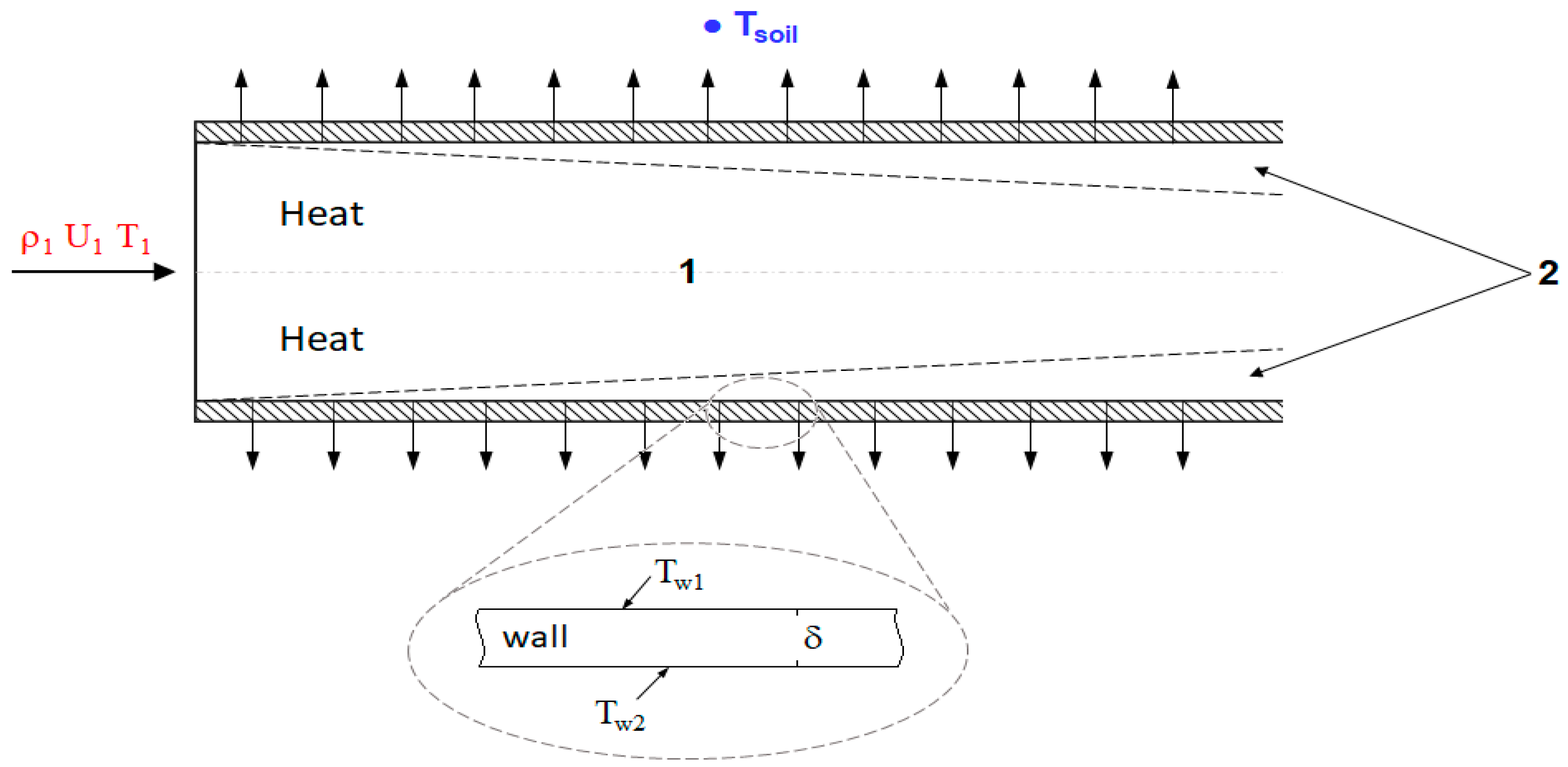
2.1. Formulation of the Problem
2.2. The Bingham–Papanastasiou Model
2.3. Basic Heat Transfer Equations
2.4. Boundary Conditions
3. The Numerical Solution
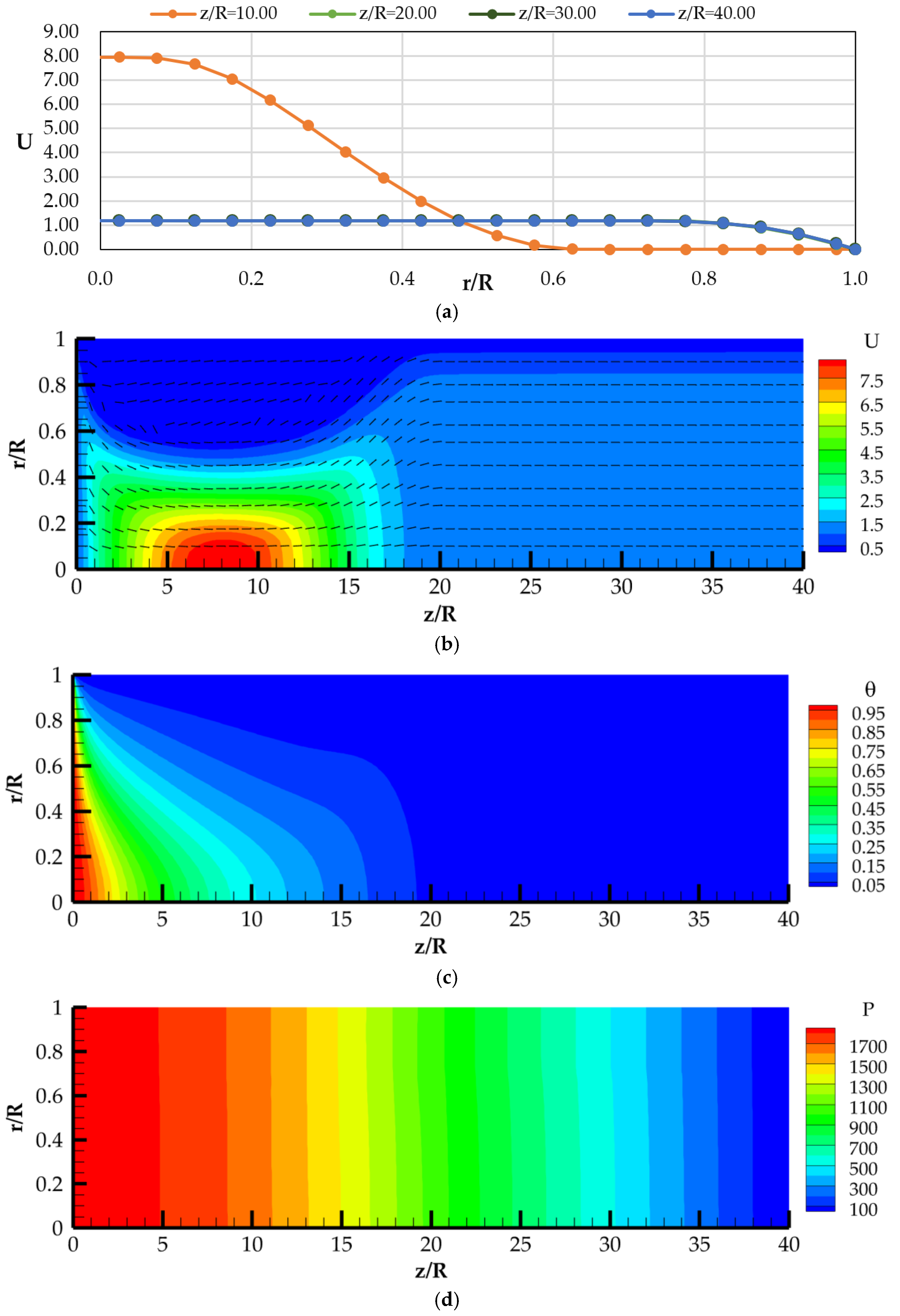
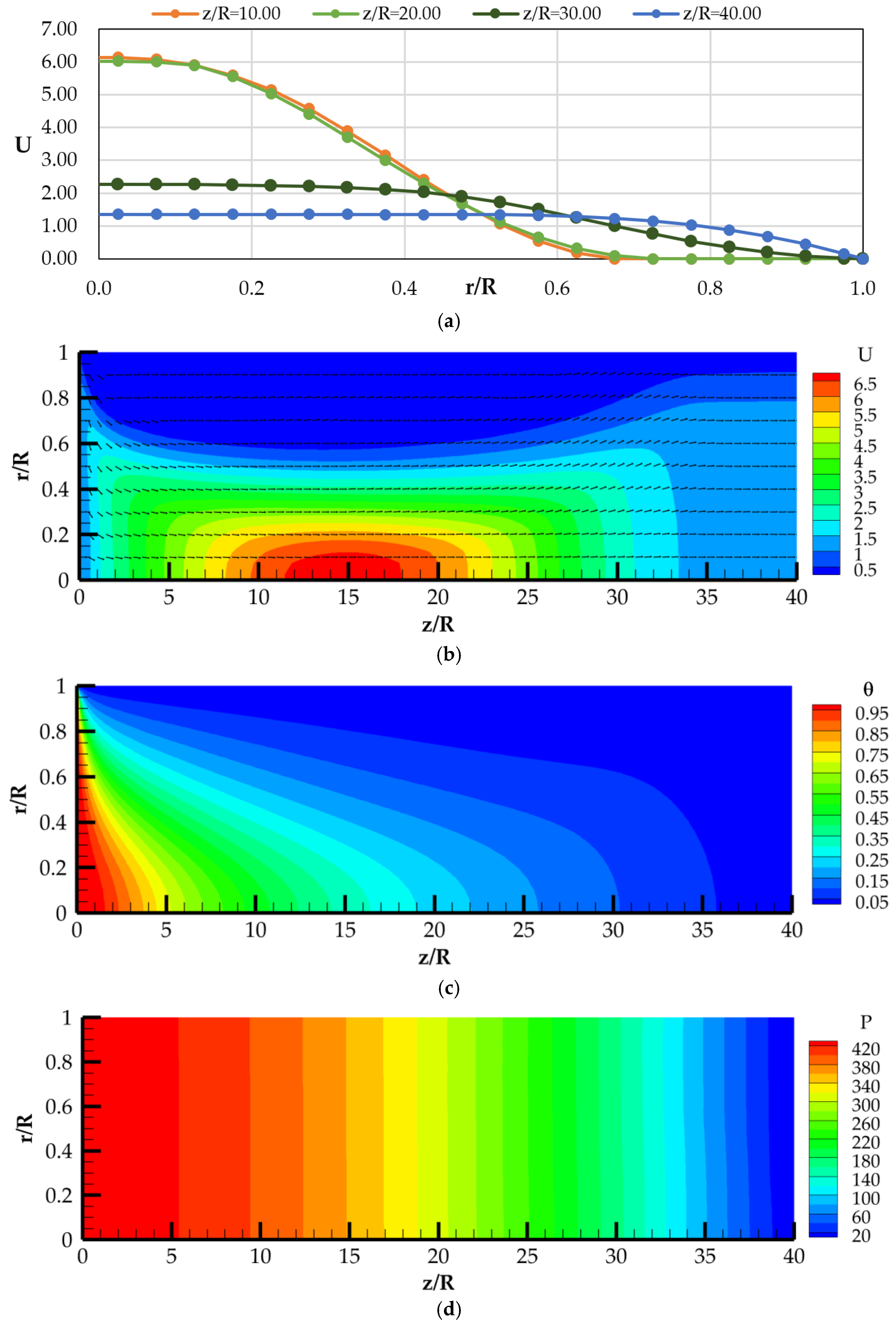
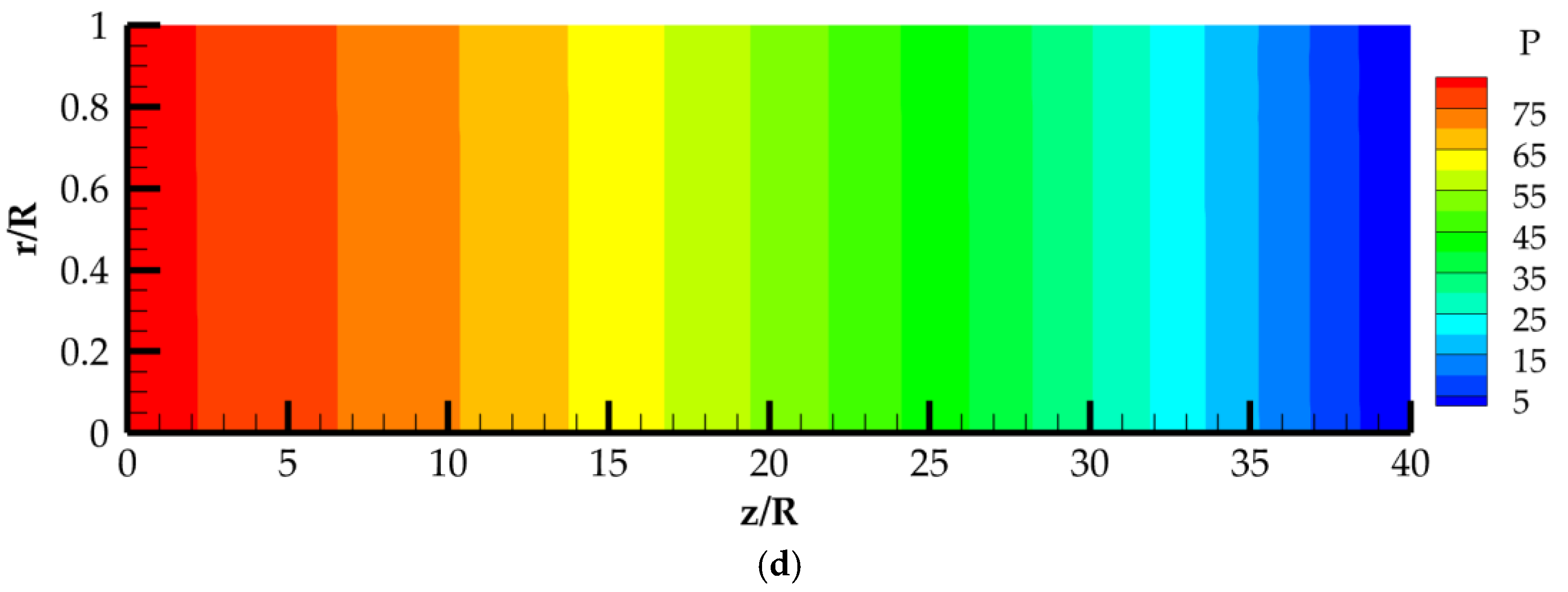
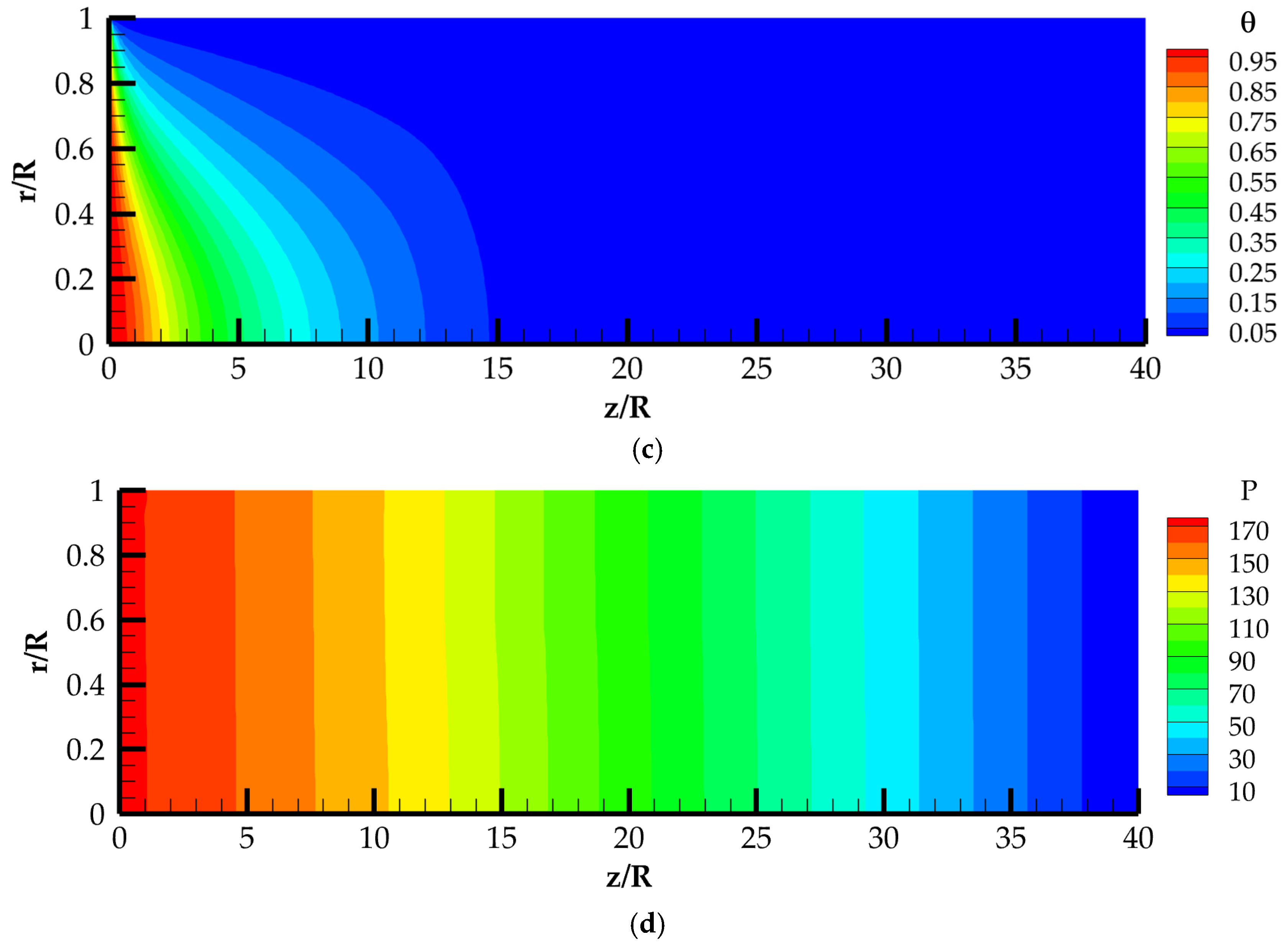
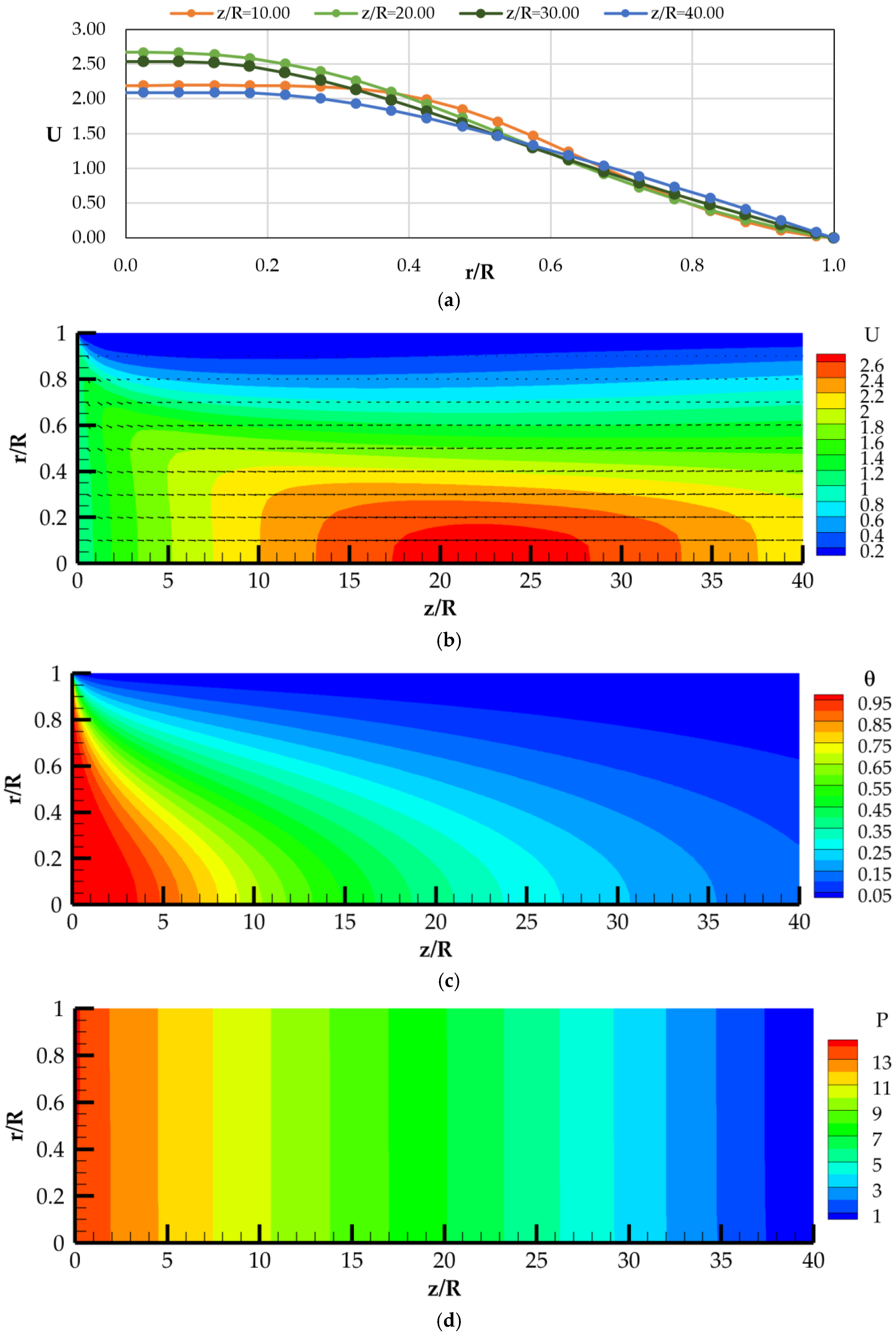
4. Discussion of Calculated Data
4.1. Calculation Data at Different Velocities and Constant Wall Temperatures
4.2. Relationship between the Nusselt Number and the Reynolds and Bingham Numbers
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Latin | |
| Bn | Bingham number |
| Br | Brinkman number |
| heat capacity, J/(kg·°C) | |
| D | inner diameter of pipe, m |
| L | pipe length, m |
| Nu | Nusselt number |
| Pe | Peclet number |
| Pr | Prandtl number |
| Re | Reynolds number |
| R | inner radius of pipe, m |
| Greek | |
| strain rate tensor, 1/s | |
| effective molecular viscosity, Pa·s | |
| plastic viscosity, Pa·s | |
| Λ | thermal conductivity, W/m·°C |
| ρ | density, kg/m3 |
| yield shear stress, Pa | |
| τ | shear stress, Pa |
References
- Barnes, H.A. The Yield Stress—A Review or ‘παντα ρει’−Everything Flows? J. Non-Newton. Fluid Mech. 1999, 81, 133–178. [Google Scholar] [CrossRef]
- Zhapbasbayev, U.K.; Ramazanova, G.I.; Bossinov, D.Z.; Kenzhaliyev, B.K. Flow and Heat Exchange Calculation of Waxy Oil in the Industrial Pipeline. Case Stud. Therm. Eng. 2021, 26, 101007. [Google Scholar] [CrossRef]
- Tugunov, P.I.; Novoselov, V.I. Transportation of Viscous Oil and Petroleum Products Through Pipelines; Nedra: Moscow, Russia, 1972. (In Russian) [Google Scholar]
- Aiyejina, A.; Chakrabarti, D.P.; Pilgrim, A.; Sastry, M.K.S. Wax formation in oil-pipelines: A critical review. Int. J. Multiph. Flow 2011, 37, 671–694. [Google Scholar] [CrossRef]
- Letelier, M.F.; Siginer, D.A.; Barrera, C.; González, A.; Boutaous, M. Forced convection in non-circular tubes with non-linear viscoelastic fluids including viscous dissipation. Int. J. Therm. Sci. 2020, 150, 106122. [Google Scholar] [CrossRef]
- Vradis, G.C.; Dougher, J.; Kumar, S. Entrance pipe flow and heat transfer for a Bingham plastic. Int. J. Heat Mass Transf. 1993, 36, 543–552. [Google Scholar] [CrossRef]
- Boutra, A.; Ragui, K.; Benkahla, Y.K.; Labsi, N. Mixed convection of a Bingham fluid in differentially heated square enclosure with partitions. Theor. Found. Chem. Eng. 2018, 52, 286–294. [Google Scholar] [CrossRef]
- Kefayati, G. Lattice Boltzmann method for natural convection of a Bingham fluid in a porous cavity. Phys. A Stat. Mech. Appl. 2019, 521, 146–172. [Google Scholar] [CrossRef]
- Coelho, P.M.; Poole, R.J. Heat transfer of Bingham fluids in an annular duct with viscous dissipation. Heat Transf. Eng. 2017, 39, 1749–1765. [Google Scholar] [CrossRef]
- Min, T.; Choi, H.G.; Yoo, J.Y.; Choi, H. Laminar convective heat transfer of a Bingham plastic in a circular pipe II. Numerical approach hydrodynamically developing flow and simultaneously developing flow. Int. J. Heat Mass Transfer. 1997, 41, 3689–3701. [Google Scholar] [CrossRef]
- Adnan, M.; Asadullah, U.; Khan, N.; Ahmed, S.T. Mohyud-Din, Analytical and numeri-cal investigation of thermal radiation effects on flow of viscous incompressible fluid with stretchable convergent/divergent channels. J. Mol. Liq. 2016, 224, 768–775. [Google Scholar] [CrossRef]
- Hermany, L.; Lorenzini, G.; Klein, R.; Zinani, F.; dos Santos, E.; Isoldi, L.; Rocha, L. Constructal design applied to elliptic tubes in convective heat transfer cross-flow of viscoplastic fluids. Int. J. Heat Mass Transf. 2018, 116, 1054–1063. [Google Scholar] [CrossRef]
- Sahu, K.C. Linear instability in a miscible core-annular flow of a Newtonian and a Bingham fluid. J. Non-Newton. Fluid Mech. 2019, 264, 159–169. [Google Scholar] [CrossRef]
- Kefayati, G.; Tang, H. MHD mixed convection of viscoplastic fluids in different aspect ratios of a lid-driven cavity using LBM. Int. J. Heat Mass Transf. 2018, 124, 344–367. [Google Scholar] [CrossRef]
- Kefayati, G.R.; Tang, H. Lattice Boltzmann simulation of viscoplastic fluids on natural convection in inclined enclosure with inner cold circular/elliptical cylinders (Part II: Two cylinders). Int. J. Heat Mass Transf. 2018, 123, 1163–1181. [Google Scholar] [CrossRef]
- Kefayati, G.; Tang, H. Lattice Boltzmann simulation of viscoplastic fluids on natural convection in inclined enclosure with inner cold circular/elliptical cylinders (Part III: Four cylinders). Int. J. Heat Mass Transf. 2018, 123, 1182–1203. [Google Scholar] [CrossRef]
- Kefayati, G.; Tang, H. Lattice Boltzmann simulation of viscoplastic fluids on natural convection in an inclined enclosure with inner cold circular/elliptical cylinders (Part I: One cylinder). Int. J. Heat Mass Transf. 2018, 123, 1138–1162. [Google Scholar] [CrossRef]
- Turan, O.; Chakraborty, N. The effects of bottom wall heating on mixed convection of yield stress fluids in cylindrical enclosures with a rotating end wall. Int. J. Heat Mass Transf. 2018, 121, 759–774. [Google Scholar] [CrossRef]
- Ragui, K.; Boutra, A.; Bennacer, R.; Benkahla, Y.K. Progress on numerical simulation of yield stress fluid flows (Part I): Correlating thermosolutal coefficients of Bingham plastics within a porous annulus of a circular shape. Int. J. Heat Mass Transf. 2018, 126, 72–94. [Google Scholar] [CrossRef]
- Kefayati, G. Double-diffusive natural convection and entropy generation of Bingham fluid in an inclined cavity. Int. J. Heat Mass Transf. 2018, 116, 762–812. [Google Scholar] [CrossRef]
- Hu, K.-X.; He, M.; Chen, Q.-S.; Liu, R. On the stability of thermocapillary convection of a Bingham fluid in an infinite liquid layer. Int. J. Heat Mass Transf. 2018, 122, 993–1002. [Google Scholar] [CrossRef]
- Coelho, P.; Pinho, F.; Oliveira, P. Fully developed forced convection of the Phan- Thien–Tanner fluid in ducts with a constant wall temperature. Int. J. Heat Mass Transf. 2002, 45, 1413–1423. [Google Scholar] [CrossRef]
- Fusi, L.; Farina, A.; Rajagopal, K.R.; Vergori, L. Channel flows of shear-thinning fluids that mimic the mechanical response of a Bingham fluid. Int. J. Non-Linear Mech. 2022, 138, 103847. [Google Scholar] [CrossRef]
- Bingham, E.C. Fluidity and Plasticity; McGraw-Hill: New York, NY, USA, 1922. [Google Scholar]
- Wilkinson, W.L. Non-Newtonian fluids. In Fluid Mechanics, Mixing and Heat Transfer; Pergamon Press: London, UK, 1960. [Google Scholar]
- Klimov, D.M.; Petrov, A.G.; Georgievsky, D.V. Viscoplastic Flows: Dynamic Chaos, Stability and Mixing; Publishing House Nauka: Moscow, Russia, 2005. (In Russian) [Google Scholar]
- Zhapbasbayev, U.K.; Bekibayev, T.T.; Pakhomov, M.A.; Ramazanova, G.I. Numerical Modeling of Non-Isothermal Laminar Flow and Heat Transfer of Paraffinic Oil with Yield Stress in a Pipe. Energies 2024, 17, 2080. [Google Scholar] [CrossRef]
- Papanastasiou, T.C. Flows of materials with yield. J. Rheol. 1987, 31, 385–404. [Google Scholar] [CrossRef]
- Vinay, G.; Wachs, A.; Agassant, J.-F. Numerical simulation of non-isothermal viscoplastic waxy crude oil flows. J. Non-Newton. Fluid Mech. 2005, 128, 144–162. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhapbasbayev, U.; Bekibayev, T.; Pakhomov, M.; Ramazanova, G. Heat Transfer of Crude Waxy Oil with Yield Stress in a Pipe. Energies 2024, 17, 4687. https://doi.org/10.3390/en17184687
Zhapbasbayev U, Bekibayev T, Pakhomov M, Ramazanova G. Heat Transfer of Crude Waxy Oil with Yield Stress in a Pipe. Energies. 2024; 17(18):4687. https://doi.org/10.3390/en17184687
Chicago/Turabian StyleZhapbasbayev, Uzak, Timur Bekibayev, Maksim Pakhomov, and Gaukhar Ramazanova. 2024. "Heat Transfer of Crude Waxy Oil with Yield Stress in a Pipe" Energies 17, no. 18: 4687. https://doi.org/10.3390/en17184687
APA StyleZhapbasbayev, U., Bekibayev, T., Pakhomov, M., & Ramazanova, G. (2024). Heat Transfer of Crude Waxy Oil with Yield Stress in a Pipe. Energies, 17(18), 4687. https://doi.org/10.3390/en17184687







