Abstract
This paper presents a numerical study of natural convection in an annular cavity filled with a hybrid nanofluid under the influence of a magnetic field. This study is significant for applications requiring enhanced thermal management, such as in heat exchangers, electronics cooling, and energy systems. The inner cylinder, equipped with fins and subjected to uniform volumetric heat generation, contrasts with the adiabatic outer cylinder. This study aims to investigate how different nanoparticle combinations (Fe3O4 with Cu, Ag, and Al2O3) and varying Hartmann and Rayleigh numbers impact heat transfer efficiency. The finite volume method is employed to solve the governing equations, with simulations conducted using Fluent 6.3.26. Parameters such as volume fraction (ϕ2 = 0.001, 0.004, 0.006), Hartmann number (0 ≤ Ha ≤ 100), Rayleigh number (3 × 103 ≤ Ra ≤ 2.4 × 104), and fin number (N = 0, 2, 4, 6, 8) are analyzed. Streamlines, isotherms, and induced magnetic field contours are utilized to assess flow structure and heat transfer. The results reveal that increasing the Rayleigh number and magnetic field enhances heat transfer, while the presence of fins, especially at N = 2, may inhibit convection currents and reduce heat transfer efficiency. These findings provide valuable insights into optimizing nanofluid-based cooling systems and highlight the trade-offs in incorporating fins in thermal management designs.
1. Introduction
Hybrid nanofluid has emerged as a promising heat transfer medium due to its enhanced heat transfer capabilities compared to conventional fluids.
These nanofluids are carefully engineered mixtures in which nanoscale solid particles are meticulously dispersed in a base fluid, typically water, oil, or ethylene glycol. These particles can be composed of a wide range of materials, including metals such as copper, silver, or gold; non-metals like carbon nanotubes or graphene oxide; and metal oxides such as titanium dioxide or alumina. The primary goal of nanofluid formulation is to improve the thermal and physical properties of the base fluid. As a result, nanofluids are widely used in heat transfer applications, including the cooling of electronics, automotive engines, and industrial processes, as well as in solar thermal systems and various manufacturing processes where precise temperature control and efficient heat transfer are crucial. They also find applications in the automotive and aerospace industries.
Since the introduction of the concept by Choi and Eastman [1], who suggested enhancing a base fluid’s thermal conductivity by dispersing nanoparticles, the field has seen significant advancements. Research has focused on understanding the behavior of nanofluids in various configurations and their role in enhancing heat transfer [2,3,4,5].
Table 1 [6,7,8,9,10,11,12,13,14] summarizes nanoparticles, base fluid, and improvement of thermal conductivity reported by researchers and scientists in recent studies.

Table 1.
Literature review of improvement of thermal conductivity.
Recent research has increasingly focused on hybrid nanofluids, which are fluids where nanoparticles of varying compositions are combined to create a hybrid system. These hybrid nanofluids are particularly useful in heat transfer applications requiring high thermal conductivity. Over the past few decades, extensive numerical and experimental research has been conducted on hybrid nanofluids, encompassing their preparation, characterization, modeling, convective heat transfer, and various applications. For instance, Esfe et al. [15] experimentally investigated the thermal conductivity of CNTs-Al2O3/water nanofluid using a statistical approach, revealing that the thermal conductivity of the nanofluid increases with both temperature and solid volume fraction.
Numerous experimental and numerical studies have been conducted to investigate the natural convection of hybrid nanofluids in enclosures, focusing on parameters such as nanoparticle concentration, fluid properties, and enclosure geometry, all of which significantly impact heat transfer performance. For instance, Esfe et al. [16] experimentally examined the thermal conductivity and dynamic viscosity of Ag-MgO/water hybrid nanofluid. Scott et al. [17] performed detailed measurements and analyses of temperature distributions and flow patterns within a square cavity containing Al2O3-MWCNT/water hybrid nanofluids. Similarly, Al-Maliki et al. [18] investigated heat transfer phenomena in an inclined rectangular cavity filled with (CuO-Al2O3/water) hybrid nanofluids, focusing on the combined effects of inclined orientation, hybrid nanofluid composition, and PCM integration on heat transfer performance. Through experimental work, Zadkhast et al. [19] developed a novel correlation to estimate the thermal conductivity of MWCNT-CuO/water hybrid nanofluid. In another study, Afrand et al. [20] investigated the effect of temperature and nanoparticle concentration on the rheological behavior of Fe3O4-Ag/EG hybrid nanofluids. Giwa et al. [21] explored the thermoconvection performance of Al2O3-MWCNT hybrid nanofluids at various nanoparticle concentrations within a differentially heated square cavity, aiming to understand how hybrid nanoparticle mixtures influence convective heat transfer under different thermal boundary conditions. Additionally, an extensive literature review by Scott et al. [22] summarized recent research and discussed strategies for improving heat transfer with hybrid nanofluids in cavities. Many studies have also been conducted on natural convection of hybrid nanofluids in complex geometries [23,24,25].
In parallel, other researchers have focused on Magnetohydrodynamics (MHD). For instance, Nepal Chandra Roy [26] investigated (MHD) natural convection of hybrid nanofluids in a multi-heat source enclosure. This study utilized mathematical modeling and numerical simulations with the finite difference method to analyze the behavior of hybrid nanofluids under the influence of magnetic fields, fluid flow, and heat transfer. The results offered valuable insights into optimizing multi-source thermal management systems using hybrid nanofluids and (MHD) effects. Another study, led by Abdel-Nour and colleagues [27], examined (MHD) natural convection of an Al2O3-Cu/water hybrid nanofluid in a porous enclosure with sinusoidally varying boundary temperatures. The Navier–Stokes equations were discretized using the Galerkin finite element method, with a particular focus on analyzing entropy generation as a measure of irreversibility within the system. Mansour et al. [28] conducted a numerical investigation on the effects of heat sources and sinks on entropy generation and (MHD) natural convection in a square porous cavity filled with Al2O3-Cu/water hybrid nanofluid. The study employed the finite difference method to solve the dimensionless partial differential equations governing the problem. The results were analyzed in terms of entropy production, considering the Hartmann number, nanoparticle volume fraction, and the geometrical parameters of the cavity. Similarly, Rashad et al. [29] numerically studied (MHD) natural convection in a triangular cavity filled with Al2O3-Cu/water hybrid nanofluid and subjected to constant heat flux. Their research focused on the impact of localized heating from below and internal heat generation on fluid flow and heat transfer phenomena. The governing equations, formulated in terms of the stream function and vorticity, were solved using the finite difference method. The results indicated that under conditions of low natural convection, increasing the nanoparticle volume fraction significantly enhances heat transfer. Furthermore, a wealth of valuable information on natural convection can be found in the works of Roy et al. [30] and Majeed et al. [31,32].
Furthermore, the effects of Fe3O4 nanoparticles on hydrothermal processes under a magnetic field have been investigated in several studies [33,34,35,36,37].
The primary objective of this study is to simulate natural convection in an annular cavity filled with hybrid nanofluids under the influence of a magnetic field. This configuration is relevant to applications such as heat exchangers, electronic cooling, and solar energy systems. The aim of the study is to investigate how the interaction between hybrid nanoparticles, fins, and magnetic fields affects the natural convection and heat transfer performance within the cavity. By analyzing parameters such as the Hartmann number, the number of fins, and the volume fraction of nanoparticles, this research will provide insights into the optimization of the use of hybrid nanofluids in practical applications where magnetic fields and complex geometries are crucial.
2. Physical Model
Figure 1 shows a schematic view of a 2D annular cavity equipped with fins and filled with hybrid nanofluid. It is a cross-section of a heat exchanger with longitudinal fins. As can be seen in this figure, the inner cylinder Di is submitted to volumetric heat generation. The outer cylinder Do is maintained adiabatic with a magnetic field applied in a horizontal direction. The aspect ratio AR is defined as (AR = D0/Di = 3), and the fin dimensions are (0.0139, 0.02).
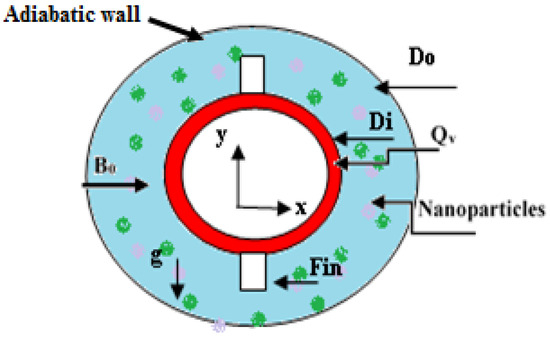
Figure 1.
Schematic of the annular cavity.
The heat transfer takes place from the heated wall of the inner diameter to the fluid filling the cavity initially at ambient temperature T0 = 298 K.
The fluid enclosed between the inner and outer cylinders is water-based and contains various nanoparticle combinations of Fe3O4, Cu, Ag, and Al2O3 that are in thermal equilibrium. Nanoparticles have spherical and uniform shapes. Thermophysical properties of the fluid and nanoparticles are defined in the following Table 2.

Table 2.
Water and nanoparticles thermophysical properties [30,34].
3. Governing Equations
The flow under consideration is Newtonian, incompressible, steady, and laminar. The dimensional governing equations under Boussinesq’s approximation are continuity, momentum, and the energy equations in the two-dimensional Cartesian coordinate system for the case of a single-phase fluid, are as follows [38]:
- Continuity equation
- Momentum equations
x-Component
y-Component
- Energy equation
- Energy equation for solid wall
Qv is the uniform volume heat generation imposed on the inner cylinder.
The adopted boundary conditions are as follows:
The fluid is initially at ambient temperature To = 298 K;
The no-slip boundary condition is applied at walls: (u = 0, v = 0);
An adiabatic condition for the outer cylinder D0.
The conduction heat-flux continuity is considered in the solid–fluid interface.
The thermophysical properties of mono- and hybrid nanofluids are assumed in accordance with the Tiwari–Das model and are presented as follows [30] (Table 3):

Table 3.
Thermophysical characteristics of mono and hybrid nanofluid [30].
Data acquisitions
The key parameters controlling the phenomenology of natural convection appear to be as follows:
The Rayleigh number: ;
The Prandtl number: ;
The Hartmann number: ;
The Nusselt number: .
h is the heat transfer coefficient defined as .
: is the average surface heat flux.
Tw and Tb are, respectively, the mean temperature of the wall and the mean bulk temperature of the fluid calculated as follows: , .
The Nusselt number becomes: .
4. Numerical Procedure
The finite volume method is used to solve the governing equations using the commercially available software Fluent 6.3.26. The Simple algorithm proposed by Patankar [39] is used for coupling between pressure and velocity with the third-order MUSCL scheme, which improves on the second-order scheme in terms of more effective gradient resolution and less numerical diffusion. The convergence requirement for the iteration of a non-linear system is given by: .
Φk are u, v, *T, and p, k is the number of iterations. The steady-state computations are performed on a 64 GB RAM8.00 Go, 2.5 GHz, Intel®, Core(TM) i5-3210 M CPU desktop computer. Six meshes were considered in order to study the effect of the mesh on the numerical solution. Table 4 presents the average Nusselt number Nuavg and le maximum temperature of the fluid in the annulus for pure water and Ra = 1.2 × 104. The grid size (22, 500) is found to meet the requirement of both the grid independence study and the computational time limits. Figure 2 illustrates the mesh representation (a) for the annulus without fins, (b) for the annulus with two fins, and (c) for the annulus with four fins.

Table 4.
Nuavg, Tmax, deviation Nuavg% and Tmax% for various grid resolution, N = 2, Ra = 1.2 × 104.
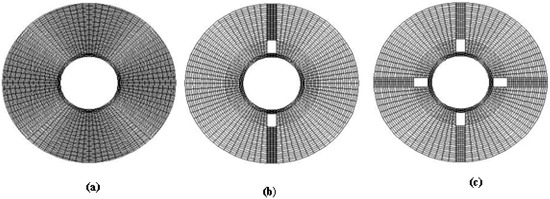
Figure 2.
Mesh of the annulus: (a) annulus without fins, (b) annulus with N = 2 fins, (c) annulus with N = 4 fins.
The quantitative results are compared with those of Vahl-Davis et al. [40] and Kumar [41] for an annular vertical cylinder with the geometric parameters (A: aspect ratio and λ = re/ri: radius ratio). The results of Table 5 show that with a percentage between 8% and 9%, our results are in agreement with those of the literature. Also, the present study is compared with other works reported in [42,43], as seen in Figure 3 and Figure 4.

Table 5.
Comparison of for annular cylinder (A = 1, λ = 1).
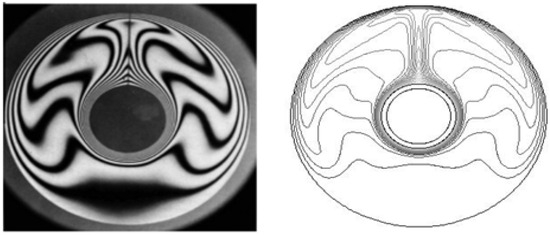
Figure 3.
Comparison of the isotherms between the present study and the experimental study carried out by Grigull and Hauf [42].
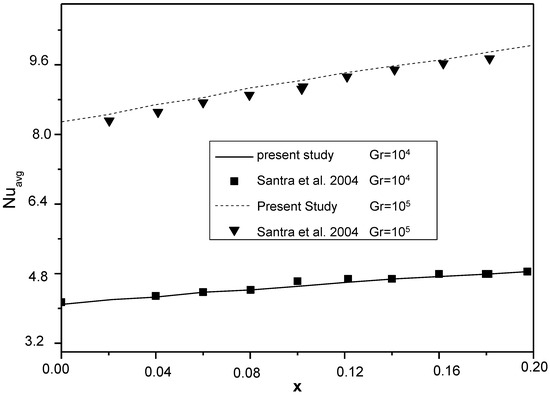
Figure 4.
Comparison of the Nusselt number between the present study and results obtained by Santra et al. [43].
5. Results and Discussion
The focus of this section is on natural convection in a finned annular cavity filled with hybrid nanofluid. The base fluid is water with a Prandtl number Pr = 5.63, containing a combination of nanoparticles; the Fe3O4 with volume fraction ϕ1 = 0.2% mixed with Al2O3; and Cu or Ag with volume fraction ϕ2 = 0.1%, 0.4%, and 0.6%. The numerical results are presented in the form of isotherms, stream function, velocity contours, and average Nusselt number distribution for different Hartmann numbers (0 ≤ Ha ≤ 100), Rayleigh numbers (3 × 103 ≤ Ra ≤ 2.4 × 104), and the number of fins (N = 2, 4, 6, 8).
5.1. Hartmann Number
The effect of the Hartmann number (Ha = 0, 25, 55, 100) on the streamlines, velocity contours, and isotherms is shown in Figure 5, Figure 6 and Figure 7 for the three mixtures of hybrid nanofluid. Firstly, it is shown that Ha has no effect on the velocity and on the temperature when Ha is equal to zero. The streamlines are smooth, indicating stable natural convection. The temperature distribution is uniform with smooth gradients. The isotherms are relatively dense, indicating a high rate of heat transfer and moderate velocities driven purely by temperature differences. As the Hartmann number increases, the effect of the Lorentz force in the annulus becomes more pronounced for the three mixtures, indicating a suppression of fluid motion and the formation of recirculation zones by a slight decrease in temperature and increase in velocity fields. The isotherms in Figure 5, Figure 6 and Figure 7 show that with increasing Ha, the temperature contours become more spaced out, indicating a thicker thermal boundary layer. Each nanoparticle type (Cu, Ag, Al2O3) responds differently to the increasing Hartmann number. The differences between the nanofluids Ag, Cu, and Al2O3 are primarily due to their varying thermal conductivities. It is shown that the isotherms become denser near heated surfaces, showing effective heat transfer maintained or even enhanced. The velocity contours may show localized increases in velocity gradients in specific regions due to the complex interaction between the magnetic field and fluid flow, aiding in maintaining adequate heat transfer rates.
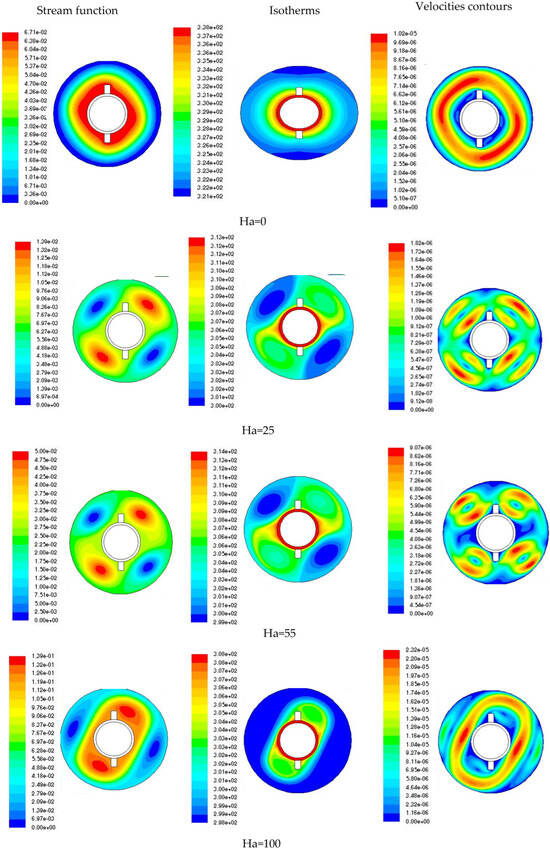
Figure 5.
Variation of the stream function (m2/s), Temperature (K) of velocities (m/s) with Hartmann number for Ag nanoparticles, ϕ2 = 0.004.
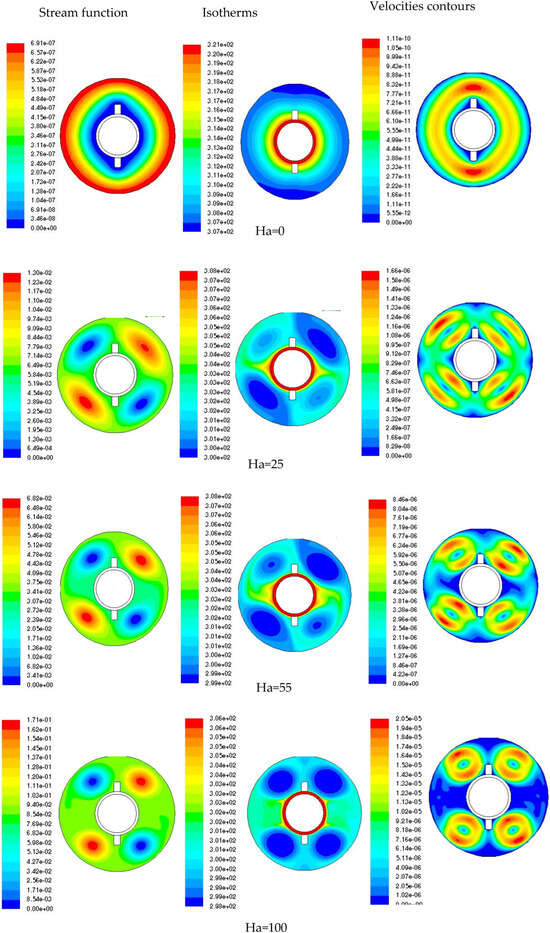
Figure 6.
Variation of the stream function (m2/s), Temperature (K) of velocities (m/s) with Hartmann number for Cu nanoparticles, ϕ2 = 0.004.
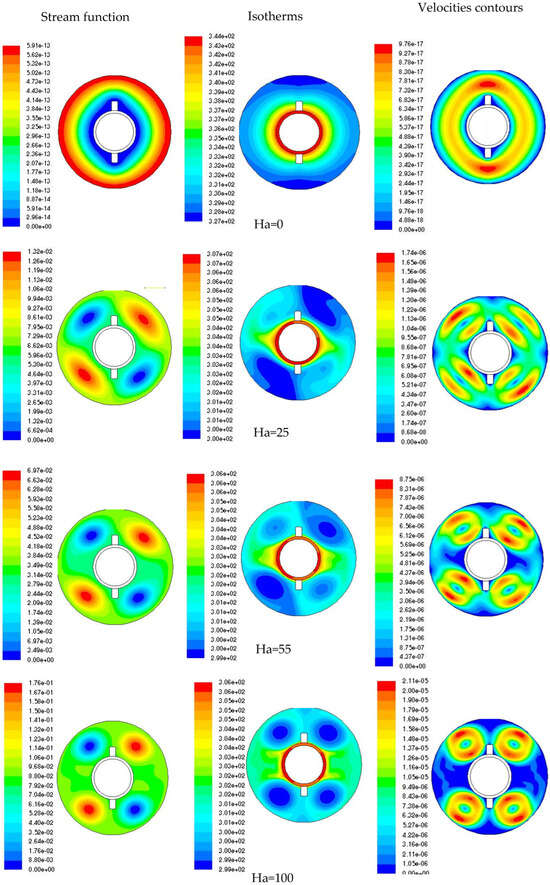
Figure 7.
Variation of the stream function (m2/s), Temperature (K) of velocities (m/s) with Hartmann number for Al2O3 nanoparticles, ϕ2 = 0.004.
Copper, with the highest thermal conductivity, shows the most significant reduction in temperature gradients as Ha increases, making it the most effective at achieving thermal uniformity in the presence of a magnetic field. The extension of these figures allows us to see the full effect of the magnetic field strength on the temperature profile along a vertical line in the annular cavity in Figure 8. As it is seen in this figure, in the absence of a magnetic field (Ha = 0), natural convection dominates, leading to a more significant temperature gradient. For the Fe3O4-Cu and Fe3O4-Ag mixtures, Figure 8a,b show that the temperature at the center line of the cavity decreases significantly with increasing Ha. This trend suggests that the magnetic field has a significant effect on the heat distribution, probably due to the high thermal conductivity of Cu and Ag, which enhances the effect of suppressed convection. On the other hand, the temperature profile of the Fe3O4-Al2O3 mixture shows the least variation with Ha, reflecting the lowest thermal conductivity among the three nanofluids.
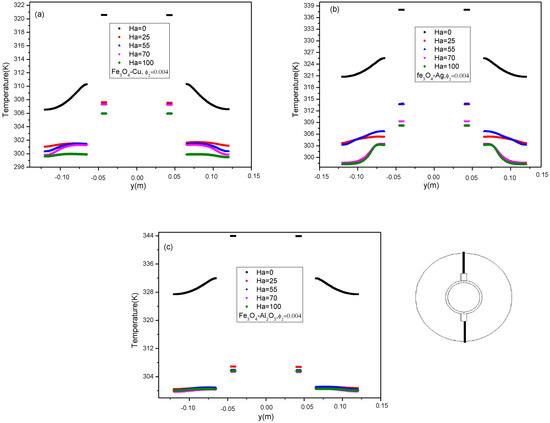
Figure 8.
Variation of the Temperature (K) in the center line of the cavity with Hartmann number for, ϕ2 = 0.004, (a) Fe3O4-Cu, (b) Fe3O4-Ag, (c) Fe3O4-Al2O3.
The induced magnetic field is a response to the movement of the fluid within the applied magnetic field; their interaction results in the Lorentz force, which influences flow patterns and heat transfer. Figure 9, Figure 10 and Figure 11 illustrate the contours of the induced magnetic field B for different Hartmann numbers (Ha = 25, 55, 70, and 100) for the three mixtures cited above. From these figures, it is seen that, as the Hartmann number increases, the influence of the induced magnetic field on the fluid flow becomes more pronounced. This results in more complex and intense convection patterns, with stronger gradients and localized high-intensity areas in the contours of the induced magnetic field B. The variations in the contours reflect the distinct thermal and magnetic properties of the nanoparticles used, affecting the natural convection and magnetic field distribution uniquely for each mixture.
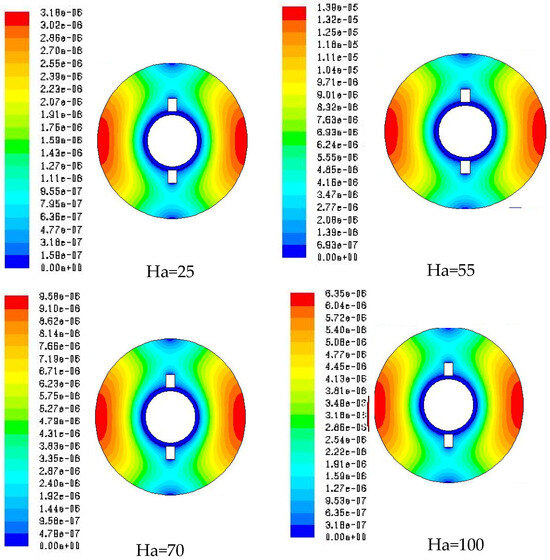
Figure 9.
Variation of the induced magnetic field B (T) with the Hartmann number for the mixture Fe3O4-Cu, ϕ2 = 0.004.
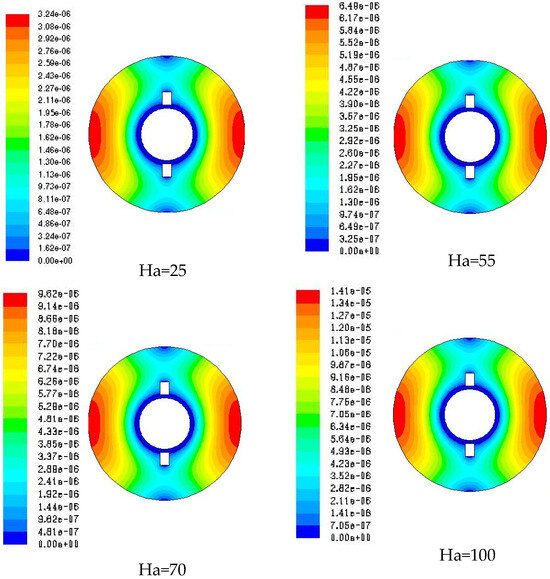
Figure 10.
Variation of the induced magnetic field B (T) with the Hartmann number for the mixture Fe3O4-Ag, ϕ2 = 0.004.
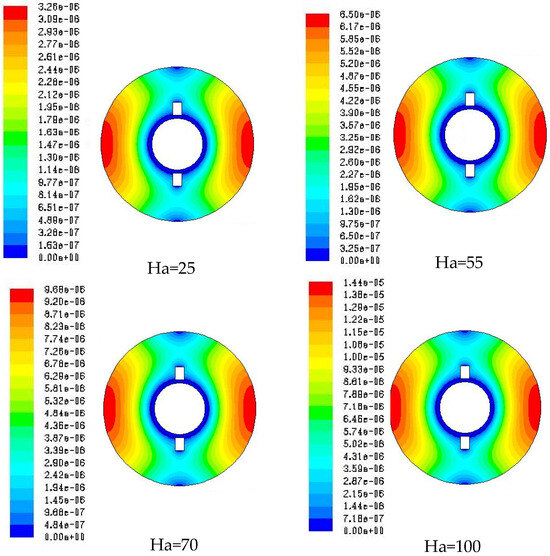
Figure 11.
Variation of the induced magnetic field B (T) with the Hartmann number for the mixture Fe3O4-Al2O3, ϕ2 = 0.004.
For a better understanding of the phenomenon, Figure 12 depicts the variations in the induced magnetic field B along a vertical line in the cavity for the three mixtures of hybrid nanofluids at various Hartmann numbers (Ha). The curves indicate that adding different nanoparticles significantly alters the distribution of the induced magnetic field in the cavity. Increasing the Hartmann number amplifies these effects, making the variations more pronounced. The differences among the mixtures highlight the importance of the specific properties of the nanoparticles in natural convection and the distribution of the magnetic field. The percentage differences between the induced magnetic field B values at Ha = 100 and Ha = 70 for Fe3O4-Ag, Fe3O4-Cu, and Fe3O4-Al2O3 mixtures is around 18.18% for the Fe3O4-Cu hybrid nanofluid and around 15.38% for both Fe3O4-Ag and Fe3O4-Al2O3 hybrid nanofluid.
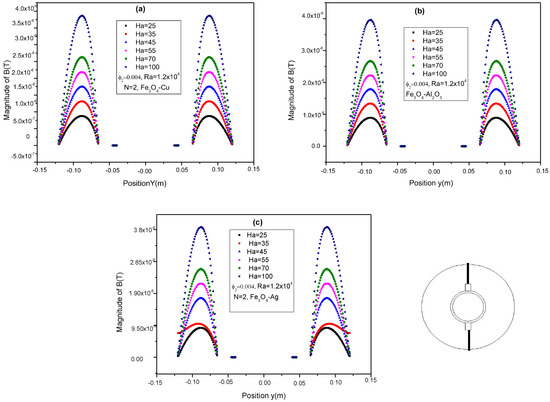
Figure 12.
Variation of the profiles of induced magnetic field B (T) in the center line of the cavity at different Hartmann number for ϕ2 = 0.004 and for the three mixtures: (a) Fe3O4-Cu, (b) Fe3O4-Al2O3, (c) Fe3O4-Ag.
Figure 13 depicts the variation in the average Nusselt number with the magnetic parameter Ha for the three different mixtures at different nanoparticle volume fractions (ϕ2 = 0.001, 0.004, and 0.006). It is shown that the Nusselt number increases not only with Ha but also with the nanoparticle volume fraction ϕ2. A higher concentration of nanoparticles leads to a greater increase in thermal conductivity, thereby improving the fluid’s ability to conduct heat. This effect is particularly important in regions where the magnetic field suppresses fluid motion. The enhanced conduction compensates for the reduced convection.
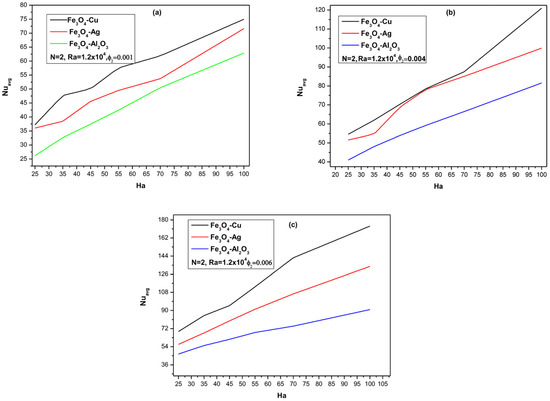
Figure 13.
Variation in the Nusselt number with the Hartmann number and nanoparticles volume fraction (a) ϕ2 = 0.001, (b) ϕ2 = 0.004, (c) ϕ2 = 0.006.
The magnetic properties of nanoparticles such as Fe3O4 can interact with the applied magnetic field and affect the overall flow and heat transfer. This interaction can lead to changes in the velocity field, as seen in Figure 5, Figure 6 and Figure 8, and may contribute to localized improvements in heat transfer.
From these results, the observation that the Nusselt number Nu increases with the Hartmann number Ha despite the suppression of fluid motion and a shift toward conduction-dominated heat transfer might seem contradictory at first glance. However, this phenomenon can be understood by considering several key factors:
- The thermal conductivity of the nanoparticles is higher than the base fluid, allowing the fluid to transfer heat more efficiently. This increase in thermal conductivity reduces the thermal resistance of the fluid, improving heat transfer even when convective currents are suppressed by the magnetic field—a higher Hartmann number.
- The inclusion of nanoparticles can thin the thermal boundary layer or maintain a steep temperature gradient across it, increasing the overall heat transfer rate.
Silver (Ag) and copper (Cu) typically possess higher thermal conductivity than aluminum oxide (Al2O3). Consequently, copper nanoparticles in the Fe3O4-Cu/water hybrid nanofluid can transfer heat to the fluid more efficiently. Compared to silver or alumina nanoparticles, copper nanoparticles may interact differently with the fluid.
The relationship between the thermal conductivity ratio khnf/kf and the Hartmann number Ha is an essential aspect of understanding how magnetic fields influence the thermal performance of nanofluids. Figure 14 illustrates the variation in the thermal conductivity ratio (khnf/kf) with Ha for different concentrations ϕ2. The three specific concentrations of ϕ2 are 0.001, 0.004, and 0.006. In all figures, an increase in Ha generally leads to an increase in the thermal conductivity ratio khnf/kf. This indicates that applying a magnetic field enhances the thermal conductivity of the hybrid nanofluid relative to the base fluid. Contrary to what might be expected, the thermal conductivity ratio (khnf/kf) decreases as the concentration of the second nanoparticles ϕ2 increases from 0.001 to 0.006 for all types of mixtures.
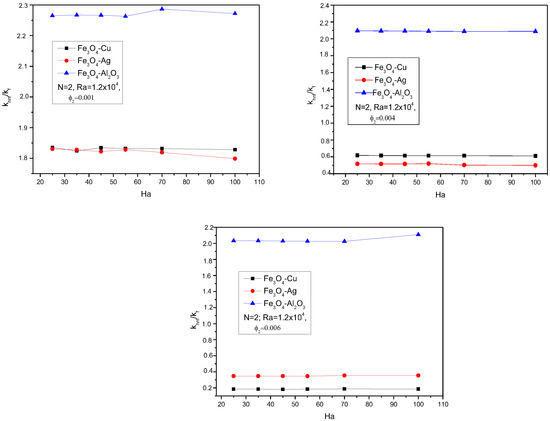
Figure 14.
Variation of the thermal conductivity ratio with Ha, for ϕ2 = 0.001, 0.004 and 0.006.
For ϕ2 = 0.001, 0.004 and 0.006, the thermal conductivity ratio starts at a higher value and increases with Ha. Fe3O4-Cu and Fe3O4-Ag nanofluids show a higher increase compared to Fe3O4-Al2O3.
5.2. Nanoparticles Concentration
As the concentration of nanoparticles in the hybrid nanofluid increases, this can lead to an increase in the average Nusselt number Nuavg. Figure 15 shows how the Nuavg varies with the concentration ϕ2. The analysis is conducted for a Rayleigh number Ra of 1.2 × 104 and a Hartmann number Ha of 35. For the three mixtures, Nuavg increases with an increase in nanoparticle concentration ϕ2. Increasing nanoparticle concentration in a nanofluid generally leads to enhancements in thermal conductivity and convective heat transfer, which contribute to higher Nusselt numbers [29]. The increase in Nusselt number with higher nanoparticle concentration is primarily due to the improved thermal conductivity provided by the nanoparticles. The specific type of nanoparticle used (Fe3O4 combined with Cu, Ag, or Al2O3) influences the extent of this improvement, with Fe3O4-Cu providing the most significant improvement.
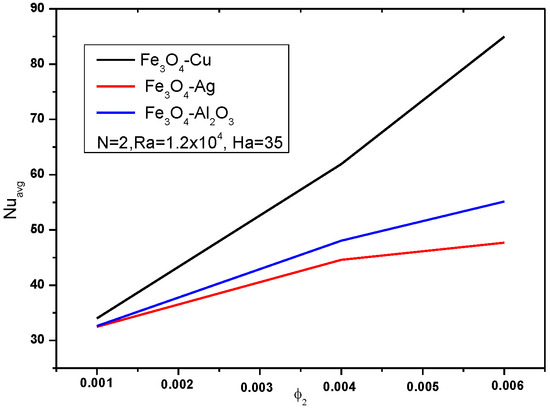
Figure 15.
Variation of the average Nusselt number Nuavg with the nanoparticles concentration ϕ2.
Among the three hybrid nanofluids, Fe3O4-Cu shows the highest enhancement in Nusselt number with increasing ϕ2, followed by Fe3O4-Ag and then Fe3O4-Al2O3. This reflects the inherent differences in the thermal conductivities and heat transfer enhancement capabilities of the Cu, Ag, and Al2O3 nanoparticles.
5.3. Rayleigh Number
The parameter of natural convection is the Rayleigh number, which is defined as a function of volumetric heat generation and the thickness of the inner diameter.
Figure 16 represents the variation in the rate of heat transfer with the Rayleigh number Ra for the three hybrid nanofluids at a fixed nanoparticles concentration ϕ2 = 0.004, N = 2, and a Hartmann number Ha = 35. The Rayleigh number represents the influence of buoyancy forces on natural convection. As expected, Nuavg increases with Ra for all nanofluids, indicating enhanced convective heat transfer with stronger buoyancy effects. The difference in Nuavg among the three nanofluids becomes more pronounced as the Rayleigh number increases, suggesting that the effectiveness of these nanofluids in enhancing natural convection is more significant at higher Ra values. Similar to Figure 15, Fe3O4-Cu shows the highest Nuavg across the range of Rayleigh numbers, followed by Fe3O4-Ag, and then Fe3O4-Al2O3. This consistent trend further reinforces the superior heat transfer capability of the Cu-based nanofluid.
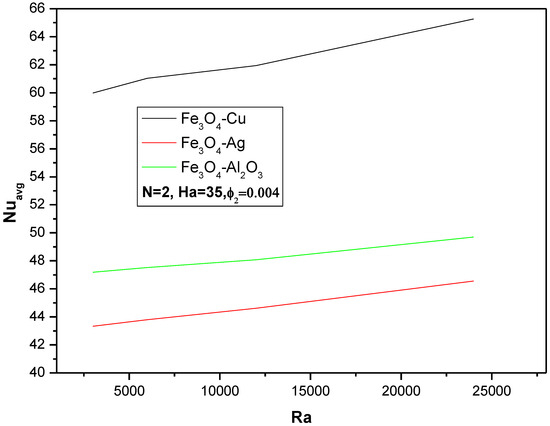
Figure 16.
Variation of the average Nusselt number Nuavg with the Rayleigh number for N = 2, ϕ2 = 0.004 and Ha = 35.
5.4. Fin Number
Figure 17 depicts the effect of varying the number of fins (N = 0, 2, 4, 6) on the temperature distribution on the left, the velocity field in the middle, and the induced magnetic field on the right inside the cavity filled with Fe3O4-Cu hybrid nanofluid under a magnetic field characterized by Ha = 55 at Ra = 1.2 × 104 and ϕ2 = 0.004. This figure shows a noticeable reduction in the temperature within the cavity as fin numbers increase. The fins improve heat transfer by increasing the surface area available for conduction, allowing for more efficient cooling. The increased number of fins disrupts the thermal boundary layer, resulting in a more uniform temperature distribution and preventing the formation of hot spots within the fluid. The velocity of the fluid is also affected by the number of fins. With more fins, the flow becomes more constrained, resulting in a reduction in velocity. This is because the fins act as barriers, restricting the free movement of the fluid, especially near the walls where the boundary layers form. The magnetic field further suppresses fluid motion due to the Lorentz force, which becomes more pronounced as the number of fins increases. On the other hand, the induced magnetic field tends to become stronger as the number of fins increases. This can be attributed to the interaction between the magnetic field and the fluid flow, where the suppression of the velocity by both the fins and the magnetic field increases the concentration of the magnetic field distribution.
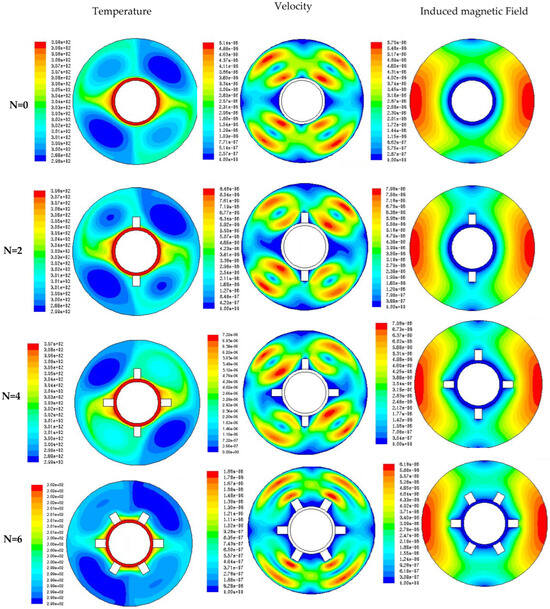
Figure 17.
Effect of the fin number on temperature, velocity and magnetic field Ra = 1.2 × 104, Fe3O4-Cu nanohybrid at ϕ2 = 0.004, Ha = 55.
Table 6 presents the variation in the average Nusselt number with different nanoparticle concentrations and fin numbers under a magnetic field. As shown in this table, for each nanoparticle type Fe3O4-Cu, Fe3O4-Ag, and Fe3O4-Al2O3, Nuavg tends to decrease as the number of fins N increases. This indicates that the addition of more fins generally results in a reduction in heat transfer efficiency. The reduction could be due to the increased obstruction to fluid flow within the cavity, which reduces the convective currents responsible for heat transfer. Higher concentrations of nanoparticles (ϕ2 = 0.006) typically result in higher Nusselt numbers compared to lower concentrations (ϕ2 = 0.001). This effect is more pronounced when the number of fins is lower, indicating that the improvement in thermal conductivity due to the nanoparticles is more effective when the number of fins is lower. Among the mixtures, Fe3O4-Cu has the highest Nusselt numbers over all fin numbers. This suggests that this combination is the most effective in improving heat transfer within the cavity. This aligns with the decrease in Nusselt number observed in Table 6. Table 7 presents the percentage decrease (PD%) across various fin numbers N and the concentrations ϕ2. The percentage decrease in the average heat transfer rate (PD%) for different nanoparticle types compared to the baseline case of N = 0 (no fins) is calculated from the formula cited below.

Table 6.
Variation in the Nusselt number with the nanoparticles concentration and the fin numbers for Ha = 55, Ra = 1.2 × 104.

Table 7.
Percentage decrease in the Nusselt PD% for each fin number for Ha = 55, Ra = 1.2 × 104.
It is clear from these values that introducing fins and nanoparticles actually leads to a decrease in Nuavg compared to the baseline case without fins (N = 0). The presence of nanoparticles may alter the thermal boundary layer in such a way as to reduce the effectiveness of the fins. As can be seen in this table, in the case of the mixture Fe3O4-Cu, for ϕ2 = 0.001 and N = 8, PD% is around 60.93%, 60.01% for Fe3O4-Ag, and 65.078% for Fe3O4- Al2O3. Regarding N = 6 and the mixture Fe3O4-Ag, the PD% is around 49.84% and 53.36%, respectively, for ϕ2 = 0.001 and ϕ2 = 0.006. We can say that at higher concentrations, nanoparticles may agglomerate. This reduces their surface area and thermal conductivity. This may counteract the benefits of the additional fin, resulting in a net reduction in heat transfer. In conclusion, in engineering applications, simply adding fins or nanoparticles does not always guarantee enhanced performance.
6. Conclusions
This article presents a 2D numerical study on natural convection in an annular cavity filled with a hybrid nanofluid under the influence of a magnetic field. The geometry analyzed for the cavity represents a cross-section of a heat exchanger equipped with longitudinal fins. The inner cylinder is subjected to uniform volumetric heat generation, while the outer cylinder is kept adiabatic, subjected to uniform volumetric heat generation, while the outer cylinder is kept adiabatic. The objective of this study was to analyze the flow structure and quantify the heat transfer rate within the annular cavity, while also evaluating the effect of nanoparticles under the action of the magnetic field. To achieve this, a single-phase model was used to consider the following particle mixtures: Fe3O4-Cu, Fe3O4-Ag, and Fe3O4-Al2O3, taking into account key parameters such as nanoparticle concentration, ϕ2; Hartmann number, Ha; Rayleigh number, Ra; and the number of fins, N. The results of this study revealed the following:
- ➢
- As the Hartmann number increases, temperature decreases while velocity increases, indicating a stronger magnetic influence that intensifies convective currents. Each type of nanoparticle (Cu, Ag, Al2O3) reacts differently to this increase, with Cu nanoparticles appearing to be the most sensitive to magnetic fields. The Nusselt number and the thermal conductivity ratio also increase with the rise in Hartmann number, nanoparticle concentration, and Rayleigh number, leading to an improvement in heat transfer rate.
- ➢
- The addition of fins up to N = 2 can slow down natural convection currents, thereby reducing heat transfer efficiency. A configuration with two fins (N = 2) might therefore be the most suitable for this study. Thus, the magnetic field not only influences the contribution of nanoparticles to heat transfer but can also enhance it.
Finally, as a perspective and continuation of this study, experimental work could be carried out to validate the numerical results. This would involve constructing a physical model of the annular cavity with hybrid nanofluids on the one hand and, on the other, measuring heat transfer rates under different magnetic field intensities. Furthermore, examining the influence of different orientations and intensities of the magnetic field on heat transfer and fluid flow could provide deeper insights for optimizing magnetic control in practical applications. We also recommend that future studies incorporate multiphase models to better understand the effects of nanoparticles under more realistic conditions.
Author Contributions
Methodology, S.B.; software, S.B.; formal analysis, A.B.; investigation, S.A.; writing—original draft, S.Z.; project administration, C.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| A | Cross section area of the flow (m2) |
| B0 | Magnetic field (Tesla) |
| Cp | Specific heat (J/kg·K) |
| Dh | Hydraulic diameter (m) |
| Dio | Inner, outer diameter (m) |
| g | Gravitational acceleration (m/s2) |
| Ha | Hartmann number |
| kf, ks | Fluid and solid thermal conductivities (W/mK) |
| Nu | Nusselt number |
| P | Pressure (N/m2) |
| PD% | Percentage decrease (%) |
| Pr | Prandtl number |
| Ra | Rayleigh number |
| The average surface heat flux (W/m2) | |
| Qv | Volumic heat generation (W/m3) |
| T | Temperature (K) |
| u, v | Velocity component in x and y directions (m/s) |
| x, y | Caetesian coordinates (m) |
| β | Thermal expansion coefficient (1/K) |
| δ | gap of the annular space (m) |
| ϕ | Solid volume concentration |
| μ | Dynamic viscosity (Pa·s) |
| ν | Kinetic viscosity (m2/s) |
| ρ | Density (kg/m3) |
| α | Thermal diffusivity (m2/s) |
| σ | Electrical conductivity (S/m) |
| bf | Base fluid |
| f | Fluid |
| max | Maximum |
| hnf | Hybrid nanofluid |
| o | Reference |
| w | Wall |
References
- Choi, S.U. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Laboratory (ANL): Argonne, IL, USA, 1995. [Google Scholar]
- Choi, S.U.S.; Zhang, Z.G.; Yu, W.; Lockwood, F.E.; Grulke, E.A. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 2001, 79, 2252–2254. [Google Scholar] [CrossRef]
- Masuda, H.; Ebata, A.; Teramae, K. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Dispersion of Al2O3, SiO2 and TiO2 ultra-fine particles. Netsu Bussei 1993, 7, 227–233. [Google Scholar] [CrossRef]
- Benkherbache, S.; Si-Ameur, M. Numerical solution on mixed convection flow of nanofluid around a finned angular sector of heat sink. Comput. Therm. Sci. Int. J. 2023, 15, 23–44. [Google Scholar] [CrossRef]
- Santra, A.K.; Sen, S.; Chakraborty, N. Study of heat transfer due to laminar flow of copper–water nanofluid through two isothermally heated parallel plates. Int. J. Therm. Sci. 2009, 48, 391–400. [Google Scholar] [CrossRef]
- Garbadeen, I.; Sharifpur, M.; Slabber, J.; Meyer, J. Experimental study on natural convection of MWCNT-water nanofluids in a square enclosure. Int. Commun. Heat Mass Transf. 2017, 88, 1–8. [Google Scholar] [CrossRef]
- Ghodsinezhad, H.; Sharifpur, M.; Meyer, J.P. Experimental investigation on cavity flow natural convection of Al2O3–water nanofluids. Int. Commun. Heat Mass Transf. 2016, 76, 316–324. [Google Scholar] [CrossRef]
- Glory, J.; Bonetti, M.; Helezen, M.; Mayne-L’Hermite, M.; Reynaud, C. Thermal and electrical conductivities of water-based nanofluids prepared with long multiwalled carbon nanotubes. J. Appl. Phys. 2008, 103, 094309. [Google Scholar] [CrossRef]
- Pang, C.; Jung, J.-Y.; Lee, J.W.; Kang, Y.T. Thermal conductivity measurement of methanol-based nanofluids with Al2O3 and SiO2 nanoparticles. Int. J. Heat Mass Transf. 2012, 55, 5597–5602. [Google Scholar] [CrossRef]
- Sharifpur, M.; Solomon, A.B.; Ottermann, T.L.; Meyer, J.P. Optimum concentration of nanofluids for heat transfer enhancement under cavity flow natural convection with TiO2–Water. Int. Commun. Heat Mass Transf. 2018, 98, 297–303. [Google Scholar] [CrossRef]
- Sundar, L.S.; Singh, M.K.; Sousa, A.C. Investigation of thermal conductivity and viscosity of Fe3O4 nanofluid for heat transfer applications. Int. Commun. Heat Mass Transf. 2013, 44, 7–14. [Google Scholar] [CrossRef]
- Wei, B.; Zou, C.; Li, X. Experimental investigation on stability and thermal conductivity of diathermic oil based TiO2 nanofluids. Int. J. Heat Mass Transf. 2017, 104, 537–543. [Google Scholar] [CrossRef]
- Xie, H.; Wang, J.; Xi, T.; Liu, Y.; Ai, F.; Wu, Q. Thermal conductivity enhancement of suspensions containing nanosized alumina particles. J. Appl. Phys. 2002, 91, 4568–4572. [Google Scholar] [CrossRef]
- Yu, W.; Xie, H.; Li, Y.; Chen, L.; Wang, Q. Experimental investigation on the thermal transport properties of ethylene glycol based nanofluids containing low volume concentration diamond nanoparticles. Colloids Surf. A Physicochem. Eng. Asp. 2011, 380, 1–5. [Google Scholar] [CrossRef]
- Esfe, M.H.; Saedodin, S.; Biglari, M.; Rostamian, H. Experimental investigation of thermal conductivity of CNTs-Al2O3/water: A statistical approach. Int. Commun. Heat Mass Transf. 2015, 69, 29–33. [Google Scholar] [CrossRef]
- Esfe, M.H.; Arani, A.A.A.; Rezaie, M.; Yan, W.-M.; Karimipour, A. Experimental determination of thermal conductivity and dynamic viscosity of Ag–MgO/water hybrid nanofluid. Int. Commun. Heat Mass Transf. 2015, 66, 189–195. [Google Scholar] [CrossRef]
- Scott, T.O.; Ewim, D.R.; Eloka-Eboka, A.C. Experimental investigation of natural convection Al2O3-MWCNT/water hybrid nanofluids inside a square cavity. Exp. Heat Transf. 2024, 37, 294–312. [Google Scholar] [CrossRef]
- Al-Maliki, M.; Al-Farhany, K.; Sarris, I.E. Heat transfer in an inclined rectangular cavity filled with hybrid nanofluid attached to a vertical heated wall integrated with PCM: An experimental study. Symmetry 2022, 14, 2181. [Google Scholar] [CrossRef]
- Zadkhast, M.; Toghraie, D.; Karimipour, A. Developing a new correlation to estimate the thermal conductivity of MWCNT-CuO/water hybrid nanofluid via an experimental investigation. J. Therm. Anal. Calorim. 2017, 129, 859–867. [Google Scholar] [CrossRef]
- Afrand, M.; Toghraie, D.; Ruhani, B. Effects of temperature and nanoparticles concentration on rheological behavior of Fe3O4–Ag/EG hybrid nanofluid: An experimental study. Exp. Therm. Fluid Sci. 2016, 77, 38–44. [Google Scholar] [CrossRef]
- Giwa, S.O.; Sharifpur, M.; Meyer, J.P. Experimental study of thermo-convection performance of hybrid nanofluids of Al2O3-MWCNT/water in a differentially heated square cavity. Int. J. Heat Mass Transf. 2020, 148, 119072. [Google Scholar] [CrossRef]
- Scott, T.O.; Ewim, D.R.; Eloka-Eboka, A.C. Hybrid nanofluids flow and heat transfer in cavities: A technological review. Int. J. Low-Carbon Technol. 2022, 17, 1104–1123. [Google Scholar] [CrossRef]
- Alomari, M.A.; Al-Farhany, K.; Hashem, A.L.; Al-Dawody, M.F.; Redouane, F.; Olayemi, O.A. Numerical Study of MHD Natural Convection in Trapezoidal Enclosure Filled With (50% MgO-50% Ag/Water) Hybrid Nanofluid: Heated Sinusoidal from Below. Int. J. Heat Technol. 2021, 39, 1271–1279. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Miroshnichenko, I.V.; Sheremet, M.A. Numerical analysis of unsteady conjugate natural convection of hybrid water-based nanofluid in a semicircular cavity. J. Therm. Sci. Eng. Appl. 2017, 9, 041004. [Google Scholar] [CrossRef]
- Majeed, A.H.; Mahmood, R.; Liu, D. Finite element simulations of double diffusion in a staggered cavity filled with a power-law fluid. Phys. Fluids 2024, 36, 033101. [Google Scholar] [CrossRef]
- Roy, N.C. MHD natural convection of a hybrid nanofluid in an enclosure with multiple heat sources. Alex. Eng. J. 2022, 61, 1679–1694. [Google Scholar] [CrossRef]
- Abdel-Nour, Z.; Aissa, A.; Mebarek-Oudina, F.; Rashad, A.; Ali, H.M.; Sahnoun, M.; El Ganaoui, M. Magnetohydrodynamic natural convection of hybrid nanofluid in a porous enclosure: Numerical analysis of the entropy generation. J. Therm. Anal. Calorim. 2020, 141, 1981–1992. [Google Scholar] [CrossRef]
- Mansour, M.; Siddiqa, S.; Gorla, R.S.R.; Rashad, A. Effects of heat source and sink on entropy generation and MHD natural convection of Al2O3-Cu/water hybrid nanofluid filled with square porous cavity. Therm. Sci. Eng. Prog. 2018, 6, 57–71. [Google Scholar] [CrossRef]
- Rashad, A.; Chamkha, A.J.; Ismael, M.A.; Salah, T. Magnetohydrodynamics natural convection in a triangular cavity filled with a Cu-Al2O3/water hybrid nanofluid with localized heating from below and internal heat generation. J. Heat Transf. 2018, 140, 072502. [Google Scholar] [CrossRef]
- Roy, N.C.; Amin, R.; Ishak, A. Magnetohydrodynamic Natural Convective Hybrid Nanofluid Flow in a Square Enclosure with Different Blocks. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023, 47, 841–858. [Google Scholar] [CrossRef]
- Majeed, A.H.; Mahmood, R.; Eldin, S.M.; Saddique, I.; Saleem, S.; Jawad, M. Natural Convection and Irreversibility of Nanofluid Due to Inclined Magnetohydrodynamics (MHD) Filled in a Cavity with Y-Shape Heated Fin: FEM Computational Configuration. CMES-Comput. Model. Eng. Sci. 2024, 139, 1505. [Google Scholar] [CrossRef]
- Majeed, A.H.; Liu, D.; Ali, A.R.; Alotaibi, H.; Yin, Z.J.; Yi, R.H. Numerical simulations of energy storage performance in a close configuration: A Galerkin finite element-based computation. Alex. Eng. J. 2024, 104, 56–65. [Google Scholar] [CrossRef]
- Goharkhah, M.; Ashjaee, M.; Shahabadi, M. Experimental investigation on convective heat transfer and hydrodynamic characteristics of magnetite nanofluid under the influence of an alternating magnetic field. Int. J. Therm. Sci. 2016, 99, 113–124. [Google Scholar] [CrossRef]
- Mebarek-Oudina, F.; Aissa, A. Convective heat transfer of magneto flow of Fe3O4-MWCNT/H2O hybrid nanofluid in a porous space between two concentric cylinders. Math. Fluid Mech. 2021, 7, 55–74. [Google Scholar]
- Mohebbi, R.; Izadi, M.; Amiri Delouei, A.; Sajjadi, H. Effect of MWCNT–Fe3O4/water hybrid nanofluid on the thermal performance of ribbed channel with apart sections of heating and cooling. J. Therm. Anal. Calorim. 2019, 135, 3029–3042. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rashidi, M.; Ganji, D. Effect of non-uniform magnetic field on forced convection heat transfer of Fe3O4–water nanofluid. Comput. Methods Appl. Mech. Eng. 2015, 294, 299–312. [Google Scholar] [CrossRef]
- Shi, L.; He, Y.; Hu, Y.; Wang, X. Thermophysical properties of Fe3O4@ CNT nanofluid and controllable heat transfer performance under magnetic field. Energy Convers. Manag. 2018, 177, 249–257. [Google Scholar] [CrossRef]
- Mohebbi, R.; Rashidi, M. Numerical simulation of natural convection heat transfer of a nanofluid in an L-shaped enclosure with a heating obstacle. J. Taiwan Inst. Chem. Eng. 2017, 72, 70–84. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Davis, G.D.V.; Thomas, R. Natural convection between concentric vertical cylinders. Phys. Fluids 1969, 12, II-198–II-207. [Google Scholar] [CrossRef]
- Kumar, R.; Kalam, M. Laminar thermal convection between vertical coaxial isothermal cylinders. Int. J. Heat Mass Transf. 1991, 34, 513–524. [Google Scholar] [CrossRef]
- Grigull, U.; Hauf, W. Natural convection in horizontal cylindrical annuli. In International Heat Transfer Conference Digital Library; Begel House Inc.: Danbury, CT, USA, 1966. [Google Scholar]
- Santra, A.K.; Sen, S.; Chakraborty, N. Analysis of laminar natural convection in a square cavity using nanofluid. In Proceedings of the 31st National Conference on Fluid Mechanics & Fluid Power, Kolkata, India, 16–18 December 2004; pp. 240–248. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).