1. Introduction
Electrical load forecasting plays a pivotal role in the management, scheduling, and operation of power systems [
1]. Accurate load forecasting can optimize the dispatch of generating units, reduce the operational costs, and ensure the balance between power supply and demand, which is essential for maintaining system stability [
2,
3]. Moreover, improving load forecasting accuracy can significantly reduce the risk of system overload and economic losses. According to the literature [
4] and [
5], even a 1% reduction in forecast error can save the UK power industry about GBP 10 million in the operational costs. Therefore, enhancing the accuracy of load forecasting has become a crucial research topic for reducing costs in the power system and power market [
6].
Electrical load forecasting can be categorized into three types based on the prediction time horizon: short-term (1 h to 1 week), medium-term (1 week to 1 year), and long-term (1 year to 20 years) [
7,
8]. Among these, short-term load forecasting is vital for power grid planning and smart grid construction. It has a profound impact on the stability, reliability, and economic operation of the system. Thus, it has become a focal point for research and technological development in the power industry [
9,
10]. However, short-term load forecasting faces numerous challenges, such as handling high-dimensional data with significant volatility and accounting for various influencing factors, including weather, economic activities, and holidays [
11,
12]. The interactions among these factors are complex, thus making accurate short-term load forecasting an extremely challenging task.
To address these challenges, many scholars have conducted extensive research and proposed various effective prediction methods for short-term load forecasting. These methods can be broadly classified into three categories: classical statistical prediction methods, machine learning prediction methods, and modern hybrid prediction methods [
13].
Classical statistical prediction methods include the Kalman Filter (KF) [
14], Linear Regression (LR) [
15], Exponential Smoothing (ES) [
16], Grey Model (GM) [
17], and Autoregressive Moving Average (ARMA) [
18]. These methods predict electrical loads by building and analyzing mathematical relationships between data points, involving pattern identification, data characterization, and the application of time-series methods. While classical statistical models are simple, easy to understand, and offer rapid calculations, they fall short when dealing with nonlinear data and complex features, especially the high-frequency, non-smooth characteristics of power loads. As the complexity of power load forecasting requirements increases, the limitations of these traditional methods become more apparent, underscoring the need for more effective methods to improve forecast accuracy.
With the rapid development of artificial intelligence technology, machine learning has effectively overcome the limitations of classical statistical models. It excels in nonlinear learning and has a lower dependence on complex mathematical modeling. Machine learning methods can be divided into two categories: traditional machine learning and deep learning. Traditional methods include Support Vector Machines (SVMs) [
19], Random Forests (RFs) [
20], Decision Trees (DTs) [
21], Extreme Learning Machines (ELMs) [
22], and Feed-Forward Neural Networks (FFNNs) [
23]. These methods, based on probability theory and statistics, utilize powerful computing capabilities to extract features from historical data and build models that achieve accurate predictions of future loads. Traditional machine learning models have a high processing speed and a strong ability to capture nonlinear relationships in power load forecasting. However, they have limitations when it comes to handling changes in data distribution and time-series characteristics.
Recurrent Neural Networks (RNNs) [
24], Long Short-Term Memory networks (LSTMs) [
25], and Gated Recurrent Units (GRUs) [
26] are deep learning models widely applied in modern power system load forecasting. These models are favored for their unique memory capabilities. Through recursive and gating mechanisms, they effectively capture temporal dependencies and accommodate the time-series and nonlinear characteristics of load data. However, despite their strong performance in load forecasting, each standalone method has inherent limitations. For instance, complex deep learning architectures like deep RNNs or LSTMs may suffer from overfitting. This overfitting reduces their generalization ability. Additionally, these standalone models often exhibit poor robustness to outliers or noisy data. As a result, they become susceptible to external disturbances, leading to unstable prediction outcomes.
In recent years, with the diversification of forecasting models, new architectures based on hybrid forecasting methods have gradually emerged. These methods combine the strengths of different standalone models, demonstrating excellent performance in improving prediction accuracy and robustness. For example, the CNN-LSTM hybrid model is first based on Convolutional Neural Networks (CNNs) to extract the local features from the input data, and then, on Long Short-Term Memory networks (LSTMs) to capture the temporal dependencies. The model has been successfully applied to short-term load forecasting for individual households and regional power systems [
27,
28]. Experimental results show that this hybrid model achieves a significantly higher prediction accuracy compared to standalone LSTM models. Similarly, the GRU-CNN hybrid model extracts time-series features using Gated Recurrent Units (GRUs) and processes high-dimensional data through CNNs. Research indicates that this model outperforms traditional Backpropagation Neural Networks (BPNNs) as well as standalone GRU or CNN models in terms of error metrics [
29].
While CNNs have significant advantages in extracting local features, such as daily or hourly load patterns, their limited receptive field makes it difficult to effectively capture long-term seasonal trends and time-series characteristics across time steps. To address this issue, Temporal Convolutional Networks (TCNs) utilize causal dilation convolutions and residual connections [
30]. These techniques markedly enhance TCNs’ ability to capture long-term temporal features in power load data. The TCN-GRU hybrid model described in the literature [
31] leverages a TCN’s capability to extract temporal features, combined with a GRU’s short-term load forecasting functionality. Research indicates that a TCN outperforms the traditional CNNs in handling one-dimensional features. Moreover, the combination of a TCN and GRU shows significant advantages in capturing complex temporal relationships, thereby further improving the prediction accuracy [
32,
33,
34].
However, the application of the conventional TCN-GRU model in power load forecasting still has certain limitations. One limitation is that the stacked structure of TCN layers—where the output of one layer serves as the input to the next—performs poorly when handling multidimensional input data, such as historical load, meteorological, economic, and date features. Integrating the interactive relationships among these different features is challenging. For example, the impact of weather changes and economic fluctuations on load is both nonlinear and interrelated. The TCN-GRU model, when dealing with these complex features, shows limited performance, which may potentially affect prediction accuracy. Another challenge is that a TCN is primarily designed for one-dimensional time-series data. This design makes it difficult to distinguish and process temporal-dependent features from non-temporal-dependent features, such as holidays or sudden events. This limitation could further weaken the accuracy of the predictions.
When designing effective hybrid forecasting models, it is crucial to focus not only on the model’s architecture and its ability to extract temporal features but also on the optimization of model parameters. Although the aforementioned hybrid models have made significant progress in structural design, optimizing their parameters is equally critical to fully realizing their potential. To address this issue, researchers have combined metaheuristic algorithms with hybrid forecasting models. This combination allows for the automated and efficient optimization of model parameters, thereby significantly enhancing model performance. For example, the literature [
35] employs the Particle Swarm Optimization (PSO) algorithm to optimize the hyperparameters of the CNN-BiGRU model. This approach significantly improves the accuracy of remaining life prediction under complex operating conditions. Similarly, the literature [
36] integrates the Grey Wolf Optimization (GWO) algorithm to optimize the CNN-BiLSTM model, which has been successfully applied to building energy consumption forecasting. This integration effectively enhances the model’s generalization ability and accuracy. Furthermore, the literature [
37] developed a hybrid Genetic Whale Optimization Algorithm (GCWOA) to optimize the hyperparameters of the CNN-GRU-AM model, leading to improvements in both the accuracy and robustness of ship motion prediction. Despite these effective optimization strategies, metaheuristic algorithms still have limitations, such as a tendency to fall into local optima or a failure to find the global optimum, which can adversely affect the model’s overall performance.
Based on the analysis and discussion above, the existing TCN-GRU model exhibits limitations in handling multidimensional features, especially when it comes to integrating the interactive relationships among different features. Additionally, traditional metaheuristic algorithms are prone to falling into local optima during the optimization process, which can negatively impact model performance. To address these challenges, this paper proposes an IDBO-PTCN-GRU short-term power load forecasting method. By introducing a parallel TCN structure, this method utilizes TCNs with different kernel sizes to comprehensively extract temporal features from multiple scales. These features are then effectively fused, overcoming the limitations of conventional TCNs in handling multidimensional input data (such as historical load, meteorological conditions, economic indicators, and date features). This approach particularly addresses the challenge of fully capturing and integrating complex interactions among different features. To enhance the optimization process, this paper incorporates Latin hypercube sampling to increase the diversity of the initial population. It also combines the Golden Sine Algorithm to optimize the rolling behavior and introduces a Cauchy–Gaussian mutation strategy in the later stages of iteration. These improvements effectively enhance the optimization performance and global search capability of the traditional Dung Beetle Optimization (DBO) algorithm.
To better understand the method proposed in this paper and its advantages, the following sections provide a detailed overview of the content’s organization. The remainder of this paper is organized as follows.
Section 2 introduces the PTCN-GRU model proposed in this study.
Section 3 elaborates on the improved Dung Beetle Optimization (IDBO) algorithm and tests of its optimization capability.
Section 4 presents the structure and principles of the PTCN-GRU model, which is optimized by the IDBO algorithm.
Section 5 outlines the experimental setup, results, and comparative analysis. Finally,
Section 6 summarizes the research findings and discusses future research directions.
2. PTCN-GRU Model
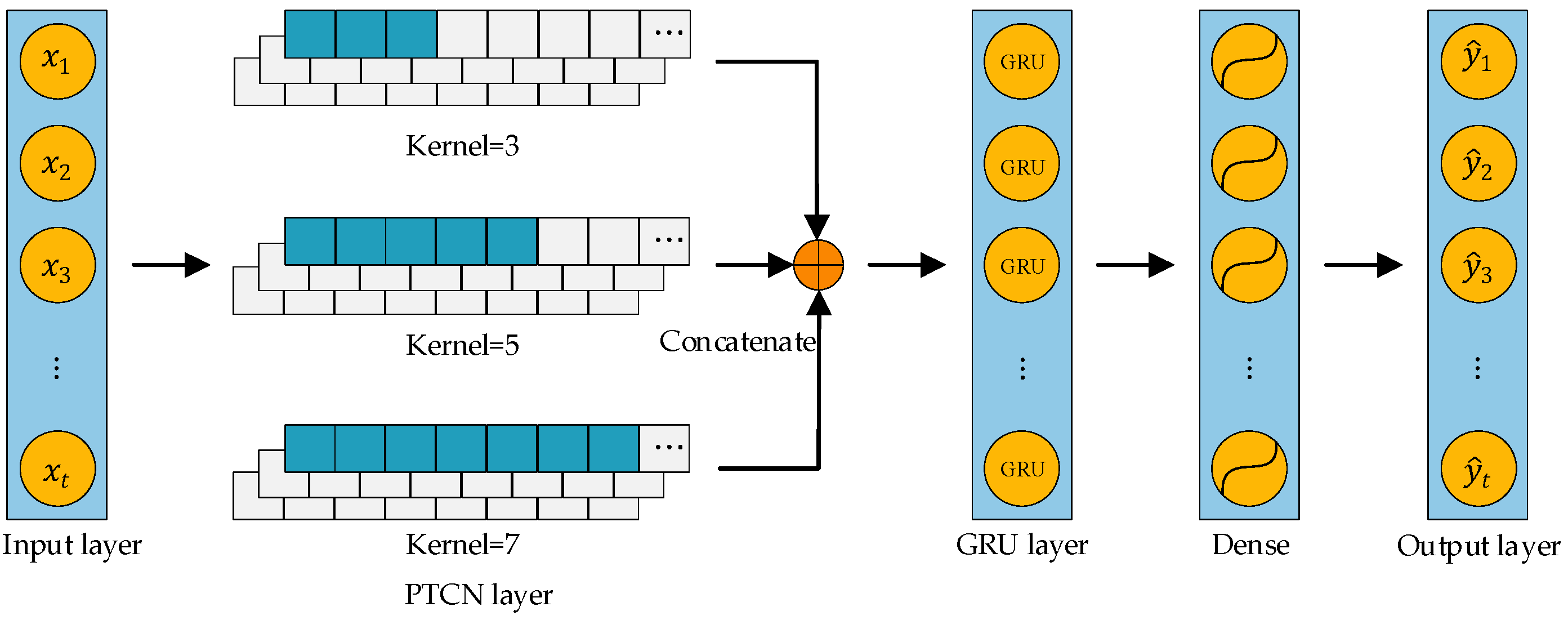
The structure of the PTCN-GRU hybrid network model proposed in this paper is illustrated in
Figure 1. It primarily consists of five key modules: the input layer, PTCN layer, GRU layer, fully connected (Dense) layer, and output layer. This architectural design aims to fully leverage the advantages of each layer, achieving efficient feature extraction and nonlinear relationship modeling.
2.1. Multi-Scale Temporal Feature Extraction Based on PTCN
The input layer of the model integrates multidimensional features, including historical load data, holiday information, and meteorological conditions. Unlike the classic layered stack hybrid model, where the output of one layer serves as the input to the next (commonly referred to as the traditional TCN-GRU model), the PTCN layer introduces a parallel TCN structure. This structure employs convolution kernels of different sizes, such as 3, 5, and 7. These varying kernels comprehensively extract temporal features across multiple scales. Feature fusion and output are achieved through parallel concatenation.
Specifically, the parallel structure of the PTCN applies differentiated temporal convolution kernels based on the specific characteristics of each feature. This approach effectively avoids the common issues in the traditional TCN-GRU model, such as feature confusion and the inadequate capture of complex inter-feature relationships when processing multidimensional data. Additionally, the PTCN utilizes a multi-scale convolution strategy. By applying convolution kernels of varying sizes, it extracts features across multiple temporal scales. This allows the model to simultaneously capture short-term fluctuations, medium-term variations, and long-term trends. As a result, it overcomes the limitations of single-scale feature extraction seen in traditional TCN models. Lastly, the feature fusion mechanism in the PTCN effectively integrates features from different temporal scales. It also captures complex feature interactions, enhancing the model’s ability to represent multidimensional features. This mechanism ensures the full utilization of information across different temporal scales, addressing the shortcomings of the traditional TCN-GRU model in feature integration and representation.
To better understand the operations of the PTCN layer, the following mathematical expressions can be used to represent it:
Here, represents the convolution operation with a kernel size of , where takes the values 3, 5, and 7, respectively. The variable denotes the input data to the model, and represents the output of the PTCN layer. The function is used to concatenate the convolution results across different scales.
2.2. Capturing Complex Nonlinear Changes Based on GRU
The fused features are transmitted to the GRU layer for processing. Through its unique update gate and reset gate mechanisms, the GRU can simultaneously consider multiple influencing factors and their nonlinear interactions. By dynamically adjusting the state of memory units, the GRU adaptively reflects these complex relationships. This mechanism enables the GRU to effectively learn and simulate complex nonlinear patterns in load variations, providing a robust foundation for accurate prediction.
The computational process of the GRU is as follows:
where
represents the sigmoid activation function;
,
, and
denote the weight matrices;
indicates element-wise multiplication;
and
are the outputs of the update gate and reset gate, respectively;
is the input at the current time step; and
is the hidden state from the previous time step. The candidate hidden state
is computed based on the current input and the adjusted hidden state from the previous time step, reflecting the information at the current time step. The updated hidden state
is derived by combining the candidate hidden state with the update gate
, thereby balancing the influence of current information and past information [
38].
2.3. Fully Connected Layer and Final Output
The output from the GRU layer is processed through a fully connected layer. This layer employs the sigmoid function as its activation function, compressing multidimensional features into a one-dimensional output to generate the final predicted value
. This process can be represented by the following equation:
where
denotes the sigmoid activation function;
represents the output from the GRU layer;
is the weight matrix; and
represents the bias vector.
4. IDBO-Optimized PTCN-GRU Model
Through the aforementioned research, we conducted a comprehensive performance evaluation of various algorithms. The results demonstrate that the proposed IDBO algorithm exhibits superior performance across multiple key indicators. The critical hyperparameters of the PTCN-GRU model, such as the number of convolutional filters, the number of GRU hidden layer units, and the learning rate, significantly influence the model’s network structure and prediction accuracy.
However, in practical applications, selecting these parameters often relies on experience, which introduces considerable uncertainty and may significantly affect the model’s predictive performance. To address this issue and enhance the model’s prediction accuracy, we employed the IDBO algorithm to systematically optimize the key parameters of the PTCN-GRU model. As a result, we constructed an IDBO-optimized PTCN-GRU model for electrical load forecasting.
The entire process of IDBO optimization is illustrated in
Figure 4. The specific steps for hyperparameter optimization are as follows:
Determine the structure of the PTCN-GRU network and specify the hyperparameters to be optimized;
Based on the network’s hyperparameter settings, define the IDBO algorithm’s population size, search space dimension, search range, and maximum number of iterations, then initialize the population;
Input the initialized hyperparameters into the PTCN-GRU network for training;
Use the trained network to make predictions on the validation set, and employ the mean squared error between the predicted results and actual values on the validation set as the fitness function to evaluate model performance;
Rank the obtained fitness values and adjust individual positions according to the corresponding update formulas;
Determine whether the preset maximum number of iterations has been reached. If so, terminate the optimization process and output the optimal network parameters; otherwise, transmit the position information of the new generation of individuals back to the PTCN-GRU network for continued training until the stopping criterion is met.
In conclusion, the method combining the PTCN-GRU network with the IDBO algorithm, through automated hyperparameter optimization and an efficient search mechanism, not only significantly enhances the model’s predictive performance and training efficiency but also ensures that the model possesses strong stability and good generalization capabilities.
5. Experiments
To validate the feasibility and superiority of the proposed model, this study selected electrical load and weather data from a specific region in Australia. The data were collected between January 2006 and December 2010 for short-term electrical load forecasting research. The sampling interval was 30 min, resulting in 48 data points per day. The first 80% of the dataset was used for model training, while the remaining 20% was used for model validation. Data from 20 to 26 December 2010 were chosen as the test sample.
This study employed a direct multi-output prediction method. It used the historical load data from the previous day, combined with weather and date features of the forecast day, as inputs to directly predict the electrical load for that day.
The hardware configuration for this experiment was identical to that described in
Section 3. The deep learning architecture was implemented based on the TensorFlow framework, using TensorFlow GPU version 2.10.0.
5.1. Feature Engineering
5.1.1. Pearson Correlation Analysis
The initial feature set comprised 13 dimensions of data. These included meteorological features (such as dry-bulb temperature and dew point temperature), economic features (e.g., electricity price), and date-related features (such as year and season). To mitigate the impact of redundant features on prediction accuracy, we used Pearson correlation coefficients to calculate the correlation between each feature and the electrical load. This analysis formed the basis for selecting the model’s input variables. The results of the correlation analysis are presented in
Figure 5.
Based on these results, we identified and eliminated features with low correlation to the electrical load. After carefully considering feature importance and model complexity, we selected features with absolute correlation coefficients greater than 0.1 as input variables for the model. The final selected input variables included 8 dimensions of data features, such as time of day, weekend indicator, and day of the week.
5.1.2. K-Means Clustering
The K-means clustering algorithm is a widely used unsupervised learning algorithm. Its core objective is to iteratively optimize the assignment of samples into K clusters to minimize the sum of squared errors within each cluster. By performing clustering analysis on the selected feature data and using the clustering results as inputs to the model, the algorithm can effectively reduce noise and outliers in the data. This process also helps to identify underlying patterns and structures, thereby enhancing the model’s stability and predictive accuracy.
To determine the optimal number of clusters, this study employed the Bayesian Information Criterion (BIC) and the Akaike Information Criterion (AIC). These methods help balance model complexity and goodness of fit. The analysis results indicated that the optimal number of clusters is 5. To visually demonstrate the clustering effect, we used Principal Component Analysis (PCA) to reduce the high-dimensional data to two dimensions and plotted the clustering results, as shown in
Figure 6. For a more detailed understanding of the dataset, examples are provided in
Appendix A.
5.2. Feature Preprocessing
The classification and processing methods for input features are presented in
Table 4. Firstly, the Min–Max normalization method was applied to scale the historical load from the previous day, electricity price, dew point temperature, humidity, and forecast time data to the interval [0, 1]. This ensures that numerical values of different features are on the same scale, avoiding errors caused by disparate magnitudes.
Secondly, days of the week were represented using numbers 1 to 7 (with 1 representing Monday and 7 representing Sunday). Weekends and holidays were encoded using binary representation: 1 for weekends and 0 for weekdays; 1 for holidays and 0 for non-holidays.
Lastly, the clustering results were encoded as integers from 0 to 4 to distinguish different categories. This systematic feature processing approach ensures consistency and interpretability of the data throughout the model training process.
5.3. Evaluation Metrics
This study employs mean absolute percentage error (MAPE), root mean square error (RMSE), mean absolute error (MAE), and coefficient of determination (R
2) as performance evaluation metrics for the load forecasting model. The specific formulas are as follows:
where
represents the predicted load value at time
,
is the actual load value at the corresponding time,
is the mean of the load values, and
denotes the total number of test samples.
5.4. Experiment 1: Performance Comparison between PTCN-GRU and Other Deep Learning Models
In Experiment One, we provide a detailed list of hyperparameters for various deep learning models, as shown in
Table 5. For models such as LSTM and GRU, we initially evaluated their performance based on the relevant literature. After that, we conducted extensive experiments through hyperparameter tuning and determined that the optimal number of layers is two.
For specific configurations, the learning rate for all models was uniformly set to 0.001 to ensure robust convergence. The dropout parameter was set to 0.2, effectively preventing overfitting and improving generalization capability. We set the batch size to 128, balancing the training speed and memory usage. The number of training epochs was set to 100, and we used an early stopping mechanism to enhance the training efficiency and avoid resource waste.
We chose mean squared error (MSE) as the loss function due to its effectiveness in regression tasks. The Adam optimizer was used to adjust the model parameters on the validation set, as it can adapt the learning rate during training.
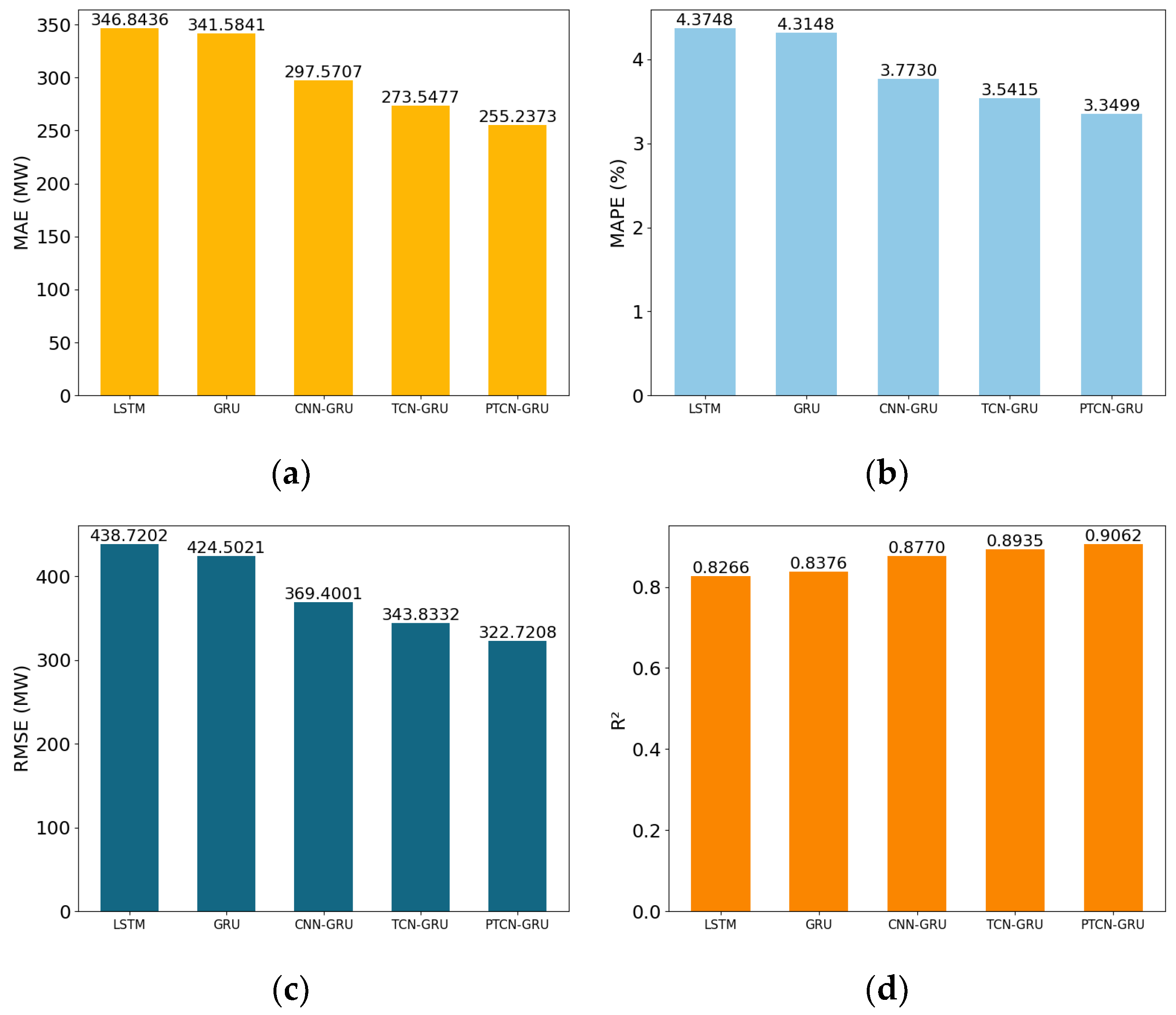
Figure 7 illustrates the results of different models in the task of electric load forecasting. To provide a more intuitive comparison of the predictive performance of these models,
Table 6 presents the MAE, MAPE, RMSE, and R
2 for each model. Additionally,
Figure 8 offers a visual representation of these performance metrics, facilitating a clearer understanding of each model’s performance.
Based on the data from
Figure 7 and
Table 6, we conducted a detailed analysis of the performance of each model in electric load forecasting. After an in-depth examination of these performance metrics, we draw the following conclusions:
The PTCN-GRU model achieves a mean absolute error (MAE) of 255.2373 MW. This is significantly lower than all other models, indicating that the PTCN-GRU can more accurately approximate actual values when predicting electric load, minimizing the mean absolute error.
In terms of the mean absolute percentage error (MAPE), the PTCN-GRU model outperforms other models with a result of 3.3499%. This demonstrates its excellence in controlling relative errors and providing more reliable and stable predictions.
The root mean square error (RMSE) of the PTCN-GRU model is 322.7208 MW. This is 6.14% (21.1124 MW) lower than the second-best TCN-GRU and 26.44% (115.9994 MW) lower than the poorest-performing LSTM. These results indicate that the PTCN-GRU model effectively reduces fluctuations in prediction errors, providing more stable forecasting results.
Regarding the R2 metric, the PTCN-GRU achieves a score of 0.9062. This is an improvement of 1.27 percentage points over the second-best TCN-GRU and 7.96 percentage points over the poorest-performing LSTM. This implies that the PTCN-GRU model better explains data variance, showing the strongest correlation between predicted and actual values.
In conclusion, the PTCN-GRU model demonstrates superior performance in electric load forecasting. It outperforms other comparative models, including LSTM, GRU, CNN-GRU, and TCN-GRU, across key metrics such as the MAE, MAPE, RMSE, and R2. The superior performance of the PTCN-GRU model stems from its combination of the TCN’s long-term dependency modeling and GRU’s nonlinear feature extraction. Its parallel structure and multi-scale convolution strategy prevent feature confusion, thereby enhancing the model’s expressive power. The feature fusion mechanism integrates information across the different temporal scales and captures the complex feature interactions. These improvements enable the PTCN-GRU model to excel in electric load forecasting. It offers higher prediction accuracy and reliability, making it highly valuable for power system planning and operation.
5.5. Experiment 2: Performance Comparison of PTCN-GRU Model under Different Optimization Algorithms
In this study, we fixed the temporal dimension kernel sizes of the first and second TCN layers in the PTCN-GRU model to 5 and 3, respectively. Subsequently, we applied five optimization algorithms—PSO, WOA, GWO, DBO, and IDBO—separately to optimize six hyperparameters. The iteration count for each algorithm was set to 6.
Table 7 presents the optimization results for each algorithm and the time taken for optimization.
To evaluate the effectiveness of different optimization algorithms in tuning the hyperparameters of the PTCN-GRU model, we applied the optimal hyperparameters obtained by each algorithm to train the model and conducted predictions on the test set.
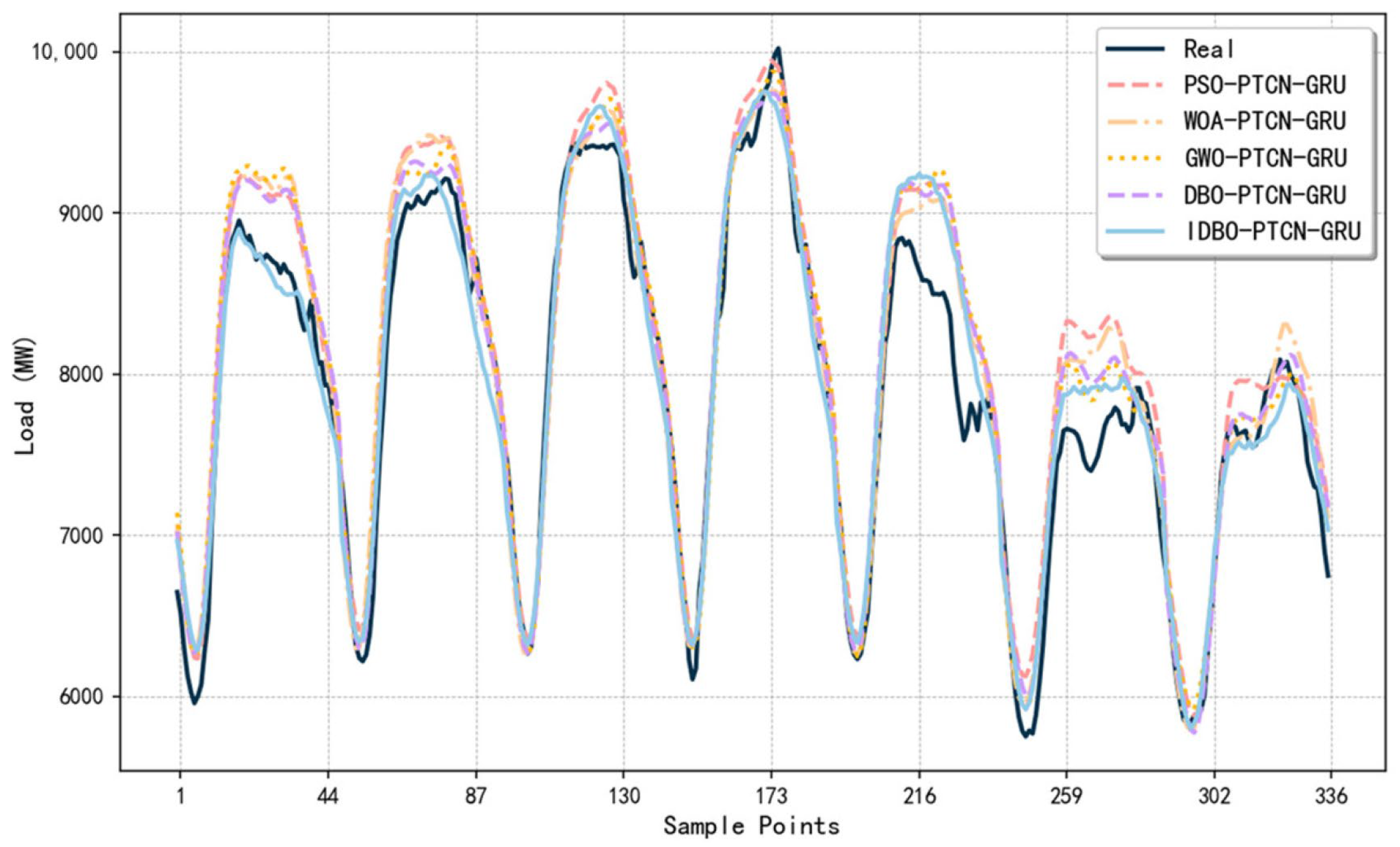
Figure 9 illustrates the prediction results under different optimization algorithms,
Table 8 lists the specific values of various performance metrics, and
Figure 10 provides a graphical comparison of these metrics.
Through an in-depth analysis of the prediction results, we found that the PTCN-GRU model optimized by the IDBO achieved significant improvements across all evaluation metrics. Specifically, the MAE decreased from 255.2373 to 191.1733, representing a reduction of 25.1%. The MAPE reduced from 3.3499% to 2.4694%, marking a decrease of 26.3%. The RMSE declined from 322.7208 to 244.6529, a reduction of 24.2%. Additionally, the R2 value increased from 0.9062 to 0.9461, an improvement of 4.4%. These data convincingly demonstrate the superior effect of the IDBO algorithm in enhancing the performance of the PTCN-GRU model.
When comparing the performance of the IDBO-PTCN-GRU with the second-best model, DBO-PTCN-GRU, we observed significant advantages across all metrics. The MAE, MAPE, and RMSE of the IDBO-PTCN-GRU were lower than those of the DBO-PTCN-GRU by 15.01%, 14.44%, and 14.42%, respectively. This highlights the outstanding capability of the IDBO algorithm in reducing prediction errors. Meanwhile, the R2 value of the IDBO-PTCN-GRU improved by approximately 2.13%. This further enhances the model’s goodness of fit and demonstrates the effectiveness of the IDBO algorithm in optimizing the overall model performance.
In conclusion, the IDBO algorithm leverages its improved exploration and exploitation capabilities to demonstrate exceptional performance in optimizing the PTCN-GRU model. It not only significantly enhances the model’s predictive accuracy but also shows distinct advantages over other optimization algorithms. This indicates that the IDBO algorithm possesses outstanding adaptability and efficiency in optimizing complex nonlinear systems such as electric load forecasting.
6. Conclusions and Future Prospects
To address the limitations of current short-term electric load forecasting models in capturing multi-scale features and handling complex influencing factors, such as holiday effects and weather conditions, this study proposes an IDBO-optimized PTCN-GRU electric load forecasting model. We conducted an empirical analysis using an electric load dataset from a region in Australia. The proposed model was then compared with advanced deep learning algorithms, including LSTM and GRU. The experimental results show that our model achieves superior predictive accuracy across key performance metrics, such as the MAPE, RMSE, MAE, and R2. These findings confirm the model’s effectiveness in improving electric load forecasting accuracy, as well as its strong adaptability and stability.
Although the IDBO-PTCN-GRU model demonstrates significant improvements in prediction accuracy, some limitations of this study must be acknowledged. Firstly, the performance of the model is highly dependent on the quality and quantity of the input data. If the data are sparse or contain high levels of noise, the accuracy of the model may decrease. In such cases, more advanced data preprocessing techniques may be required to improve the results. Secondly, the computational complexity of the model increases with the introduction of the IDBO algorithm. This could result in longer training times, making it less suitable for certain real-time applications. Additionally, while the IDBO algorithm enhances the global search capabilities and helps avoid the local optima, it may still struggle in extremely complex or high-dimensional optimization scenarios. Finally, the performance of the model has been evaluated on a specific dataset. Its generalizability to other datasets or different forecasting tasks may need further validation and adjustment.
To address the aforementioned limitations, future research can focus on the following areas:
Improving Data Quality and Preprocessing: develop more advanced data augmentation and noise-filtering techniques to enhance the model’s performance in sparse or noisy data environments and explore methods for integrating multi-source data.
Optimizing Computational Efficiency: reduce computational complexity and improve the model’s real-time application capabilities through efficient algorithms, distributed computing, or new model architectures.
Enhancing the Robustness of the IDBO Algorithm: improve parameter adjustment mechanisms and incorporate other optimization techniques to enhance the algorithm’s performance in complex and high-dimensional scenarios.
Validating and Adjusting Model Generalizability: test the model across different datasets and application scenarios and optimize as necessary to ensure its broad applicability.