Comparative Analysis of Magnetic Field Distribution Characteristics of Two Shapes of Air-Core Bridge Arm Reactors
Abstract
1. Introduction
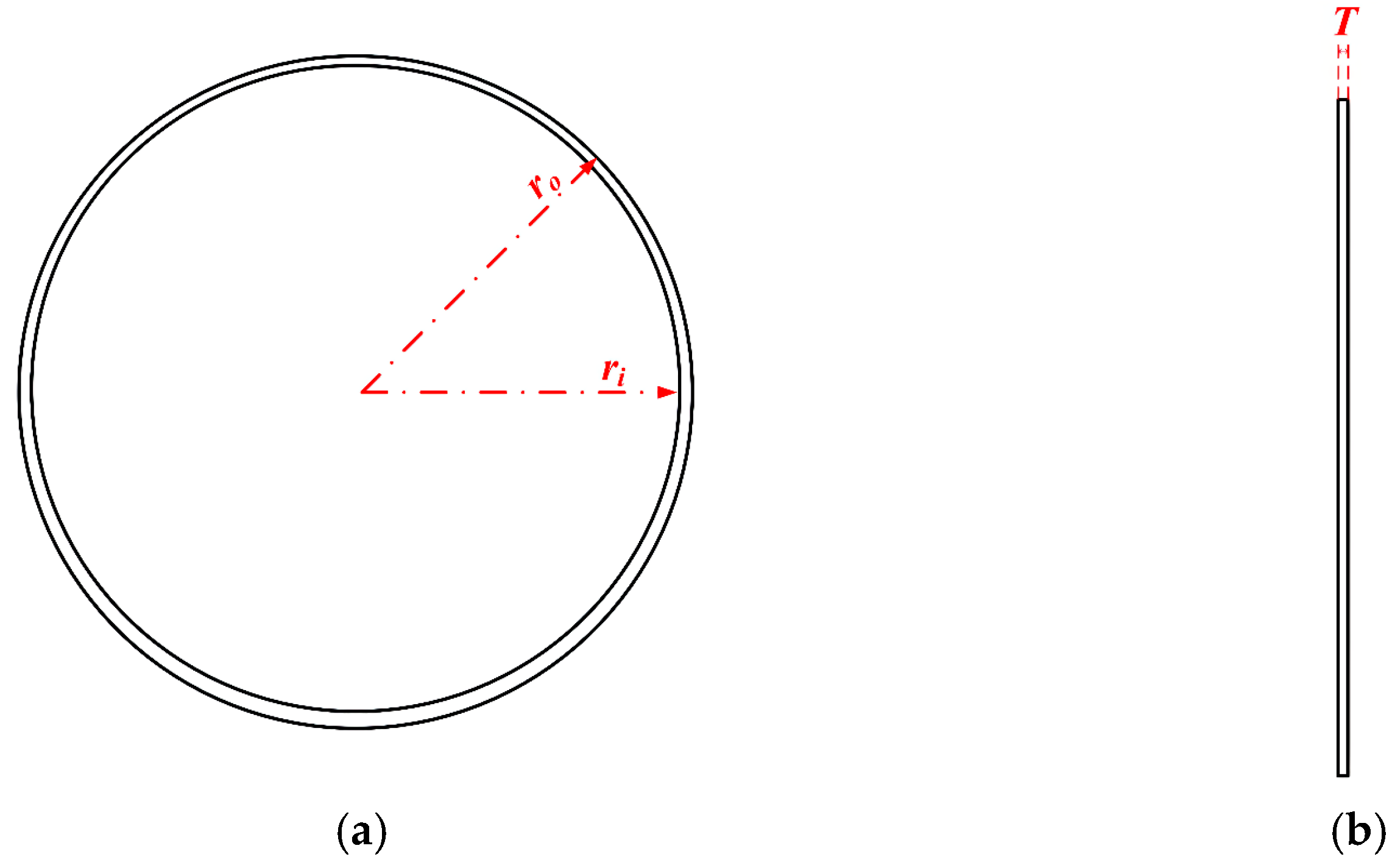
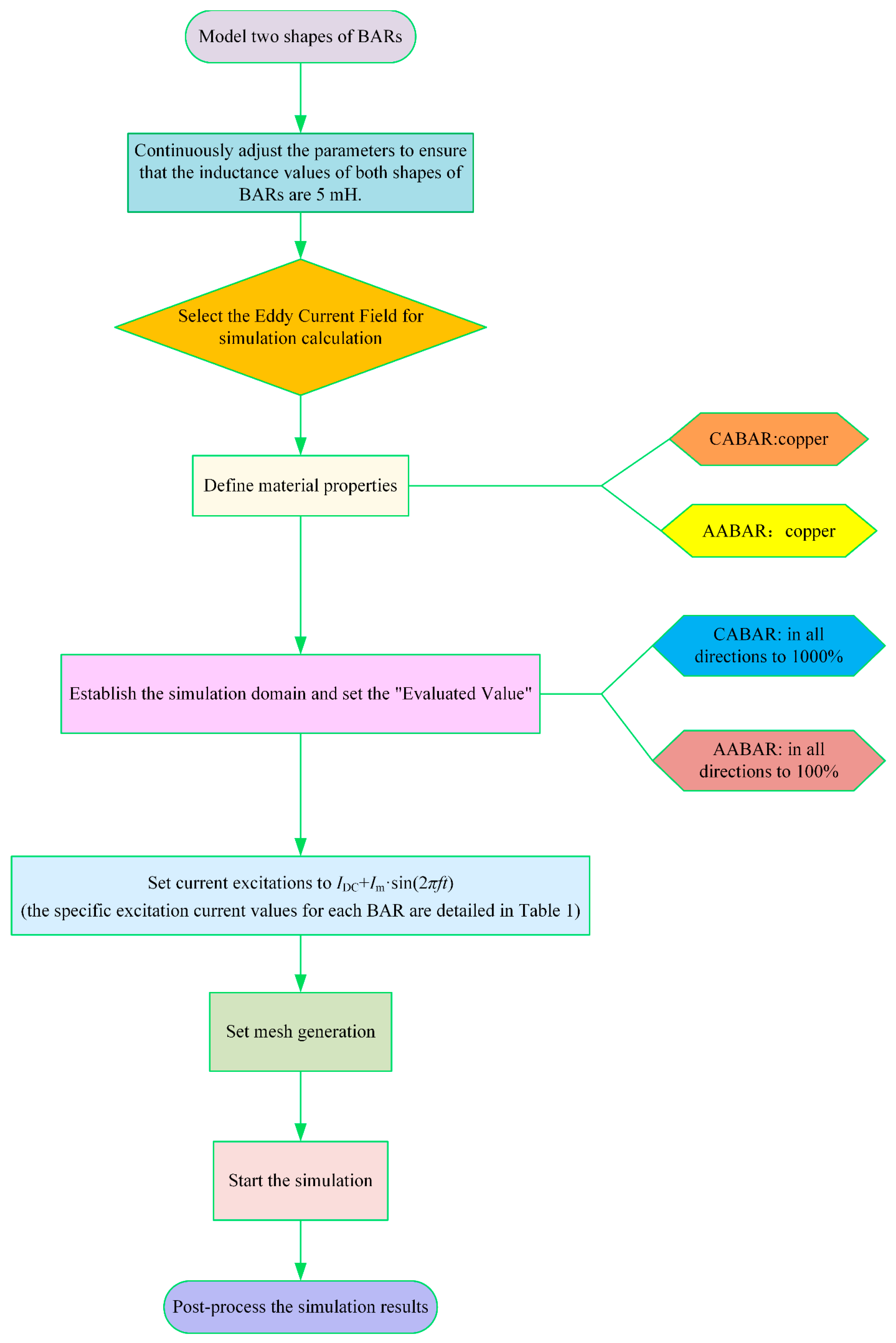
2. Establishment of Finite Element Models for Two Shapes of BARs
3. Comparative Analysis of Magnetic Field Characteristics of Two Types of BARs
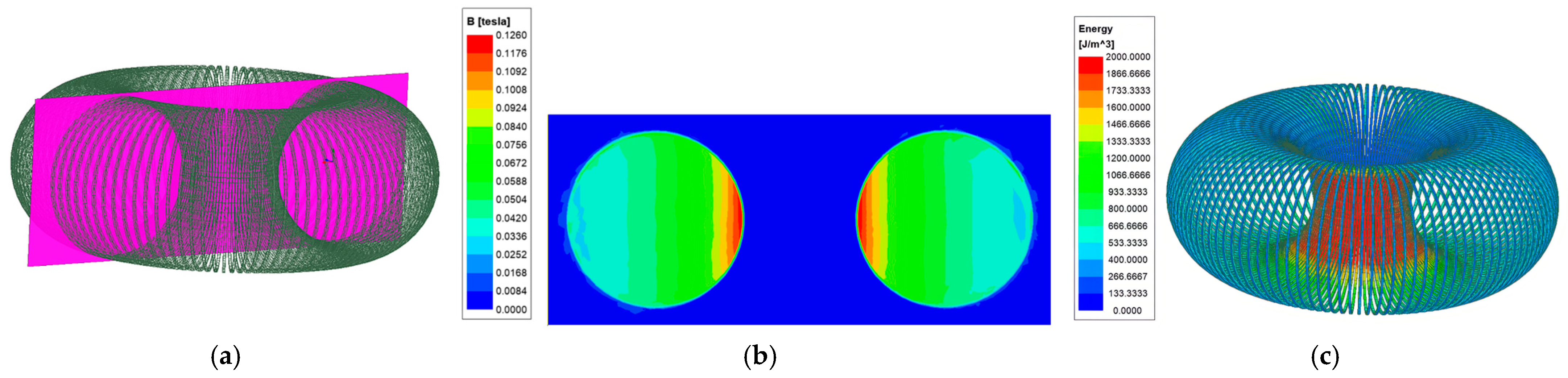
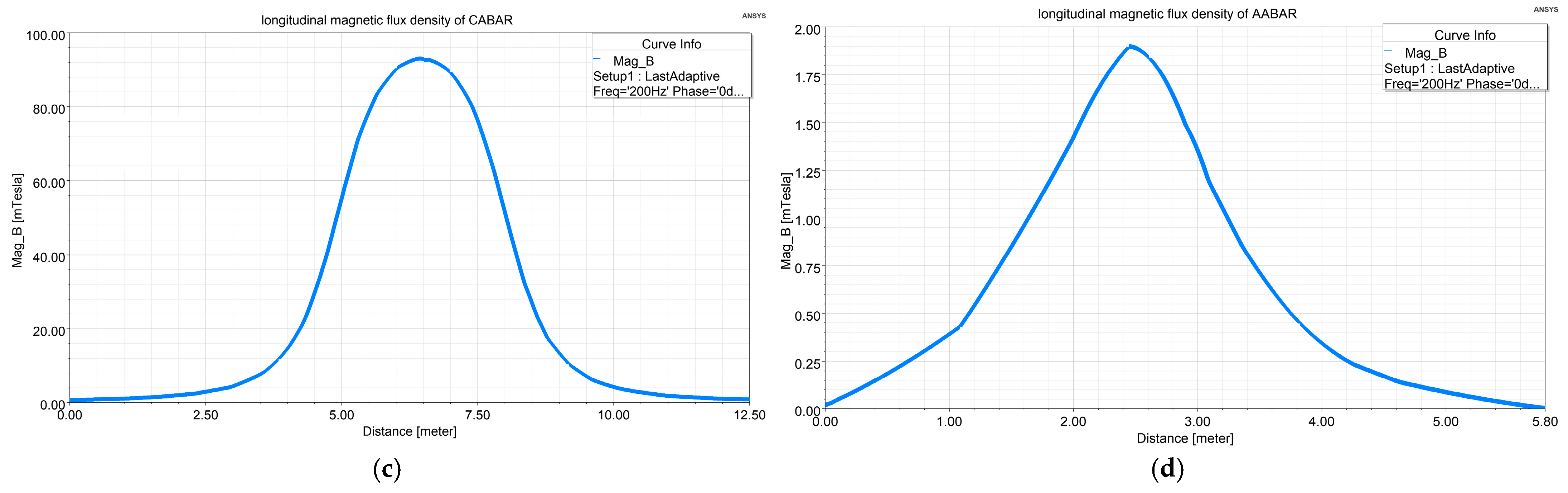
3.1. Calculation and Analysis of Magnetic Flux Density Distribution for Different Shapes of Air-Core Reactors
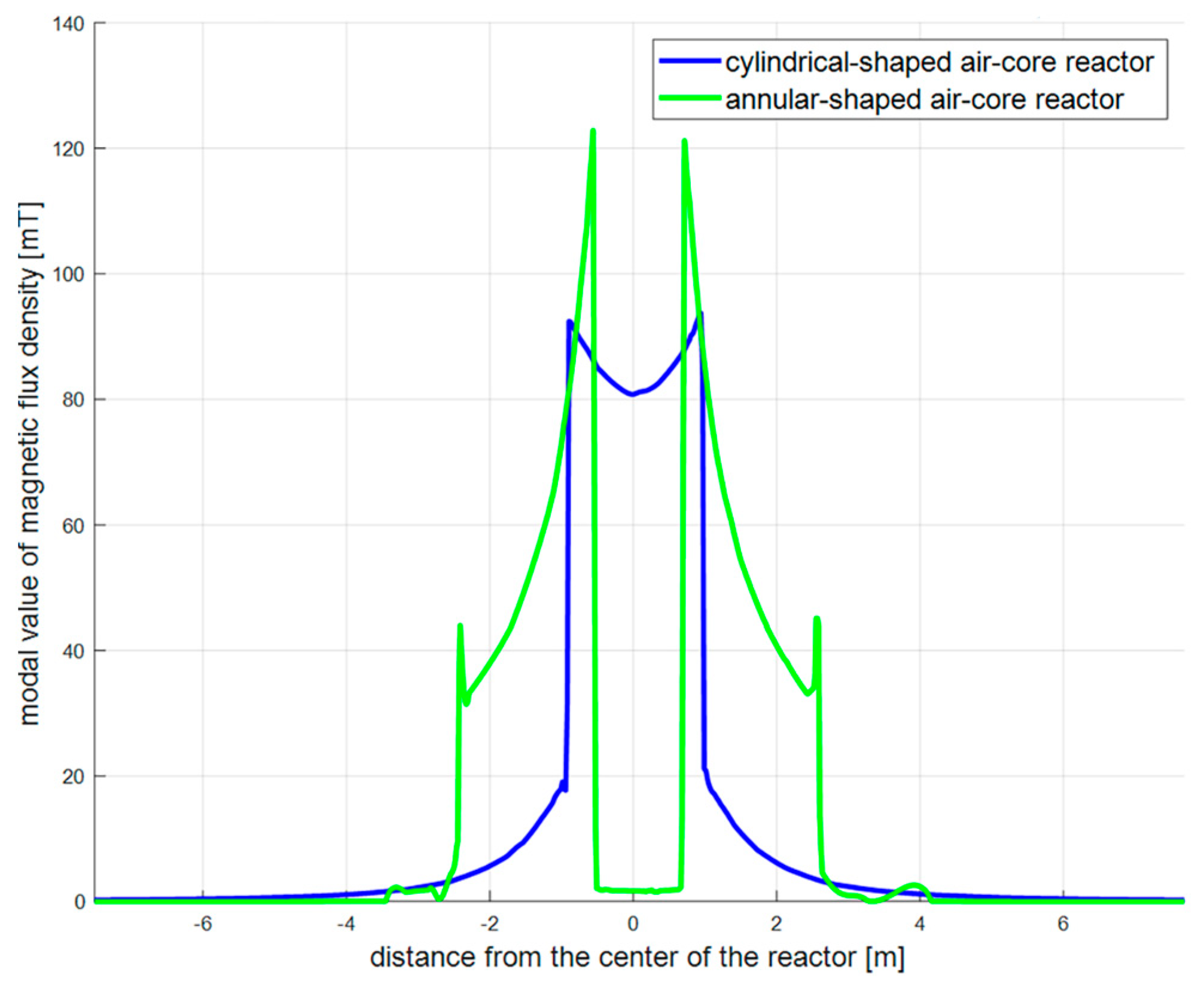
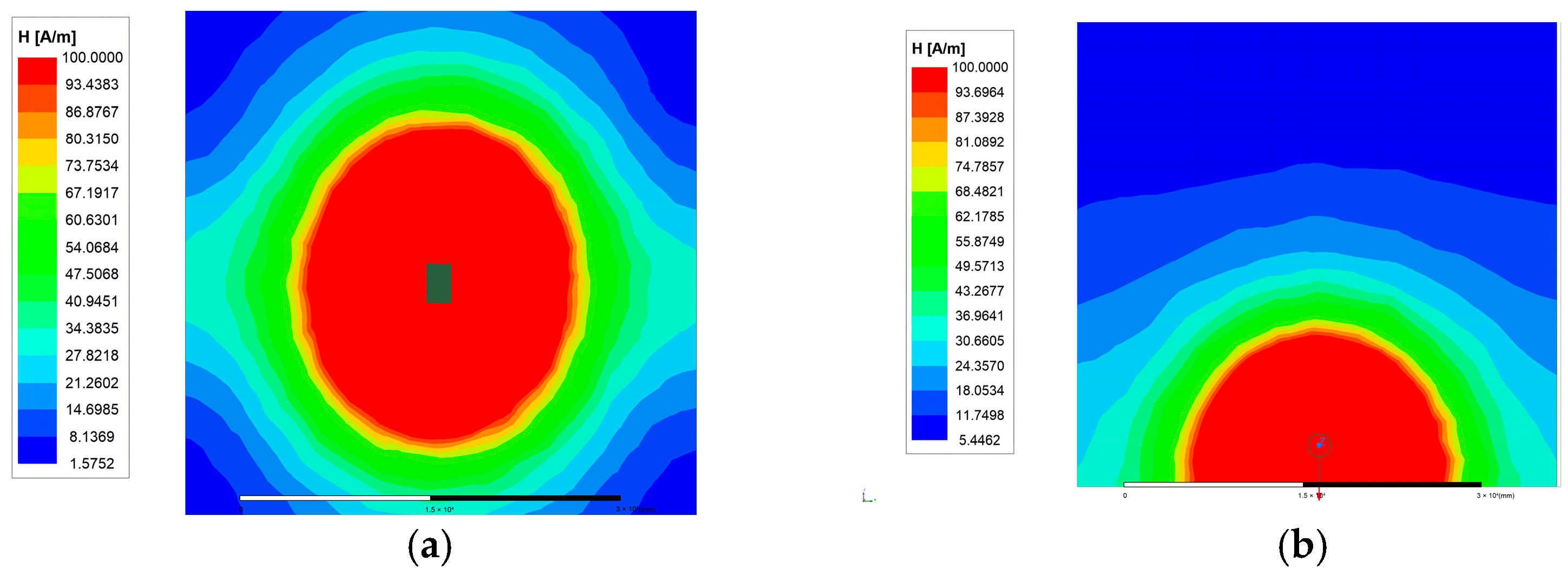
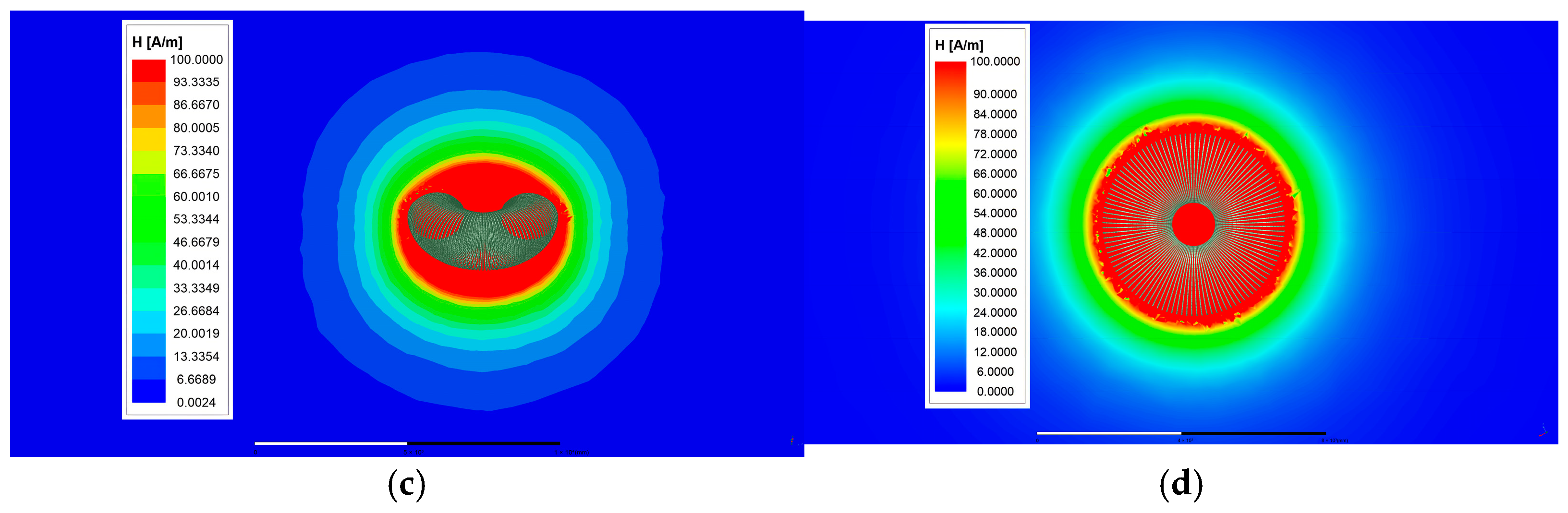
3.2. Calculation and Analysis of the Radiation Range of Different Shapes of BARs
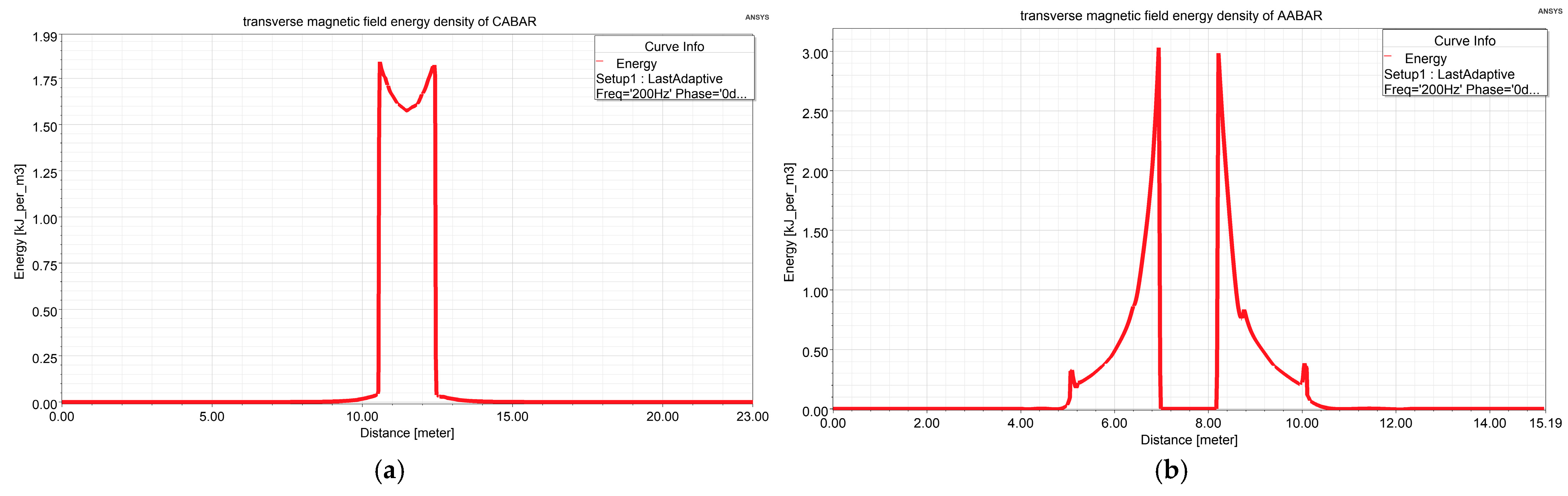
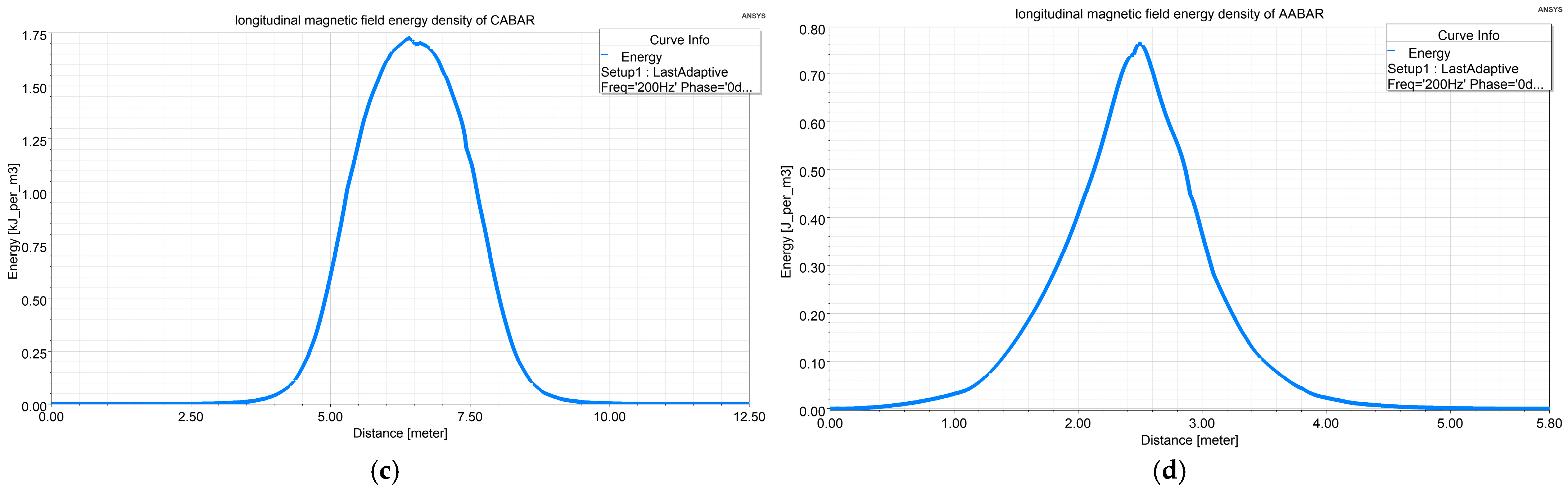
3.3. Calculation and Analysis of Magnetic Field Energy Distribution of Different Shapes of BARs
4. Conclusions
- (1)
- The magnetic clearance of the AABAR was reduced by 90% compared with the CABAR. This indicates that the AABAR structure can significantly reduce the magnetic clearance of large-capacity BARs.
- (2)
- The internal energy of the AABAR was found to be higher than that of the CABAR; however, the energy influence range of the AABAR was reduced by 40% and 37.5% in the transverse and longitudinal directions, respectively, compared with the CABAR. This demonstrates that the AABAR has lower external magnetic field energy leakage and a smaller influence distance than the CABAR.
- (3)
- Under the same radiation standard (100 A/m), the radiation area of the AABAR was reduced by approximately 90.69% compared with the CABAR. This shows that under the same radiation standard, the radiation range of the CABAR far exceeds that of the AABAR, making the AABAR structure advantageous in terms of radiation protection design.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiao, D.; Chen, B.; Li, Z.; Fu, X.; Wei, C.; Lu, D. Editorial: Control, operation, and trading strategies for intermittent renewable energy in smart grids. Front. Energy Res. 2023, 11, 1139238. [Google Scholar] [CrossRef]
- Youngquist, R.C.; Ihlefeld, C.M.; Starr, S.O. A DC transformer. IEEE Trans. Power Electron. 2014, 29, 42–44. [Google Scholar] [CrossRef]
- Cao, Y.; Ngo, K.; Dong, D. A scalable electronic-embedded transformer, a new concept toward ultra-high-frequency high-power transformer in DC–DC converters. IEEE Trans. Power Electron. 2023, 38, 9278–9293. [Google Scholar] [CrossRef]
- Purgat, P.; Prakoso, R.A.; Mackay, L.; Qin, Z.; Ramirez-Elizondo, L.; Bauer, P. A partially rated DC-DC converter for power flow control in meshed LVDC distribution grids. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1591–1596. [Google Scholar] [CrossRef]
- Denniston, N.; Massoud, A.M.; Ahmed, S.; Enjeti, P.N. Multiple-module high-gain high-voltage DC–DC transformers for offshore wind energy systems. IEEE Trans. Ind. Electron. 2011, 58, 1877–1886. [Google Scholar] [CrossRef]
- Sessa, S.D.; Chiarelli, A.; L’Abbate, A.; Benato, R. Availability assessment methods for HVDC systems: A review. In Proceedings of the 2019 AEIT HVDC International Conference (AEIT HVDC), Florence, Italy, 9–10 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Li, R.; Yu, L.; Xu, L.; Adam, G.P. Coordinated control of parallel DR-HVDC and MMC-HVDC systems for offshore wind energy transmission. IEEE J. Emerging Sel. Top. Power Electron. 2020, 8, 2572–2582. [Google Scholar] [CrossRef]
- Yuan, J.; Zhang, W.; Sun, Y.; Zhou, H.; Liu, J.; Liu, Y.; Tan, J. Topological design of a novel magnetically saturated bridge arm reactor with controllable inductance. In Proceedings of the 2024 IEEE 21st Biennial Conference on Electromagnetic Field Computation (CEFC), Jeju, Republic of Korea, 2–5 June 2024; pp. 1–2. [Google Scholar] [CrossRef]
- Zhao, W.; Xie, N.; Zhao, B.; Xie, Z.; Yue, J.; Xie, W. Finite element simulation analysis of three-phase bridge arm reactor of modular multilevel converter. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 2920–2924. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, W.; Zou, L.; Wang, Y.; Sun, Y.; Feng, Y. Research on distribution and shielding of spatial magnetic field of a DC air core smoothing reactor. Energies 2019, 12, 937. [Google Scholar] [CrossRef]
- Yuan, F.; Yuan, Z.; Chen, L.; Wang, Y.; Liu, J.; He, J.; Pan, Y. Thermal and electromagnetic combined optimization design of dry type air core reactor. Energies 2017, 10, 1989. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, J.; Zhao, L. Study on checking calculation of temperature field based on body winding and metal accessories for bridge arm reactor. In Proceedings of the 2022 IEEE International Conference on High Voltage Engineering and Applications (ICHVE), Chongqing, China, 25–29 September 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Pan, Z.; Lu, H.; Wen, X.; Jiang, Z.; Chen, B.; Chen, T. Theoretical and experimental evaluation of the temperature distribution in a dry type air core smoothing reactor of HVDC station. Energies 2017, 10, 623. [Google Scholar] [CrossRef]
- Wu, J.; Chang, Z.; Zhang, H.; Zhang, M.; Peng, Y.; Liao, J.; Huang, Q. Thermal simulation and analysis of dry-type air-core reactors based on multi-physics coupling. Energies 2023, 16, 7456. [Google Scholar] [CrossRef]
- Chen, C.; Shang, X.; Chen, P.; Zhou, G.; Liang, Y.; Yang, J.; Ma, L.; Qi, L. Simulation analysis on heating of metal structure in leakage magnetic field of arm inductor in converter station. In Proceedings of the 2021 International Conference on Advanced Electrical Equipment and Reliable Operation (AEERO), Beijing, China, 15–17 October 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Burke, P.; Lau, T.; Fawzi, T. Shielding of air core-reactors. IEEE Trans. Magn. 1983, 19, 2070–2072. [Google Scholar] [CrossRef]
- IEEE. IEEE Standard for Requirements, Terminology, and Test Code for Dry-Type Air-Core Series-Connected Reactors; IEEE Std C57.16-2011 (Revision of IEEE Std C57.16-1996); IEEE: Piscataway, NJ, USA, 2012; pp. 1–127. [Google Scholar] [CrossRef]
- IEEE. IEEE Approved Draft Guide for Recommended Electrical Clearances and Insulation Levels in Air Insulated Electrical Power Substations; IEEE P1427/D5.1; IEEE: Piscataway, NJ, USA, 2020; pp. 1–49. [Google Scholar]
- Cui, Z.; Qian, G.; Liu, Y.; Hao, C.; Yang, C.; Liu, Y. Study on electromagnetic shielding of the distributed current sensor for dry-type air-core reactor. In Proceedings of the 2020 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 6–10 September 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Zhou, K.; Li, Z.; Gong, W.; Zhao, S.; Wen, C.; Song, Y. Influence of magnetic field generated by air core reactors in SVC-based substation and an optimal suppression method based on fuzzy comprehensive evaluation. IEEE Trans. Electromagn. Compat. 2020, 62, 1961–1970. [Google Scholar] [CrossRef]
- Sun, X.; Guo, L.; Zou, C.; Cheng, J.; Zhu, J.; Zhang, W.; Huang, K.; Zhao, L.; Rao, H.; Lv, J. Design selection research on LCC-MMC multiterminal hybrid HVDC dry-type air-core reactors. In Proceedings of the 2020 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 6–10 September 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Zhao, C.; Jiang, S.; Xie, Y.; Wang, L.; Zhang, D.; Ma, Y.; Zhang, Y.; Li, M. Analysis of fault and protection strategy of a converter station in MMC-HVDC system. Sustainability 2022, 14, 5446. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Y. Optimal configuration of smoothing reactors and current limiting reactors in LCC-MMC HVDC network. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nanjing, China, 27–29 May 2022; pp. 1540–1544. [Google Scholar] [CrossRef]
- Kontos, E.; Bauer, P. Reactor design for DC fault ride-through in MMC-based multi-terminal HVDC grids. In Proceedings of the 2016 IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5–8 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Solak, K.; Rebizant, W.; Mieske, F. Development and validation of the high-voltage direct-current modular multilevel converter (HVDC-MMC) model for converter transformer protection studies. Sensors 2024, 24, 3126. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Wang, D.; Zhou, X.; Tao, L. Suppression of negative sequence current on HVDC modular multilevel converters in offshore wind power. J. Mar. Sci. Eng. 2024, 12, 383. [Google Scholar] [CrossRef]
- Hu, W.; Li, F. Improved topology and control strategies for DC converters in wind power full DC systems. Electronics 2024, 13, 400. [Google Scholar] [CrossRef]
- Jiang, Q.; Tao, Y.; Li, B.; Liu, T.; Chen, Z.; Blaabjerg, F.; Wang, P. Joint limiting control strategy based on virtual impedance shaping for suppressing DC fault current and arm current in MMC-HVDC systems. J. Mod. Power Syst. Clean Energy 2023, 11, 2003–2014. [Google Scholar] [CrossRef]
- Sun, S.; Wang, S.; Sun, Y.; Yu, X.; Yin, R.; Hu, H.; Ding, H.; Li, J.; Cao, L. Analysis of the hybrid-MMC-HVDC short-circuit current under MMC AC system symmetrical fault. In Proceedings of the 2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 26–29 March 2021; pp. 41–45. [Google Scholar] [CrossRef]
- Huang, X.; Liu, Q.; Pan, X.; Jin, S.; Chen, H.; Wang, X.; Zhao, F.; Chen, L.; Zhang, H. An equivalent modeling method for wideband magnetic radiation interference of power-electronic equipment. Electronics 2024, 13, 2481. [Google Scholar] [CrossRef]
- Liang, J.; Zhou, Z.; Xiao, Z.; Liu, H.; Lu, Z.; Su, L.; Guo, W.; Deng, X. Analysis of electromagnetic interference for anti-medal UHF RFID temperature tag in high power electronic equipment. Electronics 2023, 12, 3577. [Google Scholar] [CrossRef]
- Yang, J.; He, Z.; Pang, H.; Tang, G. The hybrid-cascaded DC–DC converters suitable for HVdc applications. IEEE Trans. Power Electron. 2015, 30, 5358–5363. [Google Scholar] [CrossRef]
- GB/T 17626.8-2006; Electromagnetic Compatibility—Testing and Measurement Techniques—Power Frequency Magnetic Field Immunity Test. Standards Press of China: Beijing, China, 2006.
- Gao, L.; Ji, S.; Zhu, L.; Yang, H.; Zhang, F.; Li, J.; Hui, S. Vibration and noise characteristics of air-core reactor used in HVDC converter stations. IEEE Trans. Power Deliv. 2022, 37, 1068–1077. [Google Scholar] [CrossRef]

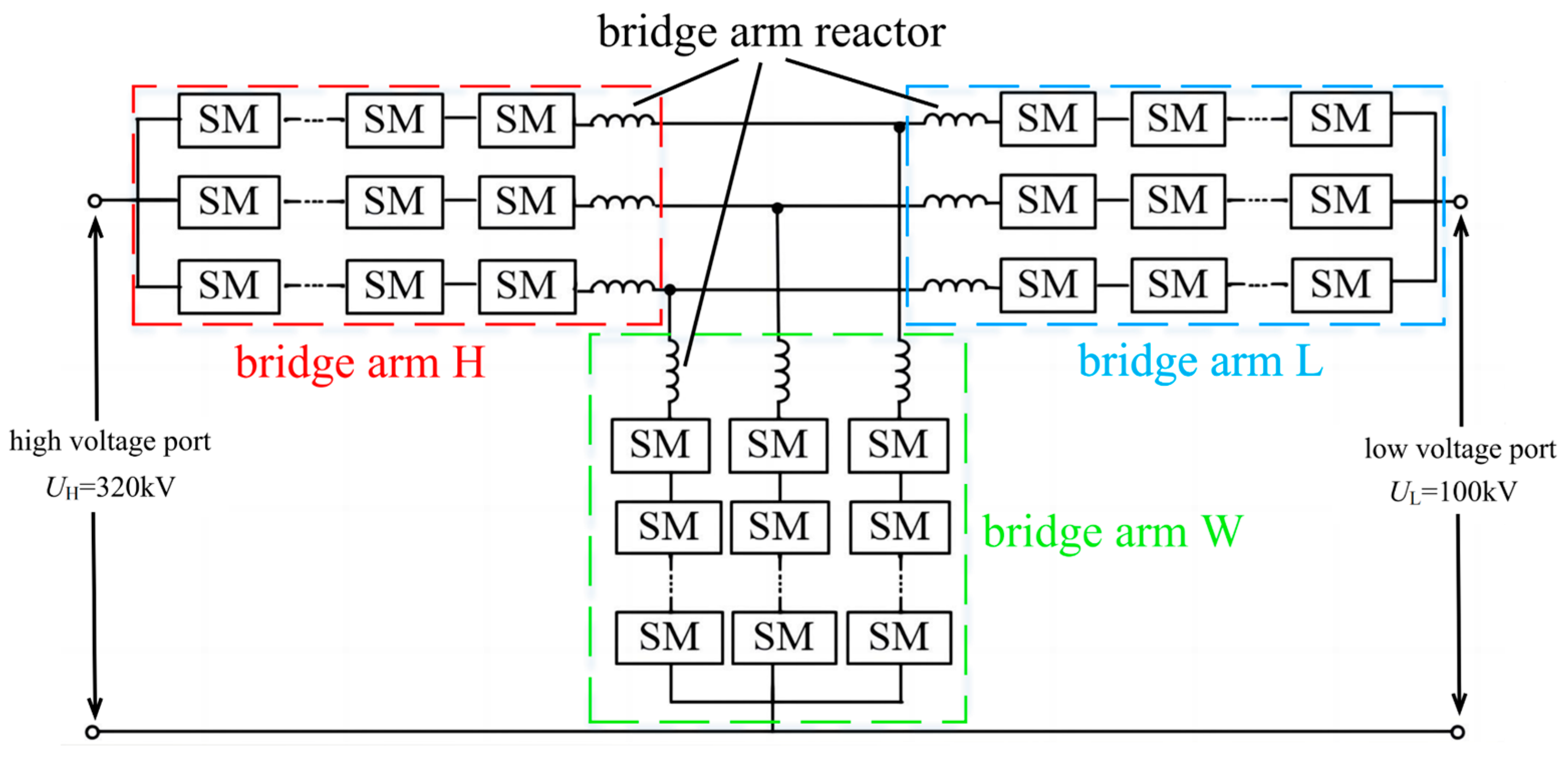

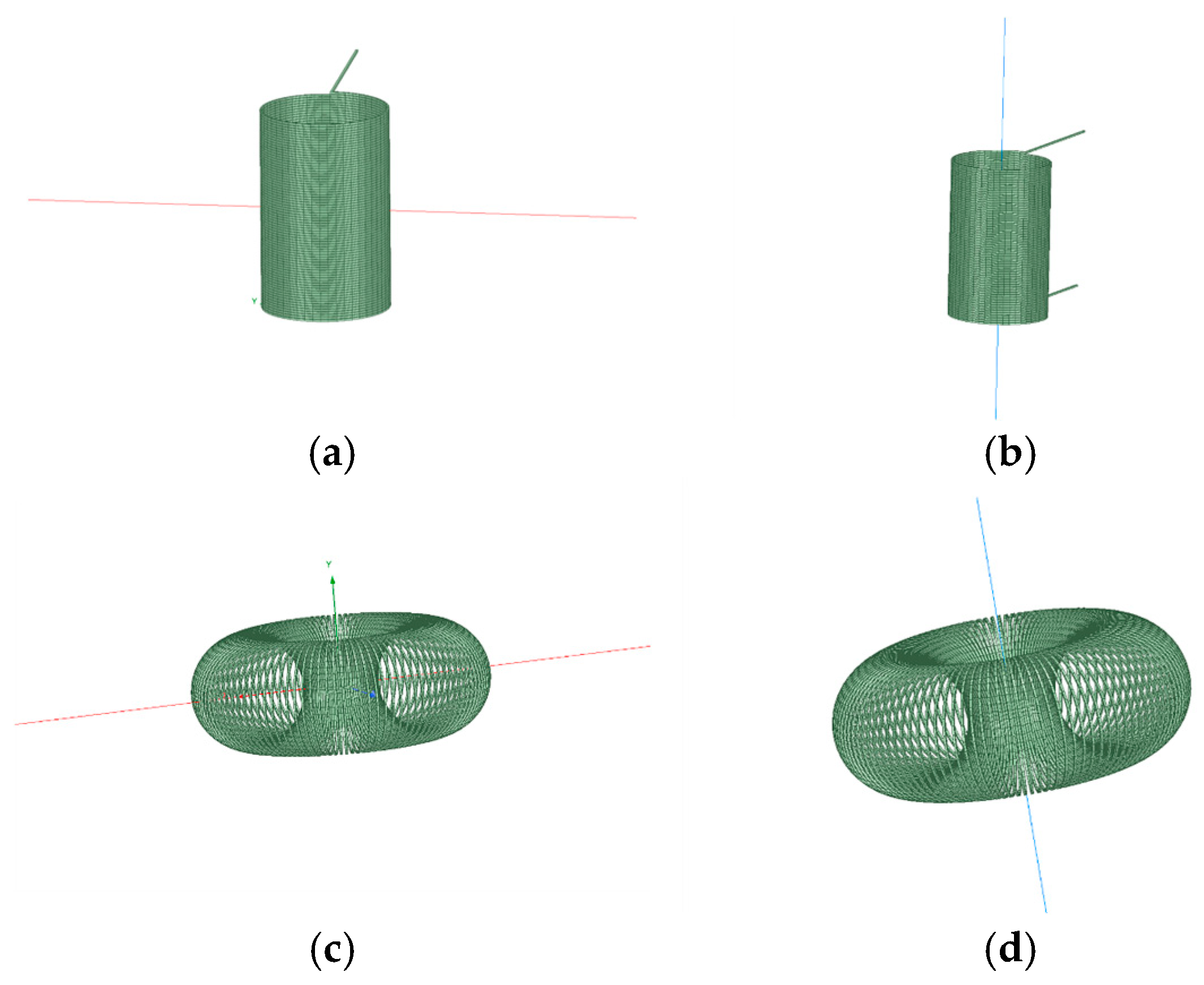

| Name | Value/Requirement | Remarks | |
|---|---|---|---|
| Bridge arm H | Design inductance value of the H-BAR | 5 mH | |
| Steady-state current | −0.43 kA (DC) + 2.47 kA (AC) | AC component frequency is 200 Hz | |
| Transient-state current | 6 kA 7.13 kA/ms and 0.21 kA/ms | Peak fault Current rise rate and decline rate | |
| Steady-state voltage | 22 kV | Peak value | |
| Transient-state voltage | 12 kV | Peak value | |
| Bridge arm W | Design inductance value of the W-BAR | 5 mH | |
| Steady-state current | 1.27 kA (DC) + 2.49 kA (AC) | AC component frequency is 200 Hz | |
| Transient-state current | 5 kA 4.03 kA/ms and 0.25 kA/ms | Peak fault Current rise rate and decline rate | |
| Steady-state voltage | 22 kV | Peak value | |
| Transient-state voltage | 50 kV | Peak value | |
| Bridge arm L | Design inductance value of the L-BAR | 5 mH | |
| Steady-state current | −0.85 kA (DC) + 0.06 kA (AC) | AC component frequency is 200 Hz | |
| Transient-state current | 1.08 kA 0.23 kA/ms and 0.34 kA/ms | Peak fault Current rise rate and decline rate | |
| Steady-state voltage | 1.7 kV | Peak value | |
| Transient-state voltage | 30 kV | Peak value | |
| (mH) | N | (mm) | (mm) | (mm) | (m) | (m) | (m) | (mm) | (mm) | (mm) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CABAR | 5 | 75 | 950 | 980 | 35 | 0.95 | 0.98 | 3.035 | 5 | / | / |
| AABAR | 5 | 111 | 950 | 980 | 35 | 0.6 | 2.56 | 1.96 | / | 4.29 | 141.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, T.; Yang, Z. Comparative Analysis of Magnetic Field Distribution Characteristics of Two Shapes of Air-Core Bridge Arm Reactors. Energies 2024, 17, 4652. https://doi.org/10.3390/en17184652
Jiang T, Yang Z. Comparative Analysis of Magnetic Field Distribution Characteristics of Two Shapes of Air-Core Bridge Arm Reactors. Energies. 2024; 17(18):4652. https://doi.org/10.3390/en17184652
Chicago/Turabian StyleJiang, Tao, and Zhe Yang. 2024. "Comparative Analysis of Magnetic Field Distribution Characteristics of Two Shapes of Air-Core Bridge Arm Reactors" Energies 17, no. 18: 4652. https://doi.org/10.3390/en17184652
APA StyleJiang, T., & Yang, Z. (2024). Comparative Analysis of Magnetic Field Distribution Characteristics of Two Shapes of Air-Core Bridge Arm Reactors. Energies, 17(18), 4652. https://doi.org/10.3390/en17184652





