Abstract
Addressing the challenges of significant speed overshoot, stability issues, and system oscillations associated with the sliding mode control (SMC) strategy in maximum power point tracking (MPPT) for permanent magnet synchronous wind power systems, this paper introduces a fuzzy sliding mode control (FSMC) method employing an innovative exponential convergence law. By incorporating a velocity adjustment function into the traditional exponential convergence law, a novel convergence law was designed to mitigate oscillations during the sliding phase and expedite the convergence rate. Additionally, a fuzzy controller was developed to implement a fuzzy adaptive SMC strategy, optimizing the MPPT for permanent magnet synchronous wind power generation systems. Simulation results indicated that this approach offered a faster response and superior interference rejection capabilities, compared to conventional and modified SMC strategies. The improved FSMC strategy demonstrated a swift, dynamic response and excellent steady-state performance, improving the efficiency of MPPT, thus confirming the effectiveness of the proposed method.
1. Introduction
Compared to conventional fossil fuels, wind energy offers economic, environmental, and renewable benefits. Utilizing wind power as a clean energy technology is crucial for addressing environmental pollution and conserving non-renewable energy resources. Consequently, wind power generation is progressively emerging as a key player in the power generation sector. Given the stochastic, time-variant, and abrupt characteristics of wind energy signals, it is imperative to investigate the MPPT of wind power systems to enhance the efficiency of wind energy utilization [1,2].
In current wind power systems, the prevalent types of generators are doubly-fed induction generators (DFIG) and permanent magnet direct-drive synchronous generators (D-PMSG). The D-PMSG, in comparison to the DFIG, eliminates the need for a gearbox, allowing the wind turbine to directly drive the generator [3]. This approach not only reduces maintenance costs but also significantly enhances the system’s operational reliability [4], thus emerging as a significant developmental trend in the wind energy sector.
Owing to the permanent magnet synchronous generator’s nature as a nonlinear, highly coupled, multivariable system, it is subject to numerous external disturbances [5,6]. The presence of such disturbances can impact the generator’s rotor speed, consequently affecting the quality of MPPT and the efficiency of wind energy utilization [7,8]. Traditional linear proportional-integral (PI) controllers are inadequate for precise speed tracking, due to their limited capacity to suppress disturbances and their slow response, which fails to meet the demands of high-performance control. Therefore, a control loop with rapid response is necessary to ensure the system’s stability, accuracy, and dynamic responsiveness [9,10]. To address these challenges, scholars have proposed various nonlinear control strategies as alternatives to conventional PI controllers, including SMC [11], predictive control [12], fuzzy logic control [13], and neural network control [14].
Given the stochastic and abrupt nature of wind speeds, SMC is extensively utilized in permanent magnet synchronous wind power systems, due to its rapid response and robustness against parameter variations and disturbances [15,16]. However, when traditional SMC strategies are employed in the speed regulation systems of permanent magnet synchronous motors, the inherent simplicity of the system structure and the imprecise control over the convergence speed can result in pronounced chattering. However, the application of traditional SMC in D-PMSG speed regulation systems can lead to significant overshoot, stemming from the system’s singular structure and the lack of precise control over the convergence rate. To address these challenges, researchers have proposed innovative approaches, such as a novel variable-exponential convergence law [17], which incorporates system state variables to accelerate convergence while reducing oscillations. Despite these advancements, the issue of overshoot remains unresolved.
Further contributions include the integration of fuzzy adaptive control into the sliding mode observer [18], the application of a super-twisting high-order sliding mode algorithm [19], and the design of a power-law convergence law [20], all aimed at enhancing control precision and robustness. Additionally, the use of a disturbance observer [21] and a nonlinear extended state observer [22] has shown promise in improving system robustness, albeit with trade-offs in flexibility and adaptability. The employment of an extended Kalman filter in conjunction with fuzzy control [23] has refined MPPT for permanent magnet synchronous generator (PMSG)-based wind turbines, yet it is sensitive to initial parameter estimation. Lastly, Reference [24] integrates an enhanced sliding mode exponential reaching law with a disturbance observer to counteract the reference voltage variations that arise from motor parameter perturbations, thereby bolstering the system’s robustness to parametric variations.
In light of this, to enhance the MPPT performance of permanent magnet synchronous wind power systems, a speed regulation function was introduced into the SMC, which employs a traditional exponential reaching law. This introduction aimed to mitigate the chattering during the sliding mode approaching process and to expedite the convergence rate. Furthermore, by incorporating fuzzy logic control, an improved FSMC strategy was developed for MPPT. To substantiate the efficacy of this control strategy, a simulation model was established in Matlab/Simulink (version 9.7.0.1190202, R2019b), and the improved FSMC strategy was compared with both traditional SMC and other improved SMC strategies.
The main contributions of this paper can be outlined as follows:
(1) In this study, we optimized the traditional SMC by introducing a novel exponential approaching rate, which diminished the chattering during the MPPT process and expedited the system’s convergence rate, thereby enhancing the responsiveness of the control system.
(2) To further augment the control performance, we integrated fuzzy logic control with the refined SMC, resulting in an improved FSMC strategy. This integration capitalized on the adaptive nature of fuzzy logic, enhancing the system’s robustness to parameter variations and external disturbances.
(3) Through a comparative analysis of three control strategies under varying wind speeds, we confirmed the efficacy of the improved FSMC control strategy in elevating the wind energy utilization coefficient, optimizing the tip-speed ratio (TSR), and the rotor speed.
(4) The findings of the study demonstrated that the improved FSMC strategy can effectively enhance the MPPT capability of permanent magnet synchronous wind power generation systems, thus bolstering the overall system performance.
2. Permanent Magnet Synchronous Wind Power System
2.1. Wind Turbine Model
The structure of the maximum power tracking control system for the permanent magnet synchronous wind power generation system is depicted in Figure 1.
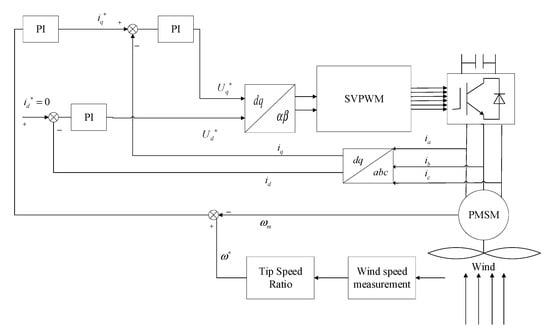
Figure 1.
Wind power system.
In the wind turbine model, the turbine is directly connected to the generator [25]. According to Bates’ theory, the following relationships hold:
In Equation (1), air density is denoted by , the blade radius of the wind turbine by , the wind energy utilization coefficient by , and the optimal tip-speed ratio by . The mechanical power captured is represented by , the mechanical torque by , and the rotational speed of the turbine by . Wind speed is denoted by , and the pitch angle of the blades is denoted by .
represents the efficiency of wind energy conversion and can be expressed as:
In Equation (2), represents an intermediate variable.
Equation (2) illustrates that the power coefficient is determined by both the tip-speed ratio and the pitch angle . As depicted in Figure 2, the power coefficient exhibits a nonlinear relationship with the TSR when the pitch angle is held constant. Each pitch angle is associated with an optimal TSR that maximizes the wind energy utilization coefficient. Notably, when the pitch angle , the system’s power coefficient reaches its peak value of 0.48, coinciding with an optimal TSR of 8.1. Thus, by adjusting the TSR, the wind energy utilization coefficient can be maximized, consequently achieving the objective of MPPT.
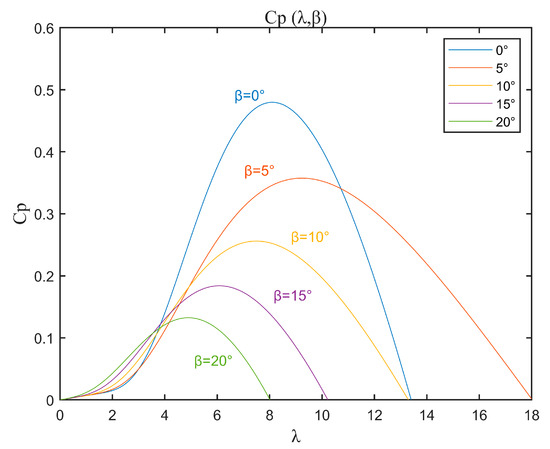
Figure 2.
Curve of .
2.2. Mathematical Model of PMSG
To elucidate the control mechanisms of a PMSG, it is essential to formulate a mathematical model that is conducive to the implementation of control strategies [26]. Initially, the following assumptions were made:
- The magnetic field in the air gap was assumed to be uniformly distributed.
- The generator structure was three-phase, uniformly symmetrical.
- The motor’s core had no magnetic saturation in the magnetic circuit.
- The slotting effect of the motor was ignored.
- The eddy current and hysteresis losses in the core were neglected.
In the interest of research and analytical expediency, this study adopted a mathematical model predicated on the d-q rotating reference frame, a standard approach in the analysis of PMSG dynamics [27]. The stator voltage equations of the motor, which are pivotal for the control strategy, were articulated by:
The motor magnetic chain equation was:
From this, the mathematical model of the PMSG in the d-q rotating reference frame can be obtained as:
The electromagnetic torque expression for PMSG was:
Due to the , Equation (6) can be simplified to:
Among them, . The motion equation for the PMSG was given by:
The d-q-axis voltages are denoted as and , respectively; the currents on the d-q-axis are represented by and , respectively; and the inductances of the d-q-axes are given by and , respectively. The stator resistance is signified by R. The number of pole pairs is designated as . The flux linkages on the d-q-axes are and , respectively; the magnetic flux is denoted by ; the electrical angular velocity is indicated by ; the damping coefficient is represented by ; and the moment of inertia is represented by .
3. Design of the Improved Sliding Mode Controller
3.1. Design of the Improved Convergence Rate
In the context of the speed loop’s SMC for PMSG wind power systems, a novel approach was developed to expedite convergence and mitigate oscillations. This approach refined the existing convergence law by integrating a velocity regulation function, thereby enhancing the performance of the system. Such advancements set the stage for the evolution of effective MPPT control strategies within wind energy systems.
In the process of constructing a speed-tracking SMC for a PMSG wind power generation system, it was essential to first identify a state variable. This study selected the tracking error relative to the reference angular velocity as the state variable, denoted by , and is defined as the derivative of with respect to time. To facilitate analysis and modeling and to reduce the complexity of the model, the damping winding of the rotor was neglected. The corresponding equation can be expressed as follows:
The reference speed of the generator, denoted as , varied with the wind speed. Substituting the aforementioned expression into the dynamic equation of the PMSG yielded the following equation:
denotes the control input, . Thus, we can derive the state equation as follows:
The system’s sliding surface was delineated by the following equation:
Taking the derivative, we obtained:
Applying the conventional exponential reaching law yielded the controller expression as follows:
In light of the limitations associated with traditional convergence laws, the present study introduced an innovative velocity modulation function. This function was designed to enhance the performance of the conventional exponential convergence law by providing a more nuanced control over the rate of approach. The details of this improvement are articulated in Equation (15), where the refined law is presented in a mathematical framework that addresses the identified deficiencies:
Here, f (s) represents the function superimposed on the constant velocity term, with its graphical representation depicted in Figure 3.
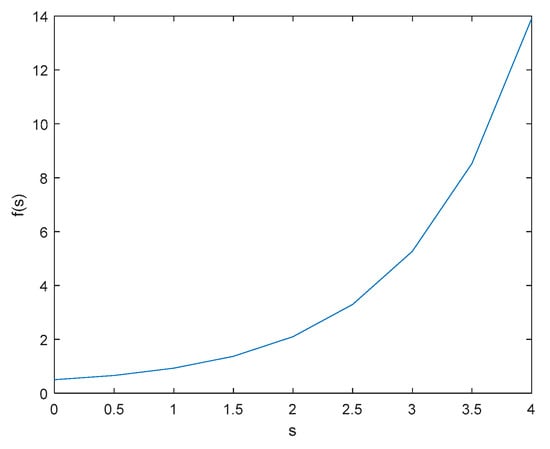
Figure 3.
Function image.
The following conclusions can be drawn regarding Equation (15):
(1) When the system operated at a considerable distance from the sliding surface, , and ; the convergence rate of the motion point at a distance can be accelerated. At this time, f (s) was a positive number; hence, the convergence speed exceeded that of the traditional exponential convergence law. This enhancement led to an improvement in the system’s response speed.
(2) As the system neared the sliding surface, , and , becoming a negative number. This resulted in the system’s convergence speed to the sliding surface being less than that of the traditional exponential convergence law. Consequently, this was advantageous for reducing the inertial distance the motion point must traverse to cross the sliding surface, which helped to minimize the system’s oscillations and enhanced the control precision.
The expression for the controller, after improvement, was as follows:
Figure 4 displays the structural diagram of the improved exponential reaching law controller.
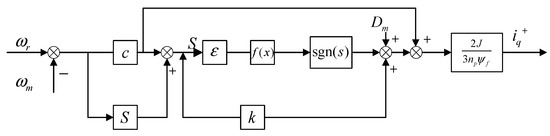
Figure 4.
Improved exponential approach law control structure diagram.
The q-axis reference current can be represented as:
3.2. Comparison of Convergence Speeds of the Improved Exponential Reaching Law
The variable speed term of the improved exponential convergence law after introducing the regulatory function was:
After solving the integral for it, the convergence time t was obtained as:
In the conventional exponential convergence law, the uniform speed term was:
The uniform speed term in the conventional exponential reaching law was:
, creating a function plot of ‘t’ and Δt with respect to the system’s initial state , as shown in Figure 5.
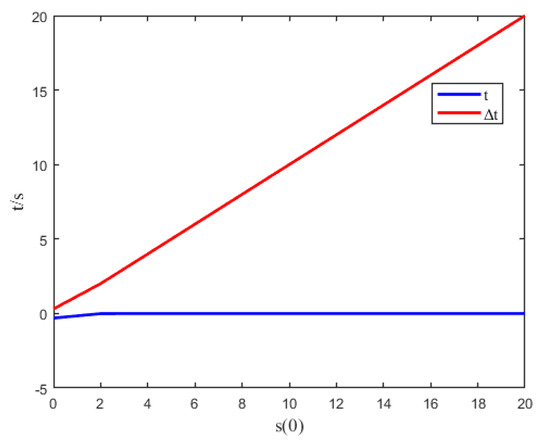
Figure 5.
Comparing the curves.
From the figure, it can be seen that Δt > 0, indicating that under the control of the improved exponential convergence law, the system reached the sliding mode surface faster and in a shorter time compared to the control under the traditional exponential convergence law.
3.3. Verification of Sliding Mode Controller Stability
According to the Lyapunov stability principle, to ensure the stability of the SMC, it is necessary to satisfy the following conditions:
From the conditions above, it can be concluded that:
It can be observed that the signs of and in the first term were the same, and the second term was greater than 0; therefore the condition was satisfied.
4. Fuzzy Controller Design
4.1. Fuzzification in Fuzzy Logic Systems
According to the Lyapunov stability principle, the following is known:
When the system reaches the sliding surface, it is necessary to determine whether component will remain on the sliding surface. To ensure that the system’s motion reaches the sliding surface, the control gain must be sufficiently high to counteract the effects of uncertainty terms. The fuzzy rules for this are as follows:
- If , then should be increased.
- If , then should be decreased.
In the process of fuzzification, precise data must first be mapped to fuzzy quantities through the establishment of appropriate fuzzy rules. Based on the logical relationship between and , the fuzzy sets for the inputs and outputs of the fuzzy control system can be defined as follows:
In the equations, ‘Negative Big’ is denoted by NB, ‘Negative Medium’ by NM, ‘Zero’ by ZO, ‘Positive Medium’ by PM, and ‘Positive Big’ by PB. The membership functions for both the inputs and outputs are illustrated in Figure 6 and Figure 7.
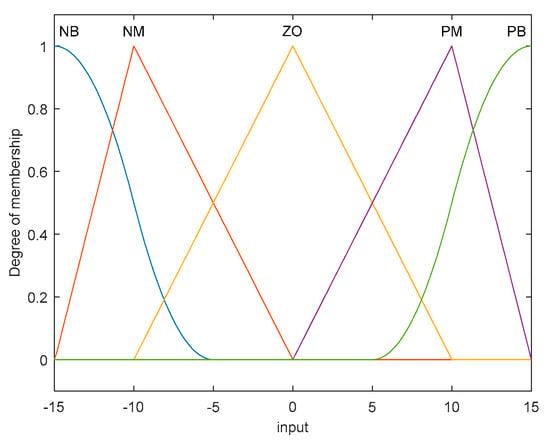
Figure 6.
Membership functions of fuzzy inputs.
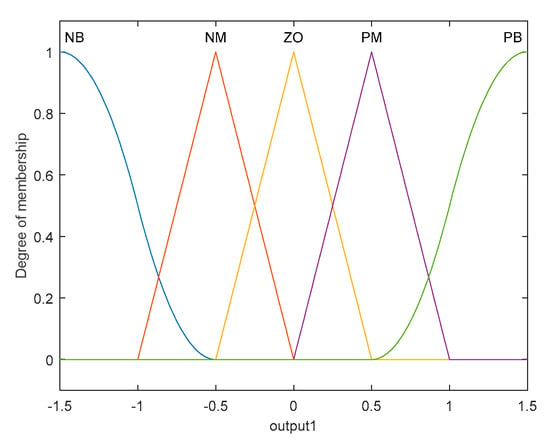
Figure 7.
Membership functions of fuzzy outputs.
Based on Figure 6 and Figure 7, when the system is tending towards stability, the gain K should be set to a higher value. Conversely, when the system deviates from the reference trajectory, a lower value for the gain K is appropriate. Additionally, in the presence of disturbances, to prevent excessive system oscillations, the gain K should also be selected to be relatively high.
4.2. Fuzzy Rules
Based on the logical relationship between and , the fuzzy rules were derived, as shown in Table 1.

Table 1.
Fuzzy rules.
An estimation of the upper bound of can be made using the following integration:
where R is the proportional function, and .
Replacing in Equation (20) with , the control law became:
The structure diagram of the established combined strategy of sliding mode control and fuzzy control is shown in Figure 8.
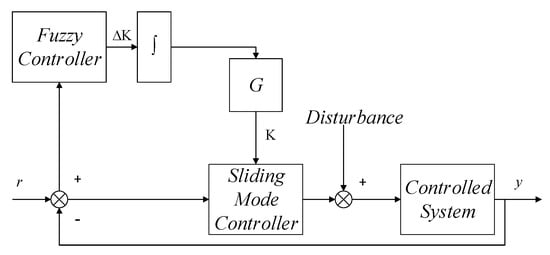
Figure 8.
Controller structure.
5. Simulation and Results
To evaluate the efficacy of the proposed control strategy, comparisons were made between the improved FSMC approach and both the traditional SMC and other improved SMC strategies. The parameter design was as follows: Simulations were conducted in the MATLAB/Simulink environment using the control system configuration outlined in Figure 9, with motor parameters specified in Table 2 [26]. In the SMC, the parameters were designed to be , , and .
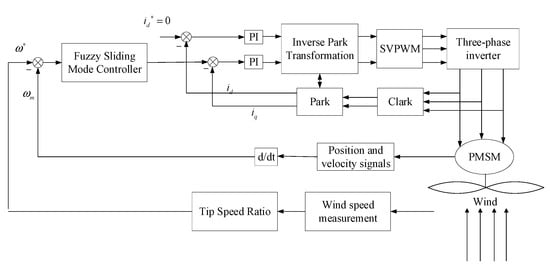
Figure 9.
Control system structure diagram.

Table 2.
Settings of wind power system parameters.
The performances under both stepped and composite wind speed conditions were evaluated based on key indicators, including the wind energy utilization coefficient, rotor speed, and TSR. This comparative analysis was conducted to validate the effectiveness of the proposed control method and to highlight its advantages over existing strategies.
Furthermore, the step wind speed was set to transition from 6 m/s to 10 m/s at 1 s. To more accurately capture the stochastic and intermittent characteristics of wind energy, the spatiotemporal model of wind speed fluctuations typically delineated the composite wind into four distinct components: the base wind, gust, random wind, and gradient wind, as depicted in Figure 10, with an additional illustration provided in Figure 11 for clarity.
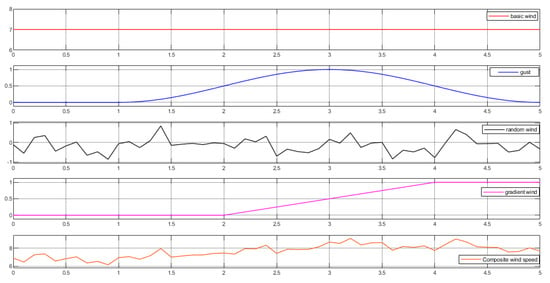
Figure 10.
Composite wind speed composition.
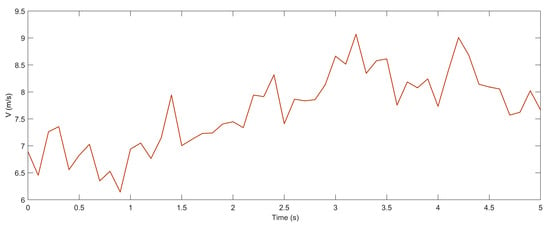
Figure 11.
Composite wind speed.
Simulation Result Analysis
Initially, the system was validated under step-change wind speed conditions. Figure 12, Figure 13 and Figure 14 present comparative diagrams of the wind energy utilization coefficient, generator rotational speed tracking, and TSR, respectively, under traditional SMC, improved SMC, and improved FSMC strategies. The relationship between d-axis and q-axis currents under the three control strategies is depicted in Figure 15 and Figure 16.
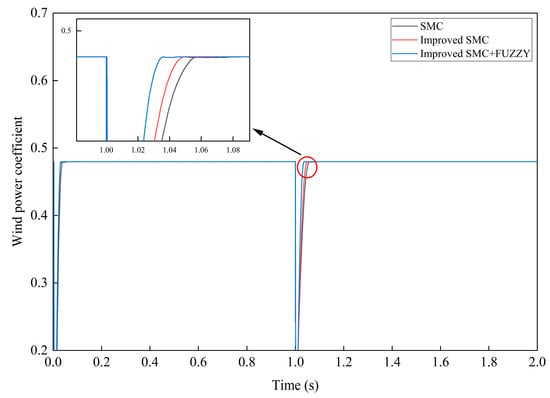
Figure 12.
Wind power coefficient comparison.
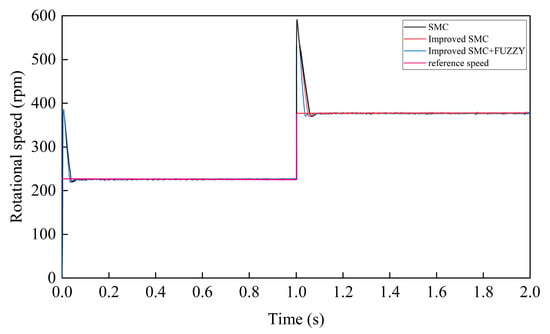
Figure 13.
Motor rotation speed comparison.
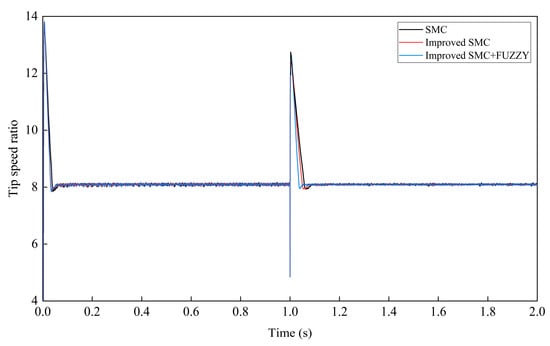
Figure 14.
Tip-speed ratio comparison.
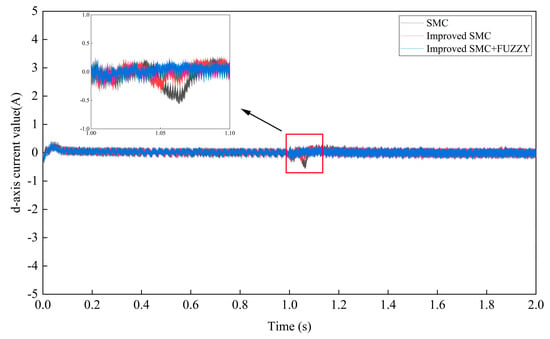
Figure 15.
The d-axis current under three control strategies.
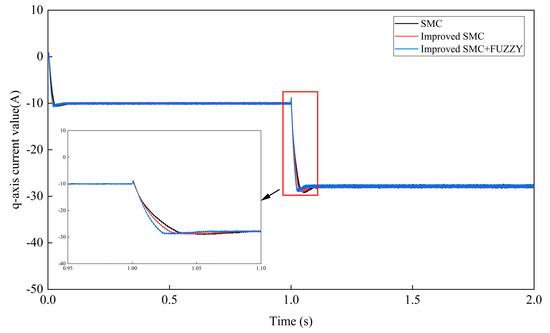
Figure 16.
The q-axis current under three control strategies.
Figure 12 illustrates a comparison of the wind energy utilization coefficient under three control strategies. The improved FSMC strategy and the improved SMC strategy exhibited a faster response, compared to the traditional SMC strategy. Initially, the difference between the improved FSMC and the improved SMC was not significant, but over time, the improved FSMC adapted its parameters autonomously, resulting in a quicker response for the wind power system. At 1 s, when the wind speed stepped up to 10 m per second, the increase in rotational speed caused the wind energy utilization coefficient to deviate from its optimal state. The permanent magnet direct-drive wind power system automatically adjusted the blade pitch through pitch control and adjusted the rotor speed through variable speed control to bring the wind energy utilization coefficient back to its optimal state. Consequently, the wind energy utilization coefficient initially decreased and then stabilized at 1.035 s, whereas other strategies stabilized after 1.04 s, as shown in Figure 12. Therefore, the improved FSMC strategy demonstrated shorter response times and a faster stabilization efficiency.
Figure 13 illustrates a comparison of rotational speeds for the three control strategies. During the initial second of static stable operation, the rotational speed was maintained at 225 rad/s. At the wind speed step change at 1 s, the improved FSMC strategy showed a faster tracking speed, reaching the reference rotational speed and stabilizing at 376 rad/s by 1.05 s. While all three control methods ensured the static rotational stability of the wind power system, they exhibited differences in response speed. The improved FSMC strategy more effectively tracked the reference rotational speed, with a significantly better response and tracking performance, compared to the others.
Figure 14 shows a comparison of the TSRs for the three control strategies. Under steady wind conditions, the system’s TSR stabilized at the standard value of approximately 7.8 for all strategies, with the wind energy utilization coefficient stabilizing at around 0.48. However, the improved strategy proposed in this study reached the maximum value of the wind energy utilization coefficient more rapidly, offering higher power output efficiency and achieving optimal power output.
Figure 16 indicates that the overshoot of the current was relatively small for all three control strategies. However, the improved FSMC strategy exhibited a shorter response time to reach a stable state upon wind speed change at 1 s. Additionally, Figure 15 shows that the fluctuations of the d-axis current were significantly less at 1 s, compared to the other strategies. Therefore, the improved FSMC strategy was considered more stable.
The system was subsequently tested under composite wind speed conditions. Figure 17, Figure 18 and Figure 19 present comparative waveforms of generator rotational speed, wind energy utilization coefficient, and TSR, respectively, under traditional SMC, improved SMC, and improved FSMC strategies.
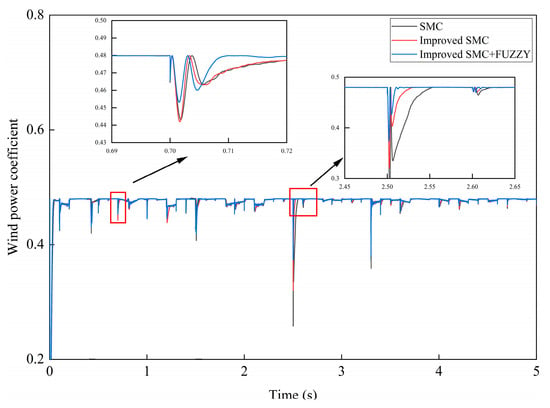
Figure 17.
Wind power coefficient comparison under composite wind speed.
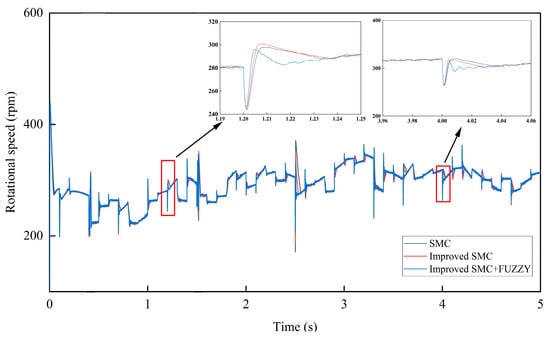
Figure 18.
Motor rotation speed comparison under composite wind speed.
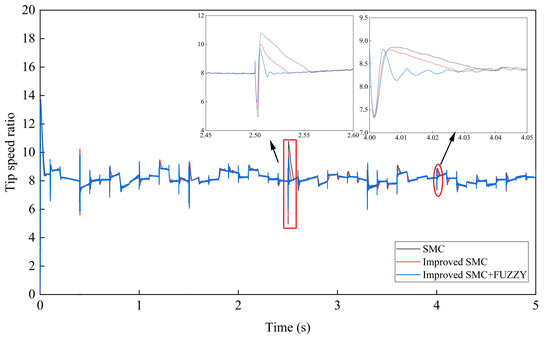
Figure 19.
Tip-speed ratio comparison under composite wind speed.
From Figure 17, it is evident that the wind energy utilization coefficient under the improved FSMC strategy exhibited a significantly reduced overshoot, compared to the other two methods, under varying natural wind speeds. Although all three methods can maintain the wind energy utilization coefficient around 4.8, randomly selected segments from the waveform for local magnification revealed that the improved FSMC strategy had a shorter response time, reached a steady state more quickly, and also reduced the overshoot.
Figure 18 demonstrates that the permanent magnet synchronous wind power generation system under the improved FSMC strategy rapidly responded to wind speed changes, showing a significantly enhanced response speed, compared to the other two strategies. Comparing from the locally magnified plots, it was found that the proposed improved FSMC strategy reduced the overshoot and increased the approach speed, showing the best performance, compared to the other two control strategies.
In Figure 19, the TSR under the improved FSMC strategy quickly entered a narrow range close to the optimal value. The TSR was maintained close to the set optimal value of 8.1. As can be seen from the local magnified plots, it reduced the overshoot and improved the response speed, compared to the other two methods, thus providing the best power output efficiency and system stability. Therefore, it can be observed that regardless of step change or composite wind speeds, the improved FSMC strategy performed well and was significantly superior to the other two control strategies.
6. Conclusions
This study addressed the challenges of speed overshoot, stability, and system oscillation in the MPPT of permanent magnet synchronous wind power generation systems, which are commonly encountered with SMC strategies. We proposed an enhancement to the traditional exponential convergence rate used in sliding mode controllers by incorporating a speed regulation function to design a novel convergence rate. The improved SMC strategy not only mitigated the chatter during the sliding surface reaching phase but also expedited the convergence process. To further refine the performance, a strategy integrating fuzzy logic control with the improved SMC was introduced. Simulation results demonstrated that the application of the improved FSMC strategy in permanent magnet synchronous wind power generation systems, under diverse wind speed conditions, offered a swift dynamic response and a superior steady-state performance, thus enhancing the efficiency of MPPT.
The limitations of this paper lie in the modeling and analysis of the permanent magnet synchronous generator, where the damping winding was omitted, thereby neglecting the transmission friction. The wind power generation system we established was relatively idealized. In practical engineering, the impact of transmission friction needs to be further considered. Moreover, our research focused on the control of the speed loop in the permanent magnet synchronous wind power system, without improvements to the current loop, which continued to use traditional PI control. In our future work, we plan to take a practical approach, aiming to simultaneously improve both the speed loop and current loop of the permanent magnet synchronous wind power generation system, and consider the effects of transmission friction on the system.
Author Contributions
Software, X.W.; Validation, L.L.; Formal analysis, L.L.; Data curation, A.L.; Writing—review & editing, L.L.; Supervision, H.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chang, Y.-C.; Chang, H.-C.; Huang, C.-Y. Design and implementation of the permanent-magnet synchronous generator drive in wind generation systems. Energies 2018, 11, 1634. [Google Scholar] [CrossRef]
- Qiao, W.; Lu, D. A survey on wind turbine condition monitoring and fault diagnosis—Part II: Signals and signal processing methods. IEEE Trans. Ind. Electron. 2015, 62, 6546–6557. [Google Scholar] [CrossRef]
- Wang, G.; Valla, M.; Solsona, J. Position sensorless permanent magnet synchronous machine drives—A review. IEEE Trans. Ind. Electron. 2019, 11, 5830–5842. [Google Scholar] [CrossRef]
- Wang, Y.; Meng, J.; Zhang, X.; Xu, L. Control of PMSG-based wind turbines for system inertial response and power oscillation damping. IEEE Trans. Sustain. Energy 2015, 6, 565–574. [Google Scholar] [CrossRef]
- Ghouraf, D.E. An advanced control applied to PMSG wind energy conversion system implemented under graphical user interface. Electr. Eng. 2023, 105, 3841–3852. [Google Scholar] [CrossRef]
- Mayilsamy, G.; Lee, S.R.; Joo, Y.H. An improved model predictive control of back-to-back three-level NPC converters with virtual space vectors for high power PMSG-based wind energy conversion systems. ISA Trans. 2023, 143, 503–524. [Google Scholar] [CrossRef]
- Xiong, L.; Shi, H.; Zhu, Q. Maximum power tracking strategy of a wind energy conversion system based on resonant with active disturbance rejection control. Robot. Intell. Autom. 2023, 43, 637–647. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Zhang, Y.; Chen, J.; Sang, Y.; Jiang, L. Passivity-based sliding-mode control design for optimal power extraction of a PMSG based variable speed wind turbine. Renew. Energy 2018, 119, 577–589. [Google Scholar] [CrossRef]
- Jiang, P.; Zhang, T.; Geng, J.; Wang, P.; Fu, L. An MPPT Strategy for Wind Turbines Combining Feedback Linearization and Model Predictive Control. Energies 2023, 16, 4244. [Google Scholar] [CrossRef]
- Le, X.C.; Duong, M.Q.; Le, K.H. Review of the modern maximum power tracking algorithms for permanent magnet synchronous generator of wind power conversion systems. Energies 2022, 16, 402. [Google Scholar] [CrossRef]
- Li, S.; Wang, H.; Li, H.; Yang, C. PMSM sliding mode control based on novel reaching law and extended state observer. Adv. Mech. Eng. 2022, 14, 1–16. [Google Scholar] [CrossRef]
- Chen, J.; Liu, J.; Zhang, Y. Predictive control of permanent magnet synchronous motor based on optimization model algorithmic control. Int. J. Adv. Comput. Technol. 2013, 50, 1027–1035. [Google Scholar]
- Wang, C.; Zhu, Z.Q. Fuzzy logic speed control of permanent magnet synchronous machine and feedback voltage ripple reduction in flux-weakening operation region. IEEE Trans. Ind. Appl. 2020, 56, 1505–1517. [Google Scholar] [CrossRef]
- Kumar, V.; Gaur, P.; Mittal, A.P. ANN based self-tuned PID like adaptive controller design for high performance PMSM position control. Expert Syst. Appl. 2014, 41, 7995–8002. [Google Scholar] [CrossRef]
- Mobayen, S.; Tchier, F. Nonsingular fast terminal sliding mode stabilizer for a class of uncertain nonlinear systems based on disturbance observer. Sci. Iran. D 2019, 24, 1410–1418. [Google Scholar] [CrossRef]
- Zheng, X.; Song, R.; Feng, Y.; Ben, H.; Zhu, M. Nonsingular terminal sliding mode control for Uncertain Actuator Systems. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; IEEE: New York, NY, USA, 2016; Volume 42, pp. 247–251. [Google Scholar]
- Wang, A.; Jia, X.; Dong, S. A new exponential reaching law of sliding mode control to improve performance of permanent magnet synchronous motor. IEEE Trans. Magn. 2013, 49, 2409–2412. [Google Scholar] [CrossRef]
- Peng, S.Q.; Song, Y.Y. Sensorless vector control of PMSM based on adaptive fuzzy sliding mode observer. Control Decis 2018, 33, 644–648. [Google Scholar]
- Lin, X.; Zhang, B.; Fang, S.; Xu, R.; Guo, S.; Liu, J. Adaptive generalized super twisting sliding mode control for PMSMs with filtered high-gain observer. ISA Trans. 2023, 138, 639–649. [Google Scholar] [CrossRef]
- Dash, P.K.; Patnaik, R.K.; Mishra, S.P. Adaptive fractional integral terminal sliding mode power control of UPFC in DFIG wind farm penetrated multimachine power system. Prot. Control Mod. Power Syst. 2018, 3, 1–14. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, J.; Li, H.; Liu, J.; Tian, D. Adaptive sliding mode current control with sliding mode disturbance observer for PMSM drives. ISA Trans. 2019, 88, 113–126. [Google Scholar] [CrossRef]
- Liu, C.; Luo, G.; Tu, W.; Wan, H. Servo systems with double closed-loops based on active disturbance rejection controllers. Proc. Chin. Soc. Electr. Eng. 2017, 37, 7032–7039. [Google Scholar]
- Honarbari, A.; Najafi-Shad, S.; Saffari Pour, M.; Ajarostaghi, S.S.M.; Hassannia, A. MPPT improvement for PMSG-based wind turbines using extended Kalman filter and fuzzy control system. Energies 2021, 14, 7503. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, B.; Mei, Y. Deadbeat predictive current control of permanent-magnet synchronous motors with stator current and disturbance observer. IEEE Trans. Power Electron. 2016, 32, 3818–3834. [Google Scholar] [CrossRef]
- Ran, H.; Wei, W.; Gao, Y. Design of Permanent Magnet Synchronous Wind Power Control System. Prog. Electromagn. Res. C 2023, 139, 11–21. [Google Scholar] [CrossRef]
- Yuan, S. Research on MPPT Method of Directly-Driven Permanent Magnet Synchronous Generator Based on Improved Sliding Mode Controller. Master’s Thesis, Jiangnan University, Wuxi, China, 2022; p. 68. [Google Scholar]
- Yin, M.; Li, G.; Zhang, J. Modeling and control strategies of directly driven wind turbine with permanent magnet synchronous generator. Power Syst. Technol. 2007, 31, 61. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).