Abstract
The deployment of photovoltaic (PV) systems has increased globally to meet renewable energy targets. Intermittent PV power generated due to cloud-induced variability introduces reliability and grid stability issues at higher penetration levels. Variability in power generation can induce voltage fluctuations within the distribution system and cause adverse effects on power quality. Therefore, it is essential to quantify resource variability to mitigate an intermittent power supply. In this study, we propose a new scheme to classify the sky conditions that are based on two common variability metrices: daily clear-sky index and normalized aggregate ramp rates. The daily clear-sky index estimates the cloudiness in the sky, and ramp rates account for the variability introduced in the system generation due to sudden cloud movements. This classification scheme can identify clear-sky, highly variable, low intermittent, high intermittent and overcast days. By performing a Chi-square test on the training and test sets, we obtain Chi-square statistic values greater than 3 with p-value > 0.05. This indicates that the distribution of the training and test clusters are similar, indicating the robustness of the proposed sky classification scheme. We have demonstrated the applicability of the scheme with diverse datasets to show that the proposed classification scheme can be homogenously applied to any dataset globally despite their temporal resolution. Using various case studies, we demonstrate the potential applications of the scheme for understanding resource allocation, site selection, estimating future intermittency due to climate change, and cloud enhancement effects. The proposed sky classification scheme enhances the precision and reliability of solar energy forecasts, optimizing system performance and maximizing energy production efficiency. This improved accuracy is crucial for variability control and planning, ensuring optimal output from PV plants.
1. Introduction
The global capacity of solar photovoltaic (PV) systems has increased exponentially in recent years and is expected to grow more than tenfold by 2050 [1]. With the increase in PV penetration levels in the existing electricity grid, weather-induced variability in power output has become extremely significant. Variability in the amount of power generated can impact the supply–demand ratio and grid stability by influencing the voltage and frequency [2]. Periods of high energy demand combined with high variability from solar sources strain the grid, making it difficult to balance supply and demand. This increases the risk of instability, leading to higher operational costs and potential power outages. To address these sudden changes in the voltage caused due to sudden fluctuations in the power output (called ramps), plant operators usually use ramp control devices [2,3]. Battery energy storage (BES) systems are effective for storing excess generation during clear-sky days and then supplying this excess during energy deficit periods. BES can charge/discharge depending on the PV generation during the day. Countries such as Germany and Denmark rely on grid interconnections with other countries and thermo-electric generators to mitigate energy deficit periods due to lower renewable energy generation [4].
The variability in solar resources is studied on multiple timescales depending on the requirement. Understanding short-term solar resource variability (seconds to minutes) is important for ramp detection and forecasting, while long-term variability studies (daily to decadal scale) is important for resource estimation, site assessment, system design, and estimating storage requirements [2,5,6]. The grid-connected PV systems are usually designed based on their highest generating capacity, such as those observed during clear-sky conditions.
In the past, there have been several studies dedicated towards developing and improving the clear-sky models [7,8,9,10,11]. The latest clear-sky models take into account the complex atmospheric composition, are dependent on the location, and can precisely forecast clear-sky irradiance. However, despite having some of the best-performing clear-sky models [7,8], identifying daily sky conditions remains a challenge. The daily clear-sky index (DCI) is one of the most commonly used sky classification metrics [12,13]. It considers the ratio of the daily all-sky global horizontal irradiance (GHI) and daily clear-sky GHI to distinguish clear, cloudy, and overcast days. When the DCI is close to one, it is considered as a clear-sky day, and when it is close to zero, it is classified as an overcast day. Even though the DCI is one of the simplest metrics for sky classification, it does not account for the variability in irradiance due to clouds.
Ramps are a widely used metric for understanding variability in the power generated from a PV system. They are sudden fluctuations in the irradiance or the amount of power generated during the day due to cloud movements. The expected ramp rates observed in a utility-scale PV plant are a function of the timescale, time of day, the plant’s size, cloud coverage, and movement. Ramps can increase electricity prices by creating an imbalance in the grid. This usually requires expensive and fast-responding backup generation to quickly meet the demand or stabilize supply, thereby driving up costs. Most solar plants have ramp control devices to stabilize the voltage fluctuations and ensure power quality, thereby increasing the installation and maintenance costs. To characterize the daily variability of utility-scale PV plants, van-Harren et al. [4] proposed a metric called the Daily Aggregate Ramp Rate (DARR). They classified the days into five categories ranging from very stable days (category 1) to highly variable days (category 5). One of the problems with these categories is that they are arbitrary and have no rationale as to how they were chosen. While DARR captures variability, it fails to distinguish clear-sky and cloudy days. Both these days are categorized as very stable days, which can be misleading while determining the generation capacity. We would expect very low power generation on a cloudy day as opposed to a clear day. Furthermore, DARR values vary depending on the geographic location of the plant, length of the day, and seasons. DARR values depend on the interval in which the data is recorded. For example, DARR calculated using data collected at every five minutes will have a higher value as opposed to DARR calculated with data recorded every hour for the same location.
Stein et al. [14] used an “arrowhead plot” classification based on the variability index and daily clearness index to identify the prevalent daily sky conditions for a location. The variability index is the ratio of the length of the all-sky GHI to a clear-sky GHI over a time interval. An arrowhead plot can categorize a day into either of these four categories: clear-sky day, overcast day, highly variable day, and variable day based on the daily variability index and DCI value. Even though this method can capture the variability observed during the day and accurately categorize the sky condition, this metric works only for data with a higher resolution. The arrowhead plot classification fails when applied to data with a resolution of 30 min or higher. Kreuwel et al. [15] have proposed a classification scheme for categorizing PV yield. They use normalized daily variability index and surface integral of PV output or GHI to categorize high yield, highly variable yield, and low yield days. Their classification scheme considers partially intermittent days as highly variable days. It is critical for the plant owners and grid operators to distinguish highly variable days from low intermittent and high intermittent days to accurately estimate the storage requirements and schedule for the battery charge/discharge time.
The application of machine learning clustering technique for the solar energy industry has been widely studied in the past for grouping regions with similar resource potential [16,17] and forecasting [18,19,20,21,22,23]. The machine learning clustering method k-means has been previously used to categorize the days into clear, cloudy, cloudy in the morning, and cloudy in the afternoon categories for Malaga, Spain [19]. They combine this clustering method with regression algorithms like decision trees, support vector machines, and artificial neural networks to forecast the day-ahead clearness index for the region. Similarly, k-means clustering combined with a multilayer neural network has been used to analyze the hourly GHI from daily GHI profiles for six locations in North Africa [23]. Ayodele et al. [24] combine the k-means clustering technique with support vector regression to improve the GHI forecasts.
Hartman et al. [25] performed a comparative study for different clustering techniques (k-means clustering, fuzzy c-means, and multiple fuzzy c-means) to categorize clear, cloudy, and partial cloudy days for Budapest, Hungary using 1-year time series data. This study lacks a robust comparison with long-term data to comment on the mean clear, cloudy, and partial-cloudy days annually. This is because the analysis of short-term data period like 1-year of data can have interannual variability in them. A non-hierarchical clustering method using the clearness index and DARR was proposed by da Rocha et al. [26] to calculate cloudless percentage days (CPD). CPD quantifies cloud cover variability based on the percentage of days showing the best condition for solar power generation. It can be useful for identifying suitable locations for deploying concentrated solar power plants. This cluster only considers four sky categories, and it is mostly suitable for high resolution temporal data. Temporal resolution of the data corresponds to frequency in which the data is recorded. For example, data recorded every second or every few minutes are higher temporal resolution data, unlike lower temporal resolution data recorded at every 30 min, 1 h, 3 h, daily, etc.
To date, all the studies dedicated towards identifying sky conditions are based on high resolution temporal data ranging from seconds to minutes. While meteorological station data are widely used for validating, forecasting, and data analysis in the solar energy industry, these stations are often sparsely spaced and most of them have issues such as missing periods, lack of timely calibration, and maintenance. As a result, researchers use freely available global datasets from satellites, reanalysis, and climate projections, which are available at 1-hourly or lower temporal resolutions. This makes it challenging to use the previous sky conditions that are developed for high temporal resolution data. Moreover, a vast majority of the studies using machine learning in the solar energy industry are heavily focused on improving forecasts and most importantly validating the best model for this purpose. There are very limited studies on clustering for identifying sky conditions and all of them are performed for a single location. This limits the sky classifications from the previous studies to be applied to other regions of interest. In order to address these limitations, this study aims to propose a new sky classification scheme that can be homogenously applicable to datasets with any temporal resolution globally. This study uses a clustering technique to classify sky conditions into five days: clear days, overcast days, low intermittent days, high intermittent days, and highly variable days. The proposed method can also be applied for spatial analysis of the different sky conditions globally. In addition, the potential applications of this novel classification scheme are assessed to demonstrate its advantages. We show the application of this scheme in resource assessment and determining new site locations, understanding future intermittency and cloud enhancement studies.
2. Data Used
The sky condition of a region is dominated by the local weather conditions, and, hence, depending on their location, one might experience more frequent clear-sky, overcast, or intermittent days. Therefore, we have examined various sky conditions across different regions by analyzing weather data from diverse locations and datasets. We use weather station data from the Australian Bureau of Meteorology (BOM) for six Australian cities situated in distinct climatic zones according to the Koppen climate classification for creating clusters and classification scheme. An overview of the location of the weather stations is given in Table 1. We have analyzed 20 years of data spanning from 2000 to 2020 for these locations at 5 min, 30 min, and 60 min resolutions. Additionally, we use the European Centre for Medium Range Weather Forecasts (ECMWF) Reanalysis (ERA5) 1-hourly data for 2022 and PV power data from a monocrystalline silicon system located in the Desert Knowledge Australia Solar Centre (DKASC), Alice Springs (time period 2010–2016) recorded at 5 min to demonstrate the applications of the proposed scheme. ERA5 reanalysis dataset has 0.25° latitude X 0.25° longitude spatial resolution. We use ACCESS1.3 regional climate model projections from Coordinated Regional Downscaling Experiment (CORDEX) to demonstrate the use of the proposed scheme for understanding future intermittency for the largest solar farm in the world, Powell Creek. Powell Creek solar farm is under construction in Northern Territory, Australia. We use climate projection data for the historical period (1976–2005) and future period (2030–2059) under a high emission RCP8.5 scenario. Under RCP8.5, the surface warming is projected up to 4.8 °C by the end of the century. Climate projections from ACCESS1.3 have 0.44° latitude X 0.44° longitude spatial resolution and 1-hourly data have been used in this study. These data have been previously used for renewable energy studies and has been validated for the historical period [2,5,27].

Table 1.
List of the BOM weather stations used in this study along with their climate type. The climate type is based on the Köppen–Geiger climate classification [28].
3. New Sky Classification Scheme
We propose a new sky classification scheme based on the DCI and normalized DARR (nDARR). The cloudiness at a location can be known by its DCI value. The DCI is close to one under clear-sky conditions and decreases with the decrease in daily radiation. On an overcast day, the DCI value is close to 0. The DCI can be estimated according to the following equation [12]:
The GHIcs is obtained from the Simplified SOLIS clear-sky model that has been validated in previous studies and was found to have the least bias [2,8,29].
To have a standardized sky classification scheme, it is important to have a location-independent variability metric. Since DARR values depend on the climatic conditions of that region and the interval in which the data is recorded, we make use of the nDARR metric in this study. The nDARR can be calculated using power output or the GHI data of a location. On a highly intermittent day with high cloud activity, the nDARR value will be closer to 1. The nDARR can be estimated according to the following equations:
The previous sky classification schemes define sky conditions as cloudy, clear-sky, and intermittent based on an arbitrary combination of the DCI, variability index, or PV output values without any justification as to how these were grouped [14,15]. In this study, we use a machine learning k-means clustering algorithm to identify the number of classes defined for the sky condition. The k-means clustering algorithm [30] is a technique for grouping data into clusters based on specified parameters. This method requires two user-defined inputs: the number of clusters (k) and the initial positions of the centroids of the clusters. In k-means clustering algorithm, each cluster is represented by its center, called the centroid. The centroid corresponds to the arithmetic mean of data points assigned to the cluster. Initially, centroids are randomly placed, and then each data point is assigned to the nearest centroid. Subsequently, the centroids are iteratively updated based on the data points assigned to each cluster, optimizing until the convergence is reached. The convergence is determined when the centroids stabilize, minimizing the weighted sum of squared deviations. The k-means algorithm essentially divides the time series data into different clusters with similarities, organizing the data based on minimum distances within a cluster and maximum distance among different clusters. It is important to note that the k-means algorithm assigns each data point to a cluster without considering scenarios outside the predefined clusters. It is one of the most popular and widely used unsupervised classification methods due to its applicability on large datasets. Apart from k-means, several other unsupervised clustering methods are commonly used, including hierarchical clustering, density based spatial clustering of applications with noise (DBSCAN), gaussian mixture models (GMM), and spectral clustering. Hierarchical clustering is particularly beneficial when forming a cluster hierarchy is necessary, especially when the cluster count is undefined, making it effective for smaller datasets where interpretability is key. DBSCAN is ideal for datasets with noise and irregularly shaped clusters, as it groups points based on density while identifying outliers. GMM is well suited for cases where clusters overlap, as it assigns data points to clusters probabilistically, allowing for greater flexibility in cluster shape. Spectral clustering is useful when dealing with complex data structures, such as non-convex clusters, and utilizes graph theory to efficiently separate data into distinct clusters. Hence, we use k-means clustering method in this paper. We use the freely available scikit-learn machine learning library in Python (version 3.12) programming language for this research [31]. This library has several functions on clustering (determining the optimal cluster), classification, regression, model selection, etc., and is fairly simple computationally.
The greatest difficulty for the application of k-means clustering lies in the prescription of the optimal number of clusters for data classification. We determine the number of clusters (the number of sky classification categories) by using the within-cluster sum of squares (WCSS) [32]. WCSS is also referred to as the elbow method. It runs k-means clustering on the dataset for a range of values for k (e.g., from 2 to 10) and then each value of k computes an average score for all clusters. It is based on the square distance between the centroid of the cluster and each cluster’s sample points. The optimal value of the cluster is found when the WCSS value drops on the curve drastically and forms a smaller angle. Figure 1 shows the WCSS for six locations in Australia. We can see an exponentially decreasing curve for the elbow method in Figure 1. The curve shows a significant decrease in the WCSS value at the third cluster (k = 3) and then a second dip for k = 5. It is inaccurate to use only three classes for sky classification as it wouldn’t account for the different intermittent conditions. It is important for the solar industry to obtain an accurate estimation of intermittent conditions that can be optimally determined if there are sub classifications for intermittent conditions. Further classification of intermittent sky conditions to high intermittent, low intermittent, and high variability can precisely indicate the variability due to cloud activity. Thus, this indicates that five clusters is the optimal value.
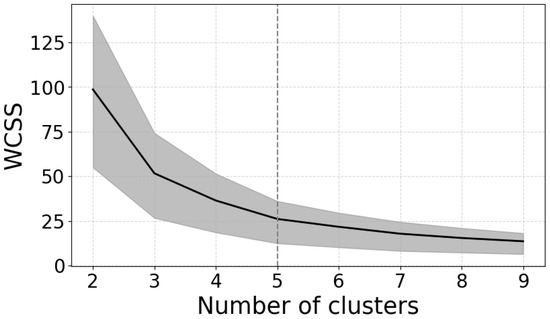
Figure 1.
Optimal number of clusters suggested by the elbow method. This figure shows the WCSS for different numbers of clusters formed with the data. The mean and the quantiles are represented with solid line and shading, respectively.
We use k-means clustering with k = 5 to obtain the five distinct clusters using all the locations. Figure 2 shows the five clusters obtained using k-means clustering algorithm for all the sites. Using combinations of the DCI and the nDARR value, the daily sky condition can be qualitatively categorized into five categories: clear-sky day (cluster 1), overcast day (cluster 2), low intermittent day (cluster 3), high intermittent day (cluster 4), and high variability day (cluster 5). On a perfect clear-sky day, the DCI value is very high (close to 1 or greater than 1) and has a lower nDARR. While on a cloudy day, one can expect lower DCI and nDARR values. On a low intermittent day, we would expect clear-sky conditions most of the time during the day, and hence it has low to medium variability. On the other hand, a high intermittent day is expected to have lower DCI with more frequent ramps. The high variability days have the highest nDARR values due to more frequent cloud activities during the day.
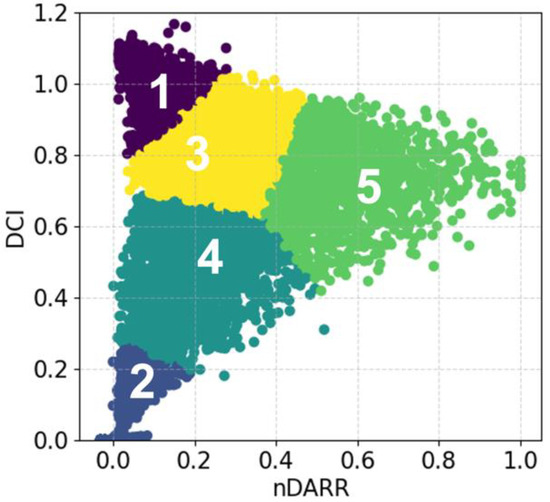
Figure 2.
DCI versus nDARR plot presenting data classes obtained using k-means algorithm applied to data from all sites. Different colors indicate different clusters.
We statistically assess how well the clusters performed by using a Chi-square test on testing and training sets. Chi-square test is performed to assess if two datasets are independent or similar. We randomly split two-third of the data from all the six stations into the training set and one-third of the data into the test set. We apply k-means clustering on both the test and training set and obtain five as the optimal number of clusters for both the sets. By performing the Chi-square test on the test and training set, we obtain the Chi-square test statistic to be 2.939 with a p-value of 0.58, indicating that the distributions in both the sets are similar. The distributions of clusters between the train and test sets are significantly different when the p-value is <0.05. We perform the Chi-square test for each location individually and test their significance. The Chi-square and p-values are mentioned in Table 2. We find that Chi-square statistic values are greater than 3 with p-value > 0.05 for all the locations. This indicates that the distributions of the clusters are similar for the train and test sets at every location.

Table 2.
Chi-square test statistic and p-value for the test and training sets obtained for different BOM weather stations used in this study.
To propose a simple scheme, we plot an “arrowhead” diagram using DCI and nDARR. We use the clusters created by the k-means method (Figure 2) to identify the boundary and the centroids. The classification scheme is shown in Figure 3 and the DCI and nDARR values for each category are explained below:
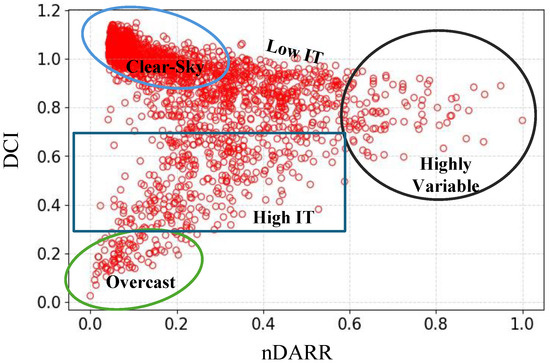
Figure 3.
Proposed sky classification scheme with five categories: clear-sky days, overcast days, low intermittent (low IT) days, high intermittent (high IT) days, and high variability days. This figure is obtained using BOM weather data for Alice Springs, Northern Territory, Australia for the period 2000–2020. Data points falling under the green, black, and light blue circle represent overcast, highly variable, and clear-sky days, respectively. The data points bounded by blue square represent high intermittent days and unbounded data points represent low intermittent days.
- Clear-Sky: nDARR ≤ 0.35 and DCI ≥ 0.9
- Overcast: nDARR ≤ 0.3 and DCI ≤ 0.3
- Low Intermittent: 0.35 < nDARR < 0.6 and DCI > 0.9 or nDARR < 0.6 and 0.7 < DCI < 0.9
- High Intermittent: nDARR ≤ 0.6 and 0.3 < DCI < 0.7
- High Variability: nDARR > 0.6
4. Case Study: Sky Classification for Alice Springs Using Data with Different Temporal Resolutions
We use BOM GHI data at a 5 min, 30 min, and 1 h temporal resolution for Alice Springs to evaluate if our classification scheme can be applicable to data with a lower temporal resolution. We show the GHI profiles for clear-sky, overcast, low intermittent, high intermittent, and highly variable days for Alice Springs in Figure 4. GHI values corresponding to all-sky and clear-sky conditions are plotted using blue and black lines, respectively. We randomly choose points corresponding to the cluster obtained above (Figure 3) and plot their GHI profiles for the data recorded at different time intervals. On a clear-sky day, the GHI profiles for clear-sky and all-sky radiation match perfectly. Similarly, we can see very low GHI values for overcast days. We can see that the overall GHI variability profile is preserved for the same day plotted with different data at different time intervals. However, the sudden changes in GHI or “ramps” observed in intermittent and highly variable days reduces with low temporal resolution data. By comparing the DCI values calculated for the data with a 5 min, 30 min, and 60 min time interval, we find that there is no to minimal difference in the DCI values calculated for different data with temporal resolutions for all the five categories (Table 3). We find that the maximum difference in the DCI among the different temporal datasets for clear-sky days is 0.005, overcast days is 0.016, high intermittent days is 0. 051, low intermittent days is 0.007, and highly variable days is 0.125. On the contrary, we find higher differences for the nDARR values recorded for the data with a different temporal resolution (Table 3). We find that the maximum difference in the nDARR among the different temporal datasets for clear-sky days is 0.238, overcast days is 0.03, high intermittent days is 0.064, low intermittent days is 0.063, and highly variable days is 0.211. This is because a lower temporal resolution data records one point from a 30 min or 60 min period which can be either too close or far away from the previous value. As expected, the clear-sky days have a low nDARR and a high DCI while high variability days have a high nDARR. It should be noted that some low intermittent days might have a very similar curve as that of clear-sky days when plotted with a lower resolution data. This is because the variability becomes averaged or smooths out in a lower resolution dataset. However, these days will have a moderate to high DCI and a low nDARR as opposed to clear days that have a low nDARR and a high DCI.
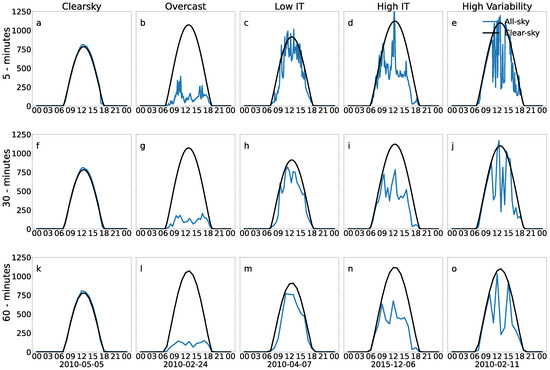
Figure 4.
GHI profiles for Alice Spring plotted using data recorded at 5 min (a–e), 30 min (f–j), and 60 min (k–o) interval. Panel (a,f,k) represent clear day (5 May 2010). Panel (b,g,l) represent overcast day (24 February 2010). Low intermittent days are plotted in panels (c,h,m) (7 April 2010). High intermittent days and highly variable days are plotted in panels (d,i,n) (6 December 2015) and (e,j,o) (11 February 2010), respectively.

Table 3.
DCI and nDARR values for clear, overcast, low intermittent, high intermittent, and highly variable days corresponding to the days shown in Figure 3 for Alice Springs. These values are calculated for data with different temporal resolution.
5. Applications of the New Scheme
5.1. Resource Assessment and Site Allocation
In solar energy planning, traditional assessments often prioritize clear-sky and overcast conditions as representing the extreme cases for power generation. However, overlooking intermittent conditions can lead to underestimating the stress solar energy systems places on the electricity grid. Therefore, adopting a sky classification system becomes crucial for resource assessment, as it allows for a more comprehensive understanding of solar energy generation patterns and their impact on grid stability. Accounting for a wider range of atmospheric conditions that includes intermittent and highly variable generation days enables a more accurate estimation of low generation periods, ultimately facilitating better grid design and management strategies for integrating solar energy into the power system. This new scheme facilitates a better understanding of how clear-sky, intermittent, and variable days vary globally both seasonally and annually. This can be highly useful for planning optimum locations for new solar plants and planning storage solutions for the existing plants.
As an example, we show the number of clear-sky, cloudy, low intermittent, high intermittent, and highly variable days in 2022 using ERA5 reanalysis data in Figure 5. The frequency of these days is obtained using the proposed classification scheme. We can see that the tropics have a higher number of clear days followed by high intermittent days. The tropics have higher convective activity and hence we can expect higher variability in that region. The north of Australia has a higher number of clear days compared to the rest of the continent. The southern and eastern regions of Australia have a higher number of intermittent and high variability due to a higher cloud cover. These metrics can be useful to calculate the seasonal frequency of days in each category for effective grid management and understanding seasonal variability in energy generation globally. The grid operators can combine this information with other variability metrics like ramp duration and daily ramp frequency to maintain grid stability especially for the days with higher intermittency. This metric can be further studied along with battery size determination and optimization to understand the region-specific requirement of the battery size and frequency of charge and discharge periods required to maintain a stable energy supply.
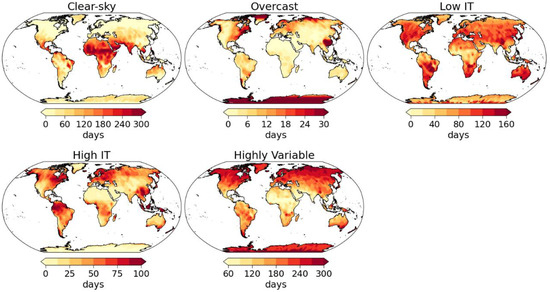
Figure 5.
Frequency of clear, overcast, low intermittent, high intermittent, and highly variable days globally for the year 2022 obtained using the proposed classification scheme. This figure is obtained using ERA5 reanalysis dataset.
5.2. Understanding Future Intermittency Induced by Climate Change
Understanding future intermittency due to climate change is crucial for solar plants because it helps predict how reliable and consistent their energy output will be in the long term. As our climate changes, we expect more extreme weather events like storms, heatwaves, and fluctuations in cloud cover. These changes can directly impact the amount of solar radiation reaching solar panels, causing variability in energy generation. The future projection dataset are usually available at a 1-hourly or lower temporal resolution due to computational and storage challenges. As mentioned above, previous sky classification schemes were limited to high resolution data (up to sec to 30 min). This often led to the use of simpler classification schemes [5] that did not account for variability while projecting future changes in sky conditions. Since our scheme classifies the sky conditions irrespective of the temporal resolution of the data, it will be highly suitable for estimating future changes in the intermittent, variable, clear, and overcast days. By understanding these potential changes, solar plant operators can better prepare for periods of reduced output, ensuring they have backup plans in place to maintain a steady supply of electricity to the grid. This understanding will also help in decision-making process for the site selection of new solar plants and how to design existing ones to be more resilient in the face of changing environmental conditions.
We show the application of our proposed scheme for identifying future changes in intermittent, overcast, clear-sky, and highly variable days for the Powell Creek solar farm in the Northern Territory, Australia (Figure 6). It is currently the world’s largest proposed solar farm under construction. We have analyzed the radiation data for the historical period (1976–2005) and future period (2030–2059) under RCP8.5 for the solar farm location. We calculate the DCI and nDARR for the historical and future periods and apply the proposed classification scheme for both the periods. We calculate the annual frequency of clear-sky, overcast, low intermittent, high intermittent, and high variability days for both the periods and plot the density distribution plots in Figure 6. Figure 6 shows a reduction in the number of future clear-sky days for the location with negligible changes in mean overcast, low intermittent, and highly variable days. The average high intermittent days are expected to increase in the future. The distribution plots show that the future overcast, and high intermittent days have a fat tail, indicating higher probability of increase in extreme overcast and high intermittent days in the future. This indicates that the Powell Creek solar farm has higher chances of future intermittency. It is therefore recommended to carefully estimate storage options to optimize energy supply to the grid during low generation periods. The results shown here fall within the uncertainty range of clear-sky, overcast, and intermittent day/year shown in the previous study by Poddar et al. [5].
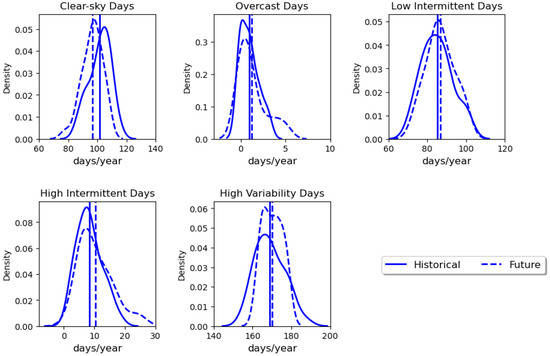
Figure 6.
Density distribution plots of number of clear-sky, overcast, high intermittent, low intermittent, and highly variable days for Powell Creek solar farm located in Northern Territory, Australia for historical (1976–2005) and future (2030–2059) periods. The distribution for the historical period is shown in bold line. The future scenario used here corresponds to high-emission RCP8.5 future scenario and is shown by the dashed line. The vertical lines indicate the mean for that period.
6. Discussion
The variability of solar resource is highly dependent on the location of study and the regional climate conditions. It is important to quantify the frequency of intermittent and high variability days seasonally and annually to plan grid management strategies, estimate storage requirements, and plan their charging and discharging times. The proposed scheme can be useful in categorizing clear, overcast, low and high intermittent, and highly variable days using data for different timescales.
The distribution of clear-sky, overcast, and intermittent days over Australia for the historical and future periods is shown in the previous work by Poddar et al. [5]. Their study used a simple sky classification method based on the DCI. Their results indicate higher clear-sky days near the northern parts of Australia and higher intermittent days near the eastern coastal regions of Australia. By applying our latest sky classification scheme, we observe a similar pattern over Australia. The similarity in the spatial pattern makes it credible to be used in resource assessment studies for both historical and future periods.
The regions with higher intermittency should be avoided as solar PV sites. However, some of these regions like New York, Pennsylvania in USA, coastal regions near New South Wales, and Victoria in Australia, despite having higher solar resource variability, have pre-existing transmission lines. The plants are set up in close proximity to the grid for cheaper distribution prices. This metric can be helpful in understanding the daily, seasonal and annual distribution of intermittent and variable days, and estimating energy deficit periods to plan backup energy storage options.
Sky classification can also play a crucial role in understanding cloud enhancement effects, particularly in the context of solar energy generation. Besides the general presence of cloud cover causing variability and hence impacting irradiance levels, clouds can scatter and diffuse sunlight, leading to an increase in solar irradiance, which is greater than what is expected under clear-sky conditions and thereby increases solar energy generation. This over-irradiance leads to the cloud enhancement effect. With the use of a sky classification scheme such as the one developed in this study, we can study the distribution of the energy generation during different days. This might be beneficial in planning inverter sizing and storage options for regions more prone to variability, thereby ensuring a stable power supply on low generation and variable days. To demonstrate the application of this new scheme for cloud enhancement studies, we examined the PV generation data from the Desert Knowledge Australia Solar Centre, Alice Springs. We examined the performance of a monocrystalline silicon system (period 2010–2016). The arrowhead plot for normalized energy generation and nDARR (Figure 7a) shows a similar pattern like the arrowhead plot for DCI and nDARR. Thus, our classification scheme can be applied to the power generation data. We use our scheme to identify the various days and plot the kernel density functions of the PV output data for each of these five categories, as shown in Figure 7b. From the distributions, it can be observed that power generation is higher for low intermittent days, indicating a potential cloud enhancement effect. Cloud enhancement temporarily increases PV generation by increasing solar irradiance beyond clear-sky levels due to scattered and reflected sunlight from the edges of passing clouds. We recommend a detailed investigation on cloud data and its role on understanding cloud enhancement effect for future work. This metric should be correlated with the cloud type, cloud amount, and recorded radiation/power output to provide insights on the excess energy generation and how it can be used.
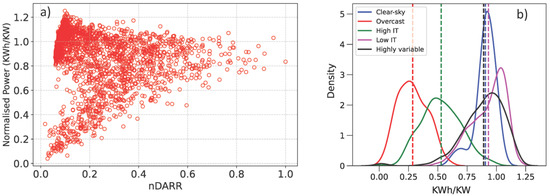
Figure 7.
(a) Arrowhead plot for power output and nDARR. (b) Density distribution plots of system generation on clear-sky, overcast, high intermittent, low intermittent, and highly variable days for a PV system located in Desert Knowledge Australia Solar Centre, Alice Spring. The dashed lines indicate the mean generation of the system for each of the five categories.
This improved method of sky classification provides a detailed understanding of the sky conditions, which translates into more accurate and reliable solar farm forecasts. We can develop efficient predictive models for energy forecasting with a higher skill score by adapting sky classification conditions that have higher precision. This leads to more accurate short-term and long-term solar energy production forecasts. Solar farms can use this information to optimize their operation, such as managing energy storage systems effectively and energy bidding.
7. Conclusions
Understanding both the solar resource potential and its variability across different timeframes and geographical areas is essential for effective PV power generation planning. Reliable information regarding solar resource availability is critical for determining the technical feasibility of specific solar technologies in a given region. Additionally, considering seasonal and daily variations is crucial for energy planning and meeting demand. Knowledge of solar resource variability and identifying times of increased cloudiness are vital for optimizing the performance of PV plants. This information can significantly help decision making in solar energy projects.
This study presents a new method to quantify sky conditions globally that can be applicable to any dataset. We use the nDARR and DCI metrics to identify five categories of sky conditions: clear-sky, overcast, low intermittent, high intermittent, and highly variable days. This study uses k-means clustering approach to determine the optimal number of clusters. We use the WCSS method to identify the optimal number of clusters (k = 5). We apply k-means clustering method with k = 5 to identify the boundaries of the five clusters and define our new scheme. We randomly split the data into training set (two-third of the data) and test set (one-third of data) and then apply the Chi-square test. We find that the p-value of the Chi test is 0.58. This indicates a similar distribution pattern among the test and training sets, thereby indicating the proposed scheme is robust. Global reanalysis and climate projections data usually have 1 h as their highest resolution, which made it difficult to use the previous methods for sky classification. We use data from different temporal resolutions to demonstrate that the proposed method can be widely applicable to any dataset irrespective of their resolution. We find that the DCI values for all the datasets (recorded at 5 min, 30 min, and 60 min) have similar values; however, the nDARR value usually varies within the range. This is because the variability smoothens for the lower temporal resolution data.
In this study, we show that the proposed method can be applicable to study global sky conditions using ERA5 reanalysis. We can determine the number of low intermittent to high variable days/year for a location using our proposed method. We observe high variability near the tropics with a higher frequency of high intermittent (up to 75 days in the year 2022) and highly variable days (up to 150 days in the year 2022). The proposed scheme can also be applied to identify future changes in intermittent conditions over a solar plant. We observe that the mean clear-sky days are projected to increase in the Powell Creek solar farm (mean increase by 5 days/year), suggesting stable energy generation in the future period.
This method can be an useful tool in understanding the influence of large-scale climate drivers like El-Nino Southern Oscillation (ENSO), Indian Ocean Dipole (IOD), Southern Annular Mode (SAM), North Atlantic Oscillation (NAO), etc. on the frequency and category of variable energy generation days for existing and proposed solar farms. This is extremely valuable for maintaining grid stability. The existing solar plants in high intermittent regions can use this method for long-term planning either by investing in storage systems or ramp control devices.
With the increasing probability of a future warmer climate, the resource variability is highly likely to change in the future [2,5]. This can result in changes in the intermittent days observed historically for different regions across the world. Hence, it is highly recommended to perform long-term future feasibility analysis considering climate change before investing in a new solar plant. This method can be applied to global and regional climate projection data to study future changes in the sky conditions due to climate change. This work has important applications for solar energy management, resource allocation, and future site selection.
Author Contributions
Conceptualization, S.P., M.K. and J.B.; methodology, S.P. and J.B.; software, S.P.; validation, S.P.; formal analysis, S.P.; investigation, S.P.; data curation, S.P.; writing—original draft preparation, S.P.; writing—review and editing, S.P., M.K. and J.B.; visualization, S.P.; supervision, M.K. and J.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were generated in the study. The CORDEX-Australasia data used for the analysis are available from the Earth System Grid Federation (https://esgf-data.dkrz.de/search/cordex-dkrz/, accessed on 5 November 2023). ERA5 data were obtained from the ECMWF Climate Data Store.
Acknowledgments
We sincerely thank the Australian National Computational Infrastructure (NCI) for providing computational resources for this work. The authors acknowledge the World Climate Research Program’s initiative to produce regional climate modeling projections (CORDEX), and the authors thank the climate modeling groups for producing and making their model output.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- IRENA, Future of Solar Photovoltaic: Deployment, Investment, Technology, Grid Integration and Socio-Economic Aspects (A Global Energy Transformation: Paper). 2019. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2019/Oct/IRENA_Future_of_wind_2019.pdf (accessed on 5 April 2024).
- Poddar, S.; Evans, P.J.; Kay, M.; Prasad, A.; Bremner, S. Assessing Australia’s future solar power ramps with climate projections. Sci. Rep. 2023, 13, 11503. [Google Scholar] [CrossRef] [PubMed]
- Dickeson, G.; McLeod, L.; Dobb, A.; Frearson, L.; Herteleer, B.; Scheltus, D. Ramp Rate Control for PV Plant Integration: Experience from Karratha Airport’s Hybrid Power Station. In Proceedings of the 36th European Photovoltaic Solar Energy Conference and Exhibition, Marseille, France, 9–13 September 2019; pp. 1351–1356. [Google Scholar] [CrossRef]
- van Haaren, R.; Morjaria, M.; Fthenakis, V. Empirical assessment of short-term variability from utility-scale solar PV plants. Prog. Photovolt. Res. Appl. 2014, 22, 548–559. [Google Scholar] [CrossRef]
- Poddar, S.; Kay, M.; Prasad, A.; Evans, J.P.; Bremner, S. Changes in solar resource intermittency and reliability under Australia’s future warmer climate. Sol. Energy 2023, 266, 112039. [Google Scholar] [CrossRef]
- Poddar, S.; Evans, J.P.; Kay, M.; Prasad, A.; Bremner, S. Estimation of future changes in photovoltaic potential in Australia due to climate change. Environ. Res. Lett. 2021, 16, 114034. [Google Scholar] [CrossRef]
- Antonanzas-Torres, F.; Urraca, R.; Polo, J.; Perpiñán-Lamigueiro, O.; Escobar, R. Clear sky solar irradiance models: A review of seventy models. Renew. Sustain. Energy Rev. 2019, 107, 374–387. [Google Scholar] [CrossRef]
- Engerer, N.A.; Mills, F.P. Validating nine clear sky radiation models in Australia. Sol. Energy 2015, 120, 9–24. [Google Scholar] [CrossRef]
- Ineichen, P. A broadband simplified version of the Solis clear sky model. Sol. Energy 2008, 82, 758–762. [Google Scholar] [CrossRef]
- Reno, M.J.; Hansen, C.W.; Stein, J.S. Global Horizontal Irradiance Clear Sky Models: Implementation and Analysis; Sandia Report SAND2012-2389; Sandia National Laboratories: Albuquerque, NM, USA; Livermore, CA, USA, 2012; pp. 1–66. [Google Scholar]
- Lefèvre, M.; Oumbe, A.; Blanc, P.; Espinar, B.; Gschwind, B.; Qu, Z.; Wald, L.; Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Arola, A.; et al. McClear: A new model estimating downwelling solar radiation at ground level in clear-sky conditions. Atmos. Meas. Tech. 2013, 6, 2403–2418. [Google Scholar] [CrossRef]
- Huang, J.; Troccoli, A.; Coppin, P. An analytical comparison of four approaches to modelling the daily variability of solar irradiance using meteorological records. Renew. Energy 2014, 72, 195–202. [Google Scholar] [CrossRef]
- Bai, F.; Yan, R.; Saha, T.K. Variability study of a utility-scale PV plant in the fringe of grid, Australia. In Proceedings of the 2017 IEEE Innovative Smart Grid Technologies—Asia (ISGT-Asia), Auckland, New Zealand, 4–7 December 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Stein, J.S.; Hansen, C.W.; Reno, M.J. The variability index: A new and novel metric for quantifying irradiance and pv output variability. In Proceedings of the World Renewable Energy Forum, WREF 2012, Including World Renewable Energy Congress XII and Colorado Renewable Energy Society (CRES) Annual Conference, Denver, CO, USA, 13–17 May 2012; pp. 2764–2770. [Google Scholar]
- Kreuwel, F.P.M.; Knap, W.H.; Visser, L.R.; van Sark, W.G.J.H.M.; de Arellano, J.V.-G.; van Heerwaarden, C.C. Analysis of high frequency photovoltaic solar energy fluctuations. Sol. Energy 2020, 206, 381–389. [Google Scholar] [CrossRef]
- Nga, P.T.T.; Ha, P.T.; Hang, V.T. Satellite-Based Regionalization of Solar Irradiation in Vietnam by k-Means Clustering. J. Appl. Meteorol. Climatol. 2021, 60, 391–402. [Google Scholar] [CrossRef]
- Maldonado-Salguero, P.; Bueso-Sánchez, M.C.; Molina-García, Á.; Sánchez-Lozano, J.M. Spatio-temporal dynamic clustering modeling for solar irradiance resource assessment. Renew. Energy 2022, 200, 344–359. [Google Scholar] [CrossRef]
- Abuella, M.; Chowdhury, B. Forecasting Solar Power Ramp Events Using Machine Learning Classification Techniques. In Proceedings of the 2018 9th IEEE International Symposium on Power Electronics for Distributed Generation Systems, Charlotte, NC, USA, 25–28 June 2018. [Google Scholar] [CrossRef]
- Jiménez-Pérez, P.F.; Mora-López, L. Modeling and forecasting hourly global solar radiation using clustering and classification techniques. Sol. Energy 2016, 135, 682–691. [Google Scholar] [CrossRef]
- Shi, J.; Lee, W.-J.; Liu, Y.; Yang, Y.; Wang, P. Forecasting power output of photovoltaic system based on weather classification and support vector machine. In Proceedings of the 2011 IEEE Industry Applications Society Annual Meeting, Orlando, FL, USA, 9–13 October 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Marquez, R.; Pedro, H.T.C.; Coimbra, C.F.M. Hybrid solar forecasting method uses satellite imaging and ground telemetry as inputs to ANNs. Sol. Energy 2013, 92, 176–188. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S.; Cai, T.; Liu, B. Online 24-h solar power forecasting based on weather type classification using artificial neural network. Sol. Energy 2011, 85, 2856–2870. [Google Scholar] [CrossRef]
- Hassan, M.A.; Abubakr, M.; Khalil, A. A profile-free non-parametric approach towards generation of synthetic hourly global solar irradiation data from daily totals. Renew Energy 2021, 167, 613–628. [Google Scholar] [CrossRef]
- Ayodele, T.R.; Ogunjuyigbe, A.S.O.; Amedu, A.; Munda, J.L. Prediction of global solar irradiation using hybridized k-means and support vector regression algorithms. Renew. Energy Focus 2019, 29, 78–93. [Google Scholar] [CrossRef]
- Hartmann, B. Comparing various solar irradiance categorization methods—A critique on robustness. Renew. Energy 2020, 154, 661–671. [Google Scholar] [CrossRef]
- da Rocha, V.R.; Costa, R.S.; Martins, F.R.; Gonçalves, A.R.; Pereira, E.B. Variability index of solar resource based on data from surface and satellite. Renew. Energy 2022, 201, 354–378. [Google Scholar] [CrossRef]
- Poddar, S.; Rougieux, F.; Evans, P.J.; Kay, M.; Prasad, A.; Bremner, S. Accelerated degradation of photovoltaic modules under a future warmer climate. Prog. Photovolt. Res. Appl. Under Rev. 2024, 32, 456–467. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future köppen-geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed]
- Mabasa, B.; Lysko, M.D.; Tazvinga, H.; Zwane, N.; Moloi, S.J. The performance assessment of six global horizontal irradiance clear sky models in six climatological regions in South Africa. Energies 2021, 14, 2583. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. J. R. Stat. Society. Ser. C Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Louppe, G.; Prettenhofer, P.; Weiss, R.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Kodinariya, T.M.; Makwana, P.R. Review on determining number of Cluster in K-Means Clustering. Int. J. 2013, 1, 90–95. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).