High-Switching-Frequency SiC Power Conversion Systems with Improved Finite Control Set Method Prediction Control

Abstract

With the development of power conversion systems or bidirectional grid-connected inverters characterized by high DC voltage, high efficiency, and high-power density, high-switching-frequency SiC power switches are being widely used, and these require a short computational time of control algorithm. Based on the sector judgment of a space voltage vector and the midpoint potential control balancing of a DC bus, an improved finite control set method prediction control (FCS-MPC) method was proposed for a T-type three-level PCS. This improved FCS-MPC first judges the sector of the space voltage vector and locates the position of the corresponding large sector according to phase lock information; then, it analyzes the sampled voltage of the upper and lower bus capacitors to obtain the midpoint potential situation and selects appropriate small vectors based on the midpoint potential situation. This simple improved strategy can reduce the computational complexity of traditional MPC for rolling optimization, resulting in a reduction in the vectors from 27 to 8. A SiC-based 10 kW bidirectional PCS prototype verified the improved FCS-MPC, and the computational time was reduced about by 56% in comparison to traditional FCS-MPC.

1. Introduction

The dual carbon target is driving many countries to vigorously develop new energy, and this has made new energy to occupy an important position in the new power system [1]. With the improvement of the efficiency and reliability of new energy generation, coupled with the reduction in industrial manufacturing costs and government policy subsidies, significant growth in new energy generation has been greatly promoted [2,3]. However, random fluctuations in new energy generation would have an impact on the reliability and quality of the power grid [4]. At this point, energy storage can suppress these fluctuations, effectively improve power generation efficiency, and strengthen the stability of new energy grid connection [5].

Currently, with the increasing capacity of electrochemical energy storage systems [6] and the requirements for high efficiency and power density, the bidirectional energy storage converters or power converter systems (PCSs) are developing towards high voltage and high switching frequency [7]. However, silicon (Si)-based semiconductor power switches cannot meet this development trend due to their own material characteristics [8]. By contrast, SiC wide-bandgap semiconductor power switches has advantages in high-efficiency and high-power-density PCSs due to their high blocked voltage, high switching frequency, and good high-temperature and thermal characteristics. Silicon carbide power switches are gradually to be used in PCSs [9].

Model predictive control (MPC) is a method that uses rolling optimization to output the optimal control vector [10,11,12]. According to whether the output voltage vector is continuous, it can be divided into continuous control set model predictive control (CCS-MPC) and finite control set model predictive control (FCS-MPC). CCS-MPC is a discrete model that modulates a continuous voltage vector in a complex vector plane. FCS-MPC uses rolling optimization to determine the optimal value of the value function vector. MPC utilizes the output characteristics of a grid-connected PCS to avoid the shortcomings of space voltage vector modulation technology, making the control method more direct and simpler [13,14,15]. Compared with other control strategies, such as SVPWM or SPWM, it also has the characteristics of predictive control, optimal vector output, and a fast dynamic response.

When using the FCS-MPC strategy for a grid-connected PCS, it is necessary to first derive a predictive model from a mathematical model of the circuit topology and then build a value function on the predictive model. The value function generally takes the minimum error of the grid-connected current as the main control objective, and other control objectives can be added at the same time, such as bus midpoint voltage. In each control cycle, various electrical signals of the PCS, such as grid voltage and grid-connected current, are sampled and input into the prediction model. The output state of the PCS in the next control cycle is predicted, and the optimal value of the value function is used as the judgment criterion to roll and optimize all switches’ states to obtain one control switch state. There are 27 types of switch states for a T-type three-level PCS, which means that 27 rounds of rolling optimization are required to obtain the optimal switch state for the next control cycle.

A high-switching-frequency SiC based PCS has a short switching cycle time, which requires high speed and short time for the operation of the PCS control algorithm. The computational complexity of MPC is relatively large compared to other control strategies and requires higher performance of MCU, especially for a high-frequency SiC PCS. Therefore, the computational complexity of the algorithm needs to be appropriately reduced. This paper studies the predictive control strategy of a high-switching-frequency SiC PCS with smaller computational complexity and a shorter operating time.

For the problem of high computational complexity and slow computation in MPC, reference [16] proposed an improved optional three-vector fixed frequency model predictive control strategy. This study drew inspiration from the idea of deadbeat control and converted grid-connected current control in a rotating coordinate system to voltage control in a stationary coordinate system. Then, by judging the sectors of the space reference voltage, different vector sets were selected to reduce the computational complexity of model predictive control. In order to reduce the impact of delay, reference [17] achieved good control by using sector judgment to shorten the calculation time. Reference [18] applied model predictive control to NPC-type three-level converters and proposed a modulation-based model predictive control strategy. After obtaining the optimal vector through rolling optimization, the duty cycle of the vector was calculated, and then the vector synthesis modulation method was used to output PWM. Reference [19] calculated the distance between the space voltage vector and the space voltage reference vector and selected a finite set of space voltage vectors to participate in model prediction rolling optimization based on this distance in order to reduce the computational complexity of model prediction control. Reference [20] determined a finite set of space voltage vectors for rolling optimization by determining the size of the sectors and reduced the number of rolling times of space voltage vectors from 27 to 10, resulting in a significant reduction in computational complexity. Reference [21] reduced the number of rolling optimized space voltage vectors from 27 to 8 by designing a new direct torque control switch table. Reference [22] utilized a branch definition algorithm for multi-step model predictive control, which directly output the optimal switch state and reduced the computational complexity of MPC.

The PCS in this paper adopts a T-type three-level topology and improved model predictive control. The remaining contents of this paper are as follows: Section 2 presents and derivates the model predictive control of the T-type three-level SiC bidirectional PCS. Section 3 proposes an improved model predictive control strategy based on simplified rolling optimization using sector judgment and bus midpoint potential control. Section 4 validates the proposed method through experiments. Finally, Section 5 concludes the paper.

2. Traditional Model Predictive Control of T-Type Three-Level PCS Topology

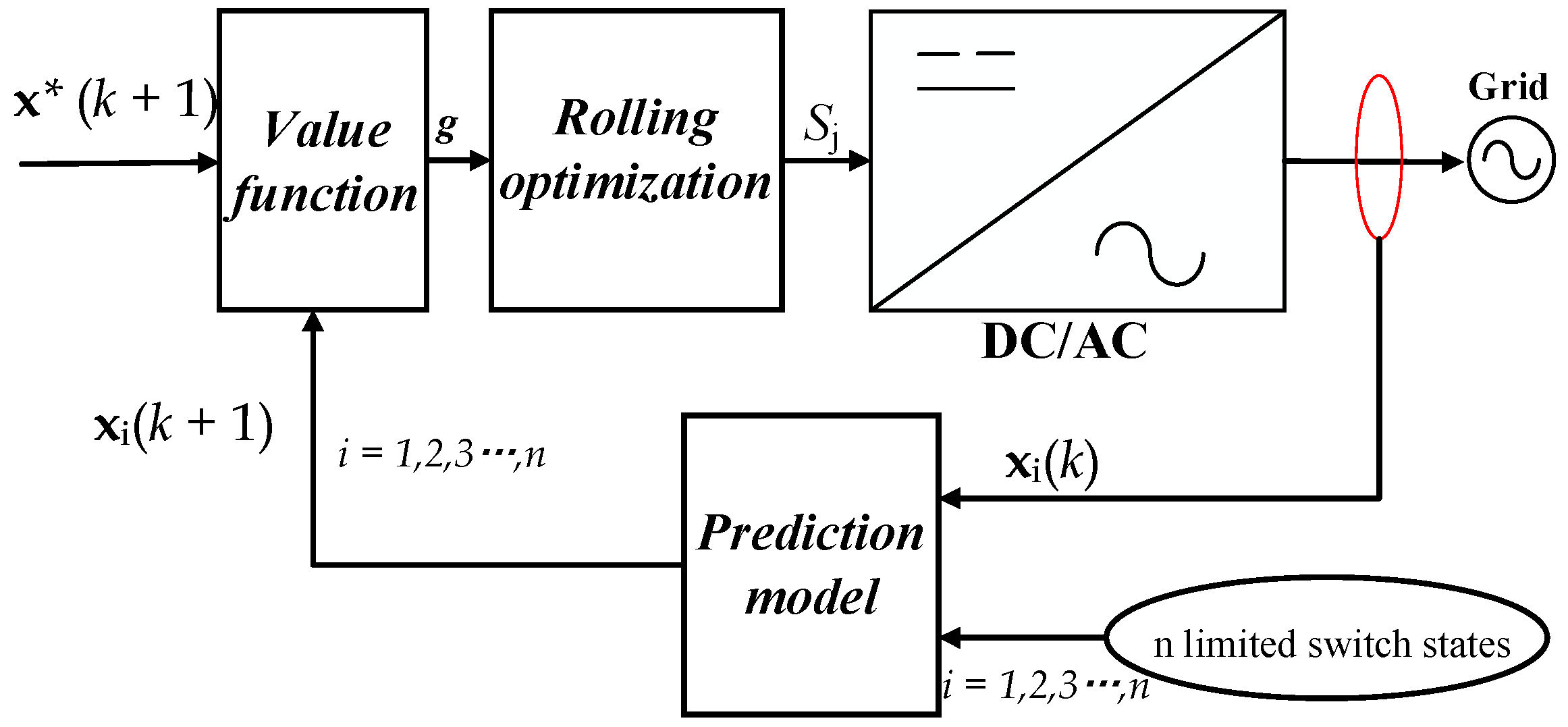
The overall control diagram of model predictive control for DC/AC converters is shown in Figure 1. Among them, x^*(k + 1) represents the reference value, x_i(k) represents the current sampling value, x_i(k + 1) represents the predictive value for the next cycle, g represents the calculated value of the value function, and S_j represents the switches’ action [23,24].

When using MPC for PCS control, the first step is to build a mathematical model of the PCS’s topology. Then, the next step is to design the value function for evaluating the control object, which serves as a criterion for optimizing and selecting the optimal output vector. MPC can simultaneously control multiple objectives. For the current source PCS, the main control object is grid-connected current and the bus midpoint potential.

As for the T-type three-level power conversion system (PCS) of DC/AC converters, the above detailed model predictive control will be derived as follows. In order to present the MPC model, the operation principle of the T-type three-level topology is briefly outlined. The main circuit of the PCS adopts a T-type three-level topology, as shown in Figure 2. The DC bus’s upper and lower capacitance is C_DC1 and C_DC2, and C_DC1 = C_DC2. The positive, negative, and midpoint potentials of the DC bus voltage are represented by points P, N, and O, respectively. Taking phase A as an example, the operation principle of the T-type three-level PCS circuit is simply analyzed. The vertical switches of S_a1 and S_a4 in the A-phase withstand the entire DC bus voltage U_DC, and the horizontal switches of S_a2 and S_a3 withstand half of the DC bus voltage U_DC. In the configuration described, the switches of S_a1 and S_a4 are connected in series, with their midpoint designated as point A. Similarly, the switches of S_a2 and S_a3 are connected in series between points A and O.

According to the circuit topology operation principle, the state equation in the three-phase stationary coordinate system can be obtained as follows:

$$\{\begin{array}{l}{u}_a=u_{\mathit{aN}}-L{\displaystyle \frac{d{i}_a}{\mathit{dt}}}-R\times i_a\\ u_b=u_{\mathit{bN}}-L{\displaystyle \frac{d{i}_b}{\mathit{dt}}}-R\times i_b\\ u_c=u_{\mathit{cN}}-L{\displaystyle \frac{d{i}_c}{\mathit{dt}}}-R\times i_c\end{array}$$

(1)

here, L = L_a = L_b = L_c is the three-phase filtering inductance; R = R_a = R_b = R_c is the equivalent series resistance; i_a, i_b, and i_c are the three-phase grid-connected currents; u_a, u_b, and u_c are the phase voltage; and u_aN, u_bN, and u_cN are the AC output voltage of the PCS.

Equation (1) is obtained by Park transformation into Equation (2) in a two-phase stationary coordinate system.

$$\{\begin{array}{l}L{\displaystyle \frac{d{i}_{\alpha }}{dt}}=u_{\alpha N}-u_{\alpha }-R\times i_{\alpha }\\ L{\displaystyle \frac{d{i}_{\beta }}{\mathit{dt}}}=u_{\beta N}-u_{\beta }-R\times i_{\beta }\end{array}$$

(2)

Among them, u_α and u_β represent the αβ axis component of the power grid phase voltage; u_αN and u_βN represent the αβ axis component of the PCS output voltage; and i_α and i_β represent the αβ axis component of the grid-connected current.

For model predictive control, if sampling frequency is high and the time interval is short, the current in Equation (2) can be discretized as follows:

$$\{\begin{array}{l}{\displaystyle \frac{d{i}_{\alpha }}{\mathit{dt}}}\approx {\displaystyle \frac{i_{\alpha }(k+1)-i_{\alpha }\left(k\right)}{T_s}}\\ {\displaystyle \frac{d{i}_{\beta }}{\mathit{dt}}}\approx {\displaystyle \frac{i_{\beta }(k+1)-i_{\beta }\left(k\right)}{T_s}}\end{array}$$

(3)

Among them, i_α(k), i_β(k), i_α(k + 1), and i_β(k + 1) represent the grid-connected current at time k and time k + 1 under a two-phase stationary coordinate system; T_s represents the sampling period.

By substituting (3) into (2), the following can be derived:

$$\{\begin{array}{l}L{\displaystyle \frac{i_{\alpha }(k+1)-i_{\alpha }\left(k\right)}{T_s}}=u_{\alpha N}\left(k\right)-u_{\alpha }\left(k\right)-R\times i_{\alpha }\left(k\right)\\ L{\displaystyle \frac{i_{\beta }(k+1)-i_{\beta }\left(k\right)}{T_s}}=u_{\beta N}\left(k\right)-u_{\beta }\left(k\right)-R\times i_{\beta }\left(k\right)\end{array}$$

(4)

In general, if the sampling frequency of the circuit system is high enough, it can be considered that the three-phase grid voltage at time k + 1 is the same as at time k. Therefore, the reference voltage value for the next cycle can be obtained as follows:

$$\{\begin{array}{l}{u_{\alpha N}}^{*}(k+1)={\displaystyle \frac{L}{T_s}}{i_{\alpha }}^{*}(k+1)+u_{\alpha }(k)+(R-{\displaystyle \frac{L}{T_s}})\times i_{\alpha }(k)\\ {u_{\beta N}}^{*}(k+1)={\displaystyle \frac{L}{T_s}}{i_{\beta }}^{*}(k+1)+u_{\beta }(k)+(R-{\displaystyle \frac{L}{T_s}})\times i_{\beta }(k)\end{array}$$

(5)

At the same time, it is also necessary to transform the current component under the dq coordinate into the component in the αβ coordinate system. Therefore, the current reference value, i*_α(k + 1), i*_β(k + 1), is shown in Equation (6), as follows:

$$\left[\begin{array}{l}{i^{*}}_{\alpha }\\ {i^{*}}_{\beta }\end{array}\right]=\left[\begin{array}{cc}\cos \mathsf{\theta }& -\sin \mathsf{\theta }\\ \sin \mathsf{\theta }& \cos \mathsf{\theta }\end{array}\right]\left[\begin{array}{l}{i}_d\\ i_q\end{array}\right]$$

(6)

Among them, θ represents the PLL angle or angle between the d-axis of the grid-connected current in the dq coordinate and the α-axis of the αβ coordinates.

As Equation (5), there is a certain relationship between the output voltage and the grid-connected current. Therefore, by controlling the output voltage, the grid-connected current can be controlled. This paper selects voltage constraints to design the value function in MPC. Then, the sum of absolute squared errors of each control variable can be used as the expression for the value function g. Therefore, the value function of the grid-connected current control can be designed as the following equation:

$$\mathbf{g}={\left|{u^{*}}_{\alpha }(k+1)-u_{\alpha }(k+1)\right|}^2+{\left|{u^{*}}_{\beta }(k+1)-u_{\beta }(k+1)\right|}^2$$

(7)

Among them, u^*_α(k + 1), u^*_β(k + 1) is the reference value of the PCS output voltage at time k + 1, and u_α(k + 1), u_β(k + 1) is the predicted output voltage of the PCS at time k + 1. Therefore, the value function is built.

Because in T-type three-level PCS topology the potential of midpoint O will greatly affect the grid-connected current THD and the topology operation’s stability, the potential of midpoint O is the key control object. Considering the potential of midpoint O, ideally, it can be assumed that the voltage of the upper bus capacitor is equal to that of the lower bus capacitor. Therefore, using the weight method to control both the grid-connected current and the midpoint potential simultaneously, the unified value function is constructed as follows:

$$\mathbf{g}={\left|{u^{*}}_{\alpha }(k+1)-u_{\alpha }(k+1)\right|}^2+{\left|{u^{*}}_{\beta }(k+1)-u_{\beta }(k+1)\right|}^2+\lambda \times {\left|{\mathrm{U}}_{\mathrm{DC}1}(k+1)-{\mathrm{U}}_{\mathrm{DC}2}(k+1)\right|}^2$$

(8)

In Equation (8), the |U_DC1(k + 1) − U_DC2(k + 1)|² of the value function for midpoint potential control is also constructed by the sum of absolute squared errors. Here, U_DC1(k + 1) and U_DC2(k + 1), respectively, represent the upper and lower bus capacitor voltage; λ is the weight control coefficient of the midpoint potential. The coefficient is related to the constraint of the control object of the midpoint potential. The stronger the constraint, the larger its value. Therefore, by adjusting the weight coefficient, different weights of multiple control objects can be controlled in the model predictive control algorithm. This article takes the grid-connected current as the main control object, and the midpoint potential control is secondary; therefore, the weight coefficient range is 0 < λ < 1.

Therefore, the MPC block diagram of the T-type three-level PCS can be obtained as shown in Figure 3.

3. Improved Model Predictive Control Strategy

According to the operation principle of the T-type three-level PCS topology, point A can be connected to points P, O, and N, resulting in U_AO having three different potentials, U_DC/2, 0, and −U_DC/2, respectively. Therefore, there are three states at points A, B, and C, which are combined to form 27 space voltage vectors. These 27 space voltage vectors can be divided into six large sectors based on their different effects. On the basis of each large sector, it can be further divided into six small sectors. According to the magnitude of space vectors, they can be further divided into six large vectors, six medium vectors, twelve positive and negative small vectors, and three zero vectors. A space voltage vector sector diagram can be obtained, as shown in Figure 4.

According to the principle of space voltage vector action, under the action of large vectors (PNN, PPN, NPN, NNP, NPP, PNP) and zero vectors (PPP, NNN, OOO), they have no effects on the midpoint potential, while the medium vectors (PON, OPN, NPO, ONP, PNO, NOP) and small vectors have effects on the midpoint potential. Moreover, the effects of the medium vectors depend on the phase current connected to the midpoint O, and the positive (POO, PPO, OPO, OPP, OOP, POP) and negative (ONN, OON, NNO, NOO, NON, ONO) small vectors have opposite effects on the midpoint potential. Therefore, different small vectors can be used under different midpoint potentials. When the voltage of the upper capacitor is greater than that of the lower capacitor, e.g., U_DC1 > U_DC2, the upper capacitor is discharged, and the lower capacitor is charged by applying a positive vector, reducing U_DC1 and raising U_DC2, thereby balancing the midpoint potential. Similarly, when the voltage of the upper capacitor is lower than that of the lower capacitor, U_DC1 < U_DC2, the lower capacitor is discharged, and the upper capacitor is charged by applying a negative vector, reducing U_DC2 and raising U_DC1, thereby balancing the midpoint potential. Based on the above analysis, the vector action table can be obtained under different midpoint potentials, as shown in

Table 1. Vector table based on the bus midpoint potential control.

Judging Conditions	UDC1 > UDC2	UDC1 < UDC2
Zero vector	PPP, NNN, OOO
Small vector	POO, PPO, OPO, OPP, OOP, POP	ONN, OON, NNO, NOO, NON, ONO
Medium vector	PON, OPN, NPO, ONP, PNO, NOP
Large vector	PNN, PPN, NPN, NNP, NPP, PNP

.

For the space voltage vector, the location can be determined in some large sector by the PLL angel θ. Therefore, based on simplifying the number of small vectors in midpoint potential control, an improved MPC strategy combining midpoint potential control and large sector judgment is proposed. The improved MPC strategy first judges the sector of the space voltage vector and locates the position of the large sector where the space voltage vector is located, according to phase lock information. Then, it will analyze the sampled voltage of the upper and lower bus capacitors to obtain the midpoint potential situation and select appropriate small vectors based on the midpoint potential situation. A list of vectors that enter rolling optimization under various control decision conditions can be obtained, as shown in

Table 2. Vector table under various control conditions. Bold and italics emphasize the small vectors.

Conditions	UDC1 > UDC2	UDC1 < UDC2	Conditions	UDC1 > UDC2	UDC1 < UDC2
Sector I	PNN, PON, PPN, POO, PPO, OOO, PPP, NNN	PNN, PON, PPN, ONN, OON, OOO, PPP, NNN	Sector IV	NPP, NOP, NNP, OPP, OOP, OOO, PPP, NNN	NPP, NOP, NNP, NOO, NNO, OOO, PPP, NNN
Sector II	PPN, OPN, NPN, PPO, OPO, OOO, PPP, NNN	PPN, OPN, NPN, OON, NON, OOO, PPP, NNN	Sector V	NNP, ONP, PNP, POP, OOP, OOO, PPP, NNN	NNP, ONP, PNP, ONO, NNO, OOO, PPP, NNN
Sector III	NPN, NPO, NPP, OPO, OPP, OOO, PPP, NNN	NPN, NPO, NPP, NON, NOO, OOO, PPP, NNN	Sector VI	PNO, PNN, PNP, POP, POO, OOO, PPP, NNN	PNO, PNN, PNP, ONO, ONN, OOO, PPP, NNN

; for instance, under the conditions of Sector I and U_DC1 > U_DC2, the vectors of (PNN, PON, PPN, POO, PPO, OOO, PPP, NNN) will be used, and the small vectors of POO and PPO are indicated in bold italic font. From the Table, it can be analyzed that there are only eight space voltage vectors that enter MPC rolling optimization under each control condition, and the small vectors that can be selected to act on different midpoint potentials in the same sector are different. Therefore, the improved MPC strategy significantly reduces the computational complexity of model predictive control, reducing the number of space voltage vectors that need to be substituted into the value function for rolling optimization from 27 to 8.

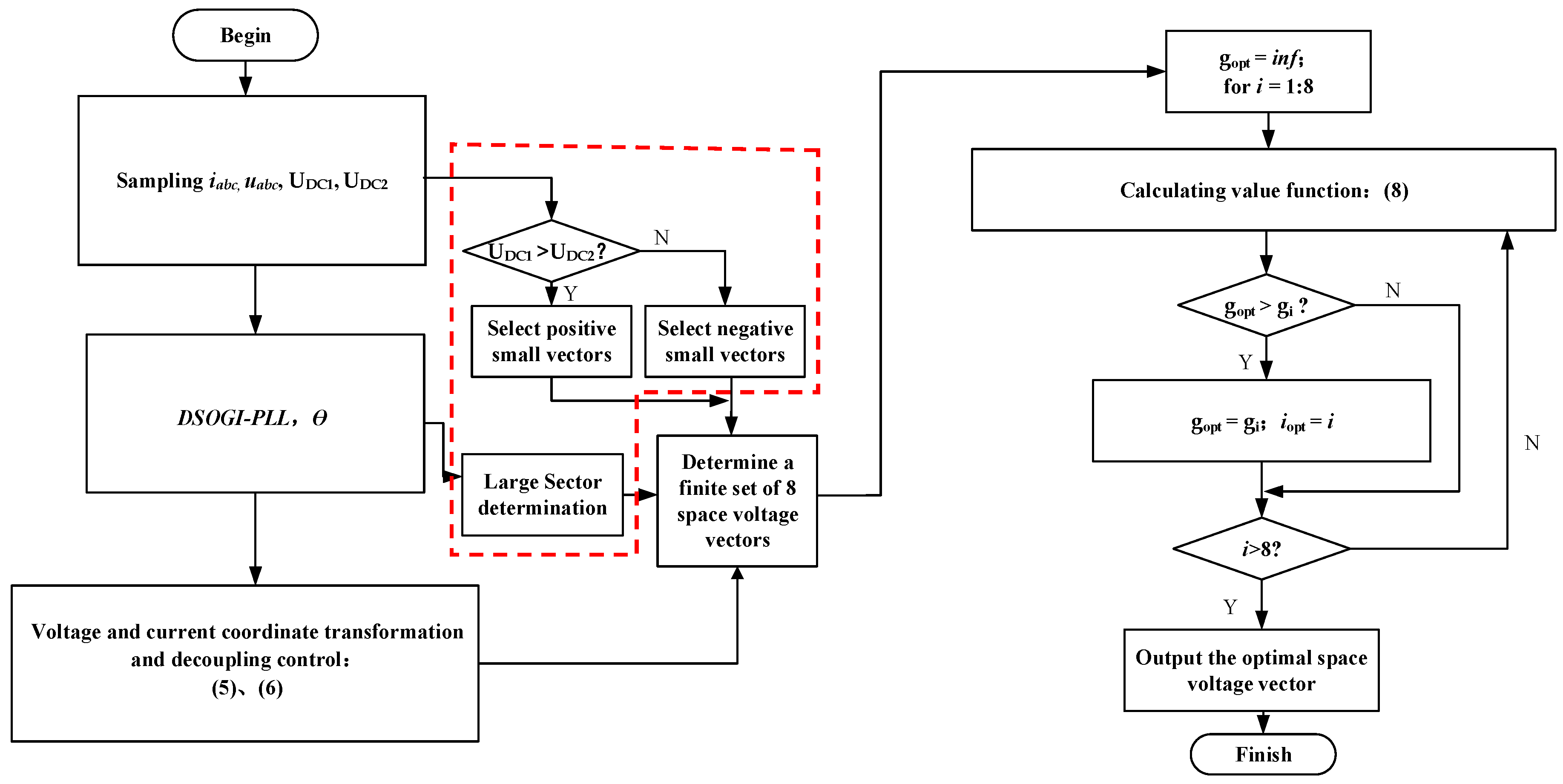
The corresponding control flow diagram of the improved MPC strategy is shown in Figure 5, which is divided into the following steps:

(1)

At the beginning of each sampling cycle, perform signal sampling on the three-phase grid-connected current i_abc, grid three-phase voltage u_abc, and DC bus upper and lower capacitor voltages of U_DC1 and U_DC2 in the PCS.

(2)

Based on the bus midpoint potential condition, select a small vector of Table 2.

(3)

Perform DSOGI-PLL (dual second-order generalized integrator phase-locked loop) [25] on the sampled grid voltage to achieve phase lock and PLL angel θ.

(4)

Based on the phase lock information θ, perform sector determination to locate the position of the large sector.

(5)

Substitute the phase lock angle θ for voltage and current decoupling control.

(6)

Combine Steps 2, 4, and 5 to determine the limited control set for eight space voltage vectors that enter the rolling optimization of model predictive control.

(7)

Substitute the eight finite control sets of the space voltage vectors determined by the rolling optimization of the method predictive model, calculating the value function value g of each space voltage vector, and compare to obtain the minimum value function value g_opt.

(8)

The space voltage vector that obtains the minimum value function value is the optimal control vector; then use it to control the inverter.

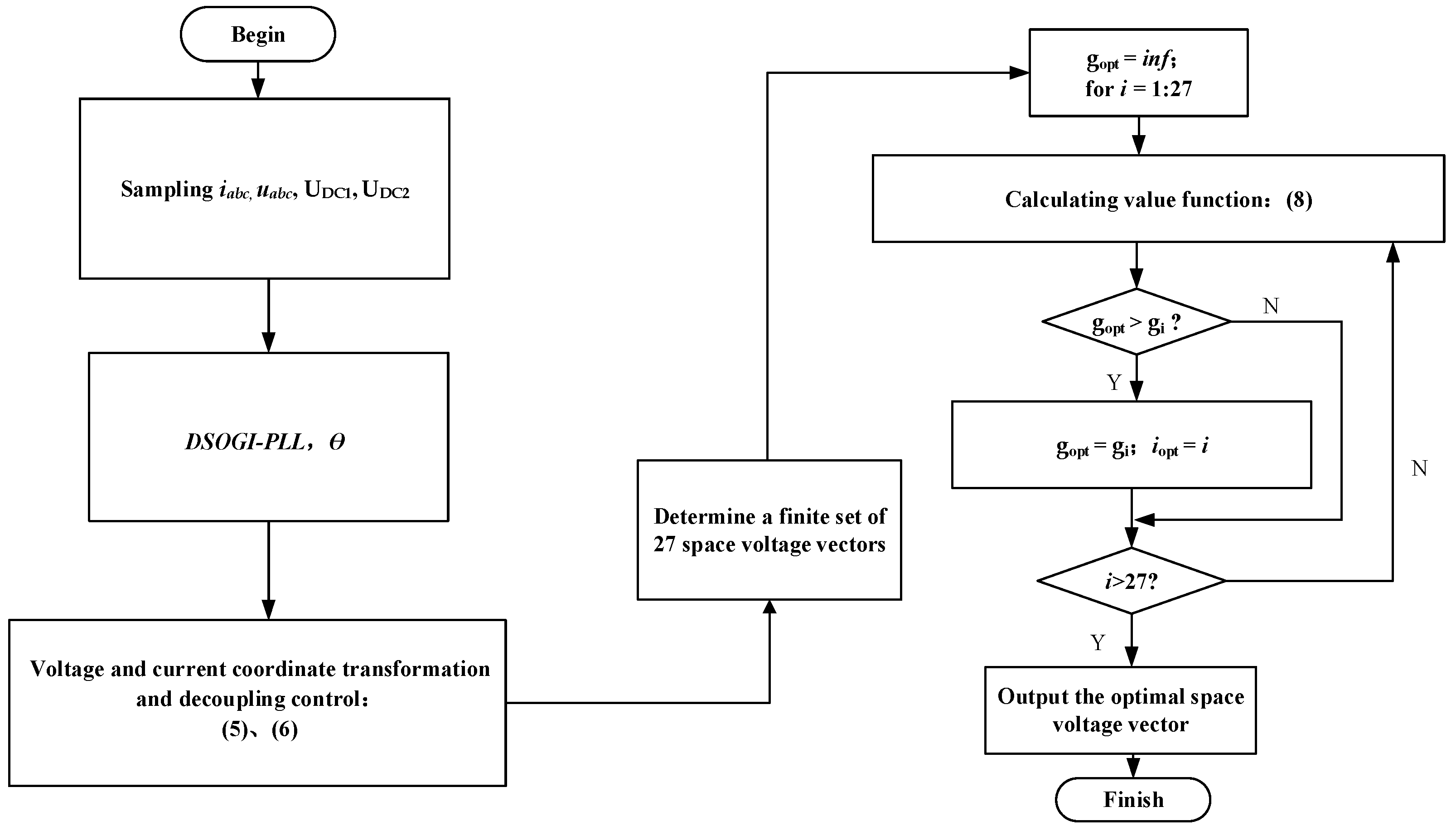
Compared with the control flow diagram of the improved MPC strategy, in traditional MPC, the strategy requires rolling optimization of all space voltage vectors. All 27 space voltage vectors are substituted into the value function and compared, and the optimal output vector is the space voltage vector with the smallest value function among the 27. Therefore, the control flow diagram of the traditional MPC strategy can be obtained, as shown in Figure 6.

It can be easily seen that the main difference is within the red dashed line in the control flow. The proposed improved MPC strategy is simple and can reduce the number of vectors that need to be substituted into the value function for rolling optimization from 27 to 8 by adding two steps—bus midpoint potential situation judgment and large sectors judgment—greatly reducing the computational complexity of the control process. Moreover, the control method does not incorporate too many complex algorithms, and the control strategy is still relatively simple and direct, which can achieve similar grid-connected output control effects for a bidirectional PCS.

4. Experimental Results

The key parameters of the built SiC-based T-type three-level PCS prototype are shown in

Table 3. Key parameters of T-type three-level bidirectional PCS.

Description	Value	Description	Value
Rated output power	10 kW	Grid phase voltage	220 Vac ± 10%/50 Hz
Bus voltage UDC	720 Vdc	Switching frequency	60 kHz
La, Lb, Lc	1 mH	Ra, Rb, Rc	10 mΩ
CDC1, CDC2	470 uF	Controller	TMS32F28377D
Sx1, Sx4 (x = a, b, c)	1.2 kV/Rds(on) = 40 mΩ (UF3C120040K4S)	Sx2, Sx3 (x = a, b, c)	750 V/Rds(on) = 23 mΩ (UJ4C075023K4S)

, and controller TMS320F28377 is used. Based on the proposed control strategy, the control program was coded. The prototype is shown in Figure 7.

The key waveforms of the prototype bidirectional PCS are tested, including inversion mode and rectification mode. Under inversion mode, Figure 8 and Figure 9 show the waveforms of the three-phase grid-connected phase current and grid line voltage at 10 kW and 5 kW, respectively, when the two different MPC strategies are used, under V_ac = 220 V.

Among them, relevant experimental data were obtained through testing with a three-phase power analyzer. Taking the A-phase current as an example, the grid-connected current iTHD was 2.02% and 2.88% for traditional MPC and 1.54% and 2.24% for the improved MPC strategy under the output of 10 kW and 5 kW, respectively. The power factor, PF, is 0.999 and 0.997 for traditional MPC and 0.999 and 0.997 for the improved MPC strategy. It can be observed that the improved MPC strategy has better control on iTHD in the inversion mode; moreover, the improved MPC strategy has smaller computational complexity and a shorter algorithm running time compared to traditional MPC.

The rectification mode waveform of the prototype is also tested. Figure 10 and Figure 11 show the waveforms of 10 kW and 5 kW three-phase phase currents and grid line voltage, respectively, when the two different MPC strategies are used, under V_ac = 220 V.

Among them, relevant experimental data were obtained through testing with a three-phase power analyzer. Taking the A-phase current as an example, the grid-connected current iTHD was 1.49% and 2.31% for traditional MPC, and 1.36% and 2.15% for the improved MPC strategy at 10 kW and 5 kW, respectively. The power factor, PF, is 0.999 and 0.997 for traditional MPC and 0.999 and 0.997 for the improved MPC strategy. It also can be observed that the improved MPC strategy has better control on iTHD in the inversion mode, and the improved MPC strategy has smaller computational complexity and a shorter algorithm running time compared to traditional MPC.

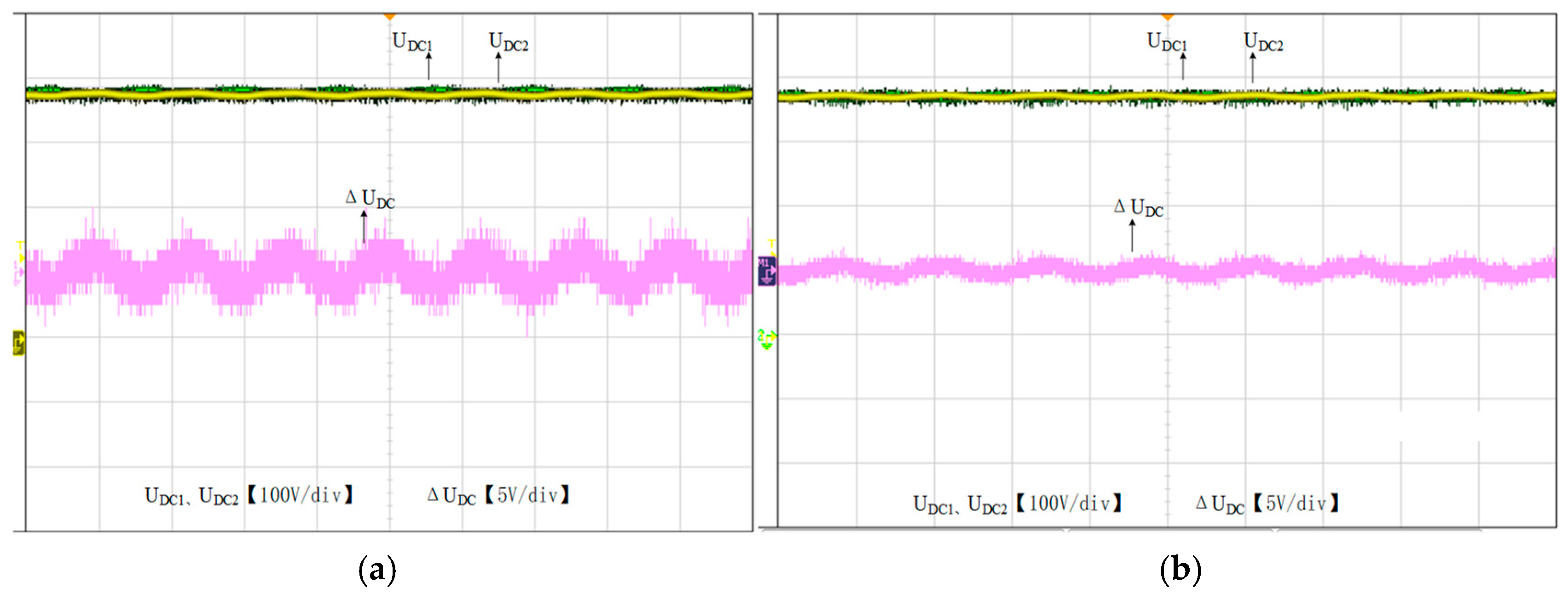
The improved MPC strategy based on midpoint potential control can be controlled through weight coefficients in the value function, achieving control of the influence of small vectors on midpoint potential. The midpoint potential control when using two different MPC strategies under the full load of 10 kW is shown in Figure 12. This Figure contains the waveform of the upper and lower bus capacitor voltage, U_DC1 and U_DC2, and the difference ΔU_DC between them. As shown in this Figure, compared with traditional MPC, when using the improved MPC strategy, the voltage control of the upper and lower bus capacitors is more balanced, and the fluctuation range between them is very small. The effective control of the midpoint potential proves the effectiveness of the improved control strategy.

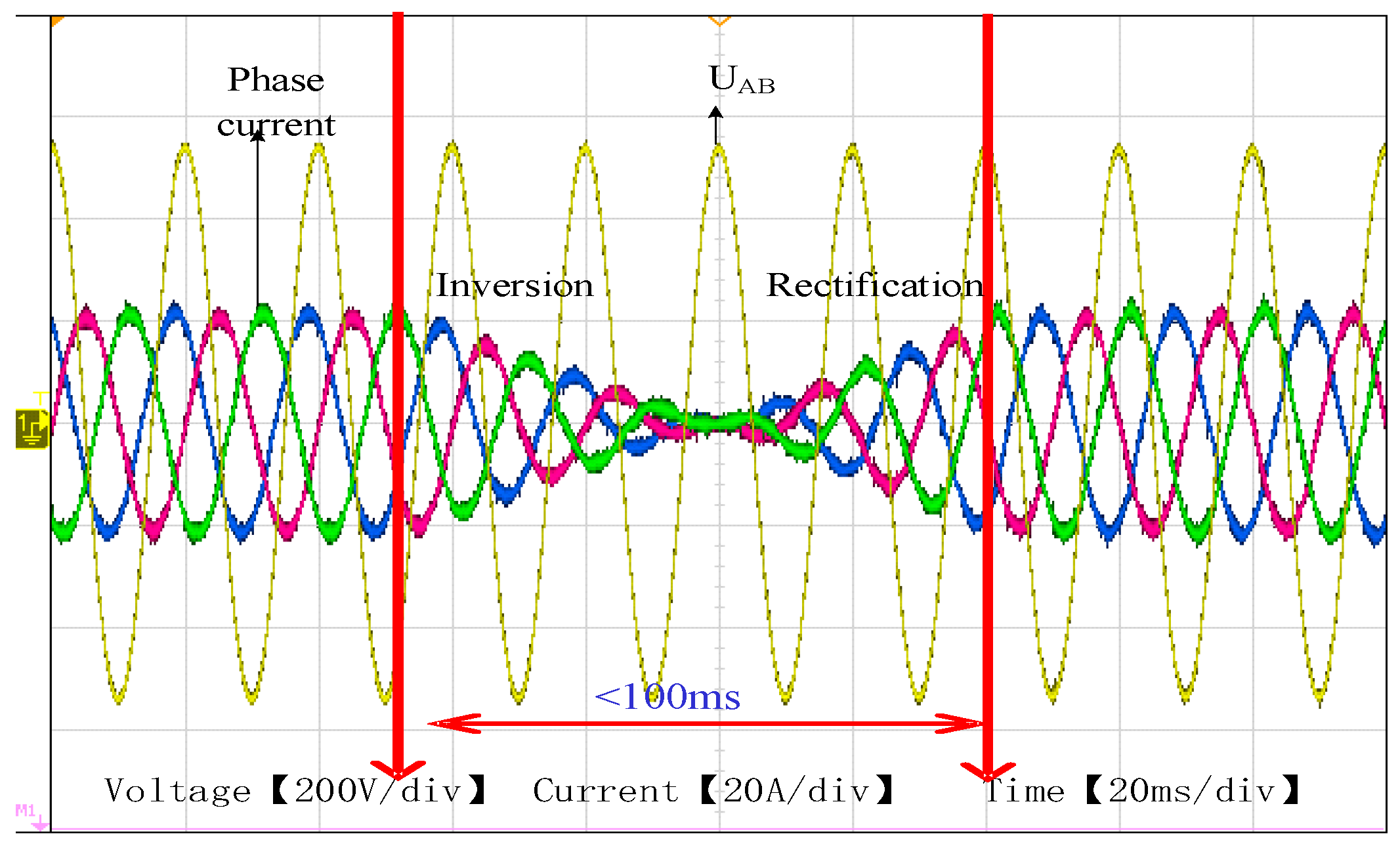
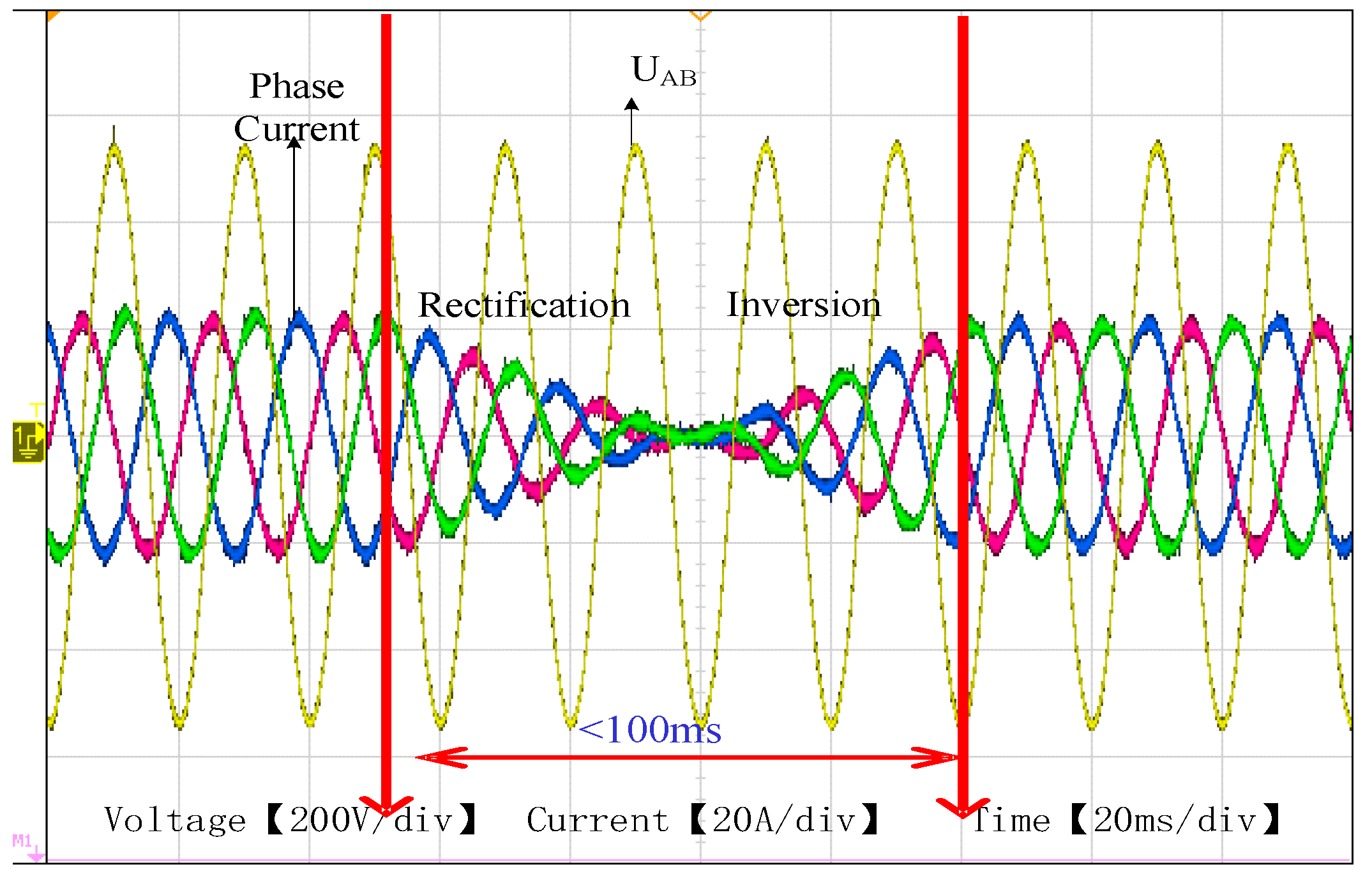
The bidirectional transition between the rectification and the inversion is tested as shown in Figure 13 and Figure 14 under the improved MPC strategy. And it can be seen that the smoothly bidirectional transition is achieved, and the transition time is less than 100 ms.

The efficiency is tested, as shown in Figure 15. It shows that the prototype has an efficiency of η = 98.32% at full load and a peak efficiency of 98.55% in the inversion mode; the efficiency is η = 98.57% at full load, and the peak efficiency is 98.73% in rectification mode.

The improved MPC strategy can reduce the computational cost of rolling optimization operations and shorten the algorithm running time. The running time of two algorithm codes can be obtained through online debugging of the microcontroller. As shown in Figure 16, the two different MPC algorithm code running times are provided, with the red part indicating the running time of the traditional MPC algorithm and the blue part indicating the running time of the improved MPC algorithm. In this Figure, the microcontroller control cycle time of the prototype with a switching frequency of 60 kHz is 16.67 μs. The former has a time of 9.87 μs, while the latter has a time of 4.31 μs, and the time is reduced about by 56%. The algorithm computation time reduction is about 36% from 64 μs to 41 μs at a switching frequency of 10 kHz in [16]. This proves that the improved MPC strategy can effectively reduce running time.

5. Conclusions

This paper researched high-performance MPC for a T-type three-level PCS. Aiming to solve the high computational complexity of traditional MPC, an improved MPC strategy based on sector judgment of the space voltage vector and midpoint potential control balancing is proposed. This improved MPC strategy can reduce the computational complexity of traditional MPC for rolling optimization, reducing the vectors from 27 to 8 in this study. The sector judgment is simple, and the improved MPC strategy is suitable for high-switching frequency operation PCSs. The prototype experiments verified that the improved MPC strategy had a better control effect of the grid connection and midpoint potential, and it effectively reduced the computational load of the MPC algorithm and shortened the algorithm running time.