Abstract
The integration of renewable energy sources, such as rooftop solar panels, into smart grids poses significant challenges for managing customer-side battery storage. In response, this paper introduces a novel reinforcement learning (RL) approach aimed at optimizing the coordination of these batteries. Our approach utilizes a single-agent, multi-environment RL system designed to balance power saving, customer satisfaction, and fairness in power distribution. The RL agent dynamically allocates charging power while accounting for individual battery levels and grid constraints, employing an actor–critic algorithm. The actor determines the optimal charging power based on real-time conditions, while the critic iteratively refines the policy to enhance overall performance. The key advantages of our approach include: (1) Adaptive Power Allocation: The RL agent effectively reduces overall power consumption by optimizing grid power allocation, leading to more efficient energy use. (2) Enhanced Customer Satisfaction: By increasing the total available power from the grid, our approach significantly reduces instances of battery levels falling below the critical state of charge (SoC), thereby improving customer satisfaction. (3) Fair Power Distribution: Fairness improvements are notable, with the highest fair reward rising by 173.7% across different scenarios, demonstrating the effectiveness of our method in minimizing discrepancies in power distribution. (4) Improved Total Reward: The total reward also shows a significant increase, up by 94.1%, highlighting the efficiency of our RL-based approach. Experimental results using a real-world dataset confirm that our RL approach markedly improves fairness, power efficiency, and customer satisfaction, underscoring its potential for optimizing smart grid operations and energy management systems.
1. Introduction
The modern power grid, or smart grid (SG), significantly improves on the traditional system by regulating and optimizing grid operations and monitoring system performance. It includes components such as electricity production stations, advanced metering infrastructure (AMI), a central system operator (SO), and transmission and distribution systems [1,2].
AMI enables efficient bidirectional communication between smart meters (SMs) in homes and the SO [3,4]. Smart meters measure and transmit detailed electricity consumption data periodically to the central system operator.
Energy management in SGs involves controlling energy generation, distribution, and consumption to ensure reliability, sustainability, and cost-effectiveness. This management is complex due to distributed energy resources (DERs), like solar panels and wind turbines, which introduce variability, and the growing use of electric vehicles (EVs) and home storage systems. Strategies must balance supply and demand, optimize renewable energy use, minimize costs, and maintain grid stability, with advanced techniques such as optimization algorithms and machine learning increasingly employed.
Various optimization techniques have been employed. Exact methods like Linear, Integer, and Binary Programs [5,6,7] utilize convex relaxation and decomposition algorithms such as branch and bound [8] and Benders decomposition [9] to reduce computational resources and achieve global optimality. Non-linear programs employ methods like Lagrangian relaxation [10], greedy search, and ADMM [11,12] to handle complex multi-objective problems. Approximate methods, including heuristic algorithms [13,14] and metaheuristics like Particle Swarm Optimization (PSO) [15,16], provide scalable solutions and near-optimal outcomes for intricate scheduling challenges. However, these techniques often face challenges such as scalability issues when applied to large-scale systems, difficulty in handling real-time dynamic changes in energy demand and pricing, and reliance on accurate system models and parameters which may not always be available or accurate in practice.
Two advanced control techniques, model predictive control (MPC) and reinforcement learning (RL), have recently been benchmarked within such a multi-energy management system context [17]. The work in [17] demonstrated that RL-based energy management systems can learn without the need for a pre-defined model and achieve better performance than linear MPC systems after a training period. However, the existing literature primarily focuses on optimizing the charging of EVs [18,19,20], often overlooking the unique challenges associated with home battery charging management. While numerous studies have proposed various strategies for EV charging to enhance grid stability and reduce costs, these approaches cannot be directly applied to home batteries, which have different usage patterns and constraints. The optimization of home battery charging requires addressing multiple objectives simultaneously, including maintaining grid stability, ensuring customer satisfaction by avoiding battery depletion, and achieving fair energy distribution among several customers. The lack of comprehensive solutions for home battery systems in the current research highlights a significant gap, necessitating novel approaches to effectively manage these distributed energy resources in an SG environment.
In this paper, we investigate the optimization of home battery charging in SGs by employing a single RL agent. Our approach treats the problem as a single-agent multi-environment scenario, where the RL agent simultaneously interacts with multiple home battery systems. This methodology allows the agent to learn and implement optimal charging policies that consider grid stability, fair energy allocation, and customer satisfaction. By integrating these objectives, our proposed solution aims to prevent grid overload, ensure fair energy distribution, and maintain battery levels above critical thresholds, providing an effective methodology for home battery management in SGs.
The primary contributions of this paper are as follows:
- Formulation as a Markov Decision Process (MDP): We formulate the home battery management problem in an SG environment as an MDP, which allows the RL agent to make optimal charging decisions based on the current system state and past actions, without requiring perfect knowledge of future events. This formulation enables the RL agent to learn effective control strategies in a dynamic and uncertain SG environment.
- Single-Agent Multi-Environment RL for Home Battery Management: We propose a novel approach utilizing a single RL agent for simultaneously optimizing the charging of multiple home batteries in an SG. This approach treats the problem as a single-agent multi-environment scenario, enabling the agent to learn optimal charging policies while considering the unique characteristics of each home battery system, and aiming to achieve the following objectives:
- –
- Enhanced Grid Stability: Our RL-based approach is designed to prevent grid overloads by learning to optimize charging schedules and avoid excessive power demand from batteries, leading to a more stable and reliable power grid.
- –
- Fair Energy Allocation: We incorporate a fairness criterion into the RL agent’s decision-making process. This ensures that all customers receive fair energy distribution, preventing significant disparities in the state of charge (SoC) levels of their home batteries.
- –
- Guaranteed Customer Satisfaction: The RL agent prioritizes maintaining battery levels above a specified threshold. This ensures customer satisfaction by preventing battery depletion and guaranteeing that energy needs are consistently met.
- Extensive Evaluations and Experiments: We have conducted extensive experiments using a real dataset to evaluate our proposed RL system. Our experimental results demonstrate significant improvements in fairness, power efficiency, and customer satisfaction compared to traditional optimization methods, highlighting the potential of RL for optimizing smart grid operations and energy management systems.
The remainder of this paper is organized as follows: Section 2 reviews the related works, providing an overview of existing research in SG energy management and the application of RL in this domain. It also discusses our motivations. Section 3 presents the key concepts and problem formulation that form the foundation of our approach. Section 4 introduces the proposed RL model, explaining the design and implementation of our single-agent multi-environment framework. Section 5 details the dataset preparation, describing the data sources and preprocessing steps used in our experiments. Section 6 evaluates the performance of our model through a series of experiments and comparisons with baseline methods. Finally, Section 7 concludes the paper by summarizing the key findings of our research and discussing potential areas for future investigation.
2. Related Works and Motivations
In this section, we first review the existing literature on energy management systems using reinforcement learning (RL) approaches. Then, we provide a comparison between our proposed approach and the current ML approaches present in the literature. The objective of this comparison is to present our motivations and the limitations inherent in the existing optimization approaches.
2.1. Related Works
Most research evaluating the effectiveness of coordinated approaches in the energy sector has focused on specific applications. Some of these applications are electric vehicle charging strategies for providing demand response (DR) services [21] or reducing peak electricity demand [22], scheduling appliance usage for load shifting [23], and coordinating heating, ventilation, and air conditioning (HVAC) systems at the building cluster level [24].
Few efforts have been devoted to coordinating the charging of home batteries at the building cluster level, despite them representing a significant energy storage resource within buildings. This lack of focus stems from the inherent challenges associated with coordinating home battery charging. Unlike a centralized system, managing numerous individual batteries necessitates accounting for diverse factors like resident energy consumption patterns, battery capacities, and varying preferences for charging times. Developing effective charging coordination strategies requires addressing these complexities to optimize energy use and maximize the benefits of distributed battery storage. The literature review can be divided into three subsections based on the scope and application of RL agents in various energy management scenarios.
2.1.1. Home Energy Management Systems
Several studies have explored home energy management systems (HEMS) using RL to optimize energy consumption and cost. These approaches can be broadly categorized into multi-agent RL (MARL) and single-agent RL. MARL leverages multiple agents, each representing a controllable device or appliance within a home. These agents interact and learn collaboratively to achieve coordinated energy management decisions. This approach is well-suited for scenarios with complex interactions between devices, such as scheduling battery charging alongside appliance operation. However, multi-agent RL can suffer from increased computational complexity due to the need for coordination among multiple agents. Single-agent RL, on the other hand, employs a single agent to manage the energy of an entire home. This simplifies the learning process but might struggle to capture the intricate interactions between various devices. Both approaches offer valuable insights for HEMS development, with the choice between them depending on the specific complexity and desired level of granularity in energy management. In the study [25], a multi-agent DDPG algorithm is leveraged to optimize EV charging schedules in a multi-home environment, demonstrating significant reductions in power consumption and costs while increasing revenue. However, implementing this method on a large scale poses substantial challenges due to the high computational time required for real-time coordination and decision making. Additionally, the system’s complexity increases with the number of prosumers, leading to scalability issues and potential delays in processing and communication. These limitations highlight the need for more efficient algorithms and infrastructure improvements to support widespread adoption. Ref. [26] presented a novel home energy management system (HEMS) that optimizes battery operation in a residential PV-Battery system using advanced load forecasting and reinforcement learning (RL). By integrating CNN and LSTM networks for load forecasting and training multiple RL agents, the system achieves a 35% cost reduction compared to traditional optimization-based methods.
2.1.2. Microgrid Management System
Recent advancements in microgrid management have leveraged a single RL agent to optimize energy distribution and storage. Studies have demonstrated that a single RL agent can effectively manage the dynamic and complex interactions within a microgrid, including load balancing, energy storage, and renewable energy integration. By continuously learning from real-time data, these RL agents adapt to fluctuations in energy supply and demand, leading to enhanced grid stability and efficiency. This approach not only reduces operational costs but also improves the overall resilience of the microgrid, making it a promising solution for future energy management systems. The study in [27] presents a two-step MPC-based RL strategy for managing residential microgrids, effectively reducing monthly collective costs by 17.5% and fairly distributing costs using the Shapley value. However, the approach faces limitations, including longer training times for complex MPCs, real-time application challenges with short sampling times, and the potential inadequacy of simple quadratic value functions for more complex problems. Additionally, computing the Shapley value can be computationally intensive, though efficient estimation methods exist.
2.1.3. EVs’ Charging Control
Efficient EV charging scheduling is crucial, focusing on cost optimization, high battery SoC, and transformer load management. The study in [28] uses a multi-agent deep reinforcement learning (DRL) with a communication neural network (CommNet) and LSTM for price prediction, which is effective in residential scenarios. Another framework, RL-Charge proposed in [29], addresses city-scale charging imbalances using multi-agent actor–critic setups and dynamic graph convolution. Additionally, the study in [30] proposed an MARL method that combines (MADDPG) and LSTM for economic energy management in charging stations, validated on real data. These studies collectively demonstrate the potential of reinforcement learning techniques in addressing the complex challenges of EV charging scheduling, offering scalable and efficient solutions for modern transportation systems. Ref. [31] introduced a multi-agent charge scheduling control framework using the cooperative vehicle infrastructure system (CVIS) to address game problems between electric vehicle charging stations (EVCSs) and EVs in complex urban environments. The proposed NCG-MA2C algorithm, incorporating a K-nearest neighbor multi-head attention mechanism, improves the efficiency of EVCSs and reduces EV charging costs, outperforming traditional methods and other multi-agent algorithms. Ref. [19] proposed a deep transfer reinforcement learning (DTRL) method to adapt pre-trained EV charging strategies to new environments, reducing retraining time while effectively meeting user demands. This approach enhances the flexibility and efficiency of RL-based charging strategies in dynamic settings. Ref. [32] presented an enhanced reinforcement learning (RL) system for managing electric vehicle (EV) charging, utilizing a Double Deep Q-learning approach to create an adaptable and scalable strategy. The proposed method significantly reduces grid load variance by 68% compared to uncontrolled charging strategies, addressing issues like overestimation in deep Q-learning and providing a flexible solution under real-world conditions. Ref. [33] introduced a two-step methodology for managing fast-charging hubs for electric vehicles (EVs). The first step uses a mixed integer–linear program (MILP) for day-ahead power commitments, while the second step employs a Markov decision process (MDP) model with deep reinforcement learning for real-time power management. The approach is tested on a fast-charging hub in the PJM power grid, demonstrating its effectiveness in handling uncertainties in electricity pricing and EV charging demand.
2.2. Motivation
The increasing penetration of renewable energy sources and the proliferation of home battery storage systems have introduced significant challenges to modern energy management. Despite extensive research, the specific issue of charging coordination for home batteries remains largely unexplored. This research aims to fill this gap by introducing a novel approach that is crucial for enhancing local grid stability, reducing costs, and promoting sustainable energy use.
Effective charging coordination can reduce peak demand, optimize energy usage to lower electricity rates, and utilize stored energy efficiently. Our approach integrates advanced reinforcement learning techniques with real-time data analytics to develop an adaptive charging strategy. Unlike previous studies, this work considers the dynamic interactions between home batteries, renewable energy sources, and the grid, offering a holistic solution to smart energy management to address the following limitations of traditional optimization methods:
- Adaptability to Real-Time Changes: Traditional methods produce static solutions that fail to adapt to real-time changes in energy consumption and generation patterns. Reinforcement learning continuously learns and adjusts policies based on new data, ensuring optimal performance in dynamic environments.
- Handling Uncertainty: The variability and uncertainty in renewable energy generation and consumption patterns pose significant challenges for traditional methods. Reinforcement learning can manage this uncertainty by optimizing policies that account for the stochastic nature of the environment.
- Scalability: As the number of batteries and the complexity of the system increase, traditional optimization methods struggle to find optimal solutions. Reinforcement learning scales effectively with system complexity, making it suitable for large-scale applications.
Reinforcement learning offers a flexible, adaptive, and scalable approach, capable of managing the dynamic and uncertain nature of smart grids. This research aims to leverage reinforcement learning to develop robust, real-time policies for efficient and effective home battery charging coordination.
Overall, this study represents a significant advancement in energy systems engineering, with the potential to improve grid reliability, reduce consumer costs, and promote environmental sustainability. The findings will benefit policymakers, utility companies, and technology developers working towards a smarter, greener energy future.
3. Preliminaries: Key Concepts and Problem Formulation
This section lays the groundwork for understanding the proposed approach in this paper. We begin by introducing the key concepts and notations used throughout the paper. Then, we delve into the details of the Proximal Policy Optimization (PPO) algorithm, as it serves as the foundation for our RL approach.
3.1. Reinforcement Learning (RL)
Reinforcement learning (RL) stands out from supervised and unsupervised learning because it can learn on its own and develop optimal decision-making strategies through trial and error [34].
3.1.1. Distinction from Traditional Optimization Techniques
Traditional optimization techniques, such as linear programming or gradient-based methods, rely on fixed parameters and explicit objective functions to find optimal solutions. In contrast, RL learns through interaction with the environment and dynamically adjusts its policies based on received rewards as shown in Equations (14), (15), and (19). In RL, optimization involves finding the best policy that maximizes cumulative rewards as shown in Equation (3). This process is guided by the reward function and value functions, with iterative updates to the Q-values to refine the policy as shown in Equation (7) where we use the received reward to update the Q-value of the state–action pair. Unlike traditional methods, RL’s optimization is driven by learning from interactions and adapting to changes in the environment.
3.1.2. Optimization in RL
An RL model has two main parts: an agent and an environment, as shown in Figure 1. Their interaction is described using three key concepts: state (s), action (a), and reward (r) [35,36]. The RL process involves a continuous interaction between the agent and the environment over time steps, as depicted in Figure 1. At each time step t, the agent takes an action and sends it to the environment. This action causes the environment’s state to change from at time t to a new state at time . The agent then receives a reward/penalty from the environment, indicating how good or bad the action was. In general, RL aims to maximize the total accumulated reward by learning a policy that maps states to actions. This total accumulated reward is expressed as follows:
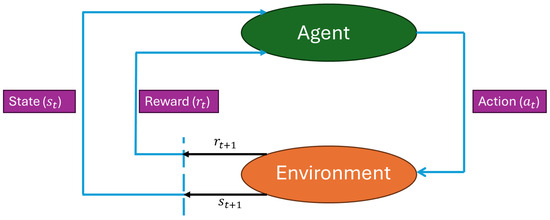
Figure 1.
The RL model block diagram.
In Equation (1), represents the total reward accumulated starting from time slot t. The term denotes the reward received at time slot , where t is the current time slot index, and l is the time step offset from the current time t. The discount factor is a real number that reflects the importance of future rewards in the agent’s decision-making process. A value of indicates that the agent is only interested in maximizing immediate rewards, while a value of closer to 1 indicates a greater focus on maximizing future rewards. This balance between immediate and future rewards is crucial for guiding the agent’s actions over time [36].
Reinforcement learning (RL) introduces the concept of the value function, denoted by in Equation (2). This function represents the expected long-term reward that the agent can achieve starting from state s and following policy , which maps states to actions. The optimal value function, , represents the highest achievable expected reward for a given state s. This is obtained when the optimal policy is used, which maximizes the reward in every state. The optimal policy and optimal value function are denoted by and , respectively, and are defined in Equations (3) and (4). These equations are standard within the reinforcement learning framework and are based on well-established principles as detailed in [37].
Similar to the value function, RL employs a Q function. This function, denoted by in Equation (5), estimates the expected cumulative reward that the agent can obtain by taking action a in state (s) and following policy thereafter. The optimal Q-value represents the highest expected cumulative reward achievable by taking action (a) in state (s) and following the optimal policy . The optimal policy and optimal Q-value are defined in Equations (5) and (6), respectively.
Similar to the value function, which is in Equation (5), Equation (6) incorporates the immediate reward received by the agent. Specifically, in Equation (6) represents the immediate reward obtained when the agent takes action (a) in state (s), causing the environment to transition to a new state . Additionally, in Equation (6) denotes the expected future reward that the agent anticipates receiving from state (), after transitioning from state (s).
Understanding how RL computes the optimal policy requires exploring the concepts of exploration and exploitation. Exploration involves the agent trying out different available actions to discover the best choices for future encounters with similar states. Conversely, exploitation involves the agent leveraging its current knowledge to select actions that maximize the total reward based on its learned Q-values.
Mathematically, the balance between exploration and exploitation is often achieved using a -greedy policy. With this policy, the agent can explore randomly selecting an action from the available options in state (s) with a probability of (exploration rate), or exploit by selecting the action with the highest estimated Q-value (considering future rewards) with a probability of ().
The exploration rate, , typically starts at its maximum value (1) and gradually decreases as the agent learns more [38,39]. This ensures that the agent initially explores a wider range of actions but eventually focuses on exploiting the knowledge it has gained for optimal performance.
One prominent model-free RL algorithm is Q-learning, introduced in [40]. It enables the agent in a Markovian decision process (where future states depend only on the current state and the action taken) to learn and act optimally through trial and error. The Q-learning algorithm aims to maximize the total accumulated reward by iteratively updating the Q-values using the Bellman equation shown in Equation (7):
The update target in the Bellman equation shown in Equation (7) is , which combines the immediate reward received at time step t with the expected future reward based on the highest Q-value in the next state (). The learning rate, , determines how much the agent incorporates the new information into its Q-value estimates. Here is a breakdown of the learning rate’s influence:
- : The agent relies solely on past knowledge and ignores the newly acquired information from the latest interaction.
- : The agent completely disregards previous knowledge and focuses entirely on exploring new actions in the current state.
The Q-function helps estimate this reward maximization when taking an action in a specific state. The core concept of the Q-learning algorithm lies in its iterative update process. The Q-values are continuously adjusted using the Bellman equation and the learning rate [35,36,38]. This update process continues until the agent reaches a terminal state (the end of an episode) at . Convergence is achieved when the difference between the current and the most recently updated Q-values becomes negligible. If convergence is not reached, the agent repeats the process in the next iteration.
In Q-learning, a data structure called a Q-table is used to store the Q-values for all possible (s, a) pairs. The Q-table has rows representing the set of states and columns representing the set of available actions in each state [38,41].
As the number of possible actions and states grows, the size of the state–action space also increases. This can lead to memory limitations when using a Q-table, especially for complex real-world problems. Fortunately, deep learning (DL) has been combined with RL to address this challenge. This marriage has led to the development of Deep Q-Networks (DQNs), which leverage the strengths of DL to offer a powerful solution [41].
3.2. Deep Learning (DL)
Deep learning (DL) is a powerful machine learning approach that utilizes artificial neural networks with multiple hidden layers. These neural networks typically consist of an input layer, one or more hidden layers, and an output layer. The hidden layers are responsible for learning complex patterns from the data. Due to their ability to learn intricate relationships and achieve high accuracy, different DL architectures are used as follows:
- Convolutional Neural Networks (CNNs) excel at tasks that involve recognizing patterns in grid-like data, making them well-suited for image and video analysis.
- Feed-forward Neural Networks (FFNNs) are general-purpose networks where information flows in one direction, from the input layer to the output layer through hidden layers. They can be applied to a wide range of problems.
- Recurrent Neural Networks (RNNs) are specifically designed to handle sequential data, where the output depends not only on the current input but also on past inputs. This makes them well-suited for tasks like language processing and time series forecasting.
These DL techniques have been successfully applied in various domains, including voice recognition and facial image analysis.
In this work, we address a novel RL problem involving a single agent interacting with multiple customers. To achieve the objectives mentioned in Section 4, the agent observes the state of each customer, which includes the customer’s battery level and the maximum amount of energy available from the grid. Based on these observations, the agent takes actions that influence the behavior of the customers, aiming to optimize the overall system performance. Thus, we leverage the power of neural networks combined with RL. Neural networks provide the function approximation capabilities needed by RL to handle complex environments and high-dimensional state spaces. This integration allows the RL agent to learn intricate relationships within the data and make effective decisions based on the learned patterns.
3.3. Proximal Policy Optimization (PPO)
To address the challenge of coordinating home battery charging, researchers have employed Proximal Policy Optimization (PPO) [42]. PPO is a type of RL algorithm that falls under the category of policy gradient methods. These methods directly optimize a policy function that is represented mathematically and can be differentiated. PPO builds upon the Actor–Critic framework [37] (illustrated in Figure 2).
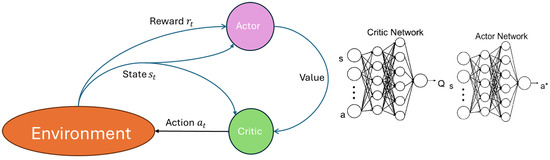
Figure 2.
Actor–critic DRL. A DDPG agent where the Actor network determines the optimal action () to take in the current state.
In this context, the learning agent aims to discover a parameterized control policy, denoted by as shown in Equation (8). This policy essentially maps a given state (the perceived state of the system) to the appropriate action that should be taken in that state (). The ultimate goal is to find a policy that maximizes the total reward received over a specified optimization horizon, starting from an initial state .
The return Equation (8) represents the total discounted reward accumulated by the agent over a trajectory generated by the policy, where represents the discount factor. The optimization horizon, T, defines the length of the trajectory considered for calculating the return.
Actor–critic methods are well-suited to problems with continuous action spaces. Unlike DQN, which typically handles discrete actions, actor–critic methods can directly optimize policies in continuous action spaces by learning separate models for the policy (actor) and the value function (critic), allowing for more precise control and exploration in complex environments.
In PPO algorithms, the policy function needs to be differentiable with respect to its parameters (represented by in Equation (9)). This differentiability allows the calculation of the gradient, which is crucial for updating the policy parameters during training. The policy itself is typically represented by a neural network, as shown in Equation (9). Here, denotes the weights of the neural network that need to be adjusted. The objective is to find the values of that will maximize the total discounted reward (return) denoted by G in Equation (8).
To achieve this, PPO utilizes a concept called the clipped surrogate objective. This objective leverages the probability ratio (pr) between the old and new policies to provide a more stable update for the policy parameters [42]. The unconstrained objective function that PPO aims to maximize is formulated in Equation (10):
Within the PPO algorithm in Equation (10), represents the probability ratio between the actions recommended by the new policy with parameters denoted by and the old policy with parameters at state and action . The term in Equation (10) represents an estimate of the advantage function, denoted by . This advantage function captures the difference between the expected reward for taking a specific action and the expected reward for simply being in that state . Both (state–action value function) and (state value function) are estimated using separate neural networks within the PPO framework.
However, the original objective function in Equation (10) can lead to significant gradient updates during training, potentially causing instability. To address this, PPO employs a clipped surrogate objective as shown in Equation (11). This objective incorporates a clipping parameter , where according to [42] to limit the magnitude of the policy updates and enhance stability.
The clipped surrogate objective is further adapted for use with neural network architectures where the policy and value functions share parameters. This is often carried out by having them share the initial hidden layers, which are responsible for extracting features from the state space. Additionally, an entropy term is introduced into the objective function Equation (12). This term encourages exploration by promoting a wider range of actions to be considered by the agent, leading to better coverage of the state space. The final objective function incorporating these modifications is presented in Equation (12).
where and are hyperparameters and H is an entropy measure. In Algorithm 1, we iteratively update the policy parameters based on advantages estimated from sampled trajectories. It restricts policy updates using a clipped objective function , ensuring changes stay within a defined threshold . This approach, optimized through minibatch stochastic gradient descent, improves convergence and performance in training neural network policies for complex environments.
| Algorithm 1: Proximal Policy Optimization [37] |
|
4. Proposed Scheme
In this paper, we address the complex problem of charging coordination for multiple customers’ batteries in an SG environment with the integration of renewable energy generators such as rooftop solar panels. Our proposed approach aims to ensure power saving, high customer satisfaction, and fairness in power distribution. This section details the methodology employed to achieve these objectives using an RL approach.
4.1. System Architecture
The considered system architecture for the SG charging coordination is illustrated in Figure 3. The figure depicts two communities, each consisting of houses equipped with rooftop solar panels and battery storage systems. The key components of the system architecture and their interactions within the SG environment are as follows:
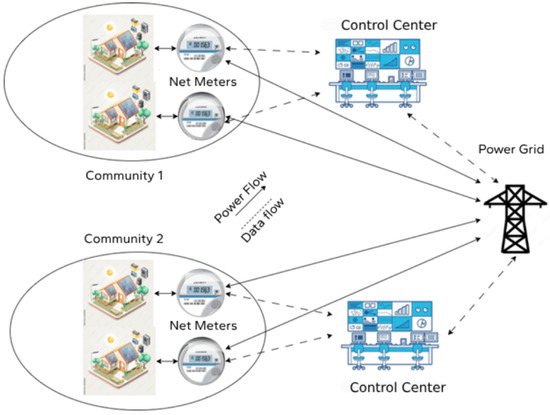
Figure 3.
The system architecture.
- Communities: Each community comprises multiple houses with solar panels generating electricity from the sun. The excess energy generated is stored in batteries for later use. If a battery stores more energy than the need of the consumer, the excess energy is sold to the electricity company.
- Net Meters: Each house has a net meter that records the amount of power generated, consumed, and stored. These meters send data to the control centers and receive power allocation instructions.
- Control Centers: Control centers are responsible for monitoring and managing the power distribution within each community. They receive real-time data from the net meters and make decisions regarding power allocation to maintain optimal operation of the grid.
- Power Grid: The power grid supplies additional power to the communities when the renewable energy generated is insufficient. It also receives excess power from the houses when their generation exceeds consumption.
Figure 3 illustrates the bidirectional flow of power and data, showcasing how the system dynamically adapts to varying energy demands and generation levels. The control centers play a crucial role in ensuring efficient power distribution by leveraging real-time data to make informed decisions on power allocation, thus achieving the objectives of power saving, customer satisfaction, and fairness.
4.2. Problem Objectives
The main objective of our paper is to design a single-agent RL model capable of coordinating the charging of multiple customers’ batteries within an SG environment. This model aims to achieve three key objectives:
- Minimize Overall Power Consumption: Minimizing overall power consumption offers significant benefits. Grid operators benefit from reduced operational costs due to lower energy generation requirements, which translates to potential delays in expensive grid infrastructure upgrades. This promotes efficient grid management and long-term power sustainability.
- Maintain Battery Level within Thresholds: Maintaining customer battery levels within pre-defined thresholds is crucial for both the grid and its customers. This ensures grid stability by allowing the grid to draw from stored energy during peak demand periods, reducing reliance solely on power generation. This can potentially delay the need for additional power plants, saving resources and promoting grid sustainability. For customers, maintaining adequate battery levels guarantees uninterrupted service and the ability to power their homes and appliances reliably, meeting their essential energy needs.
- Minimize Discrepancies in Battery Levels (Fairness): Fairness in power distribution, minimizing discrepancies among customer battery levels, is essential for both the grid and its customers. This promotes efficient utilization of available grid capacity by ensuring power is distributed fairly. It avoids overloading specific grid sectors and prevents situations where some customers face power shortages while others have surplus stored energy. This fosters overall grid stability and efficient resource management. From the customer’s perspective, fair charging power allocation builds trust in the grid management system. Customers can be confident they receive a fair share of available resources, ensuring reliable and consistent power availability.
4.3. Markov Decision Process (MDP)-Based Reinforcement Learning (RL) Approach
To tackle the charging coordination problem effectively, we propose an RL approach based on MDP formulation. MDP provides a mathematical framework for decision making in scenarios with partial randomness. Within this framework, the RL agent employs an actor–critic algorithm, which combines the strengths of policy-based and value-based methods. The RL model comprises the following components.
- Agent: The RL agent is responsible for deciding the optimal power allocation actions based on current battery levels and other relevant states.
- Environment: The environment represents the SG and includes the state of each customer’s current battery level and the maximum power available from the grid.
- State (s): The state, denoted by , provides a comprehensive snapshot of the current energy situation in the SG at a given time step t. It consists of the following key elements:
- –
- : Represents the state of the environment at a given time step t.
- –
- : Denotes the maximum power available for charging from the grid at time step t. This value defines the operational constraint on power allocation, ensuring the agent does not exceed grid capacity. The agent cannot allocate more power in total than what is available from the grid (). This constraint ensures the agent’s decisions are feasible within the physical limitations of the system and guides the agent to stay within the permissible power budget, distributing power efficiently among all customers.
- –
- : Indicates the current state of charge (battery level) for each customer i at time step t. A higher value of SoC for a customer indicates less immediate need for power allocation, allowing the agent to prioritize customers with lower levels. Knowing the SoC of all customers provides a holistic view of the system and helps avoid neglecting critical needs.
- Action (a): The action, denoted by a, represents the power allocation decisions made by the RL agent for each customer’s battery at a given time step t. The action for each customer is a value between (0,1), and the action space defines all possible power allocation combinations with a sum equal to or less than () that the agent can choose from. Each action element corresponds to the amount of power allocated to customer i during the current time step t. The agent aims to select an action that maximizes the expected cumulative reward over time, considering the previously defined objectives. By effectively selecting actions within the action space, the RL agent can learn an optimal policy for power allocation, achieving the desired balance between power saving, fairness, and customer satisfaction in the SG environment.
- State Transition Function (P(s’|(s,a))): The transition function defines the probability of transitioning from state s to state given action a. This function captures the dynamics of the SG and determines how the state evolves based on the agent’s actions and the underlying environment. The transition probabilities are influenced by factors such as power consumption patterns, renewable energy generation, and battery characteristics.
- Reward (r): The reward function, denoted by r, provides feedback to the RL agent based on the chosen actions and their impact on the system’s objectives. The reward function is designed to capture the trade-offs between power saving, customer satisfaction, and fairness. It includes the following components:where , , and denote grid reward, fairness reward, and customer satisfaction reward, respectively, and , , and are weighting factors that control the importance and priority of each component based on our objectives and constraints.
- –
- Grid Reward (): This is a penalty applied to actions that result in consuming more power than the maximum power allocated for charging, and it is a reward that increases as the difference between the maximum power allocated for charging and the consumed energy for charging increases. This component aims to prevent exceeding the maximum power and also minimize the amount of power used for charging the batteries. It is defined as follows:where is the maximum power allocated for charging at time step , and is the total allocated energy to all customers at time step . A negative reward (−10) is assigned if the total allocated power exceeds . Otherwise, the reward is equal to the percentage of the remaining available power after considering the allocated power. This encourages the agent to operate within the grid’s power limitation and save energy if the batteries are at a good level as expressed by the consumer satisfaction reward.
- –
- Fairness Reward (): A reward component that incentives actions leading to equal battery levels among customers. This component promotes fairness in power distribution and prevents disparities in battery levels. It is defined as follows:where (CV) is the Coefficient of Variation which quantifies the deviation of battery levels from an equal distribution. It is calculated using the mean and standard deviation of the SoC for all customers as follows:We use Equation (15) to calculate the reward, where CV = 0 indicates equal distribution of battery levels while CV = −1 indicates the greatest disparity in the battery levels. We multiply CV by (−) sign and add one so that the reward becomes in the range (0,1), where (1) indicates equal distribution of battery levels, while (0) indicates the greatest disparity in the battery levels. Thus, the maximum is (1) and it is achieved when CV is equal to (0) and all customers have the same battery level, and the minimum is (0) and it is achieved when CV is equal to (−1) and there is a big disparity in the battery levels. We perform this shift to normalize all the different components of the rewards by making them in the range (0,1) where (0) represents the min value of each component and (1) represents the max value.
- –
- Customer Reward (): This reward component expresses customer satisfaction by targeting adequate battery levels for each customer that ensures energy needs are met. It is defined as follows:where represents the total reward for all customers which is between (0,1). The customer’s reward is determined based on their battery SoC as shown in Equation (19). The relationship between SoC and reward is illustrated in Figure 4. The figure shows a piecewise function composed of different segments: a fixed penalty below a certain SoC threshold (), an exponential increase in reward, a linear increase, and a fixed reward above another SoC threshold ().
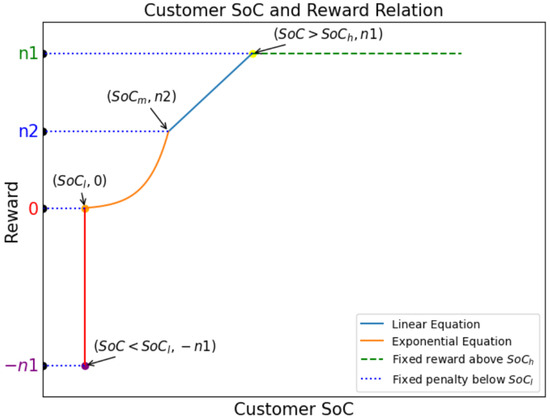 Figure 4. Customer satisfaction reward curve.
Figure 4. Customer satisfaction reward curve.- ∗
- Fixed Penalty (SoC < ): When the SoC is below a low threshold (), the reward is a fixed penalty of . This penalty discourages low battery levels, ensuring that customer satisfaction remains a priority by avoiding situations where batteries are critically low.
- ∗
- Exponential Equation (): As the SoC increases from to a medium threshold (), the reward follows an exponential curve, starting from 0 at and rising to at . This segment of the reward function aims to provide a smooth and increasing incentive as the battery charge increases, reflecting an improved customer experience.
- ∗
- Linear Equation (): When the SoC is between and , the reward increases linearly from to . This linear increment incentivizes maintaining battery levels within this range, which is considered optimal for balancing power supply and customer satisfaction.
- ∗
- Fixed Reward (): Once the SoC exceeds , the reward is fixed at . This fixed reward ensures that there is no incentive to overcharge the batteries above . We want the agent to keep the SoC between and .
5. Dataset Preparation
This section details the dataset used to train our RL agent and the preprocessing steps applied to prepare it.
5.1. Data Source
We leveraged a publicly available dataset from Ausgrid [43], a prominent Australian electricity provider. This dataset encompasses real-world power consumption and generation readings for residential solar panel installations in Sydney and New South Wales. Each participating home was equipped with two meters: one to measure power consumption from the grid and another to measure power generation from the solar panels. The readings were collected every 30 min from 1 July 2010 to 30 June 2013. The dataset additionally includes details about the maximum power generation capacity (per hour) for each home’s solar panels and their respective locations. We acknowledge the reviewer’s concern regarding the age of the dataset (2010–2013). However, the Ausgrid solar home electricity dataset remains highly relevant and has been widely used in recent research due to its comprehensive and detailed data on solar generation and residential electricity consumption. Several recent studies have effectively utilized this dataset, demonstrating its continued relevance in the field such as [44] which utilized the dataset for home energy management through stochastic control methods, Ref. [45] which employed it for anomaly detection in smart meter data, and [46] which used the dataset for detecting false-reading attacks in smart grid net-metering systems These studies highlight the dataset’s applicability in addressing current challenges in energy management and smart grid optimization. Furthermore, the dataset’s public availability and its rich features, including detailed consumption and generation readings, provide a valuable resource for simulations that are both accurate and reproducible.
5.2. Data Preprocessing
To create a clean training dataset suitable for our agent’s learning process, we performed the following preprocessing steps on the Ausgrid dataset:
- Outlier Removal: We eliminated anomalous measurements potentially caused by malfunctioning equipment. This is a standard practice for enhancing the training efficacy of machine learning models.
- Net Metering: For each house, we computed the net difference between the power consumption readings and the solar panel generation readings. This essentially simulates having a single meter that reflects the net power usage by the house (consumption minus generation).
- Data Resampling: We down-sampled the data from half-hourly readings to hourly readings (24 readings per day). This reduction in data granularity helps preserve customer privacy.
Through these steps, we constructed a refined training dataset encompassing net meter readings for 10 houses, collected over a period of 1096 days (hourly data).
5.3. Data Visualization
To gain a deeper understanding of the processed data, we employed visualization techniques to identify patterns and relationships. Figure 5 illustrates the net energy consumption (in kWh) for four randomly selected houses. The term “Net Energy Consumption (kWh)” refers to the net energy flow measured by the meter for each house, which can be either positive or negative. Positive values indicate that the power consumed from the grid is larger than the power generated from solar panels, while negative values indicate that the generated power exceeds the power consumed from the grid. In Figure 5, the quantified energy values show a recurring seasonal pattern, where each house exhibits similar patterns across months within the same season (e.g., September to January or January to May) regardless of the year. For instance, during certain months, House 1 absorbs an average of 300–500 kWh from the grid, while during others, it may feed back up to 200 kWh into the grid. This seasonal variation is influenced by factors such as the day of the week and solar generation, both of which impact power consumption and production.
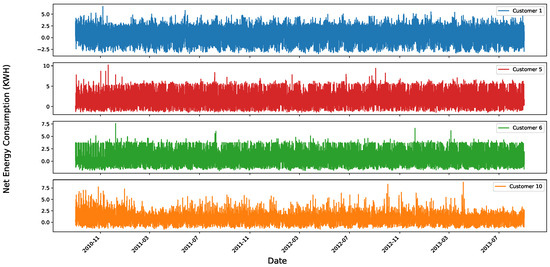
Figure 5.
Net meter readings for four randomly chosen houses.
To delve deeper into the relationships between consecutive readings within the net meter time series data for each customer, we employed the auto-correlation function (ACF). The ACF measures the correlation between a data point and subsequent data points at varying time lags within the time series. Figure 6 presents the ACFs for the same customers depicted in Figure 5.
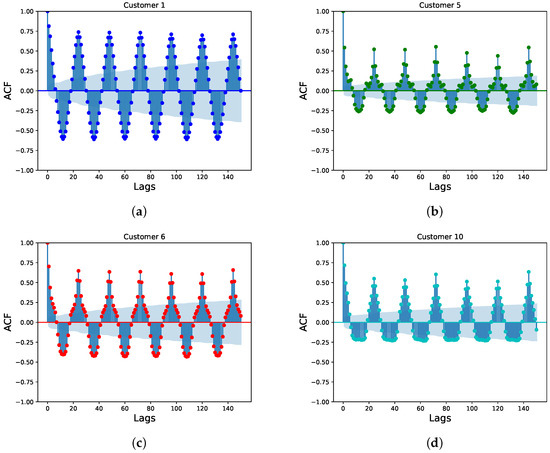
Figure 6.
The ACFs of four randomly selected customers. (a) Customer 1; (b) Customer 5; (c) Customer 6; (d) Customer 10.
The shaded blue areas in Figure 6 represent 95% confidence intervals, which are used to assess the statistical significance of the auto-correlation at specific time lags. As observed in the figure, the correlation values at lag times 1 and 2 (i.e., comparing the current reading with the readings 1 and 2 h later) for all customers fall outside the shaded area. This signifies a statistically significant correlation between a reading and the two readings that follow it in the series.
Furthermore, the overall shape of the ACF over a single day exhibits a high degree of similarity across consecutive days for all houses. This finding suggests that the net meter readings for each customer exhibit a distinct daily pattern. This pattern, along with the time correlations between the readings, can be exploited by using machine learning models capable of learning and capturing time series data to learn the consumption patterns of the consumers successfully.
6. Performance Evaluation
This section evaluates the effectiveness of our proposed RL approach. In our experiments, we consider an SG environment with 10 customers, each equipped with battery storage systems, the battery selected for the simulation is Tesla Powerwall 2, and its specifications are shown in Table 1. The aggregated load of the 10 customers is visualized in Figure 7. This section investigates the influence of the maximum power allocated for charging the batteries () on customer load management strategies. Thus, we explore three distinct scenarios for derived from Figure 7:

Table 1.
Tesla Powerwall 2 Battery Specifications.
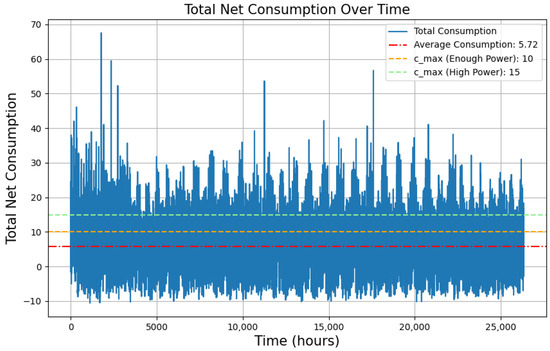
Figure 7.
Combined net consumption of the 10 customers.
- Scenario 1: is equal to average consumption. In this scenario, is set to be the average consumption of all 10 customers combined. This serves as a baseline to understand how closely customer loads can adhere to the overall power limit.
- Scenario 2: is slightly above average consumption. This scenario investigates how the system copes with a limited surplus of available power compared to the typical customer demand.
- Scenario 3: is significantly above average consumption. This scenario explores how the system manages customer loads when there is a substantial amount of excess power available.
Through these scenarios, we aim to gain insights into the effectiveness of our proposed RL approach under different power constraints. This will provide valuable information for optimizing power allocation, ensuring efficient customer service while respecting the overall power limitations, and maintaining battery levels within optimal thresholds while promoting fairness among customers.
6.1. Experimental Setup
Our simulation environment models an SG with 10 customers, each with a battery storage system. It simulates the interaction between the customers and the grid, considering parameters such as SoC and net load. The simulation environment is developed in Python using several libraries, including pandas for data handling, numpy for numerical computations, and torch for deep learning model implementation.
In our experimental setup, we imposed a constraint on the actions available to the RL agent, allowing it to explore only those actions where the sum of allocations (selected actions for all customers at the current time step t) is equal to or less than one (). This constraint ensures that the total energy allocated does not exceed the available capacity, because even though the optimal policy is defined, the agent has a possibility of exploration, which can lead to actions with a sum larger than one (), so that we enforce this constraint to prevent overloading of the system. By enforcing this limitation, we aim to:
- Ensure System Stability: By restricting the sum of actions to be within the capacity limits, we prevent drawing excessive power, thereby maintaining the overall stability and safety of the grid.
- Facilitate Learning: By providing a well-defined action space, the agent can focus on exploring viable solutions, accelerating the learning process, and improving the convergence of the training algorithm.
The optimal hyperparameters of our proposed DRL model are given in Table 2. This setup provides a comprehensive framework for simulating and analyzing the effectiveness of the RL-based load management strategies in SG.

Table 2.
Hyperparameters of the proposed DRL model.
6.2. Performance Evaluation Metrics
The performance of our proposed RL approach is assessed in terms of various evaluation metrics, including capacity utilization, battery threshold violations, fairness, and cumulative reward over the training process. Each metric provides valuable insights into the system’s performance, enabling a comprehensive evaluation of the RL framework’s effectiveness in managing smart grid energy distribution.
6.2.1. Capacity Utilization
This metric measures the amount of energy allocated to customers compared to the maximum allowed capacity (). This metric reflects the efficiency of the RL agent in utilizing the available power. High capacity utilization indicates that the agent is striving to satisfy customer demands when the maximum power allowed from the grid is not sufficient. The agent is only looking to avoid receiving penalties when the SoC drops below without giving any importance to receiving a reward from saving power. Conversely, low capacity utilization also holds significance by showing that the agent is able to save power from the grid and manage energy effectively while satisfying the customers. For this metric, lower capacity utilization is a strong indicator of efficient agent performance.
6.2.2. Battery Threshold Violations
This metric assesses the RL agent’s performance in maintaining battery levels above the critical threshold (). This metric is a key indicator of system reliability and stability. Minimizing these violations is essential to prevent battery damage and ensure continuous power supply to customers, thereby maintaining operational integrity and customer satisfaction.
6.2.3. Fairness
This metric evaluates the RL agent’s ability to maintain the customers’ batteries at the same level. Fairness is measured using Equation (15). By using this equation, an closer to one is an indication of a fair distribution of energy. Fairness ensures that no customer is disproportionately disadvantaged, fostering a balanced and fair energy distribution system.
6.2.4. Cumulative Reward over the Training Process
This metric tracks the RL agent’s performance across episodes. The cumulative reward reflects the agent’s ability to learn the optimal policy (). Higher cumulative reward indicates that the agent successfully balances the conflicting objectives of power saving, customer satisfaction, and fairness. This metric is crucial for evaluating the overall effectiveness and adaptability of the RL approach in optimizing the charging coordination of customer-side batteries.
6.3. Scenario 1: Is Equal to Average Consumption
In this subsection, we examine the first scenario where the maximum power constraint () is set to the average load of the 10 customers. This scenario serves as a baseline to understand how well the RL agent can manage customer loads when the available power is just sufficient to meet the average demand.
Figure 8 shows the simulation results for this scenario. The results highlight several key observations:
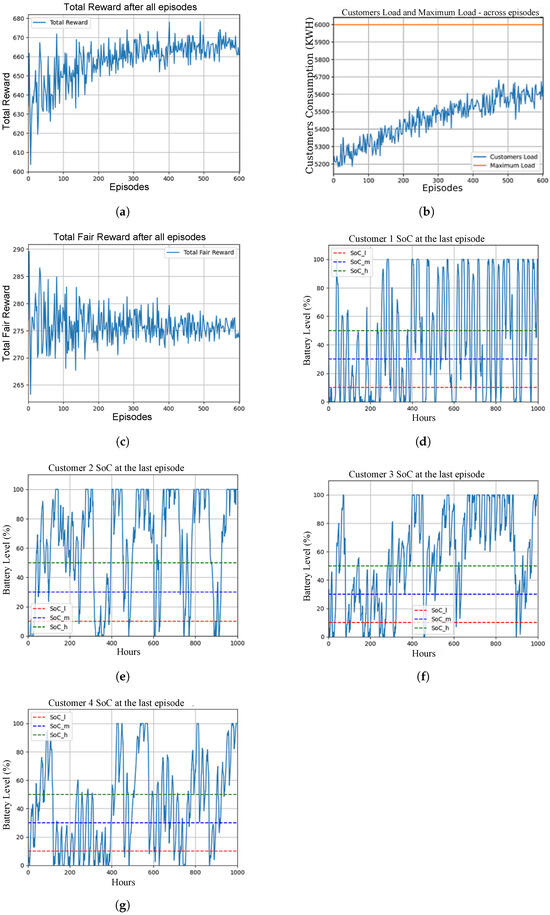
Figure 8.
Power allocation, fairness, total reward, and SoC for different customers in Scenario 1. (a) Total cumulative reward; (b) Capacity utilization; (c) Fairness; (d) Customer 1 SoC; (e) Customer 2 SoC; (f) Customer 3 SoC; (g) Customer 4 SoC.
- Battery Levels Below Critical Threshold: The batteries drop below the critical threshold (), as shown in Figure 8d–g for different customers. This occurs because the available power is insufficient to serve all customers adequately.
- Fairness as a Secondary Priority: Due to the limited power supply, the agent does not prioritize fairness in battery level distribution, as shown in Figure 8c. Instead, the primary focus is preventing the SoC from dropping below the critical threshold to avoid substantial penalties.
- Adaptive Power Utilization: The agent learns to strategically allocate more power to maintain all SoC levels above , as shown in Figure 8b. This demonstrates the agent’s ability to adapt its power usage dynamically to prevent critical battery levels despite the limited power availability.
- Reward Optimization: Although is not sufficient for all customers, the agent successfully increases the cumulative reward across episodes, as shown in Figure 8a. This indicates that the RL agent effectively learns a robust policy for action selection under constrained power conditions, optimizing the overall system performance over time.
Overall, this scenario underscores the RL agent’s capability to manage customer loads under tight power constraints, focusing on maintaining minimum battery levels and gradually improving performance through learning. The agent’s strategy to avoid critical levels highlights its effectiveness in handling power allocation challenges, even when fairness must be deprioritized due to insufficient power.
6.4. Scenario 2: Is Slightly above Average Consumption
In this subsection, we examine the second scenario in which the maximum power constraint () is set slightly above the average load of the 10 customers. Figure 9 shows the simulation results of this scenario. The results highlight several key observations. This scenario helps us understand how the RL agent performs when there is a modest surplus of available power compared to the average demand.
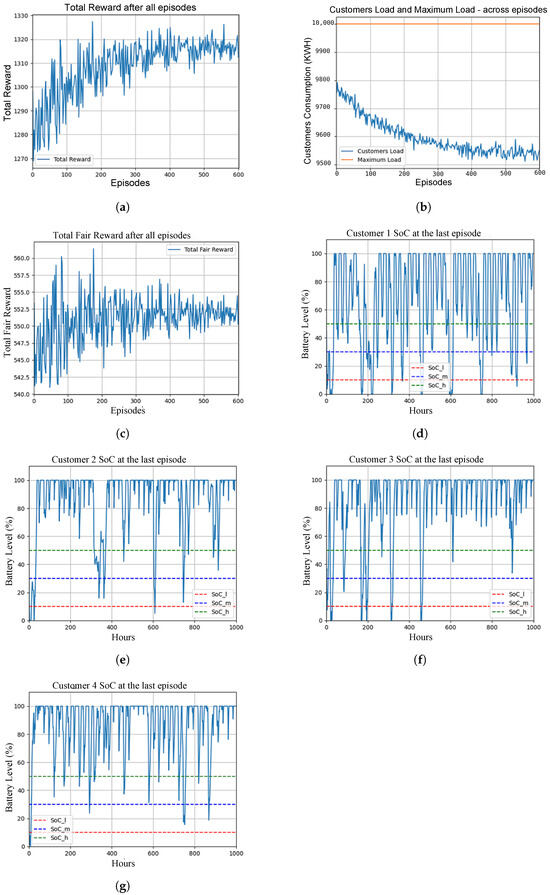
Figure 9.
Power allocation, fairness, total reward, and SoC for different customers in Scenario 2. (a) Total cumulative reward; (b) Capacity utilization; (c) Fairness; (d) Customer 1 SoC; (e) Customer 2 SoC; (f) Customer 3 SoC; (g) Customer 4 SoC.
- Improved Battery Levels: The batteries drop below the critical threshold () much less frequently than in Scenario one, as shown in Figure 9d–g for different customers. The modest surplus in available power allows the agent to better manage the battery levels, ensuring that they remain above the critical threshold more consistently.
- Enhanced Fairness: The agent achieves higher fairness in battery level distribution compared to Scenario one, as shown in Figure 9c. With slightly more power available, the agent can allocate resources more fairly among customers, reducing discrepancies in battery levels.
- Efficient Power Allocation: The agent learns to allocate less power compared to Scenario one while still maintaining sufficient battery levels for all customers, as shown in Figure 9b. This indicates that the RL agent is capable of optimizing power usage more effectively when there is a small surplus.
- Higher Cumulative Reward: The total cumulative reward is higher in this scenario compared to Scenario one due to the increased fairness, more savings in power, and higher SoC levels across episodes, as shown in Figure 9a. This demonstrates that the RL agent not only prevents critical battery levels but also enhances overall system performance by promoting fairness and efficient power utilization.
Overall, this scenario highlights the RL agent’s improved performance when given a slight surplus of available power. The agent can maintain higher battery levels, achieve better fairness among customers, and optimize power allocation, leading to a higher cumulative reward. This underscores the potential benefits of providing a modest surplus in power availability to enhance SG operations.
6.5. Scenario 3: Is Significantly above Average Consumption
In this subsection, we investigate the third scenario where the maximum power allocated for charging () is set significantly higher than the average load of 10 customers. This scenario explores the RL agent’s performance when ample power is available to meet the demands of all customers.
Figure 10 shows the simulation results for this scenario. The results highlight several key observations:
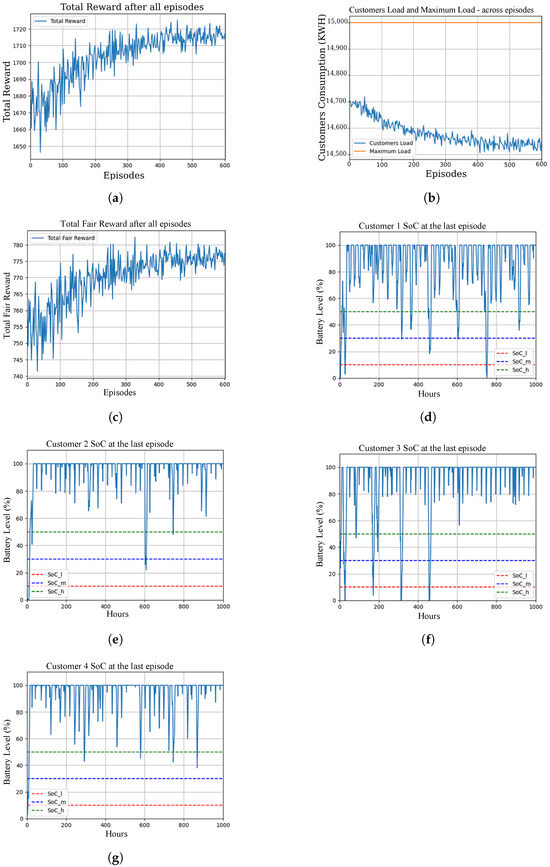
Figure 10.
Power allocation, fairness, total reward, and SoC for different customers in Scenario 3. (a) Total cumulative reward; (b) Capacity utilization; (c) Fairness; (d) Customer 1 SoC; (e) Customer 2 SoC; (f) Customer 3 SoC; (g) Customer 4 SoC.
- Rare Critical Battery Levels: As shown in Figure 10d–g, the value is mostly above with occasional drops below . These happen due to the nature of consumption patterns of certain customers. These drops are typically from very high SoC levels to low levels, reflecting sudden changes in individual consumption.
- Enhanced Fairness: The agent achieves significantly higher fairness in power distribution compared to the two previous scenarios as shown in Figure 10c. The ample power supply allows for fair energy distribution among all customers, minimizing discrepancies in battery levels.
- Optimized Power Utilization: The agent effectively learns to allocate power efficiently, maintaining high SoC levels across all customers while preventing wasteful energy usage as shown in Figure 10b.
- Highest Cumulative Reward: The overall cumulative reward is the highest among all scenarios, indicating the agent’s successful learning and adaptation to the optimal power allocation policy, as shown in Figure 10a.
Overall, Scenario 3 demonstrates the RL agent’s capability to optimize power distribution under abundant power conditions, achieving high fairness, maintaining battery levels, and maximizing the cumulative reward.
6.6. Discussion
In this section, we have conducted a thorough experimental evaluation for our proposed RL approach for optimizing the charging coordination of customer-side battery storage in SGs. We have explored three distinct scenarios with varying levels of available power () and analyzed the RL agent’s performance in terms of capacity utilization, battery level maintenance, fairness in power distribution, and overall system reward. In Scenario one, where is set to the average consumption of the total net load, the agent demonstrated a primary focus on preventing critical battery levels () at the expense of fairness. Despite the limited power, the RL agent managed to optimize the cumulative reward by learning to avoid severe penalties associated with low battery levels. In Scenario two, where the available power is slightly above the average consumption, the results show a marked improvement in fairness and battery level maintenance. The agent achieved higher cumulative rewards by balancing the power distribution more fairly among customers while ensuring that batteries do not frequently fall below the critical threshold. In Scenario three, with set significantly above the average consumption, the RL agent’s performance reached its peak. The ample power supply allowed the agent to maintain consistently high battery levels, achieve the highest fairness in energy distribution, and optimize the overall system reward. The instances of battery levels falling below were very rare. However, such drops occasionally occurred due to specific consumption patterns of certain customers, where sudden changes in consumption led to significant drops in SoC from high levels to critical levels. These experimental results underscore the effectiveness of our RL-based approach in managing customer-side battery storage under different power constraints. The approach’s ability to adapt to varying conditions, prioritize critical battery maintenance, and achieve fairness in power distribution highlights its robustness and versatility. The insights gained from these experiments pave the way for further enhancements and practical implementations of RL in SG energy management.
7. Conclusions and Future Work
This study addressed the significant challenges posed by the integration of renewable energy sources, such as rooftop solar panels, into smart grids, particularly in managing customer-side battery storage. We proposed a novel reinforcement learning (RL) approach using an actor–critic algorithm to optimize the charging coordination of these batteries. The method was rigorously tested across three distinct scenarios with varying levels of available power ().
In Scenario One, where was set to the average consumption of the total net consumption, the RL agent primarily focused on preventing critical battery levels (), even at the expense of fairness in power distribution. Despite limited power, the agent optimized the cumulative reward by avoiding severe penalties associated with low battery levels.
In Scenario Two, where the available power was slightly above the average consumption, there was a notable improvement in both fairness and battery level maintenance, leading to a 96.5% increase in fairness and a significant rise in the total reward by 94.1% (from 680 in Scenario One to 1320).
Finally, in Scenario Three, with ample power significantly above the average consumption, the RL agent excelled, maintaining consistently high battery levels, achieving the highest fairness in energy distribution with a 173.7% increase in fairness from Scenario One, and optimizing the overall system reward, which increased by 30.3% from Scenario Two to Scenario Three (reaching 1720).
These findings underscore the robustness and versatility of our RL-based approach in managing customer-side battery storage under different power constraints. The RL agent demonstrated adaptability to varying conditions, prioritizing critical battery maintenance while ensuring fairness in power distribution. The approach not only optimized the system reward but also revealed recurring seasonal patterns in energy consumption, highlighting the need for seasonally adaptive power management strategies.
Future research will focus on making power constraints dynamic to better reflect real-world scenarios where power availability fluctuates. Additionally, we plan to study the impact of malicious attacks on the system, such as rational or selfish attacks, where an attacker reports false SoC levels to prioritize their own energy allocation, and irrational attacks that manipulate the agent’s learning policy through false feedback. By examining these scenarios, we aim to develop more robust RL algorithms capable of withstanding adversarial behaviors and further enhancing the efficiency and reliability of smart grid operations.
Author Contributions
Conceptualization, M.M.B., M.M., M.A. and M.I.I.; Methodology, A.A.E., M.M.B., M.M., W.E., M.A. and M.I.I.; Software, A.A.E.; Validation, A.A.E., M.M.B., M.M. and M.A.; Investigation, A.A.E., M.M.B., M.M., W.E., M.A. and M.I.I.; Writing—original draft, A.A.E.; Writing—review & editing, A.A.E., M.M.B., M.M., W.E., M.A. and M.I.I.; Supervision, M.M. and W.E.; Project administration, M.M. and W.E.; Funding acquisition, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Researchers Supporting Project number (RSPD2024R636), King Saud University, Riyadh, Saudi Arabia.
Data Availability Statement
The data presented in this study are openly available in https://www.ausgrid.com.au/Industry/Our-Research/Data-to-share (accessed on 20 December 2023).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SG | Smart Grid |
| SM | Smart Meter |
| AMI | Advanced Metering Infrastructure |
| SO | System Operator |
| ML | Machine Learning |
| DL | Deep learning |
| RL | Reinforcement learning |
| DRL | Deep reinforcement learning |
| EVs | Electric Vehicles |
| DERs | Distributed Energy Resources |
| CNN | Convolutional Neural Network |
| FFNs | Feed-forward Neural Networks |
| RNNs | Recurrent Neural Networks |
| PSO | Particle Swarm Optimization |
| ADMM | Alternating Direction Method of Multipliers |
| MPC | Model-Predictive Control |
| MDP | Markov Decision Process |
| DR | Demand Response |
| HVAC | Heating, Ventilation, and Air Conditioning |
| HEMS | Home energy management systems |
| MARL | Multi-Agent Reinforcement Learning |
| DDPG | Deep Deterministic Policy Gradient |
| CommNet | Communication Neural Network |
| LSTM | Long Short-Term Memory |
| MADDPG | Multi-Agent Deep Deterministic Policy Gradient |
| PPO | Proximal Policy Optimization |
References
- Ibrahem, M.I.; Nabil, M.; Fouda, M.M.; Mahmoud, M.M.; Alasmary, W.; Alsolami, F. Efficient privacy-preserving electricity theft detection with dynamic billing and load monitoring for AMI networks. IEEE Internet Things J. 2020, 8, 1243–1258. [Google Scholar] [CrossRef]
- Takiddin, A.; Ismail, M.; Nabil, M.; Mahmoud, M.M.; Serpedin, E. Detecting electricity theft cyber-attacks in AMI networks using deep vector embeddings. IEEE Syst. J. 2020, 15, 4189–4198. [Google Scholar] [CrossRef]
- Ibrahem, M.I.; Badr, M.M.; Fouda, M.M.; Mahmoud, M.; Alasmary, W.; Fadlullah, Z.M. PMBFE: Efficient and privacy-preserving monitoring and billing using functional encryption for AMI networks. In Proceedings of the 2020 International Symposium on Networks, Computers and Communications (ISNCC), Montreal, QC, Canada, 20–22 October 2020; pp. 1–7. [Google Scholar]
- Ibrahem, M.I.; Badr, M.M.; Mahmoud, M.; Fouda, M.M.; Alasmary, W. Countering presence privacy attack in efficient AMI networks using interactive deep-learning. In Proceedings of the 2021 International Symposium on Networks, Computers and Communications (ISNCC), Dubai, United Arab Emirates, 31 October–2 November 2021; pp. 1–7. [Google Scholar]
- Yao, L.; Lim, W.H.; Tsai, T.S. A real-time charging scheme for demand response in electric vehicle parking station. IEEE Trans. Smart Grid 2016, 8, 52–62. [Google Scholar] [CrossRef]
- Arias, N.B.; Sabillón, C.; Franco, J.F.; Quirós-Tortós, J.; Rider, M.J. Hierarchical optimization for user-satisfaction-driven electric vehicles charging coordination in integrated MV/LV networks. IEEE Syst. J. 2022, 17, 1247–1258. [Google Scholar] [CrossRef]
- Xu, Z.; Su, W.; Hu, Z.; Song, Y.; Zhang, H. A hierarchical framework for coordinated charging of plug-in electric vehicles in China. IEEE Trans. Smart Grid 2015, 7, 428–438. [Google Scholar] [CrossRef]
- Malisani, P.; Zhu, J.; Pognant-Gros, P. Optimal charging scheduling of electric vehicles: The co-charging case. IEEE Trans. Power Syst. 2022, 38, 1069–1080. [Google Scholar] [CrossRef]
- Saner, C.B.; Trivedi, A.; Srinivasan, D. A cooperative hierarchical multi-agent system for EV charging scheduling in presence of multiple charging stations. IEEE Trans. Smart Grid 2022, 13, 2218–2233. [Google Scholar] [CrossRef]
- Chen, W.; Wang, J.; Zhang, T.; Li, G.; Jin, Y.; Ge, L.; Zhou, M.; Tan, C.W. Exploring symmetry-induced divergence in decentralized electric vehicle scheduling. IEEE Trans. Ind. Appl. 2023, 60, 1117–1128. [Google Scholar] [CrossRef]
- Wang, H.; Shi, M.; Xie, P.; Lai, C.S.; Li, K.; Jia, Y. Electric vehicle charging scheduling strategy for supporting load flattening under uncertain electric vehicle departures. J. Mod. Power Syst. Clean Energy 2022, 11, 1634–1645. [Google Scholar] [CrossRef]
- Afshar, S.; Disfani, V.; Siano, P. A distributed electric vehicle charging scheduling platform considering aggregators coordination. IEEE Access 2021, 9, 151294–151305. [Google Scholar] [CrossRef]
- Zhao, T.; Ding, Z. Distributed initialization-free cost-optimal charging control of plug-in electric vehicles for demand management. IEEE Trans. Ind. Inform. 2017, 13, 2791–2801. [Google Scholar] [CrossRef]
- Akhavan-Rezai, E.; Shaaban, M.F.; El-Saadany, E.F.; Karray, F. Online intelligent demand management of plug-in electric vehicles in future smart parking lots. IEEE Syst. J. 2015, 10, 483–494. [Google Scholar] [CrossRef]
- Kang, Q.; Feng, S.; Zhou, M.; Ammari, A.C.; Sedraoui, K. Optimal load scheduling of plug-in hybrid electric vehicles via weight-aggregation multi-objective evolutionary algorithms. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2557–2568. [Google Scholar] [CrossRef]
- Chen, J.; Huang, X.; Tian, S.; Cao, Y.; Huang, B.; Luo, X.; Yu, W. Electric vehicle charging schedule considering user’s charging selection from economics. IET Gener. Transm. Distrib. 2019, 13, 3388–3396. [Google Scholar] [CrossRef]
- Ceusters, G.; Rodríguez, R.C.; García, A.B.; Franke, R.; Deconinck, G.; Helsen, L.; Nowé, A.; Messagie, M.; Camargo, L.R. Model-predictive control and reinforcement learning in multi-energy system case studies. Appl. Energy 2021, 303, 117634. [Google Scholar] [CrossRef]
- Zhao, X.; Liang, G. Optimizing electric vehicle charging schedules and energy management in smart grids using an integrated GA-GRU-RL approach. Front. Energy Res. 2023, 11, 1268513. [Google Scholar] [CrossRef]
- Wang, K.; Wang, H.; Yang, Z.; Feng, J.; Li, Y.; Yang, J.; Chen, Z. A transfer learning method for electric vehicles charging strategy based on deep reinforcement learning. Appl. Energy 2023, 343, 121186. [Google Scholar] [CrossRef]
- Hossain, M.B.; Pokhrel, S.R.; Vu, H.L. Efficient and private scheduling of wireless electric vehicles charging using reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4089–4102. [Google Scholar] [CrossRef]
- Verschae, R.; Kawashima, H.; Kato, T.; Matsuyama, T. Coordinated energy management for inter-community imbalance minimization. Renew. Energy 2016, 87, 922–935. [Google Scholar] [CrossRef]
- Zhou, K.; Cheng, L.; Wen, L.; Lu, X.; Ding, T. A coordinated charging scheduling method for electric vehicles considering different charging demands. Energy 2020, 213, 118882. [Google Scholar] [CrossRef]
- Chang, T.H.; Alizadeh, M.; Scaglione, A. Real-time power balancing via decentralized coordinated home energy scheduling. IEEE Trans. Smart Grid 2013, 4, 1490–1504. [Google Scholar] [CrossRef]
- Pinto, G.; Piscitelli, M.S.; Vázquez-Canteli, J.R.; Nagy, Z.; Capozzoli, A. Coordinated energy management for a cluster of buildings through deep reinforcement learning. Energy 2021, 229, 120725. [Google Scholar] [CrossRef]
- Kaewdornhan, N.; Srithapon, C.; Liemthong, R.; Chatthaworn, R. Real-Time Multi-Home Energy Management with EV Charging Scheduling Using Multi-Agent Deep Reinforcement Learning Optimization. Energies 2023, 16, 2357. [Google Scholar] [CrossRef]
- Real, A.C.; Luz, G.P.; Sousa, J.; Brito, M.; Vieira, S. Optimization of a photovoltaic-battery system using deep reinforcement learning and load forecasting. Energy AI 2024, 16, 100347. [Google Scholar] [CrossRef]
- Cai, W.; Kordabad, A.B.; Gros, S. Energy management in residential microgrid using model predictive control-based reinforcement learning and Shapley value. Eng. Appl. Artif. Intell. 2023, 119, 105793. [Google Scholar] [CrossRef]
- Zhang, Z.; Wan, Y.; Qin, J.; Fu, W.; Kang, Y. A Deep RL-Based Algorithm for Coordinated Charging of Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18774–18784. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, H.; Xiong, H.; Xu, T.; Wang, F.; Xin, H.; Wu, H. RLCharge: Imitative Multi-Agent Spatiotemporal Reinforcement Learning for Electric Vehicle Charging Station Recommendation. IEEE Trans. Knowl. Data Eng. 2023, 35, 6290–6304. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Q.; An, D.; Li, D.; Wu, Z. Multistep Multiagent Reinforcement Learning for Optimal Energy Schedule Strategy of Charging Stations in Smart Grid. IEEE Trans. Cybern. 2023, 53, 4292–4305. [Google Scholar] [CrossRef]
- Fu, L.; Wang, T.; Song, M.; Zhou, Y.; Gao, S. Electric vehicle charging scheduling control strategy for the large-scale scenario with non-cooperative game-based multi-agent reinforcement learning. Int. J. Electr. Power Energy Syst. 2023, 153, 109348. [Google Scholar] [CrossRef]
- Sultanuddin, S.; Vibin, R.; Kumar, A.R.; Behera, N.R.; Pasha, M.J.; Baseer, K. Development of improved reinforcement learning smart charging strategy for electric vehicle fleet. J. Energy Storage 2023, 64, 106987. [Google Scholar] [CrossRef]
- Paudel, D.; Das, T.K. A deep reinforcement learning approach for power management of battery-assisted fast-charging EV hubs participating in day-ahead and real-time electricity markets. Energy 2023, 283, 129097. [Google Scholar] [CrossRef]
- El-Toukhy, A.T.; Badr, M.M.; Mahmoud, M.M.E.A.; Srivastava, G.; Fouda, M.M.; Alsabaan, M. Electricity Theft Detection Using Deep Reinforcement Learning in Smart Power Grids. IEEE Access 2023, 11, 59558–59574. [Google Scholar] [CrossRef]
- Kumari, A.; Tanwar, S. A reinforcement-learning-based secure demand response scheme for smart grid system. IEEE Internet Things J. 2021, 9, 2180–2191. [Google Scholar] [CrossRef]
- Lu, R.; Hong, S.H.; Yu, M. Demand response for home energy management using reinforcement learning and artificial neural network. IEEE Trans. Smart Grid 2019, 10, 6629–6639. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Dong, S.; Xia, Y.; Peng, T. Network abnormal traffic detection model based on semi-supervised deep reinforcement learning. IEEE Trans. Netw. Serv. Manag. 2021, 18, 4197–4212. [Google Scholar] [CrossRef]
- Lopez-Martin, M.; Carro, B.; Sanchez-Esguevillas, A. Application of deep reinforcement learning to intrusion detection for supervised problems. Expert Syst. Appl. 2020, 141, 112963. [Google Scholar] [CrossRef]
- Kokar, M.M.; Reveliotis, S.A. Reinforcement learning: Architectures and algorithms. Int. J. Intell. Syst. 1993, 8, 875–894. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Reddi, V.J. Deep reinforcement learning for cyber security. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 3779–3795. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Available online: https://www.ausgrid.com.au/Industry/Our-Research/Data-to-share (accessed on 20 December 2023).
- Blonsky, M.; McKenna, K.; Maguire, J.; Vincent, T. Home energy management under realistic and uncertain conditions: A comparison of heuristic, deterministic, and stochastic control methods. Appl. Energy 2022, 325, 119770. [Google Scholar] [CrossRef]
- Maatug, F. Anomaly Detection of Smart Meter Data. Master’s Thesis, University of Stavanger, Stavanger, Norway, 2021. [Google Scholar]
- Badr, M.M.; Ibrahem, M.I.; Mahmoud, M.; Fouda, M.M.; Alsolami, F.; Alasmary, W. Detection of false-reading attacks in smart grid net-metering system. IEEE Internet Things J. 2021, 9, 1386–1401. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).