Utilizing Connection of Multiple Peltier Cells to Enhance the Coefficient of Performance
Abstract
1. Introduction
2. Materials and Methods
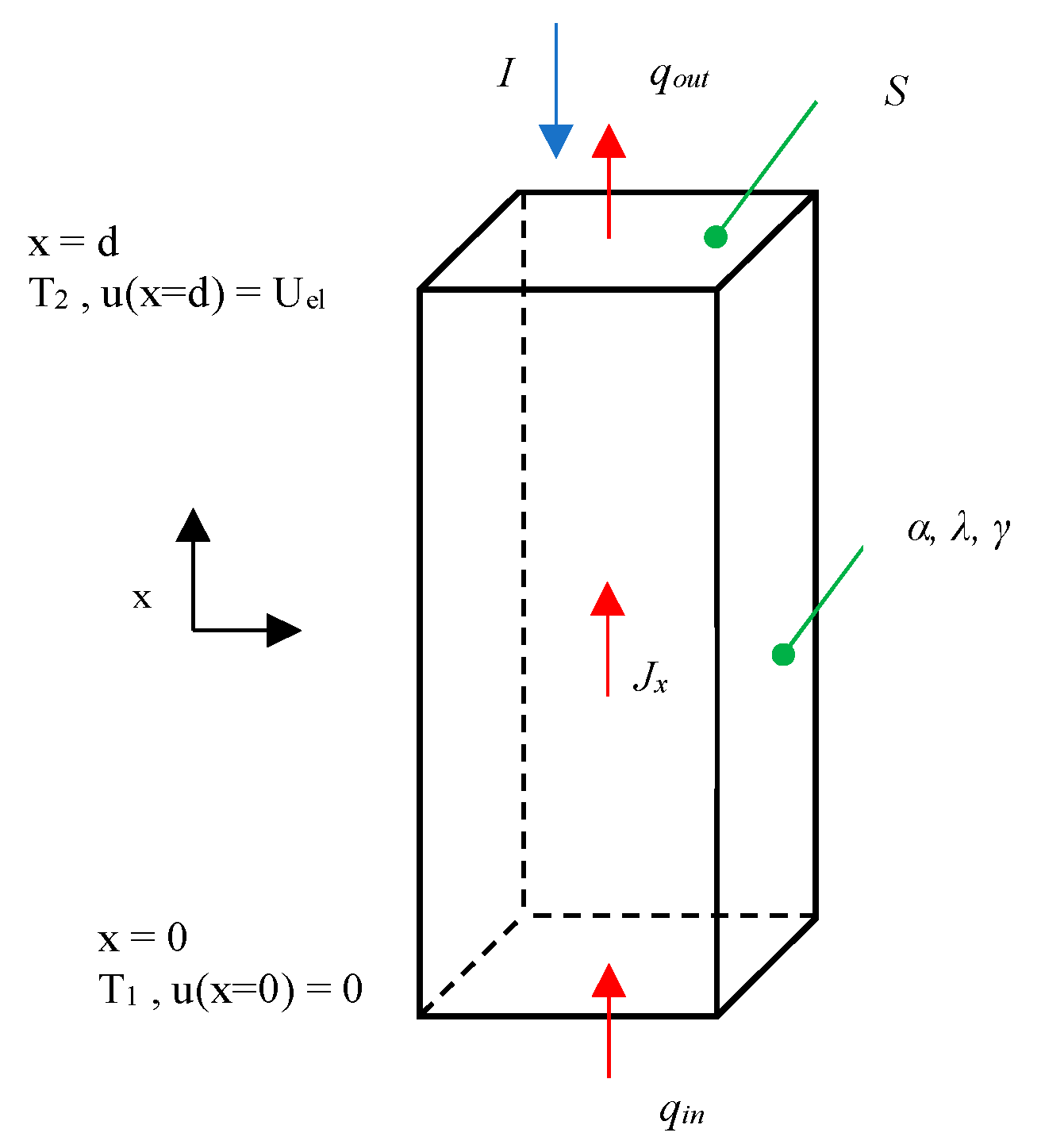
3. Model of Series Connection of Peltier Cells and Considered Parameters of Individual Layers
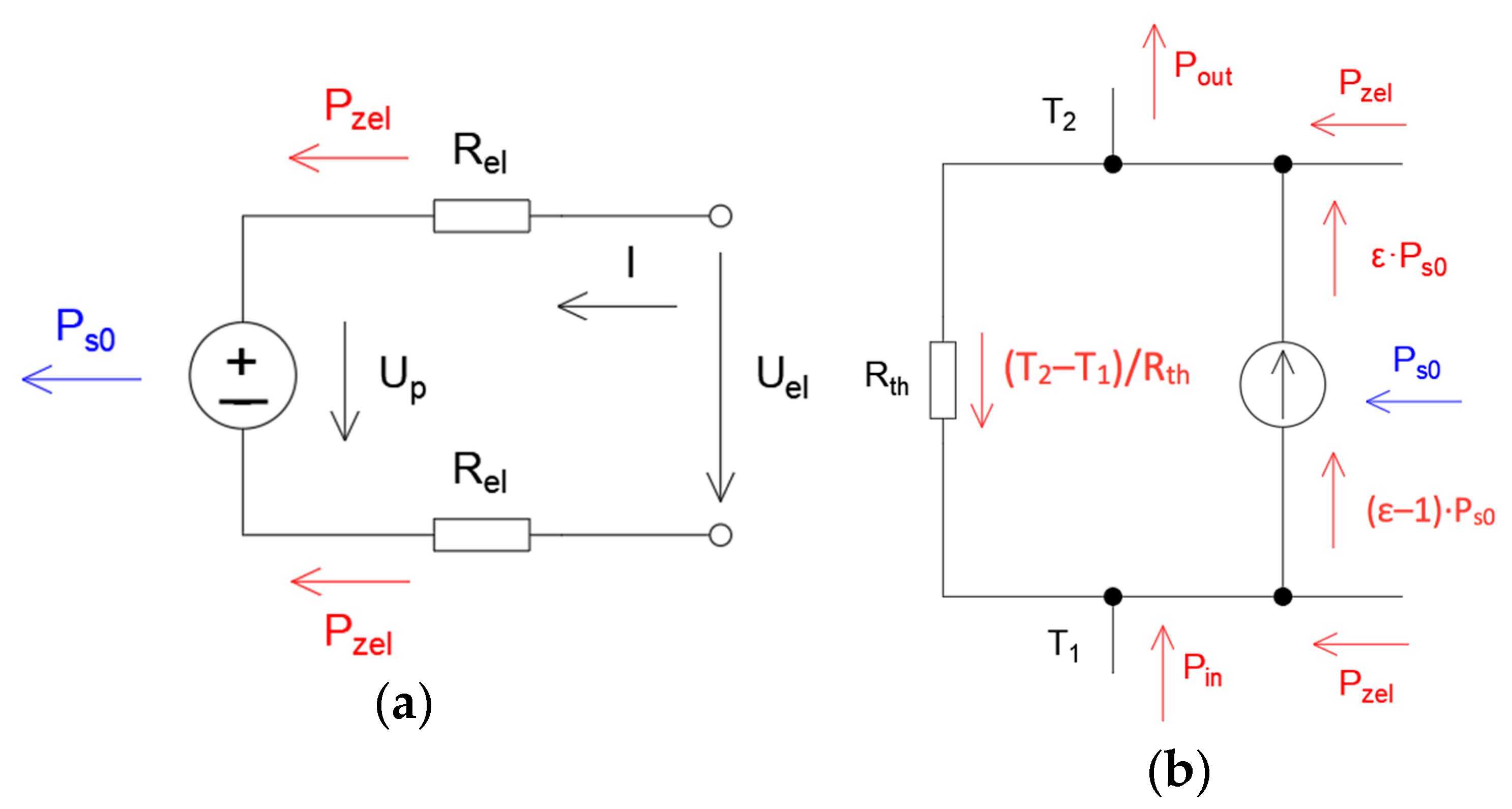
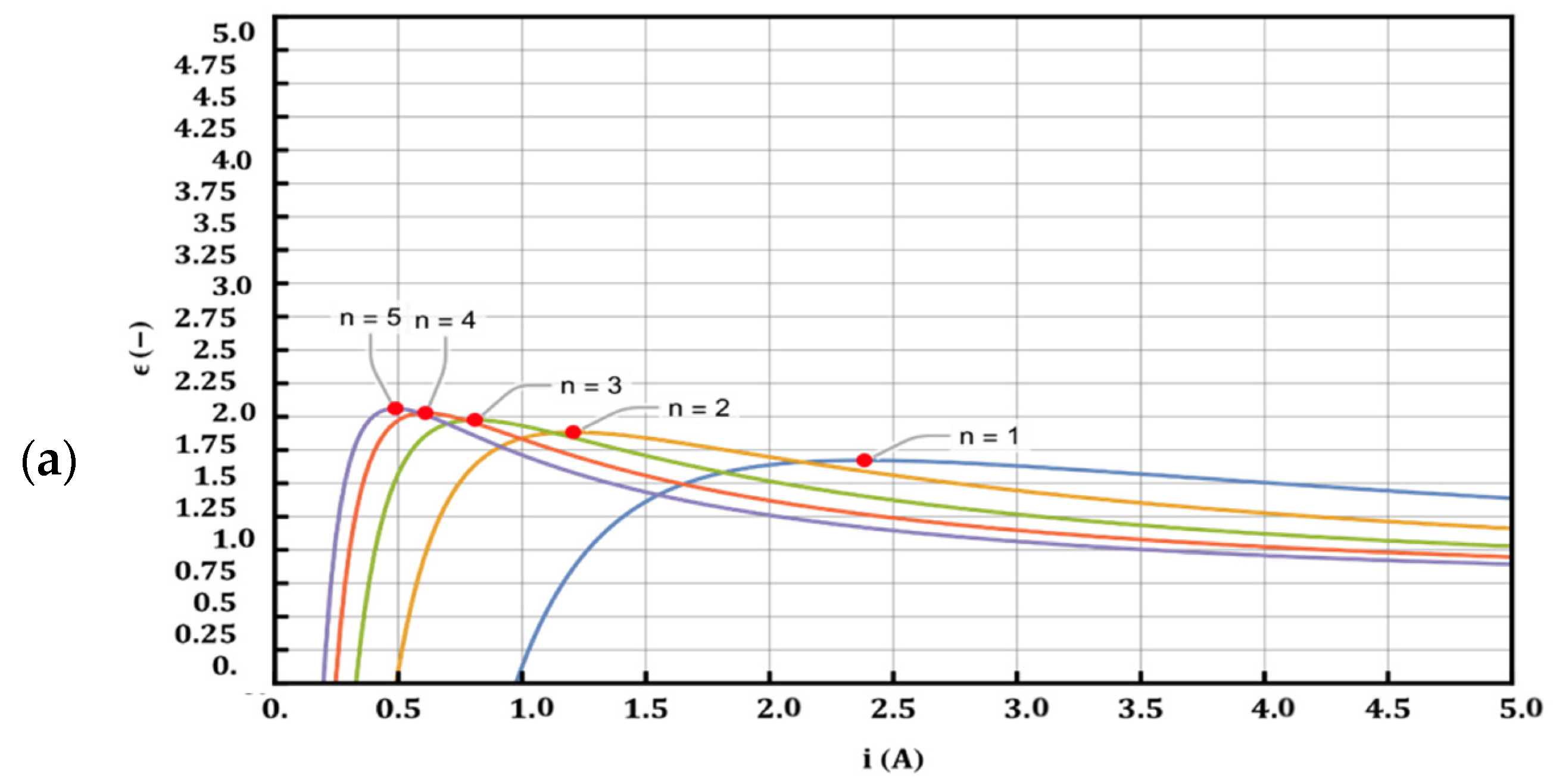
4. Optimization of the Operation of Series-Connected Peltier Cells
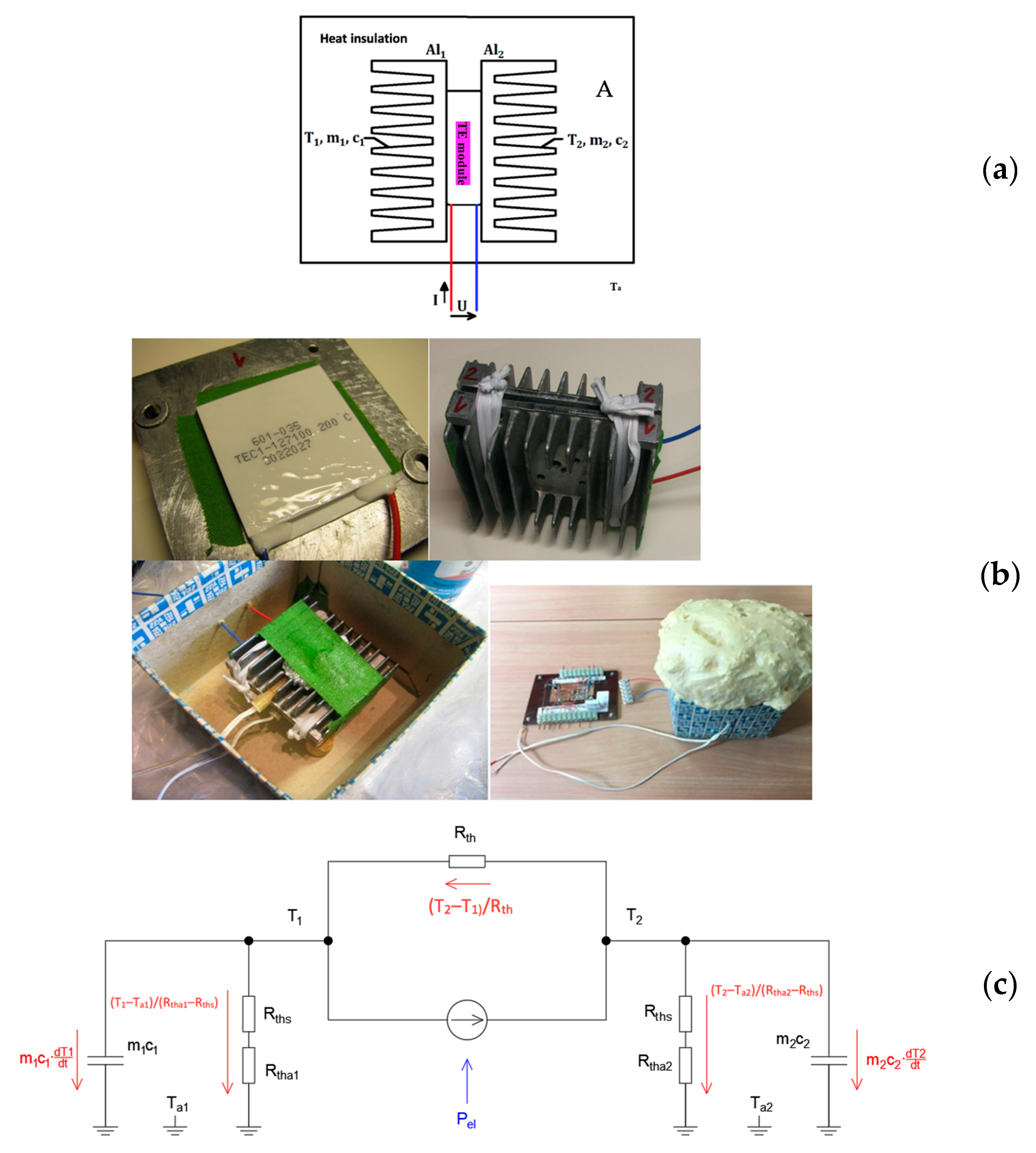
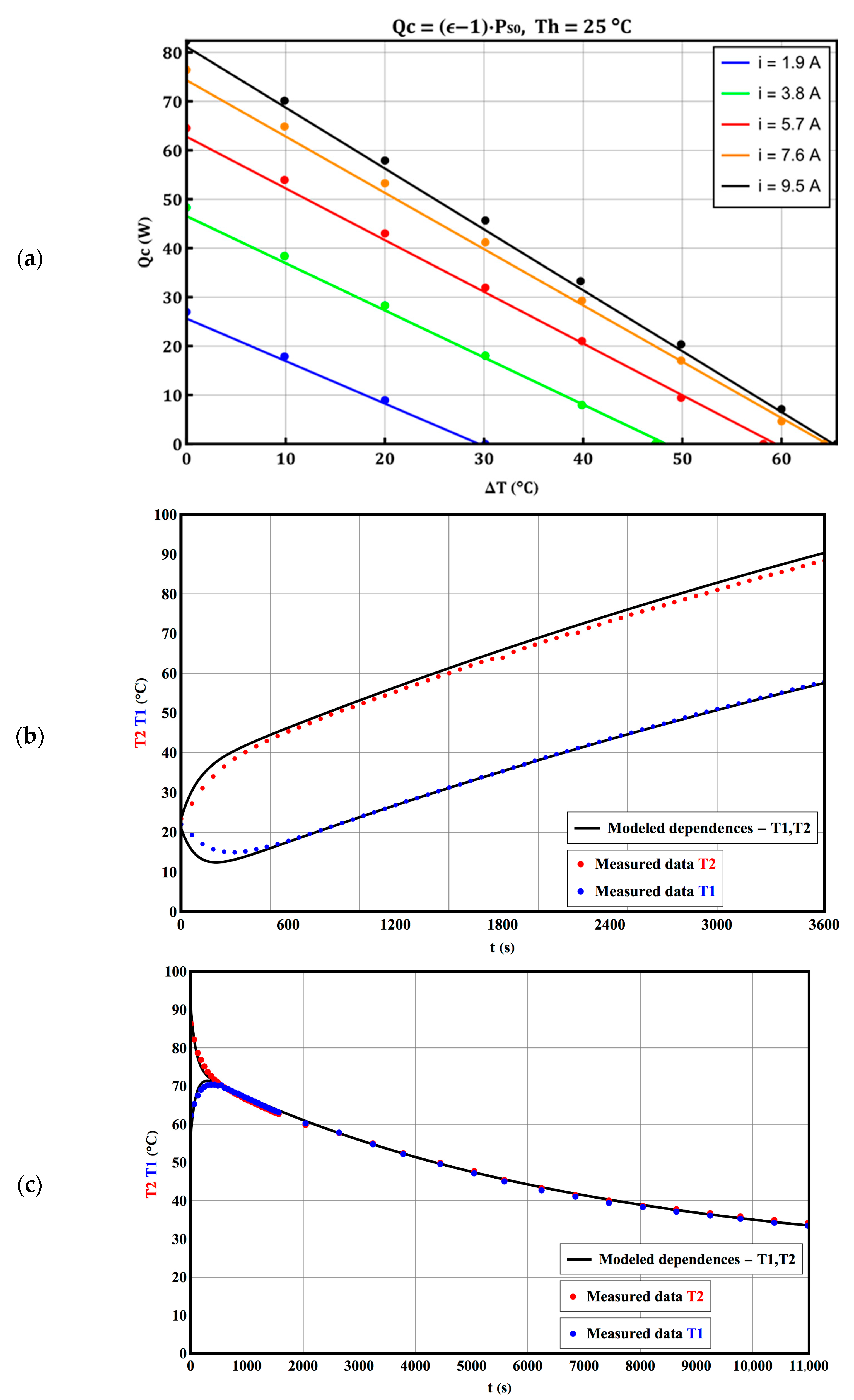
5. Parameter Identification for a Specific Peltier Cell
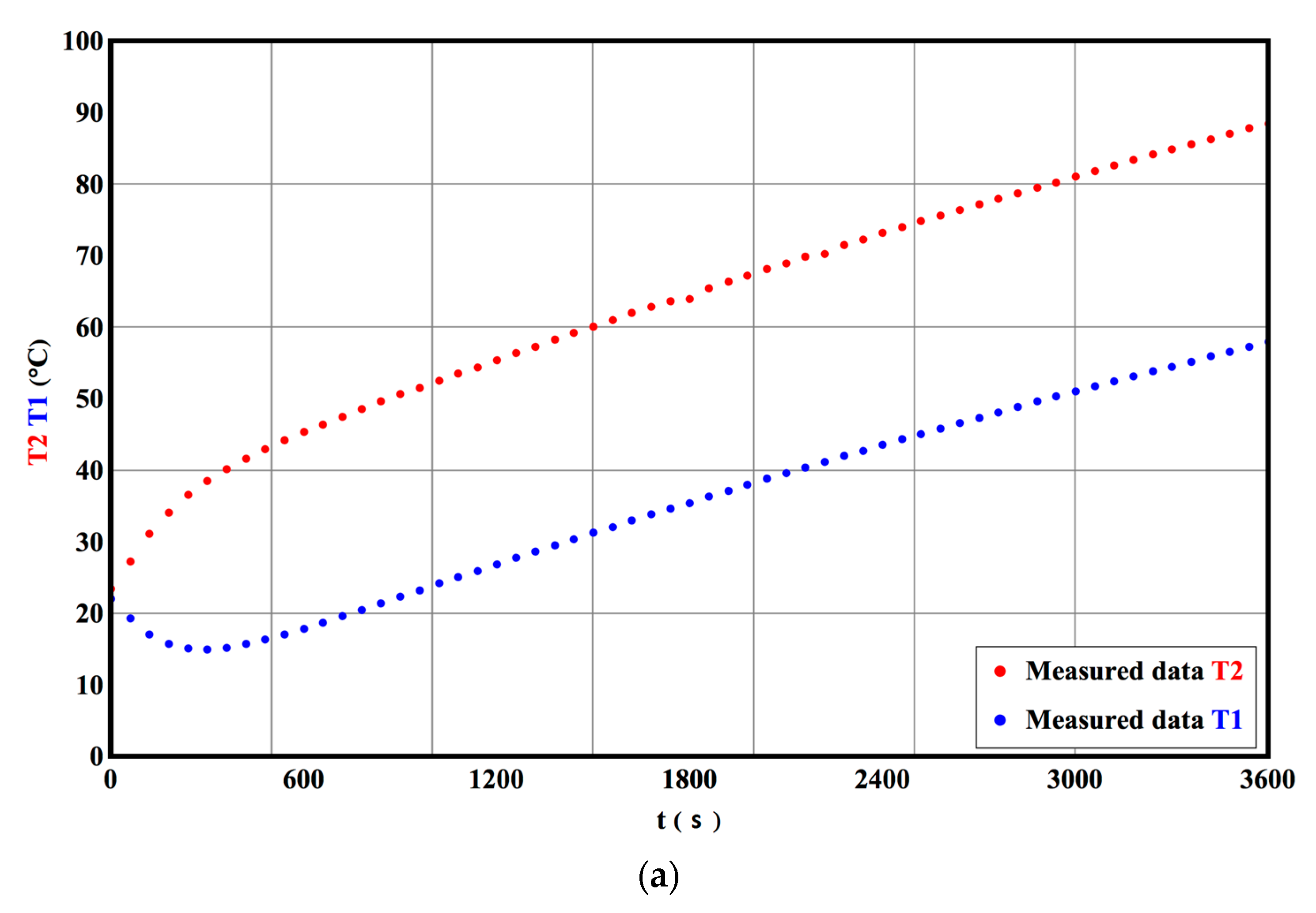
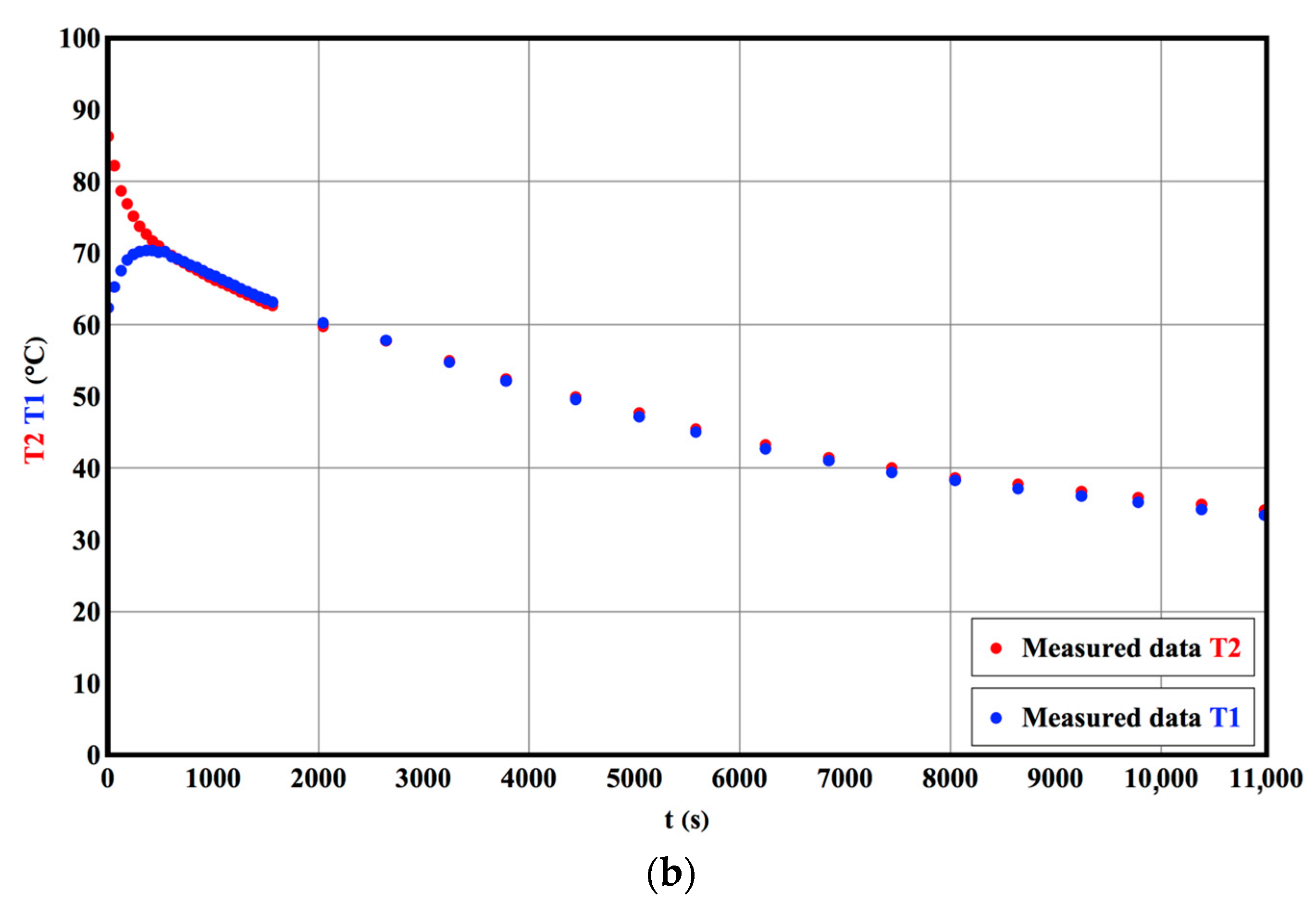
6. Determination of Peltier Module Parameters Based on Measured Data
7. Determination of Peltier Module Parameters Based on Manufacturer’s Datasheet Data
8. Case Study
9. Case Study Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.; Liu, Y.; Li, R.; Li, Y.; Bai, S. Strategies to Improve the Thermoelectric Figure of Merit in Thermoelectric Functional Materials. Front. Chem. 2022, 10, 865281. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Yu, Z.; Yuan, Y.; Zhang, J.; Lee, J. Electrical performance optimization of a transverse-Seebeck-effect-based tubular thermoelectric generator for waste heat recovery. Energy Rep. 2022, 8, 7589–7599. [Google Scholar] [CrossRef]
- Riffat, S.B.; Ma, X. Improving the coefficient of performance of thermoelectric cooling systems: A review. Int. J. Energy Res. 2004, 28, 753–768. [Google Scholar] [CrossRef]
- Renge, S.; Barhaiya, Y.; Pant, S.; Sharma, S. A Review on Generation of Electricity using Peltier Module. Int. J. Eng. Res. 2017, V6, 453–457. [Google Scholar] [CrossRef]
- Zhu, K.; Bai, S.; Kim, H.S.; Liu, W. Module-level design and characterization of thermoelectric power generator. Chin. Phys. B 2022, 31, 048502. [Google Scholar] [CrossRef]
- Luo, D.; Wang, R.; Yu, W.; Zhou, W. Parametric study of a thermoelectric module used for both power generation and cooling. Renew. Energy 2020, 154, 542–552. [Google Scholar] [CrossRef]
- Sandoz-Rosado, E.; Stevens, R. Robust Finite Element Model for the Design of Thermoelectric Modules. J. Electron. Mater. 2010, 39, 1848–1855. [Google Scholar] [CrossRef]
- Ge, Y.; He, K.; Xiao, L.; Yuan, W.; Huang, S.-M. Geometric optimization for the thermoelectric generator with variable cross-section legs by coupling finite element method and optimization algorithm. Renew. Energy 2021, 183, 294–303. [Google Scholar] [CrossRef]
- Tohidi, F.; Holagh, S.G.; Chitsaz, A. Thermoelectric Generators: A comprehensive review of characteristics and applications. Appl. Therm. Eng. 2021, 201, 117793. [Google Scholar] [CrossRef]
- Huang, G.-Y.; Hsu, C.-T.; Fang, C.-J.; Yao, D.-J. Optimization of a waste heat recovery system with thermoelectric generators by three-dimensional thermal resistance analysis. Energy Convers. Manag. 2016, 126, 581–594. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, H.; Feng, B.; Song, X.; Zhang, X.; Zhang, R. Numerical simulations and optimized design on the performance and thermal stress of a thermoelectric cooler. Int. J. Refrig. 2023, 146, 314–326. [Google Scholar] [CrossRef]
- Afshari, F. Experimental Study for Comparing Heating and Cooling Performance of Thermoelectric Peltier. J. Polytech. 2020, 23, 889–894. [Google Scholar] [CrossRef]
- Yin, T.; He, Z.-Z. Analytical model-based optimization of the thermoelectric cooler with temperature-dependent materials under different operating conditions. Appl. Energy 2021, 299, 117340. [Google Scholar] [CrossRef]
- Trancossi, M.; Kay, J.; Cannistraro, M. Peltier cells based acclimatization system for a container passive building. Tec. Ital. J. Eng. Sci. 2018, 61, 90–96. [Google Scholar] [CrossRef]
- Cai, Y.; Huang, X.-Y.; He, J.-W.; Huang, Y.-X.; Zhao, F.-Y. Investigation of thermoelectric ventilated building envelope for simultaneously passive cooling and energy savings: Critical analysis and parametric characteristics. Energy Build. 2023, 297, 113421. [Google Scholar] [CrossRef]
- Rittner, E.S. On the Theory of the Peltier Heat Pump. J. Appl. Phys. 1959, 30, 702–707. [Google Scholar] [CrossRef]
- Maryani, S.; Kusumanto, R.; Rs, C. Solar Panel Optimization Using Peltier Module TEC1-12706. J. Mech. Civ. Ind. Eng. 2023, 4, 43–50. [Google Scholar] [CrossRef]
- Ficker, T. Simplified Peltier heat pump. Eur. J. Phys. 2022, 43, 045102. [Google Scholar] [CrossRef]
- Ibañez-Puy, M.; Bermejo-Busto, J.; Martín-Gómez, C.; Vidaurre-Arbizu, M.; Sacristán-Fernández, J.A. Thermoelectric cooling heating unit performance under real conditions. Appl. Energy 2017, 200, 303–314. [Google Scholar] [CrossRef]
- Barako, M.T.; Park, W.; Marconnet, A.M.; Asheghi, M.; Goodson, K.E. Thermal Cycling, Mechanical Degradation, and the Effective Figure of Merit of a Thermoelectric Module. J. Electron. Mater. 2012, 42, 372–381. [Google Scholar] [CrossRef]
- Barako, M.T.; Park, W.; Marconnet, A.M.; Asheghi, M.; Goodson, K.E. A reliability study with infrared imaging of thermoelectric modules under thermal cycling. In Proceedings of the 13th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Orlando, FL, USA, 30 May–2 June 2012; pp. 86–92. [Google Scholar]
- Sun, Y.; Meng, F.; San, B.; Xu, C. Performance Analysis of Multistage Thermoelectric Cooler with Water-Cooled. J. Phys. Conf. Ser. 2023, 2442, 12028. [Google Scholar] [CrossRef]
- Karimi, G.; Culham, J.; Kazerouni, V. Performance analysis of multi-stage thermoelectric coolers. Int. J. Refrig. 2011, 34, 2129–2135. [Google Scholar] [CrossRef]
- Hwang, G.; Gross, A.; Kim, H.; Lee, S.; Ghafouri, N.; Huang, B.; Lawrence, C.; Uher, C.; Najafi, K.; Kaviany, M. Micro thermoelectric cooler: Planar multistage. Int. J. Heat Mass Transf. 2009, 52, 1843–1852. [Google Scholar] [CrossRef]
- Bergman, T.L.; Incropera, F.P. Introduction to Heat Transfer, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 9780470501962. [Google Scholar]
- Petkov, T.; Belovski, I.; Ivanov, K.; Aleksandrov, A. Modeling the Parameters of a Cascaded Peltier Module using Neural Network. In Proceedings of the 21st International Symposium on Electrical Apparatus & Technologies (SIELA), Bourgas, Bulgaria, 3–6 June 2020; pp. 1–4. [Google Scholar]
- Wang, Y.T.; Liu, W.; Fan, A.W.; Li, P. Performance Comparison between Series-Connected and Parallel-Connected Thermoelectric Generator Systems. Appl. Mech. Mater. 2013, 325-326, 327–331. [Google Scholar] [CrossRef]
- Ivanov, K.; Belovski, I.; Aleksandrov, A. Study of Multi-stage Peltier Module in Generator Mode. In Proceedings of the 7th International Conference on Energy Efficiency and Agricultural Engineering (EE&AE), Ruse, Bulgaria, 12–14 November 2020; pp. 1–4. [Google Scholar]
- Fan, X.; Sun, H.; Yuan, Z.; Li, Z.; Shi, R.; Razmjooy, N. Multi-objective optimization for the proper selection of the best heat pump technology in a fuel cell-heat pump micro-CHP system. Energy Rep. 2020, 6, 325–335. [Google Scholar] [CrossRef]
- Lucas, S.; Bari, S.; Marian, R.; Lucas, M.; Chahl, J. Cooling by Peltier effect and active control systems to thermally manage operating temperatures of electrical Machines (Motors and Generators). Therm. Sci. Eng. Prog. 2022, 27, 100990. [Google Scholar] [CrossRef]
- Lineykin, S.; Ben-Yaakov, S. Analysis of Thermoelectric Coolers by a Spice-Compatible Equivalent-Circuit Model. IEEE Power Electron. Lett. 2005, 3, 63–66. [Google Scholar] [CrossRef]
- Zhang, H.; Mui, Y.; Tarin, M. Analysis of thermoelectric cooler performance for high power electronic packages. Appl. Therm. Eng. 2010, 30, 561–568. [Google Scholar] [CrossRef]
- Tozaki, K.-I.; Sou, K. Novel Determination of Peltier Coefficient, Seebeck Coefficient and Thermal Resistance of Thermoelectric Module. Jpn. J. Appl. Phys. 2006, 45, 5272. [Google Scholar] [CrossRef]
- Arora, R.; Kaushik, S.; Arora, R. Multi-objective and multi-parameter optimization of two-stage thermoelectric generator in electrically series and parallel configurations through NSGA-II. Energy 2015, 91, 242–254. [Google Scholar] [CrossRef]


| Number of neTEi | COP (-) | Pout (W) | Relative Material Cost (-) |
|---|---|---|---|
| 100 | 1.9 | 14.34 | 1 |
| 100, 110 | 2.15 | 8.51 | 3.54 |
| 100, 106, 113 | 2.26 | 6.04 | 7.58 |
| 100, 106, 112, 118 | 2.32 | 4.77 | 13.11 |
| 100, 105, 110, 115, 121 | 2.36 | 3.92 | 20.14 |
| Utilizing Formulas | Utilizing Formulas | Based on Measured Data | |
|---|---|---|---|
| (38)–(40) TH = 25 °C | (38)–(40) TH = 50 °C | ||
| α (mV·K−1) | 51.65 | 50.75 | 49.36 |
| Rel (Ω) | 0.597 | 0.642 | 0.650 |
| Rth (kW−1) | 1.122 | 1.090 | 1.290 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rimbala, J.; Kyncl, J.; Koller, J.; Fandi, G. Utilizing Connection of Multiple Peltier Cells to Enhance the Coefficient of Performance. Energies 2024, 17, 4509. https://doi.org/10.3390/en17174509
Rimbala J, Kyncl J, Koller J, Fandi G. Utilizing Connection of Multiple Peltier Cells to Enhance the Coefficient of Performance. Energies. 2024; 17(17):4509. https://doi.org/10.3390/en17174509
Chicago/Turabian StyleRimbala, Jan, Jan Kyncl, Jan Koller, and Ghaeth Fandi. 2024. "Utilizing Connection of Multiple Peltier Cells to Enhance the Coefficient of Performance" Energies 17, no. 17: 4509. https://doi.org/10.3390/en17174509
APA StyleRimbala, J., Kyncl, J., Koller, J., & Fandi, G. (2024). Utilizing Connection of Multiple Peltier Cells to Enhance the Coefficient of Performance. Energies, 17(17), 4509. https://doi.org/10.3390/en17174509







