Evaluation Method for Voltage Regulation Range of Medium-Voltage Substations Based on OLTC Pre-Dispatch
Abstract
1. Introduction
2. Overview of the Principle of Substation Voltage Regulation Range Calculation
3. Zbus Linearized Power Flow Model Based on Fixed-Point Iteration and Voltage Sensitivity Analysis Method
3.1. Zbus Power Flow Model
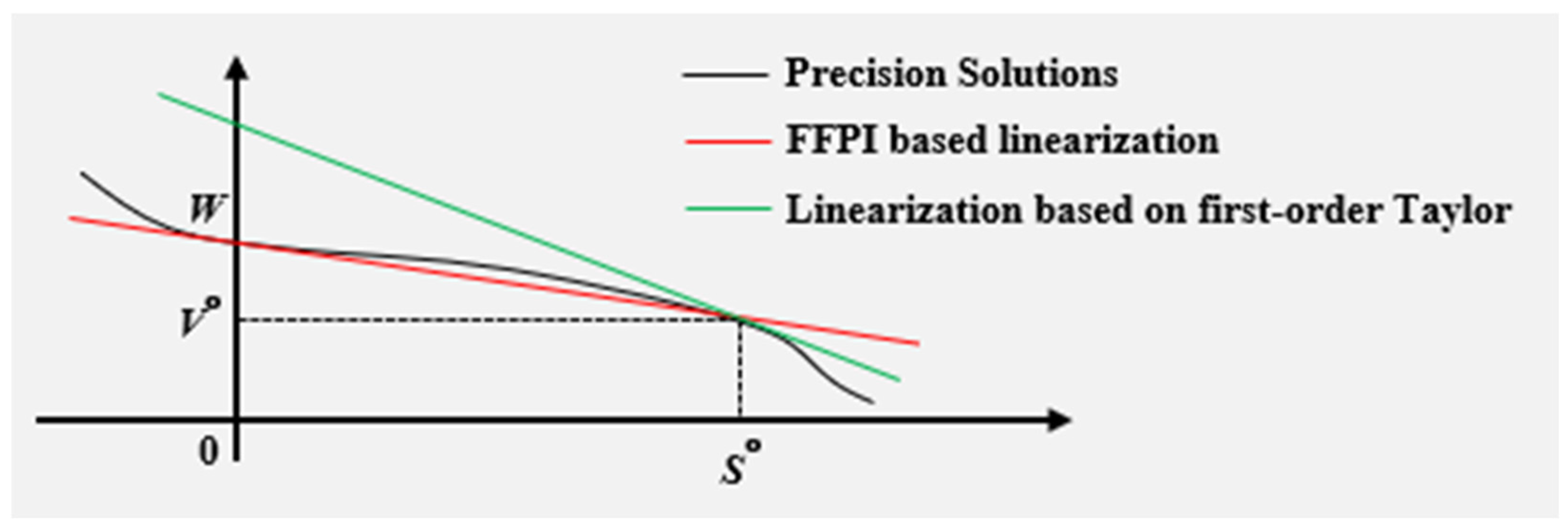
3.2. Zbus Linearized Power Flow Model Based on Fixed-Point Power Iteration
3.3. Voltage Sensitivity Analysis Method
4. Day-Ahead Dispatch Optimization Strategy
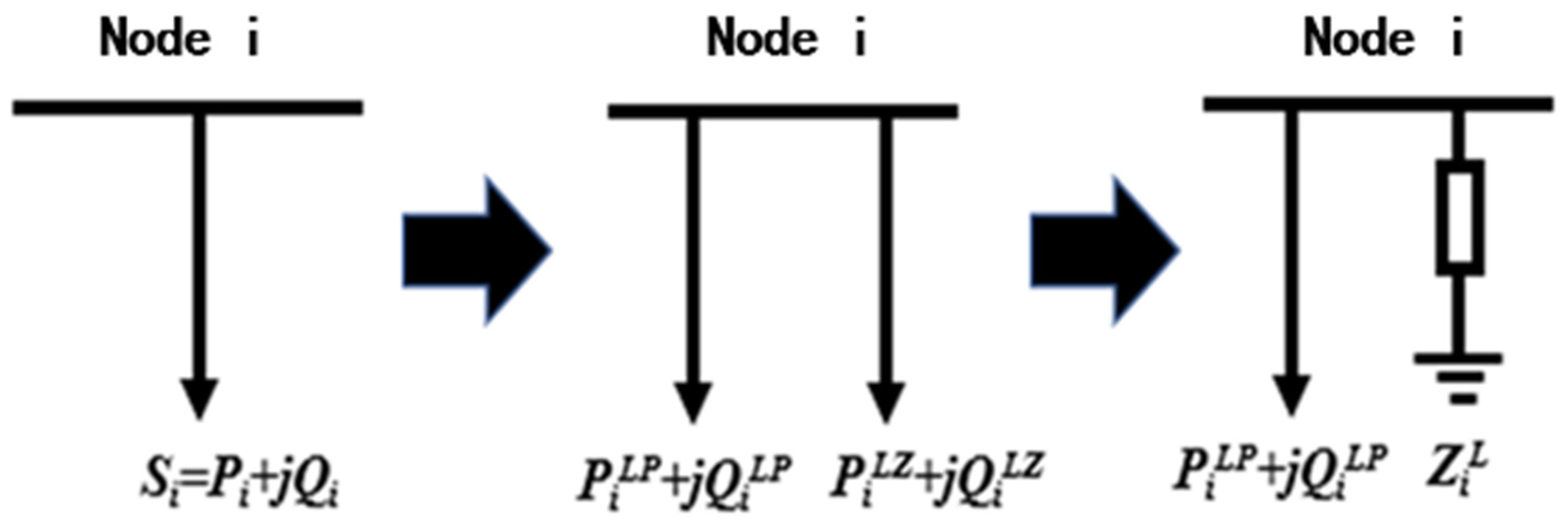
4.1. Considering the Load Active Power–Voltage Coupling Characteristics in the Power Flow Equation Correction
4.2. Constructing the Objective Function for Minimizing Network Loss
4.3. Modeling Constraint Conditions
5. Methods for Assessing Voltage Regulation Range at Substations
5.1. Constructing an Optimization Objective Function
5.2. Modeling Constraint Conditions
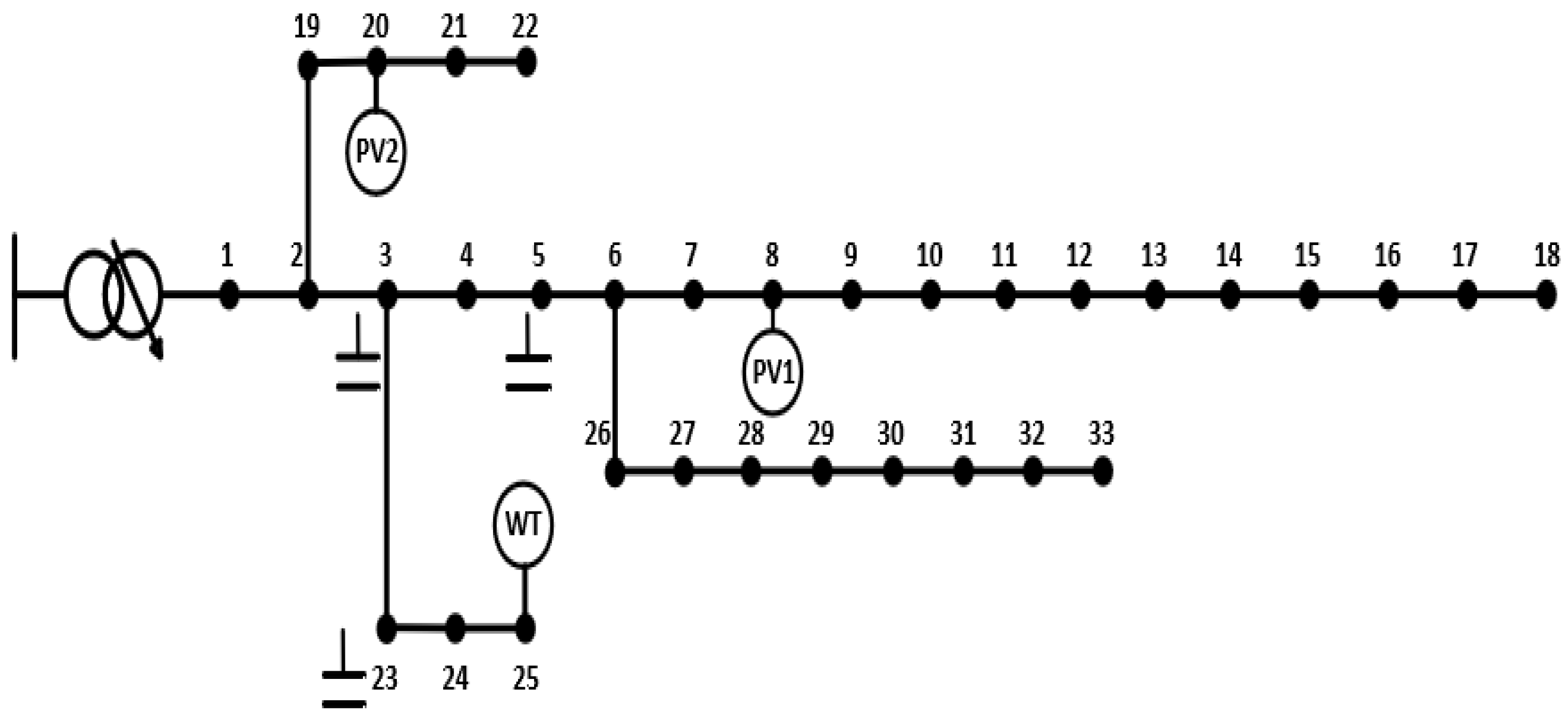
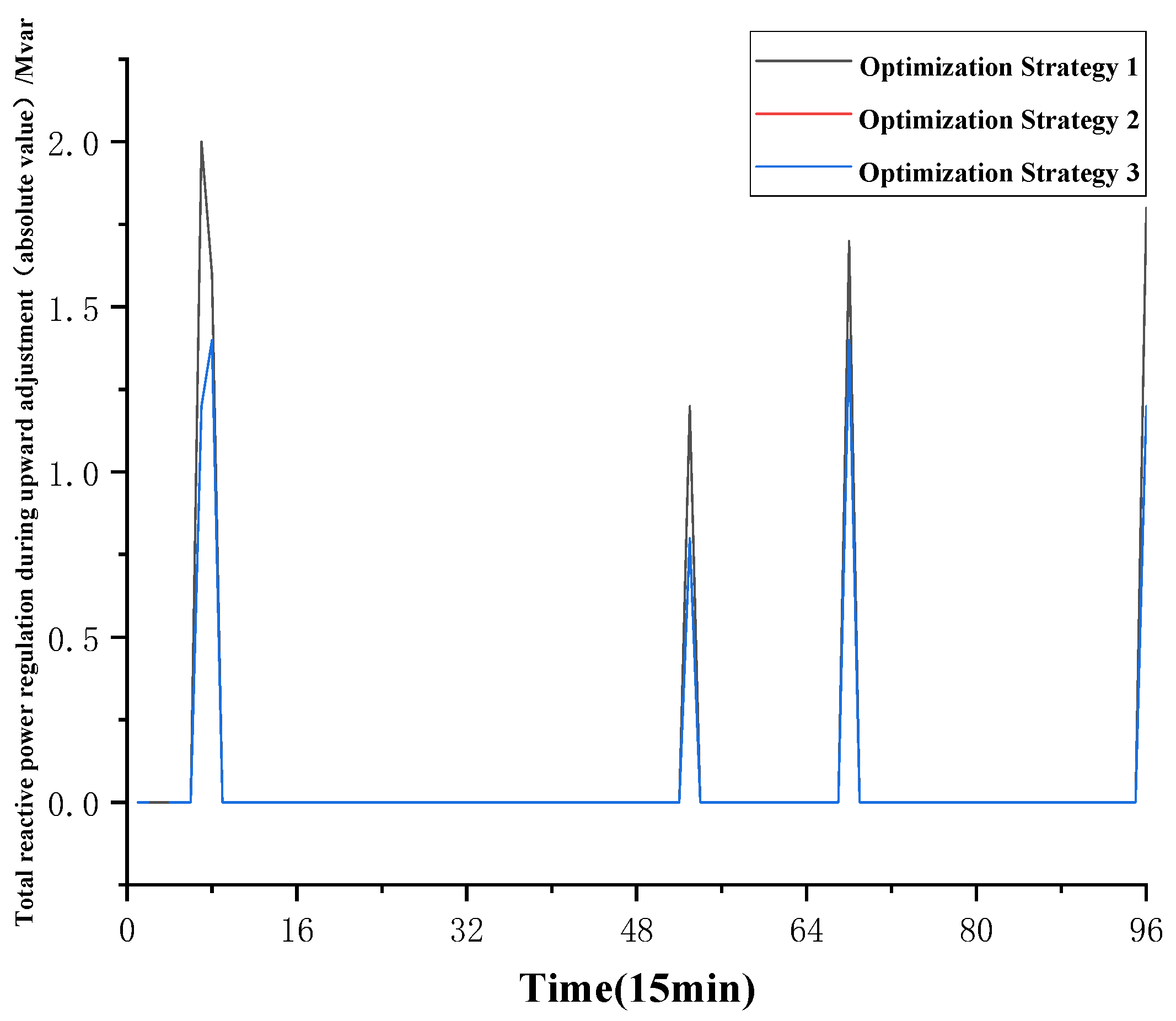
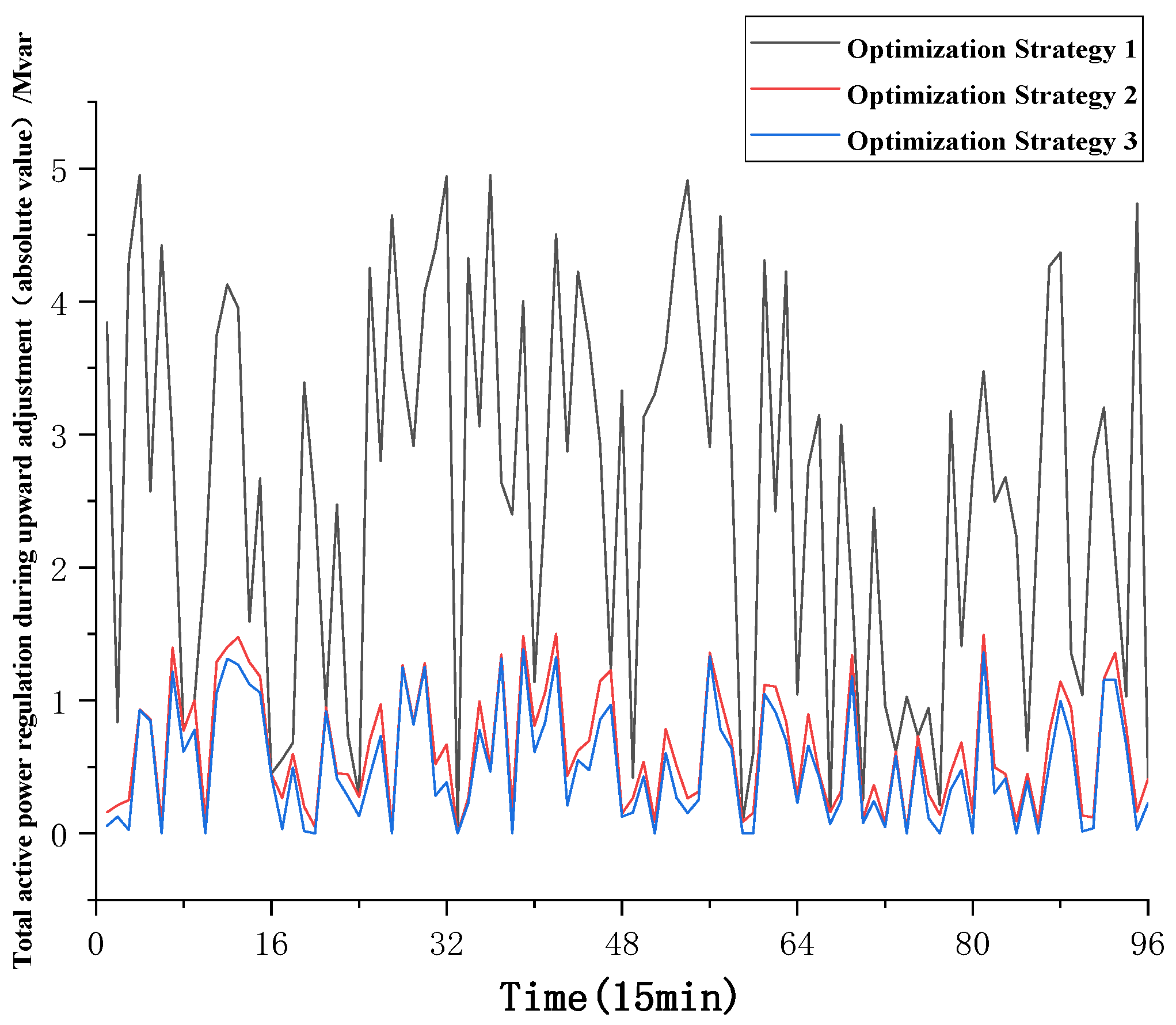
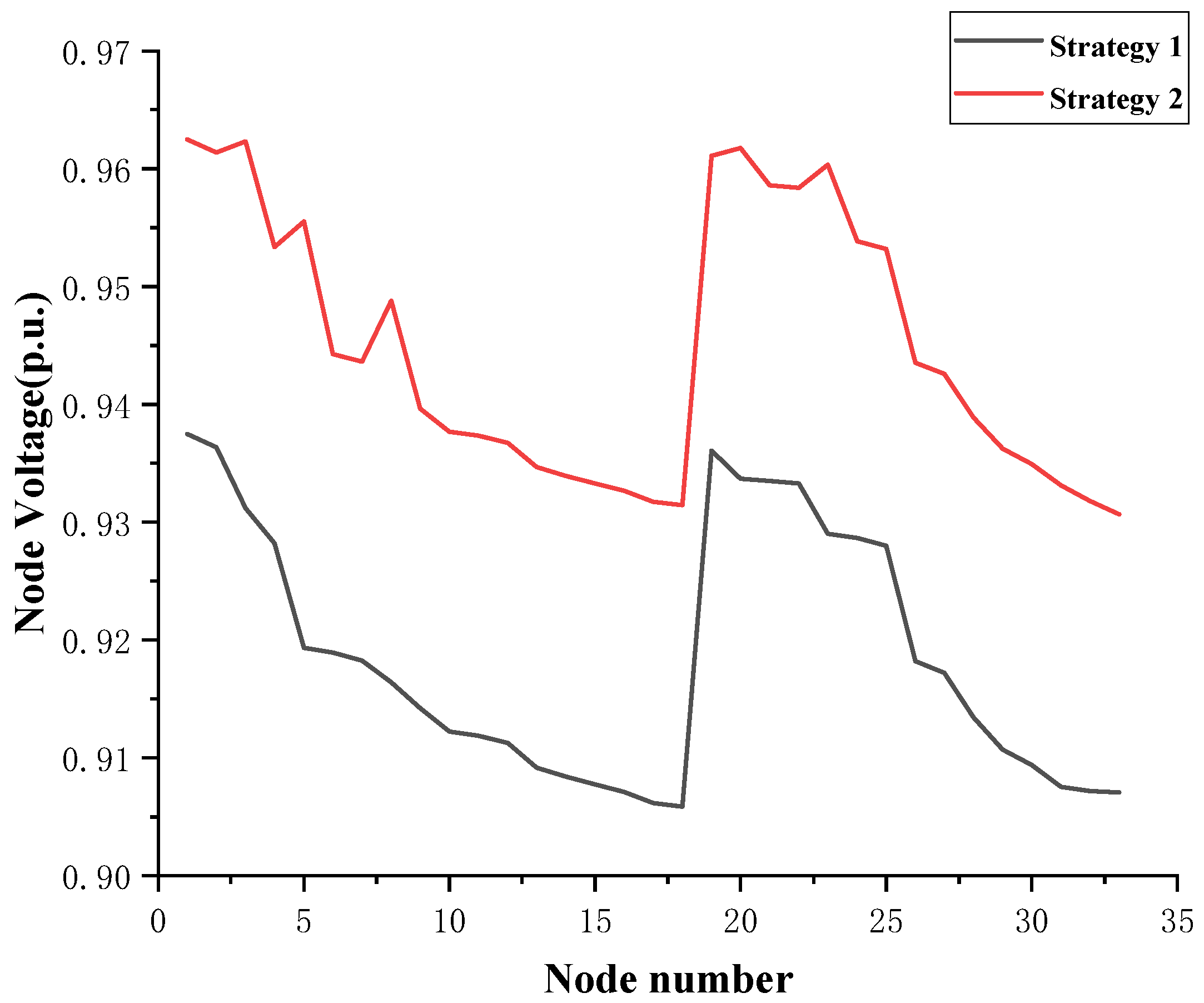
6. Case Analysis
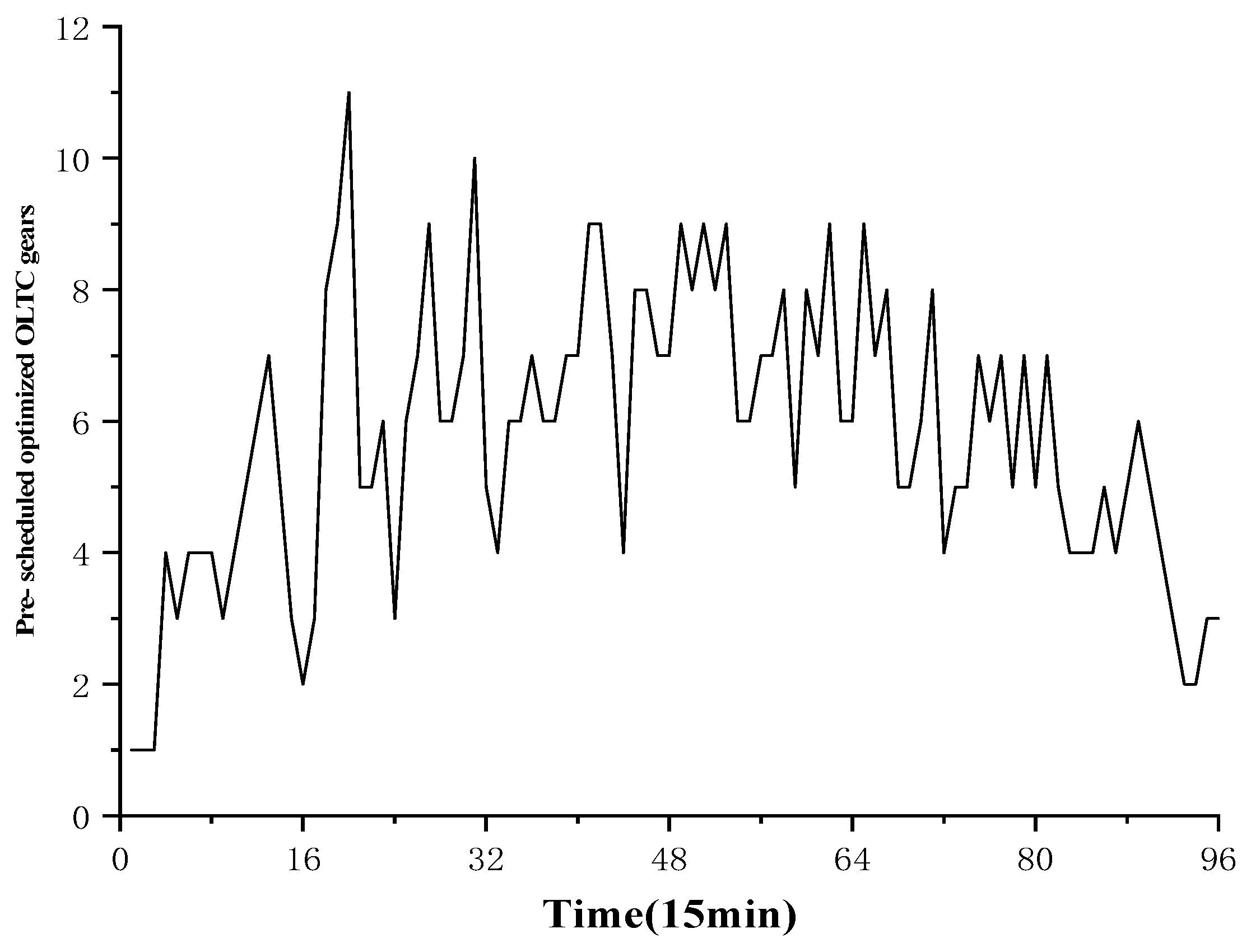
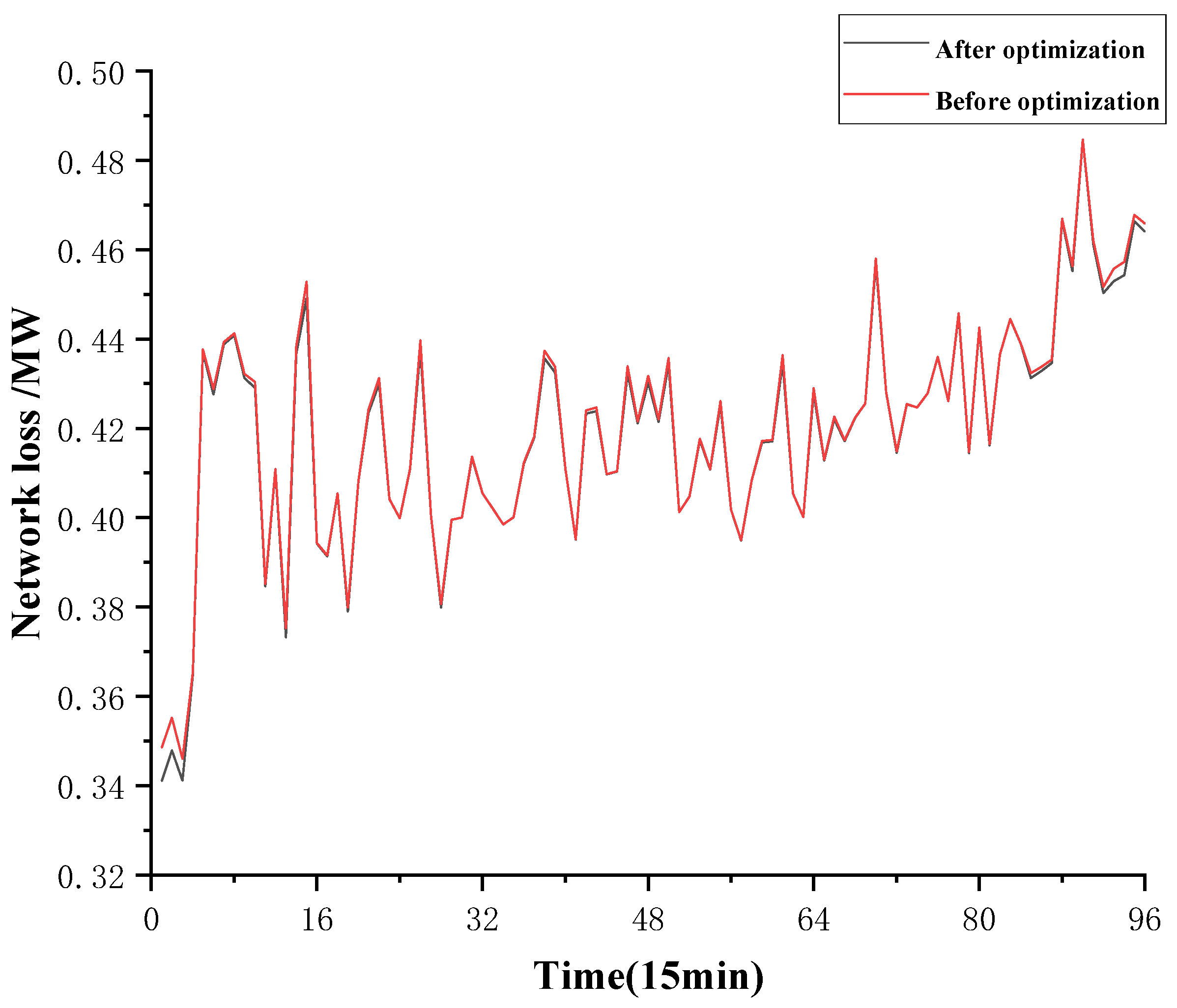
6.1. Day-Ahead Dispatching Results
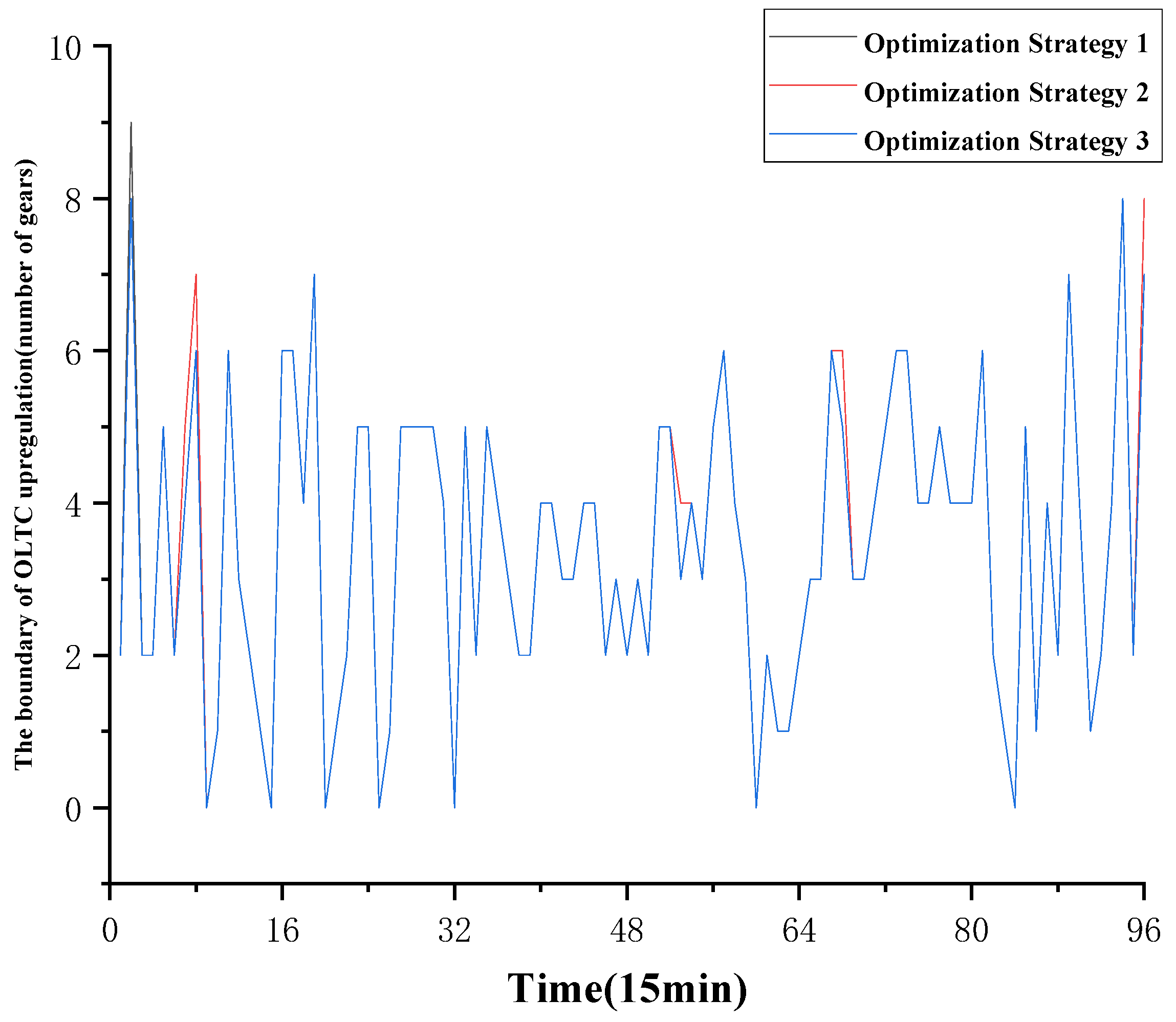
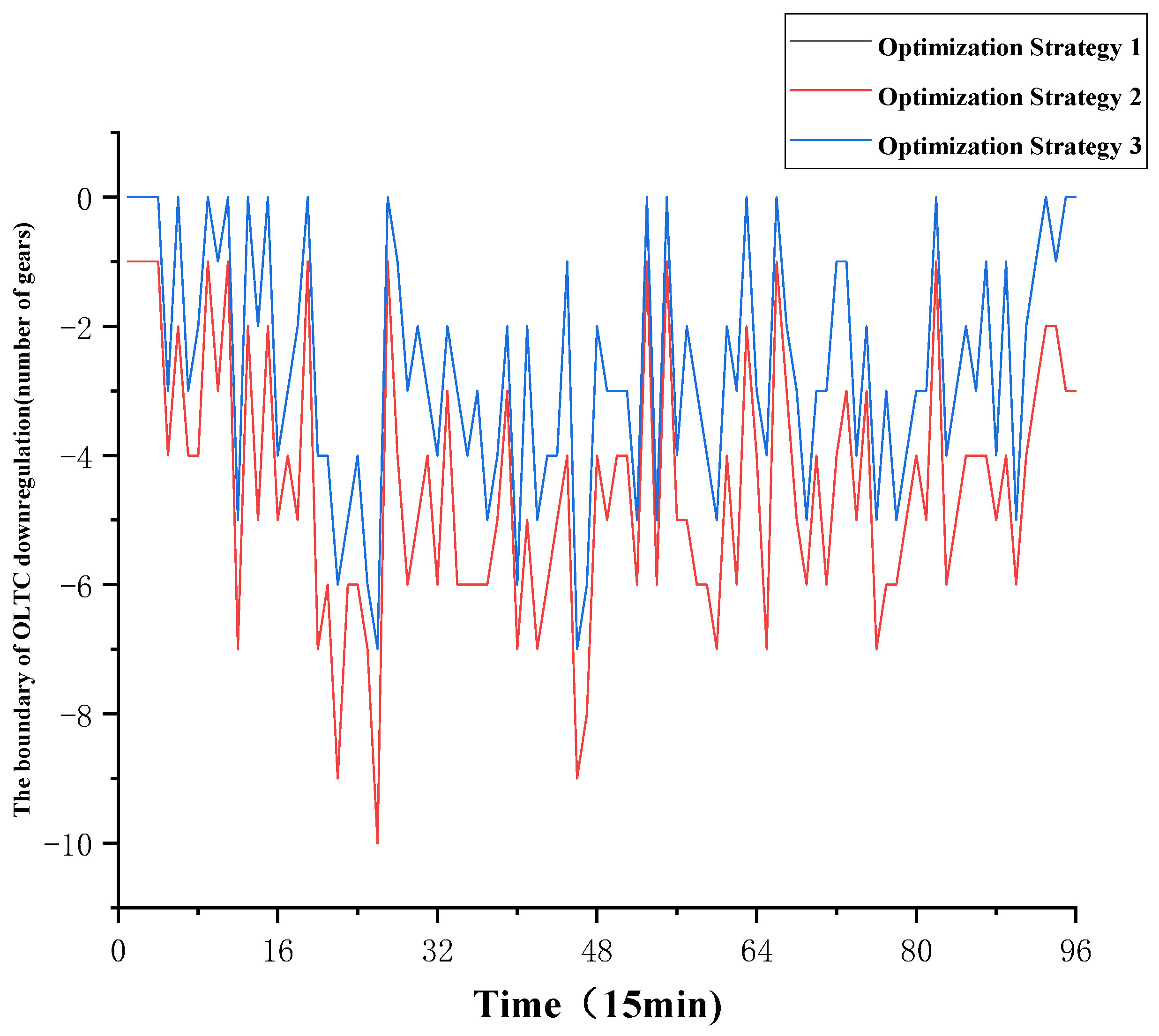
6.2. Intraday Tap Range Calculation
6.3. Analysis of Voltage Exceeding Limits
7. Conclusions
- Development of a Linearized Power Flow Model: A Zbus linearized power flow model based on fixed-point iteration is established and an analytical voltage sensitivity expression is derived from this model. This model establishes a linear relationship between node voltages, node powers, and the root node voltage, clarifying the impact of adjusting the root node voltage and reactive power on the voltages of each PQ node.
- Pre-Scheduling Optimization: In the day-ahead stage, an OLTC pre-scheduling model is constructed based on resource and network state forecasts. This optimization model targets the tap positions as optimization variables and aims to minimize network losses.
- Real-Time Optimization: In the intraday stage, reactive power control devices such as photovoltaic inverters, SVCs, and circuit breakers are optimized. The goal is to maximize the voltage adjustment range of the medium-voltage substation while minimizing the total reactive power adjustment. This provides boundary conditions for grid control commands.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, T.; Gao, Z.; Du, W.; Hu, S. Multi-dimensional evaluation method for new power system. Energy Rep. 2022, 8, 618–635. [Google Scholar] [CrossRef]
- Boyu, X.I.E. Study on the Peaking and Power Fluctuation Smoothing Strategy of High-Proportion New Energy Distribution Grid Based on Feeder Load Power Control. Ph.D. Thesis, Wuhan University, Wuhan, China, 2022. [Google Scholar]
- Hou, J.; Yu, W.; Xu, Z.; Ge, Q.; Li, Z.; Meng, Y. Multi-time scale optimization scheduling of microgrid considering source and load uncertainty. Electr. Power Syst. Res. 2023, 216, 109037. [Google Scholar] [CrossRef]
- Yang, M.; Wang, T.; Wang, Z.B. Considering dynamic perception of fluctuation trend for long-foresight-term wind power prediction. Energy 2024, 289, 130016.1–130016.11. [Google Scholar] [CrossRef]
- Wu, Y.F.; Liu, H.T.; Xiao, Z.F. Review of incremental distribution network planning considering the uncertainty of source-network-load. Power Syst. Prot. Control. 2021, 49, 177–187. [Google Scholar]
- Mosca, C.; Arrigo, F.; Mazza, A.; Bompard, E.; Carpaneto, E.; Chicco, G.; Cuccia, P. Mitigation of frequency stability issues in low inertia power systems using synchronous compensators and battery energy storage systems. IET Gener. Transm. Distrib. 2019, 13, 3951–3959. [Google Scholar] [CrossRef]
- Tian, S.M.; Wang, B.B.; Zhang, J. Key Technologies for Demand Response in Smart Grid. Proc. CSEE 2014, 34, 3576–3589. [Google Scholar]
- Xu, J.; Cao, H.Q.; Tang, C.H.; Wei, C.; Jiang, H.; Liao, S. Optimal Dispatch of Power System Considering Uncertainty of Demand Response Based on Extended Sequence Operation. Autom. Electr. Power Syst. 2018, 42, 152–160. [Google Scholar]
- Hosseini, Z.S.; Khodaei, A.; Fan, W.; Hossan, M.S.; Zheng, H.; Fard, S.A.; Paaso, A.; Bahramirad, S. Conservation voltage reduction and volt-var optimization: Measurement and verification benchmarking. IEEE Access 2020, 8, 50755–50770. [Google Scholar] [CrossRef]
- Han, B.M.; Choi, N.S.; Lee, J.Y. New Bidirectional Intelligent Semiconductor Transformer for Smart Grid Application. IEEE Trans. Power Electron. 2014, 29, 4058–4066. [Google Scholar] [CrossRef]
- Ghosh, A.; Ledwich, G. Compensation of distribution system voltage using DVR. IEEE Trans. Power Deliv. 2002, 17, 1030–1036. [Google Scholar] [CrossRef]
- Ding, M.; Wang, W.S.; Wang, X.L.; Song, Y.T.; Chen, D.Z.; Sun, M. A Review on the Effect of Large-scale PV Generation on Power Systems. Proc. CSEE 2014, 34, 1–14. [Google Scholar]
- Chen, W.J.; Gan, W.; Zhang, J.; Shen, C.; Lin, C.; Wu, M.; Sun, L.; Gu, W.; Zhang, R.; Yang, L.; et al. Divisional and Hierarchical Voltage Regulation Strategy Based on HEM Sensitivity for Distribution Network. Electr. Power Constr. 2022, 43, 42–52. [Google Scholar]
- Samadi, A.; Eriksson, R.; Söder, L.; Rawn, B.G.; Boemer, J.C. Coordinated Active Power-Dependent Voltage Regulation in Distribution Grids With PV Systems. IEEE Trans. Power Delivery. 2014, 29, 1454–1464. [Google Scholar] [CrossRef]
- Feng, Y.; Li, Y.; Cao, Y.; Zhou, Y. Automatic voltage control based on adaptive zone-division for active distribution system. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 278–282. [Google Scholar]
- Ku, T.; Lin, C.; Chen, C.; Hsu, C.T.; Hsieh, W.L.; Hsieh, S.C. Coordination of PV Inverters to Mitigate Voltage Violation for Load Transfer Between Distribution Feeders With High Penetration of PV Installation. IEEE Trans. Ind. Appl. 2016, 52, 1167–1174. [Google Scholar] [CrossRef]
- GB/T 12325-2008; Power Quality-Deviation of Supply Voltage. Standardization Administration of China: Beijing, China, 2008.
- Mccarthy, C.; Josken, J. Applying capacitors to maximize benefits of conservation voltage reduction. In Proceedings of the IEEE Rural Electric Power Conference, Raleigh, NC, USA, 4–6 May 2003; pp. C4-1–C4-5. [Google Scholar]
- Kulworawanichpong, T. Simplified Newton–Raphson power-flow solution method. Int. J. Electr. Power Energy Syst. 2010, 32, 551–558. [Google Scholar] [CrossRef]
- Mu, S.X.; Liu, J. Improved Algorithm of Load Flow Calculation for Distribution Networks. Mod. Electr. Power 2009, 26, 47–50. [Google Scholar]
- Bernstein, A.; Wang, C.; Dall’Anese, E.; Le Boudec, J.Y.; Zhao, C. Load flow in multiphase distribution networks: Existence, uniqueness, non-singularity and linear models. IEEE Trans. Power Syst. 2018, 33, 5832–5843. [Google Scholar] [CrossRef]
- Wang, C.; Bernstein, A.; Boudec, J.; Paolone, M. Explicit conditions on existence and uniqueness of load-flow solutions in distribution networks. IEEE Trans. Smart Grid 2018, 9, 953–962. [Google Scholar] [CrossRef]
- Liu, J.H.; Li, Z.H. Distributed Voltage Security Enhancement Using Measurement-Based Voltage Sensitivities. IEEE Trans. Power Syst. 2023, 39, 836–849. [Google Scholar] [CrossRef]
- Kashem, M.A.; Ganapathy, V.; Jasmon, G.B.; Buhari, M.I. A novel method for loss minimization in distribution networks. In Proceedings of the International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, London, UK, 4–7 April 2000. [Google Scholar]


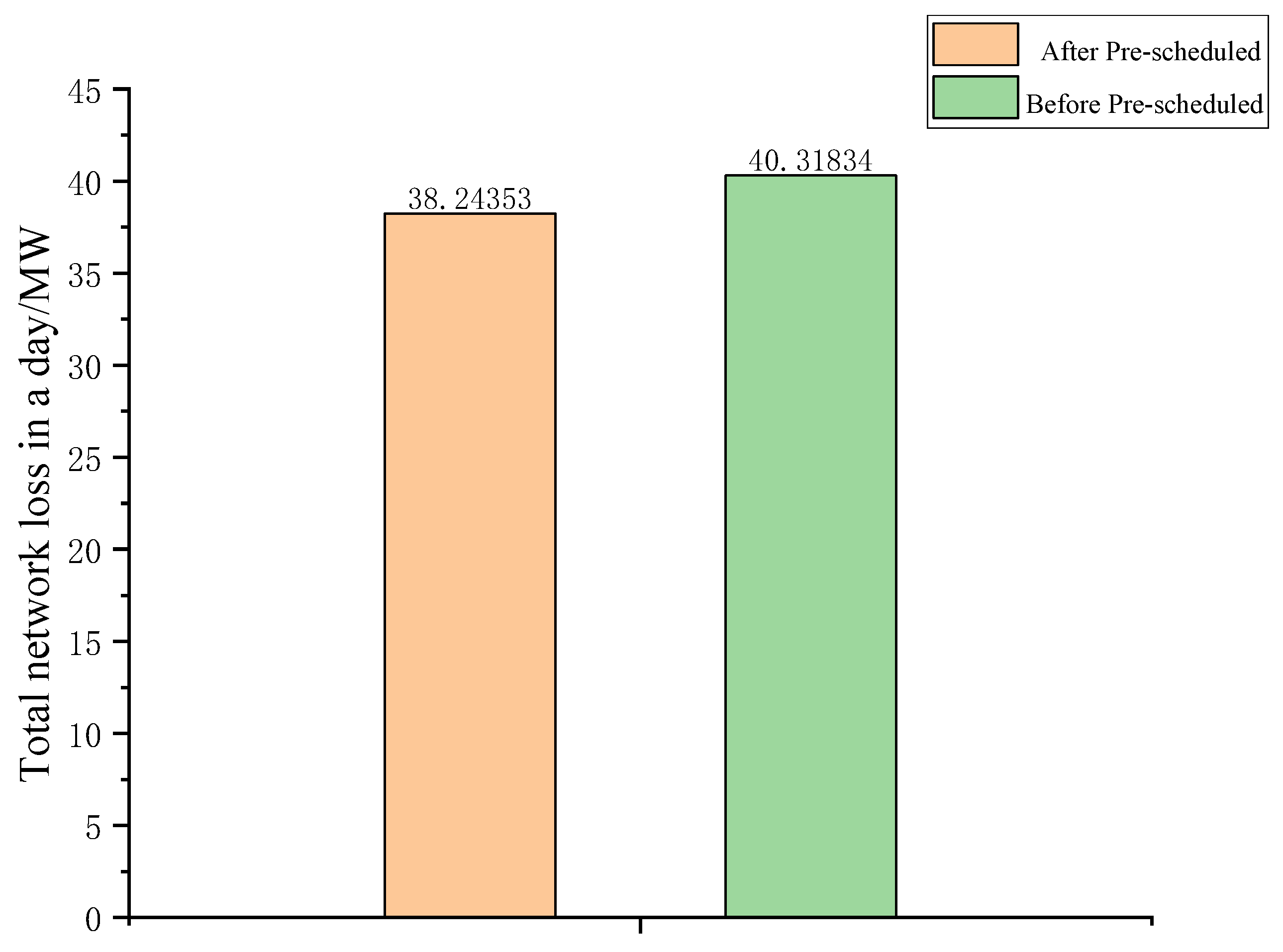

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Yang, S.; Wang, L.; Meng, Z.; Shi, F.; Liao, S. Evaluation Method for Voltage Regulation Range of Medium-Voltage Substations Based on OLTC Pre-Dispatch. Energies 2024, 17, 4494. https://doi.org/10.3390/en17174494
Hu X, Yang S, Wang L, Meng Z, Shi F, Liao S. Evaluation Method for Voltage Regulation Range of Medium-Voltage Substations Based on OLTC Pre-Dispatch. Energies. 2024; 17(17):4494. https://doi.org/10.3390/en17174494
Chicago/Turabian StyleHu, Xuekai, Shaobo Yang, Lei Wang, Zhengji Meng, Fengming Shi, and Siyang Liao. 2024. "Evaluation Method for Voltage Regulation Range of Medium-Voltage Substations Based on OLTC Pre-Dispatch" Energies 17, no. 17: 4494. https://doi.org/10.3390/en17174494
APA StyleHu, X., Yang, S., Wang, L., Meng, Z., Shi, F., & Liao, S. (2024). Evaluation Method for Voltage Regulation Range of Medium-Voltage Substations Based on OLTC Pre-Dispatch. Energies, 17(17), 4494. https://doi.org/10.3390/en17174494





