Evaluation of Distributed Photovoltaic Economic Access Capacity in Distribution Networks Considering Proper Photovoltaic Power Curtailment

Abstract

The high proportion of distributed photovoltaic (DPV) access has changed the traditional distribution network structure and operation mode, posing a huge threat to the stable operation and economy of the distribution network. Aiming at a reasonable access capacity of DPV in the distribution network, this paper proposes an economic access capacity evaluation method for DPV in the distribution network considering proper PV power curtailment. Firstly, a method for generating typical joint light intensity and load power operation scenarios based on an improved K-means clustering algorithm is proposed, which provides comprehensive scenario support for the evaluation. Secondly, based on active and reactive power regulation, this paper proposes a DPV access capacity enhancement method to improve the DPV access capacity. Thirdly, considering proper PV power curtailment, an evaluation model of DPV economic access capacity in the distribution network is established to solve the maximum DPV economic access capacity in the distribution network. And aiming at the nonlinear problem in the model, the second-order cone relaxation method is employed to transform the model into the second-order cone programming model, so as to solve the objective function conveniently and efficiently. Finally, based on the improved IEEE 33-node distribution network analysis, the results show that the proposed method can be more comprehensive and effective in evaluating the DPV economic access capacity in the distribution network, and proper PV power curtailment can significantly increase the DPV economic access capacity in the distribution network.

1. Introduction

With the worsening of the global energy crisis and the aggravation of environmental pollution, the global energy transition process has accelerated significantly. The scale of renewable energy applications represented by wind and photovoltaic power generation has accelerated expansion; the power system has become an important way of renewable energy planning.

The large-scale connection of DPVs with intermittency and strong uncertainty to the distribution network makes the operating characteristics of the power system more complex. The load characteristics of some nodes will be transformed into power characteristics, which will lead to problems such as node voltage overruns, the blockage of power transmission, and the return of tidal currents, as well as difficulties in local consumption [1,2,3]. This poses a great threat to the safe and stable operation of the distribution network and creates an unpredictable risk to the economy, so it is necessary to make a reasonable evaluation of the DPV economic access capacity in the distribution network.

The DPV access capacity evaluation model usually takes the maximum access capacity as the objective, and after considering a variety of safe operation constraints, the optimal solution is obtained by using various optimization algorithms [4,5,6,7,8]. However, when the constraints considered by this method are not comprehensive or the operational scenarios are considered to be limited, the results are relatively inaccurate. In engineering practice, transmission lines and some power equipment are allowed to slightly exceed the limit for a short time. Therefore, opportunity constraints can be introduced to avoid the influence of the calculation of the ultimate maximum access capacity due to the consideration of the occurrence of small-probability events [9,10].

Many researchers and scholars have analyzed the maximum DPV access capacity in distribution networks from different dimensions, and the research results of evaluation methods are quite rich at this stage. References [11,12] establish a new power system distributed power supply maximum-access capacity-evaluation model in the context of dual-carbon, which carries out DPV access capacity evaluation from the energy-use characteristics and mutual coupling relationship of multiple access bodies. The grid integration of large-scale DPV access also results in higher requirements for flexibility [13,14]. Flexible control and the optimal scheduling of demand-side, grid-side, and energy storage construction can be used to meet the flexibility requirements of the distribution network, and the DPV access capacity can be reasonably evaluated and increased.

References [15,16,17,18] consider user-side demand response and propose measures to optimize active power through demand response to increase the utilization of distributed power sources. References [19,20] comprehensively consider the regulation potential of flexible loads and energy storage systems, establish the impact of different energy storage configuration schemes on the system’s renewable energy access capacity, and propose an optimization strategy for source–grid–load–storage interaction. References [21,22,23,24] comprehensively consider the flexible characteristics of intelligent soft switches and propose effective methods to enhance the access capacity of renewable energy in the distribution network.

For the problems that the models find difficult to solve due to nonlinear/non-convex parts, most of research adopts different relaxation methods and linearizes the nonlinear parts of the models to improve the speed and quality of the solution [25,26,27].

When some of the security constraints in the distribution network are on the verge of being exceeded, proper PV power curtailment can be performed to reduce the output of DPV units. Such an approach can avoid the operational risks caused by the access of a large number of DPV units [28]. The economic issues brought by PV power curtailment cannot be ignored. Reference [29] proposes a DPV access capacity model considering PV power curtailment which takes into account the revenue of the DPV investor and the network loss of the operator. However, the single scenario in this paper makes the economic index representative, and the maximum DPV access capacity conservative.

In summary, existing studies have explored different aspects of DPV access capacity evaluation and enhancement methods in distribution networks. However, the analysis of the factors affecting the DPV access capacity is not comprehensive enough and has certain limitations. Moreover, there are few in-depth studies on the impact of PV power curtailment on access capacity and economic indicators.

An evaluation method of DPV access capacity in the distribution network considering proper PV power curtailment is presented in this paper. The main contributions of this paper are as follows:

(1)

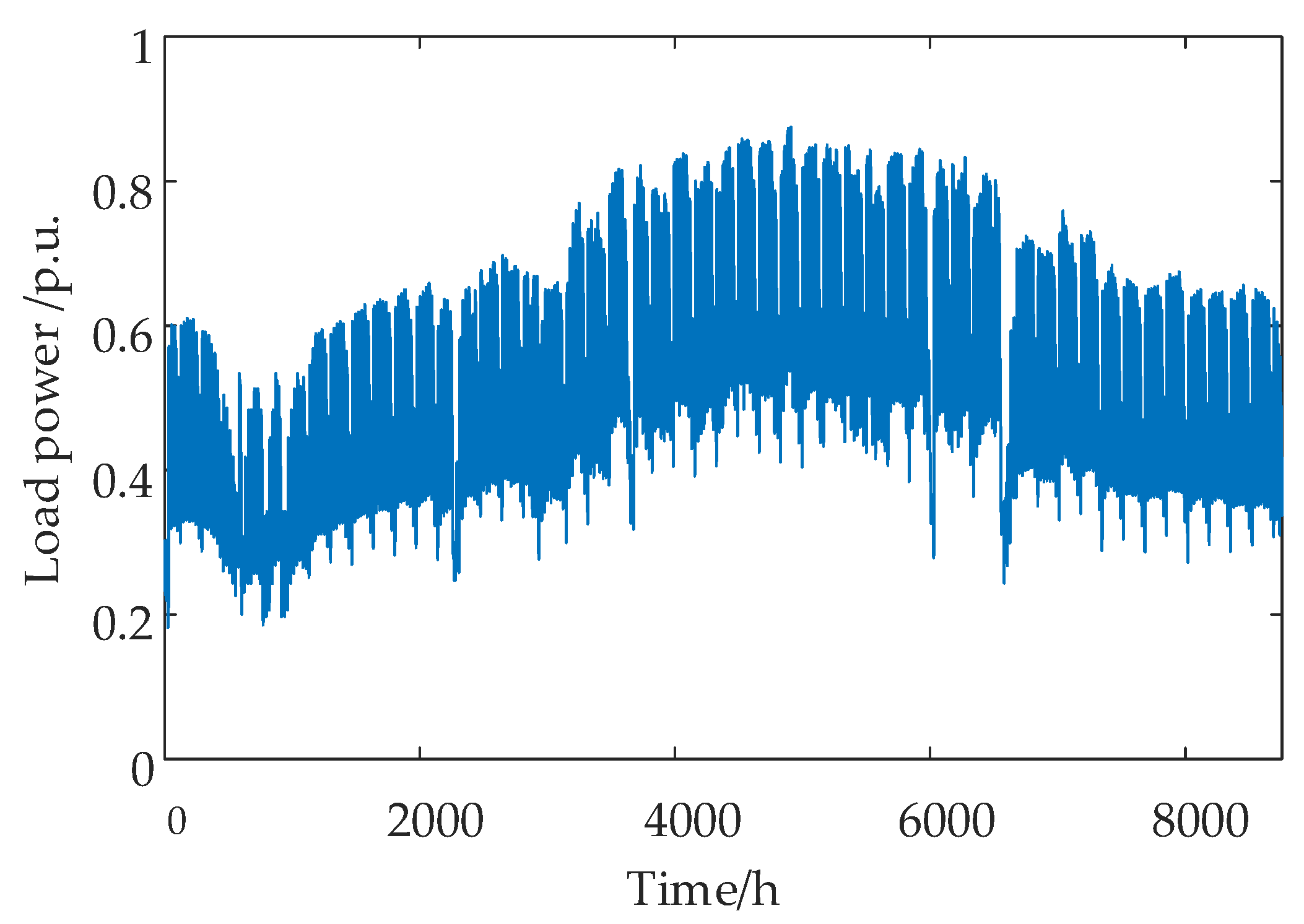
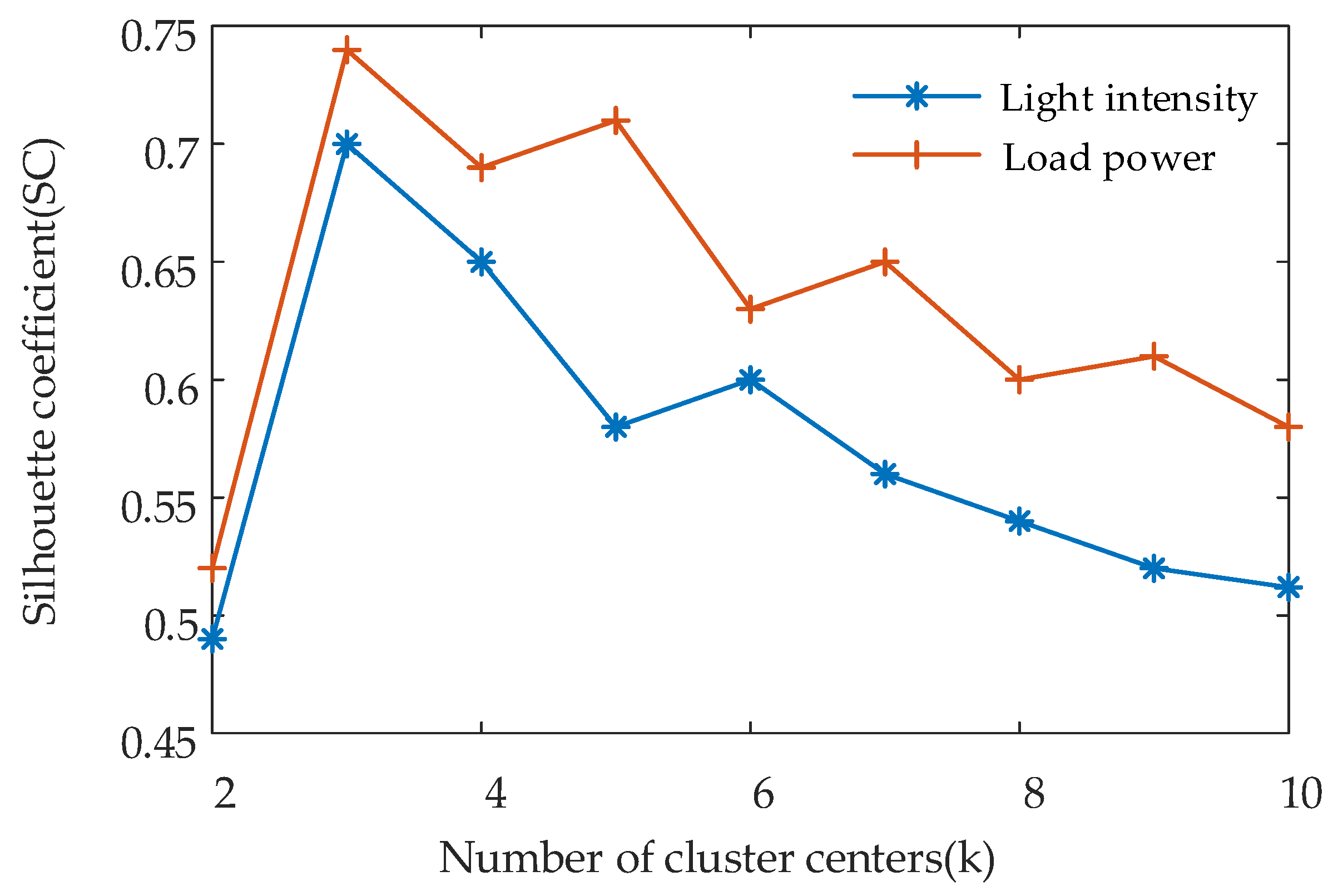
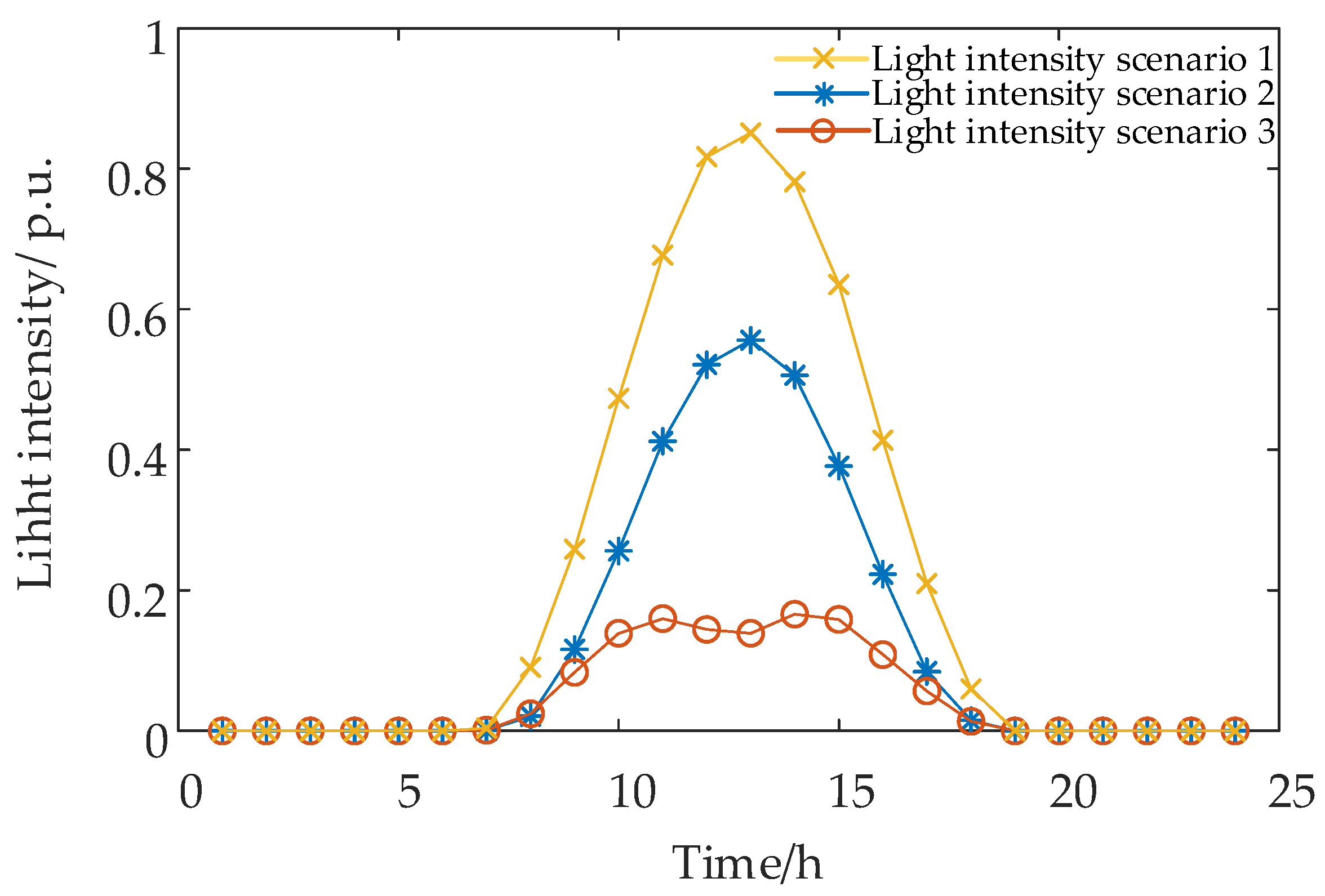
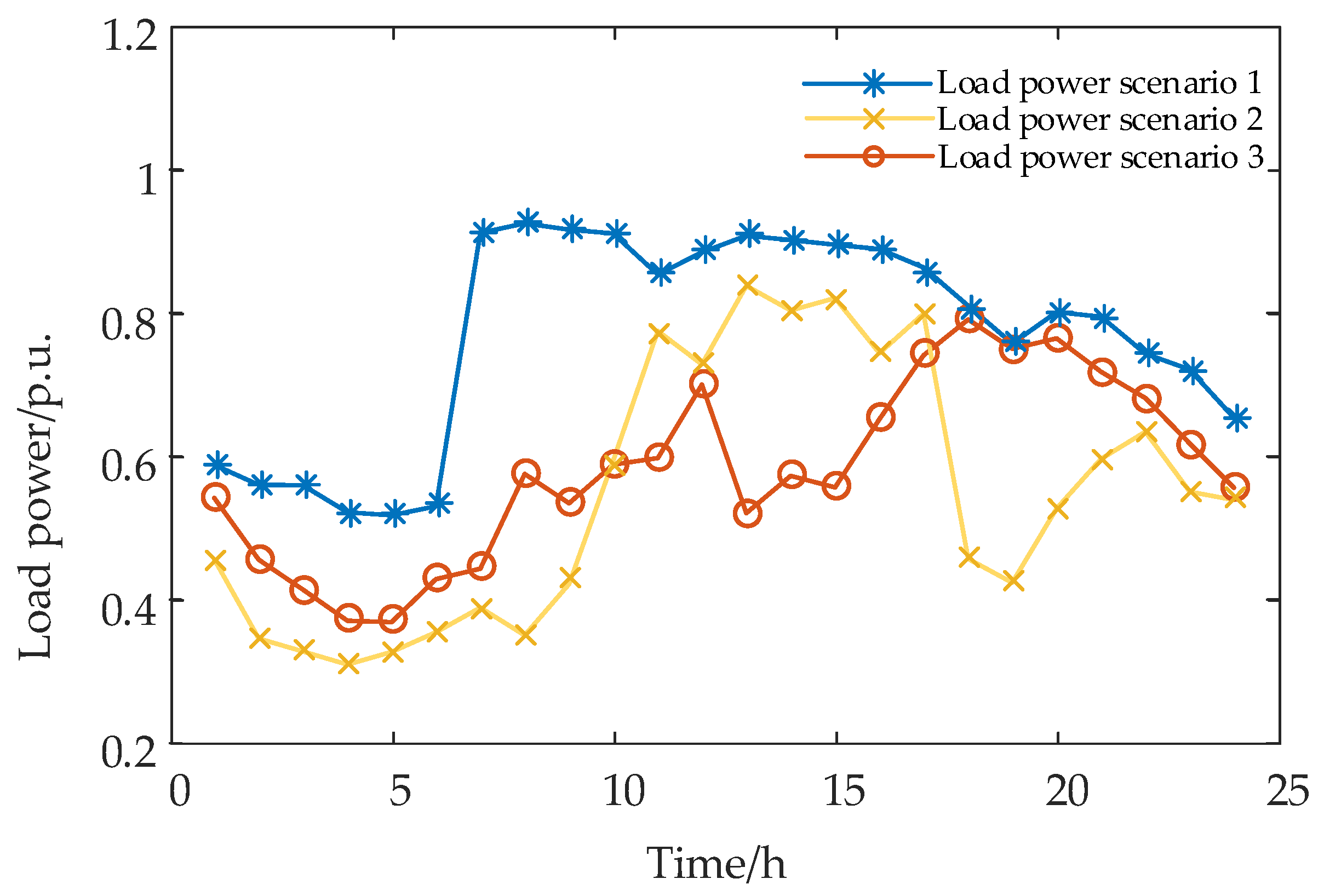
In this paper, a method for generating typical joint light intensity and load power operation scenarios based on the K-means algorithm is proposed. The typical joint operation scenario set for light intensity and load power and the probability set for these scenarios are obtained by clustering and combining the historical data of annual light intensity and load power to provide comprehensive scenario support for the evaluation.

(2)

Based on the perspective of active and reactive power regulation, this paper proposes a DPV access capacity-enhancement method to improve the DPV access capacity and increase economic revenue. From the perspective of regulating active power, this paper proposes a strategy that combines the configuration of energy storage devices with demand responses based on electricity prices. From the perspective of regulating reactive power, this paper proposes a reactive power control method for inverters based on the node voltage.

(3)

Innovatively, proper PV power curtailment is considered as one of the factors that deeply influences the evaluation of DPV economic access capacity. This paper comprehensively considers the relationship between PV power curtailment, the maximum DPV access capacity, and economic revenue, and establishes an evaluation model of maximum DPV economic access capacity in the distribution network.

This paper is organized as follows. Section 2 proposes a typical joint light intensity and load power operation scenario generation method; Section 3 proposes a DPV access capacity enhancement method for a distribution network based on active and reactive power regulation; Section 4 establishes an economic access capacity evaluation model for DPV in the distribution network that takes into account the proper PV power curtailment; Section 5 gives the model’s solution idea and process; Section 6 verifies the proposed evaluation method through example analysis and case comparison for its validity; Section 7 draws the conclusions.

2. Generation of Typical Operation Scenarios for Light Intensity and Load Power

The DPV and load outputs not only have diurnal differences in the intraday time scale, but also seasonal differences in the annual time scale. The similarity between the outputs of DPV units and loads each year is very high. To ensure that the typical scenarios of DPV and load output generated in this paper have validity and accuracy in practical applications, this paper takes 8760 h of annual light intensity and load power historical data as the original data, and then puts 24 h of daily light intensity and load power data in the same unit for class clustering to obtain the class clustering unit. An improved K-means clustering algorithm is used to cluster the light intensity and load power historical data to obtain the typical daily scenarios.

Because of the large amount of data and high correlation between the 8760 h of annual light intensity and load power, the number of clusters plays a crucial role in the clustering analysis. If the number of clusters is large, the similarity of the samples within the clusters is high, but the difference in the samples between the clusters is small and the clustering effect is not significant. If the number of clusters is small, the similarity of the samples within the clusters is low, and the clustering effect is also poor. Therefore, this paper introduces the silhouette coefficient (SC) as an index to balance the similarity within clusters and the variability between clusters to determine the number of clusters [30,31]. When in the optimal value, the sample points within clusters are close enough and the sample points between clusters are dispersed enough. The formula of SC_i for a sample point is as follows, where $S{C}_i\in \left[-1,1\right]$:

$$S{C}_i={\displaystyle \frac{{\mathrm{a}}^i-b^i}{\max (a^i,b^i)}}$$

(1)

where $d^i$ is the average distance from a point in the cluster to all other cluster points outside the cluster; $b^i$ is the average distance from a point in the cluster to other points in the cluster.

The profile coefficients of all sample points are averaged as the average clustering coefficient, which is expressed as

$$S{C}_k={\displaystyle \frac{1}{n}}S{C}_i$$

(2)

where $k$ is the number of clustering centers; $n$ is the number of samples in the dataset.

3. Methods for Enhancing DPV Access Capacity in Distribution Networks

The amount of DPV feed-in power directly affects the economics of DPV access. Therefore, this section gives methods to enhance the DPV access capacity from the perspective of regulating active and reactive power, to improve the DPV access capacity in the distribution network, and increase the economic revenue.

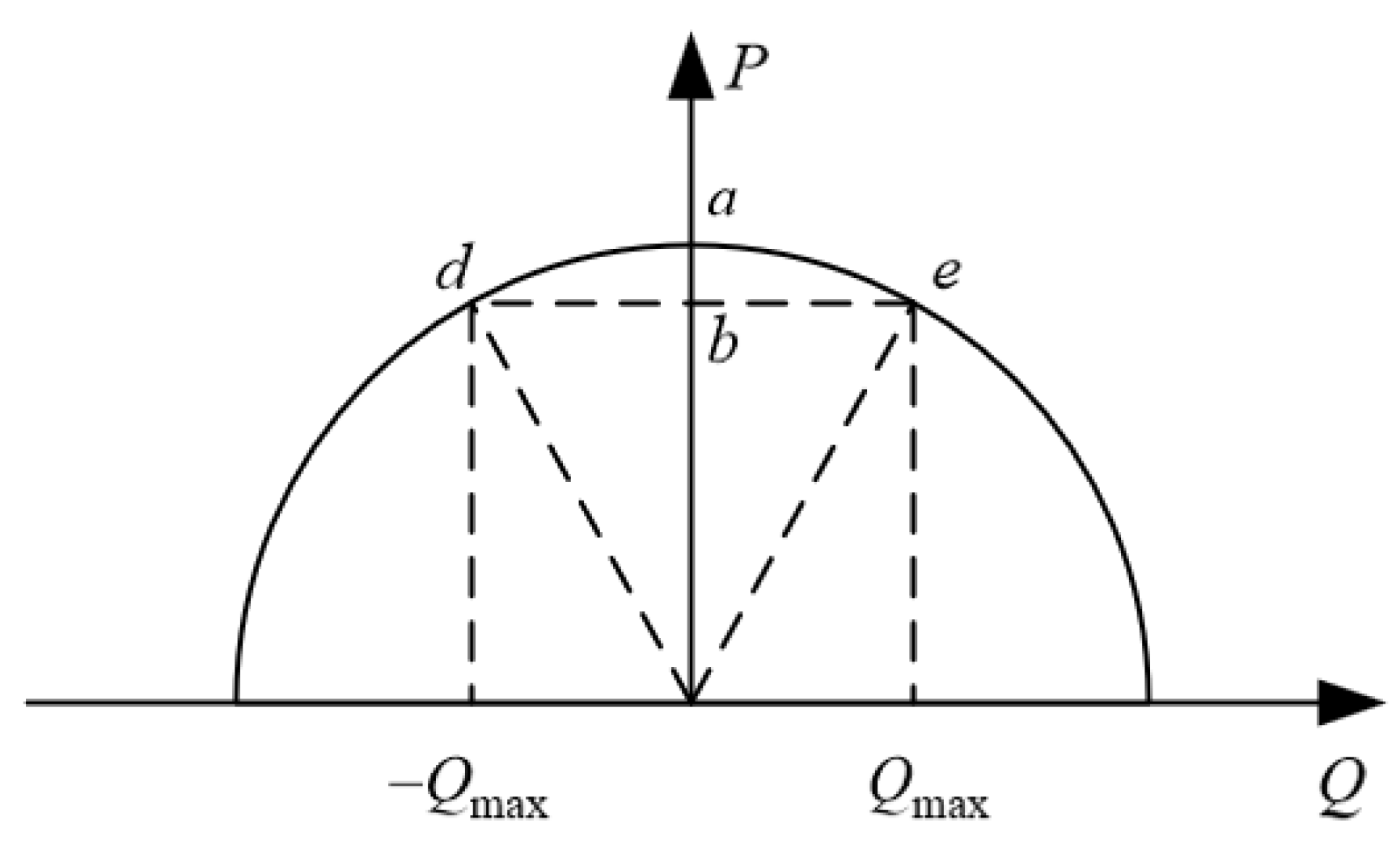
3.1. Method from the Perspective of Reactive Power Regulation

The nodal voltage exceeding the limit is one of the main factors limiting the DPV access to the distribution network. At the moment of sufficient light intensity in the middle of the day, the output of DPV units is large, which may cause the voltage of some nodes to exceed the limit. In this section, the DPV inverter is controlled to achieve the purpose of reactive power regulation, and then adjusts the node voltage magnitude to minimize the node voltage overrun phenomenon caused by the large PV output. This control method can make use of as much DPV output as possible, improve the DPV access capacity in the distribution network, and increase the economy of DPV access.

For the most part, the node voltage of the distribution network may exceed the limit at noon when there is sufficient light intensity. At this time, the active capacity is reduced by controlling the inverter, and the phase angle is adjusted to increase the reactive capacity of the inverter. When the node voltage is lower than the allowed operating voltage, the inverter sends out reactive power to play a reactive power support role for the distribution network. The relationship between inverter capacity and active and reactive power from DPV power is shown in Figure 1 below, and the magnitude of reactive power regulation is shown in Equation (3).

As shown in Figure 1, when the maximum active output of DPV is at point a, at this time the reactive capacity is 0. When the active capacity is appropriately reduced to point b, the DPV inverter has a certain reactive power regulation capability.

The specific control method of inverter reactive power based on a distribution network node voltage regulation inverter is as follows:

$$\left|Q_{pv}\right|=\sqrt{S_{\max }^2-P_{pv}^2}$$

(3)

$$(P,Q)=\left\{\begin{array}{l}(0,Q_{\max })\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}U<U_{\min }\hfill \\ (P_1,{\displaystyle \frac{U-U_{\min }}{U_{\min }-U_1}}{Q}_{\max }+Q_{\max })\hspace{1em}\hspace{1em}{U}_{\min }\le U\le U_1\hfill \\ (P_{\max },0)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{U}_1<U\le U_2\hfill \\ (P_2,{\displaystyle \frac{U-U_2}{U_2-U_{\max }}}{Q}_{\max })\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{U}_2<U\le U_{\max }\hfill \\ (0,-Q_{\max })\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{U}_{\max }<U\hfill \end{array}\right.$$

(4)

where $S_{\max }$ is the inverter capacity, generally 1.0–1.1 times the active rated capacity, $P_{pv}$ is the active power generated by the DPV inverter, and $Q_{pv}$ is the reactive power that can be issued or absorbed. $(P,Q)$ is the active and reactive power generated by the DPV inverter at a certain moment. $Q_{\max }$ is the maximum value of reactive power output. $U$ is the actual value of the DPV grid-connected point voltage monitored in real time. $U_{\max }$ and $U_{\min }$ are the upper and lower limits of the grid-connected point voltage, respectively. When $U<U_{\min }$ or $U_{\max }<U$, the DPV inverters absorb or emit reactive power to the maximum extent according to their own reactive capacity. $U_1$ and $U_2$ are the upper and lower limits of the node voltage target range, respectively. For the node voltage, it is difficult, and there needs to be a large amount of reactive power consumed, to set it to a specific value. Setting it in a specific range can ensure voltage quality and reduce reactive power consumption. Since the voltage in the target range meets the grid demand, no reactive power compensation is required and the reactive power output of the DPV inverters is zero.

The operational constraints of the DPV inverter are as follows:

$$0\le P_{pv}\le P_{pv,\max }$$

(5)

$$P_{pv}^2+Q_{pv}^2\le S_{\max }^2$$

(6)

$$-P_{pv}\tan {\theta }_{pv}\le Q_{pv}\le P_{pv}\tan {\theta }_{pv}$$

(7)

$$-{\theta }_{pv,\max }\le {\theta }_{pv}\le {\theta }_{pv,\max }$$

(8)

where ${\theta }_{pv}$ is the power angle during the operation of the DPV inverter.

3.2. Method from the Perspective of Active Power Regulation

From the active regulation point of view, this subsection considers the combination of demand response and the allocation of energy storage to admit as much DPV output as possible and increase the DPV feed-in gains.

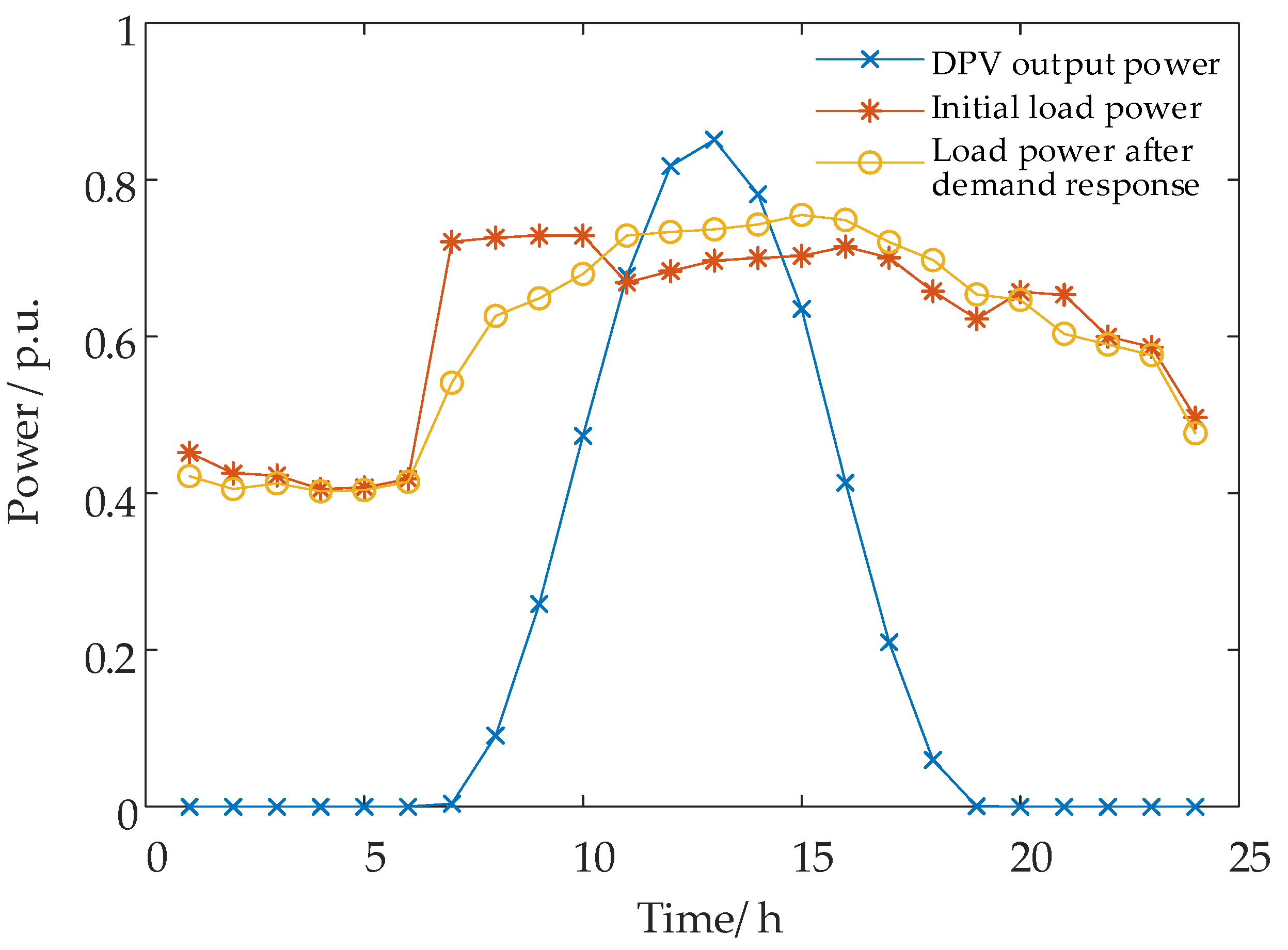
3.2.1. Demand Response Model

To promote the orderly access of DPV power generation to the grid and bring considerable economic benefits, and thus bring considerable economic revenue, this subsection proposes to guide the time of the power consumption of some users through demand-side tariff management. The purpose of this move is to increase the power consumption when the DPV output is large, increase the utilization rate of DPV power generation, and thus increase the economic revenue brought by DPV access. The demand response proposed in this subsection is based on transferable loads, which can be transferred and adjusted on time according to the change in electricity price. The total electricity demand of the scheduling cycle remains unchanged. The demand response model is expressed as follows:

$$-{\tau }_{i,t}={\displaystyle \frac{\mathsf{\Delta }{P}_{i,t}^{pur}}{\mathsf{\Delta }{\rho }_{i,t}}}={\displaystyle \frac{\mathsf{\Delta }{P}_{i,t}^{pur}}{{\rho }_{i,t}^{cur}-{\rho }_{i,t}}}$$

(9)

$$P_{i,t}^{sum}=P_{i,t}^{bas}+(P_{i,t}^{pur}-\mathsf{\Delta }{P}_{i,t}^{pur})$$

(10)

$$\mathsf{\Delta }{P}_{i,t}^{pur,\min }\le \mathsf{\Delta }{P}_{i,t}^{pur}\le \mathsf{\Delta }{P}_{i,t}^{pur,\max }$$

(11)

$$\mathsf{\Delta }{P}_{i,t}^{pur}=P_{i,t}\times {\tau }_{i,t}\times {\displaystyle \frac{{\rho }_{i,t}^h-{\rho }_{i,t}^l}{{\rho }_{i,t}^h}}$$

(12)

$${\rho }_{i,t}^{cur}=\left\{\begin{array}{c}{\rho }_{i,t}^h,t\in T^{high}\\ {\rho }_{i,t}^l,t\in T^{low}\end{array}\right.$$

(13)

where ${\tau }_{i,t}$ is the electricity price elasticity coefficient of node $i$ at the time $t$, $\mathsf{\Delta }{\rho }_{i,t}$ is the change in electricity price, ${\rho }_{i,t}$ is the initial electricity price before demand response, and ${\rho }_{i,t}^{cur}$ is the electricity price after demand response. $P_{i,t}^{sum}$, $P_{i,t}^{bas}$, $P_{i,t}^{pur}$, and $\mathsf{\Delta }{P}_{i,t}^{pur}$ are the total value of the load active power, the value of the base uncontrollable load active power, the value of the transferable load active power, and the value of the transferred load active power of node $i$ at the time $t$, respectively. $\mathsf{\Delta }{P}_{i,t}^{pur,\max }$ and $\mathsf{\Delta }{P}_{i,t}^{pur,\min }$ are the upper and lower limits of active power of transferable load, respectively. ${\rho }_{i,t}^h$ is the electricity price for the peak period of DPV output, and ${\rho }_{i,t}^l$ is the electricity price for the valley period of DPV output. $T^{high}$ is the peak period of DPV output, and $T^{low}$ is the valley period of DPV output.

Price demand elasticity refers to the sensitivity of demand to price changes. The electricity price elasticity coefficient ${\tau }_{i,t}$ in Equation (9) is used to characterize the relationship between the change in load demand and the change in electricity price. There is a certain degree of negative correlation between the change in electricity price and the change in load active power. Equation (10) is the total load active power balance of node i, which is the sum of the basic uncontrollable load active power and the transferable load active power minus the transferred load active power. The upper and lower limits of the active power of the transferable load are reflected in Inequality (11). The method for calculating the active power of the transferable load is expressed in Equation (12), which increases with the increase in the electricity price elasticity coefficient ${\tau }_{i,t}$.

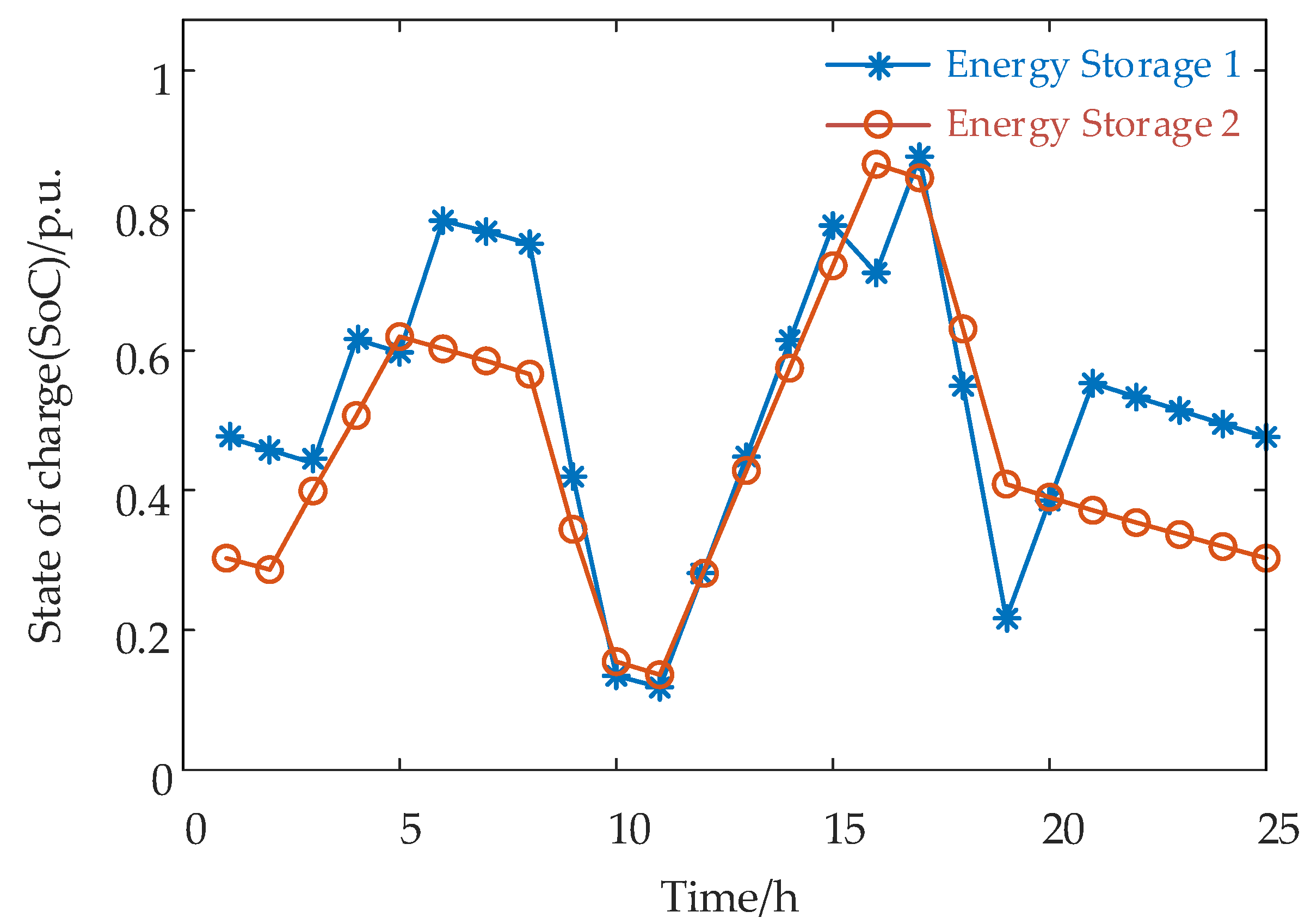
3.2.2. Energy Storage Model

When the light intensity is sufficient in a day, DPV output is large, which is a great threat to the safe and stable operation of the distribution network. In the evening and at night, when there is a lack of light intensity and a high load, DPV output is relatively small or non-existent.

Therefore, this subsection adopts the allocation of energy storage to coordinate the active power allocation at different times. The participation of energy storage in active power supply and demand regulation can reduce the risk of security overruns due to the difficulty of consuming DPV power at the peak time, allow DPV power to be accepted to a greater extent, and obtain a greater DPV power generation online revenue. However, the cost of energy storage equipment is relatively high. Its equipment investment and operation and maintenance costs cannot be ignored when evaluating the economic DPV access capacity in the distribution network.

The energy storage operation model is as follows:

$${\gamma }_{dch,it}+{\gamma }_{\mathrm{ch},it}\le 1$$

(14)

$$E_{i,t+\mathsf{\Delta }t}=E_{i,t}+({\eta }_{i,ch}\times P_{i,ch}-{\eta }_{i,dch}\times P_{i,dch})$$

(15)

$$E_{i,t0}=E_{i,t\tau }$$

(16)

where ${\gamma }_{dch,it}$ and ${\gamma }_{\mathrm{ch},it}$ are the charging and discharging states of the energy storage device $i$ at the time $t$, respectively, taking the values of 0 or 1. $E_{i,t}$ is the stored energy of the energy storage device $i$ at the time $t$. ${\eta }_{i,ch}$ and ${\eta }_{i,dch}$ are the charging and discharging efficiencies of the energy storage device $i$, respectively. $E_{i,t0}$ and $E_{i,t\tau }$ are the stored energy of the energy storage device $i$ at the initial and final moments of scheduling, respectively.

To ensure the service life of energy storage equipment, it is necessary to restrict the charge and discharge levels of energy storage equipment, which is represented by the state of charge (SoC), which is expressed as follows:

$$So{C}_{i,t}={\displaystyle \frac{E_{i,t}}{E_N}}$$

(17)

$$So{C}_{\min }\le So{C}_{i,t}\le So{C}_{\max }$$

(18)

where $E_{i,t}$ is the capacity of energy storage $i$ at the time $t$, and $E_N$ is the rated capacity of the energy storage. $So{C}_{i,t}$ is the state of charge of energy storage $i$ at the time $t$, $So{C}_{\max }$ and $So{C}_{\min }$ are the upper and lower limits of the energy storage charge state, respectively.

4. Evaluation Model of DPV Economic Access Capacity in Distribution Networks Considering Proper PV Power Curtailment

4.1. Objective Function

The objective function of this model is the maximum capacity of total DPV access in the distribution network when the net economic revenue is non-negative, taking into account proper PV power curtailment.

Because the constraints are most likely to exceed the limit in the extreme typical scenario with minimum load power and maximum light intensity, this paper takes the access capacity obtained in this scenario as the basic constant. The maximum construction capacity of the DPV power-curtailment unit is introduced as a variable. The DPV economic access capacity considering proper PV power curtailment proposed in this paper is the access capacity obtained in the above scenario plus the construction capacity of the maximum DPV power curtailment unit, which is given by Equations (19) and (20).

$$f_1=\max {\displaystyle \sum _{i=1}^N{S}_i^{pv}}$$

(19)

$$f=f_1+\max f_x$$

(20)

where $S_i^{pv}$ is the DPV capacity accessed at node $i$, and $N$ is the total number of nodes in the distribution network that are allowed to access DPV units. $f_1$ is the maximum access capacity of DPV in the extreme scenario of minimum load power and maximum light intensity, without considering proper PV power curtailment and economics, and each constraint is not crossed. $f$ is the DPV economic access capacity in the distribution network considering proper PV power curtailment, and $f$ is the objective function sought in this paper. $f_x$, as a variable, is the maximum capacity of the power-curtailment units that can be added to the distribution network on the basis of $f_1$, taking into account proper PV power curtailment and economics.

4.2. Constraints

Considering the security operation in actual working conditions and the uncertain effects of DPV power and load output, this model adopts opportunity constraints for node voltage constraints and branch line capacity margin constraints. Compared with rigid constraints, flexible opportunity constraints can avoid affecting the calculation of DPV access capacity due to the occurrence of small-probability events.

(1)

DPV construction capacity of node constraints:

$$0\le N_i^{pv}\le N_i^{pv,\max }$$

(21)

where $N_i^{pv}$ is the capacity of DPV units constructed at node $i$ and $N_i^{pv,\max }$ is the maximum capacity of DPV units allowed at node $i$.

(2)

DPV output constraints:

$$0\le P_{i,t}^{pv}\le P_{i,t}^{pv,\max }$$

(22)

where $P_{i,t}^{pv}$ is the DPV output of the $i$th node at the time $t$, and $P_{i,t}^{pv,\max }$ represents the maximum DPV output of the $i$th node at the time $t$.

(3)

Node voltage constraints:

$$\mathrm{Pr}\{U_{i,\min }^2\le U_i^2\le U_{i,\max }^2\}\ge {\alpha }_1$$

(23)

where $U_i^2$ represents the square of the voltage amplitude at the $i$th node. $U_{i,\max }^2$, $U_{i,\min }^2$ represent the square of the maximum and minimum values allowable at the $i$th node, respectively; ${\alpha }_1$ represents the confidence level at which the constraint is established.

(4)

Power flow constraints:

Figure 2 shows the operating state and power flow of a branch in a radial distribution network at time $t$. The constraints are as follows:

$$U_{j,t}^2=U_{i,t}^2-2(r_{ij}{P}_{ij,t}+x_{ij}{Q}_{ij,t})+(r_{ij}^2+x_{ij}^2)I_{ij,t}^2$$

(24)

$$p_{j,t}=P_{ij,t}-r_{ij}{I}_{ij,t}^2-{\displaystyle \sum _{j:z}{P}_{jz,t}}$$

(25)

$$q_{j,t}=Q_{ij,t}-r_{ij}{I}_{ij,t}^2-{\displaystyle \sum _{j:z}{Q}_{jz,t}}$$

(26)

$$I_{ij,t}^2={\displaystyle \frac{P_{ij,t}^2+Q_{ij,t}^2}{U_{i,t}^2}}$$

(27)

where $U_{i,t}$ and $U_{j,t}$ are the voltages at nodes $i$ and $j$, respectively. $r_{ij}$ is the resistance of branch of $ij$, and $x_{ij}$ is the reactance of branch $ij$.$p_{j,t}$ and $q_{j,t}$ are the active and reactive power injected into the node $j$, respectively. $P_{ij,t}$ and $Q_{ij,t}$ are the active and reactive power at the head end of the branch $ij$, respectively. $P_{jz,t}$ and $Q_{jz,t}$ are the active and reactive power at the head end of the branch $jz$, respectively. $I_{ij,t}$ is the branch current of the branch $ij$. $j:z$ is the set of child nodes with $j$ as the parent node.

(5)

Distribution network flexibility constraints:

Distribution networks need to have a certain regulation capability to minimize or eliminate the problems caused by the uncertainty of renewable energy output, such as peak shaving and climbing difficulties [32,33].

In this paper, two indicators are introduced: branch line capacity margin and net load power adaptation rate. The branch line capacity margin is evaluated and quantitatively constrained to avoid branch line blockage caused by large DPV output; the net load power adaptation rate reflects the degree of fluctuation of net load power in the distribution network after DPV access. The net load power adaptation rate constraints are used to respond to and regulate the upward and downward demand for distribution network flexibility at different times.

$$M_i^t={\displaystyle \frac{I_{\max ,li}-I_{li}^t}{I_{\max ,li}}}\text{×}100\%$$

(28)

$$\mathrm{Pr}\{I_{i,\min }^2\le I_i^2\le I_{i,\max }^2\}\ge {\alpha }_2$$

(29)

where $M_i^t$ is the capacity margin of branch line $i$ at the time $t$, $I_{\max ,li}$ is the maximum transmission current of branch line $i$, $I_{li}^t$ is the current of branch line $i$ at the time $t$, and ${\alpha }_2$ is the confidence level that the constraint holds.

$$F_{FSD}={\displaystyle \frac{F_{up}+F_{down}}{T}}$$

(30)

$$\left\{\begin{array}{l}{F}_{up}={\displaystyle \sum _{t=1}^T\frac{w_t{H}_U^t}{P_{t+1}^{n1}-P_t^{n1}}}\\ F_{down}={\displaystyle \sum _{t=1}^T\frac{(1-w_t)H_U^t}{P_t^{n1}-P_{t+1}^{n1}}}\end{array}\right.$$

(31)

$$F_{FSD}\ge F_{set}$$

(32)

where $F_{up}$ and $F_{down}$ correspond to the sum of the ratio of flexible resource schedulable margin to net load power variation when net load power increases or decreases in a scheduling cycle.$H_U^t$ is the amount of flexible resources that can be adjusted up or down at the time $t$. $w_t$ is the state variable for the power change in the net load power at the time $t$, which takes a value of 0 or 1. $P_t^{n1},P_{t+1}^{n1}$ are the net load power magnitudes at the time $t$ and $t+1$, respectively. $F_{set}$ is the minimum net load power adaptation rate allowed for the system.

4.3. Economic Model

For the economic indicators of DPV access in the distribution network, this paper considers the DPV generation on-grid revenue, network loss cost due to DPV access, DPV unit construction and O&M cost, energy storage construction cost, demand response cost, and PV power curtailment cost. In this paper, the economic revenue is the annual revenue of each scenario combined under the consideration of proper PV power curtailment.

$$F=B-C_1-C_2-C_3-C_4-C_{loss}^{pv}$$

(33)

where $F$ is the total economic revenue, $B$ is the DPV feed-in revenue, $C_1$ is the difference in increased or decreased power loss costs due to DPV access, $C_2$ is the DPV unit construction and O&M costs, $C_3$ is the construction cost of energy storage equipment, $C_4$ is the demand response costs, and $C_{loss}^{pv}$ is the penalty cost of PV power curtailment. Since DPV unit construction and O&M costs, power loss costs, and the penalty cost of PV power curtailment are all related to allowable abandonable unit capacity, the DPV economic revenue is a dependent variable that changes in a complex way with the change in the power-curtailment unit construction capacity.

Each of the above economic indicators is expressed as follows:

$$B=b\times 365\times {\displaystyle \sum _{s=1}^S{\displaystyle \sum _{i=1}^{24}(P_{s,t}^{pv}\times p_s)}}$$

(34)

where $b$ is the unit price of the DPV generation feed-in tariff. $P_{s,t}^{pv}$ is the DPV generation feed-in tariff at the time $t$ under scenario $s$. $p_s$ is the probability corresponding to scenario $s$ after clustering is performed.

$$C_1={\displaystyle \sum _{s=1}^S{\displaystyle \sum _{t=1}^{24}[(C_{s,t}^{sum}-C_{s,t}^{bas})}}\times p_s\times 365]$$

(35)

where $C_1$ is the cost of power loss caused by DPV access. $C_{s,t}^{bas}$ is the base power loss when the distribution network is supplied by the power system without DPV access. $C_{s,t}^{sum}$ is the total power loss after DPV access.

$$C_2=f\times c_2\times [{\displaystyle \frac{r\times {(1+r)}^n}{{(1+r)}^n-1}}+I_g]$$

(36)

where $f$ is the total installed capacity, $n$ is the DPV unit payback period, $r$ is the discount rate. $c_2$ is the unit investment cost. $I_g$ is the operation and maintenance rate of the DPV unit, which is taken as 3%.

$$C_3=c_3\times E_3\times {\displaystyle \frac{r{(1+r)}^{n_3}}{{(1+r)}^{n_3}-1}}$$

(37)

where $c_3$ is the construction cost of energy storage equipment per unit capacity, $E_3$ is the total construction capacity of energy storage, and $n_3$ is the life span of energy storage equipment.

$$C_4=({\rho }_{s,t}^h-{\rho }_{s,t}^l)\times {\displaystyle \sum _{s=1}^S{\displaystyle \sum _{t=1}^{24}(P_{s,t}^{pur}}\times p_s\times 365})$$

(38)

$$C_{loss}^{pv}=\mu \times {\displaystyle \sum _{s=1}^S{\displaystyle \sum _{t=1}^{24}(P_{s,t}^{pv}\times }}{p}_s\times 365)$$

(39)

where $P_{s,t}^{pv}$ is the amount of PV power curtailment at the time $t$ in scenario $s$, and $\mu$ is the penalty cost per unit of power curtailment.

Since then, on the basis of meeting the constraints of the safe and stable operation of the distribution network, the DPV economic access capacity and the revenue it brings can be quantitatively analyzed.

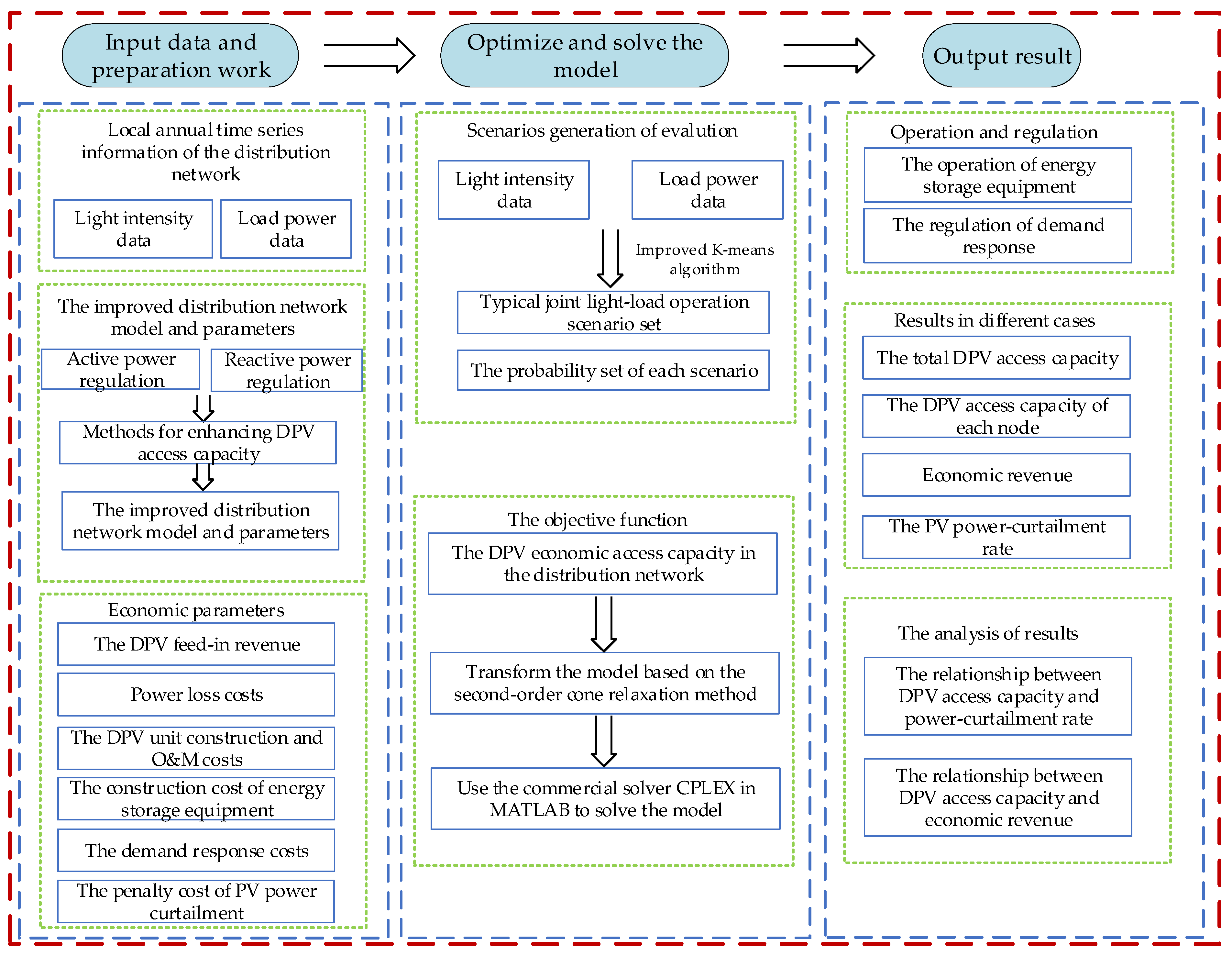
5. Solving Process of the Model

5.1. Model Solving Ideas and Process

In this paper, the light intensity and load power typical scenarios generated in Section 1 are combined to generate joint typical operating scenarios. Denote as generating $m$ load power typical scenarios, each with a probability of $M={\left[p_1,p_2,p_3\cdots p_{\mathrm{m}}\right]}^{-1}$, and those generating $n$ light intensity typical scenarios, each with a probability of $N=\left[p_1,p_2,p_3\cdots p_n\right]$. To avoid the conservative results obtained and to improve the problem of large calculation volume when analyzing 365 days of the year by the traditional method, this paper takes all joint typical scenarios into account and the probability of each joint scenario separately, which is shown as follows:

$$p_{M\times N}=M\times N=\left[\begin{array}{cccc}{p}_{11}& p_{12}& \cdots & p_{1n}\\ p_{21}& p_{22}& \cdots & p_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ p_{m1}& p_{m2}& \cdots & p_{mn}\end{array}\right]$$

(40)

With this method, the total amount of PV power curtailment is as below:

$$f_{loss}^{pv}=365\times {\displaystyle \sum _{s=1}^{m\times n}(f_{sx}\times P_s^{pv}\times p_s)}$$

(41)

$$f_{sx}=\left\{\begin{array}{l}f-f_{s,\max },\hspace{1em}f>=f_{s,\max }\\ \hspace{1em}f,\hspace{1em}\hspace{1em}\hspace{1em}f<f_{s,\max }\end{array}\right.$$

(42)

where $f_{sx}$ is the capacity of the power-curtailment unit in the $s$th joint scenario. $f_{s,\max }$ is the maximum installable unit capacity of DPV without power curtailment in the $s$th joint scenario. $P_s^{pv}$ is the amount of electricity that can be generated per unit of DPV unit in a 24 h day under the $s$th joint scenario, and $p_s$ is the probability of the sth joint scenario.

Considering the proper PV power curtailment, the total electricity generation of all the scenarios is shown in Equation (43).

$$f_{sum}^{pv}=365\times {\displaystyle \sum _{s=1}^{\mathrm{m}\times n}{\displaystyle \sum _{t=1}^{24}(f}}\times P_{s,t}^{pv}\times p_s)$$

(43)

Then, obtain the total power-curtailment rate of all the scenarios, as shown in Equation (44).

$${\eta }^{pv}={\displaystyle \frac{f_{loss}^{pv}}{f_{sum}^{pv}}}$$

(44)

In this paper, the total revenue is calculated as the revenue of each joint scenario multiplied by the probability of the respective joint scenario and then multiplied by 365 days, which is the annual total revenue. The formula is shown in Equation (45).

$$\begin{array}{c}{F}_{sum}=365\times [F_{11}\times P_{11}+F_{12}\times P_{12}+\cdots +\\ F_{m(n-1)}\times P_{m(n-1)}+F_{mn}\times P_{mn}]\end{array}$$

(45)

$$F_{sum}\ge 0$$

(46)

The equivalent total revenue $F_{sum}$ in Equation (45) should be set to be greater than 0, which means that negative revenue should not occur during the evaluation of economic access capacity. Due to the increase in $f_x$, the proportion of power-curtailment generation is increasing. When the DPV feed-in revenue is completely offset with various costs, the main cost of the penalty is for PV power curtailment. That is, when $F_{sum}=0$, the access capacity $f$ obtained at this time is the maximum economic access capacity of DPV in the distribution network.

5.2. Model Transformation Based on Second-Order Cone Relaxation

Since the power flow constraints in the established model contain quadratic as well as integer terms, it is a mixed integer nonlinear planning problem model, in which case the optimal flow is poorly solved by conventional optimization algorithms. In this paper, second-order cone relaxation is utilized to transform it into a convenient and efficient programming model.

First, the variables ${\varsigma }_{i,t}$ and ${\xi }_{ij,t}$ are introduced to represent the square of the voltage at node and the square of the current value at branch ij at the time $t$, respectively, which are shown as follows:

$${\varsigma }_{i,t}=U_{i,t}^2$$

(47)

$${\xi }_{ij,t}=I_{ij,t}^2$$

(48)

Then, constraints (24) to (27) can be transformed into Equations (49)–(53), respectively.

$${\varsigma }_{j,t}={\varsigma }_{i,t}-2(r_{ij}{P}_{ij,t}+x_{ij}{Q}_{ij,t})+(r_{ij}^2+x_{ij}^2){\xi }_{ij,t}$$

(49)

$$p_{j,t}=P_{ij,t}-r_{ij}\xi i_{j,t}-{\displaystyle \sum _{j:k}{P}_{jk,t}{\xi }_{ij,t}}$$

(50)

$$q_{j,t}=Q_{ij,t}-x_{ij}{\xi }_{ij,t}-{\displaystyle \sum _{j:k}{Q}_{jk,t}}$$

(51)

$${\xi }_{ij,t}={\displaystyle \frac{P_{ij,t}^2+Q_{ij,t}^2}{{\varsigma }_{i,t}}}$$

(52)

$$U_{i,t,\min }^2\le {\xi }_{i,t}\le U_{i,t,\max }^2$$

(53)

It can be seen that constraint (52) is still a nonlinear equality constraint, which is further treated and rewritten as a standard second-order cone form by using the second-order cone relaxation method, as shown in Equations (54) and (55).

$$\xi \ge {\displaystyle \frac{P_{ij,t}^2+Q_{ij,t}^2}{{\varsigma }_{i,t}}}$$

(54)

$${‖\begin{array}{c}2P_{ij,t}\\ 2Q_{ij,t}\\ {\xi }_{ij,t}-{\varsigma }_{i,t}\end{array}‖}_2\le {\varsigma }_{i,t}+{\xi }_{ij,t}$$

(55)

Finally, based on YALMIP Toolbox R20230622 in MATLAB 2018a, the relaxed model is solved by CPLEX solver 12.10.0.

The solution process for the model proposed in this paper is shown in Figure 3.

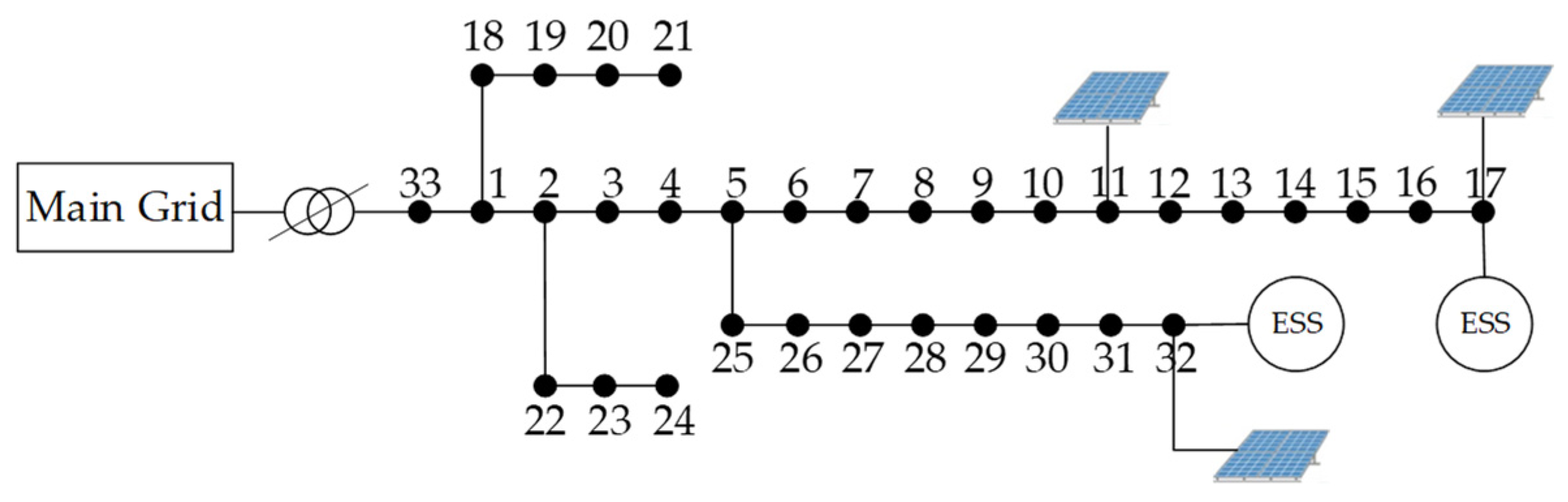
6. Example Analysis

6.1. Introduction to the Algorithmic Environment and Parameters

The example analysis in this paper is based on an improved IEEE 33-node system, as shown in Figure 4.

In this paper, the example used analyzes the DPV access of multiple nodes; compared with the DPV access of a single node, multi-node access to DPV power can avoid the single node accessing a larger number of DPV nodes caused by the difficulty of dissipation, single-node serious voltage overruns, and other problems. The distribution network node voltage range values mentioned in Section 3.1 are $U_{\min }$ = 0.94 p.u., $U_1$ = 0.96 p.u., $U_2$ = 1.04 p.u., and $U_{\max }$ = 1.06 p.u. The chance constraint confidence level is ${\alpha }_1={\alpha }_2=0.98$.

The distribution of voltage at each node is shown in Figure 5; considering that the distribution network has low voltage amplitude at the end nodes when DPV generator sets are not configured, this paper configures three DPV units, which are configured relatively at the end nodes 11, 32, and the middle node 17. The maximum installation capacity of a single node is set to 2 MW; Node 17 and 32 are equipped with energy storage devices with a capacity of 800 kW, respectively, and nodes 5, 18, and 31 are equipped with static reactive power compensation devices with a capacity of 500 kVar, respectively.

In the model of this paper, when analyzing the typical operating conditions of the distribution network for 24 h, the maximum output of the DPV in each period is equal to the DPV access capacity multiplied by the corresponding time-sequence value, and the load in each period is the basic load of this distribution network multiplied by the corresponding time-sequence value, which is a reasonable representation of the operating conditions of the distribution network in each scenario.

6.2. Example Results

6.2.1. Generation of Typical Joint Operation Scenarios for Light Intensity and Load Power

In this paper, one year’s light intensity and load power data of a place in Hebei are used as raw data for typical scenario extraction, and the light intensity is recorded every hour as a sampling point, with a total of 8760 sampling points throughout the year. The three-dimensional map of solar light intensity for the whole year is shown in Figure 6.

From Figure 6, the light intensity has obvious diurnal and seasonal differences, and the random volatility of adjacent dates is large. Such large and random data are not convenient for analyzing the maximum access capacity of DPV in the distribution network. Therefore, it is necessary to extract typical scenarios, which need to maintain the temporal order of the original initial data, but also require a good fit to the volatility and stochasticity of the DPV output.

For the analysis of loads, this paper similarly analyzes the data of 8760 h in a region of Hebei for the whole year in steps of 1 h, and its annual time series diagram is shown in Figure 7.

For load data, there are also seasonal and diurnal variations, and electricity consumption is relatively high in the summer.

The improved K-means clustering algorithm is employed to analyze the data to achieve the purpose of describing the large dataset with small samples. The silhouette coefficient is used as the clustering index, and its size ranges is [−1, 1]. The clustering effect is positively correlated with the value of $SC$. The relationship between the silhouette coefficient and the number of clusters after clustering is shown in Figure 8.

As can be seen from Figure 8, when $k=3$, the silhouette coefficient values of both light intensity data and load data are closest to 1, and the clustering effect is the best. Therefore, in this paper, the light intensity data and load data are reduced to three typical scenarios, and the timing diagrams of the power output under the typical scenarios of light intensity and load power are shown in Figure 9 and Figure 10.

Typical scenarios 1, 2, and 3 of light intensity and load power in

Table 1. Probability table for typical joint light intensity and load power scenarios.

Load Power	Light Intensity
	1 (35.89%)	2 (33.15%)	3 (30.96%)
1 (32.60%)	0.1170	0.1080	0.1009
2 (51.51%)	0.1849	0.1707	0.1595
3 (15.89%)	0.0570	0.0526	0.0492

are arranged according to light intensity and load power from largest to smallest and the probability of each typical scenario has been indicated. From the probability table, it can be seen that the joint scenario probability for the smallest load and the largest light intensity is only 0.0570, which is a relatively small percentage. Regarding the maximum construction capacity of the DPV unit obtained from this scenario, where each constraint not crossing the boundary is a criterion to characterize the maximum DPV access capacity in the distribution network, the result is unrepresentative and relatively conservative.

Therefore, this paper proposes an evaluation method of the DPV economic access capacity of distribution networks considering proper PV power curtailment. The following analyzes the DPV access capacity under the extreme scenario and all scenarios, respectively.

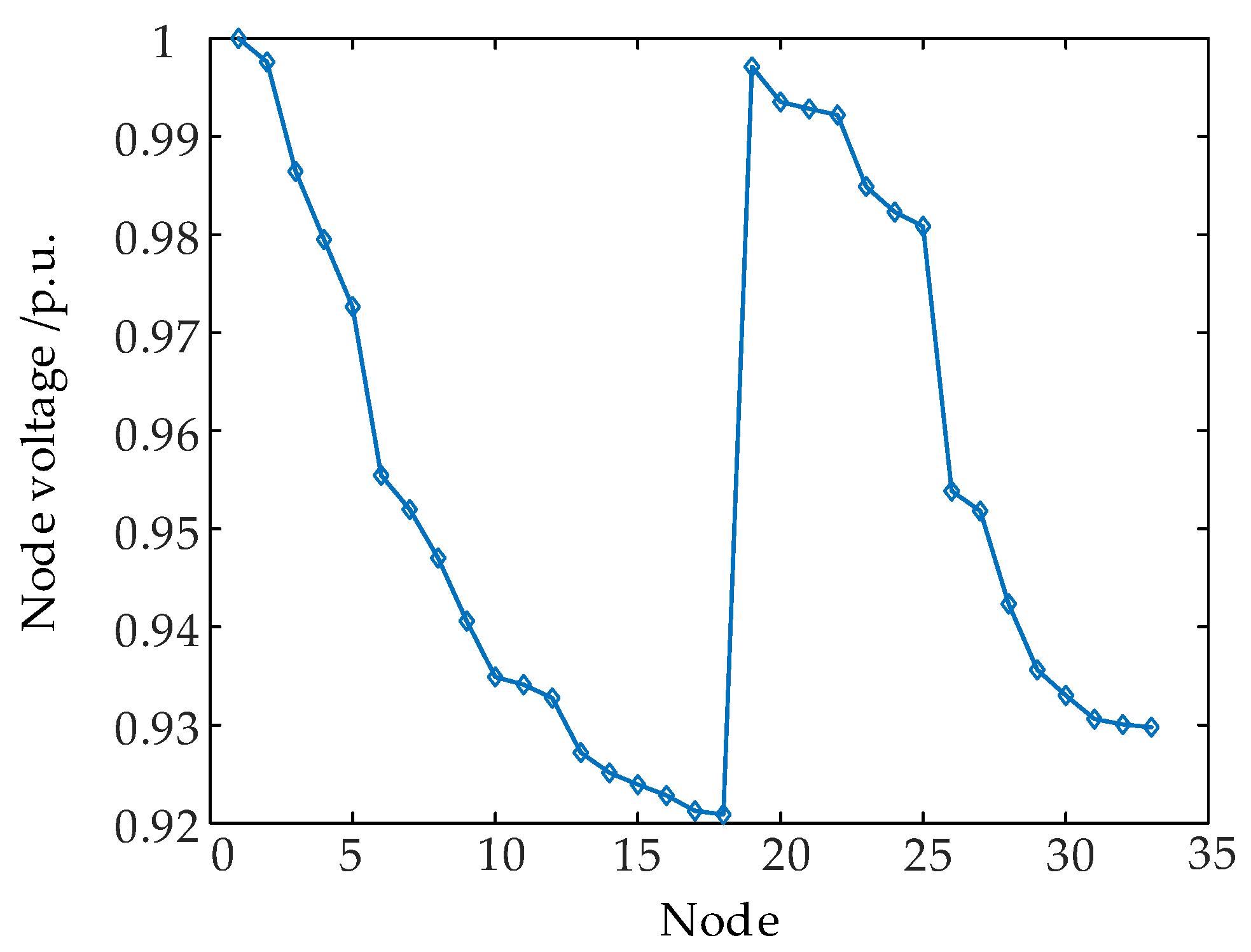
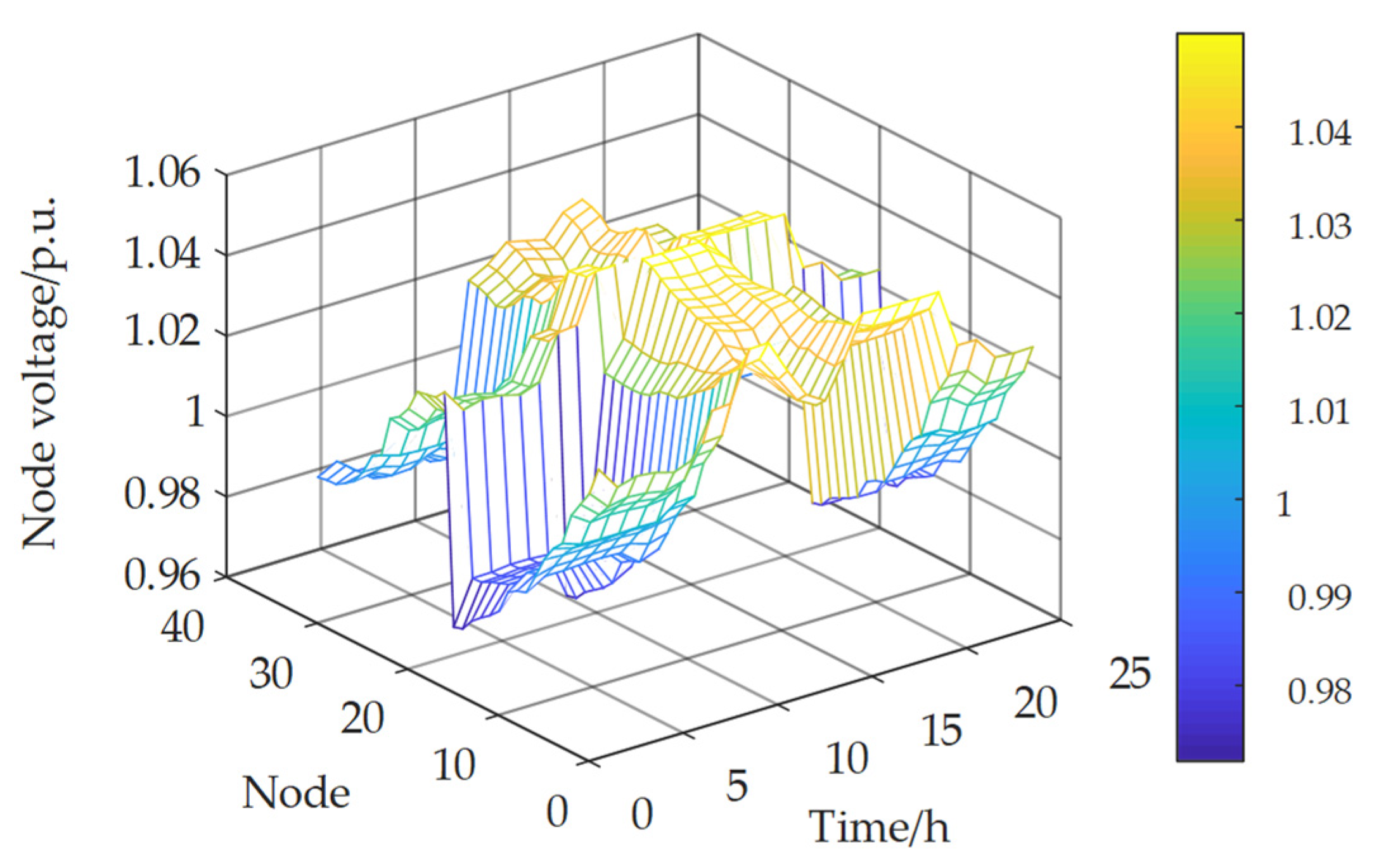
6.2.2. Analysis of the Effectiveness of the Proposed Model

To verify the effectiveness of the optimization model based on second-order cone relaxation proposed in this paper, this subsection compares and analyzes the model proposed in this paper with the model containing quadratic terms and constant terms in the same environment. In the above IEEE 33-node distribution network, the photovoltaic access points are set to nodes 11, 17, and 32. The rest of the parameters and configurations are the same as those set in Section 6.1. And the evaluation is conducted under the scenario with the maximum light intensity and the minimum load power obtained in Section 6.2.1.

Table 2. Comparison of the solution effects of two different models.

	The Optimization Model Proposed in This Paper	The Model without Relaxation
DPV access capacity/MW	2.772	2.791
Solution time/s	5.794	18.461

shows a comparison of the solution effects of two different models and shows the comparison between the proposed optimization model based on second-order cone relaxation and the unrelaxed model with quadratic and constant terms. In terms of calculation accuracy, the difference between the two models is only 0.019 MW. The calculation accuracy error is only 0.86%. And compared to the solving time of 18.461 s for the model without relaxation, the optimization model proposed in this paper can obtain the result in only 5.794 s. The solution efficiency has been greatly improved.

6.2.3. Analysis of Maximum DPV Access Capacity in Extreme Scenarios

Based on the typical scenario reduction results in Section 1 the extreme typical scenario with maximum light intensity and minimum load power is selected. The IEEE 33-node distribution network is used to evaluate the maximum DPV access capacity of distributed photovoltaics in the distribution network based on the constraint condition of not exceeding the limit. The calculation results are analyzed as follows.

As can be seen from Figure 11, since 8:00 a.m., the voltage of each node is obviously elevated, which is most obvious at the node of accessing DPV units, which is at the edge of the voltage threshold. At the time of high light intensity at noon, while the voltage at DPV access points in some scenarios is elevated, the voltage at the top end of the distribution network is relatively low. This is due to the fact that the output of the conventional electric unit is reduced to accommodate the DPV generation capacity to a greater extent, and the original power trend start point becomes the end of the trend. In the evening, though the intensity of light tends to zero, the voltage at each node is still much higher than in the morning. This is because the distribution network is equipped with energy storage devices, which release the energy stored in the stronger light intensity at noon.

Figure 12 shows the comparison between the initial load and the load after the demand response in the typical extreme operating scenario. From Figure 12, the tariff-based demand response strategy proposed in this paper changes the electricity consumption time of the original initial users. It can transfer part of the load to the time when the DPV output is large, thereby increasing the DPV access capacity in the distribution network.

According to Figure 12, it can be seen that during the period of 7–10 o’clock, the initial load power is relatively high, while the DPV output is relatively low. At this time, the load power is mainly supplied by the main power grid; during the period of 11–16 o’clock, the photovoltaic output is high, while the load power is relatively low. The DPV output is not fully utilized. Therefore, the demand response based on electricity prices is proposed in this paper to improve the utilization of DPV output from the perspective of regulating active power. From the comparison of load power curves before and after demand response, it can be seen that this method transfers some of the load power to the period with high DPV output, reducing the purchase of electricity from the main power grid and increasing the utilization of DPV output.

Figure 13 shows the operation of the configured energy storage in the extreme typical scenario. To maximize the use of DPV power, the energy storage is fully discharged before the photovoltaic output is large. When the DPV output is large and the safety constraints of the distribution network are about to exceed the limit, the energy storage absorbs active power for charging. When the DPV output is small or non-existent in the evening, the electric energy stored during the day is released and utilized, and the energy storage state of charge is maintained at a small value to make full use of the DPV output of the next day.

Figure 14 shows the capacity of DPV units accessed at each node when the PV power curtailment is 0 in this limit scenario. Nodes 11, 17, and 32 are accessed with 0.693, 0.850, and 1.229 MW, respectively, for a total capacity of 2.772 MW. This part serves as the control group for subsequent analysis, so as to clearly understand the impact of proper PV power curtailment on the DPV economic access capacity and economy.

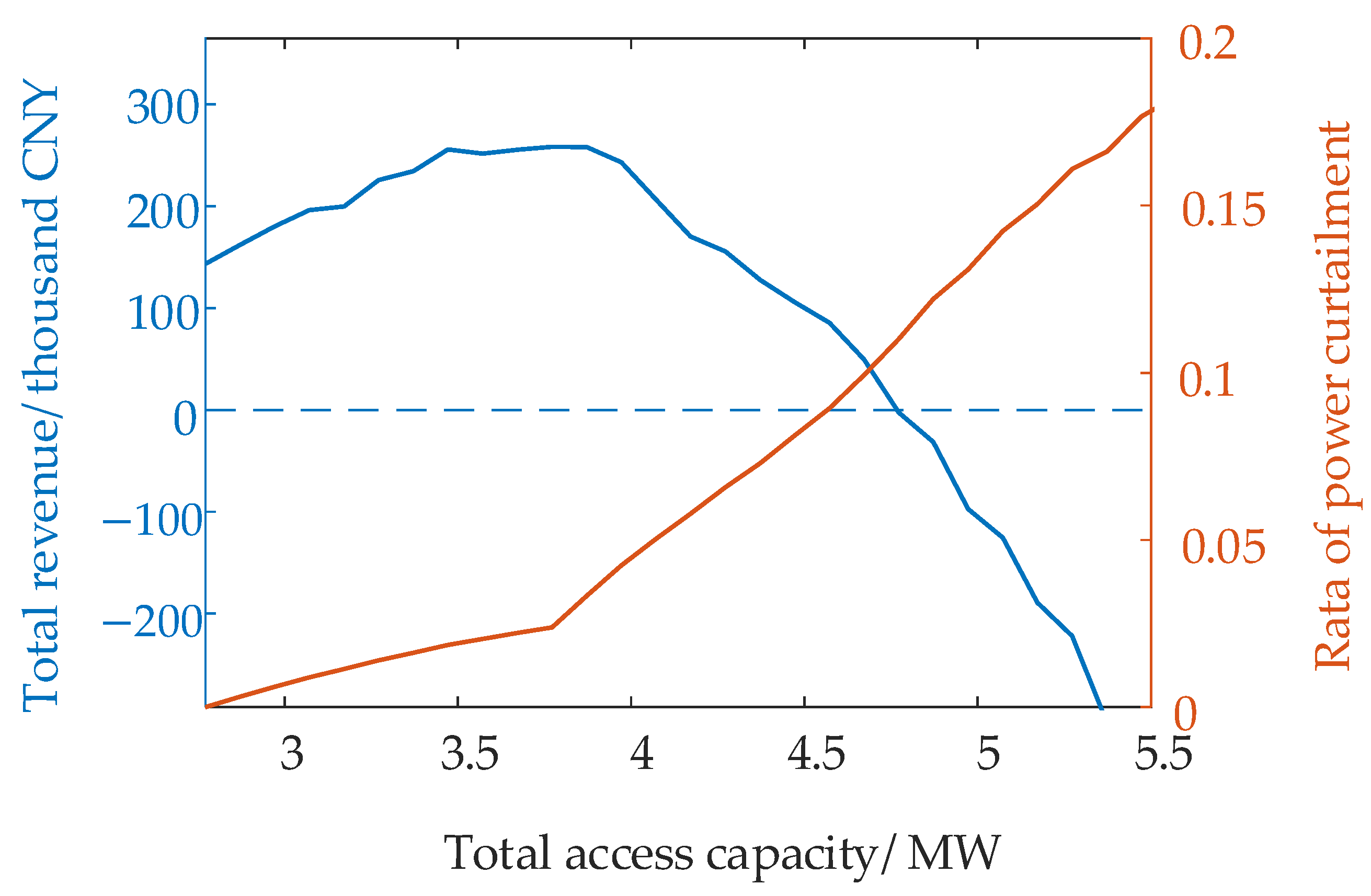
6.2.4. Analysis of DPV Economic Access Capacity Considering Proper PV Power Curtailment

Because the example in the previous subsection only considered the condition of exceeding the limit constraints under extreme weather conditions, and did not take into account PV power curtailment and economic indicators, the result obtained is relatively conservative and less representative.

Therefore, the maximum construction capacity of the DPV power-curtailment unit is introduced as the decision variable. The economic benefits brought by DPV access are considered when determining the maximum DPV access capacity in the distribution network.

Table 3. Economic parameters.

Economic Indicators	Unit Price
DPV Feed-in Tariff	0.39 CNY/kW·h
Network Loss Costs	0.5 CNY/kW·h
DPV Unit Construction Costs	3.79 CNY/W
Energy Storage Construction Costs	1.47 CNY/W·h
Penalty Costs for PV Power Curtailment	0.6 CNY/kW·h
Peak–Flat–Valley Tariff	0.8, 0.5, 0.3 CNY/kW·h

shows the economic parameters, where the service life of both the DPV unit and the energy storage equipment is 15 years.

This subsection considers the following three situations in conjunction with Section 6.2.3 and analyzes them in comparison.

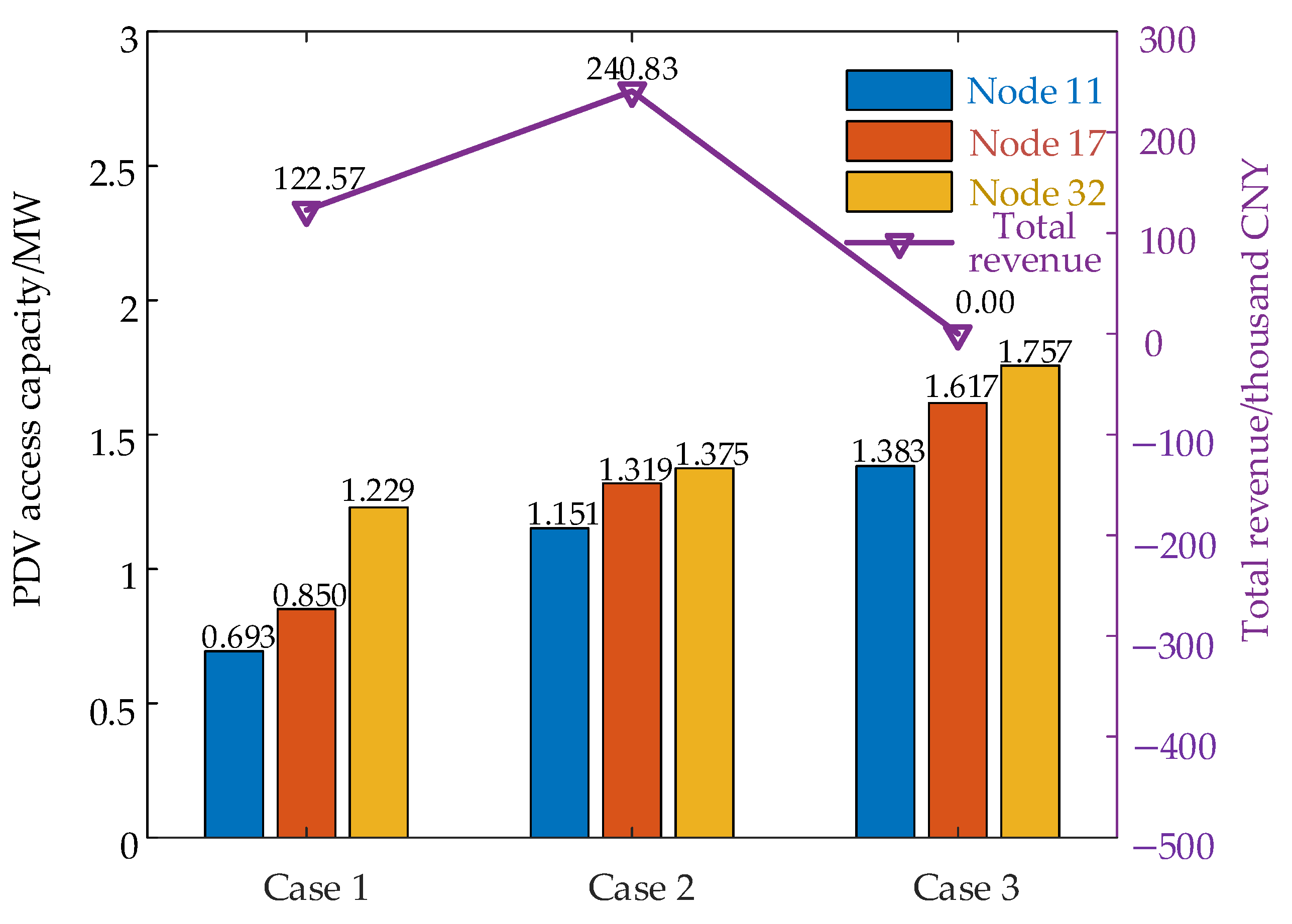
(1)

Only in the extreme operating scenario with the strongest light intensity and the smallest load power, the maximum access capacity of the DPV unit in the distribution network is determined with the criterion that each constraint is not exceeded. The result is analyzed in Section 6.2.3.

(2)

The DPV access capacity in the distribution network is obtained with the objective of maximizing the total economic revenue while considering proper PV power curtailment.

(3)

Considering proper PV power curtailment, the maximum access capacity of the DPV unit in the distribution network is obtained when the total economic revenue is non-negative. This situation focuses on finding the balance between economy and maximum DPV access capacity.

Figure 15 shows the relationship between the total amount of DPV access and total revenue, and the total amount of access and the power-curtailment rate. The starting points of the folded lines are the maximum total amount of DPV access obtained from the extreme scenarios, which is 2.772 MW, and the annual revenue is CNY 122.57 thousand. With the increase in DPV access capacity, proper PV power curtailment is carried out in some scenarios, but the on-grid power in other scenarios will increase at the same time, and the trend in the total revenue will increase first and then decrease. When the maximum point of revenue occurs, the access capacity is 3.845 MW, and at this time the total economic revenue is CNY 240.53 thousand. When DPV access capacity continues to increase, the phenomenon of PV power curtailment will be more and more significant, and the cost of PV power curtailment increases greatly. When the gains and the costs are offset, that is, the total revenue is 0, this is the critical value for the economic break-even point, and at this point the total DPV access capacity is 4.757 MW.

From Figure 15, it can also be seen that, with the increase in DPV access, the increase in the power-curtailment rate is gentler at first, and then increases more sharply. This is due to the fact that, initially, with the increase in DPV access, only some joint operation scenarios need to perform PV power curtailment properly, while other scenarios of DPV output will be fully online. However, as the total amount of DPV access continues to increase, the number of scenarios with power-curtailment will also increase, so the curve of the power-curtailment rate will be steeper in the later stage.

Table 4. Comparison results in different cases.

	Access Capacity/MW	Amount of PV Power Curtailment/MW	On-Grid Energy/MW	Rate of Power Curtailment	Total Revenue/CNY 1000
Case 1	2.772	0	3296.31	0	122.57
Case 2	3.845	183.96	4460.67	0.040	240.83
Case 3	4.757	652.07	5054.52	0.129	0

and Figure 16 show the comparison of the results for the three cases analyzed as the focus of this paper.

Through comparison, it can be seen that in Case 1, using only the criterion that each constraint does not cross the limit as a criterion for the DPV maximum access capacity calculation, the results obtained are 2.772 MW and an annual total revenue of CNY 122.57 thousand; the results are not only more conservative, but unrepresentative, and the economics needs to be improved. Scenarios 2 and 3 are evaluated for the DPV economic access capacity proposed in this paper that allows PV power curtailment. In terms of the economics, Case 2 has the largest annual gain of CNY 240.83 thousand, with an improvement in the access capacity, and the total power-curtailment rate of the whole scenario is only 0.040, resulting in an access capacity of 3.845 MW, which is a 38.7% increase in the total access capacity compared to Case 1. The DPV access capacity of Case 3 is 4.757 MW, which is 71.6% higher compared to Case 1 and 23.7% higher compared to Case 2. At this time, the power-curtailment rate is 12.9%, and the economic revenue is 0. That is, 4.757 MW is the maximum DPV access economic capacity in the distribution network when the economic revenue is non-negative.

Cases 2 and 3 are two solutions that can be obtained by the optimization model proposed in this paper. When considering the long-term planning and operation of a distribution network, Case 2 has more advantages, because it can obtain the maximum economic revenue. The result of Case 3 is a balance point between non-negative economic revenue and the maximum DPV access capacity. If the DPV access capacity continues to increase, negative revenue will occur. Case 3 can provide a certain reference for the planning and operation of the distribution network.

Compared with the evaluation of only a single extreme scenario, the results of the DPV economic access capacity evaluation considering all the scenarios proposed in this paper are more representative. Through case analysis, it can be seen that the DPV economic access capacity and economy of the distribution network are significantly improved by proper PV power curtailment. And this example verifies the effectiveness and practicality of the method proposed in this paper.

7. Conclusions

Focusing on the safe operation and economic problems caused by the large amount of DPV access to distribution networks, this paper proposes a DPV economic access capacity evaluation method of the distribution network, considering proper PV power curtailment, and obtains the following conclusions:

(1)

The selected operation scenarios are important factors affecting the scientificity and representativeness of the results, when carrying out DPV economic access capacity evaluation in the distribution network. In this paper, a method for generating typical joint light intensity and load power operation scenarios based on an improved K-means algorithm was proposed. The typical joint operation scenario set of light intensity and load power and the probability set of the scenarios were obtained by clustering and combining the historical data of annual light intensity and load power. This method comprehensively considers all the scenarios in a year, and solves the problem that the evaluation result is inaccurate and unrepresentative caused by having a single evaluation scenario.

(2)

To improve the DPV access capacity in the distribution network, this paper proposes a method to enhance the DPV access capacity in the distribution network based on active and reactive power regulation. From the perspective of active power regulation, by combining energy storage with demand response, the power consumption time on the load side is changed, so that the DPV output can be fully utilized. From the perspective of reactive power regulation, the inverter control method based on the node voltage of the distribution network can reduce the risk of the node voltage exceeding the limit, thereby improving the DPV access capacity in the distribution network.

(3)

This paper establishes a model for evaluating the DPV economic access capacity in the distribution network that considers multi-dimensional constraints and performs proper PV power curtailment. By analyzing the impact of proper PV power curtailment on the DPV economic access capacity and economy revenue, the maximum DPV economic access capacity in the distribution network and the DPV access capacity when the economy is optimal are obtained. Considering proper PV power curtailment, the DPV access capacity in Case 2 is 3.845 MW, which is 38.7% higher than that in Case 1; the economic revenue is CNY 240.83 thousand, which is 96.5% higher than that in Case 1. The maximum DPV access capacity in Case 3 is 4.757 MW, which is 71.6% higher than that in Case 1. It can be seen from the analysis that proper PV power curtailment can significantly improve the DPV economic access capacity in the distribution network.

The DPV economic access capacity evaluation method proposed in this paper can effectively evaluate the economic access capacity of DPV power in the distribution network and provides guidance for DPV configuration in the distribution network via gradually increasing the spread of DPV power.