Influence of Structural Parameters of Tesla Valve Flow Field on Performance of Fuel Cells
Abstract
1. Introduction
2. Numerical Simulation
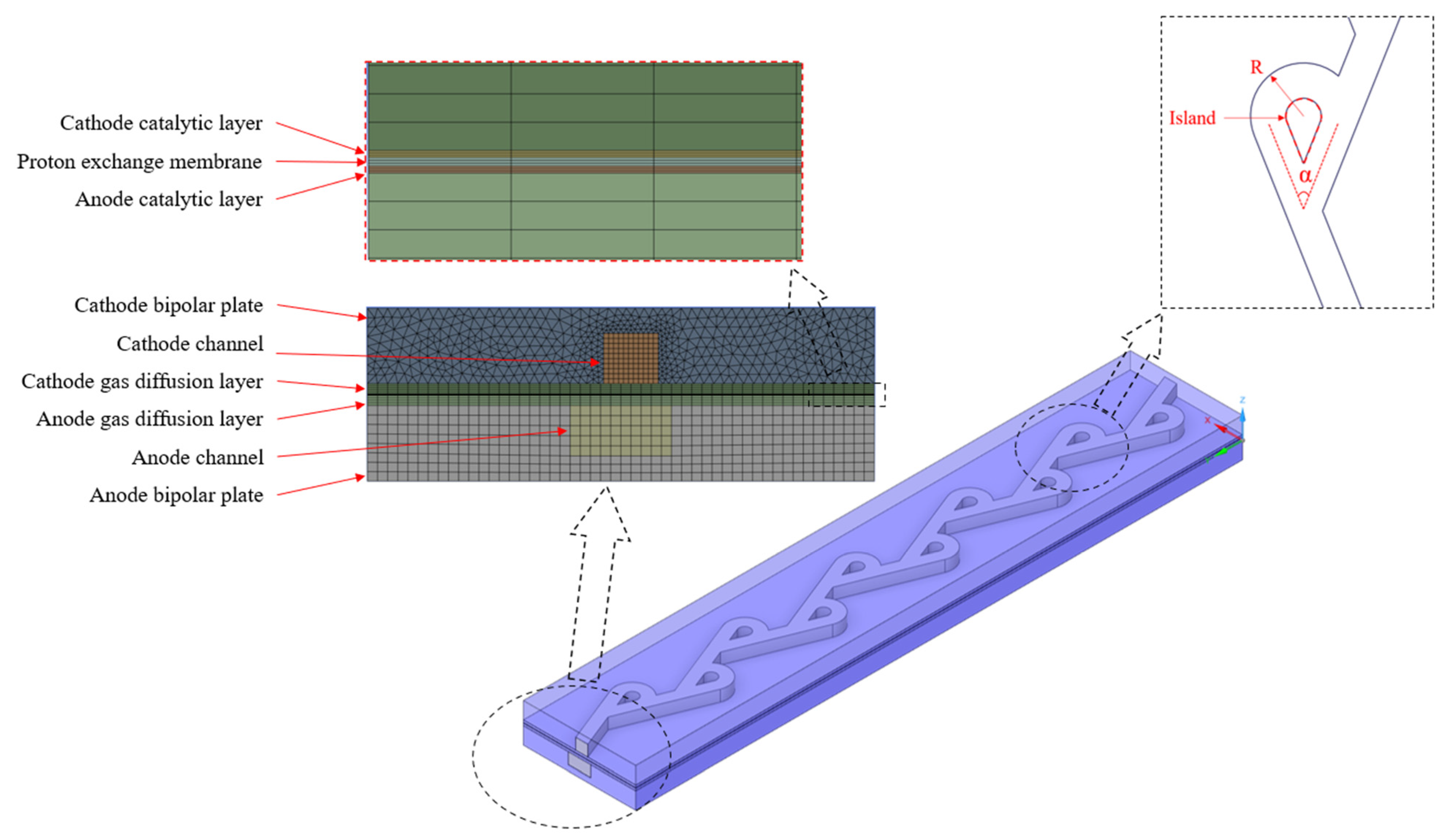
2.1. Computational Geometry and Grid
2.2. Model Assumption and Numerical Approach
- The reactant gases are assumed to be ideal gases.
- The fluid flow is assumed to be laminar.
- The effects of gravity and contact resistance are ignored.
- The Butler–Volmer equation is employed to solve the electrochemical reactions.
- The temperature in the surface boundary is set as constant.
- The materials of the GDL and CL are assumed to be homogeneous and isotropic.
2.3. Model Validation and Grid Independence Analysis
3. Results and Discussion
3.1. The Effect of Loop Inclination Angles on the PEMFC Performance
3.2. The Effect of Loop Radius on the PEMFC Performance
3.3. The Effect of Island Removal on the PEMFC Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Q.; Lan, F.; Zeng, C.; Chen, J.; Wang, J. A review of proton exchange membrane fuel cell’s bipolar plate design and fabrication process. J. Power Sources 2022, 538, 231543. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, B. Investigation of optimization and evaluation criteria for flow field in proton exchange membrane fuel cell: A critical review. Renew. Sustain. Energy Rev. 2023, 185, 113584. [Google Scholar] [CrossRef]
- Li, Y.; Chen, H.; Lu, C.; Zhou, H.; Liu, Z.; Chen, B. Multi-objective optimization design of a planar membrane humidifier based on NSGA-II and entropy weight TOPSIS. J. Therm. Anal. Calorim. 2023, 148, 7147–7161. [Google Scholar] [CrossRef]
- Chandan, A.; Hattenberger, M.; El-Kharouf, A.; Du, S.; Dhir, A.; Self, V.; Bujalski, W. High temperature (HT) polymer electrolyte membrane fuel cells (PEMFC)–A review. J. Power Sources 2013, 231, 264–278. [Google Scholar] [CrossRef]
- Yang, Z.; Jiao, K.; Wu, K.; Shi, W.; Jiang, S.; Zhang, L. Numerical investigations of assisted heating cold start strategies for proton exchange membrane fuel cell systems. Energy 2021, 222, 119910. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, X.; Yang, J.; Zhu, X.; Tai, S.; Shuai, S. Effect of liquid water in flow channel on proton exchange membrane fuel cell: Focusing on flow pattern. Energy Convers. Manag. 2022, 258, 115528. [Google Scholar] [CrossRef]
- Min, C.; He, J.; Wang, K.; Xie, L.; Yang, X. A comprehensive analysis of secondary flow effects on the performance of PEMFCs with modified serpentine flow fields. Energy Convers. Manag. 2019, 180, 1217–1224. [Google Scholar] [CrossRef]
- Liu, H.; Li, P.; Van Lew, J. CFD study on flow distribution uniformity in fuel distributors having multiple structural bifurcations of flow channels. Int. J. Hydrogen Energy 2010, 35, 9186–9198. [Google Scholar] [CrossRef]
- Singdeo, D.; Dey, T.; Gaikwad, S.; Andreasen, S.J.; Ghosh, P.C. A new modified-serpentine flow field for application in high temperature polymer electrolyte fuel cell. Appl. Energy 2017, 195, 13–22. [Google Scholar] [CrossRef]
- Liu, Z.; Zeng, X.; Ge, Y.; Shen, J.; Liu, W. Multi-objective optimization of operating conditions and channel structure for a proton exchange membrane fuel cell. Int. J. Heat Mass Transf. 2017, 111, 289–298. [Google Scholar] [CrossRef]
- Wang, X.D.; Duan, Y.Y.; Yan, W.M.; Lee, D.J.; Su, A.; Chi, P.H. Channel aspect ratio effect for serpentine proton exchange membrane fuel cell: Role of sub-rib convection. J. Power Sources 2009, 193, 684–690. [Google Scholar] [CrossRef]
- Xia, Z.; Chen, H.; Zhang, T.; Pei, P. Effect of channel-rib width ratio and relative humidity on performance of a single serpentine PEMFC based on electrochemical impedance spectroscopy. Int. J. Hydrogen Energy 2022, 47, 13076–13086. [Google Scholar] [CrossRef]
- Lim, B.H.; Majlan, E.H.; Daud, W.R.W.; Rosli, M.I.; Husaini, T. Numerical analysis of modified parallel flow field designs for fuel cells. Int. J. Hydrogen Energy 2017, 42, 9210–9218. [Google Scholar] [CrossRef]
- Manso, A.P.; Marzo, F.F.; Barranco, J.; Garikano, X.; Mujika, M.G. Influence of geometric parameters of the flow fields on the performance of a PEM fuel cell. A review. Int. J. Hydrogen Energy 2012, 37, 15256–15287. [Google Scholar] [CrossRef]
- Yu, Z.; Xia, L.; Xu, G.; Wang, C.; Wang, D. Improvement of the three-dimensional fine-mesh flow field of proton exchange membrane fuel cell (PEMFC) using CFD modeling, artificial neural network and genetic algorithm. Int. J. Hydrogen Energy 2022, 47, 35038–35054. [Google Scholar] [CrossRef]
- Han, S.H.; Choi, N.H.; Choi, Y.D. Simulation and experimental analysis on the performance of PEM fuel cell by the wave-like surface design at the cathode channel. Int. J. Hydrogen Energy 2014, 39, 2628–2638. [Google Scholar] [CrossRef]
- Mojica, F.; Rahman, M.A.; Sarker, M.; Hussey, D.S.; Jacobson, D.L.; LaManna, J.M.; Chuang, P.Y.A. Study of converging-diverging channel induced convective mass transport in a proton exchange membrane fuel cell. Energy Convers. Manag. 2021, 237, 114095. [Google Scholar] [CrossRef]
- Yoshida, T.; Kojima, K. Toyota MIRAI fuel cell vehicle and progress toward a future hydrogen society. Electrochem. Soc. Interface 2015, 24, 45. [Google Scholar] [CrossRef]
- Shen, J.; Tu, Z.; Chan, S.H. Performance enhancement in a proton exchange membrane fuel cell with a novel 3D flow field. Appl. Therm. Eng. 2020, 164, 114464. [Google Scholar] [CrossRef]
- Wu, H.W.; Shih, G.J.; Chen, Y.B. Effect of operational parameters on transport and performance of a PEM fuel cell with the best protrusive gas diffusion layer arrangement. Appl. Energy 2018, 220, 47–58. [Google Scholar] [CrossRef]
- Wang, B.; Chen, W.; Pan, F.; Wu, S.; Zhang, G.; Park, J.W.; Xie, B.; Yin, Y.; Jiao, K. A dot matrix and sloping baffle cathode flow field of proton exchange membrane fuel cell. J. Power Sources 2019, 434, 226741. [Google Scholar] [CrossRef]
- Heidary, H.; Kermani, M.J.; Prasad, A.K.; Advani, S.G.; Dabir, B. Numerical modelling of in-line and staggered blockages in parallel flowfield channels of PEM fuel cells. Int. J. Hydrogen Energy 2017, 42, 2265–2277. [Google Scholar] [CrossRef]
- Chen, H.; Guo, H.; Ye, F.; Ma, C.F. A numerical study of orientated-type flow channels with porous-blocked baffles of proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2021, 46, 29443–29458. [Google Scholar] [CrossRef]
- Li, H.W.; Liu, J.N.; Yang, Y.; Fan, W.; Lu, G.L. Research on mass transport characteristics and net power performance under different flow channel streamlined imitated water-drop block arrangements for proton exchange membrane fuel cell. Energy 2022, 251, 123983. [Google Scholar] [CrossRef]
- Roshandel, R.; Arbabi, F.; Moghaddam, G.K. Simulation of an innovative flow-field design based on a bio inspired pattern for PEM fuel cells. Renew. Energy 2012, 41, 86–95. [Google Scholar] [CrossRef]
- Liu, S.; Chen, T.; Xie, Y.; Zhang, J.; Wu, C. Numerical simulation and experimental study on the effect of symmetric and asymmetric bionic flow channels on PEMFC performance under gravity. Int. J. Hydrogen Energy 2019, 44, 29618–29630. [Google Scholar] [CrossRef]
- Kang, H.C.; Jum, K.M.; Sohn, Y.J. Performance of unit PEM fuel cells with a leaf-vein-simulating flow field-patterned bipolar plate. Int. J. Hydrogen Energy 2019, 44, 24036–24042. [Google Scholar] [CrossRef]
- Guo, N.; Leu, M.C.; Koylu, U.O. Bio-inspired flow field designs for polymer electrolyte membrane fuel cells. Int. J. Hydrogen Energy 2014, 39, 21185–21195. [Google Scholar] [CrossRef]
- Bethapudi, V.S.; Hack, J.; Trogadas, P.; Cho, J.I.S.; Rasha, L.; Hinds, G.; Coppens, M.O. A lung-inspired printed circuit board polymer electrolyte fuel cell. Energy Convers. Manag. 2019, 202, 112198. [Google Scholar] [CrossRef]
- Li, N.; Wang, W.; Xu, R.; Zhang, J.; Xu, H. Design of a novel nautilus bionic flow field for proton exchange membrane fuel cell by analyzing performance. Int. J. Heat Mass Transf. 2023, 200, 123517. [Google Scholar] [CrossRef]
- Monika, K.; Chakraborty, C.; Roy, S.; Sujith, R.; Datta, S.P. A numerical analysis on multi-stage Tesla valve based cold plate for cooling of pouch type Li-ion batteries. Int. J. Heat Mass Transf. 2021, 177, 121560. [Google Scholar] [CrossRef]
- Qian, J.Y.; Chen, M.R.; Gao, Z.X.; Jin, Z.J. Mach number and energy loss analysis inside multi-stage Tesla valves for hydrogen decompression. Energy 2019, 179, 647–654. [Google Scholar] [CrossRef]
- Thompson, S.M.; Paudel, B.J.; Jamal, T.; Walters, D.K. Numerical investigation of multistaged tesla valves. J. Fluid Eng. 2014, 136, 081102. [Google Scholar] [CrossRef]
- Bao, Y.; Wang, H. Numerical study on flow and heat transfer characteristics of a novel Tesla valve with improved evaluation method. Int. J. Heat Mass Transf. 2022, 187, 122540. [Google Scholar] [CrossRef]
- Gong, F.; Yang, X.; Zhang, X.; Mao, Z.; Gao, W.; Wang, C. The study of Tesla valve flow field on the net power of proton exchange membrane fuel cell. Appl. Energy 2023, 329, 120276. [Google Scholar] [CrossRef]
- Guo, H.; Tian, S.; Wang, L.; Xiao, C.; Yang, S. Numerical study of Tesla valve flow field on proton exchange membrane fuel cell performance. Int. J. Hydrogen Energy 2024, 50 Pt C, 1573–1583. [Google Scholar] [CrossRef]
- Li, W.; Yang, S.; Chen, Y.; Li, C.; Wang, Z. Tesla valves and capillary structures-activated thermal regulator. Nat. Commun. 2023, 14, 3996. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Shao, W.Q.; Sun, Y.; Sun, B.H. Scaling law of the one-direction flow characteristics of symmetric Tesla valve. Eng. Appl. Comput. Fluid Mech. 2022, 16, 441–452. [Google Scholar] [CrossRef]
- Kulikovsky, A.A.; Divisek, J.; Kornyshev, A.A. Modeling the cathode compartment of polymer electrolyte fuel cells: Dead and active reaction zones. J. Electrochem. Soc. 1999, 146, 3981. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer Electrolyte Fuel Cell Model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- Mazumder, S.; Cole, J.V. Rigorous 3-D mathematical modeling of PEM fuel cells: II. model predictions with liquid water transport. J. Electrochem. Soc. 2003, 150, A1510. [Google Scholar] [CrossRef]
- Um, S.; Wang, C.Y.; Chen, K.S. Computational fluid dynamics modeling of proton exchange membrane fuel cells. J. Electrochem. Soc. 2000, 147, 4485. [Google Scholar] [CrossRef]
- Ramin, F.; Sadeghifar, H.; Torkavannejad, A. Flow field plates with trap-shape channels to enhance power density of polymer electrolyte membrane fuel cells. Int. J. Heat Mass Transf. 2019, 129, 1151–1160. [Google Scholar] [CrossRef]
- Baz, F.B.; Ookawara, S.; Ahmed, M. Enhancing under-rib mass transport in proton exchange membrane fuel cells using new serpentine flow field designs. Int. J. Hydrogen Energy 2019, 44, 30644–30662. [Google Scholar] [CrossRef]
- Islam, M.N.; Mansoor Basha, A.B.; Kollath, V.O.; Soleymani, A.P.; Jankovic, J.; Karan, K. Designing fuel cell catalyst support for superior catalytic activity and low mass-transport resistance. Nat. Commun. 2022, 13, 6157. [Google Scholar] [CrossRef] [PubMed]










| Parameters | Values | Units |
|---|---|---|
| Length and width of model | 54 × 10 | mm |
| Height of anode and cathode BPs | 1.5 | mm |
| Depth of anode and cathode channels | 1 | mm |
| Thickness of anode and cathode GDLs | 0.2 | mm |
| Thickness of anode and cathode CLs | 0.01 | mm |
| Thickness of membrane | 0.012 | mm |
| Serial Number | Angle of Inclination α (deg) | Radius of Loop (mm) | Channel Area with Island (mm2) | Channel Area without Island (mm2) | The Ratio of Area Increase (%) |
|---|---|---|---|---|---|
| T1 | 77.32 | 1.5 | 111.14 | 119.88 | 7.86 |
| T2 | 61.93 | 1.5 | 105.94 | 115.75 | 9.26 |
| T3 | 43.6 | 1.5 | 104.62 | 114.44 | 9.39 |
| T4 | 77.32 | 2 | 137.93 | 172.94 | 25.38 |
| T5 | 77.32 | 2.5 | 164 | 243.52 | 48.49 |
| Name | Values | Units |
|---|---|---|
| Faraday constant | 96,487 | C/mol |
| Reference current density of anode/cathode | 10,000/10 | A/m2 |
| Reference concentration of anode/cathode | 0.5/0.1 | kmol/m3 |
| GDL porosity | 0.8 | - |
| CL porosity | 0.4 | - |
| Absolute permeability of GDL | 3 × 10−12 | m2 |
| Absolute permeability of CL | 2 × 10−13 | m2 |
| Contact angle of GDL | 110 | deg |
| Contact angle of CL | 95 | deg |
| Equivalent weight | 1100 | Kg/mol |
| Operation temperature | 353 | K |
| Operation pressure | 10,1325 | Pa |
| Open-circuit voltage | 0.95 | V |
| Mass flow rate of anode/cathode inlet | 6 × 10−7/5 × 10−6 | kg/s |
| Relative humidity of anode/cathode | 10%/80% | - |
| Stoichiometric ratio of anode/cathode | 2/2 | - |
| Electrical conductivity of GDL/CL | 5000 | S/m |
| Electrical conductivity of BP | 20,000 | S/m |
| PEM/ Liquid density | 1980/982 | kg/m3 |
| Surface/volume ratio | 200,000 | 1/m |
| Leverett function coefficients (a/b/c) | 1.417/2.12/1.263 | - |
| Element Number | Voltage (V) | Relative Deviation | |
|---|---|---|---|
| Mesh 1 | 285,120 | 0.5601 | 0.34% |
| Mesh 2 | 499,500 | 0.5598 | 0.28% |
| Mesh 3 | 2,754,000 | 0.5582 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Tian, S.; Wang, L.; Xiao, C.; Pan, Y.; Xie, W.; Yang, S. Influence of Structural Parameters of Tesla Valve Flow Field on Performance of Fuel Cells. Energies 2024, 17, 4442. https://doi.org/10.3390/en17174442
Guo H, Tian S, Wang L, Xiao C, Pan Y, Xie W, Yang S. Influence of Structural Parameters of Tesla Valve Flow Field on Performance of Fuel Cells. Energies. 2024; 17(17):4442. https://doi.org/10.3390/en17174442
Chicago/Turabian StyleGuo, Hui, Shaopeng Tian, Long Wang, Congda Xiao, Yuxin Pan, Wenlong Xie, and Shujin Yang. 2024. "Influence of Structural Parameters of Tesla Valve Flow Field on Performance of Fuel Cells" Energies 17, no. 17: 4442. https://doi.org/10.3390/en17174442
APA StyleGuo, H., Tian, S., Wang, L., Xiao, C., Pan, Y., Xie, W., & Yang, S. (2024). Influence of Structural Parameters of Tesla Valve Flow Field on Performance of Fuel Cells. Energies, 17(17), 4442. https://doi.org/10.3390/en17174442






