Energy Hub Model for the Massive Adoption of Hydrogen in Power Systems
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Contribution
- (1)
- A versatile framework based on multi-carrier energy hubs for simulation and optimization of design and operation. In detail, many components can be compared and assessed;
- (2)
- A detailed economic analysis for both design and operation;
- (3)
- A multi-objective approach aimed at balancing the minimization of costs, the grid interactions, primary energy use, and the impact on the greenhouse effect;
- (4)
- The consideration of the uncertainty on the most unpredictable input data (energy production from RES and final energy demands) is introduced in both case studies.
- Section 2. Materials and Methods, with the description of the energy hub model developed for this study and the main assumptions, showing the coordinated optimization of a multi-carrier energy system including hydrogen, power, and heating final demands. The data collection phase is also described;
- Section 3. Results, illustrating the results of the study for the reference case and for the stochastic scenarios;
- Section 4. Discussion and conclusions, recapping the main aspect of this paper and giving some insights for further deepen the topic.
2. Materials and Methods
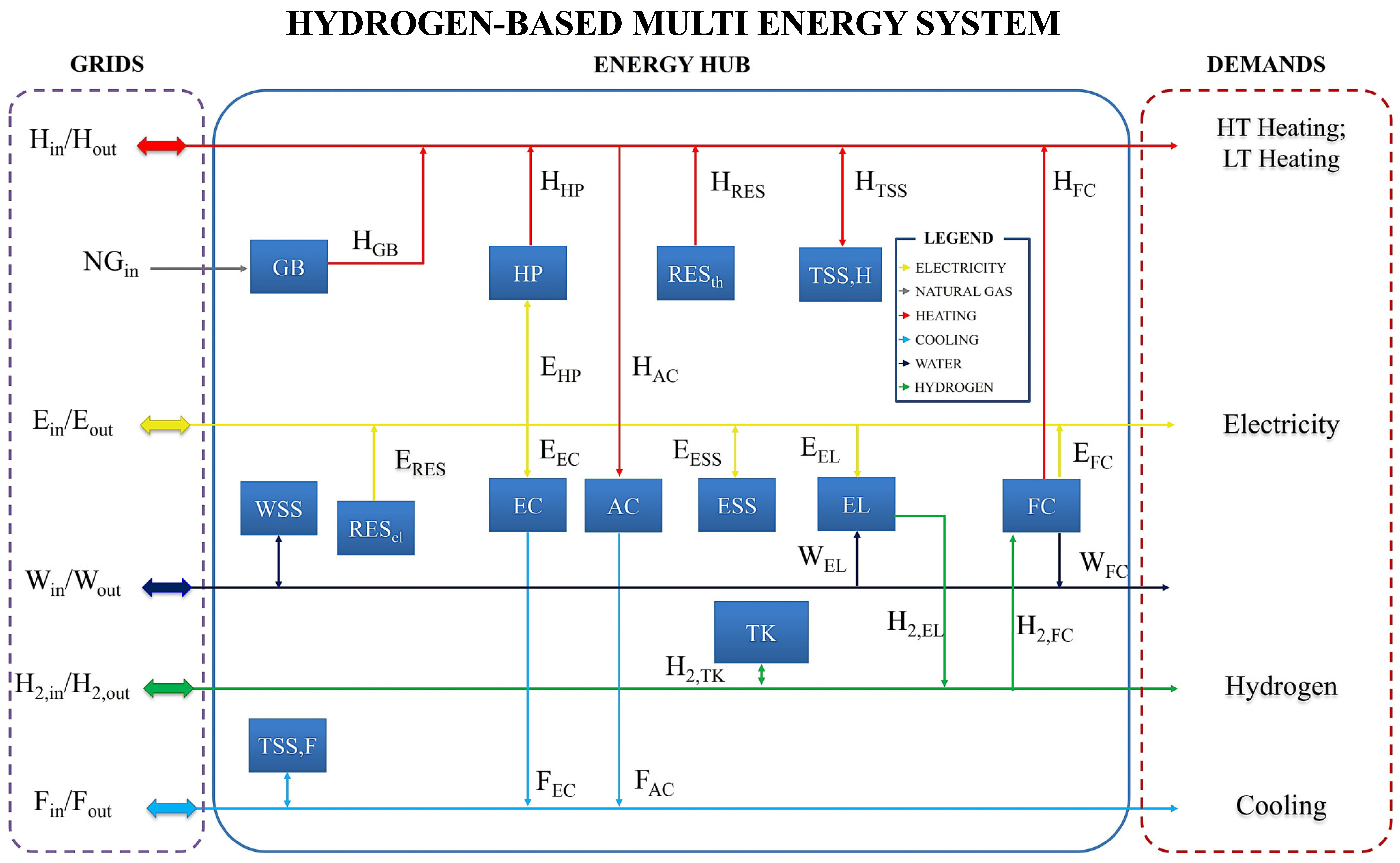
2.1. Energy Hub
- Increased efficiency through optimal interaction of various energy vectors and conversion units. For example, an electrical system with massive non-predictable renewable energy penetration might use the excess energy to charge electricity storage devices such as electric vehicles or to produce hydrogen;
- Increased security of supply through high availability of multiple power sources. MES are designed in such a way that each load does not depend on a single energy source or technology and can be met by the cheapest and most available energy carrier;
- Increased flexibility through greater degree of freedom in powering loads. An apparently polluting or expensive energy source might be substituted with a cleaner energy source.
- The hub operation is analyzed in several timesteps in steady-state conditions, when all transients or fluctuating conditions have damped out and all quantities remain essentially constant in each timestep;
- Within the EH, losses are considered only in converters and storages, although it is possible to include line gas/electricity lines losses;
- Unidirectional flows from the inputs to the outputs of the converters are usually assumed;
- Power flow through converter devices is univocally identified using the power and energy quantities, using constant efficiency terms to consider energy transformations and losses.
2.2. Objective Functions
2.3. Final Demands
2.4. Constraints
2.4.1. Constraints Describing Energy and Mass Balance Equations
− H2,dem,fl (t) = H2,dem,fix (t)
− WWSS,in (t) + WWSS,out (t) − Wdem,fl (t) = Wdem,fix (t)
− EEL (t) − Edem,fl (t) = Edem,fix (t)
+ HTSS,out (t) + EHP (t) · KHP,eh − FAC (t)/KAC,hf − Hdem,fl (t) = Hdem,fix (t)
= Fdem,fix (t)
2.4.2. Renewable Energy Sources
- -
- Photovoltaic Systems (PV)
- -
- Solar Thermal Collector (STC)
- -
- Concentrating Solar Power (CSP)
2.4.3. Energy Conversion Components
- -
- Gas-fired Boiler (GB)
- -
- Reversible Heat Pump (HP)
- -
- Absorption Chiller (AC)
- -
- Electrolyzer (EL)
- -
- Fuel Cell (FC)
2.4.4. Storage Systems
- -
- Electricity Storage System (ESS)
− EESS,out (t + 1)/KESS,out
- -
- Thermal Energy Storage System (TSS)
- -
- Hydrogen storage tank (TK)
2.5. Case Study Description and Data Collection

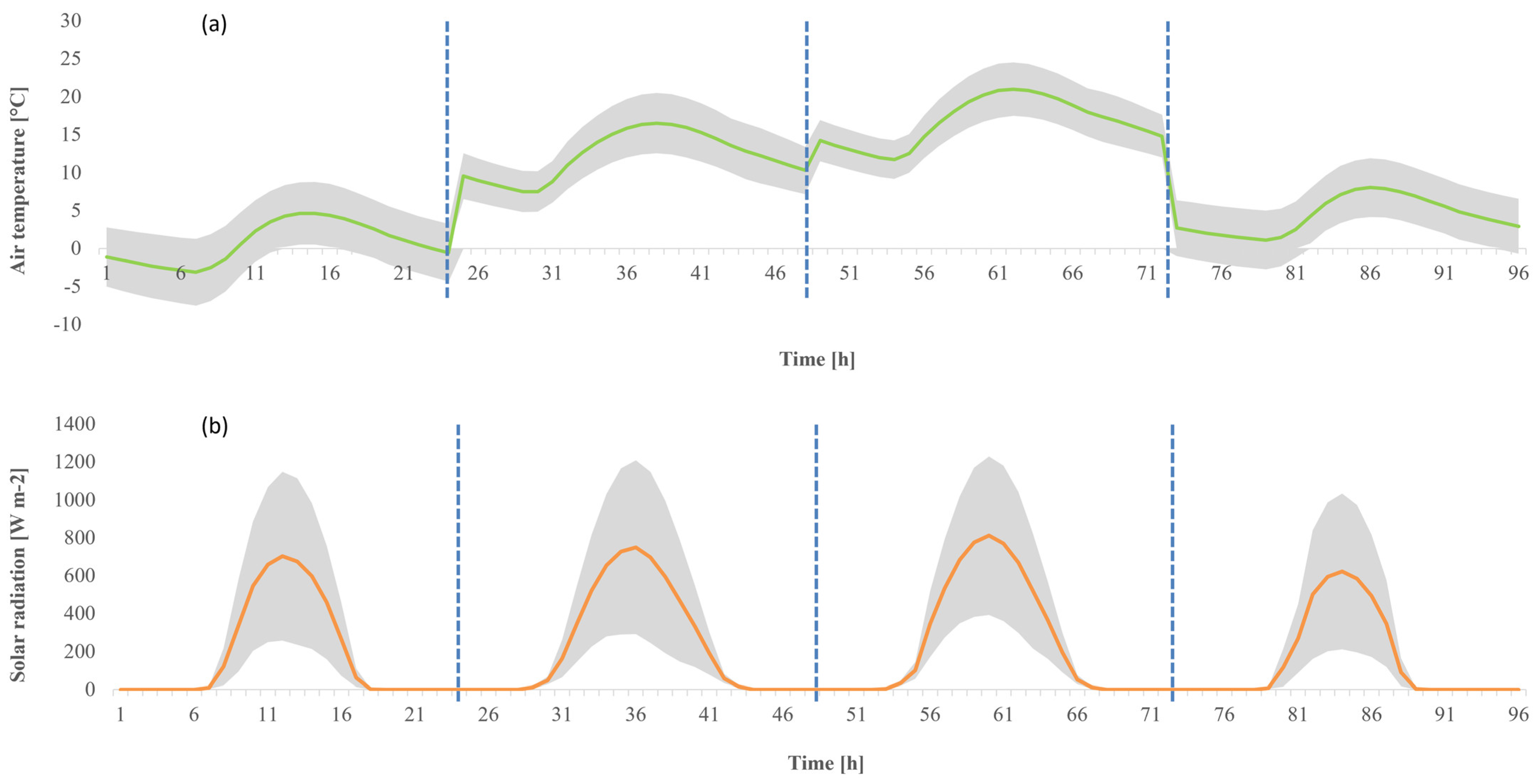
3. Results
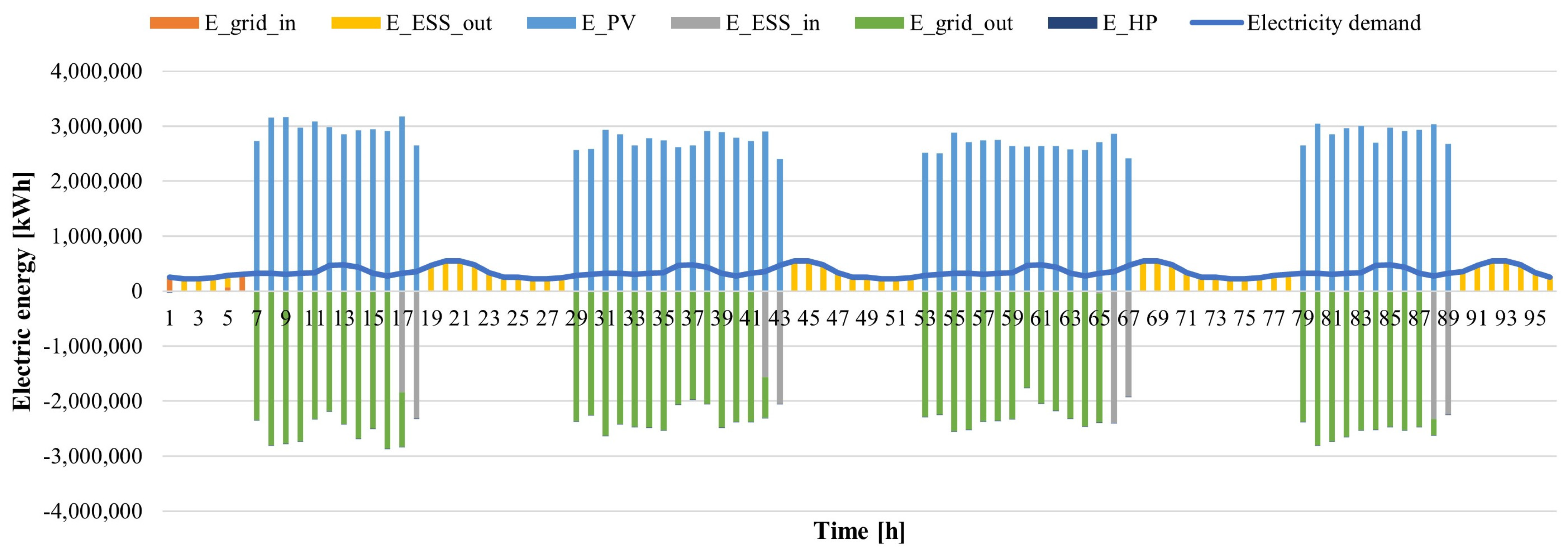
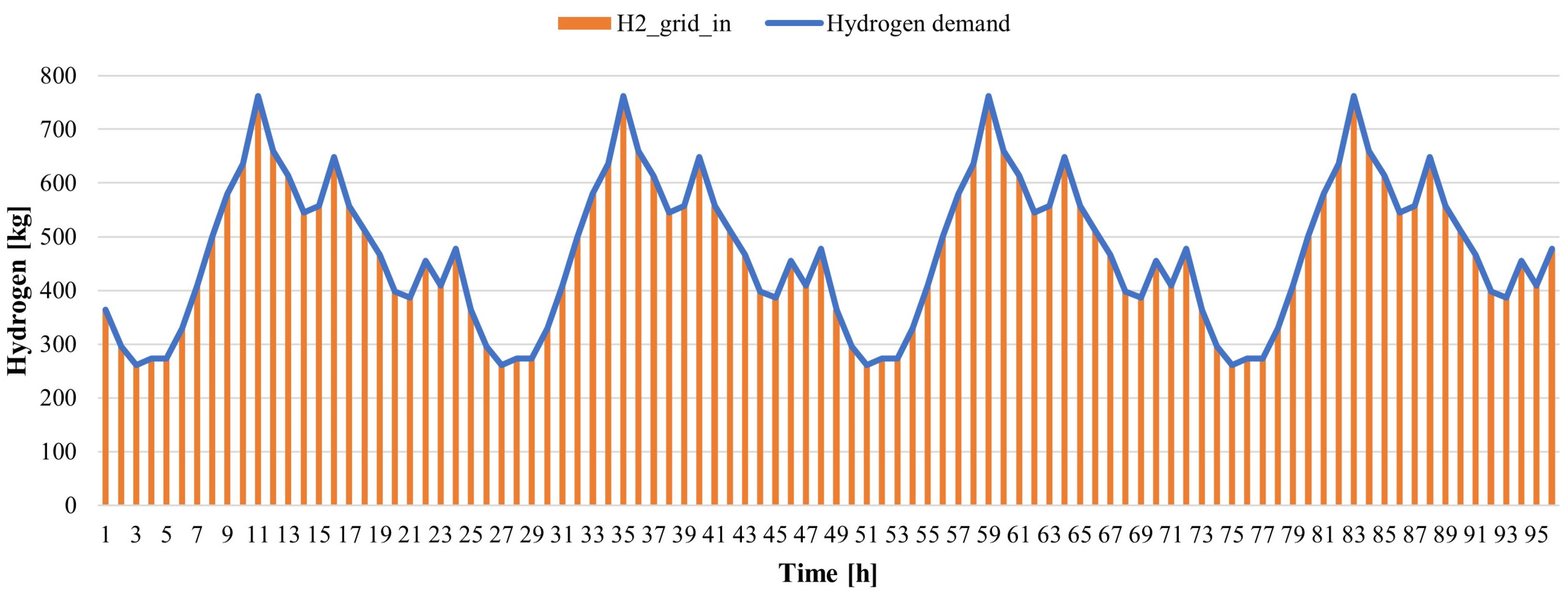
3.1. Results for the Reference Case
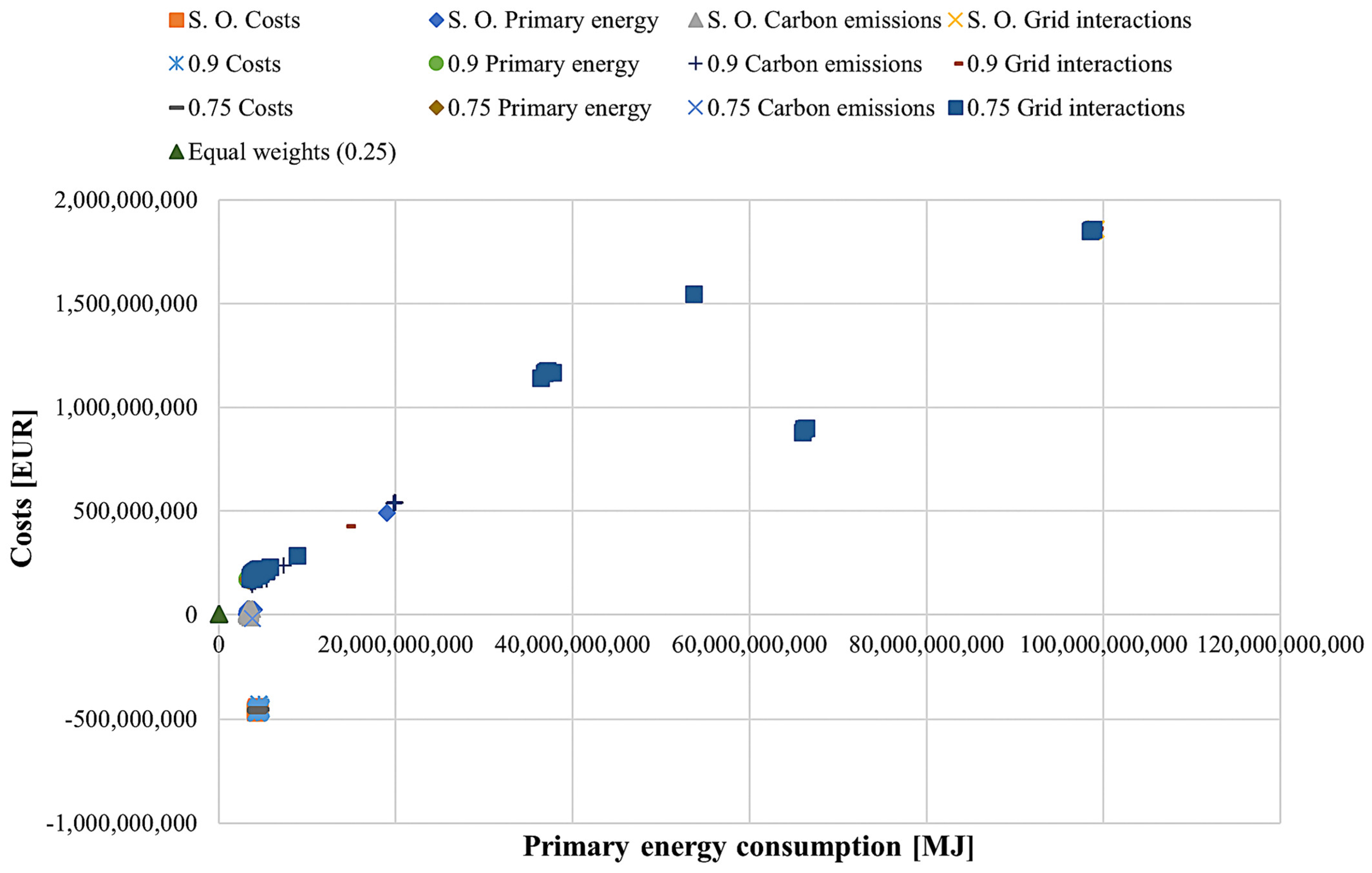
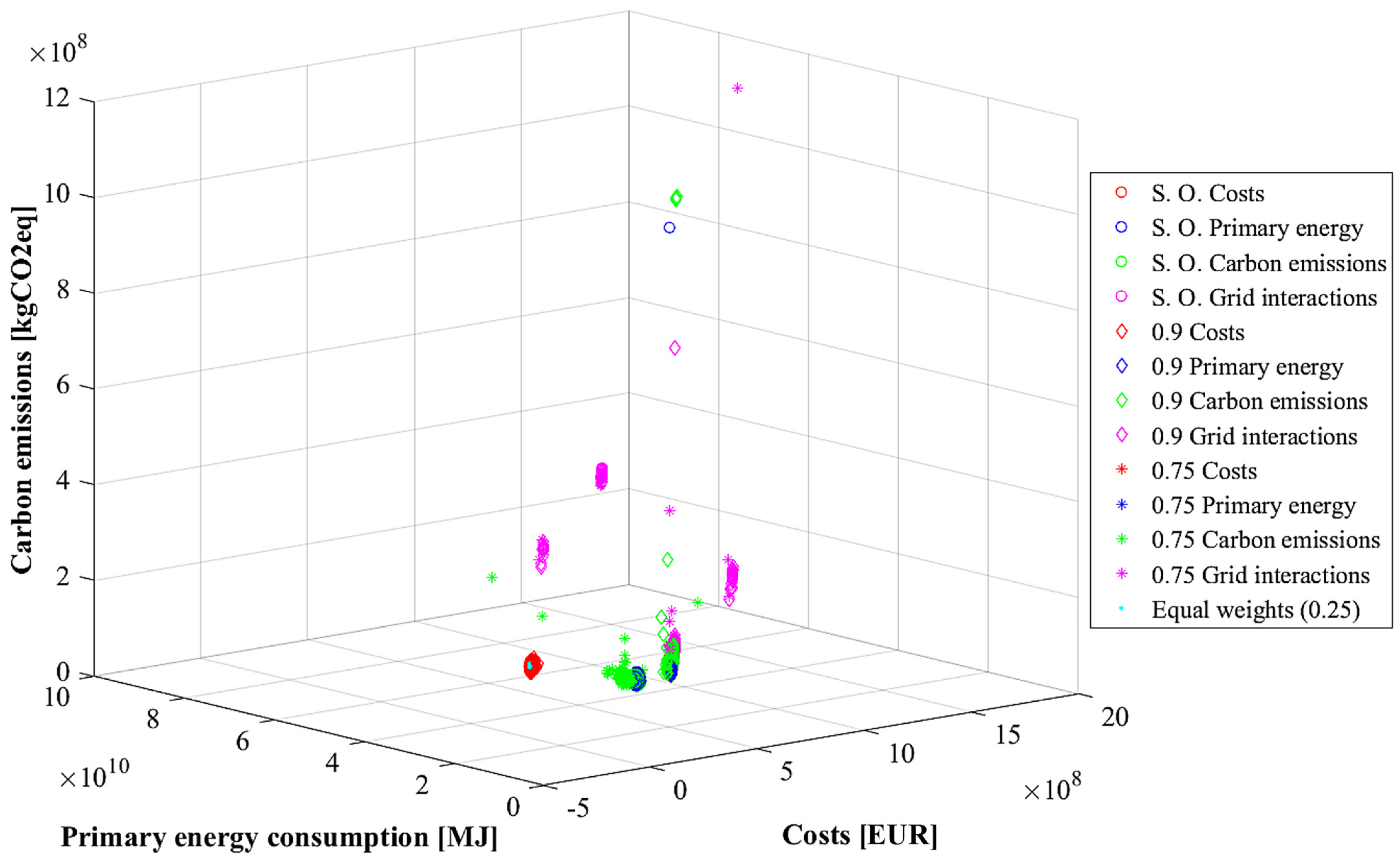
3.2. Uncertainty Assessment
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IEA. Global Hydrogen Review 2022; IEA: Paris, France, 2022. [Google Scholar]
- Thapa, B.S.; Neupane, B.; Yang, H.S.; Lee, Y.H. Green Hydrogen Potentials from Surplus Hydro Energy in Nepal. Int. J. Hydrogen Energy 2021, 46, 22256–22267. [Google Scholar] [CrossRef]
- Holden, N.; Costa, D.; Guimarães Da Silva, M.; Maniscalco, M.P.; Longo, S.; Cellura, M.; Miccichè, G.; Ferraro, M. Critical Review of Life Cycle Assessment of Hydrogen Production Pathways. Environments 2024, 11, 108. [Google Scholar] [CrossRef]
- Ajanovic, A.; Sayer, M.; Haas, R. The Economics and the Environmental Benignity of Different Colors of Hydrogen. Int. J. Hydrogen Energy 2022, 47, 24136–24154. [Google Scholar] [CrossRef]
- Howarth, R.W.; Jacobson, M.Z. How Green Is Blue Hydrogen? Energy Sci. Eng. 2021, 9, 1676–1687. [Google Scholar] [CrossRef]
- Palmer, G.; Roberts, A.; Hoadley, A.; Dargaville, R.; Honnery, D. Life-Cycle Greenhouse Gas Emissions and Net Energy Assessment of Large-Scale Hydrogen Production via Electrolysis and Solar PV. Energy Environ. Sci. 2021, 14, 5113–5131. [Google Scholar] [CrossRef]
- Di Carlo, S.; Genna, A.; Massaro, F.; Montana, F.; Riva Sanseverino, E. Optimizing Renewable Power Management in Transmission Congestion. An Energy Hub Model Using Hydrogen Storage. In Proceedings of the 21st IEEE International Conference on Environment and Electrical Engineering and 2021 5th IEEE Industrial and Commercial Power System Europe, EEEIC/I and CPS Europe 2021—Proceedings, Bari, Italy, 7–10 September 2021. [Google Scholar] [CrossRef]
- Esquivel-Elizondo, S.; Hormaza Mejia, A.; Sun, T.; Shrestha, E.; Hamburg, S.P.; Ocko, I.B. Wide Range in Estimates of Hydrogen Emissions from Infrastructure. Front. Energy Res. 2023, 11, 1207208. [Google Scholar] [CrossRef]
- 2050 Long-Term Strategy—European Commission. Available online: https://climate.ec.europa.eu/eu-action/climate-strategies-targets/2050-long-term-strategy_en (accessed on 14 March 2024).
- Snam. The Hydrogen Challenge. The Potential of Hydrogen in Italy; Snam: Milan, Italy, 2019; pp. 1–13. [Google Scholar]
- Massaro, F.; Ferraro, M.; Montana, F.; Riva Sanseverino, E.; Ruffino, S. Techno-Economic Analysis of Clean Hydrogen Production Plants in Sicily: Comparison of Distributed and Centralized Production. Energies 2024, 17, 3239. [Google Scholar] [CrossRef]
- Terna; Snam. Documento Di Descrizione Degli Scenari 2022; Terna: Rome, Italy, 2022; pp. 1–87. [Google Scholar]
- European Commission. Commission Staff Working Document—Implementing The Repower EU Action Plan: Investment Needs, Hydrogen Accelerator And Achieving The Bio-Methane Targets; European Commission: Brussels, Belgium, 2022. [Google Scholar]
- Hydrogen City. Available online: https://www.ghi-corp.com/projects/hydrogen-city (accessed on 1 April 2024).
- Crainz, M.; Curto, D.; Franzitta, V.; Longo, S.; Montana, F.; Musca, R.; Sanseverino, E.R.; Telaretti, E. Flexibility Services to Minimize the Electricity Production from Fossil Fuels. A Case Study in a Mediterranean Small Island. Energies 2019, 12, 3492. [Google Scholar] [CrossRef]
- He, C.; Liu, T.; Wu, L.; Shahidehpour, M. Robust Coordination of Interdependent Electricity and Natural Gas Systems in Day-Ahead Scheduling for Facilitating Volatile Renewable Generations via Power-to-Gas Technology. J. Mod. Power Syst. Clean Energy 2017, 5, 375–388. [Google Scholar] [CrossRef]
- Zeng, Q.; Fang, J.; Li, J.; Chen, Z. Steady-State Analysis of the Integrated Natural Gas and Electric Power System with Bi-Directional Energy Conversion. Appl. Energy 2016, 184, 1483–1492. [Google Scholar] [CrossRef]
- Bai, L.; Li, F.; Cui, H.; Jiang, T.; Sun, H.; Zhu, J. Interval Optimization Based Operating Strategy for Gas-Electricity Integrated Energy Systems Considering Demand Response and Wind Uncertainty. Appl. Energy 2016, 167, 270–279. [Google Scholar] [CrossRef]
- Hang, L.; Yuqiang, W.; Yifan, Z.; Ming, Z.; Rulei, H.; Junfei, H. Using Hydrogen Energy Storage System to Improve Wind Power Consumption and Low Voltage Ride through Capability. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference: Energy Transition for Carbon Neutrality, iSPEC 2021, Nanjing, China, 23–25 December 2021; pp. 274–280. [Google Scholar] [CrossRef]
- Dadkhah, A.; Van Eetvelde, G.; Vandevelde, L. Optimal Investment and Flexible Operation of Power-to-Hydrogen Systems Increasing Wind Power Utilisation. In Proceedings of the 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe, EEEIC/I and CPS Europe 2022, Prague, Czech Republic, 28 June–1 July 2022. [Google Scholar] [CrossRef]
- Sun, W.; Harrison, G.P. Active Load Management of Hydrogen Refuelling Stations for Increasing the Grid Integration of Renewable Generation. IEEE Access 2021, 9, 101681–101694. [Google Scholar] [CrossRef]
- Ahmed, N.; Weber, H. Frequency Regulation by the Distributed Hydrogen Storage Power Plant (HSPP); IET: London, UK, 2022; pp. 497–502. [Google Scholar] [CrossRef]
- Wang, F.; Yang, H.; Yu, H.; Li, C.; Ren, W. Coordinated Optimization Model of the Wind Power Plant with Hydrogen Storage System and Demand Response. In Proceedings of the 5th IEEE Conference on Energy Internet and Energy System Integration: Energy Internet for Carbon Neutrality, EI2 2021, Taiyuan, China, 22–24 October 2021; pp. 1948–1954. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, H.; Wang, S.; Ge, B.; Li, J.; Liu, S.; Gao, R.; Su, X. Fast Power Flow Calculation Method for Electricity Hydrogen Storage Integrated Energy Network. In Proceedings of the 5th IEEE Conference on Energy Internet and Energy System Integration: Energy Internet for Carbon Neutrality, EI2 2021, Taiyuan, China, 22–24 October 2021; pp. 1783–1788. [Google Scholar] [CrossRef]
- Sun, H.; He, C.; Yu, X.; Wu, M.; Ling, Y. Optimal Siting and Sizing of Hydrogen Refueling Stations Considering Distributed Hydrogen Production and Cost Reduction for Regional Consumers. Int. J. Energy Res. 2019, 43, 4184–4200. [Google Scholar] [CrossRef]
- Coveri, M.; Di Silvestre, M.L.; Ferraro, M.; Massaro, F.; Montana, F.; Sanseverino, E.R.; Ruffino, S. Economic Optimization of the Hydrogen Demand in a Hard-to-Abate Industrial Sector. In Proceedings of the 2023 Asia Meeting on Environment and Electrical Engineering (EEE-AM), Hanoi, Vietnam, 13 November 2023; pp. 1–6. [Google Scholar]
- Mokaramian, E.; Shayeghi, H.; Sedaghati, F.; Safari, A.; Alhelou, H.H. A CVaR-Robust-Based Multi-Objective Optimization Model for Energy Hub Considering Uncertainty and E-Fuel Energy Storage in Energy and Reserve Markets. IEEE Access 2021, 9, 109447–109464. [Google Scholar] [CrossRef]
- Heris, M.N.; Mirzaei, M.A.; Asadi, S.; Mohammadi-Ivatloo, B.; Zare, K.; Jebelli, H.; Marzband, M. Evaluation of Hydrogen Storage Technology in Risk-Constrained Stochastic Scheduling of Multi-Carrier Energy Systems Considering Power, Gas and Heating Network Constraints. Int. J. Hydrogen Energy 2020, 45, 30129–30141. [Google Scholar] [CrossRef]
- Kholardi, F.; Assili, M.; Lasemi, M.A.; Hajizadeh, A. Optimal Management of Energy Hub with Considering Hydrogen Network. In Proceedings of the 2018 International Conference on Smart Energy Systems and Technologies, SEST 2018—Proceedings, Seville, Spain, 10–12 September 2018; pp. 5–10. [Google Scholar] [CrossRef]
- Zhang, W.; Han, D.; Sun, W.; Li, H.; Tan, Y.; Yan, Z.; Dong, X. Optimal Operation of Wind-Solar-Hydrogen Storage System Based on Energy Hub. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017. [Google Scholar]
- Geng, S.; Vrakopoulou, M.; Hiskens, I.A. Optimal Capacity Design and Operation of Energy Hub Systems. Proc. IEEE 2020, 108, 1475–1495. [Google Scholar] [CrossRef]
- Nasir, M.; Rezaee Jordehi, A.; Tostado-Véliz, M.; Mansouri, S.A.; Sanseverino, E.R.; Marzband, M. Two-Stage Stochastic-Based Scheduling of Multi-Energy Microgrids with Electric and Hydrogen Vehicles Charging Stations, Considering Transactions through Pool Market and Bilateral Contracts. Int. J. Hydrogen Energy 2023, 48, 23459–23497. [Google Scholar] [CrossRef]
- Mansour-Saatloo, A.; Agabalaye-Rahvar, M.; Mirzaei, M.A.; Mohammadi-Ivatloo, B.; Abapour, M.; Zare, K. Robust Scheduling of Hydrogen Based Smart Micro Energy Hub with Integrated Demand Response. J. Clean. Prod. 2020, 267, 122041. [Google Scholar] [CrossRef]
- Daneshvar, M.; Mohammadi-Ivatloo, B.; Zare, K. An Innovative Transactive Energy Architecture for Community Microgrids in Modern Multi-Carrier Energy Networks: A Chicago Case Study. Sci. Rep. 2023, 13, 1529. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Chen, Y.; Li, Z.; Jiang, T.; Li, X. Two-Stage Robust Operation of Electricity-Gas-Heat Integrated Multi-Energy Microgrids Considering Heterogeneous Uncertainties. Appl. Energy 2024, 371, 123690. [Google Scholar] [CrossRef]
- Jiang, Y.; Ren, Z.; Li, W. Committed Carbon Emission Operation Region for Integrated Energy Systems: Concepts and Analyses. IEEE Trans. Sustain. Energy 2024, 15, 1194–1209. [Google Scholar] [CrossRef]
- Geidl, M.; Andersson, G. Optimal Power Flow of Multiple Energy Carriers. IEEE Trans. Power Syst. 2007, 22, 145–155. [Google Scholar] [CrossRef]
- Genna, A.; Di Carlo, S.; Massaro, F.; Montana, F.; Riva Sanseverino, E. Optimizing the Generation System in a Microgrid with Power, Thermal Energy and Mobility Demands. In Proceedings of the 21st IEEE International Conference on Environment and Electrical Engineering and 2021 5th IEEE Industrial and Commercial Power System Europe, EEEIC/I and CPS Europe 2021—Proceedings, Bari, Italy, 7–10 September 2021. [Google Scholar] [CrossRef]
- Tebibel, H. Methodology for Multi-Objective Optimization of Wind Turbine/Battery/Electrolyzer System for Decentralized Clean Hydrogen Production Using an Adapted Power Management Strategy for Low Wind Speed Conditions. Energy Convers. Manag. 2021, 238, 114125. [Google Scholar] [CrossRef]
- Huo, D.; Gu, C.; Yang, G.; Blond, S. Le Combined Domestic Demand Response and Energy Hub Optimisation with Renewable Generation Uncertainty. Energy Procedia 2017, 142, 1985–1990. [Google Scholar] [CrossRef]
- Favre-Perrod, P.; Geidl, M.; Koeppel, G.; Klöckl, B.; Andersson, G.; Fröhlich, K. The energy hub—A powerful concept for future energy systems. In Proceedings of the Third Annual Carnegie Mellon Conference on the Electricity Industry, Pittsburgh, PA, USA, 13–14 March 2007. [Google Scholar]
- Geidl, M. Integrated Modeling and Optimization of Multi-Carrier Energy Systems; ETH Library: Zurich, Switzerland, 2007. [Google Scholar] [CrossRef]
- MATLAB Webpage—Intlinprog Algoritm. Available online: https://www.mathworks.com/help/optim/ug/intlinprog.html (accessed on 9 August 2024).
- Short, W.; Packey, D.J.; Holt, T. A Manual for the Economic Evaluation of Energy Efficiency and Renewable Energy Technologies; NREL: Golden, Colorado, 1995.
- Cannata, N.; Cellura, M.; Longo, S.; Montana, F.; Riva Sanseverino, E.; Luu, Q.L.L.; Nguyen, N.Q. Multi-Objective Optimization of Urban Microgrid Energy Supply According to Economic and Environmental Criteria. In Proceedings of the 2019 IEEE Milan PowerTech, PowerTech 2019, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar]
- Burachik, R.S.; Kaya, C.Y.; Rizvi, M.M. A New Scalarization Technique and New Algorithms to Generate Pareto Fronts. SIAM J. Optim. 2017, 27, 1010–1034. [Google Scholar] [CrossRef]
- Zubo, R.H.A.; Mokryani, G.; Abd-Alhameed, R. Optimal Operation of Distribution Networks with High Penetration of Wind and Solar Power within a Joint Active and Reactive Distribution Market Environment. Appl. Energy 2018, 220, 713–722. [Google Scholar] [CrossRef]
- Faraji, J.; Hashemi-Dezaki, H.; Ketabi, A. Optimal Probabilistic Scenario-Based Operation and Scheduling of Prosumer Microgrids Considering Uncertainties of Renewable Energy Sources. Energy Sci. Eng. 2020, 8, 3942–3960. [Google Scholar] [CrossRef]
- Di Somma, M.; Buonanno, A.; Caliano, M.; Jin, L.; Rossi, M.; Graditi, G.; Comodi, G. Stochastic Energy Management for the Italian UNIVPM Campus as a Multi-Carrier Energy Hub Participating in the Day-Ahead Market. In Proceedings of the IEEE EUROCON 2023—20th International Conference on Smart Technologies, Torino, Italy, 6 July 2023; pp. 251–256. [Google Scholar]
- Ju, L.; Tan, Z.; Yuan, J.; Tan, Q.; Li, H.; Dong, F. A Bi-Level Stochastic Scheduling Optimization Model for a Virtual Power Plant Connected to a Wind–Photovoltaic–Energy Storage System Considering the Uncertainty and Demand Response. Appl. Energy 2016, 171, 184–199. [Google Scholar] [CrossRef]
- EN 15316-4-3:2017; Energy performance of buildings—Method for calculation of system energy requirements and system efficiencies—Part 4-3: Heat generation systems, thermal solar and photovoltaic systems, Module M3-8-3, M8-8-3, M11-8-3. European Committee for Standardization: Brussels, Belgium, 2017.
- Masterplan Idrogeno. Euregio Tirolo-Alto Adige-Trentino Corridoio Dell’idrogeno Lungo l’asse Del Brennero; Tyrol–South Tyrol–Trentino Euroregion: Bolzano, Italy, 2021. [Google Scholar]
- Terna. Annuario Statistico CONSUMI; Terna: Rome, Italy, 2020. [Google Scholar]
- GSE (Gestore dei Servizi Energetici). Nota Teleriscaldamento e Teleraffrescamento 2020; GSE: Rome, Italy, 2022. [Google Scholar]
- UNI 10349-3:2016; Riscaldamento e Raffrescamento Degli Edifici—Dati Climatici—Parte 3: Differenze Di Temperatura Cumulate (Gradi Giorno) Ed Altri Indici. UNI: Milan, Italy, 2016.
- European Union Joint Research Centre (JRC) European Reference Life Cycle Database (ELCD). Available online: https://nexus.openlca.org/database/ELCD (accessed on 28 April 2020).
- ARERA Prezzi Dell’energia Elettrica per Usi Industriali Nel 2021 (al Netto e al Lordo Delle Imposte)—Da 2.000 a 20.000 MWh Annui. Available online: https://www.arera.it/fileadmin/allegati/dati/ra21/eepcfr2.xlsx (accessed on 7 April 2024).
- ARERA Prezzi Finali Del Gas Naturale per i Consumatori Industriali Nel 2021—Utenti Con Consumi Da 260-2.600 Migliaia Di Metri Cubi Annui. Available online: https://www.arera.it/fileadmin/allegati/dati/gas/gpcfr2.xlsx (accessed on 7 April 2024).
- Enel X Web Page. Available online: https://www.enelxstore.com/it/it/prodotti/ (accessed on 7 April 2024).
- Biancardi, A. The Cost of Capital in the Energy and Water Sectors in Italy; ARERA: Milan, Italy, 2016. [Google Scholar]
- Beccali, M.; Cellura, M.; Longo, S.; Nocke, B.; Finocchiaro, P. LCA of a Solar Heating and Cooling System Equipped with a Small Water—Ammonia Absorption Chiller. Solar Energy 2012, 86, 1491–1503. [Google Scholar] [CrossRef]
- Mcmanus, M.C. Environmental Consequences of the Use of Batteries in Low Carbon Systems: The Impact of Battery Production. Appl. Energy 2012, 93, 288–295. [Google Scholar] [CrossRef]
- Mavromatidis, G.; Orehounig, K.; Carmeliet, J. Design of Distributed Energy Systems under Uncertainty: A Two-Stage Stochastic Programming Approach. Appl. Energy 2018, 222, 932–950. [Google Scholar] [CrossRef]




| Ref. | Optimization | Objective Function/Main Target | Hydrogen | Renewable Energies | Flexibility/Ancillary Services/Demand Response | Phases | Sensitivity or Uncertainty Assessment | Multi-Carrier (>2 Carriers) | Mathematical Model |
|---|---|---|---|---|---|---|---|---|---|
| [19] | No | Wind curtailment (costs) | Yes | Yes | No | Operation | No | No | Nonlinear |
| [7] | Yes | Wind curtailment (costs) | Yes | Yes | No | Operation | No | No | Linear |
| [20] | Yes | Costs | Yes | Yes | No | Design and operation | Yes (Sensitivity) | No | Linear |
| [21] | No | Costs | Yes | Yes | Yes | Operation | No | No | Linear |
| [22] | No | Grid interactions | Yes | Yes | Yes | Operation | No | No | Nonlinear |
| [23] | Yes | Costs | Yes | Yes | Yes | Operation | No | No | MILP |
| [24] | No | Power flow | Yes | Yes | No | Operation | No | No | Nonlinear |
| [25] | Yes | Costs | Yes | No | No | Design | No | No | Nonlinear |
| [26] | Yes | Costs | Yes | Yes | No | Design and operation | Yes (Sensitivity) | No | Linear |
| [27] | Yes | Costs and emissions | Yes | Yes | Yes | Operation | Yes (Uncertainty) | Yes (4) | MINLP |
| [28] | Yes | Costs | Yes | Yes | No | Operation | Yes (Uncertainty) | Yes (4) | Nonlinear |
| [29] | Yes | Costs and emissions | Yes | Yes | No | Operation | No | Yes (4) | MILP |
| [30] | Yes | Costs | Yes | Yes | No | Operation | No | Yes (4) | Linear |
| [31] | Yes | Costs | Yes | Yes | No | Design and operation | Yes (Uncertainty) | Yes (4) | MILP |
| [32] | Yes | Costs | Yes | Yes | Yes | Operation | Yes (Uncertainty) | Yes (4) | MILP |
| [33] | Yes | Costs | Yes | Yes | Yes | Operation | Yes (Uncertainty) | Yes (4) | MILP |
| [34] | Yes | Costs | Yes | Yes | No | Operation | Yes (Uncertainty) | Yes (5) | MILP |
| [35] | Yes | Costs | Yes | Yes | No | Operation | Yes (Uncertainty) | Yes (4) | MILP |
| [36] | Yes | Emissions | Yes | Yes | Yes | Operation | Yes (Uncertainty) | Yes (5) | MILP |
| This study | Yes | Costs, primary energy, emissions, grid interactions | Yes | Yes | Yes | Design and operation | Yes (Uncertainty) | Yes (7) | MILP |
| Abbreviation | Meaning |
|---|---|
| AC | Absorption chiller |
| BOP | Balance of plant |
| C | Cost |
| CED | Cumulative energy demand |
| CVaR | Conditional value at risk |
| DC | District cooling |
| DH | District heating |
| DHW | Domestic hot water |
| E | Electricity |
| EH | Energy hub |
| EL | Electrolyzer |
| ESS | Electrical energy storage |
| F | Cooling |
| FC | Fuel cell |
| GB | Gas-fired boiler |
| GWP | Global warming potential |
| H | Heating |
| H2 | Hydrogen |
| HP | Heat pump |
| K | Constant |
| MES | Multi-carrier energy system |
| NG | Natural gas |
| PEMFC | Proton exchange membrane fuel cell |
| RES | Renewable energy source |
| TSS | Thermal energy storage |
| TK | Tank |
| TR | Transformer |
| TSO | Transmission system operator |
| W | Water |
| Grid/Network | Costs | CED | GWP | Grid Interactions |
|---|---|---|---|---|
| E | Copex,E = 0.30 EUR/kWhel | CEDE = 11.8 MJ/kWh | GWPE = 0.071 kgCO2eq/kWh | 100,000 |
| NG | Copex,NG = 0.09 EUR/kWhth | CEDNG = 4.12 MJ/kWh | GWPNG = 0.037 kgCO2eq/kWh | 100,000 |
| H | - | - | - | 100,000 |
| F | - | - | - | 100,000 |
| H2 | Copex,H2 = 20 EUR/kg | CEDH2 = 213.52 MJ/kg | GWPH2 = 11.95 kgCO2eq/kg | 100,000 |
| W | Copex,W = 2.19 EUR/kg | CEDW = 0 MJ/kg (negligible) | GWPW = 0 kgCO2eq/kg (negligible) | 100,000 |
| Equipment | Conversion Factors | Costs | CED [MJ/kWh or MJ/kg] | GWP [kgCO2eq/kWh or kgCO2eq/kg] |
|---|---|---|---|---|
| GB | KGB gh = 0.9 | Ccapex,GB = 55.51 EUR/kW Ccapex,GB (0) = 118.8 EUR | 92.65 | 19.5 |
| HP | KHP eh = 5.7 | Ccapex,HP = 111.93 EUR/kW Ccapex,HP (0) = 630.63 EUR | 1250.4 | 239.4 |
| AC | KAChf = 0.9 | Ccapex,AC = 216.9 EUR/kW | 2338.42 | 147.5 |
| EL | KEL eh2 = 0.016 kg/kWh 1 KEL h2w = 8.55 kg/kg | Ccapex,EL = 1274 EUR/kW | 168,635 | 28 |
| FC | KFC h2e = 12.23 kWh/kg KFC h2h = 20.11 kWh/kg KFC h2w = 9.47 kg/kg | Ccapex,FC = 1532.44 EUR/kW | 71,466 | 11.87 |
| PV | NOCT = 47 °C APV = 1.2 m2 ηPV = 0.21 β PV = −3.7 10−3 °C−1 ηBOP = 0.95 PPV = 0.25 kW/unit | Ccapex,PV = 311.95 EUR/unit | 4582 | 358 |
| CSP | KCSP,se = 0.1394 KCSP,sh = 0.3964 ACSP = 400 m2 PCSP = 1000 kW/unit | Ccapex,CSP = 273,002.73 EUR/unit | 7210.6 | 3545.04 |
| STC | ASTC = 1.867 m2 η0 = 0.734 a1 = 1.529 W/m2 K a2 = 0.0166 W/m2 K2 Tm = 40 °C | Ccapex,STC = 500 EUR/unit | 3745.52 | 210.56 |
| TK | KTK,in = 1 KTK,out = 1 H2 TK,loss = 0.02 | Ccapex,TK = 171.33 EUR/kg Ccapex,TK (0) = 716,859 EUR | 3222.2 | 0.048 |
| ESS | KESS,in = 0.97 KESS,out = 0.97 ESS,loss = 0.01 DoDESS = 0.2 | Ccapex,ESS = 419.37 EUR/kWh Ccapex,ESS(0) = 677,502.83 EUR | 540 | 76.28 |
| TSS | KTSS,in = 1 KTSS,out = 1 TSS,loss = 0.01 | Ccapex,TSS,H = 26.18 EUR/kWh Ccapex,TSS,F = 65.46 EUR/kWh Ccapex,TSS(0) = 266 | CEDTSS,H = 201 CEDTSS,F = 504 | GWPTSS,H = 11 GWPTSS,F = 27 |
| Minimum Cost | Minimum Primary Energy Consumption | Minimal Carbon Emissions | Minimal Grid Interactions | 0.25 Weights Multi-Objective Optimization | |
|---|---|---|---|---|---|
| GB [kWth] | 37,879 | 29,065 | 29,064 | 447,681 | 29,065 |
| HP [kWfr] | 5107 | 6390 | 6390 | 6390 | 6390 |
| AC [kWfr] | 6390 | 63 | 63 | 6390 | 6390 |
| EL [kWel] | 0 | 73 | 73 | 5,488,336 | 0 |
| FC [kWel] | 0 | 0 | 0 | 5,488,336 | 0 |
| PV [n.] PV [kW] | 5,488,336 1,383,061 | 1,300,865 327,818 | 1,299,567 327,491 | 1,511,170 380,815 | 1,375,615 346,655 |
| CSP [n.] CSP [kW] | 0 0 | 2 2000 | 2 2000 | 0 0 | 0 0 |
| STC [n.] STC [m2] | 92 171.8 | 0 0 | 0 0 | 0 0 | 0 0 |
| TK [kg] | 0 | 0 | 0 | 7,624 | 0 |
| ESS [kWhel] | 5,488,336 | 5,488,336 | 5,488,336 | 5,488,336 | 5,488,336 |
| TSSH [kWhth] | 447,681 | 447,681 | 447,681 | 447,681 | 447,681 |
| TSSF [kWhfr] | 0 | 2902 | 2944 | 6390 | 6390 |
| Non-Optimized Base Scenario | Minimum Cost | Minimum Primary Energy Consumption | Minimal Carbon Emissions | Minimal Grid Interactions | 0.25 Weights Multi-Objective Optimization | |
|---|---|---|---|---|---|---|
| Costs [million euros/year] | 1007 | −455.39 (−145%) | 0.83 (−100%) | 13.27 (−99%) | 1818 (+81%) | 190.6 (−81%) |
| Primary energy consumption [TJ/year] | 37,252 | 4488 (−88%) | 3369 (−91%) | 3369 (−91%) | 98,138 (+163%) | 3965 (−89%) |
| Carbon emissions [t CO2eq/year] | 268,383 | 236,642 (−12%) | 173,588 (−35%) | 173,289 (−35%) | 194,924 (−27%) | 209,702 (−22%) |
| Grid interaction penalty function [-] | - | 1.3 × 1013 | 2.2 × 1012 | 2.2 × 1012 | 6.0 × 1010 | 3.7 × 1011 |
| Minimum Cost | Minimum Primary Energy Consumption | Minimal Carbon Emissions | Minimal Grid Interactions | 0.25 Weights Multi-Objective Optimization | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Without Uncertainty | With Uncertainty | Without Uncertainty | With Uncertainty | Without Uncertainty | With Uncertainty | Without Uncertainty | With Uncertainty | Without Uncertainty | With Uncertainty | |
| GB [kWth] | 37,879 | 34,693 | 29,065 | 27,872 | 29,064 | 27,821 | 447,681 | 447,681 | 29,065 | 447,681 |
| HP [kWfr] | 5107 | 5108 | 6390 | 6390 | 6390 | 6390 | 6390 | 6390 | 6390 | 6390 |
| AC [kWfr] | 6390 | 6390 | 63 | 62 | 63 | 62 | 6390 | 6390 | 6390 | 6390 |
| EL [kWel] | 0 | 0 | 73 | 73 | 73 | 73 | 5,488,336 | 5,488,336 | 0 | 0 |
| FC [kWel] | 0 | 0 | 0 | 0 | 0 | 0 | 5,488,336 | 5,488,336 | 0 | 0 |
| PV [n.] | 5,488,336 | 5,488,336 | 1,300,865 | 1,048,726 | 1,299,567 | 1,216,872 | 1,511,170 | 1,332,143 | 1,375,615 | 5,488,336 |
| CSP [n.] | 0 | 0 | 2 | 0 | 2 | 2 | 0 | 0 | 0 | 0 |
| STC [n.] | 92 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 54.64 |
| TK [kg] | 0 | 0 | 0 | 0 | 0 | 0 | 7624 | 7624 | 0 | 0 |
| ESS [kWhel] | 5,488,336 | 5,488,336 | 5,488,336 | 5,488,336 | 5,488,336 | 5,488,336 | 5,488,336 | 5,488,336 | 5,488,336 | 5,488,336 |
| TSSH [kWhth] | 447,681 | 447,681 | 447,681 | 447,681 | 447,681 | 447,681 | 447,681 | 447,681 | 447,681 | 447,681 |
| TSSF [kWhfr] | 0 | 0 | 2902 | 0 | 2944 | 52.22 | 6390 | 6390 | 6390 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Massaro, F.; Di Silvestre, M.L.; Ferraro, M.; Montana, F.; Riva Sanseverino, E.; Ruffino, S. Energy Hub Model for the Massive Adoption of Hydrogen in Power Systems. Energies 2024, 17, 4422. https://doi.org/10.3390/en17174422
Massaro F, Di Silvestre ML, Ferraro M, Montana F, Riva Sanseverino E, Ruffino S. Energy Hub Model for the Massive Adoption of Hydrogen in Power Systems. Energies. 2024; 17(17):4422. https://doi.org/10.3390/en17174422
Chicago/Turabian StyleMassaro, Fabio, Maria Luisa Di Silvestre, Marco Ferraro, Francesco Montana, Eleonora Riva Sanseverino, and Salvatore Ruffino. 2024. "Energy Hub Model for the Massive Adoption of Hydrogen in Power Systems" Energies 17, no. 17: 4422. https://doi.org/10.3390/en17174422
APA StyleMassaro, F., Di Silvestre, M. L., Ferraro, M., Montana, F., Riva Sanseverino, E., & Ruffino, S. (2024). Energy Hub Model for the Massive Adoption of Hydrogen in Power Systems. Energies, 17(17), 4422. https://doi.org/10.3390/en17174422








