Short-Circuit Conditions and Thermal Behaviour of Different Cable Formations
Abstract
1. Introduction
- (1)
- SC current calculated for each formation using cable parameters and a standard power system impedance (for start temperatures of 30 and 70 °C) (case 1);
- (2)
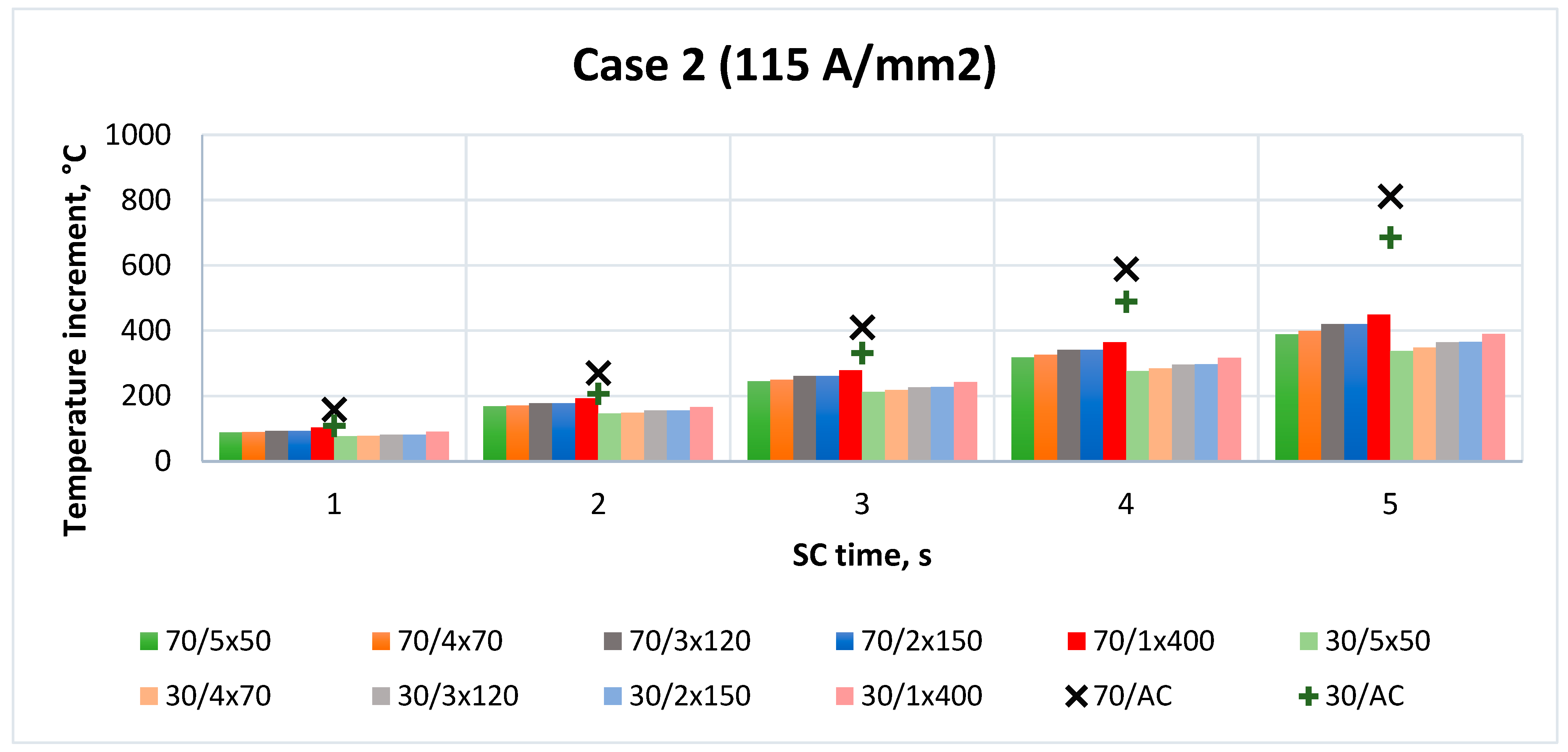
- Short-circuit current corresponding to a constant current density equal to 115 A/mm2 (for start temperatures of 30 and 70 °C) (case 2);
- (3)
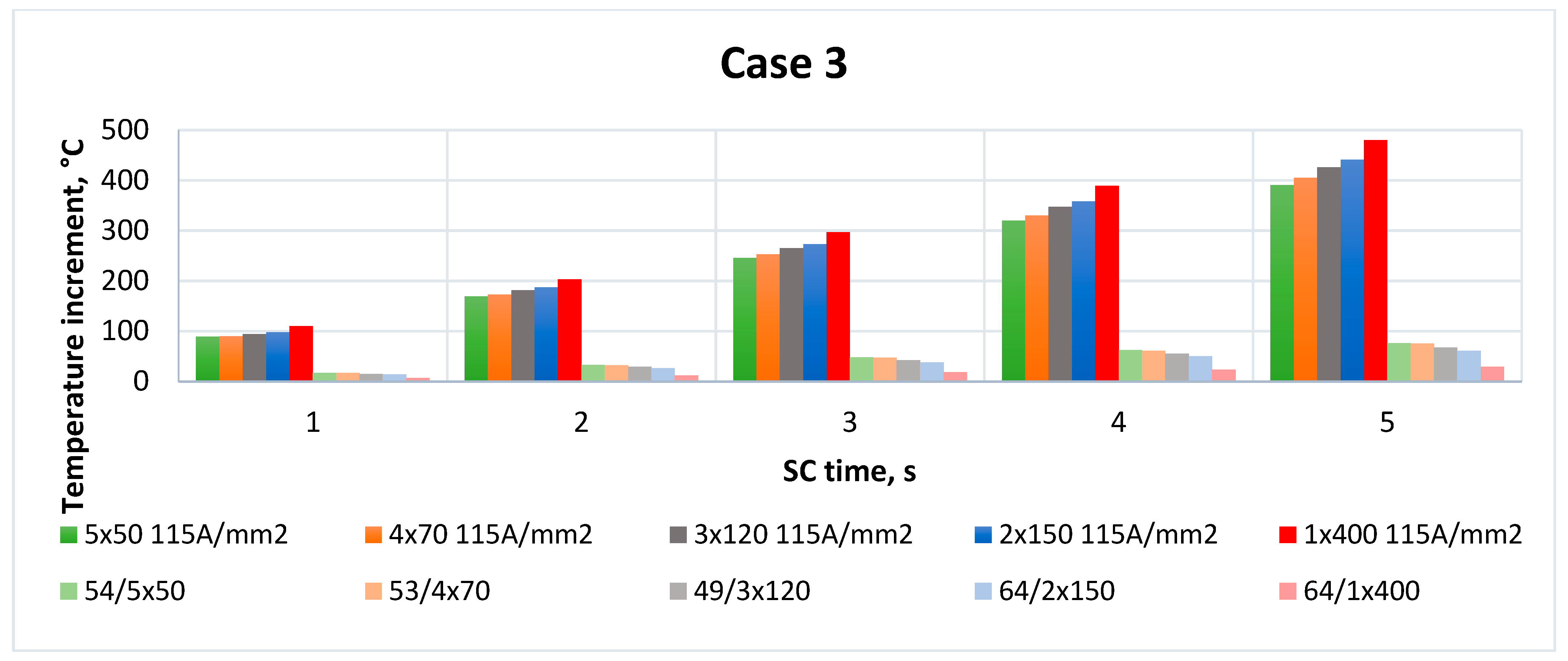
- SC current calculated for each formation for the temperature of the cable after a long-lasting rated load before a fault (case 3).
2. Materials and Methods
2.1. Calculation Methods
2.2. Cable Arrangement Parameters
3. Results
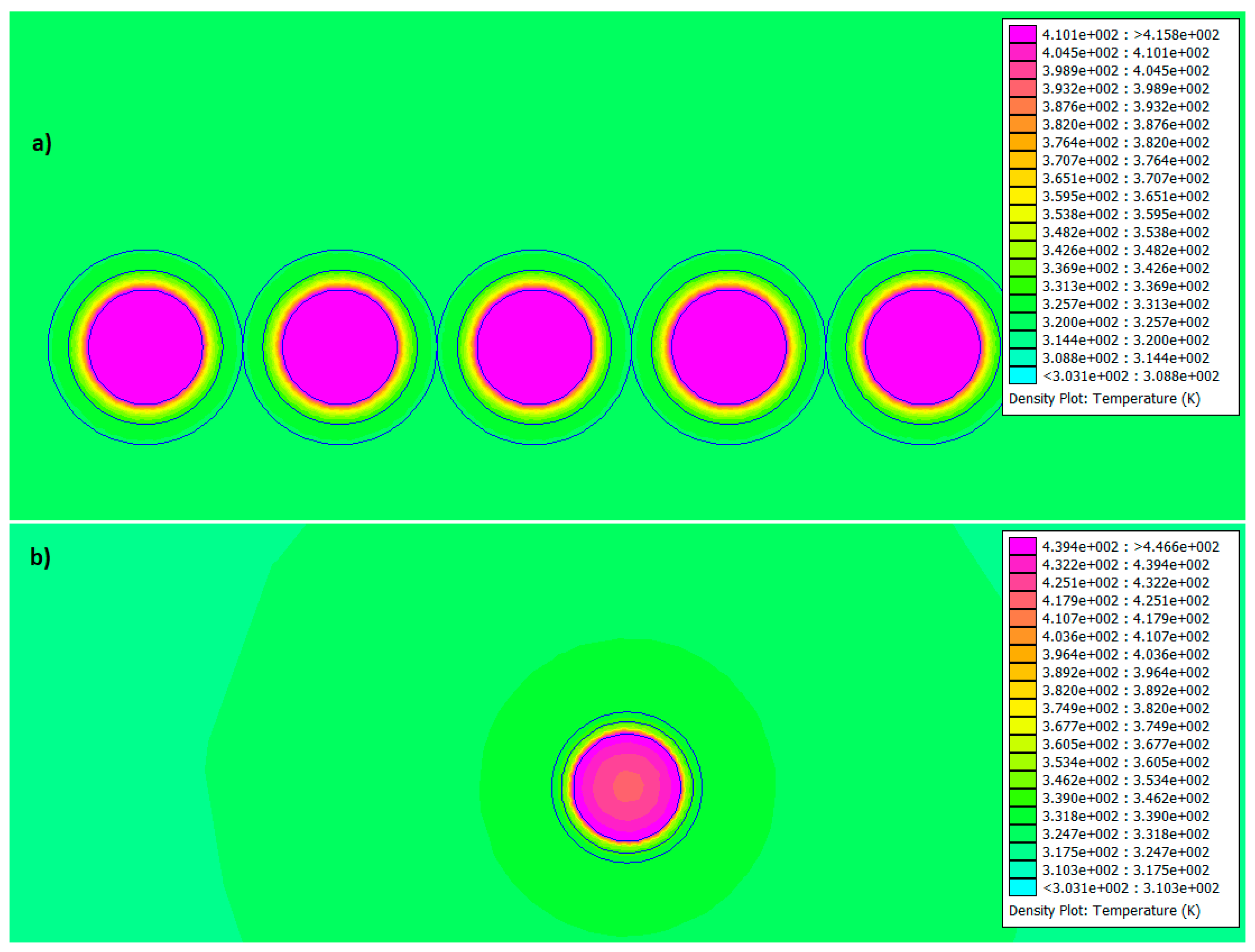
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IEC 60364-5-52:2009; Low-Voltage Electrical Installations—Part 5-52: Selection and Erection of Electrical Equipment—Wiring systems. International Standard: Geneva, Switzerland, 2009.
- Fangrat, J.; Kaczorek-Chrobak, K.; Papis, B.K. Fire Behavior of Electrical Installations in Buildings. Energies 2020, 13, 6433. [Google Scholar] [CrossRef]
- IEC TR 62095:2003; Electric Cables-Calculations for Current Ratings-Finite Element Method. International Standard: Geneva, Switzerland, 2003.
- Rerak, M.; Ocłoń, P. Thermal analysis of underground power cable system. J. Therm. Sci. 2017, 26, 465–471. [Google Scholar] [CrossRef]
- Ocłoń, P.; Pobędza, J.; Walczak, P.; Cisek, P.; Vallati, A. Experimental Validation of a Heat Transfer Model in Underground Power Cable Systems. Energies 2020, 13, 1747. [Google Scholar] [CrossRef]
- Anders, G.J. Rating of Electric Power Cables: Ampacity Computations for Transmission, Distribution, and Industrial Application; IEEE PRESS: New York, NY, USA, 1997. [Google Scholar]
- Bates, C.; Malmedal, K.; Cain, D. Cable ampacity calculations: A comparison of methods. IEEE Ind. Appl. 2016, 52, 112–118. [Google Scholar] [CrossRef]
- Wang, P.-Y.; Ma, H.; Liu, G.; Han, Z.-Z.; Guo, D.-M.; Xu, T.; Kang, L.-Y. Dynamic thermal analysis of high-voltage power cable insulation for cable dynamic thermal rating. IEEE Access 2019, 7, 56095–56106. [Google Scholar] [CrossRef]
- Zhan, Q.; Ruan, J.; Tang, K.; Tang, L.; Liu, Y.; Li, H.; Qu, X. Real-time calculation of three cable conductor temperature based on thermal circuit model with thermal resistance correction. J. Eng. 2019, 16, 2036–2041. [Google Scholar] [CrossRef]
- Wang, J.; Liang, Y.; Ma, C. A novel transient thermal circuit model of buried power cables for emergency and dynamic load. Energy Rep. 2023, 9 (Suppl. S1), 963–971. [Google Scholar] [CrossRef]
- Olsen, R.S.; Holboll, J.; Gudmundsdóttir, U.S. Dynamic Temperature Estimation and Real Time Emergency Rating of Transmission Cables. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Luo, L.; Cheng, X.; Zong, X.; Wei, W.; Wang, C. Research on Transmission Line Loss and Carrying Current Based on Temperature Power Flow Model, 3rd International Conference on Mechanical Engineering and Intelligent Systems; Atlantis Press: Amsterdam, The Netherlands, 2015; pp. 120–127. [Google Scholar] [CrossRef]
- Sarajcev, I.; Majstrovic, M.; Medic, I. Calculation of Losses in Electric Power Cables as the Base for Cable Temperature Analysis; WIT, Transactions on Engineering Sciences; WIT Press: Waterford, Ireland, 2020; Volume 27, pp. 529–537. [Google Scholar]
- Wang, X.W.; Zhao, J.P.; Zhang, Q.G.; Lv, B.; Chen, L.C.; Zhang, Y.; Yang, J.H. Real-time Calculation of Transient Ampacity of Trench Laying Cables Based on the Thermal Circuit Model and the Temperature Measurement. In Proceedings of the 2019 IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP), Xi’an, China, 21–24 October 2019; pp. 1647–1651. [Google Scholar] [CrossRef]
- Kacejko, P.; Machowski, J. Short Circuits in the Electroenergetic System; WNT: Warszawa, Poland, 2020. (In Polish) [Google Scholar]
- Mamcarz, D.; Albrechtowicz, P.; Radwan-Pragłowska, N.; Rozegnał, B. The Analysis of the Symmetrical Short-Circuit Currents in Backup Power Supply Systems with Low-Power Synchronous Generators. Energies 2020, 13, 4474. [Google Scholar] [CrossRef]
- Rozegnał, B.; Albrechtowicz, P.; Mamcarz, D.; Radwan-Pragłowska, N.; Cebula, A. The Short-Circuit Protections in Hybrid Systems with Low-Power Synchronous Generators. Energies 2021, 14, 160. [Google Scholar] [CrossRef]
- Wu, Y. Numerical Simulation and Characteristics Test of Temperature Field under Short-circuit Fault. In Proceedings of the 2017 2nd International Conference on Modelling, Simulation and Applied Mathematics (MSAM2017), Advances in Intelligent Systems Research, Bangkok, Thailand, 26–27 March 2017. [Google Scholar] [CrossRef]
- Hao, J.; Zhou, J.; Wang, Y. Thermal Stability Analysis and Design for Electrical Product in Short-Circuit Fault. Elektron. Ir Elektrotechnika 2022, 28, 18–26. [Google Scholar] [CrossRef]
- Vikharev, A.P. Calculation of the Admissible Short Circuit Current for the Protected Wires of an OHL. Power Technol. Eng. 2018, 52, 357–360. [Google Scholar] [CrossRef]
- Brakelmann, H.; Anders, G.J. Transient Thermal Response of Multiple Power Cables With Temperature Dependent Losses. IEEE Trans. Power Deliv. 2021, 36, 3937–3944. [Google Scholar] [CrossRef]
- Brakelmann, H.; Anders, G.J. Ampacity Calculations of Underground Power Cables With End Effects. IEEE Trans. Power Deliv. 2023, 38, 1968–1976. [Google Scholar] [CrossRef]
- Riba, J.-R. Analysis of formulas to calculate the AC resistance of different conductors’ configurations. Electr. Power Syst. Res. 2015, 127, 93–100. [Google Scholar] [CrossRef]
- Chaganti, P.; Yuan, W.; Zhang, M.; Xu, L.; Hodge, E.; Fitzgerald, J. Modelling of a High-Temperature Superconductor HVDC Cable Under Transient Conditions. IEEE Trans. Appl. Supercond. 2023, 33, 5400805. [Google Scholar] [CrossRef]
- Albrechtowicz, P.; Szczepanik, J. The analysis of the effectiveness of standard protection devices in supply systems fed from synchronous generator sets. In Proceedings of the 2018 International Symposium on Electrical Machines (SME): SME 2018, Andrychów, Poland, 10–13 June 2018; pp. 1–5. [Google Scholar]
- Lubośny, Z. Virtual Inertia in Electric Power Systems. Autom. Elektr. Zaklocenia 2020, 11, 1. [Google Scholar] [CrossRef]
- NKT Group. NKT Cable Calatogue, Low Voltage Cables and Wires; NKT S.A.: Warszowice, Poland, 2017. [Google Scholar]
- IEC 60502-1:2021; Power Cables with Extruded Insulation and their Accessories for Rated Voltages from 1 kV (Um = 1.2 kV) up to 30 kV (Um = 36 kV)—Part 1: Cables for Rated Voltages of 1 kV (Um = 1.2 kV) and 3 kV (Um = 3.6 kV). International Standard: Geneva, Switzerland, 2021.
- IEC 60724:2000; Short-Circuit Temperature Limits of ELECTRIC Cables with Rated Voltages of 1 kV (Um = 1.2 kV) and 3 kV (Um = 3.6 kV). International Standard: Geneva, Switzerland, 2000.
- Lejdy, B.; Skibko, Z. Determine of thermal time-constant based on temperature measuring. In Pomiary Automatyka Kontrola; Wydawnictwo PAK: Warszawa, Poland, 2010; Volume 56, pp. 143–145. [Google Scholar]
- Chybowski, R.; Jaskółowski, W.; Kustra, P. Wpływ grubości tynku na funkcjonalność pojedynczego przewodu elektrycznego poddanego oddziaływaniu promieniowania cieplnego. Zesz. Nauk. SGSP/Szkoła Główna Służby Pożarniczej 2012, 43, 5–12. [Google Scholar]
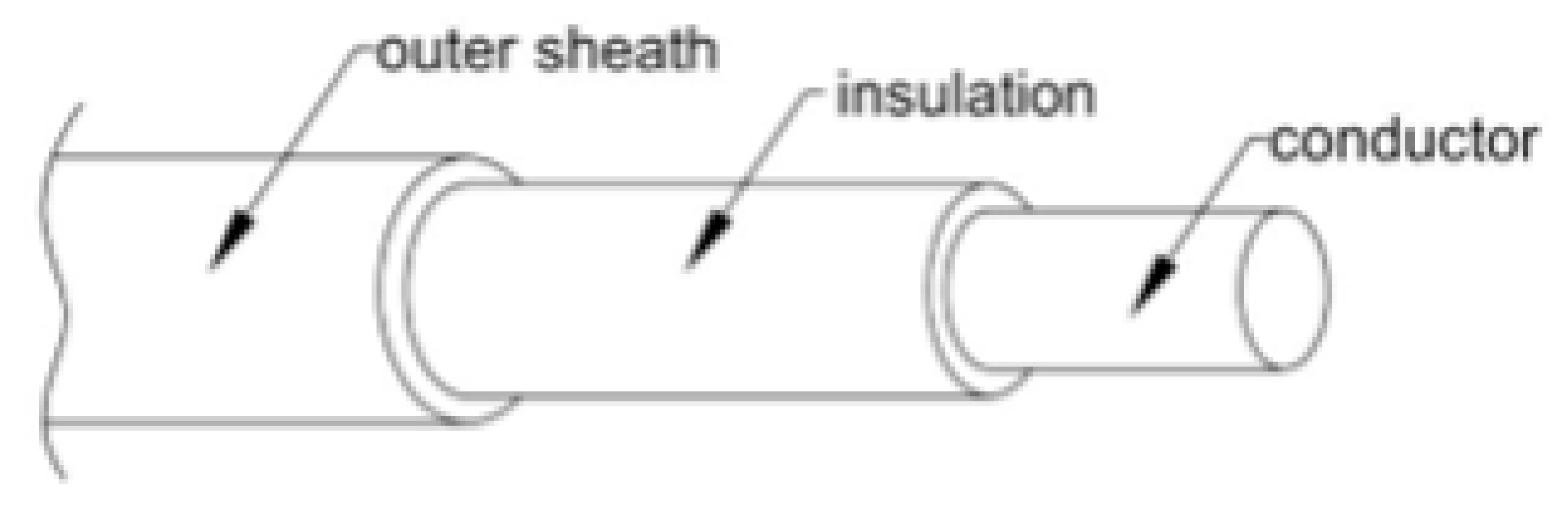

| CSA, mm2 | Current Capacity in Air, A | Current Capacity in Ground, A | Maximal Conductor Resistance, Ω/km | Inductivity, mH/km |
|---|---|---|---|---|
| 50 | 215 | 293 | 0.387 | 0.294 |
| 70 | 272 | 363 | 0.268 | 0.279 |
| 120 | 389 | 496 | 0.153 | 0.270 |
| 150 | 447 | 559 | 0.124 | 0.266 |
| 400 | 845 | 962 | 0.047 | 0.251 |
| Number of Cables and CSA | Derating Factor, - | Calculated Current Capacity, A | Load Current per Cable, A |
|---|---|---|---|
| 5 × 50 | 0.75 | 807 | 148.4 |
| 4 × 70 | 0.77 | 838 | 185.5 |
| 3 × 120 | 0.82 | 957 | 247.3 |
| 2 × 150 | 0.88 | 787 | 371 |
| 1 × 400 | 1 | 845 | 742 |
| CSA, mm2 | Insulation Thickness, mm | Sheath Thickness, mm | Approx. Outer Diameter, mm |
|---|---|---|---|
| 50 | 1.4 | 1.4 | 14 |
| 70 | 1.4 | 1.5 | 16 |
| 120 | 1.6 | 1.6 | 20 |
| 150 | 1.8 | 1.6 | 22 |
| 400 | 2.0 | 2.0 | 34 |
| Parameter | Value |
|---|---|
| Conductivity of core material, m/(Ωmm2) | 55 |
| Relative permeability, - | 1 |
| Insulation and sheath thermal conductivity, W/(mK) | 0.285 |
| Heat transfer coefficient, W/(m2 K) | 10 |
| Ambient cooling temperature of air, °C | 30 |
| Thermal conductivity of air, W/(mK) | 0.025 |
| Formation | Case 1 | Case 2 | Case 3 | ||||
|---|---|---|---|---|---|---|---|
| dP30, W | dP70, W | dP30, W | dP70, W | Tin, °C | dPRX, W | dPJd=115, W | |
| 5 × 50 | 2837.7 | 2553.6 | 12,481.1 | 14,382.2 | 54 | 2822.4 | 14,457.1 |
| 4 × 70 | 3727.5 | 3400.5 | 17,496.7 | 20,088.8 | 53 | 3771.3 | 20,313.1 |
| 3 × 120 | 5234.0 | 4937.7 | 29,994.3 | 34,564.9 | 49 | 5545.5 | 35,077.4 |
| 2 × 150 | 6100.1 | 5835.6 | 37,492.9 | 43,146.6 | 64 | 6298.0 | 45,159.2 |
| 1 × 400 | 6351.9 | 6777.5 | 99,452.0 | 114,264.0 | 64 | 7348.7 | 122,139.8 |
| Formation | Case 1 | Case 3/RX | |
|---|---|---|---|
| J30, A/mm2 | J70, A/mm2 | JRX, A/mm2 | |
| 5 × 50 | 55 | 48 | 51 |
| 4 × 70 | 53 | 47 | 50 |
| 3 × 120 | 48 | 43 | 46 |
| 2 × 150 | 46 | 42 | 43 |
| 1 × 400 | 29 | 28 | 28 |
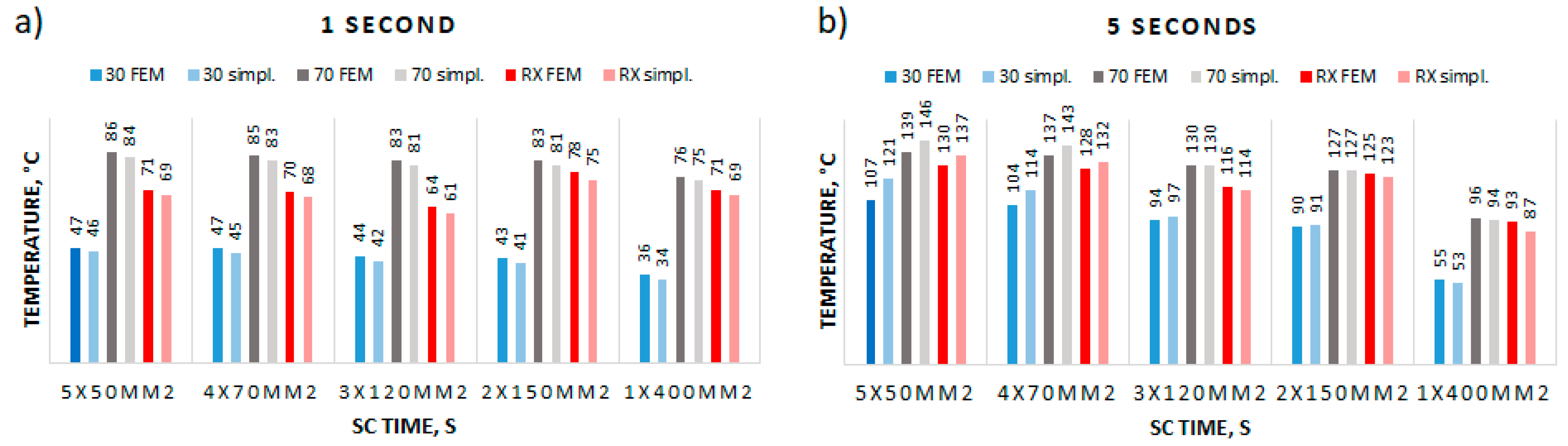
| Formation | Case 1/30 °C SC Time, s | Case 1/70 °C SC Time, s | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | |
| 5 × 50 mm2 | 47 | 63 | 78 | 93 | 107 | 86 | 100 | 113 | 126 | 139 |
| 4 × 70 mm2 | 47 | 62 | 76 | 91 | 104 | 85 | 99 | 112 | 125 | 137 |
| 3 × 120 mm2 | 44 | 57 | 69 | 82 | 94 | 83 | 95 | 107 | 119 | 130 |
| 2 × 150 mm2 | 43 | 55 | 67 | 78 | 90 | 83 | 94 | 105 | 116 | 127 |
| 1 × 400 mm2 | 36 | 41 | 45 | 50 | 55 | 76 | 81 | 86 | 91 | 96 |
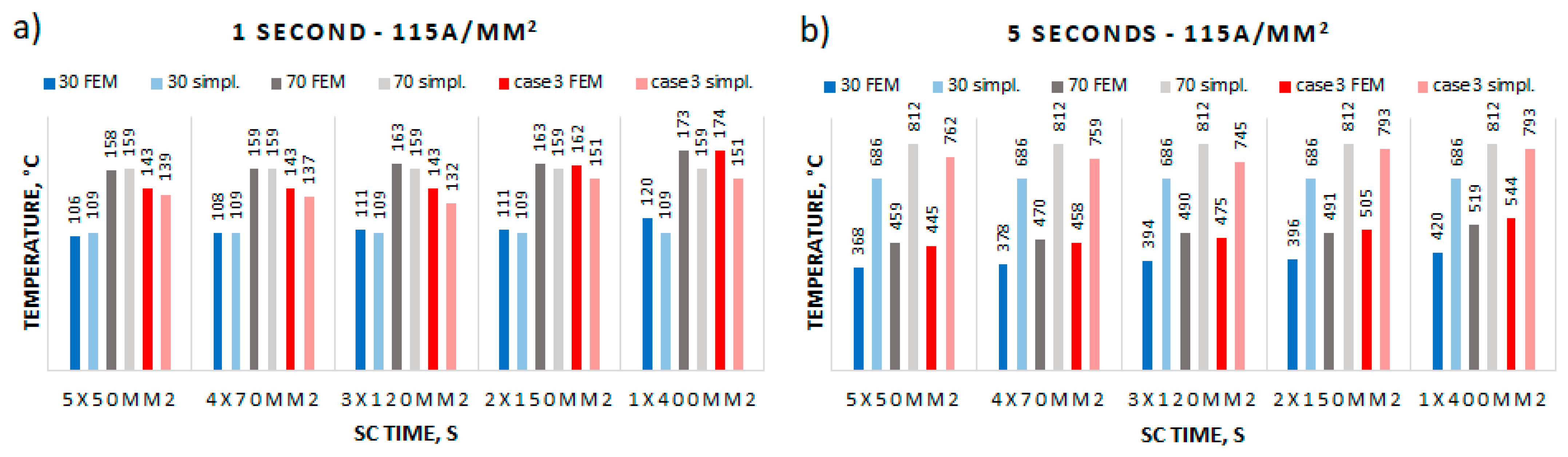
| Formation | Case 2/30 °C SC Time, s | Case 2/70 °C SC Time, s | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | |
| 5 × 50 mm2 | 106 | 176 | 242 | 306 | 368 | 158 | 238 | 315 | 388 | 459 |
| 4 × 70 mm2 | 108 | 179 | 248 | 314 | 378 | 159 | 241 | 320 | 396 | 470 |
| 3 × 120 mm2 | 111 | 185 | 256 | 326 | 394 | 163 | 248 | 331 | 411 | 490 |
| 2 × 150 mm2 | 111 | 185 | 257 | 327 | 396 | 163 | 248 | 331 | 412 | 491 |
| 1 × 400 mm2 | 120 | 196 | 272 | 347 | 420 | 173 | 262 | 349 | 434 | 519 |
| Formation | Case 3/JRX SC Time, s | Case 3/Jd = 115 A/mm2 SC Time, s | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | |
| 5 × 50 mm2 | 71 | 87 | 102 | 116 | 130 | 143 | 223 | 300 | 374 | 445 |
| 4 × 70 mm2 | 70 | 85 | 100 | 114 | 128 | 143 | 226 | 306 | 383 | 458 |
| 3 × 120 mm2 | 64 | 78 | 91 | 104 | 116 | 143 | 230 | 314 | 396 | 475 |
| 2 × 150 mm2 | 78 | 90 | 102 | 114 | 125 | 162 | 251 | 337 | 422 | 505 |
| 1 × 400 mm2 | 71 | 76 | 82 | 87 | 93 | 174 | 267 | 361 | 453 | 544 |
| Formation | Case 1/30 °C SC Time, s | Case 1/70 °C SC Time, s | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | |
| 5 × 50 mm2 | 46 | 64 | 82 | 101 | 121 | 84 | 99 | 114 | 130 | 146 |
| 4 × 70 mm2 | 45 | 61 | 78 | 96 | 114 | 83 | 97 | 112 | 127 | 143 |
| 3 × 120 mm2 | 42 | 55 | 69 | 83 | 97 | 81 | 93 | 105 | 117 | 130 |
| 2 × 150 mm2 | 41 | 53 | 65 | 78 | 91 | 81 | 92 | 103 | 115 | 127 |
| 1 × 400 mm2 | 34 | 39 | 44 | 48 | 53 | 75 | 79 | 84 | 89 | 94 |
| Formation | Case 3/JRX SC Time, s | Case 3/Jd = 115 A/mm2 SC Time, s | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | |
| 5 × 50 mm2 | 69 | 85 | 102 | 119 | 137 | 139 | 245 | 380 | 549 | 762 |
| 4 × 70 mm2 | 68 | 83 | 99 | 115 | 132 | 137 | 244 | 378 | 546 | 759 |
| 3 × 120 mm2 | 61 | 74 | 87 | 100 | 114 | 132 | 237 | 370 | 536 | 745 |
| 2 × 150 mm2 | 75 | 86 | 98 | 110 | 123 | 151 | 261 | 400 | 574 | 793 |
| 1 × 400 mm2 | 69 | 73 | 78 | 83 | 87 | 151 | 261 | 400 | 574 | 793 |
| Cable Type | Time Heating Constant, s | |
|---|---|---|
| Manufacturer Value [27] | Simulation Value | |
| 50 mm2 | 350 | 343 |
| 70 mm2 | 426 | 409 |
| 120 mm2 | 616 | 610 |
| 150 mm2 | 727 | 745 |
| 400 mm2 | 1447 | 1455 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albrechtowicz, P.; Smugała, D. Short-Circuit Conditions and Thermal Behaviour of Different Cable Formations. Energies 2024, 17, 4395. https://doi.org/10.3390/en17174395
Albrechtowicz P, Smugała D. Short-Circuit Conditions and Thermal Behaviour of Different Cable Formations. Energies. 2024; 17(17):4395. https://doi.org/10.3390/en17174395
Chicago/Turabian StyleAlbrechtowicz, Paweł, and Dariusz Smugała. 2024. "Short-Circuit Conditions and Thermal Behaviour of Different Cable Formations" Energies 17, no. 17: 4395. https://doi.org/10.3390/en17174395
APA StyleAlbrechtowicz, P., & Smugała, D. (2024). Short-Circuit Conditions and Thermal Behaviour of Different Cable Formations. Energies, 17(17), 4395. https://doi.org/10.3390/en17174395







