Sensitivity Analysis and Distribution Factor Calculation under Power Network Branch Power Flow Exceedance

Abstract

As the scale of power systems continue to expand and their structure becomes increasingly complex, it is likely that branch power flow exceedance may occur during the operation of power systems, posing threats to the safe and stable operation of entire systems. This paper addresses the issue of branch flow exceedance in power networks. To enhance the operational efficiency and optimize the adjustment effects, this paper proposes a method for eliminating branch power flow exceedance by improving the particle swarm optimization (PSO) algorithm through the introduction of sensitivity and distribution factors. Firstly, it introduces the basic theory and calculation methods of sensitivity analysis, focusing on deriving the calculation principles of power flow sensitivity and voltage sensitivity, used to predict the responses of power flow at each branch in the power network to power or voltage changes. Subsequently, the paper provides a detailed derivation of the calculation principles for the line outage distribution factor (LODF), which effectively assesses the changes in branch power flow in the power network under specific conditions. Finally, a method for eliminating branch power flow exceedance based on a combination of sensitivity analysis and PSO algorithm is proposed. Through case analysis, it is demonstrated how to use the sensitivity and distribution factor to predict and control the power flow exceedance issues in power systems, verifying the efficiency and practicality of the proposed method for eliminating branch power flow exceedance. The study shows that this method can rapidly and accurately predict and address branch power flow exceedance in power system, thereby enhancing the operational safety of the power system.

1. Introduction

As the scale and complexity of power systems continue to expand, the safety and stability of their operation have become important topics in electrical engineering research [1,2,3]. Throughout the operation of power systems, factor such as load fluctuations [4,5], equipment failures, the uncertainty of renewable energy [6], or power market transactions could lead to branch flow exceedances, thereby threatening the safety and stability of the entire power system [7,8]. Therefore, effectively predicting and controlling branch flow exceedances is key to enhancing the safety and economic efficiency of the grid [9,10].

Sensitivity analysis and distribution factor calculations are significant technical methods in power systems. Sensitivity analysis is a crucial tool for studying how changes in input parameters affect system performance and stability [11], while the distribution factor can predict the impacts of specific network operations on the flow distribution [12].

Many studies currently utilize sensitivity analysis. In the context of integrating renewable energies, the literature [13] indicates that the correlation between renewable sources such as wind and solar significantly affects the voltage stability of power systems. The higher the correlation, the greater the sensitivity of renewable energy generation to voltage stability. Reference [14] proposes a method for wind capacity sensitivity analysis in large-scale grid-connected wind power for multi-energy, strongly coupled integrated energy systems based on unified optimal power flow. Using a sensitivity matrix, the study analyzes the impact of the capacity of the energy-coupling units on wind power absorption capacity. This method provides auxiliary information for integrated energy systems’ safe and stable operation. Reference [15] introduces a method for calculating the delay margin sensitivity to system parameters. By incorporating the normalization condition of eigenvectors into the differential characteristic equation, a set of sparse linear equations is solved to obtain the delay margin sensitivity to any given parameter, suitable for various power system models and control issues. Reference [16] conducts a sensitivity analysis on hydropower units under comprehensive operational conditions, showing that the mechanical parameters of generators are most sensitive under power control modes, while electrical parameters are more sensitive under frequency control modes. This analysis aids in understanding the stability and safety of hydropower operations.

Currently, distribution factor is mainly used in power trading research. Literature [17] provides an algorithm that calculates the cost of electrical energy in transmission networks using alternating current power transfer distribution factors. Reference [18] introduces a new application of PTDFs in deregulated electricity markets for transmission pricing assessment, establishing a “hybrid analysis and decision framework” for transmission costs and pricing. Reference [19] proposes an enhanced STF-LODF method to address transmission line congestion. Pricing and sensitivity methods are used for price management while managing the optimal location and voltage instability issues associated with blocking transmission.

Concerning branch power flow exceedance elimination, the literature [3] employs a branch switching method to identify candidate branches for switching, thereby eliminating branch flow exceedances. Reference [20] establishes a risk assessment system based on probabilistic flow calculations, identifying key risk branches with flow exceedances. This is crucial for enhancing grid stability and preventing major blackout incidents. Literature [21] proposes a method that utilizes reinforcement learning and sensitivity analysis to overcome the local optima issues common in artificial intelligence methods, thereby correcting flow exceedance behaviors in grid branches. Reference [22] develops an optimization-based program to determine the maximum power flow that each branch in the network can withstand, helping to identify branches prone to exceedances.

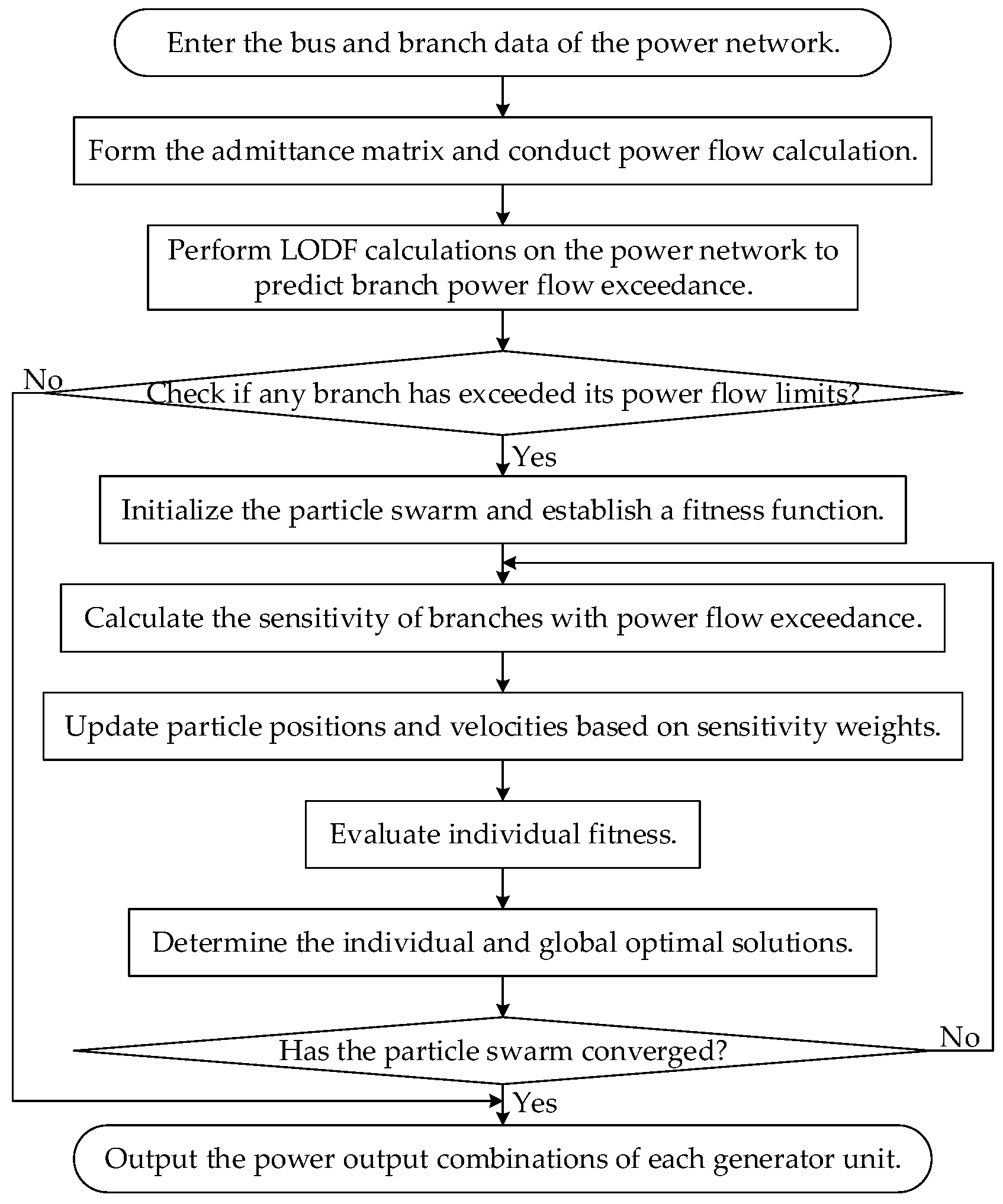
The methods for branch power flow exceedance elimination discussed in the above literature focus on different aspects and achieve corresponding results. However, they face challenges such as complex modeling, large computational loads, and difficulty in implementation. This paper applies a sensitivity analysis and distribution factors to the issue of branch power flow exceedance and proposes a branch exceedance elimination method based on sensitivity weighting, building upon the foundation of the particle swarm optimization (PSO) algorithm. This method features high operational efficiency, effective optimization results, and suitability for practical engineering applications, enabling rapid and accurate prediction and management of branch power flow exceedances in power systems.

Firstly, the paper introduces the basic theory and computational methods of sensitivity analysis, focusing on power flow sensitivity and voltage sensitivity calculation principles. Applying these theories not only helps us predict changes in power flow within the power network but also provides a scientific basis for the planning and operational optimization of power systems. Subsequently, the paper details the derivation of the calculation principles for the line outage distribution factor (LODF), which is crucial for assessing and predicting the distribution of the power flow in a power grid under specific circumstances. Finally, it utilizes the proposed method for branch power flow exceedance elimination and validates its efficiency and practicality through case studies. This method can handle branch power flow exceedance in power systems more efficiently, ensuring the stable operation of the grid and the safety of power transactions.

2. Sensitivity Calculation

Sensitivity refers to the degree to which a change in one quantity causes a change in a response quantity and is an important indicator of the numerical relationship between these two quantities. Sensitivity analysis is widely applied in power system networks. Through sensitivity calculations, it is possible to predict the power flow and voltage in weak links of the network before equipment is added or removed, thus preventing potential network failures due to improper actions. Additionally, if a fault has already occurred in the system, sensitivity analysis can be utilized to quickly and effectively identify the best strategies for restoring network operations.

2.1. Basic Principles of Sensitivity Calculation

The process of a sensitivity calculation is based on power flow calculations. The calculation process is derived by utilizing the constraint equations and relationships from the power flow analysis, combined with the definitions of various sensitivities.

For any power system network, the characteristic operational equation can be expressed as follows:

$$\left\{\begin{array}{l}f(x,u)=0\\ y=y(x,u)\end{array}\right.$$

(1)

In this equation, f(x, u) = 0 represents the node power constraint equation, reflecting the conservation of node power; y = y(x, u) relates the bus voltages to line power flows; u is the control variables, such as generator output power, bus voltage, and the set values of active and reactive power at each node, classified as independent variables; x is the state variables, such as the magnitude and phase angle of the node voltages, classified as dependent variables; and y is the dependent variables that depend on changes in state variables and control variables, such as line power.

When the dependent variables are directly related only to the state variables, Equation (1) can be rewritten as follows:

$$\left\{\begin{array}{l}f(x,u)=0\\ y=y(x)\end{array}\right.$$

(2)

Assuming the system operates in a steady state, where the state variables and control variables are $(x_0,u_0)$, then, in this state, we have the following:

$$\left\{\begin{array}{l}f(x_0,u_0)=0\\ y_0=y(x_0)\end{array}\right.$$

(3)

To derive the relationships between the control variables and state variables, Equation (2) is Taylor expanded [23] around $(x_0,u_0)$, and higher-order terms are ignored, resulting in the following:

$$\left\{\begin{array}{l}f(x_0+\Delta x,u_0+\Delta u)=f(x_0,u_0)+{\displaystyle \frac{\partial f}{\partial x}}\Delta x+{\displaystyle \frac{\partial f}{\partial u}}\Delta u\\ y_0+\Delta y=y(x_0)+{\displaystyle \frac{\partial y}{\partial x}}\Delta x\end{array}\right.$$

(4)

By substituting Equation (3) into Equation (4), the following can be obtained:

$$\left\{\begin{array}{l}{\displaystyle \frac{\partial f}{\partial x}}\Delta x+{\displaystyle \frac{\partial f}{\partial u}}\Delta u=0\\ \Delta y={\displaystyle \frac{\partial y}{\partial x}}\Delta x\end{array}\right.$$

(5)

Upon organizing Equation (5), we can derive the following:

$$\left\{\begin{array}{l}\Delta x={-\left({\displaystyle \frac{\partial f}{\partial x}}\right)}^{-1}{\displaystyle \frac{\partial f}{\partial u}}\Delta u=L_m\Delta u\\ \Delta y={\displaystyle \frac{\partial y}{\partial x}}\Delta x=L_n\Delta u\end{array}\right.$$

(6)

In this equation, L_m represents the sensitivity matrix for changes in x due to the changes in u, and L_n represents the sensitivity matrix for changes in y due to changes in u. The specific relationships are as follows:

$$\left\{\begin{array}{l}{L}_m={-\left({\displaystyle \frac{\partial f}{\partial x}}\right)}^{-1}{\displaystyle \frac{\partial f}{\partial u}}\\ L_n=-{\displaystyle \frac{\partial y}{\partial x}}{\left({\displaystyle \frac{\partial f}{\partial x}}\right)}^{-1}{\displaystyle \frac{\partial f}{\partial u}}\end{array}\right.$$

(7)

2.2. Power Flow Sensitivity

Power flow sensitivity reflects the change in line power flow caused by changes in the injected power of the node. Depending on the type of injected power, power flow sensitivity can be divided into active power sensitivity and reactive power sensitivity. Additionally, the observed line power flow can be categorized into active power, reactive power, and apparent power. Therefore, power flow sensitivity is defined as the change in the active power, reactive power, and apparent power of the line caused by the change in active power or reactive power injected into the node.

According to the basic principles of sensitivity, in the calculation of power flow sensitivity, u acts as the control variable, which is the power injected at the nodes by the load and generators; x acts as the state variable, which is the bus voltage under steady state conditions; y acts as the dependent variable, which represents the line power flow. Thus, f(x, u) = 0 is equivalent to the unbalanced quantity in power flow calculation, reflecting the constraints between node injected power and node voltage; y = y(x) represents the relationship between node voltage and line power flow, and using node voltage, the corresponding line power flow can be determined. Therefore, ${\displaystyle \frac{\partial f}{\partial x}}$ is the Jacobian matrix, J, in the power flow calculation [24].

In ${\displaystyle \frac{\partial f}{\partial x}}$, f represents the unbalance quantity, noted as follows:

$$\Delta \dot{S}={[\begin{array}{cccccccc}\Delta P_1& \Delta Q_1& \Delta P_2& \Delta U_2^2& \cdots & \cdots & \Delta P_n& \Delta Q_n\end{array}]}^T$$

(8)

and u represents the node-injected power, noted as follows:

$${\dot{S}}_s=[\begin{array}{cccccccc}{P}_{s1}& Q_{s1}& P_{s2}& Q_{s2}& \cdots & \cdots & P_{sn}& Q_{sn}\end{array}]$$

(9)

Derived from the power flow equation of the power system, the following can be obtained:

$${\displaystyle \frac{\partial f}{\partial u}}={\displaystyle \frac{\partial \Delta \dot{S}}{\partial {\dot{S}}_s}}=\left[\begin{array}{cccccccc}{\displaystyle \frac{\partial \Delta P_1}{\partial P_{s1}}}& {\displaystyle \frac{\partial \Delta P_1}{\partial Q_{s1}}}& {\displaystyle \frac{\partial \Delta P_1}{\partial P_{s2}}}& {\displaystyle \frac{\partial \Delta P_1}{\partial Q_{s2}}}& \cdots & \cdots & {\displaystyle \frac{\partial \Delta P_1}{\partial P_{sn}}}& {\displaystyle \frac{\partial \Delta P_1}{\partial Q_{sn}}}\\ {\displaystyle \frac{\partial \Delta Q_1}{\partial P_{s1}}}& {\displaystyle \frac{\partial \Delta Q_1}{\partial Q_{s1}}}& {\displaystyle \frac{\partial \Delta Q_1}{\partial P_{s2}}}& {\displaystyle \frac{\partial \Delta Q_1}{\partial Q_{s2}}}& \cdots & \cdots & {\displaystyle \frac{\partial \Delta Q_1}{\partial P_{sn}}}& {\displaystyle \frac{\partial \Delta Q_1}{\partial Q_{sn}}}\\ {\displaystyle \frac{\partial \Delta P_2}{\partial P_{s1}}}& {\displaystyle \frac{\partial \Delta P_2}{\partial Q_{s1}}}& {\displaystyle \frac{\partial \Delta P_2}{\partial P_{s2}}}& {\displaystyle \frac{\partial \Delta P_2}{\partial Q_{s2}}}& \cdots & \cdots & {\displaystyle \frac{\partial \Delta P_2}{\partial P_{sn}}}& {\displaystyle \frac{\partial \Delta P_2}{\partial Q_{sn}}}\\ {\displaystyle \frac{\partial \Delta U_2^2}{\partial P_{s1}}}& {\displaystyle \frac{\partial \Delta U_2^2}{\partial Q_{s1}}}& {\displaystyle \frac{\partial \Delta U_2^2}{\partial P_{s2}}}& {\displaystyle \frac{\partial \Delta U_2^2}{\partial Q_{s2}}}& \cdots & \cdots & {\displaystyle \frac{\partial \Delta U_2^2}{\partial P_{sn}}}& {\displaystyle \frac{\partial \Delta U_2^2}{\partial Q_{sn}}}\\ ⋮& ⋮& ⋮& ⋮& & & ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& & & ⋮& ⋮\\ {\displaystyle \frac{\partial \Delta P_n}{\partial P_{s1}}}& {\displaystyle \frac{\partial \Delta P_n}{\partial Q_{s1}}}& {\displaystyle \frac{\partial \Delta P_n}{\partial P_{s2}}}& {\displaystyle \frac{\partial \Delta P_n}{\partial Q_{s2}}}& \cdots & \cdots & {\displaystyle \frac{\partial \Delta P_n}{\partial P_{sn}}}& {\displaystyle \frac{\partial \Delta P_n}{\partial Q_{sn}}}\\ {\displaystyle \frac{\partial \Delta Q_n}{\partial P_{s1}}}& {\displaystyle \frac{\partial \Delta Q_n}{\partial Q_{s1}}}& {\displaystyle \frac{\partial \Delta Q_n}{\partial P_{s2}}}& {\displaystyle \frac{\partial \Delta Q_n}{\partial Q_{s2}}}& \cdots & \cdots & {\displaystyle \frac{\partial \Delta Q_n}{\partial P_{sn}}}& {\displaystyle \frac{\partial \Delta Q_n}{\partial Q_{sn}}}\end{array}\right]=\left[\begin{array}{cccccccc}1& & & & & & & \\ & 1& & & & & & \\ & & 1& & & & & \\ & & & 0& & & & \\ & & & & \ddots & & & \\ & & & & & \ddots & & \\ & & & & & & 1& \\ & & & & & & & 1\end{array}\right]$$

(10)

where ${\displaystyle \frac{\partial y}{\partial x}}$ represents the partial derivative of the line power flow with respect to the node voltage, obtained from the power flow equations in rectangular coordinates, as follows:

$${\dot{S}}_{ij}=(e_i^2+f_i^2)y_{i0}^{*}+(e_i+j{f}_i)(e_i-j{f}_i-e_j+j{f}_j)y_{ij}^{*}$$

(11)

Taking the partial derivatives of each term in the rectangular coordinate phasor $\dot{U}={[\begin{array}{ccccccc}{e}_1& f_1& e_2& f_2& \cdots & e_n& f_n\end{array}]}^T$ of the node voltage with respect to ${\dot{S}}_{ij}$, we can obtain the following:

$${\displaystyle \frac{\partial y}{\partial x}}={\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial \dot{U}}}=\left[\begin{array}{ccccccccccc}{\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial e_1}}& {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial f_1}}& \cdots & {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial e_i}}& {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial f_i}}& \cdots & {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial e_j}}& {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial f_j}}& \cdots & {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial e_n}}& {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial f_n}}\end{array}\right]$$

(12)

Substituting Equation (11) into Equation (12), we obtain the following:

$$\left\{\begin{array}{l}{\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial e_i}}=2e_i{y}_{i0}^{*}+(2e_i-e_j+j{f}_j)y_{ij}^{*}\\ {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial f_i}}=2f_i{y}_{i0}^{*}+(2f_i-j{e}_j-f_j)y_{ij}^{*}\\ {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial e_j}}=-(e_i+j{f}_i)y_{ij}^{*}\\ {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial f_j}}=(j{e}_i-f_i)y_{ij}^{*}\\ {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial e_x}}={\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial f_x}}=0x\ne i,j\end{array}\right.$$

(13)

Substituting Equations (10)–(12) into Equation (7), we can obtain the following:

$$L_n={\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial {\dot{S}}_s}}=-{\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial \dot{U}}}{J}^{-1}{\displaystyle \frac{\partial \Delta \dot{S}}{\partial {\dot{S}}_s}}=\left[\begin{array}{cccccccc}{\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial P_{s1}}}& {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial Q_{s1}}}& \cdots & {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial P_{sx}}}& {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial Q_{sx}}}& \cdots & {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial P_{sn}}}& {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial Q_{sn}}}\end{array}\right]$$

(14)

In this equation, ${\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial P_{sx}}}$ represents the active power sensitivity for line i-j at node x, and ${\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial Q_{sx}}}$ represents the reactive power sensitivity for line i-j at node x, where the real part represents the observed active power, and the imaginary part represents the observed reactive power.

The apparent power $\dot{S}=P+jQ$, whose value is $\sqrt{P^2+Q^2}$. The formula derivation for the power flow sensitivity of the apparent power as the observed object is as follows:

$${\displaystyle \frac{\partial \dot{S}}{\partial A}}={\displaystyle \frac{\partial \sqrt{P^2+Q^2}}{\partial A}}={\displaystyle \frac{P\frac{\partial P}{\partial A}+Q\frac{\partial Q}{\partial A}}{\sqrt{P^2+Q^2}}}$$

(15)

In this equation, A represents the injected power at the node, which can be either active power or reactive power.

Taking the IEEE 5-bus case as an example, the IEEE 5-bus case consists of 5 nodes and 5 branches, with the branches in the forward direction being 1–5, 2–4, 2–5, 3–4, and 4–5, respectively. Node 1 serves as the slack bus, and its structural topology and network data are shown in Figure 1.

According to the analytical principles of sensitivity calculation, it is necessary to compute three partial derivatives: ${\displaystyle \frac{\partial f}{\partial x}}$, ${\displaystyle \frac{\partial f}{\partial u}}$, and ${\displaystyle \frac{\partial y}{\partial x}}$.

For ${\displaystyle \frac{\partial f}{\partial x}}$, this represents the partial derivative of the node imbalance quantity with respect to the node voltage, which corresponds to the Jacobian matrix in power flow calculations.

For ${\displaystyle \frac{\partial f}{\partial u}}$, this represents the partial derivative of the node imbalance quantity with respect to the node injected power. In the IEEE 5-bus case, node 3 is a PV node, and its voltage imbalance quantity’s derivative with respect to the initial injected power is 0, while the rest are 1.

For ${\displaystyle \frac{\partial y}{\partial x}}$, this represents the partial derivative of the line flow with respect to the node voltage, which can be derived and calculated accordingly.

$$L_{15}=-{\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial \dot{U}}}{J}^{-1}{\displaystyle \frac{\partial \Delta \dot{S}}{\partial {\dot{S}}_s}}={\left[\begin{array}{c}-1.1265-j0.7756\\ -0.0954-j1.0965\\ -1.0076-j0.0765\\ 0\\ -1.0139-j0.1065\\ -0.0115-j0.2732\\ -1.0179-j0.1488\\ -0.023-j0.7775\end{array}\right]}^T.$$

In these results, the odd rows represent the sensitivity when there is a unit change in the active power injection at a node, known as the active power sensitivity; the even rows represent the sensitivity when there is a unit change in the reactive power injection at a node, known as the reactive power sensitivity. It should be noted that in the calculation results, each term is in a complex form, where the real part represents the active power and the imaginary part represents the reactive power.

2.3. Voltage Sensitivity

Voltage sensitivity reflects the changes in line power flows caused by changes in the magnitude of the generator node voltages. Similarly observed objects include active power, reactive power, and apparent power. Therefore, voltage sensitivity is defined as follows: when there is a change in the voltage magnitude at a generator node, it causes changes in the active, reactive, and apparent power flows in the line.

Voltage sensitivity analysis is similar to power flow sensitivity analysis, with the only difference being in the control variables u. For voltage sensitivity, u represents the voltage at the generator node.

For ${\displaystyle \frac{\partial f}{\partial x}}$, thi is also the Jacobian matrix, J, used in power flow calculations.

For ${\displaystyle \frac{\partial f}{\partial u}}$, f represents the unbalanced quantity, which is still noted as Equation (8). u is the node voltage of the generator, and for convenience in calculating the value of ${\displaystyle \frac{\partial f}{\partial u}}$, let u represent the voltage magnitude at all nodes, noted as follows:

$$u=\left[\begin{array}{cccc}{u}_1& u_2& \cdots & u_n\end{array}\right]$$

(16)

To find the relationship between the unbalanced quantity and voltage magnitude, represent the node voltage in polar coordinates and derive the expression for the unbalanced quantity in polar coordinates as follows:

$$\left\{\begin{array}{l}\Delta P_i=P_{si}-P_i=P_{si}-u_i\cos {\delta }_i{\displaystyle \sum _{j=1}^n(G_{ij}{u}_j\cos {\delta }_j-B_{ij}{u}_j\sin {\delta }_j)}-u_i\sin {\delta }_i{\displaystyle \sum _{j=1}^n(G_{ij}{u}_j\sin {\delta }_j+B_{ij}{u}_j\cos {\delta }_j)}\\ \Delta Q_i=Q_{si}-Q_i=Q_{si}-u_i\sin {\delta }_i{\displaystyle \sum _{j=1}^n(G_{ij}{u}_j\cos {\delta }_j-B_{ij}{u}_j\sin {\delta }_j)}+u_i\cos {\delta }_i{\displaystyle \sum _{j=1}^n(G_{ij}{u}_j\sin {\delta }_j+B_{ij}{u}_j\cos {\delta }_j)}\end{array}\right.$$

(17)

In this equation, if node i represents a PV node, then $\Delta Q_i$ should be replaced with 0.

Deriving the partial derivative of the unbalanced quantity with respect to the voltage magnitude at the nodes yields a new matrix, denoted as follows:

$$Ju=\left[\begin{array}{cccc}{\displaystyle \frac{\partial \Delta P_1}{\partial u_1}}& {\displaystyle \frac{\partial \Delta P_1}{\partial u_2}}& \cdots & {\displaystyle \frac{\partial \Delta P_1}{\partial u_n}}\\ {\displaystyle \frac{\partial \Delta Q_1}{\partial u_1}}& {\displaystyle \frac{\partial \Delta Q_1}{\partial u_2}}& \cdots & {\displaystyle \frac{\partial \Delta Q_1}{\partial u_n}}\\ {\displaystyle \frac{\partial \Delta P_2}{\partial u_1}}& {\displaystyle \frac{\partial \Delta P_2}{\partial u_2}}& \cdots & {\displaystyle \frac{\partial \Delta P_2}{\partial u_n}}\\ 0& 0& \cdots & 0\\ ⋮& ⋮& & ⋮\\ ⋮& ⋮& & ⋮\\ {\displaystyle \frac{\partial \Delta P_n}{\partial u_1}}& {\displaystyle \frac{\partial \Delta P_n}{\partial u_2}}& \cdots & {\displaystyle \frac{\partial \Delta P_n}{\partial u_n}}\\ {\displaystyle \frac{\partial \Delta Q_n}{\partial u_1}}& {\displaystyle \frac{\partial \Delta Q_n}{\partial u_2}}& \cdots & {\displaystyle \frac{\partial \Delta Q_n}{\partial u_n}}\end{array}\right]$$

(18)

In this matrix, 0 represents the partial derivative of the reactive unbalance at equilibrium nodes with respect to the voltage magnitude. The expressions for other elements in the matrix are as follows:

1.

When i = j:

$$\left\{\begin{array}{l}{\displaystyle \frac{\partial \Delta P_i}{\partial u_i}}=-\cos {\delta }_i{\displaystyle \sum _{j=1}^n(G_{ij}{u}_j\cos {\delta }_j-B_{ij}{u}_j\sin {\delta }_j)}-\sin {\delta }_i{\displaystyle \sum _{j=1}^n(G_{ij}{u}_j\sin {\delta }_j+B_{ij}{u}_j\cos {\delta }_j)}-u_i{G}_{ii}\\ {\displaystyle \frac{\partial \Delta Q_i}{\partial u_i}}=-\sin {\delta }_i{\displaystyle \sum _{j=1}^n(G_{ij}{u}_j\cos {\delta }_j-B_{ij}{u}_j\sin {\delta }_j)}+\cos {\delta }_i{\displaystyle \sum _{j=1}^n(G_{ij}{u}_j\sin {\delta }_j+B_{ij}{u}_j\cos {\delta }_j)}+u_i{B}_{ii}\end{array}\right.$$

(19)

2.

When i ≠ j:

$$\left\{\begin{array}{l}{\displaystyle \frac{\partial \Delta P_i}{\partial u_j}}=-u_i{G}_{ij}\cos ({\delta }_i-{\delta }_j)-u_i{B}_{ij}\sin ({\delta }_i-{\delta }_j)\\ {\displaystyle \frac{\partial \Delta Q_i}{\partial u_j}}=-u_i{G}_{ij}\sin ({\delta }_i-{\delta }_j)+u_i{B}_{ij}\cos ({\delta }_i-{\delta }_j)\end{array}\right.$$

(20)

When i is a PV node, and j is any node, the following applies:

$${\displaystyle \frac{\partial \Delta Q_i}{\partial u_j}}=0$$

(21)

where ${\displaystyle \frac{\partial y}{\partial x}}$ represents the partial derivative of the line power flow with respect to node voltage, consistent with the calculation of the power flow sensitivity, aligning with the reasoning process in Equation (12).

By incorporating the Jacobian matrix from the Newton–Raphson power flow calculation method with Equations (12) and (18) into Equation (7), we can obtain the following:

$$L_n={\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial u}}=-{\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial \dot{U}}}{J}^{-1}{\displaystyle \frac{\partial \Delta \dot{S}}{\partial u}}=\left[\begin{array}{cccc}{\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial u_1}}& {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial u_2}}& \cdots & {\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial u_n}}\end{array}\right]$$

(22)

Following the above calculation process, the voltage sensitivity of each node to the power flow in the lines can be determined. However, it should be noted that typically only the slack and PV nodes have generators connected, so the voltage sensitivity calculated at the PQ nodes may be considered irrelevant and can be disregarded. Additionally, each element in Equation (22) is divided into real and imaginary parts, where the real part represents the observed active power, and the imaginary part represents the observed reactive power. Similar to the power flow sensitivity, when the observed object is apparent power, the derivations can also be based on Equation (15), in which ${\displaystyle \frac{\partial P}{\partial A}}$ represents the sensitivity of the line’s active power to node voltage, and ${\displaystyle \frac{\partial Q}{\partial A}}$ represents the sensitivity of the line’s reactive power to node voltage.

Taking the IEEE 5-bus case as an example, again, similar to power flow sensitivity, it is necessary to calculate the three partial derivatives ${\displaystyle \frac{\partial f}{\partial x}}$, ${\displaystyle \frac{\partial f}{\partial u}}$, and ${\displaystyle \frac{\partial y}{\partial x}}$. Considering that the only difference between voltage sensitivity and power flow sensitivity lies in the control variables, the calculations for ${\displaystyle \frac{\partial f}{\partial x}}$ and ${\displaystyle \frac{\partial y}{\partial x}}$ are the same as those for power flow sensitivity; only ${\displaystyle \frac{\partial f}{\partial u}}$ needs to be computed.

For ${\displaystyle \frac{\partial f}{\partial u}}$, this is the partial derivative of the node imbalance quantity with respect to the voltage amplitude at the generator nodes. From the principle analysis, to understand the relationship between the imbalance quantity and the voltage amplitude, the node voltage needs to be represented in polar coordinates. Referring to Equations (18)–(21), the derivative of the imbalance quantity with respect to the voltage amplitude is derived and, by substituting the data, the derivative for all nodes can be calculated. For the slack node, its power imbalance with respect to the voltage amplitude is generally not considered and should be omitted. Also, it is important to note that typically only the slack and PV nodes have generators connected, so the voltage sensitivity calculated at PQ nodes is irrelevant and can be disregarded. Therefore, for this case, the result of this derivative ultimately has only two columns of data.

After calculating these three partial derivatives, the data are substituted into Equation (22) to obtain the following:

$$L_n=-{\displaystyle \frac{\partial {\dot{S}}_{ij}}{\partial \dot{U}}}{J}^{-1}{\displaystyle \frac{\partial \Delta \dot{S}}{\partial u}}=\left[\begin{array}{cc}-9.5503-j39.3722& -0.8440-j27.0184\end{array}\right],$$

where the two data points represent the voltage sensitivities of line 1–5 with respect to nodes 1 (slack node) and 3 (PV node), respectively. Here, the real part represents the observed object as active power, and the imaginary part as reactive power.

3. Distribution Factor Calculation

The study of distribution factor is based on power flow equations operating at steady-state points, and from this basis, it explores the relationships among variables of interest. These variables often reflect the operating conditions of the power network and may arise from changes in bus active power injections, adjustments in inter-regional power transactions, or the opening and closing of branches. Through distribution factor, one can clearly and intuitively observe the impact of various power transactions on the system [25,26].

Any change in the status of a branch, whether it is opened or closed, will cause a change in the power flow distribution of the entire system, which requires an indicator to measure the degree to which each component of the system is affected by changes in the state of the branch. line outage distribution factor (LODF) reflects the change in active power flow in other branches when a specific line in the power network is disconnected. LODF uses the change in the power flow of the selected line as a baseline to calculate the percentage change in the power flow of other components relative to this baseline, typically used to indicate the impact of the disconnection of one branch on the power flow in other branches of the network.

The LODF is generally calculated using the direct current method. Let the active power flow in branch l under the base state be denoted as $P_l$; if branch l is disconnected, the power flow on branch k will change accordingly. This change is denoted as $\Delta P_k^l$, and the relationship between them is as follows:

$$\Delta P_k^l=D_{k-l}\times P_l$$

(23)

In this equation, $D_{k-l}$ represents the line outage distribution factor.

In the analysis using the direct current method, the sensitivity equation relating the change in active power injection to the change in the angular displacement of node voltages can be derived [27], as follows:

$$\left\{\begin{array}{l}\Delta P=B\Delta \delta \hfill \\ \Delta \delta =X\Delta P\hfill \end{array}\right.$$

(24)

In this equation, B is the admittance matrix obtained under the DC method, and X is the inverse matrix of B. In the construction of matrix B, it is assumed that the reactance in the line (i,j) is much greater than the resistance, and all shunt branches to ground are neglected, with the transformer per-unit ratios consistently considered to be 1. The elements in the matrix are as follows:

$$\left\{\begin{array}{l}{B}_{ii}={\displaystyle \sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^n\frac{1}{x_{ij}}}\\ B_{ij}=-{\displaystyle \frac{1}{x_{ij}}}\end{array}\right.$$

(25)

Note that when the line’s starting or ending point is a slack node, both its self-admittance, $B_{ii}$, and mutual admittance,$B_{ij}$, are 0.

Assuming that the disconnection of a branch does not cause a change in the injected power at the nodes, before the disconnection, taking a stable state as the baseline, the change in active power at each node is 0, and the line power flow in the branch, $l(i,j)$, is denoted as $P_l$, with the direction of the power flow going from i to j. When the branch $l(i,j)$ is disconnected, changes occur in the power at the nodes on both ends of the branch; the change at node i is denoted as $P_i-(P_i-P_l)=P_l$ and at node j as $P_l-(P_j+P_l)=-P_l$. Hence, the change in injected power at the new network nodes is the following:

$$\Delta P=\left[\begin{array}{ccccccc}0& \cdots & P_l& \cdots & -P_l& \cdots & 0\end{array}\right]$$

(26)

Which can be expressed as the following:

$$\Delta P={\left[\begin{array}{ccccccc}0& \cdots & 1& \cdots & -1& \cdots & 0\end{array}\right]}^T{P}_l=M_l{P}_l$$

(27)

In this equation, $M_l$ is the node–branch incidence vector, where rows correspond to node numbers and columns to branches. Assuming the direction of line power flow is from the starting node toward the ending node, the value of $M_l$ at the starting node of the branch is set to 1, indicating only power injection there; at the ending node, it is set to −1, indicating only power output; the other values are 0, representing a balance of injection and output.

For example, in the IEEE 5-bus case, it is possible to represent the following:

$$\begin{array}{cccccc}& l(1,5)& l(2,4)& l(2,5)& l(3,4)& l(4,5)\\ Node1& 1& 0& 0& 0& 0\\ Node2& 0& 1& 1& 0& 0\\ Node3& 0& 0& 0& 1& 0\\ Node4& 0& -1& 0& -1& 1\\ Node5& -1& 0& -1& 0& -1\end{array}.$$

By excluding the slack node, the result can be expressed as follows:

$$M=\left[\begin{array}{ccccc}0& 1& 1& 0& 0\\ 0& 0& 0& 1& 0\\ 0& -1& 0& -1& 1\\ -1& 0& -1& 0& -1\end{array}\right].$$

In the matrix M, each column represents the node–branch association column vector corresponding to the branch in that column.

When the branch $l(i,j)$ in the network is disconnected, the new network’s admittance matrix will also change, specifically, $B_{ii}$ and $B_{jj}$ will be reduced by the admittance $x_l^{-1}$ of branch l; $B_{ij}$ and $B_{ji}$ become 0, which is equivalent to adding the admittance $x_l^{-1}$ of branch l. Using $M_l$, the modification to the admittance matrix can be represented as follows:

$$\Delta B=M_l{x}_l^{-1}{M}_l^T$$

(28)

The new admittance matrix then becomes the following:

$$B_{new}=B-\Delta B=B-M_l{x}_l^{-1}{M}_l^T$$

(29)

Substituting Equation (29) into Equation (24) results in the following:

$$\Delta \delta =B_{new}^{-1}\Delta P={(B-M_l{x}_l^{-1}{M}_l^T)}^{-1}\Delta P$$

(30)

For the line $k(m,n)$, before disconnection, the line power flow is the following:

$$P_k={\displaystyle \frac{1}{x_k}}({\delta }_m-{\delta }_n)$$

(31)

When the line is disconnected, changes in the node voltage angles lead to a change in the line power flow to the following:

$$\begin{array}{ll}{P}_{k-new}& ={\displaystyle \frac{1}{x_k}}({\delta }_m+\Delta {\delta }_m-{\delta }_n-\Delta {\delta }_n)\\ & ={\displaystyle \frac{1}{x_k}}({\delta }_m-{\delta }_n)-{\displaystyle \frac{1}{x_k}}(\Delta {\delta }_m-\Delta {\delta }_n)\\ & =P_k-{\displaystyle \frac{1}{x_k}}(\Delta {\delta }_m-\Delta {\delta }_n)\\ & =P_k-{\displaystyle \frac{1}{x_k}}{M}_k^T\Delta \delta \end{array}$$

(32)

Combining Equations (27), (29), (30), and (32), the change in power flow for line k is as follows:

$$\begin{array}{ll}\Delta P_k^l& =P_k-P_{k-new}\\ & ={\displaystyle \frac{1}{x_k}}{M}_k^T\Delta \delta \\ & ={\displaystyle \frac{M_k^T{B}_{new}^{-1}\Delta P}{x_k}}\\ & ={\displaystyle \frac{M_k^T{(B-M_l{x}_l^{-1}{M}_l^T)}^{-1}{M}_l}{x_k}}{P}_l\end{array}$$

(33)

From Equation (23), the expression for the LODF is the following:

$$D_{k-l}={\displaystyle \frac{M_k^T{(B-M_l{x}_l^{-1}{M}_l^T)}^{-1}{M}_l}{x_k}}$$

(34)

Using the matrix inversion lemma ${(A+B)}^{-1}=B^{-1}{(A^{-1}+B^{-1})}^{-1}{A}^{-1}$, Equation (34) can be written as follows:

$$\begin{array}{ll}{D}_{k-l}& ={\displaystyle \frac{M_k^T{(B-M_l{x}_l^{-1}{M}_l^T)}^{-1}{M}_l}{x_k}}\\ & =-{\displaystyle \frac{M_k^T{(M_l{x}_l^{-1}{M}_l^T)}^{-1}{(B^{-1}-{(M_l{x}_l^{-1}{M}_l^T)}^{-1})}^{-1}{B}^{-1}{M}_l}{x_k}}\\ & =-{\displaystyle \frac{M_k^T{(M_l^T)}^{-1}{x}_l{M}_l^{-1}{(B^{-1}-{(M_l^T)}^{-1}{x}_l{M}_l^{-1})}^{-1}{B}^{-1}{M}_l}{x_k}}\end{array}$$

(35)

Letting $B^{-1}=X$, then it is as follows:

$$\begin{array}{ll}{D}_{k-l}& =-{\displaystyle \frac{M_k^T{(M_l^T)}^{-1}{x}_l{M}_l^{-1}{(X-{(M_l^T)}^{-1}{x}_l{M}_l^{-1})}^{-1}X{M}_l}{x_k}}=-{\displaystyle \frac{M_k^T{(M_l^T)}^{-1}{x}_l{M}_l^{-1}{(X-{(M_l^T)}^{-1}{x}_l{M}_l^{-1})}^{-1}{(M_l^T)}^{-1}{M}_l^{T}X{M}_l}{x_k}}\\ & =-{\displaystyle \frac{M_k^T{(M_l^T)}^{-1}{x}_l{(M_l^{T}X{M}_l-x_l)}^{-1}{M}_l^{T}X{M}_l}{x_k}}={\displaystyle \frac{M_k^T{(M_l^T)}^{-1}{({(M_l^{T}X{M}_l)}^{-1}-x_l^{-1})}^{-1}}{x_k}}={\displaystyle \frac{M_k^T{(M_l^T)}^{-1}(M_l^{T}X{M}_l)x_l}{x_k(x_l-M_l^{T}X{M}_l)}}\\ & ={\displaystyle \frac{M_k^{T}X{M}_l{x}_l}{x_k(x_l-M_l^{T}X{M}_l)}}={\displaystyle \frac{M_k^{T}X{M}_l/x_k}{1-M_l^{T}X{M}_l/x_l}}={\displaystyle \frac{X_{k-l}/x_k}{1-X_{l-l}/x_l}}\end{array}$$

(36)

where $X_{k-l}=M_k^{T}X{M}_l$ represents the mutual impedance between nodes k and l; $X_{l-l}=M_l^{T}X{M}_l$ represents the self-impedance at port l.

4. Branch Power Flow Exceedance and Simulation Analysis

4.1. Method for Eliminating Branch Power Flow Exceedance

Branch power flow exceedance is a common type of fault in power networks. A prolonged overload operation may lead to line breakage and, in severe cases, cause the power network to collapse. There are many causes of power flow exceedance, such as changes in load, inappropriate power transactions, generator unit disconnections, and line faults. In general, any action that causes changes in branch power flows can create the potential for exceedance.

If branch power flow exceedance has already occurred in the system, timely measures must be taken to restore the branch power flow.

The PSO algorithm [28] boasts advantages such as fast convergence, simple parameter adjustments, and ease of implementation, which are highly beneficial for practical engineering dispatch applications in power systems. To ensure that branch power flows are controlled within a safe range (within 80%) and that variations in generator units are minimized for practical engineering adjustments, these two objectives serve as the target functions for the optimization search by the PSO algorithm, namely, the following:

$$\left\{\begin{array}{l}PF\le 80\%\\ \min {\displaystyle \sum _{i=1}^n\left|\Delta P_i\right|}\end{array}\right.$$

(37)

In the formula, PF represents the branch power flow vector, which includes the power flow status of all branches in the system; $\left|\Delta P_i\right|$ represents the active power adjustment amount for generator at node i. Moreover, PF and ${\displaystyle \sum _{i=1}^n\left|\Delta P_i\right|}$ represent the fitness functions of the algorithm.

The core aspect of the PSO algorithm is the continuous updating of particles’ velocities and positions based on the optimal values of the fitness function. Building upon the conventional PSO framework, sensitivity coefficients are introduced as weights for updating particles, thereby accelerating the optimization speed. $\left|S_k\right|$ represents the absolute value of the active power sensitivity coefficient at node k, serving as an additional weight set during particle updates. The improved method of particle updating is as follows:

$$\left\{\begin{array}{l}{v}_i^d=w{v}_i^{d-1}+c_1{r}_1\left(pBes{t}_i^d-x_i^d\right)+c_2{r}_2\left(gBes{t}^d-x_i^d\right)\\ x_i^{d+1}=x_i^d+\left|S_k\right|v_i^d\end{array}\right.$$

(38)

In the formula, $v_i^d$ represents the velocity of the i-th particle during the d-th iteration cycle; $x_i^d$ represents the position of the i-th particle during the d-th iteration cycle; $c_1$ is the particle’s cognitive learning factor; $c_2$ is the particle’s social learning factor; $w$ is the inertia weight of the velocity; $pBes{t}_i^d$ is the personal best of the i-th particle up to the d-th iteration; and $gBes{t}^d$ is the global best of all particles up to the d-th iteration.

The specific flowchart of the designed branch power flow exceedance elimination algorithm, which integrates the LODF and is based on sensitivity-weighted PSO, is shown in Figure 2.

4.2. Simulation Analysis

This article uses a typical 37-node network as a case study, which includes 8 generator nodes and 57 transmission lines, with node 20 being the slack node. The node data and branch data of this network are shown in

Table A1. Typical 37-node network bus parameters (all parameters are per unit).

Node	Type	PG	PL	QG	QL	U	Compensate
1	PQ	0	0	0	0	-	0
2	PQ	0	0.123	0	0.05	-	0
3	PQ	0	0.153	0	0.032	-	0
4	PQ	0	0.168	0	0.025	-	0
5	PQ	0	0.229	0	0.065	-	0
6	PQ	0	0.12	0	0.033	-	0.048
7	PU	0.1	0.222	-	0.152	1.02	0.072
8	PQ	0	0.582	0	0.363	-	0.126
9	PQ	0	0.578	0	0.404	-	0.288
10	PQ	0	0.328	0	0.129	-	0.156
11	PQ	0	0.602	0	0.19	-	0.144
12	PQ	0	0.183	0	0.05	-	0
13	PQ	0	0.153	0	0.05	-	0.072
14	PQ	0	0.372	0	0.134	-	0
15	PQ	0	0.363	0	0.104	-	0
16	PQ	0	0.39	0	0.13	-	0
17	PU	3	0	-	0	1.03	0
18	PQ	0	0	0	0	-	0
19	PQ	0	0.234	0	0.062	-	0
20	Slack	-	0	-	0	1.03	0
21	PQ	0	0	0	0	-	0
22	PQ	0	0.14	0	0.03	-	0
23	PQ	0	0.4464	0	0	-	0
24	PQ	0	0	0	0	-	0
25	PQ	0	0.334	0	0.096	-	0
26	PQ	0	0	0	0	-	0
27	PQ	0	0	0	0	-	0
28	PQ	0	0	0	0	-	0
29	PQ	0	0	0	0		0
30	PU	0.2	0.598	-	0.123	1.02	0
31	PQ	0	0	0	0	-	0
32	PU	0.16	0.558	-	0.125	1	0
33	PU	0.388	0.141	-	0.02	1.02	0
34	PU	1.4	0.595	-	0.278	1.02	0
35	PU	1.005	0.1243	-	0.0573	1.01	0
36	PQ	0	0.453	0	0.123	-	0
37	PQ	0	0.14	0	0.037	-	0

and

Table A2. Typical 37-node network branch parameters (all parameters are per unit).

ID	Branch	R	X	G	B	TR	Limit
1	1–28	0.001	0.0623	0	0	1	2.5
2	1–20	0.00117	0.017	0	0.182		5.97
3	2–28	0.0048	0.0368	0	0.0182		2.33
4	2–29	0.00902	0.0571	0	0.0135		2.33
5	3–11	0.03133	0.07675	0	0.0015		0.82
6	3–30	0.03463	0.08253	0	0.0016		0.82
7	4–6	0.03375	0.0789	0	0.0012		0.82
8	4–27	0.00106	0.03949	0	−0.0041	1.00625	1.867
9	4–12	0.0405	0.0953	0	0.0021		0.72
10	5–16	0.0142	0.07557	0	0.0695		1.12
11	5–28	0.00107	0.04039	0	−0.0042	1.025	1.87
12	5–28	0.00107	0.04039	0	−0.0042	1.025	1.87
13	5–10	0.02172	0.06935	0	0.0019		0.82
14	5–11	0.02747	0.08909	0	0.0019		1.06
15	6–36	0.02216	0.0904	0	0.0017		0.9
16	7–30	0.04211	0.08545	0	0.0474		0.81
17	7–23	0.02625	0.06429	0	0.0012		0.72
18	8–35	0.00859	0.00472	0	0.0214		0.8
19	8–35	0.00855	0.0047	0	0.0213		0.8
20	8–35	0.00846	0.00465	0	0.021		0.8
21	8–15	0.01835	0.02845	0	0.0221		0.74
22	8–9	0.00753	0.02582	0	0.0206		0.93
23	9–16	0.00366	0.01312	0	0.046		1.12
24	10–12	0.02703	0.03613	0	0.002		0.5
25	11–25	0.01017	0.00559	0	0.0253		0.68
26	11–25	0.01017	0.00559	0	0.0253		0.68
27	13–33	0.0424	0.07509	0	0.0008		0.82
28	13–32	0.02133	0.0521	0	0.0009		0.82
29	13–23	0.02423	0.05862	0	0.0011		0.72
30	14–32	0.01829	0.04246	0	0.0078		0.72
31	14–32	0.01824	0.04236	0	0.0075		0.72
32	15–30	0.03993	0.09965	0	0.002		0.82
33	17–18	0.00087	0.051	0	0	1	2.2
34	17–18	0.00087	0.051	0	0	1	2.2
35	18–29	0.01868	0.1259	0	0.0356		1.91
36	19–29	0.00735	0.04395	0	0.0123		1.91
37	19–21	0.00225	0.0134	0	0.004		1.91
38	20–26	0.00075	0.01092	0	0.117		5.97
39	20–17	0.00224	0.03268	0	0.35		6
40	21–18	0.0103	0.05681	0	0.0164		1.91
41	22–33	0.0502	0.101	0	0.0025		0.82
42	22–21	0.0025	0.0723	0	0	1	1.01
43	24–37	0.01243	0.07847	0	0.0192		2.33
44	24–27	0.01028	0.07253	0	0.0176		2.88
45	24–20	0.00087	0.051	0	0	1	2.2
46	27–31	0.00775	0.05244	0	0.0154		2.33
47	27–28	0.01161	0.08085	0	0.0225		2.33
48	27–26	0.00095	0.05116	0	−0.0124	1	2.24
49	27–26	0.00094	0.05107	0	−0.0127	1	2.24
50	30–29	0.00244	0.06829	0	−0.006	1.02125	1.01
51	30–29	0.0025	0.07144	0	−0.0045	1.02125	1.01
52	31–34	0.00204	0.00692	0	0.1601		1.85
53	32–35	0.01473	0.036	0	0.0744		1.05
54	32–31	0.00101	0.03925	0	−0.0035	1.05	1.87
55	35–36	0.06246	0.08246	0	0.0003		0.9
56	35–34	0.00134	0.04988	0	−0.0004	1	1.87
57	37–18	0.00771	0.0544	0	0.0138		2.33

, respectively. Its structure is illustrated in Figure 3.

Under the initial parameters of the network, the power flow results are displayed as a percentage of the power flow to the transmission power limit of the line (see Table A2), as shown in Figure 4. The dashed line in Figure 4 represents the safe operating limit of −80%.

To demonstrate how to use sensitivity and distribution factors to predict and control power flow exceedance issues in power systems, as well as to validate the effectiveness and practicality of the designed branch exceedance elimination method based on the sensitivity-weighted PSO algorithm, this section sets up three simulation scenarios:

• Scenario One: for the branch 31–32, the exceedance is eliminated using a method based solely on sensitivity;
• Scenario Two: prediction of faults after branch disconnection for the branch 8–35 using LODF and elimination of the predicted exceedance;
• Scenario Three: for the branch 31–32, the branch power flow exceedance elimination algorithm based on the sensitivity-weighted PSO algorithm is employed, and it is compared with the conventional PSO algorithm in terms of computation speed and optimization of the results.

4.2.1. Scenario One

For the branch 31–32, its initial power flow reached 86% of the line limit, and operations should be taken to control the power flow within a reasonable range (80%). The complete results for the sensitivity of each node, including active power sensitivity and apparent power sensitivity, are shown in

Table A3. Power flow sensitivity and voltage sensitivity for active power on the 31–32 branch.

Node	Active Power Sensitivity	Reactive Power Sensitivity	Voltage Sensitivity	Node	Active Power Sensitivity	Reactive Power Sensitivity	Voltage Sensitivity
1	−0.00686	−0.00175		20	0		−0.17503
2	−0.05289	−0.00638		21	−0.08741	−0.00881
3	−0.09337	−0.00432		22	−0.1476	−0.02316
4	0.007815	−0.01505		23	−0.2744	0.00341
5	−0.04808	−0.00983		24	0.004762	−0.00131
6	−0.03698	−0.01418		25	−0.07499	−0.00894
7	−0.20876		0.150233	26	0.010889	−0.0008
8	−0.13182	−0.00227		27	0.03655	−0.00286
9	−0.11389	−0.00568		28	−0.03281	−0.0073
10	−0.03048	−0.00992		29	−0.08392	−0.00391
11	−0.07471	−0.00888		30	−0.112		−0.59893
12	−0.01939	−0.01376		31	0.197276	−0.00725
13	−0.33019	0.004083		32	−0.43496		3.343062
14	−0.43796	−0.00104		33	−0.2421		−0.26799
15	−0.12821	−0.00262		34	0.156165		0.163822
16	−0.10418	−0.0073		35	−0.13252		−2.62575
17	−0.02287		−0.19795	36	−0.0859	−0.01837
18	−0.04119	−0.00564		37	−0.02247	−0.00357
19	−0.08673	−0.00768

and

Table A4. Power flow sensitivity and voltage sensitivity for apparent power on the 31–32 branch.

Node	Active Power Sensitivity	Reactive Power Sensitivity	Voltage Sensitivity	Node	Active Power Sensitivity	Reactive Power Sensitivity	Voltage Sensitivity
1	−0.003208	0.0016462		20	0		1.300237
2	−0.0252231	0.0052053		21	−0.04290051	−0.002175
3	−0.04504556	0.001673		22	−0.07174481	−0.009925
4	0.0101297	0.0206346		23	−0.13330199	0.0016413
5	−0.02214604	0.0060874		24	0.00247078	0.0115733
6	−0.01343932	0.0125611		25	−0.03479019	0.0029609
7	−0.10184101		0.072543	26	0.00645263	0.0101153
8	−0.0673539	−0.001037		27	0.02183636	0.0338566
9	−0.05731779	−0.000222		28	−0.01498744	0.0082815
10	−0.01159486	0.0121458		29	−0.04133184	0.0008946
11	−0.03467613	0.002985		30	−0.05542897		−0.17137
12	−0.00438245	0.0133892		31	0.12123206	0.1236553
13	−0.16000731	0.0019609		32	−0.21024014		4.68501
14	−0.21169207	−0.000505		33	−0.11768251		−0.11665
15	−0.06507795	−0.001308		34	0.06512354		18.613
16	−0.05195921	0.0002182		35	−0.06803347		−1.00593
17	−0.01150374		−0.01258	36	−0.03858477	0.0005452
18	−0.02057981	−0.000675		37	−0.01120441	0.0045001
19	−0.04259299	−0.001464

, with the generator node sensitivities presented in

Table 1. Sensitivity of generator nodes to active power and apparent power of the branch 31–32.

Node	Active Power		Apparent Power
	Active Power Sensitivity	Voltage Sensitivity	Active Power Sensitivity	Voltage Sensitivity
7	−0.20876	0.150233	−0.10184	0.072543
17	−0.02287	−0.19795	−0.0115	−0.01258
20	0	−0.17503	0	1.300237
30	−0.112	−0.59893	−0.05543	−0.17137
32	−0.43496	3.343062	−0.21024	4.68501
33	−0.2421	−0.26799	−0.11768	−0.11665
34	0.156165	0.163822	0.065124	18.613
35	−0.13252	−2.62575	−0.06803	−1.00593

.

The sensitivity results were grouped into positive and negative categories. Nodes from the negatively correlated group were selected to increase the output, and nodes from the positively correlated group were chosen to decrease the output. The generator units with larger absolute values for adjustments were prioritized. Based on the ratio of the exceedance power to sensitivity, the active power output or voltage levels were adjusted in stages.

Based on the active power sensitivity of the generator nodes to the branch 31–32, the priorities of the generator adjustments were determined. Then, the active power output was adjusted in steps. The active power sensitivities of nodes 32 and 33 were negatively correlated and have the largest absolute values, while node 34 has the highest positive correlation. Therefore, it is possible to choose to increase the output sequentially from nodes 32 and 33, and decrease the output from node 34. In the first step, the outputs of the generators at nodes 32 and 34 were adjusted to 36 MW and 120 MW, respectively. The operating status of each branch was then checked; at this time, the exceedance branch was 31–32, with a power flow of 83.6%. In the second step, the outputs of the generators at nodes 32 and 34 are adjusted to 58 MW and 100 MW, respectively. The operating status of each branch was checked again; at this time, the exceedance branches were 31–34 and 31–32, with power flows of 80.5% and 81.4%, respectively. In the third step, the sensitivity of the newly exceeded branch is calculated, and the adjustment units were determined based on the sensitivity. The outputs of generators at nodes 32, 33, and 34 are adjusted to 58 MW, 60 MW, and 100 MW, respectively, with the active power difference balanced by slack node 20, bringing the power flow of all network branches within a reasonable range. The power flow of each branch during the adjustment process is shown in Figure 5.

The optimization effect of this method is quite good; however, it is difficult to determine the appropriate step size for adjustments. If the step size is too small, the computation speed is slow, and if it is too large, the optimal adjustment amount may be missed.

In addition to adjusting the active power output of generators, the voltage can also be adjusted based on voltage sensitivity to control the power flow. Adjusting the voltage at node 32 from 1.00 to 1.02 resulted in all branch power flow being below 80%, with the power flow distribution remaining reasonable.

4.2.2. Scenario Two

In Scenario Two, we evaluated the changes in other branch power flows when a specific branch was disconnected by implementing the LODF calculation. The LODF was used to predict changes in the power flow distribution on other lines when a transmission line failed. The LODF results calculated in this simulation show that, after the disconnection of a specific line, the flow on several lines in the system changed dramatically, especially on those lines that were closely electrically connected to the failed line. For example, there were three lines connecting between nodes 8 and 35. When the first line was disconnected, its LODF was calculated, and the results are as shown in

Table 2. LODF calculation results for the first branch of 8–35.

Branch	LODF (%)	Branch	LODF(%)	Branch	LODF (%)
1–20	0.3	8–35	−100	19–21	0.2
1–28	−0.3	8–35	49.3	19–29	−0.2
2–28	0	8–35	49	24–20	−0.1
2–29	0	9–16	0.9	20–26	0.3
3–11	0	10–12	0.2	22–21	−0.2
3–30	0	11–25	0	22–33	0.2
4–6	0.3	11–25	0	24–27	0.1
4–12	−0.2	13–23	−0.4	24–37	−0.1
4–27	−0.1	13–32	0.5	27–26	−0.2
5–10	0.2	13–33	−0.2	27–26	−0.2
5–11	0	14–32	0	27–28	−0.4
5–16	−0.9	14–32	0	27–31	0.8
5–28	0.3	15–30	0.8	30–29	0.2
5–28	0.3	17–18	−0.1	30–29	0.2
6–36	0.3	17–18	−0.1	32–31	−0.2
7–23	0.4	20–17	−0.1	31–34	0.6
7–30	−0.4	21–18	0.1	32–35	0.8
8–9	0.9	18–29	−0.1	35–34	−0.6
8–15	0.8	37–18	−0.1	35–36	−0.3

.

Based on the calculated LODF values, it can be observed that the second and third lines between nodes 8 and 35 had LODFs of around 49%. This means that the majority of the power flow originally on the first line was redistributed to these two lines. Such a redistribution of power flow may lead to new power flow exceedance issues, particularly under high load conditions, thereby posing greater demands on the stable operation and safety management of the power grid.

By simulating the operation after disconnecting the branch, the operational status of each branch in the network is shown in Figure 6 (status after branch disconnection). It is observed that the flow reached up to 87% of the limit, exceeding the safe operational range. With the above LODF results, it is possible to more accurately identify key lines that may affect system stability following a specific line fault, helping to prioritize which lines need special attention in emergency response plans.

To eliminate this fault, the sensitivity of the second line between nodes 8 and 35 after disconnecting the first line was calculated, with the generator node sensitivities are shown in

Table 3. Sensitivity of the generator node to the active power and apparent power of the second branch of 8–35.

Node	Active Power		Apparent Power
	Active Power Sensitivity	Voltage Sensitivity	Active Power Sensitivity	Voltage Sensitivity
7	0.012247	0.052515	−0.01004	−0.04975
17	0.007686	0.025028	−0.00697	−0.04721
20	0	0.006698	0	−0.23132
30	0.07591	0.469387	−0.0698	−1.04621
32	−0.13424	−0.23002	0.127489	0.213316
33	−0.04154	−0.08848	0.040165	0.076956
34	−0.12678	0.133002	0.120344	−0.16483
35	−0.19211	89.96357	0.18219	−94.7489

.

According to the active power sensitivity of the generator nodes to the second branch of 8–35, the order of the generator adjustments was determined, and the active power output was adjusted in steps. In the first step, the outputs of generators at nodes 35 and 30 are adjusted to 78 MW and 42 MW, respectively. The operating status of each branch was then checked; at this time, the exceedance branch was 31–32, with a power flow of 86.5%. In the second step, referring to Scenario One, the outputs of generators at nodes 32, 33, and 34 were adjusted to 58 MW, 60 MW, and 100 MW, respectively. At this time, the exceedance branches included not only 31–34 and 31–32 but also the two branches between 8 and 35. The failure to control the power flow below 80% was due to the adjustment of the generators at nodes 35 and 30, which also impacts other branches, thus not being effectively controlled as in Scenario One. Furthermore, the adjustments at nodes 32, 33, and 34 affect the two branches between 8 and 35, causing them to exceed limits again. Further adjustments are needed. In the third step, the generator voltage at node 32 was adjusted to 1.005, and the outputs of the generators at nodes 35 and 30 were adjusted to 72 MW and 48 MW, respectively, bringing the power flow in all branches to within a reasonable range. The flow in each branch during the adjustment process is shown in Figure 6.

4.2.3. Scenario Three

For the branch 31–32, both the sensitivity-weighted PSO algorithm for branch power flow exceedance elimination and the conventional PSO algorithm were applied. The comparative results of the calculations are illustrated in Figure 7.

Both methods achieved the set requirements for eliminating branch exceedance; however, there was a significant difference in the adjustment of generator outputs. In practice, smaller adjustments are more in line with actual needs. The total adjustment amount for the generators using the sensitivity-weighted PSO algorithm was 144.78 MW, compared to 327.87 MW for the conventional PSO algorithm, demonstrating that the algorithm designed in this paper is more efficient and practical. In terms of computation speed, the sensitivity-weighted PSO algorithm took 0.82 s, while the conventional PSO algorithm took 1.45 s, indicating a significant improvement in the computation speed for the algorithm designed in this paper.

Moreover, compared to the method using sensitivity alone in Scenario One, the sensitivity-weighted PSO algorithm allows for easier parameter adjustment and is more straightforward to implement.

5. Conclusions

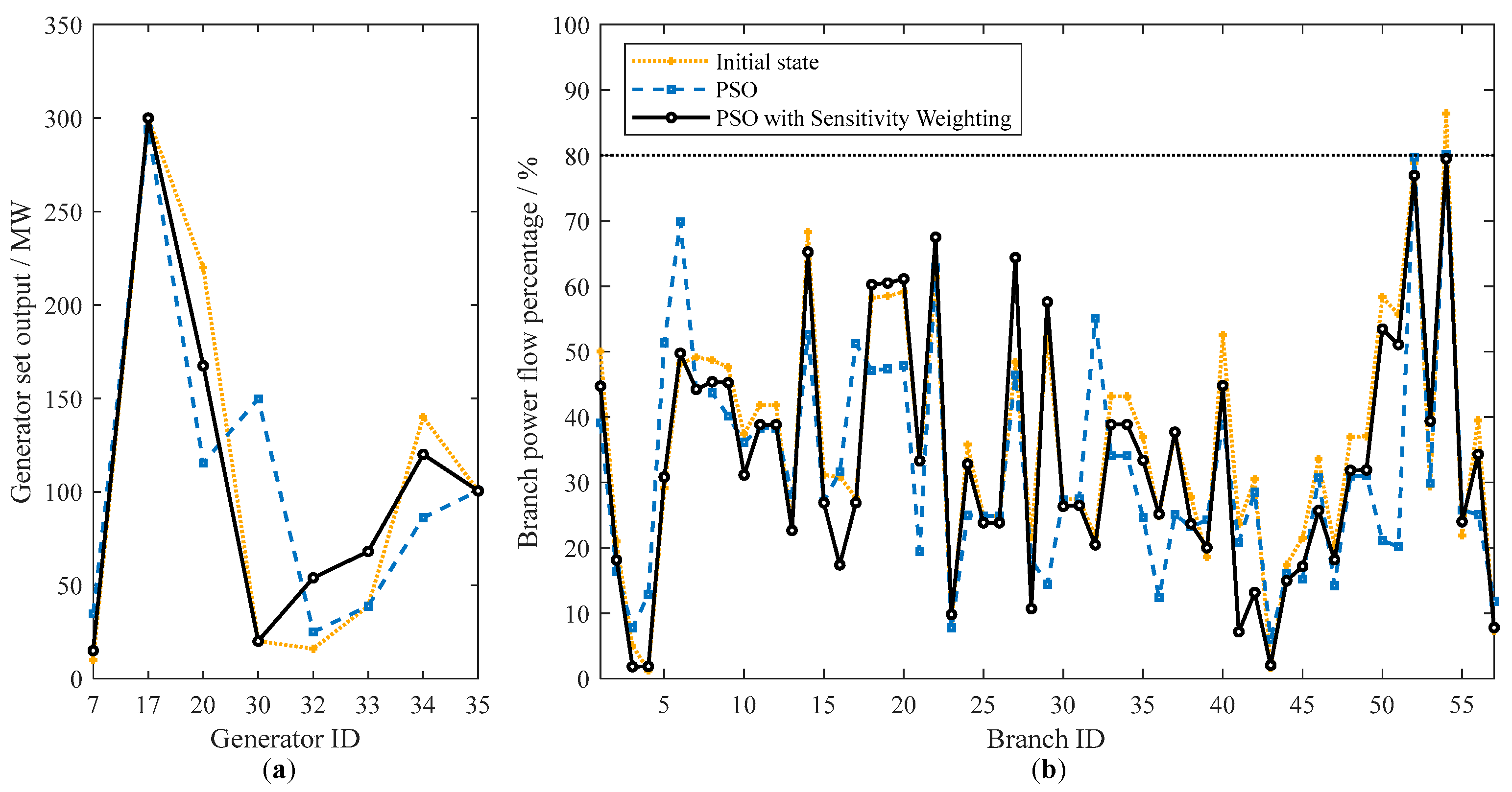
This study, through the integrated use of sensitivity analysis and distribution factors, has designed a branch exceedance elimination method based on sensitivity-weighted PSO algorithm. This method offers the advantages of high operational efficiency, effective optimization results, and ease of application in practical engineering projects, playing a key role in preventing and addressing branch flow exceedances in power systems.

The article thoroughly analyzes and derives power flow sensitivity, voltage sensitivity, and LODF. Sensitivity analysis enables the prediction of power flow responses at various nodes within the power system due to power or voltage changes, providing a scientific basis and priority determination for generator output scheduling after branch exceedances. Additionally, the calculation of the distribution factor offers a quantitative assessment of the impact on the power flow distribution of the power system under specified circumstances, enhancing the predictive capability for system stability. Through the LODF results, it is possible to more accurately identify key lines that may affect system stability following a specific line fault, thus providing a scientific basis for grid operations. This helps prioritize which lines require special attention in emergency response plans. Additionally, this also emphasizes the need to consider the interdependencies among lines when designing and implementing grid operation strategies, particularly in highly interconnected networks.

The article demonstrates how the sensitivity and distribution factor can predict and control the branch power flow exceedance in the power system through simulation of actual power network cases. By combining theory and simulation, the designed method was verified to effectively and practically address branch power flow exceedance issues in power systems, also highlighting its practical application value in power system optimization and fault recovery processes. Through this research, the paper provides an effective analytical and operational strategy for branch power flow management in a power system, contributing significantly to enhancing the safety and reliability of power systems both theoretically and practically.