Multi-Objective Energy Management in Microgrids: Improved Honey Badger Algorithm with Fuzzy Decision-Making and Battery Aging Considerations
Abstract
1. Introduction
1.1. Motivation and Background
1.2. Related Works and Research Gap
- Despite the application of various optimization methods to EMS problems, research on improved and hybrid algorithms such as the improved honey badger algorithm (IHBA) that could potentially offer better performance is lacking.
- The literature rarely addresses the impact of battery aging costs on the overall operating cost, emission cost, and the sizing of energy resources and storage devices in MGs. The literature, including references [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25], does not address this cost. We need more research to comprehensively evaluate these effects.
1.3. Contributions of the Study
- Proposing a multi-objective, efficient EMS: This paper introduces an advanced EMS designed to optimize day-ahead energy planning and management using forecasted data. By incorporating a fuzzy decision-making approach, the proposed EMS can handle the different objectives of the EMS. This results in a more reliable and cost-effective energy management solution that balances multiple objectives, such as minimizing costs and reducing emissions.
- Presenting a new, improved optimization technique (the IHBA): The conventional HBA is an effective optimization tool due to its ability to balance exploration and exploitation, mimicking the honey badger’s dynamic foraging and digging behavior to navigate complex optimization landscapes. It maintains population diversity throughout the search process, preventing premature convergence and ensuring a comprehensive exploration of the solution space. Despite its robust capabilities, HBA features a simple and intuitive structure, making it easy to implement and computationally efficient. Additionally, its adaptability allows it to dynamically adjust its search strategy, making it well suited for a wide range of optimization problems. Moreover, according to the no free lunch (NFL) theory, no single optimization method is effective for solving all types of optimization problems [26]. Therefore, this paper introduces the improved honey badger algorithm (IHBA) as an innovative and efficient optimization technique designed to address the limitations of the basic honey badger algorithm (HBA), particularly when dealing with increased problem complexity and the risk of getting trapped in local optima. The IHBA incorporates advanced features like chaotic sequences and fuzzy decision-making, making it particularly effective in tackling complex, nonlinear optimization challenges in MG energy management.
- Considering multi-objective functions: Operating and emission expenses are both factored into the research’s all-encompassing multi-objective function within the context of MG energy management. This dual focus ensures that the EMS not only aims to minimize financial expenditures but also seeks to lessen its effect on the environment, ultimately producing a greener and more long-lasting energy management system.
- Evaluating battery aging cost effects: The study evaluates the impact of battery aging costs, which are influenced by the frequency of charging and discharging cycles, on MG energy management. By incorporating battery aging costs into the EMS, the paper provides a more accurate and realistic assessment of total operational costs, promoting more efficient and sustainable battery usage strategies.
- Comparative analysis of IHBA: Engineering studies utilizing NSGA-II and MOPSO for optimization problems have demonstrated that both methods exhibit strong and competitive performance compared with other advanced algorithms. These studies often compare the proposed algorithms against NSGA-II or MOPSO to highlight their effectiveness. In this paper, the performance of the proposed optimizer is evaluated in comparison with MOPSO, emphasizing its potential advantages and improvements over the established methods. The paper includes a thorough comparative analysis of the IHBA’s performance against classic methods for optimizing like the conventional honey badger algorithm (HBA) and particle swarm optimization (PSO). This comparison demonstrates the superior capability of IHBA in handling the complexities of MG energy management, highlighting its efficiency, reliability, and overall effectiveness in optimizing energy resource allocation and management strategies.
1.4. Paper Organization
2. Problem Formulation
2.1. Objective Function
2.2. Constraints
2.3. DGs Model
2.3.1. Microturbine and Fuel Cell
2.3.2. Diesel Generator
2.3.3. WT and PV
3. Proposed Optimization Approach
3.1. Overview of the HBA
3.1.1. First Step: Initial Setting
3.1.2. Second Step: Definition of Intensity
3.1.3. Third Step: Updating the Density Coefficient
3.1.4. Fourth Step: Escape from the Local Optimum
3.1.5. Fifth Step: Update the Representative’s Position
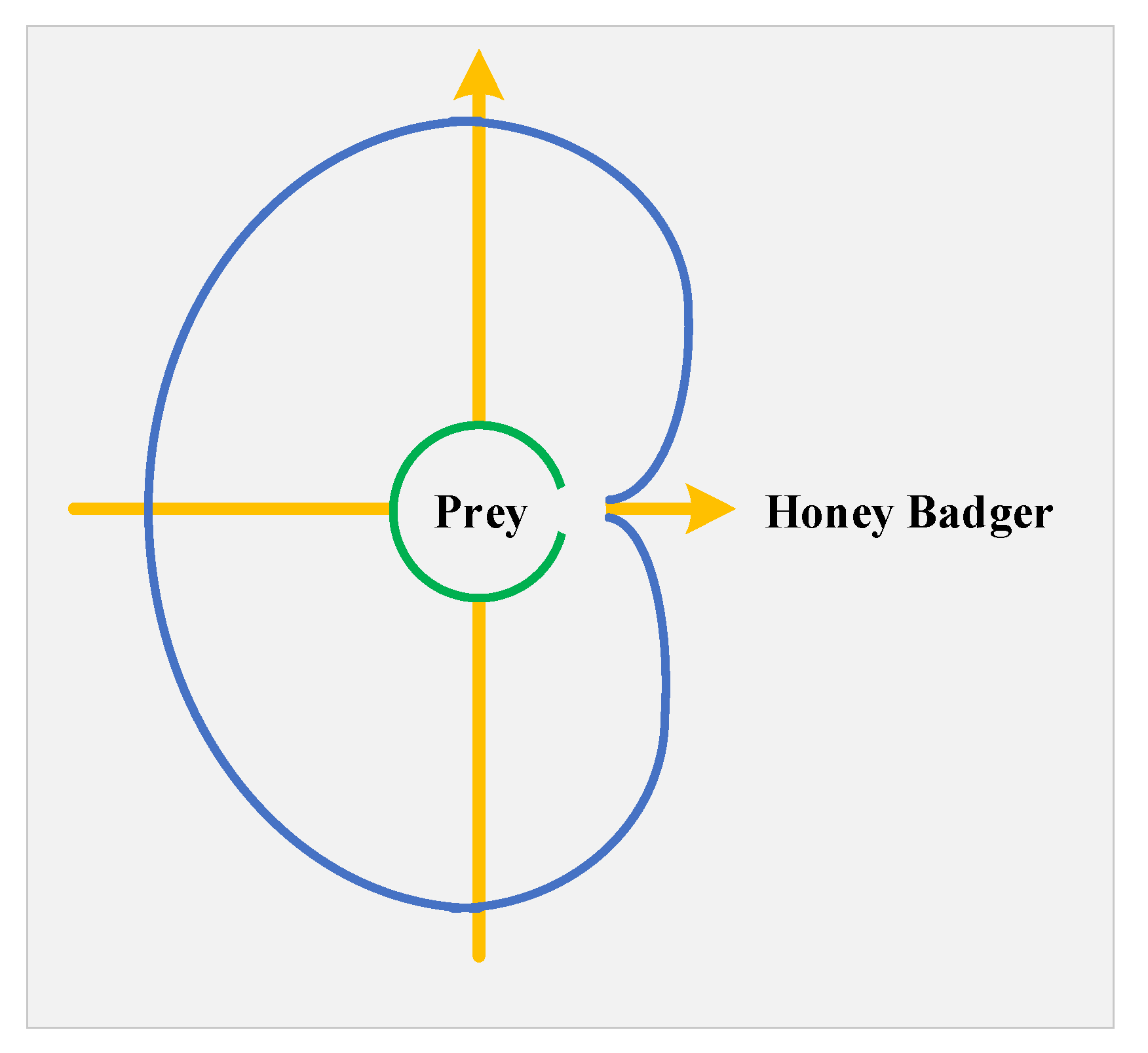
- Drilling phase
- Honey phase
3.2. Overview of the Improved HBA (IHBA)
- The search phases in the HBA can adapt based on the problem’s complexity. For example, in IHBA, the vector changes are made exponentially rather than linearly, following a chaotic sequence. This leads to faster convergence as the search process progresses, which is particularly useful for difficult optimization tasks.
- The enhanced version of HBA, IHBA, includes features like chaotic sequences and fuzzy decision-making. These features further improve the algorithm’s ability to handle complex optimization problems by enhancing the exploration and decision-making capabilities.
3.3. Multi-Objective Optimization Approach
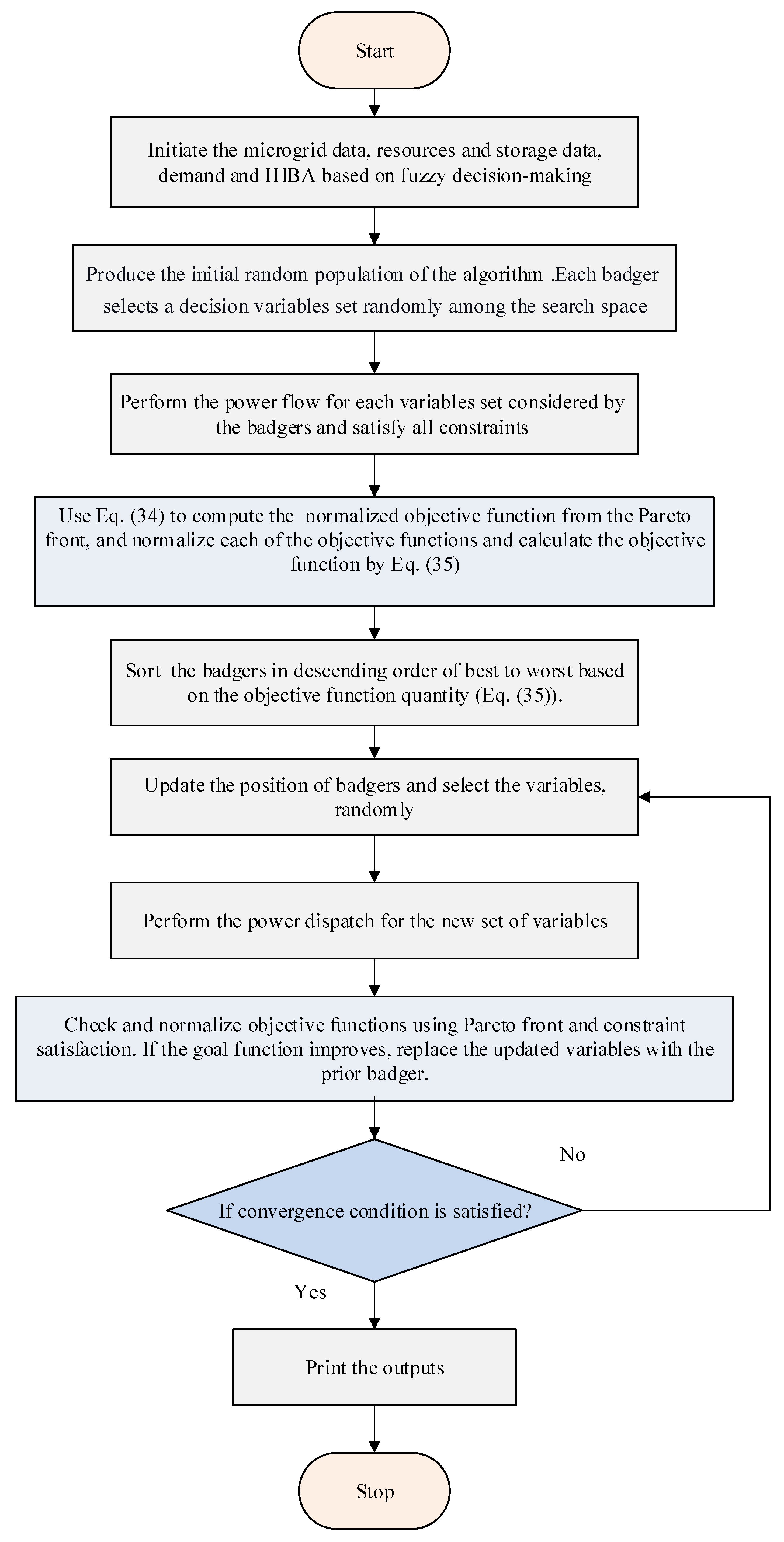
3.4. Implementation of the Fuzzy Multi-Objective IHBA
4. Results and Discussion
4.1. MG Data
4.2. Evaluating the IHBO’s Performance on the Benchmark Test Functions
4.3. Simulation Scenarios
- First scenario: MG energy management and scheduling with operation cost reduction
- Second scenario: MG energy management and scheduling with emission reduction
- Third scenario: MG energy management and scheduling with operation and emission cost reduction based on fuzzy multi-objective function
- Fourth scenario: MG energy management and scheduling with operation and emission cost reduction based on fuzzy multi-objective function incorporating battery aging.
4.3.1. Results of First Scenario
4.3.2. Results of Second Scenario
4.3.3. Results of Third Scenario
4.3.4. Results of Fourth Scenario
5. Conclusions
- In the first scenario, the single-objective IHBA was utilized for energy management and scheduling of the MG, aiming to reduce operating costs. The results demonstrated that the IHBA delivers high consistency and accuracy, which are crucial for achieving the most optimal solution. Furthermore, this method outperforms many other approaches by achieving lower costs. The findings also indicated that the outcomes from the IHBA are superior to those from traditional HBA and PSO methods as well as from previous studies. The optimization process led to a decrease in operating costs compared with the baseline state.
- In the second scenario, the single-objective IHBA was used for planning and energy management of the MG with a focus on minimizing emission costs. The results demonstrated that, like in the first scenario, the IHBA achieved a lower objective function and exhibited superior convergence compared with traditional HBA and PSO algorithms. This scenario successfully minimized emission costs while adhering to the constraints of the optimization problem. Although the optimization process led to a reduction in emission costs compared with the initial scenario, it also resulted in an increase in operating costs.
- The third scenario was implemented using the suggested multi-objective method by striking a compromise between different objectives, as evidenced by the results of the third scenario’s implementation with the multi-objective optimization of the MG, which considers the objectives of minimizing emissions and operation costs. The results showed that the emission cost decreased more than the operating cost, despite the fact that the multi-objective optimization increased the operating cost in comparison with the first scenario.
- The assessment of battery aging effects on MG optimization in the fourth scenario showed that the problem’s objective function experienced a rise in production and emission costs due to the battery’s power injection constraints. Specifically, these costs increased by 7.44% and 3.58%, respectively, compared with scenarios without battery aging.
- The IHBA shows superior performance compared with two conventional algorithms, HBA and PSO, by exhibiting more favorable and rapid convergence, overcoming local minima, and effectively balancing exploration and exploitation. This is evident from the results of applying the new, improved optimization method, which is based on chaotic sequences, to the EMS problem and the standard test functions. The IHBA’s ability to navigate complex problem spaces more efficiently and to consistently achieve optimal solutions underscores its potential for enhancing energy management systems and addressing challenges in optimization tasks.
- Future research is recommended to focus on robust optimization and energy management for multi-energy MGs that incorporate hydrogen storage, incorporating machine learning and RBF networks to forecast the renewable and load data. This involves minimizing operational and emission costs through the application of a novel optimization algorithm. By leveraging advanced techniques, the researchers aim to enhance the efficiency and sustainability of MG systems, ensuring optimal performance while reducing environmental impact. The development of such algorithms will address the complexities associated with integrating hydrogen storage, ultimately leading to more effective and cost-efficient energy management strategies.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | |
| Total number of measured periods (hours) during the period under consideration. | |
| Total number of distributed generations, including storage units. | |
| Active power purchased or sold from the network at time (kW). | |
| Auction value based on the th DG unit’s active power at time and the average power trade price between micro- and macro-grids. | |
| Control variable vector representing the active generation power and storage device inside the microgrid (MG). | |
| Variable representing the energy actively drawn from or sent to the power grid. | |
| Emissions from the th generator at time (kg/MWh). | |
| Emissions from the storage device at time (kg/MWh). | |
| Emissions from the power company at time (kg/MWh). | |
| Cost of battery aging. | |
| Battery investment cost. | |
| Usable energy of the battery at time . | |
| DOD | Battery’s depth of discharge relative to its maximum capacity. |
| Minimum state of charge of the battery. | |
| Specific parameters of the battery (empirically determined values, and for lithium-ion batteries). | |
| Load level of demand . | |
| Total number of load levels. | |
| Minimum active power of the th DG at time . | |
| Minimum active power of the network at time . | |
| Maximum active power of the th DG at time . | |
| Maximum active power of the network at time . | |
| Energy storage capacity of the battery at hour . | |
| Energy storage capacity of the battery at hour . | |
| Permissible charge/discharge rate of the battery during time interval . | |
| Efficiency of the battery during charging/discharging processes. | |
| Minimum energy storage limit of the battery. | |
| Maximum energy storage limit of the battery. | |
| Maximum charge/discharge rate of the battery for each period . | |
| Power acquired from the grid at time . | |
| Limiting variable of grid power at time . | |
| Penalty factor. | |
| Output electrical power from distributed generation sources such as microturbines and fuel cells (kW). | |
| Electrical efficiency of the generation source. | |
| Fuel price (EUR per kWh). | |
| Hourly repayment rate for investment costs related to distributed generation (EUR per hour). | |
| Setup cost of distributed generation. | |
| Depreciation period in years. | |
| Interest rate. | |
| Thermodynamic potential of the fuel cell (0.9 V). | |
| Potential of the selected cell at rated power (0.45 to 0.75 V). | |
| Power level, . | |
| Rated power of the fuel cell. | |
| Diesel generator fuel consumption (liters per hour). | |
| Diesel generator output power (kW). | |
| Characteristic coefficients of diesel generator fuel consumption. | |
| Rated power of the wind turbine. | |
| Wind speed. | |
| Nominal wind speed. | |
| Cut-in wind speed. | |
| Cut-out wind speed. | |
| Maximum photovoltaic output power under standard test conditions (STCs). | |
| Solar radiation on the surface of the photovoltaic module (W/m2). | |
| Temperature coefficient of the photovoltaic module for power (1/°C). | |
| Temperature of the photovoltaic module (°C). | |
| Ambient temperature (°C). | |
| Nominal operating cell temperature (°C). | |
| Symbols related to Section 3: | |
| Random number ranging from 0 to 1. | |
| Lower and upper boundaries of the search area, respectively. | |
| Location of the th honey badger, representing a potential solution within the population size . | |
| Intensity of the prey’s smell, as perceived by the th honey badger. | |
| Focus power source, representing the prey’s location. | |
| Distance between the prey and the th honey badger. | |
| Best position discovered so far, or the most advantageous location, with (usually set to 6) indicating the honey badger’s capacity to obtain food. | |
| Three separate random numbers ranging from 0 to 1. | |
| Flag that modifies the search direction. | |
| Location of the prey. | |
| Odor intensity of the prey. | |
| Time-dependent search impact element. | |
| Upper value of the th objective function, corresponding to non-dominated solutions. | |
| Lower value of the th objective function, corresponding to non-dominated solutions. | |
| Value ranging from 0 to 1, where indicates the sum of incompatibilities and indicates full ability for the th Pareto solution. | |
| Number of objective functions. | |
| Number of non-dominated solutions. | |
References
- Suresh, V.; Janik, P.; Jasinski, M.; Guerrero, J.M.; Leonowicz, Z. Microgrid Energy Management Using Metaheuristic Optimization Algorithms. Appl. Soft Comput. 2023, 134, 109981. [Google Scholar] [CrossRef]
- Aghajani, G.R.; Shayanfar, H.A.; Shayeghi, H. Demand side management in a smart micro-grid in the presence of renewable generation and demand response. Energy 2017, 126, 622–637. [Google Scholar] [CrossRef]
- Karimi, H.; Jadid, S.; Hasanzadeh, S. Optimal-Sustainable Multi-Energy Management of Microgrid Systems Considering Integration of Renewable Energy Resources: A Multi-Layer Four-Objective Optimization. Sustain. Prod. Consum. 2023, 36, 126–138. [Google Scholar] [CrossRef]
- Sepehrzad, R.; Rahimi, M.K.; Al-Durra, A.; Allahbakhshi, M.; Moridi, A. Optimal Energy Management of Distributed Generation in Micro-Grid to Control the Voltage and Frequency Based on PSO-Adaptive Virtual Impedance Method. Electr. Power Syst. Res. 2022, 208, 107881. [Google Scholar] [CrossRef]
- Sepehrzad, R.; Mahmoodi, A.; Ghalebi, S.Y.; Moridi, A.R.; Seifi, A.R. Intelligent Hierarchical Energy and Power Management to Control the Voltage and Frequency of Micro-Grids Based on Power Uncertainties and Communication Latency. Electr. Power Syst. Res. 2022, 202, 107567. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, Y.; Yuan, K.; Khayatnezhad, M.; Ghadimi, N. Efficient Design of Energy Microgrid Management System: A Promoted Remora Optimization Algorithm-Based Approach. Heliyon 2024, 10, e23394. [Google Scholar] [CrossRef]
- Moghaddam, A.A.; Seifi, A.; Niknam, T.; Pahlavani, M.R.A. Multi-Objective Operation Management of a Renewable MG (Micro-Grid) with Back-up Micro-Turbine/Fuel Cell/Battery Hybrid Power Source. Energy 2011, 36, 6490–6507. [Google Scholar] [CrossRef]
- Kumar, R.P.; Karthikeyan, G. A Multi-Objective Optimization Solution for Distributed Generation Energy Management in Microgrids with Hybrid Energy Sources and Battery Storage System. J. Energy Storage 2024, 75, 109702. [Google Scholar] [CrossRef]
- Hai, T.; Zhou, J.; Khaki, M. Optimal Planning and Design of Integrated Energy Systems in a Microgrid Incorporating Electric Vehicles and Fuel Cell System. J. Power Sources 2023, 561, 232694. [Google Scholar] [CrossRef]
- Dey, B.; Misra, S.; Marquez, F.P.G. Microgrid System Energy Management with Demand Response Program for Clean and Economical Operation. Appl. Energy 2023, 334, 120717. [Google Scholar] [CrossRef]
- Alamir, N.; Kamel, S.; Megahed, T.F.; Hori, M.; Abdelkader, S.M. Developing Hybrid Demand Response Technique for Energy Management in Microgrid Based on Pelican Optimization Algorithm. Electr. Power Syst. Res. 2023, 214, 108905. [Google Scholar] [CrossRef]
- Lu, Z.; Gao, Y.; Xu, C.; Li, Y. Configuration optimization of an off-grid multi-energy microgrid based on modified NSGA-II and order relation-TODIM considering uncertainties of renewable energy and load. J. Clean. Prod. 2023, 383, 135312. [Google Scholar] [CrossRef]
- Parvin, M.; Yousefi, H.; Noorollahi, Y. Techno-economic optimization of a renewable micro grid using multi-objective particle swarm optimization algorithm. Energy Convers. Manag. 2023, 277, 116639. [Google Scholar] [CrossRef]
- Ferahtia, S.; Rezk, H.; Abdelkareem, M.A.; Olabi, A.G. Optimal Techno-Economic Energy Management Strategy for Building’s Microgrids Based Bald Eagle Search Optimization Algorithm. Appl. Energy 2022, 306, 118069. [Google Scholar] [CrossRef]
- Dey, B.; Raj, S.; Mahapatra, S.; Márquez, F.P.G. Optimal Scheduling of Distributed Energy Resources in Microgrid Systems Based on Electricity Market Pricing Strategies by a Novel Hybrid Optimization Technique. Int. J. Electr. Power Energy Syst. 2022, 134, 107419. [Google Scholar] [CrossRef]
- Sun, S.; Wang, C.; Wang, Y.; Zhu, X.; Lu, H. Multi-Objective Optimization Dispatching of a Micro-Grid Considering Uncertainty in Wind Power Forecasting. Energy Rep. 2022, 8, 2859–2874. [Google Scholar] [CrossRef]
- Eskandari, H.; Kiani, M.; Zadehbagheri, M.; Niknam, T. Optimal Scheduling of Storage Device, Renewable Resources and Hydrogen Storage in Combined Heat and Power Microgrids in the Presence Plug-in Hybrid Electric Vehicles and Their Charging Demand. J. Energy Storage 2022, 50, 104558. [Google Scholar] [CrossRef]
- Xiaoluan, Z.; Farajian, H.; Xifeng, W.; Latifi, M.; Ohshima, K. Scheduling of Renewable Energy and Plug-in Hybrid Electric Vehicles Based Microgrid Using Hybrid Crow—Pattern Search Method. J. Energy Storage 2022, 47, 103605. [Google Scholar] [CrossRef]
- Dey, B.; Márquez, F.P.G.; Panigrahi, P.K.; Bhattacharyya, B. A Novel Metaheuristic Approach to Scale the Economic Impact of Grid Participation on a Microgrid System. Sustain. Energy Technol. Assess. 2022, 53, 102417. [Google Scholar] [CrossRef]
- Taghikhani, M.A.; Khamseh, J. Multi-Objective Optimal Energy Management of Storage System and Distributed Generations via Water Cycle Algorithm Concerning Renewable Resources Uncertainties and Pollution Reduction. J. Energy Storage 2022, 52, 104756. [Google Scholar] [CrossRef]
- Liao, N.; Hu, Z.; Mrzljak, V.; Arabi Nowdeh, S. Stochastic Techno-Economic Optimization of Hybrid Energy System with Photovoltaic, Wind, and Hydrokinetic Resources Integrated with Electric and Thermal Storage Using Improved Fire Hawk Optimization. Sustainability 2024, 16, 6723. [Google Scholar] [CrossRef]
- Nowdeh, S.A.; Naderipour, A.; Davoudkhani, I.F.; Guerrero, J.M. Stochastic optimization–based economic design for a hybrid sustainable system of wind turbine, combined heat, and power generation, and electric and thermal storages considering uncertainty: A case study of Espoo, Finland. Renew. Sustain. Energy Rev. 2023, 183, 113440. [Google Scholar] [CrossRef]
- Sun, H.; Cui, X.; Latifi, H. Optimal management of microgrid energy by considering demand side management plan and maintenance cost with developed particle swarm algorithm. Electr. Power Syst. Res. 2024, 231, 110312. [Google Scholar] [CrossRef]
- Habibi, S.; Effatnejad, R.; Hedayati, M.; Hajihosseini, P. Stochastic energy management of a microgrid incorporating two-point estimation method, mobile storage, and fuzzy multi-objective enhanced grey wolf optimizer. Sci. Rep. 2024, 14, 1667. [Google Scholar]
- Upadhyay, S.; Ahmed, I.; Mihet-Popa, L. Energy Management System for an Industrial Microgrid Using Optimization Algorithms-Based Reinforcement Learning Technique. Energies 2024, 17, 3898. [Google Scholar] [CrossRef]
- Adam, S.P.; Alexandropoulos, S.A.N.; Pardalos, P.M.; Vrahatis, M.N. No free lunch theorem: A review. In Approximation and Optimization: Algorithms, Complexity and Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 57–82. [Google Scholar]
- Schwenk, K.; Meisenbacher, S.; Briegel, B.; Harr, T.; Hagenmeyer, V.; Mikut, R. Integrating Battery Aging in the Optimization for Bidirectional Charging of Electric Vehicles. IEEE Trans. Smart Grid 2021, 12, 5135–5145. [Google Scholar] [CrossRef]
- Aghajani, G.R.; Shayanfar, H.A.; Shayeghi, H. Presenting a Multi-Objective Generation Scheduling Model for Pricing Demand Response Rate in Micro-Grid Energy Management. Energy Convers. Manag. 2015, 106, 308–321. [Google Scholar] [CrossRef]
- Yahiaoui, A.; Fodhil, F.; Benmansour, K.; Tadjine, M.; Cheggaga, N. Grey Wolf Optimizer for Optimal Design of Hybrid Renewable Energy System PV-Diesel Generator-Battery: Application to the Case of Djanet City of Algeria. Sol. Energy 2017, 158, 941–951. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New Metaheuristic Algorithm for Solving Optimization Problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Mokeddem, D. A New Improved Salp Swarm Algorithm Using Logarithmic Spiral Mechanism Enhanced with Chaos for Global Optimization. Evol. Intell. 2021, 15, 1745–1775. [Google Scholar] [CrossRef]
- Nowdeh, S.A.; Davoudkhani, I.F.; Moghaddam, M.J.H.; Najmi, E.S.; Abdelaziz, A.Y.; Ahmadi, A.; Razavi, S.E.; Gandoman, F.H. Fuzzy Multi-Objective Placement of Renewable Energy Sources in Distribution System with Objective of Loss Reduction and Reliability Improvement Using a Novel Hybrid Method. Appl. Soft Comput. 2019, 77, 761–779. [Google Scholar] [CrossRef]
- Golalipour, K.; Nowdeh, S.A.; Akbari, E.; Hamidi, S.S.; Ghasemi, D.; Abdelaziz, A.Y.; Kotb, H.; Yousef, A. Snow Avalanches Algorithm (SAA): A New Optimization Algorithm for Engineering Applications. Alex. Eng. J. 2023, 83, 257–285. [Google Scholar] [CrossRef]
















| Type | Min Power (kW) | Max Power (kW) | a (EURct/kW h2) | b (EURct/kW h) | c (EURct/h) | CO2 (kg/kWh) | SO2 (kg/kWh) | NOx (kg/kWh) |
|---|---|---|---|---|---|---|---|---|
| MT | 6 | 30 | 0 | 0.457 | 0 | 720 | 0.0036 | 0.1 |
| PV | 0 | 25 | 0 | 2.584 | 0 | 0 | 0 | 0 |
| FC | 3 | 30 | 0 | 0.294 | 0 | 460 | 0.003 | 0.0075 |
| WT | 0 | 15 | 0 | 1.073 | 0 | 0 | 0 | 0 |
| Battery | −30 | 30 | 0 | 0.380 | 0 | 10 | 0.0002 | 0.001 |
| Grid | −30 | 30 | 0 | - | 0 | 950 | 0.5 | 2.1 |
| Function | Dim | Type | Range | fmin |
|---|---|---|---|---|
| 30 | U | [−100,100] | 0 | |
| 30 | U | [−10,10] | 0 | |
| 30 | U | [−100,100] | 0 | |
| 30 | U | [−100,100] | 0 | |
| 30 | M | [−5.12,5.12] | 0 | |
| 30 | M | [−600,600] | 0 | |
| 30 | M | [−32,32] | 0 | |
| 4 | F | [−5,5] | 0.003 | |
| 4 | F | [0,10] | −10 |
| Functions | Quantity | PSO | HBA | IHBA |
|---|---|---|---|---|
| F1 | Best | 7.8077 × 10−8 | 3.0019 × 10−153 | 9.7372 × 10−223 |
| Mean | 1.5307 × 10−6 | 6.322 × 10−147 | 6.2472 × 10−219 | |
| STD | 1.7177 × 10−6 | 2.0911 × 10−146 | 0 | |
| Rank | 3 | 2 | 1 | |
| F2 | Best | 0.00019619 | 1.941 × 10−81 | 1.7628 × 10−113 |
| Mean | 0.0022842 | 2.4113 × 10−78 | 5.8859 × 10−111 | |
| STD | 0.0038183 | 3.2957 × 10−78 | 8.9739 × 10−111 | |
| Rank | 3 | 2 | 1 | |
| F3 | Best | 3.7395 | 1.3108 × 10−116 | 5.7235 × 10−214 |
| Mean | 8.1127 | 7.1951 × 10−108 | 4.6432 × 10−209 | |
| STD | 2.7794 | 2.8384 × 10−107 | 0 | |
| Rank | 3 | 2 | 1 | |
| F4 | Best | 0.18804 | 1.3434 × 10−65 | 1.9347 × 10−109 |
| Mean | 0.28315 | 6.4748 × 10−62 | 6.5422 × 10−107 | |
| STD | 0.074822 | 1.5819 × 10−61 | 1.877 × 10−106 | |
| Rank | 3 | 2 | 1 | |
| F5 | Best | 0.055889 | 9.7363 × 10−6 | 3.4035 × 10−6 |
| Mean | 0.097544 | 0.00032382 | 0.00023109 | |
| STD | 0.029638 | 0.00043249 | 0.00020734 | |
| Rank | 2 | 1 | 1 | |
| F6 | Best | 22.2673 | 0 | 0 |
| Mean | 42.5727 | 0 | 0 | |
| STD | 13.3025 | 0 | 0 | |
| Rank | 2 | 1 | 1 | |
| F7 | Best | 7.9936 × 10−15 | 8.8818 × 10−16 | 8.8818 × 10−16 |
| Mean | 2.4993 × 10−13 | 8.8818 × 10−16 | 8.8818 × 10−16 | |
| STD | 3.0874 × 10−13 | 0 | 0 | |
| Rank | 2 | 1 | 1 | |
| F8 | Best | 2.436 | 0 | 0 |
| Mean | 6.9443 | 0 | 0 | |
| STD | 2.7788 | 0 | 0 | |
| Rank | 2 | 1 | 1 | |
| F9 | Best | 0.00030751 | 0.00030749 | 0.00030749 |
| Mean | 0.00056656 | 0.005241 | 0.0032009 | |
| STD | 0.0002199 | 0.0088553 | 0.0072998 | |
| Rank | 3 | 2 | 1 |
| Time (h) | Load | Power (kW) | Cost (EURct/h) | Emission (kg/h) | |||||
|---|---|---|---|---|---|---|---|---|---|
| PV | WT | MT | FC | Battery | Utility | ||||
| 1 | 52 | 0 | 1.785 | 6 | 30 | −15.785 | 30 | 14.379 | 46.5411 |
| 2 | 50 | 0 | 1.785 | 6 | 30 | −17.785 | 30 | 12.419 | 46.5211 |
| 3 | 50 | 0 | 1.785 | 6 | 30 | −17.785 | 30 | 10.919 | 46.5211 |
| 4 | 51 | 0 | 1.785 | 6 | 30 | −16.785 | 30 | 10.699 | 46.5311 |
| 5 | 56 | 0 | 1.785 | 6 | 30 | −11.785 | 30 | 12.599 | 46.5811 |
| 6 | 63 | 0 | 0.915 | 6 | 30 | −3.9150 | 30 | 17.0561 | 46.6598 |
| 7 | 70 | 0 | 1.785 | 6 | 30 | 2.215 | 30 | 21.219 | 46.7211 |
| 8 | 75 | 0.2 | 1.305 | 6 | 30 | 15.3714 | 22.1236 | 27.7272 | 28.8545 |
| 9 | 76 | 3.75 | 1.785 | 30 | 30 | 30 | −19.535 | 16.2328 | 17.0944 |
| 10 | 80 | 7.525 | 3.09 | 30 | 30 | 30 | −20.615 | −25.7698 | 16.0656 |
| 11 | 78 | 10.45 | 8.775 | 28.775 | 30 | 30 | −30.000 | −50.2115 | 6.2434 |
| 12 | 74 | 11.95 | 10.41 | 21.64 | 30 | 30 | −30.000 | −47.8418 | 1.1062 |
| 13 | 72 | 23.9 | 3.915 | 14.185 | 30 | 30 | −30.000 | 47.6609 | −4.2630 |
| 14 | 72 | 21.05 | 2.37 | 18.58 | 30 | 30 | −30.000 | −34.3527 | −1.0981 |
| 15 | 76 | 7.875 | 1.785 | 30 | 30 | 30 | −23.660 | 8.8743 | 13.1649 |
| 16 | 80 | 4.225 | 1.305 | 30 | 30 | 30 | −15.530 | 15.9639 | 20.9096 |
| 17 | 85 | 0.55 | 1.785 | 30 | 30 | 30 | −7.3350 | 32.8655 | 28.7161 |
| 18 | 88 | 0 | 1.785 | 6 | 30 | 30 | 20.215 | 33.1655 | 37.6778 |
| 19 | 90 | 0 | 1.302 | 6 | 30 | 22.698 | 30 | 32.0843 | 46.9259 |
| 20 | 87 | 0 | 1.785 | 6 | 30 | 30 | 19.215 | 33.1398 | 36.7252 |
| 21 | 78 | 0 | 1.3005 | 30 | 30 | 30 | −13.300 | 19.7639 | 23.0334 |
| 22 | 71 | 0 | 1.3005 | 30 | 30 | 30 | −20.300 | 24.3632 | 16.3652 |
| 23 | 65 | 0 | 0.915 | 6 | 30 | −1.9150 | 30 | 20.8161 | 46.6798 |
| 24 | 56 | 0 | 0.615 | 6 | 30 | −10.615 | 30 | 15.9882 | 46.5928 |
| Total (per/day): | 269.7599 | 706.87 | |||||||
| Objective | Method | Best Solution |
|---|---|---|
| Cost (EURct) | GA [7] | 277.7444 |
| PSO [7] | 277.3237 | |
| FSAPSO [7] | 276.7867 | |
| CPSO-T [7] | 275.0455 | |
| CPSO-L [7] | 274.7438 | |
| AMPSO-T [7] | 274.5507 | |
| AMPSO-L [7] | 274.4317 | |
| GSA [7] | 275.5369 | |
| SGSA [7] | 269.76 | |
| HBA | 269.76 | |
| IHBA | 269.7599 |
| Time (h) | Load | Power (kW) | Cost (EURct/h) | Emission (kg/h) | |||||
|---|---|---|---|---|---|---|---|---|---|
| MT | FC | PV | WT | Battery | Utility | ||||
| 1 | 52 | 20.215 | 30 | 0 | 1.785 | 30 | −30 | 24.47356 | 0.079245 |
| 2 | 50 | 18.215 | 30 | 0 | 1.785 | 30 | −30 | 24.75956 | −1.36096 |
| 3 | 50 | 18.215 | 30 | 0 | 1.785 | 30 | −30 | 26.25956 | −1.36096 |
| 4 | 51 | 19.215 | 30 | 0 | 1.785 | 30 | −30 | 27.31656 | −0.64086 |
| 5 | 56 | 24.215 | 30 | 0 | 1.785 | 30 | −30 | 29.60156 | 2.95966 |
| 6 | 63 | 30 | 30 | 0 | 0.915 | 30 | −27.915 | 29.3288 | 9.11163 |
| 7 | 70 | 30 | 30 | 0 | 1.785 | 30 | −21.785 | 30.83476 | 14.95107 |
| 8 | 75 | 30 | 30 | 0.2 | 1.305 | 30 | −16.505 | 29.57517 | 19.9808 |
| 9 | 76 | 30 | 30 | 3.75 | 1.785 | 30 | −19.535 | 16.23281 | 17.09442 |
| 10 | 80 | 30 | 30 | 7.525 | 3.09 | 30 | −20.615 | −25.7698 | 16.06561 |
| 11 | 78 | 28.775 | 30 | 10.45 | 8.775 | 30 | −30 | −50.2115 | 6.243332 |
| 12 | 74 | 21.64 | 30 | 11.95 | 10.41 | 30 | −30 | −47.8418 | 1.105393 |
| 13 | 72 | 14.185 | 30 | 23.9 | 3.915 | 30 | −30 | 47.66094 | −4.26298 |
| 14 | 72 | 18.58 | 30 | 21.05 | 2.37 | 30 | −30 | −34.3527 | −1.09812 |
| 15 | 76 | 30 | 30 | 7.875 | 1.785 | 30 | −23.66 | 8.874305 | 13.16494 |
| 16 | 80 | 30 | 30 | 4.225 | 1.305 | 30 | −15.53 | 15.96417 | 20.90958 |
| 17 | 85 | 30 | 30 | 0.55 | 1.785 | 30 | −7.335 | 32.86551 | 28.71614 |
| 18 | 88 | 30 | 30 | 0 | 1.785 | 30 | −3.785 | 34.29346 | 32.09787 |
| 19 | 90 | 30 | 30 | 0 | 1.302 | 30 | −1.302 | 34.87135 | 34.46317 |
| 20 | 87 | 30 | 30 | 0 | 1.785 | 30 | −4.785 | 33.78776 | 31.14527 |
| 21 | 78 | 30 | 30 | 0 | 1.3005 | 30 | −13.300 | 19.76385 | 23.0334 |
| 22 | 71 | 30 | 30 | 0 | 1.3005 | 30 | −20.300 | 24.36317 | 16.3652 |
| 23 | 65 | 30 | 30 | 0 | 0.915 | 30 | −25.915 | 27.1373 | 11.01683 |
| 24 | 56 | 25.385 | 30 | 0 | 0.615 | 30 | −30 | 24.68084 | 3.802181 |
| Total (per/day): | 384.4691 | 293.5819 | |||||||
| Time (h) | Load | Power (kW) | Cost (EURct/h) | Emission (kg/h) | |||||
|---|---|---|---|---|---|---|---|---|---|
| MT | FC | PV | WT | Battery | Utility | ||||
| 1 | 52 | 6 | 30 | 0 | 1.785 | 30 | −15.785 | 21.24676 | 3.384182 |
| 2 | 50 | 6 | 30 | 0 | 1.785 | 30 | −17.785 | 21.49816 | 1.478982 |
| 3 | 50 | 6 | 3 | 0 | 1.785 | 30 | 9.215 | 13.24101 | 34.37081 |
| 4 | 51 | 6 | 3 | 0 | 1.785 | 30 | 10.215 | 13.021 | 34.38082 |
| 5 | 56 | 6 | 3 | 0 | 1.785 | 30 | 15.215 | 14.92101 | 34.43082 |
| 6 | 63 | 6 | 30 | 0 | 0.915 | 30 | −3.915 | 23.1608 | 14.69154 |
| 7 | 70 | 6 | 30 | 0 | 1.785 | 30 | 2.215 | 25.38676 | 20.53098 |
| 8 | 75 | 6 | 30 | 0.2 | 1.305 | 30 | 7.495 | 27.72717 | 25.56071 |
| 9 | 76 | 30 | 30 | 3.75 | 1.785 | 30 | −19.535 | 16.23281 | 17.09442 |
| 10 | 80 | 30 | 30 | 7.525 | 3.09 | 30 | −20.615 | −25.7698 | 16.06561 |
| 11 | 78 | 28.77501 | 30 | 10.45 | 8.775 | 30 | −30 | −50.2033 | 6.266408 |
| 12 | 74 | 21.64001 | 30 | 11.95 | 10.41 | 30 | −30 | −47.8418 | 1.10539 |
| 13 | 72 | 14.185 | 30 | 23.9 | 3.915 | 30 | −30 | 47.66094 | −4.26298 |
| 14 | 72 | 18.58002 | 30 | 21.05 | 2.37 | 30 | −30 | −34.3504 | −1.08075 |
| 15 | 76 | 30 | 30 | 7.875 | 1.785 | 30 | −23.66 | 8.874305 | 13.16494 |
| 16 | 80 | 30 | 30 | 4.225 | 1.305 | 30 | −15.53 | 15.96417 | 20.90958 |
| 17 | 85 | 30 | 30 | 0.55 | 1.785 | 30 | −7.335 | 32.86551 | 28.71614 |
| 18 | 88 | 30 | 30 | 0 | 1.785 | 30 | −3.785 | 34.29346 | 32.09787 |
| 19 | 90 | 6 | 30 | 0 | 1.302 | 30 | 22.698 | 32.30335 | 40.04309 |
| 20 | 87 | 30 | 30 | 0 | 1.785 | 30 | −4.785 | 33.78776 | 31.14527 |
| 21 | 78 | 30 | 30 | 0 | 1.3005 | 30 | −13.300 | 19.76385 | 23.0334 |
| 22 | 71 | 30 | 30 | 0 | 1.3005 | 30 | −20.3 | 24.36317 | 16.3652 |
| 23 | 65 | 6 | 30 | 0 | 0.915 | 30 | −1.915 | 23.3693 | 16.59674 |
| 24 | 56 | 6 | 30 | 0 | 0.615 | 30 | −10.615 | 20.862 | 8.309124 |
| Total (per/day): | 312.3778 | 434.3983 | |||||||
| Method | Cost (EURct/h) | Emission (kg/h) |
|---|---|---|
| NSGA-II | 314.1799 | 435.7832 |
| MOPSO | 314.8394 | 436.362 |
| MOHBA | 314.2022 | 436.2702 |
| MOIHBA | 312.3778 | 434.3983 |
| Time (h) | Load | Power (kW) | Cost (EURct/h) | Emission (kg/h) | |||||
|---|---|---|---|---|---|---|---|---|---|
| MT | FC | PV | WT | Battery | Utility | ||||
| 1 | 52 | 6 | 30 | 0 | 1.785 | 30 | −15.785 | 13.88786 | 3.384182 |
| 2 | 50 | 6 | 30 | 0 | 1.785 | 30 | −17.785 | 13.81646 | 1.478982 |
| 3 | 50 | 6 | 12.215 | 0 | 1.785 | 0 | 30 | 8.498414 | 38.51765 |
| 4 | 51 | 6 | 13.21498 | 0 | 1.785 | 0 | 30 | 8.756708 | 38.97765 |
| 5 | 56 | 6 | 18.21499 | 0 | 1.785 | 0 | 30 | 10.22671 | 41.27771 |
| 6 | 63 | 6 | 30 | 0 | 0.915 | 30 | −3.915 | 12.7268 | 14.69154 |
| 7 | 70 | 6 | 30 | 0 | 1.785 | 30 | 2.215 | 13.88786 | 20.53098 |
| 8 | 75 | 6 | 30 | 0.2 | 1.305 | 30 | 7.495 | 14.05097 | 25.56071 |
| 9 | 76 | 30 | 30 | 3.75 | 1.785 | 30 | −19.535 | 38.23781 | 17.09442 |
| 10 | 80 | 30 | 30 | 7.525 | 3.09 | 30 | −20.615 | 60.50967 | 16.06561 |
| 11 | 78 | 28.775 | 30 | 10.45 | 8.775 | 30 | −30 | 97.45955 | 6.243332 |
| 12 | 74 | 21.64 | 30 | 11.95 | 10.41 | 30 | −30 | 106.9392 | 1.105393 |
| 13 | 72 | 14.185 | 30 | 23.9 | 3.915 | 30 | −30 | 96.21544 | −4.26298 |
| 14 | 72 | 18.57988 | 30 | 21.05 | 2.37 | 30 | −29.9999 | 91.72622 | −1.0981 |
| 15 | 76 | 30 | 30 | 7.875 | 1.785 | 30 | −23.66 | 51.35681 | 13.16494 |
| 16 | 80 | 30 | 30 | 4.225 | 1.305 | 30 | −15.53 | 38.99792 | 20.90958 |
| 17 | 85 | 30 | 30 | 0.55 | 1.785 | 30 | −7.335 | 27.14651 | 28.71614 |
| 18 | 88 | 30 | 30 | 0 | 1.785 | 30 | −3.785 | 25.17716 | 32.09787 |
| 19 | 90 | 6 | 30 | 0 | 1.302 | 30 | 22.698 | 13.41475 | 40.04309 |
| 20 | 87 | 30 | 30 | 0 | 1.785 | 30 | −4.785 | 25.21286 | 31.14527 |
| 21 | 78 | 30 | 30 | 0 | 1.3005 | 30 | −13.3005 | 25.44702 | 23.0334 |
| 22 | 71 | 30 | 30 | 0 | 1.3005 | 30 | −20.3005 | 24.62771 | 16.3652 |
| 23 | 65 | 6 | 30 | 0 | 0.915 | 30 | −1.915 | 12.8183 | 16.59674 |
| 24 | 56 | 6 | 30 | 0 | 0.615 | 30 | −10.615 | 12.3818 | 8.309124 |
| Total (per/day): | 335.6221 | 449.9484 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alanazi, M.; Alanazi, A.; Memon, Z.A.; Awan, A.B.; Deriche, M. Multi-Objective Energy Management in Microgrids: Improved Honey Badger Algorithm with Fuzzy Decision-Making and Battery Aging Considerations. Energies 2024, 17, 4373. https://doi.org/10.3390/en17174373
Alanazi M, Alanazi A, Memon ZA, Awan AB, Deriche M. Multi-Objective Energy Management in Microgrids: Improved Honey Badger Algorithm with Fuzzy Decision-Making and Battery Aging Considerations. Energies. 2024; 17(17):4373. https://doi.org/10.3390/en17174373
Chicago/Turabian StyleAlanazi, Mohana, Abdulaziz Alanazi, Zulfiqar Ali Memon, Ahmed Bilal Awan, and Mohamed Deriche. 2024. "Multi-Objective Energy Management in Microgrids: Improved Honey Badger Algorithm with Fuzzy Decision-Making and Battery Aging Considerations" Energies 17, no. 17: 4373. https://doi.org/10.3390/en17174373
APA StyleAlanazi, M., Alanazi, A., Memon, Z. A., Awan, A. B., & Deriche, M. (2024). Multi-Objective Energy Management in Microgrids: Improved Honey Badger Algorithm with Fuzzy Decision-Making and Battery Aging Considerations. Energies, 17(17), 4373. https://doi.org/10.3390/en17174373









