Numerical Investigations into the Homogenization Effect of Nonlinear Composite Materials on the Pulsed Electric Field
Abstract
1. Introduction
2. Theory and Formulations
3. Numerical Simulations of the Homogenization Effect of Nonlinear Composite Materials
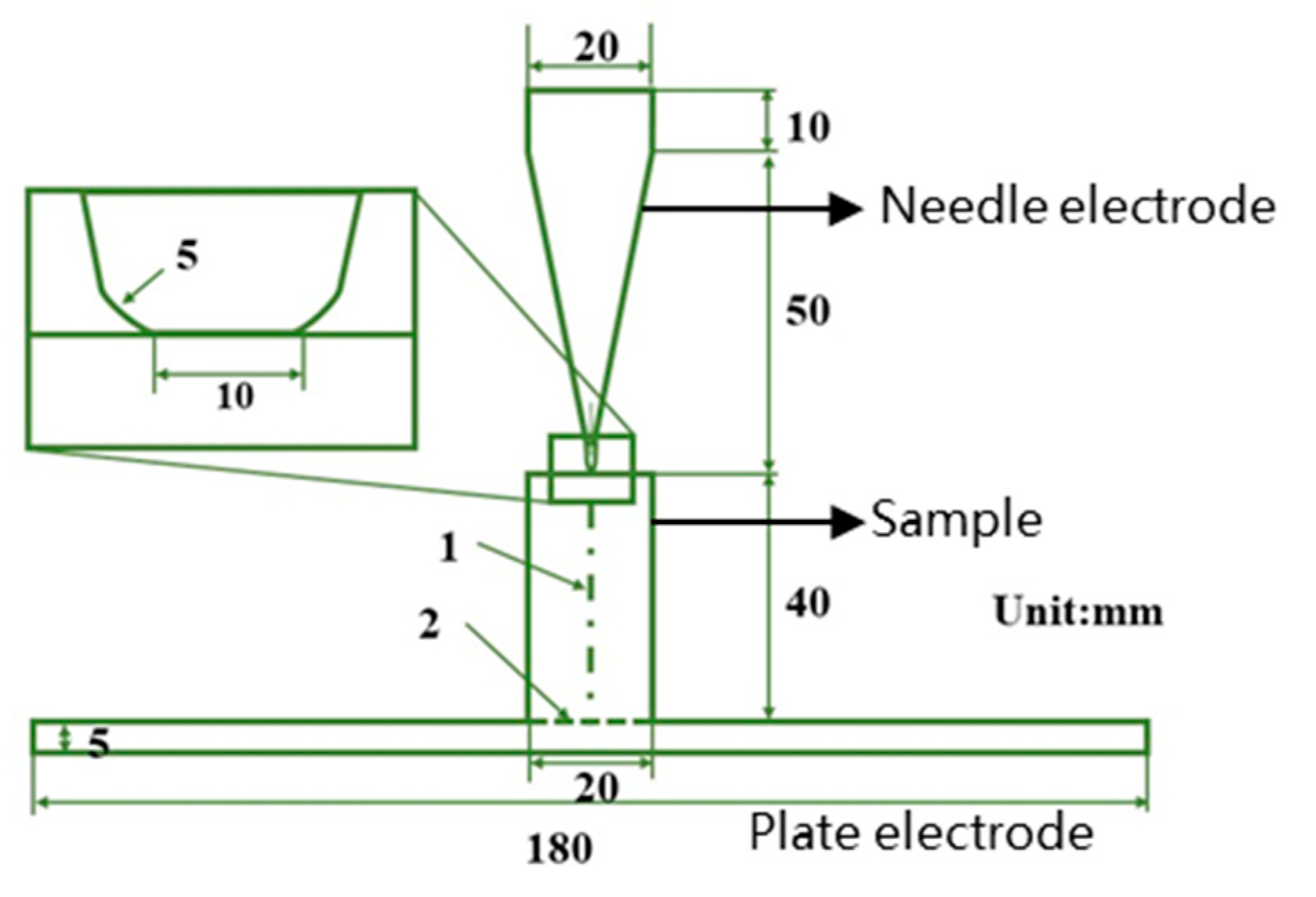
3.1. Configurations of the FEM Simulations
3.2. Needle-Plate Electrode Model
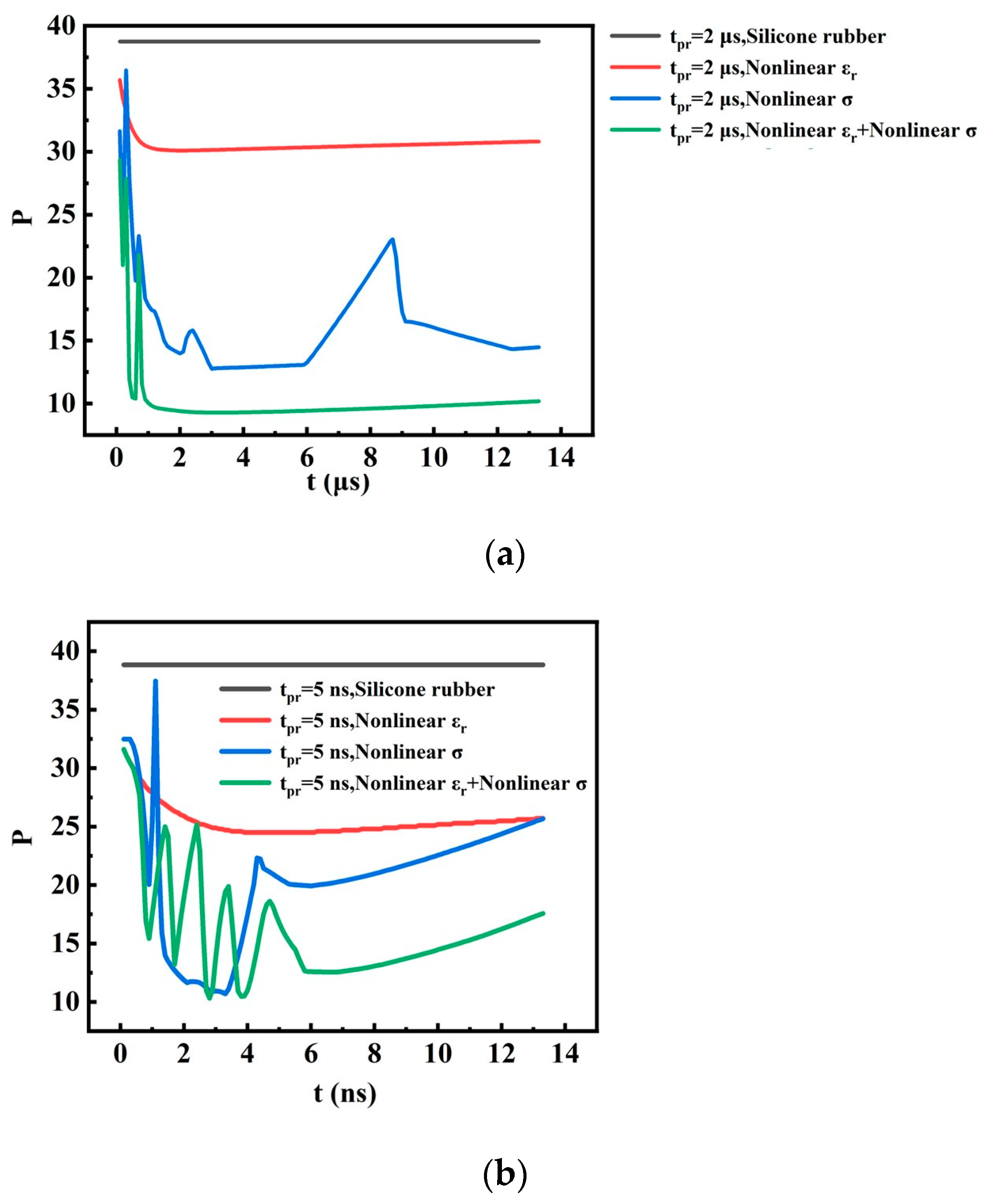
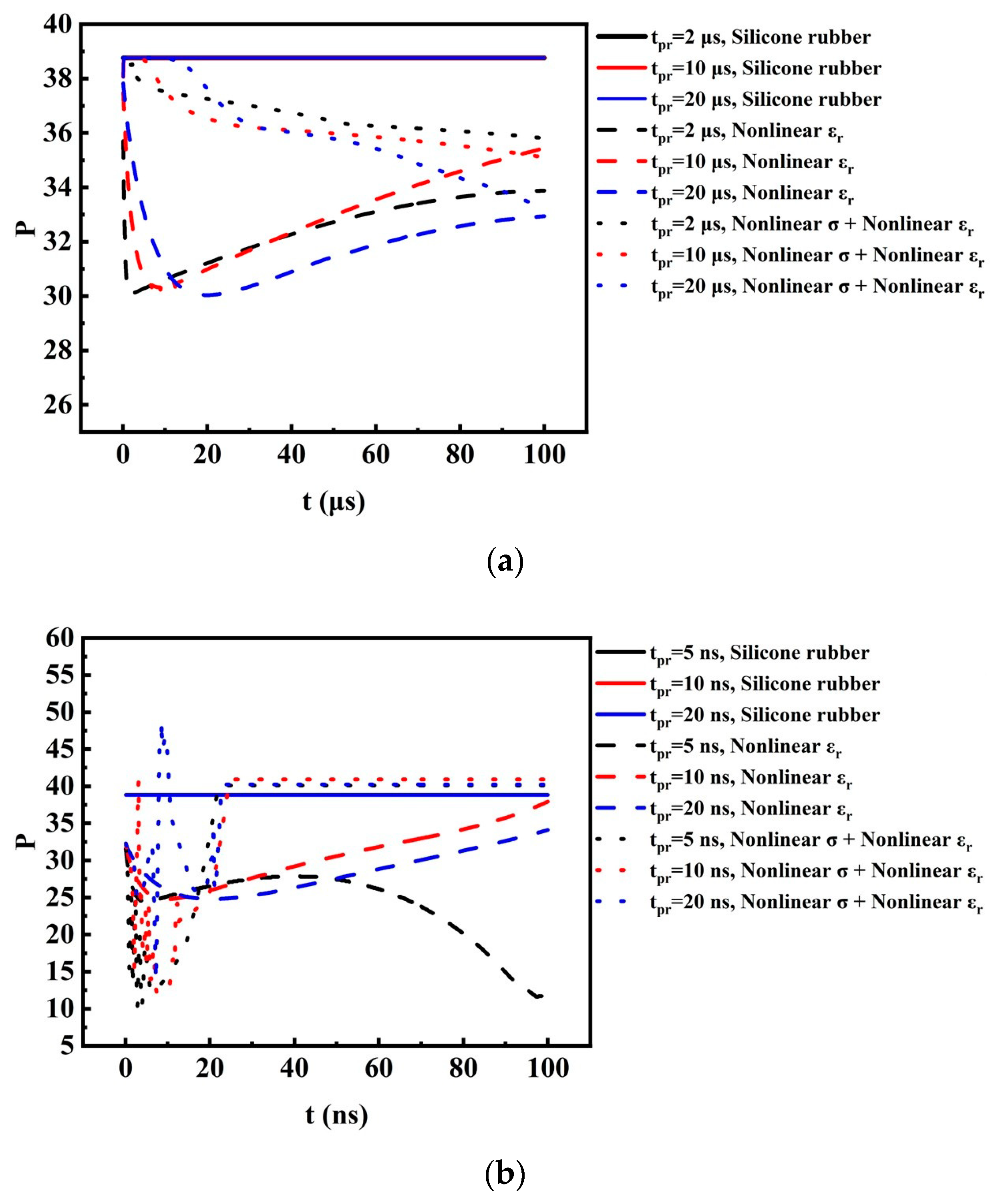
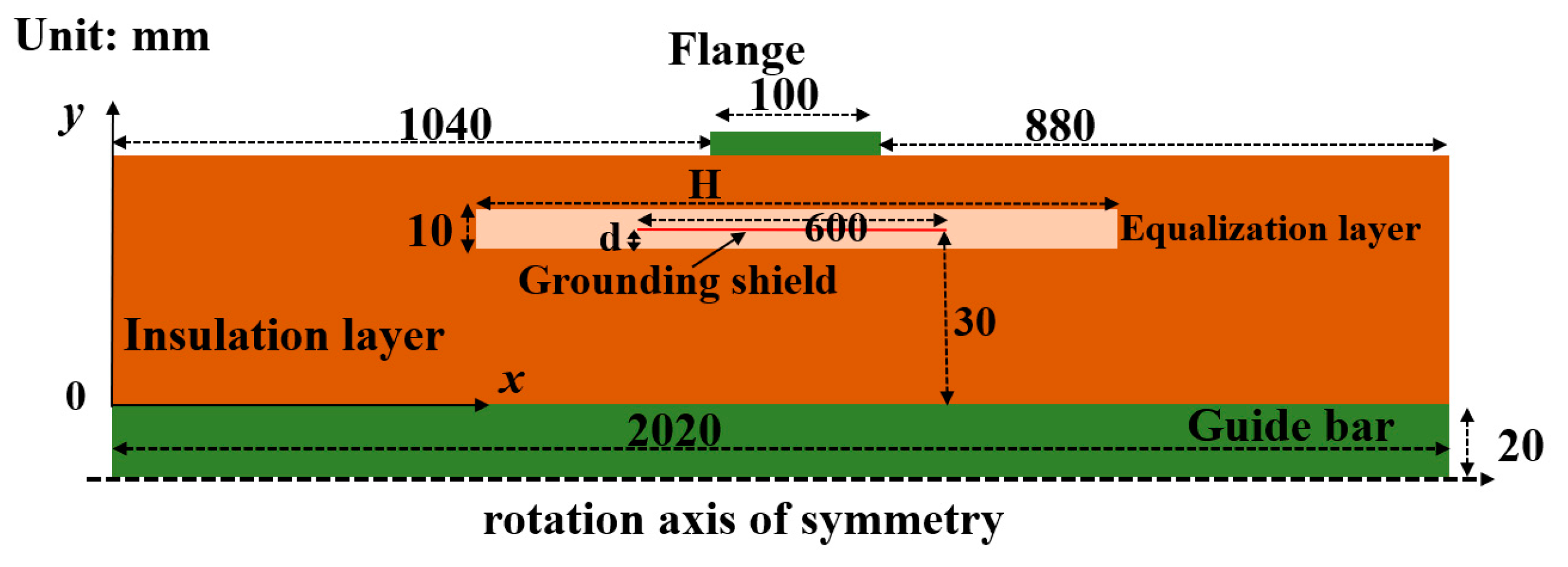
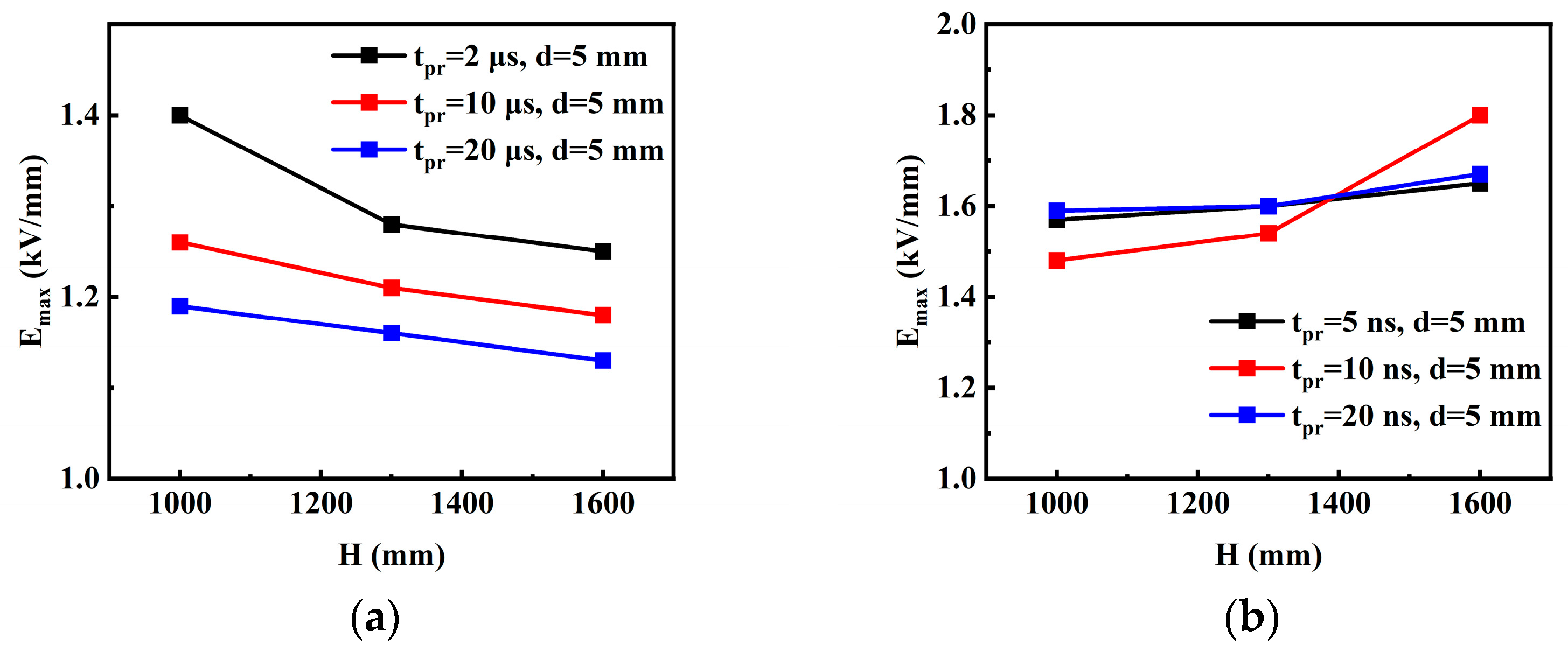
3.3. High-Voltage Bushing Model
4. Conclusions
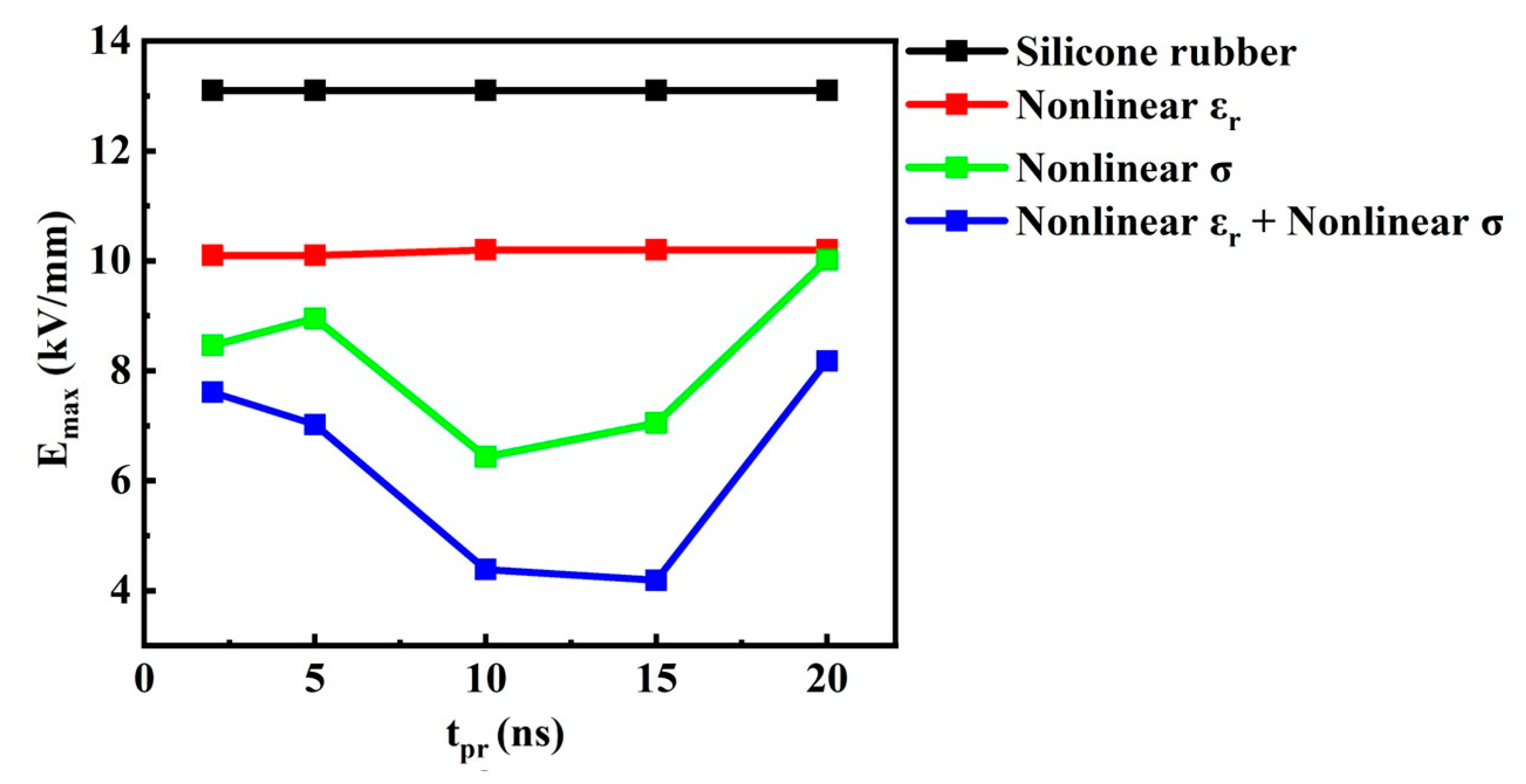
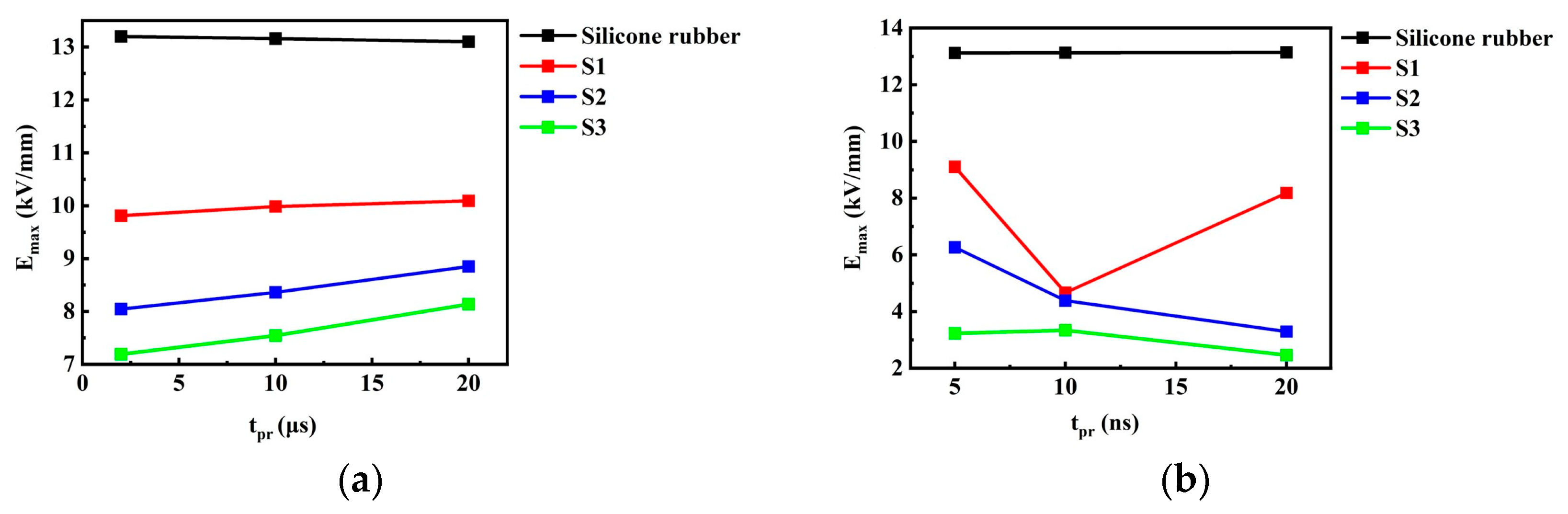
- The nonlinear composite materials with field-dependent and exhibit a significantly improved homogenization effect compared to those of the linear materials, e.g., silicone rubber, and materials with merely nonlinear or . In addition, enhancement of the nonlinearity of the materials is generally favorable for field homogenization.
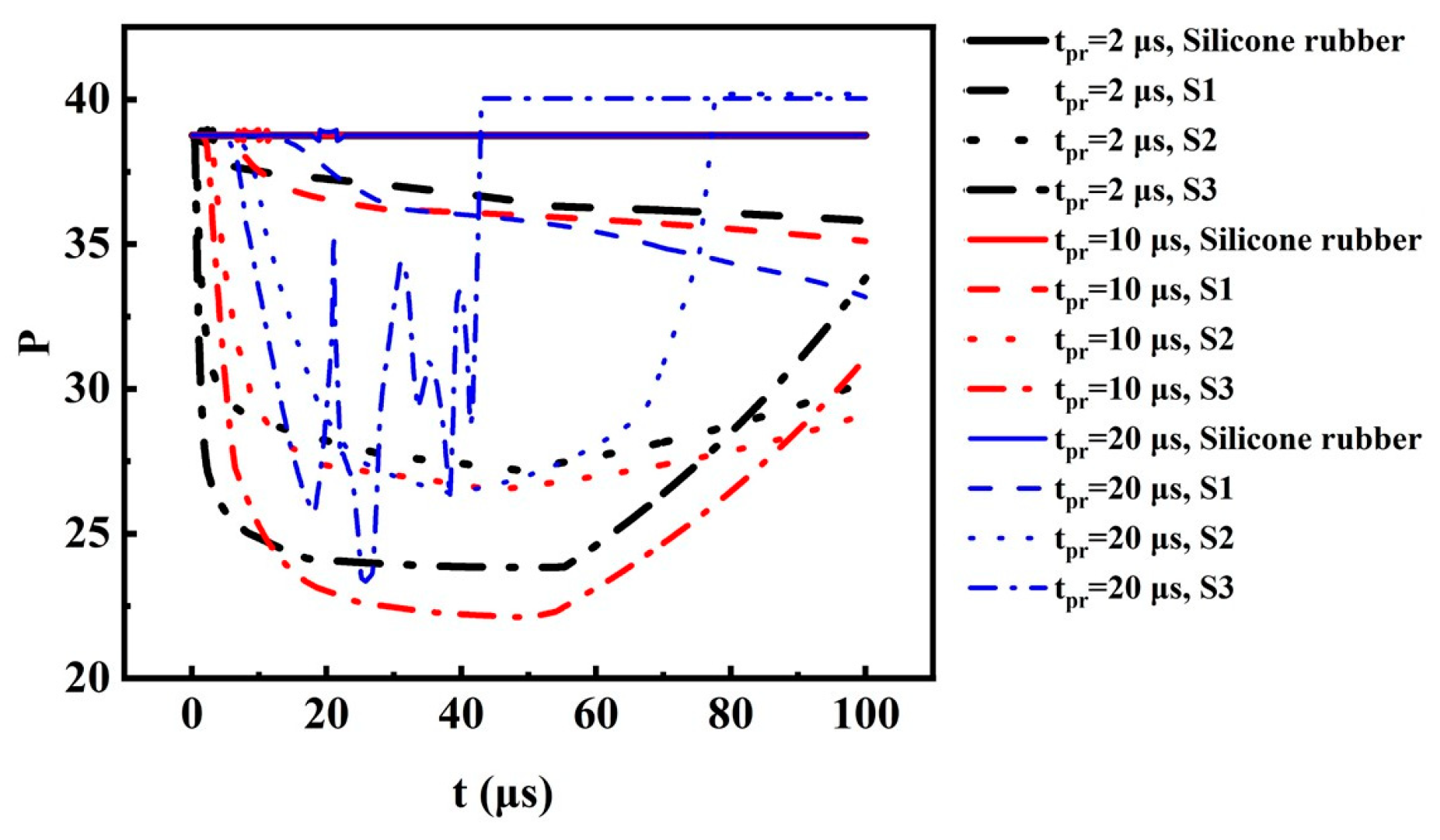
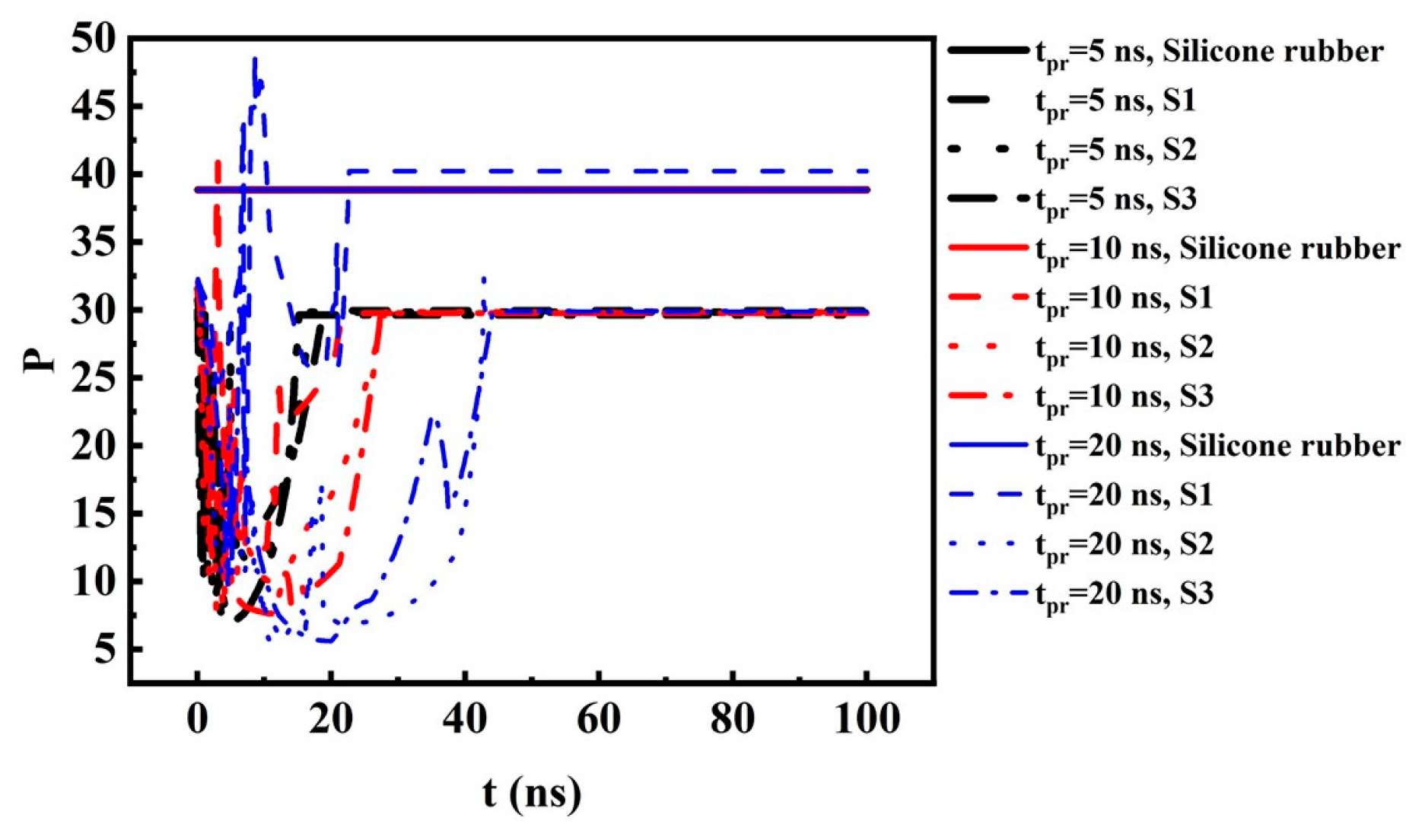
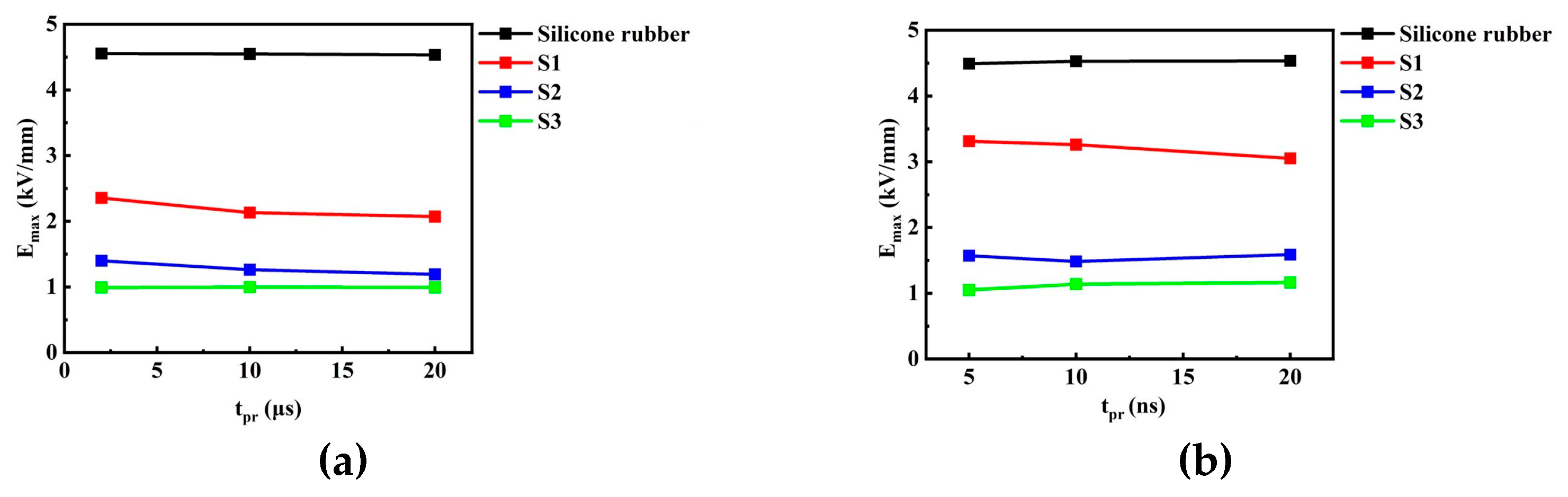
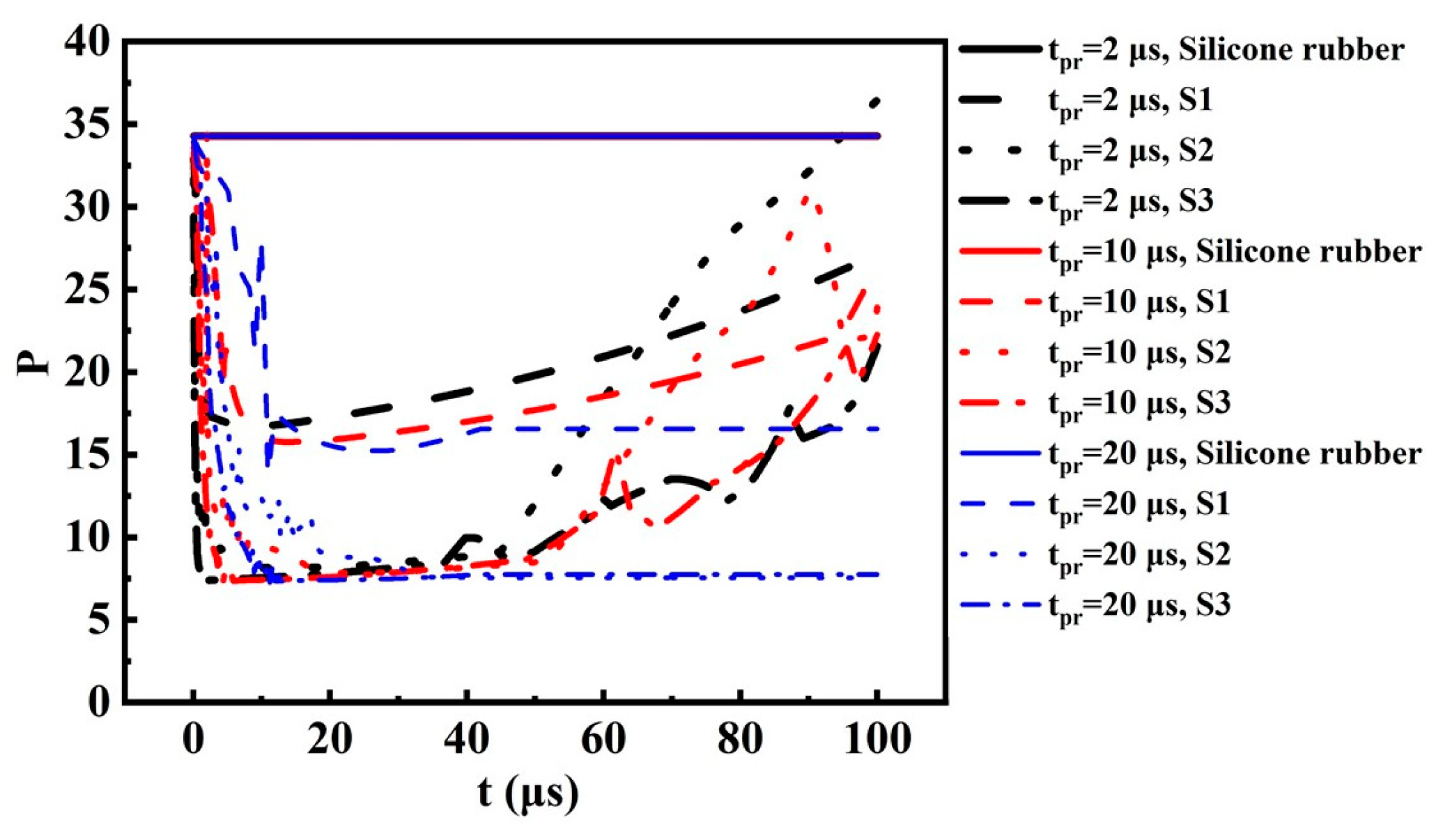
- The distribution of the internal physical field of the linear material, i.e., silicone rubber, is determined mostly by its material properties, and the non-uniformity P changes very little under various tpr. On the other hand, the nonlinear variations in the material properties are in fact a reflection of the charge relaxation process; thus, tpr and the time profile of the pulsed excitations have significant influence on the non-uniformity P of the nonlinear materials, especially when the timescale of the pulsed field is comparative or shorter than the time-constant of the relaxation process. It can be seen that the influence of tpr is more obvious for nanosecond-scale pulses, which is consistent with the above explanation.
- Existing experience for homogenization of the electric field intensity under DC or power frequencies is still valid in the presence of pulse excitations of microsecond scale. However, compared with the electric field generated by DC or power frequency sources, the pulsed electric field of nanosecond scale behaves in a different manner; thus, some abnormal phenomena appear. Therefore, inheritance of the measures commonly adopted in DC or power frequency scenarios demands cautious evaluation and implementation when applied to the homogenization of the pulsed electric field of nanosecond scale.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Akiyama, H.; Katsuki, S.; Redondo, L.; Akiyama, M.; Pemen, A.J.M.; Huiskamp, T.; Beckers, F.J.C.M.; van Heesch, E.J.M.; Winands, G.J.J.; Voeten, S.J.; et al. Pulsed Power Technology. In Bioelectrics; Akiyama, H., Heller, R., Eds.; Springer: Tokyo, Japan, 2017. [Google Scholar] [CrossRef]
- Li, L.; Wei, X. Power Interference Suppression Method for Measuring Partial Discharges under Pulse Square Voltage Conditions. Energies 2022, 15, 3437. [Google Scholar] [CrossRef]
- Mikrut, P.; Zydroń, P. Numerical Modeling of PD Pulses Formation in a Gaseous Void Located in XLPE Insulation of a Loaded HVDC Cable. Energies 2023, 16, 6374. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, X.H.; Zhao, X.; Yang, X.; Liu, S.; Xuan, J. Flashover of Insulation Materials Induced by Electrostatic Electromagnetic Pulse. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2023, 42, 169–180. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, C.; Jia, W.; Cheng, L.; Guo, F.; Xie, L.; Wu, W.; Chen, W. Flashover Voltage of Epoxy FRP Insulators with Different Surface Roughness and Groove under Nanosecond Pulses in SF6. Energies 2022, 15, 2022. [Google Scholar] [CrossRef]
- Ren, H.W.; Tanaka, Y.; Miyake, H.; Endo, K.; Li, Q.; Gao, H.; Li, C.; Wang, Z. Research on the Effect of Unipolar Pulse Wave Voltage on Space Charge Characteristics for High-Frequency Equipment Insulation. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 150–157. [Google Scholar] [CrossRef]
- Tang, C.; Huang, B.; Hao, M.; Xu, Z.; Hao, J.; Chen, G. Progress of Space Charge Research on Oil-Paper Insulation Using Pulsed Electroacoustic Techniques. Energies 2016, 9, 53. [Google Scholar] [CrossRef]
- Du, B.X.; Jiang, J.P.; Zhang, J.G.; Liu, D.S. Dynamic Behavior of Surface Charge on Double-layer Oil-paper Insulation under Pulse Voltage. IEEE Trans. Dielectr. Electr. Insul. 2017, 23, 2712–2719. [Google Scholar] [CrossRef]
- Du, B.X.; Liu, Z.X.; Xiao, M. Effect of Pulse Duration on Surface Charge of Direct-Fluorinated Polyimide Films. IEEE Trans. Dielectr. Electr. Insul. 2016, 22, 3481–3487. [Google Scholar] [CrossRef]
- He, J.L.; Yang, X.; Hu, J. Progress of Theory and Parameter Adjustment for Nonlinear Resistive Field Grading Materials. Trans. China Electrotech. Soc. 2017, 32, 44–60. (In Chinese) [Google Scholar]
- Fuse, N.; Morita, S.; Miyazaki, S.; Takahashi, T.; Hozumi, N. Estimation Accuracy of the Electric Field in Cable Insulation Based on Space Charge Measurement. Energies 2022, 15, 4920. [Google Scholar] [CrossRef]
- Florkowski, M.; Kuniewski, M. Analysis of Space Charge Signal Spatial Resolution Determined with PEA Method in Flat Samples including Attenuation Effects. Energies 2023, 16, 3592. [Google Scholar] [CrossRef]
- Dascalescu, L.; Ribardière, P.; Duvanaud, C.; Paillot, J.M. Electrostatic Discharges from Charged Cylindrical Bodies to Grounded or Floating Surfaces. IEEE Trans. Ind. Appl. 2001, 37, 1483–1491. [Google Scholar] [CrossRef]
- Winter, A.; Kindersberger, J. Transient Field Distribution in Gas-Solid Insulation Systems under DC Voltages. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 116–128. [Google Scholar] [CrossRef]
- Li, H.; Zebouchi, N.; Haddad, M.; Reid, A.; Ekkel, E. Development of Future Compact and Eco-Friendly HVDC Gas Insulated Systems: Test Verification of Shape-Optimized DC Spacer Models. Energies 2022, 15, 8563. [Google Scholar] [CrossRef]
- Nath, D.; Yang, Q.; Montanari, G.; Yin, W.; Xiong, H.; Younsi, K. Modeling and Characterization of Surface Discharges in Insulating Material for Spacers: Electrode Shape, Discharge Mode, and Revision of the Creepage Concept. Materials 2023, 16, 989. [Google Scholar] [CrossRef]
- Monga., S.; Gorur, R.S.; Hansen, P.; Massey, W. Design Optimization of High Voltage Bushing Using Electric Field Computations. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 1217–1224. [Google Scholar] [CrossRef]
- Huang, X.Z.; Zhan, J.Y.; Zheng, N.; Zhang, G.J.; Kobayashi, S.; Yamano, Y. Dielectric Characteristics of Typical Organic Insulating Materials for Pulsed Power Field under Different Temperatures in Vacuum. Insul. Mater. 2012, 45, 55–59. (In Chinese) [Google Scholar]
- Wang, G.; Chen, Q.; Gao, M.; Yang, B.; Hui, D. Generalized Locally-Exact Homogenization Theory for Evaluation of Electric Conductivity and Resistance of Multiphase Materials. Nanotechnol. Rev. 2019, 9, 1–16. [Google Scholar] [CrossRef]
- Xie, J.C.; Hu, J.; He, J.L.; Guo, Z.C.; Yin, Y. Simulation Analyse of Modification Effect of Nonlinear Composites on Nonuniform Electrical Fields. High Volt. Eng. 2014, 40, 741–750. (In Chinese) [Google Scholar]
- Mesgarpour Tousi, M.; Ghassemi, M. Effects of Frequency and Temperature on Electric Field Mitigation Method via Protruding Substrate Combined with Applying Nonlinear FDC Layer in Wide Bandgap Power Modules. Energies 2020, 13, 2022. [Google Scholar] [CrossRef]
- Hoang, A.T.; Serdyuk, Y.V.; Gubanski, S.M. Charging and Discharge Currents in Low-Density Polyethylene and its Nanocomposite. Energies 2020, 13, 1518. [Google Scholar] [CrossRef]
- Xue, Y.; Guo, W.; Sun, Y.; Li, Z.; Han, Y.; Jia, H. Study on Nonlinear Dielectric Properties of Micro Silica. Energies 2023, 16, 2479. [Google Scholar] [CrossRef]
- Tavernier, K.; Varlow, B.R.; Auckland, D.W.; Ugur, M. Improvement in Electrical Insulators by Nonlinear Fillers. IEEE Proc.-Sci. Meas. Technol. 1999, 146, 88–94. [Google Scholar] [CrossRef]
- Alexander, V.; Kudrin, Y.; Petrov, E.Y. Cylindrical Electromagnetic Waves in a Nonlinear Nondispersive Medium: Exact Solutions of the Maxwell Equations. J. Exp. Theor. Phys. 2010, 110, 537–548. [Google Scholar]
- He, J.L.; Sun, G.; Yuan, Z.K.; Huang, Z.W.; Hu, J. Electric Field Distribution Characteristics of High-Voltage Bushing with Nonlinear Electric Field Grading Layer. High Volt. Eng. 2023, 49, 179–187. (In Chinese) [Google Scholar]
- Yang, X.; Zhao, X.; Li, Q.; Hu, J.; He, J. Nonlinear Effective Permittivity of Field Grading Composite Dielectrics. J. Phys. D Appl. Phys. 2018, 51, 075304. [Google Scholar] [CrossRef]
- de Oliveira, R.M.S.; de Lima, T.S.; Nascimento, J.A.S.; Girotto, G.G. Modeling Time-Evolving Electrical Conductivity in Air Ionization Plasma under DC Voltage: A Finite-Difference Time-Domain Approach for Needle-Plate Setup Based on Laboratory Experiments. Energies 2024, 17, 1799. [Google Scholar] [CrossRef]
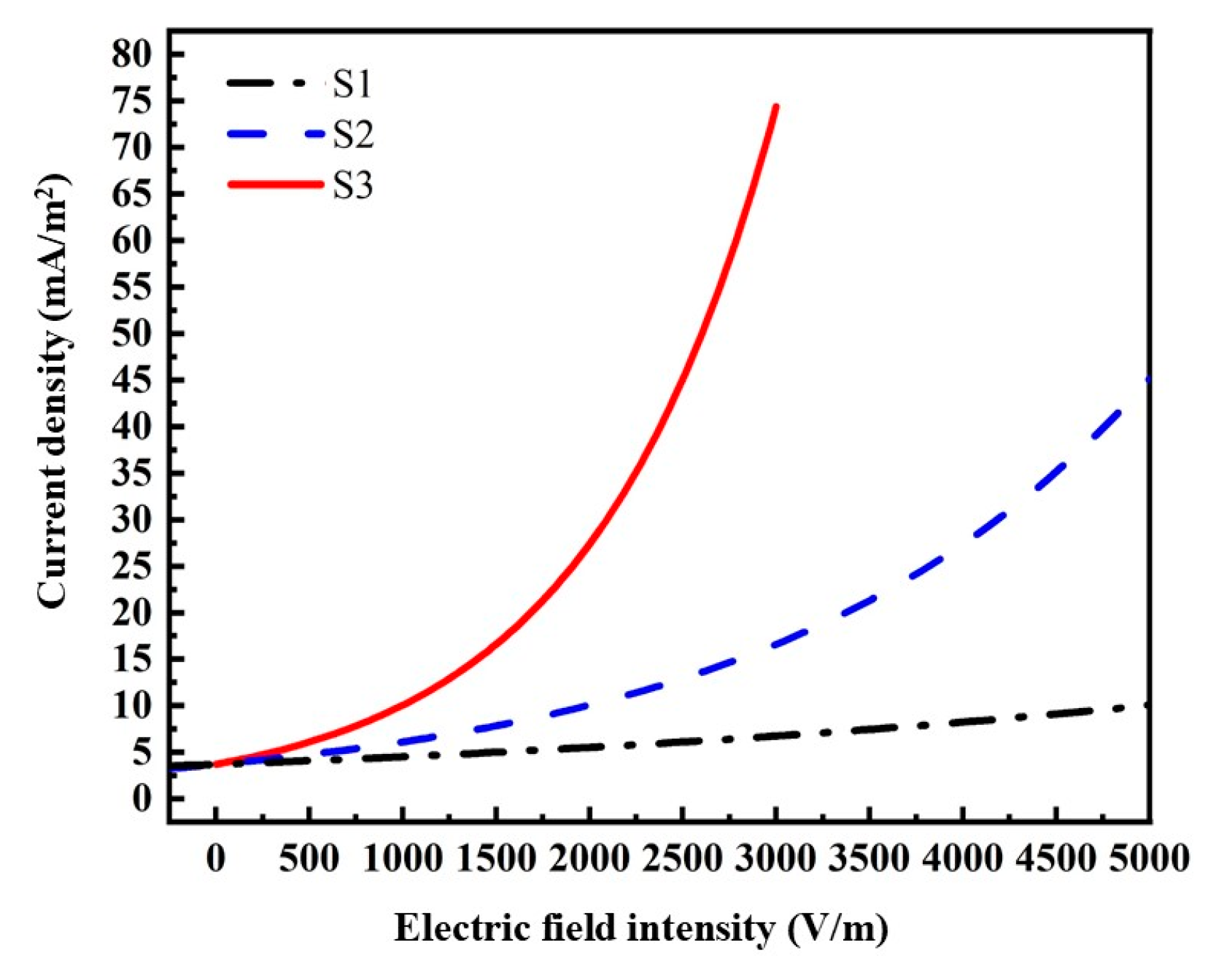
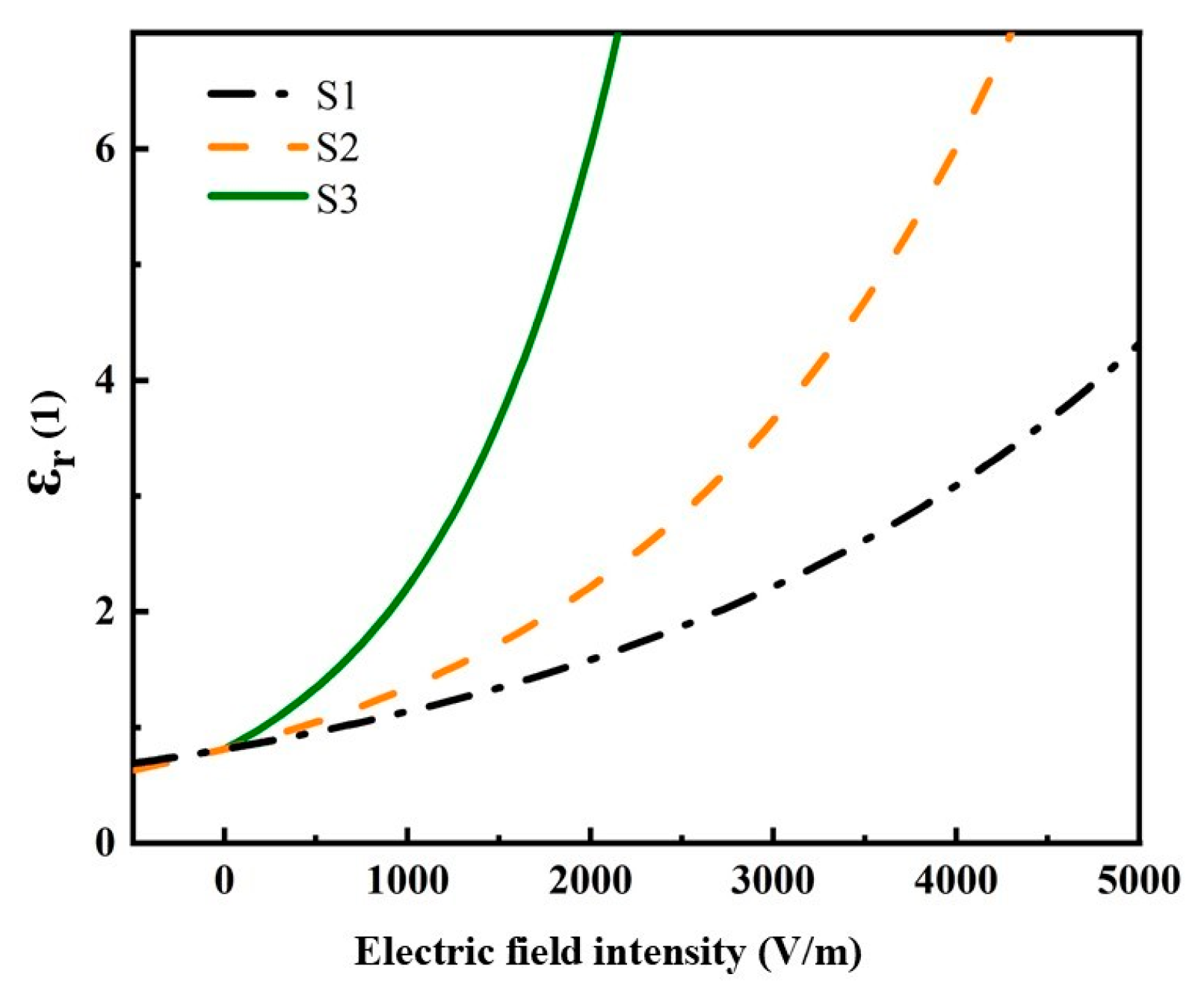




| Linear Material | (S/m) | (1) |
|---|---|---|
| Silicone rubber | 1.00 × 10−14 | 4.3 |
| Copper | 5.80 × 106 | 1.0 |
| Air | 0 | 1.0 |
| Nonlinear Material | (1) | (S/m) | (m/V) | |
|---|---|---|---|---|
| S1 | 4.3 | 10−14 | 10−5 | 10−7 |
| S2 | 2 × 10−5 | 2 × 10−7 | ||
| S3 | 3 × 10−5 | 3 × 10−7 | ||
| Number of Elements | Maximum Edge Length (mm) | Emax (kV/mm) | P |
|---|---|---|---|
| 3468 | 10.51 | 6.246 | 15.985 |
| 5172 | 7.04 | 6.276 | 14.614 |
| 9210 | 3.89 | 6.253 | 14.537 |
| 17,725 | 2.10 | 6.265 | 14.211 |
| 61,377 | 1.05 | 6.288 | 14.219 |
| Time-Stepping Method | Maximum Time-Step Size (ns) | Time Iterations | Emax (kV/mm) | P |
|---|---|---|---|---|
| Backward difference | 2 | 326 | 6.265 | 14.211 |
| 0.1 | 1161 | 6.275 | 14.608 | |
| 0.01 | 10,170 | 6.263 | 14.41 | |
| Generalized alpha | 0.01 | 10,022 | 6.268 | 14.482 |
| 0.001 | 100,011 | 6.258 | 14.373 |
| Time-Stepping Method | Maximum Time-Step Size (μs) | Time Iterations | Emax (kV/mm) | P |
|---|---|---|---|---|
| Backward difference | 2 | 128 | 8.363 | 29.270 |
| 0.1 | 1114 | 8.367 | 29.365 | |
| 0.01 | 10,017 | 8.365 | 29.175 | |
| Generalized alpha | 0.01 | 10,022 | 8.363 | 29.168 |
| 0.001 | 100,009 | 8.353 | 29.099 |
| Excitations | Sample Material | Maximum Field Intensity Emax (kV/mm) | Electric Field Non-Uniformity (P) |
|---|---|---|---|
| tpr = 5, 10, 20 ns | tpr = 5, 10, 20 ns | ||
| Nanosecond pulse | Silicone rubber | 13.122, 13.126, 13.140 | 32.490, 32.490, 32.490 |
| S1 | 9.103, 4.664, 8.180 | 16.760, 12.400, 29.555 | |
| S2 | 6.265, 4.385, 3.293 | 14.211, 10.257, 7.236 | |
| S3 | 3.228, 3.342, 2.463 | 7.203, 7.707, 5.611 | |
| tpr = 2, 10, 20 μs | tpr = 2, 10, 20 μs | ||
| Microsecond pulse | Silicone rubber | 13.200, 13.158, 13.100 | 38.888, 38.590, 38.871 |
| S1 | 9.813, 9.986, 10.092 | 38.497, 37.530, 37.624 | |
| S2 | 8.046, 8.363, 8.853 | 32.143, 29.270, 28.986 | |
| S3 | 7.191, 7.544, 8.139 | 27.731, 25.267, 29.250 |
| Number of Elements | Maximum Edge Length (mm) | Emax (kV/mm) | P |
|---|---|---|---|
| 6087 | 711 | 1.482 | 11.75 |
| 8298 | 216 | 1.485 | 12.15 |
| 11,234 | 144 | 1.483 | 11.18 |
| 36,613 | 21.6 | 1.482 | 11.25 |
| Time-Stepping Method | Maximum Time-Step Size (ns) | Time Iterations | Emax (kV/mm) | P |
|---|---|---|---|---|
| Backward difference | 2 | 105 | 1.483 | 11.18 |
| 0.1 | 1023 | 1.485 | 11.23 | |
| 0.01 | 10,017 | 1.487 | 11.20 | |
| Generalized alpha | 0.1 | 1125 | 1.485 | 12.06 |
| 0.01 | 10,007 | 1.481 | 11.16 |
| Time-Stepping Method | Maximum Time-Step Size (μs) | Time Iterations | Emax (kV/mm) | P |
|---|---|---|---|---|
| Backward difference | 2 | 153 | 1.261 | 9.463 |
| 0.1 | 1041 | 1.265 | 9.451 | |
| 0.01 | 10,017 | 1.265 | 9.445 | |
| Generalized alpha | 0.01 | 10,022 | 8.363 | 9.426 |
| 0.001 | 100,009 | 8.353 | 9.351 |
| Excitations | Length and Position of the Layer | Maximum Field Intensity Emax (kV/mm) | Electric Field Non-Uniformity (P) | |
|---|---|---|---|---|
| tpr = 5, 10, 20 ns | tpr = 5, 10, 20 ns | |||
| Nanosecond pulse | H1(1000 mm) | d1(0 mm) | 2.14,2.57,2.11 | 16.17,19.33,15.89 |
| d3(10 mm) | 1.89,1.85,1.84 | 14.24,13.93,13.87 | ||
| d2(5 mm) | 1.57,1.48,1.59 | 11.91,11.24,11.96 | ||
| H2(1300 mm) | 1.60,1.54,1.60 | 12.09,11.61,12.02 | ||
| H3(1600 mm) | 1.65,1.80,1.67 | 12.52,13.52,12.60 | ||
| tpr = 2, 10, 20 μs | tpr = 2, 10, 20 μs | |||
| Microsecond pulse | H1(1000 mm) | d1(0 mm) | 1.88,1.75,1.82 | 14.13,13.29,13.75 |
| d3(10 mm) | 1.57,1.48,1.48 | 11.78,11.19,11.09 | ||
| d2(5 mm) | 1.40,1.26,1.19 | 10.47,9.46,8.96 | ||
| H2(1300 mm) | 1.26,1.21,1.16 | 9.40,9.11,8.76 | ||
| H3(1600 mm) | 1.25,1.18,1.13 | 9.37,8.90,8.51 | ||
| Conclusions | Explanations | |
|---|---|---|
| Findings |
|
|
|
| |
|
| |
| Limitations |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Mao, M.; Shao, J.; Ma, X. Numerical Investigations into the Homogenization Effect of Nonlinear Composite Materials on the Pulsed Electric Field. Energies 2024, 17, 4252. https://doi.org/10.3390/en17174252
Wang J, Mao M, Shao J, Ma X. Numerical Investigations into the Homogenization Effect of Nonlinear Composite Materials on the Pulsed Electric Field. Energies. 2024; 17(17):4252. https://doi.org/10.3390/en17174252
Chicago/Turabian StyleWang, Jiawei, Minyu Mao, Jinghui Shao, and Xikui Ma. 2024. "Numerical Investigations into the Homogenization Effect of Nonlinear Composite Materials on the Pulsed Electric Field" Energies 17, no. 17: 4252. https://doi.org/10.3390/en17174252
APA StyleWang, J., Mao, M., Shao, J., & Ma, X. (2024). Numerical Investigations into the Homogenization Effect of Nonlinear Composite Materials on the Pulsed Electric Field. Energies, 17(17), 4252. https://doi.org/10.3390/en17174252






