Evaluating the Effects of Proppant Flowback on Fracture Conductivity in Tight Reservoirs: A Combined Analytical Modeling and Simulation Study
Abstract
1. Introduction
2. Methodology
2.1. Analytical Models
2.1.1. Critical Velocity
Physical Model and Assumptions
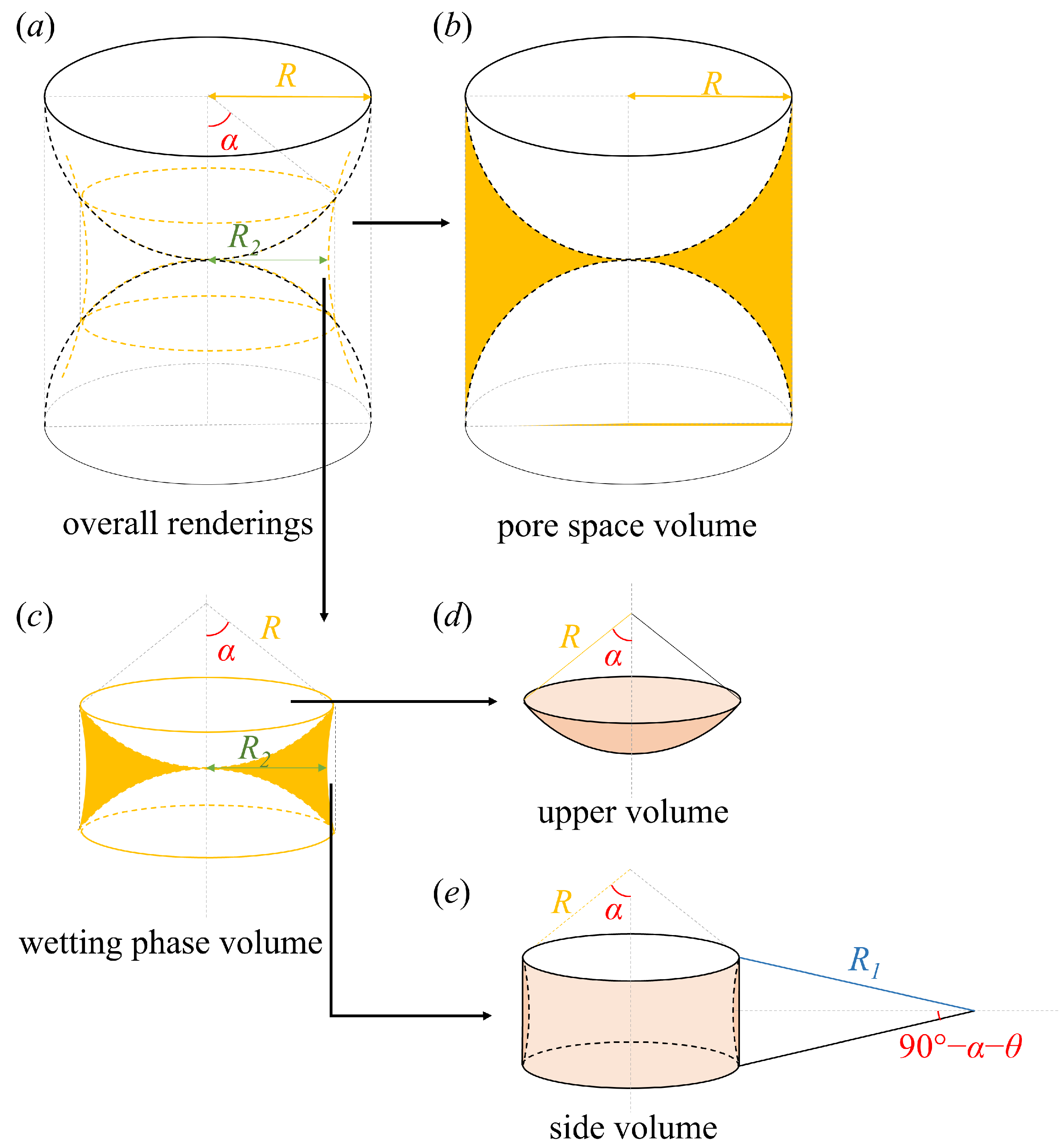
Equivalent Capillary Force
Critical Velocity of Proppant Flowback
- (1)
- Before fracture closure
- (2)
- After fracture closure
2.1.2. Fracture Conductivity
- (1)
- Before fracture closure
- (2)
- After fracture closure
2.2. Finite-Element Simulation
2.2.1. Assumptions
2.2.2. Mesh Geometry and Conditions
3. Application and Results
3.1. Field and Well Information
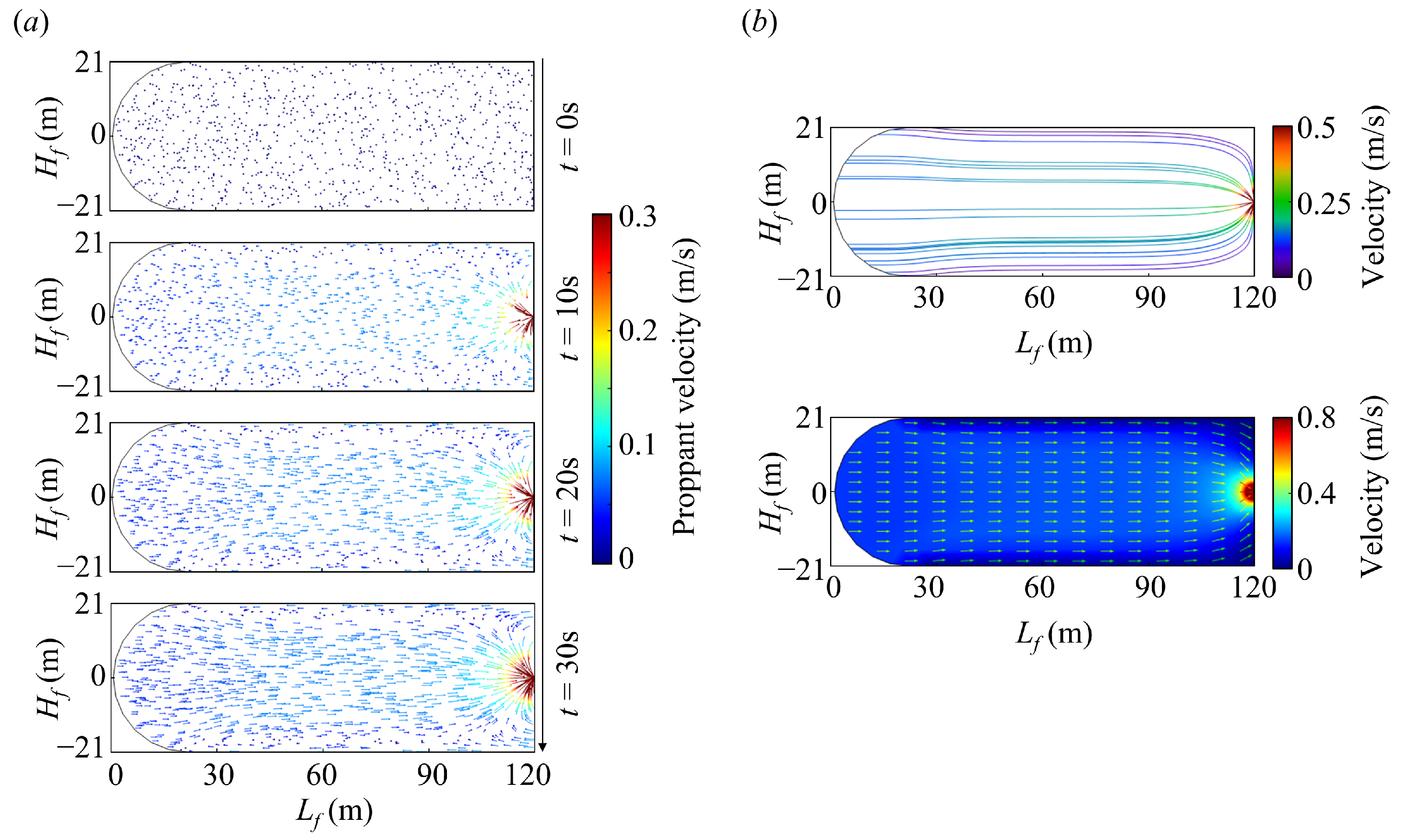
3.2. Results of Base Case
3.3. The Effects of Water Saturation in Fractures
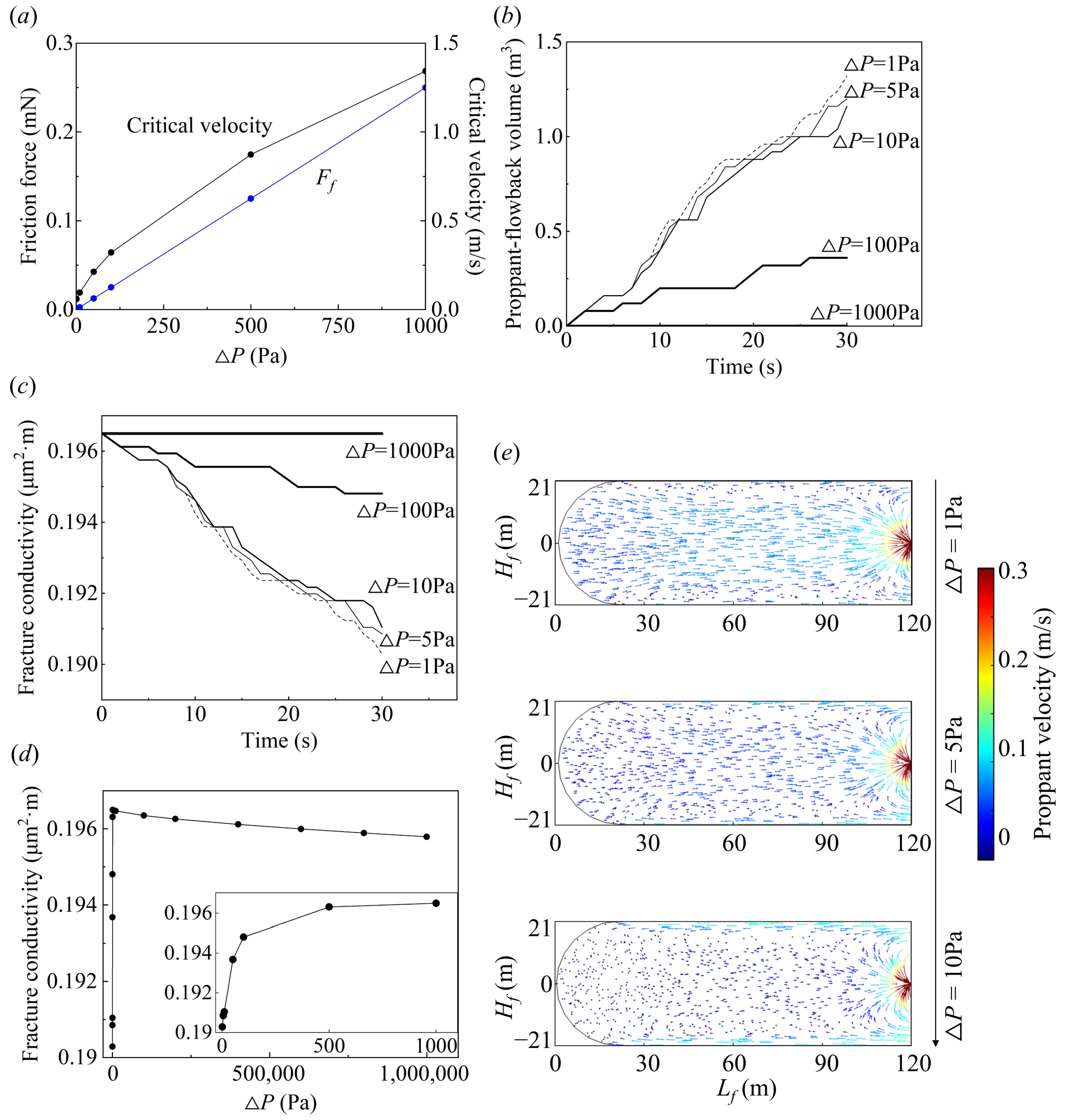
3.3.1. Critical Velocity
3.3.2. Proppant Flowback Volume and Fracture Conductivity
3.4. The Effects of Net Pressure in Fractures
3.4.1. Critical Velocity
3.4.2. Proppant Flowback Volume and Fracture Conductivity
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Capillary pressure, in Pa. | |
| R | Radius of proppant, in m. |
| Radius of curved interface between wetting and non-wetting phases, in m. | |
| Radius related to , in m. | |
| Interfacial tension, in mN/m. | |
| Contact angle, in °. | |
| Angle for the interface between two phase fluid and proppant, in °. | |
| Volume of wetting phase saturation, dimensionless. | |
| Volume of pore space, in m3. | |
| Volume of wetting phase, in m3. | |
| Cylinder volume, in m3. | |
| Volume at the upper and lower cylinder, in m3. | |
| Volume at the side of cylinder, in m3. | |
| Equivalent capillary force, in N. | |
| G | Net gravity, in N. |
| Viscous dragging force, in N. | |
| Proppant density, in g/cm3. | |
| Fracturing fluid density, in g/cm3. | |
| v | Flowback velocity, in m/s. |
| Resistance coefficient, dimensionless. | |
| Re | Reynolds number, dimensionless. |
| Viscosity of fracturing fluid, in mPa·s. | |
| Resistance moment, in m. | |
| Driving force moment, in m. | |
| Bonding force, in N. | |
| Friction force, in N. | |
| Down force of liquid, in N. | |
| Net pressure in fractures, in Pa. | |
| Friction coefficient, dimensionless. | |
| Film parameter, in cm. | |
| Coefficient of bonding force, in dyn/cm. | |
| Fracture conductivity, in m3. | |
| Permeability of propped fracture, in m2. | |
| Width of propped fracture, in m. | |
| Fracture porosity, dimensionless. | |
| r | Radius of pore throat, in m. |
| Tortuosity, dimensionless. | |
| without any proppant embedment or deformation, in m. | |
| m | Total number of proppant layer, dimensionless. |
| N | Total number of proppant, dimensionless. |
| Fracture half length, in m. | |
| Fracture height, in m. | |
| Loss in fracture width, in m. | |
| Proppant deformation, in m. | |
| Proppant embedment, in m. | |
| Poisson ratio of proppant, dimensionless. | |
| Elastic modulus of proppant, in Pa. | |
| Poisson ratio of formation, dimensionless. | |
| Formation elastic modulus, in Pa. |
References
- Li, Q.; Wang, Y.; Wang, F.; Wu, J.; Tahir, M.U.; Li, Q.; Yuan, L.; Liu, Z. Effect of thickener and reservoir parameters on the filtration property of CO2 fracturing fluid. Energy Sources Part A Recover. Util. Environ. Eff. 2020, 42, 1705–1715. [Google Scholar] [CrossRef]
- Li, Q.; Liu, J.; Wang, S.; Guo, Y.; Han, X.; Li, Q.; Cheng, Y.; Dong, Z.; Li, X.; Zhang, X. Numerical insights into factors affecting collapse behavior of horizontal wellbore in clayey silt hydrate-bearing sediments and the accompanying control strategy. Ocean Eng. 2024, 297, 117029. [Google Scholar] [CrossRef]
- Howard, P.R.; King, M.T.; Morris, M.; Feraud, J.-P.; Slusher, G.; Lipari, S. Fiber/proppant mixtures control proppant flowback in south texas. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 22–25 October 1995. [Google Scholar]
- Mayerhofer, M.J.; Wolhart, S.L.; Rogers, J.D. Results of U.S. department of energy deep gas well stimulation study. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005. [Google Scholar]
- Campos, M.; Potapenko, D.; Moncada, K.; Krishnamurthy, J. Advanced flowback in the powder river basin: Securing stimulation investments. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019; OnePetro: Richardson, TX, USA, 2019. [Google Scholar]
- Chuprakov, D.; Belyakova, L.; Iuldasheva, A.; Alekseev, A.; Syresin, D.; Chertov, M.; Spesivtsev, P.; Suarez, F.I.S.; Velikanov, I.; Semin, L.; et al. Proppant flowback: Can we mitigate the risk? In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 4–6 February 2020; OnePetro: Richardson, TX, USA, 2020. [Google Scholar]
- Fu, Y.; Dehghanpour, H.; Motealleh, S.; Lopez, C.M.; Hawkes, R. Evaluating fracture volume loss during flowback and its relationship to choke size: Fastback vs. slowback. SPE Prod. Oper. 2019, 34, 615–624. [Google Scholar] [CrossRef]
- Potapenko, D.I.; Williams, R.D.; Desroches, J.; Enkababian, P.; Theuveny, B.; Willberg, D.M.; Moncada, K.; Deslandes, P.; Wilson, N.; Neaton, R.; et al. Securing long-term well productivity of horizontal wells through optimization of postfracturing operations. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017; OnePetro: Richardson, TX, USA, 2017. [Google Scholar]
- Canon, J.M.; Romero, D.J.; Pham, T.T.; Valko, P.P. Avoiding proppant flowback in tight-gas completions with improved fracture design. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 3–4 October 2003. [Google Scholar]
- Guo, S.; Wang, B.; Li, Y.; Hao, H.; Zhang, M.; Liang, T. Impacts of proppant flowback on fracture conductivity in different fracturing fluids and flowback conditions. ACS Omega 2022, 7, 6682–6690. [Google Scholar] [CrossRef] [PubMed]
- James, S.G.; Samuelson, M.L.; Reed, G.W.; Sullivan, S.C. Proppant flowback control in high temperature wells. In Proceedings of the 1998 SPE Rocky Mountain Regional/Low-Permeability Reservoirs Symposium and Exhibition, Denver, CO, USA, 5–8 April 1998. [Google Scholar]
- Bagci, S.; Stolyarov, S. Flowback production optimization for choke size management strategies in unconventional wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Calgary, AB, Canada, 30 September–2 October 2019; OnePetro: Richardson, TX, USA, 2019. [Google Scholar]
- Deen, T.; Daal, J.; Tucker, J. Maximizing well deliverability in the eagle ford shale through flowback operations. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015; OnePetro: Richardson, TX, USA, 2015. [Google Scholar]
- Karantinos, E.; Sharma, M.M.; Ayoub, J.A.; Parlar, M.; Chanpura, R.A. Choke-management strategies for hydraulically fractured wells and frac-pack completions in vertical wells. SPE Prod. Oper. 2018, 33, 623–636. [Google Scholar] [CrossRef]
- Rojas, D.; Lerza, A. Horizontal well productivity enhancement through drawdown management approach in vaca muerta shale. In Proceedings of the SPE Canada Unconventional Resources Conference, Calgary, AB, Canada, 15–16 March 2018; OnePetro: Richardson, TX, USA, 2018. [Google Scholar]
- Wilson, K.; Ahmed, I.; MacIvor, K. Geomechanical modeling of flowback scenarios to establish best practices in the midland basin horizontal program. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, San Antonio, TX, USA, 1–3 August 2016; OnePetro: Richardson, TX, USA, 2016. [Google Scholar]
- Shor, R.J.; Sharma, M.M. Reducing proppant flowback from fractures: Factors affecting the maximum flowback rate. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2014; OnePetro: Richardson, TX, USA, 2014. [Google Scholar]
- Wang, Z.; Wang, X.; Shan, W.; Lu, Y. Development and research on fracturing technology in low-permeability ultra-deep wells in china. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Brisbane, Australia, 16–18 October 2000. [Google Scholar]
- Daneshy, A. Proppant distribution and flowback in off-balance hydraulic fractures. SPE Prod. Facil. 2005, 20, 41–47. [Google Scholar] [CrossRef]
- Milton-Tayler, D.; Stephenson, C.; Asgian, M.I. Factors affecting the stability of proppant in propped fractures: Results of a laboratory study. In Proceedings of the Society of Petroleum Engineers SPE Annual Technical Conference and Exhibition, Washington, DC, USA, 4–7 October 1992. [Google Scholar]
- Wang, H.; Wen, L. Experimental investigation on the factors affecting proppant flowback performance. J. Energy Resour. Technol. Trans. ASME 2020, 142, 053001. [Google Scholar] [CrossRef]
- Chun, T.; Zhu, D.; Zhang, Z.; Mao, S.; Wu, K. Experimental study of proppant transport in complex fractures with horizontal bedding planes for slickwater fracturing. SPE Prod. Oper. 2021, 36, 83–96. [Google Scholar] [CrossRef]
- Chuprakov, D.; Iuldasheva, A.; Alekseev, A. Criterion of proppant pack mobilization by filtrating fluids: Theory and experiments. J. Pet. Sci. Eng. 2021, 196, 107792. [Google Scholar] [CrossRef]
- Garagash, I.A.; Osiptsov, A.A.; Boronin, S.A. Dynamic bridging of proppant particles in a hydraulic fracture. Int. J. Eng. Sci. 2019, 135, 86–101. [Google Scholar] [CrossRef]
- Stephenson, C.J.; Rickards, A.R.; Brannon, H.D. Increased resistance to proppant flowback by adding deformable particles to proppant packs tested in the laboratory. In Proceedings of the 1999 SPE Annual Technical Conference and Exhibition: ‘Drilling and Completion’, Houston, TX, USA, 3–6 October 1999. [Google Scholar]
- Hu, J.; Zhao, J.; Li, Y. A proppant mechanical model in postfrac flowback treatment. J. Nat. Gas Sci. Eng. 2014, 20, 23–26. [Google Scholar] [CrossRef]
- Richefeu, V.; Youssoufi, M.S.E.; Radjaï, F. Shear strength properties of wet granular materials. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2006, 73, 051304. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Zhang, M.; Wang, B.; Shi, J. A proppant flowback mechanical model based on different wettability of the proppant particle surface. In Proceedings of the International Field Exploration and Development Conference 2020; Springer: Singapore, 2021; pp. 3374–3384. [Google Scholar]
- Wang, M.; Guo, B. Effect of fluid contact angle of oil-wet fracture proppant on the competing water/oil flow in sandstone-proppant systems. Sustainability 2022, 14, 3766. [Google Scholar] [CrossRef]
- Zhou, Y.; Ni, H.; Shen, Z.; Wang, M. Study on proppant transport in fractures of supercritical carbon dioxide fracturing. Energy Fuels 2020, 34, 6186–6196. [Google Scholar] [CrossRef]
- Fu, Y. Study on Proppant Backflow Mechanism during the Production Process of Fracturing Gas Well; Southwest Petroleum University: Chengdu, China, 2006. [Google Scholar]
- Han, G.; Dusseault, M.B.; Cook, J. Quantifying rock capillary strength behavior in unconsolidated sandstones. In Proceedings of th SPE/ISRM Rock Mechanics Conference, Irving, TX, USA, 20–23 October 2002. [Google Scholar]
- Han, G.; Dusseault, M.B. Quantitative analysis of mechanisms for water-related sand production. In Proceedings of the SPE International Symposium and Exhibition on Formation Damage Control, Lafayette, LA, USA, 20–21 February 2002. [Google Scholar]
- Liu, Y.; Leung, J.Y.; Chalaturnyk, R. Geomechanical simulation of partially propped fracture closure and its implication for water flowback and gas production. SPE Reserv. Eval. Eng. 2018, 21, 273–290. [Google Scholar] [CrossRef]
- Boyer, F.; Guazzelli, E.; Pouliquen, O. Unifying suspension and granular rheology. physical review letters. Phys. Rev. Lett. 2011, 107, 188301. [Google Scholar] [CrossRef] [PubMed]
- Lecampion, B.; Garagash, D.I. Confined flow of suspensions modelled by a frictional rheology. J. Fluid Mech. 2014, 759, 197–235. [Google Scholar] [CrossRef]
- Cao, G.; Bai, Y.; Du, T.; Yang, T.; Yan, H. Study on proppant backflow based on finite element simulation. Xinjiang Pet. Geol. 2019, 40, 10–12. [Google Scholar]
- Dontsov, E.V.; Peirce, A.P. Slurry flow, gravitational settling and a proppant transport model for hydraulic fractures. J. Fluid Mech. 2014, 760, 567–590. [Google Scholar] [CrossRef]
- Vega, F.G.; Carlevaro, C.M.; Sánchez, M.; Pugnaloni, L.A. Stability and conductivity of proppant packs during flowback in unconventional reservoirs: A cfd—dem simulation study. J. Pet. Sci. Eng. 2021, 201, 108381. [Google Scholar] [CrossRef]
- Wang, J.; Elsworth, D.; Denison, M.K. Propagation, proppant transport and the evolution of transport properties of hydraulic fractures. J. Fluid Mech. 2018, 855, 503–534. [Google Scholar] [CrossRef]
- Kozeny, J.; Carmen, P.C. Ueber kapillare leitung des wassers im boden sitzungsber akad. Wien 1927, 136, 271–306. [Google Scholar]
- Gao, Y.; Lv, Y.; Wang, M.; Li, K. New mathematical models for calculating the proppant embedment and fracture conductivity. In Proceedings of theSPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–10 October 2012. [Google Scholar]
- Jia, L.; Li, K.; Zhou, J.; Yan, Z.; Wan, F.; Kaita, M. A mathematical model for calculating rod-shaped proppant conductivity under the combined effect of compaction and embedment. J. Pet. Sci. Eng. 2019, 180, 11–21. [Google Scholar] [CrossRef]
- Meng, Y.; Li, Z.; Guo, Z. Calculation model of fracture conductivity in coal reservoir and its application. J. China Coal Soc. 2014, 39, 1852–1856. [Google Scholar]
- Leverett, M.C. Capillary behavior in porous solids. Trans. AIME 1941, 142, 152–169. [Google Scholar] [CrossRef]
- Ehlig-Economides, C.A.; Economides, M.J. Water as proppant. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011; OnePetro: Richardson, TX, USA, 2011. [Google Scholar]
- Fu, Y.; Dehghanpour, H.; Ezulike, D.O.; Jones, R.S., Jr. Estimating effective fracture pore volume from flowback data and evaluating its relationship to design parameters of multistage-fracture completion. SPE Prod. Oper. 2017, 32, 423–439. [Google Scholar] [CrossRef]
- Almasoodi, M.; Vaidya, R.; Reza, Z. Drawdown-management and fracture-spacing optimization in the meramec formation: Numerical-and economics-based approach. SPE Reserv. Eval. Eng. 2020, 23, 1251–1264. [Google Scholar] [CrossRef]
- Mirani, A.; Marongiu-Porcu, M.; Wang, H.; Enkababian, P. Production-pressure-drawdown management for fractured horizontal wells in shale-gas formations. SPE Reserv. Eval. Eng. 2018, 21, 550–565. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| Half-length of the fracture, (m) | 118.95 |
| Fracture height, (m) | 42 |
| Volume of pumped proppant, (m3) | 40 |
| Proppant radius, R (m) | 350 |
| Proppant density, (g/cm3) | 3.16 |
| Volume density of proppant, (g/cm3) | 1.74 |
| Fracturing fluid density, (g/cm3) | 1.03 |
| Fracturing fluid viscosity for gel breaking, (mPa·s) | 3.5 |
| Friction coefficient of quartz, | 0.75 |
| Film parameter of quartz, (cm) | 0.0000213 |
| Bonding force coefficient of quartz, (dyne/cm) | 2.56 |
| Surface tension of gel breaking fracturing fluid, (mN/m) | 24.4 |
| Wetting angle, (°) | 2 |
| Net pressure in fractures, (Pa) | 1 |
| Wetting-phase saturation in the fracture, (%) | 14.7 |
| Poisson’s ratio of proppant, | 0.25 |
| Elastic modulus of proppant, ( Pa) | 100 |
| Poisson’s ratio of formation, | 0.19 |
| Elastic modulus of formation, ( Pa) | 34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Li, Z.; Fu, Y.; Xu, L. Evaluating the Effects of Proppant Flowback on Fracture Conductivity in Tight Reservoirs: A Combined Analytical Modeling and Simulation Study. Energies 2024, 17, 4250. https://doi.org/10.3390/en17174250
Cheng Y, Li Z, Fu Y, Xu L. Evaluating the Effects of Proppant Flowback on Fracture Conductivity in Tight Reservoirs: A Combined Analytical Modeling and Simulation Study. Energies. 2024; 17(17):4250. https://doi.org/10.3390/en17174250
Chicago/Turabian StyleCheng, Yishan, Zhiping Li, Yingkun Fu, and Longfei Xu. 2024. "Evaluating the Effects of Proppant Flowback on Fracture Conductivity in Tight Reservoirs: A Combined Analytical Modeling and Simulation Study" Energies 17, no. 17: 4250. https://doi.org/10.3390/en17174250
APA StyleCheng, Y., Li, Z., Fu, Y., & Xu, L. (2024). Evaluating the Effects of Proppant Flowback on Fracture Conductivity in Tight Reservoirs: A Combined Analytical Modeling and Simulation Study. Energies, 17(17), 4250. https://doi.org/10.3390/en17174250





