A Blockchain and PKI-Based Secure Vehicle-to-Vehicle Energy-Trading Protocol

Abstract

With the increasing awareness for sustainable future and green energy, the demand for electric vehicles (EVs) is growing rapidly, thus placing immense pressure on the energy grid. To alleviate this, local trading between EVs should be encouraged. In this paper, we propose a blockchain and public key infrastructure (PKI)-based secure vehicle-to-vehicle (V2V) energy-trading protocol. A permissioned blockchain utilizing the proof of authority (PoA) consensus and smart contracts is used to securely store data. Encrypted communication is ensured through transport layer security (TLS), with PKI managing the necessary digital certificates and keys. A multi-leader, multi-follower Stackelberg game-based trade algorithm is formulated to determine the optimal energy demands, supplies, and prices. Finally, we propose a detailed communication protocol that ties all the components together, enabling smooth interaction between them. Key findings, such as system behavior and performance, scalability of the trade algorithm and the blockchain, smart contract execution costs, etc., are presented through numerical results by implementing and simulating the protocol in various scenarios. This work not only enhances local energy trading among EVs, encouraging efficient energy usage and reducing burden on the power grid, but also paves a way for future research in sustainable energy management.

1. Introduction

With the pressing global concern over greenhouse gas (GHG) emissions and their impact on the environment, a great amount of research effort is being focused on developing technologies to reduce GHG, such as green or renewable energy [1,2]. Fossil fuels, e.g., coal, oil, and natural gas, are major contributors to GHG emissions. They are not only contributing to climate change and global temperature rising but are also degrading nature, posing significant risks to the ecosystem and biodiversity, and creating health issues [3,4]. A large portion of these fossil fuels are consumed by the transportation sector [5].

While traditional vehicles only rely on fossil fuels, EVs can use electricity generated from rHossainenewable sources such as solar, wind, hydroelectric, or geothermal sources. This is why EVs present a promising solution to mitigate the environmental damage caused by fossil fuels and reduce harmful particles and pollutants in the environment. Due to the numerous benefits of EVs [6], the global adoption of EVs is rapidly growing, with sales reaching record levels in recent years. For instance, the global EV stock in 2023 was 40 million, with an average increment of approximately 60% per year for the 2013–2023 period [7]. However, this widespread adoption of EVs presents significant challenges for the power grid. The increased demand for electricity to charge EVs can strain existing grid infrastructure, leading to potential issues with grid stability. To address these challenges, developing improved EV charging infrastructure and efficient energy management solutions is of paramount importance.

The recent developments in vehicle-to-grid EV charging technologies and protocols such as ISO 15118 [8,9] are very promising. V2V energy trading is an emerging concept that has a great potential for transforming the energy and transport sectors’ landscape, particularly in the context of EVs [10]. V2V energy sharing allows EVs to trade energy directly with each other, thereby optimizing energy distribution, reducing energy wastage and range anxiety, and enhancing the utilization of green energy. One very notable feat of V2V energy trading is that it can help balance the load on the power grid, reducing the strain on the grid, especially during peak demand periods, and helps prevent grid overloads and blackouts [11]. Also, by facilitating decentralized energy transactions, V2V trading reduces the need for extensive grid infrastructure upgrades, leading to more resilient and efficient energy distribution systems.

Like any interaction involving monetary transactions, a V2V energy-trading system will have to be secure while maintaining the privacy of the participants. Adversarial entities in the energy market pose a significant risk to security and privacy through various malicious exploitations such as privacy leakage, data manipulation, impersonation, fraudulent advertising, etc. [12,13]. Traditional centralized systems are easier to attack or compromise because of a single point of failure, emphasizing the importance of decentralization, an attribute commonly associated with blockchain [14]. Due to the distributed nature and the anonymity, transparency, and reliability of blockchain, in recent years it has gained significant popularity among both researchers and developers. In a V2V energy-trading platform, blockchain can be used to provide distributed data storage, authenticate participants, secure transactions, and preserve anonymity, among many other things [15].

1.1. Related Work

The rapid adoption of EVs has attracted the interest of researchers, as has been made evident from the exponential growth in related publications [16,17]. In [18], the authors focus on game theory-based distributed charging strategies aimed at enhancing efficiency while considering location factors. A mixed-integer program is designed in [19] to optimize vehicle upgrade policies in the electric car rental market, aiming to maximize total profit by balancing demand and supply, considering factors such as revenue, potential demand loss, dispatching cost, energy consumption, etc. A secure EV charging solution for smart communities, utilizing a permissioned energy blockchain, a reputation-based consensus algorithm, and optimized contracts tailored to individual EV energy preferences, is introduced in [20]. This solution is further extended in [21] by incorporating a game-theoretic approach to optimally schedule EV charging services within the smart community. In [22], the authors propose a deep-reinforcement-learning-based framework to enable users to optimally adjust their charging behavior and significantly reduce their energy costs. The issue of charging schedule management is explored in [23], addressing grid challenges and optimizing cost, demand, and greenhouse gas emissions for sustainable and efficient operation in industrial energy systems. The authors in [24] were able to design a coordinated charging scheme to reduce power grid load and, thus, support more friendly power supply–demand interactions. The stochastic charging behavior of EVs were captured by a Markov decision process in [25], where the authors studied the impact of uncertainties using a policy gradient-based reinforcement learning method. A cooperative charging scenario is explored in [26] that deals with the coordinated handover of charging spots and improves charging station (CS) utilization.

Blockchain’s application ranges from database management [27,28,29], healthcare [30], and supply-chain management [31] to internet of things [32], cybersecurity [33], and the energy sector [15,34,35]. As the EV energy market is expanding, the number of consumers and producers (prosumers) is growing, also causing their interactions to become more complex. Such a complex market will be harder to control and scale if only managed centrally and demands decentralized solutions such as blockchain. In [36], the authors claim that the use of blockchain for energy trading can solve the problem of scalability and mobility. In addition to this, due to short, local energy transfer, a distributed energy exchanging system can reduce energy loss, as shown in [37]. The authors of [38] present a blockchain-based energy-trading platform for EVs, utilizing smart contracts and a private Ethereum network. Ref. [39] discusses an adaptive blockchain-based EV participation system, which focuses on minimizing power fluctuations and charging costs. A blockchain based energy-trading scheme using decentralized identifiers and verifiable credentials was proposed in [40], where the authors chose to use the blockchain only for the authentication of users, but not for storing transaction records. A blockchain-enabled scalable, secure, and decentralized peer-to-peer energy-trading solution is proposed in [41] while considering the existing technical, regulatory, and economic challenges. The proposed solution outperformed traditional models in scalability, encouraging the utilization of decentralized and sustainable energy systems with broader environmental and economic benefits. In [42], the authors propose a blockchain-enabled model, DeepICE, which utilizes vehicles’ trajectory data to enhance private car users’ commute experience by predicting optimal departure and arrival times. In this context, blockchain is used to preserve privacy while ensuring trust among users. Multilayer sharding blockchain technology was used in [43] to enhance the scalability and compatibility of decentralized identity (DID) solutions in Web3. The proposed SS-DID architecture achieved high performance with low latency and high throughput.

V2V energy-trading mechanisms have also been explored in previous studies, albeit in a somewhat incomprehensive manner. In [44], a V2V authentication protocol was designed that will utilize key exchange among users without relying on certificates. A V2V energy sharing framework is introduced in [45], along with a prosumer matching algorithm, reducing energy costs while increasing user satisfaction and social welfare. The authors in [46] propose a new consensus algorithm to ensure high throughput and deter Sybil attacks in a V2V energy-trading scheme. In [47], the authors modeled the seller selection process by a variant of the knapsack problem and then solved it using a linear approach, gaining significant improvement in metrics like charging latency, service availability, etc. An iterative bidirectional auction mechanism was designed in [48] to solve a social welfare maximization problem and make optimal charging and discharging decisions in a local V2V trading scenario.

The importance of robust pricing mechanisms in V2V energy-trading markets lies in their ability to provide higher user satisfaction and better resource utilization while maximizing social welfare and overall system efficiency. Ref. [49] proposes a decentralized Bayesian game-based pricing mechanism with incomplete information, achieving a reduced communication overhead with better approximation of user satisfaction. An algorithm named Limited Neighborhood Search with Memory (LNSM) is introduced in [50] to schedule EV charging services and ensure better profits for energy companies. In [51], the authors modeled an adaptive pricing mechanism to learn from the users reaction to price changes and achieved better performance compared to current pricing mechanisms. A privacy preserving soft actor–critic-based deep-reinforcement-learning algorithm was used in [52] to determine adaptive profitable price and charging–discharging schedules. Ref. [53] presents a dynamic EV charging and pricing system where the users are rewarded with virtual currency for using congestion-free routs and charging stations. Some widely used pricing mechanisms in the literature are as follows: single auction [54,55], double auction [22,28,56,57,58], Bayesian game [49,59], stochastic game [60,61], Stackelberg game [62,63,64], etc.

The adoption of electric vehicles faces significant challenges, such as poor range [65], limited charging infrastructure [66], recharge duration [65], increased stress on the power grid [66], security concerns [67], and particularly, the lack of standardized communication protocols [68,69,70]. Effective energy trading requires data exchange between electric vehicles regarding energy levels, pricing, and demand-supply dynamics. Although still not widely adopted, the development of the ISO 15118 standard [71] provided a robust and secure communication solution to vehicle-to-grid (V2G) energy trading. However, such a standardized protocol for V2V trading is still absent, even though they are needed in parallel with V2G ones [72] to promote the load balancing of local grids and green energy utilization.

1.2. Contributions

Despite the recent advancements in research on the development of V2V energy-trading mechanisms and price–demand–supply balancing methods, it remains fragmented across various studies. While there have been efforts to explore different aspects of V2V energy trading, such as blockchain-based schemes and game-theoretic approaches, as discussed in the related works, these studies mostly focus on isolated components of the system. There is little effort spent on binding all the elements together to provide a more mature and complete solution. This indicates a significant research gap in the literature. The need for designing a fully developed protocol enabling seamless interaction among EVs engaged in energy trading, the ability to make optimal decisions regarding their demand, supply, and energy pricing in a distributed manner still remains an open research problem. In this paper, our focus is to address exactly this issue. We applied blockchain technology and public key cryptography in a V2V energy-trading scenario to enable secure communication, transaction, and data storage; proposed a game theocratic model for deciding on optimal trade parameters; and, finally, combined everything to develop a detailed, comprehensive communication protocol. Our contributions in this paper are presented below:

• We propose a V2V energy-trading framework allowing electrical energy exchange between EVs. The charging network operators (CNOs) here act as equipment suppliers and record keepers instead of energy sellers. PKI is used to provide and manage digital certificates and private keys, enabling secure communication between the end points. We also describe how a new user can securely enroll into the service of a CNO.
• We use proof-of-authority (PoA) [73] consensus algorithm-based blockchain to validate and record user and trade-related information. PoA ensures high scalability and throughput while keeping the energy consumption and latency low. The EVs themselves are kept out of the blockchain network due their computational, storage, and energy limitations. We also design smart contracts to validate and record trade data into the blockchain.
• To identify malicious entities that can attack a charging system, we perform detailed threat modeling. Then, we conduct an informal security assessment, which shows that the proposed model can prevent these attacks with proper security measures.
• To determine the optimal demands of the charging EVs and optimal supplies and prices of the discharging EVs, thus ensuring higher utility for both the buyers and the sellers, we employ a two-layer multi-leader, multi-follower Stackelberg game model, where each EV performs its own optimization in a distributed manner.
• To demonstrate how the protocol works in practice, we implement it in Python while using Geth [74] for the blockchain implementation. Then, we perform detailed experiments based on various scenarios to evaluate the performance of our proposed trade algorithm, protocol, and the blockchain in terms of utility, revenue, message transmission and processing time, smart contract execution cost, transaction throughput, latency, scalability, etc.

1.3. Outline

The rest of this paper is organized as follows. Section 2 presents the system model and architecture, detailing the components of the system and their roles. Section 3 describes the PKI, its components, and how a new user can enroll into the service of a CNO, along with the issuance of digital certificates and cryptographic keys for that user. Section 4 talks in detail about the blockchain and its particular application in our model. In Section 5, we present the V2V protocol by providing an overview of the charging process and the TLS, then describe the protocol phases along with the smart contract and message definitions. Section 6 presents the threat model and our informal security analysis. In Section 7, we propose the trade algorithm that determines the optimal trade parameters (demands, supplies, prices), while Section 8 presents the exhaustive numerical simulation results. Finally, in Section 9 we conclude the paper by summarizing its content and discussing our future plans.

2. System Model and Architecture

The charging ecosystem is comprised of these entities (Figure 1):

• The CNOs who provide and manage the charging infrastructure.
• The charging station management system (CSMS) servers, maintained by the CNO, act as back-end servers for user enrollment, web interaction, queries, processing payments, etc. They also have the authority to seal blocks in the blockchain.
• The charging stations (CSs), managed by the CNOs, provide charging services to the EVs. Each CS has multiple pieces of EV Supply Equipment (EVSE), each having a single charging port. There can be multiple types of charging cables in each EVSE, but only one can be used at a time. Each piece of EVSE is also equipped with a smart meter that can measure the incoming or outgoing energy quantity reliably and has built-in protection against tampering. For this paper, we assume the data reported by the smart meters are genuine and can be trusted.
• Blockchain-based distributed ledger, managed by the CNO, is leveraged to securely record initial trade requests, final trading information, and transactions. The CSMS servers and the CSs are all nodes of the blockchain network.
• The EVs who want to trade energy between themselves but have to use the infrastructure provided by the CNOs. The EVs are also equipped with smart meters.
• The PKI service providers who manage the TLS certificates for the other two entities.

2.1. Charging Network Operators

CNOs’ responsibilities typically include the following:

• Expanding the charging infrastructure by installing CSs and other network equipment.
• Managing the charging network by ensuring the CSs are operational and accessible.
• Managing the blockchain and the CSMS servers.
• Monitoring the performance of the various network elements.
• Managing the demands of EV users through coordinating charging activities.
• Managing grid integration and optimizing grid utilization.
• Keeping the charging infrastructure updated by implementing state-of-the-art smart EV charging technologies.

2.2. Charging Station Management System Servers

CSMS servers are deployed and maintained by the CNOs to manage the overall charging process. These servers enable the CNOs to do the following:

• Providing web interface or apps for the user so that they can manage their accounts, data, payment methods, etc.
• Managing user enrollment, identity verification, and other authentication and access control processes.
• Ensuring that the CSs are up to date with the latest security patches and software enhancements by controlling firmware updates and device settings.
• Remotely monitoring real-time CS data like energy levels, charging sessions, and transactions. These data can be analyzed to gain insights and to further improve the performance of the system.
• Processing payments.
• Acting as sealer nodes in the blockchain by verifying and adding new blocks to the blockchain.
• Interacting with the blockchain to retrieve energy trade data and provide signed confirmation to the EV users.

2.3. Charging Stations

CSs are physical devices that are connected to one or multiple power sources. Their main task is to transfer power from these sources to EVs. Normally, CSs draw power from the grid, but in our model they draw it from other EVs who are willing to discharge their batteries. The key roles of CSs are as follows:

• Transferring power from discharging EVs to charging EVs.
• Providing hardware (EVSE) for the said energy transfer.
• Recording the amount of power coming in or going out using smart meters. These records are needed in case of a depute.
• Enabling indirect communication and interaction between charging and the discharging vehicles.
• Storing power temporarily in batteries of its own. For example, a charging EV can complete charging by taking from the batteries and go on its way without waiting for the discharging vehicles to finish, or vice versa.
• Acting as signer nodes in the blockchain. They can submit data and execute smart contacts, but cannot seal a new block.

2.4. Blockchain

A blockchain-based distributed ledger is used in many applications because of its decentralized, immutable, and transparent nature. Being decentralized, it is expensive to attack a blockchain. It provides anonymity while also enabling transparency and tractability when needed. In our system, blockchain is used for the following:

• Providing a secure place for all transactions and trading data.
• Recording the initial trade request, the optimized output of the trade algorithm, and the actual traded amount of energy, along with the prices through the use of smart contracts.
• Validating the account addresses the initial trade requests are generated from, thus verifying the source of the data using smart contracts.

2.5. Electric Vehicles

EVs are the main beneficiaries of the EV charging infrastructure. The roles of EVs and their users are as follows:

• Utilizing the EV charging infrastructure by buying (charging EVs) or selling (discharging EVs) to each other and, thus, driving the demand.
• Providing feedback on the overall charging experience so that the CNO can make better decisions in future.

2.6. PKI Service Providers

PKI is used in our model to facilitate a secure and user-friendly charging process. A CNO may want to delegate the PKI management responsibilities to a third party. The PKI service providers contribute to our system via the following:

• Creating infrastructure to providing PKI-related services like certificate issuance, revocation, life cycle management, etc.
• Managing digital certificates, cryptographic keys, and the other credentials used for authentication and authorization of entities, ensuring the encryption and integrity of communication data.
• Generating, distributing, and protecting private keys.
• Ensuring that certificate authorities at different levels are not compromised by implementing safeguards against cyber and physical attacks.

3. Public Key Infrastructure (PKI)

PKI is used to generate and manage digital certificates and cryptographic keys, which are then used to secure communication over networks. It enables a system to authenticate the identities of users, services, or devices and encrypt communication data or electronic transactions while maintaining their integrity. As TLS is employed in our proposed system to secure the communication channel through the use of digital certificates and cryptography, a well-defined PKI is needed to manage these required certificates and keys. Although there are alternatives to PKI, it is the most mature and the most widely used security technology in the industry. This is why we are choosing PKI as the backbone of security, as any alternative will have to go through rigorous scrutiny and standardization processes to be accepted by the industry. Compared to that, PKI can be readily applied to the EV charging scenario, promoting quick adoption of the proposed V2V energy-trading protocol.

The participants in this V2V energy-trading scheme are as follows: (i) the charging and discharging EVs, (ii) the CSs, and (iii) the CSMS servers. All participants will need their own sets of certificates, which will be used to mutually authenticate each other. Our PKI architecture is shown in Figure 2.

3.1. PKI Components

In a PKI, there are a number of entities whose roles vary in issuing, managing, and using the digital certificates. Certificate authorities (CAs) are responsible for issuing and managing the certificates, while the end entities use them. These components are organized in a hierarchical order to ensure scalability and flexibility and, most importantly, isolate them so that compromising one entity does not collapse the whole system. The trust also follows the same order, with the root CAs being the most trustworthy. These components and their roles in our system are described next.

3.1.1. Root Certificate Authority

The root CA of the CNO is the top level entity in the hierarchy. Its certificate is self-signed, and it acts as the trust anchor for the charging ecosystem. The relying parties inherently trust the root CA if its certificate is kept in their trust store. There can be multiple root CAs, but in our model we are only showing one for simplicity. Its main task is to issue certificates for the intermediate (or subordinate) CAs (ICAs/SubCAs). It never issues any end-entity certificates. If the Root CA is compromised, the whole ecosystem will become unsecured, so it is very important to keep the root CA offline in order to disable remote attacks. The EVs, the CSs, and the CSMS servers must keep a copy of the root CA certificate in their trust stores.

3.1.2. Intermediate or Subordinate Certificate Authority

The role of ICAs or SubCAs is to issue the end-entity or leaf certificates, while their own certificates are issued by the offline root CA. In a multi-tiered hierarchy, they can also issue certificates for the SubCAs below them. In our system, we have only one tier, which means there is only one level of SubCAs. We are using separate sets of SubCAs for the CSMS servers, the CSs, and the EVs, where each SubCA issues certificates for their respective end entities. Using different SubCAs based on the end-entity certificates they manage helps to contain attacks and isolate compromised branches from uncompromised ones.

3.1.3. End-Entity Certificates

End entities are the users of the PKI, and they do not have permission to issue another certificates. End-entity certificates are used for the TLS authentication at the start of the charging process and are subsequently used for encrypting the communication channel between the EV and the CS, and also between the CSMS server and the CS. Blockchain-based energy-trading models usually deploy smart contracts to perform the authentication and authorization of users and other system components, but our use of PKI and, thus, digital certificates removes the need for such or any other kind of validation method, as possessing the associated private key is enough for authenticating the end entities.

3.2. New User Enrollment

To access the V2V charging service provided by a particular CNO, a new EV user needs to first enroll into that CNO’s system and obtain their EV trade certificates. The enrollment process (Figure 3) and its steps are described in order below.

• Initialization: A user can start the enrollment process by initializing an account creation through a web interface or an app managed by the CNO back-end (CSMS servers). The account creation process asks for the relevant personally identifiable information (PII) of the user, information about the EVs, and payment details.
• Verification: The CNO verifies the information provided. To enforce strict validation, the CNO can use government databases, e.g., motor vehicle and social security databases, to check if the user really exists and if the vehicle indeed belongs to the user. Payment details (i.e., credit/debit card or bank information) should also be validated.
• Encryption and Recording: After the verification, the CNO creates an account ID for the user, encrypts the sensitive parts of the information, and everything is then recorded into the blockchain. Sensitive information includes personally identifiable information like names, addresses, payment details, etc., which the regular blockchain nodes or the signer nodes (i.e., the CSs, which are physically accessible by the public) do not need to know. This is why this information is encrypted before being stored on the blockchain. Only the CSMS servers possess the keys to decrypt. Nonsensitive information that cannot directly be linked to a specific person or vehicle, like the charging parameters, certificate serial numbers, etc., are needed by the CSs and should be kept in plain text. Adding payment details ensures that the users will not have to manually pay each time they use a charging service. Rather, after the charging is finished, the CSMS servers can process the payment automatically using the stored payment method (which only the servers can access) and the trade information can be stored in the blockchain through the use of smart contracts.
• Certificate Issuance: The CSMS server asks the user through the web interface or app to upload a certificate signing request (CSR). The user generates a private key, creates and signs a CSR, and uploads it. The server verifies if the CSR matches the previously provided information, and if it does it forwards the CSR to an EV SubCA. The EV SubCA issues a new EV trade certificate based on the CSR and sends it back to the server. The server updates the user’s account by adding the certificate’s serial number and the associated account address. The account address can be generated from the private key associated with the EV trade certificate using Web3 features. These two pieces of information are kept unencrypted as the smart contracts need these to verify user data.
• Certificate Installation: The user downloads the newly issued EV trade certificate using the web interface or app and installs it into the EV’s trust store. The user also needs to install the Root CA certificate into the trust store of the EV as without it, the EV will not be able to authenticate the CS. This ends the enrollment process. The EV user can now go to any CS managed by that CNO and present the EV trade certificate for establishing a TLS session to start the charging process.

4. Blockchain

In this section, we discuss the blockchain technology, consensus mechanisms, and smart contracts, and also details about their application in our proposed system.

4.1. Blockchain as a Distributed Ledger

Blockchain was first proposed in [14] with the objective of managing Bitcoin accounts while ensuring security and privacy in a peer-to-peer (P2P) network. However, the technology has evolved over the years and currently is not only limited to financial applications [75] but also to scenarios where a distributed and decentralized platform allowing network participants to verify data before storing is needed. At its core, blockchain is a decentralized, distributed, and immutable electronic ledger or database based on public key cryptography. It consists of chains of data blocks. Each block is made up of a number of transactions, but they can also be empty and only contain the header data. The chain continues to grow as more blocks are added. The blocks are linked together using the Merkel hash tree, where each block contains a reference to the previous block. If someone tries to modify a particular block, its hash will change, thus unlinking it from the subsequent blocks. This is why attacking a blockchain is expensive as the attacker will have to not only modify the targeted block but also all subsequent blocks to match the hashes and keep the chain valid.

A public blockchain is completely open to everyone, totally decentralized, not owned by anyone, and is more secure and trustworthy, but is also very slow and has high energy consumption. A private blockchain is owned by a particular authority and only some authorized users can participate in it. It is faster and maintains privacy better than a public one. However, it has security concerns as there are only a few nodes controlled by the same authority. A hybrid blockchain combines both, where some parts are private and the rest are open to the public, but because of its complex nature it is harder to maintain. Finally, a consortium blockchain can also be partly open to the public and partly private. It is managed by a number of authorities instead of a single one. It has speed, privacy, and flexibility and is more decentralized than the private blockchain. The consortium blockchain can be considered as a special case of permissioned blockchain and requires participants to be pre-authorized, providing higher privacy, security, and customizing options for specific applications. Offering more privacy, speed, and energy efficiency than the public ones while also being more secure and transparent than the private ones, we use a consortium blockchain in our proposed model.

There are two types of nodes in a blockchain: miner nodes and normal nodes. A miner mode has the permission to add a new block to the blockchain, whereas the normal nodes do not. A normal node can still send transactions and view the contents in the blockchain. Nodes can choose to keep the whole blockchain data in their local storage (full nodes) or to keep only the header data of the blocks (lightweight nodes). A miner node has to maintain the whole chain data so it is a full node. In our system, the CSMS servers are miners, whereas the CSs are normal nodes. This is because the servers are more secure and can be trusted to mine blocks, whereas the CSs can be accessed physically by anyone. When transactions are submitted into the blockchain, they are first validated and then added to the current block, and finally the block is mined, which is a term for adding a new block to the blockchain. This whole process is maintained by an algorithm called the consensus mechanism.

In our system, the EVs are not a part of the blockchain, due to three important reasons. First, the number of EVs is expected to be much higher than the number of the CNO’s own nodes (servers, CSs). Therefore, it is not wise for the CNOs to hand over more than 50% of control of the blockchain to entities that they do not trust inherently. Second, EVs have limited storage and computational power. It will be difficult for the EVs to be even a lightweight node. Third, EVs are not expected to be always online and, thus, actively be a part of the blockchain. Even if they choose to be online, being a blockchain node, it will drain the limited battery constantly with all the block updates. Some of these reasons were also used in [38]. Although many studies have used already existing cryptocurrency or have proposed their own [48,76,77] as payment units, we are not using any as they tend to be very volatile [78,79]. Instead, we are using payment methods involving real money, which is processed by the CSMS servers, as detailed in Section 5.3.3.

4.2. Consensus Mechanism

Being decentralized and distributed in nature without any third party controlling, blockchain can suffer from the Byzantine generals problem [80], where reaching an agreement can prove difficult. In the context of blockchain, these agreements involve verifying transactions, validating new blocks, preventing block manipulation, adding or kicking out nodes, etc. Over the years, various consensus algorithms have been proposed to achieve consensus. Some of the widely used consensus algorithms are proof of work (PoW), proof of stake (PoS), distributed proof of stake (DPoS), PoA, practical Byzantine fault tolerance (PBFT), proof of capacity (PoC), proof of burn (PoB), etc. In our model, we choose the PoA for its high efficiency, low energy consumption, fast transaction, and highly scalable attributes, although it is less decentralized due to the small number of validators.

In the PoA consensus algorithm, a pre-approved set of authority nodes, i.e., sealers, are responsible for generating new blocks in a rotational mining routine. There can be other nodes without block generation permission, i.e., signers. In our case, CSMS servers are sealers while the CSs are signers. Also, current sealers can vote to make a signer a sealer, or vice versa. A specific sealer is elected to create the new block. If the elected sealer fails to submit a block within the required time frame, another sealer can be selected. PoA networks offer the flexibility to control the block generation time by configuring the period parameter in the genesis file.

4.3. Smart Contracts

Smart contracts are pieces of code that are deployed into and run on the blockchain network. When a smart contract is deployed, it is saved inside a block that, after being mined, cannot be modified any more. Moreover, it is verified before the deployment through the consensus mechanism. When a smart contract function is executed by a node, the corresponding call data or function parameters are visible to all the participant nodes, and they can each verify the final results. Therefore, while a traditional transaction is executed in a single server and the results or state changes are saved in one or more databases, in cases of smart contract transactions, everything related to them is verified by all the participating nodes. Every smart contract has a unique address to identify it. If a smart contract is to be modified, the only solution is to redeploy it with the modified code, and it will have a new address, essentially making it an entirely new contract. To execute a smart contract, a certain amount of computational work has to be done by the blockchain nodes. The cost to do this is measured using a unit called “gas”.

In our V2V energy-trading scenario, the smart contracts hold the logic for verifying the identities of the trade request senders (Algorithm 1) and record keeping (Algorithms 1–3). While some blockchain-based energy-trading models use smart contracts [38,49,50] to execute the core trade algorithm involving simple arithmetic operations, in our model this is not the case. Solving the Stackelberg game-based optimization method that we use involves steps that are very expensive or even impossible to execute in smart contracts, which only support basic operations like addition, subtraction, multiplication, division, modulus, and exponents. In our model, each vehicle solves their own optimization problem in a distributed manner.

Algorithm 1 Smart contract for verifying and recording order data

1: Input: msgSender   2: Initialization:   3: struct buyOrders { address cs, string sessionId, uint64 timestamp, uint32 evId, uint32 dMin, uint32 dMax}   4: struct sellOrders {address cs, string sessionId, uint64 timestamp, uint32 evId, uint32 sMax, uint16 pMax}   5: buyOrders dataB[], sellOrders dataS[]   6: uint indexB, indexS = 0, 0   7: Functions:   8: func buyRecord(string sessionId, uint64 timestamp, uint32 evId, uint32 dMin, uint32 dMax, bytes sig):   9:  bytes msghash = keccak256(abiEncodePacked(sessionId, timestamp, evId, dMin, dMax)) 10:  address userAddress = recover(msghash, sig) 11:  indexB$++$ 12:  dataB[indexB] = (msgSender, sessionId, timestamp, evId, dMin, dMax) 13:  emit indexB, sessionId, timestamp, evId, userAddress 14: func sellRecord(string sessionId, uint64 timestamp, uint32 evId, uint32 sMin, uint16 pMax, bytes sig): 15:  bytes msghash = keccak256(abiEncodePacked(sessionId, timestamp, evId, sMax, pMax)) 16:  address userAddress = recover(msghash, sig) 17:  indexS$++$ 18:  dataS[indexS] = (msgSender, sessionId, timestamp, evId, sMax, pMax) 19:  emit indexS, sessionId, timestamp, evId, userAddress

Algorithm 2 Smart contract for recording initial trade values

1: Input: msgSender   2: Initialization:   3: struct tradeInitial {address cs, string sessionId, uint64 timestamp, uint32[] cevs, uint32[] devs, uint32[] prices, uint32[][] energies}   4: tradeInitial dataTI[]   5: uint indexTI = 0   6: Function:   7: func tradeInitialRecord(string sessionId, uint64 timestamp, uint32[] cevs, uint32[] devs, uint32[] prices, uint32[][] energies):   8:  indexTI$++$   9:  dataTI[indexTI] = (msgSender, sessionId, timestamp, , cevs, devs, prices, energies) 10:  emit indexTI, sessionId, timestamp

Algorithm 3 Smart contract for recording final trade values and payment data

1: Input: msgSender   2: Initialization:   3: struct transaction {uint64 timestamp, uint32 energy, uint32 totalPrice, string transactionId}   4: struct tradeFinal {address cs, string sessionId, uint64 timestamp, uint32[] cevs, uint32[] devs, transaction[] data}   5: tradeFinal dataTF[]   6: uint indexTF = 0   7: Functions:   8: func TFInitialize(string sessionId, uint64 timestamp):   9:  indexTF$++$ 10:  dataTF[indexTF].cs = msgSender 11:  dataTF[indexTF].sessionId = sessionId 12:  dataTF[indexTF].timestamp = timestamp 13:  emit indexTF, sessionId, timestamp 14: func TFUpdateByCS(uint index, uint8 evType, uint32 evId, uint64 timestamp, uint32 energy, uint32 totalPrice): 15:  if evType then 16:   dataTF[index].dev.push(evId) 17:  else 18:   dataTF[index].cev.push(evId) 19:  end if 20:  dataTF[index].data[evId].timestamp = timestamp 21:  dataTF[index].data[evId].energy = energy 22:  dataTF[index].data[evId].totalPrice = totalPrice 23: func TFUpdateByCSMS(uint index, uint32 evId, string id): 24:  dataTF[index].data[evId].transactionId = id

5. V2V Protocol

5.1. Overview of the Charging Process

The charging EVs (CEVs) and the discharging EVs (DEVs) gather under a CS and connect the charging cable to the station. The charging cables are power-line communication (PLC) enabled, so they can handle both the power transfer and communication between the EV and the CS. Then, the EVs initiate TLS sessions with the CS using their EV trade certificates, as described in Section 5.2. After the secure TLS connections are established, the V2V communication protocol starts and goes through the three phases detailed in Section 5.3. It should be noted that no EV directly communicates with any other EV; rather, everything (both the communication and the energy) goes through the CS. Also, there is a second, persistent TLS session established between the EVSE and the CSMS server, which is used to exchange signed data for various validation purposes. A high-level overview of the charging communication is shown in Figure 4.

5.2. Security Concept

5.2.1. Transport Layer Security

In this V2V energy-trading protocol, we are making the TLS 1.3 mandatory in order to secure the private, sensitive communication between the EVs and the CS. TLS 1.3 does not support RSA key exchange and encryption; CBC cipher mode; RC4, 3DES, and Camellia encryptions; or MD5 and SHA1 hash algorithms. It also does not support any export ciphers. TLS 1.3 supports only five ciphersuites, none of which has any known vulnerabilities. Therefore, the attack surface for TLS 1.3 is reduced significantly, making it more secure than TLS 1.2.

5.2.2. TLS Channel Establishment and Authentication

When an EV user connects the charging cable to the CS’s EVSE, the EV immediately initiates a TLS connection setup using the EVSE’s predefined V2V communication port. The CS acts as the TLS server, while the EV acts as the TLS client. No application data are sent before the TLS handshake is complete. During the TLS handshake, both the EV and the CS mutually authenticate each other. This means the EVSE sends its certificate chain, which consists of the EVSE CPO certificate and the CPO SubCA certificate, to the EV, and the EV verifies it. On the other hand, the EV sends its certificate chain, which consists of the EV trade certificate and the EV SubCA certificate, to the EVSE, and the EVSE verifies it. Both the EV and the EVSE must have the root CA certificate installed in their respective trust store so that the root CA certificate is trusted by both. The certificate status or revocation status checking is carried out using the OCSP. The EV is assumed to be offline, so the CS needs to send its own OCSP response stapled with the TLS handshake messages. The EV does not have to staple an OCSP response as the CS is supposed to be online and it can fetch the OCSP response on its own. Additionally, the EV is required to check if the domain component of the EVSE CPO certificate is set to CPO. Similarly, the CS will check if the domain component of the EV trade certificate is set to the EV. This ensures that the EV knows if it is communicating with a CS, not another EV with a valid certificate, and vice versa.

5.3. Phases and Message Sequence

After the mutual authentication is done and a TLS session is in place, the main charging process starts. There are three phases in the charging process.

• Trade request submission
• Optimal price and energy determination
• Trade completion and payment processing

Each phase consists of multiple request–response pairs of messages between the EV and the EVSE, or between the EVSE and the CSMS server.

5.3.1. Trade Request Submission

In this phase, the CEVs and DEVs submit their trade requests and the CS receives the requests, verifies them, and records them into the blockchain with the help of smart contract (Figure 5). After the TLS session is established, the EV sends a SessionReq request message to the EVSE, including its EVID. The EVSE verifies if the EVID is indeed associated with the EV by matching it with the common name (CN) of the EV’s TLS certificate. If verified, the EVSE replies back with a SessionRes response message, which includes the charging session Id. In a case where the verification of the EVID fails, the EVSE sends a session Id with all zeros. Next, the EV sends a signed OrderReq request message to the EVSE specifying its demand or supply parameters. The EVSE does not have to verify the signature as the data are already protected due to the TLS, but it can choose to do so as an added layer of protection. The data are then sent to the smart contract, which checks the signature, records the data into the blockchain, and sends a transaction receipt back to the CS. The signature checking here is necessary as the data are not directly coming from the EV, and a compromised CS can modify the data before submitting it to the smart contract. While the smart contract can verify the signature, it should not be used to sign and subsequently send a confirmation that the trade order has been recorded correctly in the blockchain to the EV. Signing data using smart contracts is not recommended as the private key will have to be stored in the contract, and it is then no longer private. Instead, we make the smart contract emit an event upon verification and use the CSMS server to read the event log when the CS sends the OrderVerifyReq message to it. The server then signs the relevant data and finally sends the confirmation back to the CS through tan OrderVerifyRes message. The CS forwards this information to the EV using the OrderRes message. If any of the verification fails, the EVSE rejects the order. Whether the order is accepted or not, the EVSE notifies the EV by sending a proper OrderRes response message back. Finally, the EV verifies the signed confirmation data. If the verification steps fail, the EV can abort the session by sending the EndSessionReq message with a proper text describing the reason, while the CS will respond with an EndSessionRes message. This ends the trade request submission phase. The related smart contract is given in Algorithm 1, where the contents highlighted in blue indicate well-known functions or functions already available in solidity [81] or web3 [82] packages.

5.3.2. Optimal Price and Energy Determination

In this phase, the CS manages execution of the trading algorithm to determine the optimal price and amount of traded energy for each of the participant EVs. The optimal parameters are again recorded into the blockchain. See Figure 6 for a graphical representation. At the start of this phase, the CS waits for a starting condition to be satisfied. For example, it can wait for a particular number of charging and discharging vehicles to be connected, or it can wait for a fixed energy supply and demand from the connected vehicles. After the starting condition is met, the CS gathers all the demand and supply data and sorts them, first based on the type of service (charging or discharging) and then based on the chronological order of trade-order reception. The trade algorithm then runs in a synchronous manner following the sorted order. In each vehicle’s turn, the CS first sends the data required to run the optimization to the vehicle in a ChargingReq or DischargingReq request message, then the vehicle runs its optimization algorithm using the provided data and, finally, it sends back the updated optimized parameters to the CS in a ChargingRes or DischargingRes response message. The CS updates its local data and checks them for convergence. If convergence is reached, the converged data are sent to the smart contract (Algorithm 2), which records them in the blockchain and sends back a transaction receipt to the CS. The EVs, however, do not know if the data were stored correctly, and they need confirmations. As mentioned previously they do not trust the CS directly. Therefore, the CS sends an TradeVerifyReq message to the CSMS server, which reads the relevant data from the blockchain, signs them for each EV, and sends the signatures back to the CS via the TradeVerifyRes message. Finally, the CS sends the EndOptimizationReq request message to all the vehicles forwarding the individual signatures. Upon receiving this, each EV checks if the signature is valid and sends back a response message EndOptimizationRes back to the CS to notify that it accepts the final parameters. This ends the optimal price and energy determination phase. The related smart contract function is given in Algorithm 2.

5.3.3. Trade Completion and Payment Processing

In this phase, the CEVs and DEVs trade energy based on optimal parameters determined in the previous phase. After the trading is complete, the CS records the final trade data into the blockchain and the CSMS server processes the payments, as presented in Figure 7. In the beginning, the CS executes function TFInitialize in the smart contract (Algorithm 3) to initialize the data structure for storing the final trading data. Next, the CEVs send PrecheckReq request messages to the CS detailing their charging parameters (i.e, target voltage, maximum current limit, etc). The DEVs can leave the message body blank. When the CS receives this request, it sends the corresponding response message PrecheckRes to the EVs. After receiving the response, the EVs immediately close their high-voltage power delivery contacts and send an EnergyExchangeReq request message. Upon receiving this message, the CS closes its own power delivery contacts and the energy starts flowing. Both the EVs and the CS use smart meters to measure the amount of energy moving in or out. When the CS’s smart meter reports that the required amount of energy has been transferred, it sends the EnergyExchangeRes response message to the EVs to notify the end of energy transfer, along with the actual amount of traded energy. The EVs check their own smart meters, and the readings should match within a small tolerance. Next, the EVs send the PaymentReq request message to the CS, containing the preferred payment option. The CS verifies the payment option, calculates the total cost or payment, and submits these details to the smart contract (Algorithm 3) by calling the TFUpdateByCS function. Upon successful execution of the function, the CS reveives a transaction receipt and sends the PaymentVerifyReq message to the CSMS server. The server then reads relevant data from the blockchain and processes the payment. As the payment is processed, the server receives a transaction ID, which it stores in the blockchain using function TFUpdateByCSMS in Algorithm 3. After that, it generates confirmation signatures and sends the response message PaymentVerifyRes back to the CS. The CS forwards these pieces of information to the EVs in PaymentRes. The EVs verify the signature and, finally, the trading session ends by exchanging the last set of request–response message pairs EndSessionReq and EndSessionRes.

5.4. Message Definitions

There are two parts in each message: message header and message body. The header has the same structure for every message, whereas the structure of the body is tailored uniquely for each message. Message data are encoded and exchanged in JSON format. For data canonicalization, RFC 8785 (JSON Canonicalization Scheme (JCS)) [83] is followed.

5.4.1. Message Header

The message header contains general information about the message. The Unix timestamp is needed in order to prevent a reply attack. On the other hand, the session ID uniquely identifies the V2V energy-trading session and also prevents reply attacks. When an entity receives a message, it checks if the timestamp is larger than the timestamp of the last message sent and smaller than the current timestamp. It also checks if the session ID is consistent throughout the session and if the received message type is expected at that point of execution. Only in the case of SessionReq, where the session ID is not yet known to the EV, can the session ID field be absent.

Field Name	Data Type	Description
type	string	Name of the request or response message. For example: SessionReq.
timestamp	integer	Unix timestamp of the time of message creation in milliseconds.
sessionId	string	16 character (64 bits) hexadecimal string, all caps. Its value is the same for all EVs under the same trading session.

5.4.2. Message Body

The message body holds information unique to a specific type of message. Unless mentioned, all the fields are required. Some fields are mentioned to be only applicable to either CEVs or DEVs.

SessionReq

Field Name	Data Type	Description
evId	integer	ID of the EV (EVID). It is the same as the common name (CN) of the EV trade certificate.

SessionRes

Field Name	Data Type	Description
status	string	OK: If the EVID in the SessionReq matches the CN of the EV trade certificate. FAIL: Otherwise.

OrderReq

Field Name	Data Type	Description
bMin	float	Minimum energy demand of the cth CEV. Denoted by $b_c^{min}$ in Table 1. Summary of key notations. Notation Description $\mathcal{C}$ Set of charging EVs (CEVs) $\mathcal{D}$ Set of discharging EVs (DEVs) ${\mathbf{b}}_c$ Energy demand (to be bought) vector of CEV c ${\mathbf{s}}_d$ Energy supply (to be sold) vector of DEV d $b_c^{min}$ Minimum energy demand of CEV c $b_c^{max}$ Maximum energy demand of CEV c $s_d^{max}$ Maximum energy supply of DEV d $U_c\left(\mathbf{b}\right)$ CEV c’s utility function $A_c,B_c$ CEV c’s normalization factors $M_c,N_c$ CEV c’s satisfaction and dissatisfaction coefficients $U_d(\mathbf{s},\mathbf{p})$ DEV d’s utility function $p_d^{max}$ Maximum energy price of DEV d $E_d,F_d,G_d$ DEV d’s normalization factors r Level of other DEVs impact . Required if evType is 0.
bMax	float	Maximum energy demand of the cth CEV. Denoted by $b_c^{max}$ in Table 1. Required if evType is 0.
factorM	float	CEV’s satisfaction coefficient as denoted by $M_c$ in Table 1. Required if evType is 0.
factorx	float	DEV’s evaluation of the provided supply as used in Equation (6) and denoted by $X_c$ for the cth CEV. Required if evType is 0.
sMax	float	Maximum energy supply of the dth DEV. Denoted by $s_d^{max}$ in Table 1. Required if evType is 1.
pMax	float	Maximum energy price asked by the dth DEV. Denoted by $p_d^{max}$ in Table 1. Required if evType is 1.
factorF	float	DEV’s normalization factor $F_d$ as shown in Table 1. Required if evType is 1.
factorG	float	DEV’s normalization factor $G_d$ as shown in Table 1. Required if evType is 1.
evType	integer	0 for CEVs, 1 for DEVs.
signature	string	Hexadecimal string of the signature. See below for signature generation rules.

A signature is generated by first hashing some selected data using Web3’s keccak256 hashing function on the packed ABI encoded data. Then, the hashed data are signed using the EVs private key. For CEVs, these data, in order, are sessionId, timestamp, evId, dMin, and dMax, with data types of string, uint64, uint32, uint32, and uint32, respectively. For DEVs, these data, in order, are sessionId, timestamp, evId, sMax, and pMax, with data types of string, uint64, uint32, uint32, and uint16, respectively. While verifying the signatures, the same procedure is followed by the smart contracts, as shown in line 9 (for CEVs) and line 15 (for DEVs) of Algorithm 1.

OrderRes

Field Name	Data Type	Description
index	integer	Index of the stored order data in the blockchain.
signature	string	Hexadecimal string of the CSMS server’s signature.
csmsCert	string	Hexadecimal string of the CSMS server’s certificate in DER format.

OrderVerifyReq

Field Name	Data Type	Description
evId	integer	ID of the EV (EVID). It is the same as the common name (CN) of the EV trade certificate.
blockNumber	integer	Block number of the recorded order data. The CS receives this from the transaction receipt.

OrderVerifyRes

Field Name	Data Type	Description
signature	string	Hexadecimal string of the signature. See below for signature generation rules.

As this signature will be verified outside of the smart contract, we use the SHA256 hash algorithm, as follows (1).

$$signature=sha256(sessionId,timestamp,evId,index,address)$$

(1)

where timestamp, index, and address are emitted by the smart contract (Algorithm 1).

ChargingReq

Field Name	Data Type	Description
factorA	float	CEV’s normalization factor $A_c$, as used in Equation (5). Required when status is INITIALIZING. Optional for other status values.
pMaxMax	float	Maximum of all the maximum price attributes of the DEVs as used in the term $B_c$ in Equation (5). Required when status is INITIALIZING. Optional for other status values.
supplies	float	List of the energy supplies, $s_{d,c}$, from all the DEVs to the cth CEV, as used in Equation (7c).
prices	float	List of the energy prices of the DEVs. Denoted by $p_j$ in Equation (5)
othersDemands	float	List of total energy requested by other CEVs from each DEV, denoted by ${\mathbf{b}}_{-c}$ in Equation (5).
status	string	INITIALIZING: For the first message of this type to a CEV. RUNNING: If the trade algorithm has not converged. FINISHED: If the trade algorithm has converged.

ChargingRes

Field Name	Data Type	Description
demands	float	Demand list of the CEV. Denoted by ${\mathbf{b}}_c$ in Equation (5).

DischargingReq

Field Name	Data Type	Description
factorH	float	Denominator of DEV’s normalization factor $E_d$ in Equation (6). Required when status is INITIALIZING. Optional for other status values.
factorX	float	A list representing the DEV’s evaluation of the provided supply, as used in Equation (6) and denoted by $X_c$ for all c. Required when status is INITIALIZING. Optional for other status values.
pMaxMax	float	Same thing as in Section ChargingReq. Required when status is INITIALIZING. Optional for other status values.
sMaxSum	float	Summation of all the maximum supply values of the DEVs, $\sum s_d^{max}$ for all d. Required when status is INITIALIZING. Optional for other status values.
demands	float	List of energy demands, $b_{c,d}$, from all the CEVs to the dth DEV, as used in Equation (8a,b).
othersData	float	A combination of different parameters of other DEVs, as represented by the denominator of the first part in Equation (6).
status	string	INITIALIZING: For the first message of this type to a DEV. RUNNING: If the trade algorithm has not converged. FINISHED: If the trade algorithm has converged or timed out.

DischargingRes

Field Name	Data Type	Description
supplies	float	Supply list of the DEV.
price	float	Energy price asked by the DEV.

TradeVerifyReq

Field Name	Data Type	Description
blockNumber	integer	Block number of the recorded order data. The CS gets this from the transaction receipt.

TradeVerifyRes

Field Name	Data Type	Description
sigCEVs	string	List of hexadecimal string of signatures for CEVs. See below for signature generation rules.
sigDEVs	string	List of hexadecimal string of signatures for DEVs. See below for signature generation rules.

A unique signature is generated for each EV following (2) and (3).

For CEVs:

$$signature=sha256(sessionId,timestamp,evId,demands,prices)$$

(2)

where, demands is a list of energy the CEV demands from each DEV and prices is the corresponding prices offered by the DEVs.

For DEVs:

$$signature=sha256(sessionId,timestamp,evId,supplies,price)$$

(3)

where supplies is a list of energy the DEV supplies to each CEV and prices is the price offered by the DEV.

EndOptimizationReq

Field Name	Data Type	Description
status	string	OK: If the trade algorithm has converged successfully. TIMEOUT: If the trade algorithm has not converged within the maximum iteration limit.
sigTimestamp	integer	Timestamp of the moment when the CSMS server generated the signature.
signature	string	Hexadeimal string of the CSMS server’s signature.

EndOptimizationRes

Field Name	Data Type	Description
status	string	OK: If the signature received in EndOptimizationReq has been verified. FAIL: Otherwise.

PrecheckReq

Field Name	Data Type	Description
voltage	float	Charging voltage requested by a CEV. Required for a CEV.
maxCurrent	float	Maximum charging current allowed by a CEV. Required for a CEV.

PrecheckRes

Field Name	Data Type	Description
status	string	OK: If the station can support the charging parameters detailed in PrecheckReq. Or if the PrecheckReq is from a DEV. FAIL: Otherwise.

EnergyExchangeReq

Field Name	Data Type	Description
energy	float	Amount of total energy requested (CEV) or to be delivered (DEV).

EnergyExchangeRes

Field Name	Data Type	Description
energy	float	Actual amount of traded energy.

PaymentReq

Field Name	Data Type	Description
method	string	Name of the preferred payment method. Can be left blank to use the default one.

PaymentRes

Field Name	Data Type	Description
status	string	OK: If the payment is processed successfully. FAILED: Otherwise.
transactionId	string	ID of the monetary transaction ID for user’s convenience.
signature	string	Hexadeimal string of the CSMS server’s signature.

PaymentVerifyReq

Field Name	Data Type	Description
index	integer	Index of the final trade data record in the blockchain. The CS receives it from the transaction receipt of function TFInitialize in Algorithm 3.
evId	integer	ID of the EV (EVID). It is the same as the common name (CN) of the EV trade certificate.

PaymentVerifyRes

Field Name	Data Type	Description
transactionId	string	Bank or credit card transaction ID for the monetary exchange.
signature	string	Hexadeimal string of the CSMS server’s signature. See below for signature generation rules.

The signature generation in Section PaymentVerifyRes is shown in (4).

$$signature=sha256(sessionId,timestamp,energy,totalPrice,transactionId)$$

(4)

where timestamp, energy, and totalPrice is read from the blockchain.

EndSessionReq

Field Name	Data Type	Description
reason	string	DONE: Everything went well and the session can be stopped. Otherwise, custom reason messages can be used.

EndSessionRes

Field Name	Data Type	Description
status	string	OK: If stopping reason is accepted and understood. Otherwise, custom status can be used.

6. Threat Modelling, Security Analysis and Privacy Concerns

In this section, we first discuss what threats can be present in a generic P2P trading system and then perform a security analysis to evaluate if these threats are feasible or viable for our model. Lastly, Customers’ privacy concerns are also addressed.

6.1. Threat Modelling

An adversary can attack different points of the system depending on their motive. For example, endpoints like the EVs, the CS, and the CSMS servers can be compromised by an attacker, or there can be man-in-the-middle (MITM) or denial-of-service (DoS) attacks, which do not require direct unauthorized access to any endpoint. Replay attacks, disclosure of customers’ private information, data breach, tampering of communication, physical tampering of end-points, code injection, impersonation, consensus mechanism vulnerabilities, etc., are also important security concerns [46,84,85,86]. An entity can be malicious by itself or can be compromised by a third party. While a malicious or compromised server can pose a serious threat to the entire charging infrastructure, we can reasonably assume that they will be protected using the best industrial practices available today, and thus we are keeping them out of the scope of the threat modeling in this work.

A threat model provides a structured approach to analyze and categorize potential threats. In the attack scenarios discussed next, we used the STRIDE threat model to categorize various threats. The name STRIDE is a mnemonic that refers to six threat categories. It stands for spoofing (pretending to be someone or something else), tampering (modifying data illegally), repudiation (denying some action or responsibility), information disclosure (providing information to someone not authorized to have it), denial of service (exhausting system resources so that its normal operation is interrupted), and elevation of privilege (allowing someone to do something they are not authorized to do). The STRIDE categories in each scenario are highlighted using boldface.

6.1.1. Malicious or Compromised EV

A malicious charging EV:

• can pretend it did not consume any energy (repudiation) and refuse to pay, even though it indeed received energy from the discharging EVs.
• can pretend it is another EV (spoofing) and try to divert the charging bill to the victim EV.

A malicious discharging EV, on the other hand:

• can pretend to deliver energy and ask the charging EVs to pay for the energy it never delivered (repudiation).

6.1.2. Malicious or Compromised Charging Station

As a CS handles the interaction between EVs and the smart contracts, if it is compromised or becomes malicious, it has the potential to modify the data sent by the EVs and submit the modified data to the smart contract. For example:

• It can refuse to pay a discharging EV by pretending it did not receive any energy from the victim (repudiation). Similarly, it can charge a charging EV for the energy it never delivered.
• It can receive an energy selling request from a discharging EV (victim) but submit the data to the smart contract in the name of another EV (tampering). In this case, this other EV will get paid for the energy the victim EV delivered. This threat makes sense if the CS is compromised by the EV that is getting paid illegally.
• It can pretend to be a charging EV (spoofing) and launch a replay attack against it by resubmitting a bill some time later to the smart contract to make the victim EV pay again.
• It can release sensitive data about the EVs and the EV users to interested parties (information disclosure).

6.1.3. Malicious Third Party

A malicious third party can be anyone other than the charging network components or the EV users. We list some attacks below that can be launched by a malicious third party.

• A third party attacker can modify EV/CS hardware physically or inject malware to steal (information disclosure) or manipulate (tampering) data, or deny charging to specific groups (denial of service).
• Fake root certificates can be installed (tampering) into EVs or CSs, leading them to place trust in untrusted entities, which can open a path for other types of attack.
• If private keys and certificates are stolen from authorized EVs or CSs, they can be installed in unauthorized ones for impersonation attacks (spoofing). Also, they can be used to silently monitor trade information by decrypting the encrypted communications (information disclosure) or manipulate data in both rest and in transit (tampering).
• Blockchain attack: Blockchain networks are generally considered very secured and resistant to illegal manipulation because no single entity controls all the authorization and validation tasks alone. Rather, these tasks are distributed among various participant nodes. To launch an attack, the attacker needs to control a large portion of blockchain nodes. Therefore, although expensive, a blockchain can be compromised. Threats here includes tampering, information disclosure, elevation of privilege, denial of service, etc. Also, in public blockchain, all of the information is accessible to the public, so sensitive data should not be stored in a public ledger.
• Man-in-the-middle attack: Instead of hacking or getting illegal access into a network component, a malicious entity can seat itself between two network components, capture the private communication between them, and finally, disclose or even modify this information for its own gain. For example, if someone can modify the data in transit between a discharging EV and the CS, it can make the system pay itself rather than the original seller for the sold energy. Related threats here are spoofing, tampering, and information disclosure.
• Denial-of-service (DoS) and distributed denial-of-service (DDoS) attack: Attackers can launch denial-of-service attacks by exhausting a CS’s resources using or posing as legitimate EVs. They can send trade requests continuously or cancel and resend trade requests again and again to overwhelm the station. Also, they can temper the charging cables on the station’s side, which might cause the trade requests to be rejected automatically. A few of these methods may result in a situation where no EVs with a real need can get a free or functioning EVSE to connect.

6.2. Security Analysis

Here we analyze the feasibility and viability of the threats and attacks mentioned in the previous subsection. The security measures in each scenario are highlighted using boldface.

6.2.1. Malicious or Compromised EV

Our security requirements prevent the threat mentioned in Section 6.1.1 from the malicious charging EVs by doing the following:

• Both the EV and the EVSE are required to record the power flowing in or out using smart meters. As smart meters also use cryptographic security measures, it is difficult to compromise one; even if a hacker or an EV user can do that to the smart meter of the EV, the smart meter of the EVSE is still protected. Therefore, if a malicious EV tries to claim that it did not receive any energy, the EVSE’s smart meter will show that the EV indeed received it. Also, as the total energy coming out of the discharging EVs should be equal to the total energy going into the charging vehicles, a simple investigation will be sufficient to determine the culprit.
• For the second scenario, as we use public key cryptography and digital certificates to verify authenticity and establish TLS connection right at the beginning of the charging session, there is no other way to spoof identity than by stealing the certificate and its associated private key from a legitimate EV.

On the other hand, for the malicious discharging EVs:

• The threat mentioned is very similar to the first threat for the charging EVs’ case. Therefore, the mitigation technique is also the same.

6.2.2. Malicious or Compromised Charging Station

Our security model counters the threats described in Section 6.1.2, as explained in order below:

• The traded energy quantity is tracked by the smart meters on both sides. Therefore, the CS cannot simply deny the quantity of the traded energy. Also, the final traded energy quantity is recorded in the blockchain, and while the EV users cannot access it directly, they do receive a signed confirmation from the CSMS servers in a PaymentRes message.
• The signature (1) from the servers in OrderRes includes the evId. Therefore, the user can be sure that the correct evId was recorded in the blockchain.
• All the protocol messages contain the timestamp and the sessionId in the header. All three server signatures and the smart contracts also include these. Therefore, it is not possible to launch a replay attack.
• As described in the enrollment process in Section 3.2, the CSs cannot access any sensitive data (i.e., identifiable information, payment method details). Therefore, in this case, the counter measure is integrated in the system architecture.

6.2.3. Malicious Third Party

• EVs and CSs have to be physically secured. To prevent remote attacks like code injection they should be allowed to communicate only with selected entities like the original equipment manufacturer (OEM) or CSMS servers. Therefore, the countermeasure is a combination of physical security controls, network firewalls, server–client network configurations, etc.
• In addition to physical security of certificate stores, certificate transparency (CT) and certificate authority authorization (CAA) technologies can be used to detect fake and rogue certificates.
• Trusted platform modules (TPMs) can be used to securely store the private keys, making it infeasible to steal or alter them.
• As consortium blockchain is used in our model, sensitive data are not available to everybody. The EV users, however, can still request their personal data through the web interface. Also, only the trusted CSMS servers, which are more secured than public nodes, can seal new blocks. Therefore, compromising the majority of these secured servers is harder than compromising untrusted public nodes.
• The use of PKI and TLS enables encrypted communication between the endpoints while ensuring their identities. This prevents any man-in-the-middle to impersonate trusted entities or eavesdrop on the communication data in transit.
• PKI and TLS do not prevent DoS or DDoS attacks. Prevention of these attacks mainly depends on the implementation and the network architecture. Standard DoS and DDoS mitigation strategies can be used in our model.

6.3. Privacy Concerns

In a V2V energy-trading scenario, there can be a few ethical considerations and privacy-related concerns.

• Fairness and equity: It is very important that all customers, regardless of their race, color, nationality, religion, gender, or ethnicity, are given equal opportunity to obtain charging services from the system. In our framework, the CSs, who coordinate the charging process, do not have personal information about the customers. Therefore, it is not possible to deny service to a specific group of customers. On top of that, customers themselves do not know with whom they are trading as the EVs do not exchange information directly with each other.
• Transparency: The trading process should be transparent and the associated prices, demands, supplies, pricing mechanisms, etc., should be clear to all participants. In our framework, the EVs themselves calculate their own trade quantities and prices. They also receive signed confirmations from the CSMS servers about whether or not these values were correctly recorded in the blockchain, along with the final payment receipt (i.e., bank transaction ID) through various response messages (OrderVerifyRes, TradeVerifyRes, and PaymentVerifyRes).
• Privacy of personal information: It has already been discussed that customers’ private or personally identifiable information (PII) is not available to the CSs and other customers. Only the CSMS servers, which are assumed to be secure, have access to these. The digital certificates themselves do not contain any personal data.
• Privacy of trade information: Trade information is available to the CSs as all the trade-related information passes through them. Also, to measure if the correct amount of energy has been exchanged, the CSs have to know how much energy is coming from or going to which EV. Studies on privacy preservation of trade information usually depend on cryptocurrencies [87,88,89]. However, as stated previously, we do not want to use cryptocurrencies as they tend to be unreliable and unstable and will be a barrier to the quick adoption of V2V trading.
• Location privacy: Location data are available to the CSMS servers as they know the identity of the users and also the location of the CSs. The CSs, however, do not have access to the first information so they cannot directly link the location data to a specific user.

7. Energy-Trading Model

In this section, we present the trade algorithm that is used to determine the optimal energy demand–supply and the prices. First, the utility functions of the CEVs and the DEVs are elaborated, and then the process of determining the optimal demands of the CEVs and the optimal supplies and prices of the DEVs are described. The main notations utilized throughout the rest of the paper are summarized in Table 1.

In this setting, we have a set of CEVs, $\mathcal{C}=\{1,\dots ,c,\dots ,C\}$, having an energy demand vector ${\mathbf{b}}_c=[b_{c,1},\dots ,b_{c,d},\dots ,b_{c,D}]$ [KWh]. Also, there is a set of DEVs, $\mathcal{D}=\{1,\dots ,d,\dots ,D\}$, characterized by an energy supply vector, ${\mathbf{s}}_d=[s_{d,1},\dots ,s_{d,c},\dots ,s_{d,C}]$ [KWh], and an energy price vector, $\mathbf{p}=[p_1,\dots ,p_d,\dots ,p_D]$ [${\displaystyle \frac{\$}{KWh}}$]. The energy price requested by a particular DEV is the same for all the CEVs. Each CEV has minimum and maximum energy demands, $b_c^{min}$ and $b_c^{max}$ [KWh]. These are defined by their energy needs and battery characteristics, respectively. Also, each DEV has a maximum energy supply capacity, $s_d^{max}$ [KWh], based on its battery characteristics and can also be specified by the user according to their willingness to sell the energy.

A Stackelberg game is a game-theoretic model that is played between one or more players known as leader(s) and one or more players known as follower(s). In this sequential game, leaders take the first turn in optimizing their utility function (maximizing profit or minimizing loss) based on followers’ decision variables, and then the followers respond in the same way based on the leaders’ decision variables. The players keep taking turns until no one wants to make moves anymore, indicating a Stackelberg equilibrium. As the name suggests, a multi-leader, multi-follower game is a special case with multiple leaders and followers. In this complex variation, the leaders and the followers also play a Nash game between themselves. For example, in a trading scenario with multiple buyers and sellers, one group can be the leaders and the other one the followers. Our trade model uses a two-layer optimization method to solve a multi-leader, multi-follower Stackelberg game where the CEVs are modelled as the leaders and the DEVs as the followers. The CEVs engage in a non-cooperative game among themselves to determine their optimal demands. At the same time, the DEVs participate in a separate non-cooperative game to determine their optimal supplies and optimal prices. The iterative optimization between these two layers of non-cooperative games continues until they converge to the multi-variable Stackelberg equilibrium. At each layer, the primary goal of the model is to optimize the utility functions of both CEVs and DEVs by determining the optimal demands, supplies, and prices. These utility functions are formulated in Section 7.1, while the optimization problems for the CEVs and the DEVs are derived in Section 7.2 and Section 7.3, respectively.

7.1. CEVs and DEVs Utility Functions

The utility derived by a CEV is contingent upon meeting its energy requirements, factoring in its risk-averse nature. Therefore, the formulation of its intrinsic utility, represented by the first term in Equation (5), is characterized as a concave, non-decreasing function of the CEV’s energy demand, which includes considerations for the minimum energy demand attributes of the CEV. Additionally, the intrinsic utility of the CEV diminishes as the energy demand from other CEVs in the market increases, illustrating the competitive interactions among CEVs striving to fulfill their energy needs from the DEVs. Furthermore, the cost incurred by CEVs to procure their energy demand, while accounting for market competition from other CEVs, is encapsulated by the second term of Equation (5).

$$\begin{array}{cc}\hfill U_c({\mathbf{b}}_c,{\mathbf{b}}_{-c})=& A_c{\displaystyle \frac{log(1+M_c{\displaystyle \sum _{\forall d}}{b}_{c,d}-b_c^{min})}{{\displaystyle \sum _{\forall d}}{\displaystyle \sum _{c^{\prime }\ne c}}{b}_{c^{\prime },d}+N_c}}\hfill \\ \hfill & -B_c{\displaystyle \sum _{\forall d}}[({\displaystyle \frac{p_d}{{\displaystyle \sum _{c^{\prime }\ne c}}{b}_{c^{\prime },d}}})·b_{c,d}]\hfill \end{array}$$

(5)

where $A_c={\displaystyle \frac{{\displaystyle \sum _{\forall c^{\prime }\ne c}}{b}_{c^{\prime }}^{max}}{\underset{\forall c^{\prime }}{max}\{log(1+M_{c^{\prime }}{b}_{c^{\prime }}^{max}-b_{c^{\prime }}^{min})\}}}$ and $B_c={\displaystyle \frac{1}{\underset{\forall d}{max}\left\{p_d^{max}\right\}{b}_c^{max}}}$ are used as normalization factors. $p_d^{max}$ denotes the maximum energy price defined by federal regulations, while the satisfaction and dissatisfaction coefficients are denoted by $M_c$ and $N_c\in {\mathbb{R}}^{+}$. Lastly, the energy demand vector of all CEVs, except for the cth CEV, is captured in the term ${\mathbf{b}}_{-c}$.

The utility of the dth DEV is derived from its profit, generated by selling ${\mathbf{s}}_d$ units of energy to multiple CEVs at the price of $p_d$ while taking the costs associated with energy generation and distribution into consideration, as reflected in the second and third terms of Equation (6). The revenue of the DEV, represented by the first term in Equation (6), is influenced by the DEV’s assessment of the supplied energy, modulated by a factor $0<X_c<1$, while accounting for the market penetration of other DEVs (denominator of the first term in Equation (6)), which can ultimately reduce the revenue experienced by the DEV.

$$\begin{array}{cc}\hfill & U_d({\mathbf{s}}_d,{\mathbf{s}}_{-d},p_d,{\mathbf{p}}_{-d})=\hfill \\ \hfill & E_d{\displaystyle \frac{\frac{p_d}{{\displaystyle \sum _{\forall c}}{b}_{c,d}}{\displaystyle \sum _{\forall c}}{(s_{d,c})}^{X_c}}{{[{\displaystyle \sum _{\forall d^{\prime }}}(\frac{p_{d^{\prime }}}{{\displaystyle \sum _{\forall c}}{b}_{c,d^{\prime }}}){\displaystyle \sum _{\forall c}}{\displaystyle \sum _{\forall d^{\prime }\ne d}}{s}_{d^{\prime },c}]}^r}}-F_d{\displaystyle \sum _{\forall c}}{(s_{d,c})}^2-G_d{\displaystyle \sum _{\forall c}}{s}_{d,c}\hfill \end{array}$$

(6)

where $r>1$ captures the level of impact of the other DEVs penetration in the energy-trading market; ${\mathbf{s}}_{-d}$ and ${\mathbf{p}}_{-d}$ denote the energy supply and price vectors of all the DEVs, except for DEV d; and $E_d={\displaystyle \frac{{[{\displaystyle \sum _{\forall d^{\prime }}}{P}_{d^{\prime }}^{max}{\displaystyle \sum _{\forall d^{\prime }\ne d}}{s}_{d^{\prime }}^{max}]}^r}{H_d}}$, $F_d={\displaystyle \frac{1}{{s_d^{max}}^2}}$, $G_d={\displaystyle \frac{1}{s_d^{max}}}$, and $H_d=\underset{\forall d^{\prime }}{max}\left\{P_{d^{\prime }}^{max}\right\}{\displaystyle \sum _{\forall c}}{\left(b_c^{max}\right)}^{X_c}$ are used as normalization factors.

7.2. Optimal CEVs Demands

As mentioned earlier, the Stackelberg game is solved using a two-layer optimization technique. Each layer is solved keeping the solution of the previous layer as a constant. In the first layer, we consider that the optimal supplies ${\mathbf{s}}^{*}$ and energy prices ${\mathbf{p}}^{*}$ of the DEVs from the second layer are communicated and, thus, are known to the CEVs. The objective of the CEVs is to independently determine their optimal demand vectors, ${\mathbf{b}}_c^{*}=[b_{c,1}^{*},\dots ,b_{c,d}^{*},\dots ,b_{c,D}^{*}],\forall c\in \mathcal{C}$, in a decentralized manner. The goal of each CEV is to determine its optimal energy demand vector by maximizing its own utility (Equation (7a)) while considering its minimum and maximum energy demand constraints (Equation (7b)) and the available energy supply by each DEV (Equation (7c)). The corresponding optimization problem for each CEV is defined as follows.

$$\begin{array}{c}\hfill \underset{{\mathbf{b}}_c}{max}{U}_c({\mathbf{b}}_c,{\mathbf{b}}_{-c})\end{array}$$

(7a)

$$\begin{array}{c}\hfill \mathrm{s}.\mathrm{t}.b_c^{min}\le \sum _{\forall d}{b}_{c,d}\le b_c^{max}\end{array}$$

(7b)

$$\begin{array}{c}\hfill 0\le b_{c,d}\le s_{d,c},\forall d\in \mathcal{D}\end{array}$$

(7c)

A non-cooperative game, ${\mathrm{\Gamma }}_C=[\mathcal{C},{\left\{{\Delta }_c\right\}}_{\forall c\in \mathcal{C}},{\left\{U_c\right\}}_{\forall c\in \mathcal{C}}]$, is formulated using the optimization problems in Equation (7a–c). Here, $\mathcal{C}$ signifies the set of players, corresponding to the CEVs. Each ${\Delta }_c=[0,s_{d,c}]$ characterizes the strategy set of energy demands that will be provided by the DEVs. $U_c$ denotes the payoff or utility function of the cth CEV, as defined in Equation (5).

As Theorems A1 and A2 in Appendix A prove the existence of a unique pure Nash equilibrium, we can now use any conventional solving method to solve Equation (7) and determine the optimal demand vectors of the CEVs. These values are communicated to the DEVs to determine their corresponding optimal energy supply vectors and their optimal energy price, as analyzed in the next section.

7.3. Optimal DEVs Supplies and Price

In the second layer, we use the optimal demands of the CEVs from the first layer to determine the DEVs’ optimal supplies and prices. Here, each DEV optimizes its utility (Equation (8a)), while considering various constraints. Equation (8b,c) are for the energy constraints, while the maximum energy price limitations imposed by the federal regulations are denoted in Equation (8d). Lastly, Equation (8e) supports the requested demand by the CEVs.

$$\begin{array}{c}\hfill \underset{\{{\mathbf{s}}_d,p_d\}}{max}{U}_d({\mathbf{s}}_d,{\mathbf{s}}_{-d},p_d,{\mathbf{p}}_{-d})\end{array}$$

(8a)

$$\begin{array}{c}\hfill \mathrm{s}.\mathrm{t}.\sum _{\forall c}{s}_{d,c}\le s_d^{max}\end{array}$$

(8b)

$$\begin{array}{c}\hfill s_{d,c}\ge 0,\forall c\in \mathcal{C}\end{array}$$

(8c)

$$\begin{array}{c}\hfill {\displaystyle \frac{p_d}{{\displaystyle \sum _{\forall c}}{b}_{c,d}}}\le p_d^{max}\end{array}$$

(8d)

$$\begin{array}{c}\hfill s_{d,c}\le b_{c,d},\forall c\in \mathcal{C}\end{array}$$

(8e)

Similar to the CEVs, a non-cooperative game, ${\mathrm{\Gamma }}_D=[\mathcal{D},{\{{\mathrm{\Phi }}_d,{\mathrm{\Omega }}_d\}}_{\forall d\in \mathcal{D}},{\left\{U_d\right\}}_{\forall d\in \mathcal{D}}]$, can be formulated for the DEVs using Equation (8a–e), where $\mathcal{D}$ is the set of DEVs and ${\mathrm{\Phi }}_d=[0,s_d^{max}]$ and ${\mathrm{\Omega }}_d=[0,p_d^{max}]$ are the strategy sets of the DEVs regarding their energy supply and price, respectively. $U_d$ denotes the utility function of the DEV, as defined in Equation (6).

Theorems A3 and A4 prove the existence of a pure Nash equilibrium and its uniqueness. This means Equation (8) can be solved to determine the optimal supply vectors and energy prices of the DEVs. On the other hand, Theorem A5 proves the existence of a Stackelberg equilibrium. Therefore, iteratively solving Equations (7) and (8) based on the best responses of each other, the optimal demands, supplies, and prices can be determined where no one will have a better alternative.

8. Experimental Results and Performance Analysis

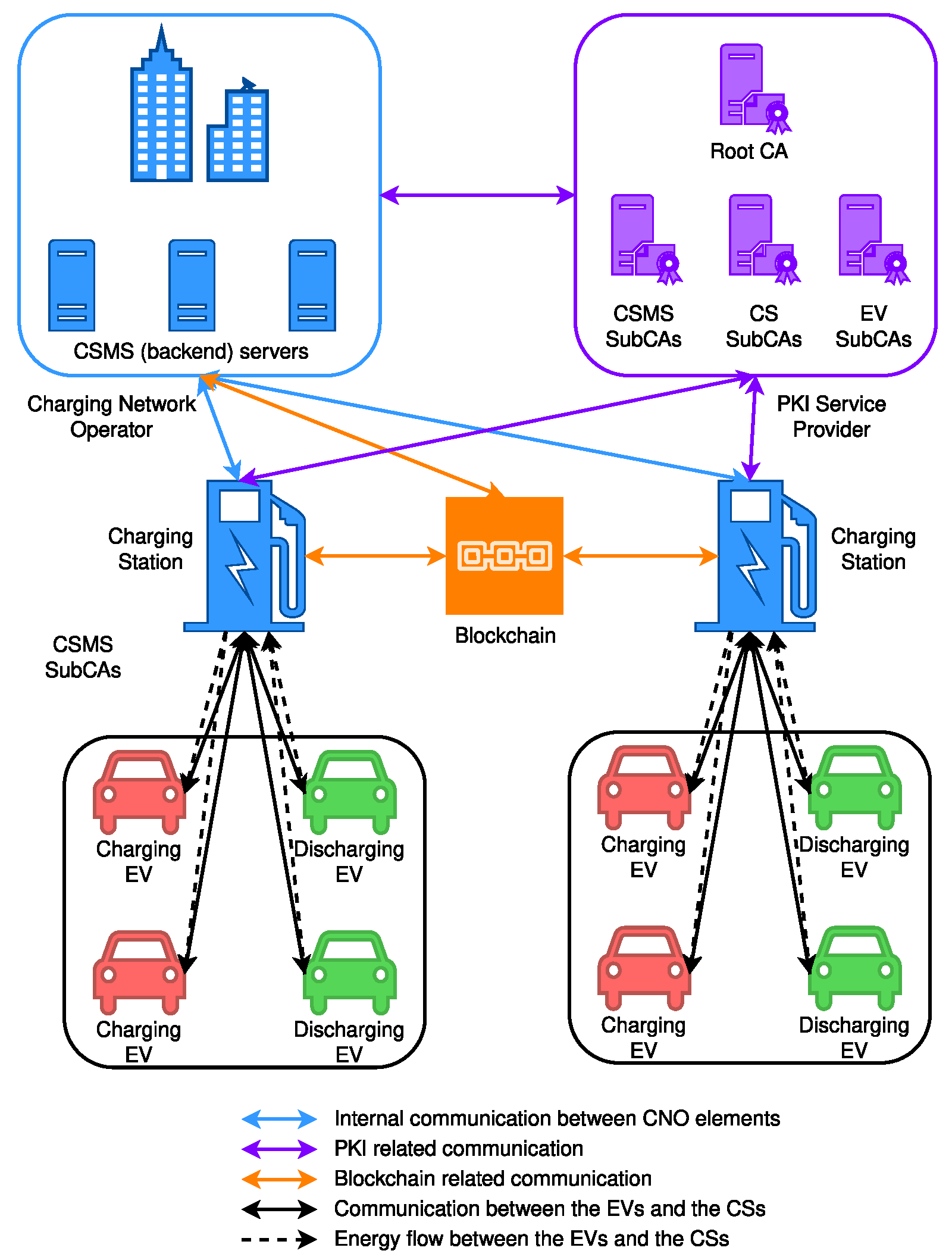
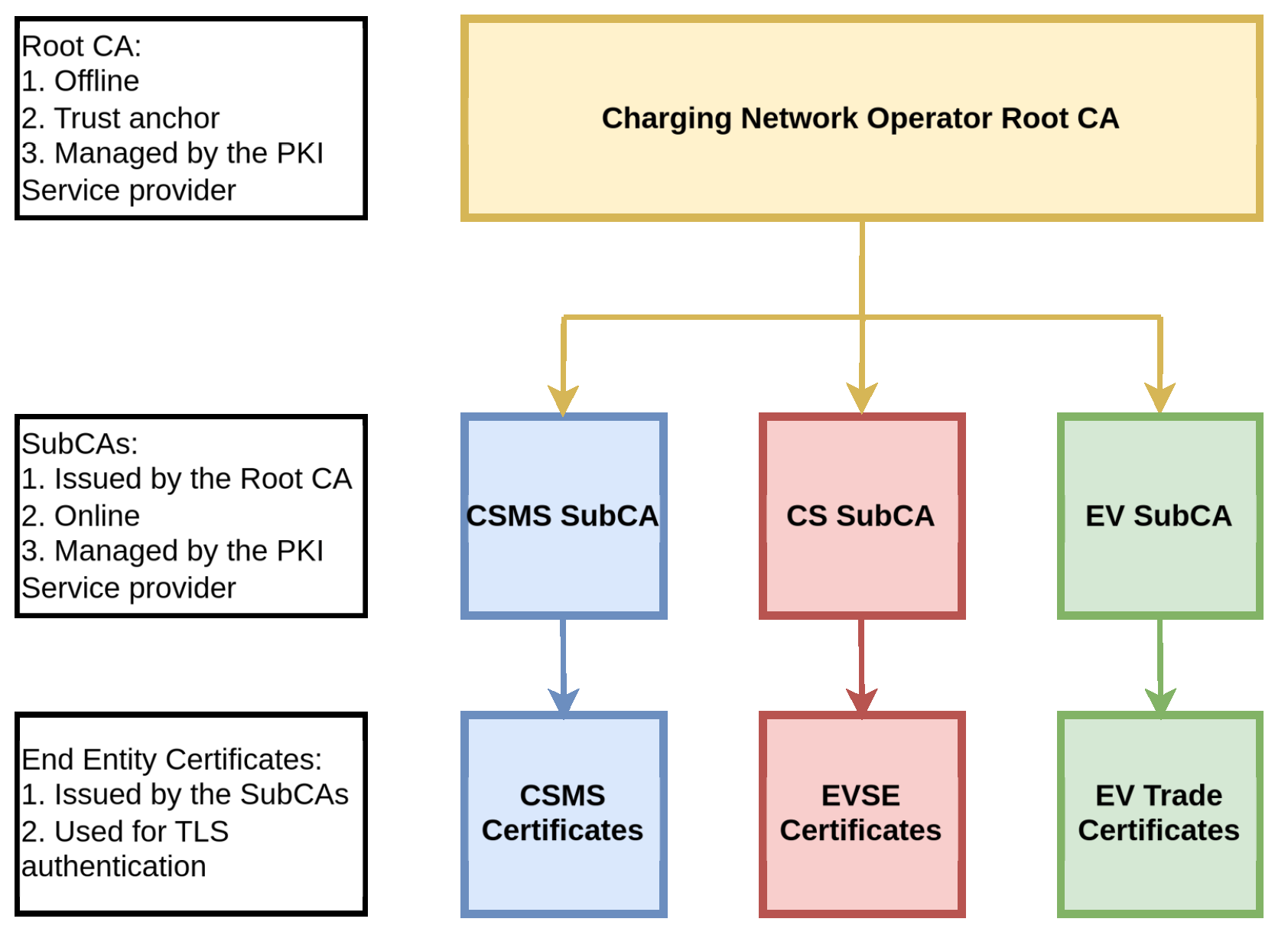
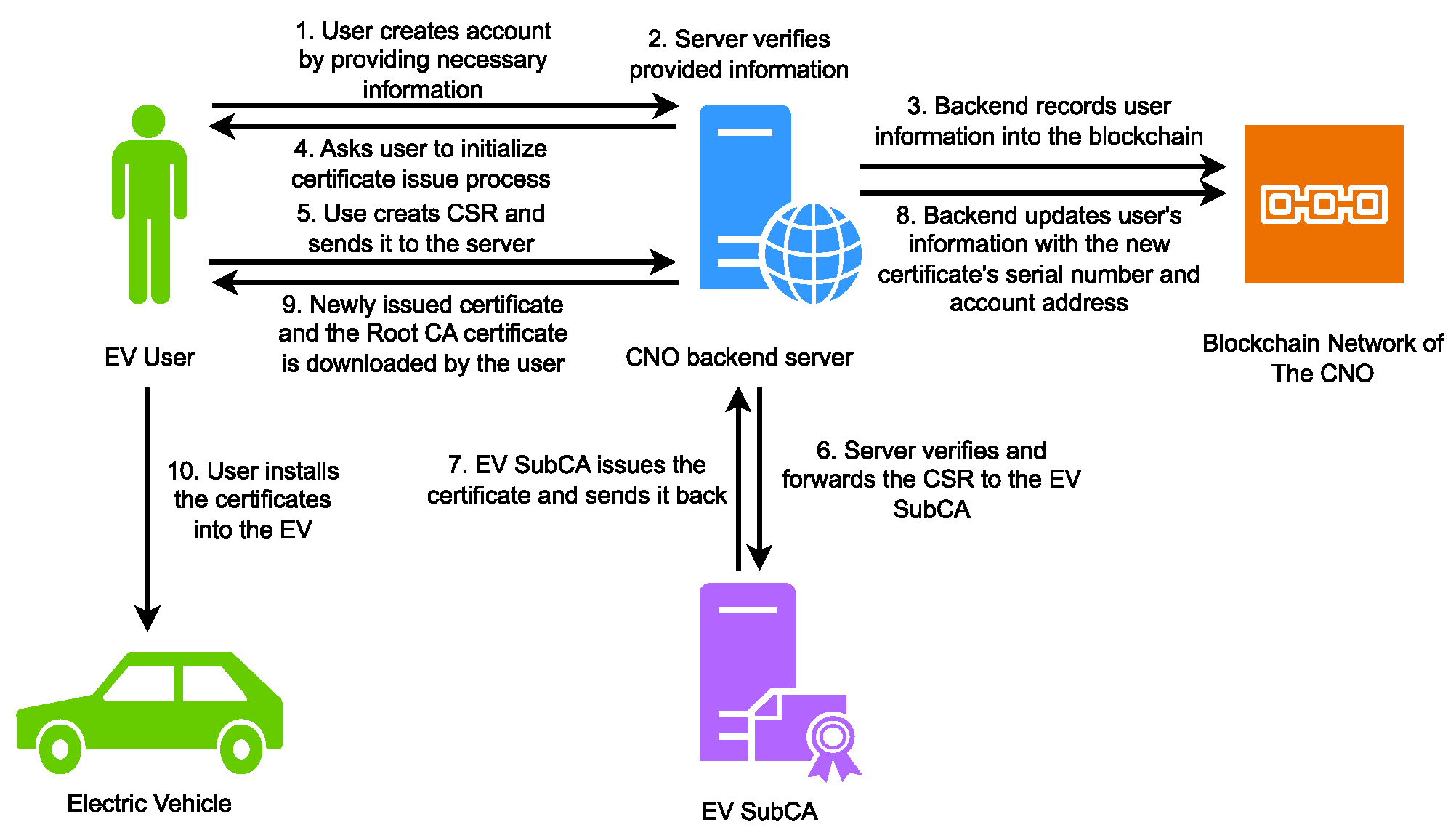
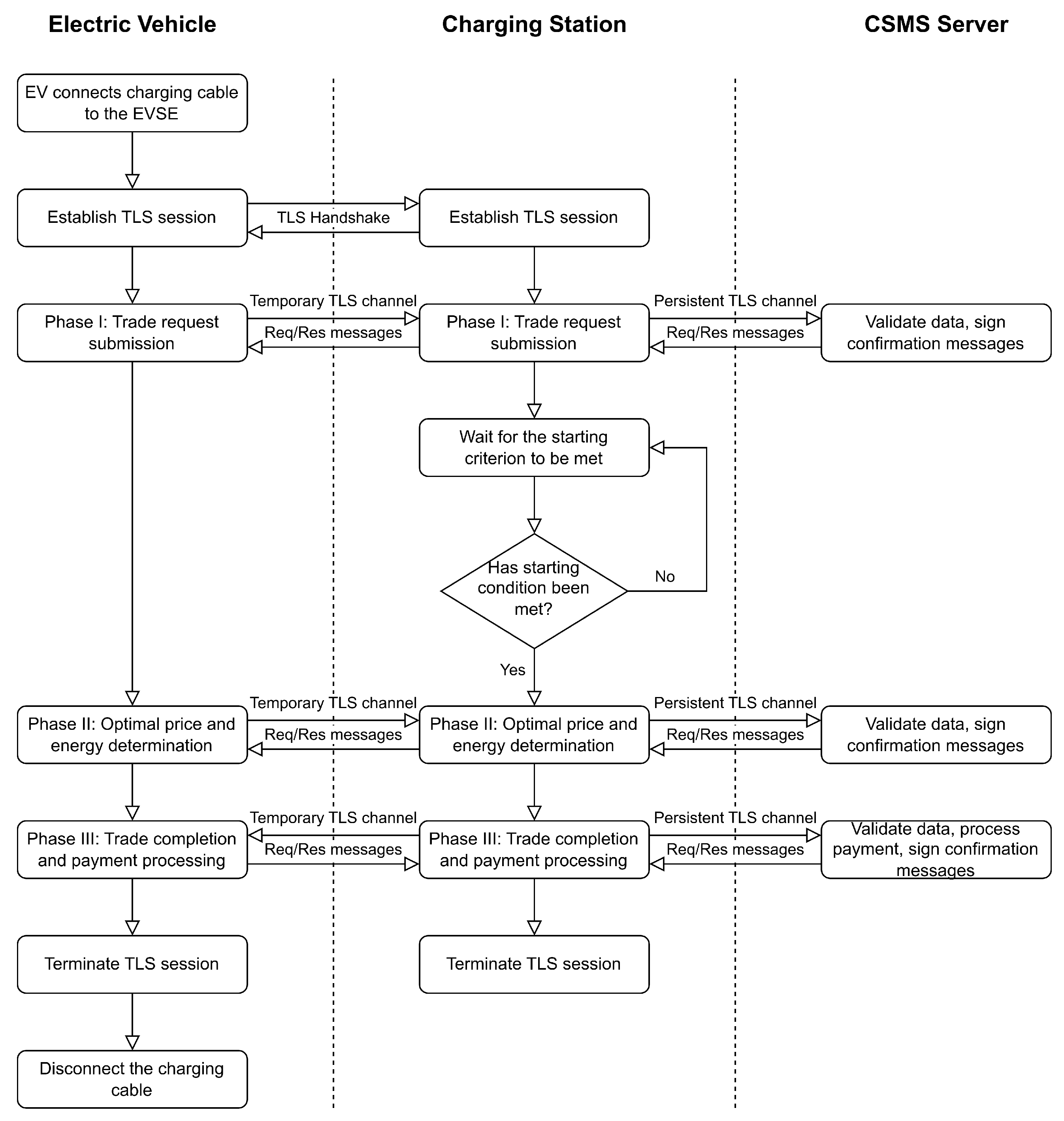
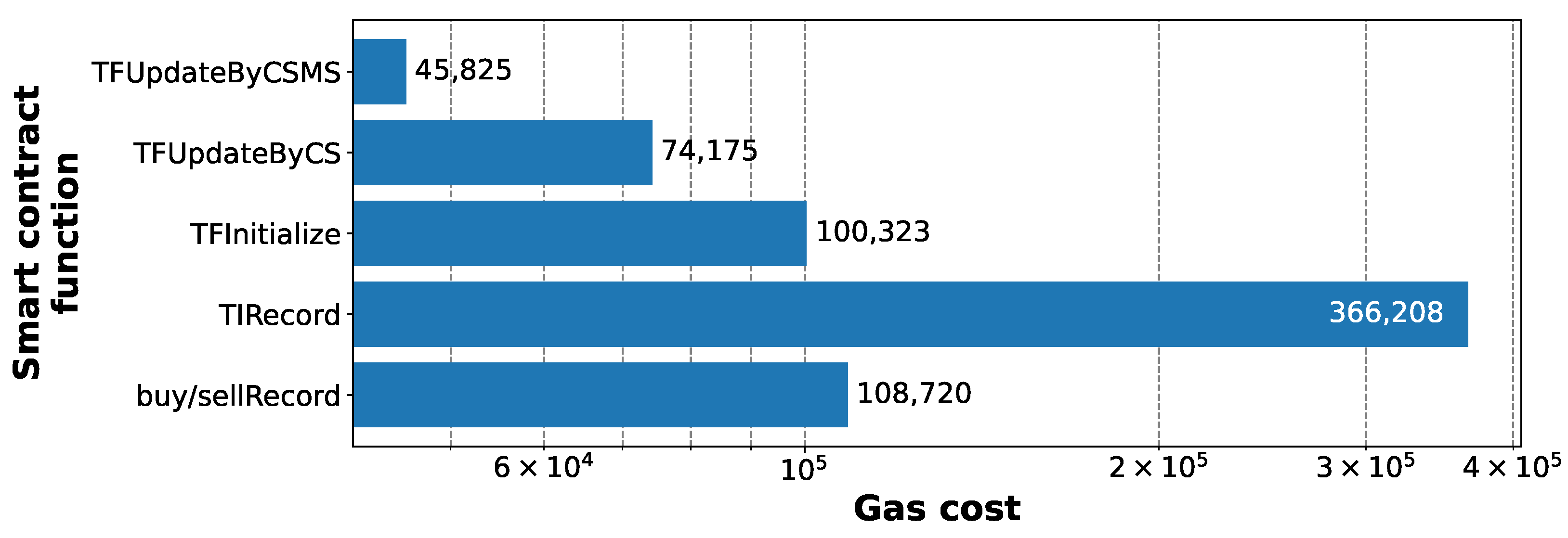In this section, we start with how we implemented the trade algorithm, the blockchain, and the full protocol. Then, we present the simulation settings and, finally, the results of the numerical experiments.

8.1. Implementation and Simulation Settings

8.1.1. Implementation of the Blockchain

We implemented the experimental Ethereum blockchain using a Go (GoLang)-based client named Geth (go-ethereum) [74]. Each blockchain node is created and run using Geth, with or without the mining or sealing option enabled. We refer to the nodes with the sealing option enabled as the “sealers” and the ones without it as the “signers”. Also, in our protocol, the CSMS servers are sealers and the CSs are signers. As mentioned previously, we used the proof-of-authority (PoA) consensus algorithm, which is implemented in Geth as Clique [90]. Each node contains an exposed http port through which they can submit transactions, listen for block generation events, and monitor various network parameters. This is how we interact with the blockchain in real-time. To write and deploy the smart contracts written in Solidity [81], Truffle [91] was used. All the contracts in Algorithms 1–3 were written in a single file and, thus, were deployed together. The deployment cost was 2,526,637 units of gas.

8.1.2. Implementation of the Trade Algorithm and the Protocol

The V2V protocol and the trade algorithm, as a part of it, are implemented in Python. There are separate scripts for the EVs, the CSs, and the CSMS servers. The latter two, being parts of the blockchain, interact with it using Python’s Web3 API [92] through the http ports. To enable the CS and the CSMS server to handle multiple TLS channels simultaneously, we used the asyncio (Asynchronous Input/Output) library of Python. Lastly, the digital certificates and associated private keys were generated locally using the OpenSSL software library.

8.1.3. Experimental Setup

We used a single computer to host all the network entities (i.e., the EVs, the CSs, the CSMS servers, and the blockchain nodes).

Table 2. Simulation environment.

Parameter	Description	Parameter	Description
Geth	v1.13.14	Truffle	v5.11.5
Solidity	v0.8.0	OpenSSL	v1.1.1l
Python	v3.9.7	TLS	1.3
TLS Cipher	ECDHE-ECDSA-AES256-GCM-SHA384
CPU	11th Gen Intel® Core™ i7-11700K @ 3.60 GHz × 16
RAM	32 GB	OS	Ubuntu 20.04.6 LTS

shows information regarding the simulation environment. In Section 8.2, Section 8.3, Section 8.4, Section 8.5 and Section 8.6, we present the performance and behavior of the full protocol as well as some of its individual components for easier comparison in future studies. Real-world parameters such as demands and supplies are chosen based on the battery capacity characteristics of the EVs currently on the market. For example, according to [93], the minimum and maximum usable battery capacities are approximately 20 kWh and 125 kWh, respectively. The maximum energy price parameters can be chosen based on the energy price of the power grid. Other algorithm-specific parameters such as $\mathbf{x}$, $\mathbf{M}$, $\mathbf{N}$, and r are chosen randomly based on the experiments. Their exact values are not as important as their effect of increment or decrement on the optimal solution, which we present in Section 8.2. In Section 8.3, we show how the algorithm scales and how the optimal solutions behave with varying numbers of CEVs, DEVs, and their respective demands, supplies, and prices. The performance of the fully implemented protocol with all the network entities running is presented in Section 8.4, while its scalability characteristics are shown in Section 8.5. In Section 8.6, we show how the blockchain behaves with an increasing number of nodes and workload. Finally, in Section 8.7 we discuss the implications of the results in future V2V energy trading. Specific details regarding the experimental parameters are discussed in their respective sections.

8.2. Pure Operation Performance of the Trade Algorithm

In this scenario, we evaluate the operational dynamics and performance of the trade algorithm. The goal is to present how the energy demand, supply, and price change for EVs with different demand and supply attributes. Here, we consider five charging EVs ($C=5$) and five discharging EVs ($D=5$) with ${\mathbf{b}}^{max}=[15,30,45,60,75]$ KWh, ${\mathbf{b}}^{min}=10\%\ast {\mathbf{b}}^{max}$, ${\mathbf{s}}^{max}=[10,25,40,55,70]$ KWh, ${\mathbf{p}}^{max}=[5,15,25,35,45]$ $/kWh, $\mathit{X}=[0.7,0.7625,0.825,0.8875,0.95]$, $\mathit{M}=[0.7,0.7625,0.825,0.8875,0.95]$, $N_c=14$, $\forall c\in \mathcal{C}$, $r=1.27$.

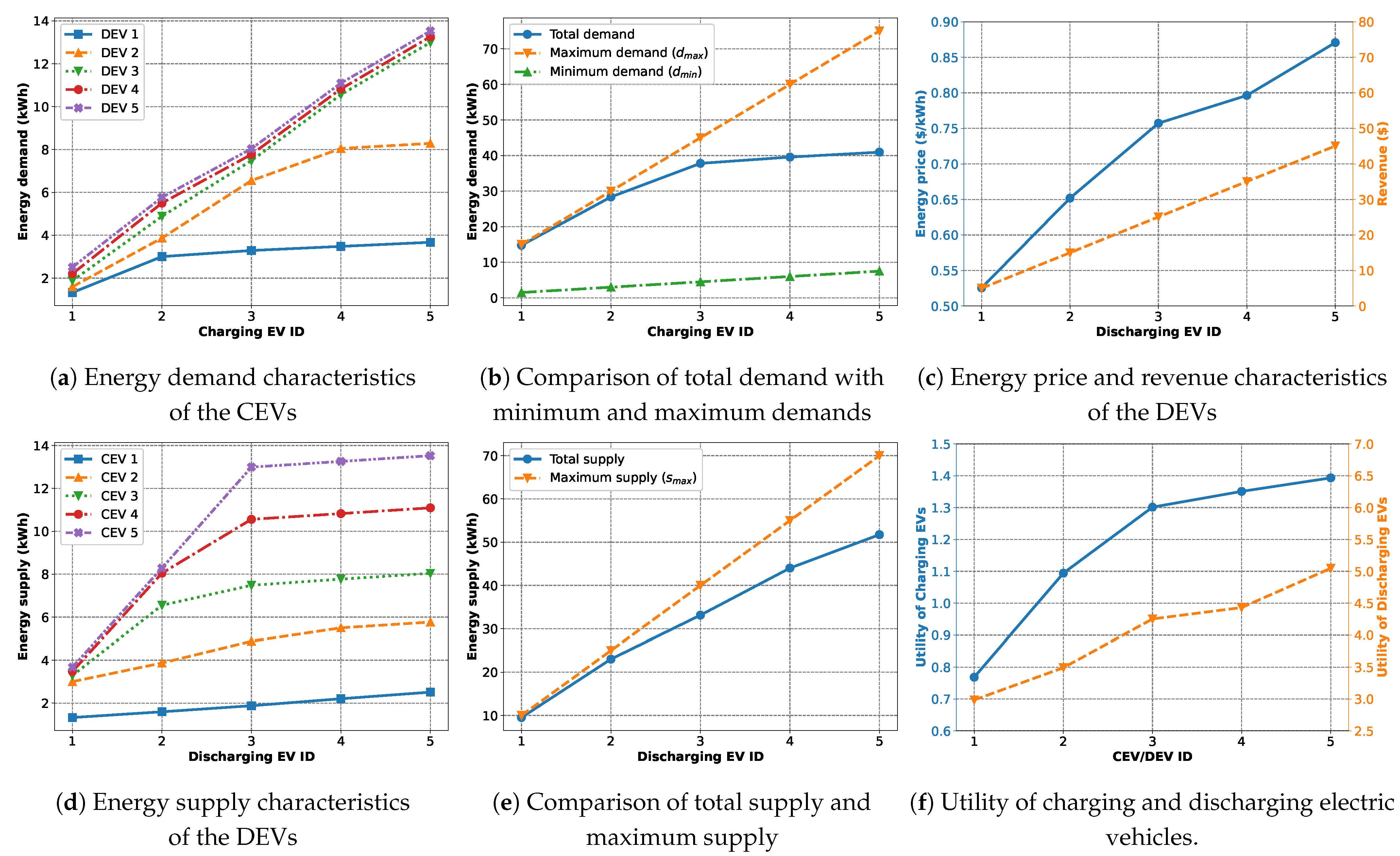
Figure 8a shows the energy demands of each charging EV (horizontal axis) from each discharging EV (separate lines). As expected, as CEVs with higher IDs have higher maximum demand, they are receiving more energy from each DEV. Also, DEVs with higher IDs offer more energy. We can see that DEVs 1 and 2 are hitting their capacity and the curves start to tapper off. On the other hand, DEVs 3 to 5 rise steadily with their higher maximum supply. Figure 8b shows the total demands of the CEVs and how they compare with the respective maximum and minimum demands. We observe that the demand curve falls between the maximum and minimum demand curves as expected. While the lower CEV IDs (1, 2) have their demands fulfilled, the higher IDs with higher demands are unable to do so. This is because those remaining demands have to be met by the higher ID DEVs, who also have a higher energy price. This is evident, as shown in Figure 8c. DEVs with higher IDs have higher energy prices and revenues.

Figure 8d presents the energy each discharging EV (horizontal axis) supplies to each charging EV (separate lines). Similarly here, as DEVs with higher IDs have a higher maximum supply capacity, they are selling more energy to each CEV, while CEVs with higher IDs are buying more energy. Also, while CEVs 1 and 2 are receiving a proportionally increasing amount of energy from the DEVs, CEVs 3 to 5 are receiving significantly less from DEVs 1 and 2. This is due to the fact that DEVs 1 and 2 have lower supply capacity. Figure 8e shows the total supply of the DEVs, comparing it with the corresponding maximum supply. Similar to the CEV case, while the lower DEV IDs (1, 2) have most of their supplies bought out, the higher IDs with higher supplies have unsold energies. This is because these DEVs also expect higher prices. As shown in Figure 8c, DEVs with higher IDs are able to generate higher revenue, although they are not selling all of their supplies.

Finally, Figure 8f presents the utility values for the CEVs and the DEVs. In both cases, we observe that the utility values increase with increasing EV IDs. This is expected as the CEVs with higher IDs are able to buy more energy, thus satisfying their higher energy demands, while the increased amount of energy sold at higher prices does the same for the DEVs.

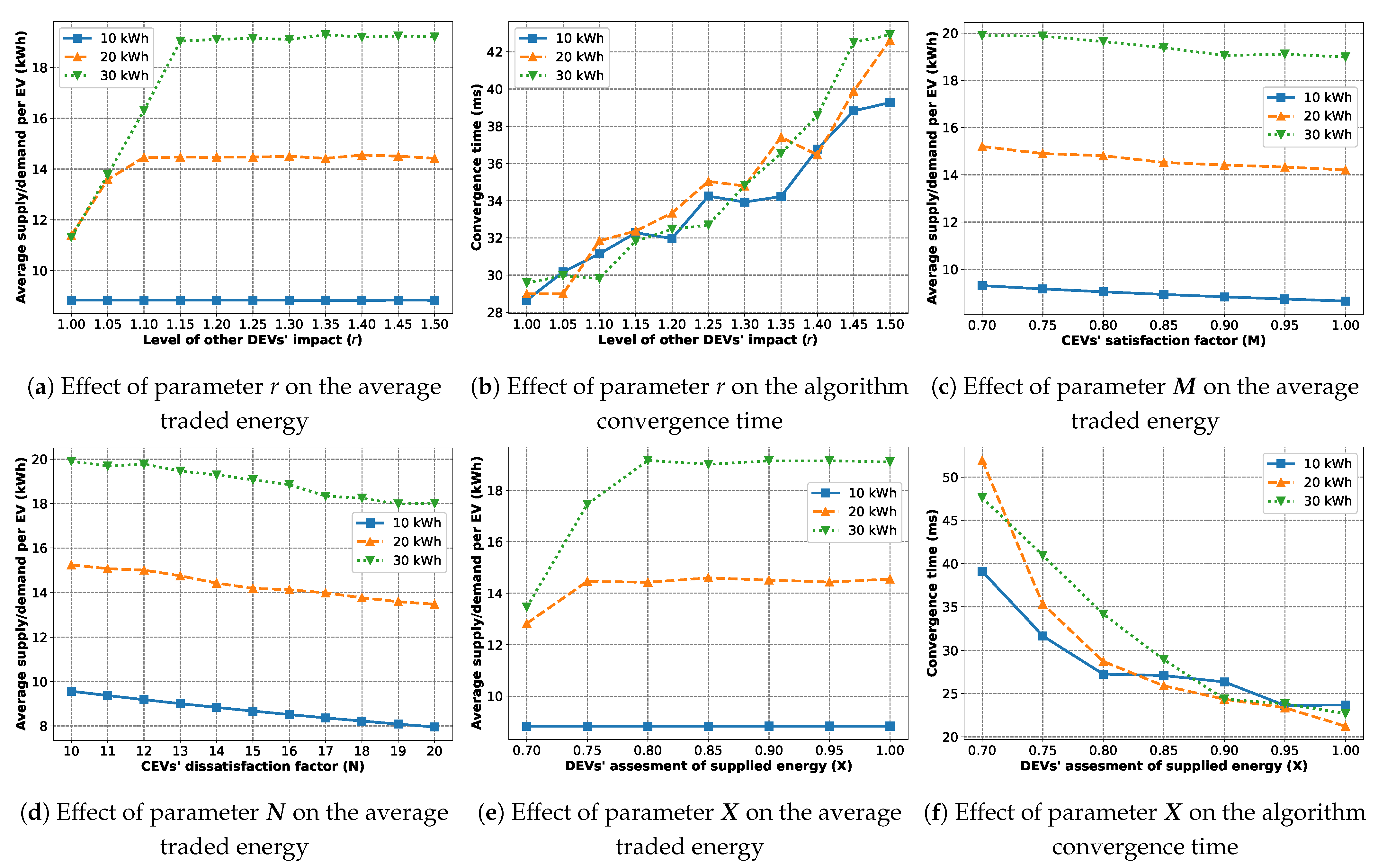
In addition to the previous scenario, we perform a sensitivity analysis in Figure 9 for algorithm-specific parameters such as r, $\mathit{M}$, $\mathit{N}$, and $\mathit{X}$. Here, we consider two CEVs and two DEVs, $b_c^{max}=[10,20,30]$ kWh, $s_d^{max}=40$ kWh, $p_d^{max}=10$ $/kWh, $X_c=0.9$, $M_c=0.9$, $N_c=14$, $r=1.27$$\forall c\in \mathcal{C}$ and $\forall d\in \mathcal{D}$, unless stated otherwise.

Figure 9a shows the effect of parameter r on the average demand/supply. For Figure 9, the average demands and average supplies are equal as we are considering an equal number of CEVs and DEVs. According to Equation (6), r affects the denominator of the positive term, which means a higher value of r will make this term smaller based on the other DEVs’ supply. To match this, a DEV will try to increase its own supply. This is why we see that the traded energy quantity is rising with increasing values of r until it becomes saturated when the CEVs have their demands satisfied. From Figure 9b, we observe that increasing r also makes the algorithm slower to converge.

Figure 9c shows the effect of parameter $\mathit{M}$, the satisfaction coefficient of the CEVs, on the average demand/supply. It captures the loss in the energy transfer. The lower the satisfaction coefficient, the higher the loss. To compensate for the higher loss, CEVs demand more energy. This is evident by the downward trend in traded energy with respect to the increasing satisfaction coefficient.

Figure 9d depicts the sensitivity of the dissatisfaction coefficient of the CEVs ($\mathit{N}$) in terms of average demand/supply. $\mathit{N}$ is a constant added to the denominator of the positive term in Equation (5). Higher $\mathit{N}$ lowers the positive term so, in response, a CEV will either have to increase the numerator by increasing the demand or decrease the negative term by decreasing the demand. Due to the logarithmic operator in the numerator of the positive term, the effect of increasing demand is weaker than that of decreasing the demand. This results in a downward trend in the traded energy with increasing $\mathit{N}$.

Finally, Figure 9e,f present the effect of $\mathit{X}$ on the quantity of traded energy and the convergence time of the trade algorithm. $\mathit{X}$ represents the DEVs’ evaluation of traded energy or, in other words, their willingness to trade with the CEVs. This is why increasing $\mathit{X}$ results in more traded energy until the CEVs’ demands are fulfilled, as shown in Figure 9e. Figure 9f informs us that increasing $\mathit{X}$ also leads to faster convergence of the trade algorithm.

8.3. Scalability of the Trade Algorithm

In this subsection, we study the scalability characteristics of the trade algorithm with varying numbers of EVs and other trade parameters like the maximum demands, supplies, and prices.

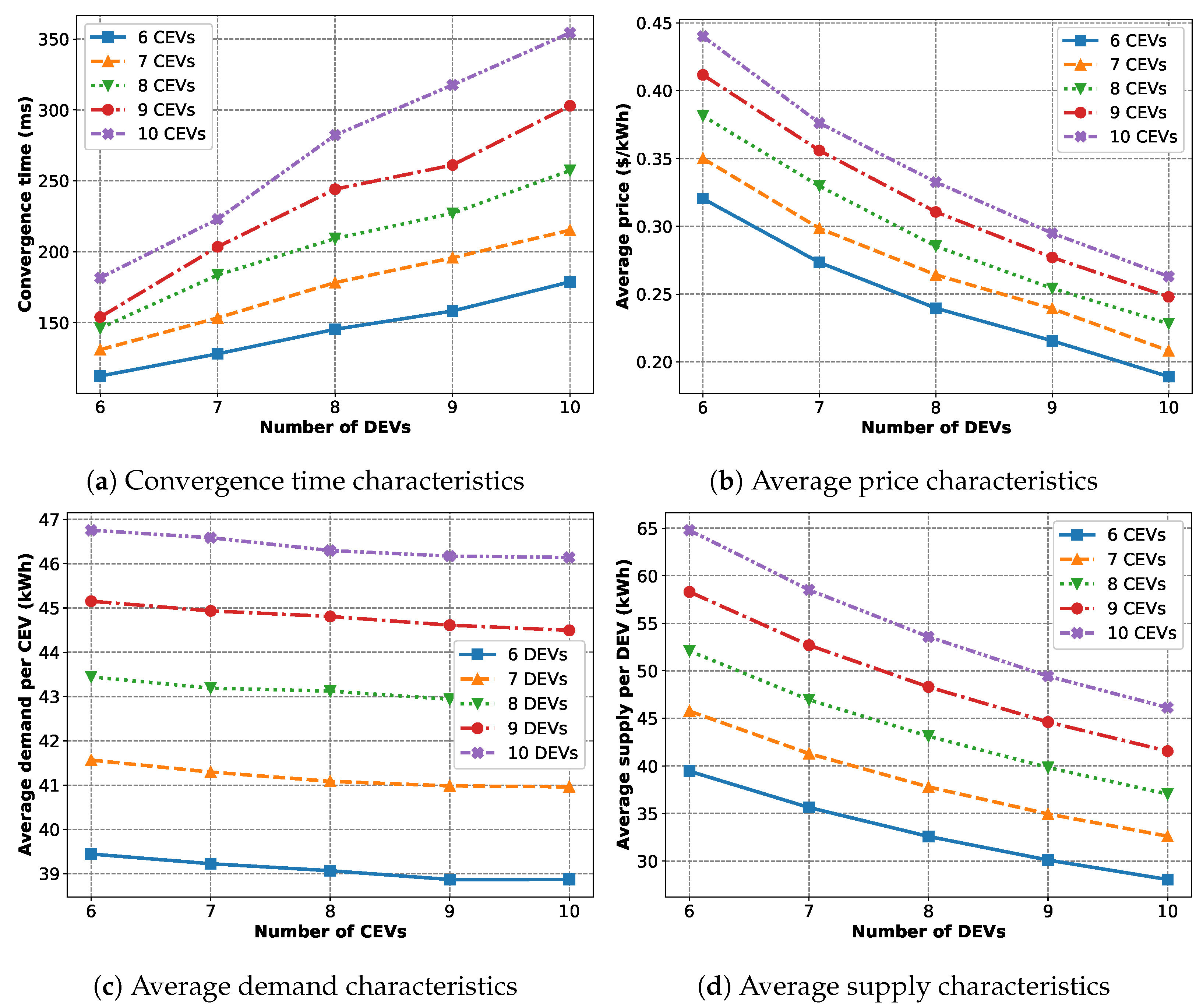
The first scenario we consider deals with varying the number of CEVs and DEVs, with the results presented in Figure 10. Here, we fixed ${\mathbf{b}}^{max}=50$ kWh, ${\mathbf{s}}^{max}=70$ kWh and ${\mathbf{p}}^{max}=12$ $/kWh for all the EVs. Figure 10a shows the convergence characteristics of the trade algorithm. We can see that, with an increased number of EVs, the convergence time also increases. Figure 10b shows that the average price decreases with an increasing number of DEVs as more DEVs mean more available supply. Also, the average price increases with an increasing number of CEVs as more CEVs mean more total demand. Figure 10c illustrates that, as the number of CEVs increases, the average amount of energy each CEV can buy decreases as the supply remains the same. On the other hand, adding more DEVs results in an increased amount of energy bought by the CEVs. Figure 10d shows the same thing but from the DEVs’ point of view.

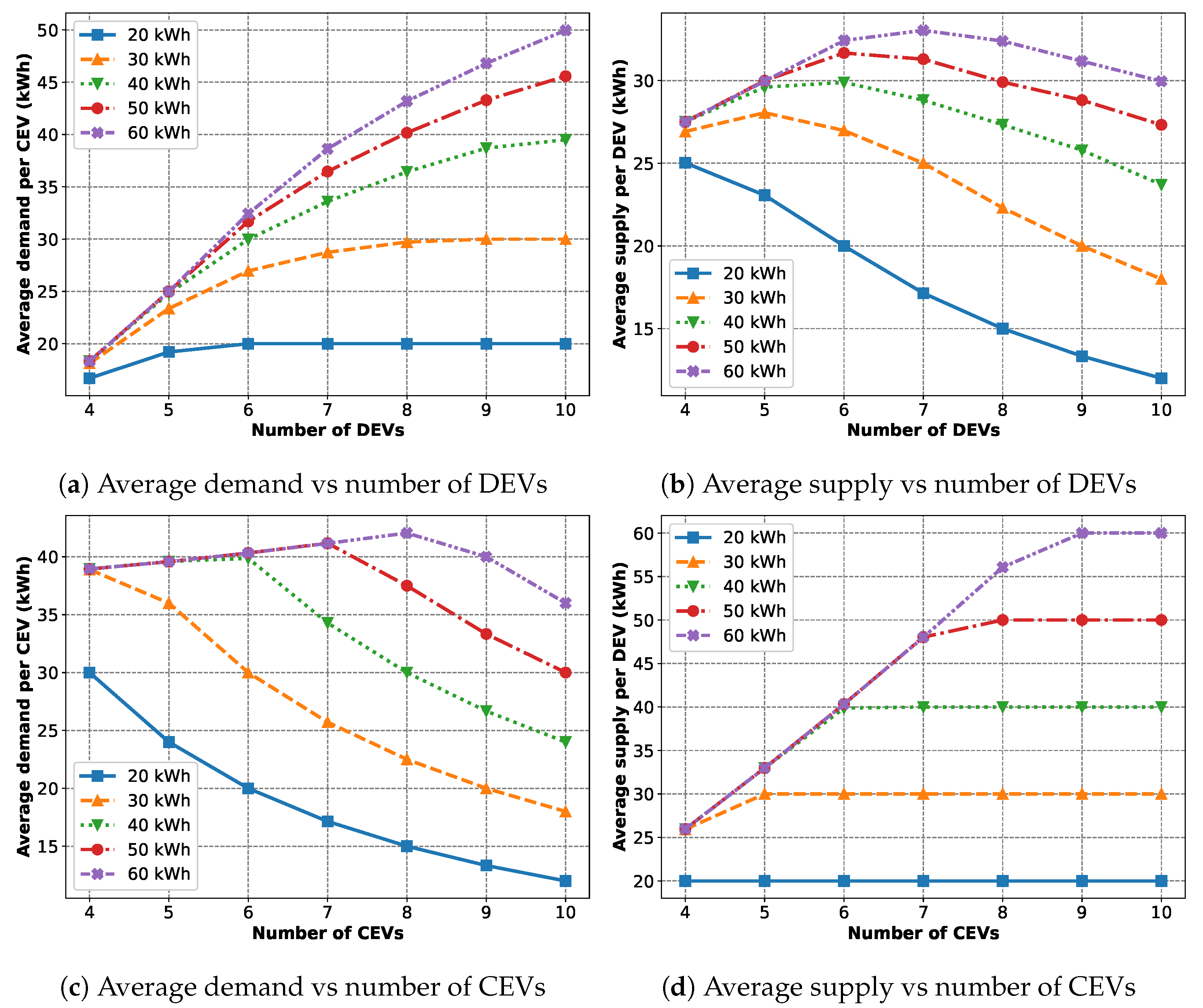
The second scenario (the results are presented in Figure 11) deals with varying the maximum demand and supply parameters along with the number of CEVs and DEVs. For Figure 11a,b, the number of DEVs and the maximum energy demand of the CEVs are varied. Each CEV ($C=6$) has the same maximum demand, while for the DEVs, ${\mathbf{s}}^{max}=[20,25,30,35,40,45]$ kWh and ${\mathbf{p}}^{max}=12$ $/kWh. Figure 11a shows that the average demand per CEV respects the maximum demand constraints. With fewer DEVs present, the demands are not fulfilled and lag behind the maximum value. However, with more DEVs present, the demands are met and follow the constraint exactly. This is why we see that the curves plateau at some point as the number of DEVs increases. Figure 11b shows that the average supply per DEV increases with more DEVs at first as they increasingly satisfy unmet demands from the CEVs. However, at some point it reaches a peak when all the CEVs’ demands are met and starts going down as, from this point forward, adding more DEVs results in a reduced amount of energy bought from each DEV. Also, as expected, the peak point is achieved later when the maximum demand of the CEVs is higher.

For Figure 11c,d, the number of CEVs and the maximum energy supply of the DEVs are varied. Each DEV ($D=6$) has the same maximum supply and price (${\mathbf{p}}^{max}=12$ $/kWh), while for the CEVs, ${\mathbf{b}}^{max}=[40,45,50,55,60,65]$ kWh. Figure 11c shows that the average demand per CEV increases with more CEVs at first as they increasingly buy more energy from the DEVs who have unsold energies. But at some point, it reaches a peak when all the DEVs’ energy is sold and starts going down, as from this point forward adding more CEVs results in a reduced amount of energy available for each CEV. Also, as expected, the peak point is achieved later when the maximum demand of the CEVs is higher. Figure 11d shows that the average supply per DEV respects the maximum supply constraints. With fewer CEVs present, there are unsold energies and the supply lags behind the maximum value. However, with more CEVs present, all the energies are sold and exactly follow the constraint. This is evident from the fact that the curves plateau as the number of CEVs increases.

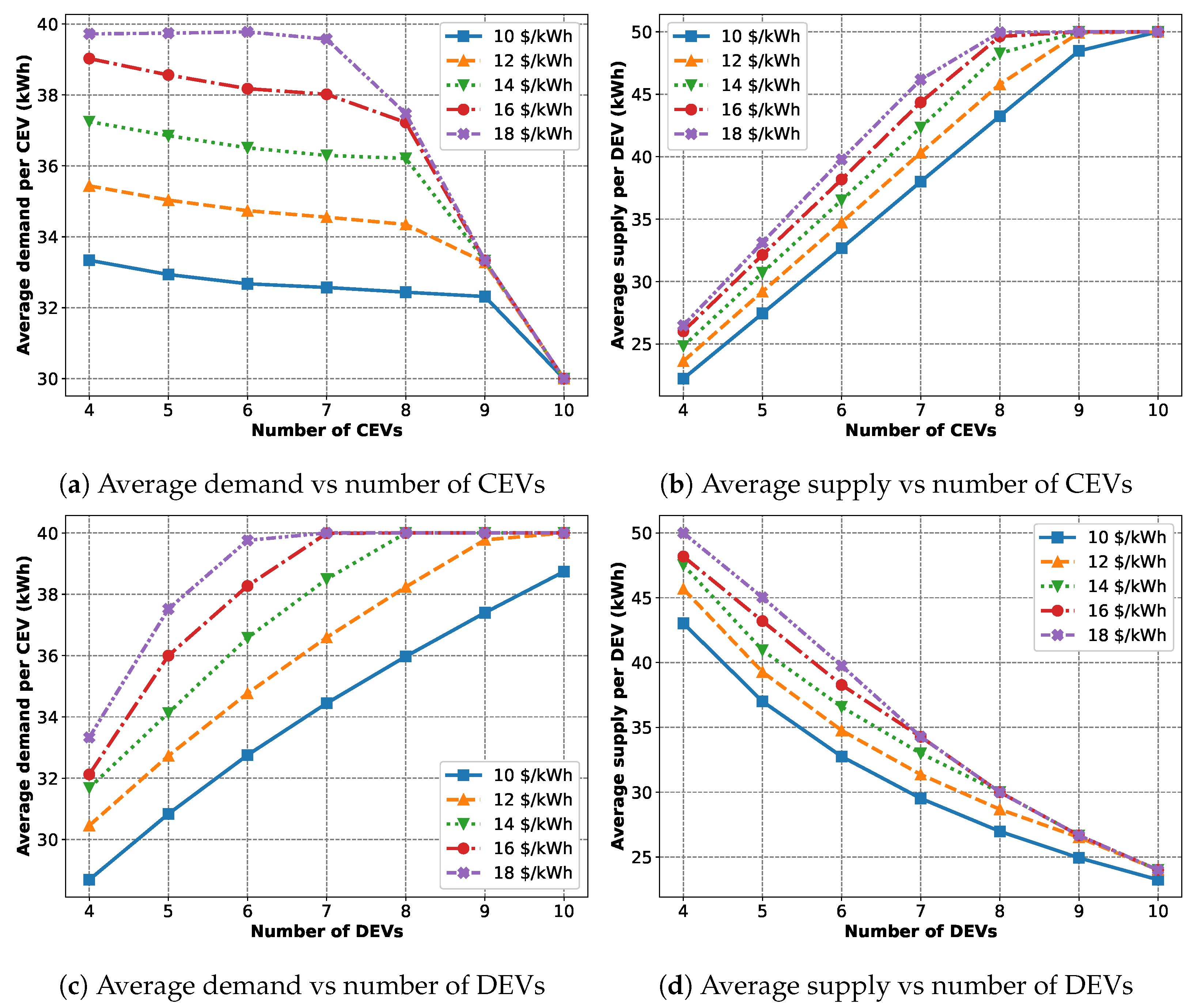
The third and final scenario (the results are presented in Figure 12) deals with varying the maximum price parameters along with the number of CEVs and DEVs. For Figure 12a,b, the number of CEVs and the maximum energy price of the DEVs are varied. Each DEV ($D=6$) has the same maximum supply, ${\mathbf{s}}^{max}=50$ kWh, and price while each CEV has the same maximum demand, ${\mathbf{b}}^{max}=40$ kWh. Figure 12a illustrates that, with an increasing number of CEVs, while the number of DEVs remains the same, the average energy bought per CEV decreases due to supply shortage. Also, we see a sudden drop in the amount of energy bought with more CEVs as the DEVs cannot supply any more energy and have hit their maximum capacity. On the other hand, as the maximum prices of the DEVs increase, they are willing to sell more energy and, as a result, the CEVs also buy more energy due to increased supply. However, as a result, the DEVs also hit their maximum capacity faster, as is evident from the fact that the 18 $/kWh curve starts to drop steeply sooner than the 10 $/kWh curve. Also, we observe that the 18 $/kWh curve has already reached the 40 kWh maximum demand constraint and thus plateaus for the first three data points. Figure 12b shows that, with increasing price, the DEVs are willing to sell more. Also, increasing the number of CEVs results in more energy sold when available while hitting the 50 kWh maximum supply constraint with too many CEVs present.

For Figure 12c,d, the number of DEVs and the maximum energy price of the DEVs are varied. Each CEV ($C=6$) has the same maximum demand, ${\mathbf{b}}^{max}=40$ kWh, while each DEV has the same maximum demand, ${\mathbf{s}}^{max}=50$ kWh, and price. In Figure 12c, adding more DEVs means more available energy; thus, the CEVs are able to buy more energy before reaching the 40 kWh maximum demand limit. Similarly to the previous case, increasing the energy price makes the DEVs willing to sell more energy, as shown in Figure 12d, causing the CEV to buy more energy as well due to unmet demands. Also, adding more DEVs lowers the average energy sold by each DEV.

8.4. Pure Operation Performance of the Protocol

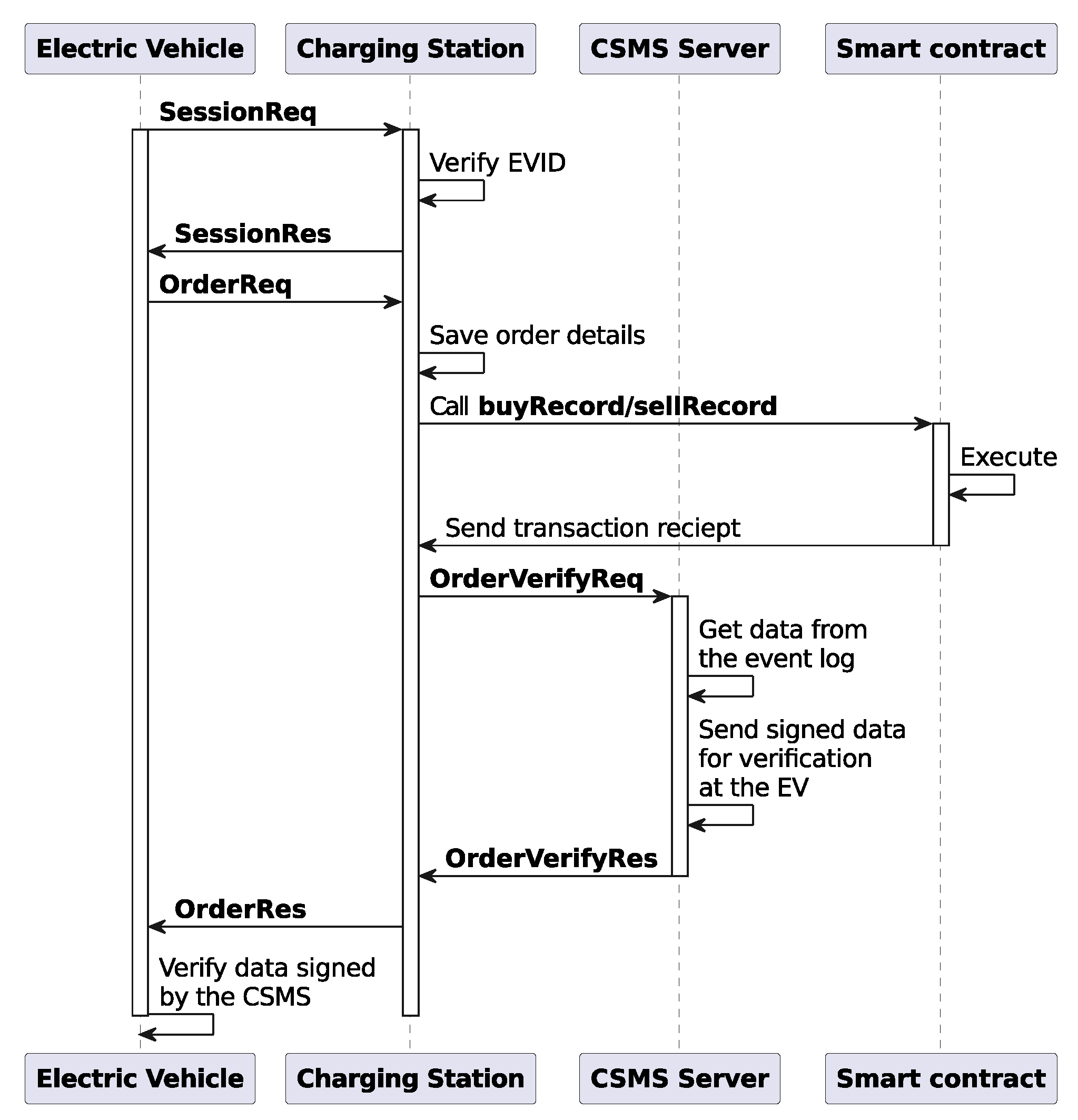
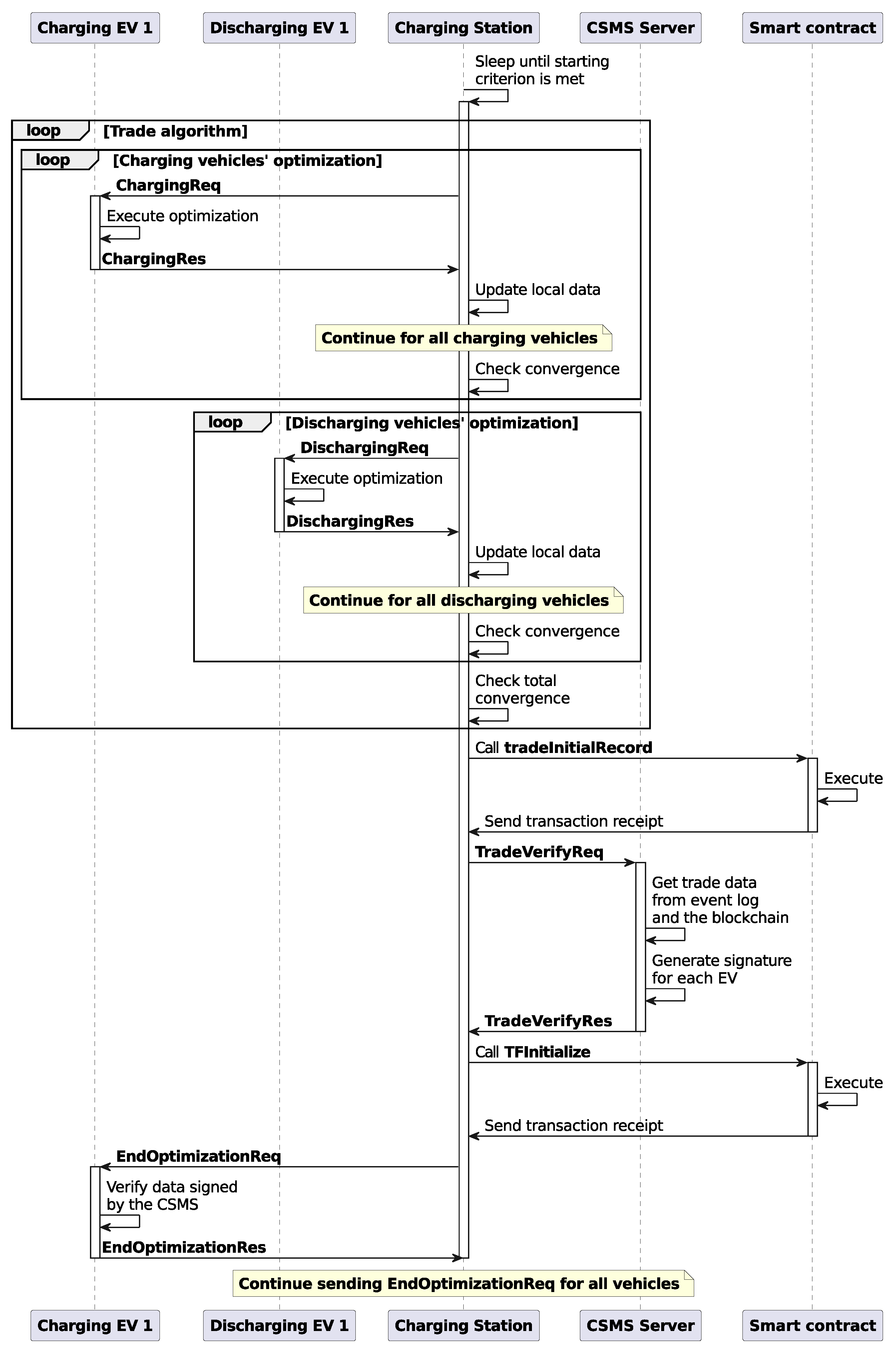
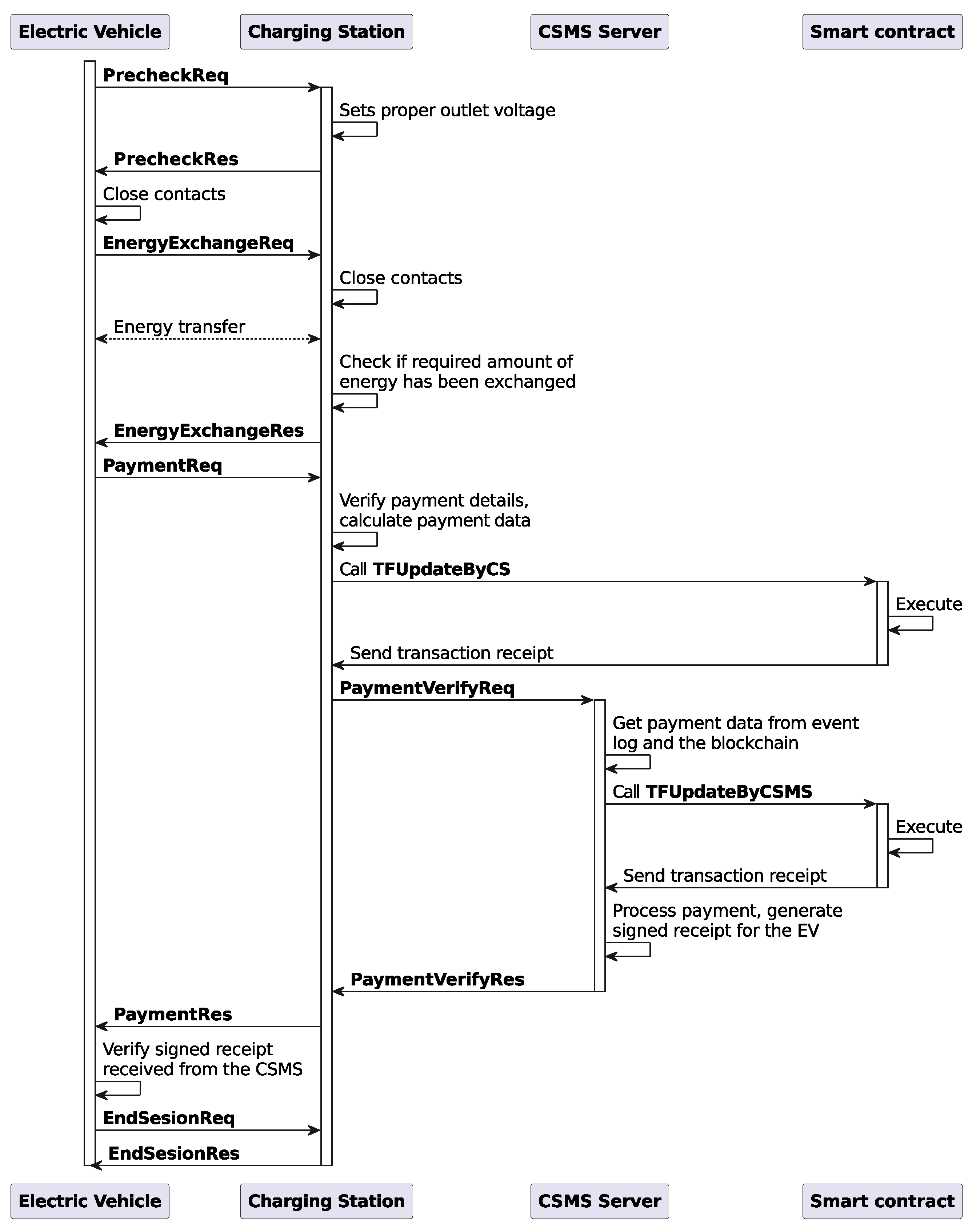
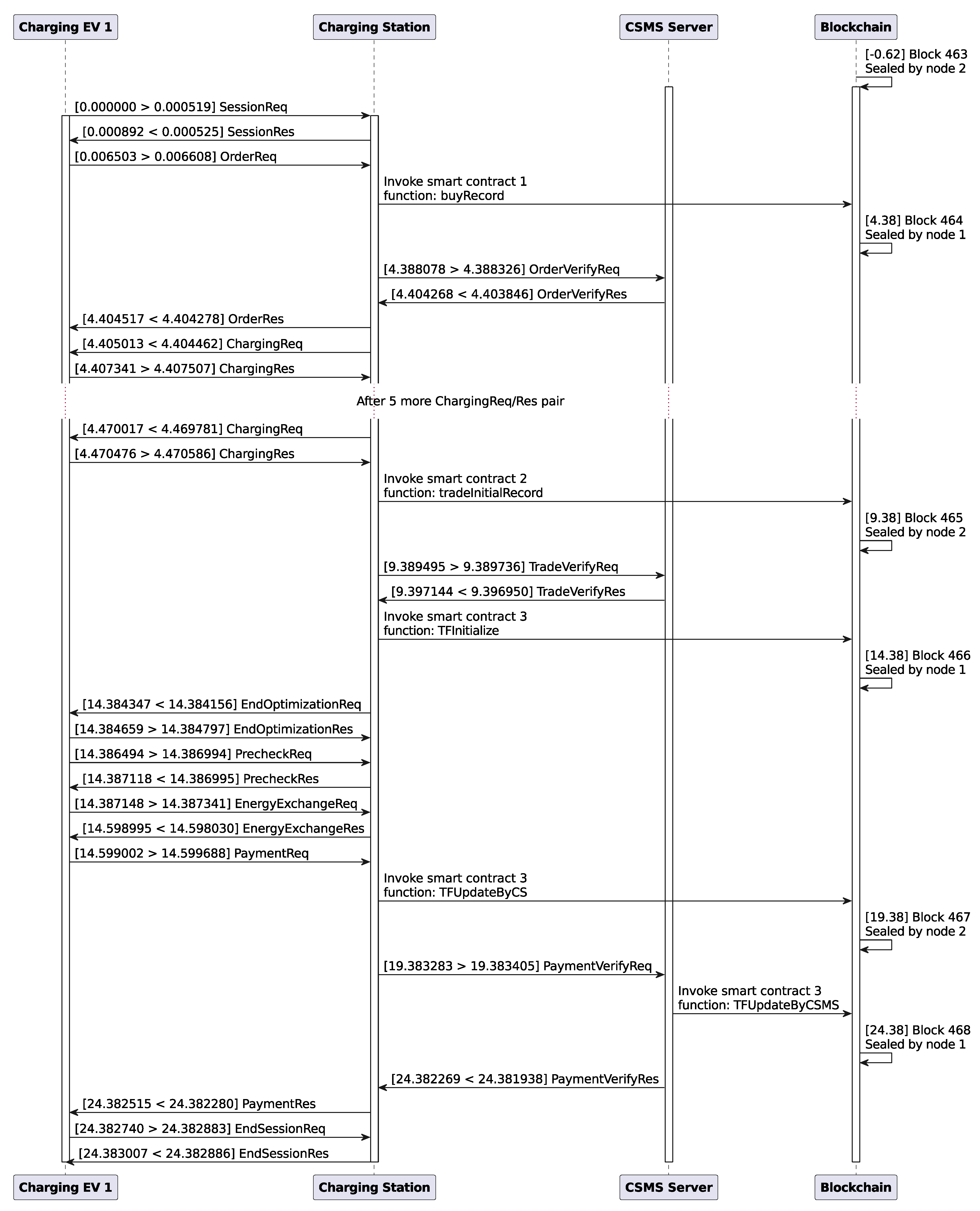
In this section, we present the pure operation characteristics of the fully implemented protocol. With two CEVs and two DEVs, Figure 13 shows the timing diagram for the communication between the first charging EV (CEV 1) and the CS. The numbers in square brackets beside most of the actions represent the relative times in seconds. For example, in the case of the blockchain line, it shows when the block was sealed. In the case of messages, there are two numbers that, depending on the direction, represent the sending time and the receiving time. The relative time counter starts when the EV sends the first message (SessionReq). The diagram is self-explanatory and gives a overview of how the protocol works in practice. To simulate the energy exchange, we instructed the EV and the CS to sleep for 10 milliseconds per kWh of energy exchanged. This is why we see approximately 200 ms of gap between the EnergyExchageReq and EnergyExchageRes message pairs, as the energy demand was approximately 20 kWh.

We can clearly understand that the blockchain used here has two sealers and a block period or interval of 5 s. The smart contract functions shown in Algorithms 1 and 3 are executed once per EV per charging session, while the function shown in Algorithm 2 is executed once per charging session. Each function is executed in a different block of the blockchain, so we need approximately 5 (number of functions) multiplied by 5 s (block period) = 25 s for the protocol execution. As shown in Figure 10a, the trade algorithm itself takes less than half a second, even for a 10 CEV and 10 DEV case. Therefore, the bottleneck can be the block generation speed, but it can be made smaller. While we experimented with two different block period (Section 8.6), we did not investigate how small it can be while operating properly. Another thing to mention here is that, while all the other smart contract functions are submitted in parallel to the blockchain, the last one (TFUpdatebyCSMS, Algorithm 3) does it sequentially for each EV. We designed it this way because parallel submission for the last smart contract means all the vehicles will have to wait until the last vehicle finishes its task. In real-life, no one will want to wait once they are finished charging or discharging their EV. This is why we submit the last contract sequentially as soon as the EV finishes its energy exchange.

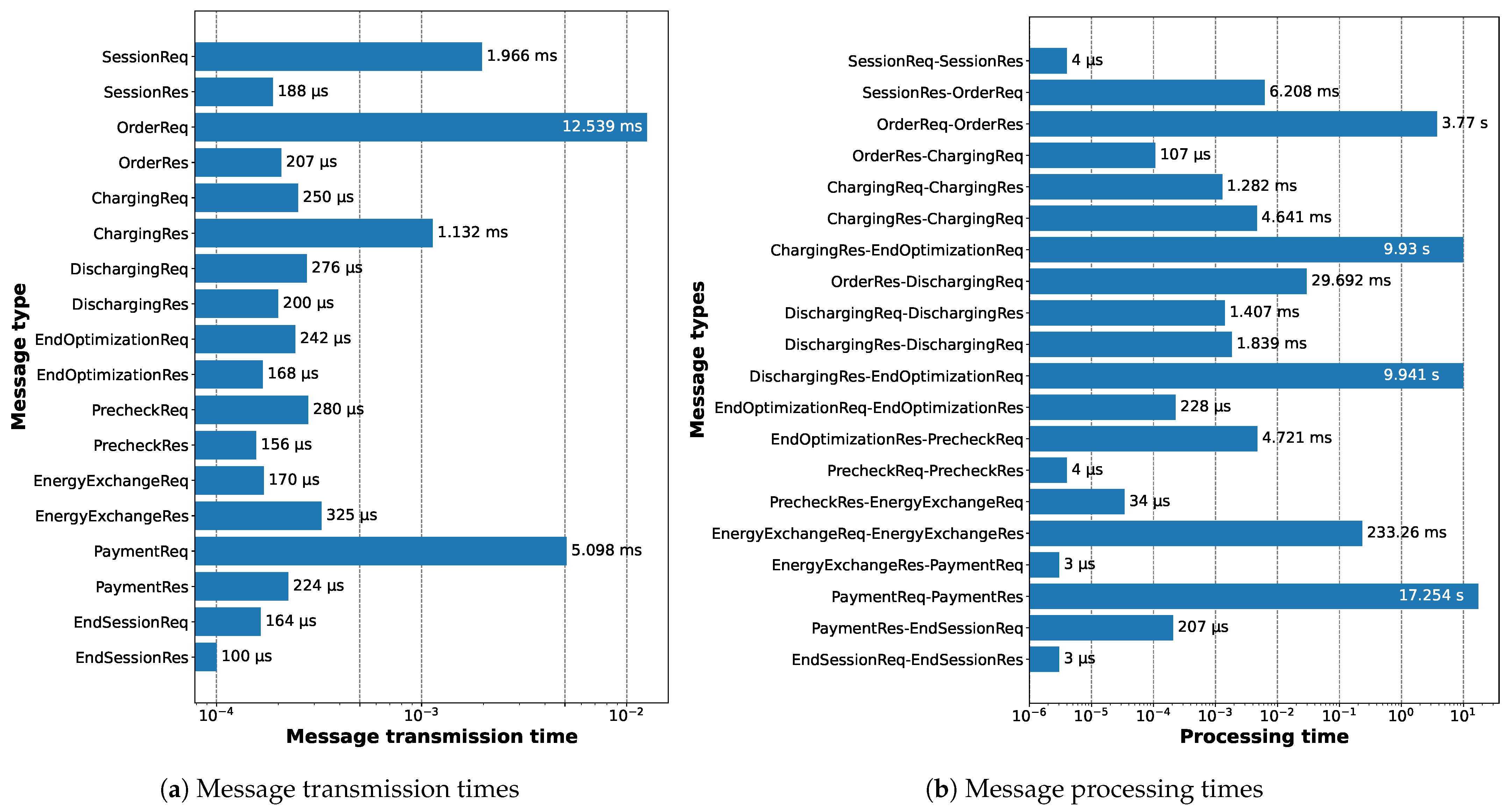
In Figure 14, we present the average data transmission and processing times for messages between the EVs and the CS. Figure 14a shows that most of the message transmission times are less than a millisecond, and at this level these values can be unreliable. However, we are showing these for reference purposes. For higher values, the reason lies in how we implemented the protocol. To control the data dependency between the CS’s multiple socket connections to the EVs, we used asynchronous locks. This causes the connections to wait for each other while performing some data-dependent tasks, thus introducing some delays in both the transmission and processing messages. Figure 14b depicts the processing time between two consecutive messages. For example, the item SessionReq-SessionRes represents the time spent by the CS between receiving the SessionReq and sending the SessionRes messages. All the significant values here are due to the smart contract execution delay. As the block period is 5 s, if we combine insights from Figure 13 and Figure 14b, we can understand that two smart contract functions are executed between the last ChargingRes/DischargingRes and the EndOptimizationReq messages, which causes approximately 10 s of delay. For OrderReq-OrderRes, the value will be less than or equal to the block period (5 s), but the exact number will depend on when the EV makes the first request. If it is right before a block is sealed, it does not have to wait long and the contract can be executed immediately. On the other hand, if it is right after a block is sealed, it has to wait a full block period to have the contract executed. PaymentReq-PaymentRes message pairs also include two smart contract executions, so the processing time here will be at least 10 s. However, as mentioned previously, the last function is called sequentially so each EV adds an extra 5 s. Therefore, for the first EV to finish charging/discharging, it should be exactly 10 (5 + 5 × 1) s, while for the fourth one (we have four EVs in total), it should be 25 (5 + 5 × 4) s. Therefore, the average is 17.5 s, which is what we see in Figure 14b. Finally, the EnergyExchangeReq-EnergyExchangeRes processsing time is approximately 200 ms, as already explained earlier.

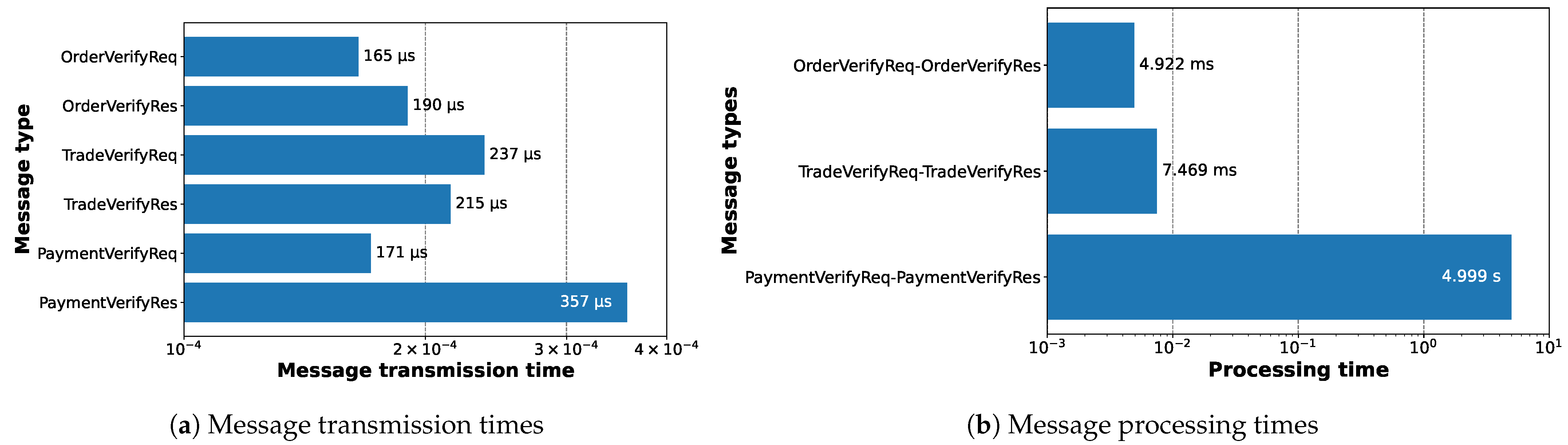
Figure 15 presents the data transmission and processing times for messages between the CS and the CSMS. As we see in Figure 15a, the values here are negligible as all of them are less than a millisecond. On the other hand, for Figure 15b, the first two involve the CSMS server retrieving logs and data from the blockchain and then signing them. Therefore, they are in the range of milliseconds. Also, as the PaymentVerifyReq-PaymentVerifyReq includes a contract execution, it needs at least a block period (5 s) worth of time.

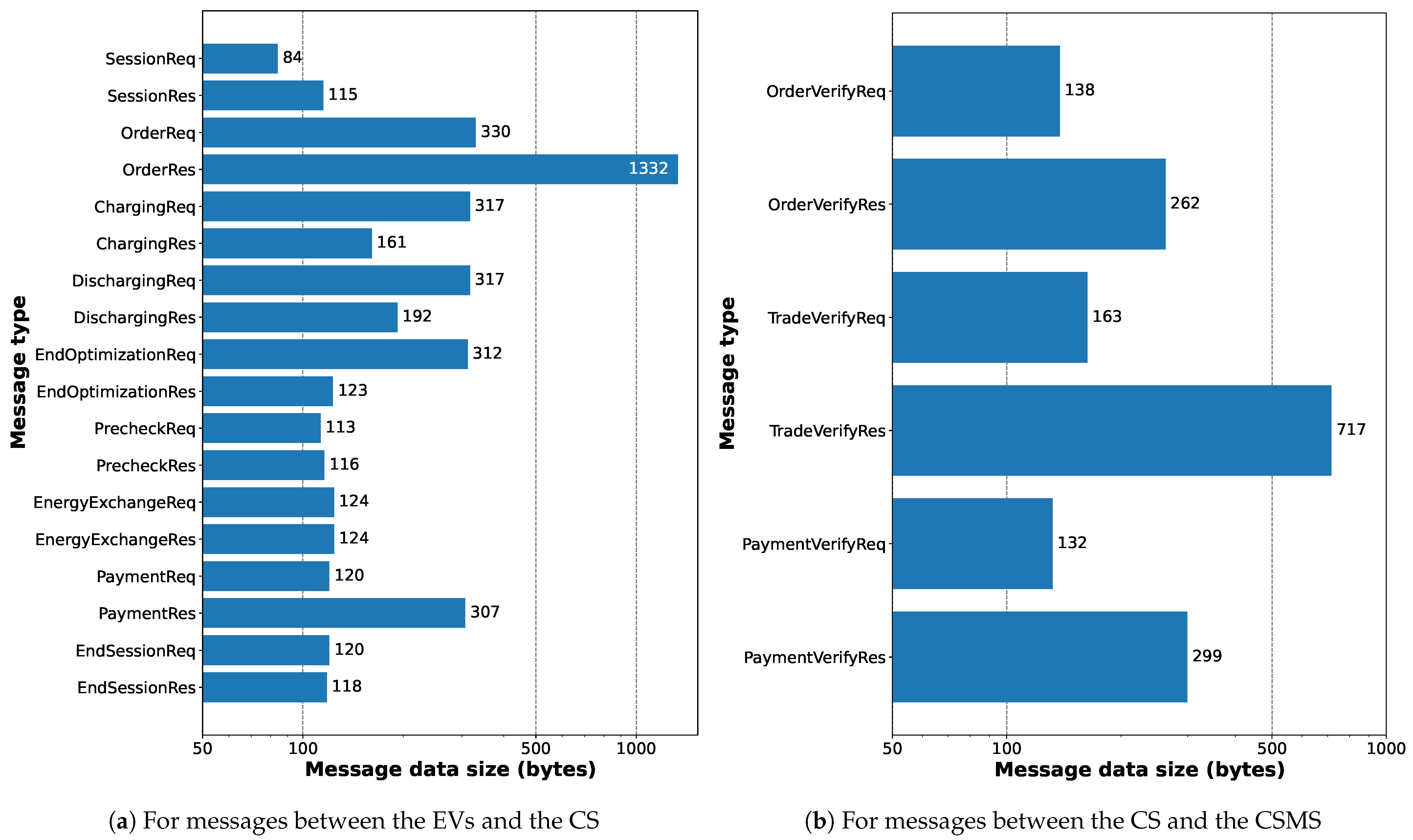
In Figure 16, we illustrate the message data sizes for messages between various entities. In Figure 16a, we see that the OrderRes message has the highest data size as it includes the CSMS server’s certificate. All of these values will make sense if compared with the message definitions described in Section 5.4. We did not round off the values of various numbers that are sent between the entities, as while doing so would reduce the data size, it would not be that significant. Also, most of the messages are between the EVs and the CS using a direct, local connection. In Figure 16b, the highest data size is for the TradeVerifyReq message as it includes separate signatures for each of the EVs.

Finally, Figure 17 shows the gas cost to execute the smart contract functions given in Algorithms 1–3. The smart contract function TIRecord (Algorithm 2) has the highest gas cost as it has the largest amount of data to be recorded in the blockchain. However, it is also executed only once per energy exchange session while the others are executed per vehicle basis. Considering this, the buy/sellRecord functions are actually the most expensive ones.

8.5. Scalability of the Protocol

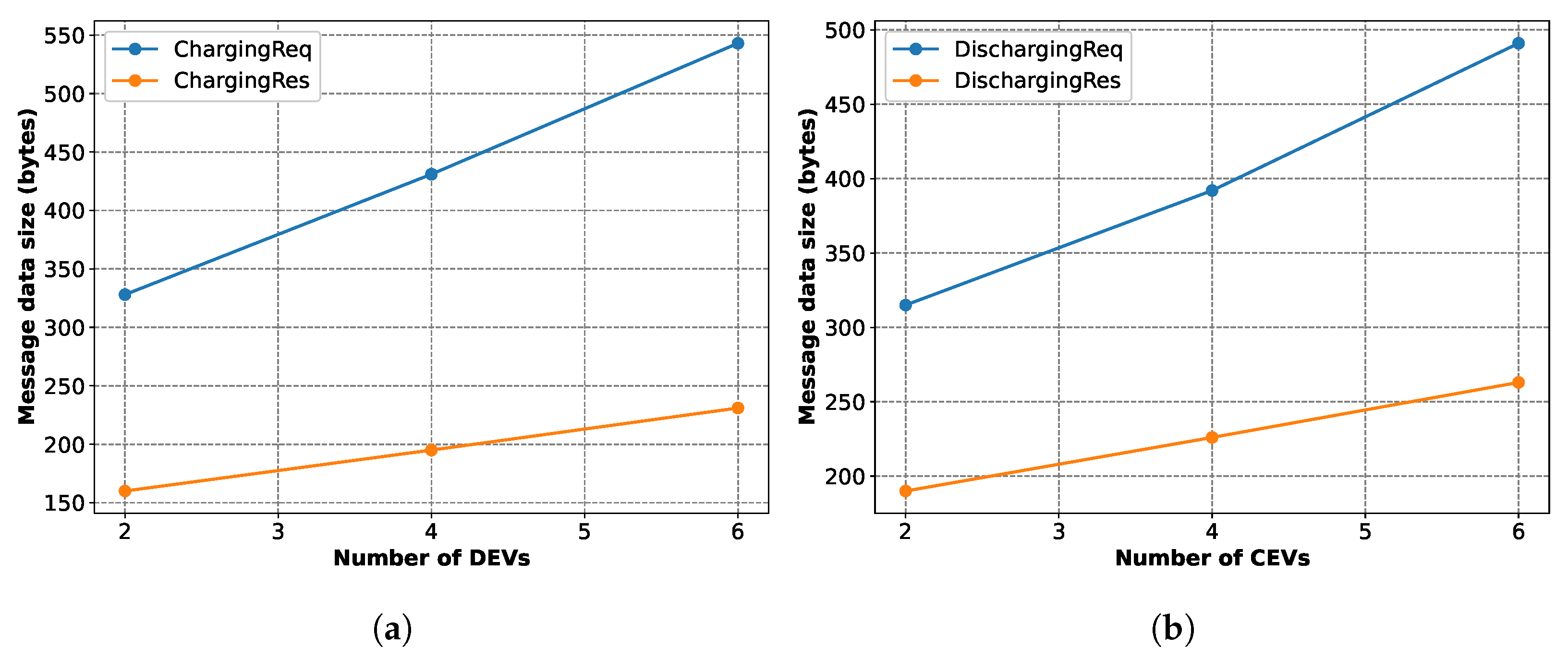
Here, we test the protocol with different numbers of CEVs and DEVs. Only the metrics that change significantly with the number of CEVs and DEVs are presented here. Figure 18 illustrates the data size variations for a few messages. The ChargingReq and ChargingRes messages have increased data size with an increased number of DEVs, as shown in Figure 18a, because each of these messages contains the supplies and prices of each DEV. For the same reason, The DischargingReq and DischargingRes messages have an increased data size with an increased number of CEVs, as shown in Figure 18b.

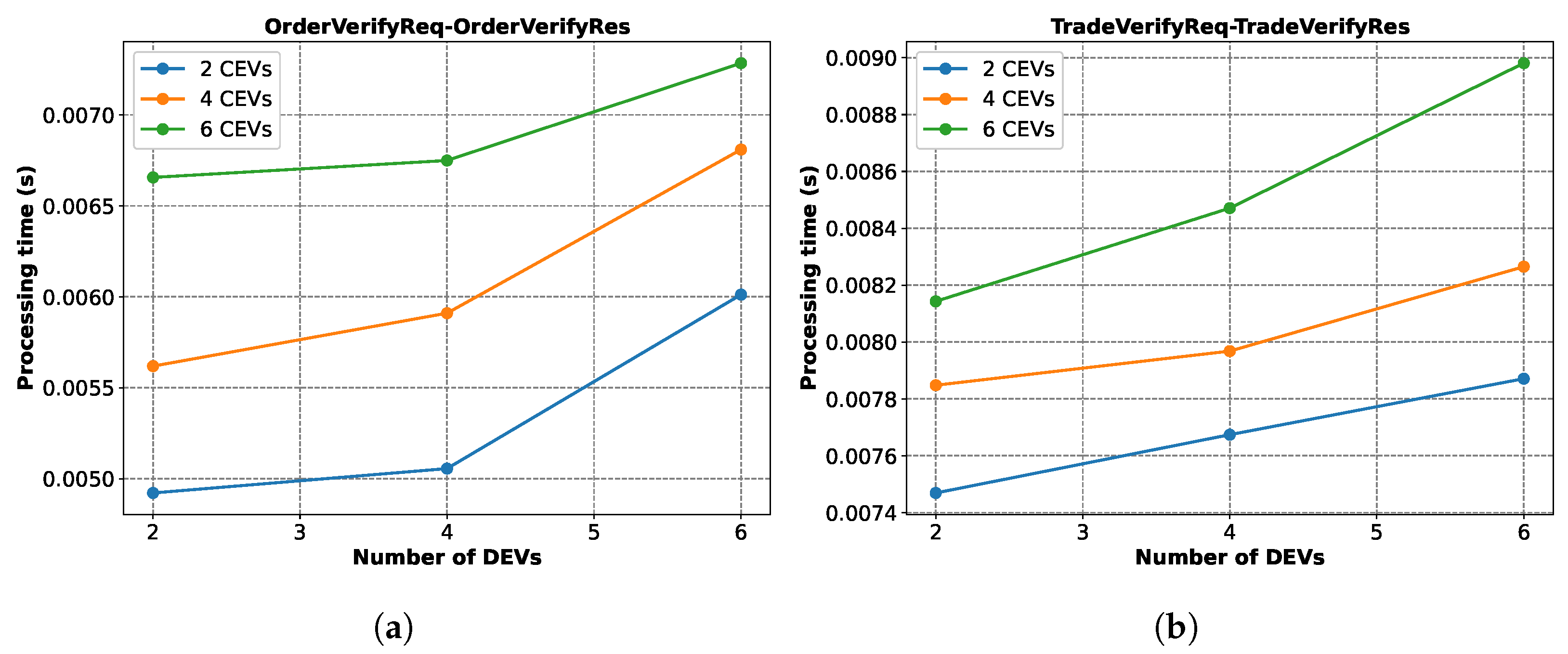
Figure 19 shows the message processing time variations for a few message pairs. In Figure 19a, we observe that the CSMS takes more time to process the OrderVerifyReq and generate the OrderVerifyRes messages as the number of CEVs and DEVs increase. Figure 19b shows the same thing for the TradeVerifyRes-TradeVerifyRes pairs. This is due to the fact that the CSMS has to generate more signatures when there are more EVs.

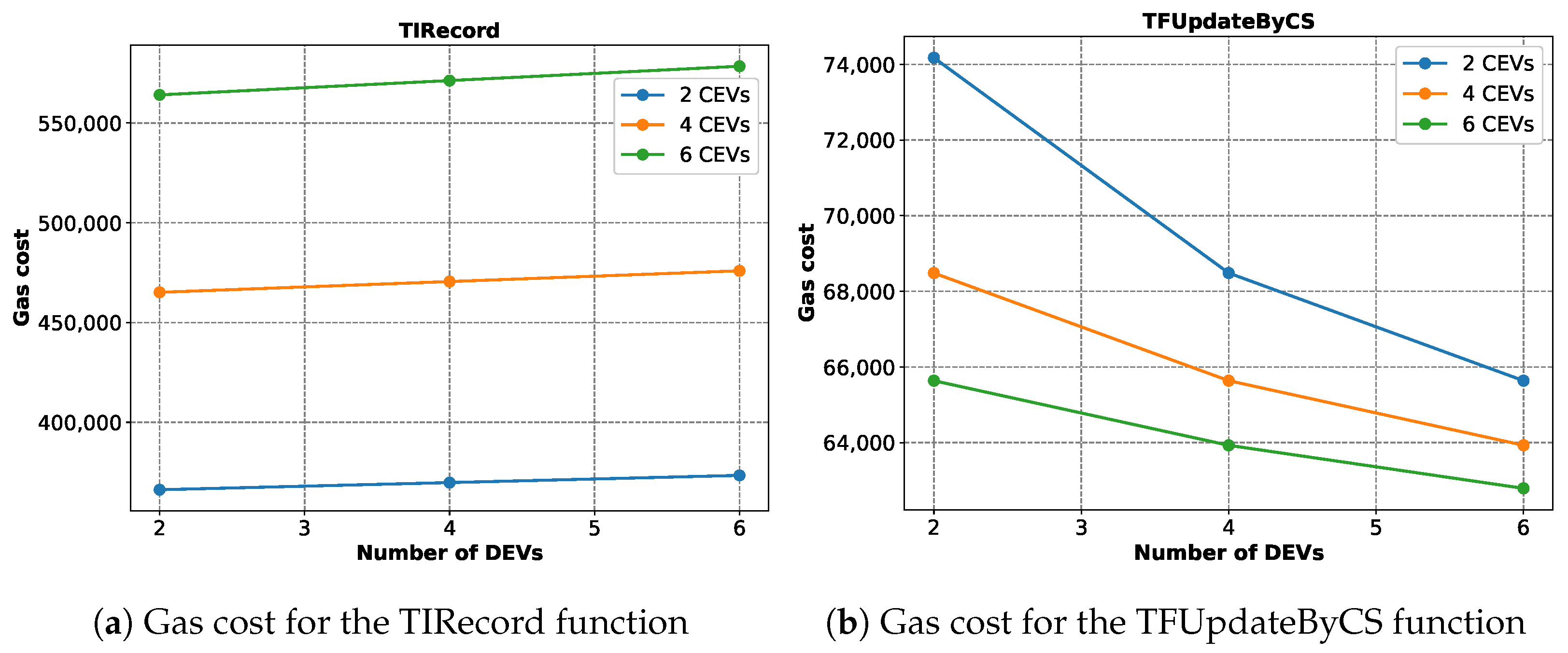
Figure 20 presents how the gas cost varies when executing a few smart contract functions. Figure 20a shows that the gas cost to execute the TIRecord (Algorithm 2) function increases for an increasing number of CEVs and DEVs. However, the jump is much larger in the case of the CEVs compared to the DEVs. This is due to the nature of Solidity. In Solidity, adding a new element to an array with at least one element costs much less than adding an element for the first time to an array. In our implementation of TIRecord, the demands for the CEVs are placed along the rows of a 2D array, while the columns represent demands from each DEV. Therefore, increasing the number of DEVs means adding additional elements to some non-empty rows, while increasing the number of CEVs means creating and then adding elements to the newly created empty rows. This is why increasing the number of CEVs is more expensive. In Figure 20b, the same thing is shown for the smart contract function TFUpdatebyCS (Algorithm 3). Here, the average gas cost decreases with the increasing number of CEVs and DEVs due to a very similar reason. We initialized the arrays to hold the CEV and DEV IDs as empty arrays. When the first EV ID is pushed to the array, it costs more, while the subsequent pushes cost less. This is why the average cost decreases with additional elements.

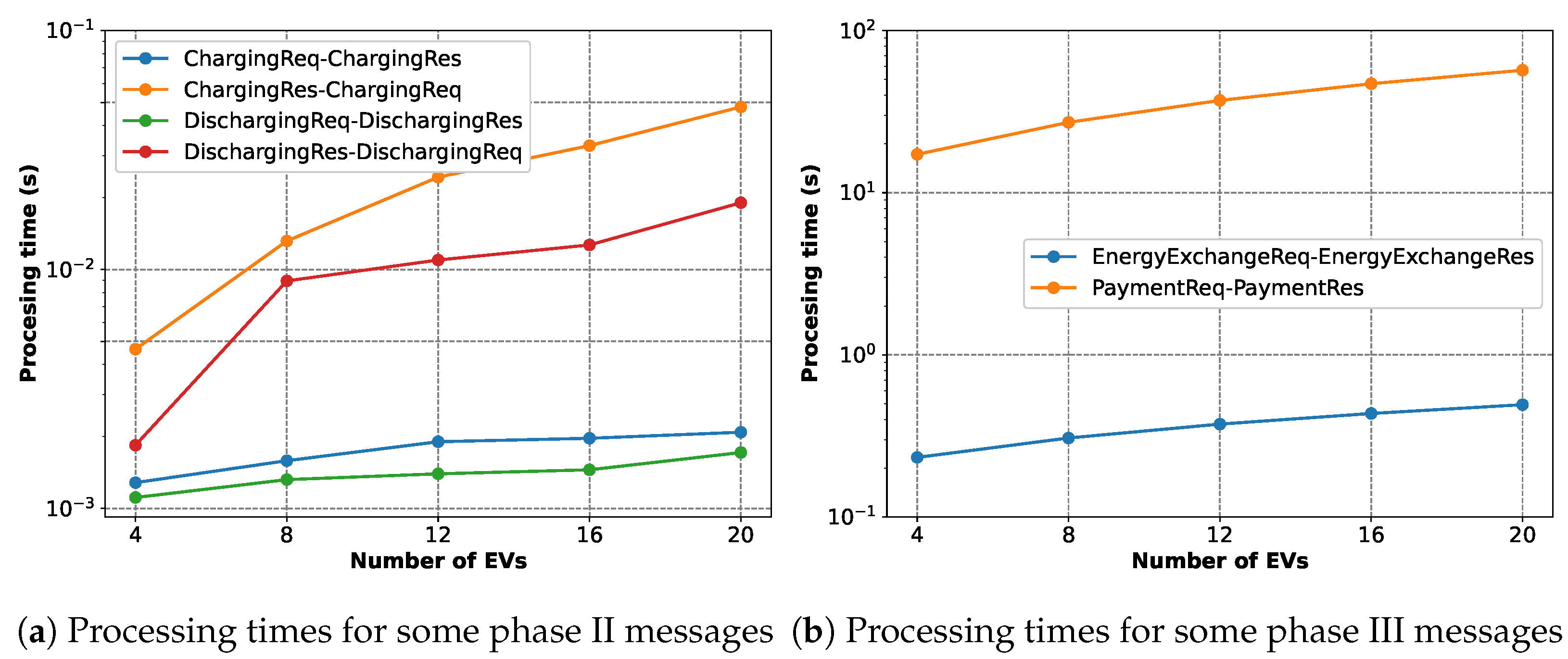
Lastly, in Figure 21, we present how some message processing times compare to each other with varying numbers of EVs (equal numbers of CEVs and DEVs). Figure 21a shows that all of the four processing times increase with the increasing number of EVs. The ChargingReq-ChargingRes and DischargingReq-DischargingRes pairs actually represent a single iteration of optimization for the charging EVs and the discharging EVs, respectively. Therefore, the charging EVs take a longer time to perform the optimization than the discharging EVs. The ChargingRes-ChargingReq and DischargingRes-DischargingReq pairs, on the other hand, represent the time an EV spends waiting for others to finish their optimization, which is, as expected, significantly higher than the time it spends for its own optimization. Figure 21b shows that the EnergyExchangeReq-EnergyExchangeRes pairs need more time as the number of EVs increases because of the increased amount of traded energy. Also, the PaymentReq-PaymentRes pairs, similarly, take more time as the final smart contract function is executed sequentially into consecutive blocks for each EV.

8.6. Scalability of the Blockchain

As blockchain plays a key role in our proposed V2V energy-trading protocol, we examined how its performance changes with increasing numbers of nodes and workload. In our experiments, we generate the workload (transactions from smart contract executions) using the signers only. This is due to the fact that the CSs play the role of signers in our system and they mainly call the smart contract functions, thus generating the transactions. Each signer node has a fixed number of workloads or transactions to be sent. Each node continues to generate and submit transactions until that fixed number is reached. To make the experiment simple, we only execute the buy/sellRecord function (Algorithm 1) that has the highest gas cost, as mentioned previously. Unless mentioned, we use a block period of 1 s and block gas limit of 1 billion. We used a few metrics to measure the performance. They are as follows:

• Transaction submission rate: It describes how fast a node can submit transactions (or execute smart contract functions). Its unit is transactions per second, or tx/sec.
• Transaction throughput: It presents how fast the blockchain can record submitted transactions to a block and seal it. For example, if the block period is 5 s and each block contains approximately 500 transactions, the transaction throughput is 100 tx/sec.
• Transaction latency: It is the time spent between submitting a transaction and having that transaction verified and included in a block.
• Average number of queued transactions: When a transaction is submitted, it is verified and added to a pending list, if its nonce is in order. For example, the very first transaction submitted from an address will have a nonce of 0. For each subsequent transaction, the nonce will be increased by 1. If transactions with a nonce of 0, 1, and 2 are in the pending list and a new transaction with a nonce of 4 is submitted, it will not be put into the pending list as the expected transaction in order should have a nonce of 3. Therefore, it will be added to a different list call queue. When the transaction with nonce 3 arrives, it will be placed on the pending list and then the transaction with nonce 4 will be taken out out the queue and be added to the pending list as well. Before a new block is sealed, the pending transactions are added to the block according to its capacity. The default maximum length of this pending list in Geth is 4096, but it can be modified. The default length of the queue is 64. If the number of queued transactions goes above this limit, the transaction will be lost and the Geth node can crash. Therefore, the average number of queued transaction is an important performance metric.

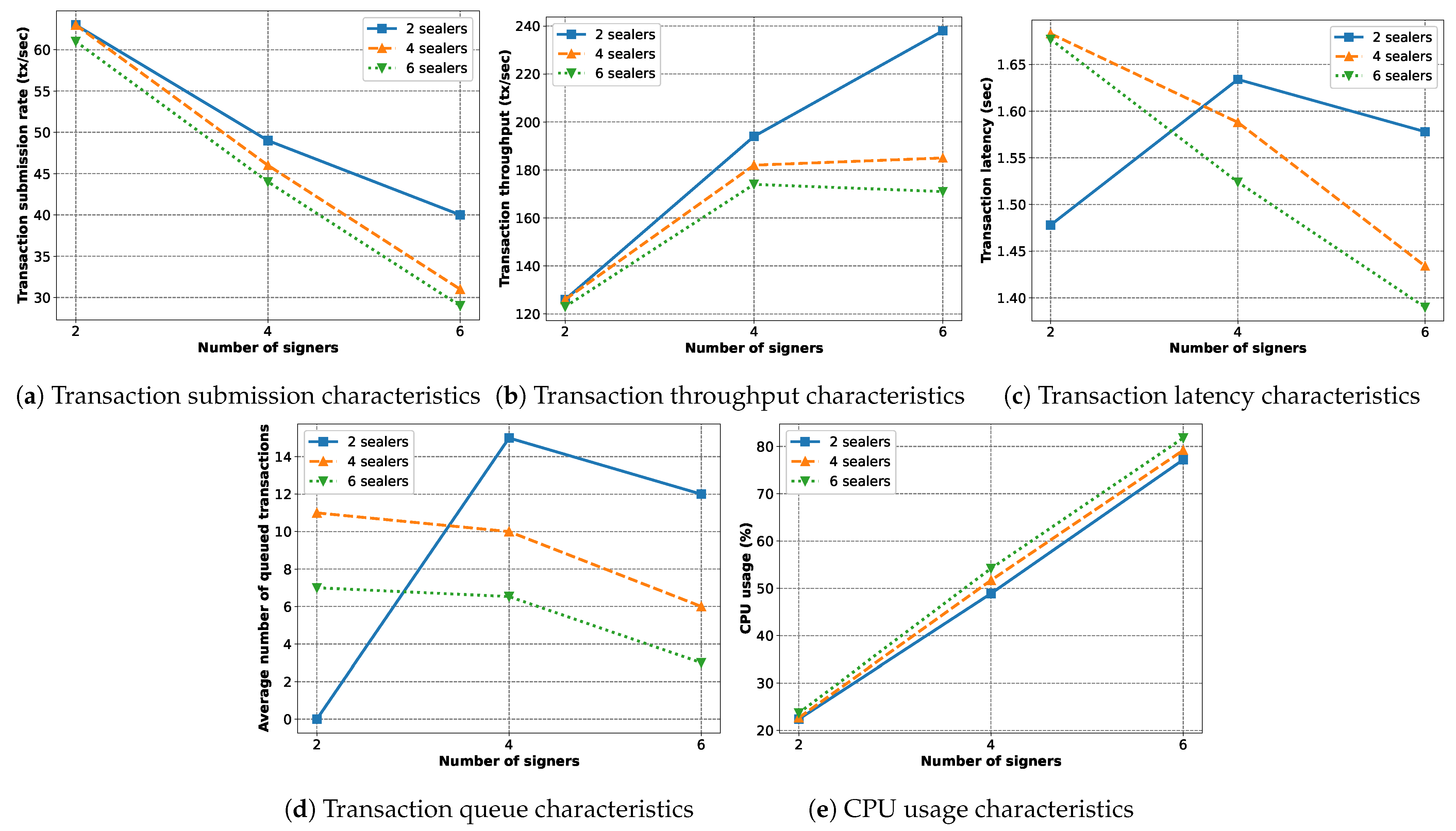
In Figure 22 is shown the behavior the implemented blockchain with varying numbers of sealers (with active mining enabled) and signers (without mining). Here, the workload is 2500 transactions per signer. Figure 22a shows that, with increasing numbers of signers (thus the total workload), the transaction submission rate decreases significantly. The number of sealers has a similar, but weaker, effect. Especially for the two-sealers case, we see that the rate of decrement is slower. Figure 22b shows that the transaction throughput initially rises as more signers are added, but later, it slows down. For six sealers, it even starts to decrease. This is expected as, with more signers, the submission rate decreases while the total amount of submitted transactions increases. For even more signers, the submission rate decreases faster than the increment of total submissions. Thus, the throughput dips. Figure 22c,d show that the transaction latency and the average number of queued transactions are correlated. The reason for this is that, when a transaction is stuck in the queue, it is not being processed, and this increases the latency. Therefore, more queued transactions results in more latency. The two-sealer and two-signer case seems to be exceptional, with a very low number of queued transactions and low latency. For other cases, with more sealers and signers, the queued transactions are split among their own transaction queues, thus lowering the average number of queued transactions and the latency. Finally, Figure 22e shows why the transaction submission rate decreases with increased sealers and signers. We can clearly see that the CPU usage increases drastically with an increasing number of signers, while the effect of sealer nodes are much weaker. We do not show the results for 8 or 10 sealers as it is obvious that the CPU will hit its limit and will not perform properly.

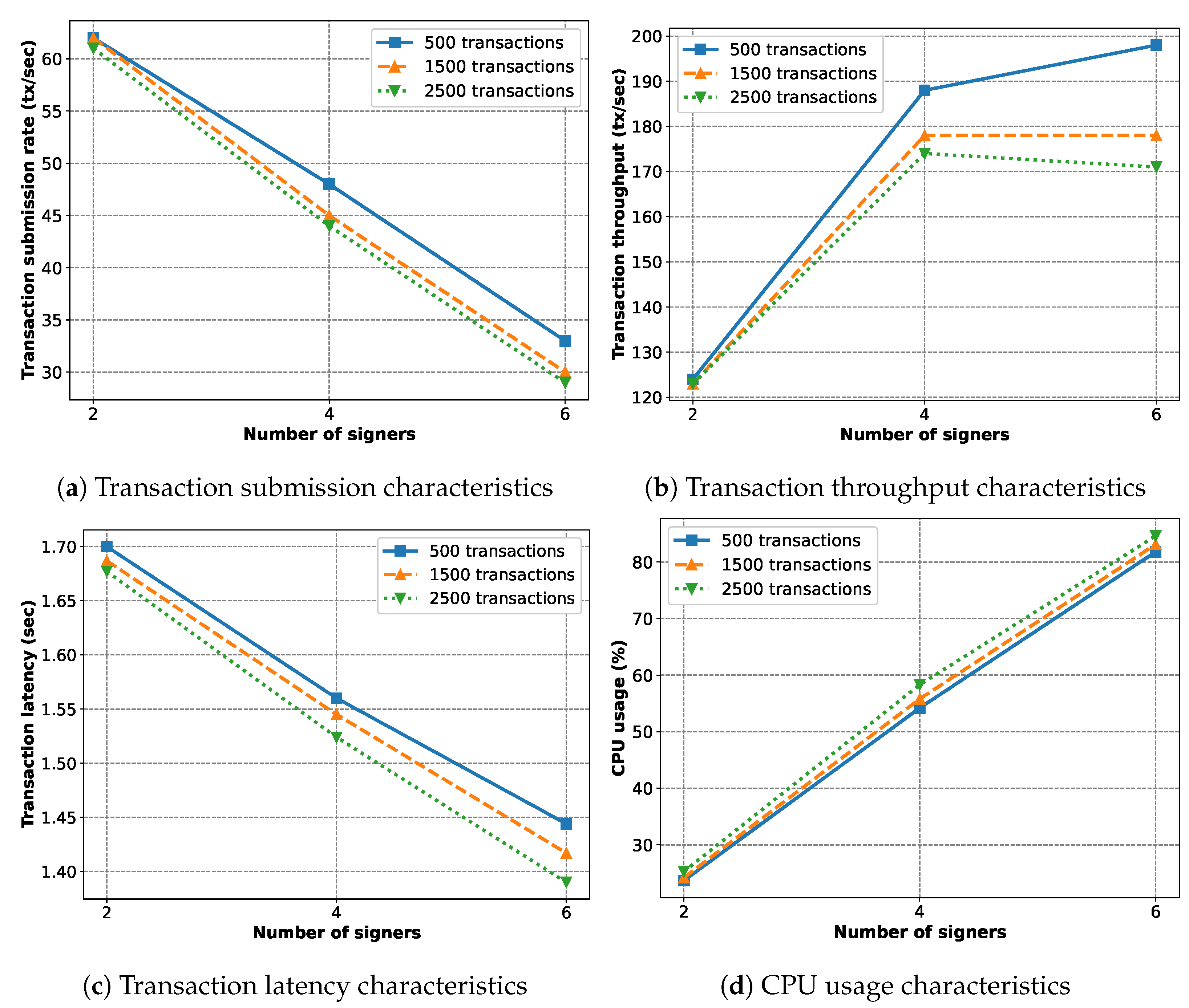
In Figure 23, we study the behavior the implemented blockchain with varying numbers of signers and workloads per signer. The number of sealers is six. The behavior is nearly similar to the previous case in Figure 22, but the effects are weaker. The decreasing submission rate (Figure 23b) stems from the rising CPU usage (Figure 23d), causing the throughput behavior in Figure 23a. The better latency in Figure 23c might be a direct result of the decreased throughput, as the blockchain is processing a lower number of transactions per second.

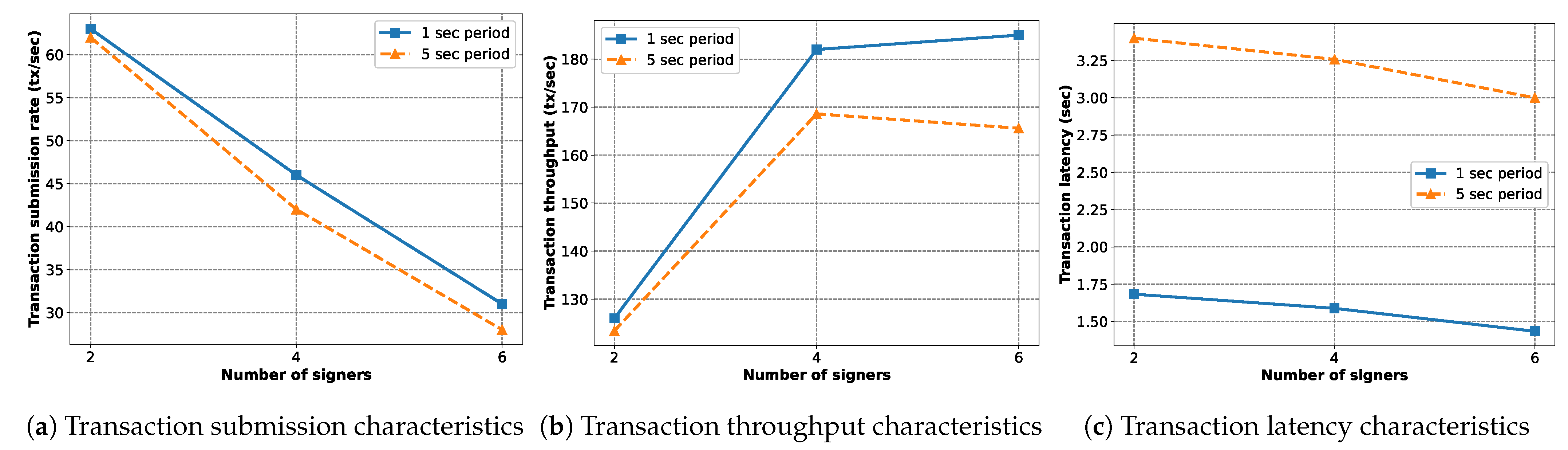
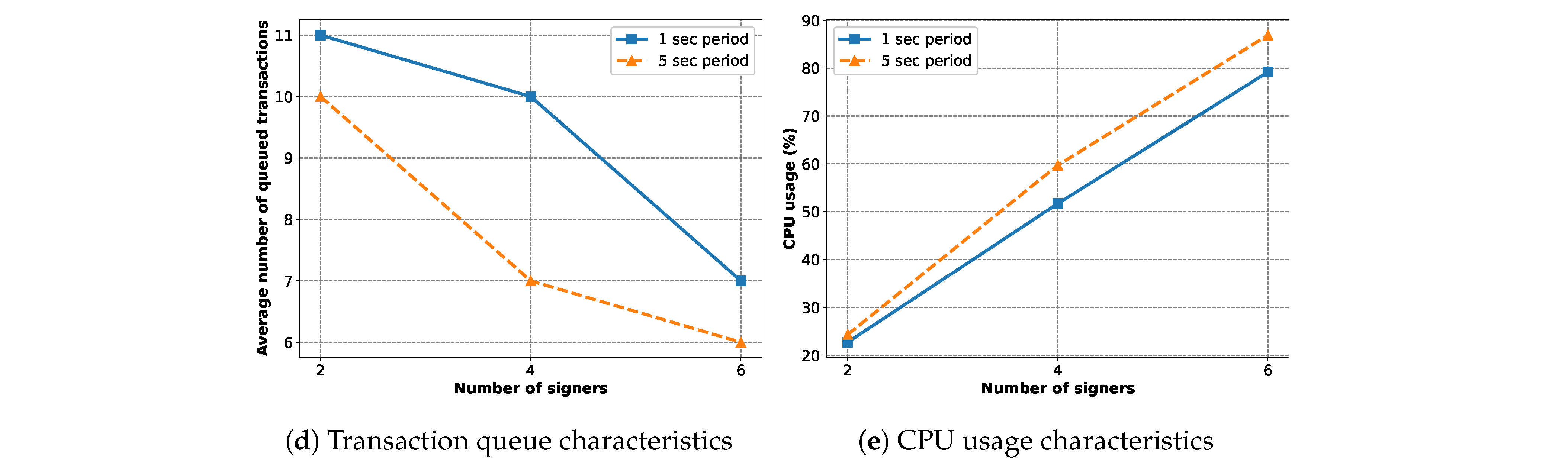
In Figure 24, we study the behavior of the implemented blockchain with varying numbers of signers and block periods. Here, the workload is 2500 transactions per signer and there are four sealers. With faster block generation, we see a higher transaction submission rate (Figure 24a) and throughput (Figure 24b). The latency also becomes lower with shorter block periods (Figure 24c) as the transactions have to wait less to be included in a block. The average number of queued transactions increases (Figure 24d) with faster block generation as the blockchain has less time to synchronize submitted transactions. Finally, Figure 24e shows that the CPU usage is considerably lower for shorter block periods.

8.7. Implication of the Results in Future V2V Trading

As mentioned earlier, there is a lack of detailed V2V energy-trading protocols in the literature. This is why we are unable to compare our protocol with previous studies. Also, our proposed trade algorithm involves three decision variables, demand, supply, and price, whereas previous studies discussed in the literature review mostly deal with two. Hopefully, our work here will be used as a benchmark in future studies and facilitate further research on this topic. We have presented the performance of individual components such as the trade algorithm and the blockchain separately so that they can be easily compared against superior technologies in the future. For example, a sharding feature, as used in [43], can be integrated into the consortium blockchain to improve the transaction rate. The results in Section 8.2 and Section 8.4 are important for participants in future V2V trading as they present the system behavior in terms of input parameters and, thus, will help them in choosing proper values. The scalability results in Section 8.3, Section 8.5 and Section 8.6, on the other hand, are useful for the industry to make implementation and system design decisions regarding the number of blockchain nodes, block generation periods, and number of CEVs and DEVs to start a charging session, etc., based on their business policy.

9. Conclusions

In this paper, we have proposed a blockchain-based V2V energy-trading protocol, along with a Stackelberg game-based algorithm to determine the optimal amount of energy to be traded and the optimal energy price. The trade algorithm iteratively optimizes the amount of energy to be bought for the charging EVs and the energy price and the amount of energy to be sold for the discharging EVs. Our model uses blockchain to record all the trading information securely through the use of smart contracts. We have described the PKI components and user enrollment process and defined the V2V protocol messages in detail. We have also presented a threat model and carried out a detailed security analysis of the proposed protocol.

To access the operational performance and scalability of the model, we have implemented the full protocol in Python while using Geth for the blockchain and then conducted several experiments on various scenarios. The pure operation performance of the trade algorithm has been presented to show how the energy demands and supplies are distributed and how the energy price, revenue, and utility changes based on EVs with varying trading parameters. The scalability tests, on the other hand, show how the algorithm behaves with increasing numbers of charging and discharging EVs. The experiments on the full protocol illustrate its performance measured in message transmission and processing time, message data size, smart contract execution cost, etc. Finally, the scalability tests on the blockchain provide us with important information about the transaction submission rate, throughput and latency, average number of queued transactions, and CPU usage. This not only helps in evaluating our model but will also act as a reference point for anyone implementing a proof-of-authority, consensus-based blockchain in Geth.

The implication of our research for the broader energy industry is that we have identified and addressed a substantial research gap in developing vehicle-to-vehicle (V2V) energy-trading protocols, which are crucial for renewable energy utilization, leading to a sustainable future. V2G trading, due to the rapidly increasing energy demand, is straining the power grid, whereas V2V trading can help in this regard by decentralizing the grid, utilizing local resources, and reducing energy cost. Our work focuses on this vital technology, proposes a V2V trading protocol, and presents detailed numerical results on different components. This work lays the groundwork for future research and facilitates further advancements through comparative analysis.

There are some limitations in our study. The interaction between the customers and the charging infrastructure could be made more anonymous. The service charge of the charging facilities and the dynamic nature of the power grid should be considered while making decisions. In the future, we plan to incorporate more practical use-cases into our protocol, such as scheduling charging or discharging sessions, reserving a spot beforehand, making decisions based on road conditions and distance to the CSs, etc. The trade algorithm can also be improved significantly by considering local and national energy buying/selling prices. The security analysis could include formal validation and attack scenario simulations. Experiments can be carried out in a cluster of computers instead of a single one for more realistic results. Experiments based on actual hardware implementation is another thing that we are looking forward to doing in the future.