CO2 Storage in Subsurface Formations: Impact of Formation Damage
Abstract
1. Introduction
2. Mathematical Model for Quasi-2D Displacement with Formation Damage
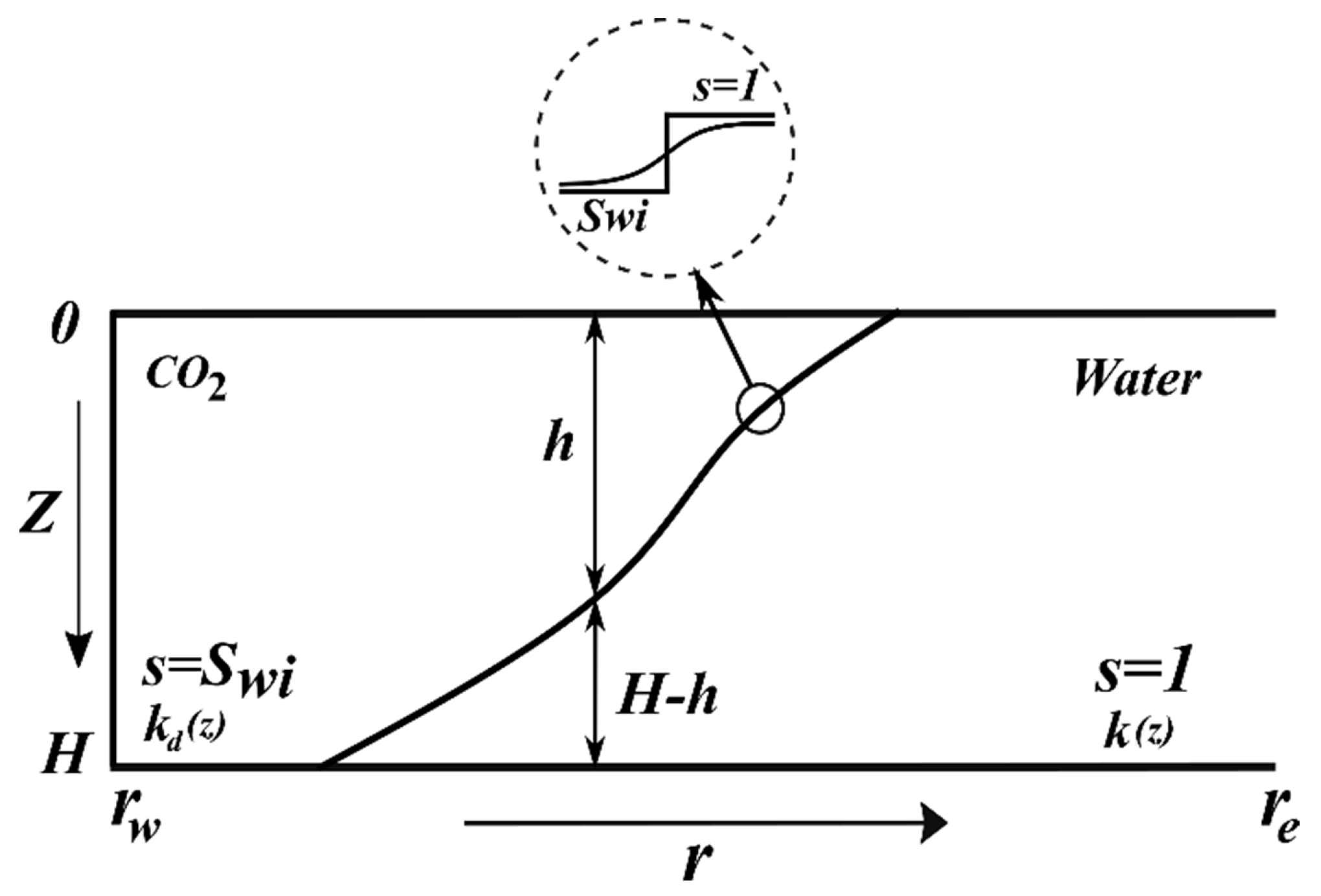
2.1. Assumptions of the Model
2.2. Governing 2D Equations
2.3. Dietz’s Model for Pseudo-Fractional Flow in a Layer-Cake Reservoir
3. Analytical Model
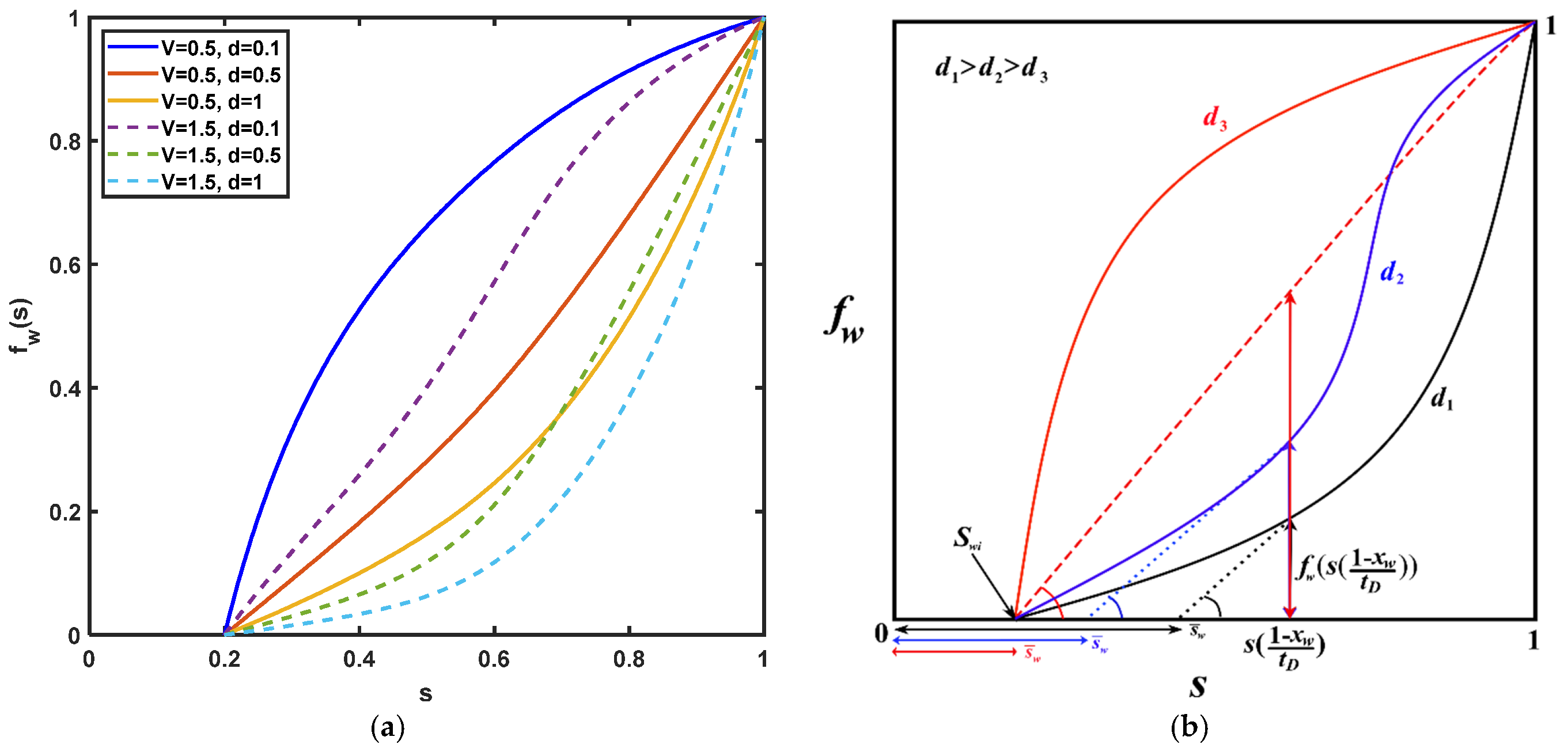
3.1. Self-Similar Solution
3.2. Average Water Saturation and Sweep Coefficient
3.3. Impedance and Skin Factor Calculations
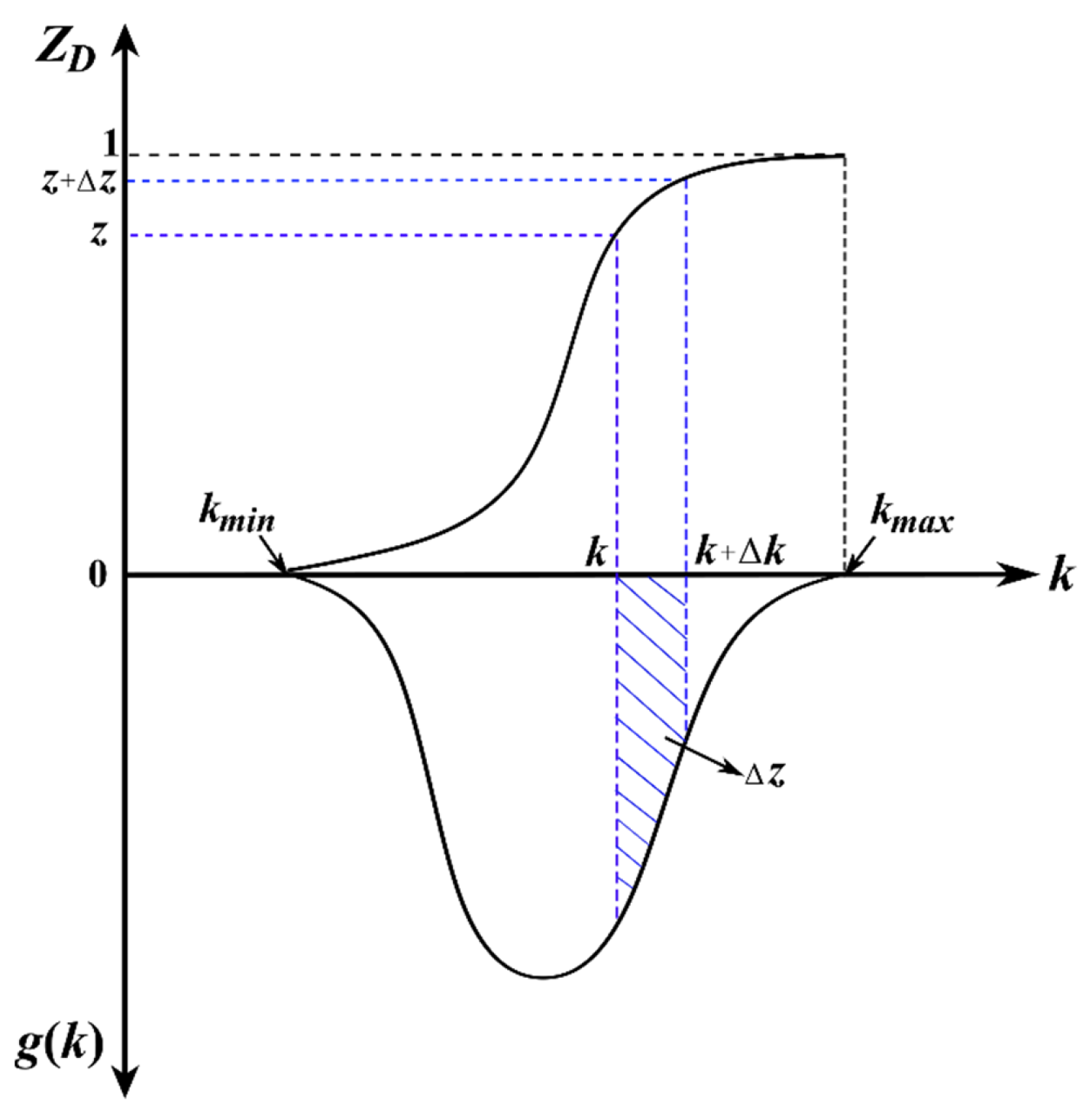
4. Practical Calculations: Power-Law Permeability Profiles
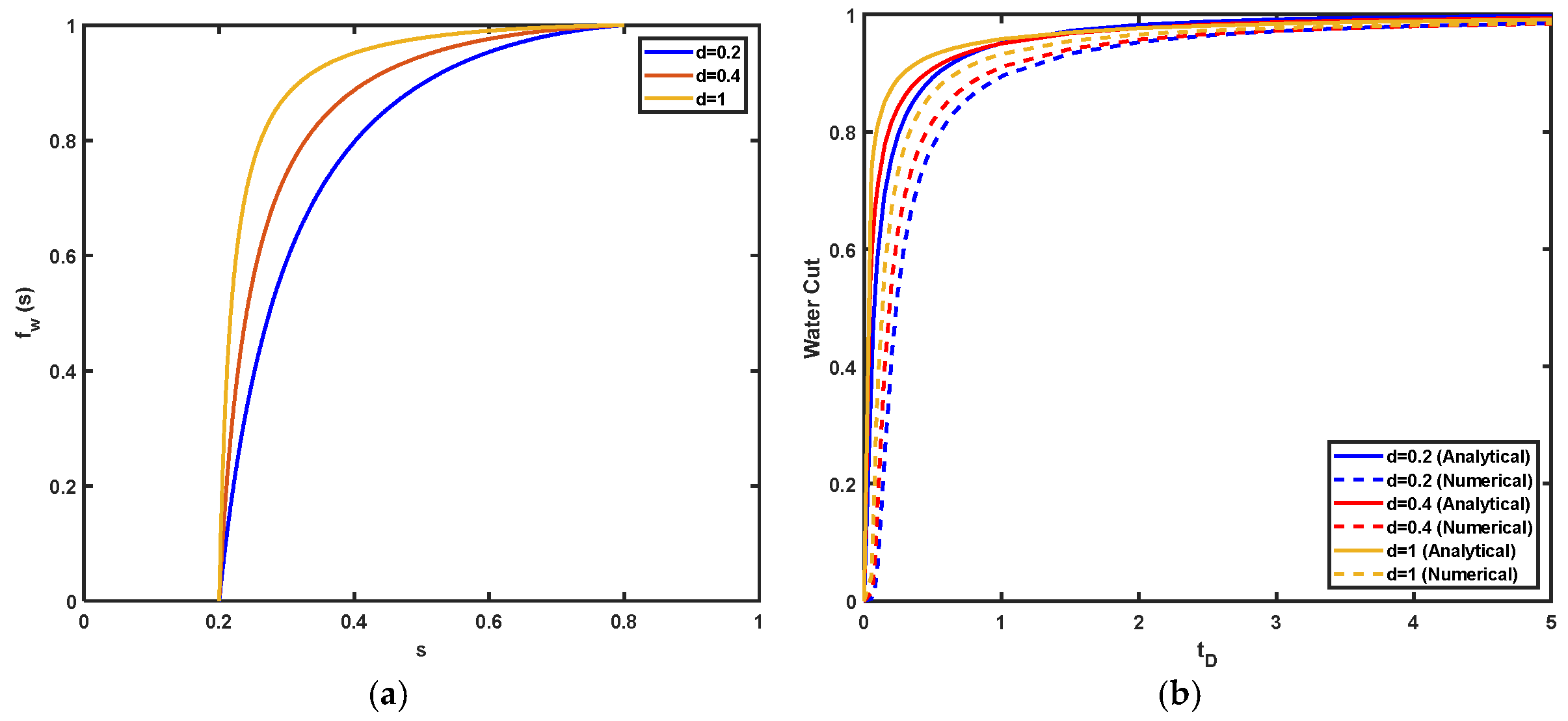
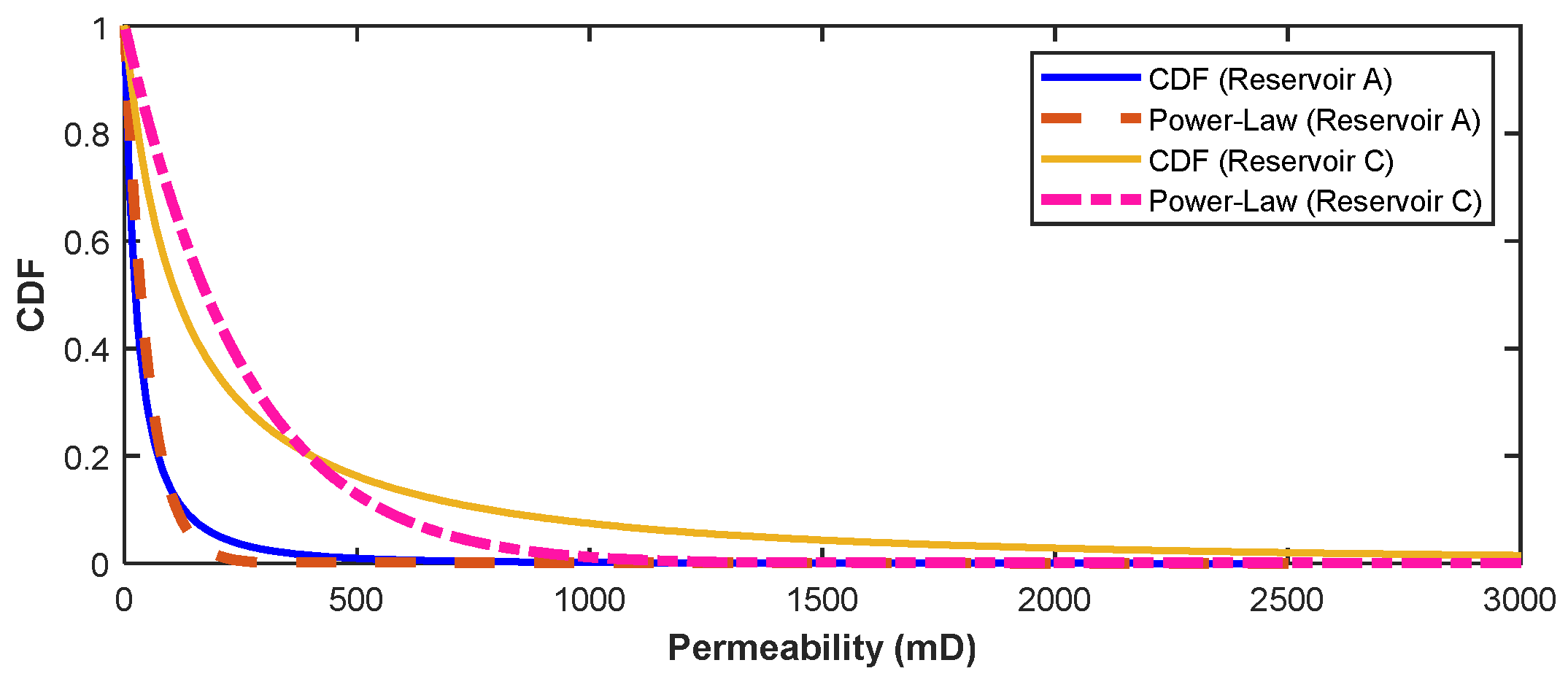
5. Validation of the Analytical Model
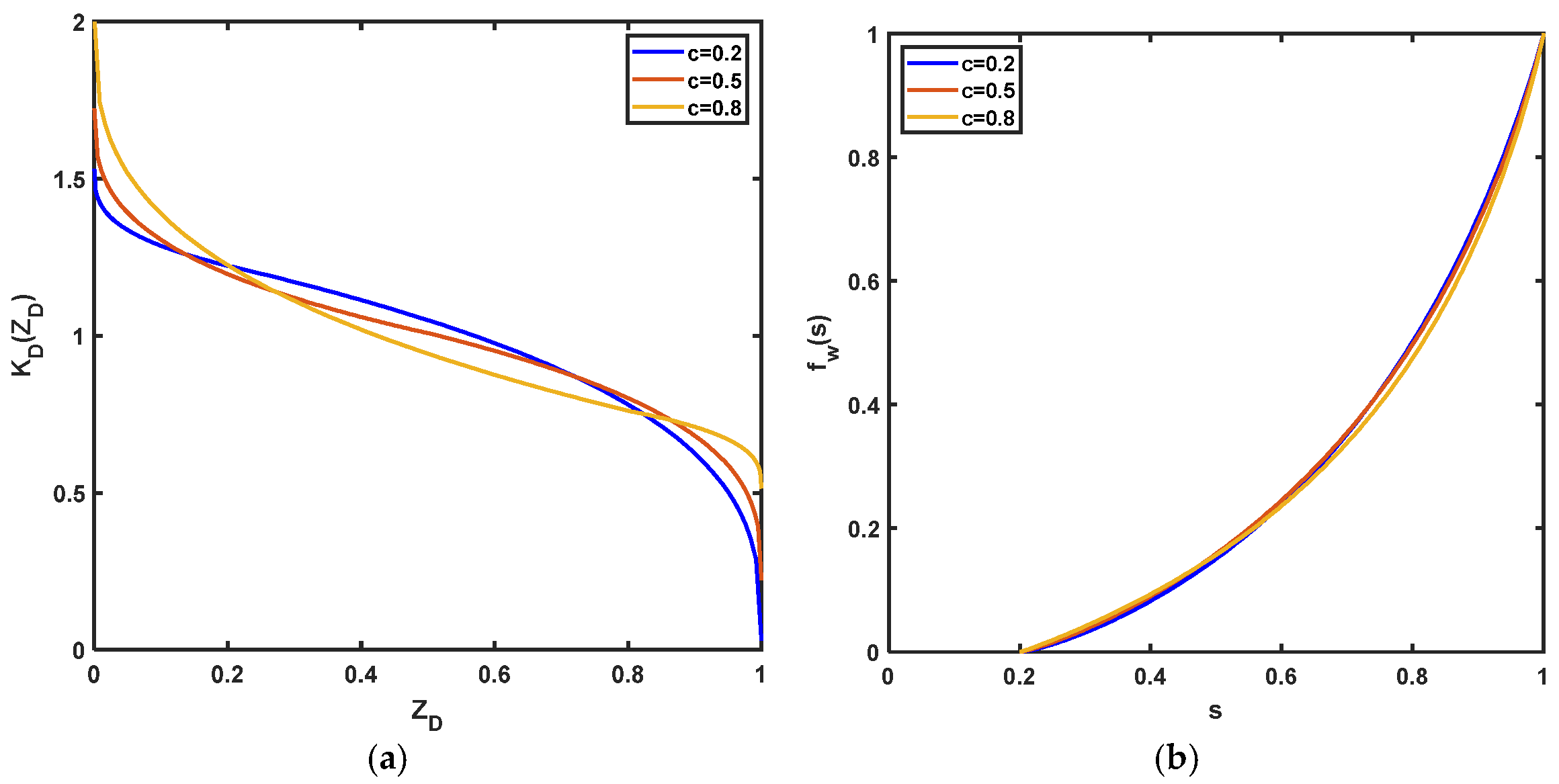
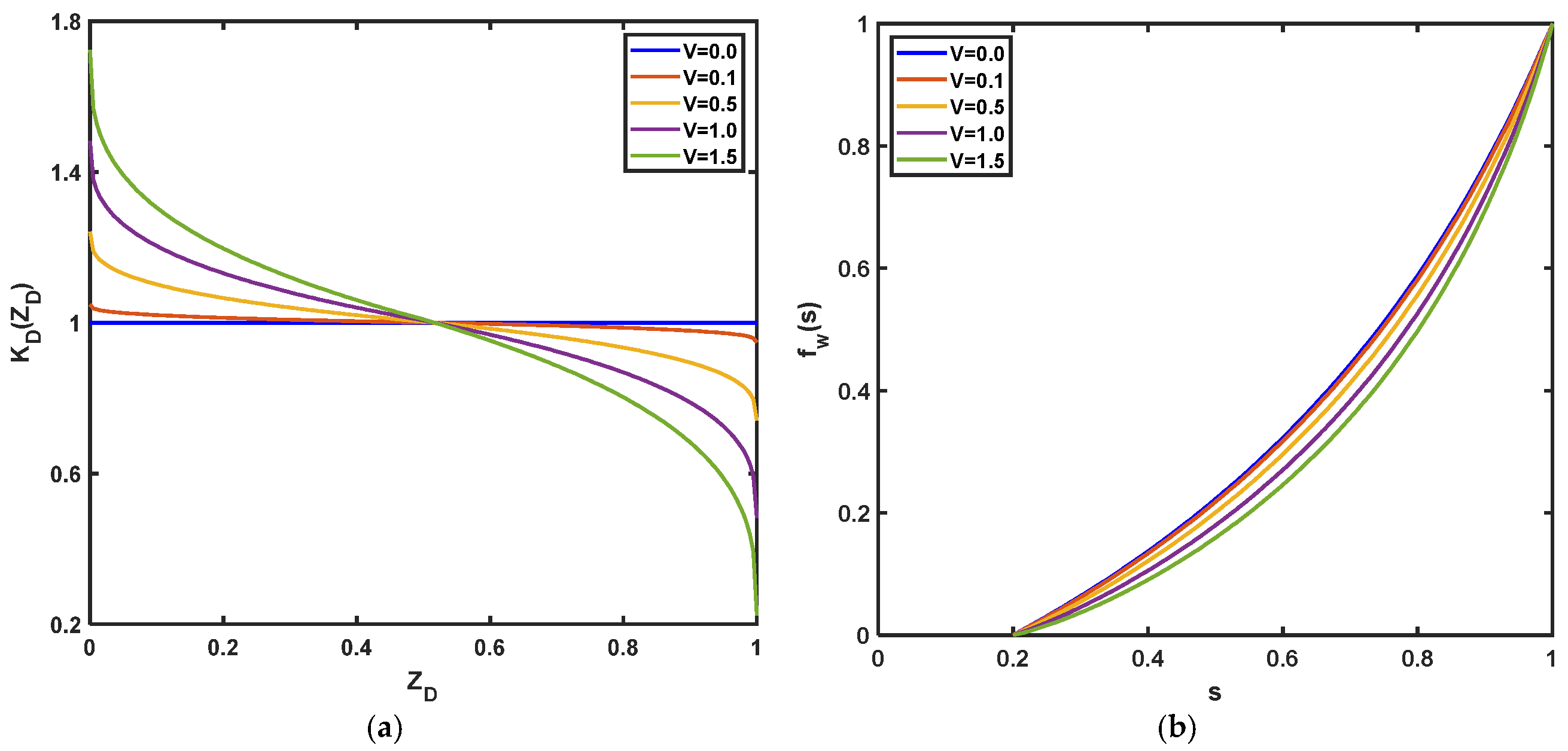
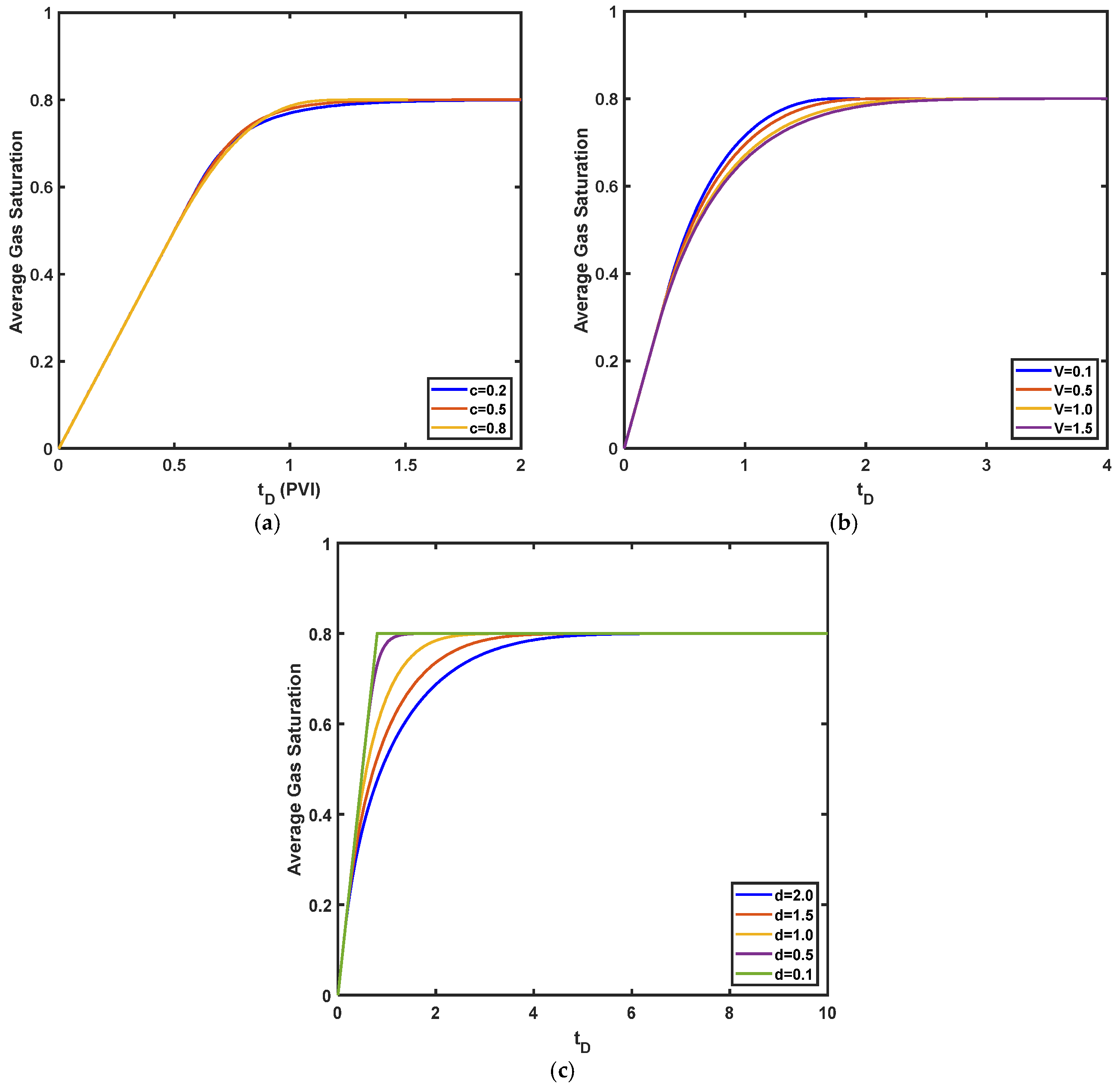
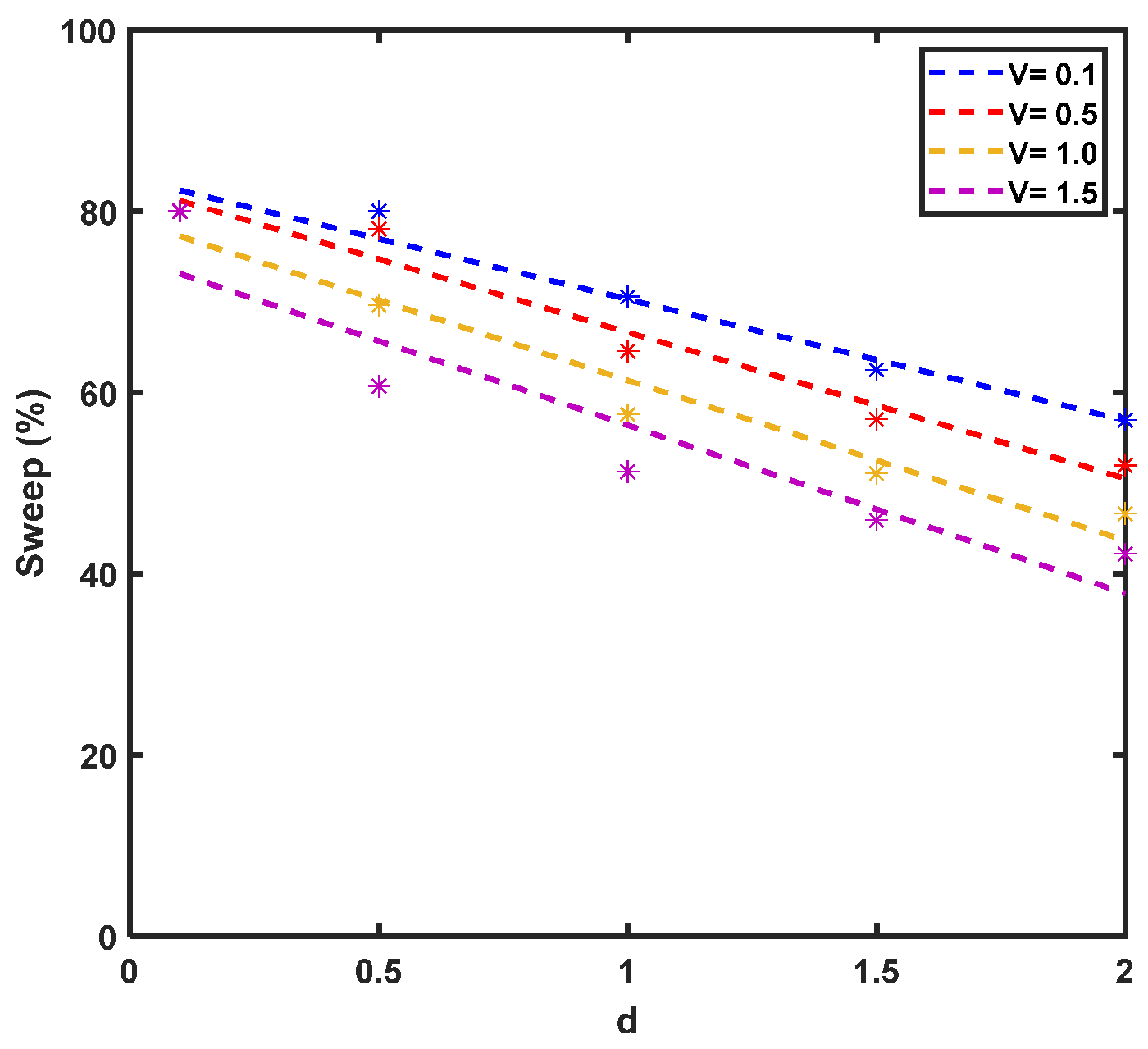
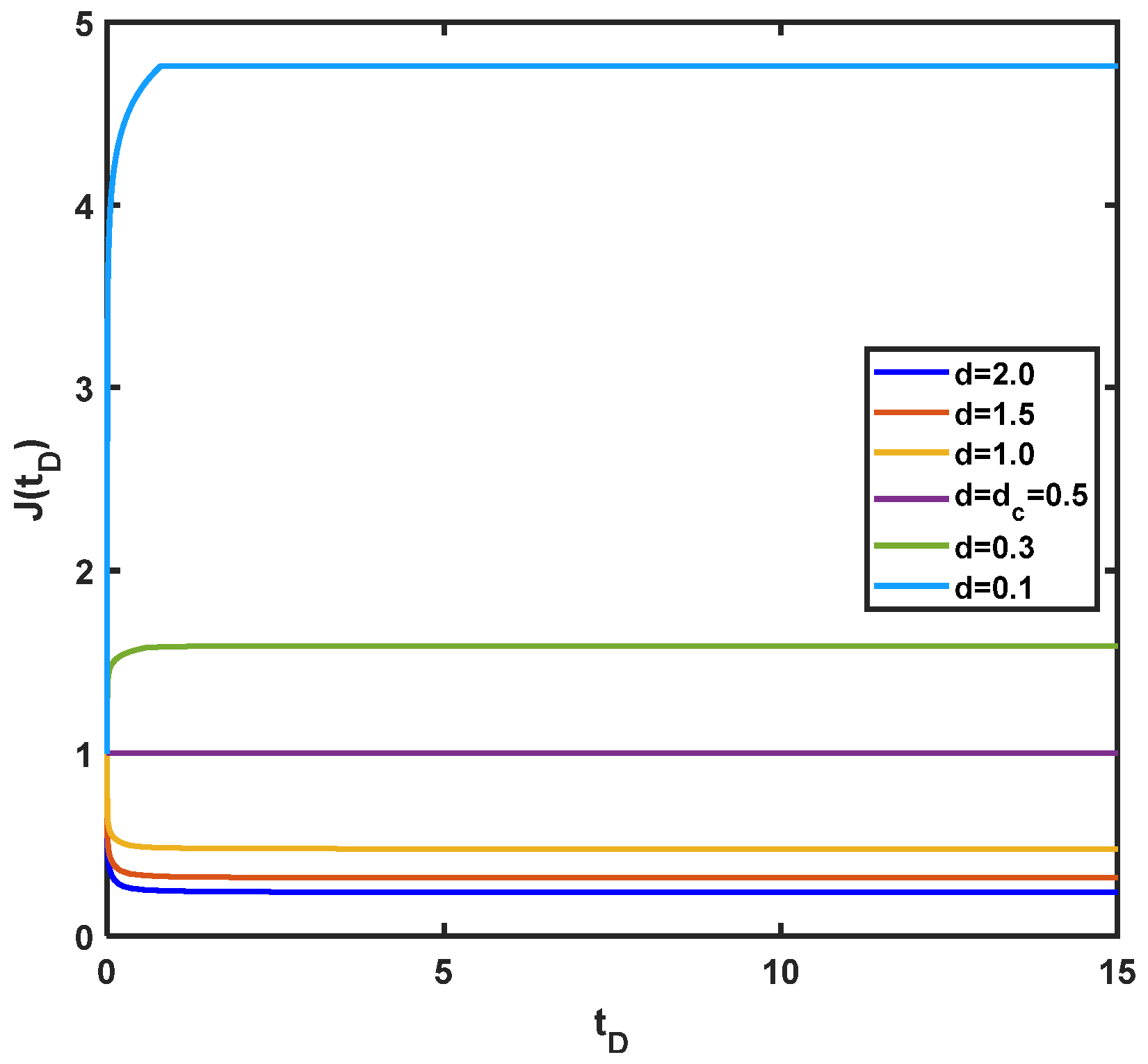
6. Results of Analytical Modelling
7. Field Case
8. Discussions
9. Conclusive Remarks
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Parameters | |
| Adjustable parameter in power-law profile, [-] | |
| Inflection point in power-law profile, [-] | |
| Constants of the integrals, [-] | |
| Formation damage factor, [-] | |
| Velocity of the front at 100% water saturation, [-] | |
| Velocity of the front at irreducible water saturation, [-] | |
| Fractional flow of water, [-] | |
| Probability distribution function of permeability, [-] | |
| Total height of reservoir, [L] | |
| Height of gas, [L] | |
| Dimensionless height of gas, [-] | |
| Well impedance, [-] | |
| Gas relative permeability at irreducible water saturation, [-] | |
| Water relative permeability, [-] | |
| Horizontal permeability as a function of depth, [L2] | |
| Horizontal damaged permeability as a function of depth, [L2] | |
| Horizontal permeability as a function of dimensionless depth, [L2] | |
| Dimensionless horizontal permeability as a function of dimensionless depth, [-] | |
| Dimensionless damaged horizontal permeability as a function of dimensionless depth, [-] | |
| Minimum permeability, [L2] | |
| Maximum permeability, [L2] | |
| Radial permeability, [L2] | |
| Vertical permeability, [L2] | |
| Average permeability, [L2] | |
| Reservoir length, [L] | |
| Core length, [L] | |
| Exponents in power-law profile, [-] | |
| Pressure, [ML−1T−2] | |
| Dimensionless pressure, [-] | |
| Injection rate, [L3T−1] | |
| Radius, [L] | |
| Drainage radius, [L] | |
| Water saturation, [-] | |
| Irreducible water saturation, [-] | |
| Skin factor, [-] | |
| Time, [T] | |
| Dimensionless time, [-] | |
| Permeability stabilization time in terms of PVI, [L3] | |
| Gas flux, [L2T−1] | |
| Water flux, [L2T−1] | |
| Total velocity, [LT−1] | |
| Gas velocity, [LT−1] | |
| Radial gas velocity, [LT−1] | |
| Velocity of gas in z direction, [LT−1] | |
| Water velocity, [LT−1] | |
| Radial water velocity, [LT−1] | |
| Velocity of water in z direction, [LT−1] | |
| Heterogeneity variation, [-] | |
| Dimensionless distance, [-] | |
| Dimensionless position of wellbore radius, [-] | |
| Defined variable, [-] | |
| Depth, [L] | |
| Dimensionless depth, [-] | |
| Dimensionless pressure drops, [-] | |
| Greek Symbols | |
| Injectivity index, [M−1L4T] | |
| Porosity, [-] | |
| Water viscosity, [ML−1T−1] | |
| Gas viscosity, [ML−1T−1] | |
| Total mobility, [-] | |
| Self-similar variable, [-] | |
| Abbreviations | |
| 1D | One-dimensional |
| 2D | Two-dimensional |
| CDF | Cumulative distribution function |
| EOR | Enhanced oil recovery |
| FFC | Fractional flow curve |
| Probability distribution function | |
| PVI | Pore volume injected |
| WGC | Water-Gas Contact |
Appendix A. Derivation of Governing Equations
Appendix B. Buckley–Leverett Solution
Appendix C. Sweep Calculations
Appendix D. Calculations of Dimensionless Pressure Drop (Impedance)
Appendix E. Calculations for Power-Law k(z)
Appendix F. Fractional Flow and Mobility Formula for Power-Law k(z)
References
- Nassan, T.H.; Freese, C.; Baganz, D.; Alkan, H.; Burachok, O.; Solbakken, J.; Zamani, N.; Aarra, M.G.; Amro, M. Integrity Experiments for Geological Carbon Storage (GCS) in Depleted Hydrocarbon Reservoirs: Wellbore Components under Cyclic CO2 Injection Conditions. Energies 2024, 17, 3014. [Google Scholar] [CrossRef]
- Song, Y.; Jun, S.; Na, Y.; Kim, K.; Jang, Y.; Wang, J. Geomechanical challenges during geological CO2 storage: A review. Chem. Eng. J. 2023, 456, 140968. [Google Scholar] [CrossRef]
- Zhang, Y.; Jackson, C.; Krevor, S. An Estimate of the Amount of Geological CO2 Storage over the Period of 1996–2020. Environ. Sci. Technol. Lett. 2022, 9, 693–698. [Google Scholar] [CrossRef]
- Ngata, M.R.; Yang, B.; Aminu, M.D.; Iddphonce, R.; Omari, A.; Shaame, M.; Nyakilla, E.E.; Mwakateba, I.A.; Mwakipunda, G.C.; Yanyi-Akofur, D. Review of Developments in Nanotechnology Application for Formation Damage Control. Energy Fuels 2022, 36, 80–97. [Google Scholar] [CrossRef]
- Ngata, M.R.; Yang, B.; Aminu, M.D.; Emmanuely, B.L.; Said, A.A.; Kalibwami, D.C.; Mwakipunda, G.C.; Ochilov, E.; Nyakilla, E.E. Minireview of Formation Damage Control through Nanotechnology Utilization at Fieldwork Conditions. Energy Fuels 2022, 36, 4174–4185. [Google Scholar] [CrossRef]
- Sbai, M.A.; Azaroual, M. Numerical modeling of formation damage by two-phase particulate transport processes during CO2 injection in deep heterogeneous porous media. Adv. Water Resour. 2011, 34, 62–82. [Google Scholar] [CrossRef]
- Tang, Y.; Hu, S.; He, Y.; Wang, Y.; Wan, X.; Cui, S.; Long, K. Experiment on CO2-brine-rock interaction during CO2 injection and storage in gas reservoirs with aquifer. Chem. Eng. J. 2021, 413, 127567. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, F.; Xu, J.; Qi, Y. Experimental Investigation and Numerical Simulation of CO2–Brine–Rock Interactions during CO2 Sequestration in a Deep Saline Aquifer. Sustainability 2019, 11, 317. [Google Scholar] [CrossRef]
- Khurshid, I.; Choe, J. Analyses of thermal disturbance and formation damages during carbon dioxide injection in shallow and deep reservoirs. Int. J. Oil Gas Coal Technol. 2016, 11, 141–153. [Google Scholar] [CrossRef]
- Baklid, A.; Korbol, R.; Owren, G. Sleipner Vest CO2 Disposal, CO2 Injection into a Shallow Underground Aquifer. In Proceedings of the SPE Annual Technical Conference and Exhibition 1996, Denver, CO, USA, 6–9 October 1996. [Google Scholar]
- Eiken, O.; Ringrose, P.; Hermanrud, C.; Nazarian, B.; Torp, T.A.; Høier, L. Lessons learned from 14 years of CCS operations: Sleipner, In Salah and Snøhvit. Energy Procedia 2011, 4, 5541–5548. [Google Scholar] [CrossRef]
- Hansen, O.; Gilding, D.; Nazarian, B.; Osdal, B.; Ringrose, P.; Kristoffersen, J.-B.; Eiken, O.; Hansen, H. Snøhvit: The History of Injecting and Storing 1 Mt CO2 in the Fluvial Tubåen Fm. Energy Procedia 2013, 37, 3565–3573. [Google Scholar] [CrossRef]
- Ringrose, P.S.; Mathieson, A.S.; Wright, I.W.; Selama, F.; Hansen, O.; Bissell, R.; Saoula, N.; Midgley, J. The In Salah CO2 Storage Project: Lessons Learned and Knowledge Transfer. Energy Procedia 2013, 37, 6226–6236. [Google Scholar] [CrossRef]
- Bjørnarå, T.I.; Bohloli, B.; Park, J. Field-data analysis and hydromechanical modeling of CO2 storage at In Salah, Algeria. Int. J. Greenh. Gas Control 2018, 79, 61–72. [Google Scholar] [CrossRef]
- Ringrose, P. How to Store CO2 Underground: Insights from Early-Mover CCS Projects; Springer International Publishing: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Smith, N.; Boone, P.; Oguntimehin, A.; van Essen, G.; Guo, R.; Reynolds, M.A.; Friesen, L.; Cano, M.-C.; O’Brien, S. Quest CCS facility: Halite damage and injectivity remediation in CO2 injection wells. Int. J. Greenh. Gas Control 2022, 119, 103718. [Google Scholar] [CrossRef]
- Russell, T.; Wong, K.; Zeinijahromi, A.; Bedrikovetsky, P. Effects of delayed particle detachment on injectivity decline due to fines migration. J. Hydrol. 2018, 564, 1099–1109. [Google Scholar] [CrossRef]
- Chequer, L.; Nguyen, C.; Loi, G.; Zeinijahromi, A.; Bedrikovetsky, P. Fines migration in aquifers: Production history treatment and well behaviour prediction. J. Hydrol. 2021, 602, 126660. [Google Scholar] [CrossRef]
- Ge, J.; Zhang, X.; Le-Hussain, F. Fines migration and mineral reactions as a mechanism for CO2 residual trapping during CO2 sequestration. Energy 2022, 239, 122233. [Google Scholar] [CrossRef]
- Ge, J.; Zhang, X.; Liu, J.; Almutairi, A.; Le-Hussain, F. Influence of capillary pressure boundary conditions and hysteresis on CO2-water relative permeability. Fuel 2022, 321, 124132. [Google Scholar] [CrossRef]
- Wang, Y.; Bedrikovetsky, P.; Yin, H.; Othman, F.; Zeinijahromi, A.; Le-Hussain, F. Analytical model for fines migration due to mineral dissolution during CO2 injection. J. Nat. Gas Sci. Eng. 2022, 100, 104472. [Google Scholar] [CrossRef]
- Wang, Y.; Almutairi, A.L.Z.; Bedrikovetsky, P.; Timms, W.A.; Privat, K.L.; Bhattacharyya, S.K.; Le-Hussain, F. In-situ fines migration and grains redistribution induced by mineral reactions—Implications for clogging during water injection in carbonate aquifers. J. Hydrol. 2022, 614, 128533. [Google Scholar] [CrossRef]
- Hajiabadi, S.H.; Bedrikovetsky, P.; Borazjani, S.; Mahani, H. Well Injectivity during CO2 Geosequestration: A Review of Hydro-Physical, Chemical, and Geomechanical Effects. Energy Fuels 2021, 35, 9240–9267. [Google Scholar] [CrossRef]
- Milad, B.; Moghanloo, R.G.; Hayman, N.W. Assessing CO2 geological storage in Arbuckle Group in northeast Oklahoma. Fuel 2024, 356, 129323. [Google Scholar] [CrossRef]
- Dietz, D. A theoretical approach to the problem of encroaching and by-passing edge water. In Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen; Elsevier: Amsterdam, The Netherlands, 1953; pp. 83–92. [Google Scholar]
- Hearn, C.L. Simulation of Stratified Waterflooding by Pseudo Relative Permeability Curves. J. Pet. Technol. 1971, 23, 805–813. [Google Scholar] [CrossRef]
- Ingsøy, P.; Gauchet, R.; Lake, L.W. Pseudofunctions and Extended Dietz Theory for Gravity-Segregated Displacement in Stratified Reservoirs. SPE Reserv. Eng. 1994, 9, 67–72. [Google Scholar] [CrossRef]
- Yuan, H.; Shapiro, A.A. Induced migration of fines during waterflooding in communicating layer-cake reservoirs. J. Pet. Sci. Eng. 2011, 78, 618–626. [Google Scholar] [CrossRef]
- Zhang, X.; Shapiro, A.; Stenby, E.H. Upscaling of Two-Phase Immiscible Flows in Communicating Stratified Reservoirs. Transp. Porous Media 2011, 87, 739–764. [Google Scholar] [CrossRef]
- Bedrikovetsky, P. Mathematical Theory of Oil and Gas Recovery: With Applications to Ex-USSR Oil and Gas Fields; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 4. [Google Scholar]
- Bruining, H. Upscaling of Single-and Two-Phase Flow in Reservoir Engineering; CRC Press: London, UK, 2021; p. 238. [Google Scholar]
- Kurbanov, A. On some generalization of the equations of flow of a two-phase liquid in porous media. Collect. Res. Pap. Oil Recovery VNINeft 1961, 15, 32–38. [Google Scholar]
- Fayers, F.J.; Muggeridge, A.H. Extensions to Dietz Theory and Behavior of Gravity Tongues in Slightly Tilted Reservoirs. SPE Reserv. Eng. 1990, 5, 487–494. [Google Scholar] [CrossRef]
- Yortsos, Y.C. Analytical Studies for Processes at Vertical Equilibrium. In Proceedings of the ECMOR III—3rd European Conference on the Mathematics of Oil Recovery, European Association of Geoscientists & Engineers, Delft, The Netherlands, 17–19 June 1992. [Google Scholar]
- Yortsos, Y.C. A theoretical analysis of vertical flow equilibrium. Transp. Porous Media 1995, 18, 107–129. [Google Scholar] [CrossRef]
- Kurbanov, A.; Atanov, G. On the problem of oil displacement by water from heterogeneous reservoirs. Oil Gas Tyumen Collect. Res. 1972, 13, 36–38. [Google Scholar]
- Kanevskaya, R.D. Asymptotic analysis of the effect of capillary and gravity forces on the two-dimensional transport of two-phase systems in a porous medium. Fluid Dyn. 1988, 23, 557–563. [Google Scholar] [CrossRef]
- Lake, L.W. Enhanced Oil Recovery; Prentice Hall: Englewood Cliffs, NJ, USA, 1989; p. 550. [Google Scholar]
- Polyanin, A.D.; Zaitsev, V.F. Handbook of Nonlinear Partial Differential Equations: Exact Solutions, Methods, and Problems, 2nd ed.; CRC Press: New York, NY, USA, 2012; p. 1912. [Google Scholar]
- Shokrollahi, A.; Prempeh, K.O.K.; Mobasher, S.S.; George, P.W.; Zulkifli, N.N.; Zeinijahromi, A.; Bedrikovetsky, P. Formation Damage during CO2 Storage: Analytical Model, Field Cases. In Proceedings of the SPE International Conference and Exhibition on Formation Damage Control, 2024, Lafayette, LA, USA, 21–23 February 2024. [Google Scholar]
- Economides, M.J.; Hill, A.D.; Ehlig-Economides, C.; Zhu, D. Petroleum Production Systems, 2nd ed.; Pearson Education: New York, NY, USA, 2013. [Google Scholar]
- Logan, J.D. An Introduction to Nonlinear Partial Differential Equations; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 89, p. 416. [Google Scholar]
- Polyanin, A.D.; Manzhirov, A.V. Handbook of Mathematics for Engineers and Scientists, 1st ed.; CRC Press: New York, NY, USA, 2006; p. 1544. [Google Scholar]
- Hussain, S.T.; Regenauer-Lieb, K.; Zhuravljov, A.; Hussain, F.; Rahman, S.S. Asymptotic hydrodynamic homogenization and thermodynamic bounds for upscaling multiphase flow in porous media. Adv. Geo-Energy Res. 2023, 9, 38–53. [Google Scholar] [CrossRef]
- Cheng, K.B.; Rabinovich, A. Optimization-based upscaling for gravity segregation with 3D capillary heterogeneity effects. J. Hydrol. 2021, 603, 127062. [Google Scholar] [CrossRef]
- Moreno, Z.; Anto-Darkwah, E.; Rabinovich, A. Semi-Analytical Modeling of Rate-Dependent Relative Permeability in Heterogeneous Formations. Water Resour. Res. 2021, 57, e2021WR029710. [Google Scholar] [CrossRef]
- Tan, Y.; Li, Y.; Rijken, M.C.M.; Zaki, K.; Wang, B.; Wu, R.; Karazincir, O.; Williams, W. Modeling of Production Decline Caused by Fines Migration in Deepwater Reservoirs. SPE J. 2020, 25, 391–405. [Google Scholar] [CrossRef]
- Carpenter, C. Fines Migration in Fractured Wells: Integrating Modeling with Field and Laboratory Data. J. Pet. Technol. 2015, 67, 129–132. [Google Scholar] [CrossRef]
- Othman, F.; Wang, Y.; Le-Hussain, F. The Effect of Fines Migration During CO2 Injection Using Pore-Scale Characterization. SPE J. 2019, 24, 2804–2821. [Google Scholar] [CrossRef]
- Alchin, L.; Lymn, A.; Russell, T.; Badalyan, A.; Bedrikovetsky, P.; Zeinijahromi, A. Near-Wellbore Damage Associated with Formation Dry-Out and Fines Migration During CO2 Injection. In Proceedings of the SPE Asia Pacific Oil & Gas Conference and Exhibition, 2022, Adelaide, Australia, 17–19 October 2022. [Google Scholar]
- Izgec, O.; Demiral, B.; Bertin, H.; Akin, S. CO2 injection into saline carbonate aquifer formations I: Laboratory investigation. Transp. Porous Media 2008, 72, 1–24. [Google Scholar] [CrossRef]
- Yu, Z.; Liu, L.; Yang, S.; Li, S.; Yang, Y. An experimental study of CO2–brine–rock interaction at in situ pressure–temperature reservoir conditions. Chem. Geol. 2012, 326–327, 88–101. [Google Scholar] [CrossRef]
- Jeddizahed, J.; Rostami, B. Experimental investigation of injectivity alteration due to salt precipitation during CO2 sequestration in saline aquifers. Adv. Water Resour. 2016, 96, 23–33. [Google Scholar] [CrossRef]
- Sim, S.S.K.; Takabayashi, K.; Okatsu, K.; Fisher, D. Asphaltene-Induced Formation Damage: Effect of Asphaltene Particle Size and Core Permeability. In Proceedings of the SPE Annual Technical Conference and Exhibition, 2005, Dallas, TX, USA, 9–12 October 2005. [Google Scholar]
- Kalantari Dahaghi, A.; Gholami, V.; Moghadasi, J.; Abdi, R. Formation Damage Through Asphaltene Precipitation Resulting from CO2 Gas Injection in Iranian Carbonate Reservoirs. SPE Prod. Oper. 2008, 23, 210–214. [Google Scholar] [CrossRef]
- Rabinovich, A.; Anto-Darkwah, E.; Mishra, A.M. Determining Characteristic Relative Permeability from Coreflooding Experiments: A Simplified Model Approach. Water Resour. Res. 2019, 55, 8666–8690. [Google Scholar] [CrossRef]
- Valavanides, M.S. Flow Rate Dependency of Steady-State Two-Phase Flows in Pore Networks: Universal, Relative Permeability Scaling Function and System-Characteristic Invariants. Transp. Porous Media 2023, 150, 521–557. [Google Scholar] [CrossRef]
- Sokama-Neuyam, Y.A.; Yusof, M.A.M.; Owusu, S.K.; Darkwah-Owusu, V.; Turkson, J.N.; Otchere, A.S.; Ursin, J.R. Experimental and theoretical investigation of the mechanisms of drying during CO2 injection into saline reservoirs. Sci. Rep. 2023, 13, 9155. [Google Scholar] [CrossRef] [PubMed]
- Chequer, L.; Vaz, A.; Bedrikovetsky, P. Injectivity decline during low-salinity waterflooding due to fines migration. J. Pet. Sci. Eng. 2018, 165, 1054–1072. [Google Scholar] [CrossRef]
- Nunes, M.; Bedrikovetsky, P.; Newbery, B.; Paiva, R.; Furtado, C.; de Souza, A.L. Theoretical Definition of Formation Damage Zone with Applications to Well Stimulation. J. Energy Resour. Technol. 2010, 132, 033101. [Google Scholar] [CrossRef]
- Kalantariasl, A.; Zeinijahromi, A.; Bedrikovetsky, P. Axi-Symmetric Two-Phase Suspension-Colloidal Flow in Porous Media during Water Injection. Ind. Eng. Chem. Res. 2014, 53, 15763–15775. [Google Scholar] [CrossRef]
- Yuan, B.; Moghanloo, R.G. Nanofluid Precoating: An Effective Method to Reduce Fines Migration in Radial Systems Saturated with Two Mobile Immiscible Fluids. SPE J. 2018, 23, 998–1018. [Google Scholar] [CrossRef]
- Yuan, B.; Moghanloo, R.G.; Wang, W. Using nanofluids to control fines migration for oil recovery: Nanofluids co-injection or nanofluids pre-flush? A comprehensive answer. Fuel 2018, 215, 474–483. [Google Scholar] [CrossRef]
- Ajoma, E.; Sungkachart, T.; Saira, -.; Yin, H.; Le-Hussain, F. A Laboratory Study of Coinjection of Water and CO2 to Improve Oil Recovery and CO2 Storage: Effect of Fraction of CO2 Injected. SPE J. 2021, 26, 2139–2147. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shokrollahi, A.; Mobasher, S.S.; Prempeh, K.O.K.; George, P.W.; Zeinijahromi, A.; Farajzadeh, R.; Zulkifli, N.N.; Mahammad Amir, M.I.; Bedrikovetsky, P. CO2 Storage in Subsurface Formations: Impact of Formation Damage. Energies 2024, 17, 4214. https://doi.org/10.3390/en17174214
Shokrollahi A, Mobasher SS, Prempeh KOK, George PW, Zeinijahromi A, Farajzadeh R, Zulkifli NN, Mahammad Amir MI, Bedrikovetsky P. CO2 Storage in Subsurface Formations: Impact of Formation Damage. Energies. 2024; 17(17):4214. https://doi.org/10.3390/en17174214
Chicago/Turabian StyleShokrollahi, Amin, Syeda Sara Mobasher, Kofi Ohemeng Kyei Prempeh, Parker William George, Abbas Zeinijahromi, Rouhi Farajzadeh, Nazliah Nazma Zulkifli, Mohammad Iqbal Mahammad Amir, and Pavel Bedrikovetsky. 2024. "CO2 Storage in Subsurface Formations: Impact of Formation Damage" Energies 17, no. 17: 4214. https://doi.org/10.3390/en17174214
APA StyleShokrollahi, A., Mobasher, S. S., Prempeh, K. O. K., George, P. W., Zeinijahromi, A., Farajzadeh, R., Zulkifli, N. N., Mahammad Amir, M. I., & Bedrikovetsky, P. (2024). CO2 Storage in Subsurface Formations: Impact of Formation Damage. Energies, 17(17), 4214. https://doi.org/10.3390/en17174214







