A New Method for Evaluating the Brittleness of Shale Oil Reservoirs in Block Y of Ordos Basin of China
Abstract
1. Introduction
2. Rock Brittleness Evaluation Method Theory
3. Experimental Materials and Method
3.1. Experimental Samples and Instruments
3.2. Experimental Steps
4. Experimental Results and Analysis
4.1. Experimental Results
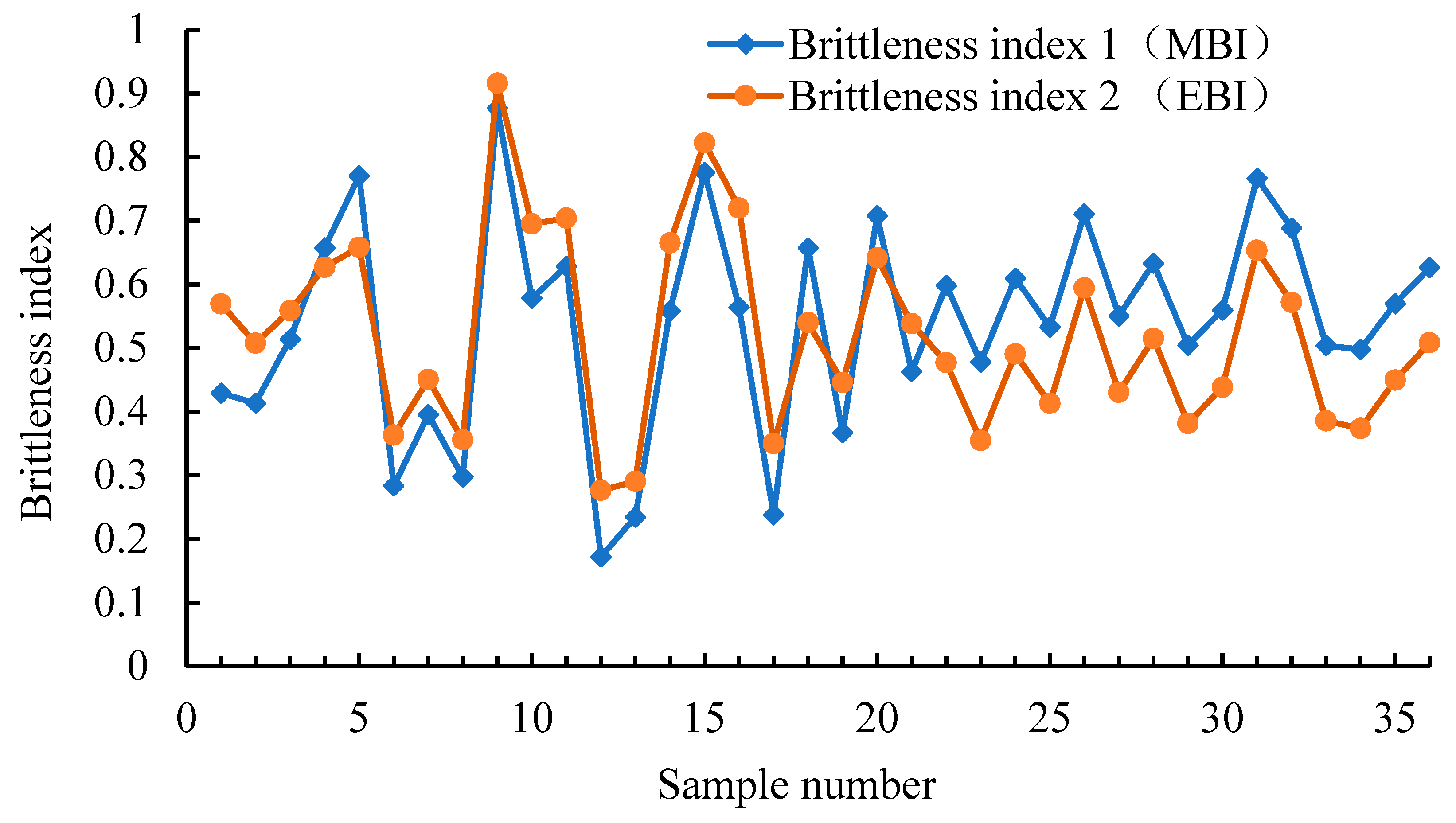
4.2. Research on Brittleness Index Evaluation Methods
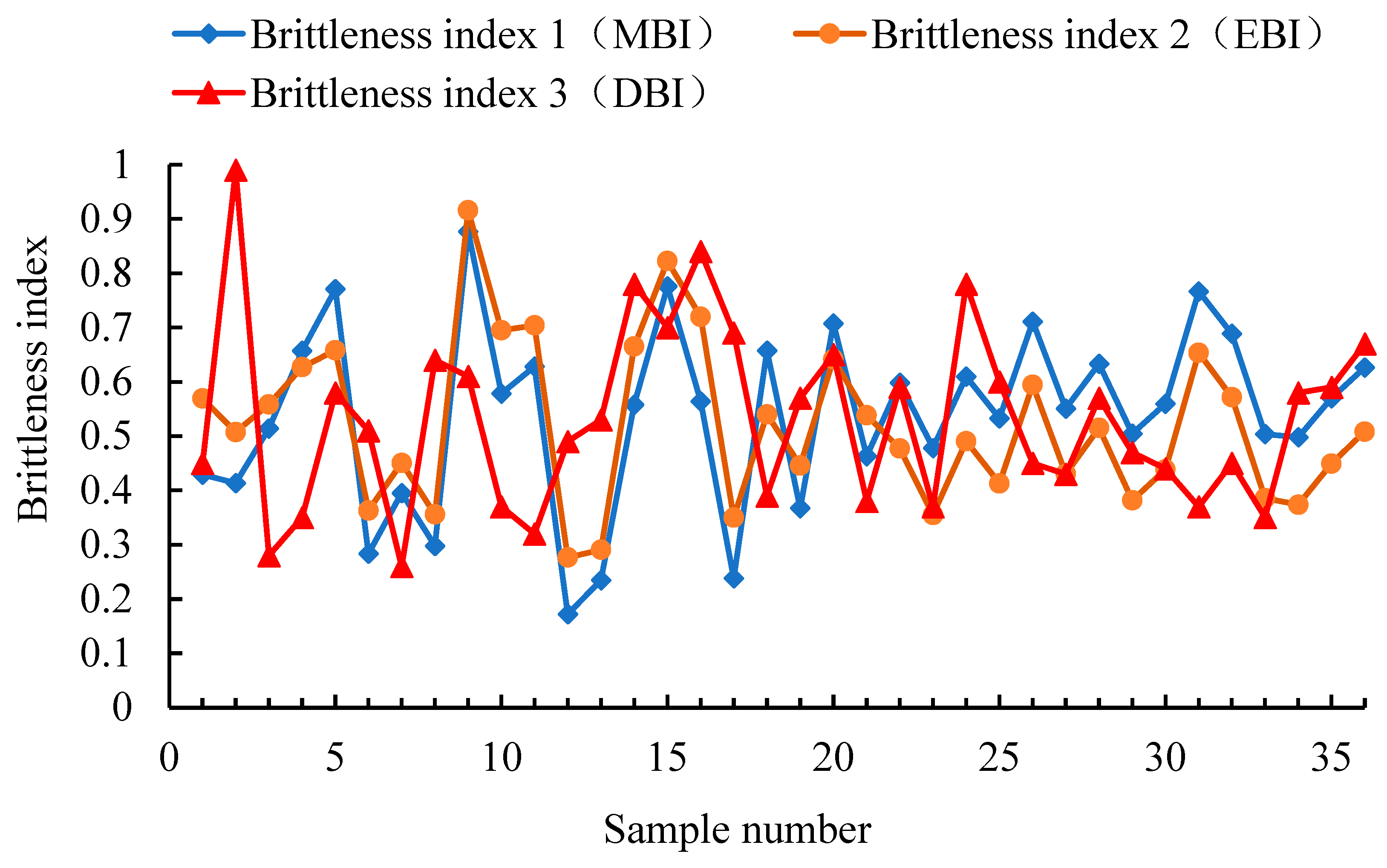
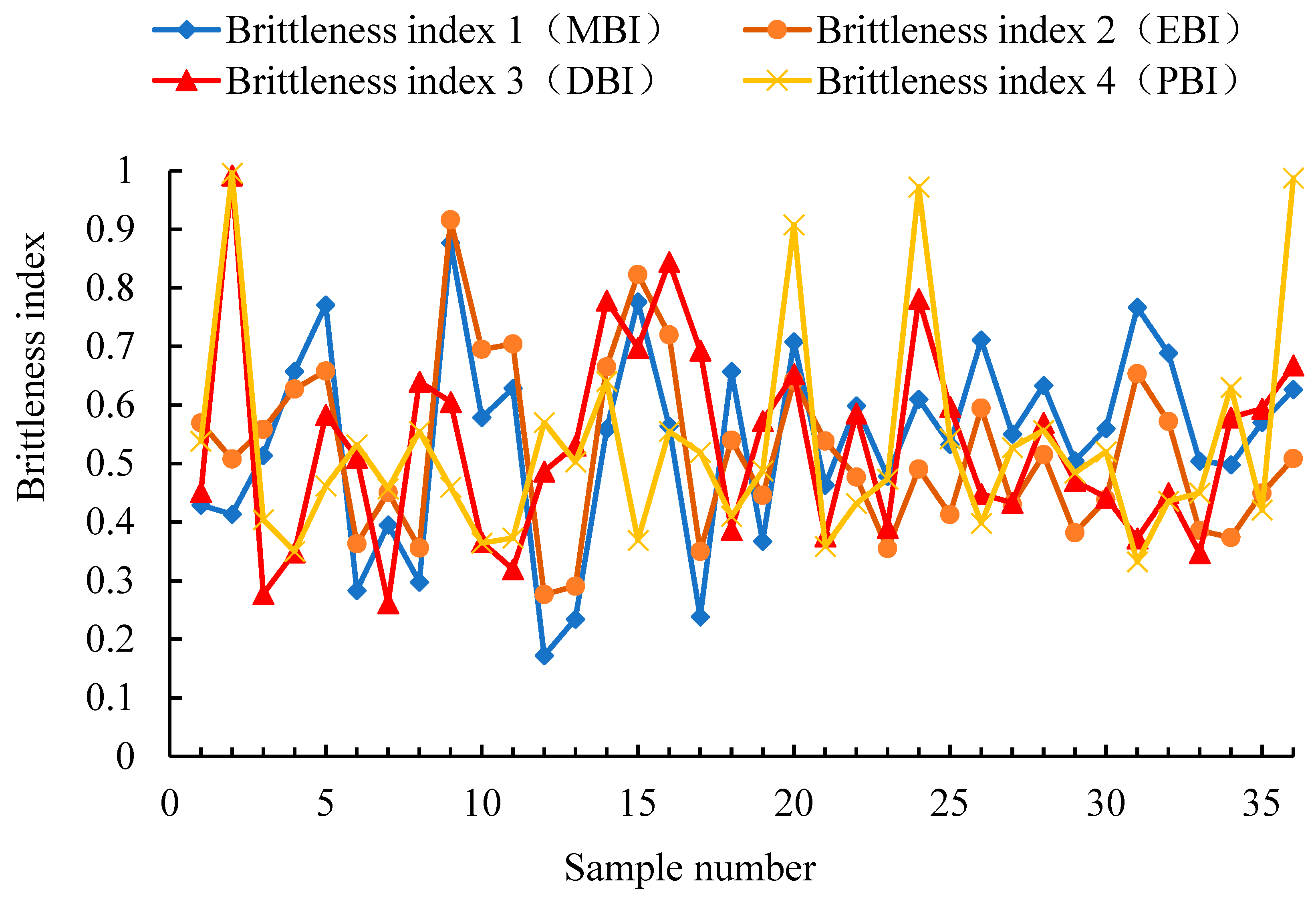
4.3. Research on New Methods for Evaluating Brittleness Index
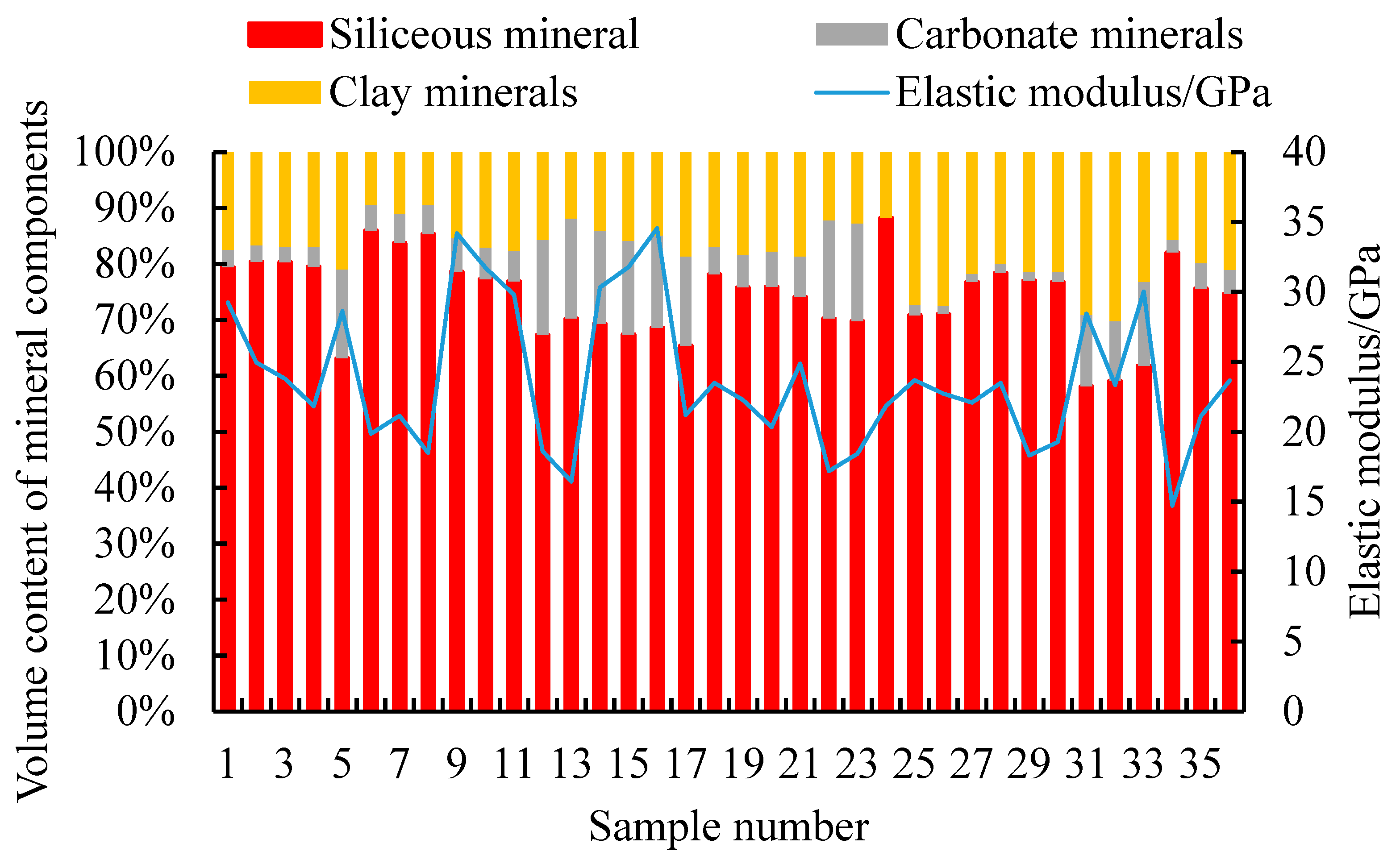
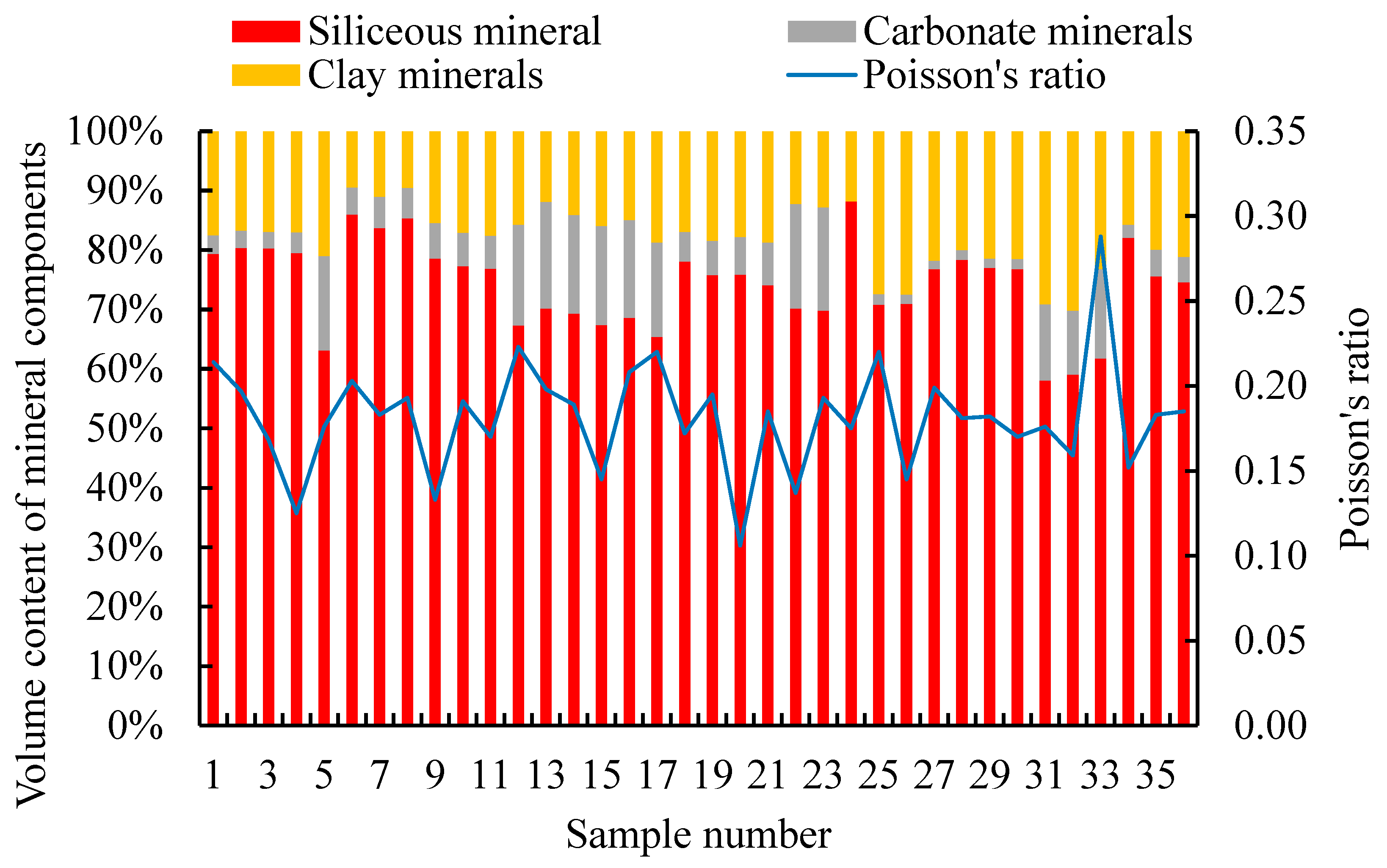
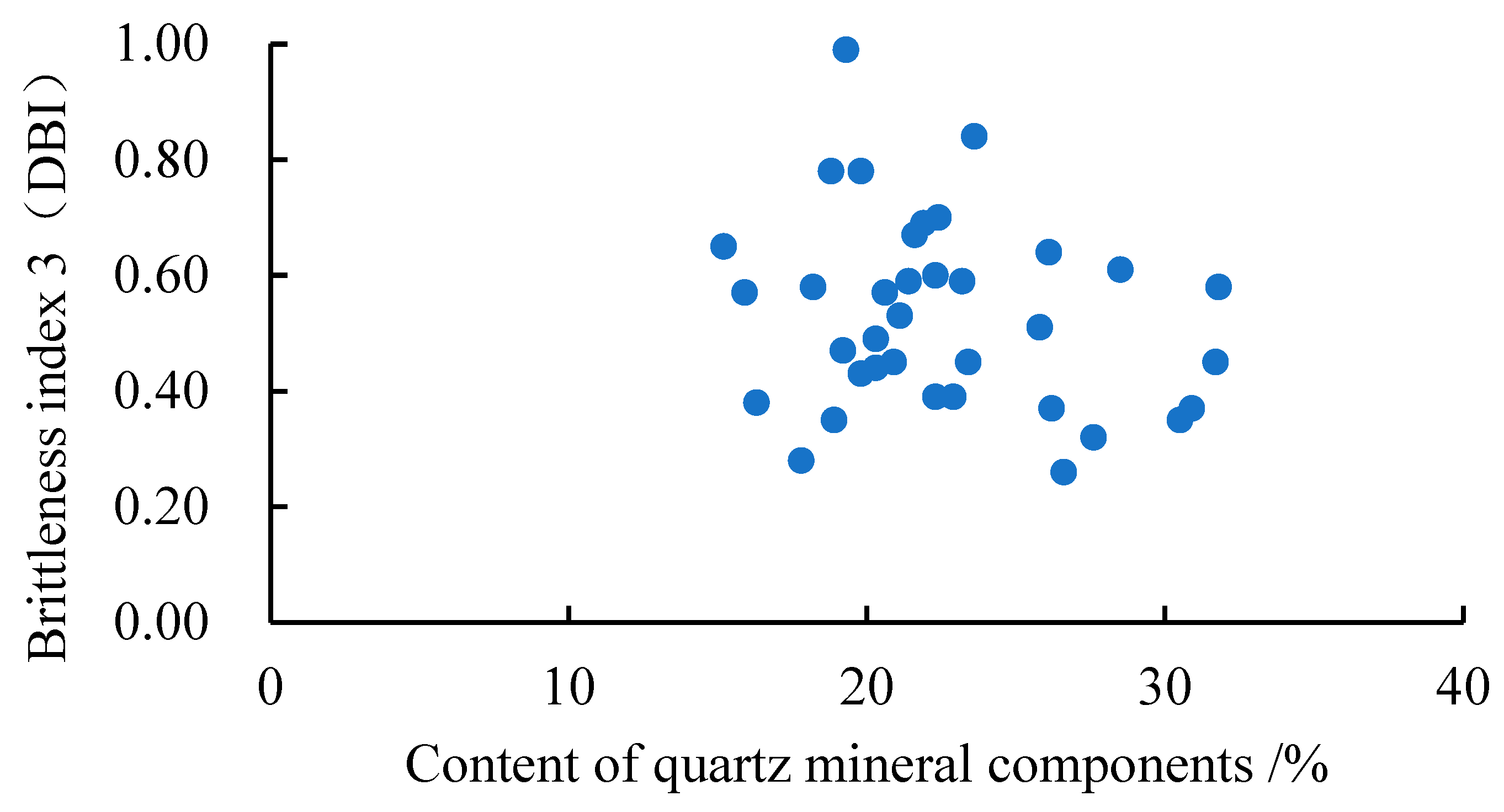
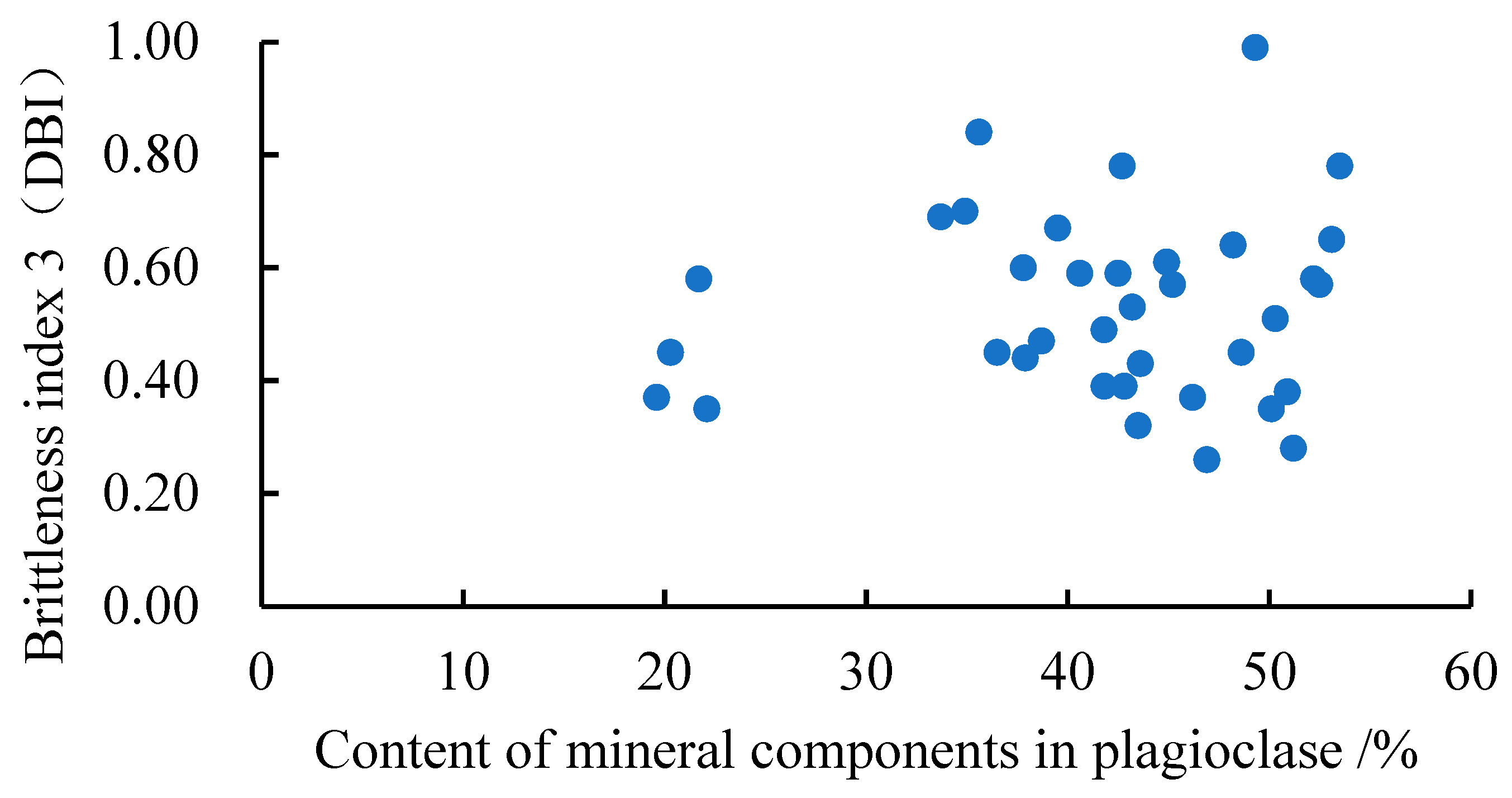
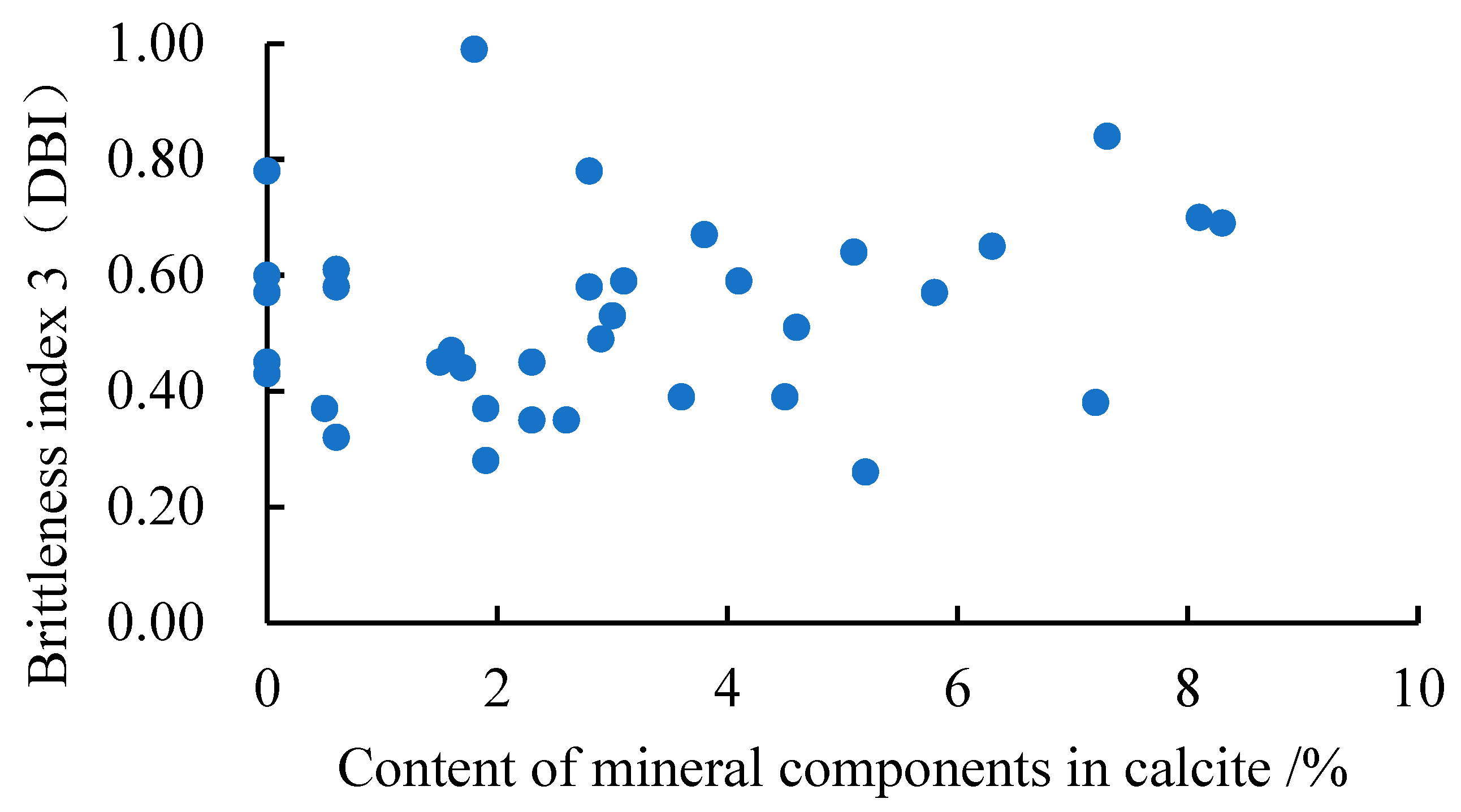
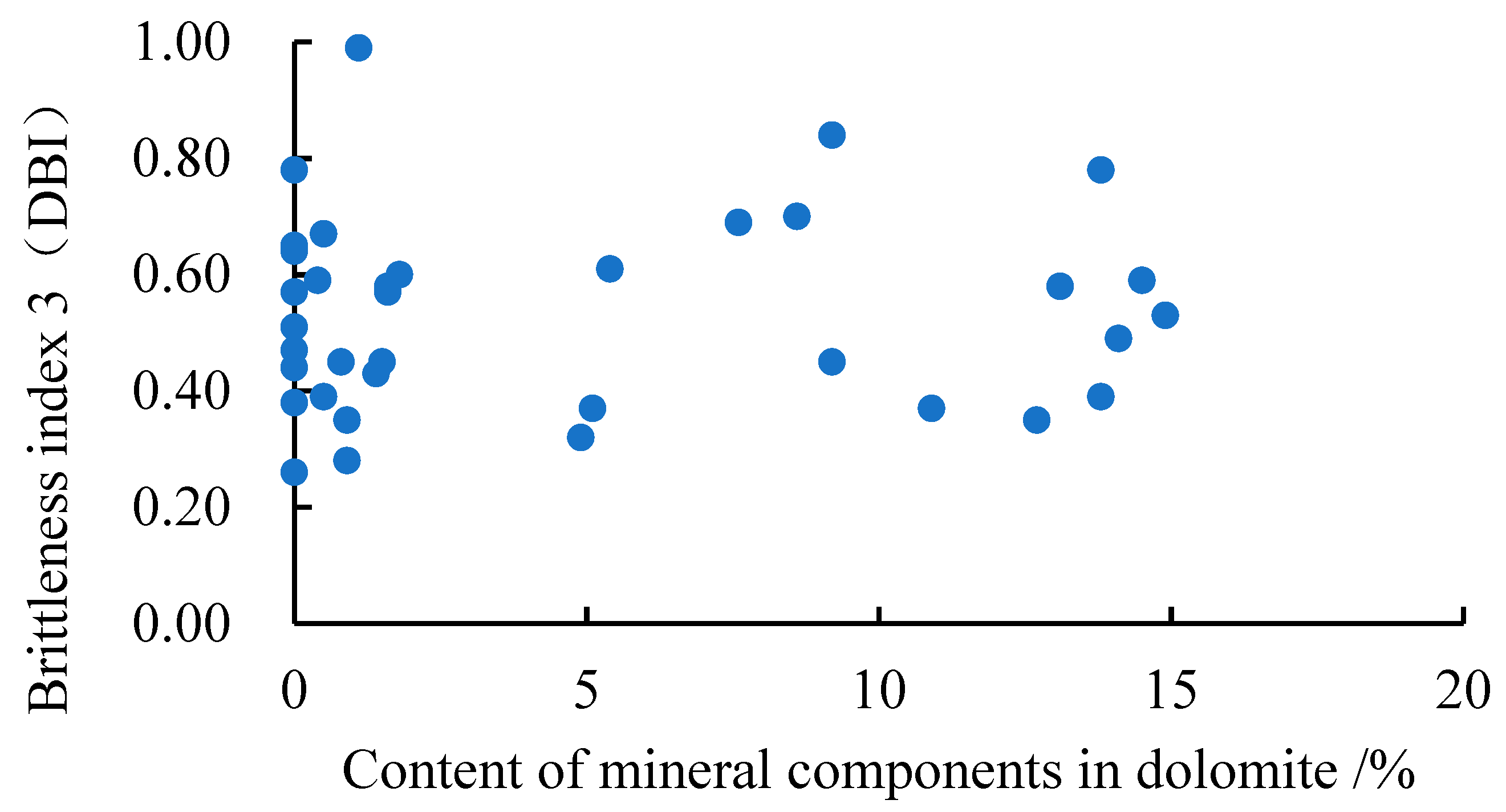
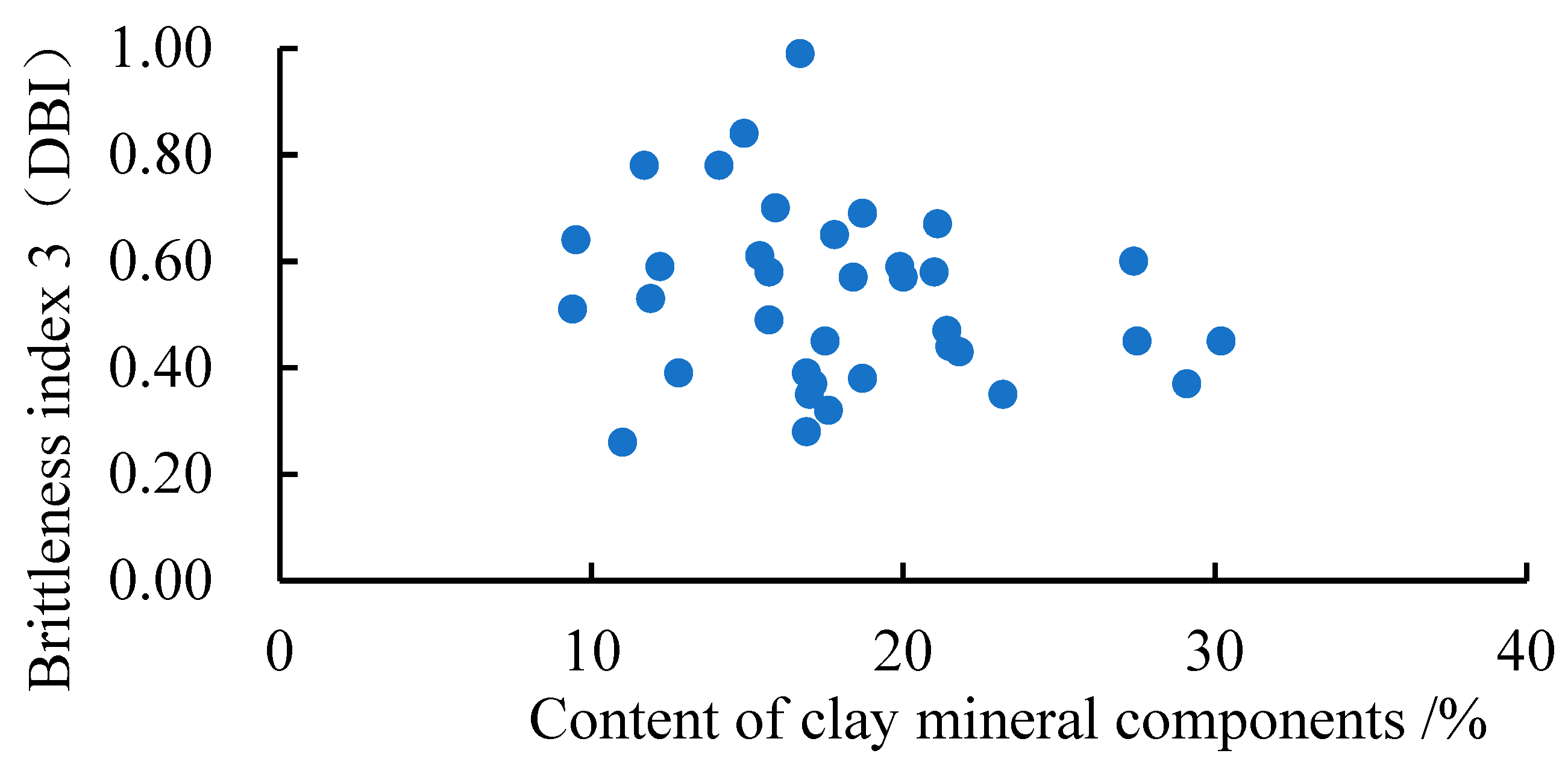
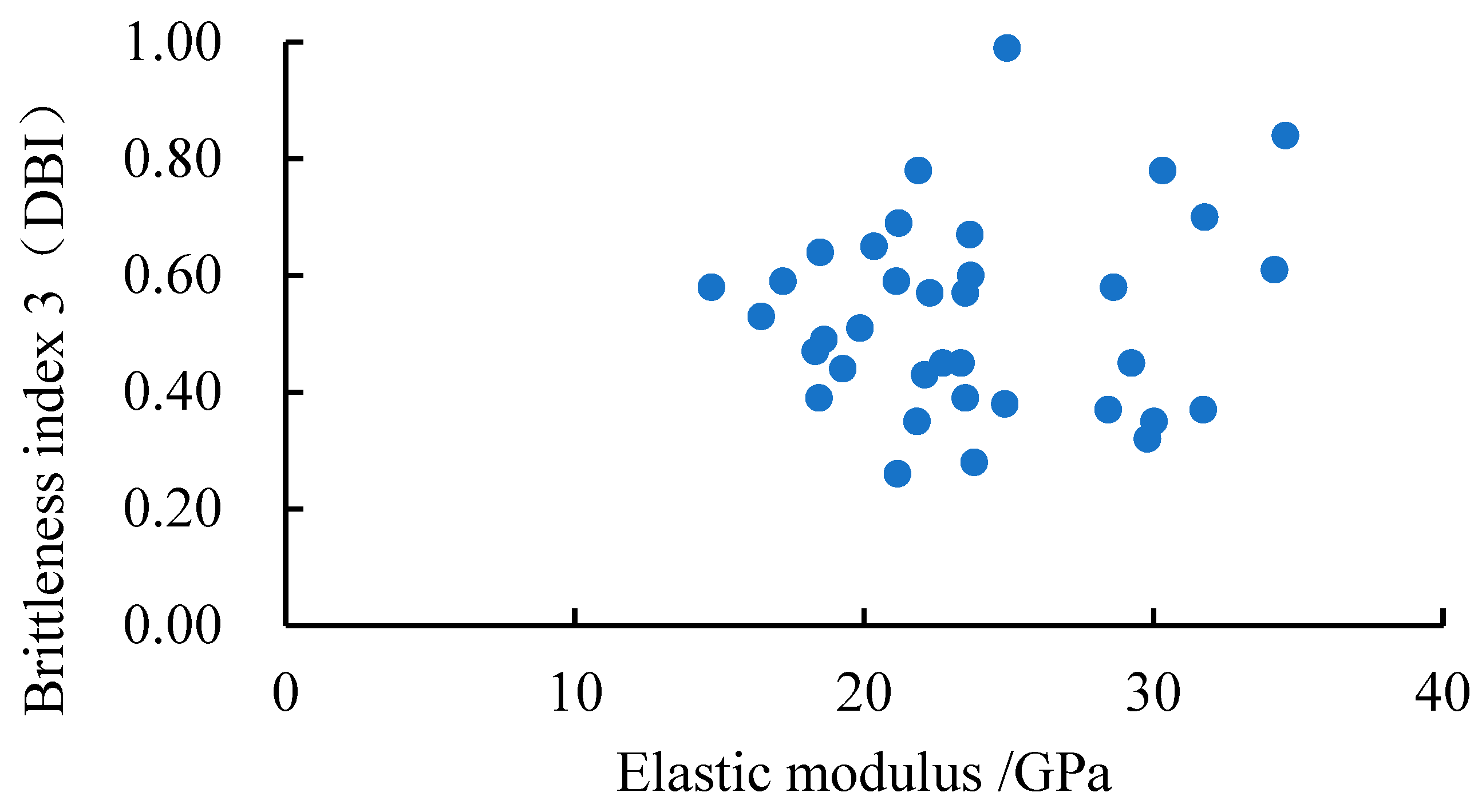
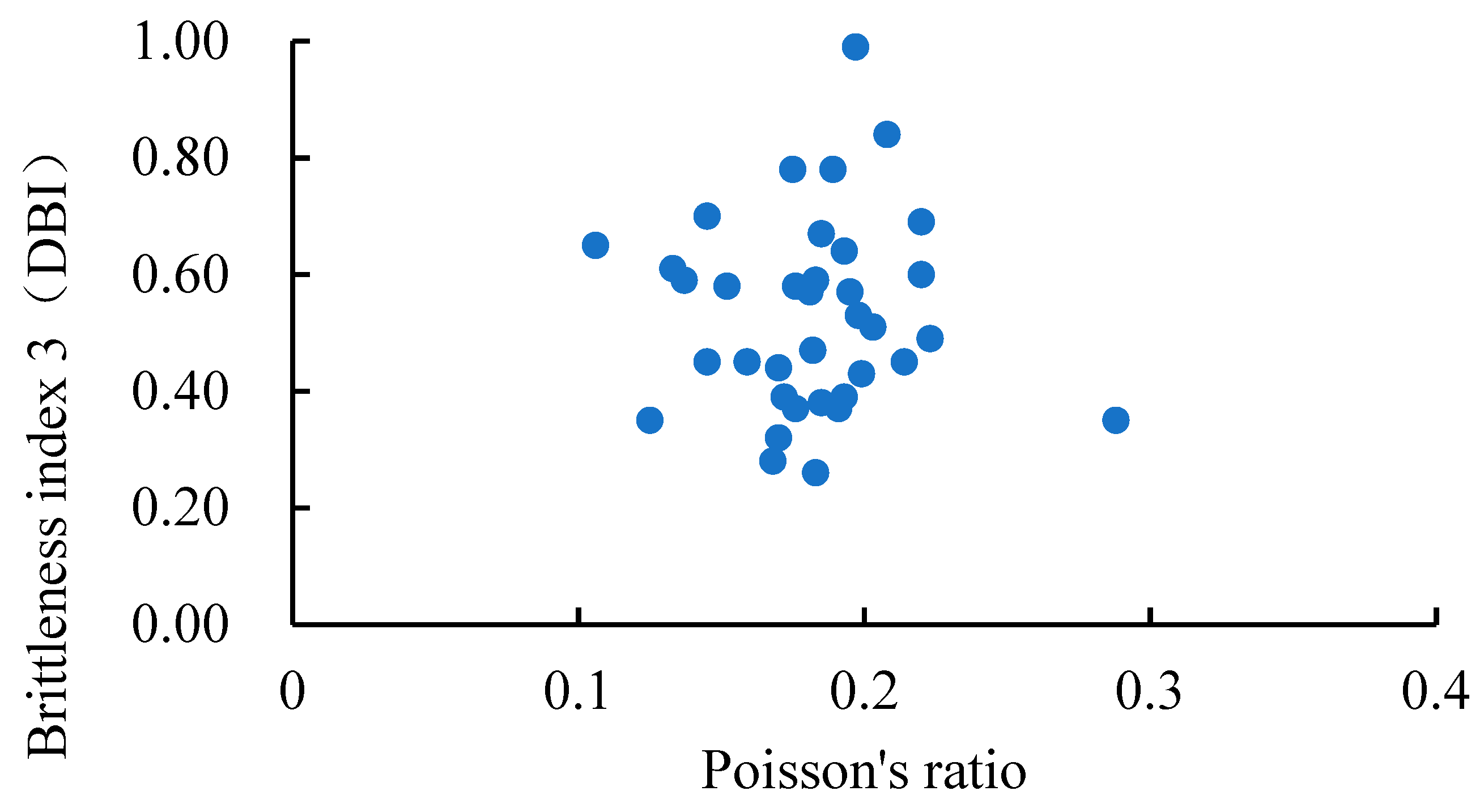
4.4. Analysis of the Main Controlling Factors of Brittleness Index
- (1)
- The influence of mineral components on brittle characteristics
- (2)
- The influence of elastic modulus and Poisson’s ratio on brittle characteristics
5. Conclusions
- (1)
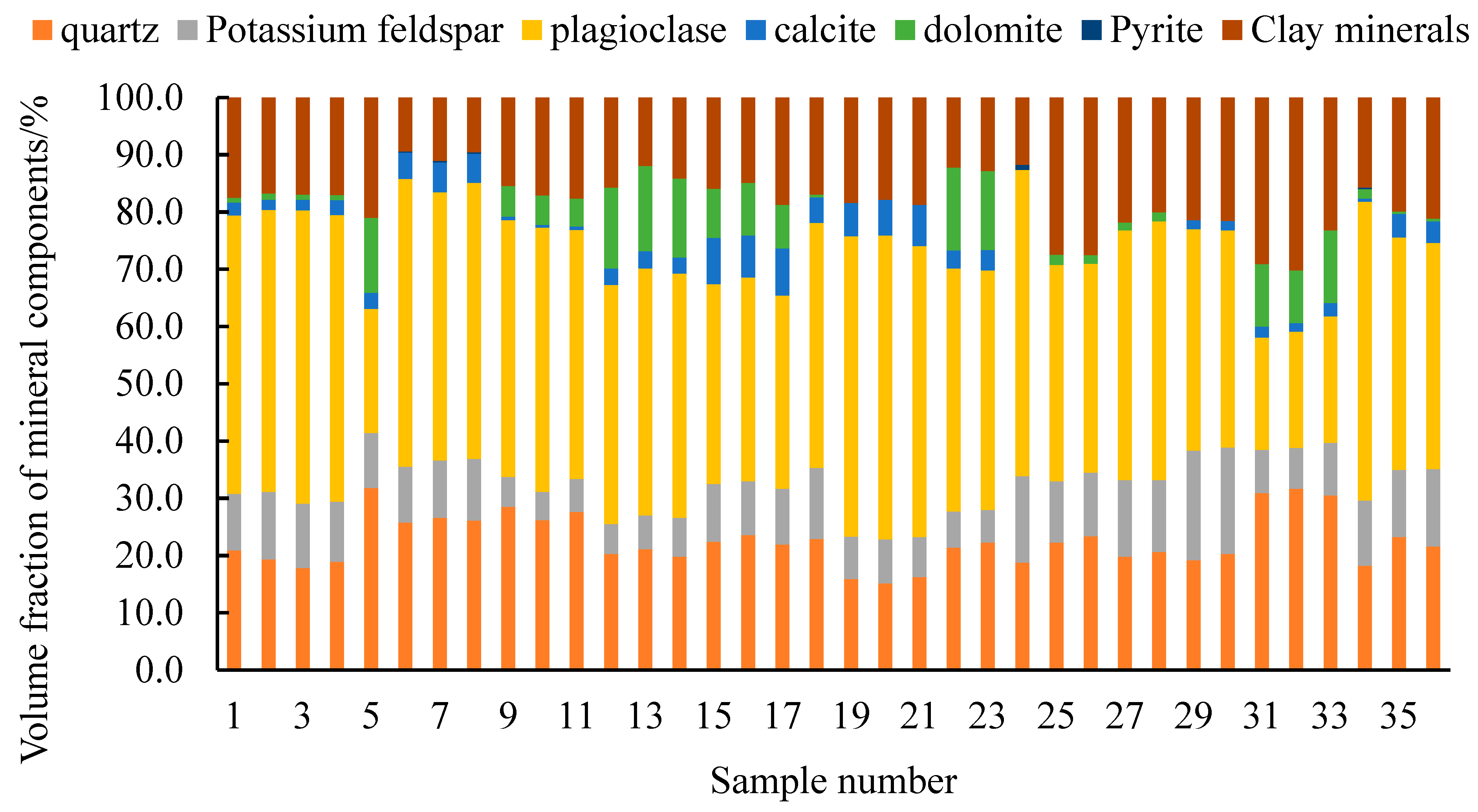
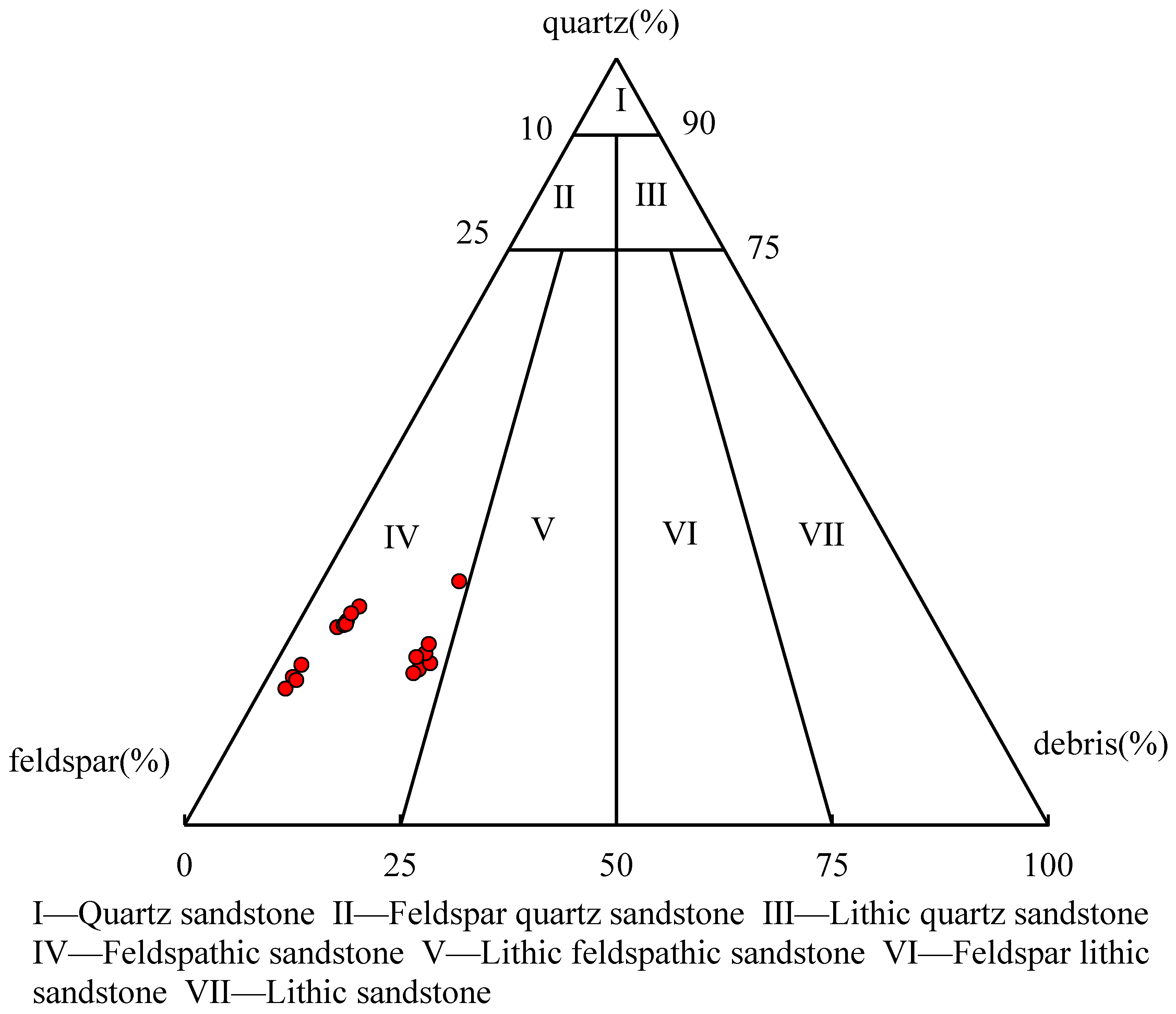
- This article takes cores from the shale oil reservoir in the Yanchang Formation Chang 7 of Block Y in the northwest of the Ordos Basin. Thirty-six samples were tested using a three-axis rock mechanics servo testing system and X-ray diffractometer. The block contains seven minerals, including quartz and feldspar, with an average volume fraction of 22.6% for quartz minerals, 51.6% for feldspar, and 18% for clay minerals. Calcite, dolomite, and pyrite are only present in a few samples. When the confining pressure is 30 MPa, the elastic modulus of the Chang 7 shale in this block is 14.72~34.58 GPa, with an average value of 23.77 GPa. The Poisson’s ratio is 0.106~0.288, with an average value of 0.182. The differential stress is 100.8~260.1 MPa, with an average value of 164.36 MPa. The peak strain ranges from 0.57 to 1.21, with an average value of 0.91.
- (2)
- Based on indoor experimental test results, the average brittleness index 1 (MBI) of 36 experimental groups was calculated using the Jarvie mineral composition method, with a value of 0.5393. Using Rickman’s normalized Young’s modulus and average Poisson’s ratio, the brittleness index 2 (EBI) was calculated to evaluate the relative brittleness of rocks. The average value of 36 experimental groups was 0.5204. Generally, in the process of selecting layers and segments, values with a brittleness index greater than or equal to 0.4 are chosen.
- (3)
- The intrinsic correlation between the elastic strain energy released during the loading process, the strain energy absorbed to the outside, and the three types of energy of fracture strain energy and rock brittleness were analyzed from the perspective of fracture mechanism. A brittle index 3 (DBI) model was established, and its feasibility was verified. The average value of 36 experimental groups can be calculated to be 0.5306, and the trend of the brittle index 3 (DBI) calculated using the energy method is basically the same as the trend calculated by the first two methods, indicating that the third method is feasible. Based on the relationship between peak stress (differential stress) and residual stress in the stress-strain curve, the brittleness index 4 (PBI) value was obtained, and the average value of 36 experimental groups was 0.5271.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, H.; Wang, T.Y.; Bao, T.; Sun, P.H.; Zhang, Z.; Wu, J.J. Effective exploitation potential of shale gas from Lower Cambrian Niutitang Formation, Northwestern Hunan, China. Energies 2018, 11, 3373. [Google Scholar] [CrossRef]
- Shi, W.R.; Wang, X.Z.; Zhang, C.M.; Feng, A.G.; Huang, Z.S. Experimental study on gas content of adsorption and desorption in Fuling shale gas field. J. Pet. Sci. Eng. 2019, 180, 1069–1076. [Google Scholar] [CrossRef]
- Zou, C.N.; Dong, D.Z.; Wang, Y.M.; Li, X.J.; Huang, J.L.; Wang, S.F.; Guan, Q.H.; Zhang, C.C.; Wang, H.Y.; Liu, H.L.; et al. Shale gas in China: Characteristics, challenges and prospects (II). Pet. Explor. Dev. 2016, 43, 182–196. [Google Scholar] [CrossRef]
- Li, Y.X.; Qiao, D.W.; Jiang, W.L.; Zhang, C.H. Gas content of gas-bearing shale and its geological evaluation summary. Geol. Bull. China 2011, 30, 308–317. [Google Scholar]
- Glorioso, J.C.; Rattia, A. Unconventional reservoirs: Basic petrophysical concepts for shale gas. In Proceedings of the SPE/EAGE European Unconventional Resources Conference and Exhibition, Vienna, Austria, 20–22 March 2012. [Google Scholar]
- Zou, C.N.; Dong, D.Z.; Yang, Y.; Wang, Y.M.; Huang, J.L.; Wang, S.F.; Fu, C.X. Conditions of shale gas accumulation and exploration practices in China. Adv. Mater. Res. 2011, 31, 26–39. [Google Scholar]
- Shi, W.; Wang, X.; Shi, Y.; Feng, A.; Zou, Y.; Young, S. Application of Dipole Array Acoustic Logging in the Evaluation of Shale Gas Reservoirs. Energies 2019, 12, 3882. [Google Scholar] [CrossRef]
- Fu, J.; Li, S.; Guo, Q.; Guo, W.; Zhou, X.; Liu, J. The enrichment conditions and optimal selection of favorable areas for continental shale oil in the Ordos Basin. J. Pet. 2022, 43, 1702–1716. [Google Scholar]
- Zhu, J.; Forrest, J.; Xiong, H.; Kianinejad, A. Cluster spacing and well spacing optimizationusing multi-well simulation for the Lower Spraberry shale in Midland Basin. In Proceedings of the SPE Liquids-Rich Basins Conference, Midland, TX, USA, 13–14 September 2017. [Google Scholar]
- Lei, Q.; Guan, B.; Cai, B.; Wang, X.; Xu, Y.; Tong, Z.; Wang, H.; Fu, H.; Liu, Z.; Wang, Z. Theoretical research progress and development direction of volume transformation technology. Pet. Explor. Dev. 2018, 45, 874–887. [Google Scholar]
- Gao, Y. Study on Brittleness Evaluation and Main Control Factors of Tight Oil Reservoirs—Taking the Yanchang Formation of the Triassic in the Dongrengou Oil Area of Dingbian, Ordos Basin as an Example. Master’s Thesis, Northwestern University, Evanston, IL, USA, 2022. [Google Scholar]
- King, G. Thirty years of gas shale fracturing: What have we learned? In Proceedings of the Society of Petroleum Engineers (SPE) Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010. [Google Scholar]
- Zhou, J.; Huang, H.; Milind, D. A new physics-based modeling of multiple non-planar hydraulic fractures propagation. In Proceedings of the Unconventional Resources Technology Conference, San Antonio, TX, USA, 20–22 July 2015. [Google Scholar]
- Ersoy, A.; Waller, M.D. Textural characterization of rocks. Eng. Geol. 1995, 39, 123–136. [Google Scholar] [CrossRef]
- Aoudia, K.; Miskimins, J.L.; Harris, N.B.; Mnich, C.A. Statistical Analysis of the Effects of Mineralogy on Rock Mechanical Properties of the Woodford Shale and the Associated Impacts for Hydraulic Fracture Treatment Design. In Proceedings of the 44th U.S. Rock Mechanics Symposium and 5th U.S.-Canada Rock Mechanics Symposium, Salt Lake City, UT, 27–30 June 2010. [Google Scholar]
- Sierra, R.; Tran, M.H.; Abousleiman, Y.N.; Slatt, R.M. Woodford Shale Mechanical Properties and the Impacts of Lithofacies. In Proceedings of the 44th U.S. Rock Mechanics Symposium and 5th U.S.-Canada Rock Mechanics Symposium, Salt Lake City, UT, 27–30 June 2010. [Google Scholar]
- Jarvie, D.M.; Hill, R.J.; Ruble, T.E.; Pollastro, R.M. Unconventional shale-gas systems: The Mississippian Barnett Shale of north-central Texas as one model for thermogenic shale-gas assessment. AAPG Bull. 2007, 91, 475–499. [Google Scholar] [CrossRef]
- Rickman, R.; Mullen, M.; Petre, E.; Grieser, B.; Kundert, D. A practical use of shale petrophysics for stimulation design optimization: All shale Plays are not clones of the Barnett shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 21–24 September 2008. [Google Scholar]
- Heng, S.; Yang, C.H.; Li, Z.; Wang, L.; Hou, Z.K. Shale brittleness estimation based on energy dissipation. J. Cent. South Univ. (Nat. Sci. Ed.) 2016, 47, 577–585. [Google Scholar]
- Hucka, V.; Das, B. Brittleness determination of rocks by different methods. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1974, 11, 389–392. [Google Scholar] [CrossRef]
- Aubertin, M.; Gill, D.E.; Simon, R. On the use of the brittleness index modified (BIM) to estimate the post-peak behavior of rocks. In Proceedings of the 1st North American Rock Mechanics Symposium, Austin, TX, USA, 1–3 June 1994. [Google Scholar]
- Bishop, A.W. Progressive failure with special reference to the mechanism causing it. Proc. Geotech. Conf. Oslo 1967, 2, 142–150. [Google Scholar]
- Hajiabdolmajid, V.; Kaiser, P. Brittleness of rock and stability assessment in hard rock tunneling. Tunn. Undergr. Space Technol. 2003, 18, 35–48. [Google Scholar] [CrossRef]
- Stavrogin, A.N.; Tarasov, B.G. Experimental Physics and Rock Mechanics; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Altindag, R. The evaluation of rock brittleness concept on rotary blast hold drills. J. S. Afr. Inst. Min. Metall. 2002, 102, 61–66. [Google Scholar]
- Honda, H.; Sanada, Y. Hardness of coal. Fuel 1956, 35, 451–461. [Google Scholar]
- Quinn, J.B.; Quinn, D.G. Indentation brittleness of ceramics: A fresh approach. J. Mater. Sci. 1997, 32, 4331–4346. [Google Scholar] [CrossRef]
- Lawn, B.; Marshall, D. Hardness, toughness, and brittleness: An indentation analysis. J. Am. Ceram. Soc. 1979, 62, 347–350. [Google Scholar] [CrossRef]
- GB/T 50266-2013; Standard for Test Methods of Engineering Rock Mass. China Planning Press: Beijing, China, 2013.
- SY/T 5163-1995; X-ray Diffraction Analysis Method for Relative Content of Clay Minerals in Sedimentary Rocks. China National Petroleum Corporation: Beijing, China, 1995.
- Ye, Y.; Tang, S.; Xi, Z. Brittleness Evaluation in Shale Gas Reservoirs and Its Influence on Fracability. Energies 2020, 13, 388. [Google Scholar] [CrossRef]
- Zheng, D.; Miska, S.; Ozbayoglu, E.; Zhang, J. Combined Experimental and Well Log Study of Anisotropic Strength of Shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 16–18 October 2023. [Google Scholar]
- Zheng, D.; Miska, S.; Ziaja, M.; Zhang, J. Study of anisotropic strength properties of shale. AGH Drill. Oil Gas 2019, 36, 93–112. [Google Scholar] [CrossRef]
- Zheng, D.; Ozbayoglu, E.; Miska, S.; Zhang, J. Experimental study of anisotropic strength properties of shale. In Proceedings of the 57th U.S. Rock Mechanics/Geomechanics Symposium, Atlanta, GA, USA, 25–28 June 2023. [Google Scholar]
- Rafieepour, S.; Zheng, D.; Miska, S.; Ozbayoglu, E.; Takach, N.; Yu, M.; Zhang, J. Combined Experimental and Well Log Evaluation of Anisotropic Mechanical Properties of Shales: An Application to Wellbore Stability in Bakken Formation. In Proceedings of the SPE Annual Technical Conference and Exhibition, Virtual, 24 October 2020. [Google Scholar]
- Peng, C.; Xiao, Y.; Fu, J.; Cao, Q.; Zhang, J.; Su, Y.; Zheng, D. Numerical validation of a novel cuttings bed impeller for extended reach horizontal wells. Pet. Res. 2024. [Google Scholar] [CrossRef]
- Wang, S. Research on the Main Controlling Factors of Brittleness in Tight Reservoirs and the Grading Evaluation of Compressibility. Ph.D. Thesis, Northeast Petroleum University, Daqing, China, 2021. [Google Scholar]
- Rahimzadeh, K.I.; Ameri, M.; Molladavoodi, H. Shale brittleness evaluation based on energy balance analysis of stress-strain curves. J. Pet. Sci. Eng. 2018, 167, 1–19. [Google Scholar] [CrossRef]



| Type | Definition of Brittleness Index | Describe | Proposer |
|---|---|---|---|
| Mineral composition analysis | B1 = Wqtz/Wtotal × 100% | The ratio of quartz to total mineral content. | Jarvie [17] |
| Mineral composition analysis | B2 = (Wqtz + Wcarb)/Wtotal | The ratio of brittle mineral content to total mineral content. | Rickman et al. [18] |
| Rock mechanics parameters | B3 = E + ν | Normalized elastic modulus and Poisson’s ratio. | Rickman et al. [18] |
| Energy dissipation, stress-strain curve | B4 = dWr/dWe | The ratio of the rupture energy consumed per unit volume to the elastic energy released internally. | Heng et al. [19] |
| stress-strain curve | B5 = Wr/W | The ratio of recoverable strain energy to total energy. | Hucka and Das [20] |
| stress-strain curve | B6 = εr/ε | The ratio of recoverable strain εr to total strain ε. | Hucka and Das [20] |
| stress-strain curve | B7 = A2/A1 | A1 is the area under the diagonal line of the peak strength point with the slope of the deformation modulus, A2 is the area under the loading curve. | Aubertin et al. [21] |
| stress-strain curve | B8 = (τp − τr)/τp | τp is Peak intensity, τr is Residual strength. | Bishop [22] |
| stress-strain curve | B9 = (εp − εr)/εp | Peak strain εp and residual strain εr function. | Hajiabdolmajid and Kaiser [23] |
| Energy dissipation, stress-strain curve | B10 = dWr/dWe = (E − M)/M | The ratio of fracture damage energy after the peak of rock fracture to pre-peak elastic strain energy. | Stavrogin and Tarasov [24] |
| Tensile strength and compressive strength | B11 = σcσt/2 | Uniaxial compressive strength σc and tensile strength σt The average value of the product. | Altindag [25] |
| Tensile strength and compressive strength | B12 = σc/σt | The ratio of Uniaxial compressive strength σc and tensile strength σt. | Hucka and Das [20] |
| Hardness testing | B13 = (Hm − H)/K | H is the macroscopic hardness, and Hm is the microscopic hardness. | Honda and Sanada [26] |
| Hardness and fracture tests | B14 = H × E/KIC2 | H is the hardness coefficient, E is the Young’s modulus, and KIC is the fracture toughness. | J.B.Quinn and G.D.Quinn [27] |
| Hardness and fracture tests | B15 = H/KIC | H is the hardness coefficient, KIC is the fracture toughness. | Lawn and Marshall [28] |
| Mohr stress circle | B16 = sinφ | Sine value of internal friction angle. | Hucka and Das [20] |
| Mohr stress circle | B17 = 45°+ φ/2 | The function of internal friction angle. | Hucka and Das [20] |
| Sample Number | Volume Fraction of Mineral Components/w% | Test Results of Triaxial Mechanical Parameters | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Quartz | Plagio-Clase | Potassium Feldspar | Calcite | Dolomite | Pyrite | Clay Minerals | Confining Pressure/MPa | Elastic Modulus/GPa | Poisson’s Ratio | Differential Stress/MPa | Peak Strain | |
| S-1 | 20.9 | 48.6 | 9.9 | 2.3 | 0.8 | - | 17.5 | 30 | 29.24 | 0.214 | 194.4 | 0.78 |
| S-2 | 19.3 | 49.3 | 11.8 | 1.8 | 1.1 | - | 16.7 | 30 | 24.94 | 0.197 | 195.5 | 1.01 |
| S-3 | 17.8 | 51.2 | 11.3 | 1.9 | 0.9 | - | 16.9 | 30 | 23.80 | 0.168 | 173.9 | 0.82 |
| S-4 | 18.9 | 50.1 | 10.5 | 2.6 | 0.9 | - | 17.0 | 30 | 21.83 | 0.125 | 121.2 | 0.57 |
| S-5 | 25.8 | 50.3 | 9.7 | 4.6 | - | 0.2 | 9.4 | 30 | 28.62 | 0.176 | 170.5 | 0.75 |
| S-6 | 26.6 | 46.9 | 10.0 | 5.2 | - | 0.3 | 11.0 | 30 | 19.86 | 0.203 | 159.9 | 1.08 |
| S-7 | 26.1 | 48.2 | 10.8 | 5.1 | - | - | 9.5 | 30 | 21.15 | 0.183 | 161.0 | 0.97 |
| S-8 | 28.5 | 44.9 | 5.2 | 0.6 | 5.4 | - | 15.4 | 30 | 18.48 | 0.193 | 154.3 | 1.04 |
| S-9 | 26.2 | 46.2 | 4.9 | 0.5 | 5.1 | - | 17.1 | 30 | 34.18 | 0.133 | 190.8 | 0.64 |
| S-10 | 27.6 | 43.5 | 5.8 | 0.6 | 4.9 | - | 17.6 | 30 | 31.72 | 0.191 | 160.8 | 0.59 |
| S-11 | 20.3 | 41.8 | 5.2 | 2.9 | 14.1 | - | 15.7 | 30 | 29.79 | 0.170 | 181.9 | 0.63 |
| S-12 | 21.1 | 43.2 | 5.9 | 3.0 | 14.9 | - | 11.9 | 30 | 18.61 | 0.223 | 142.1 | 1.11 |
| S-13 | 19.8 | 42.7 | 6.8 | 2.8 | 13.8 | - | 14.1 | 30 | 16.44 | 0.198 | 137.8 | 1.14 |
| S-14 | 22.4 | 34.9 | 10.1 | 8.1 | 8.6 | - | 15.9 | 30 | 30.32 | 0.189 | 260.1 | 1.07 |
| S-15 | 23.6 | 35.6 | 9.4 | 7.3 | 9.2 | - | 14.9 | 30 | 31.77 | 0.145 | 204.0 | 0.73 |
| S-16 | 21.9 | 33.7 | 9.8 | 8.3 | 7.6 | - | 18.7 | 30 | 34.56 | 0.208 | 209.6 | 0.72 |
| S-17 | 15.9 | 52.5 | 7.4 | 5.8 | - | - | 18.4 | 30 | 21.19 | 0.220 | 162.9 | 1.08 |
| S-18 | 15.2 | 53.1 | 7.6 | 6.3 | - | - | 17.8 | 30 | 23.50 | 0.172 | 180.7 | 0.92 |
| S-19 | 16.3 | 50.9 | 6.9 | 7.2 | - | - | 18.7 | 30 | 22.27 | 0.195 | 182.9 | 0.98 |
| S-20 | 21.4 | 42.5 | 6.3 | 3.1 | 14.5 | - | 12.2 | 30 | 20.34 | 0.106 | 100.8 | 0.58 |
| S-21 | 22.3 | 41.8 | 5.7 | 3.6 | 13.8 | - | 12.8 | 30 | 24.86 | 0.185 | 171.8 | 0.85 |
| S-22 | 18.8 | 53.5 | 15.1 | - | - | 0.9 | 11.7 | 30 | 17.19 | 0.137 | 141.6 | 1.14 |
| S-23 | 22.3 | 37.8 | 10.7 | - | 1.8 | - | 27.4 | 30 | 18.44 | 0.193 | 141.7 | 1.03 |
| S-24 | 23.4 | 36.5 | 11.1 | - | 1.5 | - | 27.5 | 30 | 21.87 | 0.175 | 151.5 | 0.97 |
| S-25 | 19.8 | 43.6 | 13.4 | - | 1.4 | - | 21.8 | 30 | 23.69 | 0.220 | 152.6 | 0.90 |
| S-26 | 20.6 | 45.2 | 12.6 | - | 1.6 | - | 20.0 | 30 | 22.72 | 0.145 | 141.0 | 0.75 |
| S-27 | 19.2 | 38.7 | 19.1 | 1.6 | - | - | 21.4 | 30 | 22.09 | 0.199 | 176.1 | 1.21 |
| S-28 | 20.3 | 37.9 | 18.6 | 1.7 | - | - | 21.5 | 30 | 23.50 | 0.181 | 167.7 | 1.10 |
| S-29 | 30.9 | 19.6 | 7.6 | 1.9 | 10.9 | - | 29.1 | 30 | 18.31 | 0.182 | 142.8 | 1.15 |
| S-30 | 31.7 | 20.3 | 7.1 | 1.5 | 9.2 | - | 30.2 | 30 | 19.26 | 0.170 | 139.6 | 1.16 |
| S-31 | 31.8 | 21.7 | 9.6 | 2.8 | 13.1 | - | 21.0 | 30 | 28.44 | 0.176 | 157.4 | 0.65 |
| S-32 | 30.5 | 22.1 | 9.2 | 2.3 | 12.7 | - | 23.2 | 30 | 23.35 | 0.159 | 150.1 | 0.71 |
| S-33 | 18.2 | 52.2 | 11.4 | 0.6 | 1.6 | 0.3 | 15.7 | 30 | 30.02 | 0.288 | 158.5 | 0.81 |
| S-34 | 23.2 | 40.6 | 11.8 | 4.1 | 0.4 | - | 19.9 | 30 | 14.72 | 0.152 | 109.3 | 0.95 |
| S-35 | 22.9 | 42.8 | 12.4 | 4.5 | 0.5 | - | 16.9 | 30 | 21.11 | 0.183 | 177.2 | 1.11 |
| S-36 | 21.6 | 39.5 | 13.5 | 3.8 | 0.5 | - | 21.1 | 30 | 23.66 | 0.185 | 192.9 | 1.17 |
| average | 22.6 | 9.8 | 41.8 | 18.0 | 23.77 | 0.182 | 164.36 | 0.91 | ||||
| Sample Number | Clay Mineral Content/w% | Illite/Montmorillonite Mixed Layer Ratio (%) | ||||
|---|---|---|---|---|---|---|
| Illite | Kaolinite | Chlorite | Illite/Montmorillonite Mixed Layer | Montmorillonite Layer S% | Illite Layer I% | |
| S-1 | 40 | 10 | 20 | 30 | 20 | 80 |
| S-2 | 42 | 12 | 18 | 28 | 20 | 80 |
| S-3 | 44 | 9 | 17 | 30 | 20 | 80 |
| S-4 | 47 | 6 | 15 | 32 | 20 | 80 |
| S-5 | 41 | 4 | 20 | 35 | 20 | 80 |
| S-6 | 35 | 16 | 38 | 11 | 20 | 80 |
| S-7 | 37 | 14 | 42 | 7 | 20 | 80 |
| S-8 | 39 | 15 | 37 | 9 | 20 | 80 |
| S-9 | 45 | 7 | 18 | 30 | 20 | 80 |
| S-10 | 47 | 4 | 20 | 29 | 20 | 80 |
| S-11 | 42 | 6 | 21 | 31 | 20 | 80 |
| S-12 | 38 | 8 | 27 | 27 | 20 | 80 |
| S-13 | 40 | 10 | 23 | 27 | 20 | 80 |
| S-14 | 45 | 9 | 24 | 22 | 20 | 80 |
| S-15 | 48 | 5 | 25 | 22 | 20 | 80 |
| S-16 | 45 | 4 | 28 | 23 | 20 | 80 |
| S-17 | 42 | 7 | 30 | 21 | 20 | 80 |
| S-18 | 25 | 16 | 53 | 6 | 20 | 80 |
| S-19 | 30 | 15 | 48 | 7 | 20 | 80 |
| S-20 | 22 | 13 | 59 | 6 | 20 | 80 |
| S-21 | 28 | 18 | 51 | 3 | 20 | 80 |
| S-22 | 33 | 9 | 47 | 11 | 20 | 80 |
| S-23 | 31 | 10 | 45 | 14 | 20 | 80 |
| S-24 | 42 | 9 | 21 | 28 | 20 | 80 |
| S-25 | 30 | 8 | 41 | 21 | 20 | 80 |
| S-26 | 32 | 10 | 35 | 23 | 20 | 80 |
| S-27 | 40 | 10 | 30 | 20 | 20 | 80 |
| S-28 | 38 | 9 | 33 | 20 | 20 | 80 |
| S-29 | 43 | 15 | 25 | 17 | 20 | 80 |
| S-30 | 47 | 13 | 28 | 12 | 20 | 80 |
| S-31 | 45 | 5 | 22 | 28 | 20 | 80 |
| S-32 | 44 | 6 | 23 | 27 | 20 | 80 |
| S-33 | 39 | 10 | 19 | 32 | 20 | 80 |
| S-34 | 33 | 13 | 35 | 19 | 20 | 80 |
| S-35 | 20 | 10 | 60 | 10 | 20 | 80 |
| S-36 | 26 | 14 | 50 | 10 | 20 | 80 |
| average | 38 | 10 | 32 | 20 | ||
| Sample Number | Volume Fraction of Mineral Components/w% | Test Results of Triaxial Mechanical Parameters | Brittleness Index 1 (MBI) | Brittleness Index 2 (EBI) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Quartz | Plagio-Clase | Potassium Feldspar | Calcite | Dolomite | Pyrite | Clay Minerals | Elastic Modulus/GPa | Poisson’s Ratio | |||
| S-1 | 20.9 | 48.6 | 9.9 | 2.3 | 0.8 | - | 17.5 | 29.24 | 0.214 | 0.4290 | 0.5693 |
| S-2 | 19.3 | 49.3 | 11.8 | 1.8 | 1.1 | - | 16.7 | 24.94 | 0.197 | 0.4134 | 0.5076 |
| S-3 | 17.8 | 51.2 | 11.3 | 1.9 | 0.9 | - | 16.9 | 23.80 | 0.168 | 0.5139 | 0.5585 |
| S-4 | 18.9 | 50.1 | 10.5 | 2.6 | 0.9 | - | 17.0 | 21.83 | 0.125 | 0.6573 | 0.6270 |
| S-5 | 25.8 | 50.3 | 9.7 | 4.6 | - | 0.2 | 9.4 | 28.62 | 0.176 | 0.7708 | 0.6580 |
| S-6 | 26.6 | 46.9 | 10.0 | 5.2 | - | 0.3 | 11.0 | 19.86 | 0.203 | 0.2835 | 0.3631 |
| S-7 | 26.1 | 48.2 | 10.8 | 5.1 | - | - | 9.5 | 21.15 | 0.183 | 0.3953 | 0.4505 |
| S-8 | 28.5 | 44.9 | 5.2 | 0.6 | 5.4 | - | 15.4 | 18.48 | 0.193 | 0.2978 | 0.3558 |
| S-9 | 26.2 | 46.2 | 4.9 | 0.5 | 5.1 | - | 17.1 | 34.18 | 0.133 | 0.8769 | 0.9162 |
| S-10 | 27.6 | 43.5 | 5.8 | 0.6 | 4.9 | - | 17.6 | 31.72 | 0.191 | 0.5784 | 0.6950 |
| S-11 | 20.3 | 41.8 | 5.2 | 2.9 | 14.1 | - | 15.7 | 29.79 | 0.170 | 0.6283 | 0.7040 |
| S-12 | 21.1 | 43.2 | 5.9 | 3.0 | 14.9 | - | 11.9 | 18.61 | 0.223 | 0.1722 | 0.2766 |
| S-13 | 19.8 | 42.7 | 6.8 | 2.8 | 13.8 | - | 14.1 | 16.44 | 0.198 | 0.2345 | 0.2906 |
| S-14 | 22.4 | 34.9 | 10.1 | 8.1 | 8.6 | - | 15.9 | 30.32 | 0.189 | 0.5582 | 0.6652 |
| S-15 | 23.6 | 35.6 | 9.4 | 7.3 | 9.2 | - | 14.9 | 31.77 | 0.145 | 0.7759 | 0.8226 |
| S-16 | 21.9 | 33.7 | 9.8 | 8.3 | 7.6 | - | 18.7 | 34.56 | 0.208 | 0.5641 | 0.7198 |
| S-17 | 15.9 | 52.5 | 7.4 | 5.8 | - | - | 18.4 | 21.19 | 0.220 | 0.2381 | 0.3499 |
| S-18 | 15.2 | 53.1 | 7.6 | 6.3 | - | - | 17.8 | 23.50 | 0.172 | 0.6573 | 0.5400 |
| S-19 | 16.3 | 50.9 | 6.9 | 7.2 | - | - | 18.7 | 22.27 | 0.195 | 0.3671 | 0.4458 |
| S-20 | 21.4 | 42.5 | 6.3 | 3.1 | 14.5 | - | 12.2 | 20.34 | 0.106 | 0.7078 | 0.6417 |
| S-21 | 22.3 | 41.8 | 5.7 | 3.6 | 13.8 | - | 12.8 | 24.86 | 0.185 | 0.4630 | 0.5385 |
| S-22 | 18.8 | 53.5 | 15.1 | - | - | 0.9 | 11.7 | 17.19 | 0.137 | 0.5983 | 0.4771 |
| S-23 | 22.3 | 37.8 | 10.7 | - | 1.8 | - | 27.4 | 18.44 | 0.193 | 0.4781 | 0.3548 |
| S-24 | 23.4 | 36.5 | 11.1 | - | 1.5 | - | 27.5 | 21.87 | 0.175 | 0.6098 | 0.4907 |
| S-25 | 19.8 | 43.6 | 13.4 | - | 1.4 | - | 21.8 | 23.69 | 0.220 | 0.5328 | 0.4129 |
| S-26 | 20.6 | 45.2 | 12.6 | - | 1.6 | - | 20.0 | 22.72 | 0.145 | 0.7109 | 0.5945 |
| S-27 | 19.2 | 38.7 | 19.1 | 1.6 | - | - | 21.4 | 22.09 | 0.199 | 0.5506 | 0.4303 |
| S-28 | 20.3 | 37.9 | 18.6 | 1.7 | - | - | 21.5 | 23.50 | 0.181 | 0.6333 | 0.5152 |
| S-29 | 30.9 | 19.6 | 7.6 | 1.9 | 10.9 | - | 29.1 | 18.31 | 0.182 | 0.5046 | 0.3817 |
| S-30 | 31.7 | 20.3 | 7.1 | 1.5 | 9.2 | - | 30.2 | 19.26 | 0.170 | 0.5598 | 0.4386 |
| S-31 | 31.8 | 21.7 | 9.6 | 2.8 | 13.1 | - | 21.0 | 28.44 | 0.176 | 0.7665 | 0.6535 |
| S-32 | 30.5 | 22.1 | 9.2 | 2.3 | 12.7 | - | 23.2 | 23.35 | 0.159 | 0.6886 | 0.5719 |
| S-33 | 18.2 | 52.2 | 11.4 | 0.6 | 1.6 | 0.3 | 15.7 | 30.02 | 0.288 | 0.5038 | 0.3856 |
| S-34 | 23.2 | 40.6 | 11.8 | 4.1 | 0.4 | - | 19.9 | 14.72 | 0.152 | 0.4979 | 0.3737 |
| S-35 | 22.9 | 42.8 | 12.4 | 4.5 | 0.5 | - | 16.9 | 21.11 | 0.183 | 0.5699 | 0.4495 |
| S-36 | 21.6 | 39.5 | 13.5 | 3.8 | 0.5 | - | 21.1 | 23.66 | 0.185 | 0.6264 | 0.5083 |
| average | 22.6 | 9.8 | 41.8 | 18.0 | 23.77 | 0.182 | 0.5393 | 0.5204 | |||
| Sample Number | Test Results of Triaxial Mechanical Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Confining Pressure/MPa | Elastic Modulus/GPa | Poisson’s Ratio | Differential Stress/MPa | Peak Strain | Residual Stress (MPa) | Residual Elastic Modulus (MPa) | Drop Modulus/GPa | Brittleness Index 3 (DBI) | Brittleness Index 4 (PBI) | |
| S-1 | 30 | 29.24 | 0.214 | 194.4 | 0.78 | 89.8 | 604.9 | −24.08 | 0.4516 | 0.5381 |
| S-2 | 30 | 24.94 | 0.197 | 195.5 | 1.01 | / | / | −3217 | 0.9923 | 0.9960 |
| S-3 | 30 | 23.80 | 0.168 | 173.9 | 0.82 | 103.6 | 945.8 | −9.14 | 0.2775 | 0.4043 |
| S-4 | 30 | 21.83 | 0.125 | 121.2 | 0.57 | 78.8 | 603.7 | −11.67 | 0.3484 | 0.3498 |
| S-5 | 30 | 28.62 | 0.176 | 170.5 | 0.75 | 91.8 | 1577.6 | −40.05 | 0.5832 | 0.4616 |
| S-6 | 30 | 19.86 | 0.203 | 159.9 | 1.08 | 74.8 | 940.9 | −20.68 | 0.5101 | 0.5322 |
| S-7 | 30 | 21.15 | 0.183 | 161.0 | 0.97 | 87.4 | 700.1 | −7.49 | 0.2615 | 0.4571 |
| S-8 | 30 | 18.48 | 0.193 | 154.3 | 1.04 | 68.7 | 733.0 | −32.82 | 0.6398 | 0.5548 |
| S-9 | 30 | 34.18 | 0.133 | 190.8 | 0.64 | 103.1 | 1993.5 | −52.39 | 0.6052 | 0.4596 |
| S-10 | 30 | 31.72 | 0.191 | 160.8 | 0.59 | 102.2 | 1437.0 | −18.30 | 0.3659 | 0.3644 |
| S-11 | 30 | 29.79 | 0.170 | 181.9 | 0.63 | 114.1 | 988.9 | −13.98 | 0.3194 | 0.3727 |
| S-12 | 30 | 18.61 | 0.223 | 142.1 | 1.11 | 61.1 | 213.2 | −17.65 | 0.4868 | 0.5700 |
| S-13 | 30 | 16.44 | 0.198 | 137.8 | 1.14 | 68.5 | 637.3 | −18.59 | 0.5307 | 0.5029 |
| S-14 | 30 | 30.32 | 0.189 | 260.1 | 1.07 | 93.6 | 986.5 | −106.55 | 0.7785 | 0.6401 |
| S-15 | 30 | 31.77 | 0.145 | 204.0 | 0.73 | 128.7 | 787.5 | −73.31 | 0.6977 | 0.3691 |
| S-16 | 30 | 34.56 | 0.208 | 209.6 | 0.72 | 93.3 | 1641.3 | −187.16 | 0.8441 | 0.5549 |
| S-17 | 30 | 21.19 | 0.220 | 162.9 | 1.08 | 78.3 | 707.9 | −47.93 | 0.6934 | 0.5193 |
| S-18 | 30 | 23.50 | 0.172 | 180.7 | 0.92 | 106.6 | 1125.2 | −14.81 | 0.3866 | 0.4101 |
| S-19 | 30 | 22.27 | 0.195 | 182.9 | 0.98 | 93.7 | 728.3 | −29.84 | 0.5726 | 0.4877 |
| S-20 | 30 | 20.34 | 0.106 | 100.8 | 0.58 | 9.3 | 781.7 | −38.20 | 0.6525 | 0.9077 |
| S-21 | 30 | 24.86 | 0.185 | 171.8 | 0.85 | 110.2 | 575.1 | −14.98 | 0.3760 | 0.3586 |
| S-22 | 30 | 17.19 | 0.137 | 141.6 | 1.14 | 80.5 | 522.5 | −24.29 | 0.5856 | 0.4315 |
| S-23 | 30 | 18.44 | 0.193 | 141.7 | 1.03 | 74.6 | 453.2 | −11.80 | 0.3902 | 0.4735 |
| S-24 | 30 | 21.87 | 0.175 | 151.5 | 0.97 | / | / | −78.15 | 0.7813 | 0.9719 |
| S-25 | 30 | 23.69 | 0.220 | 152.6 | 0.90 | 69.8 | 730.5 | −35.08 | 0.5969 | 0.5426 |
| S-26 | 30 | 22.72 | 0.145 | 141.0 | 0.75 | 84.8 | 362.9 | −18.43 | 0.4479 | 0.3986 |
| S-27 | 30 | 22.09 | 0.199 | 176.1 | 1.21 | 83.2 | 1315.9 | −16.87 | 0.4330 | 0.5275 |
| S-28 | 30 | 23.50 | 0.181 | 167.7 | 1.10 | 74.3 | 532.8 | −31.13 | 0.5698 | 0.5569 |
| S-29 | 30 | 18.31 | 0.182 | 142.8 | 1.15 | 73.7 | 649.0 | −16.25 | 0.4702 | 0.4839 |
| S-30 | 30 | 19.26 | 0.170 | 139.6 | 1.16 | 67.0 | 452.6 | −15.28 | 0.4424 | 0.5201 |
| S-31 | 30 | 28.44 | 0.176 | 157.4 | 0.65 | 105.1 | 1433.8 | −16.87 | 0.3723 | 0.3323 |
| S-32 | 30 | 23.35 | 0.159 | 150.1 | 0.71 | 84.7 | 731.7 | −19.07 | 0.4496 | 0.4357 |
| S-33 | 30 | 30.02 | 0.288 | 158.5 | 0.81 | 87.2 | 686.6 | −15.96 | 0.3471 | 0.4498 |
| S-34 | 30 | 14.72 | 0.152 | 109.3 | 0.95 | 40.4 | 2202.2 | −20.23 | 0.5788 | 0.6304 |
| S-35 | 30 | 21.11 | 0.183 | 177.2 | 1.11 | 102.6 | 290.0 | −30.83 | 0.5936 | 0.4210 |
| S-36 | 30 | 23.66 | 0.185 | 192.9 | 1.17 | 2.4 | 529.6 | −47.52 | 0.6676 | 0.9876 |
| average | 23.77 | 0.182 | 164.36 | 0.91 | 0.5306 | 0.5271 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Chen, J.; Xiong, J.; Nie, X.; Gong, D.; Li, Z.; Lei, J. A New Method for Evaluating the Brittleness of Shale Oil Reservoirs in Block Y of Ordos Basin of China. Energies 2024, 17, 4201. https://doi.org/10.3390/en17174201
Zhang J, Chen J, Xiong J, Nie X, Gong D, Li Z, Lei J. A New Method for Evaluating the Brittleness of Shale Oil Reservoirs in Block Y of Ordos Basin of China. Energies. 2024; 17(17):4201. https://doi.org/10.3390/en17174201
Chicago/Turabian StyleZhang, Jinyuan, Junbin Chen, Jiao Xiong, Xiangrong Nie, Diguang Gong, Ziyan Li, and Junjie Lei. 2024. "A New Method for Evaluating the Brittleness of Shale Oil Reservoirs in Block Y of Ordos Basin of China" Energies 17, no. 17: 4201. https://doi.org/10.3390/en17174201
APA StyleZhang, J., Chen, J., Xiong, J., Nie, X., Gong, D., Li, Z., & Lei, J. (2024). A New Method for Evaluating the Brittleness of Shale Oil Reservoirs in Block Y of Ordos Basin of China. Energies, 17(17), 4201. https://doi.org/10.3390/en17174201






