Thermoeconomic Evaluation of a High-Performance Solar Biogas Polygeneration System
Abstract
1. Introduction
- Analysis of a high-efficiency polygeneration system that recovers waste energy from an engine and a set of photovoltaic panels;
- Detailed application of the Theory of Exergy Cost to the polygeneration plant;
- Presentation of sensitivity assessments to verify the impacts of the variation in different costs.
2. Materials and Methods
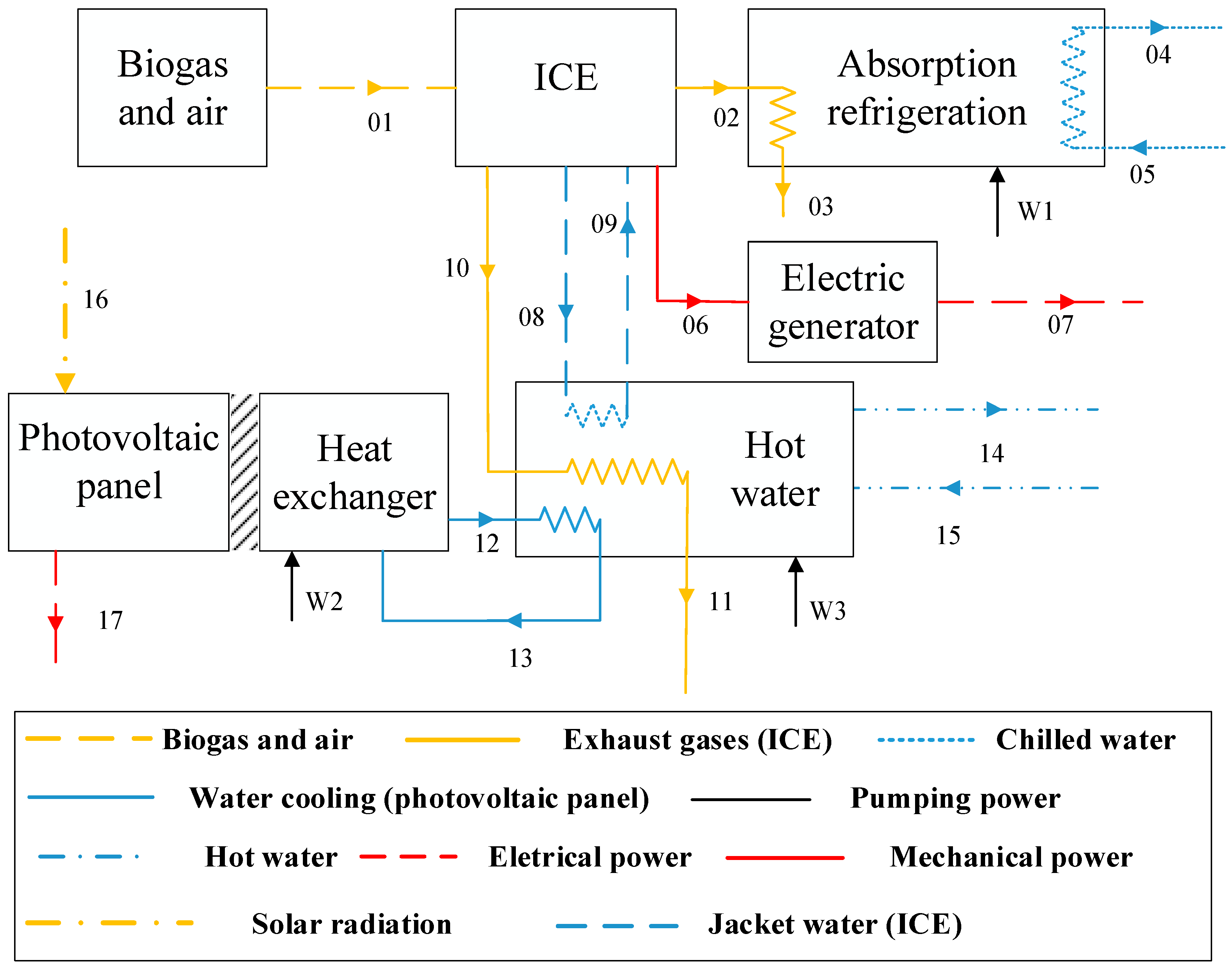
2.1. Polygeneration System
2.2. System Components
2.2.1. Internal Combustion Engine
2.2.2. Absorption Chiller
2.2.3. Photovoltaic Solar Panels
2.2.4. Thermal Storage System
2.3. Thermodynamic Analysis
- (1)
- Changes in kinetic and potential energy are negligible;
- (2)
- Pressure drops and heat dissipation through the pipes are insignificant;
- (3)
- A complete combustion process occurs in the ICE.
2.4. Thermoeconomic Analysis
2.5. Theory of the Exergetic Cost
2.6. Parameter Variation Study
3. Results and Discussion
3.1. Energy Assessment
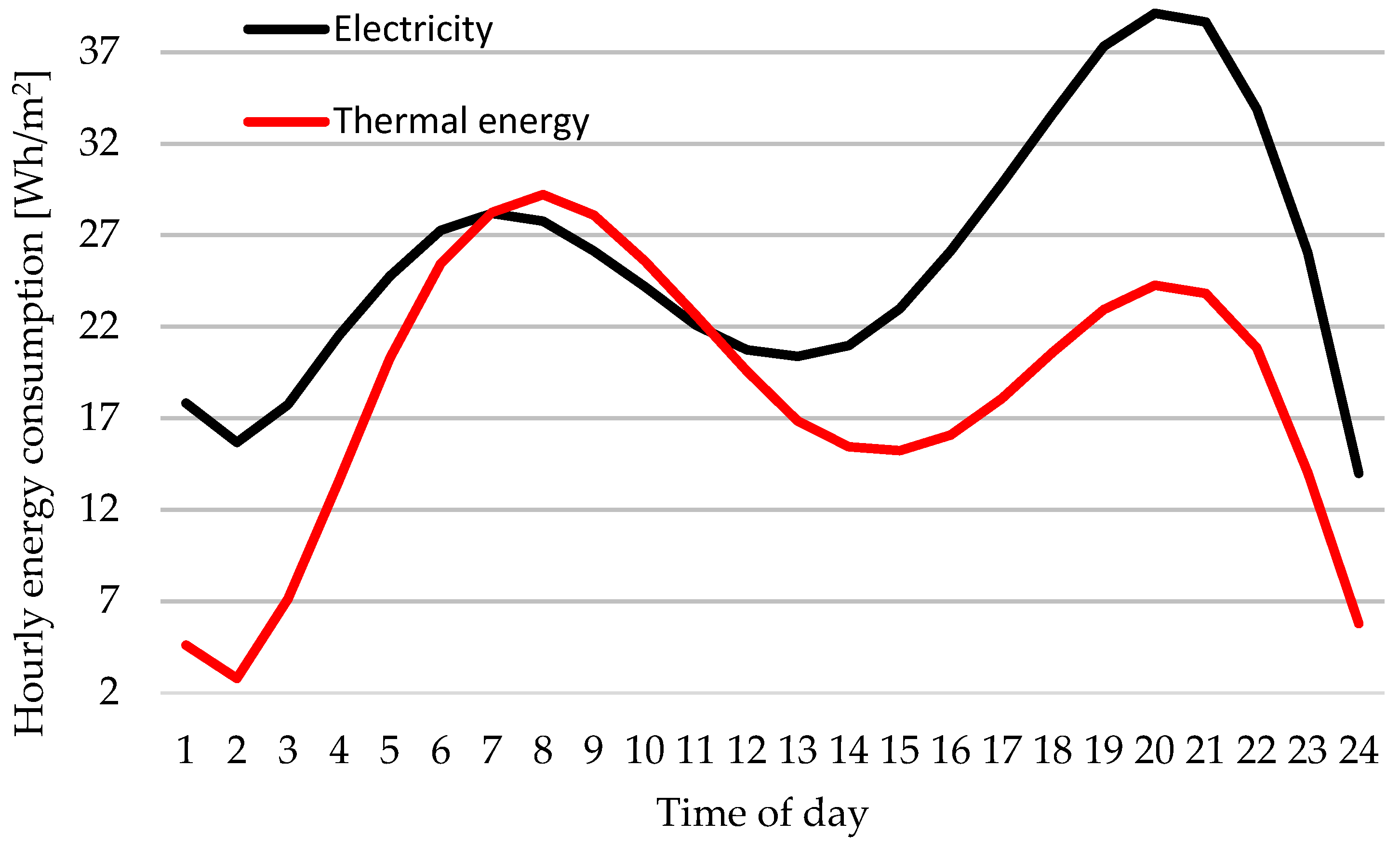
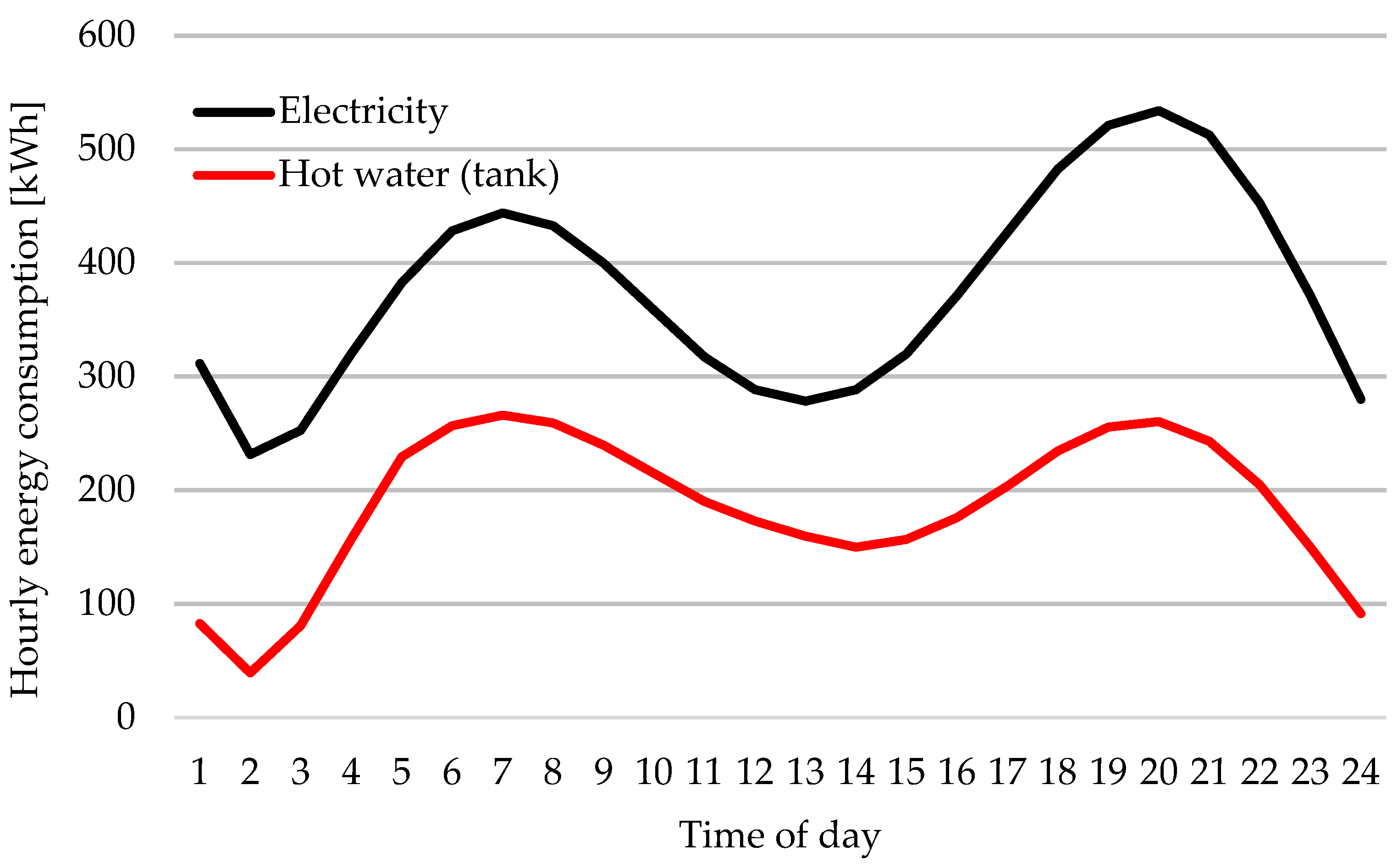
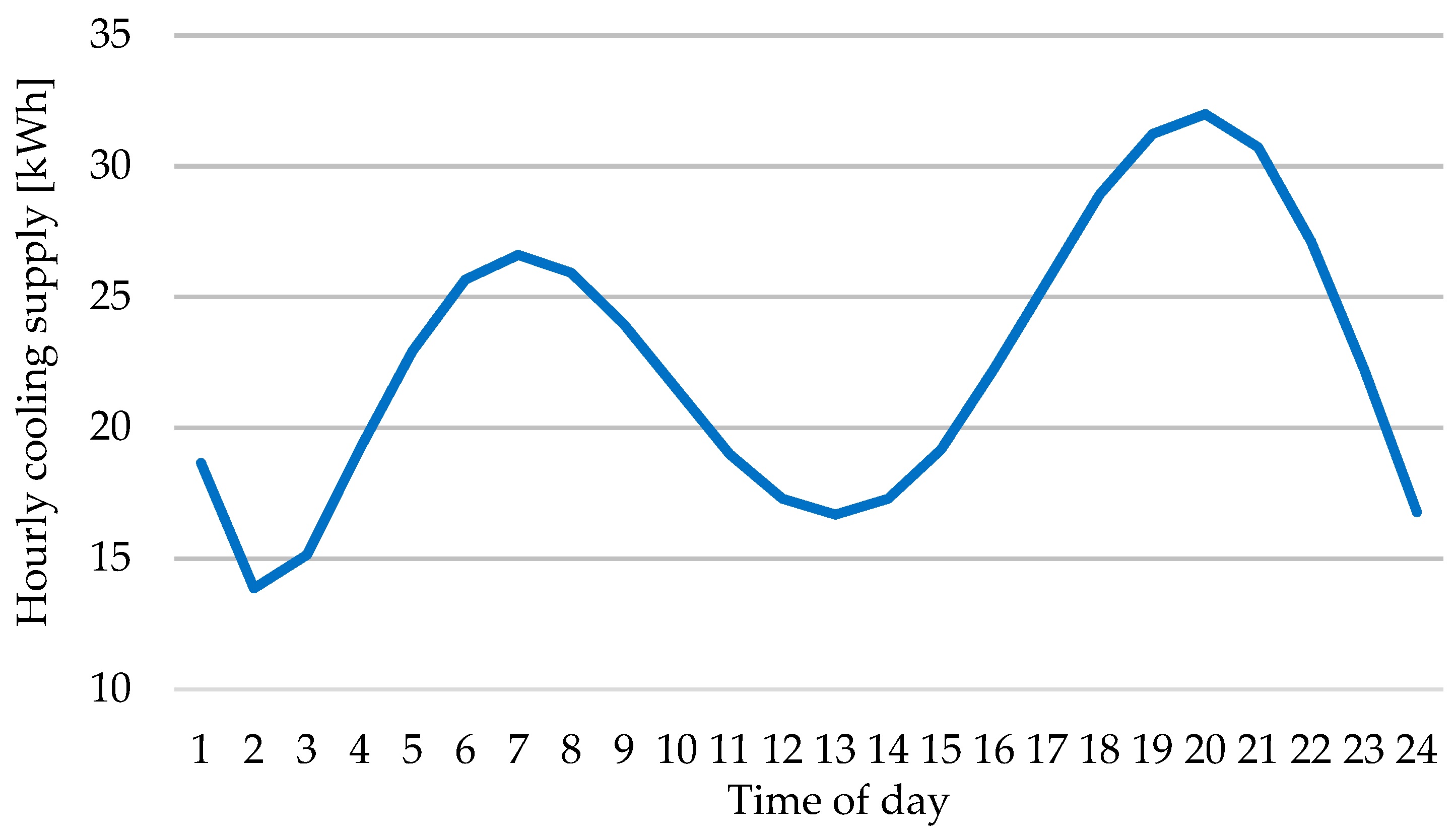
3.1.1. Average Plant Energy Consumption
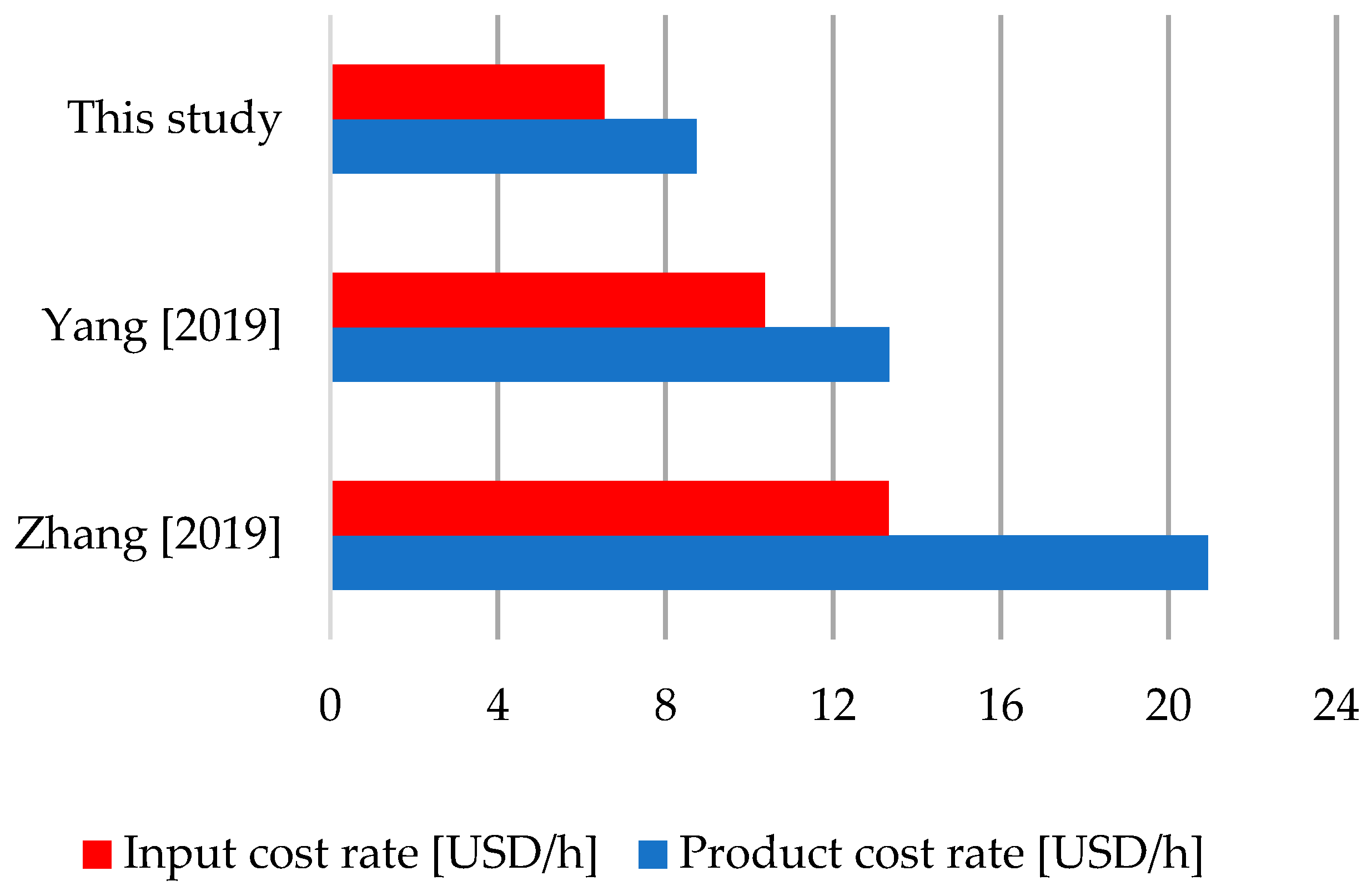
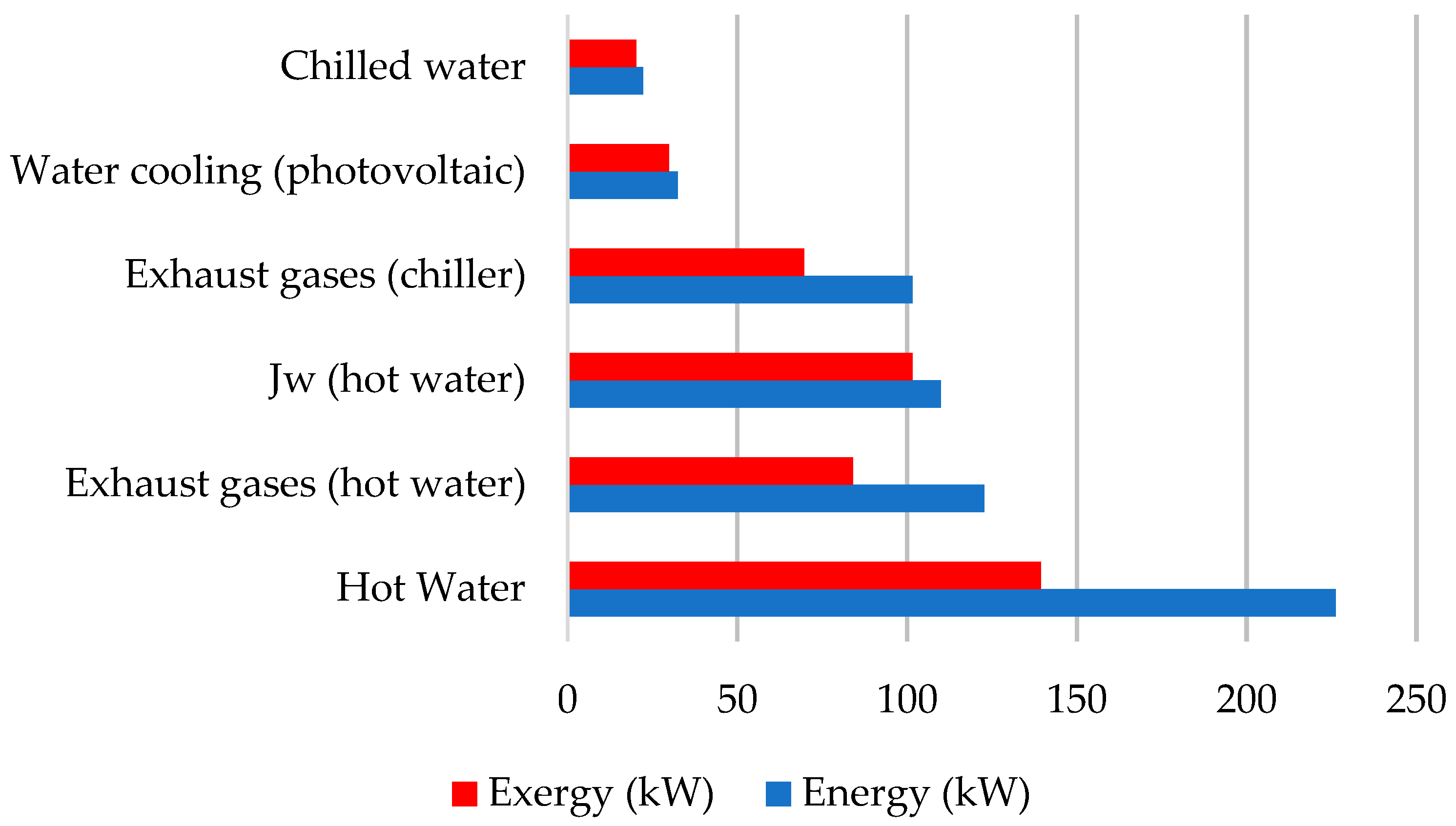
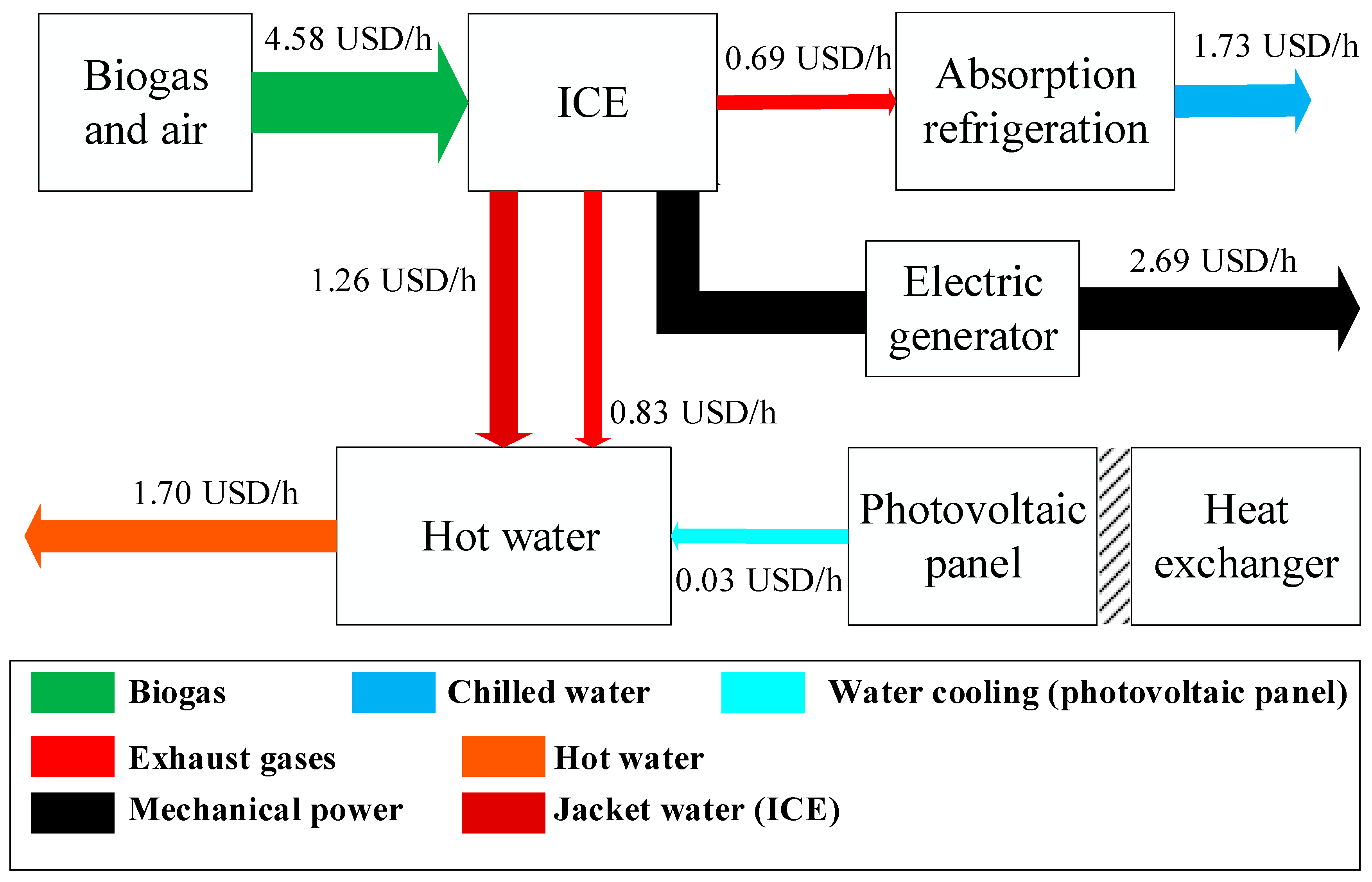
3.1.2. Thermoeconomic Evaluation
3.2. Results of the Parameter Variation Study
3.2.1. Variation in the Operation Cost Rate of ICE
3.2.2. Variation in the Cost of Fuel (Biogas)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gimelli, A.; Muccillo, M. Performance assessment of a 15 kW Micro-CHCP plant through the 0D/1D thermo-fluid dynamic characterization of a double water circuit waste heat recovery system. Energy 2019, 181, 803–814. [Google Scholar] [CrossRef]
- Yamano, S.; Nakaya, T.; Ikegami, T.; Nakayama, M.; Akisawa, A. Optimization modeling of mixed gas engine types with different maintenance spans and costs: Case study OF CCHP to evaluate optimal gas engine operations and combination of the types. Energy 2021, 222, 119823. [Google Scholar] [CrossRef]
- Marques, A.S.; Carvalho, M.; Ochoa, A.A.V.; Abrahão, R.; Santos, C.A.C. Life cycle assessment and comparative exergoenvironmental evaluation of a micro-trigeneration system. Energy 2021, 216, 119310. [Google Scholar] [CrossRef]
- Leonzio, G. An innovative trigeneration system using biogas as renewable energy. Chin. J. Chem. Eng. 2018, 26, 1179–1191. [Google Scholar] [CrossRef]
- Tang, Z.; Ly, S.; Wang, Y.; Huang, Y.; Luo, J.; Fu, C. Biofuel trigeneration with energy storage for heating, cooling and power on farms. Energy Rep. 2021, 7, 5394–5405. [Google Scholar] [CrossRef]
- Sebastián, A.; Abbas, R.; Valdés, M.; Rovira, A. Modular micro-trigeneration system for a novel rotatory solar Fresnel collector: A design space analysis. Energy Convers. Manag. 2021, 227, 113599. [Google Scholar] [CrossRef]
- Onishi, V.C.; Antunes, C.H.; Fraga, E.S.; Cabezas, H. Stochastic optimization of trigeneration systems for decision-making under long-term uncertainty in energy demands and prices. Energy 2019, 175, 781–797. [Google Scholar] [CrossRef]
- Yağli, H.; Koç, Y.; Koç, A.; Görgülü, A.; Tandiroğlu, A. Parametric optimization and exergetic analysis comparison of subcritical and supercritical organic Rankine cycle (ORC) for biogas fuelled combined heat and power (CHP) engine exhaust gas waste heat. Energy 2016, 111, 923–932. [Google Scholar] [CrossRef]
- Baghernejad, A.; Yaghoubi, M.; Jafarpur, K. Exergoeconomic optimization and environmental analysis of a novel solar-trigeneration system for heating, cooling and power production purpose. Sol. Energy 2016, 134, 165–179. [Google Scholar] [CrossRef]
- Santos, R.G.; Lourenço, A.B.; de Faria, P.R.; Barone, M.A.; Santos, J.J.C.S. A New Exergy Disaggregation Approach for Complexity Reduction and Dissipative Equipment Isolation in Thermoeconomics. Entropy 2022, 24, 1672. [Google Scholar] [CrossRef] [PubMed]
- Sala-Lizarraga, J.M.; Picallo-Perez, A. Exergy Analysis and Thermoeconomics of Buildings: Design and Analysis for Sustainable Energy Systems; Butterworth-Heinemann: Oxford, UK, 2019. [Google Scholar]
- Valero, A.; Serra, L.; Uche, J. Fundamentals of Exergy Cost Accounting and Thermoeconomics. Part I: Theory. J. Energy Resour. Technol. 2006, 128, 1–8. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, B.; Zheng, Y.; Zhang, R.; Liu, P.; An, Z. Economic assessment and regional adaptability analysis of CCHP system coupled with biomass-gas based on year-round performance. Sustain. Energy Technol. Assess. 2021, 45, 101141. [Google Scholar] [CrossRef]
- Castley, J.; Azimov, U.; Combrinck, M.; Xing, L. Modeling and optimization of combined cooling, heating and power systems with integrated biogas upgrading. Appl. Therm. Eng. 2022, 210, 118329. [Google Scholar] [CrossRef]
- Su, B.; Han, W.; Chen, Y.; Wang, Z.; Qu, W.; Jin, H. Performance optimization of a solar assisted CCHP based on biogas reforming. Energy Convers. Manag. 2018, 171, 604–617. [Google Scholar] [CrossRef]
- Pugsley, A.; Zacharopoulos, A.; Chemisana, D. Polygeneration systems in buildings. In Polygeneration Systems; Academic Press: Cambridge, MA, USA, 2022; pp. 351–410. [Google Scholar]
- Chen, Y.; Zhao, D.; Xu, J.; Wang, J.; Lund, P.D. Performance analysis and exergo-economic optimization of a solar-driven adjustable tri-generation system. Energy Convers. Manag. 2021, 233, 113873. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.; Zhang, G.; Yang, Y. Performance investigation of a solar-assisted hybrid combined cooling, heating and power system based on energy, exergy, exergo-economic and exergo-environmental analyses. Energy Convers. Manag. 2019, 196, 227–241. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Lior, N. Exergo-economic analysis method and optimization of a novel photovoltaic/thermal solar-assisted hybrid combined cooling, heating and power system. Energy Convers. Manag. 2019, 199, 111945. [Google Scholar] [CrossRef]
- Lozano, M.A.; Valero, A. Theory of the exergetic cost. Energy 1993, 18, 939–960. [Google Scholar] [CrossRef]
- da Silva Marques, A.; Carvalho, M.; Lourenço, A.B.; dos Santos, C.A.C. Energy, exergy, and exergoeconomic evaluations of a micro-trigeneration system. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 324. [Google Scholar] [CrossRef]
- Daghigh, R.; Oramipoor, H.; Shahidian, R. Improving the performance and economic analysis of photovoltaic panel using copper tubular-rectangular ducted heat exchanger. Renew. Energy 2020, 156, 1076–1088. [Google Scholar] [CrossRef]
- Zoghi, M.; Habibi, H.; Chitsaz, A.; Javaherdeh, K.; Ayazpour, M. Exergoeconomic analysis of a novel trigeneration system based on organic quadrilateral cycle integrated with cascade absorption-compression system for waste heat recovery. Energy Convers. Manag. 2019, 198, 111818. [Google Scholar] [CrossRef]
- Lima, K.M.; Delgado, D.B.M.; Martins, D.D.; Carvalho, M. Solar Energy and Biomass within Distributed Generation for a Northeast Brazil Hotel. Energies 2022, 15, 9170. [Google Scholar] [CrossRef]
- Melo, F.M.; Magnani, F.S.; Carvalho, M. Optimization of an integrated combined cooling, heat, and power system with solar and wind contribution for buildings located in tropical areas. Int. J. Energy Res. 2022, 46, 1263–1284. [Google Scholar] [CrossRef]
- Delgado, D.B.M.; Lima, K.M.; Cancela, M.C.; Siqueira, C.A.S.; Carvalho, M.; Souza, D.L.B. Trend analyses of electricity load changes in Brazil due to COVID-19 shutdowns. Electr. Power Syst. Res. 2021, 193, 107009. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Commercial and Residential Hourly Load Profiles. Available online: https://openei.org/datasets/files/961/pub/ (accessed on 13 February 2024).
- F-CHART SOFTWARE. Overview. In General Equation-Solving Program; F-CHART SOFTWARE: Madison, WI, USA, 2011; Available online: https://fchartsoftware.com/ees/ (accessed on 2 April 2024).
- Moran, J.M.; Shapiro, H.N. Fundamentals of Engineering Thermodynamics, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Mehr, A.S.; Mahmoudi, S.M.S.; Yari, M.; Chitsaz, A. Thermodynamic and exergoeconomic analysis of biogas fed solid oxide fuel cell power plants emphasizing on anode and cathode recycling: A comparative study. Energy Convers. Manag. 2015, 105, 596–606. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, R.; Mu, K.; Liu, X.; Sun, X.; Li, H. Exergetic and exergoeconomic evaluation of co-firing biomass gas with natural gas in CCHP system integrated with ground source heat pump. Energy Convers. Manag. 2019, 180, 622–640. [Google Scholar] [CrossRef]
- Alcântara, S.C.S.; Ochoa, A.A.V.; da Costa, J.A.P.; Michima, P.S.A.; Silva, H.C.N. Natural gas based trigeneration system proposal to an ice cream factory: An energetic and economic assessment. Energy Convers. Manag. 2019, 197, 111860. [Google Scholar] [CrossRef]
- Abreu, R.P.; Correia VH, L.; Lourenço, A.B.; da Silva Marques, A.; Carvalho, M. Thermoeconomic and thermoenvironmental analysis of the chilled water system in a shopping mall. Int. J. Refrig. 2022, 134, 304–311. [Google Scholar] [CrossRef]
- Yang, K.; Zhu, N.; Ding, Y.; Chang, C.; Wang, D.; Yuan, T. Exergy and exergoeconomic analyses of a combined cooling, heating, and power (CCHP) system based on dual-fuel of biomass and natural gas. J. Clean. Prod. 2019, 206, 893–906. [Google Scholar] [CrossRef]
- Delgado, D.B.M.; Carvalho, M.; Coelho Junior, L.M.; Chacartegui, R. Analysis of Biomass-fired Boilers in a Polygeneration System for a Hospital. Front. Manag. Res. 2018, 2, 1–13. [Google Scholar] [CrossRef]
- ISO 50001; Energy Management Systems—Requirements with Guidance for Use. International Organization for Standardization: Geneva, Switzerland, 2018.

| Parameter | Value | Unit |
|---|---|---|
| Mechanical efficiency | 40.6 | % |
| Rated power | 546 | kW |
| Biogas flow | 0.088 | kg/s |
| Temperature of jacket water | 90 | °C |
| Temperature of exhaust gas | 450 | °C |
| Mass flow of exhaust gas | 0.83 | kg/s |
| Parameter | Value | Unit |
|---|---|---|
| Cooling capacity | 35.16 | kW |
| Waste energy absorbed | 116.06 | kW |
| Coefficient of performance (COP) | 0.59 | - |
| Water outlet temperature in the chiller | 7.0 | °C |
| Water inlet temperature in the chiller | 12.0 | °C |
| Parameter | Value | Unit |
|---|---|---|
| Peak power | 80.00 | W |
| Operating temperature | −40.0 to 85.0 | °C |
| Monthly energy conversion rate (panel without heat exchanger) | 28.24 | kWh/m2 |
| Monthly energy conversion rate (panel with heat exchanger) | 30.34 | kWh/m2 |
| Area of PV panels | 20.90 | m2 |
| Rated power | 630 | kWh |
| Inverter | 3 | kW |
| Electrical efficiency | 12.52 | % |
| Cooling fluid inlet temperature | 35.0 | °C |
| Cooling fluid outlet temperature | 58.0 | °C |
| Average rate of solar radiation | 800.00 | kWh/m2 |
| Cooling fluid mass flow (Panel with 0.52 m2 surface area) | 0.012 | kg/s |
| Equipment | Mass Balance | Energy Balance | Exergy Balance |
|---|---|---|---|
| ICE | m1 = m2 + m10 (1) m8 = m9 (4) | Q1(biogas) = (m2 + m10)·h2 + m8·(h8 − h9) + W6 (2) | Ex1 + Ex9 = Ex2 + Ex6 + Ex8 + Ex10 + Exdestroyed (3) |
| Chiller | m2 = m3 (5) m4 = m5 (8) | m2·(h2 − h3) Qabsorber + W1(pump) = Qchiller (6) | Ex2 + Ex5 + W1(pump) + Exabsorber = Ex4 + Ex3 + Exdestroyed (7) |
| Water cooling (PV) | m12 = m13 (9) | Q16 + W2(pump) + m12 · (h13 − h12) = Qpcs (10) | Ex13 + Ex16 + W2(pump) = Ex12 + Expcs + Exdestroyed (11) |
| Tank (hot water) | - | m14 · (h14 − h15) = m12 · (h12 − h13) + m10·(h10 − h11) + m8 · (h8 − h9) + W3(pump) (12) | Ex8 + Ex10 + Ex12 + Ex15 + W3(pump) = Ex14 + Ex13 + Ex11 + Ex9 + Exdestroyed (13) |
| Proposition | Equation | Description |
|---|---|---|
| Proposition 01 | ∑Ex*(in) = ∑Ex*(out) (16) | Conservation of flows |
| Proposition 02 | (Exi*/Exi) = (Exo*/Exo) → ki = ko (17) | Input proposition |
| Proposition 03 | (Exi*/Exi) = (Exo′*/Exo’) →ki = ko′ (18) | Product proposition |
| Proposition 04 | Exi*/Exi = 0 (19) | Loss proposition |
| Proposition 05 | Exi* = Exi (20) | Proposition of lack of valuation |
| Equipment | Value (USD/h) | Reference |
|---|---|---|
| Cost of biogas: C1 | 6.54 | [30] |
| ICE: Z1 | 1.30 | [31] |
| Evaporator (chiller): Z4 | 0.48 | [31] |
| PV cooling system (Pump and heat exchanger): Z12 | 0.09 | Adapted from [23] |
| Heat recovery: Z14 | 0.55 | [31] |
| Equipment | P(1) 01 | P(1) 02 | P(1) 03 | P(1) 04 | P(1) 05 |
|---|---|---|---|---|---|
| Internal combustion engine | Ex1* = Ex2* + Ex6* +(Ex8* − Ex9*) + Ex10* (22) | (Ex1* + Ex9*)/(Ex1 + Ex9) = (Ex2* + Ex10* +Ex8* + Ex6*)/(Ex2* + Ex10* + Ex8* + Ex6*) (23) | (Ex2* + Ex10*)/ (Ex2 + Ex10) = (Ex8*-Ex9*)/ (Ex8-Ex9) (24) | Ex11* = 0 (25) | Ex1* = Ex1 (26) |
| Chiller | (Ex2* − Ex3*) + Ex5* + Exw1* = Ex4* (27) | - | - | Ex3* = 0 (28) | Ex5* = Ex5 (29) |
| Photovoltaic panels | Ex12* = Ex16* + Exw2* +Ex13* (30) | - | (Ex12*/Ex12) = (Ex13*/Ex13) (31) | - | Ex12* = Ex12 (32) |
| Hot water tank | Ex14* − Ex15* = Exw3 + (Ex8* − Ex9*) + (Ex10* − Ex11*) + (Ex12* − Ex13*) (33) | - | - | Ex15* = 0 (34) | - |
| Equipment | Cost (USD/h) | Auxiliary eq.R |
|---|---|---|
| Internal combustion engine | C1 + Z1 = C2 + C10 + C8 + C6 (35) | (C8 − C9)/(Ex8 − Ex9) = (C2 + C10)/(Ex2 + Ex10) (36) |
| Chiller | C2 + C5 + Z4 = C4 (37) | C4/Ex4 = (C2 + C5)/(Ex2 + Ex5) (38) |
| Photovoltaic panels | C12 + Z12 = C13 (39) | C12/Ex12 = C13/Ex13 (40) |
| Hot water tank | C10 + (C12 − C13) + (C8 − C9) Z14 = C14 (41) | - |
| Cost Rate | Reference [USD/h] | −10% [USD/h] | +10% [USD/h] |
|---|---|---|---|
| Biogas | 6.54 | 5.886 | 7.194 |
| Operation: ICE | 1.30 | 1.170 | 1.430 |
| Operation: Chiller | 0.48 | 0.432 | 0.528 |
| Operation: Tank | 0.11 | 0.099 | 0.121 |
| State | T [°C] | P [bar] | m [kg/s] | h [kJ/kg] | s [kJ/(kg.K)] | ex [kJ/kg] | Ex [kW] |
|---|---|---|---|---|---|---|---|
| 1 (Biogas) | 30.1 | 1.02 | 0.0613 | 4638.00 | 11.62 | 18,570.00 | 1138.34 |
| 1 (Air) | 25.0 | 1.02 | 0.528 | 298.60 | 5.69 | 0 | 0 |
| 2 | 450.0 | 2.40 | 0.258 | 465.44 | 5.85 | 385.90 | 99.56 |
| 3 | 70.0 | 1.17 | 0.258 | 72.40 | 0.91 | 116.30 | 29.23 |
| 4 | 7.0 | 1.34 | 1.060 | 29.51 | 0.11 | 93.52 | 99.13 |
| 5 | 12.0 | 1.34 | 1.060 | 50.46 | 0.18 | 112.60 | 119.36 |
| 8 | 90.0 | 2.80 | 0.438 | 377.00 | 1.19 | 413.80 | 181.24 |
| 9 | 30.0 | 2.80 | 0.438 | 125.80 | 0.44 | 181.50 | 79.50 |
| 10 | 450.0 | 2.40 | 0.331 | 465.44 | 5.85 | 385.90 | 120.57 |
| 11 | 70.0 | 1.17 | 0.331 | 72.40 | 0.91 | 116.30 | 36.34 |
| 12 | 58.0 | 1.10 | 0.480 | 242.90 | 0.81 | 289.40 | 138.91 |
| 13 | 35.0 | 1.10 | 0.480 | 146.70 | 0.51 | 200.70 | 96.34 |
| 14 | 90.0 | 1.34 | 0.599 | 377.00 | 1.19 | 413.80 | 247.87 |
| 15 | 30.0 | 1.34 | 0.599 | 125.80 | 0.44 | 181.50 | 108.72 |
| State | Exergy Ex [kW] | Thermoeconomic Cost Ex* [kW] | k [kW/kW] | ηex | C [USD/h] |
|---|---|---|---|---|---|
| 1 (biogas) | 1138.34 | 1138.34 | 1.00 | 1.00 | 4.58 |
| 2 | 99.56 | 233.15 | 2.34 | 0.43 | 0.69 |
| 3 | 29.23 | 0.00 | 0.00 | - | 0.00 |
| 4 | 99.13 | 352.60 | 3.56 | 0.28 | 1.73 |
| 5 | 119.36 | 119.36 | 1.00 | 1.00 | 0.83 |
| 6 | 385.70 | 385.70 | 1.00 | 1.00 | 2.69 |
| 7 | 373.80 | 373.80 | 1.00 | 1.00 | 2.69 |
| 8 | 181.24 | 423.28 | 2.34 | 0.43 | 1.26 |
| 9 | 79.50 | 185.65 | 2.34 | 0.43 | 0.55 |
| 10 | 120.57 | 281.56 | 2.34 | 0.43 | 0.84 |
| 11 | 36.34 | 0.00 | 0.00 | - | 0.00 |
| 12 | 138.91 | 139.34 | 1.43 | 0.70 | 0.03 |
| 13 | 96.34 | 94.79 | 1.40 | 0.71 | 0.02 |
| 14 | 247.87 | 844.19 | 3.41 | 0.29 | 1.70 |
| 15 | 108.72 | 0.00 | 0.00 | - | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreira, J.L.B.; Marques, A.d.S.; Lago, T.G.S.d.; Arruda, V.C.d.L.; Carvalho, M. Thermoeconomic Evaluation of a High-Performance Solar Biogas Polygeneration System. Energies 2024, 17, 4172. https://doi.org/10.3390/en17164172
Moreira JLB, Marques AdS, Lago TGSd, Arruda VCdL, Carvalho M. Thermoeconomic Evaluation of a High-Performance Solar Biogas Polygeneration System. Energies. 2024; 17(16):4172. https://doi.org/10.3390/en17164172
Chicago/Turabian StyleMoreira, José Luciano Batista, Adriano da Silva Marques, Taynara Geysa Silva do Lago, Victor Carlos de Lima Arruda, and Monica Carvalho. 2024. "Thermoeconomic Evaluation of a High-Performance Solar Biogas Polygeneration System" Energies 17, no. 16: 4172. https://doi.org/10.3390/en17164172
APA StyleMoreira, J. L. B., Marques, A. d. S., Lago, T. G. S. d., Arruda, V. C. d. L., & Carvalho, M. (2024). Thermoeconomic Evaluation of a High-Performance Solar Biogas Polygeneration System. Energies, 17(16), 4172. https://doi.org/10.3390/en17164172