Optimal Operation of a Novel Small-Scale Power-to-Ammonia Cycle under Possible Disturbances and Fluctuations in Electricity Prices
Abstract
1. Introduction
2. Power-to-Ammonia Optimization Background
| Authors and Year | Ammonia Application | Ammonia Production | Software Employed | Problem Formulation | Problem Type | Optimization Solver or Approach | Objective Function |
|---|---|---|---|---|---|---|---|
| Flórez-Orrego and de Oliveira Junior [29], 2017 | Methane-based ammonia production | 1000 t/d | Aspen HYSYS® V8.6 | Internally | NLP | Approach: SQP | Exergy destruction |
| Demirhan et al. [31], 2018 | Natural gas, biomass-based ammonia production, and P2A | ≤1000 t/d | GAMS® V24.4.5 | By hand | MINLP | Approach: B&B | Levelized cost of ammonia |
| Matos et al. [35], 2020 | Ammonia synthesis reactor | 5 t/d (calculated from data provided) | MATLAB® | By hand | ODE | Approach: Iteration of Runge–Kutta and Derivative-Free Direct Search Method | Nitrogen conversion and economic return |
| Osman et al. [44], 2020 | P2A | 1840 t/d | Aspen Plus® [45] with Python® [46] | By hand | DLP | GUROBI® [47] | Levelized cost of ammonia |
| Wang et al. [48], 2020 | P2A and nitric acid production | 510–680 t/d | gPROMS® [49] | Internally | DNLP | Approach: SQP [50] | Cost of ammonia |
| Kelley et al. [51], 2021 | P2A | 11–13 t/d (calculated from data provided) | gPROMS® V1.3.1 | Internally | DNLP | Not disclosed | Cost of electric power |
| Deng et al. [52], 2022 | P2A | 240 t/d (calculated from data provided) | UniSim® [53] | Internally | DNLP | Not disclosed | Energy consumption |
| Nozari et al. [54], 2022 | Energy Hub (power, heat, hydrogen, and ammonia production from natural gas and P2A) | 0.07 t/d (calculated from data provided) | GAMS® | By hand | DMILP | CPLEX® [55] | Exergy destruction and operating costs |
| Andrés-Martínez et al. [56], 2023 | P2A | 61.2 t/d (calculated from data provided) | JuMP® [57] | By hand | DNLP | Approach: time and space discretization and then IPOPT® [39] | Ammonia production |
| Wang et al. [58], 2023 | P2A | 10.8 t/d (calculated from data provided) | Not disclosed | By hand | DNLP under uncertainties | Approach: Markov Decision Process [59] | Profit |
| Kong et al. [60], 2023 | Renewable microgrid (P2H2P and P2A2P) | 2.2 t/d (calculated from data provided) | MATLAB Simulink® V2022a [61] with Pyomo® Python V3.9. [62] | Internally | DMILP | Not disclosed | Operating costs |
| This study | P2A | 0.04 t/d | MOSAIC® V3.0.1 with NEOS® | By hand | NLP and DNLP | ANTIGONE®, CONOPT®, IPOPT®, KNITRO®, MINOS®, PATHNLP® and SNOPT® | Ammonia production and profit |
3. Methods
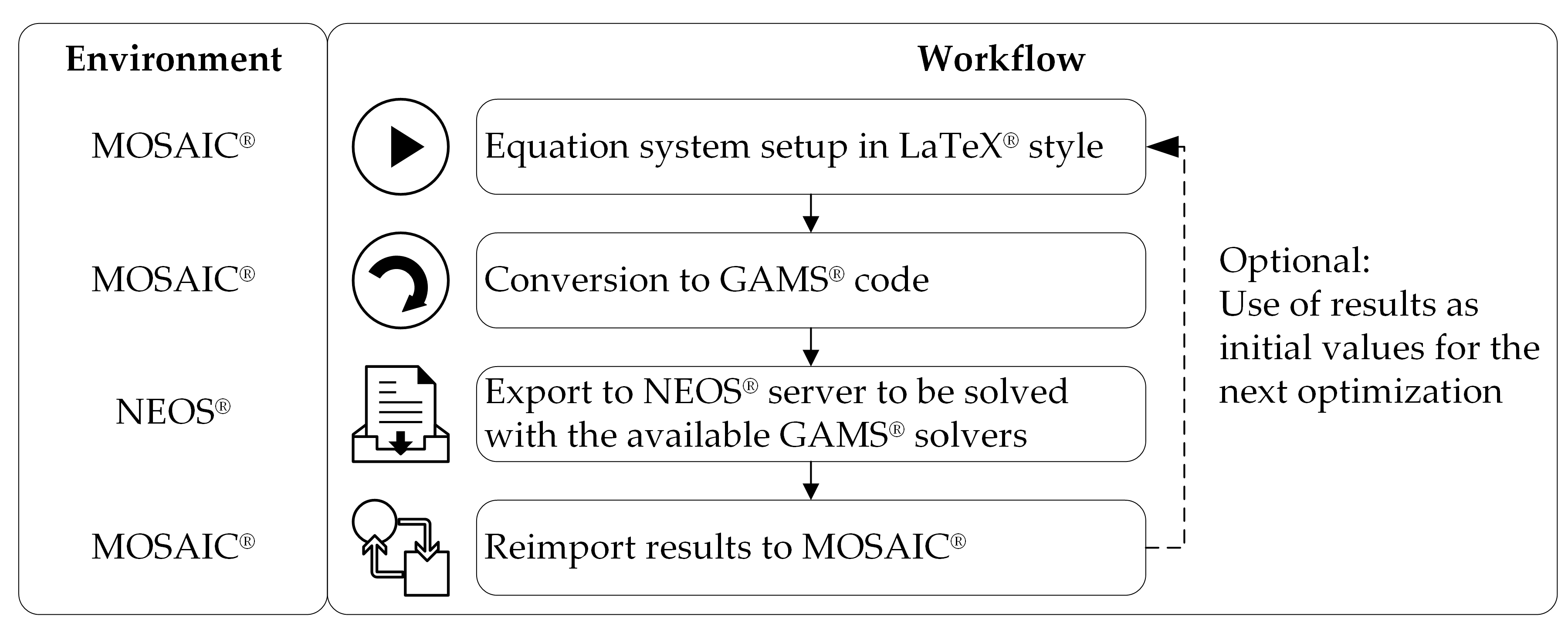
3.1. The MOSAIC®-NEOS® Optimization Approach
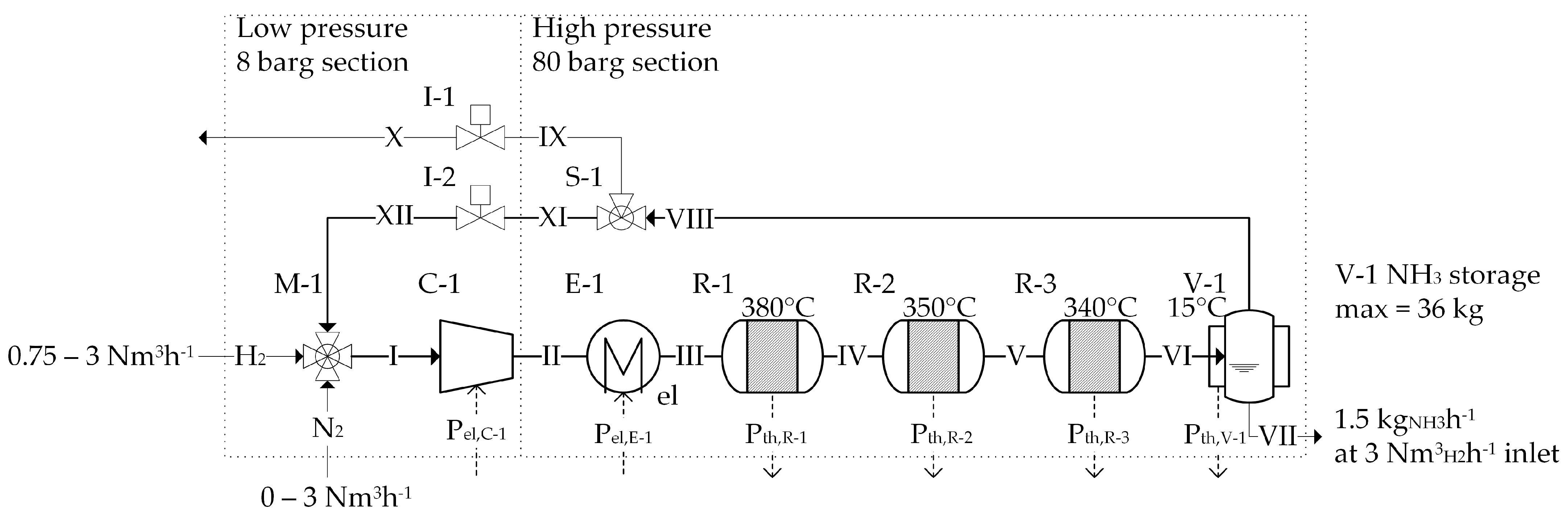
3.2. The FLEXnCONFU P2A System
3.3. MOSAIC®-NEOS® Optimization Setups
| Mole/mass balance | |
| Mole flow H2 into R-1 | |
| Mole flow H2 in R-1 (integrations steps u = 1, 2, …, 9 = U) | |
| Mole flow H2 out of R-1 | |
| Reaction kinetics rate of reaction (integrations steps u = 1, 2, …, 9 = U) [77] | |
| Reaction kinetics continued | |
| Reaction kinetics continued | |
| Reaction kinetics continued | |
| Energy balance | |
| Energy balance | |
| Mole specific enthalpy H2 III [75,76,77] | |
| Entropy balance | |
| Entropy balance | |
| Molar specific entropy H2 III [75,76,77] |
| Impulse/pressure equilibrium | |
| Pressure loss neglected | |
| Pressure loss neglected | |
| Temperature equilibrium | |
| Uniform outlet temperature | |
| Chemical equilibrium | |
| NH3 vapour–liquid equilibrium with ideal liquid and real vapor phase | |
| NH3 vapour pressure [75,76,77] | |
| Mole/mass balance | |
| Mole balance NH3 | |
| Storage of liquid NH3 |
3.3.1. Disturbance Optimization Setup
3.3.2. Dynamic Optimizations Setup
4. Results and Discussion
4.1. Disturbance Optimization Results and Discussion
4.1.1. Initial and Design Case
4.1.2. High-Pressure Case
4.1.3. Electrolyser Load Case
4.1.4. Inlet Ratio Case
4.1.5. Purge Ratio Case
4.1.6. Condensation Temperature Case
4.1.7. Low Reactor Inlet Temperature Case
4.1.8. High Reactor Inlet Temperature Case
4.2. Dynamic Optimization Results and Discussion
5. Conclusions
Author Contributions
Funding
 .
.Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
| Symbols | ||
| B&B | Branch and bound | |
| C-1 | Compressor | |
| DLP | Dynamic linear problem | |
| DMILP | Dynamic mixed integer linear problem | |
| DNLP | Dynamic nonlinear problem | |
| E-1 | Electric heater | |
| FLEXnCONFU | Flexibilize combined cycle power plant through power-to-X solutions using non-conventional fuels | |
| GHG | Greenhouse gas | |
| H2 | Hydrogen | |
| I, II, …, XII | Stream numbers | |
| I-1, I-2 | Recycle and purge valve | |
| M-1 | Mixer | |
| MILP | Mixed integer linear problem | |
| MINLP | Mixed integer nonlinear problem | |
| N2 | Nitrogen | |
| NH3 | Ammonia | |
| NLP | Nonlinear problem | |
| P2A | Power-to-Ammonia | |
| P2A2P | Power-to-Ammonia-to-Power | |
| P2H2P | Power-to-Hydrogen-to-Power | |
| R-1, R-2, R-3 | Reactor Section 1, Section 2 and Section 3 | |
| S-1 | Splitter | |
| SQP | Sequential quadratic programming | |
| V-1 | Condenser/Separator | |
| Mathematical Symbols | ||
| Equation of state polynomial enthalpy and entropy constants | ||
| Reaction kinetics variables | ||
| Reaction kinetics constants | ||
| Boundary function | ||
| Vector of constants | ||
| Reactor free cross-section | m2 | |
| Vector of constraint functions | ||
| Enthalpy flow | kmol h−1 | |
| Reaction kinetics constant | kmol h−1 kg−1 | |
| Mass stream | kg h−1 | |
| Catalyst mass | kg | |
| Molar stream | kmol h−1 | |
| Pressure | barg | |
| Electric power | kW | |
| Thermal power | kW | |
| Rate of reaction | kmol h−1 m−3 | |
| Molar gas constant | J mol−1 K−1 | |
| Entropy flow | kmol h−1 K | |
| Penalty parameter | ||
| Temperature | K | |
| Vector of variables | ||
| Molar fraction | kmol kmol−1 | |
| Objective function | ||
| Greek Symbols | ||
| R-1 integration step size forward difference method | m | |
| Energetic degree of efficiency | kJ kJ−1 | |
| Stoichiometric coefficient | ||
| Price | EUR kg−1; EUR kWh−1 | |
| Time constant of 24 h | h | |
| Fugacity coefficient | ||
| Subscripts | ||
| dep | Dependent | |
| gen | Generation | |
| i | Iteration step | |
| lb | Lower bound | |
| LV | Liquid–vapour | |
| max | Maximum | |
| Opt | Optimization | |
| T | Time step | |
| Tot | Total | |
| U | R-1 integration step forward difference method | |
| Ub | Upper bound |
References
- AVISO. Mean Sea Level. Available online: https://www.aviso.altimetry.fr/en/index.php?id=1599#c12195 (accessed on 5 January 2024).
- United Nations. World Population to Reach 8 Billion This Year, as Growth Rate Slows. Available online: https://news.un.org/en/story/2022/07/1122272 (accessed on 23 January 2024).
- Masterson, V.; Hall, S. Sea Level Rise: Everything You Need to Know. Available online: https://www.weforum.org/agenda/2022/09/rising-sea-levels-global-threat/ (accessed on 23 January 2024).
- German Federal Ministry for Economic Affairs and Energy. The National Hydrogen Strategy. Available online: https://www.bmbf.de/bmbf/shareddocs/downloads/files/bmwi_nationalewasserstoffstrategie_eng_s01.pdf?__blob=publicationFile&v=2 (accessed on 5 January 2024).
- European Commission. The Role of Hydrogen in Meeting Our 2023 Climate and Energy Targets. Available online: https://ec.europa.eu/commission/presscorner/api/files/attachment/869385/Hydrogen_Factsheet_EN.pdf.pdf (accessed on 11 August 2024).
- European Commission. The European Green Deal: Delivering the EU’s 2030 Climate Targets. Available online: https://ec.europa.eu/commission/presscorner/api/files/attachment/876248/FF55_DeliveringOnTheProposals_Factsheet.pdf.pdf (accessed on 11 August 2024).
- International Energy Agency. The Future of Hydrogen; OECD: Paris, France, 2019; ISBN 9789264418738. [Google Scholar]
- Bram, S.; de Ruyck, J. Exergy analysis tools for Aspen applied to evaporative cycle design. Energy Convers. Manag. 1997, 38, 1613–1624. [Google Scholar] [CrossRef]
- Stephan, P.; Kabelac, S.; Kind, M.; Mewes, D.; Schaber, K.; Wetzel, T. VDI-Wärmeatlas; Springer: Berlin/Heidelberg, Germany, 2019; ISBN 978-3-662-52988-1. [Google Scholar]
- Atchison, J. Large-Scale Ammonia Imports to Hamburg, Brunsbüttel. Available online: https://www.ammoniaenergy.org/articles/large-scale-ammonia-imports-to-hamburg-brunsbuttel/ (accessed on 15 May 2023).
- Atchison, J. Securing Market Access for Early Canadian Export Projects. Available online: https://ammoniaenergy.org/articles/securing-market-access-for-early-canadian-export-projects/?mc_cid=d8c7f916d7&mc_eid=d2d2750d43 (accessed on 8 April 2024).
- Tagesschau. Energieversorgung—Erster Liefervertrag für “Grünen” Wasserstoff. Available online: https://www.tagesschau.de/wirtschaft/energie/wasserstoff-import-liefervertrag-100.html (accessed on 12 July 2024).
- International Energy Agency. Ammonia Technology Roadmap: Towards More Sustainable Nitrogen Fertiliser Production. Available online: https://iea.blob.core.windows.net/assets/6ee41bb9-8e81-4b64-8701-2acc064ff6e4/AmmoniaTechnologyRoadmap.pdf (accessed on 25 April 2023).
- Rogers, M.; Delasalle, F.; Speelman, E.; Hoffman, J.; Shah, T.; Wuellenweber, J.; Miranda, J.P.; de Villepin, L.; Witteveen, M.; Isabirye, A.; et al. Making Net-Zero Ammonia Possible: An Industry-Backed, 1.5 °C-Aligned Transition Strategy. Available online: https://missionpossiblepartnership.org/wp-content/uploads/2022/09/Making-1.5-Aligned-Ammonia-possible.pdf (accessed on 15 May 2023).
- Appl, M. Ammonia, 1. Introduction. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co.: Weinheim, Germany; KGaA: Darmstadt, Germany, 2000; ISBN 3527306730. [Google Scholar]
- Appl, M. Ammonia, 2. Production Processes. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co.: Weinheim, Germany; KGaA: Darmstadt, Germany, 2000; ISBN 3527306730. [Google Scholar]
- Appl, M. Ammonia, 3. Production Plants. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co.: Weinheim, Germany; KGaA: Darmstadt, Germany, 2000; ISBN 3527306730. [Google Scholar]
- Travis, A.S. Nitrogen Capture; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-68962-3. [Google Scholar]
- Bazzanella, A.M.; Ausfelder, F. DECHEMA Gesellschaft für Chemische Technik und Biotechnologie e.V. Low Carbon Energy and Feedstock for the European Chemical Industry: Technology Study; DECHEMA e.V.: Frankfurt am Main, Germany, 2017; ISBN 978-3-89746-196-2. [Google Scholar]
- Rouwenhorst, K.H.R.; Krzywda, P.M.; Benes, N.E.; Mul, G.; Lefferts, L. Ammonia, 4. Green Ammonia Production. Ullmann’s Encyclopedia of Industrial Chemistry; Wiley: Hoboken, NJ, USA, 2000; pp. 1–20. ISBN 9783527303854. [Google Scholar]
- Verleysen, K.; Parente, A.; Contino, F. How sensitive is a dynamic ammonia synthesis process? Global sensitivity analysis of a dynamic Haber-Bosch process (for flexible seasonal energy storage). Energy 2021, 232, 121016. [Google Scholar] [CrossRef]
- Rouwenhorst, K.H.R. Flexible Ammonia Synthesis: Shifting the Narrative Around Hydrogen Storage. Available online: https://www.ammoniaenergy.org/articles/flexible-ammonia-synthesis-shifting-the-narrative-around-hydrogen-storage/ (accessed on 15 May 2023).
- Schmuecker, J. The carbon-free farm. IEEE Spectr. 2019, 56, 30–35. [Google Scholar] [CrossRef]
- Schmuecker Renewable Energy. Renewable Hydrogen and Ammonia Generation: Carbon-Free Fuel Production on the Farm. Available online: https://solarhydrogensystem.com/applications/renewable-hydrogen-and-ammonia-generation/ (accessed on 12 January 2024).
- The Fertilizer Institute. Fertilizer Product Fact Sheet Ammonia. Available online: https://www.cropscience.bayer.us/articles/bayer/fall-spring-anhydrous-ammonia-applications (accessed on 12 January 2024).
- Palys, M.J.; Wang, H.; Zhang, Q.; Daoutidis, P. Renewable ammonia for sustainable energy and agriculture: Vision and systems engineering opportunities. Curr. Opin. Chem. Eng. 2021, 31, 100667. [Google Scholar] [CrossRef]
- European Commission. FLEXnCONFU. Available online: https://flexnconfu.eu/ (accessed on 12 January 2024).
- Grant Agreement Number 884157—FLEXnCONFU. European Union’s Horizon 2020 Research and Innovation Programme. 2020. [Google Scholar]
- Flórez-Orrego, D.; de Oliveira, S., Jr. Modeling and optimization of an industrial ammonia synthesis unit: An exergy approach. Energy 2017, 137, 234–250. [Google Scholar] [CrossRef]
- Aspen Tech. Aspen HYSYS. Available online: https://www.aspentech.com/en/products/engineering/aspen-hysys (accessed on 2 February 2024).
- Demirhan, C.D.; Tso, W.W.; Powell, J.B.; Pistikopoulos, E.N. Sustainable ammonia production through process synthesis and global optimization. AIChE J. 2019, 65, e16498. [Google Scholar] [CrossRef]
- McCarl, B.A.; Meeraus, A.; van der Eijk, P.; Bussieck, M.; Dirkse, S.; Nelissen, F. McCarl Expanded GAMS User Guide Version 24.6. 2022. Available online: https://www.gams.com/mccarlGuide/mccarlgamsuserguide.pdf (accessed on 20 February 2023).
- GAMS: General Algebraic Modeling System. GAMS Development Corp. Available online: https://www.gams.com/ (accessed on 20 February 2023).
- GAMS Software GmbH. GAMS Solver Manuals. Available online: https://www.gams.com/latest/docs/S_MAIN.html (accessed on 15 September 2023).
- Matos, K.B.; Carvalho, E.P.; Ravagnani, M.A.S.S. Maximization of the profit and reactant conversion considering partial pressures in an ammonia synthesis reactor using a derivative-free method. Can. J. Chem. Eng. 2021, 99, S232–S244. [Google Scholar] [CrossRef]
- MathWorks. MATLAB: Mathematik. Grafiken. Programmierung. Available online: https://de.mathworks.com/products/matlab.html (accessed on 25 January 2024).
- Floudas, C.A.; Misener, R. ANTIGONE: Algorithms for coNTinuous/Integer Global Optimization of Nonlinear Equations. Available online: https://www.gams.com/latest/docs/S_ANTIGONE.html (accessed on 8 February 2024).
- Drud, A. CONOPT. Available online: https://www.gams.com/latest/docs/S_CONOPT.html (accessed on 8 February 2024).
- COIN-OR Initiative. Ipopt. Available online: https://github.com/coin-or/Ipopt (accessed on 6 February 2024).
- GAMS Software GmbH. KNITRO. Available online: https://www.gams.com/latest/docs/S_KNITRO.html (accessed on 8 February 2024).
- Murtagh, B.A.; Saunders, M.A.; Murray, W.; Gill, P.E. MINOS. Available online: https://www.gams.com/latest/docs/S_MINOS.html (accessed on 8 February 2024).
- GAMS Software GmbH. PATHNLP. Available online: https://www.gams.com/latest/docs/S_PATHNLP.html (accessed on 8 February 2024).
- Gill, P.E.; Murray, W.; Saunders, M.A. SNOPT. Available online: https://www.gams.com/latest/docs/S_SNOPT.html (accessed on 8 February 2024).
- Osman, O.; Sgouridis, S.; Sleptchenko, A. Scaling the production of renewable ammonia: A techno-economic optimization applied in regions with high insolation. J. Clean. Prod. 2020, 271, 121627. [Google Scholar] [CrossRef]
- Aspen Tech. Aspen Plus: Advance Circular Economy Initiatives and Respond to Global Economic Challenges, Dynamic Market Conditions and Competitive Pressures by Improving Performance, Quality and Time-to-Market with the Best-In-Class Simulation Software for Chemicals, Polymers, Life Sciences and New Sustainability Processes. Available online: https://www.aspentech.com/en/products/engineering/aspen-plus (accessed on 25 January 2024).
- Python Software Foundation. Python. Available online: https://www.python.org/ (accessed on 25 January 2024).
- Gurobi Optimization. Gurobi Optimizer. Available online: https://www.gurobi.com/solutions/gurobi-optimizer/ (accessed on 2 February 2024).
- Wang, G.; Mitsos, A.; Marquardt, W. Renewable production of ammonia and nitric acid. AIChE J. 2020, 66, e16947. [Google Scholar] [CrossRef]
- Siemens. gPROMS: Digital Process Twin Technology. Available online: https://www.siemens.com/global/en/products/automation/industry-software/gproms-digital-process-design-and-operations.html (accessed on 27 January 2024).
- Process Systems Enterprise Limited. gPROMS Optimisation Guide: Release v3.5 June 2012. Available online: https://usermanual.wiki/Document/gPROMS20Optimisation20Guide.768469482/view (accessed on 5 February 2024).
- Kelley, M.T.; Do, T.T.; Baldea, M. Evaluating the demand response potential of ammonia plants. AIChE J. 2022, 68, e17552. [Google Scholar] [CrossRef]
- Deng, W.; Huang, C.; Li, X.; Zhang, H.; Dai, Y. Dynamic Simulation Analysis and Optimization of Green Ammonia Production Process under Transition State. Processes 2022, 10, 2143. [Google Scholar] [CrossRef]
- Honeywell. UniSim Products. Available online: https://process.honeywell.com/us/en/initiative/unisim-design-suite/unisim-products (accessed on 29 January 2024).
- Nozari, M.H.; Yaghoubi, M.; Jafarpur, K.; Mansoori, G.A. Multiobjective operational optimization of energy hubs: Developing a novel dynamic energy storage hub concept using ammonia as storage. Int. J. Energy Res. 2022, 46, 12122–12146. [Google Scholar] [CrossRef]
- IBM. IBM ILOG CPLEX Optimization Studio. Available online: https://www.ibm.com/de-de/products/ilog-cplex-optimization-studio (accessed on 2 February 2024).
- Andrés-Martínez, O.; Zhang, Q.; Daoutidis, P. Optimal Operation of a Reaction-Absorption Process for Ammonia Production at Low Pressure. Ind. Eng. Chem. Res. 2023, 62, 14456–14466. [Google Scholar] [CrossRef]
- Dunning, I.; Huchette, J.; Lubin, M. JuMP: A Modeling Language for Mathematical Optimization. SIAM Rev. 2017, 59, 295–320. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, P.; Zhuo, T.; Ye, H. Scheduling power-to-ammonia plants considering uncertainty and periodicity of electricity prices. Smart Energy 2023, 11, 100113. [Google Scholar] [CrossRef]
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; Wiley-Interscience: Hoboken, NJ, USA, 2005; ISBN 0-471-72782-2. [Google Scholar]
- Kong, B.; Zhang, Q.; Daoutidis, P. Dynamic Optimization and Control of a Renewable Microgrid Incorporating Ammonia. In Proceedings of the 2023 American Control Conference (ACC), San Diego, CA, USA, 31 May 2023–2 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 3803–3808. [Google Scholar]
- MathWorks. Simulink. Available online: https://www.mathworks.com/products/simulink.html (accessed on 29 January 2024).
- Pyomo. Pyomo. Available online: https://www.pyomo.org/ (accessed on 29 January 2024).
- Process Dynamics and Operations Group. MOSAICmodeling 3.0. Available online: https://mosaic-modeling.de/ (accessed on 17 February 2023).
- Esche, E.; Hoffmann, C.; Illner, M.; Müller, D.; Fillinger, S.; Tolksdorf, G.; Bonart, H.; Wozny, G.; Repke, J.-U. MOSAIC—Enabling Large-Scale Equation-Based Flow Sheet Optimization. Chem. Ing. Tech. 2017, 89, 620–635. [Google Scholar] [CrossRef]
- Czyzyk, J.; Mesnier, M.P.; More, J.J. The NEOS Server. IEEE Comput. Sci. Eng. 1998, 5, 68–75. [Google Scholar] [CrossRef]
- Gropp, W.; Moré, J.J. Optimization Environments and the NEOS Server; Gropp, W., Moré, J.J., Eds.; Argonne National Laboratory: Lemont, IL, USA, 1997.
- Dolan, E. The NEOS Server 4.0 Administrative Guide [Technical Memorandum]. arXiv 2001. [Google Scholar] [CrossRef]
- Knuth, D.E.; Lamport, L. The LaTeX Project. Available online: https://www.latex-project.org/ (accessed on 7 August 2024).
- Koschwitz, P.; Bellotti, D.; Liang, C.; Epple, B. Steady state process simulations of a novel containerized power to ammonia concept. Int. J. Hydrogen Energy 2022, 47, 25322–25334. [Google Scholar] [CrossRef]
- Koschwitz, P.; Bellotti, D.; Liang, C.; Epple, B. Dynamic Simulation of a Novel Small-scale Power to Ammonia Concept. Energy Proceedings Volume 28: Closing Carbon Cycles—A Transformation Process Involving Technology, Economy, and Society: Part III. Energy Proc. 2022, 28, 1–10. [Google Scholar] [CrossRef]
- Koschwitz, P.; Bellotti, D.; Sanz, M.C.; Alcaide-Moreno, A.; Liang, C.; Epple, B. Dynamic Parameter Simulations for a Novel Small-Scale Power-to-Ammonia Concept. Processes 2023, 11, 680. [Google Scholar] [CrossRef]
- Koschwitz, P.; Bellotti, D.; Liang, C.; Epple, B. Exergetic Comparison of a Novel to a Conventional Small-Scale Power-to-Ammonia Cycle. IJEX 2023, 42, 127–158. [Google Scholar] [CrossRef]
- Koschwitz, P.; Anfosso, C.; Bellotti, D.; Epple, B. Exergoeconomic comparison of a novel to a conventional small-scale power-to-ammonia cycle. Energy Rep. 2024, 11, 1120–1134. [Google Scholar] [CrossRef]
- Stein, O. Grundzüge der Nichtlinearen Optimierung; Springer: Berlin/Heidelberg, Germany, 2018; ISBN 978-3-662-55592-7. [Google Scholar]
- Barin, I.; Knacke, O. Thermochemical Properties of Inorganic Substances; Springer: Berlin/Heidelberg, Germany, 1973; ISBN 3-540-06053-7. [Google Scholar]
- Barin, I. Thermochemical Properties of Inorganic Substances: Supplement; Springer: Berlin/Heidelberg, Germany, 1977; ISBN 978-3-662-02295-5. [Google Scholar]
- Barin, I.; Knacke, O.; Kubaschewski, O. Thermochemical Properties of Inorganic Substances; Knacke, O., Ed.; Springer: Berlin/Heidelberg, Germany, 1977; ISBN 3-540-54014-8. [Google Scholar]


| Optimization Study | Description |
|---|---|
| Initial 300 | The lower bound of the optimal design case reactor temperature profile, i.e., . |
| Initial 450 | The upper bound of the optimal design case reactor temperature profile, i.e., . |
| Design | The optimal design case reactor temperature profile. |
| A lower and a higher outlet pressure of the compressor C-1 than the design case (75 and 85 vs. 80 barg) emulates a faulty performance of C-1 or the investment in a stronger compressor. | |
| Three lower electrolyser loads than the design case (13.5, 14.4, and 15.3 vs. 18 kWel) corresponding to H2 inlet flows of 0.100, 0.107, and 0.114 vs. 0.134 kmol h−1 emulate a reduced availability of renewable energy. | |
| Two lower and four higher molar hydrogen to nitrogen inlet ratios of stream H2 to N2 than the design case (2.8, 2.9, 2.99, 3.01, 3.02, and 3.03 vs. 2.96 molH2 h−1/molN2 h−1) emulate a faulty inlet flow control. | |
| Two lower and one higher molar purge split ratios of stream IX to XI in S-1 (0.001, 0.004, and 0.01 vs. 0.005 molIX h−1 molXI−1 h) emulate variations in the purge line. | |
| A lower and a higher temperature of the condenser V-1 than the design case (10 and 20 vs. 15 °C) emulates the investment in a better cooling system or a faulty performance of the existing cooling system. | |
| Three lower outlet temperatures of the electric preheater E-1, as well as the same lower temperatures in R-1 compared to the design case (317, 327, and 337 vs. 360 °C), emulate a faulty, too-weak performance for E-1, as well as electrical heating in R-1. For this scenario, only and are the optimization variables. | |
| Three higher outlet temperatures of the electric preheater E-1, as well as the same higher temperatures in R-1 compared to the design case (380, 390, and 400 vs. 360 °C), emulate a faulty, too-strong performance of E-1, as well as electrical heating in R-1. For this scenario, only and are the optimization variables. |
| Case | Optimization Variables | Objective Function z | Selected Dependent Variables | Selected Constants c | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial 300 | 300 | 300 | 300 | 1.037 | 49.81 | 48.03 | 0.091 | 0.0901 | 98.72 | 0.65 | 0.23 | 80 | 0.134 | 2.96 | 0.005 | 15 |
| Initial 450 | 450 | 450 | 450 | 1.246 | 44.27 | 35.54 | 0.121 | 0.0686 | 57.06 | 0.64 | 0.24 | 80 | 0.134 | 2.96 | 0.005 | 15 |
| Design | 360 | 336 | 324 | 1.501 | 2.91 | 1.94 | 0.650 | 0.0071 | 6.04 | 0.39 | 0.48 | 80 | 0.134 | 2.96 | 0.005 | 15 |
| 363 | 339 | 327 | 1.499 | 3.21 | 2.14 | 0.633 | 0.0075 | 6.51 | 0.42 | 0.45 | 75 | 0.134 | 2.96 | 0.005 | 15 | |
| 358 | 333 | 321 | 1.503 | 2.69 | 1.79 | 0.662 | 0.0069 | 5.70 | 0.37 | 0.51 | 85 | 0.134 | 2.96 | 0.005 | 15 | |
| 352 | 327 | 316 | 1.127 | 1.99 | 1.77 | 0.665 | 0.0051 | 4.28 | 0.37 | 0.51 | 80 | 0.100 | 2.96 | 0.005 | 15 | |
| 354 | 329 | 318 | 1.202 | 2.16 | 1.80 | 0.662 | 0.0055 | 4.60 | 0.38 | 0.50 | 80 | 0.107 | 2.96 | 0.005 | 15 | |
| 356 | 331 | 319 | 1.277 | 2.35 | 1.84 | 0.658 | 0.0059 | 5.00 | 0.38 | 0.50 | 80 | 0.114 | 2.96 | 0.005 | 15 | |
| 361 | 341 | 331 | 1.485 | 7.50 | 5.05 | 0.464 | 0.0144 | 23.54 | 0.24 | 0.64 | 80 | 0.134 | 2.80 | 0.005 | 15 | |
| 360 | 337 | 326 | 1.496 | 4.46 | 2.98 | 0.573 | 0.0096 | 12.20 | 0.29 | 0.59 | 80 | 0.134 | 2.90 | 0.005 | 15 | |
| 366 | 342 | 331 | 1.500 | 2.44 | 1.63 | 0.676 | 0.0064 | 2.87 | 0.63 | 0.24 | 80 | 0.134 | 3.00 | 0.005 | 15 | |
| 370 | 346 | 335 | 1.497 | 2.64 | 1.76 | 0.663 | 0.0066 | 2.56 | 0.71 | 0.17 | 80 | 0.134 | 3.01 | 0.005 | 15 | |
| 375 | 351 | 340 | 1.493 | 3.03 | 2.03 | 0.640 | 0.0072 | 2.56 | 0.76 | 0.12 | 80 | 0.134 | 3.02 | 0.005 | 15 | |
| 379 | 355 | 344 | 1.488 | 3.55 | 2.38 | 0.611 | 0.0080 | 2.77 | 0.79 | 0.09 | 80 | 0.134 | 3.03 | 0.005 | 15 | |
| 361 | 341 | 331 | 1.507 | 7.56 | 5.02 | 0.469 | 0.0145 | 23.77 | 0.24 | 0.64 | 80 | 0.134 | 2.96 | 0.001 | 15 | |
| 360 | 336 | 324 | 1.503 | 3.16 | 2.10 | 0.637 | 0.0075 | 7.09 | 0.36 | 0.51 | 80 | 0.134 | 2.96 | 0.004 | 15 | |
| 362 | 337 | 325 | 1.490 | 2.49 | 1.67 | 0.669 | 0.0065 | 4.05 | 0.49 | 0.38 | 80 | 0.134 | 2.96 | 0.010 | 15 | |
| 358 | 333 | 321 | 1.503 | 2.72 | 1.81 | 0.661 | 0.0069 | 5.65 | 0.38 | 0.51 | 80 | 0.134 | 2.96 | 0.005 | 10 | |
| 363 | 339 | 327 | 1.498 | 3.21 | 2.15 | 0.632 | 0.0076 | 6.61 | 0.41 | 0.44 | 80 | 0.134 | 2.96 | 0.005 | 20 | |
| 317 | 354 | 335 | 1.499 | 2.97 | 1.98 | 0.646 | 0.0077 | 6.44 | 0.42 | 0.45 | 80 | 0.134 | 2.96 | 0.005 | 15 | |
| 327 | 350 | 332 | 1.499 | 2.97 | 1.98 | 0.646 | 0.0076 | 6.35 | 0.42 | 0.46 | 80 | 0.134 | 2.96 | 0.005 | 15 | |
| 337 | 345 | 330 | 1.499 | 2.94 | 1.96 | 0.648 | 0.0074 | 6.24 | 0.41 | 0.47 | 80 | 0.134 | 2.96 | 0.005 | 15 | |
| 380 | 342 | 328 | 1.500 | 3.11 | 2.07 | 0.639 | 0.0073 | 6.18 | 0.40 | 0.47 | 80 | 0.134 | 2.96 | 0.005 | 15 | |
| 390 | 347 | 331 | 1.499 | 3.24 | 2.16 | 0.632 | 0.0074 | 6.28 | 0.41 | 0.46 | 80 | 0.134 | 2.96 | 0.005 | 15 | |
| 400 | 351 | 333 | 1.499 | 3.35 | 2.23 | 0.626 | 0.0075 | 6.36 | 0.42 | 0.46 | 80 | 0.134 | 2.96 | 0.005 | 15 | |
| Case | ANTIGONE® | CONOPT® | IPOPT® | KNITRO® | PATHNLP® |
|---|---|---|---|---|---|
| Design | ✓ | ✓ | ✓ | ✓ | |
| ✓ | ✓ | ✓ | |||
| ✓ | ✓ | ✓ | |||
| ✓ | ✓ | ✓ | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | |
| ✓ | ✓ | ✓ | |||
| ✓ | ✓ | ✓ | |||
| ✓ | ✓ | ✓ | ✓ |
| Failure Scenario | Reactor Temperature Profile Must Be | ||
|---|---|---|---|
| Pressure in the high-pressure section decreases | increased | ||
| Pressure in the high-pressure section increases | decreased | ||
| Inlet hydrogen and nitrogen streams decrease | decreased | ||
| Inlet hydrogen and nitrogen streams increase | increased | ||
| Inlet hydrogen-to-nitrogen ratio decreases | increased | ||
| Inlet hydrogen-to-nitrogen ratio increases | increased | ||
| Purging decreases | increased | ||
| Purging increases | increased | ||
| Condensation temperature decreases | decreased | ||
| Condensation temperature increases | increased | ||
| Reactor inlet/first section temperature decreases | increased | ||
| Reactor inlet/first section temperature increases | increased | ||
| Scenario | Successful Solver | Time Step | Varied Price of Electricity | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Accumulated Profit | |||||||||||||||
| ANTIGONE® | 1 | 0.44 | 0.134 | 0.045 | 0.87 | 54.9 | 2.40 | 1.60 | 0.679 | 0.0063 | 3.24 | 2.99 | 1.50 | 33.1 | |
| 2 | 1.67 | 0.034 | 0.011 | 1.06 | 164.3 | 0.47 | 1.26 | 0.711 | 0.0014 | 0.48 | 3.00 | 0.38 | 16.7 | ||
| 3 | 1.42 | 0.039 | 0.013 | 1.13 | 286.5 | 0.56 | 1.28 | 0.710 | 0.0016 | 0.57 | 3.00 | 0.44 | 0 | ||
| CONOPT® | 1 | 0.44 | 0.134 | 0.045 | 1.98 | 241.4 | 2.40 | 1.60 | 0.679 | 0.0063 | 3.24 | 2.99 | 1.50 | 6.5 | |
| 2 | 1.67 | 0.034 | 0.011 | 0.49 | 255.1 | 0.47 | 1.26 | 0.711 | 0.0014 | 0.48 | 3.00 | 0.38 | 3.8 | ||
| 3 | 1.42 | 0.039 | 0.013 | 0.59 | 286.5 | 0.56 | 1.28 | 0.710 | 0.0016 | 0.57 | 3.00 | 0.44 | 0 | ||
| ANTIGONE® | 1 | 1.46 | 0.034 | 0.011 | 0.00 | −59.9 | 0.47 | 1.26 | 0.711 | 0.0014 | 0.48 | 3.00 | 0.38 | 27.0 | |
| 2 | 1.14 | 0.089 | 0.030 | 0.63 | −92.4 | 1.41 | 1.41 | 0.696 | 0.0039 | 1.65 | 3.00 | 1.00 | 35.8 | ||
| 3 | 0.34 | 0.134 | 0.045 | 2.99 | 339.5 | 2.40 | 1.60 | 0.679 | 0.0063 | 3.24 | 2.99 | 1.50 | 0 | ||
| CONOPT® | 1 | 1.46 | 0.034 | 0.011 | 0.21 | −24.9 | 0.47 | 1.26 | 0.711 | 0.0014 | 0.48 | 3.00 | 0.38 | 22.0 | |
| 2 | 1.14 | 0.089 | 0.030 | 1.39 | 70.2 | 1.41 | 1.41 | 0.696 | 0.0039 | 1.65 | 3.00 | 1.00 | 12.5 | ||
| 3 | 0.34 | 0.134 | 0.045 | 2.02 | 339.5 | 2.40 | 1.60 | 0.679 | 0.0063 | 3.24 | 2.99 | 1.50 | 0 | ||
| IPOPT® | 1 | 1.46 | 0.034 | 0.011 | 0.59 | 39.7 | 0.47 | 1.26 | 0.711 | 0.0014 | 0.49 | 3.00 | 0.38 | 12.8 | |
| 2 | 1.14 | 0.089 | 0.030 | 1.24 | 109.6 | 1.41 | 1.41 | 0.696 | 0.0039 | 1.65 | 3.00 | 1.00 | 6.9 | ||
| 3 | 0.34 | 0.134 | 0.045 | 1.79 | 339.5 | 2.40 | 1.60 | 0.679 | 0.0063 | 3.24 | 2.99 | 1.50 | 0 | ||
| ANTIGONE® | 1 | 0.95 | 0.118 | 0.040 | 0.76 | −37.1 | 2.01 | 1.52 | 0.686 | 0.0054 | 2.57 | 3.00 | 1.32 | 31.4 | |
| 2 | 0.13 | 0.134 | 0.045 | 2.48 | 352.4 | 2.40 | 1.60 | 0.679 | 0.0063 | 3.28 | 2.99 | 1.50 | 7.9 | ||
| 3 | 1.50 | 0.034 | 0.011 | 0.71 | 409.5 | 0.47 | 1.26 | 0.711 | 0.0014 | 0.48 | 3.00 | 0.38 | 0 | ||
| CONOPT® | 1 | 0.95 | 0.118 | 0.039 | 1.06 | 12.9 | 2.01 | 1.52 | 0.689 | 0.0054 | 2.57 | 3.00 | 1.32 | 24.3 | |
| 2 | 0.13 | 0.134 | 0.045 | 2.51 | 407.8 | 2.40 | 1.60 | 0.679 | 0.0063 | 3.28 | 2.99 | 1.50 | 0 | ||
| 3 | 1.50 | 0.034 | 0.011 | 0.38 | 409.5 | 0.47 | 1.26 | 0.711 | 0.0014 | 0.48 | 3.00 | 0.38 | 0 | ||
| IPOPT® | 1 | 0.95 | 0.118 | 0.040 | 1.31 | 54.8 | 2.01 | 1.52 | 0.686 | 0.0054 | 2.57 | 3.00 | 1.32 | 18.3 | |
| 2 | 0.13 | 0.134 | 0.045 | 1.51 | 281.7 | 2.40 | 1.60 | 0.679 | 0.0063 | 3.28 | 2.99 | 1.50 | 18.0 | ||
| 3 | 1.50 | 0.034 | 0.011 | 1.13 | 409.5 | 0.47 | 1.26 | 0.711 | 0.0014 | 0.48 | 3.00 | 0.38 | 0 | ||
| KNITRO® | 1 | 0.95 | 0.118 | 0.040 | 1.39 | 68.6 | 2.01 | 1.52 | 0.686 | 0.0054 | 2.57 | 3.00 | 1.32 | 16.3 | |
| 2 | 0.13 | 0.134 | 0.045 | 1.34 | 266.1 | 2.40 | 1.60 | 0.679 | 0.0063 | 3.28 | 2.99 | 1.50 | 20.2 | ||
| 3 | 1.50 | 0.034 | 0.011 | 1.22 | 409.5 | 0.47 | 1.26 | 0.711 | 0.0014 | 0.48 | 3.00 | 0.38 | 0 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koschwitz, P.; Anfosso, C.; Guedéz Mata, R.E.; Bellotti, D.; Roß, L.; García, J.A.; Ströhle, J.; Epple, B. Optimal Operation of a Novel Small-Scale Power-to-Ammonia Cycle under Possible Disturbances and Fluctuations in Electricity Prices. Energies 2024, 17, 4171. https://doi.org/10.3390/en17164171
Koschwitz P, Anfosso C, Guedéz Mata RE, Bellotti D, Roß L, García JA, Ströhle J, Epple B. Optimal Operation of a Novel Small-Scale Power-to-Ammonia Cycle under Possible Disturbances and Fluctuations in Electricity Prices. Energies. 2024; 17(16):4171. https://doi.org/10.3390/en17164171
Chicago/Turabian StyleKoschwitz, Pascal, Chiara Anfosso, Rafael Eduardo Guedéz Mata, Daria Bellotti, Leon Roß, José Angel García, Jochen Ströhle, and Bernd Epple. 2024. "Optimal Operation of a Novel Small-Scale Power-to-Ammonia Cycle under Possible Disturbances and Fluctuations in Electricity Prices" Energies 17, no. 16: 4171. https://doi.org/10.3390/en17164171
APA StyleKoschwitz, P., Anfosso, C., Guedéz Mata, R. E., Bellotti, D., Roß, L., García, J. A., Ströhle, J., & Epple, B. (2024). Optimal Operation of a Novel Small-Scale Power-to-Ammonia Cycle under Possible Disturbances and Fluctuations in Electricity Prices. Energies, 17(16), 4171. https://doi.org/10.3390/en17164171









