Abstract
The geometry of an orifice is a major determinant of nozzle internal flow and cavitation, which directly govern spray atomization and consequently affect combustion and fuel economy in internal combustion engines. In this study, simulation models of the nozzle at different angles between the normal and the injection hole inlet cross-section and the injection hole axis, as well as with different injection hole cone angles (a positive angle between the injection hole axis and its walls implies a divergent hole), were investigated by means of a previously developed numerical model that was validated based on experimental data from X-ray image technology. The results indicate that as the angle between the normal and the injection hole inlet cross-section and the injection hole axis increases, the cavitation asymmetry within the injection hole intensifies, accompanied by a decrease in the gas volume fraction. On one side of the injection hole, the hydraulic flip width expands, while, on the other side of the injection hole, the flow state gradually changes from hydraulic flip to super-cavitation flow, transitional cavitation and fully reattached flow. The divergent orifice layout intensifies cavitation, and the higher the positive injection hole cone angle, the bigger the hydraulic flip width. The convergent layout of the injection hole suppresses cavitation, and cavitation inside the nozzle disappears completely when the injection hole cone angle is less than −10°.
1. Introduction
The transport sector is one of the most important areas of energy consumption, and with the increase in car ownership worldwide, energy demand for cars is also increasing [1,2]. Researchers are striving to reduce the fuel consumption and pollutant emissions of vehicles by means of innovative control strategies involving the fuel injection system [3,4,5], the combustion process and the engine torque [6,7,8] by means of the development of new injection systems [9] and by using green fuels [10]. E-fuels, also known as synthetic fuels, are gaseous or liquid fuels, such as e-ethane, e-kerosene and e-ethanol, produced through the use of renewable energy or decarbonized electricity and can play an important role in the automotive industry [11,12]. E-fuel can be a direct replacement for conventional fossil fuels, such as gasoline and diesel, to power vehicles with internal combustion engines with reduced life-of-cycle analysis CO2 emissions [13]. GDI injectors [14] are suitable for use with liquid e-fuel [15]. The fuel spray generally plays a decisive role in the realization of the high-efficiency and low-emission combustion of liquid fuels, and spray characteristics directly determine the quality of mixture formation, which is the main factor affecting the combustion process [16]. The study of e-fuel spray characteristics can contribute to the improvement of its injection control, which is of great significance to reduce fuel consumption and pollutant emissions from internal combustion engines.
Since e-fuel is a kind of mixture with complicated physical properties, it is feasible to use pure substances to study the spray characteristics. In particular, for GDI engines with high injection pressures, cavitation inside the nozzle has an increasing influence on the atomization quality of the fuel. Cavitation is the process of the formation, development and collapse of cavities (bubbles) of vapor or gas inside the liquid and at the liquid-solid interfaces when the local pressure inside the liquid is sufficiently reduced. Fuel cavitation inside the nozzle occurs not only due to the abovementioned liquid phase change (vaporous cavitation), but also due to the passage from the dissolved gas to the undissolved one (gaseous cavitation) during the flow expansion in the nozzle [17]. The main factors affecting cavitation include the properties of the liquid substance (viscosity, density, saturated vapor pressure, vortices, etc.), the hydrodynamic properties of the liquid flow (pressure gradient in the flow field and the evolution of the pressure with time, etc.) and the properties of the walls (porosity and roughness, etc.). The highly turbulent and complex multi-phase flow inside the nozzle, due to intense cavitation, can significantly affect the flow rate through the nozzle, as well as the break-up and atomization of the liquid core [17,18]. Akira Sou et al. [19] experimentally investigated the effects of cavitation in a nozzle on liquid jet atomization. They proposed that flow in nozzles can be divided into four regimes, including no cavitation (pure liquid flow), developing cavitation (or transitional cavitation), super cavitation and hydraulic flip. Qiu et al. [20] highlighted that the discharge coefficient of the nozzle decreases once injection pressure has increased during the cavitation development period. Giannadakis et al. [21] found the presence of a dependence correlation between cavitation structures and nozzle layout. Huang et al. [22], by means of an X-ray phase-contrast imaging technique, studied the hydraulic flip and its effect on the spray in a GDI injector. Cavitation has been studied by means of the particle image velocimetry (PIV) method across a Venturi pipe [23], showing that pressure drop, the ratio of inertial to viscous forces, i.e., the flow Reynolds number, and thermal effects influence the aeriform zone in terms of morphology and length. In [24], a combined suppression effect on cavitation was identified and quantified by means of a parameter (the so-called combined suppression parameter CSP) under different experimental conditions characterized by means of the cavitation number, the turbulent level and the thermodynamic parameter; cavitation intensity decreases as the CSP value increases. Yin et al. [25] discovered that cavitation in nozzles equipped with micro holes led to a higher spray angle and a smaller spray penetration. Wang et al. [26] observed the significant influence of internal nozzle cavitation on primary breakup, as well as the obvious alteration of the spray structure in high-pressure injection diesel engines. Zhang et al. [27] conducted a comprehensive investigation utilizing an integrated experimental-numerical simulation methodology to analyze the impact of cavitation phenomena on the material of the nozzle wall. Divergent nozzles exhibited greater susceptibility to erosion damage caused by cavitation than convergent nozzles.
Studies on cavitation flow within nozzles have indicated a close correlation between cavitation characteristics and fuel physical properties, injection pressure, fuel temperature and nozzle geometry. In particular, researchers have found that optimization of the nozzle layout can lead to greater flow coefficients and better atomization [28,29,30]. Payri et al. [31] confirmed that the geometrical configuration of the nozzle has a significant effect on the internal flow characteristics and influences the development of cavitation. Benajes et al. [32] and Soyama et al. [33] were able to assess experimentally the effect of both the convergent-divergent and cylindrical nozzles on cavitation. Cavitation always led to erosion and damage to the nozzle wall surface, and convergent-divergent nozzles exhibited higher flow stability and better flow characteristics than cylindrical and convergent nozzles [34]. Chen et al. [35] investigated the effects of the nozzle orifice conicity factor, the nozzle length-to-diameter ratio and the sac chamber volume on string cavitation and spray characteristics and, in particular, found that the length-to-diameter ratio had the most significant effect (smaller length-to-diameter ratios intensified string cavitation). Liao et al. [36] quantified that the cavitation produced by a divergent nozzle was twice that produced by a convergent nozzle under the same conditions. He et al. [37] found string cavitation to be a major contributor to spray instability and fluctuations, leading to the occurrence of large spray cone angles. Finally, Liu et al. [38] and Reto Balz et al. [39] investigated the relationships between the position of the cavitation source and the nozzle geometry by a combination of simulations and experiments: the cylindrical nozzle creates a flow field with more vapor than the organ-pipe and converging–diverging nozzles.
Numerical simulations make it possible to visualize phenomena that are difficult to observe experimentally and help to explain physical phenomena occurring in structures that are not detectable using experimental devices [40,41]. Hu et al. [42] investigated the taper nozzle coefficient and found that the cylindrical nozzle improves the spray atomization performance because it has the strongest cavitation. Yu et al. [43] numerically investigated the effect of the non-circular orifice cross-section of a GDI injector with various aspect ratios on the internal flow pattern and nozzle outlet flow parameters. The total vapor phase volume fraction of the elliptical orifice is smaller than that in the circular one, and the vapor phase fraction of the elliptical orifice decreases with an increase in the aspect ratio. Guo et al. [44] numerically observed that vortex cavitation is difficult to form if the number of injection holes is too large; in fact, the swirling flow in the multi-hole nozzle is inhibited. By using numerical simulations, Yang et al. [45] found that changes in the hole layout intensified the cavitation strength and breaking effect of the jet impact; a small orifice aspect ratio promotes the conversion of pressure energy to kinetic energy, leading to an increase in cavitation intensity. The influence mechanism of injection hole cone angles on spray performance is still incomplete and needs to be investigated, though it is regarded as a fundamental factor [46,47]. In a previous study [47], a simulation model was validated by using X-ray imaging experiments to show the impact of symmetric and asymmetric inlet angles of the flow on its flow evolution and on cavitation within the nozzle.
In the present study, the abovementioned validated numerical model was used to analyze different nozzle geometrical features in order to further investigate the effects of the angle between the normal injection hole inlet cross-section and the injection hole axis (inclination angle), as well as the cone angle of the injection holes, on the flow and cavitation characteristics within the nozzle. The obtained outcomes can represent a theoretical foundation for the subsequent optimization of the injector nozzle design.
2. Numerical Methodology
The employed numerical tool, previously validated in [46,47], features a reconstructed 3D model of the nozzle with geometric boundaries derived from X-ray CT scan technology and validated by means of the data of nozzle internal flow via X-ray image technology. In particular, the void area distribution shown by the outcomes of X-ray imaging experiments was compared to the void fraction distribution determined by the internal flow model, showing good agreement. A further validation of the model was performed by comparing the experimental and numerical results of the injected flow rate, which showed great consistency. Experimental tests were performed with water instead of gasoline for safety reasons. Phase contrast images were acquired with an elevated frame rate (2000 fps) and short exposure time (32.5 μs) [47].
This approach mentioned above ensures an accurate representation of the real nozzle geometry and, therefore, of the computational domain. The simulation itself was carried out using the commercial computational fluid dynamics (CFD) code CONVERGE. The Navier-Stokes partial differential equations were numerically solved; the multiphase flow model was established by means of the volume of fluid (VOF) method [48,49,50,51], and a RNG k-ε model was implemented to simulate turbulence. The Individual Species Solution (ISS) method, also labeled as compressible VOF, a mass-fraction-based solution method for VOF simulation, was used.
2.1. Model Setup and Meshing
A number of ideal nozzle models with different layouts were developed and employed as the geometrical boundaries in the simulation model. The simulation calculations for the nozzle internal flow and near-field spray characteristics were conducted using the same grid scale and model settings. Isooctane (IC8H18) was employed as the simulation medium instead of gasoline. The fuel injection pressure (Pinj) was set at 200 bar (the same as the test value), while the ambient pressure (Pamb) was maintained at 1 bar. A rough example of the computational domain is reported in Figure 1; the provided boundary conditions and the initialization of the computational domain are reported in Table 1. From a grid dependency test performed in [46], the base grid size was set to 0.06 mm, and an AMR adaptive refinement of 6 levels was performed in the injection hole area of the injector. Table 2 reports the physical properties of isooctane and air used in the cavitation modeling.
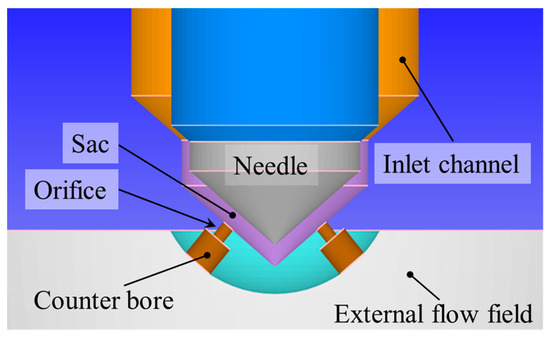
Figure 1.
The computational domain.

Table 1.
Initialization of computational domain and setting of boundary conditions for the simulation model.

Table 2.
Physical properties of the isooctane and air (T = 300 K).
2.2. Nozzle Structure Setting
The wall inclination angle and cone angle of the injection holes are important parameters that affect the cavitation characteristics of the fuel inside the nozzle, as revealed by the visualized experimental results of nozzle internal flows [46,47]. An appropriate tapering of the injection holes is effective in suppressing cavitation formation within the nozzles [52]. Different nozzle geometrical models with different wall inclinations and cone angles were designed to analyze the influence mechanism of such design features on the fuel flow characteristics inside the nozzle in depth.
The nozzle geometry is shown in Figure 2. As illustrated in Figure 2a for one of the injection holes (on the right in the picture), the inlet angle ω, which is related to the cone angle, separates the sac wall from that of the orifice. With reference to the right injection hole in the picture, the “left-side” wall indicates the hole wall that is closer to the needle axis, while the “right-side” wall refers to the wall of the hole further away from the needle axis. Specifically, the left-included angle ωin separates the sac wall from the orifice left-side wall, and the right-inlet-included angle, ωout, separates the sac wall from the right-side orifice wall. The inclination angles between the orifice walls and the direction oriented along the normal injection hole inlet section are evidenced in Figure 2b; the wall inclination angle between the normal section moving out from the orifice inlet cross-section area and the “left-side” injection hole wall is defined as φin (positive when clockwise), whereas the angle between the abovementioned normal and the “right-side” injection hole wall is labeled as φout (positive when counterclockwise). The injection hole cone angle φ0 is given by the angle included by the extension lines of the left-side and right-side walls of the orifice, and has a definite geometric relationship with the wall inclination angle, namely φ0 = φin + φout. Hence, φ0 = 0° denotes a cylindrical hole.
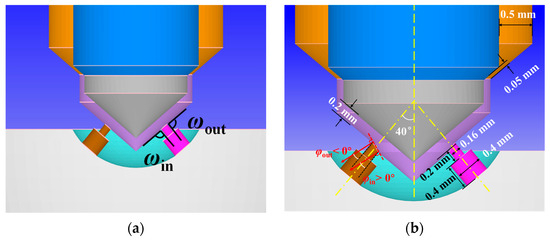
Figure 2.
Geometry schematic of the nozzle model for wall inclination angle φ ≠ 0°. (a) Left and right inlet-included angles; (b) Wall inclination angle φin = −φout > 0°.
The parameters of the five nozzles with different values of wall inclination angles are shown in Table 3. The nozzles are all equipped with two symmetrical injection holes (with the same sizes), and angles ω are equal, i.e., ωin = ωout = 90°. The injection holes of all nozzle models exhibit a cylindrical layout with equal modulus and opposite directions of left- and right-side wall inclination angles, specifically φin = −φout. The dimensions of the injection hole (hole diameter D = 0.16 mm, hole length L = 0.2 mm, counter bore diameter Dc = 0.4 mm and counter bore length Lc = 0.4 mm) are fixed for the five nozzles. Nozzle Na is used as a reference in the comparative analysis, and its wall inclination angles are φin = φout = 0°, while the injection hole inlet cross-section of the other nozzles is normally biased, with a right-side wall inclination angle φout < 0° and a left-side wall inclination angle φin > 0°, keeping φin = −φout (cylindrical hole). For this series of nozzles, when φin = −φout ≠ 0°, the normal direction of the orifice inlet cross-section deviates from the injection hole-axis.

Table 3.
The selected nozzles featuring different values of wall inclination angles.
The structural parameters for nozzle with different orifice cone angles are shown in Table 4. Figure 3 shows three different types of nozzles, including a cylindrical orifice with φ0 = 0°, a divergent orifice with φ0 > 0° and a convergent orifice with φ0 < 0°. The main dimensions of the nozzle remain constant (D = 0.16 mm, L = 0.2 mm, Dc = 0.4 mm, Lc = 0.4 mm), and the wall inclination angles of the injection holes at both sides are equal in modulus, namely ωin = ωout and φin = −φout (φ0 = 2φin = −2φout). The direction of the injection hole axis is always perpendicular to the wall of the sac, and the angle between the injection hole and the injector nozzle axes is maintained at 40°. Nozzle N3 is selected as a reference benchmark for the comparative analysis of the cylindrical nozzle layout ωin = ωout = 90° and φin = φout = 0°. By adjusting values of ωin and ωout to change the injection hole cone angle φ0, divergent nozzles N1 and N2, and convergent nozzles N4 and N5 can be obtained.

Table 4.
Structural parameters for nozzle with different orifice cone angles.
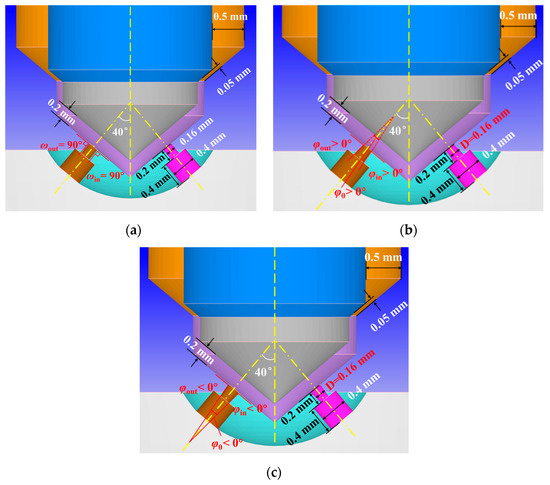
Figure 3.
Schematic structure of the nozzle geometry model with different orifice cone angles. (a) cylindrical orifice φ0 = 0°; (b) divergent orifice φ0 > 0°; (c) convergent orifice φ0 < 0°.
When the wall inclination angle φin/out increases or decreases, the size of the inlet-included angle ωin/out also changes, and the sum of ω and φ, referring to the same side, is equal to 90°, i.e., ωin + φin = ωout + φout = 90°. For a divergent nozzle (φ0 > 0°), ωin/out decreases compared to those of a cylindrical nozzle, while, for a convergent nozzle (φ0 < 0°), ωin/out increases.
Two dimensionless numbers, the void fraction αn and the cavitation asymmetry η, also defined in [47], are introduced in order to accurately characterize the cavitation inside the orifice. The void fraction αn is given by
where Vgas stands for the void in the injection hole (mm3), i.e., the injection hole volume filled with gas, and Vn is the volume of the injection hole (mm3). In order to assess if cavitation inside the orifice features a symmetrical behavior, the injection hole is split along the shaft section into two semi-cylinders. Vin indicates the void volume of the semi-cylinder closer to needle axis (mm3), and Vout is the void volume of the semi-cylinder further from the needle axis (mm3). Therefore, the parameter η is introduced:
Vin = Vout, η = 0 and the cavitation is symmetric, whereas if either Vin or Vout = 0, η = 1 and cavitation is fully asymmetric.
The presence of cavitation can reduce the flow-rate through the injection hole. The discharge coefficient, denoted as Cd, quantifies the ratio between the effective flow rate through the injection hole and the corresponding ideal liquid flow rate (which is only a function of the pressure drop across the orifice) [53]:
In the formula, is the actual flow rate (g/s), Aout is the cross-sectional area at the outlet of the injection hole (mm2), ρ is the liquid density(g/mm3), uth is Torricelli’s liquid velocity (m/s), ΔP = Pinj − Pamb is the pressure drop across the orifice, Cc is the area contraction coefficient, Pv represents the saturated vapor pressure of the fuel (bar) and CN represents the cavitation number. The link between the discharge coefficient and the cavitation number implies that the mass flow rate can serve as an indicator for the presence of cavitation phenomena [54].
3. Results and Discussion
3.1. Influence of the Wall Inclination Angle on Internal Flow and Cavitation Characteristics in Nozzle
The distribution of the void fraction (gas volume fraction) in the axial section for the considered nozzle injection hole featuring different wall inclination angles is shown in Figure 4, where a dashed line has also been added to indicate the trace of the inlet section. A void fraction equal to zero corresponds to the liquid phase; when the void fraction is equal to 1, it corresponds to the absence of the liquid phase. The simulation results of nozzle Na show that when the normal direction to the inlet section of the orifice aligns with the axis of the orifice (φin = φout = 0, Figure 4a), the gas-phase distribution within the orifice exhibits strong symmetry. Additionally, cavitation regions are formed at the orifice wall, extending from the inlet section to the outlet section. Moreover, the internal flow within the injection hole displays a distinct hydraulic flip regime for the considered pressure conditions of the test. As the normal direction of the injection hole inlet cross-section deviates from alignment with the injection hole axis, cavitation becomes progressively more asymmetric within the orifice and progressively intensifies with increasing φ (Figure 4b–e). In the picture, the cavitation on the wall side, where φout < 0° is suppressed, leads to a reduction in the size of the cavitation region; conversely, the cavitation on the wall side, where φin > 0° is intensified, results in an enlargement of the cavitation region.
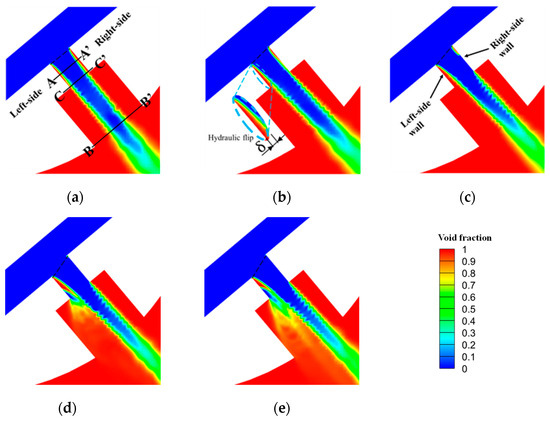
Figure 4.
Void fraction contours of orifice axial cross-section at different wall inclination angles φ. (a) Nozzle Na: φin = φout = 0°; (b) Nozzle Nb: φin = −φout = 5°; (c) Nozzle Nc: φin = −φout = 10°; (d) Nozzle Nd: φin = −φout = 15°; (e) Nozzle Ne: φin = −φout = 20°.
In order to further examine the influence of the wall inclination angle on the flow and cavitation characteristics within the injection hole, a comparative analysis was conducted on the contours depicting the gas volume distribution. These void fraction contours were generated for the central cross-section A-A′ of the orifice, the exit cross-section C-C′ of the orifice and the exit cross-section B-B′ of the counterbore, as illustrated in Figure 4a. The obtained results are presented in Figure 5. By combining Figure 4 and Figure 5, it is evident that when φin = φout = 0°, the cavitation phenomena in the 2D picture occur on both sides of the wall region of the orifice. The cavitation region extends towards the exit of the orifice, allowing downstream environment gases to enter the orifice along its wall surface; an annular gas layer is formed. During this phase, the fuel flow characteristics within the orifice can be classified as hydraulic flip [19]. Moreover, at the cross-section B-B′ of the counterbore exit, the liquid-phase fuel jet exhibits an elliptical shape, and this can be ascribed to the slight cavitation asymmetry that can be noticed in Figure 5a (cross-sections A-A′ and C-C′).

Figure 5.
Void fraction contours at different cross-sections for different wall inclination angle φ (A-A′: orifice central cross-section; B-B′: counter bore exit cross-section; C-C′: orifice exit cross-section). (a) Nozzle Na: φin = φout = 0°; (b) Nozzle Nb: φin = −φout = 5°; (c) Nozzle Nc: φin = −φout = 10°; (d) Nozzle Nd: φin = −φout = 15°; (e) Nozzle Ne: φin = −φout = 20°.
When φin = −φout = 5° (Figure 5b), several notable changes occur. The thickness of the gas layer on the left-side wall of the Nb orifice increases, while on the right-side wall, it decreases. Consequently, the fuel within the orifice becomes biased towards the right-side wall. In the orifice outlet cross-section C-C′, the red pure gas-phase region on the right side completely disappears, indicating the absence of an external downstream environment gas inlet. The gas-phase region on the right side that can be seen in section A-A′ primarily consists of vaporous fuel due to cavitation. The fuel flow characteristics on the right side of the orifice can be classified as super-cavitation flow, since the liquid flow reattaches to the nozzle wall in the proximity of the nozzle exit [55]. In contrast, the left-side wall of the orifice exhibits a hydraulic flip pattern, with an increase in the width of the hydraulic flip (δ, cf. Figure 4b). Furthermore, upon observing the cross-section B-B′ of the counterbore exit, the cross-section shape of the liquid-phase fuel jet does not exhibit significant changes, but the position of the fuel liquid core noticeably shifts towards the right side of the orifice due to the enlargement of δ.
When φin = −φout = 10° (Figure 4c and Figure 5c), the orifice semi-cylindrical side closer to the needle axis in nozzle Nc continues to exhibit a hydraulic flip state, with a further increase in δ. However, the fuel cavitation phenomenon on the opposite side is noticeably suppressed. The cavitation region experiences a significant reduction in size and does not extend up to the orifice exit. In both sections A-A′ and C-C′, the red gas-phase region on the right-side wall of Figure 5c completely disappears; this disappearance confirms that the fuel reattaches to the wall (cf. also Figure 4c). Therefore, the fuel flow state within the orifice undergoes significant changes. At this point, the fuel flow characteristics on the orifice semi-cylindrical side further from the needle can be classified as transitional cavitation flow; in fact, the fuel reattaches to the wall at around half of the nozzle height [55]. This phenomenon occurs due to the compression exerted by the cavitation region on the left side of the orifice. Along the wall of the orifice, elongation of the liquid phase takes place. Upon observing the B-B′ cross-section of the counterbore outlet, a transformation of the jet fuel cross-section from an ellipse to a crescent shape is obvious. This suggests a significant alteration in the liquid core shape. Furthermore, the interaction between the liquid phase and the gaseous phase is enhanced by a significant increase in the contact area between the downstream environment gas and the liquid-phase fuel surface.
As φ increases further to φin = −φout = 15° or 20°, the cavitation phenomena on the right side of the spray orifice disappear (cf. 2D images in Figure 4d,e). Consequently, the liquid-phase fuel comes into direct contact with the wall of the orifice, forming a turbulent boundary-layer flow. Simultaneously, the strong cavitation region formed on the orifice side, closer to the needle axis, intensifies and perturbs the liquid-phase fuel. This perturbation causes the gas-liquid interface to stretch and distort, leading to an unstable hydraulic flip. As a result, the fuel reattaches to the wall at almost half of the orifice axial length [55]. During this phase, the cross-section of the fuel jet continues to exhibit a crescent-shaped liquid core. Moreover, the degree of distortion on the jet surface increases, leading to an expanded contact area with the downstream environment gas. This change in the morphology of the liquid core, resulting from the alteration in the internal flow state, contributes to the breakup of the liquid core. Consequently, it enhances the atomization effect of the fuel jet.
The variation of void fraction (gas volume fraction) αn and cavitation asymmetry η with wall inclination angle φ normal to the inlet for each nozzle orifice are shown in Figure 6. As already mentioned, when φ augments, in the pictures in Figure 4 and Figure 5, the cavitation phenomena on the side with a negative wall inclination angle (φ < 0°), that is, the right side, are progressively suppressed. Simultaneously, the cavitation intensity on the opposite side increases, and the width of the hydraulic flip expands. As a final result, with the increment in φ, the total gas volume fraction within the orifice gradually decreases, and the η inside the orifice exhibits a significant increase. In particular, as φ increases to 20°, αn reduces by 42.7% compared to the φ = 0° condition, reaching a value of 0.171, while η approaches a value of 0.987, which is close to its theoretical maximum value of 1.0.

Figure 6.
Void fraction and cavitation asymmetry of orifice at different wall inclination angles φ.
Figure 7 reports the trends of the mass flow rate and the discharge coefficient Cd of the orifice with respect to the wall inclination angle. As φ increases, the discharge coefficient and the mass flow rate first show a monotonically increasing trend; when φin = −φout = 15°, the discharge coefficient attains its maximum value of Cd = 0.637, exhibiting a 1.93% increase compared to the φ = 0° case. As discussed, at φin = −φout = 15°, there is the complete disappearance of the cavitation area on the right side of the orifice, and further increases in φ cause the hydraulic flip width on the left side of the orifice to expand, leading to a reduction of the orifice effective flow area. The effect is a diminution of the discharge coefficient.

Figure 7.
Mass flow rate and flow coefficients of orifice with different wall inclination angles φ.
As shown in Figure 8, for comparison of the liquid core morphology between nozzles with different wall inclination angles φ, the D-D′ plane is the observation cross-section through the orifice axis. The variation in liquid core breakup length Lb with the wall inclination angle φ for each nozzle is shown in Figure 9. As φ increases, the cavitation intensity on the orifice’s left side, shown in Figure 8, intensifies, leading to an intensified gas phase. Simultaneously, the instability wave on the surface of the fuel jet gradually amplifies, leading to a reduction in the breakup length of the liquid core. As the φ surpasses 10°, the fuel in the liquid phase inside the orifice is pushed towards the right-side wall (cf. also Figure 5). The fuel jet progressively forms a semi-annular, hollow and unenclosed liquid core for the nozzles Nd and Ne. The liquid core extends and stretches on both sides of the axial cross-section of the nozzle, leading to an increase in the liquid core length Lb, with a rise in φ. In other words, the gas phase compresses the liquid core to make thickness smaller (cf. Figure 4), then the liquid core length increases.
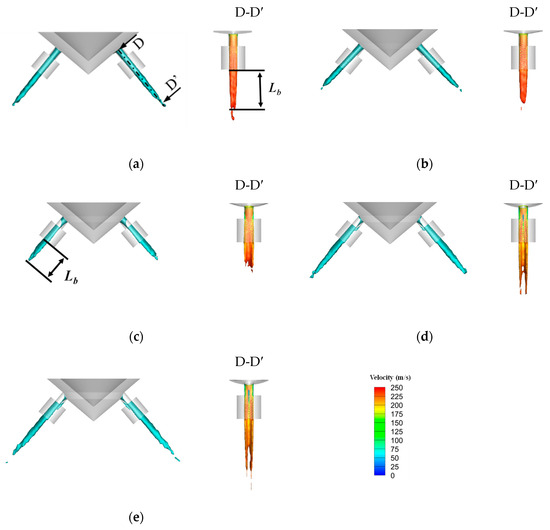
Figure 8.
Liquid core morphology of fuel jet inside nozzle with different wall inclination angles φ. (a) Nozzle Na: φin = φout = 0°; (b) Nozzle Nb: φin = −φout = 5°; (c) Nozzle Nc: φin = −φout = 10°; (d) Nozzle Nd: φin = −φout = 15°; (e) Nozzle Ne: φin = −φout = 20°.

Figure 9.
Liquid core breakup length Lb of fuel jet in nozzle with different wall inclination angles φ.
The variation of the mean turbulent kinetic energy TKE of the fuel jet with wall inclination angle φ is shown in Figure 10. As φ increases, the TKE of the liquid fuel jet gradually rises. The most significant increase in turbulence intensity occurs when φ increases from 5° to 10°. This can be attributed to the suppression of the cavitation on the right side of the orifice wall of the 2D images in Figure 4 and Figure 5, when φin = −φout = 10°. The flow state changes from super-cavitation to transitional cavitation, causing the fuel to reattach to the wall in the middle of the orifice. The liquid fuel comes into direct contact with the orifice wall, leading to the formation of a turbulent boundary layer. This turbulent boundary layer contributes significantly to the increase in the TKE of the liquid fuel. As φ continues to increase, the impact of the turbulent boundary layer on the right side continues to rise, but with a decrease in the rate of the TKE increment (the second-order derivative of TKE with respect to φ becomes negative).

Figure 10.
Mean turbulent kinetic energy TKE of liquid fuel jet at different wall inclination angles φ.
The variation of the momentum flux of the fuel jet along the axial position of the orifice for different wall inclination angles φ is shown in Figure 11, where coordinate X gives the direction of the injection hole axis. The momentum flux increases and then decreases along the axial position of the injection hole and reaches its maximum value inside the orifice, where the effective flow area of the orifice is at its minimum.
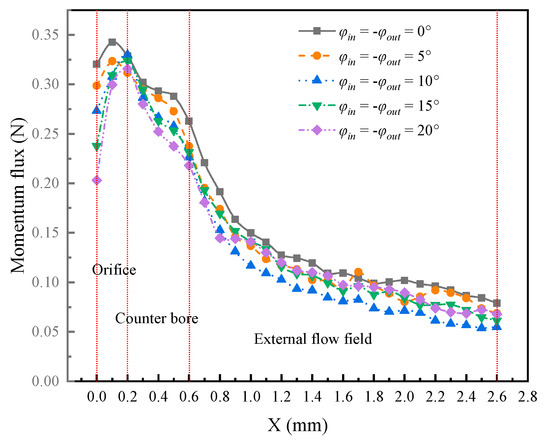
Figure 11.
Variation of momentum flux for a liquid fuel jet along the orifice axial position at different wall inclination angles φ.
The momentum flux of the fuel jet has the highest value when φ = 0°. As the wall inclination angle gradually increases, the momentum of the fuel jet decreases, reaching the lowest values when φ = 10°; this can reduce the spray penetration and decrease the overall diffusion capability of the spray. By examining Figure 8, it can be observed that the trend of the momentum flux of the liquid fuel jet with respect to φ aligns with the variation pattern of the breakup length of the liquid core. This correlation arises from the fact that as the breakup length of the liquid core diminishes, the fuel jet experiences breakup and atomization closer to the orifice outlet. Subsequently, momentum exchange occurs with the downstream environment gas, resulting in the dissipation of kinetic energy. Consequently, when the fragmentation length of the liquid core is small, the axial momentum flux of the fuel jet decreases. For φ > 10°, the jet is capable of keeping its structure more easily, even beyond the counter bore exit (Lb > 0.6 mm); therefore, a higher axial momentum can be obtained in the external flow field.
3.2. Influence of Orifice Cone Angle on Internal Flow and Cavitation Characteristics in the Orifice
The distribution of the void fraction in the axial section of each nozzle orifice with different orifice cone angles is shown in Figure 12. In comparison to the cylindrical orifice structure of nozzle N3 (Figure 12c), the introduction of a divergent orifice structure with a positive orifice cone angle (φ0 > 0°) intensifies fuel cavitation within the orifice (cf. Figure 12a,b). As φ0 increases, the cavitation region on the orifice wall surface expands, along with an increase in the hydraulic flip width (δ). Conversely, the convergent orifice structure with a negative orifice cone angle (φ0 < 0°) restrains fuel cavitation. Specifically, when φ0 = −10°, the gaseous region within the orifice completely disappears.
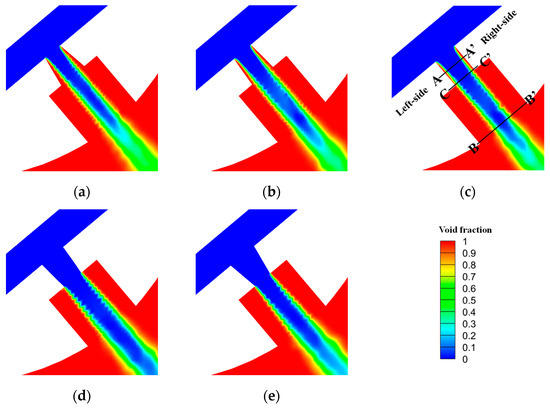
Figure 12.
Void fraction contours of orifice axial cross-section at different orifice cone angles φ0. (a) Nozzle N1: φ0 = +20°; (b) Nozzle N2: φ0 = +10°; (c) Nozzle N3: φ0 = 0°; (d) Nozzle N4: φ0 = −10°; (e) Nozzle N5: φ0 = −20°.
The distribution of the void fraction on the orifice central cross-section A-A′, the orifice exit cross-section C-C′ and the counter bore exit cross-section B-B′ for each nozzle are shown in Figure 13. Upon comparing the cross-section A-A′ at the center of each orifice, it becomes evident that the thickness of the annular gas layer within the asymptotic orifice increases correspondingly with the positive value of φ0, while displaying a symmetric distribution of the gas phase region. Simultaneously, as φ0 increases, the proportion of gas-liquid in the mixture within the jet cross-section at the counter bore exit (B-B′ cross-section) also rises. This indicates an enhanced interaction between the fuel jet and the downstream environment gas within the counter bore, facilitating sufficient mixing of the liquid fuel with the surrounding gas. Therefore, the proportion of the fuel jet in the pure liquid (blue region) decreases.
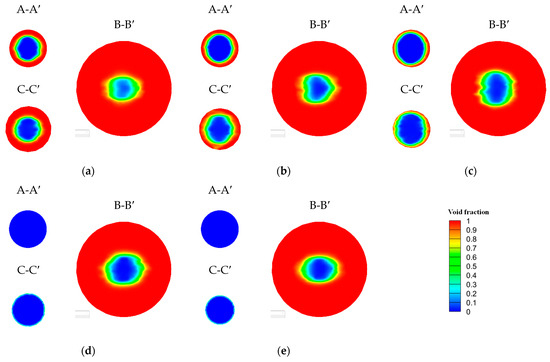
Figure 13.
Void fraction contours at different cross-sections for different orifice cone angles φ0 (A-A′: orifice central cross-section; B-B′: counter bore exit cross-section; C-C′: orifice exit cross-section). (a) Nozzle N1: φ0 = +20°; (b) Nozzle N2: φ0 = +10°; (c) Nozzle N3: φ0 = 0°; (d) Nozzle N4: φ0 = −10°; (e) Nozzle N5: φ0 = −20°.
For the convergent orifice, the fuel within the orifice remains in a pure liquid phase, as the occurrence of fuel cavitation is entirely suppressed. Furthermore, the cross-section of the liquid fuel jet at the exit of the counter bore undergoes a transition from elliptical to circular in comparison to the cylindrical orifice design. This transition is primarily a result of the effective suppression of cavitation in the wall regions of the orifice. Consequently, the liquid fuel is not subjected to any interaction inside the orifice caused by the presence of a gas region. As a result, the cross-section of the fuel jet within the counter bore exhibits an almost circular shape.
The variation of the void fraction (gas volume fraction) αn and cavitation asymmetry η with angle φ0 is shown in Figure 14. For the divergent orifice (φ0 > 0°), the void fraction within the orifice exhibits a progressive increase as φ0 increases. Specifically, when φ0 = +20°, the gas volume fraction within the orifice surpasses 50%; that is, αn = 0.575. This value represents a 93% increase compared to the cylindrical orifice (αn = 0.298). Meanwhile, the cavitation asymmetry η demonstrates a decreasing trend with the rise in φ0. For the cylindrical orifice, the cavitation phenomenon exhibits a slightly stronger occurrence on the right side of the orifice compared to the left side (reference is made to a 2D picture like in Figure 4). This discrepancy arises from the proximity of the right side of the orifice inlet to the upstream flow channel, resulting in higher fuel velocity during its entry into the orifice. However, when comparing it to the cylindrical orifice, the divergent orifice (φ0 > 0°) displays a decrease in ωin/out and an increase in φin/out > 0°, leading to an intensification of cavitation on both sides within the orifice. Hence, the relative difference in cavitation intensity, caused by the discrepancy in upstream flow velocity between the two sides of the orifice inlet, diminishes. This is why the distribution of cavitation inside the orifice exhibits improved symmetry, and the cavitation asymmetry approaches zero (η = 0.006) when φ0 = +20°. For the convergent orifice (φ0 < 0°), the cavitation inside the orifice has been completely suppressed when φ0 = −10° or −20°; therefore, αn and η inside the orifice both tend to zero.

Figure 14.
Void fraction and cavitation asymmetry of orifice at different orifice cone angles.
Figure 12 provides compelling evidence of the substantial influence of angle φ0 on the gas volume fraction in the cross-sections of the injection hole. Consequently, notable variations in discharge characteristics are observed among orifices with different φ0. Figure 15 depicts the mass flow rate and discharge coefficient trends with respect to φ0. As can be inferred, with the increase in φ0 (φ0 > 0°), the flow rate and the orifice discharge coefficient decrease, which is caused by the increase in cavitation intensity inside the orifice, resulting in a decrease in the effective flow area of the injection hole. As φ0 decreases (φ0 < 0°), the gas volume fraction inside the convergent orifice tends to zero, and the flow coefficient of the orifice increases significantly. When φ0 = −10°, the Cd reaches 0.839, which is about 34% larger than that of the cylindrical orifice (Cd = 0.625). However, when φ0 continues to decrease and reaches −20°, although the discharge coefficient of the orifice is slightly larger than that of φ0 = −10°, the flow rate of the orifice decreases significantly. This is because although the orifice diameter D measured at half the axial distance in the orifice (cf. Figure 3) is the same, the inlet and outlet diameters of the orifice, namely Din and Dout, and the actual cross-sectional area of the orifice, Aout, change as φ0 changes. Comparisons between the nozzles with the different orifice outlet diameter Dout and outlet cross-sectional area Aout are shown in Table 5. As φ0 decreases, the orifice Aout also decreases, when φ0 = −20°, the actual orifice outlet Aout is small, therefore the orifice mass flow rate decreases, even if the flow coefficient of the orifice is higher.
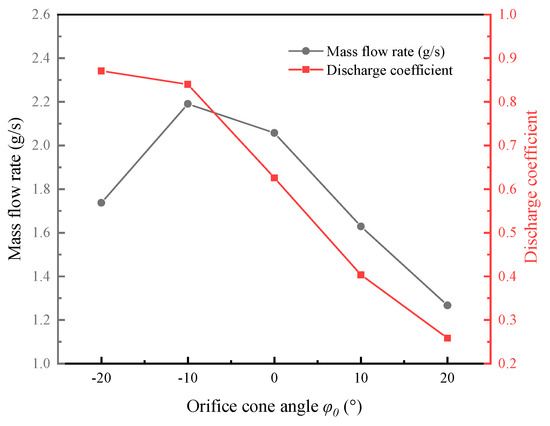
Figure 15.
Mass flow rate and cavitation asymmetry of orifice at different orifice cone angles φ0.

Table 5.
Comparison of orifice outlet diameters and outlet cross-sectional areas of each nozzle with different orifice cone angles φ0.
Figure 16 and Figure 17 show the variation of the liquid core morphology and liquid breakup length of the fuel jet for nozzles with different angles φ0, respectively. The liquid core breakup length of the divergent orifice (φ0 > 0°) is smaller than that of the cylindrical orifice. In fact, as φ0 increases, the cavitation intensity inside the orifice increases and the gas-liquid interactions are enhanced, resulting in the growth of the instability wave on the surface of the fuel jet, which contributes to the liquid core breakup.
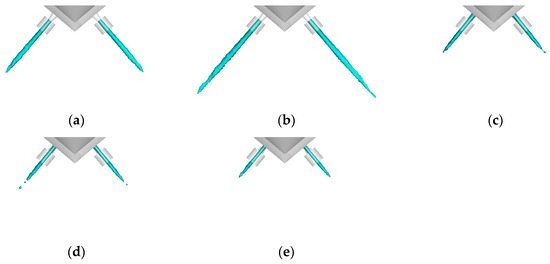
Figure 16.
Liquid core morphology of fuel jet inside nozzle with different orifice cone angles φ0. (a) Nozzle N5: φ0 = −20°; (b) Nozzle N4: φ0 = −10°; (c) Nozzle N3: φ0 = 0°; (d) Nozzle N2: φ0 = +10°; (e) Nozzle N1: φ0 = +20°.
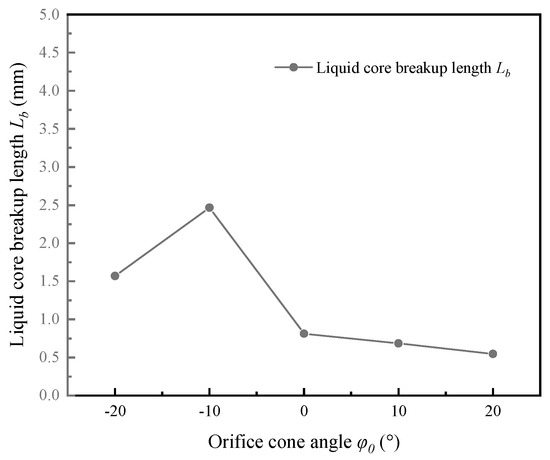
Figure 17.
Liquid breakup length Lb of fuel jet inside nozzle with different orifice cone angles φ0.
The liquid core breakup length of the convergent orifice (φ0 < 0°) is significantly larger than that of the cylindrical orifice, and the overall liquid core diameter is larger than that of the cylindrical orifice. These is because the cavitation inside the convergent orifice is suppressed, the liquid fuel is not perturbed by any gas inside the orifice to generate unstable waves, and the effective flow area of the fuel at the orifice exit is larger, thus, the diameter of the liquid core and the Lb are larger than those of the cylindrical orifice.
However, it is worth noting that when φ0 is further reduced from −10° to −20°, Lb decreases significantly. This occurs because Lb is related to the initial diameter and flow velocity of the liquid fuel in addition to the effects of the cavitation phenomena inside the orifice and the gas-liquid mutual perturbation. The flow velocity at the orifice exit diminishes, passing from φ0 = −10° to φ0 = −20°, and this on its own would lead to a reduction in the flowrate and in the Lb. The cross-sectional area of the orifice outlet for nozzle N5 (Aout = 0.012 mm2) at φ0 = −20° is obviously reduced compared with that of nozzle N4 (Aout = 0.016 mm2); therefore, the initial diameter of the liquid core is smaller, and the Lb is reduced compared with that at φ0 = −10°.
The variation of the momentum flux of the fuel jet along the axial position of the orifice for different orifice cone angles φ0 is shown in Figure 18. The fuel jet from the divergent orifice exhibits a reduced momentum flux, reaching its minimum value when φ0 = 20°. As φ0 gradually decreases, the momentum flux of the fuel jet increases, peaking when φ0 = −10° (convergent orifice). However, as φ0 is further decreased to −20°, the momentum flux of the fuel jet experiences a subsequent decrease. Compared with Figure 15, the variation of the momentum flux of the fuel jet with the orifice cone angle φ0 is consistent with that of the mass flow rate through the orifice. When keeping the orifice diameter D constant, a change in φ0 directly affects the size of the orifice outlet cross-sectional area Aout. At φ0 = +20°, since the flowrate is diminished, the axial momentum goes down due to the lower velocity and lower flow area. Compared with other design parameters (ω and φ), the mass flow rate of each nozzle varies greatly with respect to φ0. Indeed, the mass flow rate of nozzle N4 (φ0 = −10°) is 2.19 g/s, which is 73.81% larger than that of nozzle N1 (φ0 = +20°), namely 1.26 g/s. Although the divergent orifice can significantly increase the cavitation strength inside the orifice and reduce the liquid core breakup length, which may help to promote fuel atomization, the change in the orifice cone angle significantly changes the orifice mass flow rate and the momentum magnitude of the fuel jet, which in turn has an impact on the total injected volume and the overall diffusion of the spray.

Figure 18.
Variation of momentum flux for liquid fuel jet along the orifice axial position at different orifice cone angles φ0.
In summary, the wall inclination angle is an important parameter for spray characteristics. In order to keep a stable spray structure, the wall inclination angle should be controlled below 10°. Instead, if the fuel jet needs better atomization closer to the orifice outlet, the critical wall inclination angle should be selected at around 15°. Finally, the cavitation can be suppressed once the orifice cone angle reaches 0° and thoroughly disappears once the orifice cone angle is below −10°. These results define clear design keys to exploit the nozzle wall inclination angle and control spray cavitation.
4. Conclusions
In this work, different nozzle layouts with different wall inclination angles and orifice cone angles were designed, and simulation calculations of nozzle internal flow and near-field spray characteristics were carried out. The influence mechanism of the wall inclination angle and the orifice cone angle on cavitation and spray was also investigated and clarified by means of analysis of the void fraction and the asymmetry parameter . The main findings are as follows:
- (1)
- As the wall inclination angle increases, the cavitation asymmetry within the orifice intensifies, accompanied by a decrease in the gas volume fraction. On one side of the injection hole, the occurrence of cavitation is suppressed. On the other side of the injection hole, cavitation is intensified. Furthermore, the width of the hydraulic flip on one side of the orifice expands, while the flow state on the other side of the orifice gradually changes from a hydraulic flip to super-cavitation flow, transitional cavitation and an almost fully reattached flow.
- (2)
- When the wall inclination angle φ exceeds 10°, the cross-sectional profile of the jet at the counter-bore exit undergoes a transition from an ellipse to a crescent. Simultaneously, the shape of the fuel liquid core transforms from cylindrical to hollow semi-circular. Furthermore, as the wall inclination angle reaches 15°, the mass flow rate and penetration of the nozzle become larger.
- (3)
- In comparison to the cylindrical orifice, the presence of a divergent orifice intensifies fuel cavitation and leads to an enlarged hydraulic flip width as the orifice cone angle φ0 increases. Conversely, the convergent orifice configuration mitigates cavitation effects, and the complete absence of the gas region within the orifice is achieved when the orifice cone angle φ0 is below −10°.
- (4)
- When the orifice layout changes to a divergent type, the flow coefficient of the orifice reduces, together with a diminution in the fuel momentum flux and the mass flow rate. As the orifice cone angle decreases, the orifice layout becomes convergent, and the flow coefficient and momentum flux increase. The spray performance of a nozzle with an orifice cone angle of −10° is superior in terms of mass flow rate and liquid penetration.
Author Contributions
Conceptualization, Z.W. and J.D.; methodology, A.F., C.H., O.V., M.J. and Z.W.; software, C.H.; validation, C.H.; formal analysis, A.F., C.H., O.V. and Z.W.; data curation, M.J.; writing—original draft preparation, C.H. and O.V.; writing—review and editing, A.F., C.H., Z.W. and O.V.; supervision, A.F., Z.W. and M.J.; funding acquisition, Z.W and J.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China (T2241003) the Shanghai Science and Technology Program (grant number 22ZR1463000), the International Exchange Program for Graduate Students at Tongji University (No. 2023020049) and the Chinese Ministry of Science and Technology (grant number G2023133001L).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shah, K.J.; Pan, S.; Lee, I.; Kim, H.; You, Z.; Zheng, J.; Chiang, P. Green transportation for sustainability: Review of current barriers, strategies, and innovative technologies. J. Clean Prod. 2021, 326, 129392. [Google Scholar] [CrossRef]
- Zahoor, A.; Mehr, F.; Mao, G.; Yu, Y.; Sápi, A. The carbon neutrality feasibility of worldwide and in China’s transportation sector by E-car and renewable energy sources before 2060. J. Energy Storage 2023, 61, 106696. [Google Scholar] [CrossRef]
- Ferrari, A.; Novara, C.; Vento, O.; Violante, M.; Zhang, T. A novel fuel injected mass feedback-control for single and multiple injections in direct injection systems for CI engines. Fuel 2023, 334, 126670. [Google Scholar] [CrossRef]
- Ferrari, A.; Novara, C.; Paolucci, E.; Vento, O.; Violante, M.; Zhang, T. Design and rapid prototyping of a closed-loop control strategy of the injected mass for the reduction of CO2, combustion noise and pollutant emissions in diesel engines. Appl. Energy 2018, 232, 358–367. [Google Scholar] [CrossRef]
- Ferrari, A.; Novara, C.; Paolucci, E.; Vento, O.; Violante, M.; Zhang, T. A new closed-loop control of the injected mass for a full exploitation of digital and continuous injection-rate shaping. Energy Convers. Manag. 2018, 177, 629–639. [Google Scholar] [CrossRef]
- Finesso, R.; Marello, O.; Spessa, E. Development of a pressure-based technique to control IMEP and MFB50 in a 3.0 L diesel engine. Energy Procedia 2018, 148, 424–430. [Google Scholar] [CrossRef]
- Ambrosio, S.; Finesso, R.; Hardy, G.; Manelli, A.; Mancarella, A.; Marello, O.; Mittica, A. Model-Based Control of Torque and Nitrogen Oxide Emissions in a Euro VI 3.0 L Diesel Engine through Rapid Prototyping. Energies 2021, 14, 1107. [Google Scholar] [CrossRef]
- Ambrosio, S.; Mancarella, A.; Manelli, A.; Mittica, A.; Hardy, G. Experimental analysis on the effects of multiple injection strategies on pollutant emissions, combustion noise, and fuel consumption in a premixed charge compression ignition engine. Sae Int. J. Engines 2021, 14, 611–630. [Google Scholar]
- Jin, Z.; Vento, O.; Zhang, T.; Ferrari, A.; Mittica, A.; Ouyang, L.; Tan, S. Numerical-experimental optimization of the common-feeding injection system concept for application to light-duty commercial vehicles. J. Energy Resour. Technol. 2021, 143, 122304. [Google Scholar] [CrossRef]
- Mancarella, A.; Marello, O. Effect of coolant temperature on performance and emissions of a compression ignition engine running on conventional diesel and hydrotreated vegetable oil (HVO). Energies 2022, 16, 144. [Google Scholar] [CrossRef]
- Ueckerdt, F.; Bauer, C.; Dirnaichner, A.; Everall, J.; Sacchi, R.; Luderer, G. Potential and risks of hydrogen-based e-fuels in climate change mitigation. Nat. Clim. Chang. 2021, 11, 384–393. [Google Scholar] [CrossRef]
- Lindstad, E.; Lagemann, B.; Rialland, A.; Gamlem, G.M.; Valland, A. Reduction of maritime GHG emissions and the potential role of E-fuels. Transp. Res. Part D Transp. Environ. 2021, 101, 103075. [Google Scholar] [CrossRef]
- Ravi, S.S.; Brace, C.; Larkin, C.; Aziz, M.; Leach, F.; Turner, J.W. On the pursuit of emissions-free clean mobility–Electric vehicles versus e-fuels. Sci. Total Environ. 2023, 875, 162688. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, A.; Pizzo, P.; Vento, O. Investigation of a GDI injector with an innovative flowmeter for high-pressure transient flows. Int. J. Engine Res. 2023, 24, 4287–4296. [Google Scholar] [CrossRef]
- Fontanesi, S.; Shamsudheen, F.A.; Gonzalez, E.G.; Sarathy, S.M.; Berni, F.; D Adamo, A.; Borghi, M.; Breda, S. Impact of fuel surrogate formulation on the prediction of knock statistics in a single cylinder GDI engine. Int. J. Engine Res. 2024, 25, 405–423. [Google Scholar] [CrossRef]
- Huang, W.; Moon, S.; Gao, Y.; Wang, J.; Ozawa, D.; Matsumoto, A. Hole Number Effect on Spray Dynamics of Multi-Hole Diesel Nozzles: An Observation from Three- to Nine-Hole Nozzles. Exp. Therm. Fluid Sci. 2018, 102, 387–396. [Google Scholar] [CrossRef]
- Huang, W.; Pratama, R.H.; Oguma, M.; Kinoshita, K.; Takeda, Y.; Suzuki, S. Spray dynamics of synthetic dimethyl carbonate and its blends with gasoline. Fuel 2023, 341, 127696. [Google Scholar] [CrossRef]
- Huang, W.; Gong, H.; Moon, S.; Wang, J.; Murayama, K.; Taniguchi, H.; Arima, T.; Arioka, A.; Sasaki, Y. Nozzle Tip Wetting in GDI Injector at Flash-boiling Conditions. Int. J. Heat Mass Transf. 2021, 169, 120935. [Google Scholar] [CrossRef]
- Sou, A.; Hosokawa, S.; Tomiyama, A. Effects of cavitation in a nozzle on liquid jet atomization. Int. J. Heat Mass Transf. 2007, 50, 3575–3582. [Google Scholar] [CrossRef]
- Qiu, T.; Song, X.; Lei, Y.; Liu, X.; An, X.; Lai, M. Influence of inlet pressure on cavitation flow in diesel nozzle. Appl. Therm. Eng. 2016, 109, 364–372. [Google Scholar] [CrossRef]
- Giannadakis, E.; Gavaises, M.; Arcoumanis, C. Modelling of cavitation in diesel injector nozzles. J. Fluid Mech. 2008, 616, 153–193. [Google Scholar] [CrossRef]
- Pratama, R.H.; Huang, W.; Moon, S.; Wang, J.; Murayama, K.; Taniguchi, H.; Arima, T.; Sasaki, Y.; Arioka, A. Hydraulic flip in a gasoline direct injection injector and its effect on injected spray. Fuel 2022, 310, 122303. [Google Scholar] [CrossRef]
- Ge, M.; Zhang, G.; Petkovšek, M.; Long, K.; Coutier-Delgosha, O. Intensity and regimes changing of hydrodynamic cavitation considering temperature effects. J. Clean Prod. 2022, 338, 130470. [Google Scholar] [CrossRef]
- Ge, M.; Sun, C.; Zhang, G.; Coutier-Delgosha, O.; Fan, D. Combined suppression effects on hydrodynamic cavitation performance in Venturi-type reactor for process intensification. Ultrason. Sonochem. 2022, 86, 106035. [Google Scholar] [CrossRef]
- Yin, B.; Yu, S.; Jia, H.; Yu, J. Numerical research of diesel spray and atomization coupled cavitation by Large Eddy Simulation (LES) under high injection pressure. Int. J. Heat Fluid Flow 2016, 59, 1–9. [Google Scholar] [CrossRef]
- Wang, Z.; Dai, X.; Li, F.; Li, Y.; Lee, C.; Wu, H.; Li, Z. Nozzle internal flow and spray primary breakup with the application of closely coupled split injection strategy. Fuel 2018, 228, 187–196. [Google Scholar] [CrossRef]
- Zhang, L.; He, Z.; Guan, W.; Wang, Q.; Som, S. Simulations on the cavitating flow and corresponding risk of erosion in diesel injector nozzles with double array holes. Int. J. Heat Mass Transf. 2018, 124, 900–911. [Google Scholar] [CrossRef]
- Gong, H.; Huang, W.; Gao, Y.; Wang, J.; Arioka, A.; Sasaki, Y. End-of-injection fuel dribbling dynamics of multi-hole GDI injector. Fuel 2022, 317, 123406. [Google Scholar] [CrossRef]
- Gao, Y.; Huang, W.; Pratama, R.; Wang, J. Transient Nozzle-Exit Velocity Profile in Diesel Spray and Its Influencing Parameters. Int. J. Automot. Manuf. Mater. 2022, 1, 8. [Google Scholar] [CrossRef]
- Ji, M.; Wu, Z.; Ferrari, A.; Fu, L.; Vento, O. Experimental Investigation on Gasoline—Water Mixture Fuel Impingement Preparation Method and Spray Characteristics with High Injection Temperatures and Pressures. Energies 2023, 16, 6026. [Google Scholar] [CrossRef]
- Payri, F.; Bermúdez, V.; Payri, R.; Salvador, F.J. The influence of cavitation on the internal flow and the spray characteristics in diesel injection nozzles. Fuel 2004, 83, 419–431. [Google Scholar] [CrossRef]
- Benajes, J.; Pastor, J.V.; Payri, R.; Plazas, A.H. Analysis of the influence of diesel nozzle geometry in the injection rate characteristic. J. Fluids Eng. 2004, 126, 63–71. [Google Scholar] [CrossRef]
- Soyama, H. Effect of nozzle geometry on a standard cavitation erosion test using a cavitating jet. Wear 2013, 297, 895–902. [Google Scholar] [CrossRef]
- He, Z.; Guo, G.; Tao, X.; Zhong, W.; Leng, X.; Wang, Q. Study of the effect of nozzle hole shape on internal flow and spray characteristics. Int. Commun. Heat Mass Transf. 2016, 71, 1–8. [Google Scholar] [CrossRef]
- Chen, Z.; He, Z.; Shang, W.; Duan, L.; Zhou, H.; Guo, G.; Guan, W. Experimental study on the effect of nozzle geometry on string cavitation in real-size optical diesel nozzles and spray characteristics. Fuel 2018, 232, 562–571. [Google Scholar] [CrossRef]
- Liao, H.; Zhao, S.; Cao, Y.; Zhang, L.; Yi, C.; Niu, J.; Zhu, L. Erosion characteristics and mechanism of the self-resonating cavitating jet impacting aluminum specimens under the confining pressure conditions. J. Hydrodyn. 2020, 32, 375–384. [Google Scholar] [CrossRef]
- He, Z.; Hu, B.; Wang, J.; Guo, G.; Feng, Z.; Wang, C.; Duan, L. The cavitation flow and spray characteristics of gasoline-diesel blends in the nozzle of a high-pressure common-rail injector. Fuel 2023, 350, 128786. [Google Scholar] [CrossRef]
- Liu, H.; Xu, Y.; Wang, Z.; Zhang, J.; Wang, J. Experimental and numerical simulations to examine the mechanism of nozzle geometry affecting cavitation water jets. Geoenergy Sci. Eng. 2024, 233, 212511. [Google Scholar] [CrossRef]
- Balz, R.; Nagy, I.G.; Weisser, G.; Sedarsky, D. Experimental and numerical investigation of cavitation in marine Diesel injectors. Int. J. Heat Mass Transf. 2021, 169, 120933. [Google Scholar] [CrossRef]
- Wu, Z.; Zhao, W.; Li, Z.; Deng, J.; Hu, Z.; Li, L. A review of engine fuel injection studies using synchrotron radiation x-ray imaging. Automot. Innov. 2019, 2, 79–92. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, W.; Wu, Z. Understanding transient internal flow processes in high-pressure nozzles using synchrotron radiation X-ray phase contrast imaging technology. At. Sprays 2021, 31, 1–14. [Google Scholar] [CrossRef]
- Hu, B.; He, Z.; Li, C.; Deng, Y.; Guan, W.; Zhang, L.; Guo, G. Study of the effect of cavitation flow patterns in diesel injector nozzles on near-field spray atomization characteristics using a LES-VOF method. Int. J. Multiph. Flow. 2024, 174, 104791. [Google Scholar] [CrossRef]
- Yu, S.; Yin, B.; Jia, H.; Chen, C.; Xu, B. Investigation of inner cavitation and nozzle exit flow patterns for elliptical orifice GDI injectors with various aspect ratios. Int. Commun. Heat Mass 2021, 129, 105682. [Google Scholar] [CrossRef]
- Guo, G.; Lu, K.; Xu, S.; Yuan, J.; Bai, T.; Yang, K.; He, Z. Effects of in-nozzle liquid fuel vortex cavitation on characteristics of flow and spray: Numerical research. Int. Commun. Heat Mass 2023, 148, 107040. [Google Scholar] [CrossRef]
- Yang, G.; Hu, L.; Qiu, F.; Li, W.; Long, F.; Hu, D.; Cheng, Z. Numerical simulation of the effect of jet small orifice structure on cavitation characteristic and jet impact flow field. Chem. Eng. Process. Process Intensif. 2024, 200, 109775. [Google Scholar] [CrossRef]
- Zhao, W.; Li, Z.; Deng, J.; Li, L.; Wu, Z. Experimental and Numerical Study on the Effects of Nozzle Geometry Features on the Nozzle Internal Flow and Cavitation Characteristics. At. Sprays 2021, 31, 67–95. [Google Scholar] [CrossRef]
- Wu, Z.; Hu, C.; Leng, P.; Zhao, W.; Deng, J.; Li, K.; Li, L. Effect of nozzle geometry features on the nozzle internal flow and cavitation characteristics based on X-ray dynamic imaging. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2024, 1058, 168831. [Google Scholar] [CrossRef]
- Saha, K.; Som, S.; Battistoni, M.; Li, Y.; Quan, S.; Kelly Senecal, P. Modeling of Internal and Near-Nozzle Flow for a Gasoline Direct Injection Fuel Injector. J. Energy Resour. Technol. 2016, 138, 52208. [Google Scholar] [CrossRef]
- Tu, P.W.; Xu, H.; Srivastava, D.K.; Dean, K.; Jing, D.; Cao, L.; Weall, A.; Venus, J.K. Numerical Investigation of GDI Injector Nozzle Geometry on Spray Characteristics; SAE Technical Paper 2015-01-1906; SAE International: Warrendale, PA, USA, 2015. [Google Scholar] [CrossRef]
- Dong, P.; Chen, Q.; Liu, G.; Zhang, B.; Yan, G.; Wang, R. Effects of geometric parameters on flow and atomization characteristics of swirl nozzles for artificial snowmaking. Int. J. Refrig. 2023, 154, 56–65. [Google Scholar] [CrossRef]
- Bal, M.; Kayansalçik, G.; Ertunç, Ö; Böke, Y.E. Benchmark study of 2D and 3D VOF simulations of a simplex nozzle using a hybrid RANS-LES approach. Fuel 2022, 319, 123695. [Google Scholar] [CrossRef]
- Guan, W.; He, Z.; Zhang, L.; EL-Seesy, A.I.; Wen, L.; Zhang, Q.; Yang, L. Effect of asymmetric structural characteristics of multi-hole marine diesel injectors on internal cavitation patterns and flow characteristics: A numerical study. Fuel 2021, 283, 119324. [Google Scholar] [CrossRef]
- Ferrari, A.; Vento, O. Thermal effects on Common Rail injection system hydraulic performance. Int. J. Engine Res. 2023, 24, 3602–3612. [Google Scholar] [CrossRef]
- Payri, R.; Salvador, F.J.; Gimeno, J.; Venegas, O. Study of cavitation phenomenon using different fuels in a transparent nozzle by hydraulic characterization and visualization. Exp. Therm. Fluid. Sci. 2013, 44, 235–244. [Google Scholar] [CrossRef]
- Ferrari, A. Fluid dynamics of acoustic and hydrodynamic cavitation in hydraulic power systems. Proc. R. Soc. A 2017, 473, 20160345. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).