Precision Regulation Strategy for Regional Source, Grid, and Load Friendly Interaction Based on Double-Layer Sensitivity Model

Abstract

The regional source–grid–load friendly interaction and precision regulation of adjustable resources with high sensitivity provide important support for the development of a new power system, improving its regulation ability and efficiency and promoting the safe, efficient, and reliable operation. Therefore, a precision regulation strategy for a regional source–grid–load friendly interaction based on a double-layer sensitivity model is proposed in this paper. Firstly, from the two perspectives of power grid-application requirements and power node-adjustable resources, the overall implementation process of the double-layer sensitivity analysis method is described, and the layered logic architecture of the precision regulation platform for regional source–grid–load friendly interaction is constructed in order to realize and apply the proposed double-layer sensitivity model and precision-regulation strategy. Secondly, the first-layer power transmission line-sensitivity analysis model is proposed for the power grid side to obtain the power transmission line-sensitivity matrix. A fine-grained second-layer adjustable resources sensitivity-analysis model is further established for the diversified adjustable resource aggregated under the power node to complete the quantitative ranking of adjustable resource-regulation sensitivity. Then, the application process of double-layer sensitivity analysis results is designed in detail, and the regulation sequence and regulation quantity of source and load are defined. Finally, taking a power system with seven lines, five power nodes, two power sources, and seven types of adjustable resources as an example, the effectiveness and rationality of the proposed model and strategy are verified. The results indicate that the proposed precise regulation strategy can accurately select high-sensitivity power nodes and effectively sort high-sensitivity adjustable resources when solving the multiple scenarios’ application needs of power grids.

1. Introduction

With the continuous advancement towards the goals of achieving “carbon neutrality and carbon peak” in China, the construction and development of a new power system has become the main battlefield and main force of energy in the power sector [1,2,3]. The construction of a new power system is an important part of the construction of a new type of energy system, and the coordinated optimization and control of source, grid, load, and storage have become key elements in this construction process [4,5,6]. And the in-depth study of diversified adjustable-resource characteristics, source–grid, grid–load, source–grid–load friendly interaction, and precision regulation has become a current technological hotspot [3,7,8,9].

In June 2023, the National Energy Administration (China) released the Blue Book on the Development of New Power System [10,11], and the operation mode of power system form will change from “source moving with the load” to “interaction between source-grid-load-storage and multiple intelligence” [7,12,13], and the change of material basis and operation mode makes the balance, stability mechanism, and characteristics of the power system change [4,14,15]. In terms of power balance in the power system, the bilateral uncertainty of source and load in the new power system has been significantly enhanced, and the difficulty of having a reliable power supply and the efficient utilization of new energy has been greatly increased [9,16,17,18]. In order to realize the real-time power balance of the power system, it is necessary to deeply excavate the adjustment potential of each link of the source–grid–load–storage; scientifically coordinate the coordinated development of the source–grid–load–storage; and, jointly, to ensure the reliable power supply and the safe and stable operation of the system, realize the power balance of the system, and ensure the reliable power supply through the coordinated interaction of resources [10,19]. The traditional power-grid dispatching mainly starts from the power side, implements the “power source dispatching” by dispatching the conventional generator set, tracks the power load curve, and realizes and maintains the real-time balance between the power and power load of the system. The technology and resources in this aspect have been changing and excavated, and the space for improvement is getting smaller and smaller [11,20,21,22]. The traditional dispatching operation mode has been difficult to adapt to the challenges brought by the construction of the new power system with a high proportion of renewable energy and a high proportion of power electronics (double high), so it is urgent to change the existing operation regulation mode and overcome the corresponding key technologies [11,15,23]. The new dispatching technology focuses on the load side: carry out “power load dispatching”; when the power grid failure occurs, realize the rapid coordination and control between the power supply, power grid, and load; and fundamentally solve the problems of real-time balance of power supply and demand and operation safety under the emergency state [19,24,25,26].

Under the background of the construction of the new power system, there are a large number of diversified, decentralized, and adjustable flexible resources on the load side. It is urgent to mobilize the adjustable resources on the load side and realize the cooperative and friendly interaction between regional source–grid–load [6,7,27]. It is necessary to dynamically map and accurately match the distributed and diversified adjustable resources into the regional power grid topology and create the source–grid–load depth coupling map, which is very important to enhancing the complementary ability of the source and load, realizing the load with the power grid, establishing the friendly interaction between the source–grid–load, and greatly improving the operational flexibility of the new power system, and the rapid and effective adjustment ability [11,27,28].

In order to support the dispatching operation of the new power system, it is necessary to study the modeling method and regulation strategy of source, power grid, and load interaction, currently. Some basic research studies have been carried out at home and abroad, and some research results have been achieved: Reference [14] proposed a source–grid–load–storage cooperative optimization operation method taking into account the multi-stakeholder game to achieve source–grid–load–storage cooperative optimization scheduling with the objective of carbon emission and cost. The flexibility demand of the power system and flexibility supply characteristics of the source and storage were analyzed, and an optimized dispatching method of the power system with comprehensive flexibility of source and load storage was proposed in Reference [16]. In order to solve the problems of existing load reduction models, a load reduction model based on a sensitivity analysis was proposed by comprehensively considering the load importance degree and proximity principle of counting and equipment electrical coupling relationship in Reference [21]. Reference [22] proposed an economic scheduling optimization model based on energy storage and a flexible load system, along with a quantitative analysis of the impact of energy storage-resource configuration on improving the wind power-consumption capacity of the system. In the context of elaborating the energy Internet concept and system, based on the source–grid–load–storage collaborative technology of the power system, Reference [24] proposed the operation mode in a broad sense of meaning and its application of key technologies, and put forward proposals for architecture and implementation strategies. Reference [25] designed a rolling scheduling framework based on industrial load demand response to construct a multi-timescale rolling scheduling-optimization model in order to tap into the demand-side regulation potential. Reference [26] designed a large-scale source–grid–load friendly interactive system to achieve real-time accurate control of user interruptible loads in order to improve the fault defense capability under different operating states and demand scenarios of the power grid. Reference [27] analyzed the new challenges and problems faced by power dispatch in the implementation of power-balance operations in the application of a high proportion of new energy and proposed an optimal scheduling analysis method for power-balance optimization using time-dimensioned step-by-step hierarchical recursive decoupling optimization.

In summary, the existing research has primarily focused on the roles of coordination among source, power grid, and load, as well as among source, power grid, storage, and load, in enhancing the integration of renewable energy, exploring the demand-side adjustment potential, improving the fault defense capabilities, and analyzing the power balance in specific application scenarios. However, there is a lack of sensitivity analysis on adjustable resources aggregated at power nodes and below from the perspective of source, power grid, and load interactions. Furthermore, there is a dearth of studies on high-sensitivity precision regulation strategies related to source–grid and grid–load interactions. It is imperative for current research to establish a precision regulation strategy that, through adjusting the most effectively power nodes, meets the demands of specific application scenarios. Another creative motivation of this paper lies in quantificationally determining the regulatory sequence of different adjustable resources aggregated at each power node. Based on this, this paper designs the application process of a double-layer sensitivity analysis from the perspective of a power-grid control platform, elaborates the logical architecture of the double-layer sensitivity analysis technology platform, constructs the power transmission line sensitivity analysis model and adjustable resource sensitivity analysis model, elaborates the application method of the double-layer sensitivity analysis results, and carries out the validation and analysis through the arithmetic examples. Through these innovative research endeavors, the priority of adjusting power nodes and adjusting adjustable resources can be accurately sorted.

The rest of this paper is arranged as follows: Section 2 presents the overall implementation process of the double-layer sensitivity analysis method, while the first-layer power transmission line sensitivity-analysis model is established in Section 3. Furthermore, the second-layer adjustable resources sensitivity-analysis model is proposed in Section 4. After that, the application process of double-layer sensitivity-analysis results is provided in Section 5. Section 6 uses a case study to verify the effectiveness and rationality of the proposed model and strategy, and, finally, the conclusions are given in Section 7.

2. Overall Implementation Process of the Double-Layer Sensitivity Analysis Method

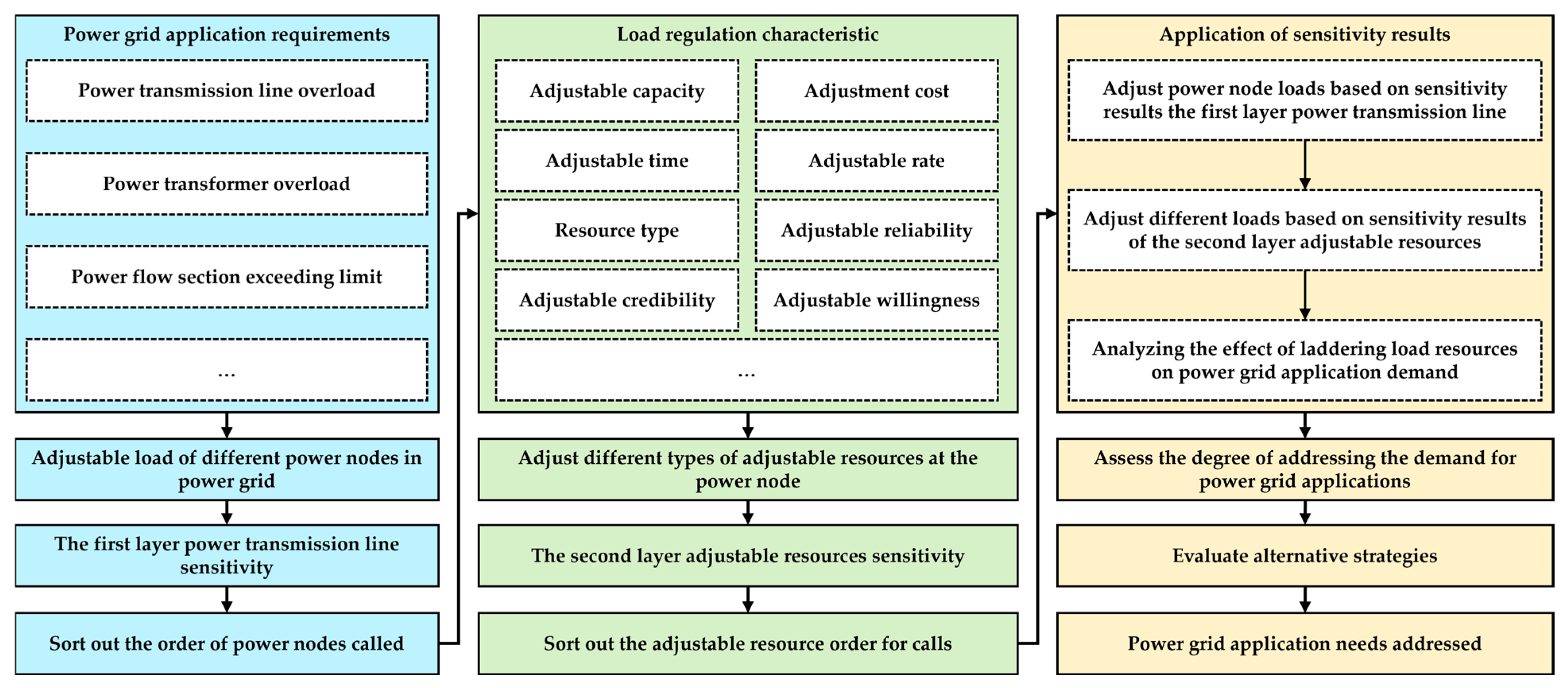
The overall implementation process of the double-layer sensitivity analysis is shown in Figure 1. From the perspective of power-grid application demand, the first-layer sensitivity analysis is carried out: according to the size of power node sensitivity, the order of power nodes invoked is sorted out. From the perspective of power-node adjustable resources, the second-layer sensitivity analysis is carried out according to the size of adjustable resources sensitivity, and the order of adjustable resources is sorted out. Based on the results of the double-layer sensitivity analysis, power-node resource regulation is carried out to address the demands of power-grid applications.

The main driving force for the double-layer sensitivity analysis comes from the actual application-demand scenarios of the power grid, including the following:

(1)

When a power transmission line transmits power, $p_{Line}$, overload, the load, $p_{Load}$, of different power nodes of power grid should be adjusted. On the premise of ensuring the security constraints of other power grids, the overload reduction of the overload line can restore the safe operation interval, and the sensitivity of $p_{Line}$ to $p_{Load}$ is analyzed, that is $\partial p_{Line}/\partial p_{Load}$, for quick judgment and selection of specific power nodes to be adjusted. After the power nodes are selected, the regulation sensitivity of various types of adjustable resources aggregated under the power node is analyzed to realize the efficient regulation of the adjustable resources.

(2)

When a transformer is overloaded with load, $p_{Trans}$, the load, $p_{Load}$, of different power nodes of power grid should be adjusted. On the premise of ensuring the security constraints of other power grids, the overload transformer restores the safe operation interval, and the sensitivity of $p_{Trans}$ to $p_{Load}$ is analyzed, that is $\partial p_{Trans}/\partial p_{Load}$, and used for quick judgment and selection of specific power nodes to be adjusted. After the power nodes are selected, the regulation sensitivity of various types of adjustable resources aggregated under the power node is analyzed to realize the efficient regulation of the adjustable resources.

(3)

When a power flow section, $p_{Sect}$, of the system exceeds the limit, the load, $p_{Load}$, of different power nodes of power grid is adjusted, and on the premise of ensuring the security constraints of other power grids, the more limited power flow section is restored to the safe operation interval, and the sensitivity of $p_{Sect}$ to $p_{Load}$ is analyzed, that is $\partial p_{Sect}/\partial p_{Load}$, for quick judgment and selection of specific power nodes that need to be adjusted. After the power nodes are selected, the regulation sensitivity of various types of adjustable resources aggregated under the power node is analyzed to realize the efficient regulation of the adjustable resources.

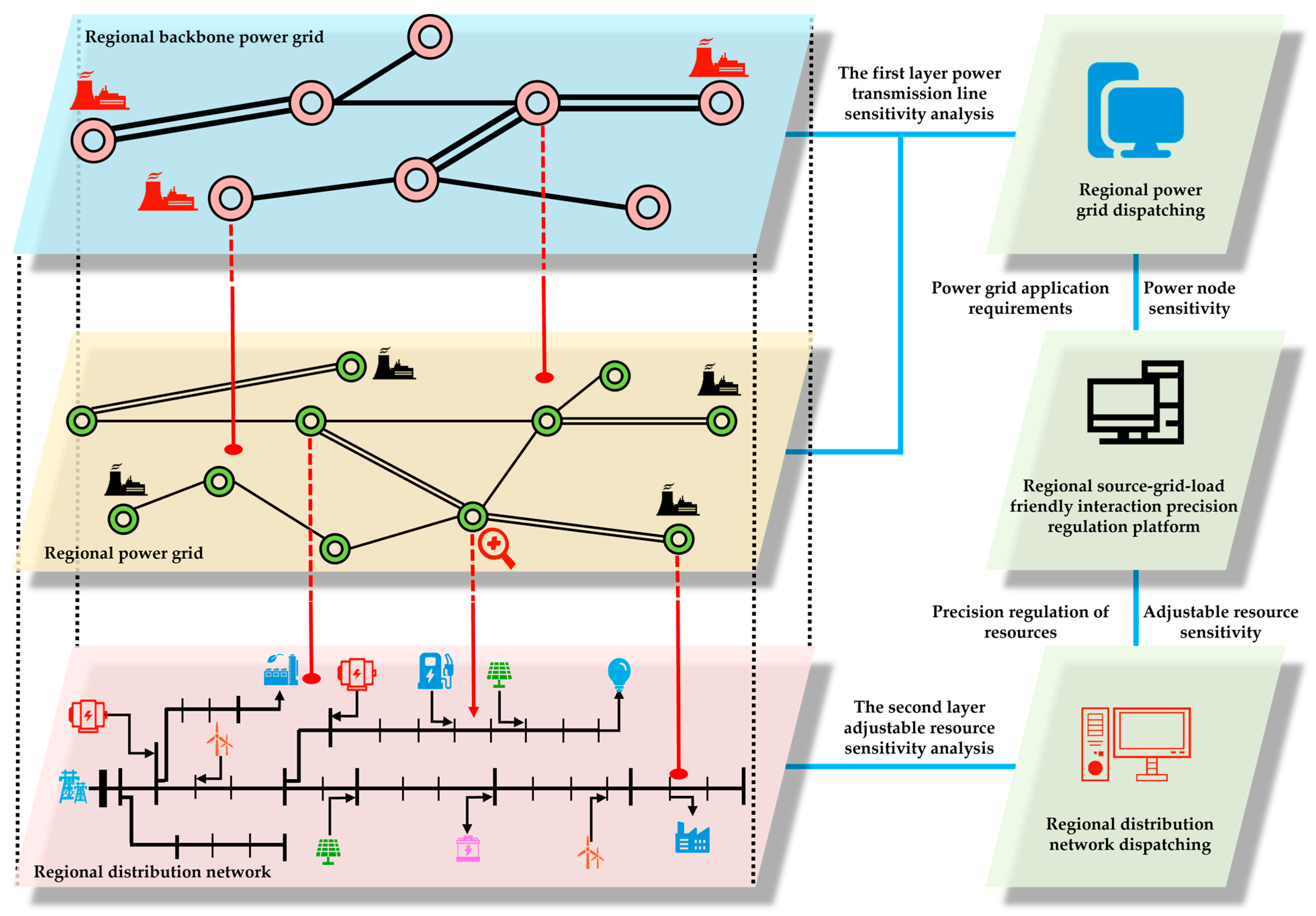
On the basis of clarifying the overall implementation process of the double-layer sensitivity analysis, it is necessary to build a regional source–grid–load friendly interaction precision regulation platform to realize the double-layer sensitivity analysis. The logical architecture of the double-layer sensitivity analysis-technology platform is shown in Figure 2.

Regional power-grid dispatching analyzes the application requirements of the regional backbone power grid and the regional power grid, and it interacts with the regional source–grid–load friendly interaction precision regulation platform. Regional distribution network dispatching analyzes the resource characteristics and topological distribution of regional distribution network, and it interacts with the regional source–grid–load friendly interaction precision regulation platform. The regional source–grid–load friendly interaction precision regulation platform supports regional power-grid dispatching to analyze power-node sensitivity, explore the potential and sensitivity of regional distribution network resource application, and realize the precise matching between power-grid application demand and regulation resources.

Regional dispatching according to the power-grid power-flow information from a specific power transmission-line overload, transformer overload, power flow section exceeding the limit, the actual application demand, on the basis of power grid application demand clear, the first layer of the power transmission line sensitivity analysis, and the first layer of the power transmission line sensitivity-analysis calculation can be determined in two ways: Dispatching Giving Method (Post Hoc Analysis) and Direct Calculation Method (Prior Analysis).

Dispatching Giving Method (Post Hoc Analysis): According to the existing evaluation, regional power-grid dispatching sorts out the specifics to adjust the order of the power nodes. And regional power-grid dispatching transmits power node-sorting information to the regional source–grid–load friendly interaction precision regulation platform. The regional source–grid–load friendly interaction precision regulation platform obtains power-flow results and the first-layer power transmission line-sensitivity information (or adjust the power grid power node sorting) from regional power-grid dispatching. On the basis of the first-layer sensitivity results provided by regional power-grid dispatching, the regional source–grid–load friendly interaction precision regulation platform primarily conducts an analysis of the second layer of the adjustable resource sensitivity.

Direct Calculation Method (Prior Analysis): The regional source–grid–load friendly interaction precision regulation platform obtains power-grid topology distribution, load prediction information, power output, power grid parameters from regional power grid dispatching, and analyses the first-layer power transmission line sensitivity. After completing the first layer of power transmission line sensitivity, the second-layer sensitivity analysis is carried out. Finally, the double sensitivity analysis results are fed back to regional power grid dispatching to provide support for an accurate analysis and precision regulation instructions.

The above Dispatching Giving Method (Post Hoc Analysis) and Direct Calculation Method (Prior Analysis) can be flexibly used in different engineering practices according to the requirements.

3. The First-Layer Power Transmission Line Sensitivity-Analysis Model

The above two methods to analyze and calculate the first-layer power transmission line sensitivity need to build the underlying mathematical model, which is constructed from the point of view of the Direct Calculation Method (Prior Analysis) in this paper. For the medium- and high-voltage power system, there are $n$ power nodes and $b$ power transmission lines, and the DC power flow model is used to solve the power-system power flow. Then, the construction process of the first-layer power transmission line sensitivity-analysis model is specified as follows.

3.1. Injected Power of Power Node

For any power node, the injected power of the power node is as follows:

$$P_i^{SP}=P_i^{Gen}-P_i^{Load}={\displaystyle \sum _{j\in i}{P}_{ij}}={\displaystyle \sum _{j\in i}\frac{{\theta }_i-{\theta }_j}{x_{ij}}}$$

(1)

where $P_i^{SP}$ denotes the injected power for the power nodes in the power system; $P_i^{Gen}$ is the active power for the power-node power in the power system; $P_i^{Load}$ stands for the power node-load active power in the power system; $P_{ij}$ stands for the power transmission line’s active power; ${\theta }_i$ and ${\theta }_j$ are the power transmission line’s voltage angle; $x_{ij}$ is the power transmission line’s reactance; and $j\in i$ represents a power transmission line connected to power node $i$, and the ends of the power transmission line are numbered $i$ and $j$.

3.2. Active Power of Power Transmission Line

For any power transmission line, the active power of the power transmission line can be expressed by the following equation:

$$P_{ij}={\displaystyle \frac{{\theta }_i-{\theta }_j}{x_{ij}}}$$

(2)

3.3. Injected Power Matricization of Power Node

For a power system, the injection power matrix form of its power nodes is as follows:

$$\{\begin{array}{l}{P}^{sp}=B\theta \\ \theta =B^{-1}{P}^{sp}\end{array}$$

(3)

Among them, we have the following:

$${\left[P^{sp}\right]}_{n\times 1}={\left[B\right]}_{n\times n}{\left[\theta \right]}_{n\times 1}$$

(4)

$${\left[\begin{array}{c}{P}_1^{SP}\\ P_2^{SP}\\ ⋮\\ P_n^{SP}\end{array}\right]}_{n\times 1}={\left[\begin{array}{llll}{B}_{11}\hfill & B_{12}\hfill & \cdots \hfill & B_{1n}\hfill \\ B_{21}\hfill & B_{22}\hfill & \cdots \hfill & B_{2n}\hfill \\ ⋮\hfill & ⋮\hfill & \cdots \hfill & ⋮\hfill \\ B_{n1}\hfill & B_{n2}\hfill & \cdots \hfill & B_{nn}\hfill \end{array}\right]}_{n\times n}{\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\\ ⋮\\ {\theta }_n\end{array}\right]}_{n\times 1}$$

(5)

$$\{\begin{array}{l}{B}_{ij}=-{\displaystyle \frac{1}{x_{ij}}}\\ B_{ii}={\displaystyle \sum _{j\in i,j\ne i}\frac{1}{x_{ij}}}\end{array}$$

(6)

where $B$ denotes an improved susceptance matrix with positive matrix diagonal elements and negative non-diagonal elements.

3.4. Active Power Matricization of Power Transmission Line

For a power system, the active power of the power transmission line has the matrix form being as follows:

$$P_r=P_{ij}=\left(D{B}_r\right)\Phi =\left(D{B}_r\right)A\theta =\left(D{B}_r\right)A{B}^{-1}{P}^{sp}$$

(7)

Among them, we have the following:

$${\left[\begin{array}{c}{P}_{r1}\\ P_{r2}\\ ⋮\\ P_{rb}\end{array}\right]}_{b\times 1}=D{\left[\begin{array}{llll}{B}_{r1}\hfill & 0\hfill & \cdots \hfill & 0\hfill \\ 0\hfill & B_{r2}\hfill & \cdots \hfill & 0\hfill \\ ⋮\hfill & ⋮\hfill & \cdots \hfill & ⋮\hfill \\ 0\hfill & 0\hfill & \cdots \hfill & B_{rb}\hfill \end{array}\right]}_{b\times b}{\left[\begin{array}{llll}{A}_{11}\hfill & A_{12}\hfill & \cdots \hfill & A_{1n}\hfill \\ A_{21}\hfill & A_{22}\hfill & \cdots \hfill & A_{2n}\hfill \\ ⋮\hfill & ⋮\hfill & \cdots \hfill & ⋮\hfill \\ A_{b1}\hfill & A_{b2}\hfill & \cdots \hfill & A_{bn}\hfill \end{array}\right]}_{b\times n}{\left[B^{-1}\right]}_{n\times n}{\left[\begin{array}{c}{P}_1^{SP}\\ P_2^{SP}\\ ⋮\\ P_n^{SP}\end{array}\right]}_{n\times 1}$$

(8)

$${\left[P_r\right]}_{b\times 1}={\left[P_{ij}\right]}_{b\times 1}=D{\left[B_r\right]}_{b\times b}{\left[\Phi \right]}_{b\times 1}=D{\left[B_r\right]}_{b\times b}{\left[A\right]}_{b\times n}{\left[\theta \right]}_{n\times 1}=D{\left[B_r\right]}_{b\times b}{\left[A\right]}_{b\times n}{\left[B^{-1}\right]}_{n\times n}{\left[P^{sp}\right]}_{n\times 1}$$

(9)

$$A_{ij}=\{\begin{array}{cc}+1,& \mathrm{power}\mathrm{nodes}\mathrm{are}\mathrm{power}\mathrm{transmission}\mathrm{line}\mathrm{start}\mathrm{points},\mathrm{namely},\mathrm{power}\mathrm{inflow}\mathrm{points}.\\ -1,& \mathrm{power}\mathrm{nodes}\mathrm{are}\mathrm{power}\mathrm{transmission}\mathrm{line}\mathrm{end}\mathrm{points},\mathrm{namely},\mathrm{power}\mathrm{outflow}\mathrm{points}.\\ 0,& \mathrm{power}\mathrm{nodes}\mathrm{are}\mathrm{not}\mathrm{directly}\mathrm{related}\mathrm{to}\mathrm{the}\mathrm{power}\mathrm{transmission}\mathrm{line}.\end{array}$$

(10)

where $P_r$ represents the power transmission-line power-flow matrix, numbered as $r1$, $r2$, …, and $rb$, respectively; $D{B}_r$ stands for a diagonal matrix composed of power transmission line susceptance, with the serial numbers being $r1$, $r2$, …, and $rb$, respectively; $A$ denotes for power transmission line–power node network correlation matrix; and $\Phi$ is the matrix composed of phase angle difference between the two ends of the power transmission line.

3.5. Sensitivity of Power Transmission Line Power to Power Node Power

For a power system, the sensitivity matrix of the power transmission line power/power flow section to the power node power is as follows:

$$S_{sp}^r={\displaystyle \frac{\partial P_r}{\partial P^{sp}}}={\displaystyle \frac{\partial P_{ij}}{\partial P^{sp}}}={\displaystyle \frac{\partial \left(\left(D{B}_r\right)A{B}^{-1}{P}^{sp}\right)}{\partial P^{sp}}}=\left(D{B}_r\right)A{B}^{-1}$$

(11)

where $S_{sp}^r$ denotes the active power sensitivity of the injected power at any power node $sp$ to the power transmission line $r$/power flow section, referred to as the power transmission line sensitivity.

3.6. Implementation Summary of Power Transmission Line-Sensitivity Algorithm

Based on the above analysis, the implementation of the power transmission line sensitivity algorithm is summarized as follows:

(1)

Select the balanced power node as the voltage phase-angle reference point.

(2)

According to the power grid and topological relations, find the power transmission line susceptance composition of the diagonal matrix $D{B}_r$, power transmission line–power node power grid correlation matrix $A$, and improved susceptance matrix $B$ of the inverse matrix $B^{-1}$.

(3)

According to matrix $D{B}_r$, matrix $A$, and matrix $B^{-1}$, find the power transmission line sensitivity, $S_{sp}^r$.

(4)

According to the power transmission line sensitivity, $S_{sp}^r$, the sensitivity is ranked in order of magnitude, and the power node that prioritizes the regulation of resources is selected.

(5)

After steps (1)–(4), calculate the first-layer sensitivity and then proceed to the second-layer-sensitivity calculation.

4. The Second-Layer Adjustable Resources Sensitivity-Analysis Model

When the ranking of the specific power nodes determined and adjusted in the “power-grid application-demand scenario” is known, the sensitivity analysis of different adjustable load resources under the same power node is conducted.

For the sensitivity analysis of adjustable load resources, consider load regulation characteristics of adjustable load resources: (1) adjustable capacity, (2) adjustable cost, (3) adjustable credibility, (4) adjustable rate, (5) adjustable time, (6) resource type, (7) adjustable reliability, (8) willingness of adjustable resources to participate in regulation, (9) adjustable control degree, etc.

The second-layer adjustable resources sensitivity calculation-system model is established directly, and its structure is shown in Figure 3: load regulation characteristics are important factors considered in the sensitivity calculation system model, the load regulation characteristics are evaluated in a standardized and unified way, and the sensitivity calculation system model forms the resource-specific sensitivity corresponding to each adjustable resource. Finally, according to the size of the sensitivity of the adjustable resources, the adjustable load resources are sorted and called.

4.1. Data Preprocessing

The data preprocessing is also called the normalization of attribute values, and its role is described below:

(1)

The attribute value types are diversified. For some data, the attribute value is more quality the smaller it is minimized, while for some data, the attribute value is more quality the larger it is maximized, and for some data, the attribute value is more quality the closer it is to a certain value. Therefore, data preprocessing of the data in the decision matrix is required to make the attribute values of the schemes or patterns transformed with a higher-quality performance for any given attribute in the data table.

(2)

The data are dimensionless. The uncommon property between multiple targets requires only the size of the value to measure the quality of the attribute.

(3)

The data are normalized. Transform all of the dimensionless normalized data in the data table into the range [0, 1].

The essence of data preprocessing is to characterize the real value of attribute value of a certain index in the decision maker or experts to evaluate the quality of the scheme.

4.2. Data Standard 0–1 Transformation Method

For the benefit attribute data (the larger the better), the standard 0–1 transformation model is as follows:

$$z_i={\displaystyle \frac{y_i-y^{\min }}{y^{\max }-y^{\min }}},\hspace{0.17em}\hspace{0.17em}i=1,\hspace{0.17em}2,\hspace{0.17em}3,\hspace{0.17em}\dots ,\hspace{0.17em}N$$

(12)

where $y^{\max }$ is the maximum value in the data $N$ before transformation, $y^{\min }$ denotes the minimum value in the data $N$ before transformation, $y_i$ is the $i$-th data in the data $N$ before transformation, and $z_i$ is the $i$-th data in the data $N$ after the standard 0–1 transformation.

For cost-type attribute data (the smaller the better), the standard 0–1 transformation model is as follows:

$$z_i={\displaystyle \frac{y^{\max }-y_i}{y^{\max }-y^{\min }}}$$

(13)

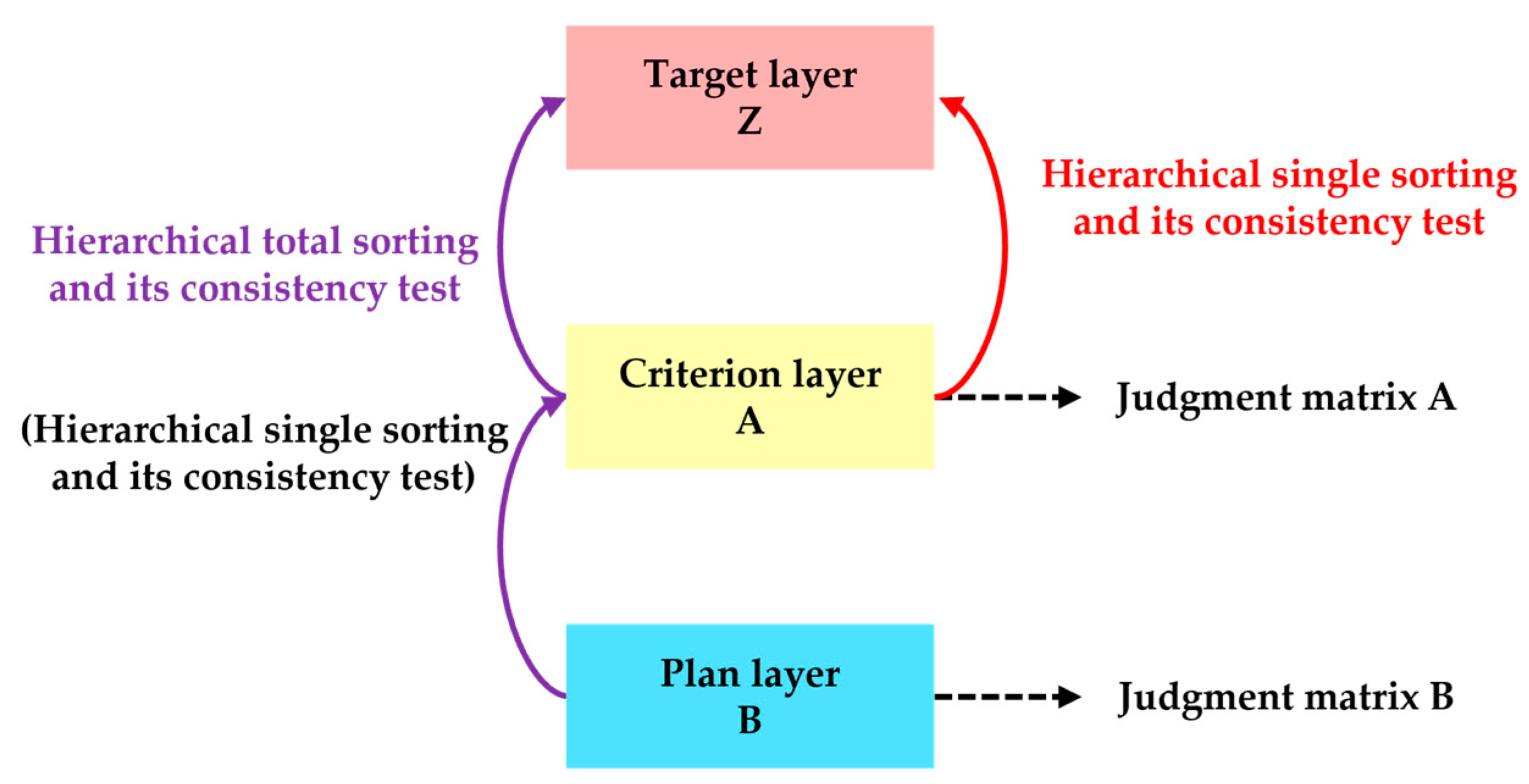
4.3. Overall Process of Hierarchy Analysis Method

The hierarchical analysis method solves the problem of dealing with the relative weight factor of plan layer or the lowest level to the target layer or the highest level. The relative weight factor can be sorted on the plan layer of different programs, modes, and measures to achieve a variety of programs to make a selection or formulate the selection of the program’s strategy, and its overall process is shown in Figure 4.

When using the hierarchical analysis method to construct the adjustable resource sensitivity model, it can be divided into the following five steps.

(1)

Building hierarchical structure model.

(2)

Constructing judgment (expert judgment and pairwise comparison) matrix.

(3)

Hierarchical single sorting and its consistency test.

(4)

Hierarchical total sorting and its consistency test.

(5)

Calculation of each adjustable resource sensitivity.

When the attribute value of each alternative scheme is known under each target, the hierarchical single-sorting result of the plan layer can be calculated directly based on the attribute value.

When it is difficult to quantify the attribute value of different candidate schemes under the corresponding target, the weight factor of each scheme under each target can be obtained by pairwise comparison, that is, priority. The total weight factor for each scheme is then calculated. The advantages and disadvantages of the scheme are determined according to the size of the overall weight factor, that is, the regulation resource sensitivity.

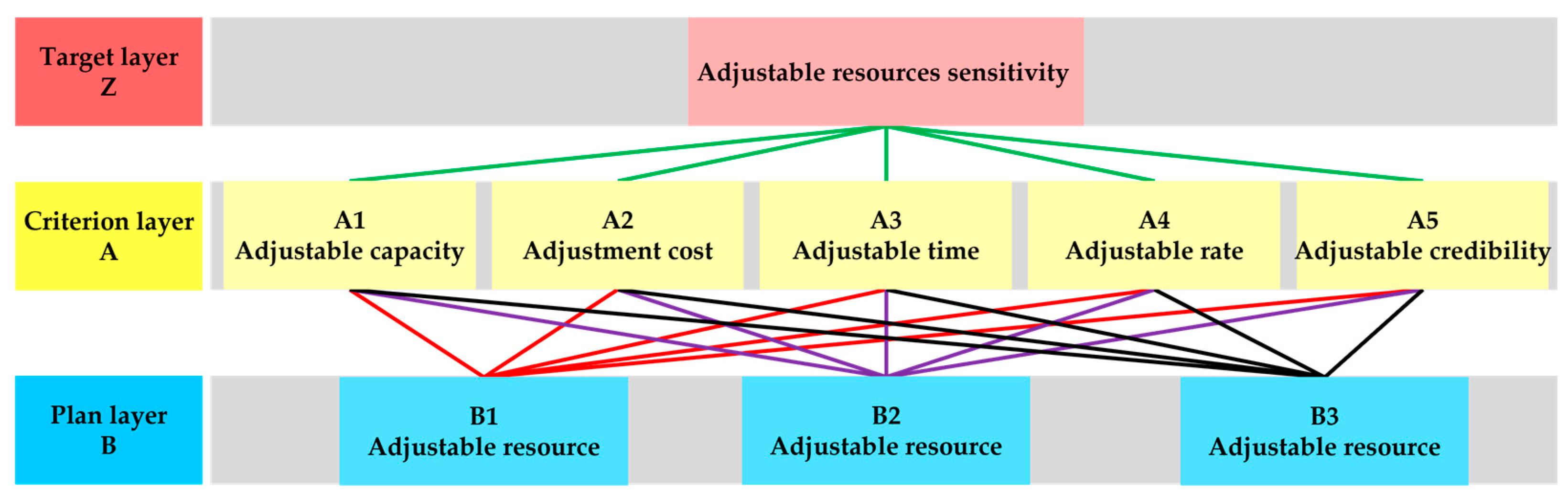
4.3.1. Building Hierarchical Structure Model

To use the hierarchical analysis method for application profiling, it is first necessary to group the factors involved, and each grouping is set into a hierarchy to hierarchize, clarify, and organize the application problem and then construct a structural model of hierarchical analysis. The said hierarchy has the following three categories in general [29]:

(1)

The highest layer (target layer): There is only one element in the target layer, usually to analyze the ideal effect or desired goal of dealing with the problem. In the second layer of the sensitivity algorithm analysis, the target layer refers to the regulatory resource sensitivity.

(2)

The intermediate layer (criterion layer): The criterion layer includes the intermediate link involved in the realization of the goal, which is generally composed of a layer that contains the criteria and sub-criteria that need to be considered. In the second layer of the sensitivity algorithm analysis, it refers to the load regulation characteristics of adjustable load resources, such as adjustable capacity, regulation cost, historical adjustable credibility, regulation rate, adjustable time, resource type, historical adjustable reliability, the willingness of adjustable resources to participate in regulation, etc.

(3)

The lowest layer (plan layer): The program layer is manifested in the various types of schemes, modes, decisions, measures, and so on, from which various options can be selected to achieve the target. In the second layer of the sensitivity algorithm analysis, this refers to each adjustable resource in a certain power-grid power node.

4.3.2. Constructing the Judgment Matrix

When determining the weight factor among various factors at different layers, if the result is purely qualitative, it may be difficult for others to accept. Therefore, SANTY proposes the consistent matrix method: instead of comparing all factors together, factors are compared in pairs to reduce the difficulty of comparing factors with different attributes, thereby improving the accuracy of the comparisons [29].

The key to the information basis of the hierarchical analysis is the judgment of the relative importance or importance of each layer and each factor, and the matrix expression form of the important degree value is the judgment matrix. When the relationship between the upper and lower layers is determined, we obtain the proportion of the lower elements associated with an upper element (target $Z$ or criterion $A$).

Assuming that the factors $A_k$ in the hierarchy $A$ are related or related to the next layer, $B_1$, $B_2$, …, and $B_n$, then the constructed judgment matrix form is shown in

Table 1. Judgment matrix form.

${\mathit{A}}_{\mathit{k}}$	${\mathit{B}}_1$	${\mathit{B}}_2$	…	${\mathit{B}}_{\mathit{n}}$	${\mathit{B}}_1$
$B_1$	$b_{11}$	$b_{12}$	…	$b_{1n}$	$b_{11}$
$B_2$	$b_{21}$	$b_{22}$	…	$b_{2n}$	$b_{21}$
$⋮$	$⋮$	$⋮$	$\ddots$	$⋮$	$⋮$
$B_n$	$b_{n1}$	$b_{n2}$	…	$b_{nn}$	$b_{n1}$

.

The $b_{ij}$ is the numerical representation of the relative importance of $B_i$ to $B_j$ for $A_k$, and the judgment matrix represents the relative importance between the factors related to it at the next layer for a factor at the previous layer. The degree of importance can be based on SANTY’s 1–9 scale (also known as importance scale), as shown in Table 1, where the pairwise comparison of factors in each layer should not exceed 9. And through the expert scoring method to obtain the value of the relative importance and ultimately to obtain the judgment matrix, $B=(b_{ij}{)}_{n\times n}$, if the ratio of the importance of the element $i$ to the element $j$ is $b_{ij}$, then the relationship between the ratio of the importance of the element $j$ to the element $i$ satisfies $b_{ji}{b}_{ij}=1$.

4.3.3. Hierarchical Single Sorting and Its Consistency Test

(1)

Hierarchical single sorting

Hierarchical single sorting refers to the weight or weight of the importance order of the factors associated with this layer for each factor at the previous layer. It is the basis for ranking the importance of all the factors at this layer relative to the previous layer.

Theorem 1.

The only nonzero eigen root of a consistent array of order $n$ is $n$.

Theorem 2.

The largest characteristic root ${\lambda }_{\max }$ of the $n$-order positive reciprocal inverse array $A$ satisfies ${\lambda }_{\max }$$\ge$$n$, and $A$ is a consistent array if and only if ${\lambda }_{\max }$=$n$.

For the pairwise comparison array $A$ (positive and reciprocal array) inconsistent within the allowable range, SANTY uses the feature vector corresponding to the maximum feature root ${\lambda }_{\max }$ as the weight vector $W$, that is, the hierarchical single order can be summarized as the feature root and feature vector problem of the calculation judgment matrix, that is, the judgment matrix $B$ should meet the following equation:

$$BW={\lambda }_{\max }W$$

(14)

where ${\lambda }_{\max }$ represents the largest eigen root of $B$. $W$ denotes the corresponding ${\lambda }_{\max }$ regularized eigenvector. The component $W_i$ of $W$ is the weight of the single sorting of the corresponding factor, i.e., the sensitivity of the factor at that layer.

(2)

Consistency test

The eigenvector corresponding to the maximum feature root, ${\lambda }_{\max }$, of the judgment matrix is then normalized as $W$. The element $B$ is the ranking weight or weight of the relative importance of the same hierarchical factor to a factor at the previous layer, which is called the hierarchical single-sorting process. Whether the hierarchical single order can be confirmed requires further consistency test. The so-called consistency test refers to the allowable range of inconsistent determination of paired comparison array (positive and reciprocal array) $A$.

In order to test the consistency of the matrix, it is necessary to calculate its consistency index, $CI$, which is defined as follows:

$$CI={\displaystyle \frac{{\lambda }_{\max }-n}{n-1}}$$

(15)

Obviously, when the judgment matrix has complete consistency, then there is $CI$= 0. The larger the ${\lambda }_{\max }-n$, the larger the $CI$ and the worse the consistency of the judgment matrix. When $CI$ = 0, there is complete consistency; at this time, the judgment matrix $A$ is a consistent matrix, the most ideal situation. When $CI$ is close to 0, there is satisfactory consistency. As $CI$ increases, the inconsistency becomes more serious.

It should be noted that the sum of the $n$ eigenvalues of matrix $B$ is exactly equal to $n$, so $CI$ is equivalent to the average of the remaining $n-1$ eigen roots, except ${\lambda }_{\max }$. In order to test whether the judgment matrix has satisfactory consistency, it is necessary to find out the criteria for measuring the consistency index, $CI$, of the matrix $B$ and introduce the stochastic consistency index, $RI$, and the selection of the stochastic consistency index ($RI$) is shown in

Table 2. Random consistency index, $RI$, and corresponding critical maximum eigen root, ${\lambda }_{\max }^{CR}$, of $n$-order matrix.

Order	1	2	3	4	5	6	7	8	9	10
$RI$	0.00	0.00	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49
${\lambda }_{\max }^{CR}$	-	-	3.116	4.27	5.45	6.62	7.79	8.99	10.16	11.34

.

The ratio of the consistency index, $CI$, of the judgment matrix to the index $RI$ of the average random consistency of the same order is called the random consistency ratio of the judgment matrix, recorded as $CR$, and the random consistency ratio is as follows:

$$CR={\displaystyle \frac{CI}{RI}}$$

(16)

when calculated $CR$ < 0.1, or calculated ${\lambda }_{\max }\le {\lambda }_{\max }^{CR}$, the judgment matrix has a satisfactory consistency; otherwise, the judgment matrix needs to be adjusted again.

4.3.4. Hierarchical Total Sorting and Its Consistency Test

Based on the results of the single sorting of all the layers in the same layer, you can calculate the weights of the importance of all the factors in the same layer for the previous layer, which is the total sorting of the hierarchy [29]. The hierarchical total sorting needs to be performed sequentially from top to bottom, layer by layer, letting the ordering of the $n$ elements on the $k-1$-th layer with respect to the total goal be calculated by the following equation:

$$w^{(k-1)}={\left[w_1^{k-1},\hspace{0.17em}\cdot \cdot \cdot ,\hspace{0.17em}{w}_n^{k-1}\right]}^T$$

(17)

The $n_k$ elements of the $k$-th layer are single-ordered vectors (as a criterion) with respect to the $j$-th element on the $k-1$-th layer being expressed by the following equation:

$$u_j^{(k)}={\left[u_{1j}^k,u_{2j}^k,\cdot \cdot \cdot ,u_{n_{k}j}^k\right]}^T,\hspace{0.17em}\hspace{0.17em}j=1,\hspace{0.17em}2,\hspace{0.17em}\dots ,\hspace{0.17em}n$$

(18)

where the weights of the elements not dominated by the $j$-th element are taken to be zero, and thus the $n_k\times n$-order matrix $U^{(k)}$ is obtained:

$$U^{(k)}=\left[u_1^{(k)},\hspace{0.17em}{u}_2^{(k)},\hspace{0.17em}\cdot \cdot \cdot ,\hspace{0.17em}{u}_n^{(k)}\right]=\left[\begin{array}{cccc}{u}_{11}^{(k)}& u_{12}^{(k)}& \cdot \cdot \cdot & u_{1n}^{(k)}\\ u_{21}^{(k)}& u_{22}^{(k)}& \cdot \cdot \cdot & u_{2n}^{(k)}\\ ⋮& ⋮& ⋮& ⋮\\ u_{n_{k}1}^{(k)}& u_{n_{k}2}^{(k)}& \cdot \cdot \cdot & u_{n_{k}n}^{(k)}\end{array}\right]$$

(19)

where column $j$ in $U^{(k)}$ stands for the single sorting vector of the $n_k$ elements of the $k$-th layer for the $j$ elements of the $k-1$-th layer as a criterion.

The total sorting of elements on the $k$-th layer for the total goal is as follows:

$$w^{(k)}={\left[w_1^{\left(k\right)},\hspace{0.17em}\cdot \cdot \cdot ,\hspace{0.17em}{w}_n^{\left(k\right)}\right]}^T$$

(20)

The $w^{(k)}$ is further expressed by the following equation:

$$w^{(k)}=U^{(k)}{w}^{(k-1)}=\left[\begin{array}{cccc}{u}_{11}^{(k)}& u_{12}^{(k)}& \cdot \cdot \cdot & u_{1n}^{(k)}\\ u_{21}^{(k)}& u_{22}^{(k)}& \cdot \cdot \cdot & u_{2n}^{(k)}\\ ⋮& ⋮& ⋮& ⋮\\ u_{n_{k}1}^{(k)}& u_{n_{k}2}^{(k)}& \cdot \cdot \cdot & u_{n_{k}n}^{(k)}\end{array}\right]\left[\begin{array}{c}{w}_1^{(k-1)}\\ w_2^{(k-1)}\\ ⋮\\ w_n^{(k-1)}\end{array}\right]$$

(21)

That is, there is the following equation:

$$w_i^{(k)}={\displaystyle \sum _{j=1}^n{u}_{ij}^{(k)}{w}_j^{(k-1)}},\hspace{0.17em}\hspace{0.17em}i=1,\hspace{0.17em}2,\hspace{0.17em}\cdot \cdot \cdot ,\hspace{0.17em}{n}_k$$

(22)

The consistency of results of the hierarchical total sorting calculations is evaluated by calculating a test quantity similar to that of the single sorting. The test is performed layer by layer from the top layer. Let the consistency index of some factors in the $k$-th layer to the single sort of the $j$-th element of the $k-1$-th layer be $C{I}_j^{(k)}$, the average random consistency index be $R{I}_j^{(k)}$ (it is not necessary to take into account the $j$-th element of the $k$-th layer when it is not related to the $j$-th element of the $k-1$-th layer), and the consistency ratio of the single sort of the $k$-th layer to the $j$-th element of the $k-1$-th layer is represented by the following equation:

$$C{R}_j^{(k)}={\displaystyle \frac{C{I}_j^{(k)}}{R{I}_j^{(k)}}}$$

(23)

when $C{R}_j^{(k)}$ $\le$ 0.1 is computed or ${\lambda }_{\max }^{(k)}\le {\lambda }_{\max }^{CR}$ is computed, the hierarchical single sorting is computed with satisfactory consistency.

Then, the consistency ratio of the total sorting at the $k$-th layer is as follows:

$$C{R}^{(k)}={\displaystyle \frac{{\displaystyle \sum _{j=1}^{n_k}{w}_j^{(k-1)}C{I}_j^{(k)}}}{{\displaystyle \sum _{j=1}^{n_k}{w}_j^{(k-1)}R{I}_j^{(k)}}}}={\displaystyle \frac{w_1^{(k-1)}C{I}_1^{(k)}+\cdots +w_j^{(k-1)}C{I}_j^{(k)}}{w_1^{(k-1)}R{I}_1^{(k)}+\cdots +w_j^{(k-1)}R{I}_j^{(k)}}}$$

(24)

In particular, when the order of $R{I}_j^{(k)}$ is the same, the above equation is equivalent to the following equation:

$$C{R}^{(k)}={\displaystyle \frac{w_1^{(k-1)}C{I}_1^{(k)}+\cdots +w_j^{(k-1)}C{I}_j^{(k)}}{1\times R{I}_j^{(k)}}}$$

(25)

Similarly, when $C{R}^{(k)}$ $\le$ 0.1, the hierarchical total sorting is calculated with satisfactory consistency.

4.3.5. Calculation of Each Adjustable Resource Sensitivity

For each adjustable resource, according to the results of the hierarchical analysis, the sensitivity of the adjustable resource is as follows:

$$S_{load}^{type}=w^{(k)}={\left[\begin{array}{cccc}{w}_1^{(k)}& w_2^{(k)}& \cdots & w_{n_k}^{(k)}\end{array}\right]}^T$$

(26)

where $S_{load}^{type}$ stands for an adjustable resource sensitivity vector, whose elements are the specific value of the sensitivity of each adjustable resource.

According to the sensitivity of adjustable resources, the regulation of adjustable resources is sorted to realize the precise regulation of adjustable resources.

5. Application Process of Double-Layer Sensitivity Analysis Results

When a power transmission line (which may include a transformer, known as a transformer power transmission line) or power flow section becomes overloaded, adjustments are required by the power grid dispatching.

The sensitivity analysis method is applied to reduce the load in the system or adjust the active power injection of the power node to eliminate the overload of the power transmission line and make the operation state of the power system return to normal.

In order to minimize the load reduction/adjustment of the system, the power transmission line overload should be eliminated by adjusting the output of the generator/power plant first, and the system load should be reduced/adjusted in the case when the generator/power-plant output regulation potential is exhausted or limited. The procedure of applying double-layer sensitivity analysis is as follows [30].

(1)

Select the line OL with the most serious overload.

(2)

Determine the adjusted generator/power-plant power nodes $m$ and $n$. The sensitivity matrix of power transmission-line power to power-node power is calculated from the first layer of the power transmission line sensitivity-analysis model. When overload occurs in the positive direction of the line OL, cut/adjust the output of the generator/power plant power node $m$ with the positive maximum sensitivity value and increase the output of the generator/power-plant power node $n$ with the negative maximum sensitivity value. When overload occurs in the negative direction of the line OL, cut/adjust the output of the generator/power-plant power node with the negative maximum sensitivity value of generator/power-plant power node $m$ and increase the output of generator/power-plant power node $n$ with a positive maximum sensitivity value. When there is an overload in the negative direction of line OL, cut/regulate the output of generator/power-plant power node EE with a negative maximum sensitivity value.

(3)

Determine the generator/power-plant power-regulation amount, $\Delta P_{gen}$, for power nodes $m$ and $n$. To eliminate the overload on the line OL, the generator/power-plant power-regulation amount, $\Delta P_{gen}$, for power nodes $m$ and $n$ is modeled as shown in the following equation:

$$\Delta P_{gen}={\displaystyle \frac{\left|P_{OL}\right|-{\overline{P}}_{OL}}{S_m^{r,+\max }-S_n^{r,-\max }}}$$

(27)

where $\Delta P_{gen}$ stands for the generator/power plant power adjustment; $\left|P_{OL}\right|$ is the current actual power of the overloaded line; ${\overline{P}}_{OL}$ represents the capacity limit of the overloaded line; $S_m^{r,+\max }$ denotes the sensitivity of the generator/power-plant power node $m$ with positive maximum sensitivity; and $S_n^{r,-\max }$ denotes the sensitivity of the generator/power plant power node $n$ with negative maximum sensitivity.

(4)

Adjust the power of generator/power-plant power nodes $m$ and $n$. After calculating the generator/power-plant power-adjustment amount, $\Delta P_{gen}$, the adjustment amounts of generator/power-plant power nodes $m$ and $n$ can be adjusted in accordance with the principles of equal proportion adjustment, priority of the absolute value of sensitivity, priority of the electrical distance, etc., so as to make the total adjustment amount reach $\Delta P_{gen}$. The power adjustment amount of the generator/power plant cannot violate the upper and lower limits of the generator/power-plant output constraints, and if the calculation exceeds them, the adjustment amount can only be adjusted in accordance with the actual adjustment value of the boundary constraints, and the adjustment amount will be reduced appropriately. If the calculation exceeds the upper and lower limits of generator/power-plant output constraints, it can only be adjusted according to the actual adjustment value of the boundary constraints, appropriately reducing the generator/power-plant adjustment amount, $\Delta P_{gen}$, and the adjustment amount is insufficient, and then there is a subsequent reduction/regulation of the adjustable resources to realize.

(5)

The calculation of power flow information can be simplified according to the actual needs. Adjust the power flow and check the effect of adjusting the generator/power plant output to achieve the effect of eliminating the line overload until the adjustment generator/power plant is not working or the adjustment generator/power plant is limited.

(6)

Reduce/regulate the number of adjustable resources in the system. When the generator/power-plant power-adjustment amount is limited or insufficient, the line overload is eliminated by cutting/adjusting the adjustable resources of the system. The reduction/adjustment method is similar to the process of adjusting generator/power-plant output. According to the sensitivity analysis model of the calculation of the load-reduction effect of the line, the calculation model of the line load reduction is as follows:

$$\Delta P_{OL}=S_{node}^{OL}\Delta P^{node}$$

(28)

where $S_{node}^{OL}$ denotes the active power sensitivity of the injected power of power node, $node$, to the line OL of the overloaded power transmission line; $\Delta P^{node}$ represents the amount of power node, $node$, adjustable resource regulation; and $\Delta P_{OL}$ stands for the amount of line-load shedding.

(7)

Adjustable resources aggregated under the sequential regulation power nodes: On the basis of the power node sensitivity of the first layer, the sensitivity analysis and calculation of the second layer are carried out, and the sensitivity analysis of the sorted power nodes is conducted out, and the adjustable resources are called one by one, according to the requirements of the line load reduction.

When the power transmission line is overloaded, when it is not feasible or feasible to adjust the active power injection of the power node by sensitivity analysis, it can directly enter the step of regulating and adjusting flexible resources to eliminate the power transmission-line overload and restore the system operation, returning it to normal.

6. Case Study

6.1. Introduction of Case

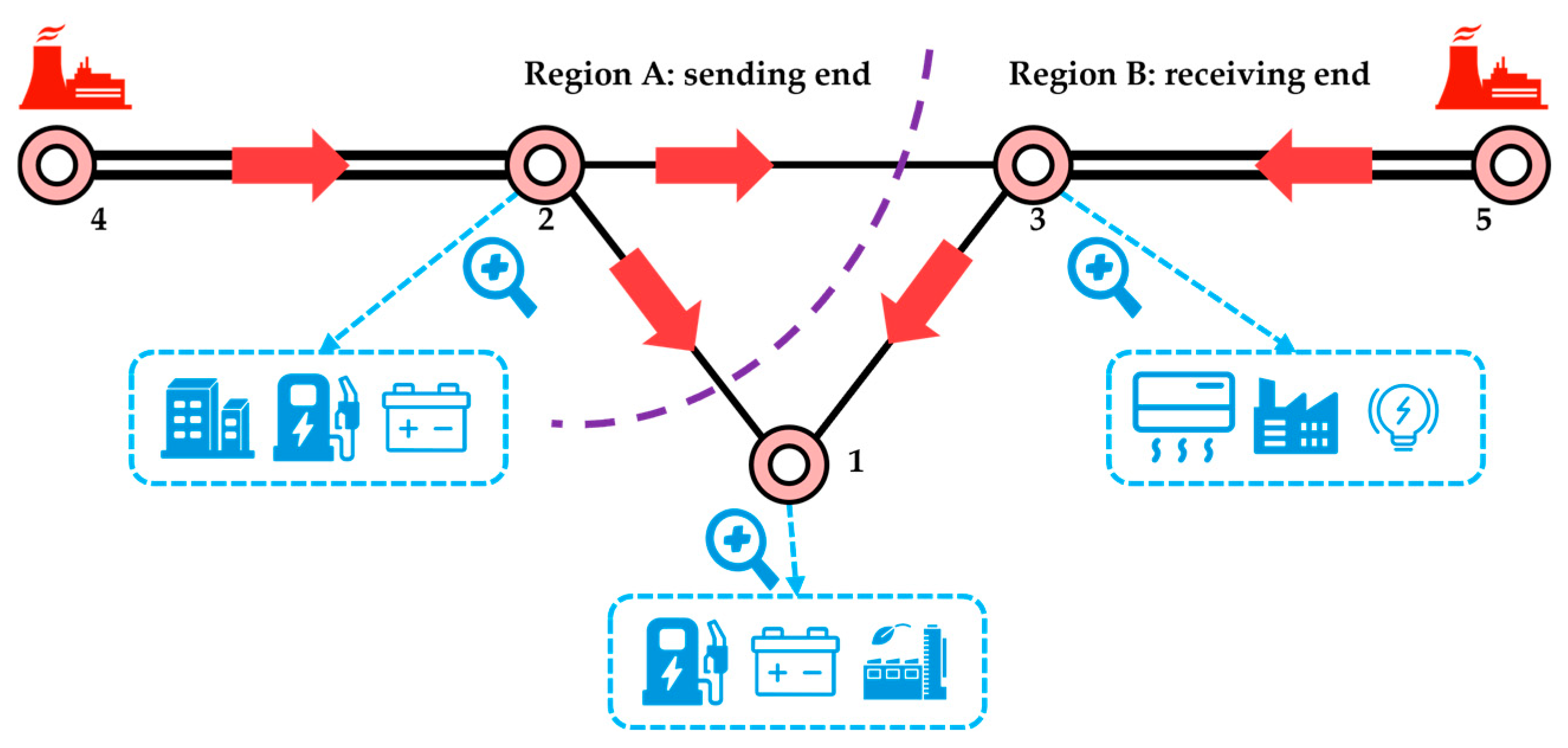
The case structure of a power system with seven lines, five power nodes, and seven types of adjustable resources is shown in Figure 5. Power node 1 is four generator sets, power node 5 is five generators and serves as the frequency modulation unit, and power node 5 is selected as the balanced power node of the system [30]. Under normal and stable operation, region A is the sending end area, region B is the receiving end area, and the active power flow of the power transmission line is shown by the red arrow.

The power transmission-line parameters of the power system shown in Figure 5 are shown in

Table 3. Power transmission-line parameters.

Power Transmission-Line Number	Power Node of Power Transmission-Line		Power Transmission-Line Reactance
	Starting Number	End Number
1	1	2	0.250
2	1	3	0.350
3	2	3	0.300
4	2	4	0.030
5	2	4	0.030
6	3	5	0.030
7	3	5	0.030

[30].

Power node 1, power node 2 and power node 3 have different types of adjustable load resources. Power node 1 mainly integrates industrial and commercial parks, charging piles/charging station, distributed energy storage, etc. Power node 2 mainly integrates residential load, charging piles/charging station, distributed energy storage, etc. Power node 3 mainly integrates cluster building air conditioning, industrial load, intelligent lighting load, etc. In this paper, the line overload of the power-system power transmission line number 2 shown in Figure 5 and Table 3 is taken as a case for the double-layer sensitivity analysis.

6.2. Calculation and Result Analysis of the First-Layer Power Transmission Line-Sensitivity Analysis

In the process of sensitivity calculation, the matrix involving reference power node is removed and then calculated. The reference power node is a known quantity. In the process of matrix operation, the reference power node will lead to matrix singular. In this case, the balanced power node is selected as the reference power node, so the balanced power node and the reference power node refer to the same node.

According to the first-layer power transmission line sensitivity-analysis model established in Section 3 above, the sensitivity matrix, $S_{sp}^r$ (where the sensitivity of balanced power node is 0 and the last column is the balanced power node), is obtained as follows:

$$S_{sp}^r=\left[\begin{array}{ccccc}0.389& -0.333& 0.000& -0.333& 0.000\\ 0.611& 0.333& 0.000& 0.333& 0.000\\ 0.389& 0.667& 0.000& 0.667& 0.000\\ 0.000& 0.000& 0.000& -0.500& 0.000\\ 0.000& 0.000& 0.000& -0.500& 0.000\\ 0.500& 0.500& 0.500& 0.500& 0.000\\ 0.500& 0.500& 0.500& 0.500& 0.000\end{array}\right]$$

The second line in the sensitivity matrix is the sensitivity of the active power of each power node power. Because the sensitivity of power node 1 is 0.611 and the largest in the same line, the power-node power regulation of power node 1 improves the overload regulation of the power transmission line number 2. Therefore, the adjustable load resources of power node 1 are adjusted first. The sensitivity of both power node 2 and power node 3 is 0.333, indicating that the line overload regulation of the power transmission line number 2 is the same. From the perspective of the aggregated resource characteristics under the power node and the electrical distance between the power node and the line, the sensitivity of power node 2 and power node 3 can be sorted again. Here, the sensitivity of power node 2 is better than the sensitivity of power node 3, according to the electrical distance.

In conclusion, according to the sensitivity analysis and sensitivity matrix calculation results, the order of power nodes in the primary-to-secondary regulated power system is power node 1, power node 2, and power node 3.

6.3. Calculation and Result Analysis of the Second-Layer Adjustable Resource-Sensitivity Analysis

According to the above analysis, preferential adjustment of the adjustable load resources of power node 1 can effectively alleviate the overload degree of power transmission line number 2. In the case that the regulation of power node 1 is limited, the adjustable resources on power node 2 and power node 3 can be regulated successively. Therefore, the aggregated resources under power node 1 are next sorted to sort out the regulation order of multiple types of resources under the same power node. Here, taking power node 1 as an example, the second-layer adjustable resource sensitivity-analysis calculation and result analysis are conducted. The regulatory sequence-processing process of multi-types of resources of power node 2 and power node 3 is similar to that of power node 1, and, thus, it is not repeated here.

Power node 1 mainly aggregates industrial and commercial parks, distributed energy storage, and the charging piles/charging station and selects five criteria, namely adjustable capacity, adjustable cost, adjustable time, adjustment rate, and adjustable credibility, as adjustment characteristics of the second-layer adjustable resources. The specific process of the second-layer adjustable resources sensitivity analysis is as follows.

6.3.1. Building the Hierarchical Structure Model

The example of a power node 1 adjustable resource sensitivity-hierarchy model is established, as shown in Figure 6.

6.3.2. Constructing the Judgment Matrix

The pairwise comparison matrix $A$ of the criterion layer to the target layer in Figure 6 is as follows:

$$A=\left[\begin{array}{ccccc}1& {\displaystyle \frac{1}{2}}& 4& 3& 3\\ 2& 1& 7& 5& 5\\ {\displaystyle \frac{1}{4}}& {\displaystyle \frac{1}{7}}& 1& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{3}}\\ {\displaystyle \frac{1}{3}}& {\displaystyle \frac{1}{5}}& 2& 1& 1\\ {\displaystyle \frac{1}{3}}& {\displaystyle \frac{1}{5}}& 3& 1& 1\end{array}\right]$$

The pairwise comparison matrices $B_1$, $B_2$, $B_3$, $B_4$, and $B_5$ of the plan layer adjustable resource B1 adjustable resource B2, and adjustable resource B3 to the criterion layer in Figure 6 are, respectively, as follows:

$$B_1=\left[\begin{array}{ccc}1& 2& 5\\ {\displaystyle \frac{1}{2}}& 1& 2\\ {\displaystyle \frac{1}{5}}& {\displaystyle \frac{1}{2}}& 1\end{array}\right],B_2=\left[\begin{array}{ccc}1& {\displaystyle \frac{1}{3}}& {\displaystyle \frac{1}{8}}\\ 3& 1& {\displaystyle \frac{1}{3}}\\ 8& 3& 1\end{array}\right],B_3=\left[\begin{array}{ccc}1& 1& 3\\ 1& 1& 3\\ {\displaystyle \frac{1}{3}}& {\displaystyle \frac{1}{3}}& 1\end{array}\right],B_4=\left[\begin{array}{ccc}1& 3& 4\\ {\displaystyle \frac{1}{3}}& 1& 1\\ {\displaystyle \frac{1}{4}}& 1& 1\end{array}\right],\mathrm{and}{B}_5=\left[\begin{array}{ccc}1& 1& {\displaystyle \frac{1}{4}}\\ 1& 1& {\displaystyle \frac{1}{4}}\\ 4& 4& 1\end{array}\right]$$

6.3.3. Hierarchical Single Sorting and Its Consistency Test

(1)

Pairwise comparison matrix $A$

The maximum eigenvalue of the pairwise comparison matrix $A$ is ${\lambda }_{\max }$ = 5.073.

The eigenvector of the pairwise comparison matrix $A$ is as follows:

$$w^2={\left[\begin{array}{ccccc}0.263& 0.475& 0.055& 0.099& 0.110\end{array}\right]}^T$$

The element of the feature vector in this hierarchy is the sensitivity value of each element of the criterion layer to the target layer, with ${\lambda }_{\max }\le$ 3.116 or $CR$ = 0.016 < 0.1, which indicates that $A$ has passed the consistency verification.

(2)

Pairwise comparison matrix $B$

The maximum eigenvalues of the pairwise comparison matrix $B_1$, $B_2$, $B_3$, $B_4$, and $B_5$ are 3.005, 3.002, 3, 3.009, and 3, respectively.

The consistency indexes of the pairwise comparison matrices $B_1$, $B_2$, $B_3$, $B_4$, and $B_5$ are 0.003, 0.001, 0, 0.005, and 0, respectively.

The eigenvectors of the pairwise comparison matrices $B_1$, $B_2$, $B_3$, $B_4$, and $B_5$ are expanded in columns and denoted by $w^3$:

$$w^3=\left[\begin{array}{ccccc}{u}_1^{(3)}& u_2^{(3)}& u_3^{(3)}& u_4^{(3)}& u_5^{(3)}\end{array}\right]=\left[\begin{array}{ccccc}0.595& 0.082& 0.429& 0.633& 0.166\\ 0.277& 0.236& 0.429& 0.193& 0.166\\ 0.129& 0.682& 0.142& 0.175& 0.668\end{array}\right]$$

Since the maximum eigenvalues of the pairwise comparison matrices $B_1$, $B_2$, $B_3$, $B_4$, and $B_5$ all satisfy ${\lambda }_{\max }\le {\lambda }_{\max }^{CR}$ = 3.116 or $B_1$, $B_2$, $B_3$, $B_4$, and $B_5$ all have $CR$ < 0.1, it is shown that $B_1$, $B_2$, $B_3$, $B_4$, and $B_5$ all pass the consistency verification.

6.3.4. Hierarchical Total Sorting and Its Consistency Test

The total sorting result of the hierarchy is presented by the following equation:

$$w^1=w^3{w}^2={\left[\begin{array}{ccc}0.300& 0.246& 0.456\end{array}\right]}^T$$

And there is the following equation:

$$C{R}^{(k)}={\displaystyle \frac{{\displaystyle \sum _{j=1}^{n_k}{w}_j^{(k-1)}C{I}_j^{(k)}}}{{\displaystyle \sum _{j=1}^{n_k}{w}_j^{(k-1)}R{I}_j^{(k)}}}}={\displaystyle \frac{w_1^{(k-1)}C{I}_1^{(k)}+\cdots +w_j^{(k-1)}C{I}_j^{(k)}}{w_1^{(k-1)}R{I}_1^{(k)}+\cdots +w_j^{(k-1)}R{I}_j^{(k)}}}={\displaystyle \frac{w_1^{(k-1)}C{I}_1^{(k)}+\cdots +w_j^{(k-1)}C{I}_j^{(k)}}{1\times R{I}_j^{(k)}}}=0.00303<0.1$$

So, the results indicate that the hierarchical total sorting passed the consistency test.

6.3.5. Calculation of Each Adjustable Resource Sensitivity

Each adjustable resource sensitivity is calculated by the following equation:

$$S_{load}^{type}=w^{(k)}=\left[\begin{array}{c}{w}_1^{(k)}\\ w_2^{(k)}\\ ⋮\\ w_{n_k}^{(k)}\end{array}\right]=w^1=\left[\begin{array}{c}0.300\\ 0.246\\ 0.456\end{array}\right]$$

where $S_{load}^{type}$ represents an adjustable resource sensitivity vector, whose elements are the specific value of the sensitivity of each adjustable resource.

According to the size of the adjustable resource sensitivity, power node 1 ranks the adjustable resource regulation. According to the above calculation results, we can see that the sensitivity of adjustable resource B1 (such as a park) aggregated under power node 1 is 0.300, the sensitivity of adjustable resource B2 (such as charging station) is 0.246, and the sensitivity of adjustable resource B3 (such as energy storage) is 0.456. Therefore, the prioritization of the aggregated adjustable resource regulation under power node 1 is as follows: adjustable resource B3 (such as energy storage) > adjustable resource B1 (such as a park) > adjustable resource B2 (such as charging station).

6.4. Analysis of Precise Regulation Effect for Regional Source–Grid–Load Friendly Interaction

The line in power transmission line number 2 of the power system shown in Figure 5 is forward overload 12.6 MW, realizing the maximum load reduction of 7.3 MW by the generator/power plant power adjustment, and the line in power transmission line number 2 is forward overload of 5.3 MW by adjusting the adjustable resources under the power node.

Combined with the Section 5 analysis and sensitivity matrix results, the adjustable resource B3 (such as energy storage) is 4.5 MW, the adjustable resource B1 (such as a park) is 3.8 MW, and the adjustable resource B2 (such as charging station) is 2.9 MW. It is known that the total adjustable resource of power node 1 is 11.2 MW to achieve the effect of 6.8432 MW and meet the forward load reduction requirements of 5.3 MW. Therefore, the application requirements of the power grid can be met by adjusting adjustable resources of power node 1. If adjustable resources under the adjustment power node 1 cannot meet the application requirements of 5.3 MW for the line of power transmission line number 2, the adjustable resources under power node 2 and power node 3 can be adjusted successively. The specific analysis results and adjustment effects are shown in

Table 4. Precision regulation effect.

Power Node	The First-Layer Power Transmission Line Sensitivity	Resource Symbol	Resource Type	The Second-Layer Adjustable Resource Sensitivity	Adjustable Capacity/MW	Load Reduction Effect/MW	Total Load Reduction Effect/MW
Power node 1	0.611		Distributed energy storage	0.456	4.5	2.7495	6.8432
			Industrial and commercial park	0.300	3.8	2.3218
			Charging piles/charging station	0.246	2.9	1.7719
Power node 2	0.333		Distributed energy storage	0.410	3.1	1.0323	2.3310
			Charging piles/charging station	0.305	1.8	0.5994
			Residential load	0.212	2.1	0.6993
Power node 3	0.333		Industrial load	0.385	2.8	0.9324	2.1645
			Cluster building air conditioning	0.352	2.4	0.7992
			Intelligent lighting load	0.285	1.3	0.4329

.

As shown in Table 4, the power node 1 adjustable resource B3 (distributed energy storage) adjustable amount of 4.5 MW can realize the effect of 2.7495 MW of positive load shedding on the line of power transmission line number 2. Power node 1 adjustable resource B1 (industrial and commercial park) with an adjustable amount of 3.8 MW can achieve a positive load shedding effect of 1.2654 MW on the line of power transmission line number 2. Power node 1 adjustable resource B2 (charging piles/charging station) can be adjusted by 2.9 MW to achieve a positive load shedding effect of 0.9657 MW on the line of power transmission line number 2. The results of other power nodes are similar. According to the sensitivity results of the first-layer power transmission line, the adjustment order of power-grid power nodes is power node 1, power node 2, and power node 3. Based on the second-layer adjustable resource sensitivity results, the resources under power node 1 are adjusted for distributed energy storage, industrial and commercial park, and charging piles/charging stations in turn. The resources under power node 2 are adjusted for distributed energy storage, charging piles/charging station, and residential load in turn. The resources under power node 3 are sequentially regulated for industrial load, cluster-building air conditioning, and intelligent lighting load.

In the process of sequential adjustment based on the sensitivity analysis results of the first-layer power transmission line and the sensitivity analysis results of the second-layer adjustable resources, if it can meet the application requirements of the power grid, no further adjustment is required. As in the above example, adjusting the resources under power node 1 can meet the requirement of 5.3 MW load reduction for the line with power transmission line number 2 under positive overload by adjusting the resources under power node 1, without the need to adjust the adjustable resources under power node 2 and power node 3.

7. Conclusions

This paper proposes a precise regulation strategy based on the double-layer sensitivity model, which shows the following:

• The proposed double-layer sensitivity analysis model and method meet the practical application requirements in solving the scenarios of regional power-grid power transmission line overload, transformer overload, and power flow section exceeding limit, and the regional source–grid–load friendly interaction precision regulation platform can realize and apply the proposed model and strategy.
• The proposed first-layer power transmission line sensitivity-analysis model can accurately address the application demands of the regional power grid, identifying the most sensitive and effective power nodes for power regulation. Additionally, the second-layer adjustable resources sensitivity-analysis model provides a unified quantification of adjustable resources and regulation sorting, enabling precise and quantifiable regulation in response to power grid-specific application demand.
• Based on the established double-layer sensitivity analysis model, the regional source–grid–load friendly interaction precision regulation platform can coordinate and unify the source, power grid, and load together to realize and carry out orderly, observable, measurable, and controllable source–grid–load friendly interactive precision regulation.

In the follow-up research, the authors will further study the precise regulation strategy of source–grid–load friendly interaction under the multi-layer power grid and multi-layer adjustable resource architecture and realize the hierarchical precise regulation of adjustable resources under the application demand scenarios of power grid voltage and frequency regulation.