A Novel Meta-Heuristic Algorithm Based on Birch Succession in the Optimization of an Electric Drive with a Flexible Shaft
Abstract
1. Introduction
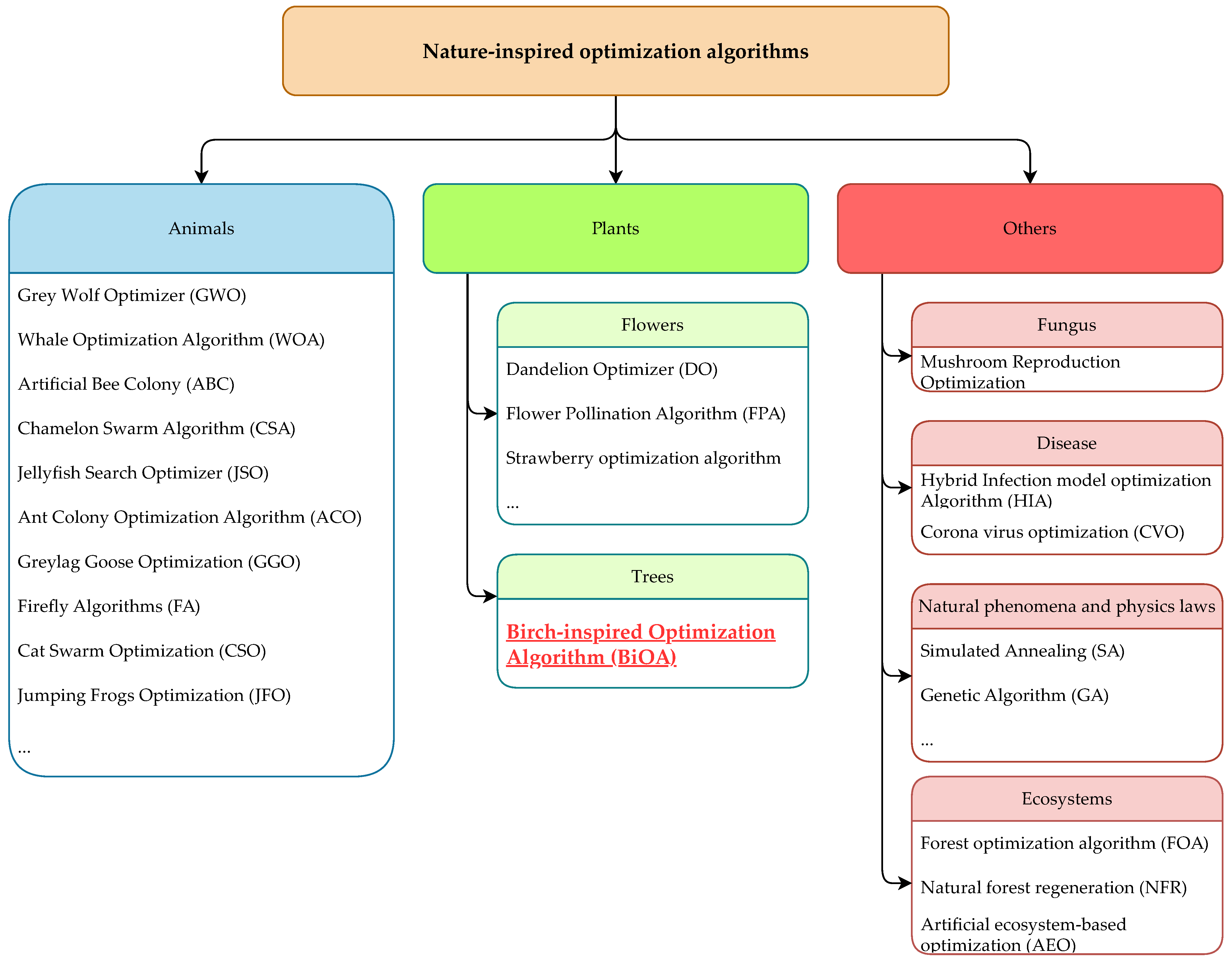
1.1. Optimization Algorithms
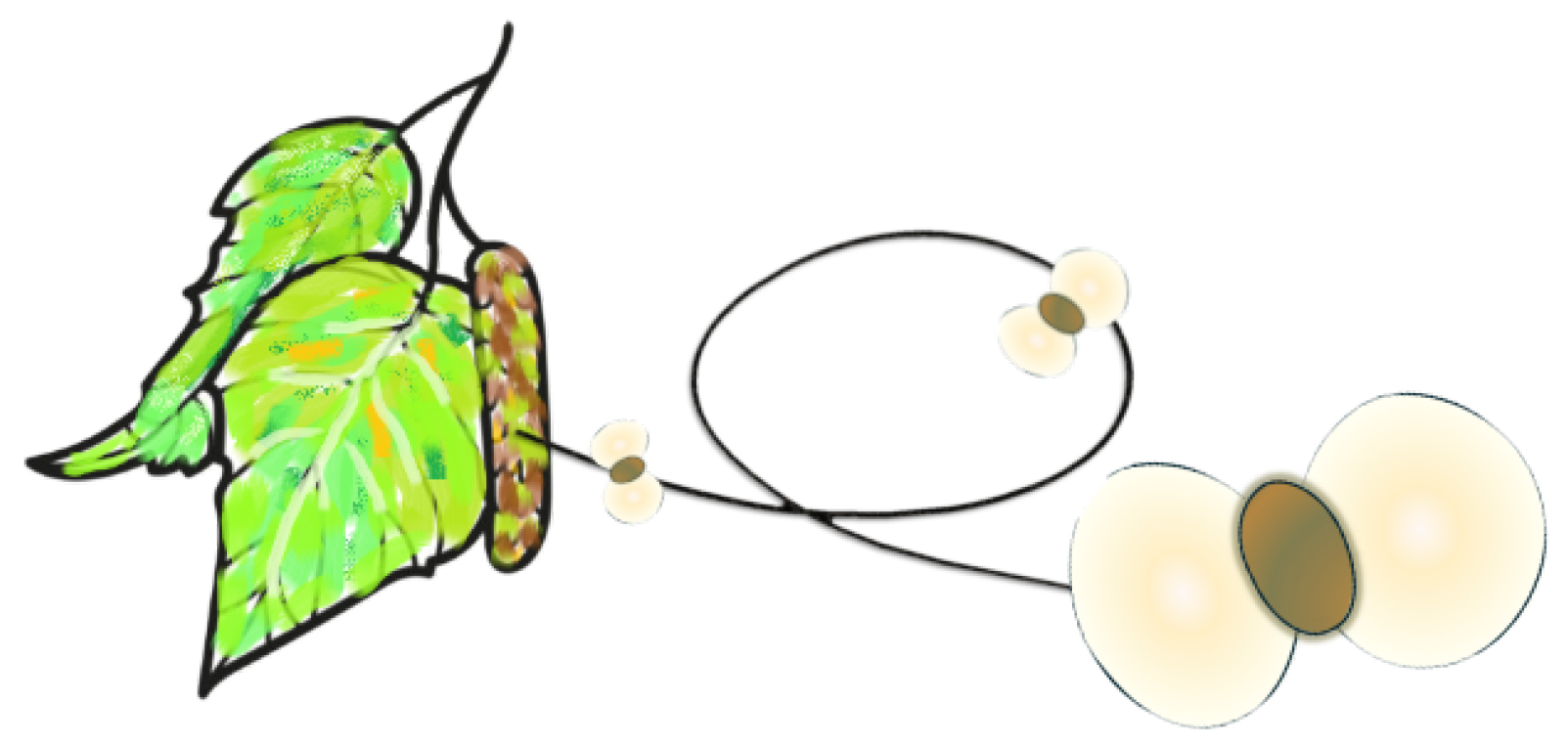
1.2. Birch Tree—Inspiration
1.3. The Example of a BiOA Application—Electrical Drives
- The foundation of a new metaheuristic algorithm inspired by propagation and pioneering capability of birch trees—the Birch-inspired Optimization Algorithm (BiOA).
- Tests based on the benchmark functions prepared for the analyzed BiOA and other well-known algorithms—a comparison.
- The BiOA implementation for the optimization of the extended control structure of the two-mass system.
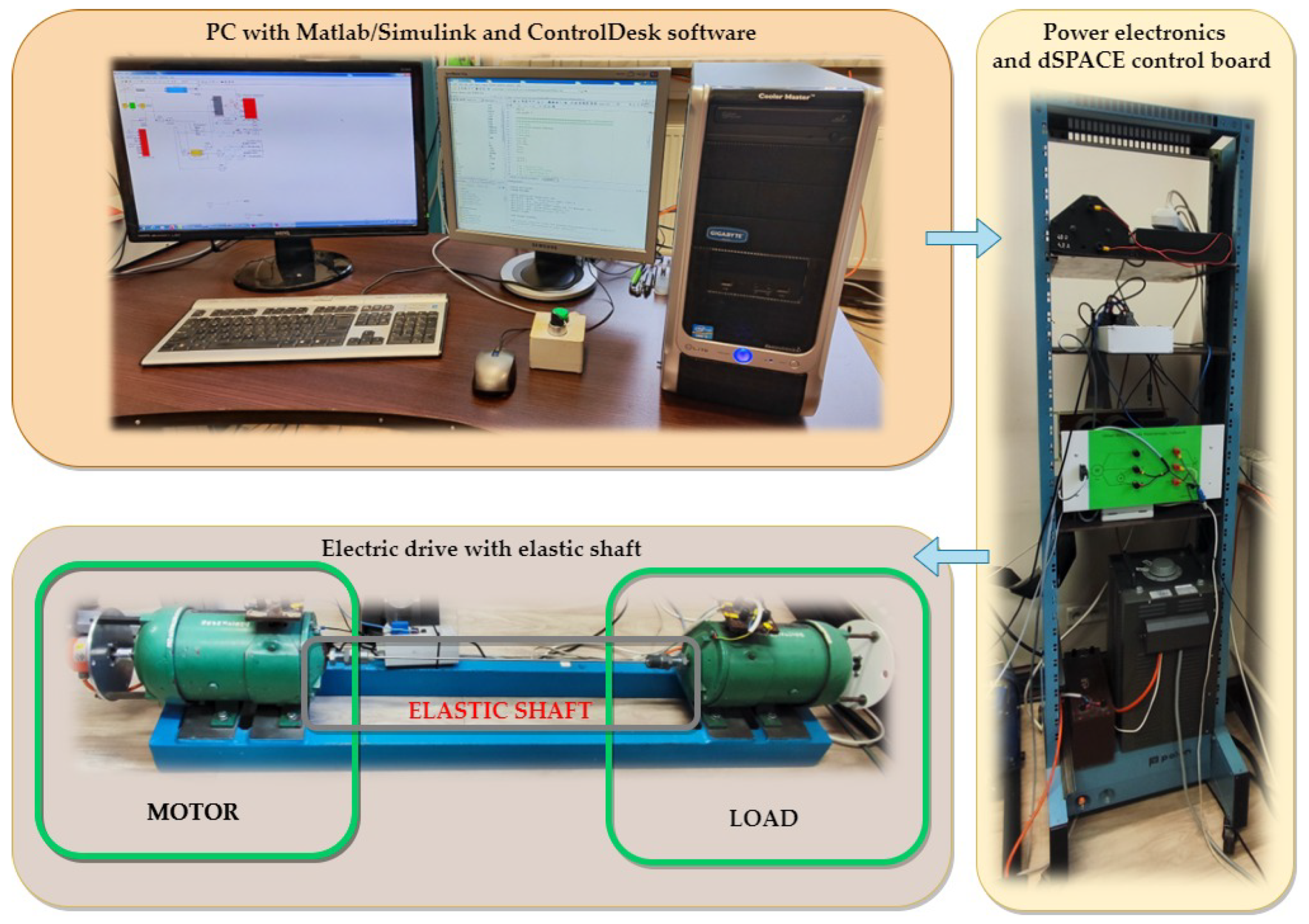
- Experimental validation of the results.
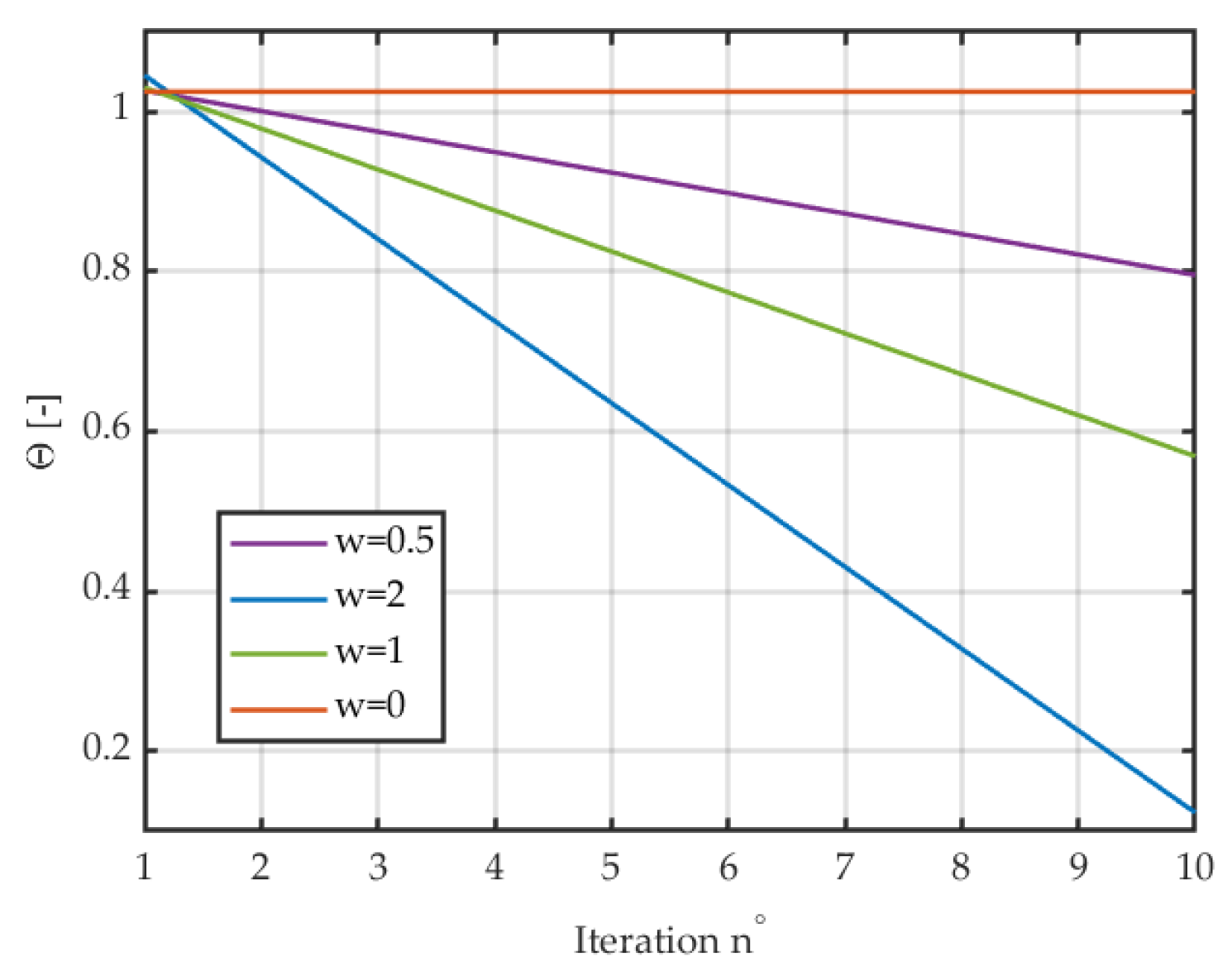
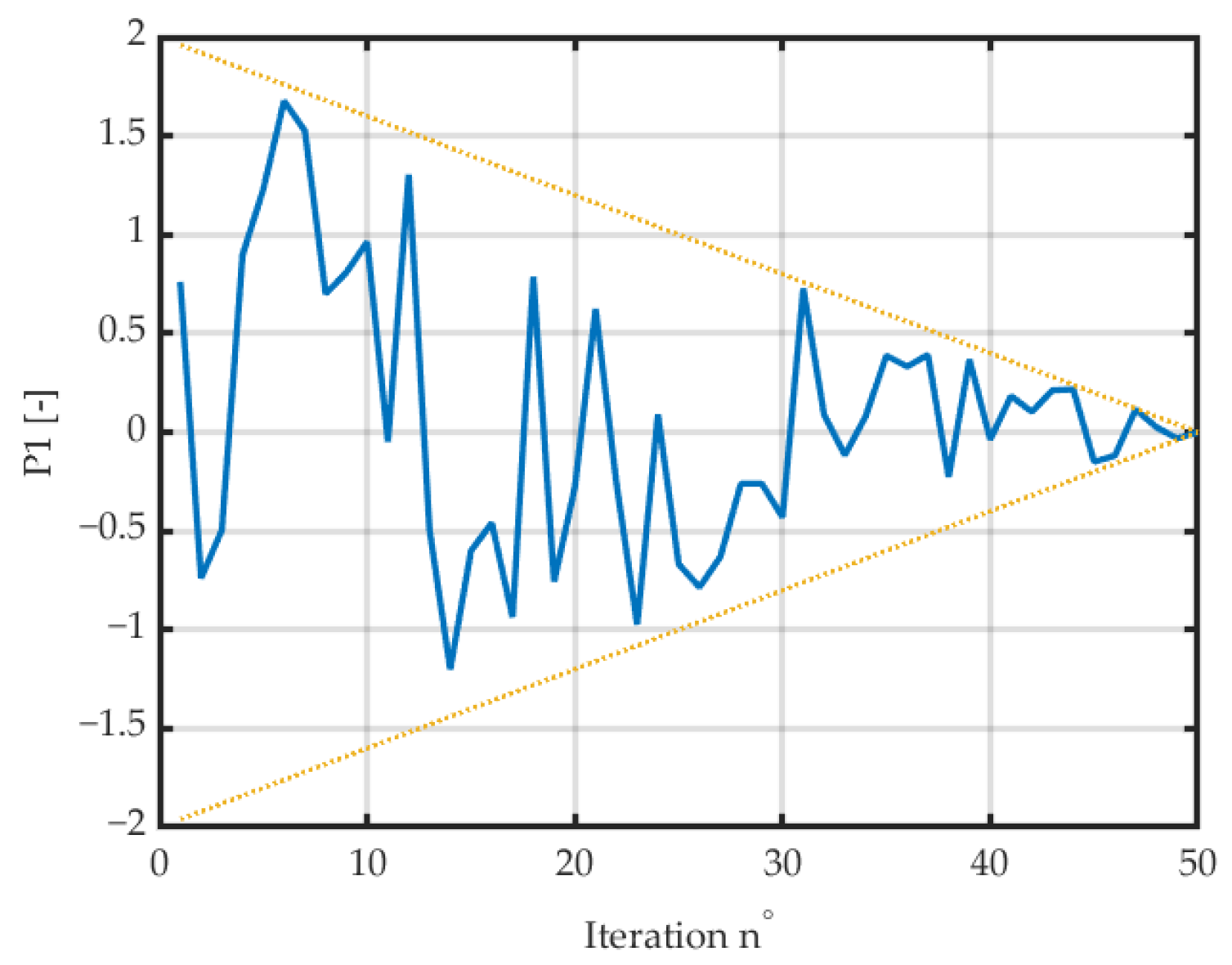
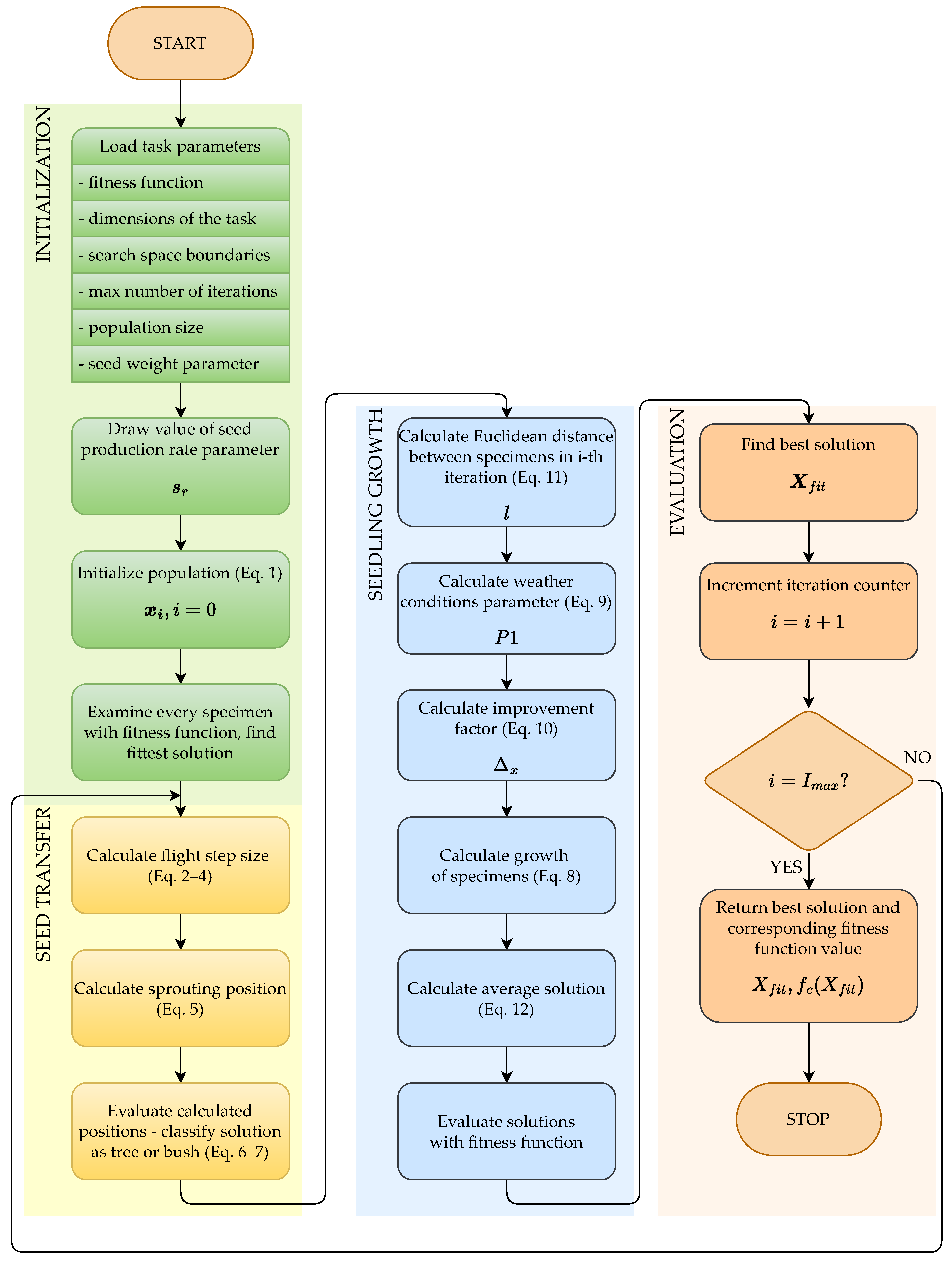
2. Mathematical Description of the Birch-Inspired Optimization Algorithm (BiOA)
3. Results
3.1. Benchmark Functions
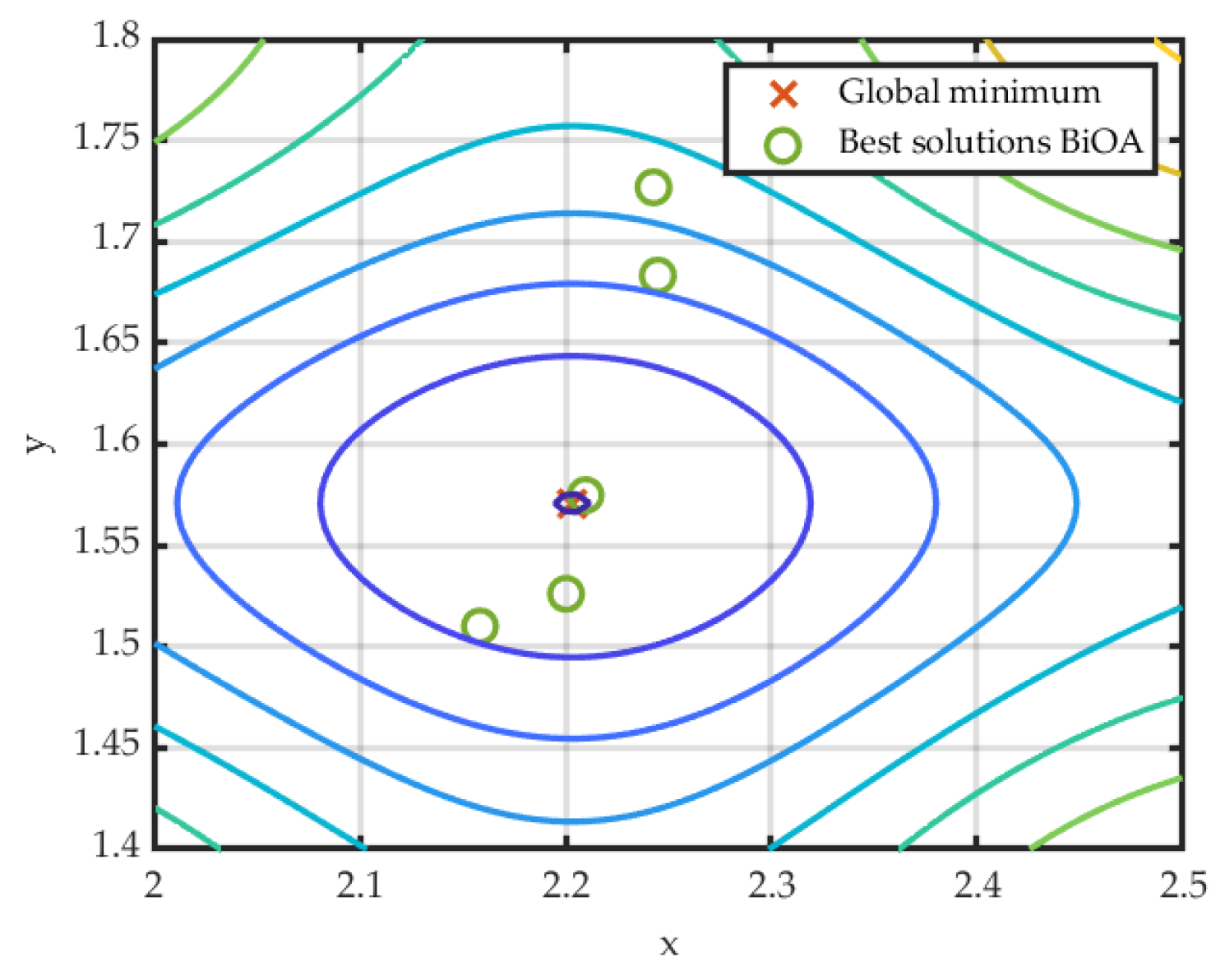
3.1.1. Michalewicz Function
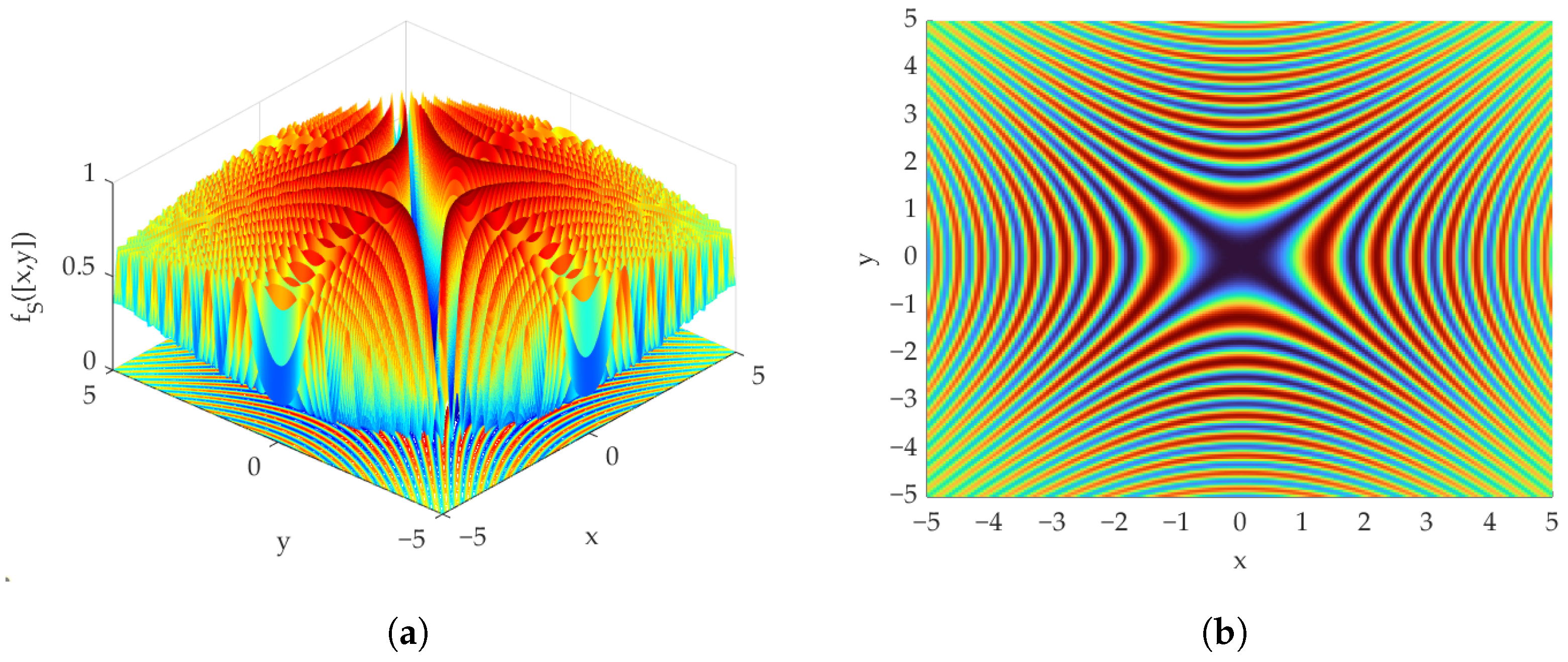
3.1.2. Schaffer Function
3.1.3. Ackley Function
3.1.4. Performance Assessment
3.2. Real-Life Applications
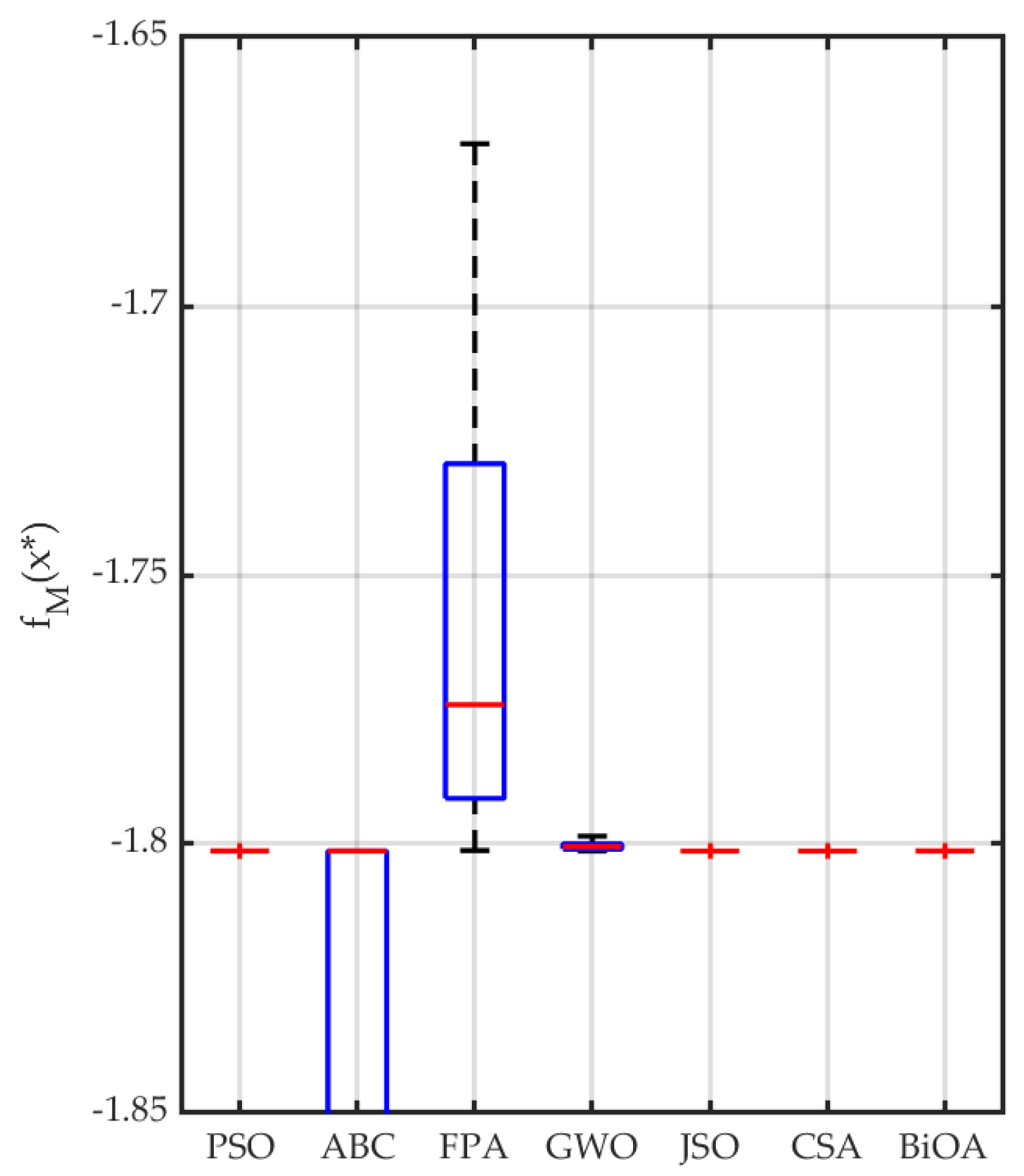
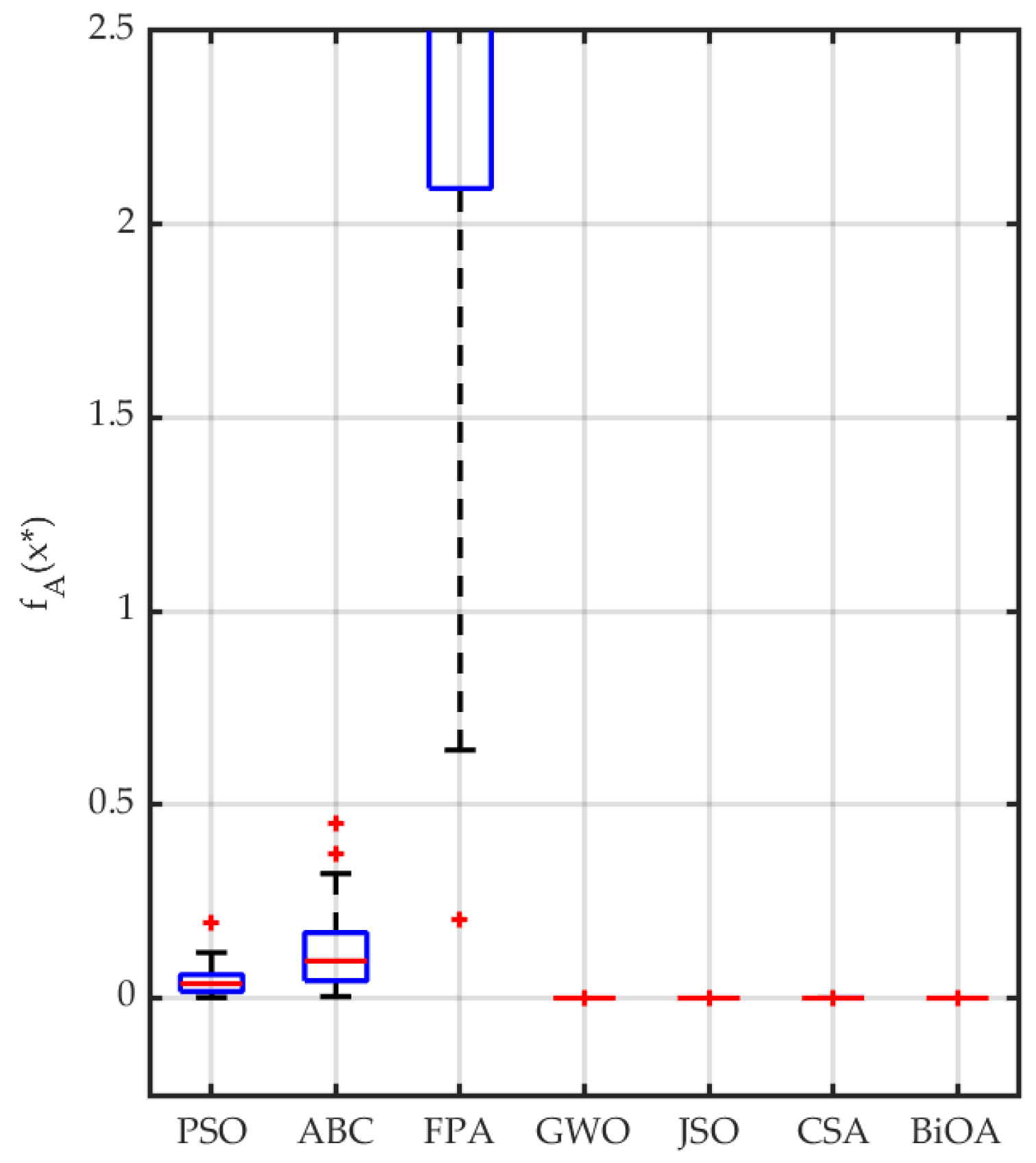
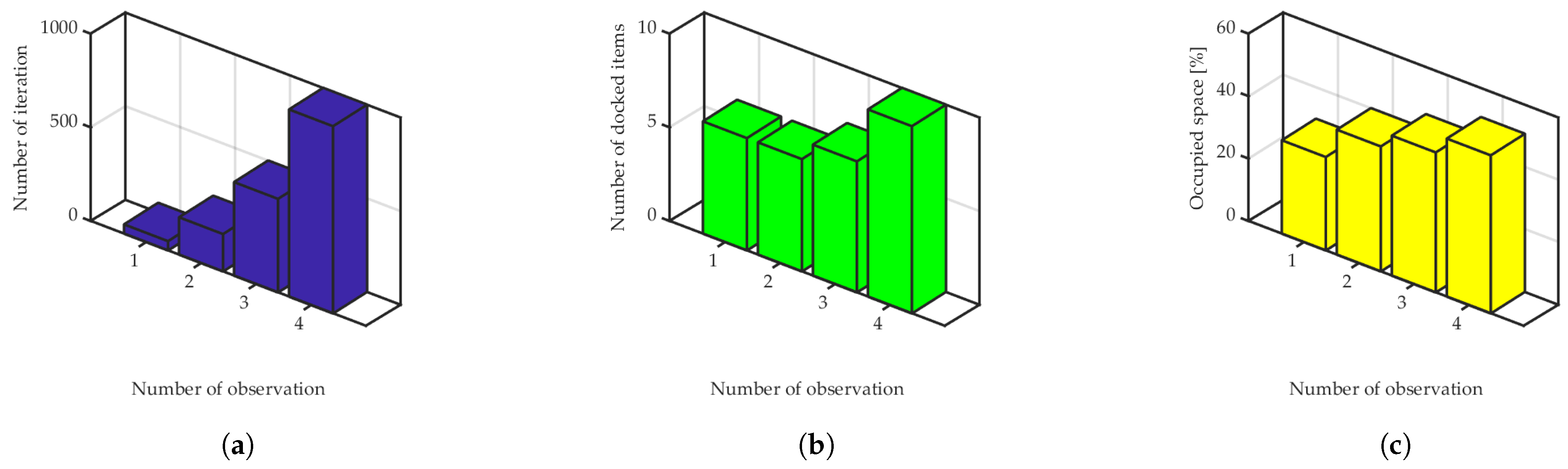
3.2.1. Bin-Packing Problem
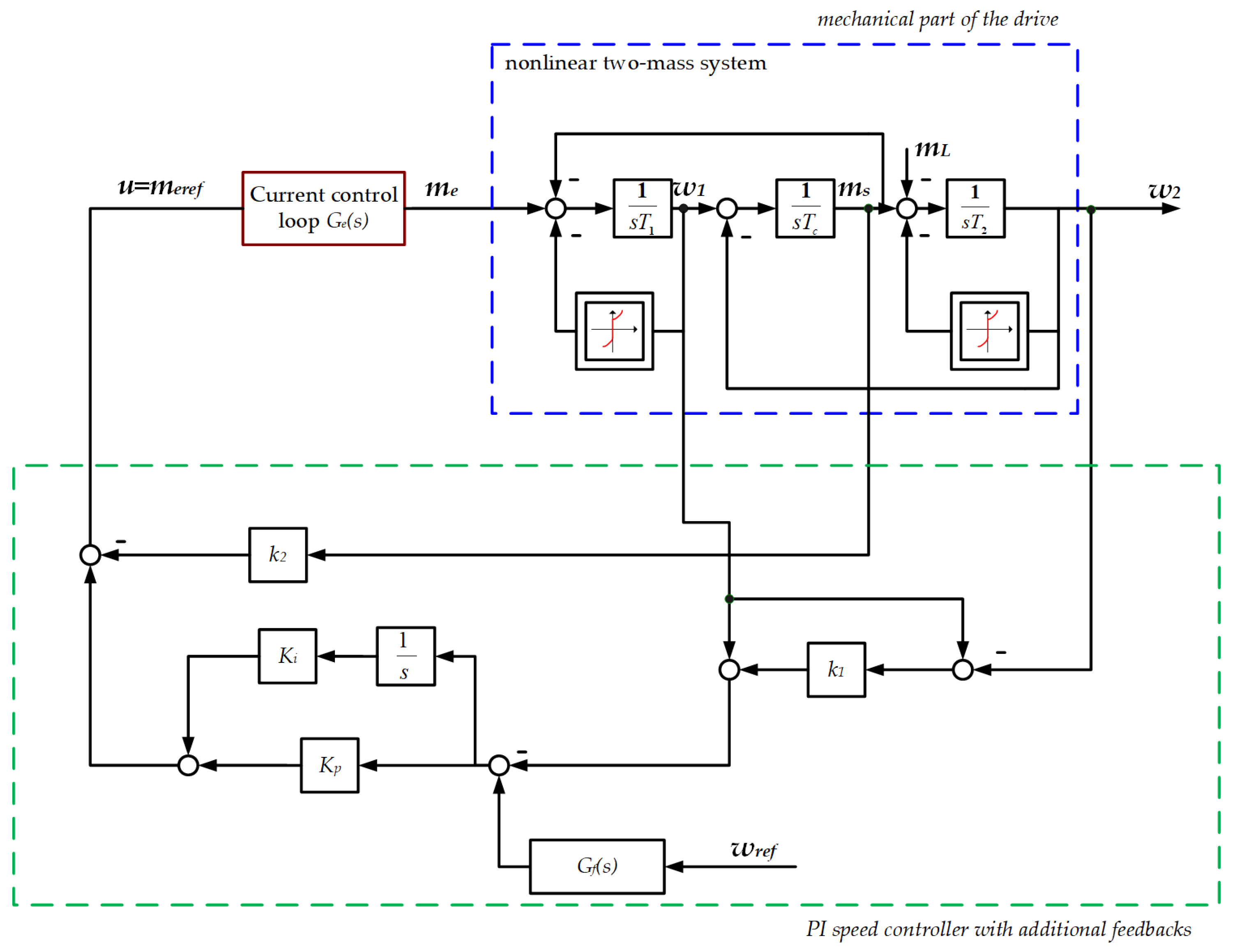
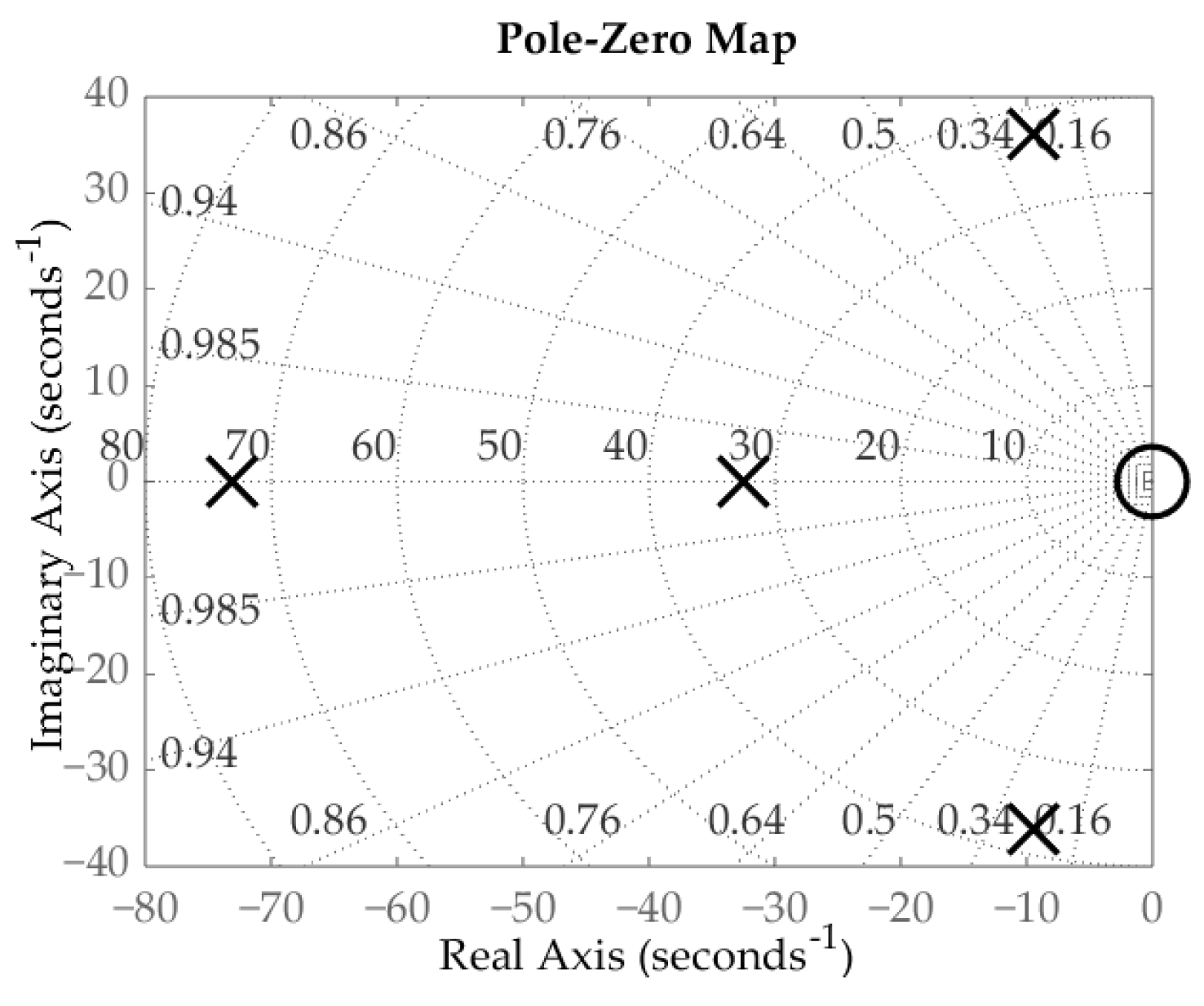
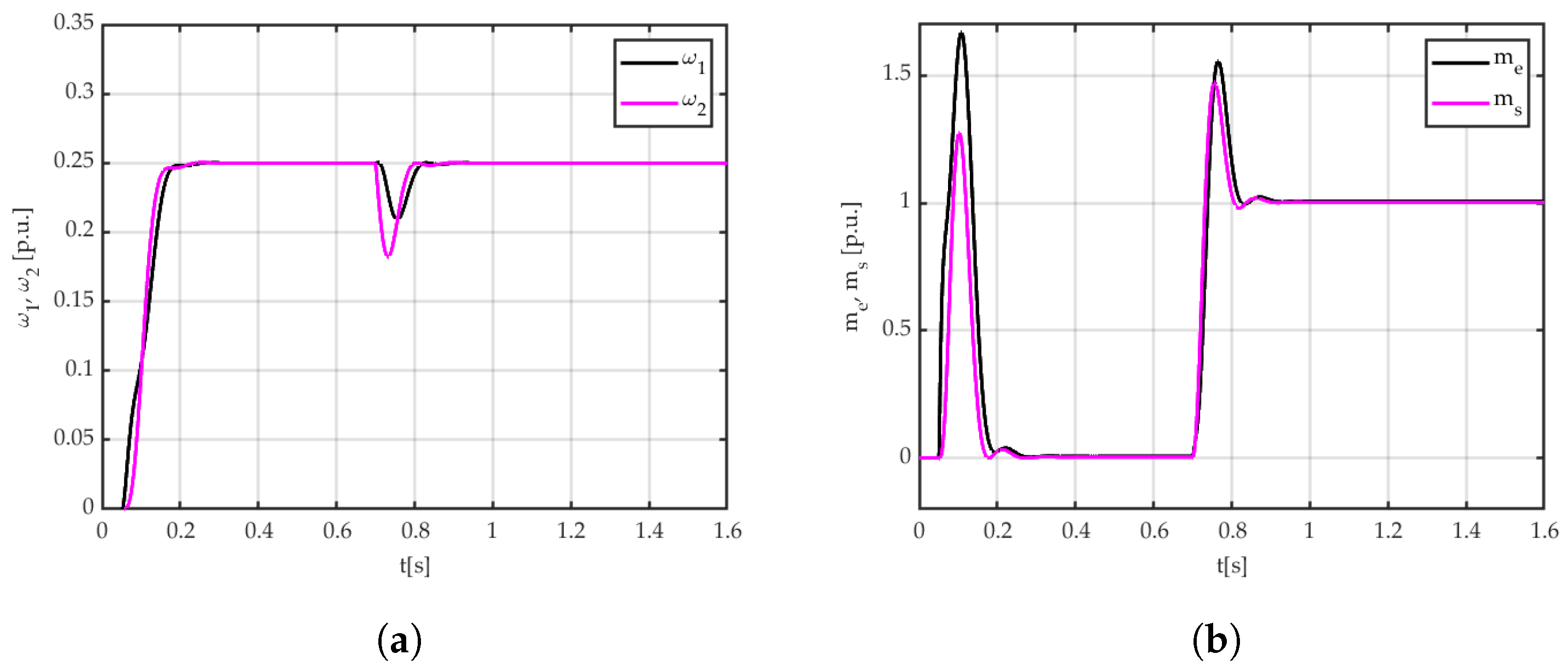
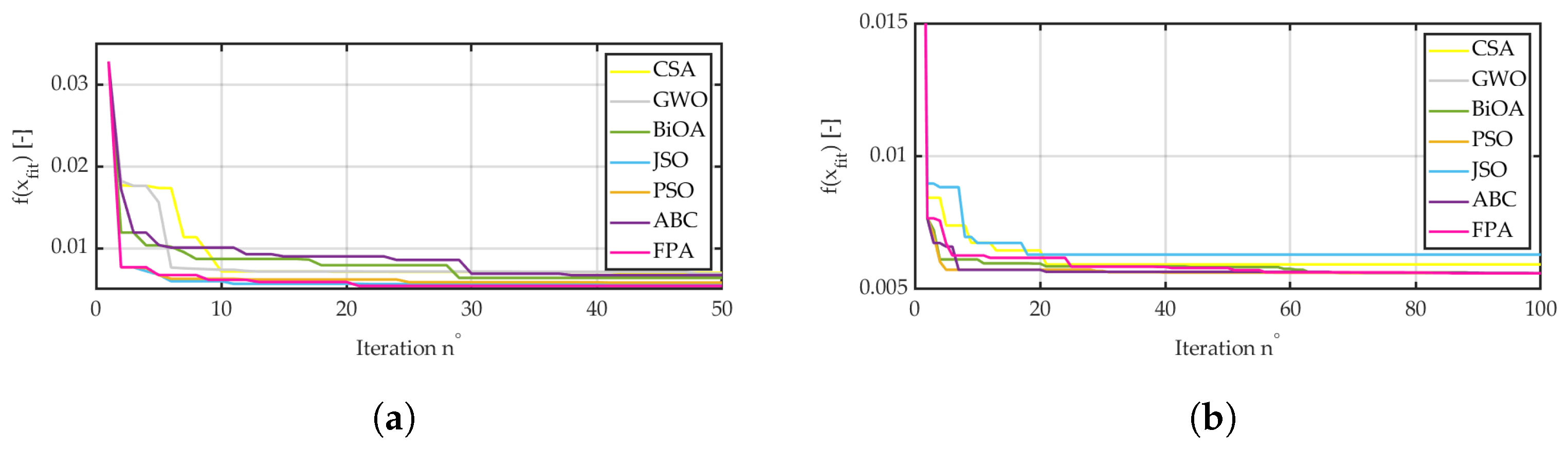
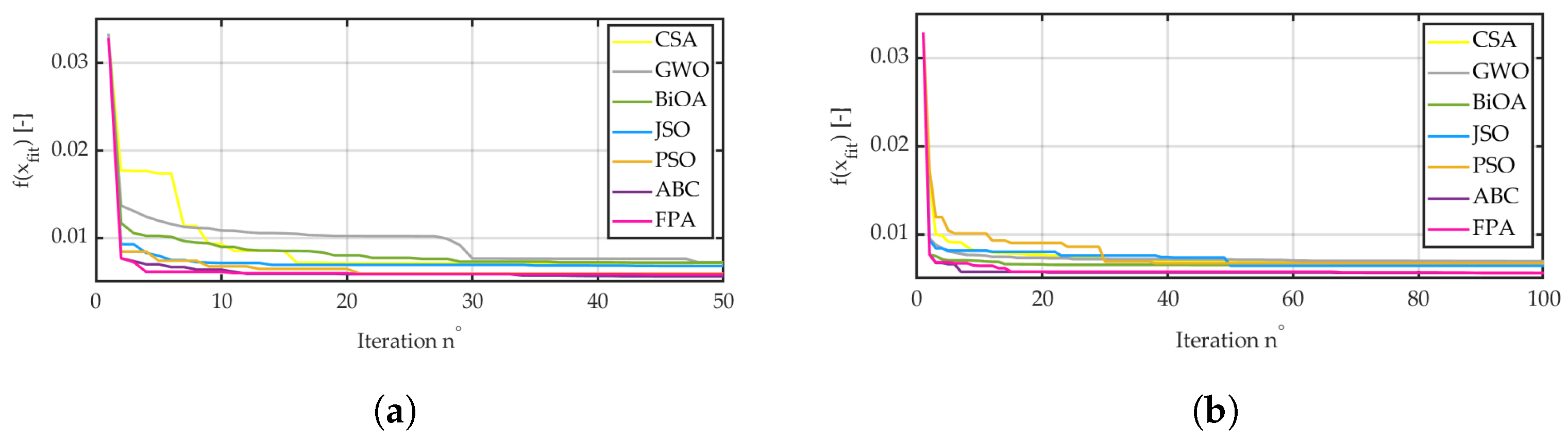
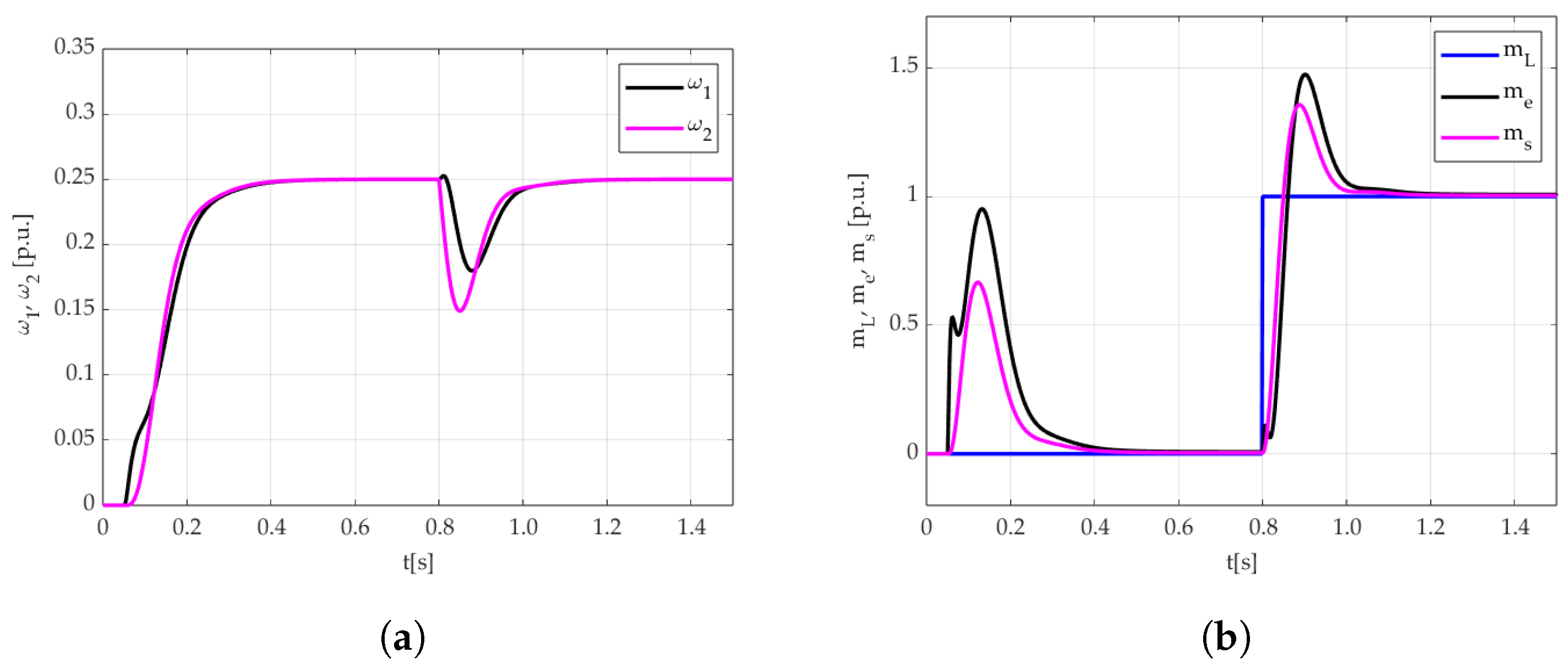
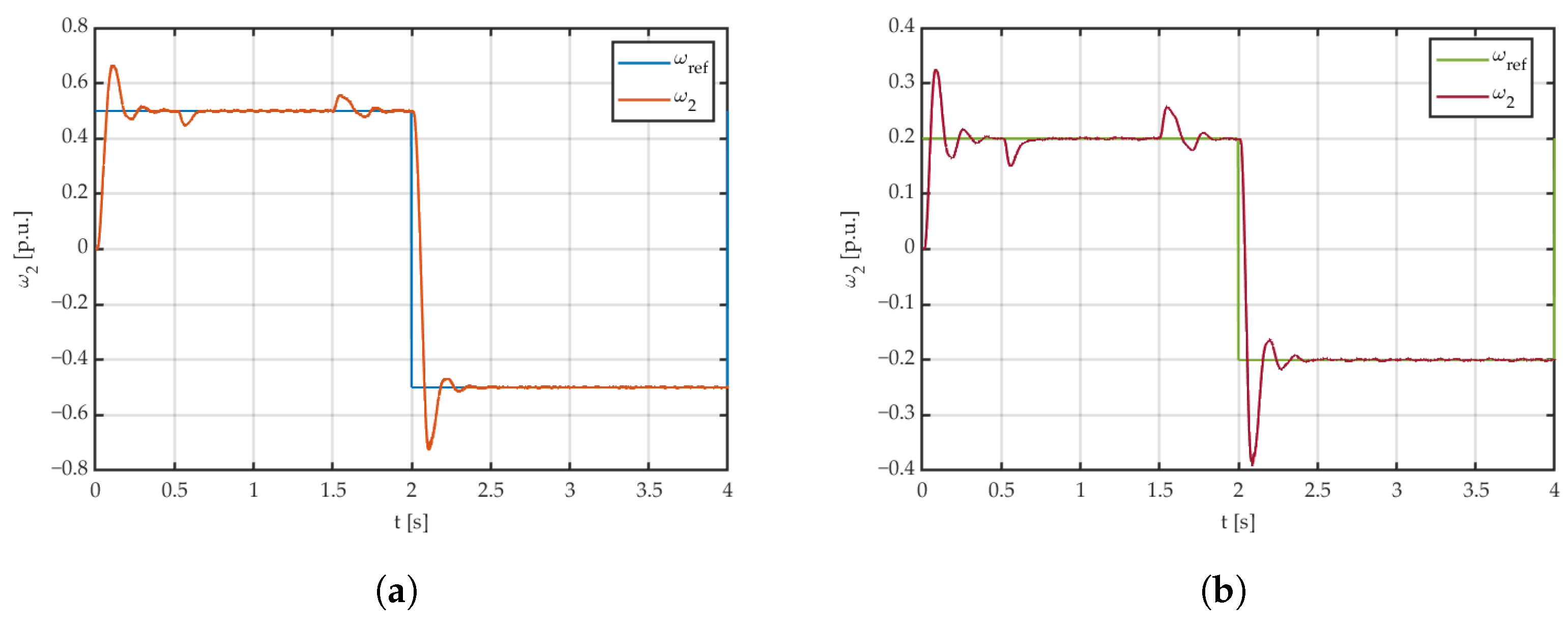
3.2.2. Engineering Application
4. Discussion
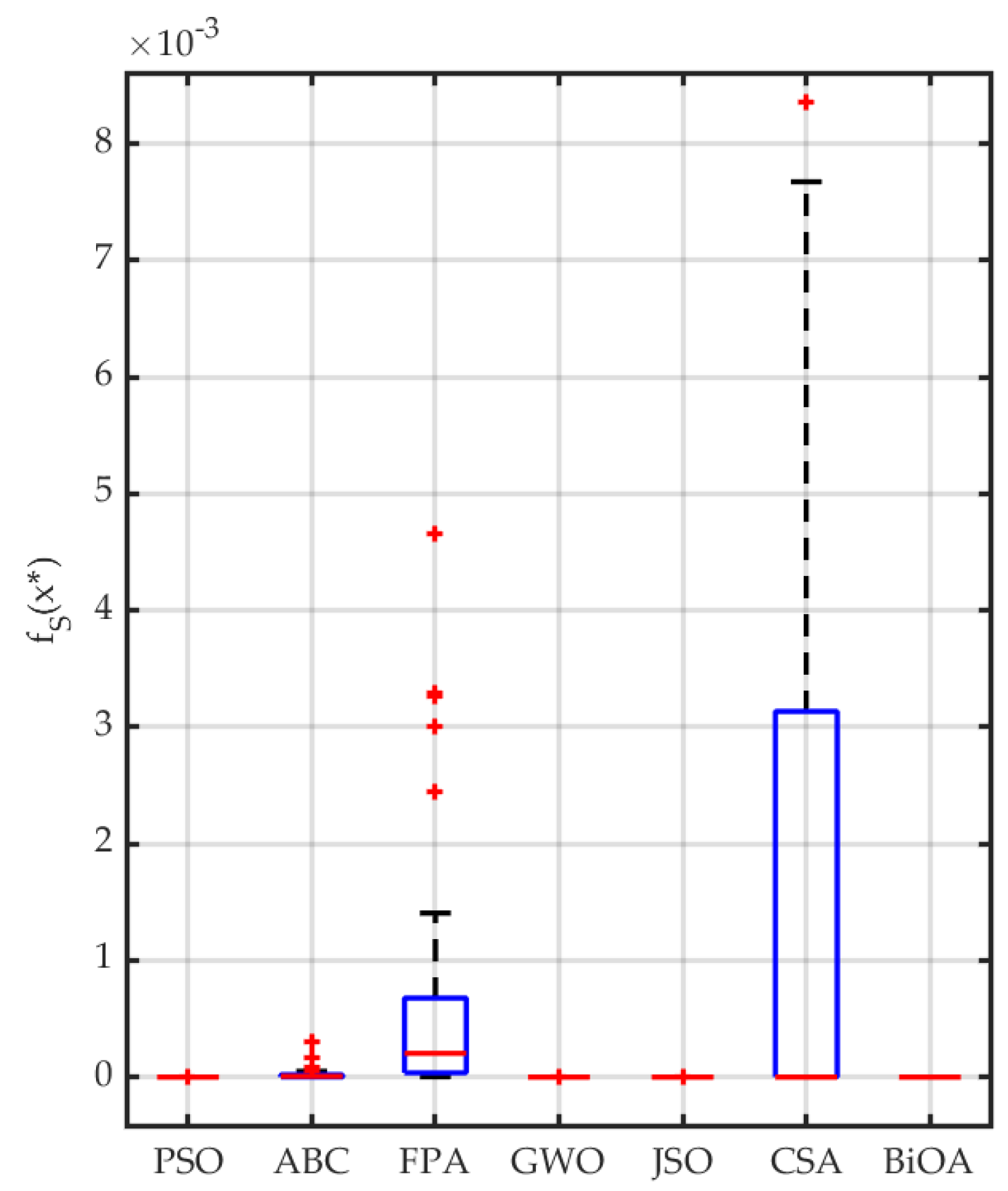
- The developed BiOA resulted in a very high precision in convergence toward the global minimum. This is caused by the parameters decreasing with the next iterations. Thus, it was observed that the BiOA was able to achieve results with even accuracy. None of the compared algorithms was characterized by such perfect results.
- An analysis of the results compiled with optimization time clearly indicates the increase in performance of the modern NIOAs. Surprisingly, the results achieved with a very popular optimizer—the ABC—were unsatisfactory. This might have been caused by the default values of algorithm parameters.
- Based on the above observations, an additional statement may be drawn: modern algorithms (except the CSA) are characterized by a reduced number of tunable parameters. This makes the application of NIOAs a simple and convenient tool.
- The performance of any algorithm should be paired with a satisfactory optimization time. The development of NIOAs (based on the chosen representatives) has significantly decreased the optimization time of benchmark functions. In this field, the JSO performed best; however, the number of adjustable parameters is rather high. This may lead to substantially longer and more difficult implementation. In the case of engineering applications, the optimization time is negligible with respect to the simulation time.
- In order to effectively dampen torsional vibrations with an elastic connection, one of the advanced control structures should be used. In the present study, a system with a PI controller and additional couplings from the torsional torque and speed difference between the working motor and the load machine was chosen. For a system with known and fixed parameters, it is possible to use the pole placement method to select the parameters of the control system and achieve the assumed pole location of the closed system. This provides the desired trajectories of closed-loop system state variables in the linear range of operation.
- If there are significant nonlinearities in the system and/or changes in the system parameters during operation, the use of the pole placement method is not optimal. This technique requires the actual parameters of the system—their change causes a change in the location of the poles of the closed system. This can result in large overshoots in the system or a significant increase in rising time.
5. Conclusions
- An analysis of control structures in terms of their robustness to changes in object parameters. Special attention will be paid to structures that are a combination of input shaping techniques and selected closed-loop control structures. A detailed verification of the effect of cost function order for optimization on system dynamics will be also conducted.
- Further development of the birch tree succession algorithm. We plan to introduce subpopulations and migration patterns between them. This is especially important for parallel processing offered by modern processors. This will ensure further shortening of the optimization process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ABC | Artificial Bee Colony |
| ACO | Ant Colony Optimization Algorithm |
| DO | Dandelion Optimizer |
| FPA | Flower Pollination Algorithm |
| GWO | Grey Wolf Optimizer |
| CSA | Chameleon Swarm Algorithm |
| BiOA | Birch-inspired Optimization Algorithm |
| PSO | Particle Swarm Optimizer |
| WOA | Whale Optimization Algorithm |
| JSO | Jellyfish Search Optimizer |
| FDC | Forced Dynamic Control |
| MPC | Model Predictive Control |
| NIOA | Nature inspired optimization algorithm |
| seed production rate | |
| shaft torque | |
| electromagnetic torque | |
| load torque | |
| motor time constant | |
| load machine time constant | |
| shaft time constant | |
| speed of motor | |
| speed of load |
Appendix A
| PSO | ABC | FPA | GWO | JSO | CSA | BiOA |
|---|---|---|---|---|---|---|
References
- Pham, T.H.; Raahemi, B. Bio-Inspired Feature Selection Algorithms with Their Applications: A Systematic Literature Review. IEEE Access 2023, 11, 43733–43758. [Google Scholar] [CrossRef]
- Roni, M.H.K.; Rana, M.S.; Pota, H.R.; Hasan, M.M.; Hussain, M.S. Recent trends in bio-inspired meta-heuristic optimization techniques in control applications for electrical systems: A review. Int. J. Dyn. Control. 2022, 10, 999–1011. [Google Scholar] [CrossRef]
- Kulejewski, J.; Rosłon, J. Optimization of Ecological and Economic Aspects of the Construction Schedule with the Use of Metaheuristic Algorithms and Artificial Intelligence. Sustainability 2023, 15, 890. [Google Scholar] [CrossRef]
- Liu, M.; Shin, D.; Kang, H.I. Parameter estimation in dynamic biochemical systems based on adaptive Particle Swarm Optimization. In Proceedings of the 2009 7th International Conference on Information, Communications and Signal Processing (ICICS), Macau, China, 8–10 December 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Jakšić, Z.; Devi, S.; Jakšić, O.; Guha, K. A Comprehensive Review of Bio-Inspired Optimization Algorithms Including Applications in Microelectronics and Nanophotonics. Biomimetics 2023, 8, 278. [Google Scholar] [CrossRef] [PubMed]
- Jayashree, R. Preventing the Early Spread of Infectious Diseases Using Particle Swarm Optimization. In Nature-Inspired Optimization Methodologies in Biomedical and Healthcare; Springer International Publishing: Cham, Switzerland, 2023; pp. 33–47. [Google Scholar] [CrossRef]
- Suguna, S.K.; Ranganathan, R.; Sangeetha, J.; Shandilya, S.; Shandilya, S.K. Application of Nature—Inspired Algorithms in Medical Image Processing. In Advances in Nature-Inspired Computing and Applications; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A physics-based optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Biswas, A.; Mishra, K.K.; Tiwari, S.; Misra, A.K. Physics-Inspired Optimization Algorithms: A Survey. J. Optim. 2013, 2013, 438152. [Google Scholar] [CrossRef]
- Henderson, D.; Jacobson, S.H.; Johnson, A.W. The Theory and Practice of Simulated Annealing. In Handbook of Metaheuristics; Springer: New York, NY, USA, 2003; pp. 287–319. [Google Scholar] [CrossRef]
- Salehan, A.; Deldari, A. Corona virus optimization (CVO): A novel optimization algorithm inspired from the Corona virus pandemic. J. Supercomput. 2022, 78, 5712–5743. [Google Scholar] [CrossRef]
- Zhang, Z. A new Hybrid Infection model optimization Algorithm. In Proceedings of the 3rd International Conference on Material, Mechanical and Manufacturing Engineering, Guangzhou, China, 27–28 June 2015; pp. 1045–1050. [Google Scholar] [CrossRef][Green Version]
- Farrag, T.A.; Farag, M.A.; Rizk-Allah, R.M.; Hassanien, A.E.; Elhosseini, M.A. An improved parallel processing-based strawberry optimization algorithm for drone placement. Telecommun. Syst. 2023, 82, 245–275. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, T.; Ma, S.; Chen, M. Dandelion Optimizer: A nature-inspired metaheuristic algorithm for engineering applications. Eng. Appl. Artif. Intell. 2022, 114, 105075. [Google Scholar] [CrossRef]
- Bidar, M.; Kanan, H.R.; Mouhoub, M.; Sadaoui, S. Mushroom Reproduction Optimization (MRO): A Novel Nature-Inspired Evolutionary Algorithm. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–10. [Google Scholar] [CrossRef]
- Nagy, Z.; Werner-Stark, A.; Dulai, T. An Artificial Bee Colony Algorithm for Static and Dynamic Capacitated Arc Routing Problems. Mathematics 2022, 10, 2205. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Anastasiadou, M.N.; Hadjimitsis, D. Measuring the Performance of Ant Colony Optimization Algorithms for the Dynamic Traveling Salesman Problem. Algorithms 2023, 16, 545. [Google Scholar] [CrossRef]
- Chou, J.S.; Molla, A. Recent advances in use of bio-inspired jellyfish search algorithm for solving optimization problems. Sci. Rep. 2022, 12, 19157. [Google Scholar] [CrossRef] [PubMed]
- Precup, R.E.; David, R.C.; Szedlak-Stinean, A.I.; Petriu, E.M.; Dragan, F. An Easily Understandable Grey Wolf Optimizer and Its Application to Fuzzy Controller Tuning. Algorithms 2017, 10, 68. [Google Scholar] [CrossRef]
- Elliott, W.M.; Wyman, R.L.; Elliott, N.B. Significance of Living Records. Bios 1984, 55, 211–218. [Google Scholar]
- Darvishpoor, S.; Darvishpour, A.; Escarcega, M.; Hassanalian, M. Nature-Inspired Algorithms from Oceans to Space: A Comprehensive Review of Heuristic and Meta-Heuristic Optimization Algorithms and Their Potential Applications in Drones. Drones 2023, 7, 427. [Google Scholar] [CrossRef]
- Kumar, A.; Nadeem, M.; Banka, H. Nature inspired optimization algorithms: A comprehensive overview. Evol. Syst. 2023, 14, 141–156. [Google Scholar] [CrossRef]
- Zakeri, H.; Nejad, F.M.; Gandomi, A.H. Nature-Inspired Optimization Algorithms (NIOAs). In Automation and Computational Intelligence for Road Maintenance and Management; Chapter 10; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2022; pp. 437–474. [Google Scholar] [CrossRef]
- Yang, X.S. Nature-Inspired Optimization Algorithms, 2nd ed.; Academic Press: Cambridge, MA, USA, 2021. [Google Scholar] [CrossRef]
- Larik, A.S.; Haider, S. A survey of nature inspired optimization algorithms applied to cooperative strategies in robot soccer. In Proceedings of the 2018 International Conference on Advancements in Computational Sciences (ICACS), Lahore, Pakistan, 19–21 February 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Rai, R.; Das, A.; Dhal, K.G. Nature-inspired optimization algorithms and their significance in multi-thresholding image segmentation: An inclusive review. Evol. Syst. 2022, 13, 889–945. [Google Scholar] [CrossRef] [PubMed]
- Dhal, K.G.; Das, A.; Ray, S.; Galvez, J.; Das, S. Nature-inspired optimization algorithms and their application in multi-thresholding image segmentation. Arch. Comput. Methods Eng. 2020, 27, 855–888. [Google Scholar] [CrossRef]
- Prach, K.; Pyšek, P. Using spontaneous succession for restoration of human-disturbed habitats: Experience from Central Europe. Ecol. Eng. 2001, 17, 55–62. [Google Scholar] [CrossRef]
- Van der Burght, L.; Stoffel, M.; Bigler, C. Analysis and modelling of tree succession on a recent rockslide deposit. Plant Ecol. 2012, 213, 35–46. [Google Scholar] [CrossRef]
- Jonczak, J.; Oktaba, L.; Pawłowicz, E.; Chojnacka, A.; Regulska, E.; Słowińska, S.; Olejniczak, I.; Oktaba, J.; Kruczkowska, B.; Kondras, M.; et al. Soil organic matter transformation influenced by silver birch (Betula pendula Roth) succession on abandoned from agricultural production sandy soil. Eur. J. For. Res. 2023, 142, 367–379. [Google Scholar] [CrossRef]
- Gasiyarov, V.R.; Radionov, A.A.; Loginov, B.M.; Zinchenko, M.A.; Gasiyarova, O.A.; Karandaev, A.S.; Khramshin, V.R. Method for Defining Parameters of Electromechanical System Model as Part of Digital Twin of Rolling Mill. J. Manuf. Mater. Process. 2023, 7, 183. [Google Scholar] [CrossRef]
- Zawirski, K.; Brock, S.; Nowopolski, K. Recursive Neural Network as a Multiple Input and Multiple Output Speed Controller for Electrical Drive of Three-Mass System. Energies 2024, 17, 172. [Google Scholar] [CrossRef]
- Liu, Y.; Song, B.; Zhou, X.; Gao, Y.; Chen, T. An Adaptive Torque Observer Based on Fuzzy Inference for Flexible Joint Application. Machines 2023, 11, 794. [Google Scholar] [CrossRef]
- Serkies, P.; Gorla, A. Implementation of PI and MPC-Based Speed Controllers for a Drive with Elastic Coupling on a PLC Controller. Electronics 2021, 10, 3139. [Google Scholar] [CrossRef]
- Łuczak, D. Mathematical model of multi-mass electric drive system with flexible connection. In Proceedings of the 2014 19th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 2–5 September 2014; pp. 590–595. [Google Scholar] [CrossRef]
- Szczepanski, R.; Kaminski, M.; Tarczewski, T. Auto-Tuning Process of State Feedback Speed Controller Applied for Two-Mass System. Energies 2020, 13, 3067. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, S.; Wang, L.; Liu, Y. Developing a Ball Screw Drive System of High-Speed Machine Tool Considering Dynamics. IEEE Trans. Ind. Electron. 2022, 69, 4966–4976. [Google Scholar] [CrossRef]
- Wang, L.; Han, J.; Ma, F.; Li, X.; Wang, D. Accuracy design optimization of a CNC grinding machine towards low-carbon manufacturing. J. Clean. Prod. 2023, 406, 137100. [Google Scholar] [CrossRef]
- Chen, L.; Du, X.; Hu, B.; Blaabjerg, F. Drivetrain Oscillation Analysis of Grid Forming Type-IV Wind Turbine. IEEE Trans. Energy Convers. 2022, 37, 2321–2337. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Y.; Wang, S.; Meng, W.; Li, G.; Xie, Y. Motion planning and tracking control of a four-wheel independently driven steered mobile robot with multiple maneuvering modes. Front. Mech. Eng. 2021, 16, 504–527. [Google Scholar] [CrossRef]
- Yamada, S.; Fujimoto, H. Precise Joint Torque Control Method for Two-inertia System with Backlash Using Load-side Encoder. IEEJ J. Ind. Appl. 2019, 8, 75–83. [Google Scholar] [CrossRef]
- Li, P.; Wang, L.; Zhong, B.; Zhang, M. Linear Active Disturbance Rejection Control for Two-Mass Systems Via Singular Perturbation Approach. IEEE Trans. Ind. Inform. 2022, 18, 3022–3032. [Google Scholar] [CrossRef]
- Sakaino, S.; Kitamura, T.; Mizukami, N.; Tsuji, T. High-Precision Control for Functional Electrical Stimulation Utilizing a High-Resolution Encoder. IEEJ J. Ind. Appl. 2021, 10, 124–133. [Google Scholar] [CrossRef]
- Yang, T.; Xu, F.; Zhao, S.; Li, T.; Yang, Z.; Wang, Y.; Liu, Y. A High-Certainty Visual Servo Control Method for a Space Manipulator with Flexible Joints. Sensors 2023, 23, 6679. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, M.; Muguro, J.; Njeri, W.; Doss, A.S.A. Adaptive Notch Filter in a Two-Link Flexible Manipulator for the Compensation of Vibration and Gravity-Induced Distortion. Vibration 2023, 6, 286–302. [Google Scholar] [CrossRef]
- Szabat, K.; Orlowska-Kowalska, T. Vibration Suppression in a Two-Mass Drive System Using PI Speed Controller and Additional Feedbacks—Comparative Study. IEEE Trans. Ind. Electron. 2007, 54, 1193–1206. [Google Scholar] [CrossRef]
- Katsura, S.; Ohnishi, K. Force Servoing by Flexible Manipulator Based on Resonance Ratio Control. IEEE Trans. Ind. Electron. 2007, 54, 539–547. [Google Scholar] [CrossRef]
- Kobayashi, H.; Katsura, S.; Ohnishi, K. An Analysis of Parameter Variations of Disturbance Observer for Motion Control. IEEE Trans. Ind. Electron. 2007, 54, 3413–3421. [Google Scholar] [CrossRef]
- Stanislawski, R.; Tapamo, J.R.; Kaminski, M. Virtual Signal Calculation Using Radial Neural Model Applied in a State Controller of a Two-Mass System. Energies 2023, 16, 5629. [Google Scholar] [CrossRef]
- Serkies, P.; Szabat, K. Effective damping of the torsional vibrations of the drive system with an elastic joint based on the forced dynamic control algorithms. J. Vib. Control 2019, 25, 2225–2236. [Google Scholar] [CrossRef]
- Wróbel, K.; Śleszycki, K.; Kahsay, A.H.; Szabat, K.; Katsura, S. Robust Speed Control of Uncertain Two-Mass System. Energies 2023, 16, 6231. [Google Scholar] [CrossRef]
- Wang, C.; Liu, F.; Xu, J.; Pan, J. An SMC-Based Accurate and Robust Load Speed Control Method for Elastic Servo System. IEEE Trans. Ind. Electron. 2024, 71, 2300–2308. [Google Scholar] [CrossRef]
- Chang, H.; Lu, S.; Huang, G.; Zheng, S.; Song, B. An Extended Active Resonance Suppression Scheme Based on a Dual-Layer Network for High-Performance Double-Inertia Drive System. IEEE Trans. Power Electron. 2023, 38, 13717–13729. [Google Scholar] [CrossRef]
- Jastrzębski, M.; Kabziński, J.; Mosiołek, P. Adaptive Position Control for Two-Mass Drives with Nonlinear Flexible Joints. Energies 2024, 17, 425. [Google Scholar] [CrossRef]
- Kabziński, J.; Mosiołek, P. Integrated, Multi-Approach, Adaptive Control of Two-Mass Drive with Nonlinear Damping and Stiffness. Energies 2021, 14, 5475. [Google Scholar] [CrossRef]
- Szabat, K.; Orlowska-Kowalska, T. Performance Improvement of Industrial Drives with Mechanical Elasticity Using Nonlinear Adaptive Kalman Filter. IEEE Trans. Ind. Electron. 2008, 55, 1075–1084. [Google Scholar] [CrossRef]
- Kamiński, M.; Szabat, K. Adaptive Control Structure with Neural Data Processing Applied for Electrical Drive with Elastic Shaft. Energies 2021, 14, 3389. [Google Scholar] [CrossRef]
- Wang, C.; Yang, M.; Zheng, W.; Long, J.; Xu, D. Vibration Suppression with Shaft Torque Limitation Using Explicit MPC-PI Switching Control in Elastic Drive Systems. IEEE Trans. Ind. Electron. 2015, 62, 6855–6867. [Google Scholar] [CrossRef]
- Yang, M.; Wang, C.; Xu, D.; Zheng, W.; Lang, X. Shaft Torque Limiting Control Using Shaft Torque Compensator for Two-Inertia Elastic System with Backlash. IEEE/ASME Trans. Mechatronics 2016, 21, 2902–2911. [Google Scholar] [CrossRef]
- Szabat, K.; Wróbel, K.; Dróżdż, K.; Janiszewski, D.; Pajchrowski, T.; Wójcik, A. A Fuzzy Unscented Kalman Filter in the Adaptive Control System of a Drive System with a Flexible Joint. Energies 2020, 13, 2056. [Google Scholar] [CrossRef]
- Serkies, P. Estimation of state variables of the drive system with elastic joint using moving horizon estimation (MHE). Bull. Pol. Acad. Sci. Tech. Sci. 2019, 67, 883–892. [Google Scholar] [CrossRef]
- Szabat, K.; Wróbel, K.; Katsura, S. Application of Multilayer Kalman Filter to a Flexible Drive System. IEEJ J. Ind. Appl. 2022, 11, 483–493. [Google Scholar] [CrossRef]
- Tzanetos, A.; Dounias, G. Nature inspired optimization algorithms or simply variations of metaheuristics? Artif. Intell. Rev. 2021, 54, 1841–1862. [Google Scholar] [CrossRef]
- Lidman, F.D.; Karlsson, M.; Lundmark, T.; Sängstuvall, L.; Holmström, E. Birch establishes anywhere! So, what is there to know about natural regeneration and direct seeding of birch? New For. 2024, 55, 157–171. [Google Scholar] [CrossRef]
- Parro, K.; Metslaid, M.; Renel, G.; Sims, A.; Stanturf, J.A.; Jõgiste, K.; Köster, K. Impact of postfire management on forest regeneration in a managed hemiboreal forest, Estonia. Can. J. For. Res. 2015, 45, 1192–1197. [Google Scholar] [CrossRef]
- Tiebel, K.; Huth, F.; Wagner, S. Is there an effect of storage depth on the persistence of silver birch (Betula pendula Roth) and rowan (Sorbus aucuparia L.) seeds? A seed burial experiment. iFor. Biogeosci. For. 2021, 14, 224–230. [Google Scholar] [CrossRef]
- Weis, I.M.; Hermanutz, L.A. Pollination dynamics of arctic dwarf birch (Betula glandulosa; Betulaceae) and its role in the loss of seed production. Am. J. Bot. 1993, 80, 1021–1027. [Google Scholar] [CrossRef]
- Tiebel, K.; Huth, F.; Frischbier, N.; Wagner, S. Restrictions on natural regeneration of storm-felled spruce sites by silver birch (Betula pendula Roth) through limitations in fructification and seed dispersal. Eur. J. For. Res. 2020, 139, 731–745. [Google Scholar] [CrossRef]
- Sagnard, F.; Pichot, C.; Dreyfus, P.; Jordano, P.; Fady, B. Modelling seed dispersal to predict seedling recruitment: Recolonization dynamics in a plantation forest. Ecol. Model. 2007, 203, 464–474. [Google Scholar] [CrossRef]
- Yang, X.S. Chapter 3—Random Walks and Optimization. In Nature-Inspired Optimization Algorithms; Yang, X.S., Ed.; Elsevier: Oxford, UK, 2014; pp. 45–65. [Google Scholar] [CrossRef]
- Yang, X.S. Flower Pollination Algorithm for Global Optimization. In Proceedings of the Unconventional Computation and Natural Computation, Orléans, France, 3–7 September 2012; Durand-Lose, J., Jonoska, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 240–249. [Google Scholar]
- Zychlewicz, M.; Stanislawski, R.; Kaminski, M. Grey Wolf Optimizer in Design Process of the Recurrent Wavelet Neural Controller Applied for Two-Mass System. Electronics 2022, 11, 177. [Google Scholar] [CrossRef]
- Jamil, M.; Yang, X.S. A literature survey of benchmark functions for global optimisation problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar] [CrossRef] [PubMed]
- Sharma, P.; Raju, S. Metaheuristic optimization algorithms: A comprehensive overview and classification of benchmark test functions. Soft Comput. 2024, 28, 3123–3186. [Google Scholar] [CrossRef]
- Yao, Z.; Wang, Z.; Wang, D.; Wu, J.; Chen, L. An ensemble CNN-LSTM and GRU adaptive weighting model based improved sparrow search algorithm for predicting runoff using historical meteorological and runoff data as input. J. Hydrol. 2023, 625, 129977. [Google Scholar] [CrossRef]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Naseem, R. Common benchmark functions for metaheuristic evaluation: A review. JOIV Int. J. Inform. Vis. 2017, 1, 218–223. [Google Scholar] [CrossRef]
- Vanaret, C.; Gotteland, J.B.; Durand, N.; Alliot, J.M. Certified Global Minima for a Benchmark of Difficult Optimization Problems. arXiv 2014, arXiv:2003.09867. [Google Scholar]
- Schaffer, J.D.; Caruana, R.A.; Eshelman, L.J.; Das, R. A study of control parameters affecting online performance of genetic algorithms for function optimization. In Proceedings of the Third International Conference on Genetic Algorithms, San Francisco, CA, USA, 1 June 1989; pp. 51–60. [Google Scholar]
- Ezugwu, A.E.; Adeleke, O.J.; Akinyelu, A.A.; Viriri, S. A conceptual comparison of several metaheuristic algorithms on continuous optimisation problems. Neural Comput. Appl. 2020, 32, 6207–6251. [Google Scholar] [CrossRef]
- Wang, Z.; Qin, C.; Wan, B.; Song, W.W. A Comparative Study of Common Nature-Inspired Algorithms for Continuous Function Optimization. Entropy 2021, 23, 874. [Google Scholar] [CrossRef] [PubMed]
- Dudakli, N.; Baykasoglu, A. A simulation—Optimization-based planning and control system for operations of fully automated parking systems. Comput. Ind. Eng. 2024, 189, 109977. [Google Scholar] [CrossRef]
- Lim, J.; Kim, H.; Han, D. Interactive Car Parking Simulation Based on On-line Trajectory Optimization. In Proceedings of the Design, User Experience, and Usability: Users, Contexts and Case Studies, Las Vegas, NV, USA, 15–20 July 2018; Marcus, A., Wang, W., Eds.; Springer: Cham, Switzerland, 2018; pp. 270–284. [Google Scholar]
- Liu, X.; Zhu, S.; Fang, Y.; Wang, Y.; Fu, L.; Lei, W.; Zhou, Z. Optimization Design of Parking Models Based on Complex and Random Parking Environments. World Electr. Veh. J. 2023, 14, 344. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Yang, J.; Meng, X.; Fu, T. Automatic parking trajectory planning based on random sampling and nonlinear optimization. J. Frankl. Inst. 2023, 360, 9579–9601. [Google Scholar] [CrossRef]
- Martin, J.G.S.; Cruz-Reyes, L.; Dorronsoro, B.; Quiroz-Castellanos, M.; Fraire, H.; Gomez-Santillan, C.; Rangel-Valdez, N. Optimization Models and Methods for Bin Packing Problems: A Case Study on Solving 1D-BPP. In New Perspectives on Hybrid Intelligent System Design Based on Fuzzy Logic, Neural Networks and Metaheuristics; Springer International Publishing: Cham, Switzerland, 2022; pp. 265–280. [Google Scholar] [CrossRef]
- Liu, D.; Tan, K.; Huang, S.; Goh, C.; Ho, W. On solving multiobjective bin packing problems using evolutionary particle swarm optimization. Eur. J. Oper. Res. 2008, 190, 357–382. [Google Scholar] [CrossRef]
- Vedenyov, M. 2d Bin Packing Problem with Genetic Algorithm. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/31789-2d-bin-packing-problem-with-genetic-algorithm (accessed on 6 August 2024).
- Żychlewicz, M. Application of the Grey Wolf Optimizer in the optimization of state space controller for three-mass drive. Interdiscip. J. Eng. Sci. 2018, 6, 12–20. [Google Scholar]
- Orlowska-Kowalska, T.; Kaminski, M. Effectiveness of Saliency-Based Methods in Optimization of Neural State Estimators of the Drive System With Elastic Couplings. IEEE Trans. Ind. Electron. 2009, 56, 4043–4051. [Google Scholar] [CrossRef]
- Grzesiak, L.; Meganck, V.; Sobolewski, J.; Ufnalski, B. Genetic Algorithm for Parameters Optimization of ANN-based Speed Controller. In Proceedings of the EUROCON 2007—The International Conference on “Computer as a Tool”, Warsaw, Poland, 9–12 September 2007; pp. 1700–1705. [Google Scholar] [CrossRef]







| Parameter | Symbol | Suggested Value |
|---|---|---|
| Seed production rate | ||
| Random Levy walk parameter | v | |
| Random Levy walk parameter | u | |
| Seed weight coefficient | w |
| d | ||
|---|---|---|
| 2 | [2.2029, 1.5708] | |
| 5 | [2.2029, 1.5708, 1.2850, 1.9231, 1.7205] | |
| 10 | [2.2029, 1.5708, 1.2860, 1.9231, 1.7205, 1.5708, 1.4544, 1.7561, 1.6557, 1.5708] |
| Number of Iterations | Calculated Solution | Value | Distance |
|---|---|---|---|
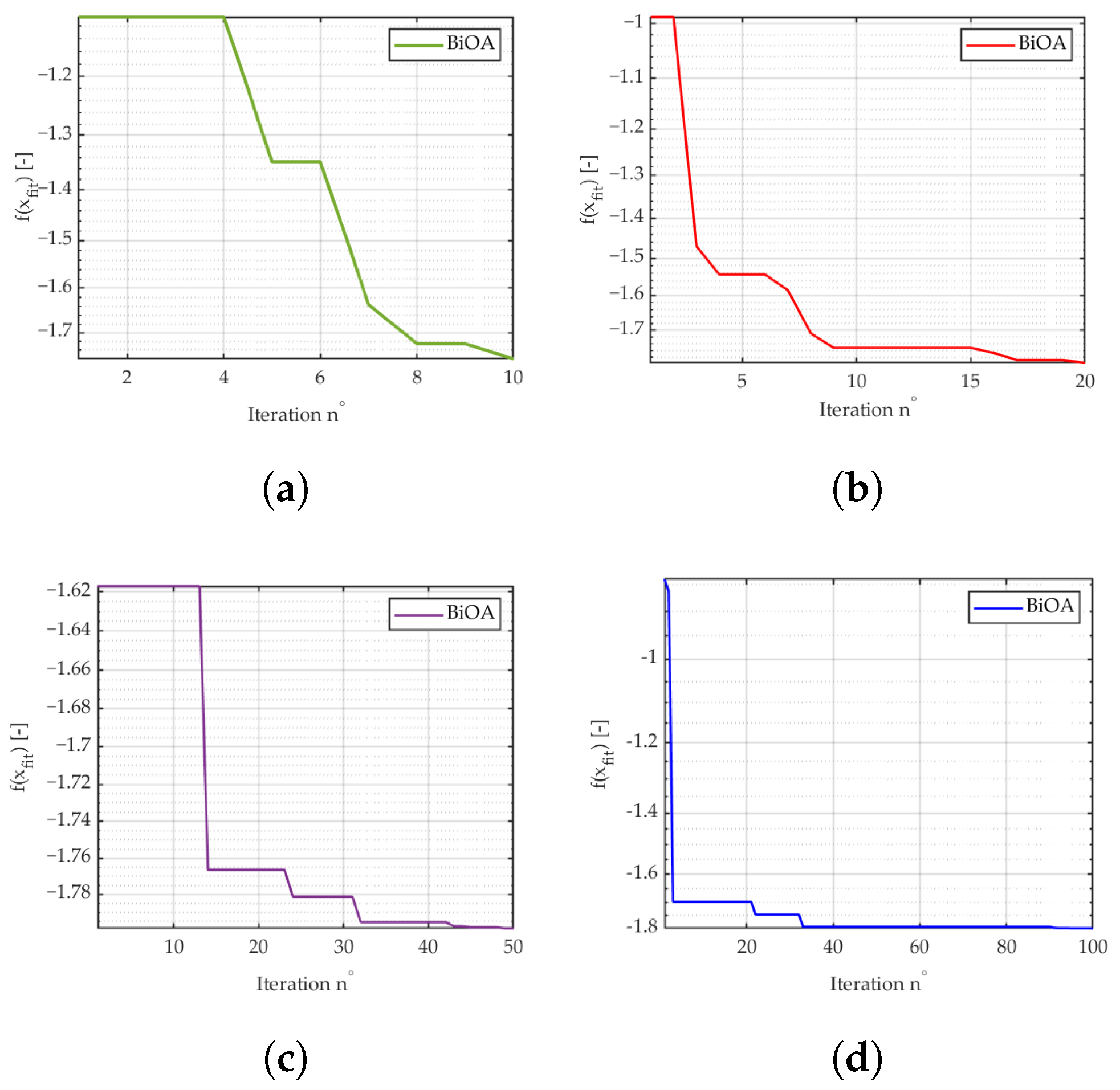
| 10 | [2.2097, 1.5748] | −1.7999 | 0.0079 |
| 20 | [2.2073, 1.5796] | −1.7979 | 0.0098 |
| 50 | [2.2027, 1.5646] | −1.7998 | 0.0062 |
| 100 | [ 2.2027, 1.5713] | −1.8013 | 0.0005 |
| Number of Iterations | Calculated Solution | Value | Distance |
|---|---|---|---|
| 10 | [0.6299, 1.6044, 2.4732, 1.9311, 0.9925] | −2.7155 | 2.1018 |
| 20 | [1.1508, 1.6068, 1.3077, 1.9387, 1.0253] | −3.5313 | 1.2619 |
| 50 | [2.2185, 1.5806, 2.2477, 1.1029, 1.7242] | −4.3539 | 1.2649 |
| 100 | [2.2225, 1.5765, 1.2921, 1.1138, 1.7230] | −4.6334 | 0.8096 |
| 200 | [2.2007, 1.5714, 1.2882, 1.9208, 1.7226] | −4.6843 | 0.0061 |
| Number of Iterations | Calculated Solution | Value | Distance |
|---|---|---|---|
| 50 | [2.2114, 1.5640, 1.2448, 1.1090, 1.0105, 0.9349, 0.8427, 1.7570, 0.9005, 0.0998] | −6.8467 | 2.1637 |
| 100 | [1.7292, 1.5560, 1.3198, 1.0730, 1.0091, 0.6368, 2.6396, 1.3574, 1.2724, 1.8586] | −6.3454 | 2.0299 |
| 200 | [2.3189, 1.5208, 1.2524, 1.9249, 2.2193, 2.0257, 0.8506, 2.0859, 2.2221, 2.1073] | −8.2403 | 1.2470 |
| d | ||
|---|---|---|
| 2 | 0 | [0, 0] |
| Number of Iterations | Calculated Solution | Value | Distance |
|---|---|---|---|
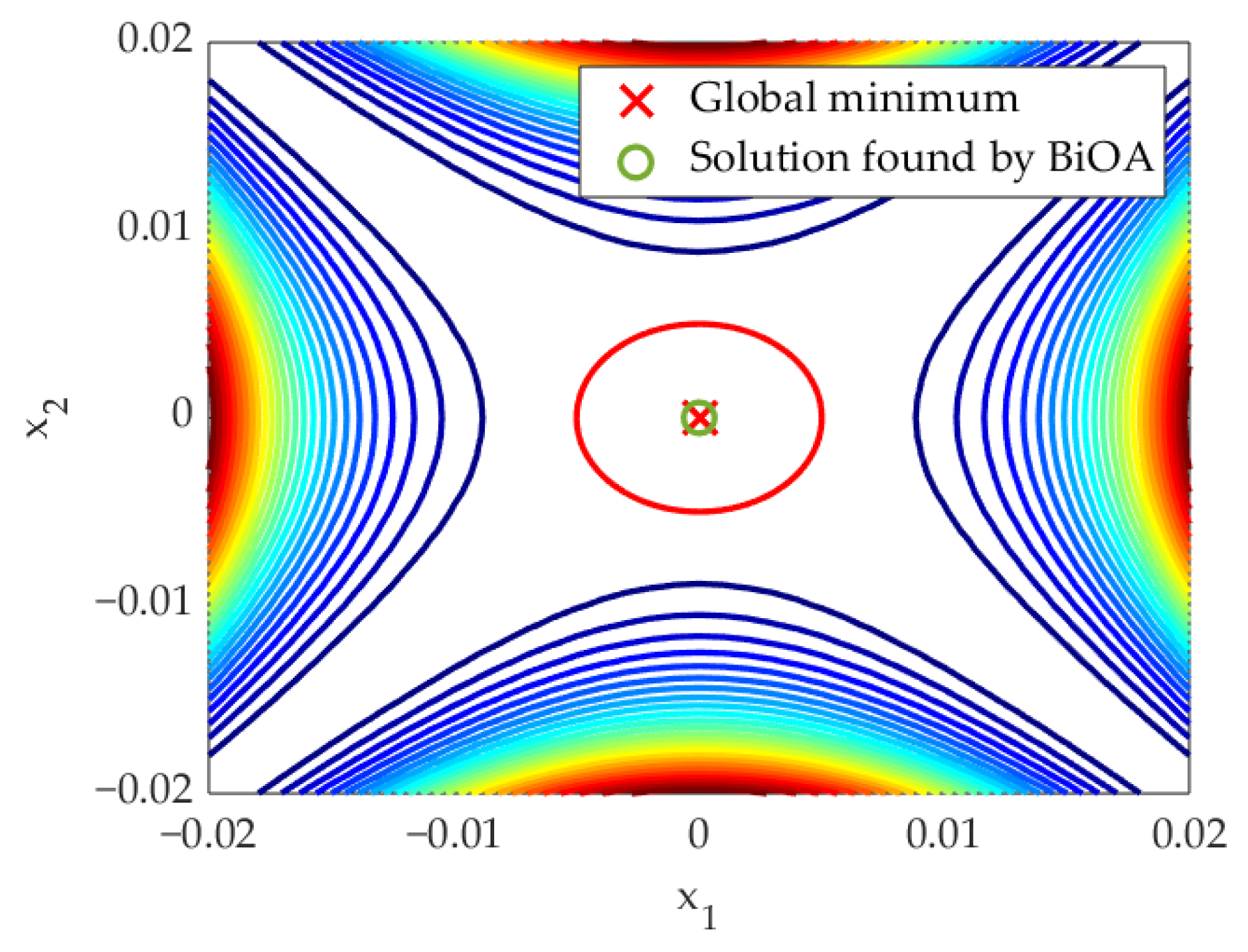
| 10 | [, ] | ||
| 20 | [, ] | 0 * | |
| 50 | [, ] | 0 * | |
| 100 | [, ] | 0 * |
| d | ||
|---|---|---|
| 2 | 0 | [0, 0] |
| Algorithm | Avg. Solution | Variance | Min. | Success Rate [%] |
|---|---|---|---|---|
| PSO | [, ] | [, ] | 70 | |
| ABC | [, ] | [, ] | 44 | |
| FPA | [ , ] | [, ] | 0 | |
| GWO | [, ] | [, ] | 100 | |
| JSO | [ , ] | [, ] | 100 | |
| CSA | [, ] | [, ] | 100 | |
| BiOA | [, ] | [, ] | 100 |
| Algorithm | Avg. Solution | Variance | Min. | Success Rate [%] |
|---|---|---|---|---|
| PSO | [, ] | [, ] | 98 | |
| ABC | [, ] | [, ] | 100 | |
| FPA | [ , ] | [, ] | 24 | |
| GWO | [, ] | [, ] | 76 | |
| JSO | [ , ] | [, ] | 100 | |
| CSA | [, ] | [, ] | 96 | |
| BiOA | [, ] | [, ] | 88 |
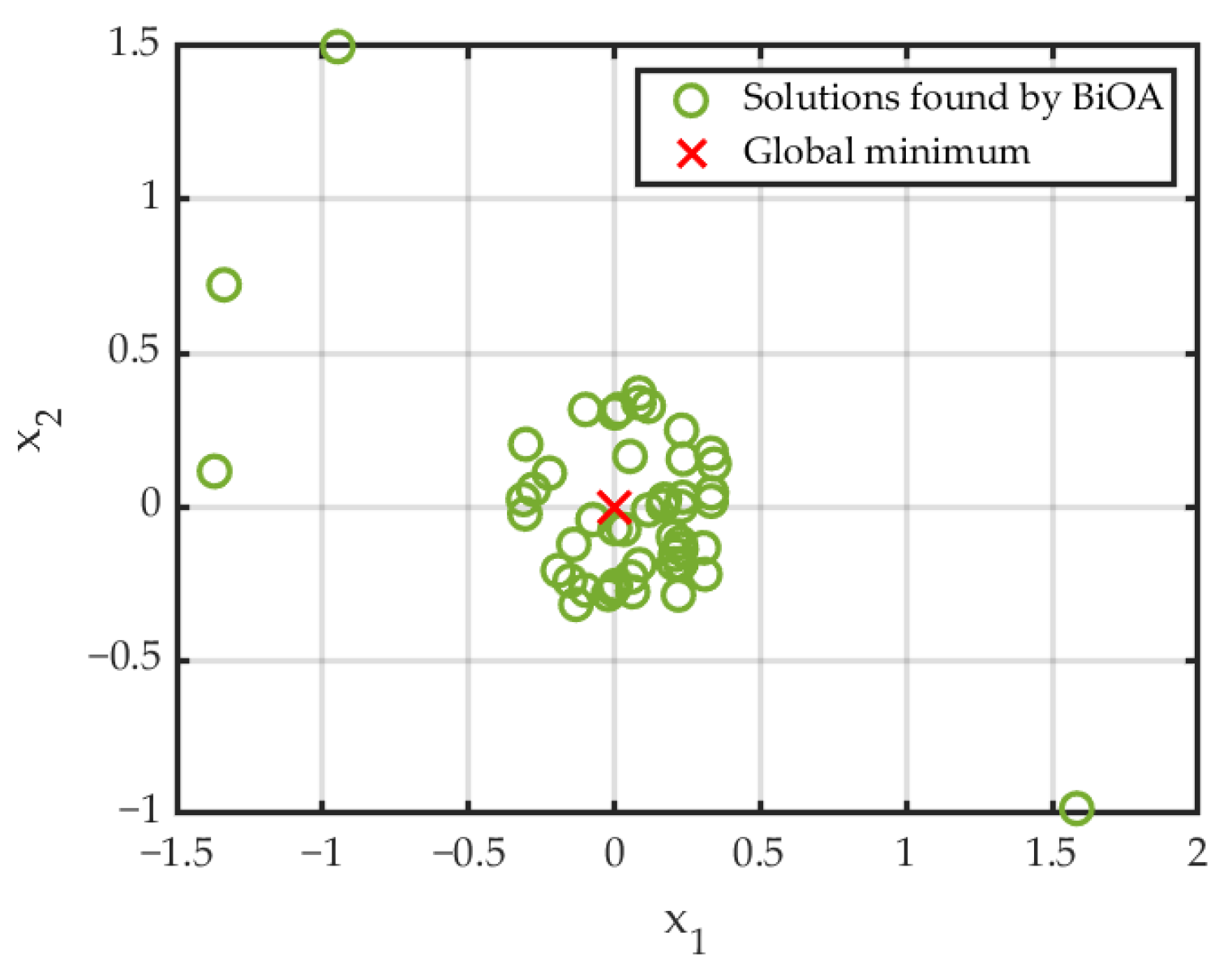
| Algorithm | Avg. Solution | Variance | Min. | Success Rate [%] |
|---|---|---|---|---|
| PSO | [ ] | [, ] | 100 | |
| ABC | [, ] | [, ] | 52 | |
| FPA | [ ] | [, ] | 6 | |
| GWO | [, ] | [, ] | 0 * | 98 |
| JSO | [ , ] | [, ] | 100 | |
| CSA | [, ] | [] | 0 * | 6 |
| BiOA | [, ] | [, ] | 0 * | 100 |
| Algorithm | Optimizer Complexity | Avg. Time | Avg. Time | Avg. Time |
|---|---|---|---|---|
| PSO | 5 | 1.867258 s | 1.743719 s | 1.736397 s |
| ABC | 4 | 2.507725 s | 2.625038 s | 2.240312 s |
| FPA | 1 | 0.601462 s | 0.584810 s | 0.642565 s |
| GWO | 4 | 0.304454 s | 0.241613 s | 0.348372 s |
| JSO | 5 | 0.012057 s | 0.007028 s | 0.004966 s |
| CSA | 7 | 0.134424 s | 0.047772 s | 0.391133 s |
| BiOA | 3 | 0.263412 s | 0.221876 s | 0.186857 s |
| Parameter | Symbol | Value |
|---|---|---|
| Motor mechanical time constant | 0.203 s | |
| Load machine mechanical time constant | 0.285 s | |
| Time constant of the shaft | 0.0026 s | |
| Shaft diameter | 5 mm | |
| Shaft length | l | 600 mm |
| Power of motor | 500 W | |
| Power of load machine | 500 W |
| Optimizer | No. of Iterations | Min. | Comp. Time |
|---|---|---|---|
| PSO | 50 | 0.005935 | 538.45 |
| 100 | 0.005612 | 1117.32 | |
| ABC | 50 | 0.005598 | 611.97 |
| 100 | 0.005600 | 1241.76 | |
| FPA | 50 | 0.005605 | 439.47 |
| 100 | 0.005593 | 864.32 | |
| GWO | 50 | 0.006914 | 714.76 |
| 100 | 0.005592 | 1438.46 | |
| JSO | 50 | 0.006037 | 217.34 |
| 100 | 0.005715 | 471.33 | |
| CSA | 50 | 0.006981 | 686.58 |
| 100 | 0.005926 | 1408.35 | |
| BiOA | 50 | 0.006374 | 386.60 |
| 100 | 0.005596 | 816.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malarczyk, M.; Katsura, S.; Kaminski, M.; Szabat, K. A Novel Meta-Heuristic Algorithm Based on Birch Succession in the Optimization of an Electric Drive with a Flexible Shaft. Energies 2024, 17, 4104. https://doi.org/10.3390/en17164104
Malarczyk M, Katsura S, Kaminski M, Szabat K. A Novel Meta-Heuristic Algorithm Based on Birch Succession in the Optimization of an Electric Drive with a Flexible Shaft. Energies. 2024; 17(16):4104. https://doi.org/10.3390/en17164104
Chicago/Turabian StyleMalarczyk, Mateusz, Seiichiro Katsura, Marcin Kaminski, and Krzysztof Szabat. 2024. "A Novel Meta-Heuristic Algorithm Based on Birch Succession in the Optimization of an Electric Drive with a Flexible Shaft" Energies 17, no. 16: 4104. https://doi.org/10.3390/en17164104
APA StyleMalarczyk, M., Katsura, S., Kaminski, M., & Szabat, K. (2024). A Novel Meta-Heuristic Algorithm Based on Birch Succession in the Optimization of an Electric Drive with a Flexible Shaft. Energies, 17(16), 4104. https://doi.org/10.3390/en17164104








