1. Introduction
To achieve carbon peaking goals, the development of renewable energy, such as wind and photovoltaic energy, is imperative [
1]. Due to the inherent volatility and intermittency of new energy, stable power generation from thermal power is crucial [
2,
3]. New energy requires thermal power units to frequently change operating conditions for deep peaking and grid frequency regulation. This deviates from the designed operating conditions of the turbine, accelerating the performance degradation of the equipment [
4]. The turbine intermediate-stage flux section, as a key component of energy conversion, directly affects the unit cycle efficiency and economy [
5]. Failure of the rotor such as through blade wear may lead to rotor imbalance and unit shutdown [
6,
7]. Therefore, accurate performance monitoring of the turbine intermediate section and sensitive early warning of faults are of great significance to ensure safe and stable operation [
8]. Traditional corrective and preventive maintenance can no longer meet the demand, so predictive maintenance systems based on early warning of failures must be developed [
9,
10].
The research on turbine anomaly detection can be generally divided into physics-based and data-driven methods [
11]. Physics-based methods need mathematical models to describe the fault process [
12]. However, building accurate physical models for the degradation process is extremely difficult. Data-driven methods are becoming increasingly popular by virtue of their simplicity and accuracy. Due to the difficulty in obtaining fault data, anomaly detection is more practical than fault diagnosis. In previous studies, the core idea of turbine flux performance assessment was mainly achieved by observing the change in Relative Internal Efficiency (RIE) [
13,
14]. Wu et al. [
15] proposed a steam turbine fault diagnosis method based on the hierarchy k-nearest neighbor model and principal component analysis. Cao et al. [
16] proposed a synthetic neural network to calculate the RIE of the stage normal values. Wang et al. [
17] used an immune system wavelet network to calculate the RIE of a low pressure cylinder. However, the RIE fluctuates dramatically during changing operating conditions, which makes it difficult to use as a stage health index. Mining the intrinsic relationship between signals based on deep learning for anomaly detection is a more effective method. Li et al. [
18] proposed a flux fault early warning method based on the long short-term memory (LSTM) model and used the correlation for feature screening. Bai et al. [
19] applied the method to gas turbine fault detection. Qiao et al. [
20] proposed a fault detection method for wind turbine generators utilizing a Convolutional Neural Network (CNN). Although the above studies achieved relatively satisfactory anomaly detection accuracy, they are not sensitive enough. How to achieve high-precision fault early warning is the first problem to be solved in this paper.
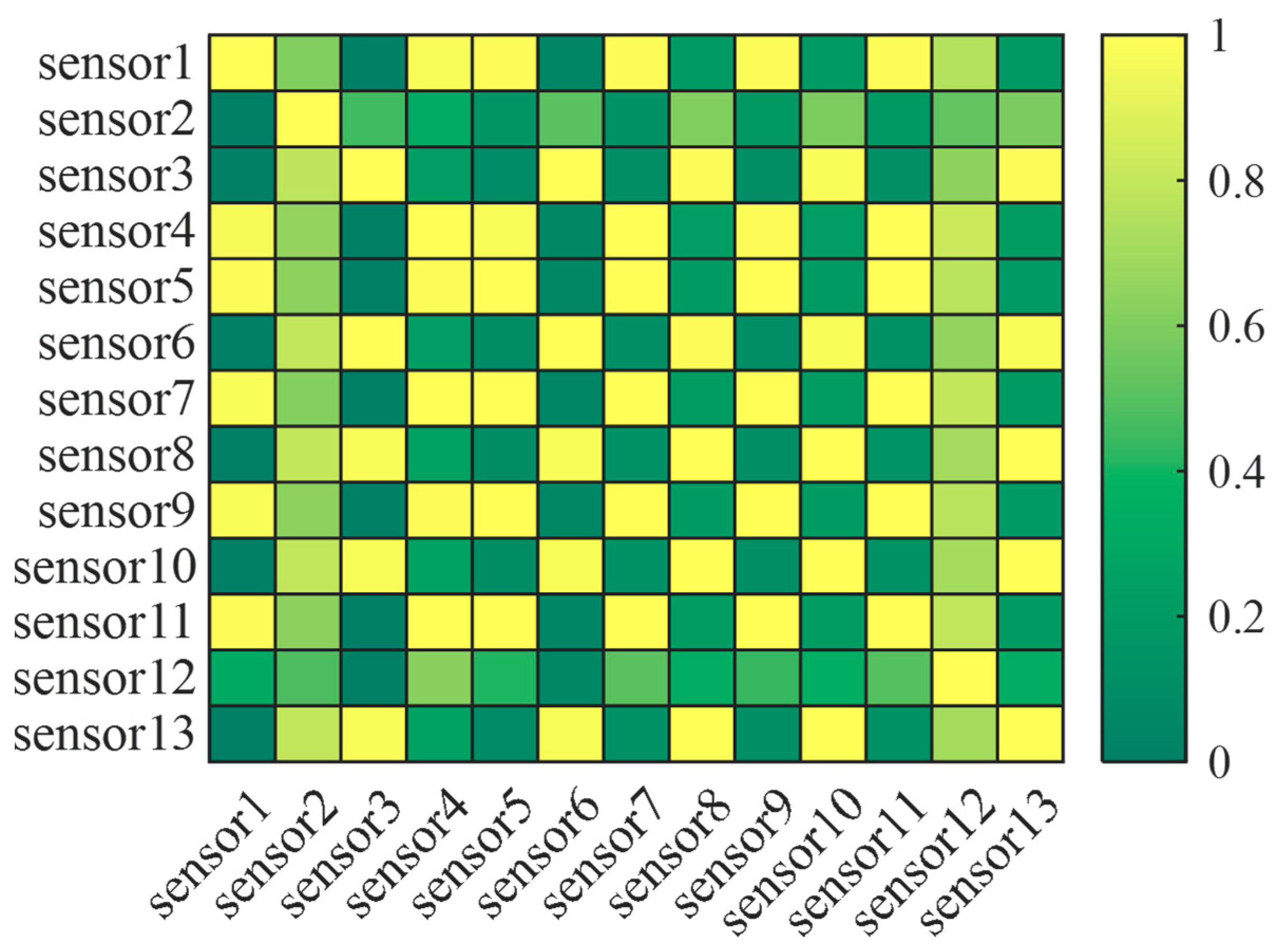
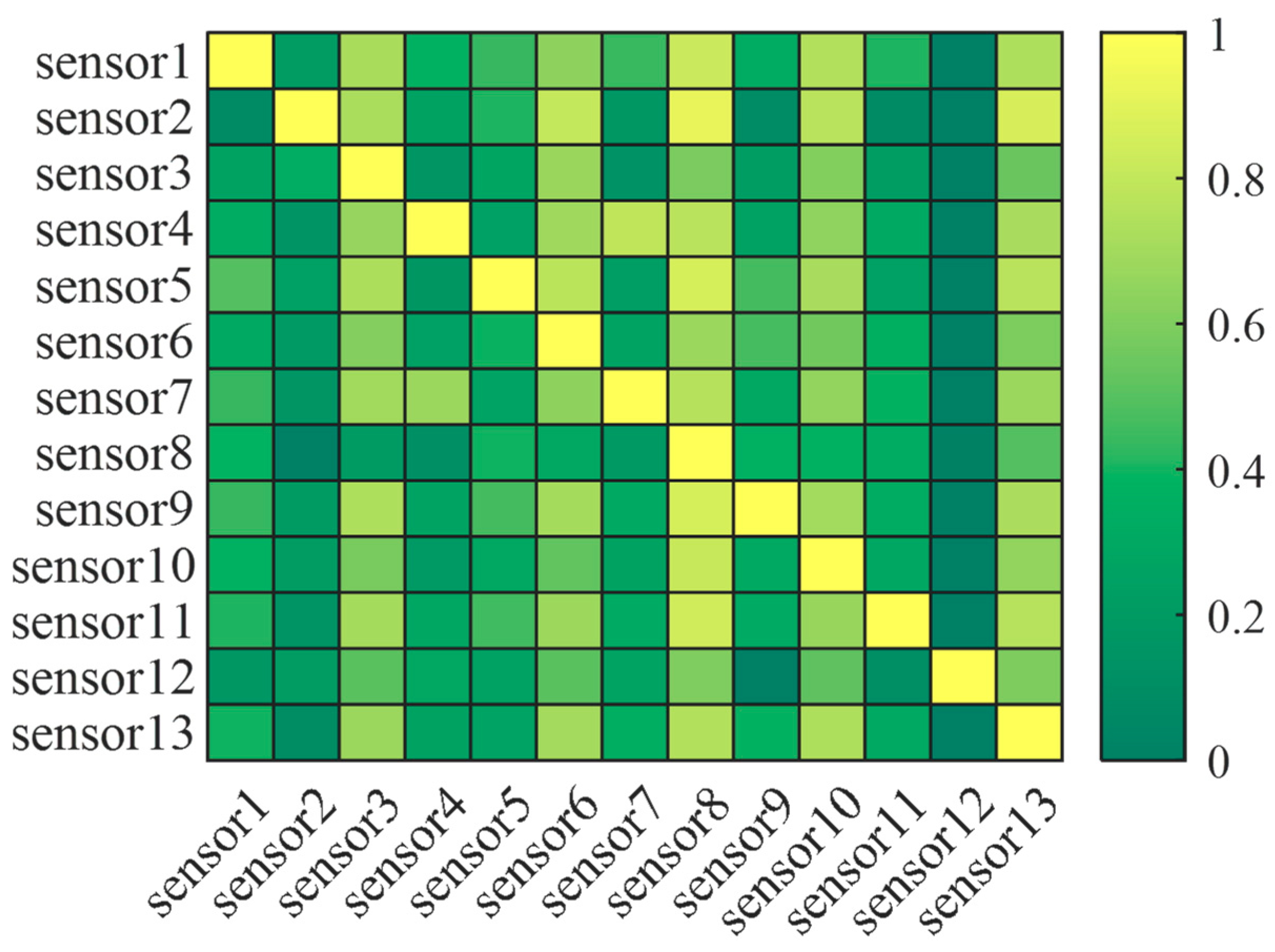
Measuring the information gain of the sensor signal for the target information is a key criterion for screening the available information, which can effectively improve the prediction accuracy of the model and the sensitivity of fault warning [
21]. Traditional screening methods include correlation [
22], information entropy [
23], monotonicity, and similarity [
24]. A reasonable sensor should have the following characteristics: (1) a high information gain for the target signal and (2) the ability to avoid introducing redundant information as much as possible [
25]. Conventional methods cannot satisfy these two requirements well. For example, the Pearson correlation coefficient can only evaluate linear correlation, which is obviously not applicable to strongly non-linear systems such as steam turbines [
26]. Only a few researchers have focused on the field. Yao et al. [
27] proposed a multi-dimensional wind turbine signal fusion method based on the Kullback–Leibler divergence. Feng et al. [
28] proposed a feature screening method based on integrated learning, and the experimental results confirmed that the method outperforms the Spearman rank correlation coefficient. There is almost no research addressing feature fusion for the turbine fault detection process. Therefore, another key issue to be addressed in this paper is how to improve the efficiency of information utilization.
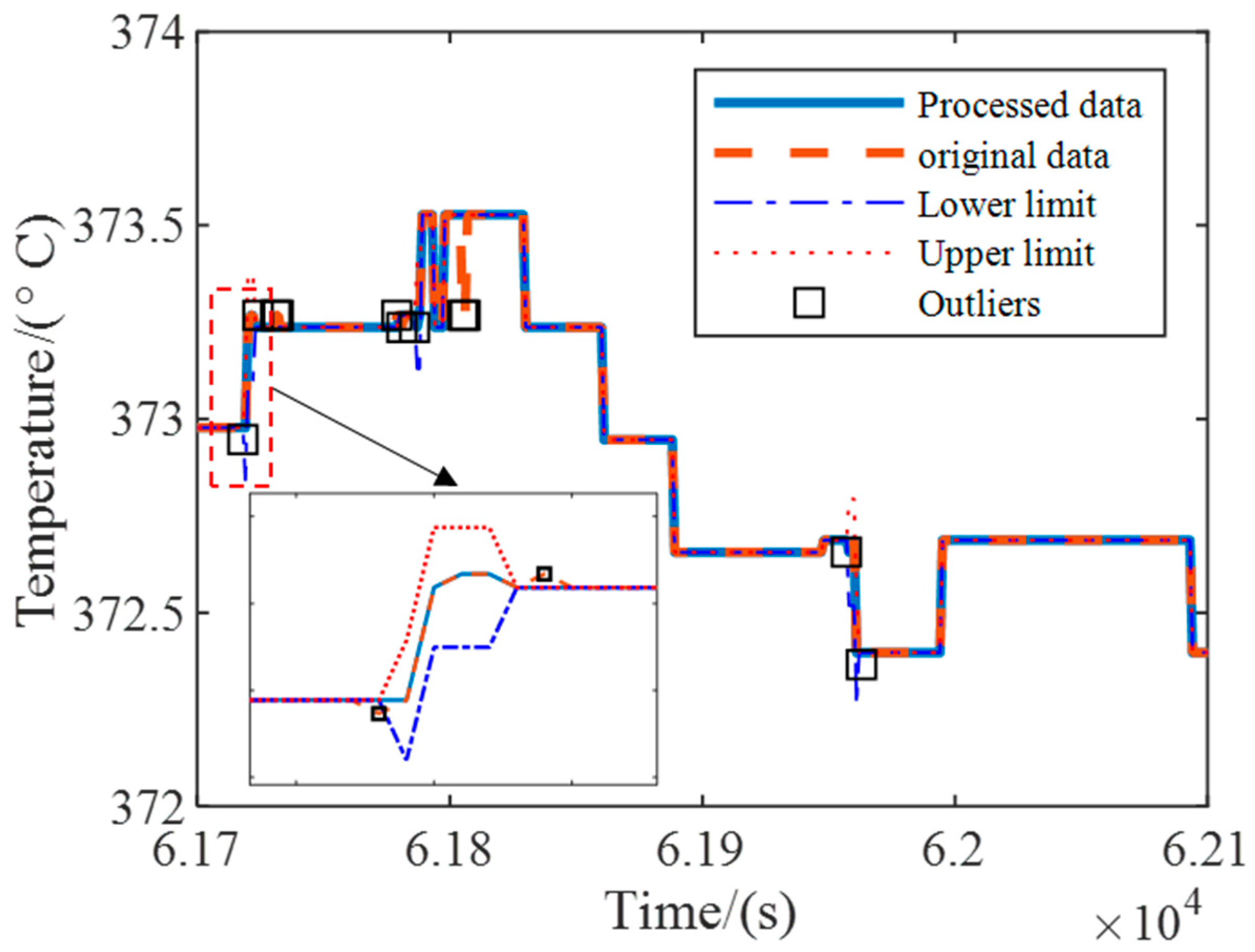
On the other hand, signal anomalies due to noise and measurement instrument failures are unavoidable. Outliers always cause a decrease in the training speed and prediction accuracy of the neural network so it is necessary to process the sensor signals for outliers [
29]. Outlier rejection and reconstruction using filters, including sliding average filters, exponential filters, Hampel filters, etc., is an effective method. Shi et al. [
30] used exponential filters to achieve data smoothing for engine degradation prediction. Zhang et al. [
31] used sliding average filters to improve the accuracy of aircraft icing identification. Hampel filtering is a test based on the degree of deviation from the median, which is more robust and stable compared to other methods. Feng et al. [
32] proposed a battery anomaly detection method using Hampel filtering. Ren et al. [
33] compared eight filters when performing traffic prediction, and the results proved that Hampel filtering performs optimally. However, there seems to be no discussion on the role of Hampel filtering in turbine flux section parameter prediction and anomaly detection, which is the third issue to be investigated in this paper.
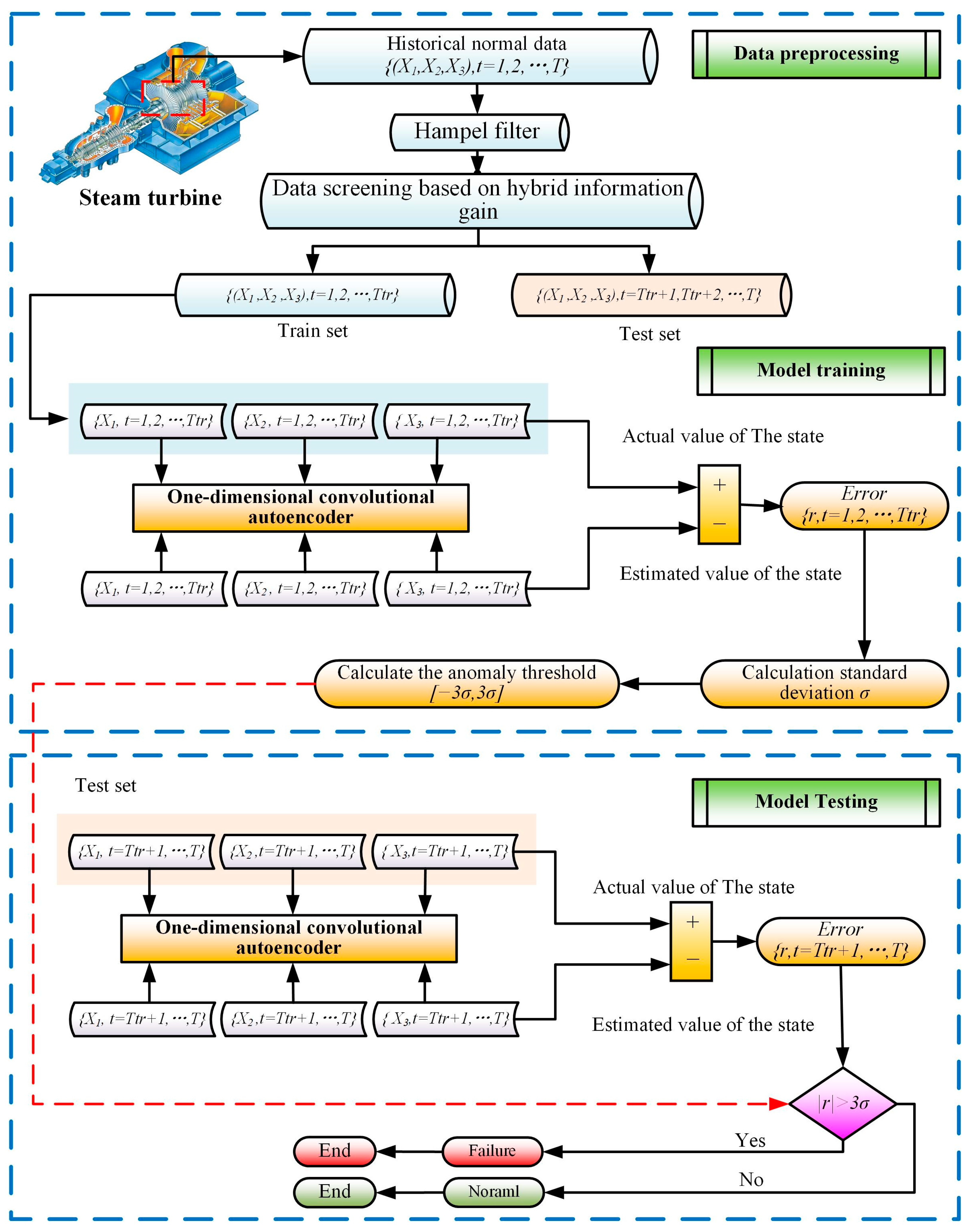
In summary, the existing turbine anomaly detection methods have problems such as insufficient anomaly detection accuracy, insufficient data utilization, and poor outlier handling. To ensure the safe and efficient operation of steam turbine equipment, an unsupervised fault early warning method based on a convolutional autoencoder and hybrid information gain calculation method is proposed. Anomaly detection and comparative experiments on real operating data of steam turbines prove the advantages of the proposed method. The main contributions of this paper are as follows:
- (1)
An unsupervised fault early warning method based on a convolutional autoencoder is proposed. The intermediate-stage flux fault detection model is implemented based on the prediction output and actual data deviation.
- (2)
A hybrid information gain calculation method based on cosine similarity and conditional entropy is proposed. Compared with the traditional methods, the proposed method can effectively improve the fault detection accuracy. Also, the proposed hybrid information gain has an improved effect on the traditional model.
- (3)
The Hampel filter is introduced for time series outlier testing. The experimental results prove that the Hampel filter can obviously eliminate data noise and abnormal data, and its performance is better than that of other methods.
- (4)
Fault detection experiments on real data demonstrate that the proposed method achieves optimal detection accuracy. The fault diagnosis accuracy of the proposed model is significantly higher than that of the traditional model and has the lowest false detection rate.
The main structure is as follows:
Section 2 introduces the principles of the methods used.
Section 3 performs a turbine intermediate-stage flux fault warning and parameter tuning experiments with actual data.
Section 4 conducts various comparative experiments between different data processing methods and data-driven models. Finally,
Section 5 presents conclusions and prospects.
5. Conclusions
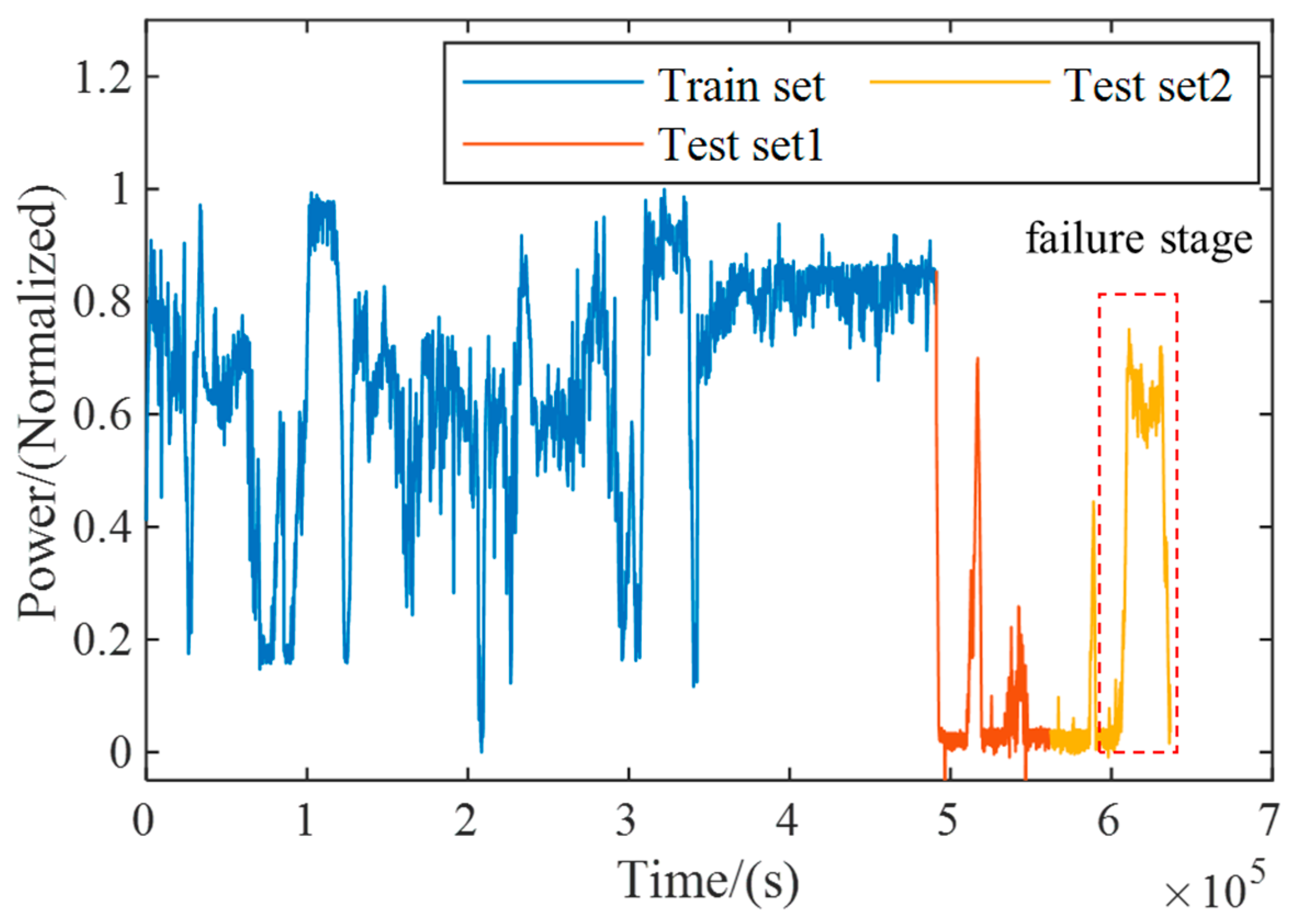
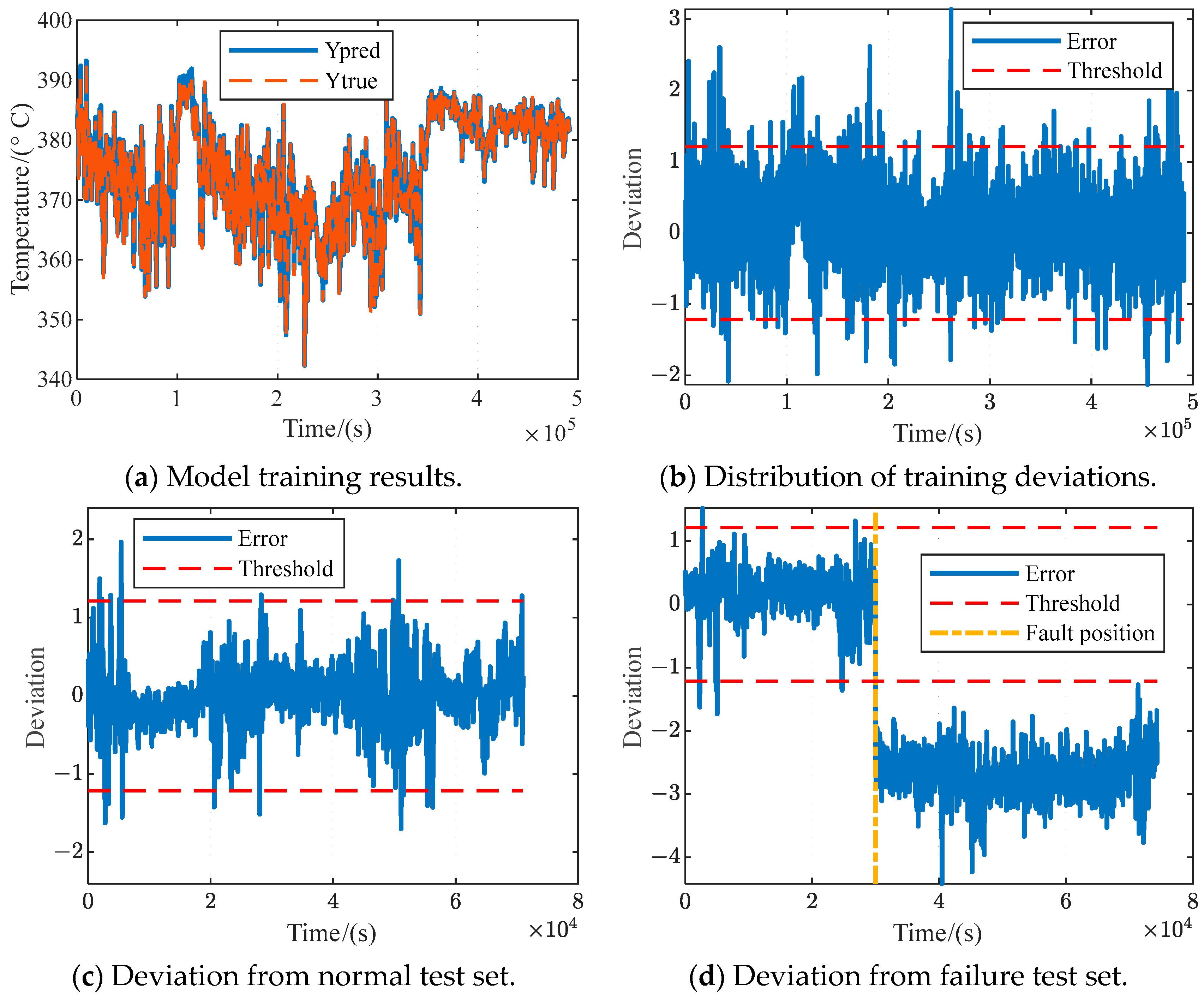
As new energy sources continue to enter the grid, their intermittent and fluctuating nature increases demand for grid frequency modulation. Frequent and large-scale load variations of thermal power units will become the norm. In the future, thermal power units will be under deep and fast frequency modulation conditions for a long period, which is a large deviation from the designed working conditions of the turbine and will also increase the possibility of turbine degradation. To improve power system stability and security, this paper proposes an unsupervised fault warning method based on a convolutional autoencoder and hybrid information gain calculation method. Meanwhile, considering factors such as sensor faults and noise, a Hampel filter is introduced for time series outlier testing. By conducting experiments on real data, the following conclusions can be drawn:
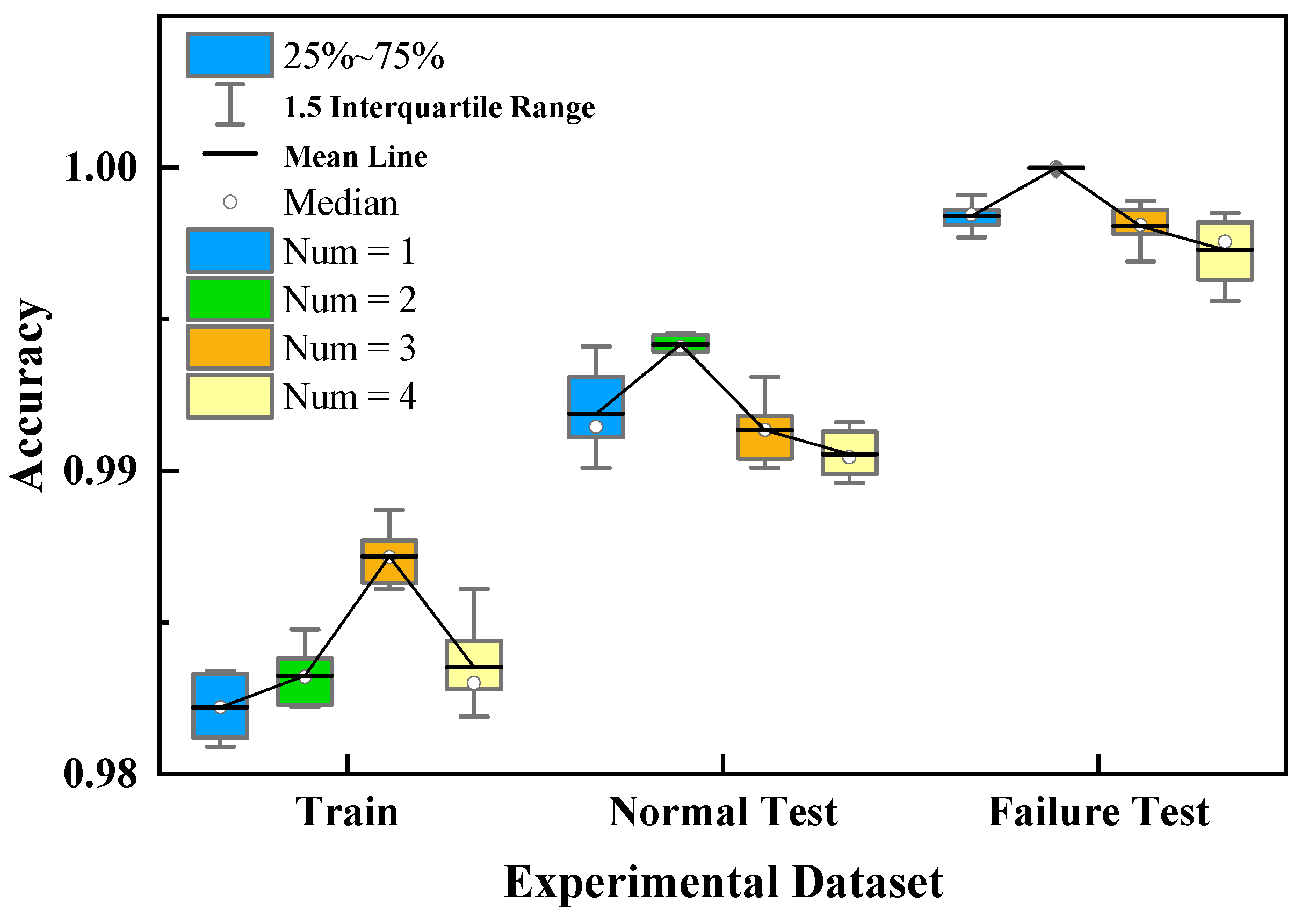
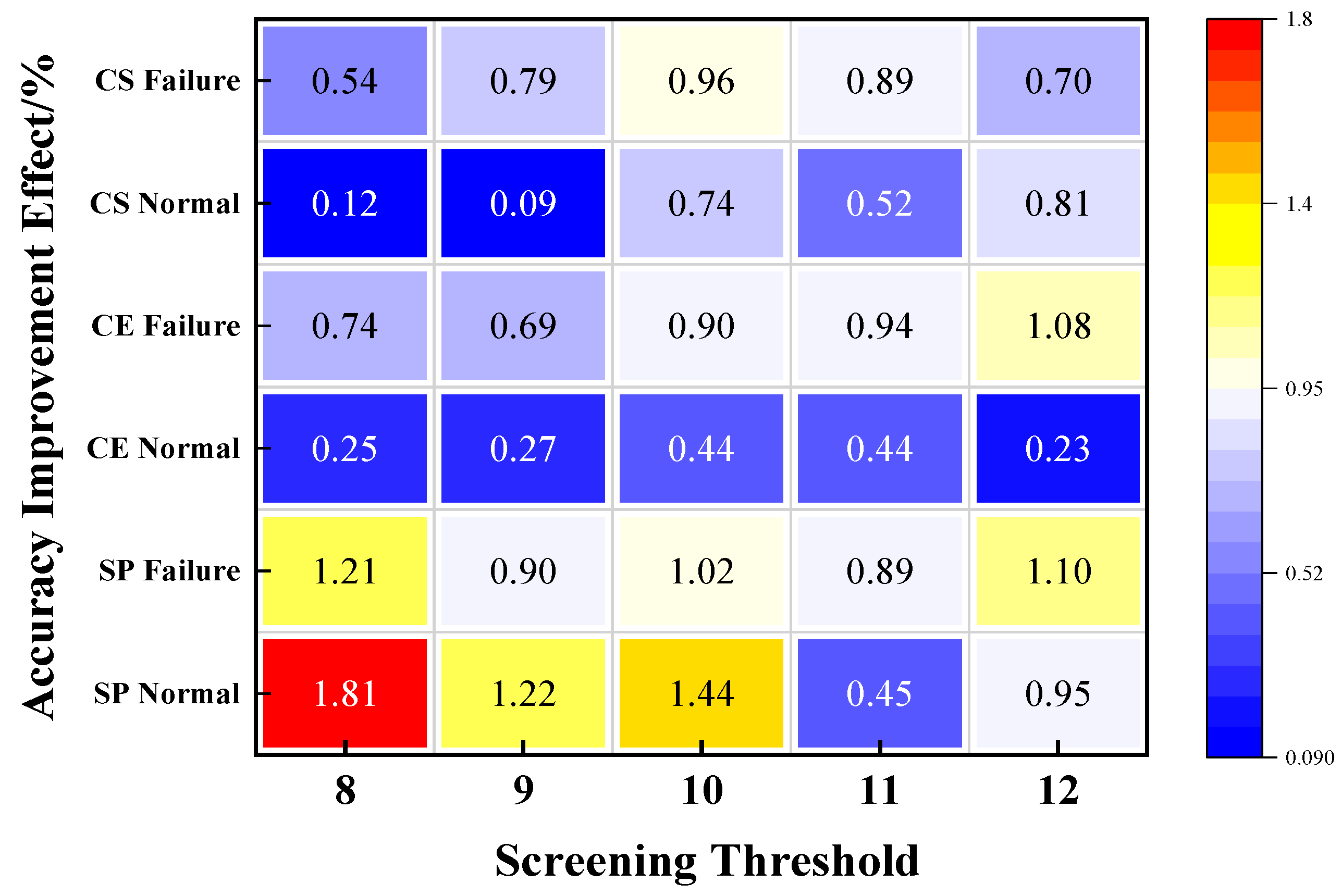
(1) The proposed hybrid information gain calculation method can evaluate data availability more effectively. Cosine similarity and conditional entropy are used in combination for feature selection, greatly improving detection accuracy. The method has the same improved effect for the traditional model, which reflects a strong adaptability.
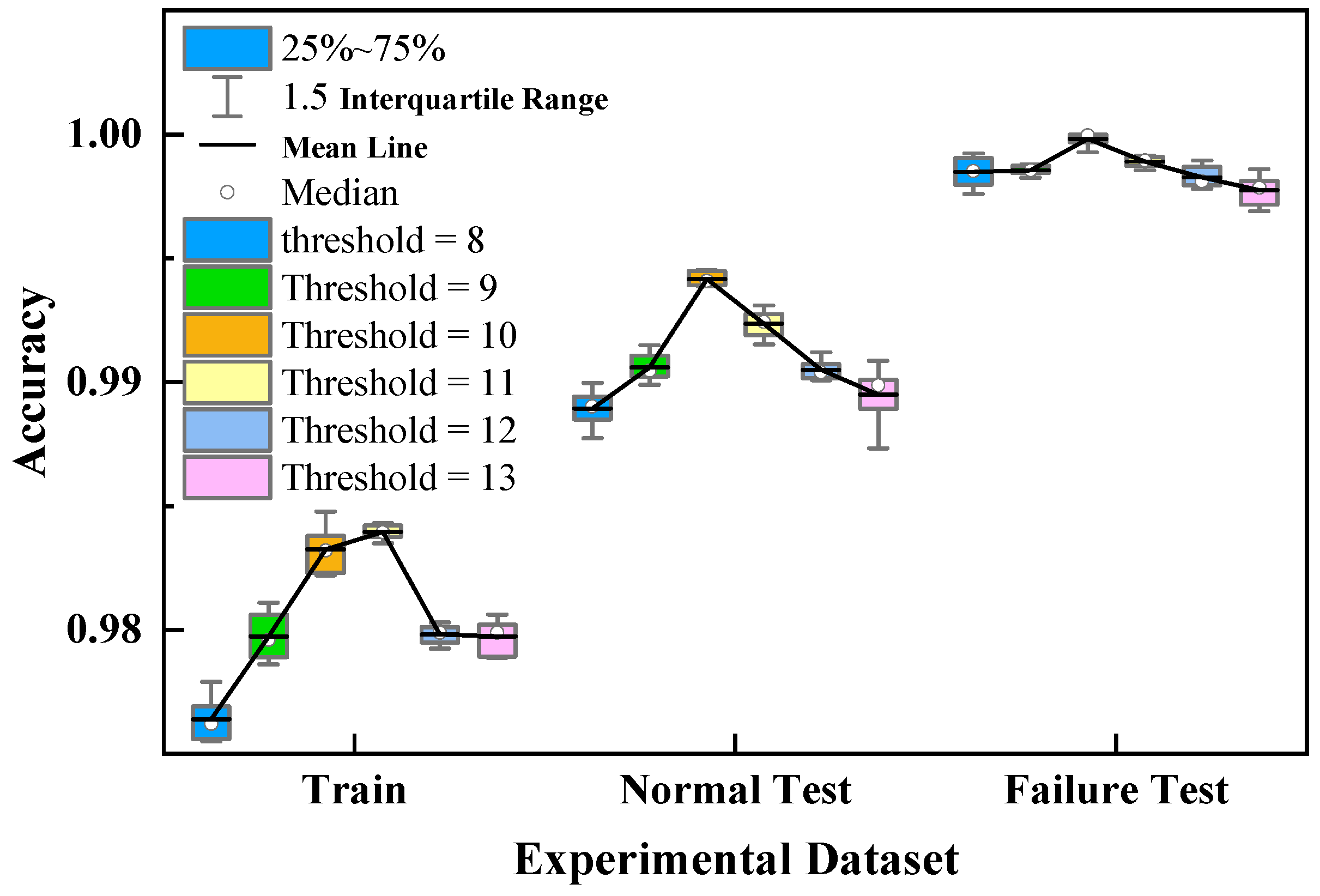
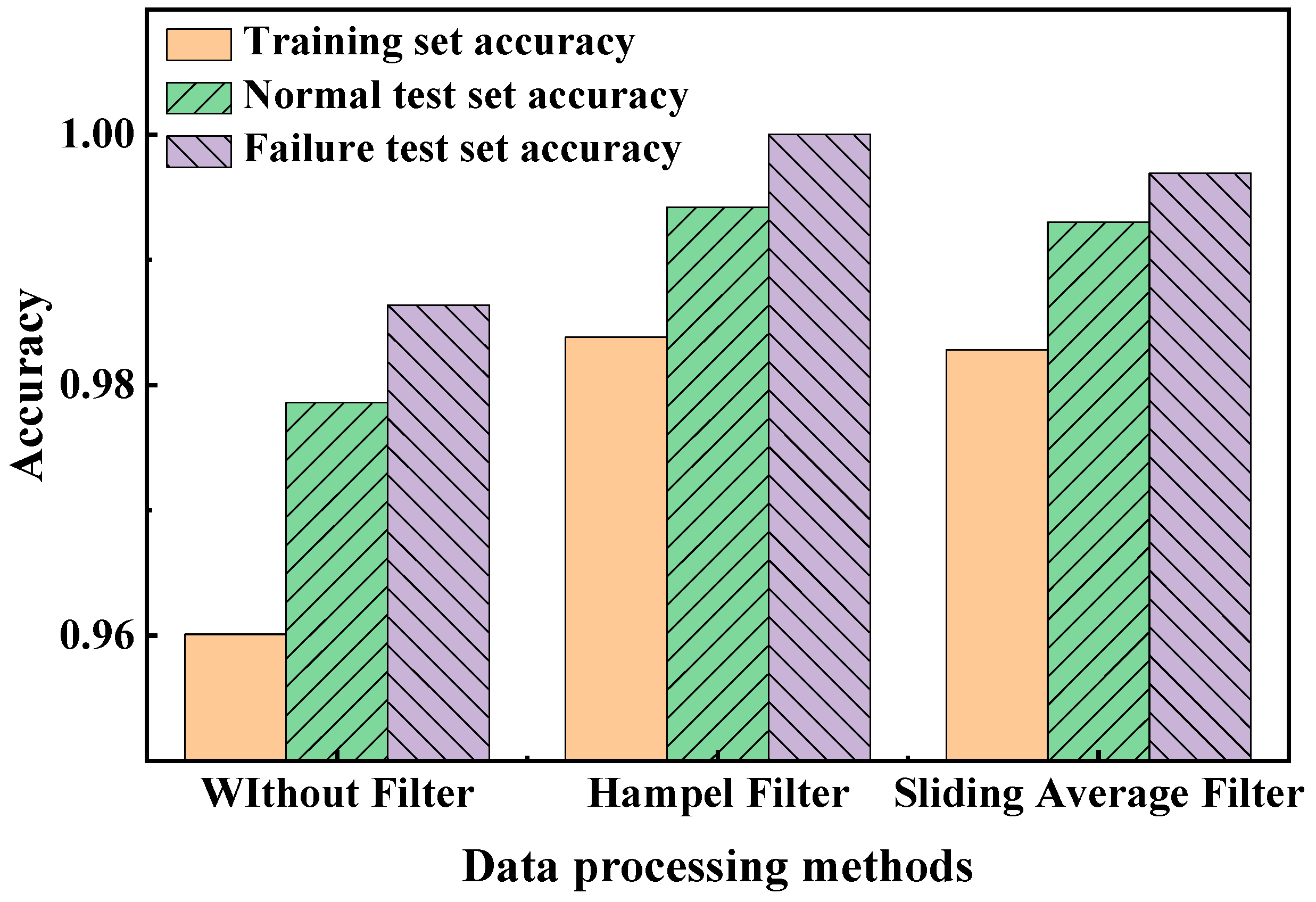
(2) The Hampel filter can effectively improve model training and fault warning stability. By eliminating and reconstructing the outliers, the accuracy of the model is relatively improved by 1.38% and 0.31% compared to the no-outlier and sliding average filter detection models on the two test datasets, respectively.
(3) The unsupervised fault warning method based on the convolutional autoencoder can detect turbine intermediate-stage flux faults effectively. The detection accuracy of the proposed method on real data is much higher than that of the traditional method, and the maximum relative improvement can reach 4.59%.
The proposed method establishes a high-precision early warning method for steam turbine intermediate-stage flux faults based on the normal operation data. It recognizes fault signs sensitively and solves the problem of insufficient fault data, which is significant for guaranteeing the safety of power grid operation. In the future, we will further investigate methods for grading the severity of faults and predict the evolution trends of degradation.